RVE-based grading of truss lattice cores in sandwich panels

Abstract

Additive manufacturing enables the fabrication of strut-based lattices that consist of periodic representative volume elements (RVE) and can be used as cores in sandwich panels. Due to the design freedom provided by additive manufacturing, the lattice strut diameter may vary through the lattice. Thus, the diameter distribution can be adapted to the stress variation in the sandwich core to achieve an efficient core design and avoid oversizing the core. Such grading approaches are required when the core is subjected to localized loads, e.g., near support points and load application areas. In this work, an analytical model is derived to determine stresses and deformations in lattice struts of RVE-based graded lattice cores in elastic sandwich panels using homogenization and dehomogenization methods. In contrast to already available models, the analytical model presented in this work allows grading the lattice strut diameter both along the sandwich length and through the core thickness. Furthermore, local stresses in the lattice struts caused by concentrated load application can be captured adequately by the present model. To highlight the benefits of graded cores, the strut stress distribution in graded cores is compared to the stress distribution in homogeneous cores.

1 Introduction

Lightweight structures made up of two skin plies enclosing a thick core layer in between are called sandwich panels. While high-strength materials are used to fabricate the face sheet layers, the cores of sandwich panels are made of lightweight cellular structures such as honeycombs and foams [1, 2]. This three-layer structural design, consisting of two thin face sheet layers and a core of low-density material, enables constructions with high bending stiffness and low weight. Therefore, these designs are widely used in various industries, such as aerospace and automotive engineering [3,4,5,6]. Due to advances in additive manufacturing, novel lattice structures with strut diameters in the micrometer scale can be fabricated [7,8,9] and used as cores in sandwich panels [10, 11]. A unit cell or a representative volume element (RVE) with a specific topology represents the basis of lattice structures [12, 13]. This unit cell can be repeated in all spatial directions to form a lattice structure. Compared to conventional honeycombs and foams, lattice structures investigated by [14, 15] provide comparable mechanical performance. However, strut-based lattices fabricated by additive manufacturing provide more flexibility to adapt the core properties to functional requirements by modifying the RVE topology and size [16,17,18]. Tailoring core properties using additive manufacturing to fabricate graded cores may improve the stiffness, impact resistance, and energy absorption of sandwich panels [19,20,21,22,23]. In particular, grading the core to prevent core failure due to locally concentrated loads is of paramount importance [24, 25]. During flexural tests, such lattice core failure in load application areas was observed by [26,27,28,29]. Local loads occur at support and load application points or through contact with other structures [30, 31]. To predict the out-of-plane stresses resulting from these localized loads, merely simulations based on finite element analysis (FEA) or costly experiments are available, since these stresses are not considered in common sandwich theories. High-order theories presented by [32,33,34,35,36] consider transverse normal stresses as well as graded cores to reduce stress concentrations in sandwich panels. However, the mentioned studies varied the core stiffness only through the core thickness. Thus, the core properties were constant along the length direction. Considering a 3-point bending test, local loads may occur on both the supporting roller points and the load application points [37, 38]. Therefore, grading the core in the sandwich length direction is required to achieve a more efficient core design. Sandwich structures with graded cores in the length direction show higher strength than non-graded structures, as observed by [39,40,41]. Since the core may account for two-thirds of the sandwich’s total weight, avoiding core oversizing is essential from a lightweight point of view [42]. Available multi-scale design strategies typically utilize finite element software to analyze cellular cores in sandwich panels [43, 44]. However, modeling and computing lattice cores are time-consuming and require high computational effort [45, 46]. Thus, models of sandwich panels with graded lattice cores allowing the determination of lattice strut stresses by a reasonable effort are needed to accelerate and simplify the development and optimization of these structures. This work presents an analytical formulation of stresses and displacements in sandwich panels with lattice cores subjected to transversal forces. All sandwich layers are assumed to show linear elastic material behavior. The modeled sandwich core is given by a lattice structure that is made up of periodic RVEs. The strut diameter of the core RVEs exhibits an arbitrary distribution through the core length and thickness. The lattice will be first replaced by an effective anisotropic material using homogenization methods. By the principle of minimum potential energy, the core deformations are determined. To obtain the lattice core strut stresses, core dehomogenization is performed and briefly discussed. The results obtained by the derived model are verified by results achieved from corresponding finite element analysis (FEA).

2 Modeling approach

Assuming a plane stress state with respect to the xz plane, merely a 2D sandwich model assembled of two face sheets and a lattice core is considered in this work, as illustrated in Fig. 1a. The quantities $h^{(f)}$ and $h^{(c)}$ denote the face sheet thickness and core thickness, respectively. The sandwich has the total length l. A global coordinate system xz at the center of the sandwich is introduced. Furthermore, each face sheet layer has a local coordinate system at the layer center. Both face sheets are made of the same isotropic material with Young’s modulus $E^{(f)}$ and Poisson’s ratio $\nu ^{(f)}$. A face-centered quadratic cell is assumed for the RVE of the considered core, as shown in Fig. 1b. The considered unit cell comprises five struts: four 45$^\circ$-inclined struts and one vertical strut. All struts within the unit cell have the strut diameter d. The ratio between the unit cell length a and the unit cell strut diameter d is considered as the aspect ratio a/d and significantly affects the mechanical properties of the cell. With the assumption of a constant unit cell length a, varying the strut diameter within the core leads to a graded core stiffness. In this work, the strut diameter within the unit cell is kept constant. Thus, the strut diameter may vary from RVE to RVE. The relationship between the strut diameter and the effective lattice stiffness is briefly introduced in Sect. 2.1. Using homogenization methods, the lattice core can be replaced by an anisotropic material with the lattice effective properties. In Sect. 2.2, the principle of minimum potential energy is used to determine the displacements of the graded core in the sandwich. The employed displacement representations, boundary conditions, and material constitutive equations are also discussed. The determined displacements are then used to determine the strut extension and, thus, the strut stresses, as shown in Sect. 2.3.

Fig. 1

Sandwich model with graded lattice core and the corresponding unit cell

2.1 Lattice homogenization

Since modeling lattice struts involves inflated cost and effort, homogenization methods provide a suitable alternative to model lattice structures. The basic idea of homogenization is to substitute the lattice on the mesoscale by an anisotropic material on the macroscale [47, 48]. The anisotropic material is assumed to be homogeneous and exhibits the same effective mechanical response as the lattice. The effective elastic properties of the unit cell are determined by considering the unit cell subjected to three elementary loads and prescribing periodic boundary conditions, as shown in Fig. 2. The effective stiffness in the horizontal direction $E^{*}_{xx}$ is obtained from a virtual uni-axial load test in the x-direction (Fig. 2a)). Analogously, the effective stiffness $E^{*}_{zz}$ is determined (Fig. 2b)). Shear Load in the xz-plane yields the effective shear stiffness $G^{*}_{xz}$ (Fig. 2c)). In this analysis, we assume that the lattice struts are ideally bonded without moment constraints, the strut material is aluminum with the corresponding linear elastic properties ($E_s=$70 GPa, $\nu _s=0.35$), and the unit cell has the unit depth $t=1$ mm. Since the considered problem in the three load cases is statically determinate, the solution can be obtained from the equilibrium equations. The unit cell shows an orthotropic material behavior. In 3D problems, 9 material constants are required to describe the orthotropic material behavior. In our 2D model, merely the three mentioned material parameters and the effective Poisson’s ratio $\nu ^{*}_{xz}$ are needed to characterize the orthotropic behavior of the unit cell. The effective stresses $\sigma ^*_{xx}$, $\sigma ^*_{zz}$ or $\tau ^*_{xz}$ resulting from the applied forces $F_x$,$F_z$ or $F_{xz}$ are obtained in each elementary load case. Similarly, the effective strains $\varepsilon ^*_{xx}$, $\varepsilon ^*_{zz}$, $\gamma ^*_{xz}$ resulting from the displacement $\Delta a_x$ and $\Delta a_z$ induced by the applied load are determined. The displacement $\Delta a_{xz}$ describes the transverse displacement in the z-direction resulting from the applied load $F_x$. In Fig. 2a), the inclined struts are loaded by the load $F_{\textrm{inclined}}=F_x/\sqrt{2}$ resulting from load $F_x$. The load in the vertical strut is $F_{\textrm{vertical}}=-F_x$. In Fig. 2b), the load $F_z$ is merely supported by the vertical strut, while the inclined struts do not transfer any load. In Fig. 2c), the load $F_{xz}$ induces the load $F_{\textrm{inclined}}=\pm F_x/\sqrt{2}$ in the inclined struts, and the vertical strut is not loaded. Using the material law $\Delta l=\frac{Fl}{EA}$, the change of the strut’s length is obtained, where l, E and A denote the strut’s length, the strut’s stiffness, and the strut’s cross section, respectively. From the boundary conditions illustrated in Fig. 2 and the change of the struts’ length, the displacements $\Delta a_x$, $\Delta a_z$, $\Delta a_{xz}$ are obtianed. Thus, the effective constants follow from

$$\begin{aligned}&E^{*}_{xx}=\frac{\sigma ^*_{xx}}{\varepsilon ^*_{xx}}, \quad \sigma ^*_{xx}=\frac{F_x}{a}, \quad \varepsilon ^*_{xx}=\frac{\Delta a_x}{a}, \quad \nu ^*_{xz}=-\frac{\Delta a_{xz}}{\Delta a_x},\quad \end{aligned}$$

(1)

$$\begin{aligned}&E^{*}_{zz}=\frac{\sigma ^*_{zz}}{\varepsilon ^*_{zz}},\quad \sigma ^*_{zz}=\frac{F_z}{a}, \quad \varepsilon ^*_{zz}=\frac{\Delta a_z}{a}, \quad \nu ^*_{zx}=\nu ^*_{xz}\frac{E^{*}_{zz}}{E^{*}_{xx}},{ \text{ and }}\quad \end{aligned}$$

(2)

$$\begin{aligned}&G^{*}_{xz}=\frac{\tau ^*_{xz}}{\gamma ^*_{xz}},\quad \tau ^*_{xz}=\frac{F_{xz}}{a}, \quad \gamma ^*_{xz}=\frac{\Delta a_x}{a}.\quad \end{aligned}$$

(3)

Fig. 2

Elementary load cases to determine the effective properties

In this analysis, the strut’s buckling and bending are neglected. Since the effective properties depend merely on the aspect ratio [49], the analysis is conducted for several aspect ratios. Therefore, the unit cell length is held constant ($a=5$ mm), and merely the strut diameter is varied. The results for the effective stiffnesses obtained by this analysis are verified by finite element simulations using 2D analysis in ABAQUS. Based on the results obtained by Eqs. (1) to (3), a dependence of the effective properties on the aspect ratio is observed. The obtained results can be plotted as a straight line for each stiffness modulus in a double logarithmic plot. These lines can be described by the following equations

$$\begin{aligned}&\frac{E^{*}_{xx}}{E_s}=1.63\, \left( \frac{a}{d}\right) ^{-2}, \quad \frac{E^{*}_{zz}}{E_s}=3.93\, \left( \frac{a}{d}\right) ^{-2}, { \text{ and }}\quad \frac{G^{*}_{xz}}{G_s}=7.49 \left( \frac{a}{d}\right) ^{-2}. \end{aligned}$$

(4)

However, the Poisson’s ratio $\nu ^{*}_{xz}$ exhibits a constant behavior for all aspect ratios, leading to $\nu ^{*}_{xz}=0.41$.

2.2 Sandwich model

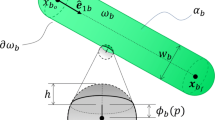
The sandwich model will be divided into subsystems to allow core grading in the length direction, as illustrated in Fig. 3. Every subsystem involves all sandwich layers (two face sheets and the core). The face sheet stiffness is kept constant in all subsystems. By contrast, the core stiffnesses may be varied along the length direction. Furthermore, every subsystem is divided into mathematical layers to enable a layerwise grading through the core thickness within the subsystem. Therefore, the core is divided into rectangular elements, and each element has the effective stiffness $E_{b}^{(c,j)}$ corresponding to the RVE strut diameter, where b is the number of the subsystem. The quantity j describes the number of the core mathematical layer through the thickness. To reduce the computing effort, each rectangular element in the subsystem may consist of more than one RVE, as illustrated in Fig. 3, where every rectangular element is composed of four RVEs. In this case, the rectangular elements have an average effective stiffness of the enclosed RVEs. Thus, the number of the lattice layers may deviate from the number of the mathematical core layers in the homogenized core. This modeling is useful when the stiffness or the strut diameter is similar between the layers and the subsystems. For the case, each rectangular element represents a single RVE, the number of the subsystems along the sandwich length p, and the number of the core mathematical layers m result from the relations $p=l/a$ and $m=h^{(c)}/a$, respectively.

Fig. 3

RVE-based homogenization of the lattice core

Assuming a three-point bending load case, the thin face sheets mainly transfer the moments’ bending stresses. In addition, shear stresses are also expected in the face sheet layers. Therefore, the face sheet layers are assumed to show similar behavior to shear-deformable beams, and the face sheet deformation is described by three independent degrees of freedom: the horizontal displacement of the layer mid-axis $u_{0,b}^{(n)}$, the vertical displacement of the layer mid-axis $w_{0,b}^{(n)}$, and the section rotational angle $\psi _{b}^{(n)}$, with n being the number of the face sheet layer. The face sheet displacement representation is given as

$$\begin{aligned}&u_{b}^{(n)}(x,z)={u}_{0,b}^{(n)}(x)+z{\psi _{b}}^{(n)}(x), { \text{ and }} \end{aligned}$$

(5)

$$\begin{aligned}&w_{b}^{(n)}(x,z)={w}^{(n)}_{0,b}(x). \end{aligned}$$

(6)

The strains in the face sheets are obtained by derivatives of the deformation functions

$$\begin{aligned}&\varepsilon ^{(n)}_{xx,b}=\frac{\partial {u}^{(n)}_{0,b}}{\partial x}+z\frac{\partial {\psi }^{(n)}_{b}}{\partial x}, { \text{ and }}\end{aligned}$$

(7)

$$\begin{aligned}&\gamma _{xz,b}^{(n)}=\frac{\partial {w}_{0,b}^{(n)}}{\partial x}+{\psi _{b}}^{(n)}. \end{aligned}$$

(8)

According to the assumption of a plane stress state, the stresses in the face sheet layers can be written in the following manner

$$\begin{aligned}&\sigma ^{(n)}_{xx,b} =\frac{E^{(f)}}{1-{\nu ^{(f)}}^2} \, \varepsilon ^{(n)}_{xx,b},{ \text{ and }} \end{aligned}$$

(9)

$$\begin{aligned}&\tau ^{(n)}_{xz,b} ={G^{(f)}} \gamma ^{(n)}_{xz,b}\,. \end{aligned}$$

(10)

In contrast to the face sheet deformation, the demanding core deformation behavior requires higher-order approaches to determine the through the thickness stresses. First, the core is decomposed into m mathematical layers through the core thickness. Therefore, new degrees of freedom, namely vertical and horizontal displacements at the mathematical layer interfaces (${\tilde{w}}^{(c,q)}_{b},{\tilde{u}}^{(c,q)}_{b}$), are introduced, with q being the number of the interface in the sandwich core. The core includes a total of $g=m+1$ interfaces, where $q=1$ and $q=g$ are the interfaces between the core and bottom and top face sheet, respectively. The core displacements can be described by interpolating the displacements between the layer interfaces. Nevertheless, due to the stiffness mismatch and concentrated loads, localized deformations with high gradients are expected in load and support areas within the core. To capture these deformations, quadratic and third-order approaches are required. Thus, for each core mathematical layer displacement, a linear interpolation term, a quadratic term (${\hat{w}}^{(c,j)}_{b},{\hat{u}}^{(c,j)}_{b}$), and a third-order term ($\grave{w}^{(c,j)}_{b},\grave{u}^{(c,j)}_{b}$) are introduced. Assuming a constant layer thickness ($a=constant$), the layer displacement representations are chosen as

$$\begin{aligned} w_{b}^{(c,j)}(x,z)=&{\tilde{f}}_w^{(c,j)}(z)\frac{m({\tilde{w}}^{(c,j+1)}_{b}(x)-{\tilde{w}}^{(c,j)}_{b}(x))}{h^{(c)}}\nonumber \\ {}&+{\hat{f}}^{(c,j)}(z)\,{\hat{w}}^{(c,j)}_{b}(x)+\grave{f}^{(c,j)}(z)\,\grave{w}^{(c,j)}_{b}(x),{ \text{ and }} \end{aligned}$$

(11)

$$\begin{aligned} u_{b}^{(c,j)}(x,z)=&{\tilde{f}}_u^{(c,j)}(z)\frac{m({\tilde{u}}^{(c,j+1)}_{b}(x)-{\tilde{u}}^{(c,j)}_{b}(x))}{h^{(c)}}\nonumber \\ {}&+ {\hat{f}}^{(c,j)}(z)\,{\hat{u}}^{(c,j)}_{b}(x)+\grave{f}^{(c,j)}(z)\,\grave{u}^{(c,j)}_{b}(x). \end{aligned}$$

(12)

The distribution functions ${\tilde{f}}_w^{(c,j)}(z)$,${\tilde{f}}_u^{(c,j)}(z)$,${\hat{f}}^{(c,j)}(z)$ and $\grave{f}^{(c,j)}(z)$ are identical for every subsystem and satisfy the displacement continuity conditions on the layer interfaces to prevent displacement discontinuities. These functions are given as

$$\begin{aligned} {\tilde{f}}_w^{(c,j)}(z)=&\; z+\frac{h^{(c)}}{m({\tilde{w}}^{(c,j+1)}_{b}(x)-{\tilde{w}}^{(c,j)}_{b}(x))}[-(-2j+m){\tilde{w}}^{(c,j)}_{b}(x)\nonumber \\ {}&+(-2j+m+2){\tilde{w}}^{(c,j+1)}_{b}(x)],\end{aligned}$$

(13)

$$\begin{aligned} {\tilde{f}}_u^{(c,j)}(z)=&\; z+\frac{h^{(c)}}{m({\tilde{u}}^{(c,j+1)}_{b}(x)-{\tilde{u}}^{(c,j)}_{b}(x))}[-(-2j+m){\tilde{u}}^{(c,j)}_{b}(x)\nonumber \\ {}&+(-2j+m+2){\tilde{u}}^{(c,j+1)}_{b}(x)],\end{aligned}$$

(14)

$$\begin{aligned} {\hat{f}}^{(c,j)}(z)=&\; [-(m-2j+2)(m-2j)-\frac{4(-2j+1+m)m}{h^{(c)}}z-\frac{4m^2}{{h^{(c)}}^2}z^2], { \text{ and }}&\end{aligned}$$

(15)

$$\begin{aligned} \grave{f}^{(c,j)}(z)=&\; {\hat{f}}^{(c,j)}(z)\,z . \end{aligned}$$

(16)

The Derivatives of the displacement functions in the following manner

$$\begin{aligned}&\varepsilon ^{(c,j)}_{xx,b}=\frac{\partial u_{b}^{(c,j)}}{\partial x},\end{aligned}$$

(17)

$$\begin{aligned}&\varepsilon ^{(c,j)}_{zz,b}=\frac{\partial w_{b}^{(c,j)}}{\partial z}, {\text {and}} \end{aligned}$$

(18)

$$\begin{aligned}&\gamma ^{(c,j)}_{xz,b}=\frac{\partial u_{b}^{(c,j)}}{\partial z}+\frac{\partial w_{b}^{(c,j)}}{\partial x} \end{aligned}$$

(19)

yield the core strains. Due to the model’s partition into subsystems, each subsystem may exhibit its own stiffness. In addition, the stiffness within the subsystem may vary through the layers due to the layerwise modeling. Assuming a linear elastic material behavior and a plane stress state, the core stresses follow from

$$\begin{aligned}&\sigma ^{(c,j)}_{xx,b} =\frac{E_{xx,b}^{(c,j)}}{(1-{\nu _{xz,b}^{(c,j)}}{\nu _{zx,b}^{(c,j)}})}\, \left[ \varepsilon ^{(c,j)}_{xx,b}+{\nu _{xz,b}^{(c,j)}}\varepsilon ^{(c,j)}_{zz,b}\right] , \end{aligned}$$

(20)

$$\begin{aligned}&\sigma ^{(c,j)}_{zz,b} =\frac{E_{zz,b}^{(c,j)}}{(1-{\nu _{xz,b}^{(c,j)}}{\nu _{zx,b}^{(c,j)}})}\, \left[ \varepsilon ^{(c)}_{zz,b}+{\nu _{zx,b}^{(c,j)}}\varepsilon ^{(c,j)}_{xx,b}\right] , { \text{ and }} \end{aligned}$$

(21)

$$\begin{aligned}&\tau ^{(c,j)}_{xz,b} ={G_{xz,b}^{(c,j)}} \; \gamma ^{(c,j)}_{xz,b}. \end{aligned}$$

(22)

Considering a three-point bending problem, the inner potential energy of the sandwich layers in a subsystem is given as

$$\begin{aligned} \Pi ^{(n)}_{i,b}=&\frac{1}{2} \int _{x_{l,b}}^{x_{r,b}}\int _{-h^{(f)}/2}^{h^{(f)}/2} \big ( \sigma ^{(n)}_{xx,b}\,\varepsilon ^{(n)}_{xx,b}+\tau ^{(n)}_{xz,b}\,\gamma ^{(n)}_{xz,b}\big ) \, \text{ d }z\; \text{ d }x,{ \text{ and }} \end{aligned}$$

(23)

$$\begin{aligned} \Pi ^{(c)}_{i,b}=&\frac{1}{2} \sum _{j=1}^{m} \int _{x_{l,b}}^{x_{r,b}}\int _{h^{(c)}(2j-m-2)/2m}^{h^{(c)}(2j-m)/2m}( \sigma ^{(c,j)}_{zz,b}\,\varepsilon ^{(c,j)}_{zz,b}+ \tau ^{(c,j)}_{xz,b}\, \gamma ^{(c,j)}_{xz,b}+\sigma ^{(c,j)}_{xx,b}\,\varepsilon ^{(c,j)}_{xx,b}) \, \text{ d }z\; \text{ d }x, \end{aligned}$$

(24)

where $x_{l,b}$ and $x_{r,b}$ are the length positions of the subsystem boundaries, as indicated in Fig. 3. The sum of the inner energies of the layers results in the total inner energy of the subsystem

$$\begin{aligned}&\Pi _{i,b}=\Pi ^{(1)}_{i,b}+\Pi ^{(2)}_{i,b}+\Pi ^{(c)}_{i,b}. \end{aligned}$$

(25)

In this study, the considered sandwich is subjected to a transverse load on the upper face sheet and simply supported at the left and right end of the bottom face sheet (Fig. 4a). Since the load case is symmetric, merely the left half of the sandwich model is considered (Fig. 4b). The external potential energy for the subsystem $b=p/2$ can be determined by

$$\begin{aligned}&\Pi _{a,p/2}=-\frac{F}{2}w_{0,p/2}^{(2)}(x=0), \end{aligned}$$

(26)

beyond this, the external potential energy of the remaining systems is zero. The sum of inner and external potential energy gives the total potential energy of the subsystem

$$\begin{aligned}&{\Pi _{b}}=\Pi _{a,b}+\Pi _{i,b}. \end{aligned}$$

(27)

Fig. 4

Three-point bending model

Using the principle of minimum potential energy, coupled differential equations of all unknown deformation functions are obtained. The number of the differential equations is $D=4+6m$. Merely second and low-order derivatives of the displacement functions occur in the differential equations. Thus, the second-order differential equation system can be represented as

$$\begin{aligned} {\underline{\underline{A}}}_b \; \underline{\ddot{\Psi }}_{b}+{\underline{\underline{B}}}_b\; \underline{\dot{\Psi }}_{b}+{\underline{\underline{C}}}_b\; \underline{{\Psi }}_{b}= \underline{{0}}, \end{aligned}$$

(28)

where $\underline{{\Psi }}_{b}$ is the vector of the undetermined deflections in the subsystem

$$\begin{aligned} {\underline{{\Psi }}_{b}}=\begin{bmatrix} u_{0,b}^{(1)}\,\,u_{0,b}^{(2)}\,\, \psi _{0,b}^{(1)} \,\, \psi _{0,b}^{(2)} \,\, w_{0,b}^{(1)} \,\, w_{0,b}^{(2)} \,\,{\hat{w}}^{c,1}_{b} \,\, {\hat{u}}^{c,1}_{b} \,\,\grave{w}^{c,1}_{b} \,\, \grave{u}^{c,1}_{b}\, ....... \end{bmatrix}^T, \end{aligned}$$

(29)

and the vectors $\underline{\dot{\Psi }}_{b},\, \underline{\ddot{\Psi }}_{b}$ are the first and second derivatives of $\underline{{\Psi }}_{b}$ with respect to the coordinate x. This second-order differential equation system can be solved by converting it to a first-order differential equation system

$$\begin{aligned} \underline{\dot{\Phi }}_{b}=\underline{\underline{E}}_b\;{\underline{\Phi }_{b}}, \end{aligned}$$

(30)

where

$$\begin{aligned}&{{\underline{\Phi }_{b}}}=\begin{bmatrix} {\underline{{\Psi }}_{b}}&{\underline{\dot{\Psi }}_{b}} \end{bmatrix}^T, \end{aligned}$$

(31)

$$\begin{aligned}&\underline{\underline{E}}_b=-\underline{\underline{D}}_{1,b}^{-1}\underline{\underline{D}}_{2,b},\end{aligned}$$

(32)

$$\begin{aligned}&{\underline{\underline{D}}}_{1,b}=\begin{bmatrix} \underline{\underline{B}}_b &{} \underline{\underline{A}}_b \\ {}\\ \underline{\underline{I}} &{} \underline{\underline{0}} \end{bmatrix},\end{aligned}$$

(33)

$$\begin{aligned}&{\underline{\underline{D}}}_{2,b}=\begin{bmatrix} \underline{\underline{C}}_b &{} \underline{\underline{0}} \\ {}\\ \underline{\underline{0}} &{} -\underline{\underline{I}} \end{bmatrix}, \end{aligned}$$

(34)

and determining the eigenvalues $\lambda _p$ and eigenvectors $v_p$ of the matrix $\underline{\underline{E}}$. The homogeneous solution of the differential equation system can be given as

$$\begin{aligned} \underline{{\Phi }}_{h,b}= \sum _{p=1}^{2D} K_{p}\underline{v_{p}}\,e^{\lambda _{p} x}. \end{aligned}$$

(35)

Further information about the procedure to solve such a differential equation system can be found in [50]. Boundary conditions to calculate the free constants $K_p$ are obtained by the condition ($\delta \Pi _{b}=0$). Since a half model is considered, symmetry boundary conditions are formulated across the symmetry line, as shown in Fig. 5. Furthermore, constraints to ensure displacement continuities at the subsystem boundaries are formulated in the following manner

$$\begin{aligned}&u_{0,b}^{(1)} (x_{r,b})=u_{0,b+1}^{(1)} (x_{l,b+1}), \quad u_{0,b}^{(2)} (x_{r,b})=u_{0,b+1}^{(2)} (x_{l,b+1}), \nonumber \\ {}&w_{0,b}^{(1)} (x_{r,b})=w_{0,b+1}^{(1)} (x_{l,b+1}), \quad w_{0,b}^{(2)} (x_{r,b})=w_{0,b+1}^{(2)} (x_{l,b+1}), \nonumber \\ {}&\psi _{0,b}^{(1)} (x_{r,b})=\psi _{0,b+1}^{(1)} (x_{l,b+1}), \quad \psi _{0,b}^{(2)} (x_{r,b})=\psi _{0,b+1}^{(2)} (x_{l,b+1}), \nonumber \\ {}&{\tilde{u}}_{b}^{(c,j)} (x_{r,b})={\tilde{u}}_{b+1}^{(c,j)} (x_{l,b+1}), \quad {\tilde{u}}_{b}^{(c,j)} (x_{r,b})={\tilde{u}}_{b+1}^{(c,j)} (x_{l,b+1}), \nonumber \\ {}&{\tilde{w}}_{b}^{(c,j)} (x_{r,b})={\tilde{w}}_{b+1}^{(c,j)} (x_{l,b+1}), \quad {\tilde{w}}_{b}^{(c,j)} (x_{r,b})={\tilde{w}}_{b+1}^{(c,j)} (x_{l,b+1}), \nonumber \\ {}&{\hat{u}}_{b}^{(c,j)} (x_{r,b})={\hat{u}}_{b+1}^{(c,j)} (x_{l,b+1}), \quad {\hat{u}}_{b}^{(c,j)} (x_{r,b})={\hat{u}}_{b+1}^{(c,j)} (x_{l,b+1}), \nonumber \\ {}&{\hat{w}}_{b}^{(c,j)} (x_{r,b})={\hat{w}}_{b+1}^{(c,j)} (x_{l,b+1}), \quad {\hat{w}}_{b}^{(c,j)} (x_{r,b})={\hat{w}}_{b+1}^{(c,j)} (x_{l,b+1}), \nonumber \\ {}&\grave{u}_{b}^{(c,j)} (x_{r,b})=\grave{u}_{b+1}^{(c,j)} (x_{l,b+1}), \quad \grave{u}_{b}^{(c,j)} (x_{r,b})=\grave{u}_{b+1}^{(c,j)} (x_{l,b+1}), \nonumber \\ {}&\grave{w}_{b}^{(c,j)} (x_{r,b})=\grave{w}_{b+1}^{(c,j)} (x_{l,b+1}), \quad \grave{w}_{b}^{(c,j)} (x_{r,b})=\grave{w}_{b+1}^{(c,j)} (x_{l,b+1}). \end{aligned}$$

(36)

Fig. 5

Boundary conditions of the sandwich model

2.3 Lattice dehomogenization

The solution of the differential equation system Eq. 35 yields all required displacements to calculate the core deformation at any arbitrary coordinate point in the core by Eqs. (11) and (12). To dehomogenize the core, the core displacements $u_{n},\, w_{n}$ at lattice nodes are of paramount importance (Fig. 6). The core displacements at all truss nodes $u_{n,l},w_{n,l},u_{n,r},w_{n,r}$ will be transformed to the respective truss local coordinate system by the transform matrix $\underline{\underline{T}}$, where $\alpha _e$ is the angle of the truss inclination in the xz plane. In this manner, the displacements $u_{e,l},w_{e,l},u_{e,r}$ and $w_{e,r}$ in the truss local coordinate system are obtained by

$$\begin{aligned}&\begin{bmatrix} u_{e,l} \\ {}\\ w_{e,l} \\ {}\\ u_{e,r} \\ {}\\ w_{e,r} \end{bmatrix}=\underbrace{\begin{bmatrix} {\cos }(\alpha _e) &{} {\sin }(\alpha _e) &{}0&{}0 \\ {}\\ {-\sin }(\alpha _e) &{} {\cos }(\alpha _e)&{}0&{}0\\ {}\\ 0 &{} 0 &{}{\cos }(\alpha _e)&{}{\sin }(\alpha _e) \\ {}\\ 0&{} 0&{} {-\sin }(\alpha _e) &{}{\cos }(\alpha _e)\end{bmatrix}}_{\underline{\underline{T}}} \begin{bmatrix} u_{n,l} \\ {}\\ w_{n,l}\\ {}\\ u_{n,r} \\ {}\\ w_{n,r} \end{bmatrix}. \end{aligned}$$

(37)

Fig. 6

Node displacements in the lattice core and at the truss nodes

When the truss node displacements are determined, the displacement difference $u_{e,r}-u_{e,l}$ yields the truss extension or compression $\Delta l_e$. The core strut stresses $\sigma _e$ then result as

$$\begin{aligned} \sigma _e= E_e\frac{\Delta l_e}{l_e}. \end{aligned}$$

(38)

Equation 38 assumes that the resulting stresses in the struts are merely caused by the axial loading. Thus, the bending stresses in the struts are neglected. This assumption applies to thin struts, which is the case in the study.

3 Lattice core stress prediction and discussion

This section presents the results of sandwich panels with graded lattice cores (GC) subjected to a transversal load. The considered sandwich lattice core contains four layers through the core thickness, with a unit cell length $a=5$ mm. Thus, the total core height is 20 mm, and the ratio of core height to face sheet height is $h^{(c)}/h^{(f)}=20$. To verify the applicability of the derived model to thick and slender sandwich beams, two slenderness ratios $SR=l/h^{(c)}$ are considered. The thick sandwich beam with $SR=4$ results in 16 unit cells along the sandwich length. The thin sandwich beam with $SR=10$ involves 40 unit cells along the sandwich length. The face sheet and the lattice solid material are assumed to have the same isotropic material properties ($E_s=E^{(f)}=70\, {\text {GPa}},\, \nu _s=\nu ^{(f)}=0.35$). The ratio of the face sheet stiffness to the core horizontal stiffness is $E^{(f)}/E^{(c)}_{xx}=1000$. As already mentioned, merely a half model is considered due to the symmetry of load and geometry. The assumed stiffness distribution in the core is that of functionally graded lattices subjected to three-point bending tests presented by [51]. In this distribution, the stiffness attains a maximum where the maximum stresses are expected, i.e., at the bearing points and load introduction. Accordingly, the stiffness varies both through the core thickness and along the core length. The stiffness variation is achieved by grading the strut diameter of the core unit cells, taking into account the correlation between the effective stiffness and the strut diameter of the unit cell. The strut diameter within the unit cell is assumed to be constant. Therefore, the stiffness variation represents a stepwise distribution. Due to the small number of the unit cells, the homogenized elements in the analytical modeling involve merely a single RVE. Thus, each homogenized element shows the corresponding effective stiffness according to the strut diameter of the RVE. In Fig. 7, the strut diameter variation in the considered core is illustrated. The stiffness in the first core layer ($j=1$, the layer over the bottom face sheet) shows a maximum value at the left sandwich boundary and decreases along the sandwich length with a constant step size. The stiffness of the last core layer ($j=4$, the layer under the top face sheet) represents a maximum value at the load application and decreases along the sandwich length. The maximum and minimum values of the first and last core layers are identical, and the ratio between the maximum and minimum stiffness values is two. The stiffnesses in the second ($j=2$) and third layer ($j=3$) are then interpolated between the maximum and minimum values with a constant step size. The stiffnesses $E^{(c)}_{zz}$ and $G^{(c)}_{xz}$ show the same variation as the stiffness $E^{(c)}_{xx}$. To highlight the effect of grading the core, a sandwich panel with a homogeneous core (HC) is also considered. The homogeneous core has the constant stiffness $E^{(c)}_{HC}= {\max }(E^{(c)}_{GC})$. Thus, the graded core is 25% lighter than the homogeneous core.

Fig. 7

FE model and the corresponding boundary conditions

The results obtained by the derived model are verified by an equivalent FE model using static analysis in ABAQUS CAE software. In the FE model, lattice struts meshed by two-node truss elements represent the sandwich core. These truss elements have merely one degree of freedom along the strut axis. Quadratic continuum elements C2D8R are used to mesh the solid face sheets. The mesh size of the face sheets was determined based on a convergence study by $h^{(f)}/3$. The lattice struts are ideally bonded with the face sheets using tie constraints. Due to the symmetry, merely a half model is used to verify the results. The vertical displacement of the bottom face sheet on the left end is prevented, and symmetry conditions are formulated along the symmetry axis, as shown in Fig. 7. Since every lattice strut is meshed by one truss element, the FE model results in 14056 degrees of freedom (DOFs) for the thin sandwich and 10546 DOFs for the thick sandwich.

In Fig. 8, the normalized absolute strut stresses (${\overline{\sigma }}=\mid \sigma _e/F\mid$) in a homogeneous core and a graded core through the sandwich length of the first and last core layer in the thin sandwich are illustrated. The blue data represent the stresses in the inclined struts, and the green data denote the stresses of the vertical struts. Since stresses are merely obtained at the strut mid-points, the connected line between the stress points serves for better clarity. High stresses occur in the vertical struts of the last core layer near the load application point. These stresses decrease with increasing distance from the load application point, both through the core thickness and along the length. Outside the boundary areas, the vertical struts are almost unloaded. Furthermore, no remarkable differences between the graded and ungraded cores are observed concerning the vertical strut stresses. By contrast to the vertical struts, the inclined struts show differences in the stress distribution. In the homogeneous core, the inclined strut stresses are almost constant outside the boundary areas. Due to the grading and, thus, the smaller strut diameter in the last core layer, the strut stresses increase along the core length from the right to the left boundary. A similar behavior is observed in the first core layer. Struts near the load application are highly stressed. Since the strut diameter variation in this layer is reversed compared to the last core layer, strut stresses of the graded core decrease from the right ($x=0$) to the left boundary ($x=-l/2$). In general, it can be shown that the strut distribution in inclined struts of the graded core follows the reversed strut diameter distribution since the stresses in the inclined struts of the homogeneous are constant through the sandwich length. Although stresses in the inclined struts are higher in the graded core, the maximum stresses in the vertical struts are almost identical in both cores. However, the graded core has a higher strength-to-weight ratio due to the lower weight.

Fig. 8

Strut stresses in the first and last core layers of the graded and homogeneous cores in the thin sandwich

As expected, the highest local stresses are observed in the support and load application area. These stresses decrease with increasing distance, both in the thickness direction and in the horizontal direction. While local stresses in the inclined and vertical struts resulting from the concentrated load are captured by the present model with reasonable accuracy, stresses in the vertical struts near the support area show deviation from FEA. Beyond the free edge area, results obtained by the present model exhibit a good agreement to FEA results. Furthermore, it can be shown that grading the core can be used to adapt the core to several load conditions in the core struts, resulting in a better core design. The strut stress distribution in the thick sandwich is shown in Fig. 9. By contrast to the thin sandwich, the strut stresses exhibit a non-uniform distribution within the core layers, even beyond the core boundaries. Nevertheless, high stresses are observed as well in the support and load application area. Since these stresses are merely localized in the load application area and support area, they decrease with a high gradient through the core thickness and length. Due to the small slenderness ratio in the thick sandwich, even struts outside the boundaries are affected by the load application or the support. Thus, the vertical struts there are not unloaded, and the difference between the graded and the homogeneous core is better recognizable than in the thin sandwich. By grading the core, stresses in the inclined struts can be adapted and show a corresponding distribution to the stiffness distribution in the graded core. In the thick sandwich, stresses in the inclined struts of the graded core are not accurately captured as in the thin sandwich since the distribution of these stresses is more demanding than in the thin sandwich. Although the stresses are not precisely determined, the deviation from the FEA is acceptable. In comparison to the inclined struts, a better agreement between the results obtained by the present model and the FEA in the vertical struts is observed.

Fig. 9

Strut stresses in the first and last core layers of graded and homogeneous cores in the thick sandwich

It could be shown that strut stresses in graded lattice cores can be predicted by the presented model using homogenization and dehomogenization methods and the results obtained are verified by detailed FEA. Furthermore, local stresses caused by concentrated load application are well rendered. Moreover, it could be demonstrated, that the strut stresses in lattice cores can be tailored by grading the core strut diameter. Thus, the derived model can be used within an optimization design procedure to determine an optimized strut diameter distribution by defining the strut diameters of the lattice unit cells as design variables. The present model can also replace FE software programs used in optimization design procedures to save time and resources since the derived model offers the opportunity to determine stresses and displacements in graded lattice cores within an abbreviated time without demanding and time-consuming modeling of lattice struts. The obtained optimized core design can be smoothly fabricated due to advances in additive manufacturing. Tailoring the core stiffness to adapt the core to the load condition would improve the sandwich’s performance and the strength-to-weight ratio. Enhancing the mechanical properties of lattices by grading the strut diameter may make these structures more attractive and competitive than honeycombs.

4 Conclusion

This work presents a novel analytical model to determine displacements and stresses in graded lattice cores of sandwich panels. Using high-order displacement approaches, localized deformations caused by concentrated loads can be captured by the derived model. By evaluating the displacements at the lattice nodes, lattice strut deformations and, thus, lattice strut stresses are determined. Due to the layerwise modeling and the partition of the sandwich model into subsystems, the core properties may vary along the core length and through the core thickness. Therefore, the lattice core properties can be customized to the functional requirements of the sandwich by varying the lattice strut diameter. Compared to the homogeneous core, strut stresses in the graded core can be adapted depending on the strut diameter variation within the core. The lattice strut stresses obtained by the present model are verified by detailed FE analysis. It could be shown that the derived model shows an satisfactory agreement with the FE results and applies to both thin and thick sandwich beams. The derived model can be used to optimize lattice cores and improve the mechanical performance of sandwich panels. For this purpose, the present model can be implemented within design optimization strategies to obtain an optimized core design. Since the present model takes localized loads into account and yields comparable results to FEA, the present approach shows advantages over conventional sandwich theories and FE in terms of computational efficiency and modeling effort. Grading approaches similar to that used in [52] may be applied to reduce the number of the design variables in the optimization. In future works, the derived model will be extended to model 3D lattices by considering a strain plane state. However, the present model does not consider the stress concentration at the interfaces between the solid face sheets and the lattice and at the lattice joints. Lattice node design recommendations presented by [53] are helpful for reducing the stress concentration at the lattice joints. Future works may address the stress concentration at the interfaces using refined modeling approaches.