Effects of the magneto-electro-elastic layer on the CNTRC cylindrical shell

Abstract

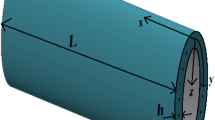
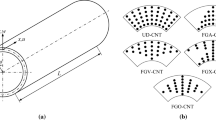
Based on the classical theory cylindrical shell, the object of the present investigation is to give analytical solutions to illustrate the effect of the magneto-electro-elastic (MEE) material layer properties on the nonlinear vibration of smart sandwich cylindrical shell supported by elastic foundations and subjected to the combination of external pressure, thermal, electric and magnetic loads. This work takes advantage of the sandwich shell configuration with three layers: two MEE face sheets and a carbon nanotube reinforced nano-composite core to analyze the vibration problem. In each MEE face sheet, the volume fraction of ${\text{BaTiO}}_{3}$–${\text{CoFe}}_{2} {\text{O}}_{4}$ is chosen to be 0.5, and for the core layer, three types of CNT distribution such as FG-O, FG-V and FG-X are considered. The reliability of present results is evaluated by comparing with the previous results based on a different approach. In addition, the special type of the cylindrical shell, elliptical cylindrical shell, is also investigated in the results section to evaluate the effect of the structural form on the nonlinear vibration when the MEE layer is added.

Appendices

Appendix 1

See Table 7,

Table 7 Mechanical properties of CNTRC material (core layer)

8

Table 8 Mechanical properties of magneto-electro-elastic material

and 9

Table 9 Names of quantities and corresponding symbols of the mechanical and physical components of the MEE material layer

.

Appendix 2

$$ \begin{aligned} \left\{ \begin{gathered} \varepsilon_{x} \hfill \\ \varepsilon_{y} \hfill \\ \gamma_{xy} \hfill \\ \end{gathered} \right\} & = \left\{ \begin{gathered} \frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} \hfill \\ \frac{\partial v}{{\partial y}} - \frac{w}{R} + \frac{1}{2}\left( {\frac{\partial w}{{\partial y}}} \right)^{2} \hfill \\ \frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}} + \frac{\partial w}{{\partial x}}\frac{\partial w}{{\partial y}} \hfill \\ \end{gathered} \right\} - z\left\{ \begin{gathered} \frac{{\partial^{2} w}}{{\partial x^{2} }} \hfill \\ \frac{{\partial^{2} w}}{{\partial y^{2} }} \hfill \\ 2\frac{{\partial^{2} w}}{\partial x\partial y} \hfill \\ \end{gathered} \right\}; \\ \left\{ {\begin{array}{*{20}c} {\sigma_{x}^{{}} } \\ {\sigma_{y}^{{}} } \\ {\sigma_{xy}^{{}} } \\ \end{array} } \right\}_{a} & = \left[ {\begin{array}{*{20}c} {Q_{11}^{a} } & {Q_{12}^{a} } & 0 \\ {Q_{12}^{a} } & {Q_{22}^{a} } & 0 \\ 0 & 0 & {Q_{66}^{a} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} - \alpha_{1} \Delta T} \\ {\varepsilon_{y} - \alpha_{2} \Delta T} \\ {\gamma_{xy} } \\ \end{array} } \right\}_{a} , \\ \end{aligned} $$

$$ \begin{aligned} \widetilde{{C_{11} }} & = C_{11} - \frac{{C_{13}^{2} }}{{C_{33} }}; \, \widetilde{{C_{12} }} = C_{12} - \frac{{C_{13} C_{23} }}{{C_{33} }}, \\ \, \widetilde{{C_{22} }} & = C_{22} - \frac{{C_{23}^{2} }}{{C_{33} }}; \, \widetilde{{C_{66} }} = C_{66} , \\ \widetilde{{e_{31} }} & = e_{31} - \frac{{C_{13} e_{33} }}{{C_{33} }}; \, \widetilde{{e_{32} }} = e_{32} - \frac{{C_{23} e_{33} }}{{C_{33} }}, \\ \, \widetilde{{q_{31} }} & = q_{31} - \frac{{C_{13} q_{33} }}{{C_{33} }}; \\ \end{aligned} $$

$$ \begin{aligned} \widetilde{{q_{32} }} & = q_{32} - \frac{{C_{23} q_{33} }}{{C_{33} }},\widetilde{{\mu_{11} }} = \mu_{11} ; \\ \, \widetilde{{\mu_{22} }} & = \mu_{22} ; \, \widetilde{{\mu_{33} }} = \mu_{33} + \frac{{q_{33}^{2} }}{{C_{33} }}; \\ \widetilde{{\alpha_{1} }} & = \alpha_{1} - \frac{{C_{13} \alpha_{3} }}{{C_{33} }}; \, \widetilde{{\alpha_{2} }} = \alpha_{2} - \frac{{C_{23} \alpha_{3} }}{{C_{33} }}, \\ \widetilde{{\eta_{11} }} & = \eta_{11} ; \, \widetilde{{\eta_{22} }} = \eta_{22} ; \, \widetilde{{\eta_{33} }} = \eta_{33} + \frac{{e_{33}^{2} }}{{C_{33} }}; \\ \widetilde{{m_{11} }} & = m_{11} ; \, \widetilde{{m_{22} }} = m_{22} ; \, \widetilde{{m_{33} }} = m_{33} + \frac{{e_{33} q_{33} }}{{C_{33} }}; \\ \end{aligned} $$

$$ \begin{aligned} N_{x} & = F_{11} \varepsilon_{x}^{0} + F_{12} \varepsilon_{y}^{0} + G_{11} k_{x}^{{}} \\ & \quad + G_{12} k_{y}^{{}} - F_{13} E_{z} - G_{13} H_{z} - \alpha_{1} \Delta T, \\ N_{y} & = F_{12} \varepsilon_{x}^{0} + F_{22} \varepsilon_{y}^{0} + G_{12} k_{x}^{{}} \\ & \quad + G_{22} k_{y}^{{}} - F_{14} E_{z} - G_{14} H_{z} - \alpha_{2} \Delta T, \\ N_{xy} & = F_{66} \gamma_{xy}^{0} + G_{66} k_{xy}^{{}} , \\ M_{x} & = G_{11} \varepsilon_{x}^{0} + G_{12} \varepsilon_{y}^{0} + H_{11} k_{x}^{{}} \\ & \quad + H_{12} k_{y}^{{}} - F_{23} E_{z} - G_{23} H_{z} - \alpha_{3} \Delta T, \\ M_{y} & = G_{12} \varepsilon_{x}^{0} + G_{22} \varepsilon_{y}^{0} + H_{12} k_{x}^{{}} \\ & \quad + H_{22} k_{y}^{{}} - F_{24} E_{z} - G_{24} H_{z} - \alpha_{4} \Delta T, \\ M_{xy} & = G_{66} \gamma_{xy}^{0} + H_{66} k_{xy}^{{}} , \\ \end{aligned} $$

$$ \begin{aligned} \left( {F_{ij} ,\,\,G_{ij} ,\,\,H_{ij} } \right) & = \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\widetilde{{C_{ij} }}(1,z,z^{2} ){\text{d}}z} + \int\limits_{{ - h_{c} /2}}^{{h_{c} /2}} {Q_{ij} (1,z,z^{2} ){\text{d}}z} \\ & \quad + \int\limits_{{h_{c} /2}}^{{h_{c} /2 + h_{f} }} {\widetilde{{C_{ij} }}(1,z,z^{2} ){\text{d}}z,} \quad \left( {ij = 11,12,22,66} \right), \\ \left( {F_{13} ,F_{23} } \right) & = \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\widetilde{{e_{31} }}\left( {1,z} \right){\text{d}}z} + \int\limits_{{h_{c} /2}}^{{h_{f} + h_{c} /2}} {\widetilde{{e_{31} }}\left( {1,z} \right){\text{d}}z} , \\ \left( {F_{14} ,F_{24} } \right) & = \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\widetilde{{e_{32} }}\left( {1,z} \right){\text{d}}z} + \int\limits_{{h_{c} /2}}^{{h_{f} + h_{c} /2}} {\widetilde{{e_{32} }}\left( {1,z,z^{3} } \right){\text{d}}z} , \\ \left( {G_{13} ,G_{23} } \right) & = \,\int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\widetilde{{q_{31} }}\left( {1,z} \right){\text{d}}z} + \int\limits_{{h_{c} /2}}^{{h_{f} + h_{c} /2}} {\widetilde{{q_{31} }}\left( {1,z} \right){\text{d}}z} , \\ \left( {G_{14} ,G_{24} } \right) & = \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\widetilde{{q_{32} }}\,\left( {1,z} \right){\text{d}}z} \quad + \int\limits_{{h_{c} /2}}^{{h_{f} + h_{c} /2}} {\widetilde{{q_{32} }}\left( {1,z} \right){\text{d}}z} , \\ \end{aligned} $$

$$ \begin{aligned} \alpha_{i} & = \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\widetilde{{\alpha_{1} }}\left( {1,z} \right){\text{d}}z} + \int\limits_{{ - h_{c} /2}}^{{h_{c} /2}} {Q_{11}^{c} \alpha_{11} \left( {1,z} \right){\text{d}}z} \\ & \quad + \int\limits_{{ - h_{c} /2}}^{{h_{c} /2}} {Q_{12}^{c} \alpha_{22} \left( {1,z} \right){\text{d}}z} + \int\limits_{{h_{c} /2}}^{{h_{f} + h_{c} /2}} {\widetilde{{\alpha_{1} }}\,\left( {1,z} \right)\,{\text{d}}z} , \\ \alpha_{j} & = \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\widetilde{{\alpha_{2} }}\,\left( {1,z} \right){\text{d}}z} + \int\limits_{{ - h_{c} /2}}^{{h_{c} /2}} {Q_{12}^{c} \alpha_{11} \left( {1,z} \right){\text{d}}z} \\ & \quad + \int\limits_{{ - h_{c} /2}}^{{h_{c} /2}} {Q_{22}^{c} \alpha_{22} \,\left( {1,z} \right){\text{d}}z} + \int\limits_{{h_{c} /2}}^{{h_{f} + h_{c} /2}} {\widetilde{{\alpha_{2} }}\left( {1,z} \right){\text{d}}z} , \\ & \quad \left( {i = 1,3;j = 2,4} \right) \\ \end{aligned} $$

Appendix 3

$$ \begin{aligned} \varepsilon_{x}^{0} & = F_{22}^{*} \frac{{\partial^{2} f}}{{\partial y^{2} }} - F_{12}^{*} \frac{{\partial^{2} f}}{{\partial x^{2} }} + G_{11}^{*} \frac{{\partial^{2} w}}{{\partial x^{2} }} \\ & \quad + G_{12}^{*} \frac{{\partial^{2} w}}{{\partial y^{2} }} + F_{13}^{*} \phi_{0} + G_{13}^{*} \psi_{0} + \alpha_{1}^{*} \Delta T, \\ \varepsilon_{y}^{0} & = F_{11}^{*} \frac{{\partial^{2} f}}{{\partial x^{2} }} - F_{12}^{*} \frac{{\partial^{2} f}}{{\partial y^{2} }} + G_{21}^{*} \frac{{\partial^{2} w}}{{\partial x^{2} }} \\ & \quad + G_{22}^{*} \frac{{\partial^{2} w}}{{\partial y^{2} }} + F_{14}^{*} \phi_{0} + G_{14}^{*} \psi_{0} + \alpha_{2}^{*} \Delta T, \\ \gamma_{xy}^{0} & = - F_{66}^{*} \frac{{\partial^{2} f}}{\partial x\partial y} + 2G_{66}^{*} \left( {\frac{{\partial^{2} w}}{\partial x\partial y}} \right), \\ \end{aligned} $$

$$ \begin{aligned} F_{11}^{*} & = \frac{{F_{11} }}{\Delta },\,F_{22}^{*} = \frac{{F_{22} }}{\Delta },\,F_{12}^{*} = \frac{{F_{12} }}{\Delta }, \\ \Delta & = F_{11} F_{22} - F_{12}^{2} ,F_{66}^{*} = \frac{1}{{F_{66} }},G_{66}^{*} = \frac{{G_{66} }}{{F_{66} }}, \\ G_{11}^{*} & = F_{22}^{*} G_{11}^{{}} - F_{12}^{*} G_{12}^{{}} ,\,G_{22}^{*} = F_{11}^{*} G_{22} - F_{12}^{*} G_{12}^{{}} , \\ G_{12}^{*} & = F_{22}^{*} G_{12}^{{}} - F_{12}^{*} G_{22}^{{}} ,G_{21}^{*} = F_{11}^{*} G_{12} - F_{12}^{*} G_{11}^{{}} ,\, \\ F_{13}^{*} & = \frac{ - 2}{{h_{f} }}\left( {F_{22}^{*} F_{13}^{{}} - F_{12}^{*} F_{14}^{{}} } \right),F_{14}^{*} = \frac{ - 2}{{h_{f} }}\left( {F_{11}^{*} F_{14}^{{}} - F_{12}^{*} F_{13}^{{}} ,} \right); \\ G_{13}^{*} & = \frac{ - 2}{{h_{f} }}\left( {F_{22}^{*} G_{13}^{{}} - F_{12}^{*} G_{14}^{{}} } \right), \\ G_{14}^{*} & = \frac{ - 2}{{h_{f} }}\left( {F_{11}^{*} G_{14}^{{}} - F_{12}^{*} G_{13}^{{}} } \right), \\ \alpha_{1}^{*} & = F_{22}^{*} \alpha_{1} - F_{12}^{*} \alpha_{2} ,\alpha_{2}^{*} = F_{11}^{*} \alpha_{2} - F_{12}^{*} \alpha_{1} . \\ \end{aligned} $$

Replacing this stress function into Eqs. (8) and (10),

$$ \left\{ \begin{aligned} & G_{21}^{*} \frac{{\partial^{4} f}}{{\partial x^{4} }} + G_{12}^{*} \frac{{\partial^{4} f}}{{\partial y^{4} }} + \left( {G_{11}^{*} + G_{22}^{*} - 2G_{66}^{*} } \right)\frac{{\partial^{4} f}}{{\partial x^{2} \partial y^{2} }} \\ & \quad - L_{11}^{*} \frac{{\partial^{4} w}}{{\partial x^{4} }} - L_{22}^{*} \frac{{\partial^{4} w}}{{\partial y^{4} }} + \frac{1}{R}\frac{{\partial^{2} f}}{{\partial x^{2} }} \\ & \quad + \frac{{\partial^{2} f}}{{\partial y^{2} }}\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w^{*} }}{{\partial x^{2} }}} \right) - \left( {L_{12}^{*} + L_{21}^{*} + 4L_{66}^{*} } \right)\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} \\ & \quad - L_{31}^{*} \frac{{\partial^{2} \Phi }}{{\partial x^{2} }} - L_{32}^{*} \frac{{\partial^{2} \Phi }}{{\partial y^{2} }}\, - L_{41}^{*} \frac{{\partial^{2} \Psi }}{{\partial x^{2} }} \\ & \quad - L_{42}^{*} \frac{{\partial^{2} \Psi }}{{\partial y^{2} }} - 2\frac{{\partial^{2} f}}{\partial x\partial y}\left( {\frac{{\partial^{2} w}}{\partial x\partial y} + \frac{{\partial^{2} w^{*} }}{\partial x\partial y}} \right) \\ & \quad + \frac{{\partial^{2} f}}{{\partial x^{2} }}\left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{{\partial^{2} w^{*} }}{{\partial y^{2} }}} \right) \\ & \quad + p - k_{1} w + k_{2} \nabla^{2} w = \rho_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }}, \\ & T_{11} \frac{{\partial^{2} w}}{{\partial x^{2} }} + T_{12} \frac{{\partial^{2} w}}{{\partial y^{2} }} + T_{13} \frac{{\partial^{2} \Phi }}{{\partial x^{2} }} + T_{14} \frac{{\partial^{2} \Phi }}{{\partial y^{2} }} \\ & \quad + T_{15} \frac{{\partial^{2} \Psi }}{{\partial x^{2} }} + T_{16} \frac{{\partial^{2} \Psi }}{{\partial y^{2} }} + \eta_{33}^{*} \Phi + m_{33}^{*} \Psi = 0, \\ & T_{21} \frac{{\partial^{2} w}}{{\partial x^{2} }} + T_{22} \frac{{\partial^{2} w}}{{\partial y^{2} }} + T_{15} \frac{{\partial^{2} \Phi }}{{\partial x^{2} }} + T_{16} \frac{{\partial^{2} \Phi }}{{\partial y^{2} }} \\ & \quad + T_{23} \frac{{\partial^{2} \Psi }}{{\partial x^{2} }} + T_{24} \frac{{\partial^{2} \Psi }}{{\partial y^{2} }} + m_{33}^{*} \Phi + \mu_{33}^{*} \Psi = 0, \\ \end{aligned} \right. $$

where the $L_{ij}^{*} \left( {\,i = 1 - 4,j = 1 - 2} \right),L_{66}^{*} ,T_{kl} \left( {k = 1 - 2,l = 1 - 4} \right)T_{15} ,T_{16} ,A_{33}^{*} \left( {A = \eta ,m,\mu } \right)$:

$$ \begin{aligned} L_{11}^{*} & = H_{11} - G_{11}^{*} G_{11} - G_{21}^{*} G_{12} , \\ L_{22}^{*} & = H_{22} - G_{12}^{*} G_{12} - G_{22}^{*} G_{22} , \\ L_{12}^{*} & = H_{12} - G_{12}^{*} G_{11} - G_{22}^{*} G_{12} , \\ L_{21}^{*} & = H_{12} - G_{11}^{*} G_{12} - G_{21}^{*} G_{22} , \\ L_{66}^{*} & = H_{66} - G_{66}^{*} G_{66} ,\,\,L_{31}^{*} = \left( { - F_{23} } \right)\beta \sin \left( {\beta z} \right), \\ L_{32}^{*} & = \left( { - F_{24} } \right)\beta \sin \left( {\beta z} \right),\,\,L_{41}^{*} = \left( { - G_{23} } \right)\beta \sin \left( {\beta z} \right), \\ L_{42}^{*} & = \left( { - G_{24} } \right)\beta \sin \left( {\beta z} \right), \\ \end{aligned} $$

$$ \begin{aligned} \eta_{33}^{*} & = - \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\eta_{33} \left( {\beta {\text{sin}}\left( {\beta z} \right)} \right)^{2} {\text{d}}z} \\ & \quad - \int\limits_{{h_{c} /2}}^{{h_{c} /2 + h_{f} }} {\eta_{33} \left( {\beta {\text{sin}}\left( {\beta z} \right)} \right)^{2} {\text{d}}z} , \\ m_{33}^{*} & = - \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {m_{33} \left( {\beta {\text{sin}}\left( {\beta z} \right)} \right)^{2} {\text{d}}z} \\ & \quad - \int\limits_{{h_{c} /2}}^{{h_{c} /2 + h_{f} }} {m_{33} \left( {\beta {\text{sin}}\left( {\beta z} \right)} \right)^{2} {\text{d}}z} , \\ \mu_{33}^{*} & = - \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\mu_{33} \left( {\beta {\text{sin}}\left( {\beta z} \right)} \right)^{2} {\text{d}}z} \\ & \quad - \int\limits_{{h_{c} /2}}^{{h_{c} /2 + h_{f} }} {\mu_{33} \left( {\beta {\text{sin}}\left( {\beta z} \right)} \right)^{2} {\text{d}}z} , \\ \end{aligned} $$

$$ \begin{aligned} T_{11} & = - \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {e_{31} z\beta \sin \left( {\beta z} \right)} {\text{d}}z \\ & \quad - \int\limits_{{h_{c} /2}}^{{h_{c} /2 + h_{f} }} {e_{31} z\beta \sin \left( {\beta z} \right)} {\text{d}}z, \\ \end{aligned} $$

$$ \begin{aligned} T_{12} & = - \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {e_{32} z\beta \sin \left( {\beta z} \right)} {\text{d}}z \\ & \quad - \int\limits_{{h_{c} /2}}^{{h_{c} /2 + h_{f} }} {e_{32} z\beta \sin \left( {\beta z} \right)} {\text{d}}z, \\ T_{13} & = \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\eta_{11} \cos^{2} \left( {\beta z} \right){\text{d}}z} \\ & \quad + \int\limits_{{h_{c} /2}}^{{h_{c} /2 + h_{f} }} {\eta_{11} \cos^{2} \left( {\beta z} \right){\text{d}}z} , \\ T_{14} & = \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\eta_{22} \cos^{2} \left( {\beta z} \right){\text{d}}z} \\ & \quad + \int\limits_{{h_{c} /2}}^{{h_{c} /2 + h_{f} }} {\eta_{22} \cos^{2} \left( {\beta z} \right){\text{d}}z} , \\ T_{15} & = \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {m_{11} \cos^{2} \left( {\beta z} \right){\text{d}}z} \\ & \quad + \int\limits_{{h_{c} /2}}^{{h_{c} /2 + h_{f} }} {m_{11} \cos^{2} \left( {\beta z} \right){\text{d}}z} , \\ T_{16} & = \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {m_{22} \cos^{2} \left( {\beta z} \right){\text{d}}z} \\ & \quad + \int\limits_{{h_{c} /2}}^{{h_{c} /2 + h_{f} }} {m_{22} \cos^{2} \left( {\beta z} \right){\text{d}}z} , \\ T_{21} & = - \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {q_{31} z\beta \sin \left( {\beta z} \right)} {\text{d}}z \\ & \quad - \int\limits_{{h_{c} /2}}^{{h_{c} /2 + h_{f} }} {q_{31} z\beta \sin \left( {\beta z} \right)} {\text{d}}z, \\ T_{22} & = - \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {q_{32} z\beta \sin \left( {\beta z} \right)} {\text{d}}z \\ & \quad - \int\limits_{{h_{c} /2}}^{{h_{c} /2 + h_{f} }} {q_{32} z\beta \sin \left( {\beta z} \right)} {\text{d}}z, \\ T_{23} & = \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\mu_{11} \cos^{2} \left( {\beta z} \right){\text{d}}z} \\ & \quad + \int\limits_{{h_{c} /2}}^{{h_{c} /2 + h_{f} }} {\mu_{11} \cos^{2} \left( {\beta z} \right){\text{d}}z} \\ T_{24} & = \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\mu_{22} \cos^{2} \left( {\beta z} \right){\text{d}}z} \\ & \quad + \int\limits_{{h_{c} /2}}^{{h_{c} /2 + h_{f} }} {\mu_{22} \cos^{2} \left( {\beta z} \right){\text{d}}z} , \\ \end{aligned} $$

By substitution of approximate solutions into the deformation compatibility equation:

$$ \begin{aligned} F_{{11}}^{*} \frac{{\partial ^{4} f}}{{\partial x^{4} }} & + F_{{22}}^{*} \frac{{\partial ^{4} f}}{{\partial y^{4} }} + \left( {F_{{66}}^{*} - 2F_{{12}}^{*} } \right)\frac{{\partial ^{4} f}}{{\partial x^{2} \partial y^{2} }} \\ & \quad + G_{{21}}^{*} \frac{{\partial ^{4} w}}{{\partial x^{4} }} + G_{{12}}^{*} \frac{{\partial ^{4} w}}{{\partial y^{4} }} + \left( {G_{{11}}^{*} + G_{{22}}^{*} - 2G_{{66}}^{*} } \right)\frac{{\partial ^{4} w}}{{\partial x^{2} \partial y^{2} }} \\ & \quad - \left( {\left( {\frac{{\partial ^{2} w}}{{\partial x\partial y}}} \right)^{2} - \frac{{\partial ^{2} w}}{{\partial x^{2} }}\frac{{\partial ^{2} w}}{{\partial y^{2} }} + 2\frac{{\partial ^{2} w}}{{\partial x\partial y}}\frac{{\partial ^{2} w^{*} }}{{\partial x\partial y}}} \right. \\ &\quad - \left. {\frac{{\partial ^{2} w}}{{\partial x^{2} }}\frac{{\partial ^{2} w^{*} }}{{\partial y^{2} }} - \frac{{\partial ^{2} w}}{{\partial y^{2} }}\frac{{\partial ^{2} w^{*} }}{{\partial x^{2} }} - \frac{1}{R}\frac{{\partial ^{2} w}}{{\partial x^{2} }}} \right) = 0; \end{aligned} $$

$$ \begin{aligned} A_{1} & = M_{1} W\left( {W + 2\mu h} \right),\,\,A_{2} = M_{2} W\left( {W + 2\mu h} \right), \\ A_{3} & = M_{3} W, \\ \end{aligned} $$

$$ \begin{aligned} M_{1} & = \frac{{\delta_{n}^{2} }}{{32F_{11}^{*} \lambda_{m}^{2} }},M_{2} = \frac{{\lambda_{m}^{2} }}{{32F_{22}^{*} \delta_{n}^{2} }}, \\ M_{3} & = - \frac{{R\left[ {G_{21}^{*} \lambda_{m}^{4} + \left( {G_{11}^{*} + G_{22}^{*} - 2G_{66}^{*} } \right)\lambda_{m}^{2} \delta_{n}^{2} + G_{12}^{*} \delta_{n}^{4} } \right] - \lambda_{m}^{2} }}{{R\left[ {F_{11}^{*} \lambda_{m}^{4} - \left( {2F_{12}^{*} - F_{66}^{*} } \right)\lambda_{m}^{2} \delta_{n}^{2} + F_{22}^{*} \delta_{n}^{4} } \right]}}. \\ \end{aligned} $$

$$ \begin{aligned} h_{11} & = - \left[ \begin{gathered} L_{11}^{*} \lambda_{m}^{4} + L_{22}^{*} \delta_{n}^{4} + \left( {L_{12}^{*} + L_{21}^{*} + 4L_{66}^{*} } \right)\lambda_{m}^{2} \delta_{n}^{2} \hfill \\ + k_{1} + k_{2} \left( {\lambda_{m}^{2} + \delta_{n}^{2} } \right) \hfill \\ \end{gathered} \right] \\ & \quad + \left[ \begin{gathered} G_{21}^{*} \lambda_{m}^{4} + G_{12}^{*} \delta_{n}^{4} + \hfill \\ \left( {G_{11}^{*} + G_{22}^{*} - 2G_{66}^{*} } \right)\lambda_{m}^{2} \delta_{n}^{2} - \frac{{\lambda_{m}^{2} }}{R} \hfill \\ \end{gathered} \right]M_{3} , \\ \end{aligned} $$

$$ \begin{aligned} h_{12} & = - \frac{{32\lambda_{m}^{{}} \delta_{n}^{{}} }}{3\pi LR}M_{3} ,\,h_{13} = - \frac{{8\lambda_{m}^{{}} \delta_{n}^{{}} }}{3\pi LR}\left( {\frac{{G_{21}^{*} }}{{F_{11}^{*} }} + \frac{{G_{12}^{*} }}{{F_{22}^{*} }}} \right), \\ h_{14} & = - \frac{1}{16}\left( {\frac{{\lambda_{m}^{4} }}{{F_{22}^{*} }} + \frac{{\delta_{n}^{4} }}{{F_{11}^{*} }}} \right), \\ h_{15} & = L_{31}^{*} \lambda_{m}^{2} + L_{32}^{*} \delta_{n}^{2} ,\,h_{16} = L_{41}^{*} \lambda_{m}^{2} + L_{42}^{*} \delta_{n}^{2} , \\ h_{41} & = - \left( {T_{11} \lambda_{m}^{2} + T_{12} \delta_{n}^{2} } \right),h_{42} = - \left( {T_{13} \lambda_{m}^{2} + T_{14} \delta_{n}^{2} - n_{33}^{*} } \right), \\ h_{43} & = - \left( {T_{15} \lambda_{m}^{2} + T_{16} \delta_{n}^{2} - m_{33}^{*} } \right),h_{51} = - \left( {T_{21} \lambda_{m}^{2} + T_{22} \delta_{n}^{2} } \right), \\ h_{52} & = - \left( {T_{23} \lambda_{m}^{2} + T_{24} \delta_{n}^{2} - \mu_{33}^{*} } \right). \\ \end{aligned} $$

Appendix 4

$$ \int\limits_{0}^{2\pi R} {\int\limits_{0}^{L} {\frac{\partial u}{{\partial x}}{\text{d}}x{\text{d}}y = 0} } , $$

$$ \begin{aligned} \frac{\partial u}{{\partial x}} & = F_{22}^{*} \frac{{\partial^{2} f}}{{\partial y^{2} }} - F_{12}^{*} \frac{{\partial^{2} f}}{{\partial x^{2} }} + G_{11}^{*} \frac{{\partial^{2} w}}{{\partial x^{2} }} \\ & \quad + G_{12}^{*} \frac{{\partial^{2} w}}{{\partial y^{2} }} + F_{13}^{*} \phi_{0} + G_{13}^{*} \psi_{0} \\ & \quad + \alpha_{1}^{*} \Delta T - \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} - \frac{\partial w}{{\partial x}}\frac{{\partial w^{*} }}{\partial x}. \\ \end{aligned} $$

$$ \begin{aligned} N_{x0} & = g_{2} \left( {W + 2\mu h} \right)W + g_{3} \phi_{0} + g_{4} \psi_{0} + g_{5} \Delta T, \\ g_{2} & = \frac{{\lambda_{m}^{2} }}{{8F_{22}^{*} }},g_{3} = - \frac{{F_{13}^{*} }}{{F_{22}^{*} }},g_{4} = - \frac{{G_{13}^{*} }}{{F_{22}^{*} }}, \\ \end{aligned} $$

$$ \begin{aligned} g_{5} & = - \frac{{\alpha_{1}^{*} }}{{F_{22}^{*} }},\,a_{1} = - \frac{{h_{41} h_{52} - h_{43} h_{51} }}{{h_{42} h_{52} - h_{43}^{2} }}, \\ a_{2} & = \frac{{h_{41} h_{43} - h_{42} h_{51} }}{{h_{42} h_{52} - h_{43}^{2} }},o_{21} = \left( {o_{11} + o_{15}^{{}} a_{1} + o_{16}^{{}} a_{2} } \right), \\ \end{aligned} $$

$$ \begin{aligned} o_{11}^{*} & = \frac{1}{{\rho_{1} }}\left( {\left( {g_{3} \lambda_{m}^{2} } \right)\phi_{0} + \left( {g_{4} \lambda_{m}^{2} } \right)\psi_{0} + \left( {g_{5} \lambda_{m}^{2} } \right)\Delta T} \right), \\ o_{11} & = - h_{11} /\rho_{1} ,o_{12} = - h_{12} /\rho_{1} , \\ o_{13} & = - h_{13} /\rho_{1} ,o_{14} = \left( { - h_{14} + g_{2} \lambda_{m}^{2} } \right)/\rho_{1} , \\ o_{15} & = - h_{15} /\rho_{1} ,o_{16} = - h_{16} /\rho_{1} . \\ \end{aligned} $$