Nonlinear vibrations and chaotic phenomena of functionally graded material truncated conical shell subject to aerodynamic and in-plane loads under 1:2 internal resonance relation

Abstract

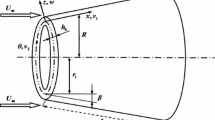
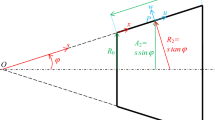
This paper focuses on the nonlinear dynamic responses of a functionally graded material (FGM) truncated conical shell under 1:2 internal resonance relation. The FGM truncated conical shell is subjected to the in-plane load and the aerodynamic load along the meridian direction. According to a power-law distribution, the material properties are assumed to be modified along the thickness direction smoothly and continuously and the material properties are temperature dependent. The aerodynamic load is obtained by the first-order piston theory with the curvature correction term. According to von Karman type nonlinear geometric relations, first-order shear deformation shell theory, Hamilton principle, the nonlinear equations of motion for the FGM truncated conical shell are established. Furthermore, the nonlinear equations of motion are reduced into a system of the ordinary differential equations by utilizing Galerkin procedure. The multiple scales method is used to obtain the averaged equations for the FGM truncated conical shell under the relations of 1:2 internal resonance and 1/2 subharmonic resonance. The frequency–response curves, time history diagrams, phase portraits, Poincare maps and bifurcation diagrams with different parameters are yielded by employing numerical calculations. The influences of exponent of volume fraction, Mach number, damping coefficient and in-plane load on the nonlinear resonance behaviors of the FGM truncated conical shell are investigated. The chaotic and periodic motions of the FGM truncated conical shell have been discussed in detail.

Appendix A

Nonlinear equations in form of generalized displacements are listed, as follows

$$\begin{aligned}&A_{11} \frac{\partial ^{2}u_{0} }{\partial x^{2}}+\mathfrak {R}^{2}A_{66} \frac{\partial ^{2}u_{0} }{\partial \theta ^{2}}+\mathfrak {R}A_{11} \frac{\partial u_{0} }{\partial x}\sin \beta -\mathfrak {R}^{2}A_{22} u_{0} \cos ^{2}\beta +\mathfrak {R}\left( {A_{12} +A_{66} } \right) \frac{\partial ^{2}v_{0} }{\partial x\partial \theta }\nonumber \\&\quad -\mathfrak {R}^{2}\left( {A_{22} +A_{66} } \right) \frac{\partial v_{0} }{\partial \theta }\sin \beta +\mathfrak {R}^{2}A_{66} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\frac{\partial w_{0} }{\partial x}+\mathfrak {R}^{2}\left( {A_{12} +A_{66} } \right) \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\frac{\partial w_{0} }{\partial \theta }\nonumber \\&\quad +2\mathfrak {R}\left( {A_{11} -A_{12} } \right) \frac{\partial ^{2}w_{0} }{\partial x^{2}}\sin \beta -2\mathfrak {R}^{3}\left( {A_{12} -A_{22} } \right) \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\sin \beta +\mathfrak {R}A_{12} \frac{\partial w_{0} }{\partial x}\cos \beta \nonumber \\&\quad -\mathfrak {R}^{2}A_{22} w_{0} \sin \beta \cos \beta +B_{11} \frac{\partial ^{2}\varphi _{x} }{\partial x^{2}}+\mathfrak {R}^{2}B_{66} \frac{\partial ^{2}\varphi _{x} }{\partial \theta ^{2}}+\mathfrak {R}B_{11} \frac{\partial \varphi _{x} }{\partial x}\sin \beta -\mathfrak {R}^{2}B_{22} \varphi _{x} \sin ^{2}\beta \nonumber \\&\quad -\mathfrak {R}^{2}\left( {B_{22} +B_{66} } \right) \frac{\partial \varphi _{\theta } }{\partial \theta }\sin \beta +\mathfrak {R}\left( {B_{12} +B_{66} } \right) \frac{\partial ^{2}\varphi _{\theta } }{\partial x\partial \theta }+A_{11} \frac{\partial ^{2}w_{0} }{\partial x^{2}}\frac{\partial w_{0} }{\partial x} \nonumber \\&\quad +\mathfrak {R}N_{xx}^{T} \sin \beta -\mathfrak {R}N_{\theta \theta }^{T} \sin \beta =I_{0} \ddot{{u}}_{0} +I_{1} \ddot{{\varphi }}_{x} , \end{aligned}$$

(A1)

$$\begin{aligned}&\mathfrak {R}\left( {A_{12} +A_{66} } \right) \frac{\partial ^{2}u_{0} }{\partial x\partial \theta }+\mathfrak {R}^{2}\left( {A_{22} +A_{66} } \right) \frac{\partial u_{0} }{\partial \theta }\sin \beta +A_{66} \frac{\partial ^{2}v_{0} }{\partial x^{2}}+\mathfrak {R}^{2}A_{22} \frac{\partial ^{2}v_{0} }{\partial \theta ^{2}}\nonumber \\&\qquad -\mathfrak {R}^{2}\left( {KA_{44} \cos ^{2}\beta +A_{66} \sin ^{2}\beta } \right) v_{0} +\mathfrak {R}A_{66} \frac{\partial w_{0} }{\partial \theta }\frac{\partial ^{2}w_{0} }{\partial x^{2}}+\mathfrak {R}^{3}A_{22} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\frac{\partial w_{0} }{\partial \theta } \nonumber \\&\qquad +\mathfrak {R}\left( {A_{12} +A_{66} } \right) \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\frac{\partial w_{0} }{\partial x}+\mathfrak {R}^{2}A_{66} \frac{\partial w_{0} }{\partial \theta }\frac{\partial w_{0} }{\partial x}\sin \beta +\mathfrak {R}^{2}A_{22} \frac{\partial w_{0} }{\partial \theta }\cos \beta \nonumber \\&\qquad +\mathfrak {R}\left( {B_{12} +B_{66} } \right) \frac{\partial ^{2}\varphi _{x} }{\partial x\partial \theta }+\mathfrak {R}^{2}\left( {B_{22} +B_{66} } \right) \frac{\partial \varphi _{x} }{\partial \theta }\sin \beta +\mathfrak {R}B_{66} \frac{\partial \varphi _{\theta } }{\partial x}\sin \beta +\mathfrak {R}B_{22} \frac{\partial ^{2}\varphi _{\theta } }{\partial \theta ^{2}}\nonumber \\&\qquad +\mathfrak {R}A_{66} \frac{\partial v_{0} }{\partial x}\sin \beta +\mathfrak {R}^{2}KA_{44} \frac{\partial w_{0} }{\partial \theta }\cos \beta +\left( {\mathfrak {R}KA_{44} \cos \beta -\mathfrak {R}^{2}B_{66} \sin ^{2}\beta } \right) \varphi _{\theta }\nonumber \\&\quad =I_{0} \ddot{{v}}_{0} +I_{1} \ddot{{\varphi }}_{\theta } , \end{aligned}$$

(A2)

$$\begin{aligned}&2\mathfrak {R}^{2}B_{66} \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\frac{\partial \varphi _{x} }{\partial \theta }+0.5\mathfrak {R}^{2}A_{11} \left( {\frac{\partial w_{0} }{\partial x}} \right) ^{3}\sin \beta -\mathfrak {R}N_{\theta \theta }^{T} \cos \beta +\mathfrak {R}\left( {B_{11} +B_{22} } \right) \frac{\partial \varphi _{x} }{\partial x}\frac{\partial w_{0} }{\partial x}\nonumber \\&\quad -\mathfrak {R}^{2}A_{66} \frac{\partial v_{0} }{\partial \theta }\frac{\partial w_{0} }{\partial x}\sin \beta -\mathfrak {R}^{3}\left( {A_{12} +A_{66} } \right) \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\frac{\partial w_{0} }{\partial x}+2\mathfrak {R}^{2}\left( {A_{12} +2A_{66} } \right) \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\frac{\partial w_{0} }{\partial \theta }\frac{\partial w_{0} }{\partial x}\nonumber \\&\quad -\mathfrak {R}^{2}B_{66} \frac{\partial \varphi _{\theta } }{\partial x}\frac{\partial w_{0} }{\partial x}\sin \beta +A_{11} \frac{\partial ^{2}u_{0} }{\partial x^{2}}\frac{\partial w_{0} }{\partial x}+B_{11} \frac{\partial ^{2}\varphi _{x} }{\partial x^{2}}\frac{\partial w_{0} }{\partial x}+\mathfrak {R}\left( {A_{12} +A_{66} } \right) \frac{\partial ^{2}v_{0} }{\partial x\partial \theta }\frac{\partial w_{0} }{\partial x}\nonumber \\&\quad +\mathfrak {R}\left( {B_{12} +B_{66} } \right) \frac{\partial ^{2}\varphi _{\theta } }{\partial x\partial \theta }\frac{\partial w_{0} }{\partial x}+\mathfrak {R}^{2}A_{66} \frac{\partial ^{2}u_{0} }{\partial \theta ^{2}}\frac{\partial w_{0} }{\partial x}+\mathfrak {R}\left( {KA_{55} +N_{xx}^{T} } \right) \frac{\partial w_{0} }{\partial x}\sin \beta \nonumber \\&\quad +\frac{3}{2}A_{11} \frac{\partial ^{2}w_{0} }{\partial x^{2}}\left( {\frac{\partial w_{0} }{\partial x}} \right) ^{2}+0.5\mathfrak {R}^{2}\left( {A_{12} +2A_{66} } \right) \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\left( {\frac{\partial w_{0} }{\partial x}} \right) ^{2}+0.5\mathfrak {R}^{2}A_{12} \left( {\frac{\partial w_{0} }{\partial x}} \right) ^{2}\cos \beta \nonumber \\&\quad +\mathfrak {R}\left( {A_{11} +A_{12} } \right) \frac{\partial w_{0} }{\partial x}\frac{\partial u_{0} }{\partial x}\sin \beta +\mathfrak {R}^{2}A_{12} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\frac{\partial u_{0} }{\partial x}-A_{12} \frac{\partial u_{0} }{\partial x}\cos \beta +A_{11} \frac{\partial ^{2}w_{0} }{\partial x^{2}}\frac{\partial u_{0} }{\partial x}\nonumber \\&2\mathfrak {R}A_{66} \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\frac{\partial v_{0} }{\partial x}-\mathfrak {R}^{2}A_{66} \frac{\partial w_{0} }{\partial \theta }\frac{\partial v_{0} }{\partial x}+\mathfrak {R}A_{12} \frac{\partial ^{2}w_{0} }{\partial x^{2}}w_{0} \cos \beta +\mathfrak {R}^{3}A_{22} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}w_{0} \cos \beta \nonumber \\&\quad -\mathfrak {R}^{2}A_{22} w_{0} \cos \beta +\mathfrak {R}B_{12} \frac{\partial ^{2}w_{0} }{\partial x^{2}}\varphi _{x} \sin \beta +\mathfrak {R}^{3}B_{22} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\varphi _{x} \sin \beta \nonumber \\&\quad +\left( {\mathfrak {R}KA_{55} -\mathfrak {R}^{2}B_{22} \cos \beta } \right) \varphi _{x} \sin \beta +\mathfrak {R}^{3}B_{66} \frac{\partial w_{0} }{\partial \theta }\varphi _{\theta } \sin ^{2}\beta -\mathfrak {R}^{2}B_{66} \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\varphi _{\theta } \sin \beta \nonumber \\&\quad +\mathfrak {R}^{3}A_{22} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}u_{0} \sin \beta -\mathfrak {R}^{3}A_{22} u_{0} \sin \beta \cos \beta +\mathfrak {R}^{2}A_{12} \frac{\partial ^{2}w_{0} }{\partial x^{2}}u_{0} \sin \beta \nonumber \\&\quad +\mathfrak {R}^{3}A_{66} \frac{\partial w_{0} }{\partial \theta }v_{0} \sin ^{2}\beta -2\mathfrak {R}^{2}A_{66} \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }v_{0} \sin \beta +\mathfrak {R}^{2}\left( {KA_{44} +N_{\theta \theta }^{T} } \right) \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\nonumber \\&\quad +\mathfrak {R}^{3}\left( {B_{22} -B_{66} } \right) \frac{\partial \varphi _{x} }{\partial \theta }\frac{\partial w_{0} }{\partial \theta }+\mathfrak {R}A_{66} \frac{\partial ^{2}v_{0} }{\partial x^{2}}\frac{\partial w_{0} }{\partial \theta }+\mathfrak {R}B_{66} \frac{\partial ^{2}\varphi _{\theta } }{\partial x^{2}}\frac{\partial w_{0} }{\partial \theta }\nonumber \\&\quad +\mathfrak {R}^{2}\left( {B_{12} +B_{66} } \right) \frac{\partial ^{2}\varphi _{x} }{\partial x\partial \theta }\frac{\partial w_{0} }{\partial \theta }+\mathfrak {R}^{3}A_{66} \frac{\partial ^{2}v_{0} }{\partial \theta ^{2}}\frac{\partial w_{0} }{\partial \theta }+\mathfrak {R}^{3}B_{22} \frac{\partial ^{2}\varphi _{\theta } }{\partial \theta ^{2}}\frac{\partial w_{0} }{\partial \theta }\nonumber \\&\quad +\left( {KA_{55} +N_{xx}^{T} -p\cos \Omega t} \right) \frac{\partial ^{2}w_{0} }{\partial x^{2}}+0.5\mathfrak {R}\left( {A_{12} +2A_{66} } \right) \frac{\partial ^{2}w_{0} }{\partial x^{2}}\left( {\frac{\partial w_{0} }{\partial \theta }} \right) ^{2}\nonumber \\&\quad +0.5\mathfrak {R}^{3}A_{22} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\left( {\frac{\partial w_{0} }{\partial \theta }} \right) ^{2}+\mathfrak {R}A_{12} \frac{\partial ^{2}w_{0} }{\partial x^{2}}\frac{\partial v_{0} }{\partial \theta }+\mathfrak {R}^{3}A_{22} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\frac{\partial v_{0} }{\partial \theta }+KA_{55} \frac{\partial \varphi _{x} }{\partial x}\nonumber \\&\quad -\mathfrak {R}^{2}\left( {KA_{44} +A_{22} } \right) \frac{\partial v_{0} }{\partial \theta }\cos \beta +B_{11} \frac{\partial ^{2}w_{0} }{\partial x^{2}}\frac{\partial \varphi _{x} }{\partial x}-\mathfrak {R}B_{12} \frac{\partial \varphi _{x} }{\partial x}\cos \beta +\mathfrak {R}^{2}B_{12} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\frac{\partial \varphi _{x} }{\partial x}\nonumber \\&\quad +2\mathfrak {R}B_{66} \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\frac{\partial \varphi _{\theta } }{\partial x}-\mathfrak {R}^{2}B_{66} \frac{\partial w_{0} }{\partial \theta }\frac{\partial \varphi _{\theta } }{\partial x}\sin \beta +\mathfrak {R}^{3}\left( {A_{22} -A_{66} } \right) \frac{\partial w_{0} }{\partial \theta }\frac{\partial u_{0} }{\partial \theta }\sin \beta \nonumber \\&\quad +\mathfrak {R}^{2}B_{66} \frac{\partial ^{2}\varphi _{x} }{\partial \theta ^{2}}\frac{\partial w_{0} }{\partial x}+\mathfrak {R}^{2}\left( {A_{12} +A_{66} } \right) \frac{\partial ^{2}u_{0} }{\partial x\partial \theta }\frac{\partial w_{0} }{\partial \theta }+0.5\mathfrak {R}^{3}A_{22} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\cos \beta \nonumber \\&\quad +2\mathfrak {R}^{3}A_{66} \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\frac{\partial u_{0} }{\partial \theta }+P_\mathrm{a} -\kappa \dot{{w}}_{0} =I_{0} \ddot{{w}}_{0} , \end{aligned}$$

(A3)

$$\begin{aligned}&B_{11} \frac{\partial ^{2}u_{0} }{\partial x^{2}}+\mathfrak {R}^{2}B_{66} \frac{\partial ^{2}u_{0} }{\partial \theta ^{2}}+\mathfrak {R}B_{11} \frac{\partial u_{0} }{\partial x}\sin \beta -\mathfrak {R}^{2}B_{22} u_{0} \sin ^{2}\beta +\mathfrak {R}\left( {B_{12} +B_{66} } \right) \frac{\partial ^{2}v_{0} }{\partial x\partial \theta }\nonumber \\&\quad -\mathfrak {R}^{2}\left( {B_{22} +B_{66} } \right) \frac{\partial v_{0} }{\partial \theta }\sin \beta +0.5\mathfrak {R}^{2}\left( {B_{11} -B_{12} } \right) \frac{\partial ^{2}w_{0} }{\partial x^{2}}\sin \beta -\mathfrak {R}^{2}B_{22} w_{0} \sin \beta \cos \beta \nonumber \\&\quad +\mathfrak {R}B_{12} \frac{\partial w_{0} }{\partial x}\cos \beta +B_{11} \frac{\partial ^{2}w_{0} }{\partial x^{2}}\frac{\partial w_{0} }{\partial x}+\mathfrak {R}^{2}B_{66} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\frac{\partial w_{0} }{\partial x}-KA_{55} \frac{\partial w_{0} }{\partial x}\nonumber \\&\quad -0.5\mathfrak {R}^{2}\left( {B_{12} +B_{22} } \right) \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\sin \beta +\mathfrak {R}^{2}\left( {B_{12} +B_{66} } \right) \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\frac{\partial w_{0} }{\partial \theta }-\left( {KA_{55} +\frac{1}{R^{2}}D_{22} } \right) \varphi _{x}\nonumber \\&\quad +\mathfrak {R}D_{11} \frac{\partial \varphi _{x} }{\partial x}\sin \beta +\mathfrak {R}^{2}D_{66} \frac{\partial ^{2}\varphi _{x} }{\partial \theta ^{2}}+D_{11} \frac{\partial ^{2}\upphi _{x} }{\partial x^{2}}+\mathfrak {R}\left( {D_{12} +D_{66} } \right) \frac{\partial ^{2}\varphi _{x} }{\partial x\partial \theta }\nonumber \\&\quad -\mathfrak {R}^{2}\left( {D_{22} +D_{66} } \right) \frac{\partial \varphi _{\theta } }{\partial \theta }\sin \beta +\mathfrak {R}M_{xx}^{T} \sin \beta -\mathfrak {R}M_{\theta \theta }^{T} \sin \beta =I_{1} \ddot{{u}}_{0} +I_{2} \ddot{{\varphi }}_{x} , \end{aligned}$$

(A4)

$$\begin{aligned}&\mathfrak {R}\left( {B_{12} +B_{66} } \right) \frac{\partial ^{2}u_{0} }{\partial x\partial \theta }+\mathfrak {R}^{2}\left( {B_{22} +B_{66} } \right) \frac{\partial u_{0} }{\partial \theta }\sin \beta +B_{66} \frac{\partial ^{2}v_{0} }{\partial x^{2}}+\mathfrak {R}^{2}B_{22} \frac{\partial ^{2}v_{0} }{\partial \theta ^{2}}\nonumber \\&\qquad +\left( {\mathfrak {R}KA_{44} \cos \beta -\mathfrak {R}^{2}B_{66} \sin ^{2}\beta } \right) v_{0} +\mathfrak {R}^{2}B_{66} \frac{\partial w_{0} }{\partial x}\frac{\partial w_{0} }{\partial \theta }\sin \beta \nonumber \\&\qquad +\left( {\mathfrak {R}^{2}B_{22} \cos \beta -\mathfrak {R}KA_{44} } \right) \frac{\partial w_{0} }{\partial \theta }+\mathfrak {R}^{3}B_{22} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\frac{\partial w_{0} }{\partial \theta }+\mathfrak {R}B_{66} \frac{\partial ^{2}w_{0} }{\partial x^{2}}\frac{\partial w_{0} }{\partial \theta }\nonumber \\&\qquad +\mathfrak {R}^{2}\left( {D_{22} +D_{66} } \right) \frac{\partial \varphi _{\theta } }{\partial \theta }+\mathfrak {R}^{2}D_{22} \frac{\partial ^{2}\varphi _{\theta } }{\partial \theta ^{2}}+\mathfrak {R}D_{66} \frac{\partial \varphi _{\theta } }{\partial x}-\left( {KA_{44} +\mathfrak {R}^{2}D_{66} \sin ^{2}\beta } \right) \varphi _{\theta }\nonumber \\&\qquad +\mathfrak {R}B_{66} \frac{\partial v_{0} }{\partial x}\sin \beta +\mathfrak {R}\left( {B_{12} +B_{66} } \right) \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\frac{\partial w_{0} }{\partial x}+\mathfrak {R}\left( {D_{12} +D_{66} } \right) \frac{\partial ^{2}\varphi _{x} }{\partial x\partial \theta }+D_{66} \frac{\partial ^{2}\varphi _{\theta } }{\partial x^{2}}\nonumber \\&\quad =I_{1} \ddot{{v}}_{0} +I_{2} \ddot{{\varphi }}_{\theta } . \end{aligned}$$

(A5)