Improving application of galloping-based energy harvesters in realistic condition

Abstract

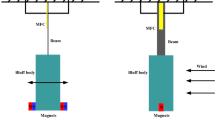
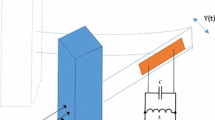
In this study, the electromechanical equation of motion for a galloping-based energy harvesting system is derived and experimentally validated. This system consists of a bluff body that elastically mounted in fluid flow and a piezoelectric energy harvesting device, which is placed inside it. To confirm dynamic behavior of the system in fluid flow, periodic response of the variables is analytically obtained by employing the harmonic balance method. The validated equations are used to study effect of changing the system parameters on electromechanical behavior of the energy harvester. Then, application of the system is investigated in a realistic condition. Employing several user-oriented charts, the energy harvesting system is optimized and it is shown that this system can optimally be used in normal wind speed.

Appendices

Appendix A

The potential energy of each piezoelectric and substructure layer is given in the following equation [39]:

$$\begin{aligned} \prod =\frac{1}{2}\int _{v_\mathrm{p} } {\sigma _\mathrm{p} \varepsilon \mathrm{d}v_\mathrm{p} } +\frac{1}{2}\int _{v_\mathrm{b} } {\sigma _\mathrm{b} \varepsilon \mathrm{d}v_\mathrm{b} } \end{aligned}$$

(A1)

where $\varepsilon$ and $\sigma$ are stress and strain, respectively. Also, Note that the integration is over the volume of the structure. Strain and stress can be written as:

$$\begin{aligned} \sigma _\mathrm{p} =E_\mathrm{p} \varepsilon +E_\mathrm{p} d_{31} E_3 ~,\quad \sigma _\mathrm{b} =E_\mathrm{b} \varepsilon ~,\quad \varepsilon =-z\frac{\partial ^{2}w_2 }{\partial x^{2}}~,\quad E_3 =\frac{V}{t_p } \end{aligned}$$

(A2)

This parameter along with electric displacement component $(D_{3})$ and electric field component in z direction $(E_{3})$. The relation, which is named as constitutive equation, is as follows:

$$\begin{aligned} D_3 =d_{31} \sigma -e_{33} E_3 \end{aligned}$$

(A3)

Substituting stress and strain relations into (A1), the final form of the potential energy for each piezoelectric and substructure layer is obtained.

$$\begin{aligned} \prod =\frac{1}{2}\int _{v_\mathrm{p} } {E_\mathrm{p} \left\{ {\left( {-z\frac{\partial ^{2}w_2 }{\partial x^{2}}} \right) ^{2}+d_{31} \frac{V}{t_\mathrm{p} }\left( {-z\frac{\partial ^{2}w_2 }{\partial x^{2}}} \right) } \right\} \mathrm{d}v_\mathrm{p} } +\frac{1}{2}\int _{v_\mathrm{b} } {E_\mathrm{b} \left( {-z\frac{\partial ^{2}w_2 }{\partial x^{2}}} \right) ^{2} \mathrm{d}v_\mathrm{b} } \end{aligned}$$

(A4)

Furthermore, using relations of Eq. (A3), the simplified form of internal electrical energy for each piezoelectric layer becomes:

$$\begin{aligned} W_\mathrm{ie} =\frac{1}{2}\int _{v_\mathrm{p} } {E_3 D_3 \mathrm{d}v_\mathrm{p} } =\frac{1}{2}\int _{v_\mathrm{p} } {\left( -\frac{V}{t_\mathrm{p} }\right) \left\{ {d_{31} E_\mathrm{p} \left( {-z\frac{\partial ^{2}w_2 }{\partial x^{2}}} \right) -e_{33} \frac{V}{t_\mathrm{p} }} \right\} \mathrm{d}v_\mathrm{p} } \end{aligned}$$

(A5)

Appendix B

Note that Eqs. (1)–(3) are integrated over the volume. In the first step, by substituting $w_{\mathrm{b}}t_{\mathrm{b}}$ and $w_\mathrm{p}t_\mathrm{p}$, respectively, as the surface of beam and piezoelectric layer, Eqs. (1)–(3) are rewritten over the length as follows:

$$\begin{aligned} \prod= & {} \int _0^L {E_\mathrm{b} w_\mathrm{b} t_\mathrm{b} \left( {-z\frac{\partial ^{2}w_2 }{\partial x^{2}}} \right) ^{2}\mathrm{d}x} +\int _0^L {E_\mathrm{p} w_\mathrm{p} t_\mathrm{p} \left( {-z\frac{\partial ^{2}w_2 }{\partial x^{2}}} \right) ^{2}\mathrm{d}x} \nonumber \\&+\,\int _0^{L_\mathrm{e} } {E_\mathrm{p} d_{31} w_\mathrm{p} V\left( {-z\frac{\partial ^{2}w_2 }{\partial x^{2}}} \right) } \mathrm{d}x+\frac{1}{2}K w_1^2 \end{aligned}$$

(B1)

$$\begin{aligned} T= & {} \int _0^L {\rho _\mathrm{b} w_\mathrm{b} t_\mathrm{b} \left( {\frac{\partial w_2 }{\partial t}+{\dot{w}}_1 } \right) ^{2}} ~ \mathrm{d}x+\int _0^L {\rho _\mathrm{p} w_\mathrm{p} t_\mathrm{p} \left( {\frac{\partial w_2 }{\partial t}+{\dot{w}}_1 } \right) ^{2}} ~ \mathrm{d}x+\frac{1}{2}M_\mathrm{bb} {\dot{w}}_1^2 \nonumber \\&+\,\frac{1}{2}m_\mathrm{tip} \left( {{\dot{w}}_1 +\left. {\frac{\partial w_2 }{\partial t}} \right| _{x=L} } \right) ^{2} \end{aligned}$$

(B2)

$$\begin{aligned} W_\mathrm{ie}= & {} \int _0^{L_\mathrm{e} } {E_\mathrm{p} d_{31} w_\mathrm{p} V} \left( -z\frac{\partial ^{2}w_2 }{\partial x^{2}}\right) \mathrm{d}x-e_{33} w_\mathrm{p} \frac{V^{2}}{t_\mathrm{p} }\int _0^L {\mathrm{d}x} \end{aligned}$$

(B3)

In the second step, by substituting Eqs. (B1)–(B3) into Eqs. (6)–(8) and using the orthogonality conditions, Eqs. (9)–(11) are obtained.

Appendix C

The fundamental Euler–Bernoulli beam equation for ith vibration mode is expressed as follows:

$$\begin{aligned} \frac{\mathrm{d}^{4}\varphi _i (x)}{\mathrm{d}x^{4}}-\omega _i ^{2}\frac{\rho A}{EI}\varphi _i (x)=0 \end{aligned}$$

(C1)

The above equation can be rewritten for rth and sth vibration modes:

$$\begin{aligned} EI\frac{\mathrm{d}^{4}\varphi _r (x)}{\mathrm{d}x^{4}}= & {} \omega _r ^{2}\rho A\varphi _r (x) \end{aligned}$$

(C2)

$$\begin{aligned} EI\frac{\mathrm{d}^{4}\varphi _s (x)}{\mathrm{d}x^{4}}= & {} \omega _s ^{2}\rho A\varphi _s (x) \end{aligned}$$

(C3)

Multiplying Eq. (C2) by $\varphi _{s}(x)$ and integrating over the length of the beam gives:

$$\begin{aligned} \int _0^L {\varphi _s (x)EI\frac{\mathrm{d}^{4}\varphi _r (x)}{\mathrm{d}x^{4}}} \mathrm{d}x=\omega _r^2 \int _0^L {\varphi _s (x)\rho A\;\varphi _r (x)\;} \mathrm{d}x \end{aligned}$$

(C4)

Integrating the left side of the above equation and using boundary conditions leads to find Eq. (C5). Multiplying Eq. (C3) by $\varphi _{r}(x)$ and integrating over the length of the beam results in find Eq. (C6):

$$\begin{aligned} \int _0^L {\frac{\mathrm{d}^{2}\varphi _s (x)}{\mathrm{d}x^{2}}EI\frac{\mathrm{d}^{2}\varphi _r (x)}{\mathrm{d}x^{2}}} \mathrm{d}x= & {} \omega _r^2 \left\{ {\int _0^L {\varphi _s (x)\rho A\;\varphi _r (x)\;} \mathrm{d}x+\varphi _s (L)m_\mathrm{tip} \;\varphi _r (L)} \right\} \end{aligned}$$

(C5)

$$\begin{aligned} \int _0^L {\frac{\mathrm{d}^{2}\varphi _s (x)}{\mathrm{d}x^{2}}EI\frac{\mathrm{d}^{2}\varphi _r (x)}{\mathrm{d}x^{2}}} \mathrm{d}x= & {} \omega _s^2 \left\{ {\int _0^L {\varphi _s (x)\rho A\;\varphi _r (x)\;} \mathrm{d}x+\varphi _s (L)m_\mathrm{tip} \;\varphi _r (L)} \right\} \end{aligned}$$

(C6)

Regarding to the above equations, in case of two distinctive mode shape ($r \ne s$), the following equation can be obtained:

$$\begin{aligned} \int _0^L {\varphi _s (x)\rho A\;\varphi _r (x)\;} \mathrm{d}x+\varphi _s (L)\frac{m_\mathrm{tip} }{2}\;\varphi _r (L)=0,\quad \omega _r^2 \ne \omega _s^2 \end{aligned}$$

(C7)

Orthogonality condition can be written as follows:

$$\begin{aligned} \int _0^L {\varphi _s (x)\rho A\;\varphi _r (x)\;} \mathrm{d}x+\varphi _s (L)\frac{m_\mathrm{tip} }{2}\;\varphi _r (L)=\delta _{rs} \end{aligned}$$

(C8)

where $\delta _{rs}$ is the Kronecker delta, defined as unity for the case of $(r=s)$ and zero for $( r \ne s$). Considering the fundamental vibration mode (the first mode shape) Eq. (21) is obtained.