Skip to main content
SpringerLink
Log in

Free vibration analysis of multi-span Timoshenko beams using the assumed mode method

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

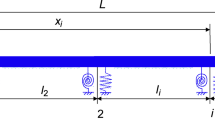
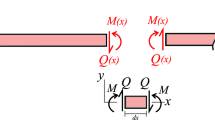
Although some investigations on the vibration properties of multi-span beams have been conducted, studies on multi-span Timoshenko beams by using the assumed mode method have been relatively few. In this paper, the multi-span Timoshenko beams are investigated, and the mode shapes of the beams are modified by the interpolation functions to model the vibration modes of the multi-span beams. Hamilton’s principle is applied to establish the equation of motion of the structure, and the natural circular frequencies and the free vibration responses of the multi-span beams are obtained. The numerical results demonstrate good agreement between the present results and those from the open literature and the ANSYS software. The influences of the length–thickness ratio, the disorder degree and the span number on the free vibration of the structure are also analyzed. It is observed that the displacement amplitude and the vibration period at the midpoint of the three-span Timoshenko beams are reduced when the disorder degree and the length–thickness ratio are reduced. The increase in the span number of the multi-span beams with equal spans leads to the decrease in the displacement amplitude and the period of the structures. Furthermore, some interesting phenomena are found, e.g., the same even-order frequencies of different three-span beams are equal under specific disorder degree.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Li, F.M., Kishimoto, K., Huang, W.H.: The calculations of natural frequencies and forced vibration responses of conical shell using the Rayleigh–Ritz method. Mech. Res. Commun. 36(5), 595–602 (2009)

    Article  MATH  Google Scholar 

  2. Lin, Y.H., Trethewey, M.W.: Finite element analysis of elastic beams subjected to moving dynamic loads. J. Sound Vib. 136(2), 323–342 (1990)

    Article  Google Scholar 

  3. Lombaert, G., Degrande, G., Kogut, J.: The experimental validation of a numerical model for the prediction of railway induced vibrations. J. Sound Vib. 297(3–5), 512–535 (2006)

    Article  Google Scholar 

  4. Cho, D.S., Kim, B.H., Kim, J.H., Vladimir, N., Choi, T.M.: Forced vibration analysis of arbitrarily constrained rectangular plates and stiffened panels using the assumed mode method. Thin-Walled Struct. 90, 182–190 (2015)

    Article  Google Scholar 

  5. Zheng, D.Y., Cheung, Y.K., Au, F.T.K., Cheng, Y.S.: Vibration of multi-span non-uniform beams under moving loads by using modified beam vibration functions. J. Sound Vib. 212(3), 455–467 (1998)

    Article  MATH  Google Scholar 

  6. Zheng, D.Y., Cheung, Y.K., Au, F.T.K., Cheng, Y.S.: Vibration of multi-span non-uniform bridges under moving vehicles and trains by using modified beam vibration functions. J. Sound Vib. 228(3), 611–628 (1999)

    Article  Google Scholar 

  7. Song, Z.G., Li, F.M.: Active aeroelastic flutter analysis and vibration control of supersonic beams using the piezoelectric actuator/sensor pairs. Smart Mater. Struct. 20(5), 055013 (2011)

    Article  Google Scholar 

  8. Li, F.M., Song, Z.G.: Flutter and thermal buckling control for composite laminated panels in supersonic flow. J. Sound Vib. 332(22), 5678–5695 (2013)

    Article  Google Scholar 

  9. Avramov, K.V., Chernobryvko, M.V., Kazachenko, O., Batutina, T.J.: Dynamic instability of parabolic shells in supersonic gas stream. Meccanica 51(4), 939–950 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  10. Lin, H.Y., Tsai, Y.C.: Free vibration analysis of a uniform multi-span beam carrying multiple spring-mass systems. J. Sound Vib. 302(3), 442–456 (2007)

    Article  Google Scholar 

  11. Lin, H.Y., Wang, C.Y.: Free vibration analysis of a hybrid beam composed of multiple elastic beam segments and elastic-supported rigid bodies. J. Mar. Sci. Technol. 20(5), 525–533 (2012)

    Google Scholar 

  12. Johansson, C., Pacoste, C., Karoumi, R.: Closed-form solution for the mode superposition analysis of the vibration in multi-span beam bridges caused by concentrated moving loads. Comput. Struct. 119, 85–94 (2013)

    Article  Google Scholar 

  13. Martínez-Castro, A.E., Museros, P., Castillo-Linares, A.: Semi-analytic solution in the time domain for non-uniform multi-span Bernoulli–Euler beams traversed by moving loads. J. Sound Vib. 294(1–2), 278–297 (2006)

    Article  Google Scholar 

  14. Biondi, B., Muscolino, G.: Component-mode synthesis method for coupled continuous and FE discretized substructures. Eng. Struct. 25(4), 419–433 (2003)

    Article  Google Scholar 

  15. Biondi, B., Muscolino, G., Sofi, A.: A substructure approach for the dynamic analysis of train-track-bridge system. Comput. Struct. 83(28–30), 2271–2281 (2005)

    Article  Google Scholar 

  16. De Salvo, V., Muscolino, G., Palmeri, A.: A substructure approach tailored to the dynamic analysis of multi-span continuous beams under moving loads. J. Sound Vib. 329(15), 3101–3120 (2010)

    Article  Google Scholar 

  17. Stancioiu, D., Ouyang, H.J., Mottershead, J.E., James, S.: Experimental investigations of a multi-span flexible structure subjected to moving masses. J. Sound Vib. 330(9), 2004–2016 (2011)

    Article  Google Scholar 

  18. Sharma, D.S., Mungla, M.J., Barad, K.H.: Vibration-based non-destructive technique to detect crack in multi-span beam. Nondestruct. Test. Eval. 30(4), 291–311 (2015)

    Article  Google Scholar 

  19. Timoshenko, S.P.: On the correction for shear of the differential equation for transverse vibration of prismatic bars. Philos. Mag. 41, 744–746 (1921)

    Article  Google Scholar 

  20. Yokoyama, T.: Vibration analysis of Timoshenko beam-columns on two-parameter elastic foundations. Comput. Struct. 61(6), 995–1007 (1996)

    Article  MATH  Google Scholar 

  21. Lee, H.P.: The dynamic response of a Timoshenko beam subjected to a moving mass. J. Sound Vib. 198(2), 249–256 (1996)

    Article  Google Scholar 

  22. Banerjee, J.R.: Development of an exact dynamic stiffness matrix for free vibration analysis of a twisted Timoshenko beam. J. Sound Vib. 270(1–2), 379–401 (2004)

    Article  MATH  Google Scholar 

  23. Avramidis, I.E., Morfidis, K.: Bending of beams on three-parameter elastic foundation. Int. J. Solids Struct. 43(2), 357–375 (2006)

    Article  MATH  Google Scholar 

  24. Zhu, X.Q., Law, S.S.: Moving forces identification on a multi-span continuous bridge. J. Sound Vib. 228(2), 377–396 (1999)

    Article  Google Scholar 

  25. Lin, H.P., Chang, S.C.: Free vibration analysis of multi-span beams with intermediate flexible constraints. J. Sound Vib. 281(1–2), 155–169 (2005)

    Article  Google Scholar 

  26. Wang, R.T.: Vibration of multi-span Timoshenko beams to a moving force. J. Sound Vib. 207(5), 731–742 (1997)

    Article  MATH  Google Scholar 

  27. Lin, H.Y.: On the natural frequencies and mode shapes of a multi-span Timoshenko beam carrying a number of various concentrated elements. J. Sound Vib. 319(1–2), 593–605 (2009)

    Article  Google Scholar 

  28. Ariaei, A., Ziaei-Rad, S., Ghayour, M.: Transverse vibration of a multiple-Timoshenko beam system with intermediate elastic connections due to a moving load. Arch. Appl. Mech. 81(3), 263–281 (2011)

    Article  MATH  Google Scholar 

  29. Zhang, Z.G., Chen, F., Zhang, Z.Y., Hua, H.X.: Vibration analysis of non-uniform Timoshenko beams coupled with flexible attachments and multiple discontinuities. Int. J. Mech. Sci. 80, 131–143 (2014)

    Article  Google Scholar 

  30. Ferreira, A.J.M.: Free vibration analysis of Timoshenko beams and Mindlin plates by radial basis functions. Int. J. Comput. Methods 2(1), 15–31 (2005)

    Article  MATH  Google Scholar 

  31. Ferreira, A.J.M., Castro, L.M.S., Bertoluzza, S.: A high order collocation method for the static and vibration analysis of composite plates using a first-order theory. Compos. Struct. 89(3), 424–432 (2009)

    Article  Google Scholar 

  32. Yildirim, V., Kiral, E.: Investigation of the rotary inertia and shear deformation effects on the out-of-plane bending and torsional natural frequencies of laminated beams. Compos. Struct. 49(3), 313–320 (2000)

    Article  Google Scholar 

  33. Pradhan, K.K., Chakraverty, S.: Free vibration of Euler and Timoshenko functionally graded beams by Rayleigh–Ritz method. Compos. B 51, 175–184 (2013)

    Article  Google Scholar 

  34. Zhou, D., Cheung, Y.K., Lo, S.H., Au, F.T.K.: Three-dimensional vibration analysis of prisms with isosceles triangular cross-section. Arch. Appl. Mech. 80(6), 699–710 (2010)

    Article  MATH  Google Scholar 

  35. Giunta, G., Koutsawa, Y., Belouettar, S., Hu, H.: Static, free vibration and stability analysis of three-dimensional nano-beams by atomistic refined models accounting for surface free energy effect. Int. J. Solids Struct. 50(9), 1460–1472 (2013)

    Article  MATH  Google Scholar 

  36. Hodges, C.H., Woodhouse, J.: Confinement of vibration by one-dimensional disorder, I: theory of ensemble averaging. J. Sound Vib. 130(2), 237–251 (1989)

    Article  Google Scholar 

  37. Pierre, C., Tang, D.M., Dowell, E.H.: Localized vibrations of disordered multi-span beams: theory and experiment. AIAA J. 25(9), 1249–1257 (1987)

    Article  Google Scholar 

  38. Yan, Z.Z., Zhang, C.Z., Wang, Y.S.: Attenuation and localization of bending waves in a periodic/disordered fourfold composite beam. J. Sound Vib. 327(1), 109–120 (2009)

    Article  Google Scholar 

  39. Li, F.M., Song, Z.G.: Vibration analysis and active control of nearly periodic two-span beams with piezoelectric actuator/sensor pairs. Appl. Math. Mech. (Engl. Ed.) 36(3), 279–292 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  40. Song, Z.G., Li, F.M.: Vibration and aeroelastic properties of ordered and disordered two-span panels in supersonic airflow. Int. J. Mech. Sci. 81, 65–72 (2014)

    Article  Google Scholar 

  41. Li, F.M., Wang, Y.S., Hu, C., Huang, W.H.: Localization of elastic waves in periodic rib- stiffened rectangular plates under axial compressive load. J. Sound Vib. 281, 261–273 (2005)

    Article  Google Scholar 

  42. Cowper, G.R.: The shear coefficients in Timoshenko’s beam theory. J. Appl. Mech. ASME 33(2), 335–340 (1966)

    Article  MATH  Google Scholar 

  43. Yesilce, Y., Demirdag, O.: Effect of axial force on free vibration of Timoshenko multi-span beam carrying multiple spring-mass systems. Int. J. Mech. Sci. 50(6), 995–1003 (2008)

    Article  MATH  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China under Grant Nos. 11761131006 and 11572007. Fengming Li is also grateful to the financial support by the Alexander von Humboldt Foundation for his scientific visit at the Chair of Structural Mechanics, University of Siegen, Germany.

Author information

Authors and Affiliations

  1. College of Mechanical Engineering, Beijing University of Technology, Beijing, 100124, China

    Zhao Zhao & Fengming Li

  2. College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin, 150001, China

    Shurui Wen & Fengming Li

  3. Department of Civil Engineering, University of Siegen, 57068, Siegen, Germany

    Fengming Li & Chuanzeng Zhang

Authors
  1. Zhao Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shurui Wen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Fengming Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Chuanzeng Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Shurui Wen or Fengming Li.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, Z., Wen, S., Li, F. et al. Free vibration analysis of multi-span Timoshenko beams using the assumed mode method. Arch Appl Mech 88, 1213–1228 (2018). https://doi.org/10.1007/s00419-018-1368-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-018-1368-8

Keywords

Search

Navigation