Ramsey Numbers and Graph Parameters

Abstract

According to Ramsey’s Theorem, for any natural p and q there is a minimum number R(p, q) such that every graph with at least R(p, q) vertices has either a clique of size p or an independent set of size q. In the present paper, we study Ramsey numbers R(p, q) for graphs in special classes. It is known that for graphs of bounded co-chromatic number Ramsey numbers are upper-bounded by a linear function of p and q. However, the exact values of R(p, q) are known only for classes of graphs of co-chromatic number at most 2. In this paper, we determine the exact values of Ramsey numbers for classes of graphs of co-chromatic number at most 3. It is also known that for classes of graphs of unbounded splitness the value of R(p, q) is lower-bounded by $(p-1)(q-1)+1$. This lower bound coincides with the upper bound for perfect graphs and for all their subclasses of unbounded splitness. We call a class Ramsey-perfect if there is a constant c such that $R(p,q)=(p-1)(q-1)+1$ for all $p,q\ge c$ in this class. In the present paper, we identify a number of Ramsey-perfect classes which are not subclasses of perfect graphs.

1 Introduction

In 1930, a 26 years old British mathematician Frank Plumpton Ramsey proved that “complete disorder is impossible”,¹ implying that for any natural p and q there is a minimum number R(p, q) such that every graph with at least R(p, q) vertices has either a clique of size p or an independent set of size q [10]. And now, nearly 100 years later, what do we know about the values of Ramsey numbers R(p, q)? Except for the trivial cases $p\le 2$ and $q\le 2$, the exact values of R(p, q) are known only for 9 combinations of p and q:

$$\begin{aligned} \begin{array}{lllll} R(3,3)=6,&{} R(3,4)=9, &{} R(3,5)=14, &{} R(3,6)=18, &{} R(3,7)=23\\ R(3,8)=28, &{} R(3,9)=36,&{} R(4,4)=18, &{}R(4,5)=25.&{}\\ \end{array} \end{aligned}$$

Paul Erdős observed that if we want to find the value of R(5, 5), “we should marshal all our computers and all our mathematicians”. However, we can do much better if we restrict ourselves to graphs in specific classes. In particular, for graphs whose vertices can be partitioned into a clique and an independent set, known as split graphs, $R(p,q)=p+q-1$ for all $p,q\ge 3$. Indeed, according to the pigeonhole principle, which itself is a special case of Ramsey’s Theorem, every split graph with $p+q-1$ vertices contains either a clique of size p or an independent set of size q. On the other hand, by creating a matching between a clique of size $p-1$ and an independent set of size $q-1$ we obtain a split graph with $p+q-2$ vertices containing neither a clique of size p nor an independent set of size q, which proves the minimality of the number $R(p,q)=p+q-1$ in the class of split graphs.

To give one more simple example, consider the class of $P_3$-free graphs, i.e. graphs containing no path on 3 vertices as an induced subgraph. Each graph in this class is a disjoint union of cliques, implying (again with the help of the pigeonhole principle) that $R(p,q)=(p-1)(q-1)+1$ in this case.

A common feature of these two classes is that both of them are hereditary, i.e. closed under taking induced subgraphs. On the other hand, there is a fundamental difference between these examples: in the first class the Ramsey numbers are linear (in p and q), while in the second class they grow with a quadratic speed.

Classes of graphs with linear Ramsey numbers have been studied in [1]. This family includes, in particular, classes of graphs of bounded co-chromatic number, where the co-chromatic number of a graph G is the the minimum k such that the vertex set of G can be partitioned into k subsets each of which is either a clique or an independent set. In particular, split graphs are graphs of co-chromatic number at most 2. The same is true for bipartite graphs and the complements of bipartite graphs. It is easy to see that in the class of bipartite graphs $R(p,q)=2q-1$ and in the class of complements of bipartite graphs $R(p,q)=2p-1$ for all $p,q\ge 3$. However, for $k\ge 3$ the exact values of R(p, q) in classes of graphs of co-chromatic number at most k are unknown. We contribute to this topic by determining Ramsey numbers for graphs of co-chromatic number at most 3 in Sect. 3.

In Sect. 4, we turn to classes where Ramsey numbers grow with at least quadratic speed. As we have seen earlier, this family includes the class of $P_3$-free graphs. The role of this class with respect to the speed of Ramsey numbers is critical in the sense that in any proper hereditary subclass of $P_3$-free graphs the Ramsey numbers are linear. The same is true for the complements of $P_3$-free graphs, known as complete multipartite graphs. These two classes, $P_3$-free graphs and complete multipartite graphs, are also critical with respect to a graph parameter known as splitness, which can be defined as follows.

For an integer $k \ge 0$, we say that a graph G is k-split if the vertex set of G can be partitioned into two subsets A and B so that A induces a graph of the clique number at most k, while B induces a graph of the independence number at most k. The splitness of G is the minimum k such that G is k-split. In particular, graphs of splitness at most 1 are precisely the split graphs. More generally, all classes of bounded co-chromatic number have bounded splitness.

In [6], it was shown that the class of $P_3$-free graphs and the class of complete multipartite graphs are the only two minimal hereditary classes of graphs of unbounded splitness. Therefore, in all classes of unbounded splitness the Ramsey numbers satisfy $R(p,q)\ge (p-1)(q-1)+1$. It is interesting that this lower bound matches the upper bound not only for two critical classes, but also for substantially more complex classes. For instance, $R(p,q)=(p-1)(q-1)+1$ in the class of perfect graphs and in any subclass of perfect graphs of unbounded splitness. We call a class Ramsey-perfect if there is a constant c such that $R(p,q)=(p-1)(q-1)+1$ for all $p,q\ge c$ in this class. In Sect. 4, we identify a number of Ramsey-perfect classes which are not subclasses of perfect graphs.

All preliminary information related to the topic of the paper can be found in Sect. 2. Section 5 concludes the paper with some open problems.

2 Preliminaries

All graphs in this paper are simple, i.e. finite, undirected, without loops and multiple edges. The vertex set and the edge set of a graph G are denoted by V(G) and E(G), respectively. The neighbourhood N(v) of a vertex $v\in V(G)$ is the set of vertices adjacent to v, and the degree of v is the size of its neighbourhood. Also, $\Delta (G)$ is the maximum vertex degree in G. In a graph,

• a matching is a subset of edges no two of which share a vertex. The size of a maximum matching in G is denoted $\mu (G)$.

• a clique is a subset of pairwise adjacent vertices. The size of a maximum clique in G is denoted $\omega (G)$.

• an independent set is a subset of pairwise non-adjacent vertices. The size of a maximum independent set in G is denoted $\alpha (G)$.

An induced subgraph of a graph G is a graph obtained from G by deleting some (possibly none) vertices. We say that G contains a graph H if H is isomorphic to an induced subgraph of G, and we say that G is H-free if G does not contain H.

A graph G is 3-colourable if the vertex set of G can be partitioned into 3 independent sets, also known as colour classes or simply parts. A complete 3-partite graph is a 3-colourable graph in which any two vertices in different colour classes are adjacent.

As usual, $K_n$, $C_n$ and $P_n$ stand for the complete graph, cycle and path with n vertices, respectively. By $K_{n,m}$ we denote the complete bipartite graph, also known as a biclique, with parts of size n and m. For two graphs G and H, we denote by $G+H$ the disjoint union of G and H.

The complement of a graph G is denoted by ${\overline{G}}$. Also, if ${{\mathcal {X}}}$ is a class of graphs, then $\overline{{{\mathcal {X}}}}$ denotes the class of complements of graphs in ${{\mathcal {X}}}$.

A class ${{\mathcal {X}}}$ of graphs is hereditary if $G\in {{\mathcal {X}}}$ implies $H\in {{\mathcal {X}}}$ for every graph H contained in G. It is well-known (and not difficult to see) that a class ${{\mathcal {X}}}$ of graphs is hereditary if and only if ${{\mathcal {X}}}$ can be characterized in terms of minimal forbidden induced subgraphs. In particular, for the class of perfect graphs the set of minimal forbidden induced subgraphs consists of odd cycles of length at least 5 and their complements [5].

The line graph of a graph $G=(V,E)$ is the graph H with $V(H)=E$ in which two vertices are adjacent if and only if the corresponding esges of G share a vertex. The class of line graphs is hereditary and the list of minimal forbidden induced subgraphs for this class consists of $K_{1,3}$ and 8 other graphs, each of which contains $K_4-e$, i.e. the graph obtained from $K_4$ by deleting an edge [3].

Given a class ${{\mathcal {X}}}$ of graphs, we denote by $R_{{{\mathcal {X}}}}(p,q)$ the Ramsey number restricted to graphs in the class ${{\mathcal {X}}}$, i.e. $R_{{{\mathcal {X}}}}(p,q)$ is the minimum number of vertices that guarantees the presence of a clique of size p or an independent set of size q for any graph in the class ${{\mathcal {X}}}$. Clearly, for any class ${{\mathcal {X}}}$, $R_{{{\mathcal {X}}}}(p,q)\le R(p,q)$.

3 Graphs of Co-chromatic Number at Most 3

Throughout this section we denote by ${{\mathcal {A}}}$ the class of 3-colourable graphs and by ${{\mathcal {B}}}$ the class of graphs partitionable into two independent sets and one clique. Any graph of co-chromatic number at most 3 belongs either to ${{\mathcal {A}}}$ or to ${{\mathcal {B}}}$ or to $\overline{{{\mathcal {A}}}}$ or to $\overline{{{\mathcal {B}}}}$. We determine Ramsey numbers for classes ${{\mathcal {A}}}$ and ${{\mathcal {B}}}$. For the remaining two classes, the result follows by complementary arguments.

Theorem 1

For any $p\ge 3$ and $q\ge 3$,

$$\begin{aligned} R_{{{\mathcal {A}}}}(p,q)=3q-2, \end{aligned}$$

unless $p=q=3$, in which case $R_{{{\mathcal {A}}}}(p,q)=6$, and $p=3$, $q=4$, in which case $R_{{{\mathcal {A}}}}(p,q)=9$.

Proof

We start with two isolated cases. Since the cycle $C_5$ is 3-colourable and contains neither $K_3$ nor ${\overline{K}}_3$, we have $R_{{{\mathcal {A}}}}(3,3)> 5$. On the other hand, $R_{{{\mathcal {A}}}}(3,3)\le R(3,3)=6$, and hence $R_{{{\mathcal {A}}}}(3,3)=6$.

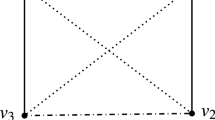
The graph in Fig. 1 is 3-colourable (the labels of the vertices are the colours) and contains neither $K_3$ nor ${\overline{K}}_4$, implying that $R_{{{\mathcal {A}}}}(3,4)> 8$. On the other hand, $R_{{{\mathcal {A}}}}(3,4)\le R(3,4)=9$, and hence $R_{{{\mathcal {A}}}}(3,4)=9$.

Fig. 1

3-colourable $(K_3,{\overline{K}}_4)$-free graph on 8 vertices

For the remaining cases, we first observe that $R_{{{\mathcal {A}}}}(p,q)\le 3q-2$, because any 3-colourable graph with at least $3q-2$ vertices contains an independent set (a colour class) of size at least q. To prove the inverse inequality, we distinguish between $p=3$ and $p\ge 4$.

If $p\ge 4$, then the complete 3-partite graph with parts of size $q-1$ provides an example of a 3-colourable graph with $3q-3$ vertices containing neither a clique of size $p\ge 4$ nor an independent set of size q, implying that $R_{{{\mathcal {A}}}}(p,q)=3q-2$ in this case.

From now on, $p=3$. To prove the result in this case, we construct a graph G with $3q-3$ vertices containing neither a clique of size 3 nor an independent set of size q. The construction depends on the parity of q.

Let $q\ge 5$ be odd. We start with two disjoint cycles of length $l=3(q-1)/2$. Since l is a multiple of 3, each cycle admits a 3-coloring with colour classes of equal size, i.e. of size $(q-1)/2$. Then we connect

• (1) Each vertex of colour 1 in the first cycle to each vertex of colour 2 in the second cycle,

• (2) Each vertex of colour 2 in the first cycle to each vertex of colour 3 in the second cycle,

• (3) Each vertex of colour 3 in the first cycle to each vertex of colour 1 in the second cycle.

Clearly, after performing steps (1), (2), (3) the graph remains $K_3$-free and the assignment of colours remains a valid 3-colouring. It remains to show that in the graph G constructed in this way every independent set A has size at most $q-1$.

If A contains at most $(q-1)/2$ vertices in each of the cycles, then $|A|\le q-1$. Now assume A contains more than $(q-1)/2$ vertices in one of the cycles. Since between any two colour classes of the cycle there is a matching of size $(q-1)/2$, and A contains at most one vertex in each edge of the matching, we conclude that A contains vertices of all three colours in the cycle. Therefore, A is disjoint from the other cycle, and hence, $|A|\le \lfloor l/2\rfloor = \lfloor 3(q-1)/4 \rfloor \le q-1$.

Now let $q\ge 5$ be even. In this case, the construction is similar, but this time we start with two disjoint cycles of different lengths: a cycle $C^1$ of length 3q/2 and a cycle $C^2$ of length $3q/2-3$. Since the length of each of the cycles is a multiple of 3, we conclude that $C^1$ admits a 3-colouring with colour classes of size q/2, and $C^2$ admits a 3-colouring with colour classes of size $q/2-1$. Then we perform steps (1), (2), (3), obtaining in this way a 3-colourable graph G containing no $K_3$. Let A be an independent set in G.

If A contains more than q/2 vertices in $C^1$, then it must contain vertices of all three colours in $C^1$ (because there is a matching of size q/2 between any two colour classes), in which case A is disjoint from $C^2$, and therefore, $|A|\le \lfloor 3q/4 \rfloor \le q-1$. Similarly, if A contains more than $q/2-1$ vertices in $C^2$, then $|A|\le q-1$. Finally, if A contains at most q/2 vertices in $C^1$ and at most $q/2-1$ vertices in $C^2$, then $|A|\le q-1$. $\square$

Corollary 1

For any $p\ge 3$ and $q\ge 3$,

$$\begin{aligned} R_{\overline{{{\mathcal {A}}}}}(p,q)=3p-2, \end{aligned}$$

unless $p=q=3$, in which case $R_{\overline{{{\mathcal {A}}}}}(p,q)=6$, and $p=3$, $q=4$, in which case $R_{\overline{{{\mathcal {A}}}}}(p,q)=9$.

Theorem 2

For any $p\ge 3$ and $q\ge 3$,

$$\begin{aligned} R_{{{\mathcal {B}}}}(p,q)=p+2q-2, \end{aligned}$$

unless $p=q=3$, in which case $R_{{{\mathcal {B}}}}(p,q)=6$.

Proof

The cycle $C_5$ belongs to ${{\mathcal {B}}}$ and hence $R_{{{\mathcal {B}}}}(3,3)>5$. Together with $R_{{{\mathcal {B}}}}(3,3)\le R(3,3)=6$ this proves the result for $p=q=3$. In what follows, we assume that at least one of p and q is greater than 3.

If a graph in the class ${{\mathcal {B}}}$ has at least $p+2q-2$ vertices, then it necessarily has either a clique of size p or an independent set of size q. Therefore, $R_{{{\mathcal {B}}}}(p,q)\le p+2q-2$.

For the inverse inequality, we construct a graph G with $p+2q-3$ vertices containing neither a clique of size p nor an independent set of size q. The construction depends on p and q.

If $p=q$, then we start with two independent sets A and B and a clique C with $|A|=|B|=|C|=p-1$. Then we create a biclique between A and B, a matching between A and C, and a matching between B and C. Taking into account that $p=q\ge 4$, it is not difficult to conclude that this graph has no cliques of size p or independent set of size q.

If $p\ne q$, then similarly we start with two independent sets $A=\{a_1,\ldots ,a_{q-1}\}$ and $B=\{b_1,\ldots ,b_{q-1}\}$ and a clique $C=\{c_1,\ldots ,c_{p-1}\}$, and create a biclique between A and B. But this time we need to be careful about the edges between C and $A\cup B$ to avoid cliques of size p and independent sets of size q.

If $p>q$, then we partition C arbitrarily into $q-1$ non-empty disjoint subsets $C^1,\ldots , C^{q-1}$, each of size at most $p-3$, which is always possible for $p\ge 5$ and $q\ge 3$ (the case $p=4,q=3$ will be analyzed later). Then for each $i=1,\ldots ,q-1$ we connect vertices $a_i$ and $b_i$ to the vertices of $C^i$. Since A dominates the graph and B dominates the graph, there is no independent set of size q in G. Now let U be a maximum clique in G. Clearly, U contains at most one vertex in A and at most one vertex in B. If $U\cap A=\emptyset$ or $U\cap B=\emptyset$, then $|U|\le p-1$, which is not difficult to see. If U contains a vertex in A and a vertex in B, their common neighbourhood in C contains at most $p-3$ vertices by construction and hence $|U|\le p-1$. For the remaining case $p=4,q=3$, we modify the construction as follows: we connect $a_1$ to $c_1$ and $c_2$, we connect $a_2$ to $c_3$, we connect $b_1$ to $c_1$, and we connect $b_2$ to $c_2$ and $c_3$. It is not difficult to check that this construction has no cliques of size 4 or independent sets of size 3.

If $q>p$, then for each $i=1,\ldots p-1$ we connect vertex $c_i$ to vertices $a_i$ and $b_i$. Again, since A dominates the graph and B dominates the graph, there is no independent set of size q in G. Also, since every vertex of A and every vertex of B has at most one neighbour in C, there is no clique of size p in G, unless $p=3$. In the latter case, we modify the construction by deleting the edges $a_1b_1$ and $a_2b_2$. It is easy to see that the graph G constructed in this way contains no triangles. Also, if W is an independent set containing a vertex in $\{a_3,\ldots ,a_{q-1}\}$, then it contains no vertex in B, in which case $|W|\le q-1$. Similarly, if W contains a vertex in $\{b_3,\ldots ,b_{q-1}\}$, then $|W|\le q-1$. Finally, if W has no vertices in $\{a_3,\ldots ,a_{q-1}\}$ and $\{b_3,\ldots ,b_{q-1}\}$, then $|W|\le 3\le q-1$ (since $q>3$). $\square$

Corollary 2

For any $p\ge 3$ and $q\ge 3$,

$$\begin{aligned} R_{\overline{\mathcal{B}}}(p,q)=2p+q-2, \end{aligned}$$

unless $p=q=3$, in which case $R_{\overline{\mathcal{B}}}(p,q)=6$.

4 Classes of Graphs of Unbounded Splitness

According to [6], every hereditary class ${{\mathcal {X}}}$ of unbounded splitness contains either all $P_3$-free graphs or all complete multipartite graphs, in which case $R_{{{\mathcal {X}}}}(p,q)\ge (p-1)(q-1)+1$. For perfect graphs, this lower bound coincides with the upper bound, because if a perfect graph contains $(p-1)(q-1)+1$ vertices and no clique of size p, then the chromatic number of the graph is at most $p-1$ and hence it contains an independent set (a colour class) of size q.

In this section, we study classes ${{\mathcal {X}}}$ of graphs for which $R_{{{\mathcal {X}}}}(p,q)=(p-1)(q-1)+1$ for “many” values of p and q. In particular, we say that a class ${{\mathcal {X}}}$ is Ramsey-perfect if $R_{{{\mathcal {X}}}}(p,q)=(p-1)(q-1)+1$ for all sufficiently large p, q, i.e. for $p,q\ge c$ for a constant c. Some Ramsey-perfect classes of graphs, which are not subclasses of perfect graphs, are identified in Sect. 4.1. Also, we say that a class ${{\mathcal {X}}}$ is Ramsey-good if $R_{{{\mathcal {X}}}}(p,q)=(p-1)(q-1)+1$ for infinitely many values of p and q and ${{\mathcal {X}}}$ is not Ramsey-perfect. One such class is identified in Sect. 4.2. All classes in the present section are defined by forbidding induced subgraphs with 4 vertices. The list of all 4-vertex graphs is represented in Fig. 2.

Fig. 2

All 4-vertex graphs

4.1 Ramsey-perfect Classes

Obviously, any class of graphs of unbounded splitness containing finitely many non-perfect graphs is Ramsey-perfect. The following result gives two examples of such classes.

Theorem 3

If ${{\mathcal {X}}}$ is the class of (paw, co-paw)-free graphs or the class of (paw, co-diamond)-free graphs, then for all $p,q\ge 3$,

$$\begin{aligned} R_{{{\mathcal {X}}}}(p,q)= (p-1)(q-1)+1, \end{aligned}$$

unless $p=q=3$, in which case $R_{{{\mathcal {X}}}}(p,q)=6$.

Proof

The class ${{\mathcal {X}}}$ contains all complete multipartite graphs, and hence $R_{{{\mathcal {X}}}}(p,q)\ge (p-1)(q-1)+1$.

For $p=q=3$, we have $R_{{{\mathcal {X}}}}(p,q)=6$, because $C_5$ belongs to ${{\mathcal {X}}}$. By direct inspection, it is easy to check that if a graph G in ${{\mathcal {X}}}$ contains a $C_5$, then $G=C_5$. On the other hand, every cycle of odd length at least 7 contains a co-paw and a co-diamond, and the complement of every cycle of odd length at least 7 contains a paw. Therefore, $C_5$ is the only non-perfect graph in ${{\mathcal {X}}}$. As a result, $R_{{{\mathcal {X}}}}(p,q)=(p-1)(q-1)+1$ for all $p,q\ge 3$, except for the case $p=q=3$. $\square$

The following two results deal with Ramsey-perfect classes containing infinitely many non-perfect graphs.

Theorem 4

If ${{\mathcal {X}}}$ is the class of (paw, 2K2)-free graphs, then

$$\begin{aligned} R_{{{\mathcal {X}}}}(p,q)= & {} (p-1)(q-1)+1 \text{ for } p\ge 4, q\ge 3,\\ R_{{{\mathcal {X}}}}(p,q)= & {} \lfloor 2.5(q-1)\rfloor +1 \ \ \text{ for } p=3, q\ge 3. \end{aligned}$$

Proof

Since $2K_2$ is forbidden, no graph in ${{\mathcal {X}}}$ contains a cycle of odd length at least 7, and since paw is forbidden, no graph in ${{\mathcal {X}}}$ contains the complement of a cycle of odd length at least 7. Therefore, if a graph $G\in {{\mathcal {X}}}$ is non-perfect, it contains a $C_5$. In order to characterize non-perfect graphs in ${{\mathcal {X}}}$, let us say that $G^*$ is an extended G (also known as a blow-up of G) if $G^*$ is obtained from G by replacing the vertices of G with independent sets.

Let $S=\{v_0,v_1,v_2,v_3,v_4\}$ induce a $C_5$ in $G\in {{\mathcal {X}}}$. To avoid an induced $2K_2$ or paw, any vertex $u\not \in S$ must have either no neighbours in S or exactly two neighbours on the cycle, which are of distance 2 from each other, i.e. $N(u)\cap S=\{v_i,v_{i+2}\}$ for some i (addition is taken modulo 5). Moreover, if $N(u)\cap S=\{v_i,v_{i+2}\}$ and $N(w)\cap S=\{v_j,v_{j+2}\}$, then

• if $i=j$ or $|i-j|>1$, then u is not adjacent to w, since G is paw-free,

• if $|i-j|=1$, then u is adjacent to w, since G is $2K_2$-free.

Also, since G is $2K_2$-free, every vertex $u\not \in S$, which has no neighbours in S, is isolated. Summarizing we conclude that G is an extended $C_5+K_1$.

Let ${{{\mathcal {X}}}}_0$ be the set of perfect graphs in ${{\mathcal {X}}}$, and let ${{{\mathcal {X}}}}_1$ be the set of non-perfect graphs in ${{\mathcal {X}}}$. Since ${{{\mathcal {X}}}}_0$ contains all complete multipartite graphs, we have $R_{{{{\mathcal {X}}}}_0}(p,q)=(p-1)(q-1)+1$.

Now we turn to graphs in ${{{\mathcal {X}}}}_1$, i.e. graphs each of which is an extended $C_5+K_1$. For an odd q, a maximum counterexample, i.e. a $(K_p,{\overline{K}}_q)$-free graph in ${{{\mathcal {X}}}}_1$ with the maximum number of vertices, is constructed from a $C_5$ by replacing each vertex with an independent set of size $(q-1)/2$. This graph has $\lfloor 2.5(q-1)\rfloor$ vertices, the independence number $q-1$ and the clique number $2<p$. For an even q, a maximum counterexample is constructed from a $C_5$ by replacing two adjacent vertices of a $C_5$ with independent sets of size q/2 and the remaining vertices of the cycle with independent sets of size $q/2-1$. This again gives in total $\lfloor 2.5(q-1)\rfloor$ vertices, and a maximum independence set of size $q-1$. By adding any vertex to any of these two constructions we obtain a graph with an independent set of size q. Therefore, $R_{\mathcal{X}_1}(p,q)=\lfloor 2.5(q-1)\rfloor +1$ for all $p,q\ge 3$.

It is not difficult to see that $R_{{{{\mathcal {X}}}}_1}(p,q)>R_{\mathcal{X}_0}(p,q)$ for $p=3$, and $R_{{{{\mathcal {X}}}}_1}(p,q)<R_{{{{\mathcal {X}}}}_0}(p,q)$ for $p\ge 4$. Hence, the result. $\square$

Theorem 5

If ${{\mathcal {X}}}$ is the class of (paw, claw)-free graphs, then

$$\begin{aligned} R_{{{\mathcal {X}}}}(p,q)= & {} (p-1)(q-1)+1 \text{ for } p\ge 4, q\ge 3,\\ R_{{{\mathcal {X}}}}(p,q)= & {} \lfloor 2.5(q-1)\rfloor +1 \ \ \text{ for } p=3, q\ge 3. \end{aligned}$$

Proof

According to [8], every connected graph in ${{{\mathcal {X}}}}$ is either $K_3$-free or a complete multipartite graph. Taking into account that graphs in ${{{\mathcal {X}}}}$ are claw-free, we conclude that every $K_3$-free graph in this class has vertex degree at most 2, and that in every complete multipartite graph in ${{\mathcal {X}}}$ all parts (colour classes) have size at most 2.

Since all $P_3$-free graphs belong to ${{\mathcal {X}}}$, we have $R_\mathcal{X}(p,q)\ge (p-1)(q-1)+1$. We claim that for $p\ge 4$, $R_\mathcal{X}(p,q)\le (p-1)(q-1)+1$. Indeed, let G be a $(K_p,{\overline{K}}_q)$-free graph in ${{\mathcal {X}}}$ with maximum number of vertices. If every connected component of G is a clique, then G is a disjoint union of $q-1$ cliques, each of size $p-1$. Now we show that by replacing some components of G by a non-complete connected graph H we cannot increase the number of vertices without avoiding $K_p$ or ${\overline{K}}_q$. To see this, notice that since H is non-complete, we need to replace at least $\alpha (H)$ components of G by H to avoid a ${\overline{K}}_q$. If H is a complete multipartite graph with parts of size at most 2, then, unless H contains a clique of size p, $|V(H)|\le 2(p-1)$ and by replacing two components of G by H we do not increase the number of vertices. If H is a path or a cycle with $\alpha (H)=k$, then the number of vertices in H is at most $2k+1$, which, for $p\ge 4$ and $k\ge 2$, is less than the number $k(p-1)$ of vertices in k components of G.

To determine $R_{{{\mathcal {X}}}}(p,q)$ for $p=3$, we may restrict ourselves to $K_3$-free graphs in ${{\mathcal {X}}}$, i.e to the class ${{{\mathcal {X}}}}_1$ of graphs every connected component of which is either a path or a cycle, different from $K_3$. For this class, the Ramsey numbers have been determined in [4, 7]: $R_{{{{\mathcal {X}}}}_1}(p,q)=\lfloor 2.5(q-1)\rfloor +1$. $\square$

4.2 Claw- and Diamond-free Graphs

In [4], the authors find Ramsey numbers for the class of line graphs. In this class, $R(p,q)> (p-1)(q-1)+1$ for all $p,q\ge 3$. In the present section, we deal with a proper subclass of line graphs defined by forbidding a claw and a diamond, and show that this class is Ramsey-good. Throughout the section we denote the class of (claw,diamond)-free graphs by ${{\mathcal {C}}}$ and start with the following characterization of the set of graphs whose line graphs belong to ${{\mathcal {C}}}$.

Lemma 1

Let H be the line graph of a graph G. Then H is (claw,diamond)-free if and only if every connected component of G is either a triangle or triangle-free.

Proof

Assume first that H is (claw,diamond)-free and suppose G contains a triangle a, b, c. If G is different from the triangle and connected, there must exist a vertex $x\not \in \{a,b,c\}$, which has a neighbour in $\{a,b,c\}$, say x is adjacent to a. Then the line graph of G induced by the vertices ab, ac, bc, ax is a diamond. This contradiction shows that if G contains a triangle and is connected, then it coincides with the triangle.

Conversely, let G be a graph every connected component of which is either a triangle or triangle-free. Since H is the line graph, it is claw-free. Suppose now that H contains a diamond induced by vertices a, b, c, d. Then in G the edges a, b, c, d form a 4-vertex connected graph containing a triangle. This contradiction completes the proof. $\square$

Lemma 2

Let G be a connected graph and let H be the line graph of G. Then

$$\begin{aligned} \omega (H)=\Delta (G) \text{ and } \alpha (H)=\mu (G), \end{aligned}$$

except for $G=K_3$, in which case $\omega (H)=3$, while $\Delta (G)=2$.

Proof

The equality $\alpha (H)=\mu (G)$ is obvious and follows from the definition of line graph.

Also, from the definition of line graph it follows that $\omega (H)\ge \Delta (G)$. For the inverse inequality, assume H contains a clique with at least 4 vertices. Let F be the set of edges of G corresponding to the vertices of that clique. Any two edges of F share a vertex. Consider any two of them, say ab and ac, and assume that there is an edge in F that does not share vertex a. Then it must be bc (to share a vertex with both ab and ac). Since F has at least 4 edges, there must be an edge sharing a vertex with each of ab, bc and ac, which is impossible. This contradiction shows that all edges of F share vertex a and hence if $\omega (H)\ge 4$, then $\omega (H)\le \Delta (G)$.

Assume now $\omega (H)=3$. If $\Delta (G)\le 2$, then G is either a path or a cycle, due to connectivity. For H to have a clique of size 3, G must be $C_3=K_3$.

For the case $\omega (H)\le 2$, the inequality $\omega (H)\le \Delta (G)$ is trivial. $\square$

Consider the graph G obtained from $K_{p-1,p-1}$ with $p\ge 3$ by deleting an edge, say xy, and adding a new vertex adjacent to x and y only. Clearly, G is triangle-free, $\Delta (G)=p-1$, $\mu (G)=p-1$ and $|E(G)|=(p-1)^2+1$. From Lemmas 1 and 2 we know that the line graph H of G is (claw,diamond)-free, $\omega (H)=p-1$, $\alpha (H)=p-1$, and by definition, H has $(p-1)^2+1$ vertices. Therefore, for the class ${{\mathcal {C}}}$ of (claw,diamond)-free graphs, $R_\mathcal{C}(p,p)>(p-1)(p-1)+1$ for all values of $p\ge 3$, showing that $\mathcal C$ cannot be Ramsey-perfect. To prove that ${{\mathcal {C}}}$ is Ramsey-good, we will show that $R_{{{\mathcal {C}}}}(p,q)=(p-1)(q-1)+1$ for all $p>q$. To this end, we prove the following lemma.

Lemma 3

Let G be a graph every connected component of which is either a triangle or triangle-free, and let $d=\Delta (G)$ and $m=\mu (G)$. If $d>m$ and $d\ge 3$, then G has at most dm edges.

Proof

We prove the lemma by induction on the number of triangle components, i.e. components which are triangles. For the induction step, consider a triangle component $K_3$ in G and denote $G'=G-K_3$ (notice that $G'$ is not empty, since $d\ge 3$). Clearly, $\Delta (G)=\Delta (G')$ and $\mu (G')=\mu (G)-1$. Therefore, by inductive assumption, $|E(G')|\le d(m-1)$ and hence $|E(G)|\le d(m-1)+3\le dm$, since $d\ge 3$.

To establish the basis of the induction, assume now that G is $K_3$-free. Let M be a matching of size m and C the subset of vertices not covered by the edges of M. Clearly, C is an independent set, since M is a maximum matching. Also, since G is triangle-free, every vertex of C has at most one neighbour in each edge of the matching M. We denote the edges of M by $a_1b_1,a_2,b_2,\ldots , a_mb_m$, where $a_j$ has no neighbours in C for all j. Also, $A=\{a_1,a_2,\ldots ,a_m\}$ and $B=\{b_1,b_2,\ldots ,b_m\}$.

If G has no edges connecting two vertices of A, then every edge of G is incident to a vertex of B, and since each vertex has degree at most d, the total number of edges is at most dm.

Now assume that G has an edge $a_ia_j$ connecting two vertices of A. One of $b_i$ and $b_j$, say $b_i$ (without loss of generality), has at most one neighbour in C, since otherwise we could choose a neighbour $c\in C$ of $b_i$ and neighbour $c'\in C$ of $b_j$ (different from c), in which case the augmenting path $c,b_i,a_i,a_j,b_j,c'$ arises, contradicting the fact that M is maximum.

• (1) If $b_i$ is adjacent to $b_j$, then we replace the edges $a_ia_j$ and $b_ib_j$ with the edges $a_ib_j$ and $a_jb_i$ (which are absent in G due to its triangle-freeness). Clearly, this transformation does not change the number of edges and the degree of the vertices.

• (2) Now suppose that $b_i$ is not adjacent to $b_j$. Then the degree of $b_i$ is at most $m<d$ (remember that $b_i$ has at most one neighbour in C, according to our assumption, and at most one neighbour in each edge of the matching, due to $K_3$-freeness), and therefore, by replacing the edge $a_ia_j$ with the edge $b_ia_j$ we do not increase $\Delta (G)$ and preserve the number of edges.

Applying (1) or (2) to every edge connecting two vertices of A, we transform G into another graph $G'$ with the same number of edges, in which every edge is incident to a vertex of B and every vertex of B has degree at most d. Therefore, $G'$ has at most dm edges, and hence G has at most dm edges too. $\square$

Theorem 6

For the class ${{\mathcal {C}}}$ of (claw,diamond)-free graphs and all $p>q$,

$$\begin{aligned} R_{{{\mathcal {C}}}}(p,q)=(p-1)(q-1)+1. \end{aligned}$$

Proof

If $p\le 2$ or $q\le 2$, the result is obvious. Therefore, we assume that $p>q\ge 3$.

Consider a (claw,diamond)-free graph H with $\omega (H)=p-1$ and $\alpha (H)=q-1$ and let G be the graph whose line graph is H. Form Lemma 1 we known that every connected component of G is either a triangle or triangle-free.

If $\Delta (G)\ge 3$, then, by Lemma 2, $\omega (H)=\Delta (G)=p-1$ and $\alpha (H)=\mu (G)=q-1$. Therefore, by Lemma 3, G has at most $(p-1)(q-1)$ edges and hence H has at most $(p-1)(q-1)$ vertices.

If $\Delta (G)\le 2$, then every connected component of G is either a cycle or a path. Therefore, every connected component of H is either a cycle or a path, and hence $\omega (H)\le 3$. Since $p>q\ge 3$, we conclude that $\omega (H)=p-1=3$ and hence $\mu (G)=\alpha (H)=q-1=2$. Since $\omega (H)=3$, both H and G contain a triangle component, and since $\mu (G)=2$, in addition to a triangle component, G contains exactly one more component with more than 1 vertex and this component has at most 3 vertices. Therefore, $H=K_3+K_1$ or $H=K_3+K_2$ or $H=K_3+K_3$. In all three cases, H contains at most $(p-1)(q-1)=6$ vertices.

The above discussion shows that if $\omega (H)=p-1$ and $\alpha (H)=q-1$, then the number of vertices of H is at most $(p-1)(q-1)$. In other words, if H has at least $(p-1)(q-1)+1$ vertices, the either $\omega (H)\ge p$ or $\alpha (H)\ge q$. Therefore, $R_{{{\mathcal {C}}}}(p,q)\le (p-1)(q-1)+1$.

For the inverse inequality, observe that the class ${{\mathcal {C}}}$ contains all $P_3$-free graphs and hence $R_{{{\mathcal {C}}}}(p,q)\ge (p-1)(q-1)+1$. $\square$

5 Conclusion

Ramsey numbers have been studied for nearly a century with a very modest success. As is often the case in research, if a problem is too complex to solve it in its whole generality, then particular cases of the problem are analyzed. Ramsey numbers for graph classes is a relatively new area of research. Up to date, the problem was solved for planar graphs [11], for perfect graphs and some of their subclasses, as well as for some subclasses of claw-free graphs [4]. We contributed to this area by determining Ramsey numbers for graphs of co-chromatic number at most 3, and some classes of unbounded splitness. Among open problems we distinguish graphs of co-chromatic number at most k for $k\ge 4$. As a step towards a solution for these graphs, the case of graphs of bounded lettericity is of particularly interest. This notion was introduced in [9], and graphs of bounded lettericity is a special case of graphs of bounded co-chromatic number. Restricted to permutation graphs, this notion is equivalent to geometric griddability of permutations [2].

One more area of interest consists of classes of bounded splitness where co-chromatic number is unbounded, such as $(C_3,C_4,\ldots ,C_k)$-free graphs for a fixed value of k. This area seems to be totally unexploared and most challenging.