1 Introduction

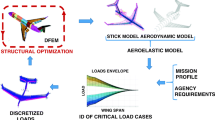
In the aerospace industry, multidisciplinary design optimisation (MDO) is increasingly being used in the preliminary design of aircraft. After a phase known as conceptual design, in which multiple models are taken into account, MDO can be used to advance these concepts in parallel and discard the least promising ones. However the need to limit the computational cost has lead to the use of coarse finite element (FE)-models with limited accuracy, which do not allow the evaluation of constraints of local details with complex geometry. Only the successive detailed modelling of these local “non-regular areas” might reveal a local infeasibility of the found optimal design, which might result in costly delays in the product development cycle.

In the preliminary design of aircraft, coarse FE-models, commonly referred as Global Finite Element Models (GFEMs) [1], are used to capture overall stiffness, global loadpaths and internal loads of large portions of the structure, like a wingbox or even the entire aircraft. The computational cost of using more accurate FE-models in an optimisation procedure would be too high [2]. Thus, GFEMs are used, even if they do not always capture the internal deformation with a sufficient level of detail. This may lead to unfeasible detail designs of some parts or to over-conservative suboptimal designs [3]. This is particularly true for “non-regular areas” [4], i.e. components like stinger run-outs, manholes and bulkheads.

To mitigate the problem, these parts are conservatively designed beforehand and kept fixed during the optimisation. Whenever this strategy fails to find a feasible solution, designers face a challenge to devise optimal solutions without violating design constraints. Modifications to the design of these components are necessary, which in the best case lead to a sub-optimal solution. But since these modifications can significantly alter the global loadpaths, constraint violations are likely propagated and designers may be forced to modify the surrounding parts or to repeat the global optimisation, leading to a long iteration process and costly delays [5,6,7].

A possible solution to this problem is to consider the design of these “non-regular areas” during global optimisation. A simple way of coupling a global analysis and a local analysis, based on a refined model, is to enforce the solution at interface. In the context of displacement based FE-analyses, this coupling is known as Specified Boundary Displacements (SBD). It can be enforced via a master–slave elimination procedure [8] or using a Lagrange multipliers formulation [9]. It is also possible to develop an iterative procedure to apply a global solution at the boundary of a local model and use the local solution to correct the global results, as in [10,11,12]. When combined with an interpolation of the solution fields, this approach can be used with non-conforming meshes [13] and to couple solution fields obtained with different numerical methods [14].

Another famous approach is static condensation [15], also known as substructuring. In this case, the stiffness of one model is condensed, by computing the Schur complement of its stiffness matrix, and used for the solution of the other model. In the case of a static analysis, this results in an exact procedure.

A third coupling strategy, known as specified boundary stiffness/force (SBSF) and introduced in [16], combines SBD and static condensation, effectively specifying the solution further from the interface and condensing the part of the structure in-between.

Strategies have also been developed to efficiently update a coarse solution with a more detailed analysis as in [17, 18].

Despite the variety of global–local analysis strategies available, the global–local optimisation approaches are often based on a standard FE-analysis. Instead of integrating a global–local approach in the optimisation, the usual approach is to split the optimisation problem in two or more levels [19, 20]. The coupling between the two optimisation problems is realised by decomposing the optimisation problem itself [21], by alternating between global and local optimisations [22] or by nesting the local optimisation in each iteration of the global procedure [23,24,25,26,27,28,29]. The coupling can also be relaxed by using response surfaces to coordinate two procedures running in parallel [30].

These methods are attractive in terms of computational cost, as they limit the size of both the analysis and the optimisation problems considered. Therefore they can be used to effectively exploit additional local design freedom at an acceptable computational cost, using gradient based as well as gradient free optimisation methods. Nevertheless, they are limited by the need to effectively couple the different levels, which can be challenging when local areas have a dramatic effect on the global loadpaths.

An exception to two-level optimization, in which global–local analysis is actually integrated in the optimisation procedure can be found in [31, 32]. The authors present an optimisation procedure, in which the analysis is solved using superelements to capture local behaviour. In this paper, to address the shortcomings of two-level approaches, we propose a similar methodology for the preliminary sizing of aircraft structures, which ensures that the design of “non-regular areas” is feasible. Contrary to the strategies presented in [31, 32], our methodology does not require the complete partition in substructures of the whole structure and is based on coupled global–local semi-analytical sensitivities. Our global–local MDO procedure is based on the use of separate FE-model for the local details to allow the accurate evaluation of local constraints. The global–local analysis methodology, based on Guyan condensation and SBD, was complemented with a novel derivation of the implied sensitivity analysis formulation, based on a semi-analytic computation of the sensitivities. Since for the specific problem of “non-regular areas” the focus is on local feasibility, rather than the exploitation of additional local design freedom, the presented approach is based on monolithic architecture, in contrast with common two-level optimization approaches. Furthermore, we present a case study, in which we compare the proposed methodology with current industry practice and highlight the inadequacies of the standard approach.

In Sect. 2, we present an integrated monolithic global–local multidisciplinary optimisation approach, based on static condensation, with a coupled global–local sensitivity analysis, in agreement with the formulation described by Sobieski et al. [33, 34]. This relies on semi-analytical sensitivities, which is crucial for accuracy and cost-effectiveness [35, 36]. We implement this using Lagrange [37, 38], an in-house software developed by Airbus, which provides access to the required sensitivities. Nevertheless, the same approach could be implemented with other tools provided that sensitivities are computed. In Sect. 3, we discuss some implementation aspects and the verification examples. In Sect. 4, we present a simple example in which global optimisation and subsequent modifications of the local design alter the loadpaths enough to cause the violation of global constraints, despite an initially conservative local design. We then prove the effectiveness of the presented methodology in finding a feasible optimal design. Lastly, our conclusions are summarised in Sect. 5.

2 Methodology

To address the challenge of insufficient level of detail in the GFEM for the early stage MDO, in our paper, we adopt a global–local design approach. In the following, a global–local multidisciplinary optimisation procedure is presented.

2.1 Problem statement and proposed MDO architecture

2.1.1 Optimisation problem

The underlying optimisation problem has the standard form:

$$\begin{aligned} \left\{ \begin{array}{ll} \text {find} &{} {{\,\textrm{argmin}\,}}_{{t}} {f}({t}) \\ \text {such that} &{} {g}({t}, {u}({t})) \ge 0 \end{array} \right. \end{aligned}$$
(1)

where \({f}\) is a functional to be minimised, \({g}\) are the constraints, \({t}\) are the design variables and \({u}\) is the solution of a multidisciplinary global–local analysis.

2.1.2 Disciplines considered

The term multidisciplinary refers to the fact that several different disciplines will be considered [39,40,41,42]. Within the scope of this paper we consider two disciples:

  1. 1.

    linear static analysis, and

  2. 2.

    static aeroelastic analysis.

These analyses are not coupled and can be solved independently. Furthermore, for a given model multiple subcases will usually be considered, i.e. the model will in general be subject to different loadcases and boundary conditions to be separately solved. The solution to each subcase \(u_i\), which might be the result either of a linear static analysis or of a static aeroelastic analysis, will affect different constraints \({g}({t}, {u}({t}))\).

Therefore, by \({u}\) we denote

$$\begin{aligned} {u}= \begin{bmatrix} {u}_1 \\ {u}_2 \\ \vdots \\ {u}_n \end{bmatrix} \end{aligned}$$
(2)

where each \({u}_i\) is the solution of a different subcase, corresponding to either one of the specified disciplines above.

2.1.3 Global–local modelling

The term global–local refers to the fact that the structure is modelled using multiple FE models, as it will be described in Sect. 2.2. Because of the subdivision in multiple models the solution of the analyses and the computation of the sensitivities require a special formulation detailed in Sects. 2.3 and 2.4.

2.1.4 Global–local MDO architecture

The approach is based on a monolithic multidisciplinary feasible architecture, therefore it is implemented as one optimisation procedure. In each optimisation iteration, the multidisciplinary global–local analysis is solved for \({u}\), the responses \({f}\) and \({g}\) are evaluated and the sensitivities \(\dfrac{\textrm{d} {f}}{\textrm{d} {t}}\), \(\dfrac{\textrm{d} {g}}{\textrm{d} {t}}\) are computed.

If the convergence criteria are not met, the optimiser uses the gradients \(\dfrac{\textrm{d} {f}}{\textrm{d} {t}}\), \(\dfrac{\textrm{d} {g}}{\textrm{d} {t}}\) to compute the design update and the procedure is repeated, as depicted in Fig. 1.

Fig. 1
figure 1

The proposed global–local MDO procedure is based on a monolithic architecture

Full size image

2.2 Modelling assumptions

In our approach we assume that the structure to be analysed requires two different levels of detail. For most of the structure a coarse modelling is deemed sufficient, while instead some parts of the model require a detailed representation of the geometry and a finer mesh. The structure is therefore represented with multiple models: one global model, which represents most of the structure using a coarse mesh, and multiple local models, used to represent detailed parts with a finer mesh. However, without loss of generality, in this paper we consider the case with only one local model. The global solution field \({u}{^{G}}\) can be partitioned in global internal solution \({z}\), and solution at the global interface \({i}\), while the local solution field \({u}{^{L}}\) is partitioned in local internal solution \({o}\), and solution at the local interface \({a}\).

We also assume that the structure is modelled following three main assumptions: (1) non-overlapping domains, (2) no local-local interfaces, and (3) conforming interfaces.

According to assumption (1) the global and local models do not overlap, so that no part of the structure is modelled twice. Hence the structure is partitioned in multiple models.

Based on the assumption (2) each local model is interfaced only with the global one, so that no local to local interfaces exist, as represented in Fig 2.

Fig. 2
figure 2

The proposed global–local MDO procedure relies on non-overlapping global–local models without local-local interfaces

Full size image

Lastly, according to assumption (3), the interface between global and local models is conforming. In practice, this means that for each FE-node at the interface of the global model, there is a matching FE-node at the interface of the local model, as represented in Fig 3. Whenever this is not the case, as long as global and local model share an interface with the same geometry, the proposed approach can still be applied, by connecting non-matching meshes using connecting elements, such as RBE2 and RBE3 elements in NASTRAN notation.

Fig. 3
figure 3

The proposed global–local MDO procedure relies on conforming interfaces. Non-matching meshes can be adapted using connecting elements like RBE2 and RBE3

Full size image

Since global and local degrees of freedom (DOFs) match, a solution field \({u}\) on the interface, defined by the global DOFs \({i}\), is represented on the local mesh by the same vector of local DOFs. The coupling at the boundary is formulated by simply matching the DOFs:

$$\begin{aligned} {i}= {a} \end{aligned}$$
(3)

therefore the mapping between \({i}\) and \({a}\) is the identity matrix.

Fig. 4
figure 4

Modelling of a structure as a single FE-model (above) and using a global and a local model (below), respectively highlighted in blue and yellow

Full size image

When considering a static aeroelasticity subcase, we will assume that it is sufficient to only interface the global degrees of freedom with the aeroelastic forces, while the local models deform as in a static analysis subcase. This is coherent with the reference procedure, in which the local model does not exist and the aeroelastic loads are injected at the global nodes.

We further assume that each design variable can be uniquely assigned to either the global or the local model. Therefore a design variable cannot be part of the global and the local model at the same time.

2.3 Global–local analysis

A global–local analysis methodology suitable for the evaluation of constraints on “non-regular areas” was developed. In the case of a linear static analysis, as well as in the case of a static aeroelastic analysis at global level, the global solution accounts for detailed local information thanks to the Guyan condensation of the non-regular areas [15]. By applying SBD [8, 9], the global solution is then used as boundary condition for the solution of a local static analysis. This approach has the advantage to only solve a static analysis of the local model, which is deemed sufficient for the evaluation of local constraints, regardless of the global subcase. Moreover, since the local condensation must not be recomputed, whenever the local design variables are not modified, this strategy allows to further contain the computational cost. For all cases, in which accurate local models are needed not for the purpose of exploiting additional design freedom, but to avoid local infeasibility at a comparable computational cost, we consider the suggested approach to be more appropriate then the two-level optimization approaches commonly found in the literature.

2.3.1 Discrete equations for static analysis

In the case of a static analysis subcase, the discrete equation is:

$$\begin{aligned} \begin{bmatrix} {K}\end{bmatrix} \begin{bmatrix} {u}\end{bmatrix} = \begin{bmatrix} {p}\end{bmatrix} \end{aligned}$$
(4)

where \({K}\) is the stiffness matrix, \({p}\) is the load vector and \({u}\) is the vector of nodal displacements.

This holds for both the global:

$$\begin{aligned} \begin{bmatrix} {K_{zz}}&{} {K_{zi}}\\ {K_{iz}}&{} {K_{ii}}\end{bmatrix} \begin{bmatrix} {z}\\ {i}\end{bmatrix} = \begin{bmatrix} {p_z}\\ {p_i}\end{bmatrix} \end{aligned}$$
(5)

and the local model:

$$\begin{aligned} \begin{bmatrix} {K_{aa}}&{} {K_{ao}}\\ {K_{oa}}&{} {K_{oo}}\end{bmatrix} \begin{bmatrix} {a}\\ {o}\end{bmatrix} = \begin{bmatrix} {p_a}\\ {p_o}\end{bmatrix} \end{aligned}$$
(6)

Solving both, while enforcing the coupling at the interface defined in Eq. 3, is equivalent to solving:

$$\begin{aligned} \begin{bmatrix} {K_{zz}}&{} {K_{zi}}&{} {\cdot }\\ {K_{iz}}&{} {K_{ii}}+ {K_{aa}}&{} {K_{ao}}\\ {\cdot }&{} {K_{oa}}&{} {K_{oo}}\end{bmatrix} \begin{bmatrix} {z}\\ {i}\\ {o}\end{bmatrix} = \begin{bmatrix} {p_z}\\ {p_i}+ {p_a}\\ {p_o}\end{bmatrix} \end{aligned}$$
(7)

which would be the system of a reference model, in which all degrees of freedom are considered at once and \({i}= {a}\) is denoted as \({i}\) (Fig. 4).

2.3.2 Discrete equations for static aeroelasticity

In the case of static aeroelasticity subcase, the discrete equation is:

$$\begin{aligned} \begin{bmatrix} {K}\end{bmatrix} \begin{bmatrix} {u}\end{bmatrix} = \begin{bmatrix} {p}\end{bmatrix} + {f^{A}_{\text {rigid}}}+ {C}\begin{bmatrix} {u}\end{bmatrix} \end{aligned}$$
(8)

where \({f^{A}_{\text {rigid}}}\) is the rigid part of the aeroelastic load vector and \({C}\) is the aeroelastic stiffness matrix.

Since we have assumed that only the global model shares an interface with the aeroelastic forces, the discrete equation of the global model is:

$$\begin{aligned} \begin{bmatrix} {K_{zz}}&{} {K_{zi}}\\ {K_{iz}}&{} {K_{ii}}\end{bmatrix} \begin{bmatrix} {z}\\ {i}\end{bmatrix} = \begin{bmatrix} {p_z}\\ {p_i}\end{bmatrix} + {f^{A}_{\text {rigid}}}+ {C}\begin{bmatrix} {z}\\ {i}\end{bmatrix} \end{aligned}$$
(9)

while instead for the local model the discrete equation is again the same as given in Eq. 6.

As for the case of a static analysis, under the assumption of direct displacement coupling at the interface (Eq. 3), it is possible to assemble a system of equations for a reference model (Fig. 4) representing the entire structure:

$$\begin{aligned}{} & {} \begin{bmatrix} {K_{zz}}&{} {K_{zi}}&{} {\cdot }\\ {K_{iz}}&{} {K_{ii}}+ {K_{aa}}&{} {K_{ao}}\\ {\cdot }&{} {K_{oa}}&{} {K_{oo}}\end{bmatrix} \begin{bmatrix} {z}\\ {i}\\ {o}\end{bmatrix}\nonumber \\{} & {} \quad = \begin{bmatrix} {p_z}\\ {p_i}+ {p_a}\\ {p_o}\end{bmatrix} + \begin{bmatrix} {{f^{A}_{\text {rigid}}}} \\ \\ {\cdot }\end{bmatrix} + \begin{bmatrix} { {C}\begin{bmatrix} {z}\\ {i}\end{bmatrix} } \\ \\ {\cdot }\end{bmatrix} \end{aligned}$$
(10)

2.3.3 On the solution approach

The global–local analysis proposed does not require any iterative procedure and is instead based on three steps: (i) condensation of the local model, depicted in Fig. 5a, (ii) global solution, depicted in Fig. 5b, and (iii) local solution, depicted in Fig. 5c

The static condensation of the local model reduces the system in Eq. 6 to:

$$\begin{aligned} \begin{bmatrix} {K_{aa}}- {K_{ao}}{K^{-1}_{oo}}{K_{oa}}\end{bmatrix} {i}&= \begin{bmatrix} {p_a}- {K_{ao}}{K^{-1}_{oo}}{p_o}\end{bmatrix} \end{aligned}$$
(11)
$$\begin{aligned} {K^{\dagger }_{aa}}{i}&= {p^{\dagger }_a} \end{aligned}$$
(12)

In the second step, the local condensed information is added to the global model:

$$\begin{aligned} \begin{bmatrix} {K_{zz}}&{} {K_{zi}}\\ {K_{iz}}&{} {K_{ii}}\end{bmatrix}&\rightarrow \begin{bmatrix} {K_{zz}}&{} {K_{zi}}\\ {K_{iz}}&{} {K_{ii}}+{K^{\dagger }_{aa}}\end{bmatrix} \end{aligned}$$
(13)
$$\begin{aligned} \begin{bmatrix} {p_z}\\ {p_i}\end{bmatrix}&\rightarrow \begin{bmatrix} {p_z}\\ {p_i}+{p^{\dagger }_a}\end{bmatrix} \end{aligned}$$
(14)

In the case of a static analysis subcase, the global system (Eq. 5) with the local contributions becomes:

$$\begin{aligned} \begin{bmatrix} {K_{zz}}&{} {K_{zi}}\\ {K_{iz}}&{} {K_{ii}}+{K^{\dagger }_{aa}}\end{bmatrix} \begin{bmatrix} {z}\\ {i}\end{bmatrix} = \begin{bmatrix} {p_z}\\ {p_i}+{p^{\dagger }_a}\end{bmatrix} \end{aligned}$$
(15)

While instead, in the case of a static aeroelasticity subcase (Eq. 9), the system is given by:

$$\begin{aligned} \begin{bmatrix} {K_{zz}}&{} {K_{zi}}\\ {K_{iz}}&{} {K_{ii}}+{K^{\dagger }_{aa}}\end{bmatrix} \begin{bmatrix} {z}\\ {i}\end{bmatrix} = \begin{bmatrix} {p_z}\\ {p_i}+{p^{\dagger }_a}\end{bmatrix} + {f^{A}_{\text {rigid}}}+ {C}\begin{bmatrix} {z}\\ {i}\end{bmatrix} \end{aligned}$$
(16)

With the condensed local contributions, the global solution can then be computed by solving either Eq. 15 or Eq. 16 for \({u}{^{G}}= \begin{bmatrix} {z}\\ {i}\end{bmatrix}\).

Lastly, the global solution (i) is applied as a Dirichlet boundary condition at the interface of the local model:

$$\begin{aligned} {K_{oo}}{o}= {p_o}- {K_{oa}}\bar{{i}} \end{aligned}$$
(17)

With this, the local system becomes solvable and \({o}\) can be computed.

Fig. 5
figure 5

Global–local analysis steps

Full size image

2.4 Global–local sensitivity analysis

2.4.1 Objective and constraints evaluation

In this paper we consider a single objective function for the MDO, where we optimise the mass of the aircraft, but the methodology could be extended to other objectives as well, e.g. range. Since we have assumed that local and global model do not overlap, the mass of the whole structure is the sum of the mass of the global model and the mass of the local model:

$$\begin{aligned} {f}= {f}{^{G}}+ {f}{^{L}}\end{aligned}$$
(18)

The constraint vector can be assembled by joining global and local constraint vectors:

$$\begin{aligned} {g}= \begin{bmatrix} {g}{^{G}}\\ {g}{^{L}}\end{bmatrix} \end{aligned}$$
(19)

In this paper, only strength constraints will be considered, but the methodology presented is applicable also to other relevant types, like buckling and flutter constraints.

2.4.2 Sensitivities of objective and constraints

When computing the sensitivities, the design variables can be divided in global \({t}{^{G}}\) and local \({t}{^{L}}\). In the case of the objective function:

$$\begin{aligned} \frac{\textrm{d} {f}}{\textrm{d} {t}} = \begin{bmatrix} \dfrac{\textrm{d} {f}}{\textrm{d} {t}{^{G}}}&\dfrac{\textrm{d} {f}}{\textrm{d} {t}{^{L}}} \end{bmatrix} \end{aligned}$$
(20)

and since the mass of a model does not depend on the design variables of other models:

$$\begin{aligned} \frac{\textrm{d} {f}}{\textrm{d} {t}} = \begin{bmatrix} \dfrac{\textrm{d} {f}{^{G}}}{\textrm{d} {t}{^{G}}}&\dfrac{\textrm{d} {f}{^{L}}}{\textrm{d} {t}{^{L}}} \end{bmatrix} \end{aligned}$$
(21)

Thus, the sensitivity of the objective function is obtained by assembling independent contributions from the global and the local model. The global–local formulation does not require any special treatment.

As for the constraints vector, computing the derivative with respect to global and local design variables one obtains:

$$\begin{aligned} \frac{\textrm{d} {g}}{\textrm{d} {t}}&= \begin{bmatrix} \frac{\textrm{d} {g}{^{G}}}{\textrm{d} {t}{^{G}}} &{} \frac{\textrm{d} {g}{^{G}}}{\textrm{d} {t}{^{L}}} \\ \frac{\textrm{d} {g}{^{L}}}{\textrm{d} {t}{^{G}}} &{} \frac{\textrm{d} {g}{^{L}}}{\textrm{d} {t}{^{L}}} \end{bmatrix} \end{aligned}$$
(22)
$$\begin{aligned}&= \begin{bmatrix} \frac{\partial {g}{^{G}}}{\partial {t}{^{G}}} + \frac{\partial {g}{^{G}}}{\partial {u}{^{G}}} \frac{d {u}{^{G}}}{\textrm{d} {t}{^{G}}} &{} \frac{\partial {g}{^{G}}}{\partial {u}{^{G}}} \frac{\textrm{d} {u}{^{G}}}{\textrm{d} {t}{^{L}}} \\ \frac{\partial {g}{^{L}}}{\partial {u}{^{L}}} \frac{\textrm{d} {u}{^{L}}}{\textrm{d} {t}{^{G}}} &{} \frac{\partial {g}{^{L}}}{\partial {t}{^{L}}} + \frac{\partial {g}{^{L}}}{\partial {u}{^{L}}} \frac{\textrm{d} {u}{^{L}}}{\textrm{d} {t}{^{L}}} \end{bmatrix} \end{aligned}$$
(23)

Within the off-diagonal sub-blocks, the terms \(\dfrac{\textrm{d} {u}{^{L}}}{\textrm{d} {t}{^{G}}}\) and \(\dfrac{\textrm{d} {u}{^{G}}}{\textrm{d} {t}{^{L}}}\) represent the coupling between global and local sensitivities. The next section explains how these can be computed.

2.5 Coupled sensitivities of the solution field

The computation of \(\dfrac{\textrm{d} {u}{^{L}}}{\textrm{d} {t}{^{G}}}\) and \(\dfrac{\textrm{d} {u}{^{G}}}{\textrm{d} {t}{^{L}}}\) requires an exchange of information between the global and the local model. As shown in Fig. 6, this information is based on the coupling between the models. The global model requires the derivative of the condensed contributions with respect to \({t}{^{L}}\) to compute \(\dfrac{\textrm{d} {u}{^{G}}}{\textrm{d} {t}{^{L}}}\). The local model requires the derivative of the global solution field with respect to \({t}{^{G}}\) to compute \(\dfrac{\textrm{d} {u}{^{L}}}{\textrm{d} {t}{^{G}}}\).

Fig. 6
figure 6

Computation of solution field sensitivities: global and local models require the sensitivities of coupling contributions

Full size image

2.5.1 Coupled sensitivity of the global solution field

The term \(\dfrac{\textrm{d} {u}{^{G}}}{\textrm{d} {t}{^{L}}}\) represents the sensitivity of the global solution field with respect to local design variables. The global solution field can be the solution of a static analysis or of a static aeroelastic analysis.

In the case of static analysis, \({u}{^{G}}\) is the solution of the linear system defined in Eq. 15.

The term \(\dfrac{\textrm{d} {u}{^{G}}}{\textrm{d} {t}{^{L}}}\) can be obtained by computing the derivative of all terms in Eq. 15 with respect to \({t}{^{L}}\). Using the fact that the components of the global stiffness matrix (\({K_{zz}}\),\({K_{zi}}\), \({K_{iz}}\) and \({K_{ii}}\)), as well as the components of the global load vector (\({p_z}\) and \({p_i}\)) do not depend on the local design variables, it follows that:

$$\begin{aligned} {K}{^{G}}\frac{\textrm{d} {u}{^{G}}}{\textrm{d} {t}{^{L}}}&= \frac{\textrm{d} {p}{^{G}}}{\textrm{d} {t}{^{L}}} - \frac{\textrm{d} {K}{^{G}}}{\textrm{d} {t}{^{L}}} {u}{^{G}}\end{aligned}$$
(24)
$$\begin{aligned} {K}{^{G}}\frac{\textrm{d} {u}{^{G}}}{\textrm{d} {t}{^{L}}}&= \begin{bmatrix} \frac{\textrm{d} {p_z}}{\textrm{d} {t}{^{L}}} \\ \frac{\textrm{d} {p_i}}{\textrm{d} {t}{^{L}}} + \frac{\textrm{d} {p^{\dagger }_a}}{\textrm{d} {t}{^{L}}} \end{bmatrix} - \begin{bmatrix} \frac{\textrm{d} {K_{zz}}}{\textrm{d} {t}{^{L}}} &{} \frac{\textrm{d} {K_{zi}}}{\textrm{d} {t}{^{L}}} \\ \frac{\textrm{d} {K_{iz}}}{\textrm{d} {t}{^{L}}} &{} \frac{\textrm{d} {K_{ii}}}{\textrm{d} {t}{^{L}}} + \frac{d {K^{\dagger }_{aa}}}{\textrm{d} {t}{^{L}}} \end{bmatrix} \begin{bmatrix} {z}\\ {i}\end{bmatrix} \end{aligned}$$
(25)
$$\begin{aligned} {K}{^{G}}\frac{\textrm{d} {u}{^{G}}}{\textrm{d} {t}{^{L}}}&= \begin{bmatrix} {\cdot }\\ \frac{\textrm{d} {p^{\dagger }_a}}{\textrm{d} {t}{^{L}}} - \frac{\textrm{d} {K^{\dagger }_{aa}}}{\textrm{d} {t}{^{L}}} {i}\end{bmatrix} \end{aligned}$$
(26)

If instead \({u}{^{G}}\) is the solution of a static aeroelasticity analysis, then the system being solved is the one defined in Eq. 16.

Since neither the matrix of aerodynamic coefficients \({C}\) nor the rigid part of the aeroelastic load vector \({f^{A}_{\text {rigid}}}\) depend on the local design variables, deriving Eq. 16 with respect to \({t}{^{L}}\) yields:

$$\begin{aligned} {K}{^{G}}{u}{^{G}}&= {p}{^{G}}+ {f^{A}_{\text {rigid}}}+ {C}{u}{^{G}}\end{aligned}$$
(27)
$$\begin{aligned} \frac{\textrm{d} {K}{^{G}}}{\textrm{d} {t}{^{L}}} {u}{^{G}}+ {K}{^{G}}\frac{\textrm{d} {u}{^{G}}}{d {t}{^{L}}}&= \frac{\textrm{d} {p}{^{G}}}{\textrm{d} {t}{^{L}}} + \frac{\textrm{d} {f^{A}_{\text {rigid}}}}{\textrm{d} {t}{^{L}}} + \frac{\textrm{d} {C}}{\textrm{d} {t}{^{L}}} {u}{^{G}}+ {C}\frac{d {u}{^{G}}}{\textrm{d} {t}{^{L}}} \end{aligned}$$
(28)
$$\begin{aligned} {K}{^{G}}\frac{\textrm{d} {u}{^{G}}}{\textrm{d} {t}{^{L}}}&= \frac{\textrm{d} {p}{^{G}}}{\textrm{d} {t}{^{L}}} - \frac{\textrm{d} {K}{^{G}}}{\textrm{d} {t}{^{L}}} {u}{^{G}}+ {C}\frac{\textrm{d} {u}{^{G}}}{\textrm{d} {t}{^{L}}} \end{aligned}$$
(29)

where the static part of the pseudo-load vector can be simplified as in the static analysis case:

$$\begin{aligned} \frac{\textrm{d} P{^{G}}}{\textrm{d} {t}{^{L}}}&= \frac{\textrm{d} {p}{^{G}}}{\textrm{d} {t}{^{L}}} - \frac{\textrm{d} {K}{^{G}}}{\textrm{d} {t}{^{L}}} {u}{^{G}}\end{aligned}$$
(30)
$$\begin{aligned}&= \begin{bmatrix} {\cdot }\\ \frac{\textrm{d} {p^{\dagger }_a}}{\textrm{d} {t}{^{L}}} - \frac{\textrm{d} {K^{\dagger }_{aa}}}{\textrm{d} {t}{^{L}}} {i}\end{bmatrix} \end{aligned}$$
(31)

yielding:

$$\begin{aligned} {K}{^{G}}\frac{\textrm{d} {u}{^{G}}}{\textrm{d} {t}{^{L}}} = \begin{bmatrix} {\cdot }\\ \frac{\textrm{d} {p^{\dagger }_a}}{\textrm{d} {t}{^{L}}} - \frac{\textrm{d} {K^{\dagger }_{aa}}}{\textrm{d} {t}{^{L}}} {i}\end{bmatrix} + {C}\frac{\textrm{d} {u}{^{G}}}{\textrm{d} {t}{^{L}}}. \end{aligned}$$
(32)

Finally, \(\dfrac{\textrm{d} {p^{\dagger }_a}}{\textrm{d} {t}{^{L}}}\) and \(\dfrac{\textrm{d} {K^{\dagger }_{aa}}}{\textrm{d} {t}{^{L}}}\) must be computed. By deriving \({K^{\dagger }_{aa}}\) and \({p^{\dagger }_a}\) as defined in Eq. 11:

$$\begin{aligned} {p^{\dagger }_a}= {p_a}- {K_{ao}}{K^{-1}_{oo}}{p_o}\end{aligned}$$
(33)
$$\begin{aligned} {K^{\dagger }_{aa}}= {K_{aa}}- {K_{ao}}{K^{-1}_{oo}}{K_{oa}}\end{aligned}$$
(34)

will lead toFootnote 1:

$$\begin{aligned} \frac{\textrm{d} {p^{\dagger }_a}}{\textrm{d} {t}}= & {} \frac{\textrm{d} {p_a}}{\textrm{d} {t}} - \frac{\textrm{d} {K_{ao}}}{\textrm{d} {t}} {K^{-1}_{oo}}{p_o}\nonumber \\{} & {} + {K_{ao}}{K^{-1}_{oo}}\frac{\textrm{d} {K_{oo}}}{\textrm{d} {t}} {K^{-1}_{oo}}{p_o}- {K_{ao}}{K^{-1}_{oo}}\frac{\textrm{d} {p_o}}{\textrm{d} {t}} \end{aligned}$$
(35)

and

$$\begin{aligned} \frac{\textrm{d} {K^{\dagger }_{aa}}}{\textrm{d} {t}}= & {} \frac{\textrm{d} {K_{aa}}}{\textrm{d} {t}} - \frac{\textrm{d} {K_{ao}}}{\textrm{d} {t}} {K^{-1}_{oo}}{K_{oa}}\nonumber \\{} & {} + {K_{ao}}{K^{-1}_{oo}}\frac{d {K_{oo}}}{\textrm{d} {t}} {K^{-1}_{oo}}{K_{oa}}- {K_{ao}}{K^{-1}_{oo}}\frac{\textrm{d} {K_{oa}}}{\textrm{d} {t}}. \end{aligned}$$
(36)

2.5.2 Coupled sensitivity of the local solution field

The remaining coupled sensitivity of the solution field to be computed is:

$$\begin{aligned} \frac{\textrm{d} {u}{^{L}}}{\textrm{d} {t}{^{G}}} = \begin{bmatrix} \frac{\textrm{d} {a}}{\textrm{d} {t}{^{G}}} \\ \frac{\textrm{d} {o}}{\textrm{d} {t}{^{G}}} \end{bmatrix}. \end{aligned}$$
(37)

To get \(\dfrac{\textrm{d} {a}}{\textrm{d} {t}{^{G}}}\), one must exploit the coupling relationship defined in Eq. 3.

It follows that:

$$\begin{aligned} \frac{\textrm{d} {a}}{\textrm{d} {t}{^{G}}} = \frac{\textrm{d} {a}}{\textrm{d} {i}} \frac{\textrm{d} {i}}{\textrm{d} {t}{^{G}}} = \frac{\textrm{d} {i}}{\textrm{d} {t}{^{G}}} \end{aligned}$$
(38)

where \(\dfrac{\textrm{d} {a}}{\textrm{d} {i}}\) cancels out because it is the identity matrix.

\(\dfrac{\textrm{d} {o}}{\textrm{d} {t}{^{G}}}\) is computed by deriving the discrete equation of the local model, for which only static analysis is considered, i.e. Eq 17. Since neither the components of the local stiffness matrix nor those of the local load vector are directly influenced by the global design variables, it follows that:

$$\begin{aligned} \frac{\textrm{d} {K_{oo}}}{\textrm{d} {t}{^{G}}} {o}+ {K_{oo}}\frac{\textrm{d} {o}}{\textrm{d} {t}{^{G}}}&= \frac{\textrm{d} {p_o}}{\textrm{d} {t}{^{G}}} - \frac{\textrm{d} {K_{oa}}}{\textrm{d} {t}{^{G}}}{i}- {K_{oa}}\frac{\textrm{d} {i}}{\textrm{d} {t}{^{G}}} \end{aligned}$$
(39)
$$\begin{aligned} \frac{\textrm{d} {o}}{\textrm{d} {t}{^{G}}}&= - {K^{-1}_{oo}}{K_{oa}}\frac{\textrm{d} {i}}{\textrm{d} {t}{^{G}}}. \end{aligned}$$
(40)

3 Implementation

3.1 Implementation strategy

The implementation is based on Lagrange, a software developed at Airbus Defense and Space for constrained gradient-based multidisciplinary design optimisation. Lagrange implements its own linear FE-solver and computes semi-analytic sensitivities. It is designed to work with one FE-model defined in one input file, but this limitation can be overcome, by using the Lagrange/Python API, which controls the analysis or optimisation procedure and provides access to the internal data.

The global–local approach is implemented by extending Lagrange through its Python interface. Multiple Lagrange instances are created:

  1. 1.

    an instance with the input file of the global model (LAGRANGE.global),

  2. 2.

    an instance for each local model (LAGRANGE.local) and

  3. 3.

    an instance for the optimiser, with a dummy input file (LAGRANGE.optimiser).

Additional information regarding the optimisation, such as design variables \({t}\) and constraints \({g}_i\), is separately defined for the global and the local model in the corresponding input files. A Python script acts as a intermediary between Lagrange instances. The main information exchanges are summarised in Figs. 7 and 8. Figure 7 represents a sequence diagram of the analysis step. This step involves a global instance a local instance and a Python script. The three operations of condensation, global and local solution are depicted as white boxes, while instead the arrows represent the information exchange between the instances. At the end of the procedure \({z}\) \({o}\) and \({i}\) are all available at Python level. Figure 8 represents a sequence diagram for the evaluation of objective, constraints and their sensitivities. Most information can be obtained from the global and local instances without any special treatment, while instead the computation of cross-sensitivities must account for the global–local information exchange and is computed at Python level. Once all the information is available, it can be provided to the optimiser.

Fig. 7
figure 7

Sequence diagram of the global–local analysis

Full size image
Fig. 8
figure 8

Sequence diagram of the global–local sensitivity analysis

Full size image

3.2 Verification example

In this section, the approach is verified by comparing the results obtained with the presented approach against the results obtained with a standard Lagrange [37]. The global–local analysis is compared against a single model representation of the same mesh. The solution fields computed with both approaches should match exactly. Similarly the designs obtained in each iteration of a global–local optimisation run can be compared with those obtained with a single model. Since the sensitivities should be the same the optimiser must follow the same path in the design space. Two models are considered a simple plate, in which the local model consists of a single element, and a plate with a finer local model, in which the internal degrees of freedom are actually condensed.

3.2.1 Coarse plate model

The structural model consists of three quadrilateral and one triangular shell element with 6 DOFs (CQUAD4 and CTRIA3 in NASTRAN notation) for a total of 54 DOFS, represented in Fig. 9a. In the global–local representation of the same structure, the middle plate, shown in yellow, is assigned to the local model, as represented in Fig. 9b. The remaining part of the structure, represented in blue, is assigned to the global model.

Fig. 9
figure 9

Alternative representations of the “coarse plate model”

Full size image

In both representations, one single point constraint (SPC) fully constrains the freedom of the right end of the plate. The same three subcases are defined for both models, a static analysis and two static aeroelastic analyses.

The aerodynamic model, shared by the reference and the global–local models, consists of three panels, which overlap the structural quadrilateral elements exactly, as represented in Fig. 10.

Fig. 10
figure 10

Aerodynamic model used in “coarse plate model”

Full size image

The optimisation problem associated to this model defines the thickness of each element as a design variable, which leads to four design variables in total.

The structure must be sized for minimal weight, which can be computed as:

$$\begin{aligned} m = \sum _i \rho _i V_i = \sum _i \rho _i t_i A_i \end{aligned}$$
(41)

where \(\rho _i\) is the material density and \(V_i\) is the volume of each element i, computed as area times thickness.

Furthermore, the structure is subject to 12 strength constraints defined as \(\sigma _\textrm{actual} < \sigma _\textrm{allowable}\). With the following definition of reserve factor (RF):

$$\begin{aligned} \textrm{RF} = \frac{\sigma _\textrm{allowable}}{\sigma _\textrm{actual}} \end{aligned}$$
(42)

and the following definition of constraints:

$$\begin{aligned} {g}= 1 - \frac{1}{\textrm{RF}} = 1 - \frac{\sigma _\textrm{applied}}{\sigma _\textrm{allowable}} \end{aligned}$$
(43)

a constraint violation is implied by RF \(< 1\) or equivalently \(g < 0\).

3.2.2 Coarse plate model analysis and optimisation results

The results of the global–local procedure match exactly those of the standard FE-solution of the whole model (Fig. 11). This is because for this particular model the global–local representation is such that the local model does not have any internal degree of freedom. In this simple case, the element stiffness matrix is identical to the condensed one and does not introduce any numerical error. Thus, as expected, the global solution (Eqs. 15–16) is identical to the solution of the whole model (Eqs. 7–10).

Fig. 11
figure 11

Results of the analyses. Each subfigure compares a different subcase with the displacement field of the reference approach represented above and the global–local solution below

Full size image

The optimised design obtained with the two approaches is the same. As it can be seen in Fig. 12 objective and maximum constraints violation follow the same optimisation history.

Fig. 12
figure 12

Histories of the “coarse plate model” optimisation

Full size image

3.2.3 Fine plate model

In the fine version of the model everything remains the same, except for the quadrilateral element in the middle, which is splitted into two, as represented in Fig. 13a.

Fig. 13
figure 13

Alternative representations of the “fine plate model”

Full size image

In the global–local representation, the local model consists of two quadrilateral elements, as represented in Fig. 13b. The optimisation problem is equivalent to the one of the coarse case, the objective remains mass minimisation, but since two quadrilateral elements have replaced a single element, two strength constraints must be specified instead of one. The local design variable is still only one and specifies the thickness of two elements. The global model remains unchanged. Therefore in total the model has 66 DOFs, 4 design variables and 15 constraints.

3.2.4 Fine plate model analysis and optimisation results

Fig. 14
figure 14

Results of the analyses. Each subfigure compares a different subcase with the displacement field of the reference approach represented above and the global–local solution below

Full size image

As the internal degrees of freedom of the local model are condensed, a negligible numerical error is introduced.

Taking the solution of Lagrange \({u}\) as a reference, we measure the absolute and relative error of the solution \({u}^{GL}\) of the global–local approach as:

$$\begin{aligned} e_\textrm{abs}= & {} \left| {u}^{GL} - {u}\right| \end{aligned}$$
(44)
$$\begin{aligned} e_\textrm{rel}= & {} \left| \frac{{u}^{GL} - {u}}{{u}} \right| . \end{aligned}$$
(45)

We then consider the \(L ^2\) and infinity norm:

$$\begin{aligned}{} & {} \Vert e \Vert _2 = \sum _{i=1}^n e_i^2 \end{aligned}$$
(46)
$$\begin{aligned}{} & {} \Vert e \Vert _{\infty } = \max ( e_1, \ldots , e_n ) \end{aligned}$$
(47)

As it can be seen from Table 1, the results are not exact, but the error is quite close to machine precision.

Figure 14 shows visual comparison of the displacement fields computed with the reference and the global–local approach.

Table 1 Error metrics for the analysis results
Full size table

The numerical error due to the condensation of the local model had a negligible effect on the optimisation results. As for the coarse model, the two approaches yield the same optimal design and the same optimisation history as shown in Fig. 15.

Fig. 15
figure 15

Histories of the “fine plate model” optimisation

Full size image

4 Case study

4.1 Model and optimisation problem

In the following, we consider a metallic wingbox, with an inspection hole in the upper skin, as an example of a “non-regular area”.

Four different subcases and two disciplines are considered. Three subcases are static analyses, named “gust-up”, “landing” and “manoeuvre”. The fourth subcase is a static aeroelastic analysis representing a steady flight at Mach 0.3 with a dynamic pressure of 2.800 kPa and an angle of attack of \(5.000^\circ\).

The optimisation problem is set up to minimise the mass of the structure, as defined in Eq. 41, subject to strength constraints, as defined in Eq. 43, by modifying one local design variable and 158 global ones.

Two modelling strategies can be used to analyse the structure. One, represented in Fig. 16a, is based on a coarse model, which does not capture the geometry of the hole, but uses equivalent material properties to match the stiffness properties of the local area. The other one, represented in Fig. 16b uses a sufficiently fine model to accurately capture the deformation of the “non-regular area”, combined with a coarse model for the remainder of the structure. Depending on modelling used, the number of constraints and degrees of freedom changes. In the coarse modelling case, the structure has 3234 global and 72 local degrees of freedom, is subject to 2956 global constraints and 24 local constraints. In the fine modelling case, the structure has 1902 local degrees of freedom instead of 72 and is subject to 1108 local constraints instead of 24.

Fig. 16
figure 16

Coarse and global–local representations of the wingbox model. In the coarse model, the non-regular area is modelled with degraded material properties so that its overall stiffness is equivalent to that of the global–local representation. In the global–local representation, separate global (blue) and local (yellow) models are used. The local model presents a finer mesh and a more accurate representation of the geometry

Full size image

In the following, two optimisation runs are compared. One, based on the coarse model, is performed by standard Lagrange and represents the current way of working. Therein the critical area (local model) is fixed and unconstrained, but sized to be initially locally feasible including a design factor of 1.3 (minimum RF = 1.3) to account for later load path changes. The other one, based on the global–local representation, follows the application of the global–local approach, which allows to define local design variables and constraints.

Figure  17 shows the thickness distribution of the initial design. The displacement fields computed for this design can be applied at the boundary of a refined local model to check for local constraints violations. As demonstrated by Fig. 18, which shows the value of minimum RF, the design is locally feasible: any constraints violation would be highlighted in red, dark blue represents a RF larger than 1.1 and green represents a RF larger than 1.3. The fact that the local model is entirely above this threshold proves not only that the design is feasible, but also that a conservative design factor provides a margin for changes of the surrounding structure.

Fig. 17
figure 17

Initial thickness distribution. The scale used in the legend is logarithmic

Full size image
Fig. 18
figure 18

Initial minimum RF distribution. The initial design is feasible and the local design is conservative, as it can be seen from the green colour which represents a RF larger than 1.3

Full size image

4.2 Feasibility of results

The optimal design found by the Lagrange optimisation procedure, while keeping the local fixed and unconstrained, as currently done during optimisation, leads to an unfeasible design as depicted in Fig. 19. This despite the fact that the local structure was conservatively sized with an initial reserve factor of 1.3.

Fig. 19
figure 19

Minimum RF of Lagrange optimum. The global design on the left is feasible, but when the local model is analysed in detail after the optimisation the unfeasiblity, highlighted in red, is revealed

Full size image

The optimal design found with the monolithic global–local optimisation procedure proposed in this paper, using local design variables and constraints, is feasible, as shown in Fig. 20, which depicts the distribution of minimum RF.

Fig. 20
figure 20

Minimum RF of global–local optimum. The design is feasible

Full size image

4.3 Comparison of designs and histories

Figure 21 shows the initial design and the two optimal designs. Starting from the same initial design, both approaches converge to a similar solution, but the global–local approach, thanks to the possibility of evaluating local constraints and modifying the local design, finds a feasible solution by designing a thicker local model.

Fig. 21
figure 21

Comparison of initial and final designs

Full size image

The optimal design found by the global–local strategy weighs 475.640 kg compared to the weight of 473.444 kg of the unfeasible design obtained by the reference approach, as shown in Fig. 22.

Fig. 22
figure 22

History comparison of the objective. The two optimisations follow a similar path. Coincidentally, the global–local approach satisfies the convergence criteria before the reference approach

Full size image

4.4 Correcting the local design

In the standard design procedure, if the optimised design was locally unfeasible, designers could attempt to resolve any constraint violation by manually modifying the design using their engineering judgement. This section will demonstrate that such an approach is non-trivial, because optimal designs are generally close to the border of the infeasible region and very sensitive to design changes.

By increasing the thickness of the local area from 3.0 mm to 4.5 mm the weight of the structure becomes 475.271 kg, while the local design is still unfeasible and the unfeasibility has propagated beyond the local model, as shown in Fig. 23. In particular the weight of the local area increases from 3.653 to 5.480 kg.

Fig. 23
figure 23

Increasing the thickness of the local model is not a viable way of correcting the design in Fig. 19. Before the local is sufficiently thick to become feasible, the additional loads attracted in that area cause elements in the surroundings to become unfeasible. This is often the case, since optimal designs are close to the boundaries of the feasible region in the design space

Full size image

A second way to mitigate the infeasible design would be to further adjust the design factor for the fixed local model. However this would require either an iterative approach by alternately optimising and increasing the design factor, which would result in a prohibitive computational cost, or by initially choosing an even higher design factor, which would increase the mass even more and lead to a sub-optimal result. For a model with multiple local areas, an estimation for the design factor proves to be even more challenging and disadvantageous.

Hence, the example demonstrates that the standard design approach fails to find optimal solutions that satisfy all the constrains, while the proposed global–local approach finds a locally feasible optimal design, overcoming the limitations of the standard procedure.

5 Conclusions

In this paper we have shown that the solution found following common industry practice can be infeasible, when MDO is used for the preliminary design of aircraft structures with “non-regular areas”. Furthermore, we introduced a novel approach to extend an existing MDO procedure, to consider local constraints defined in a separate refined model.

The reference approach is based on a coarse representation of the local model and does not consider local constraints during the optimisation. Choosing a conservative design for the local model, to be kept fixed during the optimisation procedure, as currently done, is not enough for the reference approach to find a locally feasible optimum, as shown in Sect. 4.2.

Furthermore, we have shown in Sect. 4.4 that the unfeasible design found with the standard approach cannot be easily fixed by adjusting the design of the local model. This is because optimal designs are generally sensitive to minor changes and likely to display unfeasibility elsewhere when modified.

Where the standard approach would fail, the presented global–local optimisation strategy allows to find a feasible design.

Our approach introduces a global–local coupling using static condensation, to consider detailed design of critical components for the optimisation in early design stages. Owing to the analytical derivation of a coupled sensitivity analysis, the approach is capable of accurately computing the coupled sensitivities of global and local constraints with respect to local and global design variables. It is therefore possible to consider local constraints as well as local design variables. By adopting a monolithic architecture the strong coupling between global and local disciplines is solved, maintaining multidisciplinary feasibility in each iteration. Compared to the two-level approaches found in the literature, the presented methodology is preferred, whenever the global–local coupling is strong and the focus is on local feasibility, rather than the exploitation of additional local design freedom.

The approach presented is based on the limiting assumptions presented in Sect. 2.2. In particular we assumed non-overlapping domains, conforming meshes, absence of local-local interfaces, a clear partition of design variables in global and local. Furthermore, we only considered static analysis and static aeroelasticity as disciplines and weight as a possible objective.

Future work is needed to extend this approach to more disciplines, local-local interfaces and objectives other than weight. Future work will also have to address the computational cost of such an approach. We expect the presented methodology to prove most efficient in conjunction with an active set strategy, limitations to local design changes and by skipping the local solution and constraints evaluation steps for analyses like flutter or gust analyses, which are mainly concerned with the global behaviour.