Skip to main content
SpringerLink
Log in

High-resolution compact numerical method for the system of 2D quasi-linear elliptic boundary value problems and the solution of normal derivatives on an irrational domain with engineering applications

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

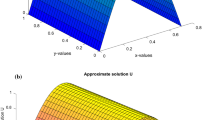
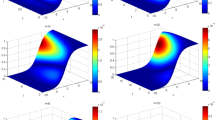
In this paper, we present a novel approach to attain fourth-order approximate solution of 2D quasi-linear elliptic partial differential equation on an irrational domain. In this approach, we use nine grid points with dissimilar mesh in a single compact cell. We also discuss appropriate fourth-order numerical methods for the solution of the normal derivatives on a dissimilar mesh. The method has been protracted for solving system of quasi-linear elliptic equations. The convergence analysis is discussed to authenticate the proposed numerical approximation. On engineering applications, we solve various test problems, such as linear convection–diffusion equation, Burgers’equation, Poisson equation in singular form, NS equations, bi- and tri-harmonic equations and quasi-linear elliptic equations to show the efficiency and accuracy of the proposed methods. A comprehensive comparative computational experiment shows the accuracy, reliability and credibility of the proposed computational approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

References

  1. Jain MK, Jain RK, Mohanty RK (1989) A fourth order difference method for elliptic equations with nonlinear first derivative terms. Numer Methods Partial Differ Equations 5:87–95

    MathSciNet  MATH  Google Scholar 

  2. Li M, Tang T, Fornberg B (1995) A compact fourth-order finite difference scheme for the steady state incompressible Navier-Stokes equations. Int J Numer Methods Fluids 20:1137–1151

    MATH  Google Scholar 

  3. Erturk E, Gökcöl C (2006) Fourth-order compact formulation of Navier–Stokes equations and driven cavity flow at high Reynolds numbers. Int J Numer Methods Fluids 50:421–436

    MATH  Google Scholar 

  4. Liu J, Wang C (2008) A fourth order numerical method for the primitive equations formulated in mean vorticity. Commun Comput Phys 4:26–55

    MathSciNet  MATH  Google Scholar 

  5. Ito K, Qiao Z (2008) A high order compact MAC finite difference scheme for the Stokes equations: augmented variable approach. J Comput Phys 227:8177–8190

    MathSciNet  MATH  Google Scholar 

  6. Spotz WF, Carey GF (1995) High order compact scheme for the steady stream function vorticity equations. Int J Numer Methods Eng 38:3497–3512

    MathSciNet  MATH  Google Scholar 

  7. Carey GF (1997) Computational grids: generation, adaption and solution strategies. Taylor & Francis, Washington, DC

    MATH  Google Scholar 

  8. Yavneh I (1997) Analysis of a fourth-order compact scheme for convection diffusion. J Comput Phys 133:361–364

    MathSciNet  MATH  Google Scholar 

  9. Zhang J (1997) On convergence of iterative methods for a fourth-order discretization scheme. Appl Math Lett 10:49–55

    MathSciNet  MATH  Google Scholar 

  10. Birkhoff G, Lynch RE (1984) The numerical solution of elliptic problems. SIAM Publications, Philadelphia

    MATH  Google Scholar 

  11. Jain MK, Jain RK, Mohanty RK (1991) Fourth order difference methods for the system of 2D nonlinear elliptic partial differential equations. Numer Methods Partial Differ Equations 7:227–244

    MATH  Google Scholar 

  12. Mohanty RK (1992) Fourth order finite difference methods for the system of 2D nonlinear elliptic equations with variable coefficients. Int J Comput Math 46:195–206

    MATH  Google Scholar 

  13. Böhmer K (2008) On finite element methods for fully nonlinear elliptic equations of second order. SIAM J Numer Anal 46(3):1212–1249

    MathSciNet  MATH  Google Scholar 

  14. Feng X, Neilan M (2009) Vanishing moment method and moment solution for fully nonlinear second order partial differential equations. J Sci Comput 38:78–98

    MathSciNet  MATH  Google Scholar 

  15. Böhmer K (2010) Numerical methods for nonlinear elliptic differential equations: a synopsis. Oxford University Press, Oxford

    MATH  Google Scholar 

  16. Jain MK, Jain RK, Krishna M (1994) Fourth order difference method for quasi-linear Poisson equation in cylindrical symmetry. Commun Numer Methods Eng 10:291–296

    MATH  Google Scholar 

  17. Ananthakrishnaiah U, Saldanha G (1995) A fourth order finite difference scheme for two-dimensional non-linear elliptic partial differential equations. Numer Methods Partial Differ Equations 11:33–40

    MATH  Google Scholar 

  18. Mohanty RK (1997) Order h4 difference methods for a class of singular two-space dimensional elliptic boundary value problems. J Comput Appl Math 81:229–247

    MathSciNet  MATH  Google Scholar 

  19. Mohanty RK, Dey S (2001) A new finite difference discretization of order four for (∂u/∂n) for two-dimensional quasi-linear elliptic boundary value problems. Int J Comput Math 76:505–576

    MathSciNet  MATH  Google Scholar 

  20. Mohanty RK, Singh S (2006) A new fourth order discretization for singularly perturbed two dimensional non-linear elliptic boundary value problems. Appl Math Comput 175:1400–1414

    MathSciNet  MATH  Google Scholar 

  21. Mohanty RK, Setia N (2013) A new compact high order off-step discretization for the system of 2D quasi-linear elliptic partial differential equations. Adv Differ Equations 2013:1–29

    MathSciNet  MATH  Google Scholar 

  22. Zhang J (1998) On convergence and performance of iterative methods with fourth order compact schemes. Numer Methods Partial Differ Equations 14:263–280

    MathSciNet  MATH  Google Scholar 

  23. Saldanha G (2001) Technical note: a fourth order finite difference scheme for a system of 2D nonlinear elliptic partial differential equations. Numer Methods Partial Differ Equations 17:43–53

    MathSciNet  MATH  Google Scholar 

  24. Arabshahi SMM, Dehghan M (2007) Preconditioned techniques for solving large sparse linear systems arising from the discretization of the elliptic partial differential equations. Appl Math Comput 188:1371–1388

    MathSciNet  MATH  Google Scholar 

  25. Mohanty RK, Kumar R (2014) A novel numerical algorithm of Numerov type for 2D quasilinear elliptic boundary value problems. Int J Comput Methods Eng Sci Mech 15:473–489

    MathSciNet  Google Scholar 

  26. Mohanty RK, Manchanda G, Khan A (2019) Operator compact exponential approximation for the solution of the system of 2D second order quasi-linear elliptic partial differential equations. Adv Differ Equations 2019:47

    MATH  Google Scholar 

  27. Mohanty RK, Manchanda G, Khan A (2019) Compact half step approximation in exponential form for 2D second order quasi-linear elliptic partial differential equations. J Differ Equations Appl 25:716–749

    MathSciNet  MATH  Google Scholar 

  28. Aziz I, Islam S, Sarler B (2013) Wavelet collocation methods for the numerical solution of elliptic BV problems. Appl Math Model 37:676–694

    MathSciNet  MATH  Google Scholar 

  29. Islam S, Aziz I, Ahmad M (2015) Numerical solution of two-dimensional elliptic PDEs with nonlocal boundary conditions. Comput Math Appl 69:180–205

    MathSciNet  MATH  Google Scholar 

  30. Aziz I, Islam S (2017) An efficient modified haar wavelet collocation method for numerical solution of two-dimensional elliptic PDEs. Differ Equations Dyn Syst 25:347–360

    MathSciNet  MATH  Google Scholar 

  31. Stephenson JW (1984) Single cell discretization of order two and four for biharmonic problems. J Comput Phys 55:65–80

    MathSciNet  MATH  Google Scholar 

  32. Mohanty RK, Evans DJ (2004) Fourth order accurate BLAGE iterative method for the solution of two dimensional elliptic equation in polar coordinates. Int J Comput Math 81:1537–1548

    MathSciNet  MATH  Google Scholar 

  33. Mohanty RK (2007) Three-step BLAGE iterative method for two-dimensional elliptic boundary value problems with singularity. Int J Comput Math 84:1613–1624

    MathSciNet  MATH  Google Scholar 

  34. Mohanty RK (2007) The smart-BLAGE algorithm for singularly perturbed 2D elliptic partial differential equations. Appl Math Comput 190:321–331

    MathSciNet  MATH  Google Scholar 

  35. Mohanty RK (2010) A new high accuracy finite difference discretization for the solution of 2D non-linear biharmonic equations using coupled approach. Numer Methods Partial Differ Equations 26:931–944

    MATH  Google Scholar 

  36. Mohanty RK (2010) Single cell compact finite difference discretizations of order two and four for multi-dimensional triharmonic problems. Numer Methods Partial Differ Equations 26:1420–1426

    MATH  Google Scholar 

  37. Mohanty RK, Jain MK, Mishra BN (2011) A compact discretization of O (h4) for two-dimensional non-linear triharmonic equations. Phys Scr 84:025002

    MATH  Google Scholar 

  38. Mohanty RK, Jain MK, Dhall D (2013) High accuracy cubic spline approximation for two-dimensional quasilinear elliptic boundary value problems. Appl Math Model 37:155–171

    MathSciNet  MATH  Google Scholar 

  39. Varga RS (2000) Matrix iterative analysis. Springer, New York

    MATH  Google Scholar 

  40. Hageman LA, Young DM (2004) Applied iterative methods. Dover, New York

    MATH  Google Scholar 

  41. Kelly CT (1995) Iterative methods for linear and non-linear equations. SIAM, Philadelphia

    Google Scholar 

  42. Saad Y (2003) Iterative methods for sparse linear systems. SIAM, Philadelphia

    MATH  Google Scholar 

Download references

Acknowledgements

The authors thank the reviewers for their valuable suggestions, which substantially improved the quality of the paper.

Author information

Authors and Affiliations

  1. Department of Electrical and Computer Science, University of Delaware, Newark, DE, 19716, USA

    Ishaani Priyadarshini

  2. Department of Applied Mathematics, South Asian University, Akbar Bhawan, Chanakyapuri, New Delhi, 110021, India

    R. K. Mohanty

Authors
  1. Ishaani Priyadarshini
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. K. Mohanty
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to R. K. Mohanty.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Priyadarshini, I., Mohanty, R.K. High-resolution compact numerical method for the system of 2D quasi-linear elliptic boundary value problems and the solution of normal derivatives on an irrational domain with engineering applications. Engineering with Computers 38 (Suppl 1), 539–560 (2022). https://doi.org/10.1007/s00366-020-01150-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-01150-4

Keywords

Mathematics subject classification

Search

Navigation