A comparison of primal- and dual-mixed finite element formulations for Timoshenko beams

Abstract

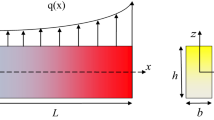
Analytical and numerical comparisons of a primal-mixed, a dual-mixed and a consistent primal-dual mixed finite element model for shear-deformable beams are presented using the lowest possible order, constant and linear, polynomial approximations. The stiffness matrices and the load vectors of the mixed elements are derived and compared analytically with each other and with that of the standard displacement-based Timoshenko beam element. It is pointed out that the element stiffness matrices of the dual-mixed and the primal-dual mixed elements are the exact ones that differ from the standard Timoshenko beam element in a geometry-, material- and mesh-dependent constant factor denoted by C _s. This constant, or its reciprocal, can be considered not only as a shear locking indicator, but can, as the results for the primal-dual mixed formulation indicate, be used to transform the standard Timoshenko beam element into a shear locking-free element, independently of the slenderness ratio and the loading of the beam.

Appendices

Appendix 1

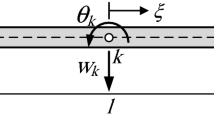
In the dual-mixed variational formulation and finite element method presented in Sect. 3.3, the continuity of the shear force Q(x) and bending moment M(x) at the element nodes with labels $i=0,1,2,\ldots,n_{e}$ is enforced by the following variational equations:

$$\sum_{i=0}^{n_{e}} \delta w_{i}\left[\!\left[Q_{i}\right]\!\right] = 0,$$

(80)

$$\sum_{i=0}^{n_{e}} \delta\phi_{i}\left[\!\left[M_{i}\right]\!\right] = 0,$$

(81)

where n _e is the number of the beam elements, δ w _i and δ ϕ _i are arbitrary virtual nodal displacements and rotations, and

$$\left[\!\left[Q_{i}\right]\!\right] =\; Q_{i}^{i+1}-Q_{i}^{i},$$

(82)

$$\left[\!\left[M_{i}\right]\!\right] = M_{i}^{i+1}-M_{i}^{i}$$

(83)

denote the jumps in the shear force and bending moment at node i, where i and i + 1 in the superscript refer to two neighboring elements with common node i in the subscript. Note that (80)–(81) represent 2 × (n _e  + 1) independent equations.

In Sect. 3.3, the virtual displacements at the nodes of element e, with nodal coordinates x ₁ and x ₂, have been denoted by δ w ₁ ≡  δ w _e−1, δ w ₂ ≡  δ w _e , and the nodal values of the element shear force Q ^e(x) have been denoted by Q ₁ ≡ Q ^e _e-1  ≡ Q ^e(x ₁) and Q ₂ ≡ Q ^e _e  ≡ Q ^e(x ₂). Employing this simplified notation, Eq. (80) for element e takes the form

$$\delta w_{1} \,Q_{1}-\delta w_{2}\, Q_{2}=0,$$

(84)

which proves (56). Applying a similar procedure and notation simplification with respect to Eq. (81), variational equation (57) is obtained for element e.

When concentrated external loads $\widetilde{Q}_{i}$ and $\widetilde{M}_{i}$ are given at node i, the jumps in the shear force and bending moment should be equal to these prescribed values. In this case, instead of (80)–(81), the modified variational equations

$$\delta w_{i}\left[\!\left[Q_{i}\right]\!\right]=\widetilde{Q}_{i}, \quad\delta\phi_{i}\left[\!\left[M_{i}\right]\!\right]= \widetilde{M}_{i}$$

(85)

hold at node i. For completeness it is noted that when displacement boundary conditions are prescribed for the nodal values w _i and ϕ _i at node i, then δ w _i  = 0 and δ ϕ _i  = 0 in Eqs. (80)–(81) and (85).

Appendix 2

The dual-mixed formulation of Sect. 3.3 leads to an equation system of the form

$$[\hbox{A}][\hbox{q}]+[\hbox{B}][\hbox{u}]+[\hbox{f}] = [0],$$

(86)

$$[\hbox{B}]^{{\rm T}}[\hbox{q}]+[\hbox{g}] = [0]$$

(87)

for each element, where, using (52), $[\hbox{q}]^{{\rm T}}=\bigl[[ \hbox{u}_{0} ]^{{\rm T}} [\hbox{s}]^{{\rm T}}\bigr]$. An equation system for the nodal variables [u], defined by (53), can be obtained performing static condensation: expressing the unknowns [q] from (86) as

$$\left[\hbox{q}\right]=-[\hbox{A}]^{-1}(\left[\hbox{B}\right]\left[ \hbox{u}\right]+\left[\hbox{f}\right])$$

(88)

and substituting (88) into (87) leads to Eq. (58) with the following matrix expressions:

$$\begin{array}{ll} \left[\hbox{K}^{{\rm DM}}\right][\hbox{u}]=[ \hbox{F}^{{\rm DM}}], & [\hbox{K}^{{\rm DM}}]=[\hbox{B}]^{{\rm T}}[ \hbox{A}]^{-1}[\hbox{B}],\\ & [\hbox{F}^{{\rm DM}}]=[\hbox{g}]-[\hbox{B}]^{{\rm T}}[ \hbox{A}]^{-1}[\hbox{f}]. \end{array}$$

(89)

When the solution for [u] is known, the bending moment and shear force of the element can be computed using (88). For the dual-mixed element of Sect. 3.3, the nodal bending moments and shear forces are obtained as

$$M_{1} =\frac{1}{C_{{\rm s}}}\left\{\frac{k_{{\rm s}}GA}{2}\Bigl[(w_{1}-w_{2} )-\frac{h}{3}(2\phi_{1}+\phi_{2})\Bigr] +\frac{EI}{h}(\phi_{2}-\phi_{1})\right\},$$

(90)

$$M_{2} =\frac{1}{C_{{\rm s}}}\left\{\frac{k_{{\rm s}}GA}{2}\Bigl[(w_{2}-w_{1} )+\frac{h}{3}(\phi_{1}+2\phi_{2})\Bigr] +\frac{EI}{h}(\phi_{2}-\phi_{1})\right\},$$

(91)

$$Q_{1} =\frac{k_{{\rm s}}GA}{C_{{\rm s}}}\left(\frac{w_{2}-w_{1}}{h}+\frac{\phi_{ 1}+\phi_{2}}{2}\right)+\frac{h}{4}\int\limits_{-1}^{+1}f_{z}^{e}(\xi)\,{\rm d}\xi,$$

(92)

$$Q_{2} =\frac{k_{{\rm s}}GA}{C_{{\rm s}}}\left(\frac{w_{2}-w_{1}}{h}+\frac{\phi_{ 1}+\phi_{2}}{2}\right)- \frac{h}{4}\int\limits_{-1}^{+1}f_{z}^{e}(\xi)\,{\rm d}\xi.$$

(93)

For the primal-dual mixed element in Sect. 3.4, the nodal bending moments can be computed according to (90)–(91) and the constant element shear force is

$$Q_{0}=\frac{k_{{\rm s}}GA}{C_{{\rm s}}}\left(\frac{w_{2}-w_{1}}{h}+\frac{ \phi_{1}+\phi_{2}}{2}\right),$$

(94)

where the mesh-dependent constant C _s is given by (61).