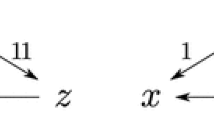Relaxed notions of Condorcet-consistency and efficiency for strategyproof social decision schemes

Abstract

Social decision schemes (SDSs) map the preferences of a group of voters over some set of m alternatives to a probability distribution over the alternatives. A seminal characterization of strategyproof SDSs by Gibbard (Econometrica 45(3):665–681, 1977) implies that there are no strategyproof Condorcet extensions and that only random dictatorships satisfy ex post efficiency and strategyproofness. The latter is known as the random dictatorship theorem. We relax Condorcet-consistency and ex post efficiency by introducing a lower bound on the probability of Condorcet winners and an upper bound on the probability of Pareto-dominated alternatives, respectively. We then show that the randomized Copeland rule is the only anonymous, neutral, and strategyproof SDS that guarantees the Condorcet winner a probability of at least 2/m. Secondly, we prove a continuous strengthening of Gibbard’s random dictatorship theorem: the less probability we put on Pareto-dominated alternatives, the closer to a random dictatorship is the resulting SDS. Finally, we show that the only anonymous, neutral, and strategyproof SDSs that maximize the probability of Condorcet winners while minimizing the probability of Pareto-dominated alternatives are mixtures of the uniform random dictatorship and the randomized Copeland rule.

1 Introduction

A pervasive phenomenon in collective decision making is strategic manipulation: voters may be better off by lying about their preferences than reporting them truthfully. This is problematic for a number of reasons: for one, spending resources on finding out other voters’ preferences and identifying beneficial manipulations is rewarded. These resources are typically not spread evenly across society and thus, voting becomes unfair. Perhaps more importantly, when a voting rule is manipulable, all of its desirable properties are in doubt because they were shown to hold under the assumption that all voters submit their preferences truthfully. Hence, it is desirable that voting rules incentivize voters to report their true preferences. Unfortunately, Gibbard (1973) and Satterthwaite (1975) have shown independently that dictatorships are the only non-imposing voting rules that are immune to strategic manipulations. However, these voting rules are unacceptable for most applications as they invariably return the most preferred alternative of a fixed voter.

A natural follow-up question is whether more positive results can be obtained when allowing for randomization. Instead of choosing a single winner deterministically, randomized voting rules return a lottery over the alternatives and the final winner is drawn according to this lottery. Gibbard (1977) calls these randomized voting rules social decision schemes (SDSs) and motivates them as follows:

“What is meant here by a combination of voting with chance? Suppose a decision is made in the following way: first, voting of some kind is used to pick out a set of one or more winning alternatives; then, in case there is more than one such winner, one of them is chosen by lot. Such a scheme, in effect, uses the way people vote to determine the probability each alternative has of being adopted. This I shall take as the defining feature of a scheme which combines voting with chance: on the basis of the way people vote, it assigns to each alternative a probability of being adopted.” (Gibbard 1977, p. 665)

Gibbard defined SDSs to be strategyproof if no voter can obtain more expected utility for any utility representation that is consistent with his ordinal preference relation. He then gave a complete characterization of strategyproof SDSs in terms of convex combinations of two types of restricted SDSs, so-called unilaterals and duples. An important consequence of this result is the random dictatorship theorem: random dictatorships are the only ex post efficient and strategyproof SDSs. Random dictatorships are convex combinations of dictatorships, i.e., each voter is selected with some fixed probability, and the top choice of the chosen voter is returned.

While this result may seem like an extension of the Gibbard–Satterthwaite theorem to the randomized context, it is in fact much more positive. In contrast to deterministic dictatorships, the uniform random dictatorship, in which every agent is picked with the same probability, enjoys a high degree of fairness and is in fact used in subdomains of social choice that are concerned with the allocation of private goods (see, e.g., Abdulkadiroğlu and Sönmez 1998; Che and Kojima 2010). Gibbard’s theorem has been the point of departure for a large body of follow-up work. In addition to several alternative proofs of the theorem (e.g., Duggan 1996; Nandeibam 1997; Tanaka 2003), there have been extensions with respect to manipulations by groups (Barberà 1979a), cardinal preferences (e.g., Hylland 1980; Dutta et al. 2007; Nandeibam 2013), weaker notions of strategyproofness (e.g., Benoît 2002; Sen 2011; Aziz et al. 2018; Brandl et al. 2018; Brandt et al. 2023a), and restricted domains of preferences (e.g., Dutta et al. 2002; Chatterji et al. 2014; Brandt et al. 2023b).

1.1 Objectives

The goal of this paper is to investigate whether there are attractive strategyproof SDSs other than random dictatorships when relaxing classic axioms. A problem of random dictatorships is that they do not allow for compromise. For example, suppose that voters strongly disagree on the best alternative but have a common second best alternative. In such a scenario, it seems reasonable to choose the second best alternative, but this alternative would never be considered by random dictatorships. On a formal level, this observation is related to the fact that random dictatorships violate Condorcet-consistency, which demands that an alternative that beats all other alternatives in pairwise majority comparisons should be selected. Unfortunately, it is a simple consequence of Gibbard’s work that no strategyproof SDS satisfies Condorcet-consistency. Our first objective thus is to study how much probability a strategyproof SDS can guarantee to the Condorcet winner.

The point of departure for our second objective is that the random dictatorship theorem demands that Pareto-dominated alternatives always receive probability 0. In particular, Gibbard’s theorem does not preclude the possibility of a strategyproof SDS that is axiomatically attractive except that it will select Pareto-dominated alternatives with astronomically small probability. If this probability is, for example, $10^{-100}$, the SDS will be ex post efficient for all practical matters and virtually indistinguishable from an ex post efficient SDS. We thus investigate whether letting Pareto-dominated alternatives be selected with negligible probability allows for more interesting SDSs than random dictatorships.

1.2 Contribution

Fig. 1

Graphical summary of our results. Points in the graphs correspond to SDSs. In both graphs the horizontal axis indicates the value of $\beta$ for which the considered SDS is $\beta$-ex post efficient. In the left graph, the vertical axis represents the $\alpha$ for which the considered SDSs are $\alpha$-Condorcet-consistent, and in the right graph, it represents the $\gamma$ for which SDSs are $\gamma$-randomly dictatorial. Theorems 4 and 6 show that no strategyproof SDS lies in the grey area of the left graph. Theorem 5 shows that no strategyproof SDS lies in the grey area below the diagonal in the right graph. Furthermore, no SDS lies in the grey area above the diagonal since a $\gamma$-randomly dictatorial SDS can put no more than probability $1 - \gamma$ on Pareto-dominated alternatives. Finally, the following SDSs are marked in the graphs: D corresponds to all random dictatorships, C to the randomized Copeland rule, B to the randomized Borda rule, and U to the uniform lottery rule

In order to formally study these problems, we introduce relaxations of Condorcet-consistency and ex post efficiency. In more detail, we say that an SDS is $\alpha$-Condorcet-consistent if a Condorcet winner will be selected with a probability of at least $\alpha$ and $\beta$-ex post efficient if a Pareto-dominated alternative will be selected with a probability no more than $\beta$. Moreover, we say a strategyproof SDS is $\gamma$-randomly dictatorial if it can be represented as a convex combination of two strategyproof SDSs, one of which is a random dictatorship that will be selected with probability $\gamma$. All of these axioms are discussed in more detail in Sect. 2.2.

Building on a characterization of strategyproof SDSs by Barberà (1979b), we then prove the following results (m is the number of alternatives and n the number of voters).

• Let $m,n\ge 3$. There is no strategyproof SDS that satisfies $\alpha$-Condorcet-consistency for $\alpha > \nicefrac {2}{m}$. Moreover, the randomized Copeland rule, which assigns probabilities proportional to Copeland scores, is the only strategyproof SDS that satisfies anonymity, neutrality, and $\nicefrac {2}{m}$-Condorcet-consistency (Theorem 4).

• Let $0 \le \varepsilon \le 1$ and $m\ge 3$. Every strategyproof SDS that is $\frac{1 - \varepsilon }{m}$-ex post efficient is $\gamma$-randomly dictatorial for $\gamma \ge \varepsilon$. If we additionally require anonymity and $m \ge 4$, then only mixtures of the uniform random dictatorship and the uniform lottery rule satisfy this bound tightly (Theorem 5).

• Let $m \ge 4$ and $n \ge 5$. No strategyproof SDS that is $\alpha$-Condorcet-consistent is $\beta$-ex post efficient for $\beta < \frac{m-2}{m-1}\alpha$. If we additionally require anonymity and neutrality, then only mixtures of the uniform random dictatorship and the randomized Copeland rule satisfy $\beta = \frac{m-2}{m-1}\alpha$ (Theorem 6).

Our findings, which are summarized in Fig. 1, show that two strategyproof SDSs perform particularly well with respect to $\alpha$-Condorcet-consistency and $\beta$-ex post efficiency: the uniform random dictatorship (and random dictatorships in general), and the randomized Copeland rule.

In more detail, the first statement characterizes the randomized Copeland rule as the “most Condorcet-consistent” SDS that satisfies strategyproofness, anonymity, and neutrality. In fact, no strategyproof SDS can guarantee more than probability $\nicefrac {2}{m}$ on the Condorcet winner, even when dropping anonymity and neutrality. Conversely, this means that every strategyproof SDS satisfies $\alpha$-Condorcet-consistency for some $\alpha \in [0,\nicefrac {2}{m}]$.

The second result can be interpreted as a continuous strengthening of Gibbard’s random dictatorship theorem: the less probability we put on Pareto-dominated alternatives, the more randomly dictatorial is the resulting SDS. In other words, any hope for attractive strategyproof SDSs by relaxing ex post efficiency is in vain: strategyproof SDSs that almost never select Pareto-dominated alternatives are almost equivalent to random dictatorships. An interesting consequence of this result is that every strategyproof SDS that has no random dictatorship component is as “inefficient” as the uniform lottery rule which always returns the uniform lottery over all alternatives. The second part of the theorem characterizes the SDSs that optimize $\beta$-ex post efficiency subject to being strategyproof, anonymous, and $\gamma$-randomly dictatorial for some $\gamma \in [0,1]$: these are mixtures of the uniform random dictatorship and the uniform lottery rule.

The last statement identifies a tradeoff between $\alpha$-Condorcet-consistency and $\beta$-ex post efficiency: the more probability a strategyproof SDS guarantees to the Condorcet winner, the less efficient it is. Thus, we can either only maximize the $\alpha$-Condorcet-consistency or minimize the $\beta$-ex post efficiency of a strategyproof SDS, which again highlights the antipodal roles of the randomized Copeland rule and random dictatorships. Furthermore, we characterize the SDSs that optimize this tradeoff under the additional assumptions of anonymity and neutrality.

2 The model

Let $N = \{1, 2, \dots , n\}$ be a finite set of voters and let $A = \{a, b, \dots \}$ be a finite set of m alternatives. Every voter i has a preference relation $\succ _i$, which is an anti-symmetric, complete, and transitive binary relation on A. We write $x\succ _i y$ if voter i prefers x strictly to y and $x\succcurlyeq _i y$ if $x \succ _i y$ or $x = y$. The set of all preference relations is denoted by $\mathcal {R}$. A preference profile $R \in \mathcal {R}^n$ contains the preference relation of each voter $i \in N$. We define the supporting size $n_{x y}(R)=|\{i \in N: x \succ _i y\}|$ for x against y in the preference profile R as the number of voters that prefer x to y. Moreover, the rank $r(x, \succ _i)=|\{y\in A:y\succcurlyeq _i x\}|$ of an alternative x in the preference relation of a voter i is the number of alternatives that are weakly preferred to x by voter i. Finally, the rank vector $r^*(x,R)$ of an alternative x in a preference profile R is the vector that contains the rank of x with respect to every voter in increasing order, i.e., $r^*(x,R)=(r(x,\succ _{i_1}), r(x,\succ _{i_2}), \dots , r(x,\succ _{i_n}))$ where the voters $i_1,\dots , i_n$ are ordered such that $r(x,\succ _{i_1})\le r(x,\succ _{i_2})\le \dots \le r(x,\succ _{i_n})$.

Given a preference profile, we are interested in the winning chance of each alternative. We therefore analyze social decision schemes (SDSs) which map each preference profile to a lottery over the alternatives. A lottery p is a probability distribution over the set of alternatives A, i.e., it assigns each alternative x a probability $p(x) \ge 0$ such that $\sum _{x \in A} p(x) = 1$. The set of all lotteries over A is denoted by $\Delta (A)$. Formally, a social decision scheme (SDS) is a function $f:\mathcal {R}^n\rightarrow \Delta (A)$. We denote by f(R, x) the probability assigned to alternative x by f for the preference profile R. The winner will eventually be selected according to these probabilities.

Two basic fairness conditions are anonymity and neutrality. Anonymity requires that voters are treated equally. Formally, an SDS f is anonymous if $f(R)=f(\pi (R))$ for all preference profiles R and permutations $\pi :N\rightarrow N$. Here, $R'=\pi (R)$ denotes the profile with ${\succ _{\pi (i)}'} = {\succ _i}$ for all voters $i\in N$. Neutrality guarantees that alternatives are treated equally and formally requires for an SDS f that $f(R, x)=f(\tau (R), \tau (x))$ for all preference profiles R and permutations $\tau :A\rightarrow A$. This time, $R'=\tau (R)$ is the profile derived by permuting the alternatives in R according to $\tau$, i.e., $\tau (x)\succ _i' \tau (y)$ if and only if $x\succ _i y$ for all alternatives $x, y \in A$ and voters $i\in N$.

2.1 Stochastic dominance and strategyproofness

This paper is concerned with strategyproof SDSs, i.e., social decision schemes in which voters cannot benefit by lying about their preferences. In order to make this formally precise, we need to specify how voters compare lotteries. To this end, we leverage the well-known notion of stochastic dominance: a voter i (weakly) prefers a lottery p to another lottery q, written as $p \succcurlyeq _i q$, if $\sum _{y\in A:y \succ _i x} p(y) \ge \sum _{y\in A:y \succ _i x} q(y)$ for every alternative $x\in A$. In other words, a voter prefers a lottery p to a lottery q if, for every alternative $x\in A$, p returns a better alternative than x with as least as much probability as q. Stochastic dominance does not induce a complete order on the set of lotteries, i.e., there are lotteries p and q such that a voter i neither prefers p to q nor q to p.

Based on stochastic dominance, we can now formalize strategyproofness. An SDS f is strategyproof if $f(R)\succcurlyeq _i f(R')$ for all preference profiles R and $R'$ and voters $i\in N$ such that ${\succ _j}={\succ _j'}$ for all $j\in N{\setminus } \{i\}$. In other words, strategyproofness requires that every voter prefers the lottery obtained by voting truthfully to any lottery that he could obtain by voting dishonestly. Conversely, we call an SDS f manipulable if it is not strategyproof. While there are other ways to compare lotteries with each other, stochastic dominance is the most common one (see, e.g., Gibbard 1977; Barberà 1979b; Bogomolnaia and Moulin 2001; Ehlers et al. 2002; Aziz et al. 2018). This is mainly due to the fact that $p \succcurlyeq _i q$ implies that the expected utility of p is at least as high as the expected utility of q for every vNM utility function that is ordinally consistent with voter i’s preferences. Hence, if an SDS is strategyproof, no voter can manipulate regardless of his exact utility function (see, e.g., Sen 2011; Brandl et al. 2018). This observation immediately implies that the convex combination $h=\lambda f+(1-\lambda )g$ (for some $\lambda \in [0,1]$) of two strategyproof SDSs f and g is again strategyproof: a manipulator who obtains more expected utility from $h(R')$ than h(R) prefers $f(R')$ to f(R) or $g(R')$ to g(R).

Gibbard (1977) shows that every strategyproof SDS can be represented as convex combinations of unilaterals and duples.¹ The terms “unilateral” and “duple” refer to special classes of SDSs: a unilateral is a strategyproof SDS that only depends on the preferences of a single voter i, i.e., $f(R)=f(R')$ for all preference profiles R and $R'$ such that ${\succ _i}={\succ _i'}$. A duple, on the other hand, is a strategyproof SDS that only chooses between two alternatives x and y, i.e., $f(R, z)=0$ for all preference profiles R and alternatives $z\in A\setminus \{x, y\}$.

Theorem 1

(Gibbard 1977) An SDS is strategyproof if and only if it can be represented as a convex combination of unilaterals and duples.

Since duples and unilaterals are by definition strategyproof, Theorem 1 only states that strategyproof SDSs can be decomposed into a mixture of strategyproof SDSs, each of which must be of a special type. In order to circumvent this restriction, Gibbard proves another characterization of strategyproof SDSs.

Theorem 2

(Gibbard 1977) An SDS is strategyproof if and only if it is non-perverse and localized.

Non-perversity and localizedness are two axioms describing the behavior of an SDS. For defining these axioms, we denote by $R^{i:yx}$ the profile derived from R by only reinforcing y against x in voter i’s preference relation. Note that this requires that $x\succ _i y$ and that there is no alternative $z\in A$ such that $x\succ _i z\succ _iy$. Then, an SDS f is non-perverse if $f(R^{i:yx},y)\ge f(R,y)$ for all preference profiles R, voters $i\in N$, and alternatives $x,y\in A$. Moreover, an SDS is localized if $f(R^{i:yx},z)=f(R,z)$ for all preference profiles R, voters $i\in N$, and distinct alternatives $x,y,z\in A$. Intuitively, non-perversity—which is now often referred to as monotonicity—requires that the probability of an alternative only increases if it is reinforced, and localizedness that the probability of an alternative does not depend on the order of the other alternatives. Together, Theorems 1 and 2 show that each strategyproof SDS can be represented as a mixture of unilaterals and duples, each of which is non-perverse and localized.

Since Gibbard’s results can be quite difficult to work with, we now state another characterization of strategyproof SDSs due to Barberà (1979b). This characterization shows that every strategyproof SDS that satisfies anonymity and neutrality can be represented as a convex combination of a supporting size SDS and a point voting SDS. A point voting SDS is defined by a scoring vector $(a_1, a_2, \dots , a_m)$ that satisfies $a_1 \ge a_2 \ge \dots \ge a_m \ge 0$ and $\sum _{i \in \{1, \dots , m\}} a_i = \frac{1}{n}$. The probability assigned to an alternative x by a point voting SDS f is $f(R, x) = \sum _{i \in N} a_{r(x,\succ _i)}$. Furthermore, supporting size SDSs also rely on a scoring vector $(b_n, b_{n-1}, \dots , b_0)$ with $b_n \ge b_{n-1} \ge \dots \ge b_0 \ge 0$ and $b_i + b_{n-i} = \frac{2}{m(m-1)}$ for all $i\in \{0,\dots ,n\}$ to compute the outcome. The probability assigned to an alternative x by a supporting size SDS f is then $f(R, x) = \sum _{y \in A {\setminus } \{x\}} b_{n_{xy}(R)}$. Point voting SDSs can be seen as a generalization of deterministic positional scoring rules and supporting size SDSs can be seen as a variant of Fishburn’s C2 functions (Fishburn 1977).

Theorem 3

(Barberà 1979b) An SDS is anonymous, neutral, and strategyproof if and only if it can be represented as a convex combination of a point voting SDS and a supporting size SDS.

Many well-known SDSs can be represented as point voting SDSs or supporting size SDSs. For example, the uniform random dictatorship $f_{ RD }$, which chooses one voter uniformly at random and returns his best alternative, is the point voting SDS defined by the scoring vector $\left( \frac{1}{n}, 0, \dots , 0\right)$. An instance of a supporting size SDS is the randomized Copeland rule $f_{C}$, which assigns probabilities proportional to the Copeland scores $c(x,R)=|\{y\in A{\setminus } \{x\}:n_{xy}(R)>n_{yx}(R)\}| + \frac{1}{2}|\{y\in A{\setminus } \{x\}:n_{xy}(R)=n_{yx}(R)\}|$. This SDS is the supporting size SDS defined by the vector $b=\left( b_n, b_{n-1}, \dots , b_0\right)$, where $b_i=\frac{2}{m(m-1)}$ if $i>\frac{n}{2}$, $b_i=\frac{1}{m(m-1)}$ if $i=\frac{n}{2}$, and $b_i=0$ otherwise. Furthermore, there are SDSs that can be represented both as point voting SDSs and supporting size SDSs. An example is the randomized Borda rule $f_B$, which randomizes proportional to the Borda scores of the alternatives. This SDS is the point voting SDS defined by the vector $\left( \frac{2(m-1)}{nm(m-1)}, \frac{2(m-2)}{nm(m-1)}, \ldots , \frac{2}{nm(m-1)},0\right)$ and equivalently the supporting size SDS defined by the vector $\left( \frac{2n}{nm(m-1)}, \frac{2(n-1)}{nm(m-1)}, \ldots , \frac{2}{nm(m-1)}, 0\right)$.²

2.2 Classic axioms and their relaxations

An alternative x Pareto-dominates another alternative y in a preference profile R if $x\succ _i y$ for all $i\in N$. The standard notion of ex post efficiency then demands that Pareto-dominated alternatives should have no chance of winning, i.e., $f(R,x)=0$ for all preference profiles R and alternatives x that are Pareto-dominated in R. Gibbard (1977) showed that Theorem 1 implies a simple characterization of strategyproof and ex post efficient SDSs. This result is commonly known as the random dictatorship theorem.

Corollary 1

(Gibbard 1977) The only strategyproof SDSs that satisfy ex post efficiency are random dictatorships, i.e., each voter is selected with a fixed probability and the most preferred alternative of this voter is returned as the winner.

When insisting on anonymity, Corollary 1 turns into a complete characterization of $f_{ RD }$. However, Corollary 1 breaks down once we allow that Pareto-dominated alternatives can have a non-zero chance $\beta >0$ of being selected. To illustrate this point, consider a random dictatorship d and another strategyproof SDS g. Then, the SDS $f^*=(1-\beta ) d + \beta g$ is strategyproof for every $\beta \in (0,1]$ and no random dictatorship, but assigns a probability of at most $\beta$ to Pareto-dominated alternatives. We call the last property $\beta$-ex post efficiency: an SDS f is $\beta$-ex post efficient if $f(R,x)\le \beta$ for all preference profiles R and alternatives x that are Pareto-dominated in R.

Our first objective is to study which strategyproof SDSs satisfy $\beta$-ex post efficiency for small values of $\beta$ because sufficiently small values of $\beta$ may be acceptable to accomplish other design goals. As it turns out, Corollary 1 is quite robust in the sense that all SDSs that satisfy $\beta$-ex post efficiency for $\beta <\frac{1}{m}$ are “similar” to random dictatorships. In order to formalize this phenomenon, we introduce $\gamma$-randomly dictatorial SDSs: a strategyproof SDS f is $\gamma$-randomly dictatorial if $\gamma \in [0,1]$ is the maximal value such that f can be represented as $f=\gamma d + (1-\gamma ) g$, where d is a random dictatorship and g is another strategyproof SDS. In particular, we require that g is strategyproof as otherwise, SDSs that seem “non-randomly dictatorial” are not 0-randomly dictatorial. For instance, the uniform lottery rule $f_U$, which always assigns probability $\frac{1}{m}$ to all alternatives, is not 0-randomly dictatorial if g is not required to be strategyproof because it can be represented as $f_U=\frac{1}{m}d_i+\frac{m-1}{m}g$, where $d_i$ is the dictatorial SDS of voter i and g is the SDS that randomizes uniformly over all alternatives but voter i’s favorite one. Moreover, it should be mentioned that the maximality of $\gamma$ implies that g is 0-randomly dictatorial if $\gamma <1$. Otherwise, we could also represent g as a mixture of a random dictatorship and some other strategyproof SDS h, which means that f is $\gamma '$-randomly dictatorial for $\gamma '>\gamma$.

The following characterization of $\gamma$-randomly dictatorial SDSs is very useful. Recall that $R^{i:yx}$ denotes the profile derived from R by only reinforcing y against x in voter i’s preference relation.

Lemma 1

A strategyproof SDS f is $\gamma$-randomly dictatorial if and only if there are non-negative values $\gamma _1,\dots , \gamma _n$ such that $\sum _{i\in N}\gamma _i=\gamma$, and $\gamma _i =\min _{x,y\in A} \min _{R \in \mathcal {R}^{i:xy}} f(R^{i:yx},y)-f(R,y)$ where $\mathcal {R}^{i:xy}\subseteq \mathcal {R}^n$ denotes the set of profiles in which voter i prefers x the most and y the second most.

The proof of this lemma can be found in the appendix. Lemma 1 provides an intuitive interpretation of $\gamma$-randomly dictatorial SDSs: it requires that there are voters who increase the winning probability of an alternative by at least $\gamma _i$ by swapping their two top-ranked alternatives. For small values of $\gamma$, this axiom seems uncontroversial and can be seen as a strict monotonicity property. However, for larger values of $\gamma$, $\gamma$-randomly dictatorial SDSs become more similar to random dictatorships. Furthermore, the proof of Lemma 1 shows that the decomposition of $\gamma$-randomly dictatorial SDSs is completely determined by the values $\gamma _1,\dots ,\gamma _n$: given these values for a strategyproof SDS f, it can be represented as $f=\sum _{i\in N}\gamma _i d_i + (1-\sum _{i\in N} \gamma _i)g$, where g is a strategyproof SDS and $d_i$ the dictatorial SDS of voter i. Thus, Lemma 1 directly provides a way to compute the value $\gamma$ for a given SDS f: we only need to determine the values $\gamma _1,\dots ,\gamma _n$ of f by computing $\gamma _i = \min _{x,y\in A} \min _{R \in \mathcal {R}^{i:xy}} f(R^{i:yx},y)-f(R,y)$ because then $\gamma = \sum _{i \in N} \gamma _i$.

Fig. 2

Condorcet-consistent SDSs violate strategyproofness when $m=n=3$. Due to the symmetry of $R'$, we may assume without loss of generality that $f(R',a) > 0$. It follows from Condorcet-consistency that $f(R,c) = 1$. Since it is not the case that $f(R)\succcurlyeq f(R')$, the left-most voter can manipulate by swapping c and b in R

Finally, we consider Condorcet-consistency. A Condorcet winner in a profile R is an alternative x that wins every majority comparison in R, i.e., $n_{xy}(R) > n_{yx}(R)$ for all $y \in A {\setminus } \{x\}$. Condorcet-consistency demands that $f(R,x)=1$ for all preference profiles R and alternatives x such that x is the Condorcet winner in R. Unfortunately, Condorcet-consistency is in conflict with strategyproofness, which can easily be derived from Gibbard’s work. A simple two-profile proof for this fact when $m=n=3$ is given in Fig. 2. To circumvent this impossibility, we relax Condorcet-consistency. Instead of requiring that the Condorcet winner always obtains probability 1, we only require that it receives a probability of at least $\alpha$. An SDS f is $\alpha$-Condorcet-consistent if $f(R,x)\ge \alpha$ for all profiles R and alternatives $x\in A$ such that x is the Condorcet winner in R. For small values of $\alpha$, this axiom is clearly compatible with strategyproofness and therefore, we are interested in the maximum value of $\alpha$ such that there are $\alpha$-Condorcet-consistent and strategyproof SDSs.

Table 1 Values of $\alpha$, $\beta$, and $\gamma$ for which specific strategyproof SDSs are $\alpha$-Condorcet-consistent, $\beta$-ex post efficient, and $\gamma$-randomly dictatorial

2.3 Examples of strategyproof SDSs

To illustrate the notions of $\alpha$-Condorcet-consistency, $\beta$-ex post efficiency, and $\gamma$-random dictatorships, let us discuss some of the values in Table 1. The uniform random dictatorship is 1-randomly dictatorial and 0-ex post efficient by definition. Moreover, it is 0-Condorcet-consistent because a Condorcet winner may not be top-ranked by any voter. The same values of $\alpha$, $\beta$, and $\gamma$ are also attained by non-uniform (and thus non-anonymous) random dictatorships. The randomized Borda rule is $\frac{2(m-2)}{m(m-1)}$-ex post efficient because it assigns this probability to an alternative that is second-ranked by every voter. Moreover, it is $\frac{2}{m(m-1)}$-randomly dictatorial as we can represent it as $\frac{2}{m(m-1)} f_ RD + \left( 1-\frac{2}{m(m-1)}\right) g$, where $f_ RD$ is the uniform random dictatorship and g is the point voting SDS defined by the scoring vector $\left( \frac{2(m-2)}{n(m(m-1) - 2)}, \frac{2(m-2)}{n(m(m-1) - 2)}, \frac{2(m-3)}{n(m(m-1) - 2)}, \dots , 0\right)$. Finally, the randomized Copeland rule is 0-randomly dictatorial because for every voter there is a profile in which he can swap his two best alternatives without affecting the outcome. Moreover, it is $\frac{2}{m}$-Condorcet-consistent because a Condorcet winner x satisfies that $n_{xy}(R)>\frac{n}{2}$ for all $y\in A\setminus \{x\}$ and hence, $f_C(R,x)=\sum _{y\in A{\setminus }\{x\}} b_{n_{xy}(R)}=(m-1)\frac{2}{m(m-1)}=\frac{2}{m}$.

The randomized Copeland and the randomized Borda rule can be interpreted as rules where two alternatives are drawn uniformly at random (see Remark 4). In the randomized Copeland rule, the majority-preferred of the two alternatives is selected, whereas in the randomized Borda rule, a randomly selected voter picks his preferred alternative. It is possible to define non-neutral variants of these rules, in which the two alternatives are not drawn independently (see Remark 3). As long as the total probability of drawing each alternative is still $\frac{2}{m}$, the resulting rules achieve the same values of $\alpha$, $\beta$, and $\gamma$ as their neutral counterparts in Table 1.

Note that Table 1 also contains a row corresponding to the uniform lottery rule $f_{ U }$ which always selects every alternative with probability $\frac{1}{m}$. We consider this SDS as a threshold with respect to $\alpha$-Condorcet-consistency and $\beta$-ex post efficiency because we can compute it without knowledge about the voters’ preferences. Hence, if an SDS performs worse than the uniform lottery rule with respect to $\alpha$-Condorcet-consistency or $\beta$-ex post efficiency, we could as well dismiss the voters’ preferences.

3 Results

We are now ready to state our results about $\alpha$-Condorcet-consistent and $\beta$-ex post efficient strategyproof SDSs.

3.1 $\alpha$-Condorcet-consistency

Our first result shows that no strategyproof SDS satisfies $\alpha$-Condorcet-consistency for $\alpha >\frac{2}{m}$. Conversely, this means that strategyproof SDSs can only be $\alpha$-Condorcet-consistent for $\alpha \in [0,\frac{2}{m}]$. This bound is tight as the randomized Copeland rule $f_C$ is $\frac{2}{m}$-Condorcet-consistent, which means that it is one of the “most Condorcet-consistent” strategyproof SDSs. Even more, we turn this observation into a characterization of $f_C$ by additionally requiring anonymity and neutrality: the randomized Copeland rule is the only strategyproof SDS that satisfies $\frac{2}{m}$-Condorcet-consistency, anonymity, and neutrality.

To prove these results, we derive several auxiliary lemmas. As the first step, we show in Lemma 2 that we can “symmetrize” any given strategyproof and $\alpha$-Condorcet-consistent SDS.

Lemma 2

Let $\alpha \in [0,1]$. If there is a strategyproof and $\alpha$-Condorcet-consistent SDS, there is also a strategyproof and $\alpha$-Condorcet-consistent SDS that satisfies anonymity and neutrality.

Proof

Let f denote an arbitrary strategyproof SDS that is $\alpha$-Condorcet-consistent for some $\alpha \in [0,1]$. In the sequel, we construct an anonymous and neutral SDS $f^*$ that satisfies strategyproofness and $\alpha$-Condorcet-consistency for the same $\alpha$ as f. For this, we define the SDSs $f^{\pi \tau }$ for all permutations $\pi :N\rightarrow N$ and $\tau :A\rightarrow A$ as follows. First, $f^{\pi \tau }$ permutes the voters in the input profile R according to $\pi$ and the alternatives according to $\tau$. Next, we compute f on the resulting profile $\tau (\pi (R))$ and finally, we define $f^{\pi \tau }(R,x)$ as the probability assigned to $\tau (x)$ by f in $\tau (\pi (R))$. More formally, $f^{\pi \tau }$ is defined as $f^{\pi \tau }(R,x)=f(\tau (\pi (R)), \tau (x))$, where the profile $\tau (\pi (R))$ satisfies for all $i\in N$ and $x,y\in A$ that $\tau (x)\succ _{\pi (i)} \tau (y)$ in $\tau (\pi (R))$ if and only if $x\succ _i y$ in R. Note that $f^{\pi \tau }$ is strategyproof for all permutations $\pi$ and $\tau$ because every manipulation of $f^{\pi \tau }$ implies a manipulation of f. Furthermore, $f^{\pi \tau }$ is $\alpha$-Condorcet-consistent because for every preference profile R with Condorcet winner x, $\tau (x)$ is the Condorcet winner in $\tau (\pi (R))$. Hence, if $f^{\pi \tau }$ violates $\alpha$-Condorcet-consistency in some profile R, then f violates this axiom in the profile $\tau (\pi (R))$.

Finally, we define the SDS $f^*$ by averaging over $f^{\pi \tau }$ for all permutations $\pi$ and $\tau$. Hence, let $\Pi$ denote the set of all permutations on N and let $\textrm{T}$ denote the set of all permutations on A. Then, $f^*$ is defined as follows.

$$\begin{aligned} f^*(R, x) :=&\sum _{\pi \in \Pi } \frac{1}{|\Pi |} \sum _{\tau \in \textrm{T}} \frac{1}{|\textrm{T}|} f^{\pi \tau }(R, x) \\ =&\sum _{\pi \in \Pi } \sum _{\tau \in \textrm{T}} \frac{1}{n!m!} f(\tau (\pi (R)), \tau (x)) \end{aligned}$$

Next, we show that $f^*$ satisfies all axioms required by the lemma. First, $f^*$ is strategyproof since all SDSs $f^{\pi \tau }$ are strategyproof. The $\alpha$-Condorcet-consistency of $f^*$ is shown by the following inequality, where R denotes a profile in which x is the Condorcet winner.

$$\begin{aligned} f^*(R, x) = \sum _{\pi \in \Pi } \sum _{\tau \in \textrm{T}} \frac{1}{n!m!} f(\tau (\pi (R)), \tau (x)) \ge \sum _{\pi \in \Pi } \sum _{\tau \in \textrm{T}} \frac{1}{n!m!} \alpha = \alpha \end{aligned}$$

Furthermore, observe that $f^*$ is anonymous because it averages over all possible permutations of the voters, i.e., for all permutations of the voters $\pi \in \Pi : f^*(R) = f^*(\pi (R))$. It follows from a similar argument that $f^*$ is neutral: since $f^*$ averages over all permutations of the alternatives, it holds that $f^*(R, x) = f^*(\tau (R), \tau (x))$ for every $\tau \in \textrm{T}$. Hence, $f^*$ is strategyproof, $\alpha$-Condorcet-consistent, anonymous, and neutral. $\square$

We next investigate the $\alpha$-Condorcet-consistency of strategyproof SDSs that satisfy anonymity and neutrality because Lemma 2 turns an upper bound on the $\alpha$-Condorcet-consistency of such SDSs into an upper bound for all strategyproof SDSs. Since Theorem 3 shows that every strategyproof, anonymous, and neutral SDS can be decomposed in a point voting SDS and a supporting size SDS, we analyze these two classes separately in the following two lemmas. First, we bound the $\alpha$-Condorcet-consistency of point voting SDSs.

Lemma 3

No point voting SDS is $\alpha$-Condorcet-consistent for $\alpha \ge \frac{2}{m}$ if $n \ge 3$ and $m \ge 3$.

Proof

Let f be a point voting SDS for $m \ge 3$ alternatives and $n \ge 3$ voters, and let $a=(a_1, \dots , a_m)$ be the scoring vector that defines f. Moreover, let $\alpha \in [0,1]$ be the maximal value such that f is $\alpha$-Condorcet-consistent. We will show that $\alpha <\frac{2}{m}$. The central observation for this is that $f(R,x)=f(R',x)$ for all profiles $R,R'$ with $r^*(x,R)=r^*(x,R')$ as f assigns probability $a_i$ to x whenever it is ranked i-th. As a consequence of this insight, we will focus on Condorcet winner candidates which are alternatives that can be made into the Condorcet winner without changing their rank vector. The reason for this is that Condorcet winner candidates must also have a probability of $\alpha$ due to our previous insights. Hence, we will construct profiles with $\lceil \frac{m}{2}\rceil$ Condorcet winner candidates because then each Condorcet winner candidate has a probability of at most $\frac{2}{m}$. Otherwise, $\sum _{x\in A} f(R,x)>1$, which contradicts the definition of an SDS. This shows that f is only $\alpha$-Condorcet-consistent for $\alpha \le \frac{2}{m}$ and, by investigating our profiles in more detail, we can also deduce that $\alpha \ne \frac{2}{m}$.

For constructing the required profiles with $k=\lceil \frac{m}{2}\rceil$ Condorcet winner candidates $x_1, \dots , x_k$, we use a case distinction with respect to the parity of n and m. Moreover, we first focus on cases with fixed n, and provide in the end an argument for generalizing our base profiles to all $n\ge 3$. Figure 3 illustrates our constructions for $n,m\in \{3,4\}$.

Case 1: $n=3$ and m is odd

In this case, we consider the profile $R^1$ which is defined as follows: for every $i \in \{1, \dots , k\}$, voters 1 and 2 rank alternative $x_i$ at position i, and voter 3 ranks it at position $m + 2 - 2i$. The remaining alternatives can be ranked arbitrarily. The sum of ranks of $x_i$ in $R^1$ is then equal to $\sum _{j\in \{1,2,3\}} r(x_i, \succ _j)=2i + m + 2 - 2i = m + 2$, which means that only $m - 1$ alternatives can be ranked above $x_i$. Hence, for every $i\in \{1,\dots , k\}$, we can reorder the alternatives in $A\setminus \{x_i\}$ such that each alternative $y\in A\setminus \{x_i\}$ is preferred to $x_i$ by a single voter. So, $x_i$ is a Condorcet winner candidate in $R^1$ and $f(R^1,x_i)\ge \alpha$ for all $i\in \{1,\dots ,k\}$. Since m is odd and $k=\lceil \frac{m}{2} \rceil =\frac{m+1}{2}$, this implies that $\alpha \le \frac{2}{m+1}<\frac{2}{m}$.

Case 2: $n=3$ and m is even

Next, suppose that $n=3$ and m is even. In this case, we first choose $m-1$ candidates from A and construct the profile $R^1$ of Case 1. Then, we add the last alternative z as the last-ranked one of voters 1 and 2 and as the first-ranked one of voter 3 to derive the profile $R^2$. The candidates $x_1, \dots , x_k$ are Condorcet winning candidates in $R^2$ as they are in $R^1$ and only voter 3 prefers z to $x_i$. Hence, there are $\frac{m}{2}$ Condorcet winner candidates and an analogous argument as in the last case shows that $\alpha \le \frac{2}{m}$. As the last step, we will show that $\alpha \ne \frac{2}{m}$. Otherwise, each of the $\frac{m}{2}$ Condorcet winner candidates has a probability of $\frac{2}{m}$, which entails that the other alternatives have a probability of 0. In particular, $f(R^2,z)=0$ even though voter 3 reports z as his best alternative. This implies for the scoring vector $a=(a_1, \dots , a_m)$ of f that $a_1=0$. However, this is not possible because the scoring vector a satisfies $\sum _{i=1}^m a_i=\frac{1}{n}$ and $a_i\ge a_j$ if $i\le j$. Hence, $\alpha <\frac{2}{m}$.

Case 3: $n=4$ and m is odd

As third case, we suppose $n=4$ and m is odd and construct the profile $R^3$ as follows: for every $i \in \{1, \dots , k\}$, voters 1 and 2 rank alternative $x_i$ at position i, and voters 3 and 4 rank it at position $\frac{m + 1}{2} + 1 - i$. The remaining alternatives can again be placed arbitrarily. For each $x_i$, it holds that $\sum _{j\in \{1,2,3,4\}} r(x_i, {\succ _j})=2i + 2\left( \frac{m + 1}{2} + 1 - i\right) = m + 3$. Consequently, only $m - 1$ alternatives can be ranked above $x_i$ for every $i\in \{1,\dots , k\}$, and all $x_i$ thus are Condorcet winner candidates. We can now derive that $\alpha \le \frac{2}{m+1}<\frac{2}{m}$ as there are $\frac{m+1}{2}$ Condorcet winner candidates.

Case 4: $n=4$ and m is even

In the last case, we construct the profile $R^4$ with $k=\frac{m}{2}$ Condorcet winner candidates as follows: we choose an alternative z, and apply the construction of Case 3 to the alternatives in $A\setminus \{z\}$. Then, voters 1 to 3 add z as their least preferred alternative and voter 4 adds it as his best alternative. Every alternative that is a Condorcet winner candidate before adding z is also a Condorcet winner candidate after adding this alternative because z is the least preferred alternative of three voters. Hence, there are $\frac{m}{2}$ Condorcet winner candidates in $R^4$, which implies that $\alpha \le \frac{m}{2}$. Finally, if $\alpha = \frac{2}{m}$, then $f(R^4, z) = 0$, which, analogous to Case 2, conflicts with the definition of point voting SDSs since voter 4 reports z as his favorite choice. Therefore, we infer again that $\alpha < \frac{2}{m}$.

Fig. 3

Profiles used in the base cases of the proof of Lemma 3 if $m\in \{3,4\}$. The profile $R^k$ shows the profile corresponding to case k

Case 5: Generalizing the impossibility to larger n

Finally, we explain how to generalize the last four cases to an arbitrary number of voters $n\ge 3$. For this, we choose the suitable base case and add repeatedly pairs of voters with inverse preferences until there are n voters. Note that voters with inverse preferences do not change the majority margins, and therefore they do not change whether an alternative is a Condorcet winner candidate. Hence, every alternative that is a Condorcet winner candidate in the base case is also a Condorcet winner candidate in the extended profile, which means that the arguments in the base cases also apply to larger numbers of voters. Therefore, no point voting SDS satisfies $\alpha$-Condorcet-consistency for $\alpha \ge \frac{2}{m}$. $\square$

The last ingredient for the proof of Theorem 4 is that no supporting size SDS can assign a probability of more than $\frac{2}{m}$ to any alternative. This immediately implies that no supporting size SDS satisfies $\alpha$-Condorcet-consistency for $\alpha >\frac{2}{m}$.

Lemma 4

No supporting size SDS can assign more than probability $\frac{2}{m}$ to an alternative.

Proof

Let f be a supporting size SDS and let $b=(b_n, \dots , b_0)$ be the scoring vector that defines f. Recall that the definition of a supporting size SDS requires that $b_n \ge \dots \ge b_0 \ge 0$ and $b_i + b_{n-i} = \frac{2}{m(m-1)}$ for all $i\in \{0,\dots , n\}$. This implies that $b_i \le \frac{2}{m(m-1)}$ for all $i\in \{0,\dots , n\}$ and hence $f(R, x) = \sum _{y \in A {\setminus } \{x\}} b_{n_{xy}(R)} \le (m - 1)\frac{2}{m(m-1)} = \frac{2}{m}$ for all preference profiles R and alternatives $x\in A$. $\square$

We now have all lemmas required to prove our first theorem.

Theorem 4

The randomized Copeland rule is the only strategyproof SDS that satisfies anonymity, neutrality, and $\frac{2}{m}$-Condorcet-consistency if $m \ge 3$ and $n \ge 3$. Moreover, no strategyproof SDS satisfies $\alpha$-Condorcet-consistency for $\alpha > \frac{2}{m}$ if $n \ge 3$.

Proof

The theorem consists of two claims: the characterization of the randomized Condorcet rule $f_C$ and the fact that no other strategyproof SDS can attain $\alpha$-Condorcet-consistency for a larger $\alpha$ than $f_C$. We prove these claims separately.

Claim 1: The randomized Copeland rule is the only strategyproof SDS that satisfies $\frac{2}{m}$-Condorcet-consistency, anonymity, and neutrality.

The randomized Copeland rule $f_C$ is a supporting size SDS and satisfies therefore anonymity, neutrality, and strategyproofness. Furthermore, it satisfies also $\frac{2}{m}$-Condorcet-consistency because a Condorcet winner x wins every pairwise majority comparison in R. Hence, $n_{xy}(R)> \frac{n}{2}$ for all $y\in A{\setminus } \{x\}$, which implies that $f_C(R,x) = \sum _{y \in A {\setminus } \{x\}}b_{n_{xy}(R)} = (m - 1)\frac{2}{m(m-1)} = \frac{2}{m}$.

Next, let f be an SDS satisfying anonymity, neutrality, strategyproofness, and $\frac{2}{m}$-Condorcet-consistency. We show that f is the randomized Copeland rule. Since f is anonymous, neutral, and strategyproof, we can apply Theorem 3 to represent f as $f=\lambda f_{ point } + (1-\lambda ) f_{ sup }$, where $\lambda \in [0,1]$, $f_{ point }$ is a point voting SDS, and $f_{ sup }$ is a supporting size SDS. Lemma 3 states that there is a profile R with Condorcet winner x such that $f_{ point }(R,x)<\frac{2}{m}$, and it follows from Lemma 4 that $f_{ sup }(R,x)\le \frac{2}{m}$. Hence, $f(R,x)=\lambda f_{ point }(R,x)+f_{ sup }(R,x)<\frac{2}{m}$ if $\lambda >0$. Therefore, f is a supporting size SDS as it satisfies $\frac{2}{m}$-Condorcet-consistency.

Next, we show that f has the same scoring vector as the randomized Copeland rule. Since f is a supporting size SDS, there is a scoring vector $b=(b_n, \dots , b_0)$ with $b_n \ge b_{n-1} \ge \dots \ge b_0 \ge 0$ and $b_i + b_{n - i} = \frac{2}{m(m-1)}$ for all $i\in \{1,\dots , n\}$ such that $f(R, x) = \sum _{y \in A{\setminus } \{x\} } b_{n_{xy}(R)}$. Moreover, $f(R, x) = \frac{2}{m}$ if x is the Condorcet winner in R because of $\frac{2}{m}$-Condorcet-consistency and Lemma 4. We derive from the definition of supporting size SDSs that the Condorcet winner x can only achieve this probability if $b_{n_{xy(R)}}=\frac{2}{m(m-1)}$ for every other alternatives $y\in A{\setminus } \{x\}$. Moreover, observe that the Condorcet winner needs to win every majority comparison but is indifferent about the exact supporting sizes. Hence, it follows that $b_{i} = \frac{2}{m(m-1)}$ for all $i>\frac{n}{2}$ as otherwise, there is a profile in which the Condorcet winner does not receive a probability of $\frac{2}{m}$. We also know that $b_{i} + b_{n-i} = \frac{2}{m(m-1)}$, so $b_{i} = 0$ for all $i<\frac{n}{2}$. If n is even, then $b_{\frac{n}{2}} = \frac{1}{m(m-1)}$ is required by the definition of supporting size SDSs as $\frac{n}{2}=n-\frac{n}{2}$. Hence, the scoring vector of f is equal to the scoring vector of $f_C$, which proves that f is $f_C$.

Claim 2: No strategyproof SDS satisfies $\alpha$-Condorcet-consistency for $\alpha >\frac{2}{m}$.

The claim is trivially true if $m \le 2$ because $\alpha$-Condorcet-consistency for $\alpha >1$ is impossible. Hence, let f denote a strategyproof SDS for $m\ge 3$ alternatives. We show in the sequel that f cannot satisfy $\alpha$-Condorcet-consistency for $\alpha >\frac{2}{m}$. As a first step, we use Lemma 2 to construct a strategyproof SDS $f^*$ that satisfies anonymity, neutrality, and $\alpha$-Condorcet-consistency for the same $\alpha$ as f. Since $f^*$ is anonymous, neutral, and strategyproof, it follows from Theorem 3 that $f^*$ can be represented as a mixture of a point voting SDS $f_{ point }$ and a supporting size SDS $f_{ sup }$, i.e., $f^* = \lambda f_{ point } + (1 - \lambda ) f_{ sup }$ for some $\lambda \in [0,1]$.

Next, we consider $f_{ point }$ and $f_{ sup }$ separately. Lemma 3 implies for $f_{ point }$ that there is a profile R with a Condorcet winner a such that $f_{ point }(R,a)<\frac{2}{m}$. Moreover, Lemma 4 shows that $f_{ sup }(R,a)\le \frac{2}{m}$. Thus, we derive the following inequality, which shows that $f^*$ fails $\alpha$-Condorcet-consistency for $\alpha > \frac{2}{m}$. Hence, no strategyproof SDS satisfies $\alpha$-Condorcet-consistency for $\alpha > \frac{2}{m}$ when $n \ge 3$.

$$\begin{aligned} \alpha \le f^*(R, a) = \lambda f_{ point }(R, a) + (1 - \lambda ) f_{ sup }(R, a) \le \lambda \frac{2}{m} + (1 - \lambda )\frac{2}{m} = \frac{2}{m} \end{aligned}$$

$\square$

Remark 1

Lemma 2 can be applied to properties other than $\alpha$-Condorcet-consistency as well. For example, given a strategyproof and $\beta$-ex post efficient SDS, one can construct another SDS that satisfies anonymity and neutrality on top of these axioms. In general, our construction maintains all axioms that can be described by linear inequalities and that are themselves closed under permutations of voters and alternatives.

Remark 2

Point voting SDSs can be interpreted as positional scoring rules that randomize in proportion to the assigned scores. A result by Smith (1973) shows that for large n, every scoring rule except Borda’s rule can assign the Condorcet winner the lowest score. Hence, for every point voting SDS except the randomized Borda rule, there is a profile where the Condorcet winner receives less than probability $\frac{1}{m}$. On the other hand, the randomized Borda rule $f_B$ is $\left( \frac{1}{m} + \frac{2 - (n\mod 2)}{nm}\right)$-Condorcet-consistent. This argument gives a more restrictive bound on the $\alpha$-Condorcet-consistency of point voting SDSs when there is a large number of voters. Moreover, it shows that $f_B$ is a point voting SDS that maximizes the $\alpha$-Condorcet-consistency when considering large electorates.

Remark 3

All axioms in the characterization of the randomized Copeland rule are independent of each other. The SDS that picks the Condorcet winner with probability $\frac{2}{m}$ if one exists and distributes the remaining probability uniformly between the other alternatives only violates strategyproofness. The randomized Borda rule satisfies all axioms of Theorem 4 but $\frac{2}{m}$-Condorcet-consistency. An SDS that satisfies anonymity, strategyproofness, and $\frac{2}{m}$-Condorcet-consistency can be defined based on an arbitrary order of alternatives $x_0,\dots , x_{m-1}$. Then, we pick an index $i\in \{0, \dots , m-1\}$ uniformly at random and return the winner of the majority comparison between $x_i$ and $x_{i+1\bmod m}$ (if there is a majority tie, a fair coin toss decides the winner). Furthermore, we can use the randomized Copeland rule $f_C$ to construct an SDS that fails only anonymity for even n: we just ignore one voter when computing the outcome of $f_C$. If n is even and x is the Condorcet winner in R, then $n_{xy}(R)\ge \frac{n+2}{2}$ for all $y\in N{\setminus } \{x\}$ and x remains the Condorcet winner after removing a single voter. Finally, the impossibility in Theorem 4 does not hold when there are only $n=2$ voters because random dictatorships are strategyproof and Condorcet-consistent in this case.

Remark 4

The randomized Copeland rule has various interesting interpretations. Firstly, it can be defined as a supporting size SDS as shown in Sect. 2.1. Alternatively, it can be defined as the SDS that picks two alternatives uniformly at random and then picks the majority winner between them; majority ties are broken by a fair coin toss. Next, Theorem 4 shows that the randomized Copeland rule is the SDS that maximizes the value of $\alpha$ for $\alpha$-Condorcet-consistency among all anonymous, neutral, and strategyproof SDSs. Finally, the randomized Copeland rule is the only strategyproof SDS that satisfies anonymity, neutrality, and assigns probability 0 to a Condorcet loser (i.e., an alternative that loses all pairwise comparisons) whenever it exists.

3.2 $\beta$-ex post efficiency and $\gamma$-random dictatorships

In this section, we show that the random dictatorship theorem (Corollary 1) is rather robust by identifying a tradeoff between $\beta$-ex post efficiency and $\gamma$-random dictatorships. More formally, we prove that for every $\varepsilon \in [0,1]$, all strategyproof and $\frac{1-\varepsilon }{m}$-ex post efficient SDSs are $\gamma$-randomly dictatorial for $\gamma \ge \varepsilon$. If we set $\varepsilon =1$, we obtain Corollary 1. Conversely, our result also entails that $\gamma$-randomly dictatorial SDSs can only satisfy $\frac{1 - \varepsilon }{m}$-ex post efficiency for $\varepsilon \le \gamma$. Moreover, one can derive from this theorem that every 0-randomly dictatorial and strategyproof SDS is $\beta$-ex post efficient for $\beta \ge \frac{1}{m}$, i.e., every such SDS is at least as inefficient as the uniform lottery rule. Finally, we also investigate the SDSs that optimize the tradeoff between being both $\gamma$-randomly dictatorial and $\beta$-ex post efficient for small values of $\gamma$ and $\beta$. In particular, from our first claim, we know that a strategyproof and $\frac{1-\varepsilon }{m}$-randomly dictatorial SDS is $\beta$-ex post efficient for $\beta \ge \varepsilon$, and we show for every $\varepsilon \in [0,1]$ that mixtures of the uniform random dictatorship and the uniform lottery rule are the only SDSs that satisfy $\beta = \varepsilon$ when additionally requiring anonymity and $m\ge 4$. These results demonstrate that relaxing ex post efficiency does not lead to interesting strategyproof SDSs.

For proving the tradeoff between $\beta$-ex post efficiency and $\gamma$-random dictatorships, we first investigate the efficiency of 0-randomly dictatorial strategyproof SDSs. In more detail, we prove next that every such SDS fails $\beta$-ex post efficiency for $\beta < \frac{1}{m}$. In particular, this means that every 0-randomly dictatorial SDS is as ”inefficient” as the uniform lottery rule and we thus interpret Proposition 1 as a negative result.

Proposition 1

No strategyproof SDS that is 0-randomly dictatorial satisfies $\beta$-ex post efficiency for $\beta < \frac{1}{m}$ if $m \ge 3$.

The proof of this result is deferred to the appendix because it is rather involved; instead, we only give a short summary here. First, we note that we cannot apply Lemma 2 as convex combinations of 0-randomly dictatorial SDSs may not be 0-randomly dictatorial. Hence, we work with Theorem 1 and decompose a strategyproof SDS into a mixture of duples and a mixture of unilaterals. For both classes, we show that if the considered SDS is 0-randomly dictatorial, it fails $\beta$-ex post efficiency for $\beta < \frac{1}{m}$. Next, we consider an arbitrary 0-randomly dictatorial SDS f and aim to show that there are a profile R and a Pareto-dominated alternative $x\in A$ such that $f(R,x)\ge \beta$. Even though Theorem 1 allows us to represent f as the convex combination of a 0-randomly dictatorial mixture of unilaterals $f_{ uni }$ and a 0-randomly dictatorial mixture of duples $f_{ duple }$, our previous observations have no direct consequences for the $\beta$-ex post efficiency of f as $f_{ uni }$ and $f_{ duple }$ may violate $\beta$-ex post efficiency for different profiles or alternatives. We solve this problem by transforming f into a more symmetric SDS $f^*$ while preserving 0-random dictatorship and $\beta$-ex post efficiency. We then decompose $f^*$ into a 0-randomly dictatorial mixture of unilaterals $f_{ uni }^*$ and a 0-randomly dictatorial mixture of duples $f_{ duple }^*$, and due to the symmetry of $f^*$, we identify a profile R where $f_{ uni }^*$ and $f_{ duple }^*$ assign both at least probability $\frac{1}{m}$ to the same Pareto-dominated alternative. Consequently, $f^*$ fails $\beta$-ex post efficiency for $\beta <\frac{1}{m}$, which implies that also f violates this axiom.

Based on Proposition 1, we next formalize the tradeoff between ex post efficiency and the similarity to random dictatorships in Theorem 5.

Theorem 5

For every $\varepsilon \in [0,1]$, every strategyproof and $\frac{1 - \varepsilon }{m}$-ex post efficient SDS is $\gamma$-randomly dictatorial for $\gamma \ge \varepsilon$ if $m\ge 3$. Moreover, when $m \ge 4$, every strategyproof and $\varepsilon$-randomly dictatorial SDS that satisfies anonymity and $\frac{1 - \varepsilon }{m}$-ex post efficiency is a mixture of the uniform random dictatorship and the uniform lottery rule.

Proof

Just as for Theorem 4, we need to show two claims: (i) for every $\varepsilon \in [0,1]$, there is no strategyproof and $\frac{1 - \varepsilon }{m}$-ex post efficient SDS that is $\gamma$-randomly dictatorial for $\gamma <\varepsilon$, and (ii) every strategyproof and $\varepsilon$-randomly dictatorial SDS that satisfies anonymity, neutrality, and $\frac{1 - \varepsilon }{m}$-ex post efficiency is a mixture of the uniform random dictatorship and the uniform lottery rule.

Claim 1: Every strategyproof and $\frac{1 - \varepsilon }{m}$-ex post efficient SDS is $\gamma$-randomly dictatorial for $\gamma \ge \varepsilon$.

Consider an arbitrary SDS f that is strategyproof and $\frac{1 - \varepsilon }{m}$-ex post efficient for some $\varepsilon \in [0,1]$. By the definition of $\gamma$-randomly dictatorial SDSs, there is a maximal $\gamma \in [0,1]$ such that f can be represented as $f = \gamma d + (1 - \gamma ) g$, where d is a random dictatorship and g is another strategyproof SDS. We need to show that $\gamma \ge \varepsilon$. If $\gamma =1$, this is trivially the case since $\varepsilon \in [0,1]$. On the other hand, if $\gamma <1$, the maximality of $\gamma$ entails that the SDS g is 0-randomly dictatorial. Hence, Proposition 1 shows that g is at most $\frac{1}{m}$-ex post efficient, i.e., there is a profile R with a Pareto-dominated alternative x such that $g(R,x)\ge \frac{1}{m}$. Since f is $\frac{1-\varepsilon }{m}$-ex post efficient, we derive therefore the following inequality.

$$\begin{aligned} \frac{1-\varepsilon }{m}\ge f(R, x) = \gamma d(R, x) + (1 - \gamma ) g(R, x) \ge \frac{1 - \gamma }{m} \end{aligned}$$

This inequality is equivalent to $\varepsilon \le \gamma$ and therefore proves the claim.

Claim 2: Every strategyproof and $\varepsilon$-randomly dictatorial SDS that satisfies anonymity and $\frac{1-\varepsilon }{m}$-ex post efficiency is a mixture of the uniform random dictatorship and the uniform lottery rule.

Consider an arbitrary $\varepsilon \in [0,1]$ and let f denote an SDS for $m\ge 4$ alternatives that satisfies all axioms listed above. In particular, f is $\varepsilon$-randomly dictatorial and therefore, it can be represented a $f=\varepsilon d + (1-\varepsilon ) g$, where d is a random dictatorship and g another strategyproof SDS. As a first step, we show that d is the uniform random dictatorship. Note for this that anonymity implies that the values $\gamma _1, \dots , \gamma _n$ introduced in Lemma 1 are equal for all voters, i.e., $\gamma _i=\gamma _j$ for all $i,j\in N$. A close inspection of the proof of Lemma 1 then reveals that d is the uniform random dictatorship because we prove for this lemma that, given the values $\gamma _i$, f can be represented as $f=\sum _{i\in N} \gamma _i d_i+ (1-\sum _{i\in N}\gamma _i)g$. Here, $d_i$ denotes the dictatorial SDS of voter i. Hence, f is the uniform random dictatorship if $\varepsilon =1$, so our claim holds in this case.

Next, assume that $\varepsilon <1$. In this case, the maximality of $\varepsilon$ implies that the SDS g is 0-randomly dictatorial. Furthermore, g needs to satisfy $\frac{1}{m}$-ex post efficiency as otherwise, there is a profile R with a Pareto-dominated alternative x such that $f(R,x)=\varepsilon d(R,x)+(1-\varepsilon )g(R,x)>\frac{1-\varepsilon }{m}$. This contradicts, however, the assumption that f is $\frac{1-\varepsilon }{m}$-ex post efficient. As the last point on g, observe that it is also anonymous as both d and f satisfy this axiom.

Since g is strategyproof, we can use Theorem 1 to represent g as a convex combination of unilateral SDSs and duple SDSs, i.e., $g = \lambda f_{ uni } + (1 - \lambda ) f_{ duple }$ for some $\lambda \in [0, 1]$, mixture of unilateral SDSs $f_{ uni }$, and mixture of duple SDSs $f_{ duple }$. We will show that both $f_{ uni }$ and $f_{ duple }$ always return the uniform lottery.

We start with the proof for $f_{ duple } = f_U$ and assume for contradiction that this is not the case. Then, a profile R and alternative x exists such that $f_{ duple }(R, x) > \frac{1}{m}$. Let $R'$ denote the profile derived from R by pushing x to the top of the preferences of all voters, and let $R^x$ denote an arbitrary profile in which all voters unanimously rank x first. By strategyproofness, $\frac{1}{m} < f_{ duple }(R, x) \le f_{ duple }(R', x) = f_{ duple }(R^x, x)$. Furthermore, for all alternatives $y \in A$ and profiles $R^y$, we have $f_{ duple }(R^y, y) \ge \frac{1}{m}$ as otherwise $\frac{1}{m}$-ex post efficiency is violated for some alternative $z \in A \setminus \{y\}$.

Next, we apply Lemma 2 to $f_{ duple }$ to construct a new SDS $f^*_{ duple }$. By construction, $f^*_{ duple }$ is a mixture of duples that satisfies anonymity, neutrality, strategyproofness, and $\frac{1}{m}$-ex post-efficiency. Hence, we derive from Theorem 3 that $f^*_{ duple }$ is a supporting size SDS. Let $b=(b_n, \dots , b_0)$ be the scoring vector such that $f^*_{ duple }(R, x) = \sum _{y \in A {\setminus } \{x\}} b_{n_{xy}(R)}$ and recall that b satisfies $b_n \ge \dots \ge b_0 \ge 0$ and $b_i + b_{n - i} = \frac{2}{m(m - 1)}$ for all $i \in \{0, \dots , n\}$. Now, since $f_{ duple }(R^y, y) \ge \frac{1}{m}$ for all $y \in A$ and $f_{ duple }(R^x, x) > \frac{1}{m}$ for some $x \in A$, it follows that $f^*_{ duple }(R^z, z) > \frac{1}{m}$ for all alternatives z and profiles $R^z$ as the construction of Lemma 2 only averages the probabilities of $f_{ duple }$. In particular, this means that $f^*_{ duple }$ is not the uniform lottery.

We will now derive a contradiction to $f^*_{ duple }\ne f_U$. For this, let $R^{xy}$ be the profile in which all agents rank x first and y second. By $\frac{1}{m}$-ex post efficiency and the definition of supporting size SDSs, $\frac{1}{m} \ge f^*_{ duple }(R^{xy}, y) = \sum _{z \in A {\setminus } \{y\}} b_{n_{yz}(R)} = b_0 + (m - 2) b_n$. This implies that $\frac{1}{m}\ge b_0 + (m - 2) \left( \frac{2}{m(m - 1)} - b_0\right) = -(m-3) b_0 + \frac{2(m-2)}{m(m-1)}$. Solving for $b_0$ then results in $b_0\ge \frac{1}{m(m-1)}$; in particular, $m\ge 4$ prevents that $m-3=0$. Since the definition of supporting size schemes requires that $b_0 + b_{n} = \frac{2}{m(m - 1)}$ and $b_i\ge b_j$ if $i>j$, we can now infer that $b_i = \frac{1}{m(m - 1)}$ for all $i \in \{0, \dots , n\}$. Hence, $f^*_{ duple }$ is the uniform lottery rule, which contradicts our previous observations. Therefore, $f_{ duple }$ must also be the uniform lottery.

Next, we turn to $f_{ uni }$. First, we note that $f_{ uni }$ must be anonymous, 0-randomly dictatorial, and $\frac{1}{m}$-ex post efficient since f satisfies these axioms and $f_{ duple }$ is the uniform lottery rule. Now, since $f_{ uni }$ is anonymous, there is a unilateral $f^*$ such that $f_{ uni }(R)=\sum _{i\in N} \frac{1}{n} f^*(\succ _i)$. This follows from the following averaging argument: given some weights $\lambda _i\ge 0$ and unilaterals $f^i$ such that $f_{ uni }=\sum _{i\in N}\lambda _i f^i$, we can construct a new representation of $f_{ uni }$ by averaging the $f^i$ over all permutations $\pi :N\rightarrow N$, i.e., ${\bar{f}}^i=\sum _{\pi \in \Pi } \frac{1}{n!} f^{\pi (i)}$. Since $f_{ uni }$ is anonymous, it holds that $f_{ uni }(R)=\sum _{\pi \in \Pi } \frac{1}{n!} f_{ uni }(\pi (R))=\sum _{i\in N}\frac{1}{n} {\bar{f}}^i$. Finally, it can be checked that ${\bar{f}}^i={\bar{f}}^j$ for all $i,j\in N$, which shows that $f_{ uni }(R)=\sum _{i\in N} \frac{1}{n} f^*(\succ _i)$.

For showing that $f_{ uni }=f_U$, we will prove that $f^*$ always returns the uniform lottery. Hence, we focus from now on a single voter i. Note here that $f^*$ is $\frac{1}{m}$-ex post efficient and 0-randomly dictatorial as otherwise, $f_{ uni }$ fails these properties, too. Hence, there are alternatives $x,y\in A$ and a preference relation $\succ _i$ with $r(x,\succ _i)=1$ and $r(y,\succ _i)=2$ such that $f^*(\succ _i) = f^*(\succ ^{i:yx}_i)$. Moreover, strategyproofness shows that this equality also holds if voter i reorders the alternatives $z\in A{\setminus } \{x,y\}$. Now, let $\succ ^{a_1}_i=a_1\succ \dots$, $\succ ^{a_1a_2}_i=a_1\succ _i a_2\succ _i\dots$, and $\succ ^{a_1a_2a_3}_i=a_1\succ _i a_2\succ _i a_3\succ _i\dots$ denote the preference relations in which voter i prefers the alternatives in the superscript the most. In particular, note that $f^*(\succ ^{xy}_i,a)=f^*(\succ ^{yx}_i,a)$ for $a\in \{x,y\}$.

Now, consider an arbitrary preference relation $\succ ^z_i$. We will show that $f^*(\succ ^z_i,z)=\frac{1}{m}$ because $\frac{1}{m}$-ex post efficiency then requires that $f^*(\succ ^z_i)$ is the uniform lottery. Note for this that this axiom immediately entails that $f^*(\succ ^z_i,z)\ge \frac{1}{m}$ because otherwise, there is a Pareto-dominated alternative $z'$ such that $f^*(\succ ^z_i,z')>\frac{1}{m}$. First, suppose that $z=x$. Then, it holds that $f^*(\succ ^x_i,x)=f^*(\succ ^{xy}_i,x)=f^*(\succ ^{yx}_i,x)\le \frac{1}{m}$, where the first equality follows from strategyproofness, the second one from the definition of x and y, and the final inequality from $\frac{1}{m}$-ex post efficiency. Together with our lower bound, we thus have that $f^*(\succ ^x_i,x)=\frac{1}{m}$. An analogous argument also holds for all preference relations $\succ ^y_i$.

Hence, suppose now that $z\not \in \{x,y\}$ and consider the preference relations $\succ _i^{xzy}$, $\succ _i^{yzx}$, $\succ _i^{zxy}$, and $\succ _i^{zyx}$. By the last case, it holds that $f^*(\succ _i^{xzy},a)=f^*(\succ _i^{yzx},a)=\frac{1}{m}$ for all $a\in A$. Localizedness thus implies that $f^*(\succ _i^{zxy},y)=f^*(\succ _i^{xzy},y)=\frac{1}{m}$ and $f^*({\succ _i^{zyx}},x)=f^*({\succ _i^{yzx}},x)=\frac{1}{m}$. On the other hand, non-perversity requires that $f^*(\succ _i^{zxy},x)\ge f^*({\succ _i^{zyx}},x)=\frac{1}{m}$. Finally, since $f^*(\succ _i^{xzy},a)=\frac{1}{m}$ for all a and since we can go from $\succ _i^{xzy}$ to $\succ _i^{zxy}$ by only swapping x and z, localizedness requires that $f^*(\succ _i^{zxy},z)\le \frac{1}{m}$. Hence, our lower bounds requires again that $f^*(\succ _i^z)=f^*(\succ _i^{zxy},z) =\frac{1}{m}$, which proves that $f^*$ always returns the uniform lottery. Thus, $f_{ uni }=f_U$.

Since $f_{ duple }$ and $f_{ uni }$ are both the uniform lottery rule, g itself is also the uniform lottery rule. So, the original SDS f is indeed a mixture of the uniform lottery rule and the uniform random dictatorship. $\square$

Remark 5

All axioms of the characterization in Theorem 5 are independent of each other if $\varepsilon \in (0, 1)$. Mixtures of the uniform random dictatorship and the Condorcet rule (choose the Condorcet winner if there is one, otherwise return the uniform lottery) satisfy all axioms except strategyproofness. Without anonymity, the uniform random dictatorship can be replaced with other random dictatorships. If we drop the constraint that $\varepsilon = \gamma$ or when $m = 3$ the randomized Copeland rule also satisfies all required axioms and the uniform lottery rule thus is not the unique choice.

Remark 6

Theorem 5 shows that the uniform lottery rule is the only strategyproof SDS that is 0-randomly dictatorial, $\frac{1}{m}$-ex post efficient, and anonymous. This insight strengthens the negative consequences of Proposition 1 as it demonstrates that every other anonymous and strategyproof 0-random dictatorship is strictly less efficient than the uniform lottery rule. We interpret this (as well as Proposition 1) as an impossibility result stating that no strategyproof and 0-randomly dictatorial SDS performs well with respect to $\beta$-ex post efficiency.

Remark 7

Another natural variant of $\beta$-ex post efficiency is to bound the sum of probabilities assigned to Pareto-dominated alternatives. When requiring anonymity and neutrality, it is easy to show that every strategyproof and 0-randomly dictatorial SDS assigns at least a total probability of $\frac{1}{2}$ to Pareto-dominated alternatives. Based on such a result, one can then also generalize Theorem 5. On the other hand, if we drop anonymity and neutrality, things become much more difficult, and the bound of $\frac{1}{2}$ does no longer hold. For example, consider the following SDS f for m alternatives and $n=\left( {\begin{array}{c}m\\ 2\end{array}}\right)$ voters: each voter is associated with a unique pair of alternatives x, y and if x or y is his first choice, the voter assigns probability $\frac{1}{2n}$ to both his best and second best alternative; otherwise, he assigns probability $\frac{1}{n}$ to his best alternative. It can be checked that f is strategyproof, 0-randomly dictatorial, and always assigns strictly less than probability $\frac{1}{2}$ to Pareto-dominated alternatives. Thus, contrary to all of our results, the availability of anonymity and neutrality plays an important role for a bound on the sum of probabilities of Pareto-dominated alternatives.

3.3 $\beta$-ex post efficiency and $\alpha$-Condorcet-consistency

As our last result, we identify a tradeoff between $\alpha$-Condorcet-consistency and $\beta$-ex post efficiency: every $\alpha$-Condorcet-consistent and strategyproof SDS fails $\beta$-ex post efficiency for $\beta < \frac{m - 2}{m - 1}\alpha$. Or, put differently, every stategyproof and $\alpha$-Condorcet-consistent SDS satisfies $\beta$-ex post efficiency only for $\beta \ge \frac{m - 2}{m - 1}\alpha$. This result follows essentially from the correlation between $\beta$-ex post efficiency and $\gamma$-random dictatorships identified in Theorem 5: since every $\frac{1-\varepsilon }{m}$-ex post efficient SDS f is at least $\varepsilon$-randomly dictatorial and since random dictatorships are 0-Condorcet-consistent, it follows immediately that f is at most $(1-\varepsilon )$-Condorcet-consistent. In our next theorem, we thus determine the exact tradeoff between $\alpha$-Condorcet-consistency and $\beta$-ex post efficiency. Moreover, we also characterize the anonymous, neutral, and strategyproof SDSs that optimize this tradeoff as mixtures of the uniform random dictatorship and the randomized Copeland rule. This result highlights the antipodal roles of the randomized Copeland rule and the uniform random dictatorship.

Theorem 6

Every strategyproof SDS that satisfies anonymity, neutrality, $\alpha$-Condorcet-consistency, and $\beta$-ex post efficiency with $\beta = \frac{m-2}{m-1}\alpha$ is a mixture of the uniform random dictatorship and the randomized Copeland rule if $m\ge 4$, $n\ge 5$. Furthermore, no strategyproof SDS satisfies $\alpha$-Condorcet-consistency and $\beta$-ex post efficiency for $\beta < \frac{m-2}{m-1}\alpha$ if $m\ge 4$, $n\ge 5$.

Proof

We again show the two claims of the theorem separately and start with the upper bound on $\beta$-ex post efficiency.

Claim 1: No strategyproof SDS is $\alpha$-Condorcet-consistent and $\beta$-ex post efficient for $\beta <\frac{m-2}{m-1}\alpha$.

Let f be a strategyproof SDS that satisfies $\alpha$-Condorcet-consistency for some $\alpha \in [0,\frac{2}{m}]$ and let $\beta \in [0,1]$ denote the minimal value such that f is $\beta$-ex post efficient. As the first step, we apply Lemma 2 to construct an SDS $f^*$ that satisfies strategyproofness, anonymity, neutrality, $\alpha$-Condorcet-consistency, and $\beta$-ex post efficiency. We will show that $\beta \ge \frac{m-2}{m-1}\alpha$.

For this, we apply Theorem 3 to represent $f^*$ as a mixture of a supporting size SDS $f_{ sup }$ and a point voting SDS $f_{ point }$, i.e., $f^* = \lambda f_{ point } + (1 - \lambda ) f_{ sup }$ for some $\lambda \in [0,1]$. Let $(a_1, \dots , a_m)$ and $(b_0, \dots , b_n)$ denote the scoring vectors describing $f_{ point }$ and $f_{ sup }$, respectively. Next, we derive a lower bound for $\alpha$ and an upper bound for $\beta$ by considering specific profiles. First, consider the profile $R^1$ in which every voter reports x as his best alternative and y as his second best alternative; the remaining alternatives can be ordered arbitrarily. It follows from the definition of point voting SDSs that $f_{ point }(R^1,y)=na_2$ and from the definition of supporting size SDS that $f_{ sup }(R^1,y)=(m-2)b_n+b_0$. Since x Pareto-dominates y in $R^1$, it holds that $\beta \ge f(R^1,y)=\lambda na_2 + (1-\lambda )((m-2)b_n+ b_0)$.

For the upper bound on $\alpha$, we will construct a profile $R^2$ in which alternative x is the Condorcet winner, wins all pairwise comparisons by a minimal margin, and is never ranked first. For this, we denote the alternatives as $A = \{ x, x_1, \dots , x_{m - 1} \}$. Now, $R^2$ is defined as follows: the voters $i \in \{1, 2, 3\}$ rank the alternatives $X_i:= \{ x_k \in A {\setminus } \{x\}: k \mod 3 = i-1 \}$ above x and all other alternatives below. The exact order of the alternatives in $A\setminus \{x\}$ does not matter. Since $m \ge 4$, no voter $i\in \{1,2,3\}$ ranks x first. Next, if the number of voters n is even, we duplicate voters 1, 2, and 3. As the last step, we add pairs of voters with inverse preferences such that no voter prefers x the most until $R^2$ consists of n voters. Since alternative x is never top-ranked in $R^2$, it follows that $f_{ point }(R^2,x) \le na_2$. Furthermore, $n_{xy}(R^2)=\lceil \frac{n + 1}{2}\rceil$ for all $y\in A{\setminus } \{x\}$ and therefore $f_{ sup }(R^2,x) = (m-1) b_{\lceil \frac{n + 1}{2}\rceil }$. Finally, we derive that $\alpha \le f(R^2,x)\le \lambda na_2+(1-\lambda )(m-1)b_{\lceil \frac{n + 1}{2}\rceil }$ because x is by construction the Condorcet winner in $R^2$.

Using these bounds, we finally show that $\beta \ge \frac{m-2}{m-1}\alpha$, which proves our first claim. In the subsequent calculation, the first and last inequality follow from our previous analysis. The second inequality is true since $\frac{m-2}{m-1}\le 1$ and $\frac{m-2}{m-1}(m-1)=m-2$. The third inequality uses the definition of supporting size SDSs.

$$\begin{aligned} \beta&\ge \lambda na_2 + (1-\lambda )((m-2)b_n+ b_0)\nonumber \\&\ge \frac{m-2}{m-1}\lambda na_2 + \frac{m-2}{m-1}(1-\lambda )((m-1)b_n + b_0)\nonumber \\&\ge \frac{m-2}{m-1}\lambda na_2 + \frac{m-2}{m-1}(1-\lambda )(m-1)b_{\lceil \frac{n + 1}{2}\rceil }\nonumber \\&\ge \frac{m-2}{m-1}\alpha \end{aligned}$$

(1)

Claim 2: Every strategyproof SDS that satisfies anonymity, neutrality, $\alpha$-Condorcet-consistency, and $\beta$-ex post efficiency with $\beta = \frac{m-2}{m-1}\alpha$ is a mixture of the uniform random dictatorship and the randomized Copeland rule.

Next, suppose that f is a strategyproof SDS that satisfies anonymity, neutrality, $\alpha$-Condorcet-consistency, and $\beta$-ex post efficiency with $\beta = \frac{m-2}{m-1}\alpha$. By Theorem 3, f can be represented as mixture of a point voting scheme $f_{ point }$ and a supporting size scheme $f_{ sup }$, i.e., there is $\lambda \in [0,1]$ such that $f=\lambda f_{ point }+(1-\lambda )f_{ sup }$. Now, by considering the profiles $R^1$ and $R^2$ of Claim 1, we infer that Equation (1) must also hold for f. Even more, since $\beta = \frac{m-2}{m-1}\alpha$, all inequalities must be tight. For the second inequality, this is only the case if $a_2=0$ and $b_0=0$, and for the third one if $b_n = b_{\lceil \frac{n + 1}{2}\rceil }$. These observations fully specify the scoring vectors of $f_{ point }$ and $f_{ sup }$. For the point voting SDS, $a_2 = 0$ implies $a_i = 0$ for all $i\ge 2$ and $a_1 = \frac{1}{n}$, i.e., $f_{ point }$ is the uniform random dictatorship. Next, $b_0 = 0$ and $b_n = b_{\lceil \frac{n + 1}{2}\rceil }$ imply that $b_i =\frac{2}{m(m-1)}$ for all $i\in \{\lceil \frac{n + 1}{2}\rceil ,\dots , b_n\}$ and $b_i = 0$ for all $i \in \{0, \dots , \lfloor \frac{n-1}{2}\rfloor \}$. Moreover, if n is even, the definition of supporting size SDSs requires that $b_{\frac{n}{2}} = \frac{1}{m(m-1)}$. Hence, f is a mixture of the uniform random dictatorship and the randomized Copeland rule. $\square$

Remark 8

All axioms of the characterization in Theorem 6 are independent of each other. Every mixture of a non-uniform random dictatorship and the randomized Copeland rule only violates anonymity. An SDS that only violates neutrality can be constructed by using a variant of the randomized Copeland rule that does not split the probability equally if there is a majority tie. Finally, the correlation between $\alpha$-Condorcet-consistency and $\beta$-ex post efficiency is required since the uniform lottery rule satisfies all other axioms. Moreover, all bounds on m and n in Theorem 6 are tight. If there are only $n=2$ voters, $m=3$ alternatives, or $m=4$ alternatives and $n=4$ voters, the uniform random dictatorship is not 0-Condorcet-consistent since a Condorcet winner is always ranked first by at least one voter. Hence, the bound on $\beta$ does not hold in these cases. By contrast, our proof shows that Theorem 6 is also true when $n = 3$.

Omitted proofs

In the following, we present the proofs of Lemma 1 and Proposition 1. Since the proof of the latter lemma is rather involved, we organize the appendix in two subsections: Appendix A.1 discusses the proof of Lemma 1 and Appendix A.2 the proof of Proposition 1. Proof sketches explaining the main ideas for these proofs can be found in the main body.

1.1 Proof of Lemma 1

We start with the proof of Lemma 1. Recall for this proof that $R^{i:yx}$ is the profile derived from R by letting voter i reinforce y against x.

Lemma 1

A strategyproof SDS f is $\gamma$-randomly dictatorial if and only if there are non-negative values $\gamma _1,\dots , \gamma _n$ such that $\sum _{i\in N}\gamma _i=\gamma$, and $\gamma _i =\min _{x,y\in A} \min _{R \in \mathcal {R}^{i:xy}} f(R^{i:yx},y)-f(R,y)$ where $\mathcal {R}^{i:xy}\subseteq \mathcal {R}^n$ denotes the set of profiles in which voter i prefers x the most and y the second most.

Proof

We first note that $\gamma _i = \min _{x,y\in A}\min _{R \in \mathcal {R}^{i:xy}} f(R^{i:yx},y)-f(R,y)$ if and only if the following two conditions hold:

• (i) $f(R^{i:yx},y)-f(R,y)\ge \gamma _i$ for all alternatives $x,y\in A$ and preference profiles R in which voter i prefers x the most and y the second most, and

• (ii) there are alternatives $x,y\in A$ and a profile R such that voter i prefers x the most and y the second most in R, and $f(R^{i:yx},y)-f(R,y)= \gamma _i$.

We use these equivalent conditions in this proof.

“$\Leftarrow$”: Assume that f is a strategyproof SDS for which there are values $\gamma _1, \dots , \gamma _n$ such that $f(R^{i:yx},y)-f(R,y)\ge \gamma _i\ge 0$ for all alternatives $x,y\in A$, voters $i\in N$, and profiles R such that voter i prefers x the most and y the second most in R. Furthermore, we assume that for every voter $i\in N$, this inequality is tight for at least one pair of alternatives $x,y\in A$ and one profile R. We show next that f is $\gamma$-randomly dictatorial for $\gamma =\sum _{i\in N} \gamma _i$.

As the first step, note that $f(R,x)\ge \sum _{i\in S} \gamma _i$ for every profile R, alternative $x\in A$, and set of voters $S\subseteq N$ such that all voters in S report x as their favorite alternative. This follows by letting the voters $i\in S$ one after another swap x with their second best alternative y (note that y might be a different alternative for every voter $i\in S$). Using our assumption on f, the probability of y has to increase by at least $\gamma _i$ during such a step, which means that the probability of x decreases by $\gamma _i$ because of localizedness. Furthermore, it holds that $f(R',x)\ge 0$, where $R'$ is the profile derived by letting all voters in S swap their best two alternatives. Combining these two facts then implies that $f(R,x)\ge \sum _{i\in S} \gamma _i$. Moreover, this observation also shows that $\gamma \le 1$ because f fails the definition of an SDS otherwise. Moreover, f is a random dictatorship if $\gamma =1$. This follows from the following reasoning: for all profiles R and alternatives $x\in A$, it holds that $f(R,x)\ge \sum _{i\in S_x} \gamma _i$, where $S_x$ denotes the set of voters who prefer x the most in R. Since the sets $S_x$ partition N and $\gamma =1$, this inequality must be tight for every alternative; otherwise, $\sum _{x\in A} f(R,x)>\sum _{x\in A} \sum _{i\in S_x} \gamma _i=1$, contradicting the definition of an SDS. Hence, if $\gamma =1$, f is 1-randomly dictatorial as $f=\sum _{i\in N}\gamma _i d_i$, where $d_i$ denotes the dictatorial SDS of voter i.

As next case, suppose that $\gamma <1$ and define $g=\frac{1}{1 - \gamma }\left( f -\sum _{i\in N}\gamma _i d_i\right)$. Note that g is a well-defined SDS: for all profiles R and alternatives $x\in A$, it holds that $g(R,x)\ge 0$ because $f(R,x)\ge \sum _{i\in S_x} \gamma _i$. Moreover, $\sum _{x\in A}g(R,x)=\frac{1}{1 - \gamma } \sum _{x\in A}f(R,x) -\sum _{x\in A}\sum _{i\in N}\frac{\gamma _i}{1 - \gamma } d_i(R,x)=\frac{1}{1 - \gamma }-\frac{\gamma }{1 - \gamma }=1$ for all profiles R. Next, we show that g is strategyproof, which implies that f is $\gamma '$-randomly dictatorial for $\gamma '\ge \gamma$ because $f=\sum _{i\in N}\gamma _i d_i + (1-\gamma ) g$. For this, it suffices to prove that g is localized and non-perverse because of Theorem 2. Now, g is localized because the SDS f and all SDSs $d_i$ are localized. Hence, swapping two alternatives in the preferences of a voter only affects the probabilities of these alternatives. For seeing that g is non-perverse, consider a voter i, two alternatives $x,y\in A$ and a profile R such that x is voter i’s k-th best alternative and y is his $k+1$-th best one. We will show that $g(R^{i:yx}, y)\ge g(R,y)$. Note for this that $d_j(R^{i:yx})=d_j(R)$ for all $j\in N{\setminus } \{i\}$ because the preferences of these voters did not change, and $f(R^{i:yx},y)- f(R,y)\ge 0$ because f is strategyproof. If x and y are not the two best alternatives of voter i, then $d_i(R^{i:yx})=d_i(R) = 0$. Hence, it immediately follows that $g(R^{i:yx},y)-g(R,y)=\frac{1}{1-\gamma }\Big (f(R^{i:yx},y)-f(R,y)\Big )\ge 0$. On the other hand, if x and y are voter i’s best and second best alternatives, we have that $d_i(R^{i:yx},y)=1$ and $d_i(R,y)=0$. Moreover, our assumptions imply that $f(R^{i:yx},y)-f(R,y)\ge \gamma _i$. Thus, we calculate that $g(R^{i:yx},y)-g(R,y)=\frac{1}{1-\gamma }\Big (f(R^{i:yx},y)-f(R,y) - \gamma _i (d_i(R^{i:yx},y) - d_i(R,y))\Big )\ge \frac{1}{1-\gamma }\Big (\gamma _i -\gamma _i\Big )=0$. This means that g is non-perverse.

Finally, we show that f cannot be $\gamma '$-randomly dictatorial for $\gamma '>\gamma$. If this was the case, we can represent f as $f=\sum _{i\in N}\gamma '_i d_i + (1-\gamma ') g'$, where $\gamma '_i\ge 0$ are values such that $\sum _{i\in N}\gamma '_i=\gamma '$ and $g'$ is a strategyproof SDS. Since $\gamma '>\gamma$, there is a voter i with $\gamma _i'>\gamma _i$. Furthermore, our assumptions state that there are a profile R and alternatives x, y such that voter i prefers x the most and y the second most in R, and $f(R^{i:yx},y)-f(R,y)=\gamma _i$. This means that $\Big (f(R^{i:yx},y)-\sum _{j\in N}\gamma '_j d_j(R^{i:yx},y)\Big )-\Big (f(R,y)-\sum _{j\in N}\gamma '_j d_j(R,y)\Big )=\gamma _i-\gamma _i'<0$ because $d_i(R^{i:yx},y)-d_i(R,y)=1$ and $d_j(R^{i:yx},y)-d_j(R,y)=0$ for all $j\in N\setminus \{i\}$. Consequently, $g'(R^{i:yx},y)-g'(R,y)<0$ which means that $g'$ violates non-perversity and therefore also strategyproofness. Hence, the assumption that f is $\gamma '$-randomly dictatorial for $\gamma '>\gamma$ is wrong and f is $\gamma$-randomly dictatorial.

“$\Rightarrow$”: Let f be a strategyproof $\gamma$-randomly dictatorial SDS. We show next that there are values $\gamma _i$ that satisfy the requirements of the lemma. Since f is $\gamma$-randomly dictatorial, it can be represented as $f=\gamma d+(1-\gamma ) g$, where d is a random dictatorship and g is another strategyproof SDS. Moreover, as d is a random dictatorship, there are values $\delta _1,\dots ,\delta _n$ such that $\delta _i\ge 0$ for all $i\in N$, $\sum _{i\in N} \delta _i=1$, and $d=\sum _{i\in N} \delta _i d_i$. Combining these two equations, we derive that $f=\gamma \sum _{i\in N} \delta _i d_i + (1-\gamma ) g$. We will show in the sequel that the values $\gamma _i=\gamma \delta _i$ satisfy all requirements of our lemma. First, note that the conditions $\gamma _i\ge 0$ for all $i\in N$ and $\sum _{i\in N}\gamma _i=\gamma$ are obviously true.

Next, consider two alternatives $x,y\in A$, an arbitrary voter $i\in N$, and a profile R in which voter i reports x as his best alternative and y as his second best one. It holds that $g(R^{i:yx},y)-g(R,y)\ge 0$ because g is strategyproof and therefore non-perverse, $d_j(R^{i:yx},y)-d_j(R,y)=0$ for all $j\in N{\setminus } \{i\}$ because ${\succ ^{i:yx}_j} = {\succ _j}$, and $d_i(R^{i:yx},y)-d_i(R,y)=1$ as y is voter i’s best alternative in $R^{i:yx}$ but not in R. Hence, $f(R^{i:yx},y)-f(R,y)\ge \gamma \delta _i = \gamma _i$ for all voters $i\in N$, alternatives $x,y\in A$, and preference profiles R in which voter i reports x as his best and y as his second best alternative.

Finally, it remains to show that there is for every voter $i\in N$ a pair of alternatives $x,y\in A$ and a profile R such that voter i prefers x the most and y the second most in R and $f(R^{i:yx},y)-f(R,y)=\gamma _i$. Assume this is not the case for some voter i, i.e., that $f(R^{i:yx},y)-f(R,y)>\gamma _i$ for all alternatives $x,y\in A$ and profiles R in which x is voter i’s best alternative and y his second best one. Hence, let $\gamma _i'>\gamma _i$ denote $\gamma _i'=\min _{x,y\in A}\min _{R\in \mathcal {R}^{i:xy}} f(R^{i:yx},y)-f(R,y)$. Moreover, we define $\gamma '=\gamma _i' + \sum _{j\in N\setminus \{i\}}\gamma _j$. We can now apply the arguments for the inverse direction to derive that f is $\gamma ''$-randomly dictatorial for some $\gamma ''\ge \gamma '>\gamma$. This contradicts our assumption that f is $\gamma$-randomly dictatorial as $\gamma$ must be the maximal value such that f can be represented as $f=\gamma d + (1-\gamma ) g$, where d is a random dictatorship and g is another strategyproof SDS. Hence, it follows that for every voter $i\in N$, there are a profile R and two alternatives $x,y\in A$ such that $f(R^{i:yx},y)-f(R,y)=\gamma _i$ and voter i reports x as his best alternative and y as his second best one in R. So, our choice of $\gamma _i$ satisfies all requirements of the lemma. $\square$

1.2 Proofs of Proposition 1

Finally, we present proof of Proposition 1, i.e., we discuss our lower bound for the $\beta$-ex post efficiency of strategyproof 0-randomly dictatorial SDSs. Since Theorem 1 allows us to represent strategyproof SDSs as mixtures of duples and unilaterals, we focus next on these two classes. To simplify the proof we put these two cases in auxiliary lemmas.

First, we investigate the $\beta$-ex post efficiency of duples. Recall therefore that a duple is a strategyproof SDS $f_{xy}$ such that $f_{xy}(R,z)=0$ for all alternatives $z \in A {\setminus } \{x,y\}$. Moreover, a mixture of duples f is defined as $f(R,x)=\sum _{y \in A \setminus \{x\}}\lambda _{xy}f_{xy}(R,x)$, where $f_{xy}=f_{yx}$ and $\lambda _{xy}=\lambda _{yx}$ denote non-negative weights that sum up to 1. Finally, note that one duple for every pair is sufficient to represent every mixture of duples because two duples $f_{xy}$ and $f_{xy}'$ can be merged into one.

Lemma 5

No SDS that can be represented as a mixture of duples satisfies $\beta$-ex post efficiency for $\beta < \frac{1}{m}$ if $m \ge 3$.

Proof

Let $f(R, x) = \sum _{y \in A {\setminus } \{x\}}\lambda _{xy}f_{xy}(R,x)$ be an SDS represented as a convex combination of duples, where $f_{xy} = f_{yx}$ is the duple SDS for the pair x and y and $\lambda _{xy} = \lambda _{yx}$ is the weight of $f_{xy}$. Furthermore, we define $R^{x,y}$ as a profile where all voters report x as best alternative and y as worst one; all other alternatives can be ranked arbitrarily. First, note that $f(R^{x,y},x)=f(R^{x,z},x)$ and $f(R^{y,x},x)=f(R^{z,x},x)$ for all distinct $x,y,z\in A$. Thus, we also write $R^{x,\cdot }$ and $R^{\cdot , x}$ to indicate that alternative x is unanimously top-ranked or bottom-ranked, respectively.

As first step, we want to bound the average probability $f(R^{x,y},x)+f(R^{x,y},y)$ over all $x,y\in A$. In more detail, the subsequent equation shows that $\sum _{x \in A}\sum _{y \in A {\setminus } \{x\}} \Big (f(R^{x,y}, x) + f(R^{x,y}, y)\Big )= 2(m - 1)$.

$$\begin{aligned}&\sum _{x \in A}\sum _{y \in A \setminus \{x\}} f(R^{x,y}, x) + f(R^{x,y}, y) \\&\quad =(m-1)\sum _{x \in A} f(R^{x,\cdot }, x) + (m-1)\sum _{y \in A} f(R^{\cdot , y}, y) \\&\quad = (m-1)\sum _{x\in A}\sum _{y\in A\setminus \{x\}} \lambda _{xy} f_{xy}(R^{x,y},x) + \lambda _{xy}f_{xy}(R^{x,y},y)\\&\quad = (m-1)\sum _{x\in A}\sum _{y\in A\setminus \{x\}} \lambda _{xy}\\&\quad = 2(m - 1) \end{aligned}$$

The first equality follows because $f(R^{x,y},x)=f(R^{x,\cdot },x)$, $f(R^{x, y},y)=f(R^{\cdot ,y},y)$ for all alternatives $x,y\in A$ and every alternative x is both unanimously top-ranked and unanimously bottom-ranked in exactly $(m-1)$ of the considered preferences profiles. For the second equality, we replace $f(R^{x,\cdot }, x)$ with $\sum _{y \in A \setminus \{x\}}\lambda _{xy}f_{xy}(R^{x, y},x)$ and $f(R^{\cdot , y}, y)$ with $\sum _{x \in A {\setminus } \{y\}}\lambda _{xy}f_{xy}(R^{x, y},y)$ according to the definition of f. Furthermore, we swap the order of the sum for the second term. We derive the third equality from the fact that $f_{xy}(R, x) + f_{xy}(R, y) = 1$ for all profiles R. Finally, the last equality uses that $\sum _{x \in A} \sum _{y \in A {\setminus } \{x\}} \lambda _{xy} = 2$, which follows from $\sum _{x\in A}f(R, x) = \sum _{x\in A}\sum _{y \in A {\setminus } \{x\}}\lambda _{xy}f_{xy}(R, x) = 1$ and $f_{xy}(R, x) + f_{xy}(R, y) = 1$ for all profiles R.

As a consequence of this observation, there is a pair of alternatives $x,y\in A$ such that $f(R^{x,y},x)+f(R^{x,y},y)\le \frac{2}{m}$. Otherwise, it holds that $\sum _{x \in A}\sum _{y \in A {\setminus } \{x\}} f(R^{x,y}, x) + f(R^{x,y}, y) > \sum _{x \in A}\sum _{y \in A {\setminus } \{x\}} \frac{2}{m} = 2(m - 1)$ contradicting our previous equation. Hence, $\sum _{z\in A{\setminus } \{x,y\}} f(R^{x,y},z)\ge \frac{m-2}{m}$. Since all alternatives $z\in A\setminus \{x,y\}$ are Pareto-dominated by x, this entails that one of these alternative receives a probability of at least $\frac{m - 2}{m(m - 2)} = \frac{1}{m}$. We conclude therefore that f fails $\beta$-ex post efficiency for $\beta < \frac{1}{m}$. $\square$

Next, we aim to show that no 0-randomly dictatorial SDS that can be represented as a mixture of unilaterals satisfies $\beta$-ex post efficiency for $\beta <\frac{1}{m}$. For this, we will first discuss a construction that allows us to construct a strategyproof, 0-randomly dictatorial, and $\beta$-ex post efficient SDS that satisfies several symmetry properties based on another strategyproof, 0-randomly dictatorial, and $\beta$-ex post efficient SDS. Unfortunately, we cannot use Lemma 2 here as this lemma does not preserve the 0-random dictatorship of an SDS. For demonstrating this point, let $A=\{x_1, \dots , x_m\}$ denote the alternatives and consider the SDS f for $n\ge 3$ voters and $m=n$ alternatives in which every voter $i\in N$ assigns probability $\frac{1}{n}$ to his favorite alternative in $A\setminus \{x_i\}$. Lemma 1 shows that this SDS is 0-randomly dictatorial because for all $i\in N$, the probability of $x_i$ does not increase if voter i reinforces it to his best alternative. However, applying the construction of Lemma 2 to f results in the point voting SDS defined by the scoring vector $(\frac{m-1}{nm}, \frac{1}{nm}, 0, \dots , 0)$. This SDS is not 0-randomly dictatorial as pushing an alternative from second place to first place increases its probability always by $\frac{m-2}{nm}>0$.

Therefore, we discuss another construction in the next lemma that preserves 0-random dictatorships while introducing new symmetries. Note that we require some additional terminology for Lemma 6: we say that voter i or his unilateral SDS $f_i$ is 0-randomly dictatorial for alternatives x, y if $f(R)=f(R^{i:yx})$ for all preference profiles R in which x is voter i’s best alternative and y is his second best alternative.

Lemma 6

Let f be a strategyproof and 0-randomly dictatorial SDS that satisfies $\beta$-ex post efficiency for some $\beta \in [0,1]$ and that can be represented as a mixture of unilaterals. Then, there is a strategyproof and 0-randomly dictatorial SDS $f^*$ for $\left( {\begin{array}{c}m\\ 2\end{array}}\right)$ voters that can be represented as a mixture of unilaterals and that is $\beta$-ex post efficient for the same $\beta$ as f. Moreover, $f^*$ satisfies the following conditions:

• (i) For every voter $i\in N$, there is a set $\{x_i, y_i\}$ such that voter i is 0-randomly dictatorial for $x_i$, $y_i$ and $\{x_i,y_i\}\ne \{x_j,y_j\}$ if $i\ne j$.

• (ii) There is a constant $\delta$ such that $f^*(R^{i:cb},c)-f^*(R,c)=\delta$ for all voters $i\in N$, alternatives $\{a,b\}=\{x_i, y_i\}$, $c\in A{\setminus }\{x_i,y_i\}$, and preference profiles R such that voter i reports a as his best alternative, b as his second best one, and c as his third best one.

• (iii) If every voter $i\in N$ reports $x_i$ and $y_i$ as their two best alternatives, there is a scoring vector $a=(a_1, \dots , a_m)$ such that $a_1 = a_2 \ge 0$, $a_3 \ge \dots \ge a_m \ge 0$, and $f^*(R, x) = \sum _{i \in N} a_{r(x, \succ _i)}$.

Proof

Let $\beta \in [0,1]$ and let f denote a strategyproof 0-randomly dictatorial SDS that is $\beta$-ex post efficient and that can be represented as a mixture of unilaterals. In the sequel, we use f to construct the SDS $f^*$ that satisfies all requirements of the lemma. Note that this proof is quite involved and therefore, we use some auxiliary claims that are proven in the end.

We start by representing f as $f(R) = \sum _{i \in N} \lambda _i f_i(\succ _i)$, where $f_i$ denotes the unilateral SDS of voter i and $\lambda _i\ge 0$ is its weight. Note that we interpret unilaterals in this proof as SDSs that take a single preference relation as input. This is possible as unilaterals only rely on the preferences of a single voter. Claim 1 states that for every voter $i\in N$ there are alternatives x, y such that $f_i$ is 0-randomly dictatorial for x and y. Even though a voter can be 0-randomly dictatorial for multiple pairs of alternatives, we associate from now on every voter i with exactly one such pair $x_i,y_i$. This pair can be chosen arbitrarily as it will not affect the rest of the proof.

Next, we define the unilaterals $f_i^\tau$ as $f^\tau _i(R,x)=f_i(\tau (R), \tau (x))$ for all voters $i\in N$ and permutations $\tau :A\rightarrow A$. Claim 2 states that every SDS $f_i^\tau$ is strategyproof and 0-randomly dictatorial for $\tau ^{-1}(x_i)$, $\tau ^{-1}(y_i)$, where $\tau ^{-1}$ is the inverse permutation of $\tau$ and $x_i$ and $y_i$ are the alternatives associated with $f_i$. Just as the SDSs $f_i$, each $f_i^\tau$ can be 0-randomly dictatorial for multiple pairs of alternatives, but we associate $f^\tau _i$ from now on only with the pair $\tau ^{-1}(x_i)$, $\tau ^{-1}(y_i)$. Then, we partition the SDSs $f^\tau _i$ with respect to the alternatives $\tau ^{-1}(x_i)$, $\tau ^{-1}(y_i)$. In more detail, let $F_{xy}=\{f^\tau _i:i\in N, \tau \in \textrm{T}, \{\tau ^{-1}(x_i), \tau ^{-1}(y_i)\}=\{x,y\}\}$ denote the multi-set of SDSs $f^{\tau }_i$ that are associated with x and y. Note that all unilaterals in $F_{xy}$ are 0-randomly dictatorial for x, y. Furthermore, these multi-sets partition the SDSs $f^\tau _i$ as each $f^\tau _i$ is only associated with a single pair of alternatives. Even more, there are for every $f_i$ exactly $2(m-2)!$ permutations $\tau$ such that $\{\tau ^{-1}(x_i), \tau ^{-1}(y_i)\}=\{x,y\}$. Hence, we derive that each set $F_{xy}$ contains $2n(m-2)!$ unilaterals.

In the next step, we merge all unilaterals in a multi-set $F_{xy}$ into a single unilateral. Thus, we define the unilateral $f_{xy}(\succ _j)$ as $f_{xy}(\succ _j)=\sum _{f^\tau _i\in F_{xy}} \frac{\lambda _i}{2(m-2)!} f^\tau _i(\succ _j)$, i.e., $f_{xy}$ chooses each SDS $f^\tau _i\in F_{xy}$ with a probability proportional to $\lambda _i$. Observe that $f_{xy}$ is strategyproof because it is a mixture of strategyproof SDSs and it is 0-randomly dictatorial for x, y because all unilaterals in $F_{xy}$ are 0-randomly dictatorial for these alternatives. Based on the SDS $f_{xy}$, we can finally define the SDS $f^*$ for $n^*=\left( {\begin{array}{c}m\\ 2\end{array}}\right)$ voters. To this end, let $N^*$ denote the electorate of $f^*$. We associate each voter $j\in N^*$ with a different pair of alternatives $x,y\in A$ and set $f^*_j=f_{xy}$. Then, the SDS $f^*$ chooses one of the voters $j\in N^*$ uniformly at random and returns $f^*_j(\succ _j)=f_{xy}(\succ _j)$, i.e., $f^*(R)=\frac{1}{n^*}\sum _{j=1}^{n^*}f_j^*(\succ _j)$. Clearly, $f^*$ is strategyproof because it is a mixture of strategyproof SDSs. Moreover, it is 0-randomly dictatorial because every voter $j\in N^*$ is 0-randomly dictatorial for the pair of alternatives x, y with which he is associated. Furthermore, Claim 3 shows that $f^*$ is $\beta$-ex post efficient for the same $\beta$ as f.

It remains to show that the SDS $f^*$ satisfies the properties (i), (ii), and (iii). First, note that it satisfies (i) by construction as every voter is 0-randomly dictatorial for a different pair of alternatives. For (ii) and (iii), we show first the auxiliary claim that $f_{xy}(R,x)=f_{\tau (x)\tau (y)}(\tau (R),\tau (x))$ for all permutations $\tau :A\rightarrow A$, preference profiles R, and alternatives $x\in A$. Hence, we fix two arbitrary alternatives x, y and a permutation $\tau :A\rightarrow A$. Moreover, consider an arbitrary SDS $f^{\tau '}_i\in F_{xy}$ and note that $f_i^{\tau '}(R,x)=f_i(\tau '(R), \tau '(x)) = f(\tau '(\tau ^{-1}(\tau (R))), \tau '(\tau ^{-1}(\tau (x))))=f_i^{\tau '\circ \tau ^{-1}}(\tau (R), \tau (x))$. Next, observe that $f^{\tau '\circ \tau ^{-1}}\in F_{\tau (x),\tau (y)}$. This is true because $f^{\tau '}_i\in F_{xy}$ implies that $\{\tau '^{-1}(x_i), \tau '^{-1}(y_i)\}=\{x,y\}$ or equivalently that $\{\tau '(x), \tau '(y)\}=\{x_i, y_i\}$. Therefore, $\{\tau '(\tau ^{-1}(\tau (x))), \tau '(\tau ^{-1}(\tau (y)))\}=\{x_i, y_i\}$ which shows that $f^{\tau '\circ \tau ^{-1}}\in F_{\tau (x)\tau (y)}$. Finally, we derive the following equality for all profiles R and alternatives $x\in A$.

$$\begin{aligned} f_{xy}(R,x)&=\sum _{f_i^{\tau '}\in F_{xy}} \frac{\lambda _i}{2(m-2)!} f_i^{\tau '}(R,x)\\&=\sum _{f_i^{\tau '}\in F_{xy}} \frac{\lambda _i}{2(m-2)!} f_i^{\tau '\circ \tau ^{-1}}(\tau (R),\tau (x))\\&=\sum _{f_i^{\hat{\tau }}\in F_{\tau (x)\tau (y)}} \frac{\lambda _i}{2(m-2)!} f_i^{\hat{\tau }}(\tau (R),\tau (x))\\&=f_{\tau (x)\tau (y)}(\tau (R),\tau (x)). \end{aligned}$$

In the third step of this equation, we define $\hat{\tau }= \tau '\circ \tau ^{-1}$. Moreover, we use here the fact that $\tau '\circ \tau ^{-1}\ne \tau ''\circ \tau ^{-1}$ if $\tau '\ne \tau ''$, which implies that every SDS $f^\tau _i\in F_{xy}$ is mapped to a unique element $f^{\hat{\tau }}_i\in F_{\tau (x)\tau (y)}$. This proves the auxiliary claim.

Subsequently, we show that $f^*$ satisfies condition (ii) and consider therefore an arbitrary voter $i\in N^*$. Moreover, let $x_i$, $y_i$ denote the alternatives associated with $f^*_i$, i.e., $f^*_i=f_{x_iy_i}$. Finally, consider a profile R in which voter i prefers $x_i$ the most, $y_i$ the second most, and some arbitrary alternative $z_i\in A\setminus \{x_i, y_i\}$ the third most. We define $\delta =f^*(R^{i:z_iy_i},z_i)-f^*(R,z_i)$. First, note that $R^{i:z_iy_i}$ and R only differ in the preferences of voter i and thus, $f^*(R^{i:z_iy_i},z_i)-f^*(R,z_i)=f^*_i(\succ ^{i:z_iy_i}_i,z_i)-f^*_i(\succ _i,z_i)$. Next, consider a second voter $j\in N^*$ ($j=i$ is possible), let $x_j$ and $y_j$ denote the alternatives which are associated with $f^*_j$, and let $z_j\in A\setminus \{x_j,y_j\}$ denote another alternative. Moreover, define $R'$ as a profile such that voter j ranks $x_j$ first, $y_j$ second, and $z_j$ third in $R'$, and let $R^+=(R')^{j:z_jy_j}$. We show in the sequel that $f^*(R^+,z_j)-f^*(R',z_j)=\delta$, which proves claim (ii). Thus, note that $f^*(R^+,z_j)-f^*(R',z_j)=f^*_j(\succ ^+_j,z_j)-f^*_j(\succ _j',z_j)$ because $f^*$ is a mixture of unilaterals and only voter j changes his preference relation. Next, let $\tau$ denote a permutation such that $\tau (\succ _j')={\succ _i}$, which means in particular that $\tau (x_j)=x_i$, $\tau (y_j)=y_i$, and $\tau (z_j)=z_i$. Now, our auxiliary claim proves (ii) since

$$\begin{aligned} f^*_j(\succ ^+_j,z_j)-f^*_j(\succ '_j,z_j)&=f_{x_jy_j}((\succ '_j)^{j:z_jy_j}, z_j)-f_{x_jy_j}(\succ '_j,z_j)\\&=f_{\tau (x_j)\tau (y_j)}(\tau ((\succ '_j)^{j:z_jy_j}), \tau (z_j)) - f_{\tau (x_j)\tau (y_j)}(\tau (\succ _j'), \tau (z_j))\\&=f_{x_iy_i}(\succ ^{i:z_iy_i}_i, z_i) - f_{x_iy_i}(\succ _i, z_i)\\&=\delta . \end{aligned}$$

Finally, we discuss why $f^*$ satisfies condition (iii). For this, consider two voters $i,j\in N^*$ and let $x_i, y_i$ and $x_j$, $y_j$ denote the alternatives associated with $f^*_i$ and $f^*_j$, respectively. We explicitly allow that $i=j$. Furthermore, consider two preference relations $\succ _i$ and $\succ _j$ such that $x_i$ and $y_i$ are top-ranked in $\succ _i$ and $x_j$ and $y_j$ are top-ranked in $\succ _j$. Finally, let $\tau$ denote a permutation such that ${\succ _i}=\tau ({\succ _j})$ and let $z^k_i$ and $z^k_j$ denote the k-th ranked alternative of voter i and j, respectively. Our auxiliary claim shows immediately that $f^*_i(\succ _i, z^k_i)=f^*_j(\succ _j, z^k_j)$. This means that for every $k\in \{1,\dots ,m\}$, the k-th ranked alternative receives the same probability from every voter if they report the alternatives $x_i$, $y_i$ as their favorite choice. Hence, there is a scoring vector $a=(a_1,\dots , a_m)$ such that $f^*(R,x)=\sum _{i \in N} a_{r(x,\succ _i)}$ for such profiles. Moreover, it follows from strategyproofness that $a_3\ge a_4\ge \dots a_m$ and from the definition of an SDS that $a_i\ge 0$ for all $i\in \{1,\dots , m\}$. Finally, $a_1=a_2$ since for all $i\in N^*$, the unilateral $f^*_i$ is 0-randomly dictatorial for $x_i$ and $y_i$. Hence, there is a scoring vector that meets all requirements of (iii).

Claim 1: For every voter i, there exists a pair of alternatives$x_i$, $y_i$ such that$f(R)=f(R^{i:y_ix_i})$ for all preference profilesR in which voteri reports$x_i$ as best alternative and$y_i$ as second best one.

Since f is a strategyproof and 0-randomly dictatorial SDS, Lemma 1 shows that for every voter $i\in N$, there is a pair of alternatives $x_i, y_i$ and a preference profile R such that $f(R,y)=f(R^{i:y_ix_i},y)$, voter i top-ranks $x_i$ in R, and second-ranks $y_i$. First, note that localizedness immediately generalizes this claim to $f(R)=f(R^{i:y_ix_i})$. Moreover, since only voter i’s preference changes and f is a mixture of unilaterals, we also infer that $f_i(R)=f_i(R^{i:y_ix_i})$ where $f_i$ is the unilateral of voter i. We show in the sequel that $f({\bar{R}})=f({\bar{R}}^{i:y_ix_i})$ for all preference profiles $\bar{R}$ in which voter i reports $x_i$ and $y_i$ as his best and second best alternatives.

Since f is a mixture of unilaterals, it follows that $f(\bar{R})=f({\bar{R}}^{i:y_ix_i})$ if $f_i({{\bar{\succ }}_i})=f_i({{\bar{\succ }}^{i:y_ix_i}_i})$ because ${{\bar{\succ }}_j}={{\bar{\succ }}_j^{i:y_ix_i}}$ for all $j\in N{\setminus } \{i\}$. Moreover, it follows from strategyproofness, which entails localizedness, that $f_i({{\bar{\succ }}_i},z)=f_i({{\succ }_i},z)=f_i({{\succ }^{i:y_ix_i}_i},z)=f_i({\bar{\succ }^{i:y_ix_i}_i},z)$ for $z\in \{x_i,y_i\}$ since ${\bar{\succ }}_i$ and $\succ _i$ only differ in the order of the alternatives in $A\setminus \{x_i,y_i\}$. On the other hand, ${\bar{\succ }}_i$ and ${\bar{\succ }}_i^{i:y_ix_i}$ differ only in the preference over $x_i$ and $y_i$, so another application of localizedness shows that $f_i({\bar{\succ }}_i)=f_i({\bar{\succ }}_i^{i:y_ix_i})$. Hence, it holds indeed that $f({\bar{R}})=f({\bar{R}}^{i:y_ix_i})$ for all preference profiles in which voter i reports $x_i$ and $y_i$ as his two best alternatives.

Claim 2: The SDS$f^\tau _i(R,x)=f_i(\tau (R), \tau (x))$ is strategyproof and0-randomly dictatorial for$\tau ^{-1}(x_i)$, $\tau ^{-1}(y_i)$.

First, note that $f^\tau _i$ is strategyproof as every manipulation of $f^\tau _i$ can be mapped to a manipulation of $f_i$. In more detail, if voter i can manipulate $f^\tau _i$ by switching from R to $R'$, he can also manipulate $f_i$ by deviating from $\tau (R)$ to $\tau (R')$. This is true because a manipulation requires an alternative x such that $\sum _{y\succ _i x} f^\tau _i(R',y)>\sum _{y\succ _i x} f^\tau _i(R,y)$, which entails by definition of $f^\tau _i$ that $\sum _{y\succ _i x} f_i(\tau (R'),\tau (y))>\sum _{y\succ _i x} f_i(\tau (R),\tau (y))$. Finally, since $y\succ _i x$ in R if and only if $\tau (y)\succ _i \tau (x)$ in $\tau (R)$, we derive that voter i can manipulate $f_i$ by deviating from $\tau (R)$ to $\tau (R')$ if he can manipulate $f_i^\tau$ by deviating from R to $R'$.

Furthermore, $f^\tau _i$ is a 0-randomly dictatorial SDS because $f_i$ is one: Claim 1 shows that for every voter i, there exists a pair of alternatives $x_i$, $y_i$ such that $f(R)=f(R^{i:y_ix_i})$ for all preference profiles R in which voter i prefers $x_i$ the most and $y_i$ the second most. It follows from this claim that $f^\tau _i(\tau ^{-1}(R),\tau ^{-1}(x))=f_i(R,x)=f_i(R^{i:y_ix_i},x)=f^\tau _i(\tau ^{-1}(R^{i:y_ix_i}), \tau ^{-1}(x))$ for all $x\in A$, where $\tau ^{-1}$ is the inverse permutation of $\tau$, i.e., $\tau ^{-1}(\tau (x))=x$ for all $x\in A$. Therefore, $f^\tau _i(\tau ^{-1}(R), \tau ^{-1}(x_i)) = f^\tau _i(\tau ^{-1}(R^{i:y_ix_i}), \tau ^{-1}(x_i))$ and $f^\tau _i(\tau ^{-1}(R), \tau ^{-1}(y_i)) = f^\tau _i(\tau ^{-1}(R^{i:y_ix_i}), \tau ^{-1}(y_i))$. Moreover, the preference profiles $\tau ^{-1}(R)$ and $\tau ^{-1}(R^{i:y_ix_i})$ only differ in the order of the two best alternatives $\tau ^{-1}(x)$ and $\tau ^{-1}(y)$ of voter i and the proof of Claim 1 entails thus that $f^\tau _i$ is 0-randomly dictatorial for these two alternatives.

Claim 3: The SDS$f^*=\frac{1}{n^*} \sum _{i=1}^{n^*} f^*_i$ is$\beta$-ex post efficient for the same $\beta$ as f.

To prove this claim, we construct first another SDS $f^+$ and show that this SDS is $\beta$-ex post efficient for the same $\beta$ as f. As the second step, we show that $f^*$ can also be derived from $f^+$ by merging voters, and thus $f^*$ inherits the $\beta$-ex post efficiency of $f^+$. Before defining $f^+$, we introduce the SDS $f^\tau$: just as the SDSs $f^\tau _i$, it is defined as $f^\tau (R,x)=f(\tau (R), \tau (x))$. In particular, $f^\tau$ is $\beta$-ex post efficient for the same $\beta$ as f. This follows by considering an arbitrary profile R in which an alternative x is Pareto-dominated. It is easy to see that $\tau (x)$ is then Pareto-dominated in $\tau (R)$, and we derive therefore that $f^\tau (R,x)=f(\tau (R),\tau (x))\le \beta$ because f is $\beta$-ex post efficient. Next, we define the SDS $f^+$ for nm! voters as follows: we partition the voters $\{1,\dots , nm!\}$ into m! sets $N_1,\dots , N_{m!}$ with $|N_i|=n$ and associate with every set a different permutation $\tau _i:A\rightarrow A$. Then, $f^+(R)=\frac{1}{m!}\sum _{i=1}^{m!} f^{\tau _i}(R_{N_i})$, where $R_{N_i}$ denotes the restriction of R to the voters in $N_i$. Observe that $f^+$ is $\beta$-ex post efficient for the same $\beta$ as f because an alternative x that is Pareto-dominated in R is also Pareto-dominated in all $R_{N_i}$ and all $f^{\tau _i}$ are $\beta$-ex post efficient. Hence, it follows that $f^+(R,x)=\frac{1}{m!}\sum _{i=1}^{m!} f^{\tau _i}(R_{N_i},x)\le \frac{1}{m!}\sum _{i+1}^{m!}\beta =\beta$.

Next, we show that $f^+$ and $f^*$ satisfy $\beta$-ex post efficiency for the same $\beta$. Therefore, we change the representation of $f^+$. The central observation here is that $f^\tau =\sum _{i\in N} \lambda _i f^\tau _i$. Hence, we can also associate every voter $j\in \{1,\dots , nm!\}$ with an index $i\in N$ and a permutation $\tau$ such that each index-permutation pair is assigned exactly once. Thus, define $f_j^+=f^\tau _i$ and $\lambda _j^+=\frac{\lambda _i}{m!}$ (i.e., the weight of $f^\tau _i$ is the proportional to the weight of $f_i$ in the original SDS f). Then, we can write $f^+$ as $f^+(R)=\sum _{j=1}^{nm!} \lambda _j^+ f_j^+(\succ _j)$. Next, note that every $f^\tau _i$ appears once in the definition of $f^+$ and once in the union of all $F_{xy}$. Therefore, we derive that $f^+(R)=\frac{1}{n^*}\sum _{\{x,y\}\in {A\atopwithdelims ()2}} \sum _{f^\tau _i\in F_{xy}} \frac{\lambda _i}{2(m-2)!} f^\tau _i(\succ _i)$, where $n^*={m\atopwithdelims ()2}$. Next, we restrict our attention to profiles R such that for all $\{x,y\}\in {A\atopwithdelims ()2}$, all voters j with $f_j\in F_{xy}$ submit the same preference relation. In this case, we may replace the preferences of all voters j with $f_j\in F_{xy}$ with a single preference relation. Then, there are exactly $m\atopwithdelims ()2$ voters left, each of which is associated with a different pair of alternatives. In particular, we can use the definition of $f_{xy}(\succ _i)=\sum _{f^\tau _i\in F_{xy}}\frac{\lambda _i}{2(m-2)!} f^\tau _i(\succ _i)$ now as we apply all unilateral SDSs in $F_{xy}$ to the same preference relation $\succ _i$. Hence, $f^+$ returns the same outcomes as $f^*$ if for each $\{x,y\}\in {A\atopwithdelims ()2}$, all voters j with $f_j\in F_{xy}$ report the same preferences. Since $f^+$ is $\beta$-ex post efficient, it follows therefore also that $f^*$ is $\beta$-ex post efficient. $\square$

Next, we use Lemma 6 to prove that no 0-randomly dictatorial SDS that can be represented as a mixture of unilaterals is $\beta$-ex post efficient for $\beta <\frac{1}{m}$.

Lemma 7

No 0-randomly dictatorial SDS that can be represented as a mixture of unilaterals satisfies $\beta$-ex post efficiency for $\beta < \frac{1}{m}$ if $m \ge 3$.

Proof

Let the SDS f denote a mixture of unilaterals. First, we apply Lemma 6 to construct the SDS $f^*$ as specified by this lemma. In the sequel, we show that $f^*$ is $\beta$-ex post efficient for $\beta \ge \frac{1}{m}$ and the same therefore holds for f. In our proof, we will construct a profile $R^*$ in which every alternative must receive a probability of at most $\beta$ which leads to a contradiction if $\beta < \frac{1}{m}$. Let N with $|N| = \left( {\begin{array}{c}m\\ 2\end{array}}\right)$ be the set of voters of $f^*$. Furthermore, Lemma 6 (i) states that every voter $j \in N$ is associated with a different pair of alternatives $\{x_j, y_j\}$ for which he is 0-randomly dictatorial.

First, we explain the construction of an auxiliary profile R. For this profile, we choose an arbitrary pair of alternatives a, b and assume without loss of generality that voter 1 is 0-randomly dictatorial for a, b, i.e., $\{a,b\}=\{x_1, y_1\}$. Voter 1 submits the preference relation ${\succ _1}=b \succ _1 a \succ _1 \dots$ in R. Furthermore, there are $m - 2$ other voters $j\in N$ with $a \in \{x_j, y_j\}$ and $b \notin \{x_j, y_j\}$. We assume without loss of generality that these are the voters in $\{2, \dots , m-1\}$ and that $a = x_j$. The preferences of the voters $j\in \{2,\dots , m-2\}$ in R is ${\succ _j}= y_j \succ _j a \succ _j b \succ _j \dots$. Also, there are $m - 2$ voters j with $a \notin \{x_j, y_j\}$ and $b \in \{x_j, y_j\}$. We assume that these voters are the ones in $\{m,\dots ,2\,m-3 \}$ and that $b=y_j$. The preferences of these voters is ${\succ _j}= b \succ _j x_j \succ _j a \succ _j \dots$. Finally, $a, b \notin \{x_j, y_j\}$ for the remaining voters $j\in \{2m-2, \dots , \left( {\begin{array}{c}m\\ 2\end{array}}\right) \}$. These voters report ${\succ _j}=x_j \succ _j y_j \succ _j b \succ _j a\succ _j\dots$ in R. Note that if $m = 3$, there are no voters of the fourth type. Furthermore, every voter $j\in N$ ranks the alternatives $x_j, y_j$ for which he is 0-randomly dictatorial at the top. The full profile for $m = 4$ is shown in Fig. 4.

Fig. 4

The preference profile R from the proof of Lemma 7 for $m = 4$. There are four groups of voters. The first group contains only the first voter who is 0-randomly dictatorial for a and b. The next two groups have both $m-2$ voters and are 0-randomly dictatorial for one of a and b. The last group contains the remaining $\left( {\begin{array}{c}m - 2\\ 2\end{array}}\right)$ voters that are not 0-randomly dictatorial a or b. All voters have the pair for which they are 0-randomly dictatorial ranked at the top

Fig. 5

The preference profile $R'$ for $m = 4$ alternatives that results from R by swapping the second and third alternatives of voters $j \in \{2, \dots , 2\,m - 3\}$. Alternative a is Pareto-dominated by alternative b

We show next that $f^*(R,a) \le \beta$ by constructing a new preference profile $R'$ such that $f^*(R, a) = f^*(R', a) \le \beta$. For the construction of $R'$, let all voters in the second group $j \in \{2,\dots , m-1\}$ swap a and b, and all voters in the third group $j \in \{m,\dots , 2m-3\}$ swap a and $x_j$. The resulting preference profile is shown in Fig. 5 for the case that $m=4$. It is easy to see that b Pareto-dominates a in $R'$ and, as $f^*$ is $\beta$-ex post efficient, $f^*(R',a) \le \beta$. Alternative a was moved from third to second and from second to third place by $m-2$ voters. It follows therefore from Lemma 6 (ii) and localizedness that the probability that alternative a gains when $m-2$ voters swap it from third to second place is the same as the probability that a looses when $m-2$ voters swap it from second to third place. Thus, we derive that $f^*(R, a) = f^*(R',a) \le \beta$.

Finally, note that in R, all voters $j\in N$ report the pair $x_j, y_j$ for which they are 0-randomly dictatorial as their two best alternatives. Hence, Lemma 6 (iii) entails the existence of a scoring vector $(a_1, \dots , a_m)$ such that $a_1 = a_2 \ge 0$, $a_3 \ge \dots \ge a_m \ge 0$, and $f^*(R, x) = \sum _{j \in N}a_{r(x,\succ _j)}$ for all $x\in A$. In particular, observe that the probability of an alternative only depends on its rank vector $r^*(x,R)$, which contains the rank of x with respect to every voter in increasing order. The rank vector of alternative a in R is

$$\begin{aligned} r^*(a, R) = (\overbrace{2, \dots , 2}^{m - 1}, \overbrace{3, \dots , 3}^{m-2}, \overbrace{4, \dots , 4}^{\left( {\begin{array}{c}m - 2\\ 2\end{array}}\right) }). \end{aligned}$$

Furthermore, observe that $f^*(\bar{R},x)\le f^*(R,a)$ in every profile $\bar{R}$ in which (i) each voter $j\in N$ reports the alternatives $x_j$, $y_j$ as his two best alternatives and (ii) $r^*(x,\bar{R})_k\ge r^*(a,R)_k$ for all $k\in \{m, \dots , \left( {\begin{array}{c}m\\ 2\end{array}}\right) \}$. Condition (i) implies that $f^*$ can be computed based on the scoring vector $(a_1, \dots , a_m)$. Furthermore, it implies that every alternative $x\in A$ is among the two best alternatives of exactly $m-1$ voters, and since $a_1=a_2$, it follows that we can ignore these entries when comparing the probability of a in R with the probability of x in $\bar{R}$. Finally, the claim follows as $a_3\ge \dots \ge a_m$ and $r^*(x,\bar{R})_k\ge r^*(a,R)_k$ for all $k\in \{m, \dots , \left( {\begin{array}{c}m\\ 2\end{array}}\right) \}$.

We use this fact to construct a new profile $R^*$ where $f^*(R^*, x) \le f^*(R,a)\le \beta$ for every $x\in A$. Let every voter $j\in N$ report the alternatives $x_j$, $y_j$ for which he is 0-randomly dictatorial as his two best alternatives. Furthermore, we distribute all other alternatives such that no alternative is ranked third by more than $m-2$ voters. This is possible as there are $m\ge 3$ alternatives and $\frac{m(m-1)}{2}$ voters. It follows from the construction that $r^*(x,R^*)_{k}\ge r^*(a,R)_k$ for every $k\in \{m, \dots , \left( {\begin{array}{c}m\\ 2\end{array}}\right) \}$ and every $x\in A$. Hence, we derive that $f^*(R^*,x)\le f^*(R,a)\le \beta$ for every $x\in A$. If $\beta <\frac{1}{m}$, this entails that $\sum _{x\in A} f^*(R^*,x) <1$, a contradiction. Thus, $f^*$ cannot satisfy $\beta$-ex post efficiency for $\beta <\frac{1}{m}$ and f therefore violates this axiom, too. This shows that there exists no 0-randomly dictatorial SDS that can be represented as a mixture of unilaterals and that satisfies $\beta$-ex post efficiency for $\beta < \frac{1}{m}$ when $m \ge 3$. $\square$

Finally, we use Lemmas 5 and 7 to prove that there are no 0-randomly dictatorial SDSs that satisfy $\beta$-ex post efficiency for $\beta <\frac{1}{m}$.

Proposition 1

No strategyproof SDS that is 0-randomly dictatorial satisfies $\beta$-ex post efficiency for $\beta < \frac{1}{m}$ if $m \ge 3$.

Proof

Let f denote a strategyproof SDS for n voters and $m\ge 3$ alternatives that is 0-randomly dictatorial. Our argument focuses mainly on the profiles $R^{x,y}$, in which all voters report x as their best choice and y as their second best choice. The reason for this is that if $f(R,y) > \beta$ for some profile R in which y is Pareto-dominated by x, then $f(R^{x,y},y) > \beta$. This is a direct consequence of strategyproofness as we can transform R into $R^{x,y}$ by reinforcing x and y. Hence, non-perversity implies that $f(R^{x,y},y)\ge f(R,y) > \beta$. Moreover, localizedness entails that the order of the alternatives $z\in A{\setminus } \{x,y\}$ in $R^{x,y}$ is not important as it does not affect the probabilities of x and y.

Next, we use Theorem 1 to represent f as mixture of duples and unilaterals, i.e., $f=\lambda f_{ uni } + (1-\lambda ) f_{ duple }$, where $\lambda \in [0,1]$, $f_{ uni }$ is a mixture of unilaterals, and $f_{ duple }$ is a mixture of duples. While Lemmas 5 and 7 imply that $f_{ uni }$ and $f_{ duple }$ are not $\beta$-ex post efficient for $\beta <\frac{1}{m}$, this does not imply that f violates $\beta$-efficiency for $\beta <\frac{1}{m}$, too. The reason for this is that $f_{ uni }$ and $f_{ duple }$ may violate $\beta$-ex post efficiency for different profiles or alternatives. We solve this problem by constructing a strategyproof SDS $f^*=\lambda f_{ uni }^*+(1-\lambda ) f_{ duple }^*$ that is 0-randomly dictatorial and $\beta$-ex post efficient for the same $\beta$ as f, and for which $f_{ uni }^*$ and $f_{ duple }^*$ denote mixtures of unilaterals and duples such that $f^{*}_{ uni }(R^{x,y},y)=f^*_{ uni }(R^{\tau (x), \tau (y)}, \tau (y))$ and $f^{*}_{ duple }(R^{x,y},y)=f^*_{ duple }(R^{\tau (x), \tau (y)}, \tau (y))$ for all permutations $\tau :A\rightarrow A$.

For this construction, we define $f^{\tau }$ as $f^\tau (R,x)=f(\tau (R),\tau (x))$ for every permutation $\tau :A\rightarrow A$. We construct the SDS $f^*$ for m!n voters as follows: we partition the electorate in m! sets $N_k$ with $|N_k|=n$ and associate each of these sets with a different permutation $\tau _k:A\rightarrow A$. Then, we choose one of these sets $N_k$ uniformly at random and consider from now on only the preference profile $R_{N_k}$ defined by the voters in $N_k$. Finally, return $f^{\tau _k}(R_{N_k})$, where $\tau _k$ denotes the permutation associated with $N_k$. More formally, $f^*(R)=\frac{1}{m!}\sum _{k=1}^{m!}f^{\tau _k}(R_{N_k})$.

First, note that $f^*$ is 0-randomly dictatorial because of Lemma 1. In more detail, since f is 0-randomly dictatorial, there is for every voter i a profile R and alternatives x, y such that voter i prefers x the most and y the second most in R, and $f(R,y)=f(R^{i:yx},y)$. Consequently, there are such profiles and alternatives for every voter in each SDS $f^\tau$. Finally, we derive that such profiles and alternatives exist also for $f^*$. For a voter $i \in N_k$, the corresponding alternatives x, y and the preferences of the voters in $N_k$ are the same as for $f^{\tau _k}$. The preferences of the remaining voters do not matter. If $f^*$ does not choose $N_k$ in the first step, the preferences of voter i do not matter, and if $f^*$ chooses $N_k$, it only computes $f^{\tau _k}(R_{N_k})$. Hence, if voter i now swaps x and y, the outcome of $f^*$ does not change as the outcome of $f^{\tau _k}$ does not change. Consequently, Lemma 1 implies that $f^*$ is 0-randomly dictatorial.

Next, observe that $f^*(R)=\frac{1}{m!}\sum _{k=1}^{m!}f^{\tau _k}(R_{N_k})$ is strategyproof as it is a mixture of strategyproof SDSs. In particular, we can interpret each term $f^{\tau _k}(R_{N_k})$ as SDS for n voters that ignores the preferences of the voters not in $N_k$. It follows immediately from this interpretation that $f^*$ is strategyproof because all $f^{\tau _k}$ are strategyproof. Hence, we can use Theorem 1 to represent $f^*$ as $f^*=\lambda f^*_{ uni } + (1-\lambda ) f^*_{ duple }$, where $f^*_{ uni }$ is a mixture of unilaterals and $f^*_{ duple }$ is a mixture of duples. In more detail, the following equation shows that $f^*_{ uni }(R)=\frac{1}{m!}\sum _{k=1}^{m!} f^{\tau _k}_{ uni }(R_{N_k})$ and $f^*_{ duple }(R)=\frac{1}{m!}\sum _{k=1}^{m!} f^{\tau _k}_{ duple }(R_{N_k})$, where $f^{\tau _k}_{ uni }$ and $f^{\tau _k}_{ duple }$ are defined analogously to $f^{\tau _k}$.

$$\begin{aligned} f^*(R)&=\frac{1}{m!}\sum _{k=1}^{m!}f^{\tau _k}(R_{N_k})\\&= \frac{1}{m!}\sum _{k=1}^{m!}\lambda f^{\tau _k}_{ uni }(R_{N_k}) + (1-\lambda )f^{\tau _k}_{ duple }(R_{N_k}) \\&=\lambda \frac{1}{m!} \sum _{k=1}^{m!} f^{\tau _k}_{ uni }(R_{N_k}) + (1-\lambda )\frac{1}{m!} \sum _{k=1}^{m!} f^{\tau _k}_{ duple }(R_{N_k})\\&=\lambda f^*_{ uni }(R) + (1-\lambda ) f^*_{ duple }(R) \end{aligned}$$

Note that the definitions of $f^*_{ uni }$ and $f^*_{ duple }$ entail that $f^*_{ uni }(R^{x,y},y)=f^*_{ uni }(R^{\rho (x),\rho (y)}, \rho (y))$ and $f^*_{ duple }(R^{x,y},y)=f^*_{ duple }(R^{\rho (x),\rho (y)},\rho (y))$ for every permutation $\rho :A\rightarrow A$. For $f^*_{ uni }$, this follows from the following equations and a symmetric argument holds for $f^*_{ duple }$.

$$\begin{aligned} f^*_{ uni }(R^{x,y},y)&=\frac{1}{m!}\sum _{k=1}^{m!} f^{\tau _k}_{ uni }(R_{N_k}^{x,y},y) \\&=\frac{1}{m!}\sum _{k=1}^{m!}f_{ uni }(\tau _k(R_{N_k}^{x,y}),\tau _k(y)) \\&=\frac{1}{m!}\sum _{k=1}^{m!} f_{ uni }(\tau _k(\rho (R_{N_k}^{x,y})),\tau _k(\rho (y))) \\&=f^*_{ uni }(R^{\rho (x), \rho (y)}, \rho (y))) \end{aligned}$$

The first two equations rely only on our definitions. The third equation follows because $\{\tau \circ \rho :\tau \in \textrm{T}\}=\textrm{T}=\{\tau _k:k \in \{1, \dots , m!\}\}$ for every permutation $\rho :A\rightarrow A$, where $\textrm{T}$ is the set of all permutations on A.

Finally, we show that $f^*$ violates $\beta$-ex post efficiency for every $\beta <\frac{1}{m}$, which entails that f also violates this axiom. We use Lemma 5 and Lemma 7 for this as these lemmas imply that $f^*_{ duple }$ and $f^*_{ uni }$ violate $\beta$-ex post efficiency. Note for this that $f^*_{ uni }$ is 0-randomly dictatorial as otherwise, $f^*$ cannot be 0-randomly dictatorial. Hence, there are profiles $R^{1}$ and $R^{2}$, and alternatives $x_1$, $y_1$, $x_2$, and $y_2$ such that $x_i$ Pareto-dominates $y_i$ in $R^i$ for $i\in \{1,2\}$, $f^*_{ uni }(R^1,y_1)\ge \frac{1}{m}$, and $f^*_{ duple }(R^2,y_2)\ge \frac{1}{m}$. We now derive from strategyproofness that $f^*_{ uni }(R^{x_1,y_1},y_1)\ge \frac{1}{m}$ and $f^*_{ duple }(R^{x_2,y_2},y_2)\ge \frac{1}{m}$. Finally, it follows from the symmetry of $f^{*}_{ uni }$ and $f^*_{ duple }$ with respect to the profiles $R^{x,y}$ that $f^*_{ uni }(R^{x,y},y)\ge \frac{1}{m}$ and $f^*_{ duple }(R^{x,y},y)\ge \frac{1}{m}$ for all alternatives $x,y\in A$. Consequently, we conclude that $f^*(R^{x,y},y)=\lambda f^*_{ uni }(R^{x,y},y)+(1-\lambda )f^*_{ duple }(R^{x,y},y)\ge \frac{1}{m}$ for all $x,y\in A$. This means that $f^*$ and therefore also f violate $\beta$-ex post efficiency for every $\beta <\frac{1}{m}$. $\square$