Abstract
The interaction between the transonic flow around a spring mounted OAT15A airfoil model and the resulting pitching motion of the model were investigated with the goal of understanding the dynamics of the occurring phenomena. The experiments were performed at a free-stream Mach number of 0.74, a Reynolds number of \(\mathrm{Re}_\mathrm {c}=3.1\times 10^6\), and a mean angle of attack of \(5.8^\circ\). A periodic pitch motion with an amplitude of the angle of attack of \(\pm \,0.9^\circ\) was observed for these flow conditions. The dominant structural frequency of the airfoil’s pitch motion was adjusted to be in the range of the natural buffet frequency of the flow with inhibited pitching motion of the model. The structural motion locks into the frequency of the shock buffet with the pitching degree of freedom at a dominant frequency of 115.5 Hz. Velocity field measurements by means of high repetition rate particle image velocimetry (PIV) were used to capture the motion of the shock and to determine the state of the boundary layer flow for the different phases of the model motion. The PIV results with high temporal resolution allow the detailed observation of the evolution of the different phases of the buffet cycle. Mean values and statistical quantities, spectra and space-time correlations were determined from the measurement data to analyze the flow effects. It was possible to estimate the convection velocity of turbulent structures in the detached boundary layer.
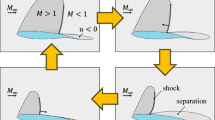
Graphical abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In transonic airfoil flow, the subsonic inflow accelerates first to sonic speed and then, due to the curvature of the airfoil, to supersonic speed. For positive angles of attack, a supersonic region initially forms only on the upper side of the airfoil (suction side), which is locally limited and changes back to subsonic flow by means of a compression shock, as illustrated in Fig. 1. Due to the shock, the pressure rises abruptly and the velocity drops accordingly. Depending on the shock strength and the state of the boundary layer, separation can occur due to the sudden increase in pressure. For a certain range of inflow Mach numbers and angles of attack, which depends on the airfoil geometry, there is no stable solution for the shock position. Instead, so-called shock buffet occurs, where the shock executes a periodic motion coupled with a shock-induced separation of the boundary layer (Giannelis et al. 2017; Lee 2001; McDevitt and Okuno 1985; Tijdeman 1977). The interaction between separation and shock motion depends on the airfoil geometry and the inflow conditions (Crouch et al. 2009; Iovnovich and Raveh 2012; Jacquin et al. 2009; Tijdeman 1977). During a buffet cycle, the boundary layer flow can alternate between fully detached and fully attached. Depending on the geometry and flow conditions, however, the boundary layer can also be detached over the complete cycle and only the size of the separated area changes.
Shock-induced buffet represents an unsteadiness which causes strong periodic pressure fluctuations and consequently alternating loads and thus limits the operating range of technical components. Due to the dynamics of the change in shock position, shock intensity and detachment of the boundary layer, periodic loads result in an increased risk of structural damage. For a safe use of components that are subject to transonic flow, such as aircraft wings and turbine blades, it is necessary to be able to predict the flow conditions under which shock buffet occurs as well as the dominant frequency. (Lee 1990, 2001) has proposed a model for estimating the buffet frequency that is based on the propagation time of pressure disturbances. Disturbances originating from the shock foot are transported in the detached shear layer to the trailing edge of the profile, where they generate upstream pressure waves that interact again with the shock. The time it takes the disturbances to move from the shock foot location to the trailing edge and back to the shock through the region above the profile suction side corresponds to the period of the shock oscillation. On the one hand, there are numerical investigations (Deck 2005; Xiao et al. 2006) and experiments (Zhao et al. 2013) that give a good agreement with Lee’s model. On the other hand, there are also flow simulations (Crouch et al. 2009; Garnier and Deck 2010) and experiments (Hartmann et al. 2013; Jacquin et al. 2009; Klinner et al. 2021) that determine a different period duration. Other approaches are based on interaction with the upper part of the shock (Hartmann et al. 2013) or on propagation of pressure perturbations along the pressure side of the profile and around the nose to the shock (Klinner et al. 2021; Crouch et al. 2009; Jacquin et al. 2009; Garnier and Deck 2010), thus modifying Lee’s model.
Since no real structures are infinitely stiff, the consideration of coupling is particularly relevant. New numerical simulations, which also consider the coupling between fluid and structure in transonic flow, show that the natural frequencies of elastic structures have an influence on the buffet frequency and on the buffet boundary (Gao and Zhang 2020; Nitzsche et al. 2019). It is the primary aim of this analysis to contribute to further understanding regarding the interaction between structure and flow. For experimental investigations, however, it is essential to know the structural properties and to characterize the model motion resulting from the coupling. For this purpose, a quasi-two-dimensional airfoil model with a pitching degree of freedom whose natural frequency is close to the buffet frequency is investigated. This allows a coupling between the change of the angle of attack and the flow field with oscillating compression shock and changing boundary layer separation.
The following section briefly describes the test facility, the wind tunnel model and the measurement approach. In Sect. 3, the measurement results are presented and discussed in detail; in Sect. 4 the work is summarized and conclusions are drawn.
2 Measurement setup
The measurements were performed in the trisonic wind tunnel at the Bundeswehr University Munich (TWM). The TWM facility is a blow-down type wind tunnel with a 300 mm wide and 675 mm high test section. Two adjustable throats, the Laval nozzle upstream of the test section and the diffuser further downstream, enable an operating range of Mach numbers from 0.2 to 3.0. The facility has two tanks with a total volume of 356 m\(^3\) that are pressurized with dry air up to 20 bar above ambient pressure. To control the Reynolds number, the total pressure in the test section is varied between 1.2 and 5 bar. The free-stream turbulence level based on streamwise velocity fluctuations in the TWM test section is approximately \(1.3\%\) for the Mach number range considered here. More details about the facility and its characterization are provided in Scheitle and Wagner (1991) and Scharnowski et al. (2019).
The airfoil model consists of a shell-like structure (carbon-fiber-reinforced plastic, CFRP) and a metal shaft (tool steel, Toolox44) located at \(25\,\%\) of the chord length. The shaft passes through the side windows of the test section and is supported by needle bearings directly outside the windows. With this support, the model can pitch around the axis of the shaft, as illustrated in Fig. 1. A steel lever with a rectangular cross section (\(6\times 10\,\mathrm {mm}^2\)) extends downwards from both shaft ends. This lever serves as a spring and its bending stiffness can be adjusted via the lever length. Balancing masses are used to ensure that the center of gravity of all moving parts is located on the axis of rotation. Thus, structural pitch and heave modes are decoupled. The natural frequency of the model’s pitch motion was set to \(105\,\mathrm{Hz}\), which is approximately the same as the buffet frequency of the rigidly suspended airfoil, according to Kokmanian et al. (2022).
For the geometry, the super-critical shape OAT15A was chosen because it has been investigated numerous times. The model has a chord length of 150 mm and is 298 mm wide. This results in a gap of one millimeter on each side, which is required to perform the pitch motion.
The Mach number of the flow was set to \(Ma_\infty =0.74\), where the static pressure port from which \(Ma_\infty\) is computed is located \(200\,\mathrm{mm}\) upstream of the model at the upper wall of the test section. A total pressure of \(p_0=1.5\,\mathrm{bar}\) was used to achieve a Reynolds number of \(\mathrm{Re}_c=3.1\times 10^6\). This value is based on the chord length \(c=150\,\mathrm{mm}\), the free-stream velocity \(u_\infty =238\,\mathrm{m/s}\) and the total temperature \(T_0=285\,\mathrm{K}\).
For the PIV measurements, the flow was seeded with Di-Ethyl-Hexyl-Sebacate (DEHS) tracer particles with a mean diameter below \(1\,{\upmu }\)m. The particles have a response time of about \(2\,{\upmu }\)s (Melling 1997; Ragni et al. 2011) and are therefore considered to be able to follow the flow sufficiently. Only for a small region downstream of the shock is the flow velocity overestimated due to the inertia of the droplets in the region with strong negative acceleration.
The particles in the TWM test section were illuminated from downstream with a light sheet generated by a PIV double pulse laser (DM 150-532, by Photonics Industries Inc.) with a light sheet width of \(0.5\,\mathrm{mm}\) measured at \(1/e^2\) of the maximum intensity. The scattered light was recorded by means of a high-speed camera (Phantom V2640, by Vision Research Inc.) which was equipped with a 50 mm lens (Planar T2/50, by Zeiss). Double images, \(2048\times 1264\,\mathrm{pixel}\) in size (corresponding to \(278\times 171\,\mathrm{mm^2}\)), were recorded with 5 kHz. Additionally, measurements with a further cropped sensor size (\(1790\times 704\,\mathrm{pixel}\)) and an increased acquisition rate (10 kHz) were performed to capture the convection of vortical structures in the separated shear layer. The data with higher repetition rate were used for the two-point correlation in Sect. 3.6, while the data with larger image sizes were used for all other results. For statistical convergence of the results both recording frequencies, 10,000 double images were acquired and analyzed. This leads to a measurement time of 2 and 1s for a recording rate of 5 and 10 kHz, respectively. This is considered to be well suited for a reliable estimation of flow statistics, since a fluid element at free-stream velocity \(u_\mathrm {\infty }\) would travel more than 3000 and 1500 times over a distance of the model’s chord length c for a recording rate of 5 and 10 kHz, respectively. The time separation between the double images was set to \(4\,{\upmu }\)s, resulting in a particle image displacement of up to 12 pixels for regions with a flow velocity of 400 m/s. Although the optical magnification and the particle image displacement were optimized to account for the richness of spatial and temporal dynamics in this kind of flow, resolving the small-scale features remains challenging due to the strong velocity gradients in the shear layers (Scharnowski and Kähler 2020). For the densely seeded PIV images, a background noise level with a standard deviation of about 12 counts was estimated from the auto-correlation function with the method presented in Scharnowski and Kähler (2016). This noise level leads to a loss-of-correlation due to image noise of \(F_\mathrm {\sigma }\approx 0.9\) and to a signal-to-noise ratio of \(\mathrm{SNR}\,\approx 3.6\), which is considered to be well suited for PIV evaluation.
3 Results and discussions
3.1 Airfoil dynamics
During the wind tunnel run, the airfoil performed a periodic oscillation around its axis of rotation. The laser light sheet touched the surface in the rear part of the model, making it clearly visible in the PIV raw images. The angle of attack over time \(\alpha (t)\) was determined by detecting the top surface from the scattered light in the PIV images and finding the best match with the known geometry. Figure 2 illustrates the change in angle of attack over the first \(50\,\mathrm{ms}\) together with a sinusoidal fit-function. Two different coordinate systems are used throughout this work: \(\left( x,y \right)\) are global coordinates and \(\left( {\hat{x}},{\hat{y}} \right)\) are rotated coordinates relative to the pitching airfoil, as indicated in Fig. 1.
Before the wind tunnel run, \(\alpha\) was set to \(7.0^\circ\) with an unloaded lever arm. During the wind tunnel run, the aerodynamic loads caused a positive aerodynamic moment that bent the lever arm and decreased \(\alpha\) on average to the desired value of \({\overline{\alpha }}\approx 5.8^\circ\). Additionally, the angle of attack is fluctuating around its mean by an amplitude of \(\Delta \alpha \approx \pm 0.9^\circ\), as can be seen in Fig. 2. Frequency and amplitude of the oscillation vary slightly over the measurement time of \(2\,\mathrm{s}\). The mean values and standard deviations are \(f=(115.5\pm 0.9)\,\mathrm{Hz}\) and \(\Delta \alpha =0.84^\circ \pm 0.09^\circ\). From the fit-function in the figure, the phase information for each time step was determined, which will be used for phase averaged flow field statistics in Sect. 3.3. The effect of \(\alpha\) on the change in the flow field is discussed in detail in the following section.
Measured angle of attack over time \(\alpha (t)\) together with a sinusoidal fit function. The open circles indicate the time instances used for the instantaneous flow fields in Fig. 3
3.2 Flow field dynamics
The PIV images were evaluated using an iterative approach with decreasing interrogation window size and subsequent image deformation. A Gaussian window weighting function was applied and a final interrogation window size of \(24^2\,\mathrm{pixel}\) with \(50\%\) overlap was used, leading to a vector grid spacing of \(1.6\,\mathrm{mm}\) corresponding to \(1.1\%\) of the chord length c. Invalid vectors were identified and removed with the method of Westerweel and Scarano (2005). For most time steps, the fraction of invalid vectors was well below \(1\%\).
Figure 3 illustrates the development of the flow field over time, showing example flow fields at every fifth time step of a full period. At \(t=0\) (top left in the figure), the shock is located at its most downstream position and the angle of attack is almost at its maximum. As time progresses, the boundary layer separates and the shock moves towards the leading edge. At \(t=3\,\mathrm{ms}\) and \(4\,\mathrm{ms}\) (bottom left in Fig. 3) the flow features a large separated region with reversing flow as fast as –200 m/s, as it can also be seen in Fig. 9. In the following, the flow reattaches on the surface of the model and the shock moves downstream again until it reaches its most downstream position again after about \(9\,\mathrm{ms}\) (bottom right in the figure).
To see if the changes in the flow field, as shown in Fig. 3, are periodic in nature, the power spectral density (PSD) of velocity was determined using the method of Welch (1967). For each vector location, the PSD was computed from the horizontal velocity component u (in airfoil coordinates) of the 10,000 vector fields by using a window length of 1000 samples, an overlap of \(50\%\) of the window length and a so-called Hamming window function. Figure 4 shows the spatially averaged PSD of the velocity fluctuation \(u-\langle u\rangle\), with \(\langle u\rangle\) being the local time-averaged mean. The PSD of the velocity shows a dominant peak at \(115\,\mathrm{Hz}\) together with its higher harmonics up to the fifth order, indicating a strictly periodic behavior. This corresponds to a reduced frequency of \(k=\pi f c/u_\infty =0.23\). The PSD of the angle of attack is also plotted in Fig. 4. It shows the same dominant peak at \(f=115\,\mathrm{Hz}\) confirming the coupling between fluid and structure.
Figure 5 illustrates the spatial distribution of the PSD amplitude of the horizontal velocity component for the dominant frequency \(f=115.5\,\mathrm{Hz}\). It can be seen from the figure that very large amplitudes are reached in the region of the shock as well as downstream of the shock in the boundary layer. These regions are subject to strong changes of the horizontal velocity component due to the movement of the shock and due to the periodically separating boundary layer, as shown in Fig. 3. The dominant frequency of the fluid at \(115.5\,\mathrm{Hz}\) is slightly larger than both the buffet frequency of the rigidly mounted airfoil for \(M_\infty =0.74\) and \(\alpha \approx 5.8^\circ\) as well as the natural frequency of the model’s pitch motion.
3.3 Phase averaged flow evolution
Since the motion of the airfoil and the changes in the flow field are highly periodic, the velocity fields can be divided into groups with similar conditions in order to analyze the periodic changes in more detail. The phase of the 10,000 velocity fields was determined from a sinusoidal fit-function applied to the temporal development of the angle of attack \(\alpha\), as shown in Fig. 2. To account for slight changes in frequency and amplitude of \(\alpha\), the fit-function was applied to successive subsets of 200 time steps (corresponding to \(0.04\,\mathrm{s}\)). This allowed the phase relation of each vector field to be reliably determined. The individual velocity fields were then divided into 50 different groups, each with 200 samples, based on their phases. For each of the groups, the mean velocity distribution and the velocity fluctuations were computed. Figure 6 shows the phase-averaged spatial distribution of the turbulent kinetic energy TKE, defined as:
where \(\sigma _\mathrm {u}\) and \(\sigma _\mathrm {v}\) are the standard deviations of the horizontal and vertical velocity component (in global coordinates), respectively. In the figure, the TKE is normalized with the free-stream velocity \(u_\infty =238\,\mathrm{m/s}\). The phases in Fig. 6 are sorted by the phase time \(t^\star\), defined as:
where t is the actual time, \(t_\mathrm {d}\) is the time when the shock was last at the downstream turning point and \(f_\mathrm {b}\) is the buffet frequency. \(t^\star\) therefore takes values between 0 and 1.
At the phase time \(t^\star =0\), the shock is located at its most downstream location at \({\hat{x}}_\mathrm {shock}/c\approx 0.48\) (in airfoil coordinates), shown in the top left of Fig. 6. The shock can be clearly identified from the iso-lines of the Mach number lying almost on top of each other. The fact that the iso-lines are not perfectly superimposed is due to the low-pass filtering of the calculated velocity fields by the PIV interrogation windows (Kähler et al. 2012) as well as due to changes in the shock location within the set of data used for the phase averaged field. With increasing phase time, the shock moves upstream. For \(t^\star \ge 0.1\), the lower part of the shock changes its type from an almost straight shock to an oblique one. Typical for an oblique shock is the abrupt deflection of the flow, which in this case can only be caused by a detachment of the boundary layer. In the phase-time range \(0.2\le t^\star \le 0.6\), the Mach number downstream of the shock is still supersonic, causing a second shock that merges into the primary one and results in a so-called \(\lambda -\) shock wave. For the sake of easy comparability, the primary shock locations from the different phases are plotted altogether in Fig. 7. Besides the phase averaged shock location, the figure also shows the region of flow separation, indicated by the iso-line of \(u=0\). It can be seen from Fig. 7 that the separated region grows with the further upstream moving shock location.
At \(t^\star \approx 0.4\), the shock has almost reached its forward turning point at \({\hat{x}}_\mathrm {shock}/c\approx 0.24\) (in airfoil coordinates) and the separation region is now at its largest. The TKE level also reaches its maximum in the separated shear layer, as shown in the bottom left of Fig. 6. The compression shock increases the pressure on the rear part of the airfoil and its forward motion increases the aerodynamic moment about the axis of rotation. As a result, the angle of attack is showing an inflection point at \(t^\star \approx 0.4\). Thus, \(\alpha\) reduces its rate of change and will start to increase soon, as it can be seen from the red circles in Fig. 8.
For \(t^\star >0.4\), the shock location starts to move back downstream and for \(t^\star >0.6\), no flow separation can be detected anymore. The orientation of the shock now changes abruptly: the oblique shock, which indicates a detachment, now becomes an almost straight shock again. In the following, the shock angle and the angle of attack increase again, as it can be seen from Fig. 8, where the shock angle \(\beta\) is the angle between the tangent of the surface and the compression shock. At \(t^\star =1.0\), the shock location is back at its most downstream location and the cycle repeats from the beginning. The shock exceeds a total of \(24\%\) of airfoil chord length during its phase averaged oscillation, which is more than observed for models without the rotational degree of freedom. The authors of this work have also performed measurements on the same model without the pitching degree of freedom. In this case, the position of the shock changes approximately \(17\%\) of the chord length for the same Mach number and a fixed angle of attack of \(\alpha = 5.8^\circ\). However, if the angle of attack is changed to the same extent as here in the experiments with a fixed model, a comparable variation of the shock location is observed (Kokmanian et al. 2022). This experimental result clearly shows that the model’s stiffness strongly influences the buffet amplitude as predicted by Gao and Zhang (2020) and Nitzsche et al. (2019). It seems, however, that the larger amplitude of the shock motion is not a dynamic effect but is caused only by the change in the angle of attack.
3.4 Boundary layer separation
The shock motion during the buffet cycle strongly affects the boundary layer flow in the rear part of the airfoil’s suction side. Figure 9 shows the temporal development of the streamwise velocity component u at a height of \(0.02\cdot c\) above the airfoil’s suction side surface for a short period of time. Flow separation takes place when the shock is moving upstream, as it can be seen from the blue regions in the figure. This corresponds to states when the shock is of an oblique type with a shock angle below \(70^\circ\), as shown by the blue circles in Fig. 8. In Fig. 9, the reversed flow region does not start directly downstream of the shock because the early separation region is very thin and lies below the slice shown in the figure. The near wall region could not be resolved for the instantaneous velocity fields with the chosen PIV setup. It can also be seen from the figure that the size of the recirculation region and the intensity of the back-flow velocity at the selected height is subject to strong changes between the different phases.
In order to characterize the change in the near wall velocity between the different phases of the buffet cycle in more detail, a single-pixel PIV evaluation was performed. Single-pixel ensemble-correlation allows for reliable estimation of the mean velocity with improved spatial resolution, compared to the classical window correlation PIV evaluation method (Westerweel et al. 2004; Kähler et al. 2012). For the single-pixel evaluation, 40,000 PIV double images were divided into 20 phases. This results in 2000 image pairs per phase, which is considered to be sufficient for a reliable velocity estimation (Scharnowski et al. 2012; Avallone et al. 2015). To enhance the signal-to-noise ratio, the single-pixel correlation functions were averaged over \(5\times 5\,\mathrm{pixel}\) (\(1/e^2\) width of a Gaussian weighting function) and flow statistics are presented for every second pixel in both directions. The resulting vector grid spacing is about \(170\,{\upmu }\)m (or 0.1\(\%\) of the airfoil chord length). Figure 10 shows the mean velocity distribution in the central region above the airfoil surface. Due to the improved spatial resolution with the single-pixel approach, a small recirculation region can be detected already for \(t^{\star }=0\). The separated region quickly grows in the following phases while the shock moves upstream. For \(t^{\star }=0.55\), the shock is weakened such that the separated region collapses, which is in agreement with the sudden increase in the shock angle as shown in Fig. 8. However, it is also possible that a small separation continues to occur without being resolved. The streamline closest to the wall shows a bump downstream of the shock that supports this possibility. Furthermore, it is also possible that separation only occurs occasionally for this phase and thus no reverse flow can be detected in the mean flow field.
For \(t^{\star }=0.8\) (second from bottom in Fig. 10) the shock is aligned rather perpendicular to the surface and moves back to its downstream turning point. At this phase, the little bump in the streamline close to the wall is further reduced. Flow separation is therefore very weak and rare. Close to the downstream turning point of the shock, at \(t^{\star }=0.9\) (bottom in Fig. 10), the streamline bump is again more pronounced. It is safe to say that a significant separation will occur in the next increments causing the shock to move upstream again.
3.5 Evolution of the wake
Downstream of the trailing edge, the flow from both the suction side and pressure side recombines. Due to the velocity differences, another shear layer is formed starting from the trailing edge of the model. The flow from the pressure side is attached all the way to the trailing edge in the visible region. It is subject to only minor changes during the different phases of the model motion. However, the flow from the suction side shows strong changes during the different phases. Figure 11 illustrates profiles of the phase averaged streamwise velocity component for three different locations downstream of the model. The line color represents the phase time \(t^\star\) defined by Eq. (2). For \(x/c=1.1\) (top row in Fig. 11), the velocity gradient in the new developing shear layer at \(-0.1\le y/c\le -0.02\) is approximately the same for all phases. However, the thickness of the shear layer varies. When the shock is at its downstream turning point (\(t^\star =0\)), the shear layer is thinnest (red line) and it grows until \(t^\star \approx 0.35\) (blue line) in width before it collapses again during the rest of the phase time. Further downstream, the velocity gradient weakens due to the mixing in the shear layer (middle and bottom rows in Fig. 11), which is in agreement with the elevated TKE values in that region, as shown in Fig. 6.
The dissipative processes in the boundary layer and in the free shear layer in the wake as well as the pressure losses over the shock prevent the velocity in the wake from reaching the same level as before the model. Instead, a velocity deficit remains, the strength of which changes with the model movement. The velocity profiles in the wake of the airfoil from Fig. 11 are used to compute the velocity deficit \(u_\mathrm {d}\) during the different phases of the model motion as follows:
The integral bounds were \(y/c=-\,0.2\) and 0.6.
Figure 12 shows \(u_\mathrm {d}\) as a function of the angle of attack \(\alpha\) for different streamwise locations in the wake. At the beginning of the phase time (\(t^\star \approx 0.1\)), the deficit increases quickly due to the developing separation. Around \(t^\star \approx 0.4\), the maximum is reached, which decreases with increasing distance from the trailing edge. At this point, the shock has reached its most upstream position. From now on, the velocity deficit in the wake decreases again, at first gradually but then rapidly at \(t^\star \approx 0.6\). In the following, the type of shock changes from an oblique shock to a rather straight shock, as it can be seen in the development of the shock angle in Fig. 8. For the rest of the phase time, the deficit slowly approaches its minimum value before increasing again in the next period.
It should be noted that the velocity deficit changes by more than a factor of two during a cycle in the evaluated region. Since the velocity deficit in the wake is directly linked to the drag, this phenomenon could lead to strong fluctuations in the loads of technical components and thus limit their operational life or even cause them to fail. The flow separation and the change in the size of the separation region are the cause of the strong fluctuations of the drag force. However, the same phenomena also cause a change in the lift force. Therefore, it can be expected that the lift is also subject to strong fluctuations, resulting in additional loads and further risks and/or limitations.
Particularly at the turning points of the shock motion, the relationship between drag and angle of attack is highly nonlinear. If the shock is close to its downstream turning point, the separation increases massively in the following, which increases the drag. At the same time, the lift decreases and the pitch moment increases, reducing the angle of attack. In the following, the shock moves upstream and becomes weaker, causing the pitch moment to decrease again. Near the upstream turning point, the separation collapses, causing an increase in the angle of attack. This nonlinear relationship limits the change in the angle of attack to relatively small values.
3.6 Convection of coherent flow structures
In order to examine which physical process causes the dominant frequency of the shock oscillation, this section investigates how turbulent structures propagate downstream from the detached boundary layer. According to Lee’s model (Lee 1990), the buffet period is composed of the time it takes pressure waves to travel from the shock foot to the trailing edge plus the time it takes pressure waves coming from the trailing edge to reach the shock again. To determine the convection velocity of coherent velocity structures associated with the pressure waves, the two-point correlation R of the velocity components was computed as follows:
where \(u^\prime\) and \(\sigma _\mathrm {u}\) are the fluctuation values about the mean and the standard deviation, respectively. The time shift \(\tau\) is used to analyze the temporal evolution of the correlation distribution. In order to be able to follow the flow structures, \(\tau\) must be small enough. Therefore, the data-set with 10 kHz repetition rate was used for this analysis.
Figure 13 illustrates the two-point correlation of the streamwise (left) and vertical (right) velocity component for a reference location above the trailing edge of the airfoil at \({\hat{x}}/c=1\) and \({\hat{y}}/c=0.1\). The middle row in the figure shows the distribution of R without any time shift, i.e. \(\tau =0\). The \(u\) component (left) shows a large region of strong correlated and anti-correlated velocity fluctuations. This correlation is caused by the strong changes in the entire flow field during the different flow phases. The negative and positive time shifts (top and bottom rows in Fig. 13) do not change the \(R_\mathrm {uu}\) distribution significantly and a clear displacement of the location with maximum correlation cannot be determined. In contrast, there is only a small area of increased correlation values around the reference location \(\left( x_0,y_0\right)\) for the correlation of the vertical velocity component \(R_\mathrm {vv}\). A fluctuation in the \(v\) component indicates the presence of vortical structures in the separated boundary layer.
Two-point correlation of the streamwise (left) and vertical (right) velocity component for negative time shift (top), without time shift (middle row), and for positive time shift (bottom). The reference location \((x_0,y_0)\) is marked by the \(x-\)shaped marker and the highest correlation is marked by the circle. Data are presented in the airfoil coordinate system \(({\hat{x}},{\hat{y}})\)
Comparing the correlation distribution of \(R_\mathrm {vv}\) at \(\tau =0\) with the correlations at a time shift of \(\tau =\pm \,0.1\,\mathrm{ms}\), a similar shape is found, but shifted in the flow direction. This shift can be related to the mean displacement of coherent structures within the time difference \(\tau\), allowing for the estimation of the mean convection velocity. Figure 14 shows the convection velocity \(u_\mathrm {c}\) for various positions above and downstream of the model determined in this way. In the figure, it can be seen that the convection velocity increases as the reference point is placed further downstream. Furthermore, it is noticeable that \(u_\mathrm {c}\) becomes larger with greater vertical distance to the model. However, the values for \(u_\mathrm {c}\) in the region downstream of the model fall on each other for all vertical positions. The increasing convection velocity is due to the increasing size of the out-flowing vortices. As they fill more and more space, they must also move faster. The different velocities at the different heights are certainly related to the fact that the detached shear layer lies at different heights depending on the phase and is developed to different degrees.
The convection velocities determined for the coherent flow structures are ranging from \(u_\mathrm {c}= 50\) to \(140\,\mathrm{m/s}\) for the region above the airfoil. This is in agreement with the findings of Simpson (1989) who stated that the convective velocity in a separated shear layer reaches approximately \(0.6\cdot u_\infty\). However, the determined convection velocities are significantly higher than the velocity of downstream propagating waves determined by Hartmann et al. (2013). Such propagating waves could not be detected from the present data set. Thus, feedback by means of acoustic waves along the upper surface of the wing, as suggested in Lee’s model, cannot be verified with the present results, but neither can it be disproved.
4 Conclusions
The transonic flow over an OAT15A airfoil model with a torsional degree of freedom was investigated by means of high repetition rate PIV measurements. At buffet flow conditions, a strongly periodic change of the angle of attack and the shock position are observed, as seen from the spectra in Fig. 4. The frequency of the model motion of 115 Hz was slightly larger than both the structural natural frequency determined before the tests without flow as well as the buffet frequency of the rigid model at similar flow conditions.
It was shown that during the buffet cycle, the flow strongly varies regarding the shape and location of the compression shock as well as the state of the boundary layer downstream of the shock. For the investigated test case, the rotational degree of freedom significantly enhances the dynamics of the flow field compared to a model with zero degree of freedom. The analysis also showed significant changes of the velocity deficit in the wake during the buffet cycle, from which strong changes in drag and lift can also be concluded. It is the nonlinear relation between angle of attack and drag, and thus with lift and pitch moment, that limits the oscillation amplitude of the airfoil model and prevents its destruction.
References
Avallone F, Discetti S, Astarita T, Cardone G (2015) Convergence enhancement of single-pixel PIV with symmetric double correlation. Exp Fluids 56(4):1–11. https://doi.org/10.1007/s00348-015-1938-2
Crouch JD, Garbaruk A, Magidov D, Travin A (2009) Origin of transonic buffet on aerofoils. J Fluid Mech 628:357–369. https://doi.org/10.1017/S0022112009006673
Deck S (2005) Numerical simulation of transonic buffet over a supercritical airfoil. AIAA J 43(7):1556–1566. https://doi.org/10.2514/1.9885
Gao C, Zhang W (2020) Transonic aeroelasticity: a new perspective from the fluid mode. Prog Aerosp Sci 113(100):596. https://doi.org/10.1016/j.paerosci.2019.100596
Garnier E, Deck S (2010) Large-eddy simulation of transonic buffet over a supercritical airfoil. In: Deville M, Lê TH, Sagaut P (eds) Turbulence and interactions. Springer, Berlin, Heidelberg, pp 135–141
Giannelis NF, Vio GA, Levinski O (2017) A review of recent developments in the understanding of transonic shock buffet. Prog Aerosp Sci 92:39–84. https://doi.org/10.1016/j.paerosci.2017.05.004
Hartmann A, Feldhusen A, Schröder W (2013) On the interaction of shock waves and sound waves in transonic buffet flow. Phys Fluids 25(2):26101. https://doi.org/10.1063/1.4791603
Iovnovich M, Raveh DE (2012) Reynolds-averaged Navier–Stokes study of the Shock-Buffet instability mechanism. AIAA J 50(4):880–890. https://doi.org/10.2514/1.J051329
Jacquin L, Molton P, Deck S, Maury B, Soulevant D (2009) Experimental study of shock oscillation over a transonic supercritical profile. AIAA J 47(9):1985–1994. https://doi.org/10.2514/1.30190
Kähler CJ, Scharnowski S, Cierpka C (2012) On the resolution limit of digital particle image velocimetry. Exp Fluids 52:1629–1639. https://doi.org/10.1007/s00348-012-1280-x
Klinner J, Hergt A, Grund S, Willert CE (2021) High-speed PIV of shock boundary layer interactions in the transonic buffet flow of a compressor cascade. Exp Fluids 62(3):58. https://doi.org/10.1007/s00348-021-03145-3
Kokmanian K, Scharnowski S, Schäfer C, Accorinti A, Baur T, Kähler CJ (2022) Investigating the flow field dynamics of transonic shock buffet using PIV. Exp Fluids, under review
Lee BHK (1990) Oscillatory shock motion caused by transonic shock boundary-layer interaction. AIAA J 28(5):942–944. https://doi.org/10.2514/3.25144
Lee BHK (2001) Self-sustained shock oscillations on airfoils at transonic speeds. Prog Aerosp Sci 37(2):147–196. https://doi.org/10.1016/S0376-0421(01)00003-3
McDevitt JB, Okuno AF (1985) Static and dynamic pressure measurements on a NACA 0012 airfoil in the Ames high Reynolds number facility. Tech. Rep
Melling A (1997) Tracer particles and seeding for particle image velocimetry. Meas Sci Tech 8:1406–1416. https://doi.org/10.1088/0957-0233/8/12/005
Nitzsche J, Ringel LM, Kaiser C, Hennings H (2019) Fluid-mode flutter in plane transonic flows. In: IFASD 2019-International forum on aeroelasticity and structural dynamics, https://elib.dlr.de/127989/
Ragni D, Schrijer F, Van Oudheusden BW, Scarano F (2011) Particle tracer response across shocks measured by PIV. Exp Fluids 50(1):53–64. https://doi.org/10.1007/s00348-010-0892-2
Scharnowski S, Kähler CJ (2016) On the loss-of-correlation due to PIV image noise. Exp Fluids 57(7):1–12. https://doi.org/10.1007/s00348-016-2203-z
Scharnowski S, Kähler CJ (2020) Particle image velocimetry: classical operating rules from today’s perspective. Opt Lasers Eng. https://doi.org/10.1016/j.optlaseng.2020.106185
Scharnowski S, Hain R, Kähler CJ (2012) Reynolds stress estimation up to single-pixel resolution using PIV-measurements. Exp Fluids 52:985–1002. https://doi.org/10.1007/s00348-011-1184-1
Scharnowski S, Bross M, Kähler CJ (2019) Accurate turbulence level estimations using PIV/PTV. Exp Fluids 60(1):1. https://doi.org/10.1007/s00348-018-2646-5
Scheitle H, Wagner S (1991) Influences of wind tunnel parameters on airfoil characteristics at high subsonic speeds. Exp Fluids 12(1–2):90–96. https://doi.org/10.1007/BF00226571
Simpson R (1989) Turbulent boundary-layer separation. Ann Rev Fl Mech 21:205–232. https://doi.org/10.1146/annurev.fl.21.010189.001225
Tijdeman H (1977) Investigations of the transonic flow around oscillating airfoils. PhD thesis, TU Delft
Welch PD (1967) The use of fast fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans Audio Electroacoust AU 15:70–73. https://doi.org/10.1109/TAU.1967.1161901
Westerweel J, Scarano F (2005) Universal outlier detection for PIV data. Exp Fluids 39:1096–1100. https://doi.org/10.1007/s00348-005-0016-6
Westerweel J, Geelhoed PF, Lindken R (2004) Single-pixel resolution ensemble correlation for micro-PIV applications. Exp Fluids 37:375–384. https://doi.org/10.1007/s00348-004-0826-y
Xiao Q, Tsai HM, Liu F (2006) Numerical study of transonic buffet on a supercritical airfoil. AIAA J 44(3):620–628. https://doi.org/10.2514/1.16658
Zhao Z, Ren X, Gao C, Xiong J, Liu F, Luo S (2013) Experimental Study of Shock Wave Oscillation on SC(2)-0714 Airfoil. https://doi.org/10.2514/6.2013-537
Acknowledgements
Financial support in the frame of the project HOMER (Holistic Optical Metrology for Aero-Elastic Research) from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 769237 is gratefully acknowledged. Furthermore, the authors would like to thank Jens Nitzsche, Yves Govers, Johannes Dillinger, Johannes Knebusch and Tobias Meier for their contributions during the model design phase of the project.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visithttp://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Scharnowski, S., Kokmanian, K., Schäfer, C. et al. Shock-buffet analysis on a supercritical airfoil with a pitching degree of freedom. Exp Fluids 63, 93 (2022). https://doi.org/10.1007/s00348-022-03427-4
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-022-03427-4