1 Introduction

Quantum systems of atom–field interaction are an increasingly significant area of research in quantum physics. The intricate relationship between atoms and electromagnetic fields has been studied in great detail, and this research has yielded significant progress in both theory and practical application. In particular, insights gained from this research have revolutionized our understanding of how light interacts with matter on an atomic level, and enabled us to comprehend the behavior of complex molecules [1]. Rabi model is a semi-classical model that has been widely studied and has yielded a deep understanding of the behavior of atoms and their interactions with electromagnetic fields [2]. This model has been used to provide explanations for phenomena, such as Rabi oscillations and the Lamb shift [3]. Due to its broad applicability, the Rabi model continues to be a key tool for researchers in the field of quantum optics. The second most important model was proposed in 1963 by physicists E.T. Jaynes and F.W. Cummings to describe the interaction between a single atom and a single photon [4]. Since its conception, it has been prominently used to explore a variety of physical phenomena, including superconductivity and quantum computation [5]. The Jaynes–Cummings model has been greatly expanded over the years, allowing for more intricate interactions between atoms and fields, as well as multiple modes of the field [6], through the addition of multiple atoms, external terms and non-linear interactions [7,8,9,10,11]. In essence, the generalization of the Jaynes–Cummings model has enabled scientists to explore a variety of possibilities that were previously not available. In particular, the interaction between a fourth-level atom and a quantized field, which is one of these generalizations, can be used to study phenomena, such as lasing, photon blockade and entanglement [12]. Additionally, this type of interaction has been used to explore the behavior of quantum systems in the presence of an external driving field and a Kerr-like non-linear medium [13].

Quantum coherence is an important concept in quantum mechanics and information processing, which describes the ability of a quantum system to remain in a superposition of multiple states [14]. It is the basis for many phenomena, such as entanglement and interference [15]. Coherence is a measure of how well the system maintains its quantum state over time. In other words, it is a measure of how well the system can maintain its quantum properties without being disturbed by external influences. Coherence has been studied extensively in recent years and has been found to be essential for many quantum systems, such as nonlinear SU(1, 1) quantum states [16], two-qubit system interacting with a deformed cavity [17], two coupled quantum dot molecules [18], and accelerated systems [19, 20].

The quantum Wigner function (W-function) is a mathematical tool originally proposed by Eugene Wigner in 1932, used to describe the quantum states of particles, such as atoms and photons [21]. This function has been used to gain insights into the quantum interference of particles, quantum system dynamics, and the interaction between atoms and light fields [22]. It has been applied across many different areas of quantum physics and has been used in recent research to control atomic and field states, such as, the classicality/ non-classicality of three qubit system [23, 24], negativity of multimode non-Gaussian states [25], and quantum correlation of light–matter interaction [26, 27]. Furthermore, the W-function has proven to be invaluable for studying the effects of atom–field interactions on atomic states, which is critical for the development of quantum technologies [28].

Building on previous studies, this paper aims to explore how an external classical field affects a W four-level atom placed in a quantized cavity field. In order to solve the physical Hamiltonian, we require certain approximations and rotations when subjecting the system to an external classical field. In our paper, we have employed a method that entails fewer approximations compared to existing approaches for solving the system. This is due to the difficulty in obtaining an exact solution for a quantum system with high dimensionality in the presence of a classical field [29]. Notwithstanding the existing research, this system continues to draw interest from both experimental and theoretical scientists, particularly with respect to its statistical properties and quantum correlations. Furthermore, the model and results presented in this study are both intriguing and promising for future research. For instance, it can be utilized to investigate the four wave mixing process, both theoretically and experimentally [30]. Notably, the observation of the tripod-configuration for a four-level atom has been instrumental in enhancing the cross-phase modulation based on a double electromagnetically induced transparency [31]. Therefore, we present a physical model and demonstrate an exact solution system in Sect. 2. In Sect. 3, 4 and 5, we discuss the mathematical quantum quantifiers associated with our model, where we defined the relative entropy of coherence, Wigner function, and Pancharatnam phase. Finally, our results are summarized and discussed in Sect. 6.

2 Hamiltonian system

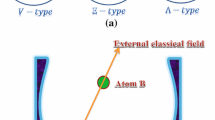
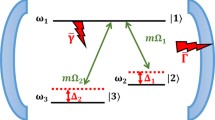
Assuming the physical system consists of interaction of a single W configuration of a four-level atom inside a single mode of a quantized field and an external classical laser field. Considering the transitions between the atomic levels are \(|1\rangle \leftrightarrow \{|3\rangle ,|4\rangle \}\), and \(|2\rangle \leftrightarrow \{|3\rangle ,|4\rangle \}\), where \(|1\rangle ,|4\rangle\) are the upper and ground states respectively, while \(|2\rangle ,|3\rangle\) are the two intermediate states. The classical field associates the upper and lower state with two intermediate states. Under the rotating wave approximation, the physical model that describes Hamiltonian system is written as \((\hbar =1)\),

$$\begin{aligned} \hat{H}=\hat{H}_{0}+\hat{H}_{I}+\hat{H}_{\text {D}}, \end{aligned}$$
(1)

where

$$\begin{aligned} \begin{aligned}&\hat{H}_{0}=\omega _{f} \hat{a}^{\dagger } \hat{a}+\sum _{i=1}^{4} \omega _{i} \hat{\sigma }_{i i}, \\&\hat{H}_{I}=\lambda _{1}\left( \hat{a}\left( \hat{\sigma }_{13}+\hat{\sigma }_{14}+\hat{\sigma }_{23}+\hat{\sigma }_{24}\right) + \text{ h.c. } \right) , \\&\hat{H}_{D}=\lambda _{2}\left( \hat{\sigma }_{12}+\hat{\sigma }_{34}+\text{ h.c. } \right) . \end{aligned} \end{aligned}$$

Here, \(\omega _{f}\) and \(\omega _{i}\) are the frequencies of the cavity field and atomic levels transition, respectively. \(\hat{a }\) and \(\hat{a}^{\dagger }\) are the bosonic annihilation and creation of the cavity field. \(\hat{\sigma }_{j i}=|j\rangle \langle i|\) are polarization operators for \(i\ne j\) and free atomic operators for \(i= j\). \(\lambda _{1}\) and \(\lambda _{2}\) represent the coupling constants of the atom-field and external field, respectively. The classical field is represented by the transition from \(|1\rangle\) to \(|2\rangle\) and from \(|3\rangle\) to \(|4\rangle\). Via denationalization for the free atomic subsystem \(\sum _{i=1}^{4}\omega _{i} \hat{\sigma }_{ii}\) and the driven Hamiltonian \(\hat{H}_{\text {driven }}\), one can obtain the following eigenstates,

$$\begin{aligned} \begin{aligned} \begin{bmatrix} |1\rangle \\ |2\rangle \\ |3\rangle \\ |4\rangle \end{bmatrix} =\begin{bmatrix} \beta _{1}^{-} &{} \beta _{1}^{+} &{} 0 &{} 0 \\ \beta _{2}^{-} &{} \beta _{2}^{+} &{} 0 &{} 0 \\ 0 &{} 0 &{} \alpha _{1}^{-} &{} \alpha _{1}^{+} \\ 0 &{} 0 &{} \alpha _{2}^{-} &{} \alpha _{2}^{+}\end{bmatrix} \begin{bmatrix} |l_{1}\rangle \\ |l_{2}\rangle \\ |l_{3}\rangle \\ |l_{4}\rangle \end{bmatrix}, \end{aligned} \end{aligned}$$
(2)

where

$$\begin{aligned} \begin{array}{c} \begin{array}{cc} \beta _{1}^{\pm }=\frac{\Delta _{1}\pm \sqrt{\Delta _{1}^{2}+4\lambda _{2}^{2}}}{\sqrt{4\lambda _{2}^{2}+(\Delta _{1}\pm \sqrt{\Delta _{1}^{2}+4\lambda _{2}^{2}})}}, \qquad &{} \beta _{2}^{\pm }=\frac{2\lambda _{2}}{ \sqrt{4\lambda _{2}^{2}+(\Delta _{1}\pm \sqrt{\Delta _{1}^{2}+4\lambda _{2}^{2}})}}, \\ \alpha _{1}^{\pm }=\frac{\Delta _{2}\pm \sqrt{\Delta _{2}^{2}+4\lambda _{2}^{2}}}{\sqrt{4\lambda _{2}^{2}+(\Delta _{2}\pm \sqrt{\Delta _{2}^{2}+4\lambda _{2}^{2}})}}, \qquad &{} \alpha _{2}^{\pm }=\frac{2\lambda _{2}}{ \sqrt{4\lambda _{2}^{2}+(\Delta _{2}\pm \sqrt{\Delta _{2}^{2}+4\lambda _{2}^{2}})}}, \end{array} \\ \text { and } \qquad \Delta _{1}=\omega _{1}-\omega _{1},\quad \Delta _{2}=\omega _{3}-\omega _{4}. \end{array} \end{aligned}$$

However, the atomic levels \(|1\rangle ,|2\rangle ,|3\rangle ,|4\rangle\) of the atomic flip operators \(\hat{\sigma }_{ij}\) in eq. (2) can be transformed into a new rotating levels \(|l_{1}\rangle ,|l_{2}\rangle ,|l_{3}\rangle ,|l_{4}\rangle\). Hence, the the atomic flip operators \(\hat{\sigma }_{ij}\) may be transformed into \(\hat{S}_{ij}=|l_i\rangle \langle l_j|\), which obey the commutation relation \(\big [\hat{S}_{ij}, \hat{S}_{nm}\big ]=\hat{S}_{im} \delta _{nj}-\hat{S}_{nj} \delta _{im}\).

Moreover, Hamiltonian (1) in the new rotating bases may be written as,

$$\begin{aligned}{} & {} \hat{\mathcal {H}}=\omega _{f}\hat{a}^{\dagger }\hat{a}+\Omega _{1}\hat{S} _{11}+\Omega _{2}\hat{S}_{22}+\Omega _{3}\hat{S}_{33}+\Omega _{4}\hat{S} _{44}\nonumber \\{} & {} \quad +\hat{a}\left( \mu _{1}\hat{S}_{13}+\mu _{2}\hat{S}_{14}+\mu _{3}\hat{S} _{23}+\mu _{4}\hat{S}_{24}\right) +h.c., \end{aligned}$$
(3)

with the new atomic transitions,

$$\begin{gathered} \Omega _{1} = \omega _{1} \beta _{1}^{{ - 2}} + \omega _{2} \beta _{2}^{{ - 2}} + 2\lambda _{2} \beta _{1}^{ - } \beta _{2}^{ - } , \hfill \\ \Omega _{2} = \omega _{1} \beta _{1}^{{ + 2}} + \omega _{2} \beta _{2}^{{ + 2}} + 2\lambda _{2} \beta _{1}^{ + } \beta _{2}^{ + } , \hfill \\ \Omega _{3} = \omega _{3} \alpha _{1}^{{ - 2}} + \omega _{4} \alpha _{2}^{{ - 2}} + 2\lambda _{2} \alpha _{1}^{ - } \alpha _{2}^{ - } ,\qquad \hfill \\ \Omega _{4} = \omega _{3} \alpha _{1}^{{ + 2}} + \omega _{4} \alpha _{2}^{{ + 2}} + 2\lambda _{2} \alpha _{1}^{ + } \alpha _{2}^{ + } , \hfill \\ \end{gathered}$$
(4)

and the new coupling interaction including the coupling of external field,

$$\begin{gathered} \mu _{1} = \lambda _{1} (\beta _{1}^{ - } + \beta _{2}^{ - } )(\alpha _{1}^{ - } + \alpha _{2}^{ - } ),\qquad \hfill \\ \mu _{2} = \lambda _{1} (\beta _{1}^{ - } + \beta _{2}^{ - } )(\alpha _{1}^{ + } + \alpha _{2}^{ + } ), \hfill \\ \mu _{3} = \lambda _{1} (\beta _{1}^{ + } + \beta _{2}^{ + } )(\alpha _{1}^{ - } + \alpha _{2}^{ - } ),\qquad \hfill \\ \mu _{4} = \lambda _{1} (\beta _{1}^{ + } + \beta _{2}^{ + } )(\alpha _{1}^{ + } + \alpha _{2}^{ + } ). \hfill \\ \end{gathered}$$
(5)

The Hamiltonian (3) can be rewritten in terms of Heisenberg constants of motion as,

$$\begin{aligned} \hat{\mathcal {H}}=\omega _{f} \hat{\mathcal {N}}+\Omega _{1} \sum _{r=1}\hat{S}_{rr}+\mathcal {H} _{i n t}. \end{aligned}$$
(6)

Here, the interaction Hamiltonian \(\mathcal {H}_{\text {int }}\) reads,

$$\begin{aligned}{} & {} \mathcal {H}_{\text {int }}=\delta _{1}\hat{S} _{22}+\delta _{2}\hat{S}_{33}+\delta _{3}\hat{S}_{44}\nonumber \\{} & {} \quad +\hat{a}\left( \mu _{1}\hat{S}_{13}+\mu _{2}\hat{S}_{14}+\mu _{3}\hat{S}_{23}+\mu _{4}\hat{S}_{24}\right) +h.c., \end{aligned}$$
(7)

with \(\delta _{1}=\sqrt{\Delta _{1}^2+4 \lambda _{2}^2}\), \(\delta _{2}=\frac{1}{2}(\Delta _{3}+\sqrt{\Delta _{1}^2+4 \lambda _{2}^2}-\sqrt{\Delta _{2}^2+4 \lambda _{2}^2})\), \(\delta _{3}=\frac{1}{2}(\Delta _{3}+\sqrt{\Delta _{1}^2+4 \lambda _{2}^2}+\sqrt{\Delta _{2}^2+4 \lambda _{2}^2})\), and using \(\Delta _{3}=2 \omega _{f}-\omega _{1}-\omega _{2}+\omega _{3}+\omega _{4}\). However, the operator \(\hat{\mathcal {N}}=\hat{a}^{\dagger }\hat{ a}-\hat{S}_{22}-\hat{S}_{33}\).

At any time \(t>0\), one can assume the wave vector of the interaction Hamiltonian (7) as a follows:

$$\begin{gathered} |\psi (t)\rangle = \sum\limits_{{n = 0}}^{\infty } ({\mathcal{C}}_{1}^{n} (t)|n,l_{1} \rangle +{\mathcal{C}}_{2}^{n} (t)|n,l_{2} \rangle \hfill \\ \;\;\;\;\;\;\;\;\;\; + {\mathcal{C}}_{3}^{n} (t)|n + 1,l_{3} \rangle +{\mathcal{C}}_{4}^{n} (t)|n + 1,l_{4} \rangle ) \hfill \\ \end{gathered}$$
(8)

The time-dependent Schrödinger equation \(i\frac{\partial }{\partial t}|\psi (t)\rangle =\mathcal {H}_{\text {int }}|\psi (t)\rangle\) provides a way to describe the behavior of a quantum system as a function of time, which can be expressed as a system of four ordinary differential equations,

$$\begin{aligned} \begin{aligned}&i\dot{\mathcal {C}}_{1}^n (t)=v_{1}\mathcal {C}_{3}^n (t)+v_{2}\mathcal {C}_{4}^n (t), \\ {}&i\dot{\mathcal {C}}_{2}^n (t)=\delta _1 \mathcal {C}_{2}^n (t)+v_{3}\mathcal {C}_{3}^n (t)+v_{4}\mathcal {C}_{4}^n (t),\\ {}&i\dot{\mathcal {C}}_{3}^n (t)=\delta _2 \mathcal {C}_{3}^n (t)+v_{1}\mathcal {C}_{1}^n (t)+v_{3}\mathcal {C}_{2}^n (t),\\ {}&i\dot{\mathcal {C}}_{4}^n (t)=\delta _3 \mathcal {C}_{4}^n (t)+v_{2}\mathcal {C}_{1}^n (t)+v_{4}\mathcal {C}_{2}^n (t), \end{aligned} \end{aligned}$$
(9)

where \(v_i=\mu _{i} \sqrt{n+1}\). It can be assumed that the initial atomic state is prepared in the upper state, while the field is initially in a coherent state \(|\alpha \rangle\) with,

$$\begin{aligned} |\alpha \rangle =\sum _{n=0}^{\infty } q_{n}|n\rangle , \quad \text { and } \ q_{n}=\frac{\alpha ^{n}}{\sqrt{n !}} e^{-\frac{|\alpha |^{2}}{2}}. \end{aligned}$$
(10)

The Laplace transform method provides the exact solution of the time-dependent probability amplitudes in differential eq (9), which can be expressed as,

$$\begin{aligned} \begin{aligned} \begin{bmatrix} \mathcal {C}_{1}^n (t) \\ \mathcal {C}_{2}^n (t) \\ \mathcal {C}_{3}^n (t)\\ \mathcal {C}_{4}^n (t) \end{bmatrix} =\begin{bmatrix} a_{11} &{} a_{12} &{} a_{13} &{} a_{14} \\ a_{21} &{} a_{22} &{} a_{23} &{} a_{24} \\ a_{31} &{} a_{32} &{} a_{33} &{} a_{34} \\ a_{41} &{} a_{42} &{} a_{43} &{} a_{44} \end{bmatrix} \begin{bmatrix} e^{\eta _{1} t} \\ e^{\eta _{2} t} \\ e^{\eta _{3} t} \\ e^{\eta _{4} t} \end{bmatrix}, \end{aligned} \end{aligned}$$
(11)

with the entries,

$$\begin{aligned}{} & {} \left[ \begin{array}{l} a_{1 j} \\ a_{2 j} \\ a_{3 j} \\ a_{4 j} \end{array}\right] =\frac{q_{n}}{\eta _{j i} \eta _{j k} \eta _{j l}}\left[ \begin{array}{c} h_{3}+\eta _{j}\left( h_{2}+\eta _{j}\left( h_{1}+\eta _{j}\right) \right) \\ -(k_{2}+k_1 \eta _{j})\\ l_{3}+\eta _{j}\left( l_{2}+\eta _{j} l_{1}\right) \\ m_{3}+\eta _{j}\left( m_{2}+\eta _{j} m_{1}\right) \end{array}\right] \\{} & {} \quad \text{ with } \eta _{j k}=\eta _{j}-\eta _{k}, i \ne j \ne k \ne l=1,2,3,4 \end{aligned}$$

with

$$\begin{gathered} \eta _{{1,2}} = \frac{{ - x_{1} }}{4} - \frac{{z_{1} }}{2} \pm \frac{1}{2}\sqrt {z_{2} - \frac{{z_{3} }}{{4z_{1} }}} , \hfill \\ \eta _{{3,4}} = \frac{{ - x_{1} }}{4} + \frac{{z_{1} }}{2} \pm \frac{1}{2}\sqrt {z_{2} + \frac{{z_{3} }}{{4z_{1} }}} , \hfill \\ z_{1} = \sqrt {f_{1} + \frac{{f_{2} }}{{3f_{3} }} + \frac{{f_{3} }}{3}} ,\quad \hfill \\ z_{2} = 2f_{1} - \frac{{f_{2} }}{{3f_{3} }} - \frac{{f_{3} }}{3},\quad \quad \hfill \\ z_{3} = 4x_{1} x_{2} - x_{1}^{3} - 8x_{3} , \hfill \\ f_{1} = \frac{{x_{1}^{2} }}{4} - \frac{{2x_{2} }}{3},\quad \hfill \\ f_{2} = x_{2}^{2} + 12x_{4} - 3x_{1} x_{3} ,\quad \quad \hfill \\ f_{3} = (\frac{{R + \sqrt {R^{2} - 4f_{2}^{3} } }}{2})^{{\frac{1}{3}}} ,{\text{and }}R = 2x_{2}^{3} + 27\left( {x_{3}^{2} + x_{1}^{2} x_{4} } \right) - 72x_{2} x_{4} - 9x_{1} x_{2} x_{3} ,x_{1} = i\left( {\delta _{1} + \delta _{2} + \delta _{3} } \right),\quad x_{2} = v_{1}^{2} + v_{2}^{2} + v_{3}^{2} + v_{4}^{2} - \delta _{1} \delta _{2} - \delta _{1} \delta _{3} - \delta _{2} \delta _{3} ,x_{3} = i\left( {\delta _{1} \left( {v_{2}^{2} + v_{4}^{2} - \delta _{2} \delta _{3} } \right) + \delta _{2} \left( {v_{1}^{2} + v_{3}^{2} } \right) + \delta _{3} \left( {v_{1}^{2} + v_{2}^{2} } \right)} \right),x_{4} = \left( {v_{1} v_{4} - v_{2} v_{3} } \right)^{2} - \delta _{1} \left( {v_{1} \delta _{3} + v_{2} \delta _{2} } \right). \hfill \\ \end{gathered}$$

Also,

$$\begin{aligned} \begin{aligned}&h_{1}=i\left( \delta _{1}+\delta _{2}+\delta _{3}\right) , \qquad h_{2}=v_{3}^{2}+v_{4}^{2}-\delta _{1}\left( \delta _{2}+\delta _{3}\right) -\delta _{2} \delta _{3}, \qquad \\&\quad h_{3}=i\left( v_{3}^{2} \delta _{3}+v_{4}^{2} \delta _{2}-\delta _{1} \delta _{2} \delta _{3}\right) , \quad \\&k_{1}=v_{1} v_{3}+v_2 v_4, \qquad k_{2}=i\left( v_2 v_4 \delta _{2}+v_1 v_3 \delta _{3}\right) , \qquad l_1=-i v_1, \quad \\&\quad l_2= v_1 (\delta _{1}+\delta _{3}),\\ {}&l_{3}=i \left( v_{2} v_{3} v_{4}-v_{1} v_{4}^2 +v_{1} \delta _{1} \delta _{3} \right) ,\quad \quad m_{1}=-i v_{2}, \quad \\&\quad m_{2}=v_{2}\left( \delta _{1}+\delta _{2}\right) , \quad m_{3}=i \left( v_{1} v_{3} v_{4}-v_{2} v_{3}^2 +v_{2} \delta _{1} \delta _{2} \right) . \end{aligned} \end{aligned}$$

To study the effect of the driven classical field and detuning parameters on the behavior of coherence, W-function, and phase, it is important to obtain the reduced density operator of the four-level atom sub-state and field sub-state. To do so, one must trace out the field sub-state, yielding the atomic sub-state \(\hat{\rho }_{A}={\text {Tr}}_{\text{ field } }|\psi (t)\rangle \langle \psi (t)|\), where \(|\psi (t)\rangle\) is defined in eq. (8). Thus, the reduced density operator can be found using the transformation (2), which is given by,

$$\begin{aligned} \hat{\rho }_{A} =\begin{bmatrix} \rho _{11} &{} \rho _{12} &{} \rho _{13} &{} \rho _{14} \\ \rho _{21} &{} \rho _{22} &{} \rho _{23} &{} \rho _{24} \\ \rho _{31} &{} \rho _{32} &{} \rho _{33} &{} \rho _{34} \\ \rho _{41} &{} \rho _{42} &{} \rho _{43} &{} \rho _{44} \end{bmatrix}, \end{aligned}$$
(12)

where,

$$\begin{aligned} \begin{aligned}&\rho _{11}= \left| \mathcal {C}_{1}^{n}(t)\right| ^{2} \left( \beta _1^-\right) ^2+ 2\beta _1^+\beta _1^- {\text {Re}}\left[ \mathcal {C}_{1}^{n}(t) \mathcal {C}_{2}^{n^{*}}(t)\right] \\&+\left| \mathcal {C}_{2}^{n}(t)\right| ^{2} (\beta _1^+)^2,\\&\rho _{22}=\left| \mathcal {C}_{2}^{n}(t)\right| ^{2} \left( \beta _2^-\right) ^2+2{\text {Re}}\left[ \mathcal {C}_{1}^{n}(t) \mathcal {C}_{2}^{n^{*}}(t)\right] \beta _2^- \beta _2^{+}\\&+\left| \mathcal {C}_{2}^{n}(t)\right| ^{2} \left( \beta _2^+\right) ^2,\\&\rho _{33}=\left| \mathcal {C}_{3}^{n}(t)\right| ^{2} \left( \alpha _1^-\right) ^2+2{\text {Re}}\left[ \mathcal {C}_{3}^{n}(t) \mathcal {C}_{4}^{n^{*}}(t)\right] \alpha _1^- \alpha _1^{+}\\&+\left| \mathcal {C}_{4}^{n}(t)\right| ^{2} \left( \alpha _1^+\right) ^2,\\&\rho _{44}=\left| \mathcal {C}_{3}^{n}(t)\right| ^{2} \left( \alpha _2^-\right) ^2+2 {\text {Re}}\left[ \mathcal {C}_{3}^{n}(t) \mathcal {C}_{4}^{n^{*}}(t)\right] \alpha _2^- \alpha _2^{+}\\&+\left| \mathcal {C}_{4}^{n}(t)\right| ^{2} \left( \alpha _2^+\right) ^2,\\&\rho _{12}=\beta _1^- \left( \beta _2^- \left| \mathcal {C}_{1}^{n}(t)\right| ^{2}+\beta _2^{+} \mathcal {C}_{1}^{n}(t) \mathcal {C}_{2}^{n^{*}}(t)\right) \\&+\beta _1^+ \left( \beta _2^- \mathcal {C}_{2}^{n}(t) \mathcal {C}_{1}^{n^{*}}(t)+\beta _2^{+}\right. \\&\left. \left| \mathcal {C}_{2}^{n}(t)\right| ^{2}\right) =\rho _{21}^{*},\\&\rho _{13}=\alpha _1^- \left( \beta _1^- \mathcal {C}_{1}^{n+1}(t) \mathcal {C}_{3}^{n^{*}}(t)+\beta _1^+ \mathcal {C}_{2}^{n+1}(t) \mathcal {C}_{3}^{n^{*}}(t)\right) \\&+\alpha _1^+ \left( \beta _1^- \mathcal {C}_{1}^{n+1}(t) \mathcal {C}_{4}^{n^{*}}(t)+\beta _1^+ \mathcal {C}_{2}^{n+1}(t) \mathcal {C}_{4}^{n^{*}}(t)\right) +\rho _{31}^{*},\\&\rho _{14}=\alpha _2^- \left( \beta _1^- \mathcal {C}_{1}^{n+1}(t) \mathcal {C}_{3}^{n^{*}}(t)+\beta _1^+ \mathcal {C}_{2}^{n+1}(t) \mathcal {C}_{3}^{n^{*}}(t)\right) +\alpha _2^{+} \\&\left( \beta _1^- \mathcal {C}_{1}^{n+1}(t) \mathcal {C}_{4}^{n^{*}}(t)+\beta _1^+ \mathcal {C}_{2}^{n+1}(t) \mathcal {C}_{4}^{n^{*}}(t)\right) =\rho _{41}^{*}, \\ {}&\rho _{23}=\alpha _1^- \left( \beta _2^- \mathcal {C}_{1}^{n+1}(t) \mathcal {C}_{3}^{n^{*}}(t)+\beta _2^+ \mathcal {C}_{2}^{n+1}(t) \mathcal {C}_{3}^{n^{*}}(t)\right) \\&+\alpha _1^+ \left( \beta _2^- \mathcal {C}_{1}^{n+1}(t) \mathcal {C}_{4}^{n^{*}}(t)+\beta _2^+ \mathcal {C}_{2}^{n+1}(t) \mathcal {C}_{4}^{n^{*}}(t)\right) =\rho _{32}^{*}, \\ {}&\rho _{24}=\alpha _2^- \left( \beta _2^- \mathcal {C}_{1}^{n+1}(t) \mathcal {C}_{3}^{n^{*}}(t)+\beta _2^+ \mathcal {C}_{2}^{n+1}(t) \mathcal {C}_{3}^{n^{*}}(t)\right) \\&+\alpha _2^+ \left( \beta _2^- \mathcal {C}_{1}^{n+1}(t) \mathcal {C}_{4}^{n^{*}}(t)+\beta _2^+ \mathcal {C}_{2}^{n+1}(t) \mathcal {C}_{4}^{n^{*}}(t)\right) =\rho _{42}^{*}, \\&\rho _{34}=\alpha _1^- \left( \alpha _2^- \left| \mathcal {C}_{3}^{n}(t)\right| ^{2}+\alpha _2^+ \mathcal {C}_{2}^{n}(t) \mathcal {C}_{4}^{n^{*}}(t)\right) \\&+\alpha _1^{+} \left( \alpha _2^- \mathcal {C}_{4}^{n+1}(t) \mathcal {C}_{3}^{n^{*}}(t)+\alpha _2^+ \left| \mathcal {C}_{4}^{n}(t)\right| ^{2}\right) =\rho _{43}^{*}, \end{aligned} \end{aligned}$$
(13)

Likewise, the reduced density field sub-state system can be obtained by tracing out the atomic sub-state, which is given by,

$$\begin{gathered} \hat{\rho }_{{{\text{field }}}} = \sum\limits_{{n,m = 0}}^{\infty } ( ({\mathcal{C}}_{1}^{n} (t){\mathcal{C}}_{1}^{{m^{*} }} (t) +{\mathcal{C}}_{2}^{n} (t){\mathcal{C}}_{2}^{{m^{*} }} (t))|n\rangle \langle m| \hfill \\ \;\;\;\;\;\;\;\; + ({\mathcal{C}}_{3}^{n} (t){\mathcal{C}}_{3}^{{m^{*} }} (t) + {\mathcal{C}}_{4}^{n} (t){\mathcal{C}}_{4}^{{m^{*} }} (t))|n + 1\rangle \langle m + 1|) \hfill \\ \end{gathered}$$
(14)

Hereinafter, we shall employ the final reduced density atomic and field states to discuss coherence, non-classicality, and phase jumps.

3 Relative entropy of coherence

Relative entropy of coherence (REC) is a measure of the amount of quantum coherence present in a quantum state, and it is defined as the relative entropy between the given state \(\hat{\rho }\) and the closest incoherent state, say all diagonal entries of a quantum state \(\hat{\rho }\) [14]. This measure has been widely applied in various areas of quantum information, such as entanglement theory, quantum cryptography, and quantum computing. In particular, REC has been used to quantify the amount of entanglement present in a bipartite system [32], to study the security of quantum key distribution protocols [33], and to characterize the performance of teleportation protocol [34]. Moreover, REC has been useful for understanding the dynamics of decoherence in open systems [35], allowing us to acquire a better insight into the effects of decoherence on the quantum nature of a system. These make REC a powerful tool for probing and understanding the behavior of quantum systems. REC is defined via von Neumann entropy as [14],

$$\begin{aligned} \mathcal {C}_{Re}= \mathcal {S}_d-\mathcal {S}, \end{aligned}$$
(15)

where \(\mathcal {S}_d=- Tr \hat{\rho }_d \log \hat{\rho }_d\) with \(\hat{\rho }_d\) is the diagonal entries of a quantum state \(\hat{\rho }\), and \(\mathcal {S}=- Tr \hat{\rho } \log \hat{\rho }\).

Fig. 1
figure 1

The dynamical behavior of REC \(\mathcal {C}_{Re}\) as a function of \(\lambda _1 t\) with \(\alpha =5\). (a) \(\Delta _1=1\), \(\Delta _2=0.1\), \(\Delta _3=0.1\), \(\lambda _{2}=0.1\) (b) \(\Delta _1=10\), \(\Delta _2=2\), \(\Delta _3=5\), \(\lambda _{2}=0.1\) (c) \(\Delta _1=1\), \(\Delta _2=0.1\), \(\Delta _3=0.1\), \(\lambda _{2}=5\) and (d) \(\Delta _1=10\), \(\Delta _2=2\), \(\Delta _3=5\), \(\lambda _{2}=5\)

Full size image

In figure 1, we used the atomic density state in Eq. (12) to investigate the impact of various detuning parameters and external classical field values on the coherence of a system, as measured by the temporal of REC with \(\alpha =5\). Our results demonstrate a direct correlation between these parameters and the degree of coherence, with some parameter values leading to maximum coherence and others to minimum coherence. This suggests that these parameters can be manipulated to control the coherence of the system, allowing users to maximize or minimize the degree of coherence as needed. This can be of great use in the development of quantum information processing, where a high degree of coherence is usually preferred. In general, the level of coherence of a system at the onset of an interaction is impacted by the intensity of the external classical field. It is shown that the REC is zero for certain values of \(\lambda _2\), as seen in figures 1 (a, b), and grows as \(\lambda _2\) increases (figures 1 (c, d)). As seen in figure 1. (a), the coherence of an atom–field interaction decreases with increasing the interaction time when the atom–field interaction is affected by small values of classical field and detuning parameters. This can be attributed to the energy exchange between the atom and the field, which causes the system to become less coherent. However, when the detuning parameters increase and the external field strength decreases, as seen in figure 1. (b), the maximum bounds of coherence increase and the minimum bounds decrease. This suggests that the increase in detuning parameters results in an increase in dispersion, which in turn leads to an expansion in the amplitude of the \(\mathcal {C}_{Re}\). This phenomenon can be explained by the fact that the atom–field interaction becomes increasingly more non-resonant, and therefore the energy exchange between them is reduced, leading to an overall increase in the coherence of the system. When considering the effect of a large classical field value (figure 1. (c)), it is apparent that the maximum bounds of relative coherence decrease as the interaction time increases, and the number of oscillations decreases with a small amplitude. The external classical field reinforces the system at specific values and reduces fluctuations in relative coherence. For example, at \(\lambda _2 = 30\) and different values of detunings, the relative coherence is a straight line at \(\ln 2\). Furthermore, figure 1. (d) indicates that higher values of the classical field and detunings can increase the coherence of the system, resulting in an extended amplitude of the coherence. This phenomenon is further supported by the fact that larger values of the classical field are capable of counteracting the destabilizing effects of the detuning parameters, thus contributing to the overall stability of the system.

4 The Wigner function (W-function)

The temporal evolution of the Wigner function (W-function) is a key characteristic of the atom–field interaction and can be used to measure the non-classicality of the system [36]. The W-function is a quasiprobability distribution in phase space that describes the quantum state of a system, and its evolution over time is determined by the Moyal equation [37]. By looking at the shape of the W-function and its evolution over time, one can measure the amount of quantum correlation present in the system. For example, the W-function can take on negative values, which is a signature of entanglement [38]. For the reduced field density state, one can defined W-function \((\mathcal {W}(\beta ) )\) as [39, 40],

$$\begin{aligned} \mathcal {W}(\beta )=\frac{2}{\pi }\sum _{k=1}^{\infty } (-1)^{k} \langle k| D^\dagger (\beta ) \hat{\rho }_{\text {field }} D(\beta ) | k\rangle , \end{aligned}$$
(16)

where \(D(\beta )\) is a displaced number state with \(\beta =x+i y\), and \(\rho _{\text {field }}\) is the reduced density matrix of the field in eq.(14). For our system, one may obtain the W-function as [41],

$$\begin{aligned} \begin{aligned} \mathcal {W}(\beta )=\frac{2}{\pi }&e^{-|\beta |^2} \sum _{k=1}^{\infty } \sum _{n=1}^{\infty } (-1)^{k} \bigg ( |(\mathcal {C}_1^{n}+\mathcal {C}_2^{n}) D_{k,n}(-\beta )|^2+ |(\mathcal {C}_3^{n}+\mathcal {C}_4^{n}) D_{k,n+1}(-\beta )|^2\bigg ), \end{aligned} \end{aligned}$$
(17)

here,

$$\begin{aligned} D_{k,n} (\beta )= \sqrt{\frac{n!}{k!}} (\beta ^*)^{k-n} L_n^{k-n}(|\beta |^2), \end{aligned}$$
(18)
Fig. 2
figure 2

The 3D plot of W-function \(\mathcal {W}\) as a function of \(\beta\) where \(\lambda _1 t=5\) and \(\alpha =4\). The detuning parameters and the coupling of classical field are the same as figure 1

Full size image

The W-function has been demonstrated to be a reliable two-fold measure for assessing the quantum and classical properties of a system. Negative values of the W-function are indicative of quantumness, while positive values are suggestive of classicality or minimal uncertainty. In figure 2, we present the effects of varying detuning parameters and different intensities of the coupling of the classical field \(\lambda _2\) on the Wigner function for a system with a scaled interaction time of \(\lambda _{1} t= 5\), which is in the middle of the collapse period in atomic inversion [42]. This analysis serves to illustrate the utility of the W-function as an effective tool for analyzing both the quantum and classical characteristics of a system. Under the same conditions as those used in figure 1, figure 2 (a) shows the W-function for the field subsystem with a small value of the detuning parameter and the coupling of the classical field. This resulted in a quantum behavior that was confined to the middle of the phase space, while the classicality of the system was visible in the middle of the phase space and around points (2, ± 4). This indicates that quantum behavior is confined to the middle of the phase space, while classicality is visible in both the middle and around points (2, ± 4). The results of figure 2 (b) display that an increase in the detuning parameters can lead to a substantial change in the W-function, where one of the separated peaks increases, while the other disappears and negative values decrease [43]. This suggests that classicality increases with large detuning, being limited to positive values of \(\beta\), i.e., \(Im[\beta ]\) and \(Re[\beta ] > 0\). This finding is consistent with previous research which has established that large detuning can increase classical correlations. It is noteworthy that these correlations are only observed for positive values of \(\beta\), thus highlighting the importance of selecting appropriate parameters to achieve the desired behavior. As figures 2 (c and d) illustrate, an increase in the classical field leads to a subsequent rise in classical correlation and a decrease in quantum correlation. Furthermore, a single positive peak appears at (4,2) for large detuning and (4,0) for smaller detuning, while the diffusion peaks in the middle of phase space have dissipated. This implies that the classicality of the system increases with increasing detuning, while the coupling of the classical field suppresses the negative behavior in the middle of the phase space. Consequently, large detuning can result in an enhancement of classical correlations and the emergence of distinct positive peaks in the middle of phase space.

5 Pancharatnam phase

The Pancharatnam phase is a mathematical concept introduced by S. Pancharatnam in 1956 [44], which can be used to quantify the relative phase between two waveforms. This concept has the potential to be employed in order to measure the phase space of a system and is related to the polarization of light. This has been found to be particularly useful for the analysis of complex systems, as well as for applications such as quantum computing, where it can be used to quantify the quantum phase of a qubit and quantum electrodynamics systems [45,46,47,48,49]. Furthermore, its potential applications extend to the study of optical properties of materials, such as the polarization of light [50]. The Pancharatnam phase encompasses the dynamical phase and the geometric phase, which is calculated as the phase acquired during the change in the wave function from the initial wave vector \(|\psi (0) \rangle\) to the final wave vector \(|\psi (t) \rangle\), which is expressed as [51],

$$\begin{aligned} \Phi (t)= \arg \big (\langle \psi (0)|\psi (t) \rangle \big ), \end{aligned}$$
(19)
Fig. 3
figure 3

The dynamical behavior of Pancharatnam phase \(\Phi (t)\) as a function of \(\lambda _1 t\) with the same parameters as displayed in figure 1

Full size image

The effects of classical field parameters and the detuning parameters on the Pancharatnam phase are clearly visible in figure 3. As shown in figures 3(a) and (c), the classical field parameter has a significant impact on the oscillation of the phase, causing a periodic saw-tooth type of oscillation in cases where the value of \(\lambda _{2}\) is lower, and a reduced number of oscillations when the effect of the classical field is larger. This indicates the phase’s capability of changing rapidly, leading to brief periods of artificial phase jumps in the lower values of the external classical field. In contrast, the effect of the detuning parameters amplifies the swift fluctuation over brief periods, thus raising the detuning effect produces random phase jumps. However, by augmenting the external classical field, the leap of the function \(\Phi (t)\) diminishes with time. This confirms that the external classical field stabilizes the interaction between the field and matter after a period of interaction.

6 Conclusions

This paper presented a study of a single four-level atom in a W-configuration interacting locally with a single-mode quantized cavity field. The initial cavity field is assumed to be in a coherent state, and the atomic system is taken to be in the upper state. By employing exact solutions of the Schrödinger equation under certain canonical conditions of dressed states, we are able to obtain the exact solution without making any assumptions. Subsequently, we investigate the effects of detuning parameters and an external classical field on coherence, non-classicality, and phase space. Our findings suggest that these three phenomena can be modified by the strength of the classical field and the detuning parameters, thereby allowing for controlled manipulation of relative coherence, Wigner function, and Pancharatnam phase.

The effect of detuning on the behaviors of coherence, quantumness, and Pancharatnam phase is discussed. It is demonstrated that the rate of decrease/increase of these three phenomena is contingent upon the detuning parameter. As the detuning increases, the lower bounds of coherence and negative values of Wigner function are observed to diminish. On the other hand, Pancharatnam phase exhibits a rapid oscillation as detuning increases, suggesting that it is more sensitive to changes in detuning than coherence and quantumness.

The effects of varying values of the external field on the general behaviors of coherence, non-classicality, and phase space in the presence of detuning parameters are investigated. We find that as the strength of the classical field increases, the effect of the detuning parameters is reduced, allowing the quantum system to remain stable at large values of the classical field. Additionally, our results indicate that the maximum bounds of coherence decrease, the classicality of the system increases, and the phase jumps decrease as the external field increases.