1 Introduction

In polar semiconductors such as GaAs, the energy state of an electron is modified by polaronic effects in which the electron is strongly coupled with lattice vibrations by emitting or absorbing longitudinal optical (LO) phonons [1]. The coupled state of the electron and the phonons is termed a polaron. Due to this interaction, the effective mass of the electron increases and the spacing between Landau levels changes, which alters the cyclotron resonance frequency [2,3,4,5]. A resonant polaron occurs when the energy of an optical phonon matches the difference between two Landau levels. Under this condition, the polaronic effect is most noticeable and can be observed in a magneto-optical experiment.

In the present work, we consider a nanowire in the presence of the spin–orbit interaction represented by the Rashba effect. The spin–orbit interaction influences many physical properties of nanostructures [6,7,8,9,10,11,12,13,14,15,16,17]. We calculate the energy of polarons and the optical absorption peaks from the ground state to higher energy states in the absence of the magnetic field. We show that the strength of the lateral quantum confinement, forming the nanowire, plays the role of the magnetic field in the magneto-optical experiments. In addition, the interplay of the Rashba and the electron–phonon interactions induces an energy gap in the dispersion relation. Under the resonant polaron conditions, this gap assumes a maximum value, and influences to a great extent the structure of the optical absorption peaks.

2 The model

Let the axis of the nanowire be parallel to the x-direction. The strength of the confinement potential \(V(y) = m\omega _0^2 y^2/2\) is characterized by the harmonic oscillator frequency \(\omega _0\), where m is the effective mass of the electron. We assume the motion of the electron is confined to a thin layer in the xy plane, so that the probability density in the z-direction takes the form \(\delta (z)\). An electric potential applied externally to a set of top gates can be used to realize this structure in two-dimensional systems such as III–V quantum wells. We shall consider GaAs in our calculations. Owing to the asymmetry produced by the different layers in this system, electrons experience Rashba spin–orbit interaction \(H_r = \alpha _{r}\left( p_x \sigma _y - p_y \sigma _x\right) /\hbar\). Here, \(p_{x}\) and \(p_{y}\) are the components of the electron momentum \(\vec {p}\), \(\alpha _r\) is the Rashba constant, and \(\sigma _x\) and \(\sigma _y\) are the components of the Pauli vector operator \(\vec {\sigma }\). Thus, for a ballistic nanowire, the single particle Hamiltonian reads [11, 16]

$$\begin{aligned} H_{0} = \dfrac{p^2}{2m} + \dfrac{1}{2} m\omega _0^2 y^2 + \dfrac{\alpha _{r}}{\hbar }\left( p_x \sigma _y - p_y \sigma _x\right) . \end{aligned}$$
(1)

The last term in the above equation is responsible for the intersubband coupling, and may be treated using the perturbation theory. Ignoring this term yields the following eigenvalues and eigenfunctions

$$\begin{aligned} E^{(0)}_{n\eta }(k)= & {} \frac{\hbar ^2 k^2}{2 m}+ \hbar \omega _0 (n + 1/2) + \eta \alpha _{r} |k|, \end{aligned}$$
(2)
$$\begin{aligned} \Psi _{n\eta k }^{(0)}= & {} \frac{\psi _{n} (y) \exp \left( i x k\right) }{\sqrt{2 L_x}} \left( \begin{array}{c} -\eta i \\ 1 \\ \end{array} \right) , \end{aligned}$$
(3)

where \(\eta = \pm 1\) the branch-splitting quantum index, k is the wave vector corresponding to the free motion of the electron along the wire axis, n is the harmonic oscillator quantum number, and \(L_x\) represents the length of the nanowire.

The optical phonons in the nanowire are generated in the layered semiconductor structure. Neglecting interface effects, the interaction of electrons with the bulk longitudinal optical (LO) phonons is given by the standard Fröhlich Hamiltonian \(H_{ep}\) [1]. So, we have

$$\begin{aligned} H_{ep} = c \sum _{\vec {q}} \frac{1}{q} \left( e^{-i \vec {q}.\vec {r}} a_{\vec {q}}^{\dagger } +e^{i \vec {q}.\vec {r}} a_{\vec {q}}\right) , \end{aligned}$$
(4)

with \(c = \sqrt{4 \pi \alpha _{f} r_p (\hbar \omega _L)^2/V}\). Here, the 3D polaron radius \(r_{p} = \sqrt{\hbar /2m\omega _{L}}\), \(\alpha _{f}\) the dimensionless polaron coupling constant, \(\omega _{L}\) the frequency of the LO phonons. The destruction and creation operators for a phonon of wave vector \(\vec {q}\) are \(a_{\vec {q}}\) and \(a_{\vec {q}}^{\dagger }\), respectively. V is the volume of the sample.

The change of the electron energy due to interaction with the LO phonons and the Rashba intersubband coupling (RIC) can be obtained by the perturbation theory. The first-order correction vanishes because of action of the phonon destruction and creation operators. For III–V quantum wells \(\alpha _{f} \ll 1\) and the system is in the weak-coupling limit, so it seems reasonable to consider perturbed states containing only one LO phonon. Since, \(H_{ep}\) does not involve the spin state of the electron, then the energy shift of an electron in the state \(|n,k,\eta \rangle\) to a second order is given by

$$\begin{aligned} E^{(2)}_{n\eta }(k) = \sum _{n^{'} = 0}^{\infty } \sum _{\vec {q}} \left( \frac{c}{q}\right) ^2 \frac{\left| \left\langle n^{'}\left| e^{-i y q_y} \right| n\right\rangle \right| ^2}{E^{(0)}_{n\eta } \left( k\right) - E^{(0)}_{n^{'}\eta ,n_q=1}\left( k - q_x\right) }. \end{aligned}$$
(5)

Here, \(E^{(0)}_{n\eta ,n_q} \left( k\right)\) represents the energy of the polaron.

Next, we measure energy and length, in units of \(\hbar \omega _{L}\) and \(r_{p}\), and introduce the length scale \(l_r=\hbar ^2/2 \alpha _{r} m\) for the Rashba. Converting the sum over the phonon momentum into an integral and using cylindrical coordinates in the \(q_{x}q_{y}\) plane [5], we obtain

$$\begin{aligned}&E^{(2)}_{n\eta }(k)\nonumber \\&\quad = -\frac{\alpha _{f} }{2 \pi }\sum _{n^{'} = 0}^{\infty } \int _{-\pi }^{\pi }\int _0^{\infty }\frac{e^{-\zeta } n_{2}! \zeta ^{n_{1}-n_{2}} \left| L_{n_{2}}^{n_{1}-n_{2}}(\zeta ) \right| ^2}{n_{1}! d_{n\eta n^{'}}\left( k,q_x\right) }\mathrm{{d}}q\, \mathrm{{d}}\phi , \end{aligned}$$
(6)

where \(\zeta = \lambda ^{-1} q^{2} \sin ^{2} \phi , \lambda =\omega _0 /\omega _L\), and \(q^{2} = q_{x}^{2} + q_{y}^{2}\). \(L_{n_{2}}^{n_{1}-n_{2}}(\zeta )\) is the associated Laguerre polynomial with \(n_{1} = \max \left( n,n^{'}\right) , n_{2} = \min \left( n,n^{'}\right)\). The quantity in the denominator is given by

$$\begin{aligned} d_{n\eta n^{'}}\left( k,q_x\right)= & {} 1 + \lambda \left( n^{'} - n\right) + q_{x}^2 -2 k q_{x} \nonumber \\&+ \eta \left( |k - q_{x}| - |k| \right) /l_r. \end{aligned}$$
(7)

Let us consider the optical absorption at \(k = 0\). The above equation indicates that \(d_{n\eta n^{'}}\) vanishes for \(\lambda = n^{-1}\) at \(n^{'} = 0\). This is the condition for resonant polaron. It can be realized by changing the lateral dimension of the nanowire via the electric voltage applied to the top gates in our case. Thus, the degree of lateral quantum confinement represented by \(\lambda\), in our model, corresponds to \(\hbar \omega _{c}\) in magneto-optical experiments, where \(\omega _{c}\) is the cyclotron resonance frequency.

Obviously, the energy of resonant polaron cannot be calculated using Rayleigh–Schrödinger theory. The Wigner–Brillouin approach overcomes this difficulty by replacing \(E^{(0)}_{n\eta }\) by \(E_{n\eta } = E^{(0)}_{n\eta } + E^{(2)}_{n\eta }\) and solve Eq. (6) iteratively. This approach is improved by rewriting the Hamiltonian in the form \(H = H_{0} + E^{(0)}_{0\eta } + H_{ep} - E^{(0)}_{0\eta }\) which modifies the denominator of Eq. (6) such that \(d_{n\eta n^{'}} \rightarrow d_{n\eta n^{'}} + E^{(2)}_{n\eta } - E^{(0)}_{0\eta }\) [3]. This improved Wigner–Brillouin method is used to calculate the energy of the electrons in the nanowire. To perform the iterative calculations, we carry out the summation. We get

$$\begin{aligned}&E^{(2)}_{n\eta }\nonumber \\&\quad = -\frac{\alpha _{f}}{2\pi }\int _0^{\infty }\mathrm{{d}}t\, \int _0^{\infty } \mathrm{{d}}q\,\int _{-\pi }^{\pi } \mathrm{{d}}\phi \, F_{n\eta }(t,q,\phi )f_{n}(t,q,\phi ), \end{aligned}$$
(8)

where

$$\begin{aligned}&F_{n\eta }(t,q,\phi ) \nonumber \\&\quad = \exp \left[ -t \left( 1 + \eta |q\cos \phi |/l_{r} + q^2 \cos ^2\phi + E^{(2)}_{0\eta } -E^{(2)}_{n\eta } \right) \right] , \end{aligned}$$
(9)

and

$$\begin{aligned} f_{0}(t,q,\phi ) =\exp \left[ -q^2 e^{-t\lambda }\sin ^2\phi \left( e^{t\lambda }-1\right) /\lambda \right] . \end{aligned}$$
(10)

Defining \(w_{1} = \lambda e^{t\lambda }\), and \(w_{2} = q^2 \left( e^{t\lambda }-1\right) ^2 \sin ^2\phi\), we have for the first three excited states

$$\begin{aligned} f_{1}(t,q,\phi )= & {} \dfrac{1}{\lambda }f_{0} e^{-t \lambda } (w_{1} + w_{2}), \end{aligned}$$
(11)
$$\begin{aligned} f_{2}(t,q,\phi )= & {} \dfrac{1}{2!\lambda ^{2}} f_{0} e^{-2 t \lambda } \left[ 2! w_{1}^{2} +w_{2}^{2}\left( w_{2}^{2} + 4w_{1} \right) \right] , \end{aligned}$$
(12)
$$\begin{aligned} f_{3}(t,q,\phi )= & {} \dfrac{1}{3!\lambda ^{3}} f_{0}e^{-3 t \lambda }\nonumber \\&\quad \left[ 3! w_{1}^{3} +w_{2}^{2}\left( w_{2}^{2} + 3w_{1} \right) \left( w_{2}^{2} + 3! w_{1} \right) \right] . \end{aligned}$$
(13)

It is straightforward to calculate the energy correction due to the RIC. We have

$$\begin{aligned} \varepsilon _{n,\eta }^{(2)} =\dfrac{1}{l_r} \frac{l_r\lambda ^{2} + 2 \eta \lambda (2 n+1) |k| }{16 k^2-4 \lambda ^2 l_r^2}. \end{aligned}$$
(14)

For \(k = 0\), this contribution represents a negative rigid shift to the energy of the electron. Since it does not affect the energy separation between the various subbands, we will neglect it in the following discussion.

According to Fermi’s golden rule, the optical absorption coefficient of electromagnetic radiations of angular frequency \(\omega\) due to the transition from state \(E_{n\eta }\) to state \(E_{n^{'} \eta ^{'}}\) is given by [1].

$$\begin{aligned}&\alpha _{n\eta } \nonumber \\&\quad = \dfrac{\pi \hbar e^{2}}{n_{0} \epsilon _{0} c m^{2}} \sum _{ n^{'}\eta ^{'}} \dfrac{1}{\hbar \omega }\left| \left\langle n^{'} \eta ^{'} | p_{y} |n\eta \right\rangle \right| ^{2} \delta \left( E_{n^{'} \eta ^{'}} - E_{n\eta } -\hbar \omega \right) . \end{aligned}$$
(15)

Here, \(n_{0}\) represents the refractive index, c is the speed of light, and \(\epsilon _{0}\) is the permittivity constant. We’ll consider only the transitions from \(E_{0\eta }\) to higher states, so we calculate the matrix elements \(\left\langle n^{'} \eta ^{'} | p_{y} |0\eta \right\rangle\) in the above equation to a first order using \(|n\eta \rangle = |n\eta , n_{q} = 0\rangle + \sum _{n^{'}\eta ^{'} n_{q}^{'} } b_{n\eta n_{q};n^{'}\eta ^{'} n_{q}^{'}}|n^{'}\eta ^{'} n_{q}^{'} \rangle\), where \(b_{n\eta n_{q}}\) are the expansion coefficients. We have

$$\begin{aligned}&\left\langle n^{'} \eta ^{'} \left| p_{y} \right| 0\eta \right\rangle = \delta _{\eta ^{'}\eta }\delta _{n^{'},1} \nonumber \end{aligned}$$
(16)
$$\begin{aligned}&+\delta _{\eta ^{'}\eta } \left( \frac{\alpha _{f}}{2\pi }\right) ^2 \iiiint _0^{\infty }\mathrm{{d}}t\,\mathrm{{d}}u\,\mathrm{{d}}q\,\mathrm{{d}}Q\iint _{-\pi } ^{\pi } \mathrm{{d}}\phi \, \mathrm{{d}}\varPhi \; \Lambda _{n^{'}}, \end{aligned}$$
(17)

where

$$\begin{aligned} \Lambda _{1}&=\dfrac{q Q e^{-\frac{s_{1}}{2 \lambda }}}{\lambda } \left[ s_{3} e^{- h_{1} t -u g_{11}} + q s_{2} \sin \phi e^{- h_{2} t - u g_{21}} \right] , \end{aligned}$$
(18)
$$\begin{aligned} \Lambda _{2}&= \dfrac{q Q s_{2} e^{-\frac{s_{1}}{2 \lambda }} }{i\sqrt{2} \lambda ^{3/2}} \,\nonumber \\&\quad \left[ 2 (\lambda +s_{3}) e^{-h_{1} t/2 - u g_{12}/2 + s_{1}/4 \lambda } + q s_{2}\sin \phi e^{-h_{2} t - u g_{22}} \right] , \end{aligned}$$
(19)

and

$$\begin{aligned}&\Lambda _{3} = -\dfrac{q Q s_{2}^{2}e^{-\frac{s_{1}}{2 \lambda }}}{\sqrt{6}\lambda ^{2}}\nonumber \\&\quad \left[ 2 (2\lambda +s_{3}) e^{-h_{1} t/2 - u g_{13}/2 + s_{1}/4 \lambda } + q s_{2}\sin \phi \,e^{-h_{2} t - u g_{23}}\right] , \end{aligned}$$
(20)

with

$$\begin{aligned} h_{1}&= 1 + \frac{\eta | q \cos \phi | }{l_{r}} + (q \cos \phi )^2, \end{aligned}$$
(21)
$$\begin{aligned} h_{2}&= h_{1} + \lambda , \end{aligned}$$
(22)
$$\begin{aligned} g_{1n}&= 1 + \frac{\eta |Q \cos \varPhi | }{l_{r}}-\lambda (n - 1) +(Q \cos \varPhi )^2, \end{aligned}$$
(23)
$$\begin{aligned} g_{2n}&= g_{1n} - \lambda , \end{aligned}$$
(24)
$$\begin{aligned} s_{1}&= q^2 \sin ^2\phi + 2 q Q \sin \phi \sin \varPhi \, e^{-(t+u) \lambda } + Q^2 \sin ^2\varPhi , \end{aligned}$$
(25)
$$\begin{aligned} s_{2}&= q \sin \phi \, e^{-(t+u) \lambda } + Q \sin \varPhi , \end{aligned}$$
(26)
$$\begin{aligned} s_{3}&=\lambda -q Q \sin \phi \sin \varPhi \, e^{-(t+u) \lambda }-Q^2 \sin ^2\varPhi . \end{aligned}$$
(27)

In the Wigner–Brillouin approach, the above equations are slightly modified such that \(h_{i} \rightarrow h_{i} - E_{0\eta }^{(2)}\) and \(g_{i,n} \rightarrow g_{i,n} - E_{n\eta }^{(2)}\), where \(i = 1,2\).

3 Results and discussion

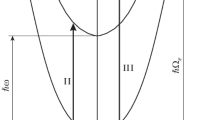
In the following, we present numerical calculations for a nanowire hosted in a GaAs layered structure. We use \(\alpha _{f} = 0.07183\), \(r_{p} =3.987\) nm, \(\hbar \omega _{L} = 36.17\) meV, and \(m = 0.067\; m_{0},\) where \(m_{0}\) is the free electron mass [18]. The bisection method is utilized to calculate \(E_{n\eta }^{(2)}\) as a function of \(\lambda\) for \(n \le 3\), keeping the relative error of the estimated values less than \(10^{-4}\). The results of this iterative calculations are shown in Fig. 1 for \(l_{r} = 2\). The thin-solid lines represent the unperturbed energy of the electron. The thick black line represents the combined state of an electron and a LO phonon. The interplay of the Rashba and electron–phonon interactions modifies the unperturbed states in two ways. First, they shift the electron states down in energy. Second, they remove the degeneracy corresponding to \(\eta = \pm 1\) at \(k = 0\) in Eq. (2), so the dispersion relation for each harmonic oscillator state splits into two branches. The splitting occurs because the last term on the RHS of Eq. (7) contributes differently to \(E_{n\eta }^{(2)}\) depending on the value of \(\eta\).

Fig. 1
figure 1

The energy of the electron in the nanowire for \(k = 0, l_{r} = 2\). Solid lines represent the unperturbed states. Broken lines include the effect of the electron–phonon interaction

Full size image

When the lateral confinement of the nanowire is weak, the energy splitting is comparable for all energy states. As \(\lambda\) increases the energy splitting increases to a great extent for \(n > 0\), but it stays roughly the same for the ground state, as indicated by the broken black lines in Fig. 1. As \(\lambda\) increases further, the degeneracy points for higher states are reached, where the unperturbed energies \(E_{n,\eta }^{(0)}\) of the electron matches the energy of the combined state \(|n = 0, n_{q} = 1 \rangle\). According to Eq. (6) \(\lambda = 1/n\) at these points. The splitting mostly reaches its maximum value and the system is in the state of resonant polaron. For larger values of \(\lambda\), the energy of the electron gradually gets pinned to the energy of the combined state.

Fig. 2
figure 2

The evolution of the energy splitting as the strength of the lateral confinement of the nanowire increases. The dots represent the numerical results. The solid lines represent analytical approximation based on the Rayleigh–Schrödinger theory

Full size image

The variation of the energy splitting as a function of the quantum confinement of the nanowire is indicated in Fig. (2). The dots represent the numerical data obtained using the improved Wigner–Brillouin approach, while the solid lines show the result of some analytical calculations based on the Rayleigh–Schrödinger theory. Since there is no degeneracy in the ground state, the analytical approximation is clearly in an excellent agreement with the numerical data. The energy splitting in this case is given by

$$\begin{aligned} \Delta _{0} = \frac{\alpha _{f} }{9 \pi l_{r}^3}\left[ 3 (\lambda + 6) l_{r}^2+2\right] , \end{aligned}$$
(28)

and thus, increases linearly with \(\lambda\). For \(n = 1\), the energy splitting is given by

$$\begin{aligned} \Delta _{1} = \frac{\alpha _{f} }{\pi l_{r}}\left[ 2 + \lambda + \dfrac{7}{9}\lambda ^{2} + \dfrac{1}{2}\lambda ^{3} + \dfrac{2}{9 l_{r}^2}\left( 1 + \dfrac{6}{5}\lambda \right) \right] . \end{aligned}$$
(29)

This form deviates from the numerical data for \(\lambda > 1/2\) because of the approaching degeneracy. As \(\lambda \rightarrow 0\), the above equations yield \(2 \alpha _{f} \left( 1 + 1/9 l_{r}^2 \right) /\pi l_{r}\) for the energy splitting for the two-dimensional system hosting the nanowire. For \(\lambda \approx 0\), the system is still practically a two dimensional and all energy states have a splitting \(\sim 0.025\; \hbar \omega _{L}\). When \(\omega _{0}\) exceeds \(\omega _{L}\), the splitting is large for states with \(n > 0\) and roughly reads \(0.1 \; \hbar \omega _{L}\).

Fig. 3
figure 3

The energy of the electron in the nanowire for \(k = 0, l_{r} = 6\). The energy splitting is much smaller than that for \(l_{r} = 2\)

Full size image

The magnitude of the energy splitting is sensitive to the strength of the spin–orbit interaction as seen from the above equations. In Fig. 3, we show the polaron energies for \(l_{r} = 6\). It is clear that the dependence of the electron energy on \(\lambda\) is the same, but with a smaller splitting. The tuning of the Rashba effect is established experimentally in low-dimensional systems using an external electric field, where in some samples it can be switched on and off [19,20,21]. This is achieved using top and bottom gates. In our model, the lateral confinement may be realized using a set of top gates, while a bottom gate can be used to change the strength of Rashba interaction and hence \(l_{r}\).

In the magneto-optical experiments investigating the polarons in bulk GaAs, cyclotron emission as well as cyclotron resonance absorption measurements are carried out [3]. The observed absorption lines are due to transitions between different Landau levels formed by applying an external magnetic field \(\vec {B}\). The effect of electron–phonon coupling is observed clearly in the neighborhood of the resonant polaron, which is achieved by varying the magnetic field. As the g value of this system is very small, the spin splitting is neglected. In our model, the effect of the variation of the quantum confinement \(\lambda\) is equivalent to the effect of changing \(\vec {B}\) in the magneto-optical experiments in every aspect except for the electron spin. The strength of the magnetic field determines the spin splitting and the separation between the Landau levels. Although the energy splitting shown in Fig. 1 is related to the electron spin, it exists at zero magnetic field. Such zero-field splitting is observed in other structures due to different mechanisms [22,23,24,25]. It can be also controlled by either changing \(\lambda\) or by tuning the spin–orbit interaction. This splitting is quite clear in the strong Rashba regime. As a consequence, this energy variations will influence the optical absorption to a great extent.

Fig. 4
figure 4

Optical absorption as a function of the photon frequency for \(\lambda = 0.1, l_{r} = 2\). For weak quantum confinement, the peaks corresponding to different \(\eta\) species coincide

Full size image
Fig. 5
figure 5

Optical absorption as a function of the photon frequency for \(\lambda = 0.4, l_{r} = 2\). The peaks for the transition \(0 \rightarrow 3\) are well resolved, since the energy splitting assume a large value for resonant polaron

Full size image

The optical absorption coefficient \(\alpha = \sum _{n\eta } \alpha _{n\eta }\) at \(k = 0\) is calculated using Eq. (15) after replacing the delta function by a Lorentzian, i.e., \(\delta (x) \rightarrow \Gamma /(\Gamma ^{2} + x^{2})\), with \(\Gamma = \Delta _{0}/5\), where \(\Delta _{0}\) is the energy splitting for the ground state at \(\lambda = 0.1\). This choice is arbitrary, but it influences the resolution of the absorption peaks. In Fig. 4 we show the optical absorption as a function of the photon energy for \(\lambda = 0.1, l_{r} = 2\). The red lines represent the transitions between states with \(\eta = -1\), while the black lines belong to \(\eta = 1\). Practically, the peaks coincide since the energy splitting for all n is roughly the same for weak confinement as indicated in Figs. 1 and 2. We notice also that the frequency separation between the peaks is almost the same. For \(\lambda = 0.4\), the resonant polaron condition is satisfied by the state \(n = 3\), so the energy splitting for that state is well developed (green dots in Fig. 2) and the peaks corresponding to the \(\eta = \pm 1\) are resolved (Fig. 5). Because the resonant polaron is accompanied by clear pinning effect which kicks in at \(\lambda \ge 1/3\), the frequency separation between the peaks is different unlike the case without resonant polaron. Figure 6 depicts the absorption peaks for \(\lambda = 0.9\), where the states with \(n > 1\) exhibit two adjacent peaks for each value of \(\eta\), while the state \(n = 1\) demonstrate well-resolved peaks. For \(\lambda = 1.5\), all states are pinned to the combined state, so the absorption peaks are resolved with approximately the same frequency separation (Fig. 7). We expect for higher values of \(\lambda\) that these six peaks will merge to form just two peaks corresponding to the different values of \(\eta\). Therefore, the pattern of the absorption peaks is largely dependent on the degree of the lateral quantum confinement forming the nanowire, which is very similar to their dependence on the magnetic field in the magneto-optical experiments.

Fig. 6
figure 6

Optical absorption as a function of the photon frequency for \(\lambda = 0.9, l_{r} = 2\). The peaks for the transition \(0 \rightarrow 1\) are well resolved, while the pinning effect is clear for the other peaks

Full size image
Fig. 7
figure 7

Optical absorption as a function of the photon frequency for \(\lambda = 1.5, l_{r} = 2\). All states are pinned to the combined state with very small frequency separation

Full size image

4 Conclusions

In summary, we investigated the effect of the electron–phonon interaction on the energy of an electron and the optical transitions in a nanowire in the presence of Rashba interaction. The energy of the electron shows a pinning behavior signaling the existence of a resonant polaron that occurs at different values of the confining potential of the wire. This is accompanied by a splitting in the energy, which assumes large values for the resonant polaron. The optical absorption peaks demonstrate such effects in terms of their frequency separation and their number.