Spectral and coherent properties of partially polarized pulsed electromagnetic beams upon turbulent atmosphere propagation for different source conditions

Abstract

The spectral and coherent properties of partially polarized pulsed electromagnetic beams propagating in a horizontal homogeneous and isotropic turbulent atmosphere channel for different source conditions are investigated in detail. Based on the extended Huygens–Fresnel principle and von Karman power spectrum, the analytical expressions for the elements of the two-frequency cross spectral density matrix, the average spectral intensity, the beam width, and the spectral degree of electromagnetic coherence are derived in turn. Finally, with the help of numerical calculations, the effects of different source conditions on the changes in the beam width, spectral and coherent properties of partially polarized pulsed Gaussian Schell-model electromagnetic beams are studied. Some theoretical results in this paper will be useful for applications involving polarized pulsed electromagnetic beams propagating through atmospheric turbulence.

1 Introduction

In the past decades, with the rapid development of femtosecond pulse laser technology, ultrashort pulse beam has aroused great interests of scholars at home and abroad [1,2,3,4,5,6]. For an optical pulse, it is commonly assumed that both its spatial and spectral components are completely coherent. However, such assumption does not stand in practice, i.e., the spatial and spectral distributions of optical pulses are usually partially coherent, which represent a class of partially coherent non-stationary wave field [7, 8]. In 2002, a scalar model of a partially coherent plane-wave pulse with a Gaussian spectrum and a Gaussian distribution of correlations between different frequency components, i.e., the Gaussian Schell-model pulse (GSMP) was introduced in the frequency domain by Paakkonen et al. [9] and later in the temporal domain by Lin et al. [10]. The so-called Gaussian Schell-model beam, is a convenient mathematical model for wave fields which are spatially partially coherent, which helps to understand the role of partial spatial coherence in physical radiometry [9]. Therefore, using analogy to this model, the spectral and temporal components of the Gaussian Schell-model pulse is obtained [11]. Since then, generation, propagation, and coherent-mode representation of such a partially coherent pulse beam have been studied in detail [12,13,14,15,16,17,18,19,20]. It is noted that the above researches are all based on scalar fields.

On the other hand, coherence and polarization are natural physical characteristics of light [21]. In 2003, Wolf proposed the unified theory of coherence and polarization of stochastic electromagnetic beams [22], i.e., vector light field. Henceforth, there has been numerous interests in studying the spectral, coherent, and polarization properties, etc., of stochastic electromagnetic (pulse) beams on propagation through different kinds of random mediums, such as a gradient-index fiber [23], an optical system [24, 25], dispersive media [26], free space [27,28,29], turbulent atmosphere [30], and oceanic turbulence [31]. Nevertheless, literature mentioned above have been restricted to the electromagnetic pulse beams by assuming that the electric vector components in the x and y directions are uncorrelated at the source plane. Recently, Voipio et al. presented the coherent-mode decomposition for pulsed electromagnetic beam fields and introduced the overall degree of coherence as a measure of the average temporal or spectral and spatial coherence of the beam [32]. However, to the best of our knowledge, rarely the references are concerned with the context of propagation properties of the partially polarized, partially spatially and spectrally coherent pulsed electromagnetic fields through turbulent atmosphere.

In this work, we take the partially polarized pulsed electromagnetic Gaussian Schell-model (PEGSM) beams as a typical example, which are also called as partially polarized electromagnetic Gaussian Schell-model pulse (EGSMP) beams. The paper is organized as follows. In Sect. 2, the beam model in source plane is established and analytical expressions of the elements of the two-frequency cross spectral density matrix and the average spectral intensity, the beam width and the spectral degree of electromagnetic coherence in the observation plane are derived in turn. Simulation results are presented and discussed in Sect. 3. The influence of different source conditions and turbulent atmosphere on the normalized spectral intensity, beam width in the x and y directions and two-frequency, two points spectral degree of electromagnetic coherence are emphasized. Finally, the main results obtained in this paper are summarized in Sect. 4.

2 Theoretical formulation

We consider optical wave field propagation from the source plane z = 0 to the observation plane z > 0 where a horizontal homogeneous and isotropic turbulent atmosphere channel exists. In space–time domain, the elements of the polarization-coherence function matrix of the partially polarized PEGSM beams in z = 0 are given by the expressions:

$$ \Gamma^{(0)} ({\mathbf{r}}_{1} ,{\mathbf{r}}_{2} ,0,t_{1} ,t_{2} ) = \left[ {\begin{array}{*{20}c} {\Gamma_{xx}^{(0)} ({\mathbf{r}}_{1} ,{\mathbf{r}}_{2} ,0,t_{1} ,t_{2} )} & {\Gamma_{xy}^{(0)} ({\mathbf{r}}_{1} ,{\mathbf{r}}_{2} ,0,t_{1} ,t_{2} )} \\ {\Gamma_{yx}^{(0)} ({\mathbf{r}}_{1} ,{\mathbf{r}}_{2} ,0,t_{1} ,t_{2} )} & {\Gamma_{yy}^{(0)} ({\mathbf{r}}_{1} ,{\mathbf{r}}_{2} ,0,t_{1} ,t_{2} )} \\ \end{array} } \right], $$

(1)

with

$$ \Gamma_{ij}^{(0)} ({\mathbf{r}}_{1} ,{\mathbf{r}}_{2} ,0,t_{1} ,t_{2} ) = A_{i} A_{j} B_{ij} \exp \left[ { - \frac{{{\mathbf{r}}_{1}^{2} }}{{4\sigma_{i}^{2} }} - \frac{{{\mathbf{r}}_{2}^{2} }}{{4\sigma_{j}^{2} }} - \frac{{\left( {{\mathbf{r}}_{1} - {\mathbf{r}}_{2} } \right)^{2} }}{{2\delta_{ij}^{2} }}} \right]\exp \left[ { - \frac{{t_{1}^{2} + t_{2}^{2} }}{{2T_{0}^{2} }} - \frac{{\left( {t_{1} - t_{2} } \right)^{2} }}{{2T_{cij}^{2} }} - i\omega_{0} (t_{1} - t_{2} )} \right]. $$

(2)

Here the variances σ_i, δ_ij are independent of position but may depend on frequency. σ_i (i = x, y) is initial beam waist width in i- direction. A_i denotes the amplitude of i-direction. In addition, the parameters B_ij have the following properties [27, 33]: B_ij ≡ 1 when i = j, |B_ij|≤ 1 when i ≠ j, and B_xy = B*_yx = |B_xy|exp(iθ), θ is the phase difference, θ ≠ kπ (k = 1, 2, 3,...). T₀ is the pulse duration, ɷ₀ is center frequency. δ_ij and T_cij are the spatial and temporal coherent width of the beam, respectively. The beam parameters σ_x, σ_y, δ_ij, and T_cij, which satisfy the following intrinsic constraints [33, 34]:

$$ \left\{ \begin{aligned} \, & \frac{1}{{4\sigma_{i}^{2} }} + \frac{1}{{\delta_{ii}^{2} }} \le \frac{{2\pi^{2} }}{{\lambda^{2} }},{(}i\,{=}\,x{,}y{),} \hfill \\ \, & \max \left\{ {\delta_{xx} ,\delta_{yy} } \right\} \le \delta_{xy} \le \min \left\{ {\frac{{\delta_{xx} }}{{|B_{xy} |}},\frac{{\delta_{yy} }}{{|B_{xy} |}}} \right\},\max \left\{ {T_{cxx} ,T_{cyy} } \right\} \le T_{cxy} \le \min \left\{ {\frac{{T_{cxx} }}{{|B_{xy} |}},\frac{{T_{cyy} }}{{|B_{xy} |}}} \right\}. \hfill \\ \end{aligned} \right. $$

(3)

In the following numerical examples, the values of σ_i, δ_ij, and T_cij, are chosen to satisfy Eq. (3).

Using the Fourier-transform [30], the element of the two-frequency cross spectral density matrix can be expressed as:

$$ {\mathbf{W}}({\mathbf{r}}_{1} ,{\mathbf{r}}_{2} ,0,\omega_{1} ,\omega_{2} ) = \iint {\Gamma ({\mathbf{r}}_{1} ,{\mathbf{r}}_{2} ,0,t_{1} ,t_{2} )}\exp [i(\omega_{1} t_{1} - \omega_{2} t_{2} )]dt_{1} dt_{2}. $$

(4)

Substituting Eqs. (1), (2) into Eq. (4), we can get

$$ W_{ij} ({\mathbf{r}}_{1} ,{\mathbf{r}}_{2} ,0,\omega_{1} ,\omega_{2} ) = \frac{{A_{i} A_{j} B_{ij} T_{0} }}{{2\pi \Omega_{0ij} }}\exp \left[ { - \frac{{{\mathbf{r}}_{1}^{2} }}{{4\sigma_{i}^{2} }} - \frac{{{\mathbf{r}}_{2}^{2} }}{{4\sigma_{j}^{2} }} - \frac{{\left( {{\mathbf{r}}_{1} - {\mathbf{r}}_{2} } \right)^{2} }}{{2\delta_{ij}^{2} }}} \right]\exp [ - {\rm T}_{ij} (\omega_{1} ,\omega_{2} )], $$

(5)

where

$$ {\rm T}_{ij} (\omega_{1} ,\omega_{2} ) = \frac{{(\omega_{1} - \omega_{0} )^{2} + (\omega_{2} - \omega_{0} )^{2} }}{{2\Omega_{0ij}^{2} }} + \frac{{(\omega_{1} - \omega_{2} )^{2} }}{{{2}\Omega_{cij}^{2} }}, $$

(6)

where, $\Omega_{0ij} = \sqrt {{1 \mathord{\left/ {\vphantom {1 {T_{0}^{2} + }}} \right. \kern-\nulldelimiterspace} {T_{0}^{2} + }}{2 \mathord{\left/ {\vphantom {2 {T_{cij}^{2} }}} \right. \kern-\nulldelimiterspace} {T_{cij}^{2} }}}$ and $\Omega_{cij} = {{T_{cij} \Omega_{0ij} } \mathord{\left/ {\vphantom {{T_{cij} \Omega_{0ij} } {T_{0} }}} \right. \kern-\nulldelimiterspace} {T_{0} }}$ describe the spectral width and the spectral coherent width of the beam, respectively.

When the partially polarized PEGSM beams propagate through a horizontal homogeneous and isotropic atmospheric turbulence from the source plane to the observation plane (z > 0) along the z-axis, the position coordinates of any two points on the z plane are expressed by ρ₁ = (x₁, y₁) and ρ₂ = (x₂, y₂), respectively. According to the extended Huygens-Fresnel principle, the elements of the two-frequency cross spectral density matrix can be expressed as [22]:

$$ \begin{aligned} W_{ij} ({{\varvec{\rho}}}_{1} ,{{\varvec{\rho}}}_{2} ,z;\omega_{1} ,\omega_{2} ) & = \frac{{k_{1} k_{2} }}{{4z^{2} \pi^{{2}} }}\exp \left[ {-i(k_{1} - k_{2} )z} \right]\int\limits_{ - \infty }^{\infty } {\iiint {d^{2} {\mathbf{r}}_{1} d^{2} {\mathbf{r}}_{2} }} W_{ij} ({\mathbf{r}}_{1} ,{\mathbf{r}}_{2} ,0;\omega_{1} ,\omega_{2} ) \hfill \\ & \times \exp \left\{ { - \frac{i}{2cz}\left[ {\omega_{1} \left( {{{\varvec{\rho}}}_{1} - {\mathbf{r}}_{1} } \right)^{2} - \omega_{2} \left( {{{\varvec{\rho}}}_{2} - {\mathbf{r}}_{2} } \right)^{2} } \right]} \right\} \times C_{\psi } ({\mathbf{r}}_{1} ,{{\varvec{\rho}}}_{1} ,{\mathbf{r}}_{2} ,{{\varvec{\rho}}}_{2} ,z,k_{1} ,k_{2} ), \end{aligned} $$

(7)

where k = ɷ/c, is the wave number, and c = 3 × 10⁸ m/s. C_ѱ (r₁, ρ₁, r₂, ρ₂, z, k₁, k₂) denotes the random phase fluctuation caused by turbulence. This paper is based on the second order statistics (i.e. mutual coherence function or cross spectral density); therefore, we will assume that the extended Huygen’s Fresnel approach is valid in all regimes of atmospheric turbulence with respect to propagation properties [35]. Paralleling the pulse wave analysis in Ref. [35], the complex phase fluctuation is given by:

$$ C_{\psi } ({\mathbf{r}}_{1} ,{{\varvec{\rho}}}_{1} ,{\mathbf{r}}_{2} ,{{\varvec{\rho}}}_{2} ,z,k_{1} ,k_{2} ) = \left\langle {\exp [\psi ({\mathbf{r}}_{1} ,{{\varvec{\rho}}}_{1} ,z,k_{1} ) + \psi^{*} ({\mathbf{r}}_{2} ,{{\varvec{\rho}}}_{2} ,z,k_{2} )]} \right\rangle \cong \Gamma_{2} \exp \left[ { - \frac{1}{2}D_{\text{sp}} ({\mathbf{r}}_{1} - {\mathbf{r}}_{2} ,{{\varvec{\rho}}}_{1} - {{\varvec{\rho}}}_{2} )} \right], $$

(8)

$$ \Gamma_{2} = \exp \left[ { - 2\pi^{2} \left( {k_{1} - k_{2} } \right)^{2} z\int_{0}^{\infty } \kappa \Phi_{n} (\kappa )d\kappa } \right], \, D_{\text{sp}} (Q) = 8\pi^{2} k_{1} k_{2} z\int_{0}^{1} {} \int_{0}^{\infty } {\kappa \Phi_{n} (\kappa )\left( {1 - J_{0} \left( {\kappa \xi |Q|} \right)} \right)}, $$

(9)

where J₀ is a Bessel function and Φ_n (κ) is the refractive index power spectrum. Dsp (Q) is the spherical wave structure function. In our analysis, we use the von Karman spectrum given by:

$$ \Phi_{n} (\kappa ) = 0.033C_{n}^{2} \frac{{\exp \left( { - \kappa^{2} /\kappa_{m}^{2} } \right)}}{{\left( {\kappa^{2} + \kappa_{0}^{2} } \right)^{11/6} }}, $$

(10)

where κ_m = 5.92/l₀, κ₀ = 1/L₀, L₀ and l₀ are the outer and inner scales of turbulence, respectively; κ is the spatial radial frequency, and $C_{n}^{2}$ is the structure parameter.

The spherical wave structure function Dsp (Q) and Γ₂ in Eq. (9) based on the von Karman spectrum have been shown to be approximated by [35]:

$$ D_{\text{sp}} (Q) \approx 2\left( {\frac{Q}{{\rho_{0} }}} \right)^{2} {,}\,\Gamma_{2} = \exp \left( { - 0.391C_{n}^{2} k_{d}^{2} zL_{0}^{5/3} } \right), $$

(11)

respectively. In Eq. (11), $\rho_{0} = \left( {0.55C_{n}^{2} k_{c}^{2} l_{0}^{ - 1/3} z} \right)^{ - 1/2}$ is the coherence length of a spherical wave propagating in the horizontal path of turbulent medium, k_c =  (k₁ + k₂)/2, k_d = k₁ − k₂.

In Ref. [35], Q only includes the points on-axis and ignores the points off-axis, therefore, it can be extended in this paper to include all points in the observation plane. i.e.,

$$ D_{\text{sp}} (Q) \cong 2 \, \frac{{({\mathbf{r}}_{1} - {\mathbf{r}}_{2} )^{2} + ({\mathbf{r}}_{1} - {\mathbf{r}}_{2} )({{\varvec{\rho}}}_{1} - {{\varvec{\rho}}}_{2} ) + ({{\varvec{\rho}}}_{1} - {{\varvec{\rho}}}_{2} )^{2} }}{{\rho_{0}^{2} }}. $$

(12)

Substituting Eqs. (5), (6) and Eqs. (8)–(12) into Eq. (7) and calculating the related integral we obtain:

$$ \begin{aligned} W_{ij} ({{\varvec{\rho}}}_{1} ,{{\varvec{\rho}}}_{2} ,z,\omega_{1} ,\omega_{2} ) & = \frac{{\omega_{1} \omega_{2} W_{0ij} \Gamma_{2} \gamma_{ij}^{4} }}{{c^{2} z^{2} \left( {4\alpha_{1ij} \alpha_{2ij} \gamma_{ij}^{4} - 1} \right)}}\exp \left. {\left[ {\frac{i}{2cz}\left( {\omega_{2} {{\varvec{\rho}}}_{2}^{2} - \omega_{1} {{\varvec{\rho}}}_{1}^{2} } \right) - \frac{{\left( {{{\varvec{\rho}}}_{1} - {{\varvec{\rho}}}_{2} } \right)^{2} }}{{\rho_{0}^{2} }}} \right.} \right]\exp \left[ {\frac{{\gamma_{ij}^{4} \left( {p^{2} \alpha_{2ij} + q^{2} \alpha_{1ij} } \right) - pq\gamma_{ij}^{2} }}{{4\alpha_{1ij} \alpha_{2ij} \gamma_{ij}^{4} - 1}}} \right] \\ & \times \exp \left[ {\frac{{-i(\omega_{1} - \omega_{2} )z}}{c} - \frac{{\left( {\omega_{1} - \omega_{0} } \right)^{2} + \left( {\omega_{2} - \omega_{0} } \right)^{2} }}{{2\Omega_{0ij}^{2} }} - \frac{{\left( {\omega_{1} - \omega_{2} } \right)^{2} }}{{2\Omega_{cij}^{2} }}} \right], \end{aligned} $$

(13)

with

$$ \begin{aligned} W_{0ij} & = \frac{{A_{i} A_{j} B_{ij} T_{0} }}{{2\pi \Omega_{0ij} }}, \, \alpha_{1ij} = \frac{1}{{4\sigma_{i}^{2} }} + \frac{1}{{2\delta_{ij}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{{i\omega_{1} }}{2cz}, \, \alpha_{2ij} = \frac{1}{{4\sigma_{j}^{2} }} + \frac{1}{{2\delta_{ij}^{2} }} + \frac{1}{{\rho_{0}^{2} }} - \frac{{i\omega_{2} }}{2cz}{, } \hfill \\ \frac{1}{{\gamma_{ij}^{2} }} & = \frac{1}{{\delta_{ij}^{2} }} + \frac{2}{{\rho_{0}^{2} }}, \, p = \frac{{i\omega_{1} }}{cz}\varvec{\rho}_{1} - \frac{{(\varvec{\rho}_{1} - \varvec{\rho}_{2} )}}{{\rho_{0}^{2} }}, \, q = \frac{{i\omega_{2} }}{cz}\varvec{\rho}_{2} - \frac{{(\varvec{\rho}_{1} - \varvec{\rho}_{2} )}}{{\rho_{0}^{2} }}. \end{aligned} $$

(14)

2.1 Average spectral intensity

The average spectral intensity at the point (ρ, z, ɷ) was given by the formula [27]:

$$ \begin{aligned} S({{\varvec{\rho}}},z,\omega ) & = Tr\left( {W_{ij} ({{\varvec{\rho}}},{{\varvec{\rho}}},z,\omega ,\omega )} \right) = \frac{{T_{0} }}{2\pi }\left\{ {\frac{1}{{\Omega_{0xx} }}\frac{{A_{x}^{2} }}{{\Delta_{xx} }}\exp \left[ { - \frac{{{{\varvec{\rho}}}^{2} }}{{2\sigma_{x}^{2} \Delta_{xx} }}} \right]\exp \left[ { - \frac{{\left( {\omega - \omega_{0} } \right)^{2} }}{{\Omega_{0xx}^{2} }}} \right]} \right. \\ & + \frac{1}{{\Omega_{0yy} }}\frac{{A_{y}^{2} }}{{\Delta_{yy} }}\left. {\exp \left[ { - \frac{{{{\varvec{\rho}}}^{2} }}{{2\sigma_{y}^{2} \Delta_{yy} }}} \right]\exp \left[ { - \frac{{\left( {\omega - \omega_{0} } \right)^{2} }}{{\Omega_{0yy}^{2} }}} \right]} \right\}, \end{aligned} $$

(15)

where

$$ \begin{aligned} \Delta_{xx} = 1 + \frac{{c^{2} }}{{2\sigma_{x}^{2} \omega^{2} }}\left( {\frac{1}{{2\sigma_{x}^{2} }} + \frac{2}{{\delta_{xx}^{2} }}} \right)z^{2} + 1.1C_{n}^{2} \sigma_{x}^{ - 2} l_{0}^{ - 1/3} z^{3} , \hfill \\ \Delta_{yy} = 1 + \frac{{c^{2} }}{{2\sigma_{y}^{2} \omega^{2} }}\left( {\frac{1}{{2\sigma_{y}^{2} }} + \frac{2}{{\delta_{yy}^{2} }}} \right)z^{2} + 1.1C_{n}^{2} \sigma_{y}^{ - 2} l_{0}^{ - 1/3} z^{3}. \end{aligned} $$

(16)

Equation (16) is similar to Eq. (15) in [30], which is employing the Kolmogorov spectrum model. By setting ρ = (0, 0), we can get on-axis average spectral intensity:

$$ S(0,z,\omega ) = \frac{{T_{0} }}{{2\pi \Omega_{0xx} }}\frac{{A_{x}^{2} }}{{\Delta_{xx} }}\exp \left[ { - \frac{{\left( {\omega - \omega_{0} } \right)^{2} }}{{\Omega_{0xx}^{2} }}} \right] + \frac{{T_{0} }}{{2\pi \Omega_{0yy} }}\frac{{A_{y}^{2} }}{{\Delta_{yy} }}\exp \left[ { - \frac{{\left( {\omega - \omega_{0} } \right)^{2} }}{{\Omega_{0yy}^{2} }}} \right]. $$

(17)

It is helpful to define the normalized spectral intensity as:

$$ S^{\prime}({{\varvec{\rho}}},z,\omega ) = S({{\varvec{\rho}}},z,\omega )/S_{\max } ({{\varvec{\rho}}},z,\omega ). $$

(18)

The average spectral intensity for the partially polarized PEGSM beam is determined in Eq. (15), and the change in the spectral property on propagation in a homogeneous and isotropic turbulent atmosphere is studied by choosing different source conditions parameters σ_i, δ_ij and T_cij, refractive index structure constant C_n², and turbulence inner scale l₀.

2.2 Beam width

Let us study how the source conditions and turbulence affect the spot size of the beam. We define the width W of the beam spot such that [36]

$$ \left\{ {S(z,{{\varvec{\rho}}}_{c} = W,{{\varvec{\rho}}}_{d} = 0)/S(z,{{\varvec{\rho}}}_{c} = {{\varvec{\rho}}}_{d} = 0)} \right\} = \exp \left( { - 2} \right), $$

(19)

where ρ_c = (ρ₁ + ρ₂)/2, ρ_d = ρ₁ − ρ₂.

Substituting Eqs. (15), (16) into Eq. (19), we obtain the following equation for the beam size W_x (z, ɷ) and W_y (z, ɷ) can be written as:

$$ \begin{aligned} W_{x} (z,\omega ) & = \sigma_{x} \sqrt {\Delta_{xx} } = \sqrt {\sigma_{x}^{2} \left[ {1 + \frac{{c^{2} }}{{2\omega^{2} \sigma_{x}^{2} }}\left( {\frac{1}{{2\sigma_{x}^{2} }} + \frac{2}{{\delta_{xx}^{2} }}} \right)z^{2} } \right] + 1.1C_{n}^{2} l_{0}^{ - 1/3} z^{3} } \hfill \\ & = \sqrt {\sigma_{x}^{2} + \frac{{\sigma_{x}^{2} z^{2} }}{{16Z_{Rx}^{2} }} + \frac{{c\sigma_{x}^{2} z^{2} }}{{2\omega Z_{Rx} \delta_{xx}^{2} }} + 1.1C_{n}^{2} l_{0}^{ - 1/3} z^{3} }, \end{aligned} $$

(20)

$$ \begin{aligned} W_{y} (z,\omega ) & = \sigma_{y} \sqrt {\Delta_{yy} } = \sqrt {\sigma_{y}^{2} \left[ {1 + \frac{{c^{2} }}{{2\omega^{2} \sigma_{y}^{2} }}\left( {\frac{1}{{2\sigma_{y}^{2} }} + \frac{2}{{\delta_{yy}^{2} }}} \right)z^{2} } \right] + 1.1C_{n}^{2} l_{0}^{ - 1/3} z^{3} } \hfill \\ & = \sqrt {\sigma_{y}^{2} + \frac{{\sigma_{y}^{2} z^{2} }}{{16Z_{Ry}^{2} }} + \frac{{c\sigma_{y}^{2} z^{2} }}{{2\omega Z_{Ry} \delta_{yy}^{2} }} + 1.1C_{n}^{2} l_{0}^{ - 1/3} z^{3} }, \end{aligned} $$

(21)

The term Z_Ri = kσ_i²/2 denotes the Rayleigh distance. It can be seen from Eqs. (20) and (21) that the second and third terms in the square root stand for diffraction of the beam on free-space propagation induced by σ_i and δ_ii (i = x, y), respectively. Diffraction in the two terms is proportional to the square of the propagation distance z. The fourth term stands for the extra diffraction induced by turbulence and proportional to the cube of the propagation distance z, also proportional to the turbulence structure parameter C_n², and inversely proportional to the one third power of the turbulence inner scale l₀.

We noticed that in free space (C_n² = 0) the beam size remains close to σ_i as long as z << Z_Ri. The beam begins to diverge rapidly in the far-field region z > Z_Ri. The presence of the turbulence medium causes the beam to diverge further.

2.3 Spectral degree of electromagnetic coherence

Correlations between different electric-field frequency components are characterized by the spectral degree of electro- magnetic coherence μ_EM (ρ₁, ρ₂, z, ω₁, ω₂) originally introduced for stationary, spatially partially coherent fields [32], but which can readily be extended to spatially and spectrally partially coherent fields as:

$$ \mu_{\text{EM}}^{2} (\varvec{\rho}_{1} ,\varvec{\rho}_{2} ,z,\omega_{1} ,\omega_{2} ) = \frac{{||\mathbf{W}(\varvec{\rho}_{1} ,\varvec{\rho}_{2} ,z,\omega_{1} ,\omega_{2} )||_{F}^{2} }}{{{S}(\varvec{\rho}_{1} ,z,\omega_{1} ){S}(\varvec{\rho}_{2} ,z,\omega_{2} )}}, $$

(22)

where ||·||_F is the Frobenius norm.

From Eq. (22), we can get three models for spectral degree of electromagnetic coherence, i.e., (1) two-frequency, single- point spectral degree of electromagnetic coherence μ_EM (ρ, ρ, z, ω₁, ω₂); (2) single-frequency, two-point spectral degree of electromagnetic coherence μ_EM (ρ₁, ρ₂, z, ω, ω); and (3) two-frequency, two-point spectral degree of electromagnetic coherence μ_EM (ρ₁, ρ₂, z, ω₁, ω₂). For the sake of simplicity, in this work, we take the two-frequency, two-point spectral degree of electromagnetic coherence as a typical example, which can be written as:

$$ \mu_{\text{EM}} (0,d,z,\omega_{1} ,\omega_{2} ) = \sqrt {\frac{{||\mathbf{W}(0,d,z,\omega_{1} ,\omega_{2} )||_{F}^{2} }}{{{S}(0,z,\omega_{1} ){S}(d,z,\omega_{2} )}}}, $$

(23)

where we set ρ₁ = (0, 0) and ρ₂ =( d, 0). When d = 0, Eq. (23) becomes the two-frequency, single-point spectral degree of electromagnetic coherence μ_EM (0, 0, z, ω₁, ω₂).

3 Numerical results and discussion

To evaluate the preceding analysis, we show the detailed variations of propagation properties parameters in a horizontal homogeneous and isotropic turbulent atmosphere channel. Here, the different conditions’ source parameters, i.e., isotropic source, semi-isotropic source and the anisotropic source [37], are adopted as:

• (1) Isotropic source: σ_x = σ_y = 2 cm, δ_xx = δ_yy = 2 mm, T_cxx = T_cyy = 30 fs;

• (2) Semi-isotropic source: σ_x = 1 cm, σ_y = 2 cm, δ_xx = δ_yy = 2 mm, T_cxx = T_cyy = 30 fs;

• (3) Anisotropic source: σ_x = 1 cm, σ_y = 2 cm, δ_xx = 2 mm, δ_yy = 3 mm, T_cxx = 20 fs, T_cyy = 30 fs.

The other parameters are choosen to be: ω₀ = 2.98 × 10¹⁵ rad/s (λ = 632.8 nm), ω = ω₁ = 3.0 × 10¹⁵ rad/s, ω₂ = 2.96 × 10¹⁵ rad/s, A_x = 1.5, A_y = 1, T₀ = 50 fs, B_xy = 0.3 exp (iπ/3), δ_xy = 4 mm, T_cxy = 50 fs, C_n² = 10^–14 m^−2/3, l₀ = 1 mm, L₀ = 10 m.

We employ the above parameters as examples for a theoretical analysis; other values can also be chosen depending on the propagation scenario. The above parameters are measured in a turbulent channel, consistent with physically realizable conditions. The results are shown in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11.

Fig. 1

Evolution of on-axis normalized spectral intensity with z for various values of C_n² and different source conditions

Fig. 2

Evolution of on-axis normalized spectral intensity with z for various values of l₀ and different source conditions

Fig. 3

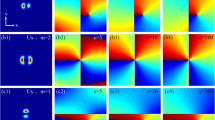
Normalized 3D-spectral intensity distribution S (x, y, z, ɷ)/S_max (x, y, z, ɷ) of a partially polarized PEGSM beam for different source conditions a isotropic source, b semi-isotropic source, and c anisotropic source at several propagation distances in a horizontal homogeneous and isotropic turbulent atmosphere

Fig. 4

Cross line (y = 0) of the normalized intensity distribution S (x, 0, z, ɷ)/S_max (x, 0, z, ɷ) of a partially polarized PEGSM beam at several propagation distances a z = 0 m, b z = 0.5 km, c z = 4.5 km, and d z = 10 km in a horizontal homogeneous and isotropic turbulent atmosphere for different source conditions

Fig. 5

Evolution of the normalized spectral intensity of partially polarized PEGSM beams as a function of (ω– /ω₀)/ω₀ at the observations a ρ = 0 m, z = 10 km and b ρ = 5 m, z = 10 km for different source conditions. The black solid curves denote the original normalized spectrum S₀(ω)

Fig. 6

Changes in the beam width W_x (z, ω) and W_y (z, ω) of partially polarized PEGSM beams versus the propagation distance z with different source conditions a isotropic source, b semi-isotropic source, and c anisotropic source for different C_n²

Fig. 7

Changes in the beam width W_x (z, ω) and W_y (z, ω) of partially polarized PEGSM beams versus the frequency ω with different source conditions a isotropic source, b semi-isotropic source, and c anisotropic source for different C_n² at z = 5 km

Fig. 8

Changes of the values of the two-frequency, two-point spectral degree of electromagnetic coherence |μ_EM (ρ₁, ρ₂, z, ɷ₁, ɷ₂)| versus propagation distance z with different refractive index structure constant C_n² and transverse distance (ρ₁ = 0, ρ₂ = d) under three different source conditions, where a isotropic source, b semi-isotropic source, and c anisotropic source

Fig. 9

Changes of the values of the two-frequency, two-point spectral degree of electromagnetic coherence |μ_EM (ρ₁, ρ₂, z, ɷ₁, ɷ₂)| versus propagation distance z with different turbulence inner scale l₀ and transverse distance d (ρ₁ = 0, ρ₂ = d) for different source conditions, where (a1, b1) isotropic source, (a2, b2) semi-isotropic source and (a3, b3) anisotropic source (a d = 0 cm, b d = 1 cm)

Fig. 10

3D-spectral degree of electromagnetic coherence distribution |μ_EM (x, y, x, y, z, ω₁, ω₂)| of a partially polarized PEGSM beam for different source conditions a isotropic source, b semi-isotropic source, and c anisotropic source at several propagation distance in a horizontal homogeneous and isotropic turbulent atmosphere

Fig. 11

Cross line (y = 0) of the spectral degree of electromagnetic coherence distribution |μ_EM (x, 0, x, 0, z, ω₁, ω₂)| of a partially polarized PEGSM beam at several propagation distances a z = 0.2 km, b z = 1.5 km, c z = 5 km, and d z = 15 km in a horizontal homogeneous and isotropic turbulent atmosphere

Now we study the evolution of the on-axis normalized spectral intensity of a partially polarized PEGSM beam in a horizontal homogeneous and isotropic turbulent atmosphere for different source conditions. By applying Eqs. (16)–(18), we calculate in Fig. 1 the on-axis normalized spectral intensity S′ (0, z, ɷ) versus the propagation distance z for different source conditions and various values of refractive index structure constant C_n². As can be seen, values of S′ (0, z, ɷ) near the source plane (z ≤ 50 m) is unchanged for different source conditions and different values of C_n². For the case of 100 m ≤ z ≤ 1000 m, the values of S′ (0, z, ɷ) decrease rapidly with the increase of z; fixing z and C_n², value of S′ (0, z, ɷ) for isotropic source is the largest and semi-isotropic source is the smallest. The smaller C_n² is, the greater the difference between the three sources will become. When C_n² is larger, the curves of S′ (0, z, ɷ) are almost overlapped for the case of the latter two sources.

In Fig. 2, the S′ (0, z, ɷ) is plotted for several values of turbulence inner scale l₀. As can be seen, the evolution of S′ (0, z, ɷ) is consistent with Fig. 1. For different l₀, the value of S′ (0, z, ɷ) is almost unchanged. In other words, the turbulence inner scale hardly affects the S′ (0, z, ɷ). On the other hand, the source parameters have great effect on the S′ (0, z, ɷ), for the case of 100 m ≤ z ≤ 1000 m.

By applying Eqs. (15) and (18), we calculate in Fig. 3 the normalized 3D-spectral intensity distribution S(x, y, z, ɷ)/S_max(x, y, z, ɷ) of a partially polarized PEGSM beam at several propagation distances in a horizontal homogeneous and isotropic turbulent atmosphere for different source conditions (a) isotropic source, (b) semi-isotropic source, and (c) anisotropic source. To learn about evolution of the average spectral intensity of a partially polarized PEGSM beam on propagation, we also calculate in Fig. 4 the cross line (y = 0) of the normalized average spectral intensity distribution S(x, 0, z, ɷ)/S_max(x, 0, z, ɷ) of a partially polarized PEGSM beam at several propagation distances during propagation for different source conditions. One sees from Figs. 3 and 4 that in the far field region, the partially polarized partially coherent PEGSM beam propagating through the turbulent atmosphere can keep its initial beam profile almost unchanged. Moreover, the beam shapes of the three sources are similar. The beam profiles of both the isotropic and the semi-isotropic source almost coincide in the far field, and the center width of spectral intensity distribution in the case of the anisotropic source is always smaller than the other two cases.

The relative spectral shift δω/ω₀ is defined as δω/ω₀ = (ω_max − ω₀)/ω₀, where ω_max denotes the frequency at which the spectrum takes the maximum value. The normalized spectral intensity S′ (ρ, z, ɷ) versus the relative spectral shift δω/ω₀ at the observations (a) ρ = 0 m, z = 10 km and (b) ρ = 5 m, z = 10 km for different values of C_n² and source conditions are given in Fig. 5 and the corresponding values of the relative spectral shift are compiled in Table 1. The other calculation parameters are the same as those in Fig. 1. It is interesting to find that the evolution of on-axis normalized spectral intensity S′ (ρ, z, ɷ) for the three source conditions almost coincide. In comparison of Fig. 5a1–a3 with Fig. 5b1–b3, we see that the spectrum is blue- and red-shifted in comparison with the original spectrum for ρ = 0 m and ρ = 5 m, respectively and the value of the blue shift (or red shift) decreases with the increase in C_n². Taking the isotropic source as an example, for ρ = 0 m, the normalized spectrum shifts in the direction of the larger frequency and the values of the relative spectral shift δω/ω₀ = 0.0007 (C_n² = 0) and 0.0003 (C_n² = 10^–14 m^−2/3), respectively; for ρ = 5 m, the normalized spectrum shifts in the direction of the smaller frequency and the values of the relative spectral shift δω/ω₀ = − 0.0141 (C_n² = 0) and − 0.0067 (C_n² = 10^–14 m^−2/3), respectively. For the case of anisotropic source, values of the red shift are bigger than the other two sources, i.e., the values of the relative spectral shift are δω/ω₀ = − 0.0282 (C_n² = 0) and − 0.0141 (C_n² = 10^–14 m^−2/3), respectively.

Table 1 The values of relative spectral shift corresponding to Fig. 5

Figure 6 presents the evolution of beam width W_x (z, ω) and W_y (z, ω) of partially polarized PEGSM beams in Eqs. (20) and (21) with the propagation distance z for different values of C_n². In the absence of turbulence (C_n² = 0 m^−2/3), the fourth term disappears and Eqs. (20) and (21) can be rewritten as:

$$ W_{i} (z,\omega ) = \sigma_{i} \sqrt {1 + \frac{{c^{2} z^{2} }}{{4\omega^{2} \sigma_{i}^{2} }} + \frac{{c^{2} z^{2} }}{{\omega^{2} \delta_{ii}^{2} }}} {,}\,i = x,y, $$

(24)

where the second term is inverse proportional to the square of σ_i and the third term is inverse proportional to the square of δ_ii. In the presence of turbulence, i.e.

$$ W_{i} (z,\omega ) = \sigma_{i} \sqrt {1 + \frac{{c^{2} z^{2} }}{{4\omega^{2} \sigma_{i}^{2} }} + \frac{{c^{2} z^{2} }}{{\omega^{2} \delta_{ii}^{2} }} + \frac{{1.1C_{n}^{2} l_{0}^{ - 1/3} z^{3} }}{{\sigma_{i}^{2} }}} {,}\,i = x,y. $$

(25)

As can be seen from Eq. (25), for z ≥ 2000 m, the value of the fourth term is greater than one, i.e., in this case, the turbulence-induced diffraction plays a significant role in the beam width. Comparing Fig. 6 with Table 2, one finds that the beam width W_x (z, ω) and W_y (z, ω) of the former two source conditions are almost the same. This implies that the partially polarized PEGSM beams with the two source conditions exhibit the same beam profile in the far field region. Moreover, the beam spreads more seriously in the presence of turbulence. On the other hand, the source condition has a great influence on the beam size (see Fig. 6c; also see Table 2). For the case of 0 m ≤ z ≤ 1000 m, the turbulence-induced diffraction is smaller than the initial beam parameters-induced diffraction, which leads to W_x (z, ω) < W_y (z, ω) within this range. For z > 2000 m, the beam width in the y direction is smaller than that in the x direction. This implies that both the source parameters and turbulence-induced diffraction impact on the beam width.

Table 2 The special spectral parameters corresponding to Fig. 6

Figure 7 examines the evolution of beam width W_x (z, ω) and W_y (z, ω) of partially polarized PEGSM beams as a function of the frequency ω for different C_n² at z = 5 km. One finds that the variation of the beam size with frequency is not obvious and the beam width in the presence of turbulence is larger than that in the absence of turbulence. This indicates that turbulence-induced diffraction has a larger effect on the beam size and the magnitude of the frequency hardly affects it. Furthermore, it is clear that the beam width W_x (z, ω) and W_y (z, ω) in the anisotropic source cases are different from that two cases. i.e., the beam width difference in the x and y directions is greater.

Now, let us examine the evolution of the two-frequency, two-point spectral degree of electromagnetic coherence μ_EM (0, d, z, ω₁, ω₂) in turbulent atmosphere. We employ Eq. (23) to compute μ_EM (0, d, z, ω₁, ω₂). The results are plotted in Figs. 8 and 9. Figure 8 presents the evolution of μ_EM (0, d, z, ω₁, ω₂) as a function of propagation distance z with different C_n² and transverse distance d for different conditions source parameters. One finds that changes of μ_EM (0, d, z, ω₁, ω₂) are similar and different from the former one for the case of latter two sources; under the same C_n², |μ_EM| of semi-isotropic source is greater than that of anisotropic source ( see Fig. 8b, c). Meanwhile, we find that |μ_EM| varies more rapidly with z as d increases. The values of |μ_EM| are kept ≈ 0 then rise with the increase of d (d > 0) in the absence of turbulence; in the presence of turbulence, values of |μ_EM| are kept smaller than 0.01 with the increase of d (d > 0). For d = 0, i.e., two-frequency, one-point spectral degree of electromagnetic coherence μ_EM (0, 0, z, ω₁, ω₂), it can be seen from Fig. 8a that, for 0 m ≤ z ≤ 100 m, the value of |μ_EM| remains constant in the absence of turbulence(C_n² = 0), then falls rapidly to 0 until z ≈ 3000 m, finally increases quickly. On the other hand, in the presence of turbulence, the value of |μ_EM| decreases slightly over a short distance, then drops sharply to 0. A comparison of Fig. 8b with Fig. 8c, in the absence of turbulence, with the increase of z, the value of |μ_EM| almost stays unchanged, secondly gradually decreases, then increases rapidly and eventually remains constant; in the presence of turbulence, the evolution of |μ_EM| agree well with the isotropic source case and the value of |μ_EM| in the semi-istropic case is the biggest. Therefore, it can be concluded that the source parameters play a great role in the spectral degree of electromagnetic coherence.

Figure 9 demonstrates the evolution of μ_EM (0, d, z, ω₁, ω₂) versus z for four kinds of turbulence scale and transverse distance d (Fig. 9a: d = 0 cm, b: d = 1 cm) under three different source conditions. As seen in Fig. 9a and recalling Fig. 8a–c, there is a slight change in |μ_EM| for z ≤ 100 m. This indicates that the turbulence scale has little effect on the |μ_EM| over the distance range. One finds from Fig. 9a1 and b1 that, for the case of l₀ = 1 mm and L₀ = 1 m, when z > 100 km, the evolution of |μ_EM| appears abnormal compared with the other three cases. Therefore, it can be concluded that for 5 km ≤ z ≤ 50 km, and L₀ fixed, the bigger the l₀ is, the larger the |μ_EM| becomes. For l₀ fixed, the smaller the L₀ is, the larger the |μ_EM| becomes; and the smaller l₀ is, the bigger the difference becomes.

Figure 9b1–b3 illustrate that, the evolution of μ_EM (0, d, z, ω₁, ω₂) versus z for four kinds of turbulence scale is similar to the corresponding former three figures (see Fig. 9a1–a3). To draw a conclusion that turbulence inner scale and outer scale play a great role in |μ_EM| in the far field region. Moreover, the source conditions have an important effect on |μ_EM|. Under the same conditions, the |μ_EM| of semi-isotropic source is higher than the other two sources.

Finally, to learn more about the coherence property, by applying Eq. (22) and choosing ρ₁ = ρ₂ = (x, y), we calculate in Fig. 10 the 3D-spectral degree of electromagnetic coherence distribution |μ_EM (x, y, x, y, z, ω₁, ω₂)| of a partially polarized PEGSM beam at several propagation distances in the turbulent atmosphere for different source conditions. Meanwhile, we also calculate in Fig. 11 the cross line (y = 0) of the spectral degree of electromagnetic coherence distribution |μ_EM (x, 0, x, 0, z, ω₁, ω₂)| of a partially polarized PEGSM beam at several propagation distances for different source conditions. One sees from Figs. 10 and 11 that, for the case of semi-isotropic source and anisotropic source, the spectral degree of electromagnetic coherence exhibits flat-topped Gaussian distribution with circular symmetry, and both the shape and the symmetry keeps unchanged during transmission; the value of |μ_EM| increases and then gradually decreases with the increase of z. For the case of isotropic source, the shape of the spectral degree of electromagnetic coherence changes during transmission: it exhibits concave distribution at a few kilometers distance; the value of |μ_EM| gradually decreases with the increase of propagation distance. It can be concluded that the source parameters play a crucial role in determining the correlation property.

4 Conclusion

In summary, the spectral and coherent properties of an isotropic, semi-isotropic, and anisotropic partially polarized pulsed electromagnetic beams propagation upon a horizontal homogeneous and isotropic atmospheric turbulence channel have been examined. With the help of numerical calculations, we have studied the changes in the beam width, spectral, and coherent properties for the beams mentioned. It is shown that, both the source parameters and turbulent atmosphere impact on the spectrum distribution, beam width, and spectral degree of electromagnetic coherence distribution of the partially polarized PEGSM beams. Within a short distance range, source parameters induced diffraction plays a major role; after further propagation, the turbulence-induced diffraction plays a dominant role. It is also found that after passing through a turbulent atmosphere, the spectrum at the far zone shifts towards red shift or blue shift, compared with the source spectrum. In particular, the findings have shown that there is a considerable difference in evolution of the three kinds of partially polarized pulsed electromagnetic beams during propagation. To draw a conclusion, source parameters have little effect on the normalized spectral distribution; the beam width in the case of anisotropic source is smaller than that of the other two sources; and the source parameters play a crucial role in determining the correlation property.

The research outlined in this work provides a better understanding of the second-order statistics of a partially polarized PEGSM beam propagating through atmospheric turbulence in the space frequency domain. Some theoretical results in this paper will be widely applied in the free-space optical communication, information encoding and exchange, and lidar system.