1 Introduction

The scientific community has recently focused on manufacturing and analyzing optical glass systems doped with heavy metal oxide (HMO) and its special applications in optics, photonic devices, and nuclear engineering [1,2,3,4,5]. Synthesis and characterization of new materials are important for several applications [6,7,8,9,10,11]. Furthermore, doping such substances with rare-earth (Re3+) ions enhances their optical and electronic properties, good stability, and flexibility characteristics, allowing an intake of elements in their formulation to be accepted. While also lasers, solid-phase lighting systems, fiber amplification, photodetectors, storage systems, dosimeters, and renewable power their uses are advancing [2, 12,13,14,15,16,17]. Moreover, trivalent rare-earth (Re3+) ions in glasses contain a substantial percentage of absorption bands in the Vis–NIR areas, making them useful as practical photonic elements for various purposes. Specifically, Er3+/Yb+3 ions activated glasses are valuable as the optical gain host, focusing on producing photonic technologies, including solid-state illumination, color displays, and broad bandwidth data storage capacities [1, 13, 18,19,20,21].

Phosphate glass doped with Re3+ ions is far from many other materials in terms of realizing photonic materials with enhanced optical gain across a short length while minimizing nonlinear optical consequences, thus leading to high-laser reliability and long-term stability [3, 22, 23]. Lead phosphate glasses with Re3+ ions are part of an enormous family of heavy metal glasses explored for potential optoelectronic characteristics as prospective laser glass hosts [24]. Glasses composed of lead-based phosphates are desirable in optoelectronics and therapeutic uses [19, 25].

Co-doping Er3+/Yb3+ has been demonstrated to be an effective strategy for producing short, efficient lasers and amplifying the entire communications wavelength region. Doping using Yb3+ enhances absorption pumping near ⁓ 980 nm and energy transfer efficiency between Er3+ and Yb3+, allowing for centimeter-long laser beams at low Er3+ contents [26]. These glasses’ optical, electrical, chemical, and fluorescence characteristics are predominantly improved by adding certain oxides, such as Al2O3, PbO, and Na2O, with rare-earth ions [27,28,29,30,31,32].

Lead oxide can operate as a glass former or a modifier based on the link between lead and oxide (covalent or ionic), and the PbO/P2O5 ratio in the glass network was found to be beneficial for spectroscopy approaches. The chemical resistance of the glass system is improved by the P–O–Pb bond and the lead phosphate’s regional geometry. Increasing the number of NBO (non-bridging oxygen) atoms in the host by adding three metal oxide elements can improve its chemical resistance. Furthermore, the presence of lead ions (Pb2+) will significantly benefit the spectroscopic characterization of Re3+ ions. Due to the S–P electronic transition of Pb2+ ions, there is also a high absorption in the UV area [12, 19, 33, 34].

When aluminum ions are integrated into glass hosts, the fluorescence of rare-earth ions, such as Re3+, is often enhanced because the Al3+ ions separate the rare-earth ions from the RE−O−RE bonds and produce Al–O–RE bonds. In contrast to the alumina-free glass hosts, this declustering action results in higher spacing between RE ions, which improves fluorescence emission [19]. In addition, because of its various qualities such as high solubility, enhanced chemical stability, and thermo-mechanical strength. Na2O is frequently used to adjust low field intensity cations, with Na+ improving the mechanical qualities necessary for effective laser glass [12, 27, 35].

Researchers studied the effects of gamma irradiation on HMO-based glasses based on the mechanisms of interactions that can be categorized as photoelectric effects, Compton scattering, or pair production [36, 37]. Gamma irradiation causes either the introduction of new active defects or the activation of existing defects and the repair of these defects by recombination or recovery. Irradiation causes changes in the glass matrix's structure, including defects [30, 38]. Optical spectra (UV–Vis light) are used to investigate the impact of radiation on glasses modified with rare-earth oxides that produce distinct emission bands in the UV–visible region [39]. Liberated electrons can pass through the glass matrix during the irradiation process, generating electron–hole pairs that are predicted to interact with non-bridging oxygen that occurs as defects in the host glass to capture the positive holes or liberated radicals, causing color centers to form in the glass network [27].

Ramesh et al. showed that the nonlinear optical (NLO) features improved with gamma irradiation doses increasing, suggesting that high-dose irradiated glasses might be valuable for photonic devices, especially optical limiters. It is worth noting that this study shows how gamma irradiation affects the NLO characteristics of lead phosphate glasses having Re3+ ions (Er3+/Yb3+ doped and co-doped). Research on the performance of radiation on Re3+ doped and co-doped glasses is increasing attention in the photonics and dosimetry investigation fields [1, 40, 41].

Herein, this study intends to reveal the impacts of gamma irradiation on the structural, linear, and nonlinear optical characteristics of 47P2O5−23Na2O−6Al2O3−22PbO−0.5Er2O3−1.5Yb2O3 glass. The Er/Yb-doped lead phosphate glass sample was produced using the traditional melt quenching procedure and then treated to different doses of gamma irradiation (0, 20, 50, and 100) kGy. Also, our study guides the commercial preparation of Er3+/Yb3+ co-doped lead phosphate glasses and active optoelectronic devices.

2 Materials and methods

2.1 Er3+/Yb3+doped lead phosphate glasses preparation

Glass sample with the composition of 47P2O5−23Na2O−6Al2O3−22PbO−0.5Er2O3−1.5Yb2O3 was prepared by the quenching melting method at 1100 °C at a muffle furnace during the melting process, the molten sample was stirred two times to obtain homogeneity for the molten components of the glassy sample. The molten glassy sample was poured into preheated stainless steel frames, followed by transferring the poured sample into another furnace at 300 °C to avoid thermal stress and let to cool gradually till it reached room temperature after 24 h. The obtained sample was divided into rectangle pieces and power for different measurements [42, 43]. According to the chemical composition formula, the sample has density of 4.15 g/cm3. The raw materials used for preparation are ammonium dihydrogen phosphate, sodium carbonate, aluminum oxide, lead oxide, erbium oxide, and ytterbium oxide.

2.2 Characterization of Er/Yb-doped lead phosphate glass samples

The structures of the Er3+/Yb3+ co-doped lead phosphate glasses were examined using X-ray diffraction (XRD; Shimadzu XRD-6000, Japan) [44,45,46,47,48,49,50,51,52,53]. FTIR absorption spectra of the Er3+/Yb3+ co-doped lead phosphate glasses samples were measured via (Thermo Nicolet 380 spectrometer). In addition, the linear and nonlinear optical characteristics were determined using (Jasco, V-570) [42, 43, 45, 54, 55].

3 Results and discussions

3.1 X-ray diffraction (XRD) studies

Figure 1 demonstrates the XRD patterns of Er/Yb-doped lead phosphate glass samples. Besides a broadening hump, XRD patterns revealed no crystalline peaks, suggesting that the Er/Yb-doped lead phosphate glass samples are noticeably amorphous. The Er/Yb-doped lead phosphate glass samples showed no crystalline peaks after being irradiated with gamma radiation. As a result of the wide hump and the absence of crystalline peaks, the Er/Yb-doped lead phosphate samples have an amorphous characteristic both before and after gamma irradiation [42, 43, 56].

Fig. 1
figure 1

XRD patterns of Er/Yb-doped lead phosphate glass samples

Full size image

4 Fourier transform infra-red (FTIR) studies

Phosphorus pentoxide has a molecular formula, P4O10, but its common name is derived from the empirical formula (P2O5). Phosphate glass is inorganic polymeric [57]. Phosphate glasses have a tetrahedral structure surrounded by four oxygen atoms, and each pair can only share one oxygen ion with the other [58, 59]. In the phosphorus tetrahedral structure, three oxygen atoms bridge to neighboring tetrahedral, and the fourth is considered non-bridging oxygen (P = O) [60].

It is based on the concept that phosphate glasses are constructed from the number of the building unit (phosphate tetrahedra) to form the structure. The PO4 unit has three bridging oxygen, which is the Q3 unit. PO4 unit with two bridging oxygen is Q2 unit (metaphosphate). PO4 unit, which has one bridging oxygen, is Q1 (pyrophosphate). However, the PO4 unit with no bridging oxygen is Q0 (orthophosphate) [61].

The tetrahedral form results from SP3 hybrid orbitals by outer electrons (3S2, 3P3), and the fifth ʹe is promoted to the third orbital to form a strong П bond with oxygen 2P electrons. The tetrahedral links from covalent bridging oxygen can form different phosphate anions. The classification of the different tetrahedral phosphate anions (Qn) according to BOs can be represented in Ref. [62].

Figure 2 shows FTIR spectra of Er/Yb-doped lead phosphate glass, whereas Table 1 illustrates the IR absorption peaks assignment for the investigated sample and compares it with other previously prepared phosphate glasses [27, 63, 64]. The spectra show two main areas; one is specific for phosphate groups located in the range from 400 to 1600 cm−1, and the other is specific for OH molecules from 1640 to 4000 cm−1.

Fig. 2
figure 2

FTIR spectra of Er/Yb lead phosphate glass samples

Full size image
Table 1 Assignment of vibrational modes of Er/Yb lead phosphate glass
Full size table

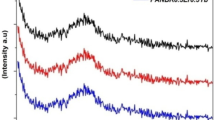
Figure 3a–d shows deconvoluted FTIR spectra of Er/Yb-doped lead phosphate glass samples before and after irradiation with 20, 50, and 100 kGy. Peaks from 400–590 cm−1 give several overlapped peaks at 463, 476, 501, 534, and 564 cm−1, where 463 cm−1 is for bending vibrations of O–P–O bond and (PO2) mode of (PO3)n chain [65] and 476 cm−1 for harmonic bending of O = P–O of the main phosphate network [66], 501 cm−1 is for Pb-metaphosphate bond due to the presence of lead oxide inside the glass network, 534 cm−1 is for harmonic bending of P–O–P and PbO6 vibration mode while 564 cm−1 is for AlO6 group vibration mode [67].

Fig. 3
figure 3

Deconvoluted FTIR spectra of Er/Yb lead phosphate glass after different gamma irradiated doses: (a) 0, (b) 20, (c) 50, and (d) 100 kGy

Full size image

Another peak at 617 cm−1 may be related to bonds of Pb–O and Pb–O–P vibration from the formed (PbO4) pyramidal groups. Also, the extended peak from 710 to 890 cm−1 is observed to deconvoluted into three peaks at 712, 764, and 889 cm−1, where the peak at 712 cm−1 is for vibration in AlO4 units as a former oxide, 764 cm−1 is for symmetric vibrations of P–O–P bond in pyrophosphate (P2O7)4− units and 889 cm−1 is considered to be due to the asymmetric vibration of bridging oxygen in P–O–P bonds of different metaphosphate units in the form of a ring, terminal, and chain units.

Two deconvoluted peaks are given at 958 cm−1, associated with symmetric PO3 and Pb–O from pyramidal groups (PbO4), while the other is at 1074 cm−1 for asymmetrical vibration of PO3 bonds in pyrophosphate units; this high intensity is due to Na ions. The other two deconvoluted peaks at 1150 cm−1 and 1247 cm−1 are for symmetrical and asymmetrical O–P–O bonds, respectively. Besides two peaks, one at 1383 cm−1 for (PO3)2− a terminal group that contains the doubly bonded oxygen P = O Stretching mode and 1617 cm−1 for the P−O−H bridge. All these peaks are assigned in Table 1. FTIR spectra concluded that the revealed characteristic vibrational bands are related to the presence of metaphosphates (PO2–) and pyrophosphate (PO3–) units, with the first in higher intensity.

In general, FTIR spectra of phosphate glasses are known to have several overlapped peaks, while the position of these peaks can be shifted owing to additives or the composition of the glass, as given in Table 2. Various induced defects have been detected relying on the intensity of radiation exposure and charged particle irradiation [68, 69]. Glasses often have a limited range of orders and suffer from defect sites. Suppose the energy of the photon is greater than the bandgap. In that case, electrons are liberated from the valence band, and the remaining energy will be transferred to kinetic energy if the glasses are irradiated to electromagnetic fields [68]. Consequently, the escaped electrons migrate through the glass network. They are either captured via pre-existing defects for generating induced defect centers in the glasses or generate secondary electron cascades through knock-on collision with the bound electrons throughout the terms of excess energy Compton electrons. The major vibrated groups appeared in almost the same numbers and positions upon irradiation to various gamma doses as they achieved in the non-treated sample. It reveals that the total phosphate structural units (metaphosphate (PO2–) and pyrophosphate (PO3–)) units of the investigated glasses continue to stay in overall with their arrangement typically [70]. The reduction in pyrophosphate groups and the corresponding rise in metaphosphate groups might be ascribed to the decrease in the peak intensity at 1074 cm–1 after progressive gamma irradiation doses. In addition, the shift of the peaks, which matched with a decrease in intensity at 764 cm−1 upon irradiation with different gamma doses, may be due to a change in bond angles besides the change in the bond length of the P–O–P bridges which means the glass network stability against radiation [64, 71,72,73]. Also, decreasing the intensity of the peaks in the area of 600–650 cm−1 and 900–1200 cm−1 may be attributed to the rearrangement of defects and NBO originated by irradiation that resulted in conversion from PO4 (tetrahedral groups) to PO3 units [5].

Table 2 Deconvolution parameters of the infra-red spectra of studied glasses; band center, relative area, and the amplitude for the samples bands
Full size table

5 Linear optical properties

5.1 The absorption spectra behavior

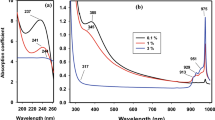
The absorption spectra of Er–Yb lead phosphate glass samples are shown in Fig. 4. For the pristine glass sample (0 kGy), the absorption bands can be categorized into three mean regions; the first one is located in the range of 190–300 nm for the oxygen deficient center (ODC), which depends on the existence of P, Pb, and Al within the matrix. Along with the presence of Yb2+ and other non-bridging oxygen hole centers (NBOC), this region is believed to be responsible for the photodarkening effect (PD) in optical amplifier glasses. Second region; show small bands at about 378 and 522 nm were assigned to transitions from ground-state 4I15/2 to 2H7/2 and 4F9/2 excited states of Er3+. The last region is for absorption peak at ~ 978 nm is ascribed to (2F7/2 → 2F5/2) of Yb3+ [74,75,76,77]. In general, irradiation causes the electrons that are already present in the glass matrix to get excited, and these excited electrons have the potential to eject themselves in accordance with the dosage, therefore, increasing the number of NBOs. Irradiation causes some of these electrons to get excited, and some of those electrons may be utilised to heal defects that are already present in the glass matrix. But in the other hand, Yb ions have the ability to captivate these electrons in during charge transfer (CT) process between Yb and Er, which will also assist in returning some of the NBOs to the BOs and beginning to form more covalent bonds between the cations and the O2− as observed by a reduction in the intensity of the bands with a small lower shift in the wavelength in the first region upon 20 and 100 kGy. The second and third areas do not produce any shift in the wavelength; rather, a rise in the band intensities is the only change that can be seen.

Fig. 4
figure 4

Absorbance spectra of Er–Yb lead phosphate glass samples

Full size image

5.2 The spectral distribution of absorption index

The extinction coefficient (k) can be deduced as a function of the absorbance coefficient α (λ) [78,79,80].

$$k=\frac{\alpha \lambda }{4\pi }$$
(1)

The extinction coefficient (k) spectra of Er/Yb lead phosphate glass samples are presented in Fig. 5. The spectral behavior of k has been observed to be influenced by gamma dosages. Irradiation of Er/Yb lead phosphate glass decreases the absorption index but has little effect on the spectra’ peak position of absorption bands. Also, it is worth noting that the value of k has never approached zero. This behavior might be considered a unique feature of free carriers’ appearances.

Fig. 5
figure 5

The extinction coefficient (k) spectra of Er/Yb lead phosphate glass samples

Full size image

5.3 The refractive index spectra (n)

The refractive index (n), which is controlled by the interaction of light with the electrons of the component atoms of the glass, is another essential characteristic of the optoelectronic properties of the studied glass. It is influence by oxides in the glass sample, cationic polarizability, and radiation doses. The rise in NBOs, created due to the effect of gamma radiation, increases the refractive indices of a standard glass system.

The following expression can derive the refractive index (n) of Er/Yb lead phosphate glass samples [78,79,80].

$$n=\frac{1+R}{1-R}+\sqrt{\frac{4R}{(1-R{)}^{2}}-{k}^{2} }$$
(2)

The spectra of the refractive index, n, for Er/Yb lead phosphate glass samples are seen in Fig. 6. We found that the value of n changes slightly after irradiation in all wavelength ranges. Also, the absorption peaks were shifted to higher wavelengths with increasing gamma radiation doses.

Fig. 6
figure 6

The refractive index spectra, n, of Er/Yb lead phosphate glass samples.

Full size image

5.4 Urbach and optical bandgap energies

The Urbach energy, Eu, may be derived in the low incident photons energy spectrum through graphing the relationship between lnα and hν (see Fig. 7) [81]:

Fig. 7
figure 7

Plot of Ln(α) vs. (hν) for Er/Yb lead phosphate glass samples.

Full size image
$$\mathrm{ln} \, \alpha =\mathrm{ln}\,{\alpha }_{0}+\frac{h\nu }{{E}_{u}}$$
(3)

The Urbach energy (Eu) values of Er/Yb lead phosphate glass samples are summarized and tabulated in Table 3. We will see that enhanced doses of up to 50 kGy improve the Urbach energy of Er/Yb lead phosphate glass samples and then declines at a dose of 100 kGy. That means the increase in the depolymerization of the glassy network up to 50 kGy making the glass samples less compacted due to more formation of NBOs amount. The Eu of Er/Yb lead phosphate glass samples increases from 10.23 eV for the pristine glass sample to 37.03 eV at 50 kGy.

Table 3 The optical bandgap Eg, Urbach energy Eu, and the dispersion parameters for the Er/Yb lead phosphate glass samples
Full size table

Using the Tauc relation, the optical band gap energy of Er/Yb lead phosphate glass samples was related to \(\alpha\) and \(h\nu\)[82]:

$$\alpha h\nu ={A(h\nu -{E}_{g})}^{t},$$
(4)

in which A is a constant, t denotes the transition type, and Eg represents the energy gap

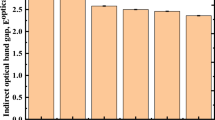
As shown in Fig. 8, the direct optical band gap energy, Eg, may be calculated by graphing (αhν)2 as a function of (hν) for Er/Yb lead phosphate glass samples. Table 3 lists the values of the energy band gaps for direct transitions. We note that by increasing the irradiation doses up to 50 kGy, a decrease in the energy gap was observed and then increased at the dose of 100 kGy. The direct optical band gap energy decreased from 4.11 eV for pristine Er/Yb lead phosphate glass to 3.42 eV at 50 kGy. These results agree with previous findings of Urbach’s energy behavior. That may explained as by increasing gamma doses, the amount of created excited electrons and non-bridging oxygen increased and moved through the already excited defects inside lead phosphate glass sample that act as tunnels between energy levels till reach 100 kGy where the excited electrons being to be captured by converting NBOs to BO that reduce the amount of net empty defects.

Fig. 8
figure 8

(αhν)2 vs. (hν) for Er/Yb lead phosphate glass samples

Full size image

A material’s optical density (Dopt) is related to its thickness and absorption coefficient. The present glass system's optical density (Dopt) may be computed using the formula below [34]:

$$D_{opt} = \alpha (v)r,$$
(5)

in which, r is the thickness of the sample.

Figure 9 illustrates the optical density (Dopt) spectrum of Er/Yb lead phosphate glass samples. The optical density of the synthetic glass rises as gamma radiation exposures rise. This rise caused the wide near-visible band to shift in the direction of a higher wavelength, which was generated by a reduction in the bandgap.

Fig. 9
figure 9

The optical density (Dopt) spectrum of Er/Yb lead phosphate glass samples

Full size image

5.5 Dispersion and the dielectric performance

The dispersion behavior plays a very important role in assessing optical materials since it is a vital factor in optical communication and the manufacturing of spectral dispersion technologies.

The single oscillator model could be used to calculate the oscillator energy Eo, dispersion energy Ed, and static dielectric constant (ε∞ = n2) for Er/Yb lead phosphate glass samples, which can then be expressed using Wemple and DiDomenico formula [83].

The relationship between (n2−1)−1 and (hν)2 for Er/Yb lead phosphate glass samples is seen in Fig. 10. Table 3 validates the (Eo, Ed, and ε∞) values. Increased the irradiated dosages up to 50 kGy resulted in a significant rise in these values, which subsequently reduced at 100 kGy. The oscillator energy Eo was found between 1.55 to 1.62 eV. Also, the dispersion energy Ed ranged from 2.11 eV at 100 kGy to 2.71 eV at the dose of 50 kGy. We observed that the dispersion constants values had been empirically related to the bandgap variation [84]. Also, the static dielectric constant varied between 2.36 and 2.66.

Fig. 10
figure 10

(n2−1)−1 vs. (hν)2 for Er/Yb lead phosphate glass samples

Full size image

The percentage of free carrier ions to effective mass (N/m*) is reliant on the lattice dielectric constant (ε), wavelength λ, and the refractive index [85]:

$${n}^{2}-{k}^{2}={\varepsilon }_{l}-\left(\frac{{e}^{2}}{4{\pi }^{2}{\varepsilon }_{0}{c}^{2}}\right)\left(\frac{N}{{m}^{*}}\right){\lambda }^{2}.$$
(6)

The relationship between (n2−k2) vs. λ2 for Er/Yb lead phosphate glass samples is seen in Fig. 11. Table 4 lists the values for these parameters. The percentage of free carrier ions to effective mass (N/m*) increased with increasing gamma doses but declined at 50 kGy, where the N/m* values in the range (4.82–8.66) × 1047 cm3/g. Besides, the lattice dielectric constant (\({\varepsilon }_{l}\)) increased from 5.54 to 6.63 with increasing the gamma doses.

Fig. 11
figure 11

(n2−k2) vs. λ2 for Er/Yb lead phosphate glass samples

Full size image
Table 4 The free carrier concentration (N), (N/m*), and the lattice dielectric constant (\({{\varvec{\varepsilon}}}_{{\varvec{l}}}\)) for Er/Yb lead phosphate glass samples
Full size table

6 Nonlinear optical properties

The following expression was used to compute the nonlinear third-order optical susceptibility (χ(3)) for Er/Yb lead phosphate glass samples using linear refractive index and dispersion parameters (Eo and Ed) [86,87,88]:

$${\upchi }^{(3)}=A{\left(\frac{{E}_{o}{E}_{d}}{4\pi ({E}_{o}^{2}-{\left(h\nu \right)}^{2}}\right)}^{4},$$
(7)

where A ~ 1.7 × 10–10 esu [89].

The relationship between χ(3) and \(h\nu\) for Er/Yb lead phosphate glass samples is shown in Fig. 12. The susceptibility χ(3) is the outcome of the Er/Yb lead phosphate glass samples reaction to the impacted electric field of light. We can see from Fig. 12 that increasing gamma doses up to 50 kGy enhances the susceptibility χ(3) and then reduces at 100 kGy, so we assume that the increase of gamma doses beyond 50 kGy reduces polarizability ability. The electrical polarizability of the irradiated Er/Yb lead phosphate glass samples opens up the prospect of using them in optoelectronics applications.

Fig. 12
figure 12

The relationship between χ(3) and \(h\nu\) for Er/Yb lead phosphate glass samples

Full size image

Figure 13 demonstrates the correlation between the nonlinear refractive index and \(\lambda\) for Er/Yb lead phosphate glass samples. The nonlinear susceptibility can be used to calculate the nonlinear refractive index, n2, using the formula [86, 87]:

Fig. 13
figure 13

The correlation between the nonlinear refractive index n2 and \(\lambda\) for Er/Yb lead phosphate glass samples

Full size image
$${n}_{2}=\frac{{12\mathrm{\pi \chi }}^{(3)}}{{n}_{o}}.$$
(8)

We can see that from Fig. 13 that increasing gamma doses up to 50 kGy reduces the nonlinear refractive index, n2, and then improves at 100 kGy,

The nonlinear absorption coefficient βC spectra for Er/Yb lead phosphate glass samples were based on their band structure. It controls the energy states and may well be derived using the formula [86, 87]:

$${\beta }_{c}=\frac{{K}_{c }{E}_{p}^{1/2}F}{{n}^{2}{E}_{g}^{3}},$$
(9)
$$F=\frac{{\left(\frac{2h\nu }{{E}_{g}}-1\right)}^{3/2}}{{(2h\nu /{E}_{g})}^{5}}.$$
(10)

Kc is constant (3100 cm/GW), Ep is the Kane energy, and the dispersion of absorption coefficient is denoted by F, which is related to photon energy. The nonlinear absorption coefficient βC varied as the gamma doses enhanced (Fig. 14).

Fig. 14
figure 14

The nonlinear absorption coefficient βC spectra for Er/Yb lead phosphate glass samples

Full size image

7 Conclusion

The purpose of this study was to reveal the effect of gamma rays on the Er/Yb lead phosphate glass system’s physical, structural, linear, and nonlinear optical characteristics. The Er/Yb lead phosphate glass’s amorphous nature was verified using XRD patterns. FTIR spectra likewise reveal the resistance of Er/Yb lead phosphate glass against radiation with slight adjustments in the intensities of specific bands. The Eu value of Er/Yb lead phosphate glass samples increases from 10.23 eV for the pristine glass sample to 37.03 eV at 50 kGy. Also, the direct optical band gap energy decreased from 4.11 eV for pristine Er/Yb lead phosphate glass to 3.42 eV at 50 kGy. The oscillator energy Eo was found between 1.55 and 1.62 eV. Also, the dispersion energy Ed ranged from 2.11 eV at 100 kGy to 2.71 eV at the dose of 50 kGy. The free carrier concentration (N) increased with increasing gamma doses but declined at 50 kGy, where the percentage of free carrier ions to effective mass (N/m*) values in the range (4.82–8.66) × 1047 cm3/g. Besides, the lattice dielectric constant (\({\varepsilon }_{l}\)) increased from 5.54 to 6.63 with increasing the gamma doses. Furthermore, increasing gamma doses up to 50 kGy enhances the susceptibility χ(3) and then reduces at 100 kGy, assuming that increasing gamma doses beyond 50 kGy reduces polarizability ability. While the increasing gamma doses up to 50 kGy reduces the nonlinear refractive index and then improves at 100 kGy. Altogether, the nonlinear and linear findings demonstrate that Er/Yb lead phosphate glass could be a potential candidate for optical applications such as gain media and optical amplifiers.