Synthesis, crystal structure, thermal and dielectric properties of tetrapropylammonium tetrabromozincate [N(C₃H₇)₄]₂[ZnBr₄] compound

Abstract

The new organic–inorganic compound tetrapropylammonium tetrabromozincate [N(C₃H₇)₄]₂ZnBr₄ has been synthesized and characterized by single-crystal X-ray diffraction, differential scanning calorimetry, IR, Raman and impedance measurements. The crystal structure refinement shows that the [N(C₃H₇)₄]₂ZnBr₄ compound is crystallized in the monoclinic system (space group C_2/c) with the following unit cell parameters: a = 33.145(5) Å, b = 14.234(3) Å, c = 15.081(2) Å, β = 110.207(5)° and Z = 8. The structural arrangement of the title compound can be described as an alternation of organic and inorganic layers along the [100] direction. Differential scanning calorimetry disclosed two order–disorder transition phases located at 340 and 393 K. Besides, an analysis of the dielectric constants ε′ and ε″, at several frequencies, shows a distribution of relaxation times. This relaxation is probably due to the reorientational dynamics of alkyl chains.

1 Introduction

Recently, attention has been drawn to a novel class of open-framework materials, namely organic–inorganic hybrid materials. These materials exhibit specific properties, such as electronic, optical, thermal and catalytic, since they combine both inorganic and organic properties [1, 2]. Inorganic materials offer the potential for a wide range of electronic properties, magnetic and dielectric transitions, substantial mechanical hardness and thermal stability, and the organic materials can provide high fluorescence efficiency, large polarizability and plastic mechanical properties [3, 4]. Moreover, the non-covalent interactions, usually observed in hybrid materials, are some of the most powerful forces to organize structural units in both natural and artificial systems, and they have important effects on the organization and properties of many materials in areas such as biology, crystal engineering and material science [5–9]. Considerable interest has been devoted to the compounds of the general formula AMX₄, where A is an organic cation, M a divalent metal (M: Zn, Cd, Cu, Mn…) and X a halogens (X: Cl, Br, and I) can be described as a sequence of alternating organic–inorganic layers. Many of these compounds exhibit successive structural phase transitions, which are associated with the reorientational dynamics of organic and inorganic part.

In this context, the present work is devoted to the synthesis, crystal structure, IR, Raman, scanning calorimetry (DSC) and dielectric proprieties on a new tetrapropylammonium tetrabromozincate [N(C₃H₇)₄]₂[ZnBr₄] sample.

2 Experimental procedures

White prismatic monocrystals of [N(C₃H₇)₄]₂ZnBr₄ compound are obtained by slow evaporation at room temperature of the aqueous solution formed by ZnBr₂ (purity 98%;) and [N(C₃H₇)₄]Br (purity 97%; FLUKA) in a molar ratio of 1:1. The reaction sequence for the synthesis is shown in the following equation:

$$2\left[ {{\text{N}}\left( {{\text{C}}_{3} {\text{H}}_{7} } \right)_{4} } \right]{\text{Br}} + {\text{ZnBr}}_{2} \,\mathop{\longrightarrow}\limits^{{\text{H}}_{2}{\text{O}}}\,\left[ {{\text{N}}\left( {{\text{C}}_{3} {\text{H}}_{7} } \right)_{4} } \right]_{2} {\text{ZnBr}}_{4}$$

X-ray structural analysis was performed on a single crystal selected with an optical microscope. The intensity data are collected on a Bruker AXS CCD area detector system equipped with graphite monochromatic MoK_α radiation (0.71073 Å) at room temperature. A total of 6063 independent reflections were collected using the ω–2θ scan technique of which 2900 have I > 2σ(I) and are used for the structure determination. Then, the structure was solved by the Patterson method using SHELXS-97 [10] and refined by SHELXL-97 [11] programs, which readily establishes the heavy atom positions and facilitates the identification of the light atoms from different Fourier maps. We note that four carbon atoms of [N(3)(C₃H₇)₄]⁺ cation are disordered. As soon as the duplication tentative of these atoms is not successful, the structure is solved with four constraints imposed on atom distances.

On the other hand, the calorimetric measurements are taken on PerkinElmer DSC-7 from 300 up to 440 K at an average heating of 5° per min with 15 mg sample weight. The infrared spectrum is obtained using a PerkinElmer FTIR 1000 spectrometer with a sample pressed in KBr pellet in the 450–4000 cm⁻¹ region. The Raman spectrum of the sample is obtained under the microscope with a T-64000 Raman spectrometer (ISA, Jobin–Yvon) with nitrogen-cooled CCD detector, in the frequency 50–3500 cm⁻¹ region with 1800 tr per mm.

The dielectrical measurements are taken using a two-electrode configuration. In fact, the [(C₃H₇)₄N]₂ZnBr₄ sample is pressed into pellets of 8 mm in diameter and 1.1 mm in thickness using 3 t cm⁻² uniaxial pressures.

The AC impedance data, |Z|, and phase angle are obtained in the frequency range of 20 Hz–1 MHz using Agilent 4284A LCR impedance analyzer over the temperature range of 303–403 K.

3 Results and discussion

3.1 Structure description

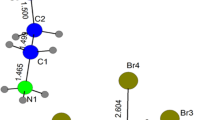
At room temperature, the title compound crystallizes in the monoclinic system (C_2/c space group) with the following unit cell parameters: a = 33.145(2) Å, b = 14.234(3) Å, c = 15.081(2) Å and β = 110.23(0)°. Diamond computer program is used to prepare the drawings. The crystal data collected reflections and the parameters of the final refinement are gathered in Table 1. The interatomic bond distances and angle schemes are listed in Table 2. It should be mentioned that atomic coordinate anisotropic displacement parameters, tables for all bond distances, and angles are deposited at the Cambridge Crystallographic Data Center (deposition number CCDC 861352). The crystallographic analysis of this compound reveals that the crystal structure of [(C₃H₇)₄N]₂ZnBr₄ consists of one and two halves of [N[(C₃H₇)₄]⁺ and one of ZnBr₄ inequivalent groups.

Table 1 Crystal data and structure refinement for [N(C₃H₇)₄]₂ZnBr₄

Table 2 Principal intermolecular distances (Å) and angles (°) for anionic part [ZnBr₄]²⁻and cationic part [N(C₃H₇)₄]⁺

A view of the asymmetric unit of the structure showing the thermal ellipsoid atom mean-square displacements of non-hydrogen is depicted in Fig. 2. The structural arrangement of the title compound can be described as an alternation of organic and inorganic layers along the [100] direction, made up of [N(C₃H₇)₄]⁺ and [ZnBr₄]²⁻ atom groups, as shown in Fig. 1, respectively. The inorganic groups are located in the (100) plane at a = 1/8 and 3/8 sandwiched between two different organics sheets. The first, which is localized at a/8, is made up of [N(2)(C₃H₇)₄]⁺ characterized by C₁ punctual symmetry, whereas the second observed at the origin is formed by two inequivalent cations [N(1)(C₃H₇)₄]⁺ and [N(3)(C₃H₇)₄]⁺. Both ammoniums present C₂ punctual symmetry. The crystal package is provided by van der Waals and ionic interaction.

Fig. 1

[010] view showing alternation of organic and inorganic sheets of [N(C₃H₇)₄]₂ZnBr₄

Fig. 2

Representation of asymmetric unit with 50% probability of the thermal ellipsoid of non-hydrogen atoms of [N(C₃H₇)₄]₂ZnBr

3.1.1 Geometry of the ZnBr ²⁻₄ anion

The zinc atom is tetrahedrally coordinated by bromine atoms. The Zn–Br bond lengths are from 2.401(2) to 2.430(2) Å. The Br–Zn–Br angles are in the range of 106.97(7)–112.16(7)°, as listed in Table 2. The average values of the distortion parameters of ZnBr ²⁻₄ tetrahedron are calculated, respectively, using Eqs. (1) and (2) [12]:

$${\text{ID}} \left( {{\text{Br}}-{\text{Zn}}-{\text{Br}}} \right) = \sum\limits_{i = 1}^{n1} {\frac{|ai - am|}{n1\,am}}$$

(1)

$${\text{ID}} \left( {{\text{Zn}}-{\text{Br}}} \right) = \sum\limits_{i = 1}^{n2} {\frac{|di - dm|}{n2\,dm}}$$

(2)

with a: (Br–Zn–Br) angle, d: (Zn–Br) distance, m: average values, n1 = 4 and n2 = 6. ID (Zn–Br–Zn) = 0.009, ID (Zn–Br) = 0.0042. The low values of the distortion indices indicate that the coordination geometry of the metal is pseudo-regular tetrahedron.

3.1.2 Geometry of the (C₃H₇)₄N⁺ cation

The organic part of [N(C₃H₇)₄]₂ZnBr₄ compound shows three inequivalent cations: N(1)(C₃H₇) ⁺₄ , N(2)(C₃H₇) ⁺₄ and N(3)(C₃H₇) ⁺₄ with C₂, C₁ and C₂ punctual symmetry, respectively, as shown in Figs. 3 and 4. The details of the principal inter-atomic distances and angles are gathered in Table 2. Chain alkyls of the first cation show a trans configuration, whereas other cations are in gauche configuration. With the exception of the third cation, the CC and CN distances and C–N–C, C–C–C and C–C–N angles are normal and usually observed. The observed distances and angles N(3)(C₃H₇) ⁺₄ are more dispersed and vary from 1.335 to 1.444 Å and from 103.3° to 141.0°, respectively. This dispersion is related to the disorder of this cation. In the literature, the range of distances and angles is observed on other chain alkyls.

Fig. 3

TPAZnBr N1 cross-configuration

Fig. 4

TPAZnBr N2 and N3 broken configuration

3.2 Calorimetric study

Figure 5 shows the DSC runs for [(C₃H₇)₄]₂ZnBr₄ upon the heating a sample (15 mg) with a scanning rate (5°min⁻¹). An overview of the results obviously shows the existence of two distinct endothermic peaks detected at 340 and 393 K corresponding to the phase transition. Enthalpy and entropy of the first phase transition are 3.838 k J mol⁻¹ and 11.32 J mol⁻¹ K⁻¹, respectively. However, those of the second phase transition are 4.101 k J mol⁻¹ and 10.41 J mol⁻¹ K⁻¹, respectively. These experimentally observed entropies can be interpreted in terms of Boltzmann’s principle ΔS = R Ln Ω = R Ln N1\N2 where N1 and N2 are the number of distinguishable orientations allowed in the high- and low-temperature phases [13]. At 340 and 393 K, the Nl/N2 ratio is equal to 4 and 3.5, respectively. Taking into account the transition entropy values, both phase transitions may be classified as “order–disorder” phase transition.

Fig. 5

DSC thermograms of [N(C₃H₇)₄]₂[ZnBr₄] compound

3.3 Infrared and Raman spectra

To gain more information about the crystal structure, we have undertaken a vibrational study using infrared spectroscopy and Raman scattering. The infrared and Raman spectra of the studied compound at room temperature are shown in Figs. 6 and 7, respectively. The assignments of the observed bands are realized by comparison with similar compounds [14–20]. Besides, the wave numbers of the registered peaks are quoted in Table 2. The bands observed at 2969 and 2988 cm⁻¹ in IR and Raman, respectively, are accredited to the asymmetric ν_as(CH₃) stretching mode. Concerning the CH stretching vibrations ν_s(CH₂) + ν_s(CH₃), they are observed at 2881 cm⁻¹ in IR. The band that appears at 1469 and 1463 cm⁻¹ in IR and Raman, respectively, is related to the asymmetric deformation δ _as(CH₃), whereas the bands that appeared at 1376 and 1326 cm⁻¹ in IR can be assigned to the symmetric deformation δ _s(CH₃) and to the ω(CH₂) wagging modes, respectively, while the weak bands observed around 1173 are assigned to the ρr (CH₃) methyl rocking modes [16, 26]. The frequencies observed at 1177 and 852 cm⁻¹ in infrared are related to the rocking ρ _r(CH₃) vibration modes. The splitting (C–C–C–N) and the blending mode at 1134 cm⁻¹ may correspond to different conformers of organic chains. The bands observed at 1116 cm⁻¹ are assigned to ν₁(NC₄) stretching modes. Moreover, the weak peak in the infrared spectrum at 1044 cm⁻¹ is related to the bending mode [ν_s(C–C–N)] [21–25]. The band observed around 970 and at 921 cm⁻¹ is assigned to ν₁(NC₄) stretching modes. A weak band that appeared at 874 cm⁻¹ is related to the ρ _r(CH₃) + ρ _r(CH₂) rocking vibration mode [16]. The deformation mode ν₃(NC₄) appears at 762 cm⁻¹ in IR. The deformation mode ν₂(NC₄) appears below 750 cm⁻¹. The band observed at 515 cm⁻¹ in IR is accredited to the ν₁₁(B_2g) stretching mode. The bands corresponding to the internal vibrational modes of the anions: ν₁, ν₂, ν₃ and ν₄ (ZnX₄) (where X = Cl and Br) appear in the spectral region below 300 cm⁻¹. The band appearing at 193 cm⁻¹ is assigned to the ν₃(ZnBr₄) mode and can be used to confirm the presence of the ZnBr₄ group in this compound.

Fig. 6

Infrared spectrum of [N(C₃H₇)₄]₂ [ZnBr₄] compound

Fig. 7

Raman spectra of [N(C₃H₇)₄]₂[ZnBr₄]

3.4 Dielectric properties

The temperature dependence of the real ε′ and imaginary ε″ parts of the dielectric permittivity of TPA₂ZnBr₄ at different frequencies is shown in Figs. 8 and 9, respectively. It is clear from these figures that there are three regions, region I (T < 340), region II (340 < T < 393) and region III (T > 393).

Fig. 8

Temperature dependence of the real part of the permittivity at various frequencies

Fig. 9

Temperature dependence of the imaginary part of the permittivity at various frequencies

At T < 340, the variations of ε′ and ε″ with temperature are almost constant. This may be explained by the restricted reorientational motions of the cation, which cannot orient themselves with respect to the direction of the applied electric field, but they acquire a weak contribution to polarization.

Over the transition temperature, T > 340 K, the reorientational dynamics of alkyl chains is activated. The cation gets enough excitation thermal energy to be able to obey the change in the external electric field more easily. This in return enhances their contribution to the polarization leading to an increase in dielectric behavior.

At T > 393, an asymmetrical dielectric loss peak is observed. This anomaly may be due to disorder in the lattice caused by the reorientational motion of the alkyl chains [27], which weakens the van der Waals interaction between the ions that departs to another unit cell and leaves a vacancy behind [28].

This dielectric anomaly appears when the jumping frequency of localized charge carriers becomes approximately equal to that of the externally applied in the electric field. Furthermore, as the frequency increases, the peak located at 393 K becomes less pronounced. This can be explained by the fact that beyond a certain frequency of external field, the charge carriers cannot follow the alternating electric field.

The dielectric relaxation is described by a non-Debye model, which gives the frequency a dependent complex permittivity in the form of [ 29, 30]:

$$\varepsilon^{*} (\omega ) = \varepsilon_{\infty } + \frac{{\varepsilon_{\text{s}} - \varepsilon_{\infty } }}{{1 + \left( {j\frac{\omega }{{\omega_{1} }}} \right)^{1 - \alpha } }} + \frac{{\sigma_{0} }}{{j\varepsilon_{0} \omega }}$$

(3)

The imaginary part of ε* is:

$$\varepsilon^{{\prime \prime }} (\omega ) = \frac{{(\varepsilon_{\text{s}} - \varepsilon_{\infty } )\left( {\frac{\omega }{{\omega_{1} }}} \right)^{1 - \alpha } \sin \left( {\frac{(1 - \alpha )\pi }{2}} \right)}}{{1 + 2\left( {\frac{\omega }{{\omega_{1} }}} \right)^{1 - \alpha } \cos \left( {\frac{(1 - \alpha )\pi }{2}} \right) + \left( {\frac{\omega }{{\omega_{1} }}} \right)^{2(1 - \alpha )} }} + \frac{{\sigma_{0} }}{{\varepsilon_{0} \omega }}$$

(4)

where ε _s is the static permittivity, ε _∞ is the permittivity at “infinitely” high frequency, ε ₀ is the permittivity of the free space, σ ₀ represents the specific conductivity, parameter α represents the tilting angle (α·π/2) of the circular arc from the real axis in the complex permittivity plane and ω is the frequency.

The first part in Eq. (4) is related to the thermal polarization and the second one to the electrical conductivity. Figure 10 shows the evolution of ε″ as a function of frequency at different temperatures. This figure shows that the imaginary part of permittivity has a low-frequency dispersive behavior when temperature increases [31]. There are no appreciable relaxation peaks in the frequency range employed in this study. Using function (4) gives a suitable fitting of the curves resulting from the experimental data.

Fig. 10

Variation of ln ε″ versus lnω at different temperatures

Figure 11 shows the tangent losses, tan δ = ε″(ω)/ε′(ω), as a function of temperatures at different frequencies. All the curves show a similar behavior that the variation of real and imaginary parts of dielectric (the presence of three regions, region I (T < 340), region II(340 < T < 393) and region III (T > 393)).

Fig. 11

Temperature dependence of the dielectric loss at various frequencies

Figure 12 shows the variation of Log (σ _dc T) with the inverse of absolute temperature (1000/T). This plot is explained by Arrhenius type. The change in the slope of the linear curve is detected around 340 and 393 K. This discontinuity is in agreement with the DSC measurements. The values of the activation energies determined in regions I, II and III are 0.27 and 1.73 and 0.45 eV, respectively.

Fig. 12

Temperature dependence of ln (σ _dc T)

4 Conclusion

The present work is devoted to the synthesis of X-ray characterization and dielectric properties of tetrapropylammonium tetrabromozincate, [N(C₃H₇)₄]₂[ZnBr₄]. The compound crystallizes at room temperature in the monoclinic system (space group C_2/c). The structural arrangement of the title compound can be described as alternation of organic and inorganic layers along the [100] direction, made up of [N(C₃H₇)₄]⁺ and [ZnBr₄]²⁻ groups. The inorganic groups are located in the (100) plane at a = 1/8 and 3/8 sandwiched between two different organics sheets. The crystal package is provided by van der Waals and electrostatic interaction. Differential scanning calorimetry revealed the presence of two order–disorder phase transitions at 340 and 393 K, resulting from the disorder of tetrapropylammonium cations. The results of the dielectric permittivity study confirm the conclusion drawn from the calorimetric measurements that the order–disorder phase transition located in the vicinity of the temperature of the dielectric relaxation is characterized by change in the dynamical state of the cations.