Stability, Periodic Solution and Kam Tori in the Circular Restricted $(N+1)$-Body Problem on ${\mathbb {S}}^3$ and ${\mathbb {H}}^3$

Abstract

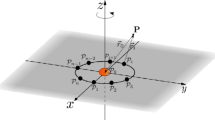
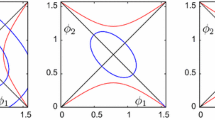
In this article, we define a circular restricted $(N+1)$-body problem on the surfaces ${\mathbb {M}}^3_{\kappa }$, with $\kappa =\pm 1$. The motion of the primaries corresponds to an elliptic relative equilibria studied in Diacu (Relative equilibria of the curved N-body problem. Atlantis Studies in Dynamical Systems, Atlantis Press, Paris, 2012), where N identical mass particles are rotating uniformly at the vertices of a regular polygon placed at a fixed parallel of a maximal sphere. By introducing rotating coordinates, this problem gives rise to a 3 d.o.f. Hamiltonian system. This problem has an equilibrium point placed at the poles of ${\mathbb {S}}^3$ and the vertex of ${\mathbb {H}}^3$, for any value of the parameters. We give information about the linear and nonlinear stability of these equilibria. Finally, we carry out a study about the existence of periodic solutions and KAM tori.

Appendices

Appendix A. Sokol’skii Stability Theorem 1977

Suppose that the Hamiltonian function in its normal form admits the following form

$$\begin{aligned} H=\frac{\delta _1}{2}q_1^2+\frac{\omega \delta _2}{2}\left( q_2^2+p_2^2\right) +\sum _{s=3}^{M}\sum _{j=0}^{[s/2]}a_{s-2j,j}\,p_1^{s-2j}\left( q_2^2+p_2^2\right) ^j+H^{M+1}+\cdots , \end{aligned}$$

where $a_{s-2j,j}$ are real constants. The normalization must be carried out up to terms of order M such that $a_{M,0}$ is different from zero.

Theorem 8

(A.G. Sokol’skii, 1977) If M is odd, the origin is a unstable equilibria solution for the system associated to H. If M is even, we have that the equilibria solution is stable if $\delta _1a_{M,0}>0$ and unstable if $\delta _1a_{M,0}<0$ (see Sokolskii 1977).

Appendix B. Perturbation Theorems

Consider the linear Hamiltonian system

$$\begin{aligned} {\dot{z}}=Az=J\nabla {\mathcal {H}}(z),\quad {\mathcal {H}}=\frac{1}{2}z^TSz, \end{aligned}$$

(58)

where S is a symmetric constant matrix and $A=JS$ is a Hamiltonian matrix.

Definition 1

(Strong stability) System (58) (or the matrix A) is strongly stable (or parametrically stable) if it and all sufficiently small linear constant Hamiltonian perturbations of it are stable. If system (58) is stable but not strongly stable, we say that it is weakly stable.

Let $\pm \alpha _1i,\,\pm \alpha _2i,\cdots ,\pm \alpha _si$ be the eigenvalues of the matrix A, and let $V_j$, $j=1,\cdots ,s$, be the maximal real linear subspace where A has eigenvalues $\pm \alpha _ji$, and ${\mathbb {R}}^{2n}=V_1\oplus V_2\oplus \cdots \oplus V_s$. Let ${\mathcal {H}}_j$ be the restriction of ${\mathcal {H}}$ to $V_j$.

Theorem 9

(Krein-Gel’fand) System (58) is strongly stable if and only if

• all the eigenvalues of A are purely imaginary,

• A is nonsingular,

• A is diagonalizable over the complex numbers, and

• Hamiltonian $H_j$ is positive or negative defined for each j.

See proof in Yakubovich and Starzhinskii (1975) or in Meyer and Offin (2017).

Let $(M,\Omega )$ be a symplectic manifold of dimension 2n, ${\mathcal {H}}_0: M \rightarrow {\mathbb {R}}$ a smooth Hamiltonian which defines a Hamiltonian vector field $Y_0 = (d{\mathcal {H}}_0)\sharp$ with symplectic flow $\phi ^t_0$. Let ${\mathbb {I}}\subset {\mathbb {R}}$ be an interval such that each $h\in {\mathbb {I}}$ is a regular value of ${\mathcal {H}}_0$ and ${\mathcal {N}}_0(h) = {\mathcal {H}}^{-1}(h)$ is a compact connected circle bundle over the orbit space B(h) with projection $\pi : {\mathcal {N}}_0(h) \rightarrow B(h)$. Assume that the vector field $Y_0$ is everywhere tangent to the fibers of ${\mathcal {N}}_0(h)$, i.e., assume that all the solutions of $Y_0$ in ${\mathcal {N}}_0(h)$ are periodic. We assume that all these periodic solutions have periods smoothly depending only on the value of the Hamiltonian, i.e., the period is a smooth function $T = T(h)$ (sometimes the dependence on h will be omitted in the notation). Now we state two of Reeb’s classic theorems (Reeb 1952) in more modern terminology. The original reduction theorem is the following.

Theorem 10

The orbit space B inherits a symplectic structure $\omega$ from $(M,\omega )$, i.e., $(B,\omega )$ is a symplectic manifold.

Now look at a perturbation of this situation. Let $\epsilon$ be a small parameter, ${\mathcal {H}}_1: M \rightarrow {\mathbb {R}}$ smooth, ${\mathcal {H}}_{\epsilon } = {\mathcal {H}}_0 + \epsilon {\mathcal {H}}_1$, $Y_{\epsilon } = Y_0 + \epsilon Y_1 = d{\mathcal {H}}_{\epsilon }^{\sharp }$, ${\mathcal {N}}_{\epsilon }(h) = {\mathcal {H}}^{-1}_{\epsilon }(h)$, and $\phi ^t_{\epsilon }$ the flow defined by $Y_{\epsilon }$. We shall refer to this as the full system.

Let the average of ${\mathcal {H}}_1$ be

$$\begin{aligned} \bar{{\mathcal {H}}} = \frac{1}{T}\int _0^T {\mathcal {H}}_1\left( \phi ^t_0\right) {\text {d}}t, \end{aligned}$$

which is a smooth function on B(h), and let ${\bar{\phi }}^t$ be the flow on B(h) defined by ${\bar{Y}} = d\bar{{\mathcal {H}}}^{\sharp }$. We refer to this as the reduced system. A critical point of $\bar{{\mathcal {H}}}$ is nondegenerate if the Hessian at the critical point is nonsingular.

Theorem 11

If $\bar{{\mathcal {H}}}$ has a nondegenerate critical point at $\pi (p) = {\bar{p}}\in B$ with $p \in {\mathcal {N}}_0$, then there are smooth functions $p(\epsilon )$ and $T(\epsilon )$ for $\epsilon$ small with $p(0) = p$, $T(0) = T$, and $p(\epsilon ) \in {\mathcal {N}}_{\epsilon }$, and the solution of $Y_{\epsilon }$ through $p(\epsilon )$ is $T(\epsilon )$-periodic.

Let the characteristic exponents of the critical point ${\bar{Y}}({\bar{p}})$ be $\lambda _1,\cdots ,\lambda _{2n-2}$. Then the characteristic multipliers of the periodic solution through $p(\epsilon )$ are

$$\begin{aligned} 1, 1, 1 + \epsilon \lambda _1T + {\mathcal {O}}\left( \epsilon ^2\right) ,\,1 + \epsilon \lambda _2T + {\mathcal {O}}\left( \epsilon ^2\right) ,\cdots ,1 + \epsilon \lambda _{2n-2}T + {\mathcal {O}}\left( \epsilon ^2\right) . \end{aligned}$$

Theorem 12

Let p and ${\bar{p}}$ as in the previous theorem. If one or more of the characteristic exponents $\lambda _i$ is real or has nonzero real part, then the periodic solution through $p(\epsilon )$ is unstable. If the matrix A is strongly stable, then the periodic solution through $p(\epsilon )$ is elliptic, i.e., linearly stable.

The proofs of Theorems 11 and 12 appear in Yanguas et al. (2008).

For a Hamiltonian with high degeneracy we will use results due to Han, Li and Yi. Starting with a Hamiltonian system of the form

$$\begin{aligned} {\mathcal {H}}(I,\varphi ,\epsilon )=h_0\left( I^{n_0}\right) +\epsilon ^{m_1}h_1\left( I^{n_1}\right) +\cdots +\epsilon ^{m_a}h_a\left( I^{n_a}\right) +\epsilon ^{m_a+1}p(I,\varphi ,\epsilon ), \end{aligned}$$

(59)

where $(I,\varphi )\in {\mathbb {R}}^n\times {\mathbb {T}}^n$ are action-angle variables with the standard symplectic structure $dI\wedge d\varphi$, and $\epsilon > 0$ is a sufficiently small parameter. The Hamiltonian ${\mathcal {H}}$ is real analytic in $(I,\varphi ,\epsilon )$ and in particular p is a smooth in $\epsilon$. The parameters $a, m, n_i$ $(i = 0,1,\cdots ,a)$ and $m_j$ $(j = 1,2,\cdots ,a)$, are positive integers satisfying $n_0 \le n_1 \le \cdots \le n_a = n$, $m_1\le m_2 \le \cdots \le m_a = m$, $I^{n_i}=(I_1,\cdots ,I_{n_i})$, for $i = 1,2,\cdots ,a$.

The Hamiltonian ${\mathcal {H}}(I,\varphi ,\epsilon )$ is considered in a bounded closed region $Z\times {\mathbb {T}}^n \times [0,\epsilon ^*]\subset {\mathbb {R}}^n \times {\mathbb {T}}^n\times [0,\epsilon ^*]$ for some fixed $\epsilon ^*$ with $0< \epsilon ^* < 1$. For each $\epsilon$ the integrable part of ${\mathcal {H}}$,

$$\begin{aligned} X_{\epsilon }(I) = h_0\left( I^{n_0}\right) + \epsilon ^{m_1}h_1\left( I^{n_1}\right) +\cdots + \epsilon ^{m_a}h_a\left( I^{n_a}\right) , \end{aligned}$$

admits a family of invariant n-tori $T^{\epsilon }_{\zeta } = \{\zeta \} \times {\mathbb {T}}^n$ with linear flows $\{x_0 +\omega ^{\epsilon }(\zeta )t\}$, where, for each $\zeta \in Z$, $\omega ^{\epsilon }(\zeta ) = \nabla X_{\epsilon }(\zeta )$ is the frequency vector of the n-torus $T^{\epsilon }_{\zeta }$ and $\nabla$ is de gradient operator. When $\omega ^{\epsilon }(\zeta )$ is nonresonant, the flow on the n-torus $T^{\epsilon }_{\zeta }$ becomes quasi-periodic with slow and fast frequencies of different scales. We refer to the integrable part $X_{\epsilon }$ and its associated tori $\left\{ T^{\epsilon }_{\zeta }\right\}$ as the intermediate Hamiltonian and tori, respectively.

Let ${\bar{I}}^{n_i} = \left( I_{n_{i-1}+1},\cdots ,I_{n_i}\right)$, $i = 0,1,\cdots ,a$ (where $n_{-1} = 0$, hence ${\bar{I}}^{n_0} = I^{n_0}$), and define

$$\begin{aligned} \Omega = \left( \nabla _{{\bar{I}}^{n_0}}h_0\left( I^{n_0}\right) ,\cdots ,\nabla _{{\bar{I}}^{n_a}} h_a\left( I^{n_a}\right) \right) \end{aligned}$$

such that for each $i = 0,1,\cdots ,a$, $\nabla _{{\bar{I}}^{n_i}}$ denotes the gradient with respect to ${\bar{I}}^{n_i}$. The following theorem gives the right setting in which one can ensure the persistence of KAM tori for the Hamiltonian (59).

Theorem 13

(Han et al. 2010) Let $\delta$ be given with $0< \delta < 1/5$. Assume there is a positive integer s such that

$$\begin{aligned} Rank\left\{ \partial ^{\alpha }_I\Omega (I): 0 \le |\alpha | \le s\right\} = n, \quad \forall I \in Z. \end{aligned}$$

Then there exists an $\epsilon _0 > 0$ and a family of Cantor sets $Z_{\epsilon } \subset Z$, $0< \epsilon < \epsilon _0$, such that each $\zeta \in Z_{\epsilon }$ corresponds to a real analytic, invariant, quasi−periodic $n-$torus ${\bar{T}}^{\epsilon }_{\zeta }$ of the Hamiltonian (59) which is slightly deformed from the intermediate n-torus $T^{\epsilon }_{\zeta }$. The measure of $Z\backslash Z_{\epsilon }$ is ${\mathcal {O}}\left( \epsilon ^{\delta /s}\right)$ and the family $\left\{ {\bar{T}}^{\epsilon }_{\zeta }: \zeta \in Z_{\epsilon },\, 0< \epsilon < \epsilon _0\right\}$ varies Whitney smoothly.