Abstract
We study the dynamic behaviour of two viscous fluid films confined between two concentric cylinders rotating at a small relative velocity. It is assumed that the fluids are immiscible and that the volume of the outer fluid film is large compared to the volume of the inner one. Moreover, while the outer fluid is considered to have constant viscosity, the rheological behaviour of the inner thin film is determined by a strain-dependent power-law. Starting from a Navier–Stokes system, we formally derive evolution equations for the interface separating the two fluids. Two competing effects drive the dynamics of the interface, namely the surface tension and the shear stresses induced by the rotation of the cylinders. When the two effects are comparable, the solutions behave, for large times, as in the Newtonian regime. We also study the regime in which the surface tension effects dominate the stresses induced by the rotation of the cylinders. In this case, we prove local existence of positive weak solutions both for shear-thinning and shear-thickening fluids. In the latter case, we show that interfaces which are initially close to a circle converge to a circle in finite time and keep that shape for later times.
Similar content being viewed by others
1 Introduction
Taylor–Couette flows describe the dynamics of viscous fluids confined between two concentric cylinders. By the end of the nineteenth century, Couette experimentally observed that the fluid flow is steady when the relative velocity of the rotating cylinders is small and the gap between the cylinders is small compared to their radii. This is the so-called Couette flow. In 1923, Taylor proved mathematically that the Couette flow becomes unstable as soon as the relative angular velocity of the cylinders exceeds a certain critical value (Taylor 1923). The more the relative angular velocity of the cylinders is increased, the more turbulent becomes the behaviour of the flow.
There is a rich literature dealing with the dynamics of one single Newtonian fluid between two concentric rotating cylinders, both in the mathematical and the physical literature, c.f. (Baumert and Muller 1997; Chandrasekhar 1961; Chossat and Iooss 1994; Drazin and Reid 2004; Schlichting and Gersten 2000; Renardy and Joseph 1985), to mention only a few contributions. Much less has been done for the two-fluid Taylor–Couette flow. The dynamics of two immiscible Newtonian fluids in a Taylor–Couette geometry has been studied in Renardy and Joseph (1985) with a combination of analytical and numerical methods. In particular, the stability of the flows for different ranges of viscosities, densities and surface tensions of the fluids in the absence of gravity is considered. The particular setting in which one of the fluids is localised in a thin layer is considered in Pernas-Castaño and Velázquez (2020) for the case in which both fluids are Newtonian.
In the present work, we formally derive a model for the dynamics of the interface separating two immiscible viscous fluids between two concentric cylinders, where one of the fluids occupies a rather thin layer and is characterised by a non-Newtonian rheology. We also study rigorously the well-posedness of the resulting model and the long-time asymptotics of its solutions.
Two physical assumptions are crucial for the derivation of the model. First, as in Pernas-Castaño and Velázquez (2020), we assume that the dynamics of the two-fluid system is described by a small perturbation of the Taylor–Couette flow for one single fluid confined between two cylinders. Second, while the outer fluid is assumed to be Newtonian, the inner fluid is assumed to be a non-Newtonian fluid with a strain-dependent viscosity \(\mu \). We consider the setting in which the inner cylinder is at rest, while the outer cylinder rotates at a fixed angular velocity.
Originally, the dynamics of both immiscible fluids are described by a Navier–Stokes system in which gravitational effects are neglected. For different regimes of the surface tension and under the assumption that the Reynolds number is small enough to avoid the aforementioned Taylor instabilities, we study the formal asymptotic limit of a vanishing thickness of the inner fluid film. To this end, we apply the so-called lubrication approximation which has been used extensively in the literature on fluid mechanics, c.f., for instance, (Ockendon and Ockendon 1995). We also refer the reader to the papers (Giacomelli et al. 2008; Günther and Prokert 2008) for rigorous mathematical results concerning the derivation of the classical Newtonian thin-film equation, taking as a starting point the Navier–Stokes equations.
The evolution equation that we derive and study in this paper has the general form
for the thickness \(h=h(t,\theta )\) of the thin strain-dependent fluid film which separates the thicker Newtonian fluid from the internal cylinder. We assume that the non-Newtonian fluid has a general strain-dependent viscosity \(\mu =\mu \bigl (\tau _{\text {char}}\left\| \,\mathbf{D } \mathbf{u }\right\| \bigr )\), where \(\mathbf{u }\) is the velocity field of the inner non-Newtonian fluid, \(\mathbf{D } \mathbf{u }=\frac{1}{2}\bigl (\nabla \mathbf{u }+\nabla (\mathbf{u })^{T}\bigr )\) is the corresponding symmetric gradient and \(\left\| \,\mathbf{D } \mathbf{u }\right\| = \sqrt{\text {tr}(|\mathbf{D } \mathbf{u }|^2)}\). Moreover, \(\tau _{\text {char}}\) is the characteristic time of the non-Newtonian fluid, i.e. it can be thought of as a characteristic value of the strains for which the nonlinear effects in the viscosity become relevant. The key assumption in the derivation of (1.1) is that the function \(s\mapsto \mu (|s|)s,\ s \in {\mathbb {R}}\), is strictly increasing. Then, the function \(\psi \) in (1.1) is defined by means of \(\psi \bigl (\mu (|s|)s\bigr ) = s\) for \(s\in {\mathbb {R}}\). It can be seen in the derivation of (1.1) that the evolution of the interface separating the two fluids is driven by the combined action of surface tension, of the shear stress induced by the rotation of the outer cylinder, and of the characteristic stress of the non-Newtonian rheology. We are interested in the interaction of these forces and on their influence on the structure of the evolutionary equation for the thickness h of the non-Newtonian fluid. Different scaling limits for these three effects are encoded in the function \(\psi \) and the parameter \(\beta \), respectively.
We first comment on the choice of the function \(\psi \). If the effect of surface tension is comparable with the characteristic stress of the non-Newtonian fluid, we can derive and study (1.1) for general smooth functions \(\psi \). If either surface tension dominates the characteristic stress of the non-Newtonian fluid or vice versa, we chose the function \(\psi \) such that
in order to allow for an appropriate time scaling. We mention that the definition of \(\psi \) in (1.2) does also correspond to the case in which the function \(\mu \) characterising the strain-dependent viscosity of the non-Newtonian fluid is given by
Fluids whose rheology is defined by (1.3) are called Ostwald–de Waele fluids. The parameter p denotes the flow behaviour exponent. These fluids are Newtonian if \(p=1\). For \(p > 1\) the corresponding fluids are called shear-thickening as their viscosity increases with increasing shear rate. Conversely, if \(p<1\), the viscosity decreases with increasing shear rate and the fluids are called shear-thinning fluids.
The parameter \(\beta \) in (1.1) measures the ratio of surface tension and shear forces induced by the rotation of the cylinders and plays a crucial role in our analysis.
In the regime in which the surface tension, the shear stress induced by the rotation of the outer cylinder, and the characteristic stress of the non-Newtonian fluid are of the same order, we have that \(\beta > 0\) is a positive constant that depends on the radii of the two cylinders, their relative velocity and the characteristic viscosities of the two fluids. In these cases the derivation of (1.1) is valid for general smooth functions \(\mu \) and \(\psi \), respectively, under the sole assumption that the map \(s\mapsto \mu (|s|)s,\ s \in {\mathbb {R}}\), is strictly increasing. Using centre manifold theory, as developed, for instance, in Mielke (1988); Haragus and Iooss (2011), we prove in this paper that solutions to (1.1) behave, for long times, after a suitable rescaling of the variables, in a manner analogous to the solutions in the Newtonian case (\(\mu \equiv 1\) and \(\psi (s)\equiv s\) or \(p=1\)) in which (1.1) reduces to the equation
Equation (1.4) is studied in Pernas-Castaño and Velázquez (2020), where the authors observe the same asymptotic behaviour for initial interfaces close to a circle. In particular, it is shown that in the Newtonian case the solution is globally defined and the interface approaches quickly a circle which is initially not concentric with the rotating cylinders. For larger times, the centre of this circle spirals towards the common centre of the cylinders as time tends to infinity. Equation (1.4) has also been obtained in Kerchman (1995) describing the motion of a single thin fluid layer evolving on the exterior of a solid cylinder.
By a straightforward adaptation of the methods used in Pernas-Castaño and Velázquez (2020), we prove in this paper that solutions to (1.1) feature the same asymptotic behaviour as solutions to (1.4). More precisely, we prove that if the interface is initially close to a circle in \(H^1(S^1)\), it is globally defined and converges in \(H^1(S^1)\) to a circle at rate 1/t which is not concentric with the rotating cylinders. However, the centre of this circle spirals at rate \(1/\sqrt{t}\) to the common centre of the cylinders as time t tends to infinity.
If either surface tension effects dominate the effects of the characteristic stresses of the non-Newtonian rheology or vice versa, we have that \(\psi \) is given by (1.2). For both settings we study the case when the effects of surface tension dominate the shear effects due to the rotation of the cylinders. This corresponds to the asymptotic limit \(\beta \rightarrow 0\), and we obtain the evolution equation
In this regime, the effect of the shear forces induced by the rotation of the cylinders is negligible and the whole dynamics of the interface is driven by the combination of surface tension and the non-Newtonian rheology of the thin fluid film.
We prove local existence of positive weak solutions to (1.5) for general positive initial data for both shear-thinning and shear-thickening fluids. Moreover, in the shear-thickening regime (\(p>1\)), we show that if the initial interface is close to a circle, there exists a global weak solution of (1.5) with the property that it converges to a circle in finite time \(t^*< \infty \). The proof is based on the derivation of a differential inequality for a certain energy functional which implies that the energy drops down to zero as \(t\rightarrow t^*\). The main obstruction in the proof of the global existence result is the possibility of the interface touching the interior cylinder, i.e. to have \(\min h\left( t,\cdot \right) =0\) at some positive time t. In this paper, we consider only solutions of positive thickness h since we are interested in the analysis of the stability of circular interfaces. In the shear-thinning case \(p<1\), we expect the solutions to (1.5) to approach asymptotically a circle as \(t\rightarrow \infty \) with a correction given by the power-law \({\mathcal {O}}(t^{-\frac{p}{1-p}})\). However, since the techniques required to obtain this result differ much from the ones used in this paper, we do not consider this case here.
Thin-film equations the solutions of which allow for film rupture have been extensively studied in the literature, c.f. (Bernis and Friedman 1990; Beretta et al. 1995; Knüpfer 2015; Giacomelli 1999), to mention only a selection. Global well-posedness for non-negative initial data has first been proved in the seminal paper (Bernis and Friedman 1990). This topic has additionally been pursued in Bertozzi et al. (1994), where the authors also study numerically the existence of singularities in finite and infinite time. The existence of global in time weak solutions to (1.4) which allow for film rupture has been studied in Marzuola et al. (2019) for a cylindrical geometry.
We remark that the surface tension forces tend to drive the interface towards a circular shape. On the contrary, the shear induced by the rotation of the cylinders has the tendency to generate ’fingering’ and to form interfaces which differ much from a circular interface. In this paper, we consider only situations in which, for large times, the contribution due to the surface tension dominates the contribution due to the shear induced by the rotation of the cylinders. Therefore, for large times the interfaces behave asymptotically as a circle.
Note that when the shape of the interface becomes close to a circle, then the surface tension forces, reflected in the term \((\partial _\theta h + \partial _\theta ^3 h)\), do no longer yield a considerable effect on the dynamics. Therefore, for sufficiently long times, the parameter \(\beta \) reflecting the shear stress induced by the rotating cylinders gives the main contribution to the deformation of the interface. Consequently, for large times the solution behaves always as in the Newtonian case, with a viscosity coefficient depending on \(\beta \). This indicates in particular that, when the shape of the interface becomes close to a circle, then the model with \(\beta =0\) is not a good approximation anymore. Moreover, even if the interface is not close to a circle, the term \((\partial _\theta h + \partial _\theta ^3 h)\) induced by the surface tension vanishes at some points. Near those points, the effect of the term \(\beta \), reflecting the shear forces, becomes the dominant one. Consequently, this might lead to small localised effects in the solution and to the creation of boundary layer regions in which the shear stress is dominant. However, these questions are addressed in future works.
The evolution Eq. (1.1), respectively (1.5), belongs to a class of non-Newtonian thin-film equations with strain-dependent viscosity. Similar equations have been studied in different settings, for instance, in Ansini and Giacomelli (2002, 2004); King (2001a, 2001b); Lienstromberg and Müller (2020). In Ansini and Giacomelli (2004), the authors consider a single thin film occupied by a power-law fluid. The governing equation is
Note that this equation is very similar to the equation (1.5) with \(\beta =0\), except that in (1.6) the nonlinearity depends only on the third-order derivative, instead of \((\partial _{\theta }^{}h+\partial _{\theta }^{3}h)\). The authors use a two-step regularisation scheme to prove global existence of non-negative weak solutions to (1.6) for general non-negative initial data. The papers Ansini and Giacomelli (2002) and Lienstromberg and Müller (2020) deal with an Ellis thin-film equation instead of a power-law thin-film equation. This is a constitutive rheological law for shear-thinning fluids which combines a power-law behaviour with a Newtonian plateau, cf. (Matsuhisa and Bird 1965; Weidner and Schwartz 1994). In Ansini and Giacomelli (2002), the authors analyse a class of quasi-self-similar solutions describing the spreading of a droplet, whose thickness h is determined by the equation
For these solutions the presence of the non-Newtonian rheology plays a fundamental role removing the well-known no-slip paradox which arises for Newtonian fluids in the presence of contact lines. However, the non-Newtonian terms become negligible except in a small region close to the contact lines. In Lienstromberg and Müller (2020), the authors prove local existence of strong solutions to (1.7) in the case \(p \in (1/2,1)\), in which the coefficients of the highest-order terms depend only Hölder continuously on the solution.
For two-phase thin-film equations, we refer the reader to the works (Bruell and Granero-Belinchón 2019; Escher et al. 2013; Laurençot and Matioc 2017) dealing with the Newtonian case. Moreover, a wide variety of two-fluid viscous flows in many different geometrical settings is described in Joseph and Renardy (1993).
The introduction is closed by a brief outline of our work. In Sect. 2, we use lubrication approximation to formally derive the evolution Eq. (1.1) and (1.5), respectively, for the interface separating the strain-dependent thin fluid film from the Newtonian fluid film. At the end of the section, we discuss the different asymptotic limits, reflected in the choice of the function \(\psi \) and the parameter \(\beta \). The resulting evolution equations are analysed in Sects. 3 and 4. More precisely, the asymptotic limit \(\beta =0\) is treated in Sect. 3. In Sect. 3.1 we prove local existence of positive weak solutions in the shear-thinning as well as in the shear-thickening regime. In Sect. 3.2 we prove, for initial interfaces close to a circle, the existence of a global weak solution of (1.5) with the property that it converges to a circle in finite time. Finally, in Sect. 4 we study the equation for \(\beta > 0\) of order one. We use centre manifold theory, to prove the aforementioned convergence to a circular interface for long times.
2 Physical Model and Derivation of the Equations
In this section we describe the physical setting of our problem and derive the evolution Eqs. (1.1) and (1.5) for the interface separating the two fluids. These evolution equations, which contain a parameter \(\beta \) that can take the value \(\beta >0\) and \(\beta =0\) in different asymptotic limits, are analysed rigorously in the subsequent sections.
2.1 Navier–Stokes System for One Newtonian and One Non-Newtonian Fluid
We consider two immiscible fluid films confined between two concentric cylinders rotating at different angular velocities. More precisely, we denote by \(R_-, R_+ > 0\) the radius of the internal and external cylinder, respectively, both cylinders being centred at the origin. The hydrodynamic behaviour of the two fluids can be described by the Navier–Stokes equations
where \(\tilde{\mathbf{u }}^\pm ({\tilde{t}},{\tilde{x}}) = ({\tilde{u}}^\pm ({\tilde{t}},{\tilde{x}}),{\tilde{v}}^\pm ({\tilde{t}},{\tilde{x}}))\) denotes the velocity field at time \({\tilde{t}} > 0\) and position \({\tilde{x}} \in {\mathbb {R}}^2\), \({\tilde{p}}^\pm \) is the pressure and \(\rho _{\pm } \ge 0\) is the density of the inner (-), respectively outer (+) fluid. The fluid next to the internal cylinder is assumed to be non-Newtonian with a shear-dependent viscosity \({\tilde{\mu }}_-\bigl (\bigl \Vert \tilde{\mathbf{D }}^- \tilde{\mathbf{u }}^-\bigr \Vert \bigr ) > 0\). Here \(\tilde{\mathbf{D }}^- \tilde{\mathbf{u }}^-=\frac{1}{2}\bigl (\nabla \tilde{\mathbf{u }}^- + (\nabla \tilde{\mathbf{u }}^-)^T\bigr )\) denotes the symmetric gradient of the velocity field \(\tilde{\mathbf{u }}^-\) of the inner fluid and \(\bigl \Vert \tilde{\mathbf{D }}^- \tilde{\mathbf{u }}^-\bigr \Vert = \sqrt{\text {tr}(|\tilde{\mathbf{D }}^- \tilde{\mathbf{u }}^-|^2)}\). We assume that the shear stress is monotonically increasing in the shear rate, i.e. the function \(s\mapsto \mu (s)s\) is monotonically increasing on \({\mathbb {R}}\). The fluid next to the external cylinder is assumed to be Newtonian with constant viscosity \(\mu _+ > 0\). In order to describe the spatial position between the two cylinders we use polar coordinates \(\tilde{\mathbf{x }} = ({\tilde{x}},{\tilde{z}}) = (r \cos \theta , r \sin \theta ) \in {\mathbb {R}}^2\). Thus, denoting by \(d > 0\) the average height of the inner fluid film and by \(h({\tilde{t}},\theta ) > 0\) the function defining the interface, the regions filled by the respective fluid may be described by
Note that we assume the function \(h({\tilde{t}},\theta )\) being strictly positive, i.e. the interface of the two fluid films cannot touch the inner cylinder. A sketch of the problem setting may be found in Fig. 1.
The Navier–Stokes system (2.1) is complemented by the following boundary conditions. We suppose that the internal cylinder is at rest, while the external cylinder rotates counterclockwise at angular velocity \(\omega > 0\). Moreover, we assume that the fluid velocities \(\tilde{\mathbf{u }}^\pm \) of the two fluids coincide at the respective cylinders with the angular velocities at which the respective cylinder rotates. That is, we have the boundary conditions
Moreover, we assume that at the interface \(\partial {\tilde{\Omega }}\) the normal velocities of the fluids coincide with the normal velocity \(V_n\) of the interface and the tangential velocities of the fluids coincide, i.e.
Finally, denoting by \({\tilde{\Sigma }}^\pm (\tilde{\mathbf{u }},{\tilde{p}})\) the stress tensor of the respective fluid, we require the tangential stress balance condition and the normal stress balance condition to be satisfied at the interface \(\partial {\tilde{\Omega }}\). These conditions read
Here, we use the notation \(\tilde{\mathbf{n }}\) and \(\tilde{\mathbf{t }}\) for the normal vector pointing from the region \({\tilde{\Omega }}_-\) occupied by the inner fluid to the region \({\tilde{\Omega }}_+\) occupied by the outer fluid and the tangential vector at the interface, respectively. Furthermore, \({\tilde{\kappa }}\) denotes the mean curvature of the interface and \({\tilde{\gamma }}\) is the constant surface tension.
The dimensionless Navier–Stokes system. In this paper we assume that the rheology of the non-Newtonian fluid is given by a viscous coefficient \(\mu _-\bigl (\tau \bigl \Vert \mathbf{D }^- \mathbf{u }^-\bigr \Vert \bigr ) = \mu _0 {\tilde{\mu }}_-\bigl (\tau _{\text {char}}\bigl \Vert \tilde{\mathbf{D }}^- \tilde{\mathbf{u }}^-\bigr \Vert \bigr )\). The function \(s \mapsto \mu _-(s)\) is a function that can describe very complicated nonlinear behaviours. The parameter \(\mu _0\) is the characteristic viscosity of the fluid when \(\tau _{\text {char}}\bigl \Vert \tilde{\mathbf{D }}^- \tilde{\mathbf{u }}^-\bigr \Vert \) is of order one. Moreover, the parameter \(\tau _{\text {char}}\) is the characteristic time of the non-Newtonian fluid that must have unit of time for dimensional reasons. Under this assumption on \({\tilde{\mu }}_-\), we have that the viscous stresses are given by \( \mu _0{\tilde{\mu }}_-\bigl (\tau _{\text {char}}\bigl \Vert \tilde{\mathbf{D }}^- \tilde{\mathbf{u }}^-\bigr \Vert \bigr ) =\frac{\mu _0}{\tau _\text {char}}\Lambda (\tau _\text {char}\tilde{\mathbf{D }}^{-}\tilde{\mathbf{u }}^{-})\), where \(\Lambda (\mathbf{A })=\mu _-(\Vert \mathbf{A }\Vert )\mathbf{A }\) with \(\mathbf{A }\in M_{3\times 3}({\mathbb {R}})\). Note that the order of magnitude of these viscous stresses is \(\frac{\mu _0}{\tau _{\text {char}}}\) if \(\tau _{\text {char}}\bigl \Vert \tilde{\mathbf{D }}^- \tilde{\mathbf{u }}^-\bigr \Vert \) is of order one.
We now rescale the original variables in order to obtain the above Navier–Stokes system in dimensionless form. To this end, we set
Consequently, \(\varepsilon > 0\) is the dimensionless thickness of the inner fluid film. By \(\text {Re} \ge 0\) we denote the Reynolds number which defines the ratio of inertial to viscous forces.
The external characteristic time \(\tau \) is induced by the relative angular velocity of the rotating cylinders. Observe that the system is now scaled such that the internal cylinder has radius 1, while the external cylinder has radius \(\eta \) and rotates with angular velocity 1, c.f. Fig. 2. Note that the non-dimensional quantities \(\rho , \text {Re}, \tau , \eta \) and \(\mu \) do not have indices.
With this change of variables, the original Navier–Stokes system (2.1) becomes
where the regions \(\Omega _-(t)\) and \(\Omega _+(t)\), filled by the inner, respectively the outer fluid, are now given by
The dimensionless boundary conditions read
2.2 Taylor–Couette Flow and Thin-Film Approximation
As already mentioned in the introduction we are interested in the case in which the volume of the liquid film \(\Omega _-(t)\) next to the internal cylinder is rather small compared to the volume of the film \(\Omega _+(t)\) next to the external cylinder. Mathematically, this corresponds to the asymptotic limit \(\varepsilon = \frac{\mathrm{d}}{R_-} \rightarrow 0\).Footnote 1 In order to obtain a nontrivial dynamic behaviour for the interfaces, we require the surface tension to scale with the non-dimensional thickness \(\varepsilon \) like
where \(b > 0\) is a constant of order one. It is worthwhile to mention that this specific rescaling strongly effects the character of the resulting evolution equation. Taking the limit \(\varepsilon \rightarrow 0\) and using formal matched asymptotic expansions, we are able to derive explicit expressions for the pressure as well as for the velocity field of each of the fluids. Consequently, we are left with a single equation for the for the interface h separating the two fluids.
Since the numerical results in Renardy and Joseph (1985), as well as the analytic results in Pernas-Castaño and Velázquez (2020), show that the laminar flow solution, i.e. the concentric circle centred at the origin, is stable for small Reynolds number, we require \(\text {Re} = \frac{\rho _+ \omega R_-^2}{\mu _+}\) to be of order one, but small enough to avoid the appearance of the Taylor instabilities. In addition, we require the parameters \(\mu = \frac{\mu _0}{\mu _+}, \eta = \frac{R_+}{R_-}\) and \(\rho = \frac{\rho _-}{\rho _+}\) to be of order one.
The dimensionless Navier–Stokes system in polar coordinates. In order to perform the formal asymptotic analysis, we first introduce polar coordinates \(\mathbf{x } = (r \cos \theta , r \sin \theta )\) and write the velocity fields \(\mathbf{u }^\pm \) as
Componentwise, the conservation of momentum equations for the fluid next to the inner cylinder, i.e. in \(\Omega _-(t)\) in these variables, read
The conservation of momentum equation for the outer fluid in \(\Omega _+(t)\) becomes, also componentwise,
and the continuity equation transforms into
Finally, the boundary conditions in polar coordinates are given by
For convenience, we perform another change of variables and set
Therewith, the system (2.5)–(2.8) transforms as follows: The conservation of momentum equation for the inner fluid in \(\Omega _-(t)\) becomes
Similarly, for the outer fluid, we obtain the conservation of momentum equations
The continuity equation in the new variables reads
and the boundary conditions transform into
For the elements of the stress tensors, we obtain
with \(c^- = \mu \mu _-(\tau |\partial _\xi w_\theta ^-|)\) and \(c^+ = 1\). Note that \(\kappa \) is the rescaled mean curvature of the interface \(r = 1 + \varepsilon h(t,\theta )\), given by
In order to determine the equation for the evolution of the interface h, separating the two fluids, we keep only the terms of order one in \(\varepsilon \) in the system derived above.
The leading-order system. In this paragraph we consider the formal asymptotic limit \(\varepsilon \rightarrow 0\). In the literature this limiting process is also referred to as lubrication approximation. For a rigorous justification of the lubrication approximation in the Newtonian case, we refer the reader to the work (Giacomelli and Otto 2003). Taking the formal asymptotic limit \(\varepsilon \rightarrow 0\), we obtain the following system. The Navier–Stokes equations reduce to
Moreover, for the boundary conditions we obtain
where we used the coefficients of the stress tensors in the leading order. Note that we keep the \(\varepsilon \) in the last boundary condition in (2.13) since \(\gamma \) depends on \(\varepsilon \) as specified in (2.4). Recalling that the mean curvature \(\kappa \) is of order one, this results in a jump of the pressures \(P^{-} - P^+\) of order \(1/\varepsilon \). Since we assume the interface being close to a circle, cf. (2.3), to the leading order the pressure jump does not depend on \(\theta \) and hence does not have any effect on the dynamics of the interface. Nevertheless, the next-order correction of the mean curvature leads to a contribution of order \(\gamma \varepsilon ^2\) which influences the dynamics of the interface.
Determination of the pressure and the velocity field by matched asymptotic expansions. With this reduced system we are able to determine explicit expressions for the pressure \(P^\pm \) and the velocity field \((w_\xi ^\pm ,w_\theta ^\pm )\). Indeed, from (2.12)\(_1\) we deduce \(P^+ = P^+(\theta )\). Thus, integrating (2.12)\(_2\) twice with respect to \(\xi \) yields
for functions \(A^+ = A^+(\theta )\) and \(B^+=B^+(\theta )\) that are to be determined. In view of the conservation of mass equation (2.12)\(_3\) we are finally able to derive an equation for \(w_\xi ^+(\xi ,\theta )\). Summarising, for the Newtonian fluid next to the external boundary we obtain
For the fluid film next to the internal cylinder, we proceed similarly. Recall that the fluid filling \(\Omega _-(t)\) is assumed to be non-Newtonian. To leading order its viscosity is a function \(\mu _- = \mu _-(\tau |\partial _\xi w_\theta ^-|)\). In order to derive a well-posed parabolic equation for the interface separating the two fluids, we assume the shear stress \(\mu _-(\tau |\partial _\xi w_\theta ^-|)\partial _\xi w_\theta ^-\) to be a monotonically increasing function of the shear rate \(\partial _\xi w_\theta ^-\). In the leading-order approximation of the Navier–Stokes system, this yields
As for the outer fluid, the first equation implies that \(P^- = P^-(\theta )\). Thus, by integration of (2.15)\(_2\) with respect to \(\xi \) we obtain
Since \(s \mapsto \mu _-(|s|)s\) is monotonically increasing on \({\mathbb {R}}\), we can define a function \(\psi \) such that \(\psi (\mu _-(|s|)s) = s\). Hence, for all \(\xi < h\) we have
By integration of this equation with respect to \(\xi \) and exploiting the boundary condition (2.13)\(_1\), we obtain
We can now use the boundary conditions in order to determine \(A^\pm (\theta ), B^+(\theta )\) and \(C^+(\theta )\) by matched asymptotics. Since the non-Newtonian liquid film next to the internal cylinder is very thin compared the Newtonian fluid film, we may assume the velocity of the outer fluid being a small perturbation of the Taylor–Couette flow for one single fluid confined between the two cylinders. This means we assume that the angular velocity, before the change of variables, is given by
Here we used that the radius of the internal cylinder is 1, the radius of the external cylinder is \(\eta \) and the external cylinder is rotating at angular velocity \(\omega =1\), while the internal cylinder is at rest. The second-order Taylor series expansion of the Taylor–Couette flow \(u^+_{\theta }(r)\) around \(r=1\) is given by
With the change of variables introduced in (2.9), this becomes
Thus, matching (2.14) with \(w^+_\theta \), we get
and consequently, \(A^+(\theta ) = D_1 - D_2 = 2\eta ^2/(\eta ^2-1)\). Moreover, since the pressure in the Taylor–Couette flow is constant, that is \(\partial _\theta P^+(\theta ) = 0\), we have
Next, we determine \(A^-(\theta )\). To this end, observe that
thanks to the fact that the pressure \(P^+\) is constant. Therefore, the tangential-stress balance condition (2.13)\(_4\), given by
yields, to leading order,
where we set \(D = D_1 - D_2 = 2D_1 = 2\eta ^2/(\eta ^2 - 1) > 0\). Using this expression in (2.16) yields
Proceeding similarly as above, we may further determine the functions \(B^+(\theta )\) and \(C^+(\theta )\) by exploiting the different boundary conditions.
However, we do not compute the explicit expressions since they are not needed in order to determine the equation for the evolution of the interface.
Derivation of the evolution equation for h. We first recall from (2.13)\(_5\) that to leading order the normal-stress balance condition is \(\sigma _{\xi \xi }]^+_- = \gamma \kappa \). This yields \(-P^+ + P^- = \varepsilon \gamma \kappa \). Using the first-order Taylor approximation \(\kappa = 1 - \varepsilon (h + \partial ^2_\theta h) + {\mathcal {O}}(\varepsilon ^2)\) of the mean curvature (2.11) of the interface around \(\varepsilon = 0\) and the fact that \(\partial _\theta P^+(\theta ) = 0\), we obtain
Moreover, up to order \(\varepsilon \) the boundary condition (2.10) for the normal velocity of the interface may be written as
Inserting into this equation the identity
which follows from the conservation of mass, we obtain that the interface evolves according to the evolution equation
Using the representation of \(w_\theta ^-(\xi ,\theta )\), derived in (2.18), and the representation of \(\partial _\theta P^-(\theta )\), derived in (2.19), this equation may further be rewritten as
for \(t > 0,\ \theta \in S^1\).
In view of Fubini’s theorem, we find that
Consequently, the evolution Eq. (2.21) reads
for \(t > 0\) and \(\theta \in S^1\).
The evolution equation for different scaling limits. We now determine the evolution equation for different scaling limits of the surface tension forces and the shear forces induced by the rotation of the cylinder. To this end, we define the parameters
and rewrite the evolution Eq. (2.21) in terms of B and \(\beta \) as
for \(t > 0\) and \(\theta \in S^1\).
We recall that, in this paper, we consider only the regime in which the radii of the cylinders are of the same order but such that the two cylinders are not too close to each other. Therefore, \(D > 0\) is just a non-dimensional geometrical constant. We now discuss the structure of the equation for different ranges of the parameters B and \(\beta \). To this end, note first that, in physical variables, B and \(\beta \) are given by
respectively, where we used the scaling for \({\tilde{\gamma }}, \tau , \text {Re}\) and \(\mu \) introduced in (2.2). Thus, the parameter B reflects the ratio of the shear forces induced by the surface tension over the characteristic shear \(\frac{\mu _0}{\tau _{\text {char}}}\) associated to the non-Newtonian fluid and \(\beta \) reflects the ratio of the shear forces induced by the rotating cylinder over the surface tension forces.
We first distinguish the asymptotic limits \(B>0\) of order one, \(B\rightarrow 0\) and \(B \rightarrow \infty \), respectively.
(I) The case \(B > 0\) of order one. In this case the effects of the surface tension are comparable with those of the characteristic stresses of the non-Newtonian fluid. Changing the variables via
and then dropping the tildes for convenience, we have that the evolution Eq. (2.23) for the interface is given by
with \({\tilde{\beta }}=B\beta = \frac{D R_- \omega ^2 \mu _+ \tau _{\text {char}}}{\mu _0}\).
(II) The cases \(B\rightarrow 0\) and \(B\rightarrow \infty \), respectively. The asymptotic limit \(B\rightarrow 0\) corresponds to the situation in which the surface tension effects are dominated by the effects of the characteristic stresses of the non-Newtonian fluid. Conversely, the limit \(B\rightarrow \infty \) represents the regime in which the surface tension forces dominate the characteristic stresses of the non-Newtonian rheology. Suppose that the function \(\psi \) is given such that
where \(p > 0\). Then, changing the times scale via
and dropping again the tilde for convenience, the evolution equation (2.23) becomes
for all \(t > 0,\ \theta \in S^1.\)
For both equations (2.25) and (2.27), we now distinguish different asymptotic limits of the parameter \(\beta = \frac{D R_- \omega \mu _+}{\varepsilon ^2 {\tilde{\gamma }}}\).
(I) The case \(\frac{D R_- \omega \mu _+}{{\tilde{\gamma }}} \approx \varepsilon ^2\). In this asymptotic limit the surface tension forces and the shear forces induced by the rotating cylinder are comparable. Thus, we obtain the evolution equations
and
for \(t > 0,\ \theta \in S^1\), with \({\tilde{\beta }}, \beta > 0\) being positive constants. These two equations are studied in Sect. 4, where we prove that if the initial interface is close to a circle, then the solution is globally defined and converges to a circle which is not necessarily concentric with the two cylinders. However, as time tends to infinity, the centre of the circle spirals towards the common centre of the cylinders.
(II) The case \(\frac{D R_- \omega \mu _+}{{\tilde{\gamma }}} \ll \varepsilon ^2\). This corresponds to the asymptotic limit \(\beta \rightarrow 0\) in which the effects of surface tension on the flow are dominating the shear effects induced by the rotation of the cylinders are negligible. The evolution equations for this setting read
and
respectively. Equation (2.31), corresponding to the function \(\psi \) defined in (2.26), is studied in Sect. 3. We prove existence of positive weak solutions for short times. For \(p>1\), we show that solutions that are originally close to a circle, converge to a circle in finite time. We recall that, as discussed in the introduction, in the regions where \(\partial _{\theta }^{}h+\partial _{\theta }^{3}h\) is small, boundary layer effects can arise.
(III) The case \(\frac{D R_- \omega \mu _+}{{\tilde{\gamma }}} \gg \varepsilon ^2\). This reflects the situation in which the shear stress induced by the rotation of the cylinders dominates the surface tension such that \(\beta \rightarrow \infty \). We remark that this asymptotic limit is not studied in the present paper.
Power-law fluids. In this paper we are particularly interested in the case in which the viscous behaviour of the thin non-Newtonian fluid film is governed by a power-law. That is, for the effective viscosity \(\mu _-\) we use the constitutive law
with \(p > 0\). Fluids with such a viscosity are usually called power-law fluids or Ostwald–de Waele fluids. Recall that a flow-behaviour exponent \(p=1\) corresponds to a Newtonian fluid. Moreover, for \(p<1\) the fluid is shear-thinning, while it is shear-thickening for \(p>1\).
3 The Case \(\beta \rightarrow 0\): Existence Result and Asymptotic Behaviour
In this section we deal with the asymptotic limit \(\beta \rightarrow 0\) in which we have derived the approximation (2.31). We first prove local in time existence of weak solutions in the shear-thickening, as well as in the shear-thinning regime. For the latter case, we then study the asymptotic behaviour of solutions that are initially not too far from a circle. We observe that they converge to a circle in finite time and then continue to exist as a circle forever. The centre of the circle is not necessarily the origin, differently from the case in which \(\beta \) is of order one, which is discussed in Sect. 4.
We recall that, as discussed in the introduction, Eq. (2.31) cannot be expected to be a good approximation of (2.27) if \(|(\partial _\theta h + \partial _\theta ^3 h)|\ll \beta \). Since for a circular interface we have that \((\partial _\theta h + \partial _\theta ^3 h)=0\), and the model (2.31) predicts that the interface becomes a circle in finite time, it follows that (2.31) cannot describe the solutions of (2.27) for long times. Therefore, (2.31) describes only the intermediate asymptotics of the interfaces when they are not yet very close to circles.
Before proving local existence of positive weak solutions, we briefly introduce the notation used throughout the paper. We identify \(S^1\) with the interval \([0,2\pi ]\). Moreover, we identity functions \(\phi \in L_p(S^1)\) with functions \(\phi \in L_{p,\text {loc}}({\mathbb {R}})\) which are periodic with period \(2\pi \). Here, \(L_p({\mathbb {R}})\) denotes the usual Lebesgue space. Finally, by \(W^k_p(S^1)\) and \(H^{k}(S^{1})\) we denote the usual Sobolev spaces. They are defined as the closure of the restriction of \(2\pi \)-periodic functions in \(C^{\infty }({\mathbb {R}})\) to the interval \([0,2\pi ]\) with respect to the norm in \(W^k_p((0,2\pi ))\), respectively \(H^{k}((0,2\pi ))\). In order to simplify notation, we consider \(W^k_p(S^1)\) and \(H^k(S^1)\) as a closed subspaces of the complex spaces \(W^{k}_p(S^{1};{\mathbb {C}})\) and \(H^{k}(S^{1};{\mathbb {C}})\), respectively. In particular, we can represent any \(f\in H^{k}(S^{1})\) by its Fourier series
3.1 Local Existence of Positive Weak Solutions
In this section we prove local existence of weak solutions to the problem
with periodic boundary conditions and for all flow behaviour exponents \(\alpha > 0\). We use the notation
such that the evolution Eq. (P) can be written as
Note that this equation is a quasilinear equation of fourth order that may degenerate in h and \(\partial _{\theta }^{}h+\partial _{\theta }^{3}h\). In the non-degenerate case of a positive film height the equation is parabolic. Moreover, the coefficients of the highest-order terms depend only \((\alpha -1)\)-Hölder-continuously on the lower-order terms. In order to prove the existence of local positive weak solutions, we follow the usual ansatz of regularising the equation and showing that the sequence of solutions to the regularised problem has an accumulation point h which is a weak solution to the original problem. The compactness arguments mainly rely on a-priori estimates that are derived from the functional
Even if E[v](t) is not necessarily non-negative, we refer to it as an energy functional. To be able to pass to the limit in the nonlinear terms, we use lower semicontinuity of the norm and apply Minty’s trick.
The main result of this subsection is the following theorem on the existence of weak solutions to (P).
Theorem 3.1
Given an initial film height \(h_0 \in H^1(S^1)\) with \(0 < C_0 \le h_0(\theta )\) for all \(\theta \in S^1\), there exist a positive time \(T > 0\) and a positive weak solution h of (P) on [0, T] in the sense that \(0 < C_1 \le h(t,\theta ) \le C_2\) for all \(t \in [0,T],\, \theta \in S^1\),
-
(i)
h has the regularity \(h \in L_{\alpha +1}\bigl ((0,T);W^3_{\alpha +1}(S^1)\bigr ) \cap C\bigl ([0,T];H^1(S^1)\bigr ), \quad \partial _t h \in L_\frac{\alpha +1}{\alpha }\bigl ((0,T);(W^1_{\alpha +1}(S^1))'\bigr ); \)
-
(ii)
h satisfies the integral equation
$$ \int _0^T \langle \partial _t h(t),\varphi (t)\rangle _{W^1_{\alpha +1}(S^1)}\, \mathrm{d}t = \int _0^T \int _{S^1} h^{\alpha +2} \psi (\partial _{\theta }^{}h+\partial _{\theta }^{3}h) \partial _{\theta }^{}\varphi \, \mathrm{d}\theta \, \mathrm{d}t $$for all test functions \(\varphi \in L_{\alpha +1}\bigl ((0,T);W^1_{\alpha +1}(S^1)\bigr )\);
-
(iii)
h satisfies the initial condition \(h(0,\theta ) = h_0(\theta )\) for all \(\theta \in S^1\).
In addition, this solution has the following properties:
-
(iv)
(Conservation of mass) The mass of the fluid is conserved in the sense that
$$ \left\| h(t)\right\| _{L_1(S^1)} = \left\| h_0\right\| _{L_1(S^1)} $$for all \(t \in [0,T]\).
-
(v)
(Energy dissipation) The solution dissipates energy in the sense that
$$\begin{aligned} E[h](t) + \int _0^T \int _{S^1} \left| h\right| ^{\alpha +2} \left| \partial _{\theta }^{}h+\partial _{\theta }^{3}h\right| ^{\alpha +1}\, \mathrm{d}\theta \, \mathrm{d}t = E[h_0]. \end{aligned}$$
The mollified problem. To overcome the problems caused by the degeneracy and the lack of regularity of (P), we introduce a mollified version of (P) as follows. Let
be the usual mollifier such that, for \(\varepsilon \in (0,1)\),
where \(*\) denotes convolution. Note that the parameter \(\varepsilon \) in this section is a regularisation parameter that is not related to the average dimensionless height \(\varepsilon \) of the film, defined in (2.2).
Moreover, we use the notation
for the average of a function \(v \in L_2(S^1)\). Since our proofs strongly rely on Fourier analysis, we use this notation frequently for the zeroth Fourier mode. Therewith, for a fixed \(\varepsilon \in (0,1)\), we replace the mobility \(h^{\alpha +2}\) by a function
and the nonlinear term \(\psi (\partial _\theta h + \partial _\theta ^3 h)= |\partial _\theta h + \partial _\theta ^3 h|^{\alpha -1}(\partial _\theta h + \partial _\theta ^3 h)\) by
Then, we also have \(\psi _\varepsilon \in C^\infty \bigl ({\mathbb {R}}_{\ge 0};{\mathbb {R}}_{\ge 0}\bigr )\). Finally, we introduce the regularised / mollified problem

with periodic boundary conditions. We are interested in solving (\(P_\varepsilon \)) for initial values \(h_0\) that are close to their constant average \({\bar{h}}_0 > 0\).
In order to solve (P), different regularisation techniques are certainly possible. In Bernis and Friedman (1990) the authors propose two different regularisation techniques for the Newtonian thin-film equation. In both approaches the regularisation is restricted to the mobility coefficient. Moreover in Ansini and Giacomelli (2004), where the authors prove global existence for a doubly nonlinear equation the nonlinearity of which contains only the third-order derivative, a two-step regularisation is chosen. The authors regularise the mobility coefficient and introduce an artificial lower-order term, to guarantee positivity of the regularised solution on the one hand and to obtain sufficient regularity of the limit problem with the non-regularised mobility.
It follows from a standard fixed-point argument (see, for instance, Majda and Bertozzi (2002)) that the regularised problem (\(P_\varepsilon \)) possesses a local solution as stated in the following theorem.
Theorem 3.2
Let \(\varepsilon \in (0,1)\). Given an initial value \(h^\varepsilon _0 = h_0 \in H^1(S^1)\), there exists a positive time \(T_\varepsilon > 0\), possibly depending on \(\varepsilon \), and a unique solution \(h^\varepsilon \) of (\(P_\varepsilon \)) on \([0,T_\varepsilon ]\) such that
and \(h^\varepsilon \) satisfies the integral equation
for all test functions \(\phi \in L_{\alpha +1}\bigl ((0,T_\varepsilon );W^1_{\alpha +1}(S^1)\bigr )\).
Note that, if in Theorem 3.2 the initial value \(h_0 \in H^1(S^1)\) satisfies \(0 < \frac{{\bar{h}}_0}{2}\le h_0 \in H^1(S^1)\), the continuity of the solution \(h^\varepsilon \in C\bigl ([0,T_\varepsilon ]\times S^1\bigl )\) implies its positivity of \(h^\varepsilon \) for very small times \(t > 0\). However, in general the solution \(h^\varepsilon \) does not necessarily remain positive on the whole time interval \([0,T_\varepsilon ]\) on existence, even if we require \(h_0 > 0\) initially.
We now prove that the sequence \((h^\varepsilon )_\varepsilon \) has an accumulation point h which is in turn a weak solution to the original problem (P). To this end, note first that (3.3) may be rewritten equivalently as
for all \(\phi \in L_{\alpha +1}\bigl ((0,T);W^1_{\alpha +1}(S^1)\bigr )\). We start by collecting some important properties of the solution \(h^\varepsilon \) to the regularised problem (\(P_\varepsilon \)). To this end, we denote by \(T_\varepsilon \) be the maximal time of existence of the solution \(h^\varepsilon \) to (\(P_\varepsilon \)). In general, \(T_\varepsilon \) depends on the parameter \(\varepsilon \).
Remark 3.3
It is worthwhile to mention that if \(h^\varepsilon \) is defined in some space \(C\bigl ([0,\tau ];H^1(S^1)\bigr )\) for some \(\tau > 0\), then the solution can be extended to a larger time interval. In particular, this implies that \(\tau < T_\varepsilon \). We will use this result frequently in order to prove that the solutions \(h^\varepsilon \) obtained in Theorem 3.2 can be defined in some small time interval [0, T], where \(T > 0\) is independent of \(\varepsilon \).
In the next lemma, we observe that solutions \(h^\varepsilon \) to (\(P_\varepsilon \)) conserve their mass.
Lemma 3.4
Let \(h^\varepsilon \) be the solution to the mollified problem (\(P_\varepsilon \)) on \([0,T_\varepsilon )\), corresponding to the initial value \(h_0\). Then \(h^\varepsilon \) conserves its mass in the sense that
Proof
This follows by testing the regularised evolution equation with \(\phi =1\) and using the periodic boundary conditions. \(\square \)
In addition to the conservation of mass property, solutions \(h^\varepsilon \) to the mollified problem dissipate energy, in the sense that the functional E introduced above is decreasing along solutions.
Lemma 3.5
(Energy dissipation) Let \(h^\varepsilon \) be a solution to (\(P_\varepsilon \)) on \([0,T_\varepsilon )\), emanating from an initial value \(h_0 \in H^1(S^1)\). Then \(h^\varepsilon \) complies with the functional equation
where the non-negative dissipation \(D_{T}[h^\varepsilon ]\) is given by
This, in particular, implies the a-priori estimate
Proof
-
(i)
That \(h^\varepsilon \) satisfies the functional equation (3.4) follows by testing the equation with \((h^\varepsilon + \partial _\theta ^2 h^\varepsilon )\).
-
(ii)
In order to prove the a-priori estimate (3.5), we use Fourier analysis and write
$$\begin{aligned} h^\varepsilon (t,\theta ) = \sum _{n\in {\mathbb {Z}}} a_n(t) e^{i n \theta } = {\bar{h}}^\varepsilon + \sum _{n\in {\mathbb {Z}}, n \ne 0} a_n(t) e^{i n \theta }, \quad t \in [0,T_\varepsilon ), \end{aligned}$$
where the Fourier coefficients \(a_n(t),\ n \in {\mathbb {Z}}\), are, for \(t \in [0,T_\varepsilon )\), given by
Using Plancherel’s theorem, i.e. the identity
we obtain
and consequently, we end up with
This yields the desired estimate and the proof is complete. \(\square \)
By means of the energy balance (3.4) we can now derive a uniform (in \(\varepsilon \)) \(L_\infty \bigl ([0,T];H^1(S^1)\bigr )\) estimate for \(h^\varepsilon \). It is worthwhile to mention that, although the energy estimate (3.4) is the natural estimate for Eq. (P), it does not provide any information on the Fourier modes \(a_{\pm 1}\).
Throughout the paper we frequently use the following elementary inequality. Given \(\varepsilon > 0\) and \(\alpha \in (0,1)\) it holds that
Lemma 3.6
Let \(\varepsilon \in (0,1)\) be fixed and let \(h^\varepsilon \) be the solution to (\(P_\varepsilon \)) on \([0,T_\varepsilon )\), emanating from the initial value \(h^\varepsilon _0 \in H^1(S^1)\). Then there exist a positive time \(T > 0\) and a positive constant \(C > 0\), both independent of \(\varepsilon \), such that
The main issue in the proof of this lemma is to observe that the \(H^1(S^1)\)-norm of \(h^\varepsilon \) is equivalent to the sum of \(E[h^\varepsilon ]\) and the low Fourier modes. In virtue of Lemma 3.4 and Lemma 3.5, we thus need to derive estimates for the Fourier modes \(n=0, \pm 1\).
Proof
As in the proof of Lemma 3.5, we use the Fourier series representation of \(h^\varepsilon \) to obtain the equation
for every \(t \in [0,T_\varepsilon )\).
Writing \(\left\| h^\varepsilon (t)\right\| _{H^1(S^1)}\) in terms of the Fourier series of \(h^\varepsilon (t)\) yields
for all \(t \in (0,T_\varepsilon )\). Thus, to get an estimate for \(\left\| h^\varepsilon (t)\right\| _{H^1(S^1)}\), we need estimates for the first Fourier modes \(a_{-1}(t)\) and \(a_1(t)\). Since \(h^\varepsilon \) is a real-valued function, we have \(a_{-1}(t) = \overline{a_1(t)}\), where the bar indicates complex conjugation. Hence, it is enough to estimate \(a_1(t)\). To this end, recall that \(a_1\) is given by
This immediately implies the estimate \(|a_1(t)| \le C \left\| h^\varepsilon (t)\right\| _{L_\infty (S^1)} \le C \left\| h^\varepsilon (t)\right\| _{H^1(S^1)}, t\in (0,T_\varepsilon )\). Moreover,
With the elementary inequality (3.6) and in view of Hölder’s inequality with exponents \(p=(\alpha +1)/\alpha \) and \(q=\alpha +1\), we deduce the estimate
for all \(t \in (0,T_\varepsilon )\). Consequently, for the derivative with respect to time of \(|a_1(t)|^2\) we find that
for all \(t \in (0,T_\varepsilon )\), with \(\beta = \frac{\alpha +2}{\alpha +1} > 1\). Due to Young’s inequality with exponents \(p = \frac{\alpha +1}{\alpha }\) and \(q=\alpha +1\) we find that, for all \(t \in (0,T_\varepsilon )\),
for arbitrarily small \(\delta > 0\), a constant \(C_{\delta ,\alpha } > 0\) that depends on \(\delta \) and \(\alpha \) and with \(\gamma = (\alpha +2)+(\alpha +1) > 1\). Integration with respect to time yields
The estimate for \(|a_{-1}(t)|^2 = |a_1(t)|^2\) is the same. In addition, Lemma 3.4 implies \(|{\bar{h}}^\varepsilon (t)| = |{\bar{h}}^\varepsilon _0|\). Inserting this into (3.7) yields for all \(t \in (0,T_\varepsilon )\)
Choosing \({\tilde{\delta }}\) small enough, such that \(C_3 - {\tilde{\delta }} = \frac{1}{2}\), we obtain
with \(\gamma = (\alpha +2)+(\alpha +1) > 2\). Thus, in view of Lemma 3.5, we have derived the estimate
for \(t \in (0,T_\varepsilon )\). Finally, using a Gronwall-type argument, we find that there exists a time \(T > 0\), independent of \(\varepsilon \), such that
In addition, we have \(h^\varepsilon \in C\bigl ([0,T];H^1(S^1)\bigr )\) due to the regularity of the divergence-term in the regularised equation (\(P_\varepsilon \)). Thus, it follows that \(T \le T_\varepsilon \) (cf. Remark 3.3). This completes the proof. \(\square \)
Our next goal is to prove that solutions \(h^\varepsilon \) of (\(P_\varepsilon \)) that emerge from a positive initial film height do not immediately drop to zero. For this purpose we need the following auxiliary result.
Lemma 3.7
Let \(p > 1\) and \(\psi \in W^2_p(S^1)\). Then for all \(\delta > 0\) there exists a constant \(C_\delta > 0\), such that the estimate
holds true.
Proof
Let \(\phi \in L_q(S^1)\) with \(q > 1\) such that \(\tfrac{1}{p}+\frac{1}{q}=1\). As usual, we identify \(S^1\) with the interval \([0,2\pi ]\) and we can identity functions \(\phi \in L_q(S^1)\) with functions \(\phi \in L_{q,\text {loc}}({\mathbb {R}})\) which are periodic with period \(2\pi \). Let \(\eta _\varepsilon \) be a standard mollifier, i.e. let
Moreover, we require that
Since the argument of \(\eta _\varepsilon \) might be negative in some of the following calculations, we extend the function \(\eta _\varepsilon \) periodically by assuming that \(\eta _\varepsilon (\theta ) = \eta _\varepsilon (\theta +2\pi )\). We define \(\phi _\varepsilon = \eta _\varepsilon *\phi \), where \(*\) denotes convolution. Then we have \(\phi _\varepsilon \in C^\infty (S^1)\) and
Moreover, since \(\int _{S^1} (\phi - \phi _\varepsilon )\, \mathrm{d}\theta = 0\), it follows that \(G_\varepsilon \in W^1_q(S^1)\) and we may use integration by parts to obtain, for every \(\psi \in W^2_p(S^1)\), the equation
In view of Hölder’s inequality, this allows us to derive the estimate
For the second summand on the right-hand side of (3.8), we have the estimate
Thus, in order to prove the desired inequality, we are left with estimating the first summand in (3.8). To this end, we write
for \(\theta \in S^1\), where we used symmetry condition of the mollifier. From this equation we may then derive the estimate
for \((s,\theta ) \in [0,2\pi ]^2\), where \(W(s,\theta ) = \int _0^{2\pi } \bigl |\chi _{\{s \le \theta \}} - \chi _{\{\xi \le \theta \}}\bigr |\, \eta _\varepsilon (\xi - s)\, \mathrm{d}\xi \). Using that the support of \(\eta _\varepsilon (\xi -s)\) is contained in the region \(\{|\xi -s| \le \varepsilon , |\xi - s \pm 2\pi |\le \varepsilon \}\), we conclude that the support of \(W(s,\theta )\) is contained in the region \(\{|s-\theta |\le \varepsilon , |s - \theta \pm 2\pi |\le \varepsilon \}\). Since in addition \(0 \le W(s,\theta ) \le 1\) for all \((s,\theta ) \in [0,2\pi ]^2\), we find that
Inserting this into (3.10), we find that the first summand in (3.8) may be estimated by
Finally, inserting (3.9) and (3.11) into (3.8), we end up with
Since the constant \(C(2\varepsilon )^{1/p}\) becomes arbitrarily small, as \(\varepsilon \rightarrow 0\), the statement follows after choosing \(\phi = (\partial _\theta \psi )^{p/q} \in L_q(S^1)\). \(\square \)
We are now able to prove the following lemma.
Lemma 3.8
Let \(s \in (0,1)\). Given \(\varepsilon \in (0,1)\), let \(h^\varepsilon \) be the corresponding solution to (\(P_\varepsilon \)) on \([0,T_\varepsilon )\) with initial value \(h^\varepsilon _0 \in H^1(S^1)\). There exist a time \(T_0 > 0\) and a function \(K_s \in C({\mathbb {R}}_+;{\mathbb {R}}_+)\) with \(\lim _{t\searrow 0} K_s(t)=0\), both independent of \(\varepsilon \), such that for any \(T \in (0,T_0)\) with \(T_\varepsilon \le T\), we have
Note that, due to the embedding \(H^s(S^1) \hookrightarrow L_\infty (S^1)\) for \(s \ge 1/2\), the estimate obtained in Lemma 3.8 implies in particular that
Proof
For convenience we work with functions \(u^\varepsilon = h^\varepsilon - {\bar{h}}_0\) with zero average, that is \(\int _{S^1} u^\varepsilon (t,\theta ) \, \mathrm{d}\theta = 0\). Given an initial value \(u_0\), consider the equation
In order to derive suitable estimates, we test the equation with the function
where the operator \(S:L_2(S^1) \rightarrow L_2(S^1)\) is defined by
Therefore, we obtain
The operator M is now a nice operator in the sense that M is non-negative, self-adjoint and may be written as \(M = A^2\), where \(A:H^1(S^1) \rightarrow L_2(S^1)\) is defined by
On the other hand, we can identify \(S (\partial _\theta + \partial ^3_{\theta })=H(\partial _{\theta }^{2}+I)\), where H is the periodic Hilbert operator given by
Testing (3.12) with the function \(\varphi = -M(u^\varepsilon - u_0)\), introduced in (3.13), respectively (3.14), we obtain
for \(t \in [0,T_\varepsilon )\). As in Lemma 3.6, the inequality (3.6) and Young’s inequality with exponents \(p=\frac{\alpha +1}{\alpha }\) and \(q = \alpha +1\) yield, for all \(\delta > 0\) the existence of some constant \(C_{\delta ,\alpha } > 0\) such that
for all \(t \in [0,T_\varepsilon )\). Next, we estimate the second integral on the right-hand side of (3.15). Using the definition of the operator S and Lemma 3.7, we find that
for arbitrarily small \({\tilde{\delta }} > 0\). Integrating (3.15) with respect to time and using that at the initial time \(t=0\) we have \(\left\| A\bigl (u^\varepsilon (0)-u_0\bigr )\right\| _{L_2(S^1)} = 0\) yield
where we use Lemma 3.6, the fact that the dissipation is bounded thanks to Lemma 3.5 and \(T_\varepsilon \le T\). Note that the right-hand side of this inequality can be made arbitrarily small by choosing \(\delta , {\tilde{\delta }}\), and then T sufficiently small. Hence, by definition of A, we find that there exists a function \(K_\frac{1}{2}(T) \ge 0\) with \(\lim _{T \rightarrow 0} K_\frac{1}{2}(T) = 0\) such that
In view of Lemma 3.6, interpolation between \(H^{1/2}(S^1)\) and \(H^1(S^1)\) leads us to the desired estimate
for all \(s \in [1/2,1]\). This completes the proof for \(s \in (0,1/2]\). \(\square \)
Note that Lemma 3.8 implies that the solution \(h^\varepsilon \) stays bounded away from zero in the sense that
for \(T > 0\) sufficiently small, i.e. with a bound independent of \(\varepsilon \), if we require \(\Vert h_0 - {\bar{h}}_0\Vert _{H^1(S^1)}\le \delta \) for \(\delta > 0\) sufficiently small (and independent of \(\varepsilon \)).
In the following lemma we collect the uniform (in \(\varepsilon \)) a-priori estimates for the approximations \(h^\varepsilon \).
Lemma 3.9
(Uniform bounds) Let \(\varepsilon \in (0,1)\) be given and let \(h^\varepsilon \) be the corresponding solution to (\(P_\varepsilon \)) on \([0,T_\varepsilon )\) with initial value \(h_0 \in H^1(S^1)\). There exist \(\delta > 0\) sufficiently small and \(T > 0\), both independent of \(\varepsilon \) such that, if \(\Vert h_0 - {\bar{h}}_0\Vert _{H^1(S^1)} \le \delta \), then \(T_\varepsilon > T\) and the functions \(h^\varepsilon \) have the following properties.
-
(i)
The family \((h^\varepsilon )_\varepsilon \) is uniformly bounded in \(L_\infty \bigl ((0,T);H^1(S^1)\bigr )\);
-
(ii)
the family \(\bigl (m_\varepsilon (h^\varepsilon )\, \psi _\varepsilon \bigl (\eta _\varepsilon \bigl (\partial _{\theta }^{}h^{\varepsilon }+\partial _{\theta }^{3}h^{\varepsilon }\bigr )\bigr )\bigr )_\varepsilon \) is uniformly bounded in \(L_\frac{\alpha +1}{\alpha }\bigl ((0,T)\times S^1\bigr )\);
-
(iii)
the family \((\partial _t h^\varepsilon )_\varepsilon \) is uniformly bounded in \(L_\frac{\alpha +1}{\alpha }\bigl ((0,T);(W^1_{\alpha +1}(S^1))'\bigr )\);
-
(iv)
the family \(\bigl (\eta _\varepsilon \bigl (\partial _{\theta }^{}h^{\varepsilon }+\partial _{\theta }^{3}h^{\varepsilon }\bigr )\bigr )_\varepsilon \) is uniformly bounded in \(L_{\alpha +1}\bigl ((0,T)\times S^1\bigr )\);
-
(v)
the family \((\eta _\varepsilon h^\varepsilon )_\varepsilon \) is uniformly bounded in \(L_{\alpha +1}\bigl ((0,T);W^3_{\alpha +1}(S^1)\bigr )\);
-
(vi)
the family \(\bigl (\partial _t(\partial _{\theta }^{}h^{\varepsilon })\bigr )_\varepsilon \) is uniformly bounded in \(L_\frac{\alpha +1}{\alpha }\bigl ((0,T);\bigl (W^1_{\alpha +1,0}(S^1)\cap W^2_{\alpha +1}(S^1)\bigr )'\bigr )\).
Proof
-
(i)
Uniform boundedness of \((h^\varepsilon )_\varepsilon \) in \(L_\infty \bigl ((0,T);H^1(S^1)\bigr )\) has already been proved in Lemma 3.6.
-
(ii)
This follows by applying (3.6), Hölder’s inequality with exponents \(p=\alpha +1\) and \(q=(\alpha +1)/\alpha \) and using the uniform bounds on the dissipation term (Lemma 3.5) and on the \(L_\infty \bigl ((0,T_\varepsilon )\times S^1\bigr )\)-norm (cf. part (i) of this lemma):
$$\begin{aligned}&\left\| m_\varepsilon (h^\varepsilon )\, \psi _\varepsilon \bigl (\eta _\varepsilon \bigl (\partial _{\theta }^{}h^{\varepsilon }+\partial _{\theta }^{3}h^{\varepsilon }\bigr )\bigr )\right\| _{L_\frac{\alpha +1}{\alpha }((0,T)\times S^1)}\\&\quad \le C \left\| h^\varepsilon \right\| _{L_\infty ((0,T)\times S^1)}^{\alpha +2} \left( D_T^\varepsilon [h^\varepsilon ]\right) ^\frac{\alpha }{\alpha +1} \le C(h_0). \end{aligned}$$ -
(iii)
Since \(h^\varepsilon \) is a weak solution to (\(P_\varepsilon \)), we have that
$$\begin{aligned} \int _0^T \langle \partial _t h^\varepsilon (t), \varphi (t) \rangle _{W^1_{\alpha +1}(S^1)}\, \mathrm{d}t = \int _0^T \int _{S^1} m_\varepsilon (h^\varepsilon )\, \psi _\varepsilon \left( \eta _\varepsilon \bigl (\partial _{\theta }^{}h^{\varepsilon }+\partial _{\theta }^{3}h^{\varepsilon }\bigr )\right) \eta _\varepsilon (\partial _{\theta }^{}\varphi )\, \mathrm{d}\theta \, \mathrm{d}t, \end{aligned}$$
for all \(\varphi \in L_{\alpha +1}\bigl ((0,T);W^1_{\alpha +1}(S^1)\bigr )\). Using again the elementary inequality (3.6) and Hölder’s inequality with exponents \(p=\alpha +1\) and \(q=(\alpha +1)/\alpha \), we obtain
Young’s inequality for convolutions and the fact that the mollifier has mass 1, thus lead to the uniform estimate
with a positive constant \(C(h^\varepsilon _0)\) that does not depend on \(\varepsilon \).
-
(iv)
We prove that \(\eta _\varepsilon \bigl (\partial _{\theta }^{}h^{\varepsilon }+\partial _{\theta }^{3}h^{\varepsilon }\bigr )\) is uniformly bounded in \(L_{\alpha +1}\bigl ((0,T)\times S^1\bigr )\). To this end, recall from Lemma 3.8 that \(h^\varepsilon \) is, for each \(\varepsilon \in (0,1)\), bounded from away from zero for short times. For \(\varepsilon >0\), we split
$$\begin{aligned} \begin{aligned}&\int _0^T \int _{S^1} \left| \eta _\varepsilon \bigl (\partial _{\theta }^{}h^{\varepsilon }+\partial _{\theta }^{3}h^{\varepsilon }\bigr )\right| ^{\alpha +1}\, \mathrm{d}\theta \, \mathrm{d}t \\&\quad =\ \iint _{\{|\eta _\varepsilon (\partial _{\theta }^{}h^{\varepsilon }+\partial _{\theta }^{3}h^{\varepsilon })| \le \varepsilon \}} \left| \eta _\varepsilon \bigl (\partial _{\theta }^{}h^{\varepsilon }+\partial _{\theta }^{3}h^{\varepsilon }\bigr )\right| ^{\alpha +1}\, \mathrm{d}\theta \, \mathrm{d}t \\&\qquad + \iint _{\{|\eta _\varepsilon (\partial _{\theta }^{}h^{\varepsilon }+\partial _{\theta }^{3}h^{\varepsilon })| > \varepsilon \}} \left| \eta _\varepsilon \bigl (\partial _{\theta }^{}h^{\varepsilon }+\partial _{\theta }^{3}h^{\varepsilon }\bigr )\right| ^{\alpha +1}\, \mathrm{d}\theta \, \mathrm{d}t. \end{aligned} \end{aligned}$$Using the inequality
$$\begin{aligned} |x|^{\alpha +1} = \left( \tfrac{1}{2} |x|^2 + \tfrac{1}{2} |x|^2\right) ^\frac{\alpha -1}{2} |x|^2 \le \left( \tfrac{1}{2}\right) ^\frac{\alpha -1}{2} \left( |x|^2 + \sigma ^2\right) ^\frac{\alpha -1}{2} |x|^2, \quad |x| > \varepsilon , \end{aligned}$$this leads us to the estimate
$$\begin{aligned} \begin{aligned}&\int _0^T \int _{S^1} \left| \eta _\varepsilon \bigl (\partial _{\theta }^{}h^{\varepsilon }+\partial _{\theta }^{3}h^{\varepsilon }\bigr )\right| ^{\alpha +1}\, \mathrm{d}\theta \, \mathrm{d}t \\&\quad \le \ 2\pi T \varepsilon ^{\alpha +1} + \int _0^T \int _{S^1} \left| \eta _\varepsilon \bigl (\partial _{\theta }^{}h^{\varepsilon }+\partial _{\theta }^{3}h^{\varepsilon }\bigr ) + \sigma ^2\right| ^\frac{\alpha -1}{2} \left| \eta _\varepsilon \bigl (\partial _{\theta }^{}h^{\varepsilon }+\partial _{\theta }^{3}h^{\varepsilon }\bigr )\right| ^2 \mathrm{d}\theta \, \mathrm{d}t \\&\quad \le \ 2\pi T \varepsilon ^{\alpha +1} + D_T[h^\varepsilon ]. \end{aligned} \end{aligned}$$Using again the uniform bound for the dissipation functional derived in Lemma 3.5, we obtain the desired bound
$$\begin{aligned} \int _0^T \int _{S^1} \left| \eta _\varepsilon \bigl (\partial _{\theta }^{}h^{\varepsilon }+\partial _{\theta }^{3}h^{\varepsilon }\bigr )\right| ^{\alpha +1}\, \mathrm{d}\theta \, \mathrm{d}t \le C(h_0). \end{aligned}$$ -
(v)
We prove the estimate
$$\begin{aligned} \int _0^T\int _{S^{1}}\left| \eta _\varepsilon \bigl (\partial _{\theta }^{3}h^\varepsilon \bigr )\right| ^{\alpha +1}\mathrm{d}\theta \, \mathrm{d}t\le & {} \int _0^T\int _{S^{1}}\left| \eta _\varepsilon \bigl (\partial _{\theta }^{}h^\varepsilon +\partial _{\theta }^{3}h^\varepsilon \bigr )\right| ^{\alpha +1}\mathrm{d}\theta \, \mathrm{d}t\\&+ C(T) \Vert \eta _\varepsilon (h^\varepsilon )\Vert _{H^{1}(S^{1})}^{\alpha +1}. \end{aligned}$$
To this end, we define \(V_0= \text {span}\{\cos (\theta ),\sin (\theta )\}\subset L_{2}(S^1)\) and \(V_1\) as the orthogonal complement of \(V_0\oplus \text {span}\{1\}\) in \(L_{2}(S^1)\). Given \(\eta _\varepsilon (h^\varepsilon )\in H^{3}(S^1)\), we can decompose \(\eta _\varepsilon (h^\varepsilon )\) as
with \(a_0\in {\mathbb {R}}\), \(\Phi \in V_0\cap H^{3}(S^1)\) and \(v\in V_1\cap H^{3}(S^1)\). In terms of the corresponding Fourier series we may write
Since m(n) is bounded, we can apply the Littlewood–Paley Theory (c.f. (Stein 1970, Chapter 4)) to obtain
with a positive constant A which is independent of v. Therefore, using (3.17) and the fact that \(\Phi =a_1(t)\cos \theta +a_{-1}(t)\sin \theta \), we can write
Indeed, for the first term on the right-hand side of (3.18) we use the structure of \(\Phi \) and Young’s inequality for convolutions to derive the pointwise estimate
For the second integral on the right-hand side of (3.18) we use that \(\partial _{\theta }^{}\Phi +\partial _{\theta }^{3}\Phi =0\) and we obtain that
Thus, we can conclude that
and we have proved the desired result.
(vi) This follows similarly as in (iii). \(\square \)
Next, we prove that the approximations \(h^\varepsilon \) converge in a suitable sense.
Lemma 3.10
(Convergence of approximations) Let \(\varepsilon \in (0,1)\) be given and let \(h^\varepsilon \) be the corresponding solution to (\(P_\varepsilon \)) on \([0,T_\varepsilon )\) with initial value \(h_0 \in H^1(S^1)\). There exist \(\delta > 0\) sufficiently small and \(T > 0\), both independent of \(\varepsilon \) such that, if \(\Vert h_0 - {\bar{h}}_0\Vert _{H^1(S^1)} \le \delta \), then \(T_\varepsilon > T\) and we may extract a subsequence \((h^\varepsilon )_\varepsilon \) (not relabelled) such that, as \(\varepsilon \searrow 0\),
-
(i)
\(h^\varepsilon \rightarrow h\) strongly in \(C\bigl ([0,T];C^{\rho }(S^1)\bigr )\);
-
(ii)
\(m_\varepsilon (h^\varepsilon ) \psi _\varepsilon \bigl (\eta _\varepsilon \bigl (\partial _{\theta }^{}h^{\varepsilon }+\partial _{\theta }^{3}h^{\varepsilon }\bigr )\bigr ) \rightharpoonup \Phi \) weakly in \(L_\frac{\alpha +1}{\alpha }\bigl ([0,T]\times S^1\bigr )\) for some limit function \(\Phi \);
-
(iii)
\(\partial _t h^\varepsilon \rightharpoonup \partial _t h\) weakly in \(L_\frac{\alpha +1}{\alpha }\bigl ((0,T)\times (W^1_{\alpha +1}(S^1))'\bigr )\);
-
(iv)
\(\eta _\varepsilon (\partial _{\theta }^{}h^{\varepsilon }+\partial _{\theta }^{3}h^{\varepsilon }) \rightharpoonup (\partial _{\theta }^{}h+\partial _{\theta }^{3}h)\) weakly in \(L_{\alpha +1}\bigl ([0,T]\times S^1\bigr )\);
-
(v)
\(\partial _t(\partial _{\theta }^{}h^{\varepsilon }) \rightharpoonup \partial _t\partial _{\theta }^{}h\) weakly in \(L_\frac{\alpha +1}{\alpha }\bigl ((0,T);\bigl (W^1_{\alpha +1,0}(S^1)\cap W^2_{\alpha +1}(S^1)\bigr )'\bigr )\).
Proof
-
(i)
In the previous Lemma 3.9 (i), (iii) we have proved that
$$\begin{aligned} {\left\{ \begin{array}{ll} (h^\varepsilon )_\varepsilon \text { is uniformly bounded in } L_\infty \bigl ((0,T);H^1(S^1)\bigr ) &{} \\ (\partial _t h^\varepsilon )_\varepsilon \text { is uniformly bounded in } L_\frac{\alpha +1}{\alpha }\bigl ((0,T);(W^1_{\alpha +1}(S^1))'\bigr ).&{} \end{array}\right. } \end{aligned}$$Moreover, thanks to the Rellich–Kondrachov theorem, cf., for instance, in Adams and Fournier (2003, Thm. 6.3), we know that

where
 indicates compactness of the embedding. This allows us to invoke (Simon 1987, Cor. 4) in order to conclude that the sequence $$\begin{aligned} (h^\varepsilon )_\varepsilon \text { is relatively compact in } C\bigl ([0,T];C^\rho (S^1)\bigr ) \end{aligned}$$
indicates compactness of the embedding. This allows us to invoke (Simon 1987, Cor. 4) in order to conclude that the sequence $$\begin{aligned} (h^\varepsilon )_\varepsilon \text { is relatively compact in } C\bigl ([0,T];C^\rho (S^1)\bigr ) \end{aligned}$$with \(\rho \in [0,1/2)\) as above.
-
(ii)
This is an immediate consequence of Lemma 3.9 (ii).
-
(iii)
Thanks to Lemma 3.9 (iii), we may extract a subsequence \((\partial _t h^\varepsilon )_\varepsilon \) such that
$$\begin{aligned} \partial _t h^\varepsilon \rightharpoonup v \quad \text {weakly in } L_\frac{\alpha +1}{\alpha }\bigl ((0,T);(W^1_{\alpha +1}(S^1))'\bigr ) \hookrightarrow {\mathcal {D}}'\bigl ((0,T);(W^1_{\alpha +1}(S^1))'\bigr ) \end{aligned}$$for some limit function \(v \in L_\frac{\alpha +1}{\alpha }\bigl ((0,T);(W^1_{\alpha +1}(S^1))'\bigr )\). Since we know in addition that
$$\begin{aligned} h^\varepsilon \longrightarrow h \quad \text {in } C\bigl ([0,T];C^\rho (S^1)\bigr ) \hookrightarrow {\mathcal {D}}'\bigl ((0,T);(W^1_{\alpha +1}(S^1))'\bigr ), \quad \rho \in [0,1/2), \end{aligned}$$we conclude that
$$\begin{aligned} \partial _t h^\varepsilon \longrightarrow \partial _t h \quad \text {in } {\mathcal {D}}'\bigl ((0,T);(W^1_{\alpha +1}(S^1))'\bigr )\bigr ), \end{aligned}$$and consequently, \(v = \partial _t h \in L_\frac{\alpha +1}{\alpha }\bigl ((0,T);(W^1_{\alpha +1}(S^1))'\bigr )\).
-
(iv)
The strong convergence \(h^\varepsilon \rightarrow h\) in \(C\bigl ([0,T];C^\rho (S^1)\bigr ),\, \rho \in [0,1/2),\) in Lemma 3.10 (i) in particular implies uniform convergence \(h^\varepsilon \rightarrow h\) in \(C\bigl ([0,T]\times S^1\bigr )\) and then, by definition of the mollifier,
$$\begin{aligned} \eta _\varepsilon h^\varepsilon \longrightarrow h \quad \text {in } C\bigl ([0,T]\times S^1\bigr ). \end{aligned}$$(3.19)
Moreover, Lemma 3.9 (v) guarantees the existence of some \({\hat{h}} \in L_{\alpha +1}\bigl ((0,T);W^3_{\alpha +1}(S^1)\bigr )\) such that
In virtue of the uniqueness of the limit function, (3.19) and (3.20) imply
Thanks to the weak lower semicontinuity of the norm and Lemma 3.9 (iv), (v), we finally obtain
for some positive generic constant \(C > 0\) that does not depend on \(\varepsilon \).
-
(v)
This follows similarly as in (iii) and the proof is complete.
\(\square \)
It remains to prove the convergence of the nonlinear flux term \(m_\varepsilon (h^\varepsilon )\, \psi _\varepsilon \bigl (\eta _\varepsilon \bigl (\partial _{\theta }^{}h^{\varepsilon }+\partial _{\theta }^{3}h^{\varepsilon }\bigr )\bigr ) \rightharpoonup \left| h\right| ^{\alpha +2} \psi \bigl (\partial _{\theta }^{}h+\partial _{\theta }^{3}h\bigr )\) in \(L_\frac{\alpha +1}{\alpha }\bigl ((0,T)\times S^1\bigr )\). This is the content of the next lemma. The main idea of the proof is to use lower semicontinuity of the norm and to apply Minty’s trick in order to be able to identify the nonlinear limit flux.
Lemma 3.11
Let \(\varepsilon \in (0,1)\) be given and let \(h^\varepsilon \) be the corresponding solution to (\(P_\varepsilon \)) on \([0,T_\varepsilon )\) with initial value \(h_0 \in H^1(S^1)\). There exist \(\delta > 0\) sufficiently small and \(T > 0\), both independent of \(\varepsilon \) such that, if \(\Vert h_0 - {\bar{h}}_0\Vert _{H^1(S^1)} \le \delta \), then \(T_\varepsilon > T\) and we may extract a subsequence \((h^\varepsilon )_\varepsilon \) (not relabelled) such that
as \(\varepsilon \searrow 0\).
Proof
We divide the proof in several steps. For convenience, we pass to a subsequence where necessary without explicitly mentioning.
-
(i)
First, in virtue of Lemma 3.10 (ii), we know that \(m_\varepsilon (h^\varepsilon )\, \psi _\varepsilon \bigl (\eta _\varepsilon \bigl (\partial _\theta h^\varepsilon + \partial ^3_\theta h^\varepsilon \bigr )\bigr )\) is weakly sequentially compact, i.e. there is an element \(\Phi \in L_\frac{\alpha +1}{\alpha }\bigl ((0,T)\times S^1)\bigr )\) such that
$$\begin{aligned} m_\varepsilon (h^\varepsilon ) \psi _\varepsilon \bigl (\eta _\varepsilon \bigl (\partial _\theta h^\varepsilon + \partial ^3_\theta h^\varepsilon \bigr )\bigr ) \rightharpoonup \Phi \quad \text {weakly in } L_\frac{\alpha +1}{\alpha }\bigl ((0,T)\times S^1)\bigr ). \end{aligned}$$It remains to identify the limit flux \(\Phi \).
-
(ii)
Next, we prove that h is bounded in \(C\bigl ([0,T];H^1(S^1)\bigr )\). We already know from Lemma 3.10 (i) that
$$\begin{aligned} h \in C\bigl ([0,T];C^\rho (S^1)\bigr ) \hookrightarrow C\bigl ([0,T];L_2(S^1)\bigr ). \end{aligned}$$Moreover,
$$\begin{aligned}&\partial _{\theta }^{}h \in L_{\alpha +1}\bigl ((0,T);W^1_{\alpha +1,0}(S^1) \cap W^2_{\alpha +1}(S^1)\bigr ) \quad \text {and}\\&\quad \partial _t\partial _{\theta }^{}h\in L_\frac{\alpha +1}{\alpha }\bigl ((0,T);\bigl (W^1_{\alpha +1,0}(S^1)\cap W^2_{\alpha +1}(S^1)\bigr )'\bigr ), \end{aligned}$$thanks to Lemma 3.10 (iv) and (v) and lower semicontinuity of the norm. Using (Bernis 1988, Remark 3.4), this implies that \(\partial _\theta h \in C\bigl ([0,T];L_2(S^1)\bigr )\). Consequently, \(h \in C\bigl ([0,T];H^1(S^1)\bigr )\).
-
(iii)
In view of the previous steps, we may choose \(\varphi = h + \partial _{\theta }^{2}h \in L_{\alpha +1}\bigl ((0,T);W^1_{\alpha +1}(S^1)\bigr )\) as a test function in the weak formulation (3.3) for \(h^\varepsilon \). This yields
$$\begin{aligned}&\int _0^T \int _{S^1} \partial _t h^\varepsilon (h + \partial _{\theta }^{2}h)\, \mathrm{d}\theta \, \mathrm{d}t\\&\quad + \int _0^T \int _{S^1} m_\varepsilon (h^\varepsilon ) \psi _\varepsilon \left( \eta _\varepsilon \bigl (\partial _\theta h^\varepsilon + \partial _\theta ^3 h^\varepsilon \bigr )\right) \eta _\varepsilon \bigl (\partial _{\theta }^{}h+\partial _{\theta }^{3}h\bigr )\, \mathrm{d}\theta \, \mathrm{d}t = 0. \end{aligned}$$As \(\varepsilon \searrow 0\), the first term satisfies
$$\begin{aligned} \int _0^T \int _{S^1} \partial _t h^\varepsilon (h + \partial _{\theta }^{2}h)\, \mathrm{d}\theta \, \mathrm{d}t \longrightarrow \int _0^T \int _{S^1} \partial _t h\, (h + \partial _{\theta }^{2}h)\, \mathrm{d}\theta \, \mathrm{d}t = E[h](T) - E[h](0), \end{aligned}$$where we have used that the limit function satisfies \(h \in C\bigl ([0,T];H^1(S^1)\bigr )\). Moreover, since \((\partial _{\theta }^{}h+\partial _{\theta }^{3}h)\) is bounded in \(L_{\alpha +1}\bigl ((0,T)\times S^1\bigr )\) by (3.21), the definition of the mollifier yields the strong convergence
$$\begin{aligned} \eta _\varepsilon \bigl (\partial _{\theta }^{}h+\partial _{\theta }^{3}h\bigr ) \longrightarrow \partial _{\theta }^{}h+\partial _{\theta }^{3}h \quad \text {in } L_{\alpha +1}\bigl ((0,T)\times S^1\bigr ). \end{aligned}$$Together with Lemma 3.10 (ii), this implies
$$\begin{aligned}&\int _0^T \int _{S^1} m_\varepsilon (h^\varepsilon )\, \psi _\varepsilon \left( \eta _\varepsilon \bigl (\partial _\theta h^\varepsilon + \partial _\theta ^3 h^\varepsilon \bigr )\right) \eta _\varepsilon \bigl (\partial _{\theta }^{}h+\partial _{\theta }^{3}h\bigr )\, \mathrm{d}\theta \, \mathrm{d}t\\&\quad \longrightarrow \int _0^T \int _{S^1} \Phi \bigl (\partial _{\theta }^{}h+\partial _{\theta }^{3}h\bigr )\, \mathrm{d}\theta \, \mathrm{d}t, \end{aligned}$$and consequently, we obtain the identity
$$\begin{aligned} E[h](t) + \left\langle \Phi | \partial _{\theta }^{}h+\partial _{\theta }^{3}h \right\rangle = E[h_0] \end{aligned}$$for almost every \(t \in [0,T]\).
-
(iv)
Monotonicity and identification of the limit flux \(\Phi \) by Minty’s trick. Observe that the operator
$$\begin{aligned} {\left\{ \begin{array}{ll} \psi _\varepsilon : L_{\alpha +1}\bigl ((0,T)\times S^1\bigr ) \longrightarrow L_{\frac{\alpha +1}{\alpha }}\bigl ((0,T)\times S^1\bigr ), &{} \\ \psi _\varepsilon (u) = \left( |u|^2 + \varepsilon ^2\right) ^\frac{\alpha -1}{2} u &{} \end{array}\right. } \end{aligned}$$
is monotone, i.e. we have
for all \(u, v \in L_{\alpha +1}\bigl ([0,T]\times S^1\bigr )\) with \(u\ne v\). This follows immediately from the monotonicity of the function \(\psi _\varepsilon :{\mathbb {R}}\rightarrow {\mathbb {R}},\ s\mapsto (s^2 + \varepsilon ^2)^\frac{\alpha -1}{2}s\). Let now \(\phi \in W^3_{\alpha +1}\bigl ((0,T)\times S^1\bigr )\). For better readability, henceforth we simply write \(\langle u | v\rangle \) for the dual pairing \(\langle u |v \rangle _{L_{\alpha +1}((0,T)\times S^1)}\) between \(u \in L_\frac{\alpha +1}{\alpha }\bigl ((0,T)\times S^1\bigr )\) and \(v \in L_{\alpha +1}\bigl ((0,T)\times S^1\bigr )\). Thanks to the monotonicity of \(\psi _\varepsilon \), we have
Let us consider the different pairings on the right-hand side separately.
First, we have proved in Lemma 3.5 that \(h^\varepsilon \) satisfies the energy dissipation formula for the problem (\(P_\varepsilon \)). We rewrite it here as
Thanks to Lemma 3.10 (i) we know that \(h^\varepsilon (t) \rightarrow h(t)\) in \(H^1(S^1)\) for almost every \(t \in [0,T]\). Thus, as \(\varepsilon \) tends to zero, we find that
for almost every \(t \in [0,T]\). Moreover, Lemma 3.10 (ii) yields
For the third pairing we use that

thanks to Lemma 3.10 (i), respectively Lemma 3.10 (iv). Here we also use the fact that \(m_\varepsilon (h^\varepsilon ) = |h^\varepsilon |^{\alpha +2}\) in the range of values attained by \(h^\varepsilon \) for times \(t \in [0,T]\), cf. (3.2). This implies
Finally, for the fourth term, we obtain
where we use again the convergence \(m_\varepsilon (h^\varepsilon ) \rightarrow h^{\alpha +2}\) strongly in \(C\bigl ([0,T]\times S^1\bigr )\). Combining (3.22)–(3.25) leads to the inequality
Thus, using the identity
proved in step (iii), for almost every \(t \in [0,T]\), we discover that
By choosing \(\phi = h - \lambda v\) for some arbitrary \(v \in W^3_{\alpha +1}\bigl ((0,T)\times S^1\bigr )\) and \(\lambda > 0\), we obtain the inequality
and hence, in the limit \(\lambda \searrow 0\):
for almost every \(t \in [0,T]\). Similarly, choosing \(\phi = h + \lambda v\), we discover that
and consequently
Since \(v \in W^3_{\alpha +1}\bigl ((0,T)\times S^1\bigr )\) is arbitrary, we are finally able to identify
This completes the proof. \(\square \)
With the previous convergence results at hand, we are now able to prove Theorem 3.1.
Proof of Theorem 3.1
-
(i)
It follows from Lemma 3.10 (iii) and (iv) and step (ii) of the proof of Lemma 3.11 that
$$\begin{aligned} h \in C\bigl ([0,T];H^1(S^1)\bigr ) \cap L_{\alpha +1}\bigl ((0,T);W^3_{\alpha +1}(S^1)\bigr )\quad \text {and}\quad \partial _t h \in L_\frac{\alpha +1}{\alpha }\bigl ((0,T);(W^1_{\alpha +1}(S^1))'\bigr ). \end{aligned}$$ -
(ii)
We now prove that h complies with the integral equation in Theorem 3.1 (ii). To this end, recall that
$$\begin{aligned} \int _0^T \langle \partial _t h^\varepsilon (t),\varphi (t)\rangle _{W^1_{\alpha +1}(S^1)}\, \mathrm{d}t = \int _0^T \int _{S^1} \eta _\varepsilon \left[ m_\varepsilon (h^\varepsilon ) \psi _\varepsilon \left( \eta _\varepsilon \bigl (\partial _{\theta }^{}h^{\varepsilon }+\partial _{\theta }^{3}h^{\varepsilon }\bigr )\right) \right] \, \partial _{\theta }^{}\phi \, \mathrm{d}\theta \, \mathrm{d}t \end{aligned}$$for all test functions \(\phi \in L_{\alpha +1}\bigl ((0,T);W^1_{\alpha +1}(S^1)\bigr )\). Since \(\partial _{\theta }^{}\phi \in L_{\alpha +1}\bigl ((0,T)\times S^1)\), we may invoke Lemma 3.11 to deduce that, on the one hand,
$$\begin{aligned} \int _0^T \langle \partial _t h^\varepsilon (t),\varphi (t)\rangle _{W^1_{\alpha +1}(S^1)}\, \mathrm{d}t \longrightarrow \int _0^T \int _{S^1} h^{\alpha +2} \psi \bigl (\partial _{\theta }^{}h+\partial _{\theta }^{3}h\bigr )\, \mathrm{d}\theta \, \mathrm{d}t. \end{aligned}$$On the other hand, Lemma 3.10 (iii) implies that
$$\begin{aligned} \int _0^T \langle \partial _t h^\varepsilon (t),\varphi (t)\rangle _{W^1_{\alpha +1}(S^1)}\, \mathrm{d}t \longrightarrow \int _0^T \langle \partial _t h(t),\varphi (t)\rangle _{W^1_{\alpha +1}(S^1)}\, \mathrm{d}t. \end{aligned}$$Combining both, we find that h satisfies the desired integral identity
$$\begin{aligned} \int _0^T \langle \partial _t h(t),\varphi (t)\rangle _{W^1_{\alpha +1}(S^1)}\, \mathrm{d}t = \int _0^T \int _{S^1} h^{\alpha +2} \psi \bigl (\partial _{\theta }^{}h+\partial _{\theta }^{3}h\bigr )\, \mathrm{d}\theta \, \mathrm{d}t \end{aligned}$$for all \(\phi \in L_{\alpha +1}\bigl ((0,T);W^1_{\alpha +1}(S^1)\bigr )\).
-
(iii)
That the initial condition is satisfied is clear since we chose them identically in (P) and (\(P_\varepsilon \)).
-
(iv)
That a solution conserves its mass follows from the convergence \(h^\varepsilon \rightarrow h\) in \(C\bigl ([0,T];C^\rho (S^1)\bigr )\), cf. Lemma 3.10 (i), and from the conservation of mass property
$$\begin{aligned} \int _{S^1} h^\varepsilon (t,\theta )\, \mathrm{d}\theta = \int _{S^1} h_0(\theta )\, \mathrm{d}\theta , \quad t \in [0,T], \end{aligned}$$for the approximations \(h^\varepsilon \).
-
(v)
That the solution satisfies the energy equality has already been proved in step (iii) of the proof of Lemma 3.11.
-
(vi)
To see that the solution is bounded away from zero for short times, we just argue as in the proof of Lemma 3.6 and Lemma 3.8. \(\square \)
3.2 Global Existence and Convergence to a Circle in Finite Time in the Shear-Thickening Regime
In this section we study the setting in which the thin film next to the internal cylinder is occupied by a shear-thickening fluid. This corresponds to the regime of flow-behaviour exponents \(\alpha < 1\). We consider solutions emerging from initial values that are close to a circle. For these solutions we show that they converge to a circle in finite time. This circle does not necessarily have to be centred at the origin. Note that this behaviour clearly differs from the Newtonian case (c.f. Sect. 4).
The main result of this section is stated in the following theorem.
Theorem 3.12
Let \(\alpha < 1\). There exists a \(\delta > 0\) such that for all initial values \(h_0 \in H^1(S^1)\) with \(\left\| h_0 - {\bar{h}}_0\right\| _{H^1(S^1)} < \delta \), there is a weak solution \(h \in C\bigl ([0,\infty );H^1(S^1)\bigr ) \cap L_{\alpha +1,\text {loc}}\bigl ((0,\infty );W^3_{\alpha +1}(S^1)\bigr )\) that exists globally in time. Moreover, there exists a time \(0< t^*< \infty \) such that
Here \(v_{\pm 1}\) denote the Fourier coefficients corresponding to the Fourier modes \(n=\pm 1\) that are constant for times \(t \ge t^*\).
The idea of the proof is to derive a differential inequality for the energy E that guarantees that the energy drops down to zero in finite time. Using Fourier analysis, we may then prove that solutions with zero average and zero energy are necessarily given by a circle. Let first
Then, the condition \(\Vert h_0 - {\bar{h}}_0\Vert _{H^1(S^1)} < \delta \) for some \(\delta > 0\) is equivalent to the condition \(\left\| v_0\right\| _{H^1(S^1)} < \delta \) for some \(\delta > 0\).
Thanks to Theorem 3.1, there exists a time \(T > 0\) and a positive weak solution \(h \in C\bigl ([0,T];H^1(S^1)\bigr ) \cap L_{\alpha +1}\bigl ((0,T);W^3_{\alpha +1}(S^1)\bigr )\) on [0, T]. We write this solution in terms of its Fourier series as
for all \(t \in (0,T]\), where the constant c is given by the average
Then it clearly holds that \({\bar{v}}=0\), i.e. \(v = h-c\) has average zero.
Lemma 3.13
Let \(\alpha < 1\). For all \(v \in C\bigl ([0,T];H^1(S^1)\bigr )\) with \({\bar{v}} = \frac{1}{2\pi } \int _{S^1} v(t,\theta )\, \mathrm{d}\theta = 0\), the energy E[v](t) satisfies the differential inequality
Proof
Using the Fourier series representation of v, we have that
for all \(t\in [0,T]\) and \(\theta \in S^1\). We define
and write
and \(a(t), b(t) \in {\mathbb {R}}\) for all \(t \in [0,T]\). Then the Fourier series representation of \(A\Phi \) is
that is, \(A\Phi \) is given by
for \(\theta \in S^1\). Moreover, since \(G \in C^1(S^1)\), we observe that the derivative \(\partial _{\theta }^{}(A\Phi )\) satisfies
Consequently, using the identities
we discover that
This yields the desired estimate. \(\square \)
Using this differential inequality for the energy, we may prove that the energy converges to zero in finite time. We obtain an upper bound of the extinction time \(t^*\) in terms of the distance \(\delta \) from the initial value \(h_0\) to its average \({\bar{h}}_0\). The Fourier coefficients \(v_{\pm 1}(t)\) converge to a constant, as \(t\rightarrow t^*\), while the remaining terms converge to zero in the \(H^1\)-norm. For times \(t \ge t^*\) the solution can be extended globally in time as the limit circle at time \(t^*\), i.e. it does not change its shape at later times. In this way we obtain a solution that is defined for arbitrarily large times.
Proof of Theorem 3.12
We divide the proof into several steps.
-
(i)
We first prove that there exists a positive time \(t^*> 0\) such that \(E[v](t)=0,\ t \ge t^*\). In the previous Lemma 3.13 we have derived the differential inequality
$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} E[v](t) \le -C \bigl (E[v](t)\bigr )^\frac{\alpha +1}{2}, \quad t \in [0,T], \end{aligned}$$for all \(v \in C\bigl ([0,T];H^1(S^1)\bigr )\) with zero average and for all flow behaviour exponents \(\alpha < 1\). This inequality implies that \(E[v](\cdot )\) is decreasing and thus
$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \bigl (E[v](t)^\frac{1-\alpha }{2}\bigr ) \le -C_\alpha , \quad t \in [0,T], \end{aligned}$$as long as \(E[v](t) > 0\), where \(C_\alpha = \frac{C(1-\alpha )}{2}\). Therefore,
$$\begin{aligned} \bigl (E[v](t)\bigr )^\frac{1-\alpha }{2} \le \bigl (E[v_0]\bigr )^\frac{1-\alpha }{2} - C_\alpha t, \quad t \in [0,T], \quad \text {if} \quad E[v](t) > 0. \end{aligned}$$(3.26)This in turn implies that
$$\begin{aligned} E[v](t) \le \left( \bigl (E[v_0]\bigr )^\frac{1-\alpha }{2} - C_\alpha t\right) ^\frac{2}{1-\alpha }, \quad t \in [0,T], \quad \text {if} \quad E[v](t) > 0. \end{aligned}$$Thus, we can conclude that there exists a time \(t^*\ge 0\) such that
$$\begin{aligned} E[v](t) = 0, \quad t \ge t^*, \quad \text {where} \quad t^*\le \frac{(E[v_0])^\frac{1-\alpha }{2}}{C_\alpha }. \end{aligned}$$Note that \(t^*> 0\) is strictly positive, if \(E[v_0]>0\), as a consequence of the continuity of the energy. Moreover, recall that we assume h to be initially close to a circle in the sense that \(\left\| h_0 - c\right\| _{H^1(S^1)} = \left\| v_0\right\| _{H^1(S^1)} < \delta \) for some small but positive \(\delta > 0\). If we choose \(\delta < (C_\alpha T)^\frac{1}{1-\alpha }\), then we find that
$$\begin{aligned} E[v](t) = 0, \quad t \ge t^*, \quad \text {where} \quad 0< t^*< \frac{\left\| v_0\right\| _{H^1(S^1)}^{1-\alpha }}{C_\alpha }< \frac{\delta ^{1-\alpha }}{C_\alpha } < T. \end{aligned}$$It is worthwhile to mention that the extinction time \(t^*\) is smaller that the maximal time T of existence if \(\delta \) is small enough.
-
(iii)
We can write h in terms of its Fourier series as
$$\begin{aligned} h(t,\theta ) = c + v_{-1}(t) e^{-i\theta } + v_1(t) e^{i\theta } + \Phi (t,\theta ) \quad \text {with} \quad \Phi (t,\theta ) = \sum _{n\in {\mathbb {Z}}, n \ne 0,\pm 1} v_n(t) e^{in\theta } \end{aligned}$$for \(t \in [0,T]\) and \(\theta \in S^1\). We show that \(\Phi \) converges to zero as time t tends to the extinction time \(t^*\). It holds that
$$\begin{aligned} \left\| \Phi (t)\right\| _{H^1(S^1)}^2&= \left\| \Phi (t)\right\| _{L_2(S^1)}^2 + \left\| \partial _{\theta }^{}\Phi (t)\right\| _{L_2(S^1)}^2\\&= 2\pi \sum _{n=\in {\mathbb {Z}},n \ne 0,\pm 1} (n^2+1) \left| v_n(t)\right| ^2 \\&\le C \pi \sum _{n\in {\mathbb {Z}}, n\ne 0,\pm 1} (n^2-1) \left| v_n(t)\right| ^2. \\&= C E[v](t). \end{aligned}$$Consequently, we discover that
$$\begin{aligned} \left\| \Phi (t)\right\| _{H^1(S^1)}^2 \le C \delta ^2, \quad t \in [0,T], \quad \text {and} \quad \left\| \Phi (t)\right\| _{H^1(S^1)}^2 \longrightarrow 0 \quad \text {as } t \rightarrow t^*\end{aligned}$$ -
(iv)
Next, we prove that \(\left| v_{\pm 1}(t)\right| \) is bounded by \(\delta \) for all \(t \in [0,t^*)\). To this end, observe first that
$$\begin{aligned} \left| v_{\pm 1}(0)\right| \le \left\| v_0\right\| _{H^1(S^1)} \le \delta . \end{aligned}$$Moreover, as in the proof of Lemma 3.6 we can derive the estimate
$$\begin{aligned} \begin{aligned} \left| \frac{\mathrm{d}}{\mathrm{d}t} v_{\pm 1}(t)\right|&= \left| \frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{1}{2\pi } \int _{S^1} h(t,\theta ) e^{\mp i\theta }\, \mathrm{d}\theta \right) \right| \\&= \left| \frac{i}{2\pi }\int _{S^1} h^{\alpha +2} \psi (\partial _{\theta }^{}h+\partial _{\theta }^{3}h) e^{\mp i\theta }\, \mathrm{d}\theta \right| \\&\le C \int _{S^1} \left| h\right| ^{\alpha +2} \left| \partial _{\theta }^{}h+\partial _{\theta }^{3}h\right| ^\alpha \, \mathrm{d}\theta . \end{aligned} \end{aligned}$$Integration with respect to time and applying Hölder’s inequality lead to the estimate
$$\begin{aligned} \begin{aligned}&\left| v_{\pm 1}(t) - v_{\pm 1}(0)\right| \\&\quad \le C \left( \int _0^t \int _{S^1} \left| h\right| ^{\alpha +2} \left| \partial _{\theta }^{}h+\partial _{\theta }^{3}h\right| ^{\alpha +1}\, \mathrm{d}\theta \, ds\right) ^\frac{\alpha }{\alpha +1} \left( \int _0^t\int _{S^1}\left| h\right| ^{\alpha +2}\, \mathrm{d}\theta \, ds\right) ^\frac{1}{\alpha +1} \\&\quad \le C t^\frac{1}{\alpha +1} \sup _{t \in (0,T)} \left\| h(t)\right\| _{L_\infty (S^1)}^\frac{\alpha +2}{\alpha +1} \left( \int _0^t\int _{S^1} \left| h\right| ^{\alpha +2} \left| \partial _{\theta }^{}h+\partial _{\theta }^{3}h\right| ^{\alpha +1}\, \mathrm{d}\theta \, ds\right) ^\frac{\alpha }{\alpha +1}, \quad t \le t^*, \end{aligned} \end{aligned}$$whence we find that
$$\begin{aligned} \left| v_{\pm 1}(t) - v_{\pm 1}(0)\right| \le C^\frac{\alpha +2}{\alpha +1} (D_t[h])^\frac{\alpha }{\alpha +1} \le C \left\| v_0\right\| _{H^1(S^1)}^\frac{2\alpha }{\alpha +1} \le C \delta ^\frac{2\alpha }{\alpha +1}. \end{aligned}$$This implies
$$\begin{aligned} \left| v_{\pm 1}(t)\right| \le \delta + C \delta ^\frac{2\alpha }{\alpha +1}, \quad t \le t^*. \end{aligned}$$ -
(v)
Next, we prove that \(v_{\pm 1}(t) \rightarrow v_{\pm 1}(t^*)\) as \(t \rightarrow t^*\). To this end, we first observe that the bound
$$\begin{aligned} \left| v_{\pm 1}(t)\right| \le C \sup _{t \in (0,T)} \left\| h(t,\theta )\right\| _{L_\infty (S^1)} \le C, \quad t \in [0,T), \end{aligned}$$implies that there exists a sequence \(t_n \rightarrow t^*\) and an element \(\chi \in {\mathbb {R}}\) such that
$$\begin{aligned} \lim _{n\rightarrow \infty } v_{\pm 1}(t_n) = \chi . \end{aligned}$$(3.27)Moreover, as in the previous step (iv), we obtain
$$\begin{aligned} \begin{aligned}&\lim _{n \rightarrow \infty } \left| v_{\pm 1}(t_n) - v_{\pm 1}(t)\right| \\&\quad \le \lim _{n \rightarrow \infty }C \sup _{s \in (t,t^*)} \left\| h(s)\right\| _{L_\infty (S^1)}^\frac{\alpha +2}{\alpha +1} \left( \int _t^{t_n}\int _{S^1} \left| h\right| ^{\alpha +2} \left| \partial _{\theta }^{}h+\partial _{\theta }^{3}h\right| ^{\alpha +1}\, \mathrm{d}\theta \, ds\right) ^\frac{\alpha }{\alpha +1} \\&\quad = C \sup _{s \in (t,t^*)} \left\| h(s)\right\| _{L_\infty (S^1)}^\frac{\alpha +2}{\alpha +1} \left( \int _t^{t^*}\int _{S^1} \left| h\right| ^{\alpha +2} \left| \partial _{\theta }^{}h+\partial _{\theta }^{3}h\right| ^{\alpha +1}\, \mathrm{d}\theta \, ds\right) ^\frac{\alpha }{\alpha +1}. \end{aligned} \end{aligned}$$Thanks to the convergence in (3.27), we also have
$$\begin{aligned} \left| \chi - v_{\pm 1}(t)\right|= & {} \lim _{n \rightarrow \infty } \left| v_{\pm 1}(t_n) - v_{\pm 1}(t)\right| \\\le & {} C \sup _{s \in (t,t^*)} \left\| h(s)\right\| _{L_\infty (S^1)}^\frac{\alpha +2}{\alpha +1} \left( \int _t^{t^*}\int _{S^1} \left| h\right| ^{\alpha +2} \left| \partial _{\theta }^{}h+\partial _{\theta }^{3}h\right| ^{\alpha +1}\, \mathrm{d}\theta \, ds\right) ^\frac{\alpha }{\alpha +1} \end{aligned}$$and the right-hand side converges to zero, as \(t \rightarrow t^*\).
-
(vi)
Now we construct a solution with infinite lifetime by defining
$$\begin{aligned} h(t,\theta ) = c + v_{-1}(t) e^{-i\theta } + v_1(t) e^{i\theta } + \Phi (t,\theta ), \quad t \ge 0, \end{aligned}$$where
$$\begin{aligned} v_{\pm 1}(t)&= {\left\{ \begin{array}{ll} v_{\pm 1}(t), &{} t \le t^*\\ v_{\pm 1}(t^*), &{} t> t^*, \end{array}\right. } \\ \Phi (t,\theta )&= {\left\{ \begin{array}{ll} \Phi (t,\theta ), &{} t \le t^*\\ 0, &{} t > t^*. \end{array}\right. } \end{aligned}$$Then h defines for all times \(t > 0\) a weak solution of (P).
-
(vii)
Finally, we prove that the extension of the solution to the time interval \([t^*,\infty )\) by
$$\begin{aligned} h(t,\theta ) = c + v_{-1}(t^*) e^{-i\theta } + v_1(t^*) e^{i\theta }, \quad t \ge t^*,\ \theta \in S^1, \end{aligned}$$
where \(v_{\pm 1} = v_{\pm 1}(t^*)\), is unique. For this purpose, assume that f is another solution of (P) on \([0,\infty )\) such that
Then also \(E[f](t) = 0\) for all \(t \ge t^*\) and f is given by
In addition, f satisfies the integral equation
Since f is, for times \(t \ge t^*\), given by a circle, cf. (3.28), it holds that \(\bigl (\partial _\theta f(t,\theta ) + \partial _\theta ^3 f(t,\theta )\bigr )=0\) pointwise for all \(t \ge t^*\) and \(\theta \in S^1\). Consequently, (3.29) implies that f is constant in time. This in turn implies that the \(w_{\pm 1}\) are constant in time. Finally, the continuity property of the solution implies that \(w_{\pm 1} = v_{\pm 1}(t^*)\) and the proof is complete. \(\square \)
4 The Case \(\beta \) of Order One: Stability and Long-Time Behaviour
In this section we study the stability of constant solutions of (2.28) and (2.29) when \(\beta \) is of order one, i.e. when the surface tension forces are comparable with the shear forces induced by the rotation of the cylinder. These constant solutions describe circular interfaces which are concentric with the confining cylinders. We prove that, in the scaling limit \(\beta \) of order one, solutions of (2.28) and (2.29) with initial data close to a constant, converge to the constant with an error of order one as \(t\rightarrow \infty .\) A more detailed analysis of the solution shows that the interface behaves, to the leading order, as a circle the centre of which moves along a spiral towards the origin O, as \(t\rightarrow \infty \) (cf. Theorem 4.3).
In the following, we denote by \({\dot{H}}^{k}(S^{1})\) the homogeneous Sobolev spaces, consisting of functions \(f\in H^{k}(S^{1})\) with zero average \(\frac{1}{2\pi }\int _{S^{1}}f\, \mathrm{d}\theta =0\).
4.1 The Case \(B>0\) of Order One
In the case \(B > 0\) of order one, the effects of the surface tension are comparable with those of the shear forces induced by the rotation of the cylinder and we have the evolution equation (2.28), i.e.
It turns out that, in this physical limit, the asymptotic behaviour of solutions, as \(t\rightarrow \infty \), is as in the Newtonian case studied in Pernas-Castaño and Velázquez (2020). However, since the involved differential operators are different, we briefly sketch the arguments yielding the long-time asymptotics in order to give a complete picture of all the possible scaling limits.
Theorem 4.1
Let \(c>0\). There exists \(\delta >0\) (depending on c) such that, for any \(h_0\in H^{4}(S^{1})\) satisfying \(\Vert h_0-c\Vert _{H^{4}(S^{1})}<\delta \) with \(\frac{1}{2\pi }\int _{S^{1}}h_0=c\), there exists a unique solution \(h\in C([0,\infty ); H^{4}(S^{1}))\cap C^{1}((0,\infty );H^{4}(S^{1}))\) of (2.28), where \(h(0,\cdot )=h_0(\cdot )\). Moreover, we have
where C depends only on c.
In order to prove Theorem 4.1, it is convenient to reformulate (2.28) in a coordinate system rotating at velocity c. Moreover, we linearise around the constant solution \(h=c\). More precisely, we define
Using the evolution Eq. (2.28), we obtain that v solves the equation
where \(L:{\dot{H}}^{k}(S^{1})\rightarrow L_{2}(S^{1})\) is a linear operator, given by
and \(R:{\dot{H}}^{k}(S^{1})\rightarrow L_{2}(S^{1})\) is the non-linear operator defined by
for \(v\in {\dot{H}}^4(S^1)\). Note that L and R are well-defined bounded operators from \({\dot{H}}^{k}(S^{1})\) to \(L_{2}(S^{1})\). Now we define
where \(\bot \) denotes the orthogonal complement in \(L_2(S^{1})\). Moreover, we introduce the following subspaces of \({\dot{H}}^4(S^1)\),
and we denote by \(P_0\) and \(P_1\) the orthogonal projections of \(L_{2}(S^{1})\) onto \(V_0\), respectively \(V_1\). Therefore, we have that \({\dot{H}}^4(S^1)={\mathcal {E}}_0\oplus {\mathcal {E}}_1\). Indeed, using Fourier expansion, it readily follows that \(P_0({\dot{H}}^4(S^1))\subset {\mathcal {E}}_0\), and \(P_1({\dot{H}}^4(S^1))\subset {\mathcal {E}}_1\). Consequently, we can write each \(v\in {\dot{H}}^4(S^1)\) as a sum \(v=v_0+v_1\) with \(v_0=P_0(v)\in {\mathcal {E}}_0\) and \(v_1=P_1(v)\in {\mathcal {E}}_{1}\). We finally introduce the quadratic operator, \(Q:{\mathcal {E}}_0\times {\mathcal {E}}_0\rightarrow {\mathcal {E}}_1\) by
for each \(v_0=a_{-1}e^{-i\phi }+a_1e^{i\phi }\in {\mathcal {E}}_0\), where \(a_1=\overline{a_{-1}}\). Since the proof Theorem 4.1 follows the lines of the proof of Pernas-Castaño and Velázquez (2020, Thm 5.1), we only sketch it here.
Proof
First, one can prove existence of solutions
on some small time interval [0, T], cf. (Pernas-Castaño and Velázquez 2020, Prop. A.1). By standard parabolic theory, one can then prove that the solution even has the better regularity
cf. (Pernas-Castaño and Velázquez 2020, Lemma 5.2). With the improved regularity, one may then derive appropriate a-priori estimates for the operators introduced above in order to obtain global existence by a continuation argument. \(\square \)
A centre manifold theory for quasilinear problems has been developed in Mielke (1988). We follow here the version of this type of theory as developed in Haragus and Iooss (2011). Similar techniques can be also found in Lunardi (1995, Chapter 9).
Theorem 4.2
Let L and R be defined as in (4.4) and (4.5). There exists a map \(\Phi \in {\mathcal {C}}^{k}({\mathcal {E}}_0,{\mathcal {E}}_1)\), where \({\mathcal {E}}_0=\text {Im} P_0=\text {Re} P_1\subset {\dot{H}}^4(S^{1})\) and \({\mathcal {E}}_1=P_1{\dot{H}}^4\subset {\dot{H}}^4(S^{1})\), with \(\Phi (0)=0\) and \(D\Phi (0)=0\). Moreover, there exists a neighbourhood \({\mathcal {O}}\) of 0 in \({\dot{H}}^4(S^{1})\) such that the manifold
has the following properties:
-
(i)
\({\mathcal {M}}_0\) is locally invariant, i.e. if v is a solution to (4.3), satisfying \(v(0)\in {\mathcal {M}}_0\cap {\mathcal {O}}\) and \(v(t)\in {\mathcal {O}}\) for all \(t\in [0,T]\), then \(v(t)\in {\mathcal {M}}_0\) for all \(t\in [0,T]\).
-
(ii)
\({\mathcal {M}}_0\) contains the set of bounded solutions of (4.3) that stay in \({\mathcal {O}}\) for all \(t\in {\mathbb {R}}\). If v is a solution to \(\frac{\mathrm{d}v}{\mathrm{d}t}=L(v)+R(v)\) that belongs to \({\mathcal {M}}_0\) for \(t\in I\), where \(I\subset {\mathbb {R}}\) is an open interval, then \(v=v_0+\Phi (v_0)\) and \(v_0\) satisfies
$$\begin{aligned} \frac{\mathrm{d}v_0}{\mathrm{d}t}=L_0(v_0)+P_0R\bigl (v_0+\Phi (v_0)\bigr ), \end{aligned}$$(4.9)where \(L_0\) is the restriction of L to \({\mathcal {E}}_0\). Moreover, \(\Phi \) satisfies
$$\begin{aligned} D\Phi (v_0)\bigl (L_0(v_0)+P_0R(v_0+\Phi (v_0))\bigr )=L_1\Phi (v_0)+P_1R\bigl (v_0+\Phi (v_0)\bigr )\quad \forall v_0\in {\mathcal {E}}_0. \end{aligned}$$(4.10) -
(iii)
\({\mathcal {M}}_0\) is locally attracting in the following sense. If \(v(0)\in {\mathcal {O}}\) and if the solution to (4.3), corresponding to this initial value, satisfies \(v(t)\in {\mathcal {O}}\) for all \(t>0\), then there exist an initial value \({\tilde{v}}(0)\in {\mathcal {M}}_0\cap {\mathcal {O}}\) and a constant \(a > 0\) such that \(\Vert v-{\tilde{v}}\Vert _{{\dot{H}}^{4}(S^{1})}\le Ce^{-at}\), as \(t\rightarrow \infty \).
Proof
In order to prove this theorem, we have to verify that the operators L and R introduced above satisfy the Hypotheses 5.1–5.3 of Pernas-Castaño and Velázquez (2020). To this end, observe first that
-
(i)
\(L\in {\mathcal {L}}\bigl ({\dot{H}}^4(S^{1});L_{2}(S^{1})\bigr )\).
-
(ii)
For some \(k\ge 2\), there exists a neighbourhood \({\mathcal {V}}\subset {\dot{H}}^4(S^{1})\) of 0 such that \(R\in {\mathcal {C}}^k\bigl ({\mathcal {V}};L_{2}(S^{1})\bigr )\), \(R(0)=0\) and \(DR(0)=0\).
Moreover, the linear operator L has the following spectral properties. First, its spectrum can be written as \(\sigma =\sigma _0\cup \sigma _-\) where \(\sigma _0=\{\lambda \in \sigma ;\, \text {Re}\lambda =0\}\) and \(\sigma _-=\{\lambda \in \sigma ;\, \text {Re}\lambda <0\}\). More precisely, the following statements are true:
-
(iii)
There exists a positive constant \(\gamma >0\) such that
$$\sup _{\lambda \in \sigma _-}(\text {Re}\lambda )<-\gamma .$$ -
(iv)
\(\sigma _0\) consists of a finite number of eigenvalues with finite multiplicities.
Finally, there exist positive constants \( s_0>0\) and \(C>0\) such that, for all \(s\in {\mathbb {R}}\) with \(|s|\ge s_0\), we have that
-
(v)
\(\Vert (i s I-L_1)^{-1}\Vert _{{\mathcal {L}}(L_2(S^{1}))}\le \frac{C}{| s|},\)
where \(L_1\) is the restriction of L to \(P_1{\dot{H}}^4(S^{1})\), \(P_1\) is the projection \(P_1:L_{2}(S^{1})\rightarrow L_{2}(S^{1})\) defined by \(P_1={\mathbb {I}}-P_0\) and \(P_0\) is the spectral projection corresponding to \(\sigma _0\) that is given by
for a simple, counterclockwise oriented Jordan curve \(\Gamma \) surrounding \(\sigma _0\) and lying entirely in \(\{\lambda \in {\mathbb {C}};\, \text {Re}\lambda >-\gamma \}\). It is worthwhile to note that, thanks to Haragus and Iooss (2011, Rem. 2.16), the only property that we need to check for the operator \(L_1\) is the one in (v). This is the case since we are working with the Hilbert spaces \(L_{2}(S^{1})\) and \({\dot{H}}^{4}(S^{1})\). The theorem is now a minor adaptation of Theorems 2.9 and 3.22 in Haragus and Iooss (2011). \(\square \)
Theorem 4.3
Let \(c>0\). There exist \(\delta >0\) and a manifold \({\mathcal {M}}_0\) as in (4.8) (both of them depending on c) such that all the properties stated in Theorem 4.2 hold true with \({\mathcal {O}}=B_{\delta }(0)\). In particular, if \(v(0,\cdot )\in {\mathcal {M}}_0\cap {\mathcal {O}}\), then the corresponding solution h of (2.28) (cf. (4.2)) satisfies:
where
and C depends only on c. Moreover, if \(v(\cdot ,0)\in {\mathcal {O}}\), we have that
with \(a=a(c)\).
Proof
Using the same techniques as in Pernas-Castaño and Velázquez (2020), we can prove that the operators L and R, given by (4.4) and (4.5), are well-defined from \({\dot{H}}^{4}(S^{1})\rightarrow L_{2}(S^{1})\) and \({\dot{H}}^{4}(S^{1})\times {\dot{H}}^{4}(S^{1})\rightarrow L_{2}(S^{1})\), respectively.
Moreover, the operator L satisfies the properties (i), (iii) and (iv) of the proof Theorem 4.2 and the operator R satisfies property (ii) for any \(k\ge 2\). Therefore, the operator \(P_0\) defined in (4.11) is the orthogonal projection of \(L_{2}(S^{1})\) onto \({\mathcal {E}}_0=\text {span}\{\cos (\theta ),\sin (\theta )\}\) and there exists a manifold \({\mathcal {M}}_0\) with the properties stated in Theorem 4.2 that can be parametrised as in (4.8) with \(\Phi \in {\mathcal {C}}^{k}({\mathcal {E}}_0,{\mathcal {E}}_1)\) for any \(k\ge 2\). Furthermore, we have \(\Phi (0)=0\), \(D\Phi (0)=0\) and, if \(v_0=a_{-1}e^{-i\theta }+a_1e^{i\theta }\in {\mathcal {E}}_0\), then
The differential equation (4.9) that describes the dynamics of v on this manifold is reduced to
where we used that \(L_0(v_0)=0\) for \(v_0\in {\mathcal {E}}_0\). Using (4.15) and (4.16), we can conclude (4.12). Finally, the estimate (4.14) is a consequence of the global existence result in Theorem 4.1 and Theorem 4.2(iii). For more details c.f. Pernas-Castaño and Velázquez (2020). \(\square \)
Remark 4.4
The asymptotic behaviour in (4.12) can be reformulated in terms of the original non-dimensional variables (cf. (2.24)) as:
where \(\lambda =\frac{1}{\sqrt{B}}\) and \(t\gg \frac{\tau }{\varepsilon \lambda }\).
Moreover, we recall that the interface separating the two fluids is given by the curve \(r=1+\varepsilon h\). Therefore, a geometrical argument shows that the interface associated to the solution described by (4.17) behaves asymptotically as the circle given by
where \(\sigma (t)= 2K\sqrt{\frac{\tau \varepsilon \lambda }{t}}\), \(\theta _0(t)=c\psi ({\tilde{\beta }})\frac{\varepsilon }{\tau }\lambda t+{\tilde{K}}\log {(\frac{\varepsilon }{\tau } \lambda t)}+C_0\) and \(r_0=1+\varepsilon \lambda c\). Note that the centre of this circle spirals towards the origin as \(t\rightarrow \infty \) (Fig. 3).
4.2 The Cases \(B\rightarrow 0\) and \(B\rightarrow \infty \)
We recall that in these cases we have the evolution Eq. (2.29). For this case we can proof exactly the analogous Theorems in Sect. 4.1. For this purpose, we consider:
Using the evolution Eq. (2.27), we obtain that v solves the equation
where \(L:{\dot{H}}^{4}(S^{1})\rightarrow L_{2}(S^{1})\) is a linear operator, given by
and \(R:{\dot{H}}^{4}(S^{1})\rightarrow L_{2}(S^{1})\) is the non-linear operator defined by
Note that L and R are well-defined bounded operators from \({\dot{H}}^{4}(S^{1})\) to \(L_{2}(S^{1})\). Moreover, we consider the quadratic operator \(Q:{\mathcal {E}}_0\times {\mathcal {E}}_0\rightarrow {\mathcal {E}}_1\) defined by
where \(a_1=\overline{a_{-1}}\). Using (4.18)-(4.22) we can prove the global existence result.
On the other hand, taking
we can prove that
Therefore, we can conclude that in the these cases, we have that the centre of the circle spirals towards the origin as in Sect. 4.1.
Notes
In Pernas-Castaño and Velázquez (2020), the case in which the layer of fluid closer to the external cylinder is much thinner than the inner one, has also been considered in the Newtonian case. However, since the analysis is similar we restrict ourselves in this paper to the case in which the thin layer is close to the internal cylinder.
References
Adams, R.A., Fournier, J.J.F.: Sobolev Spaces, volume 140 of Pure and Applied Mathematics (Amsterdam), 2nd edn. Elsevier/Academic Press, Amsterdam (2003)
Ansini, L., Giacomelli, L.: Shear-thinning liquid films: macroscopic and asymptotic behaviour by quasi-self-similar solutions. Nonlinearity 15(6), 2147–2164 (2002)
Ansini, L., Giacomelli, L.: Doubly nonlinear thin-film equations in one space dimension. Arch. Ration. Mech. Anal. 173(1), 89–131 (2004)
Baumert, B.M., Muller, S.J.: Flow regimes in model viscoelastic fluids in a circular Couette system with independently rotating cylinders. Phys. Fluids 9(3), 566–586 (1997)
Beretta, E., Bertsch, M., Dal Passo, R.: Nonnegative solutions of a fourth-order nonlinear degenerate parabolic equation. Arch. Ration. Mech. Anal. 129(2), 175–200 (1995)
Bernis, F.: Existence results for doubly nonlinear higher order parabolic equations on unbounded domains. Math. Ann. 279(3), 373–394 (1988)
Bernis, F., Friedman, A.: Higher order nonlinear degenerate parabolic equations. J. Differ. Equ. 83(1), 179–206 (1990)
Bertozzi, A.L., Brenner, M.P., Dupont, T.F., Kadanoff, L.P.: Singularities and similarities in interface flows. In: Trends and Perspectives in Applied Mathematics, Volume 100 of Appl. Math. Sci., pp. 155–208. Springer, New York (1994)
Bruell, G., Granero-Belinchón, R.: On the thin film Muskat and the thin film Stokes equations. J. Math. Fluid Mech. 21(2), 33 (2019)
Chandrasekhar, S.: Hydrodynamic and Hydromagnetic Stability: The International Series of Monographs on Physics. Clarendon Press, Oxford (1961)
Chossat, P., Iooss, G.: The Couette–Taylor problem. Applied Mathematical Sciences, vol. 102. Springer, New York (1994)
Drazin, P.G., Reid, W.H.: Hydrodynamic Stability. Cambridge Mathematical Library, 2nd edn. Cambridge University Press, Cambridge (2004)
Escher, J., Matioc, A.V., Matioc, B.V.: Thin-film approximations of the two-phase Stokes problem. Nonlinear Anal. 76, 1–13 (2013)
Giacomelli, L.: A fourth-order degenerate parabolic equation describing thin viscous flows over an inclined plane. Appl. Math. Lett. 12(8), 107–111 (1999)
Giacomelli, L., Knüpfer, H., Otto, F.: Smooth zero-contact-angle solutions to a thin-film equation around the steady state. J. Differ. Equ. 245(6), 1454–1506 (2008)
Giacomelli, L., Otto, F.: Rigorous lubrication approximation. Interfaces Free Bound. 5(4), 483–529 (2003)
Günther, M., Prokert, G.: A justification for the thin film approximation of Stokes flow with surface tension. J. Differ. Equ. 245(10), 2802–2845 (2008)
Haragus, M., Iooss, G.: Local bifurcations, center manifolds, and normal forms in infinite-dimensional dynamical systems. Universitext. Springer-Verlag London, Ltd., London; EDP Sciences, Les Ulis (2011)
Joseph, D.D., Renardy, Y.Y.: Fundamentals of two-fluid dynamics. Part I, volume 3 of Interdisciplinary Applied Mathematics. Springer-Verlag, New York, (1993). Mathematical theory and applications
Kerchman, V.: Strongly nonlinear interfacial dynamics in core-annular flows. J. Fluid Mech. 290, 131–166 (1995)
King, J.R.: The spreading of power-law fluids. Fluid Mech. Appl. 62, 153–160 (2001)
King, J.R.: Two generalisations of the thin film equation. Math. Comput. Model. 34(7–8), 737–756 (2001)
Knüpfer, H.: Well-posedness for a class of thin-film equations with general mobility in the regime of partial wetting. Arch. Ration. Mech. Anal. 218(2), 1083–1130 (2015)
Laurençot, P., Matioc, B.V.: Self-similarity in a thin film Muskat problem. SIAM J. Math. Anal. 49(4), 2790–2842 (2017)
Lienstromberg, C., Müller, S.: Local strong solutions to a quasilinear degenerate fourth-order thin-film equation. NoDEA Nonlinear Differ. Equ. Appl. 27(2), 16 (2020)
Lunardi, A.: Analytic Semigroups and Optimal Regularity in Parabolic Problems: Progress in Nonlinear Differential Equations and their Applications, vol. 16. Birkhäuser Verlag, Basel (1995)
Majda, A.J., Bertozzi, A.L.: Vorticity and Incompressible Flow. Cambridge University Press, Cambridge (2002)
Marzuola, J.L., Swygert, S.R., Taranets, R.: Nonnegative weak solutions of thin-film equations related to viscous flows in cylindrical geometries. J. Evol. Equ., (2019)
Matsuhisa, S., Bird, R.B.: Analytical and numerical solutions for laminar flow of the non-newtonian Ellis fluid. AIChE J. 11(4), 588–595 (1965)
Mielke, A.: Reduction of quasilinear elliptic equations in cylindrical domains with applications. Math. Methods Appl. Sci. 10(1), 51–66 (1988)
Ockendon, H., Ockendon, J.R.: Viscous Flow. Cambridge Texts in Applied Mathematics. Cambridge University Press, Cambridge (1995)
Pernas-Castaño, T., Velázquez, J.J.L.: Analysis of a thin film approximation for two-fluid Taylor-Couette flows. J. Differ. Equ. 269(1), 377–419 (2020)
Renardy, Y., Joseph, D.D.: Couette flow of two fluids between concentric cylinders. J. Fluid Mech. 150, 381–394 (1985)
Schlichting, H., Gersten, K., Boundary-layer theory. Springer-Verlag, Berlin, enlarged edition,: With contributions by Egon Krause and Herbert Oertel. Jr, Translated from the ninth German edition by Katherine Mayes (2000)
Simon, J.: Compact sets in the space \(L^p(0, T;B)\). Ann. Mat. Pura Appl. 4(146), 65–96 (1987)
Stein, E.M.: Singular Integrals and Differentiability Properties of Functions (PMS-30). Princeton University Press (1970)
Taylor, G.I.: VIII: stability of a viscous liquid contained between two rotating cylinders. Philos. T. R. Soc. Lond. 223, 289–343 (1923)
Weidner, D.E., Schwartz, L.W.: Contact-line motion of shear-thinning liquids. Phys. Fluids 6(11), 3535–3538 (1994)
Acknowledgements
The authors have been supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the collaborative research centre ’The mathematics of emerging effects’ (CRC 1060, Project-ID 211504053) and the Hausdorff Center for Mathematics (GZ 2047/1, Project-ID 390685813).
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Rustum Choksi.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lienstromberg, C., Pernas-Castaño, T. & Velázquez, J.J.L. Analysis of a Two-Fluid Taylor–Couette Flow with One Non-Newtonian Fluid. J Nonlinear Sci 32, 24 (2022). https://doi.org/10.1007/s00332-021-09750-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00332-021-09750-0
Keywords
- Taylor–Couette flow
- Non-Newtonian fluid
- Power-law fluid
- Degenerate parabolic equation
- Weak solution
- Long-time asymptotics
- Thin-film equation


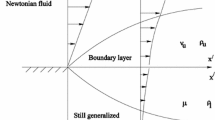
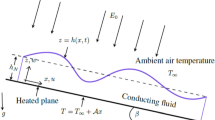




 indicates compactness of the embedding. This allows us to invoke (Simon
indicates compactness of the embedding. This allows us to invoke (Simon 