Vector-borne disease models with Lagrangian approach

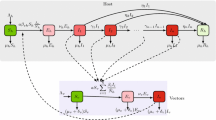
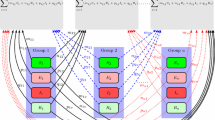
Abstract

We develop a multi-group and multi-patch model to study the effects of population dispersal on the spatial spread of vector-borne diseases across a heterogeneous environment. The movement of host and/or vector is described by Lagrangian approach in which the origin or identity of each individual stays unchanged regardless of movement. The basic reproduction number $\mathcal {R}_0$ of the model is defined and the strong connectivity of the host-vector network is succinctly characterized by the residence times matrices of hosts and vectors. Furthermore, the definition and criterion of the strong connectivity of general infectious disease networks are given and applied to establish the global stability of the disease-free equilibrium. The global dynamics of the model system are shown to be entirely determined by its basic reproduction number. We then obtain several biologically meaningful upper and lower bounds on the basic reproduction number which are independent or dependent of the residence times matrices. In particular, the heterogeneous mixing of hosts and vectors in a homogeneous environment always increases the basic reproduction number. There is a substantial difference on the upper bound of $\mathcal {R}_0$ between Lagrangian and Eulerian modeling approaches. When only host movement between two patches is concerned, the subdivision of hosts (more host groups) can lead to a larger basic reproduction number. In addition, we numerically investigate the dependence of the basic reproduction number and the total number of infected hosts on the residence times matrix of hosts, and compare the impact of different vector control strategies on disease transmission.

Appendices

Appendix A: Variable and notation index

Symbol	Meaning	Page
$H_i$	Total host population of group i	5
$S_i^h$	Number of susceptible hosts in group i	5
$I_i^h$	Number of infected hosts in group i	5
$N_j^v$	Total vector population of patch j	5
$S_j^v$	Number of susceptible vectors in group j	5
$I_j^v$	Number of infected vectors in group j	5
$I_{ik}^h$	Number of infected hosts of group i in patch k	18
$I_{jk}^v$	Number of infected vectors of patch j in patch k	18
$I_{i}^{hf}$	Number of infected hosts of group i that are frequent travelers	35
$I_{i}^{hu}$	Number of infected hosts of group i that are unfrequent travelers	35
$\Omega _h$	Set of host groups	5
$\Omega _v$	Set of vector patches	5
$\Omega _v^0$	Set of vector patches that are visited by at least one host group	5
$\Omega _v^j$	Set of vector patches that are visited by host group j	22
$\Gamma$	Positively invariant region for model (2.2)	9
$E_0$	Disease-free equilibrium of model (2.2)	9
$E^*$	Endemic equilibrium of model (2.2)	17
F	New infection matrix for model (2.2)	9
V	Transition matrix for model (2.2)	9
$\rho$	Spectral radius of a square matrix	9
${\mathscr {A}}$	Block of matrix F at position (1,2)	9
${\mathscr {B}}$	Block of matrix F at position (2,1)	9
${\mathscr {C}}$	Block of matrix V at position (1,1)	9
${\mathscr {D}}$	Block of matrix V at position (2,2)	9
$\alpha _{ij}$	The (i, j)-entry of matrix ${\mathscr {A}}{\mathscr {D}}^{-1}{\mathscr {B}}{\mathscr {C}}^{-1}$	10
$\beta _{ij}$	The (i, j)-entry of matrix ${\mathscr {B}}{\mathscr {C}}^{-1}{\mathscr {A}}{\mathscr {D}}^{-1}$	10
M	A Sign equivalent form of $FV^{-1}$	11
W	Host-vector contact matrix in terms of residence times matrices	11
${\mathcal {G}}$	Infectious disease network	13
$\mathcal {R}_0$	Basic reproduction number of model (2.2)	9
$\mathcal {R}_0^{(k)}$	Basic reproduction number of patch k in disconnection	18
$\mathcal {R}_0^{[k]}$	Basic reproduction number of patch k in isolation	19
${\hat{\mathcal {R}}}_{ijskr}$	Basic reproduction number that involves host groups i, j and	20
	vector patches s, k, r, and depends on the ratio of overall
	population sizes of vectors and hosts, i.e., V/H
${\hat{\mathcal {R}}}_{jjskr}$	${\hat{\mathcal {R}}}_{ijskr}$ in the case of $i=j$	23
${\hat{\mathcal {R}}}_{ijk}$	${\hat{\mathcal {R}}}_{ijskr}$ in the case of $s=r=k$ (no vector movement)	31
${\hat{\mathcal {R}}}_{jjk}$	${\hat{\mathcal {R}}}_{ijk}$ in the case of $i=j$	31
$\mathcal {R}_0(m/n)$	$\mathcal {R}_0$ of model (2.2) containing m host groups and n vector patches	23
$\mathcal {R}_{ijskr}$	Basic reproduction number that involves host groups i, j and vector	26
	patches s, k, r, and depends on the ratio of population sizes
	of vector patch s and host group j, i.e., $V_s/H_j$
$\mathcal {R}_{jjskr}$	$\mathcal {R}_{ijskr}$ in the case of $i=j$	28
$\mathcal {R}_{ijk}$	$\mathcal {R}_{ijskr}$ in the case of $s=r=k$ (no vector movement)	31
$\mathcal {R}_{jjk}$	$\mathcal {R}_{ijk}$ in the case of $i=j$	31
${\tilde{\mathcal {R}}}_{ijk}$	Basic reproduction number that involves host group k and vector	32
	patches i, j, depends on the ratio of population sizes of vector patch

Symbol	Meaning	Page
	i and host group k, i.e., $V_i/H_k$, and has no vector movement
${\tilde{\mathcal {R}}}_0^{(k)}$	Basic reproduction number of patch k in disconnection with only	33
	vector movement before disconnection
$h_i$	Proportion of hosts in group i, i.e., $H_i/H$	20
$v_j$	Proportion of vectors of patch j, i.e., $V_j/V$	20
$p_k$	Proportion of hosts from all host groups that commute to patch k	23
$q_k$	Proportion of vectors from all vector patches that commute to patch k	23
${\hat{L}}$	${\mathscr {A}}{\mathscr {D}}^{-1}{\mathscr {B}}{\mathscr {C}}^{-1}$ in the case of all ${\hat{\mathcal {R}}}_{ijskr}\equiv 1$	21
L	${\mathscr {A}}{\mathscr {D}}^{-1}{\mathscr {B}}{\mathscr {C}}^{-1}$ in the case of all $\mathcal {R}_{ijskr}\equiv 1$	27
${\tilde{A}}$	A spectral radius equivalent form of ${\mathscr {A}}{\mathscr {D}}^{-1}{\mathscr {B}}{\mathscr {C}}^{-1}$	51
${\tilde{L}}$	${\tilde{A}}$ in the case of all ${\hat{\mathcal {R}}}_{jjskr}\equiv 1$	51
${\check{L}}$	${\mathscr {B}}{\mathscr {C}}^{-1}{\mathscr {A}}{\mathscr {D}}^{-1}$ in the case of all ${\tilde{\mathcal {R}}}_{ijk}\equiv 1$ (no vector movement)	53

Appendix B: Derivation of matrix W

• (1) The vector-borne disease considered here cannot be directly transmitted from host to host, so the (1, 1) block in Table 2 is $0_{m\times m}$.

• (2) Suppose the hosts of group $i~(1\le i\le m)$ spend part of time in patch $j~(1\le j\le k)$. If an infected host of group i is introduced, then this infected host can visit patch j and infect the susceptible vectors of patch j. On the other hand, if an infected vector of patch j is introduced, then this infected vector can infect the susceptible hosts of group i who visit patch j. So, the (1, 2) and (2, 1) blocks in Table 2 are $P_{1}$ and $P_{1}^{\textrm{T}}$, respectively.

• (3) Since no host visits the last $n-k$ patches, the disease transmission from the infected hosts of group $i~(1\le i\le m)$ to the susceptible vectors of patch $j~(k+1\le j\le n)$ in patch j cannot occur. Similarly, the disease transmission from the infected vectors of patch j to the susceptible hosts of group i in patch j is impossible. So, the (1, 3) and (3, 1) blocks in Table 2 are $0_{m\times (n-k)}$ and $0_{(n-k)\times m}$, respectively.

• (4) Suppose the vectors of patch $j~(1\le j\le k)$ spend part of time in patch $l~(1\le l\le k)$. If an infected vector of patch j is introduced, then this infected vector can visit patch l and infect the susceptible hosts in patch l (the first k patches have host visitors). The infected hosts in patch l can then infect the susceptible vectors of patch l. On the other hand, if an infected vector of patch l is introduced, then this infected vector can infect the susceptible hosts in patch l. The infected hosts in patch l can infect the susceptible vectors of patch j who visit patch l. In other words, the visit of vectors of patch j to patch l has the same transmission impact as the visit of vectors of patch l to patch j. So, the (2, 2) block in Table 2 is $Q_1+Q_1^{\textrm{T}}$.

• (5) Suppose the vectors of patch $l~(k+1\le l\le n)$ spend part of time in patch $j~(1\le j\le k)$. If an infected vector of patch l is introduced, then this infected vector can visit patch j and infect the susceptible hosts in patch j (the first k patches have host visitors). The infected hosts in patch j can then infect the susceptible vectors of patch j. On the other hand, if an infected vector of patch j is introduced, then this infected vector can infect the susceptible hosts in patch j. The infected hosts in patch j can infect the susceptible vectors of patch l who visit patch j. Since the last $n-k$ patches are host-free, the visit of the vectors of the first k patches to the last $n-k$ patches does not cause disease transmission. So, the (3, 2) and (2, 3) blocks in Table 2 are $Q_2$ and $Q_2^{\textrm{T}}$, respectively.

• (6) The last $n-k$ patches are host-free, so the movement of the vectors of the last $n-k$ patches between the last $n-k$ patches produces no infection. So, the (3, 3) block in Table 2 is $0_{(n-k)\times (n-k)}$.

Appendix C: Proof of Theorem 3.2

Proof

Necessity. It follows from the nonnegativity of matrices $P_1$, $Q_1$, and $Q_2$ that

$$\begin{aligned} \begin{aligned} W^{2}&= \begin{pmatrix} P_{1}P_{1}^{\textrm{T}} &{}\quad P_{1}(Q_{1}+Q_{1}^{\textrm{T}}) &{}\quad P_{1}Q_{2}^{\textrm{T}} \\ (Q_{1}+Q_{1}^{\textrm{T}})P_{1}^{\textrm{T}} &{}\quad P_{1}^{\textrm{T}}P_{1}+\left( Q_{1}+Q_{1}^{\textrm{T}}\right) ^{2}+Q_{2}^{\textrm{T}}Q_{2} &{}\quad (Q_{1}+Q_{1}^{\textrm{T}})Q_{2}^{\textrm{T}} \\ Q_{2}P_{1}^{\textrm{T}} &{}\quad Q_{2}(Q_{1}+Q_{1}^{\textrm{T}}) &{} \quad Q_{2}Q_{2}^{\textrm{T}} \end{pmatrix}\\&\quad \ge \begin{pmatrix} 0 &{}\quad P_{1}Q_{1}^{\textrm{T}} &{}\quad P_{1}Q_{2}^{\textrm{T}} \\ Q_{1}P_{1}^{\textrm{T}} &{}\quad 0 &{}\quad 0 \\ Q_{2}P_{1}^{\textrm{T}} &{}\quad 0 &{} \quad 0 \end{pmatrix} =M\ge 0. \end{aligned} \end{aligned}$$

Thus, the irreducibility of the matrix M implies the irreducibility of the matrix $W^2$. Hence W is also irreducible. Suppose not, i.e., W is reducible, then there exists a permutation matrix S such that

$$\begin{aligned} \begin{aligned} S^{\textrm{T}}WS= \begin{pmatrix} {\tilde{W}}_1 &{} \quad {\tilde{W}}_3 \\ 0 &{}\quad {\tilde{W}}_2 \end{pmatrix}, \end{aligned} \end{aligned}$$

and hence

$$\begin{aligned} \begin{aligned} S^{\textrm{T}}W^2S= \begin{pmatrix} {\tilde{W}}_1^2 &{}\quad {\tilde{W}}_1{\tilde{W}}_3+{\tilde{W}}_3{\tilde{W}}_2 \\ 0 &{}\quad {\tilde{W}}_2^2 \end{pmatrix}. \end{aligned} \end{aligned}$$

Therefore $W^2$ is reducible, a contradiction.

Sufficiency. Suppose that the matrix W is irreducible, then the directed graph generated by W, denoted by ${\mathcal {G}}(W)$, is strongly connected (Horn and Johnson 2013). We write the sets of nodes of the directed graphs ${\mathcal {G}}(W)$ and ${\mathcal {G}}(M)$ as

$$\begin{aligned} \{W_{1},\dots ,W_{m},\,W_{m+1},\dots ,W_{m+n}\}\ \text{ and } \ \{M_{1},\dots ,M_{m},\,M_{m+1},\dots ,M_{m+n}\}, \end{aligned}$$

respectively. Denote $W=(w_{ij})_{(m+n)\times (m+n)}$ and $M=(m_{ij})_{(m+n)\times (m+n)}$, where

$$\begin{aligned} w_{ij}= {\left\{ \begin{array}{ll} p_{i,j-m}, &{} 1\le i\le m,\;m+1\le j\le m+k, \\ p_{j,i-m}, &{} m+1\le i\le m+k,\;1\le j\le m, \\ q_{i-m,j-m}+q_{j-m,i-m}, &{} m+1\le i,\,j\le m+k, \\ q_{i-m,j-m}, &{} m+k+1\le i\le m+n,\;m+1\le j\le m+k, \\ q_{j-m,i-m}, &{} m+1\le i\le m+k,\;m+k+1\le j\le m+n, \\ 0, &{} \text{ otherwise }, \end{array}\right. }\nonumber \\ \end{aligned}$$

(C.1)

and

$$\begin{aligned} m_{ij}={\left\{ \begin{array}{ll} \sum \limits _{r=1}^{k}p_{ir}q_{j-m,r}, &{} 1\le i\le m,\;m+1\le j\le m+n, \\ \sum \limits _{r=1}^{k}p_{jr}q_{i-m,r}, &{} m+1\le i\le m+n,\;1\le j\le m, \\ 0, &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

(C.2)

Based on the symmetry of matrices W and M, and the number of nonzero blocks in matrix W, we have three parts to show that: if there is a directed path between a given pair of nodes of graph ${\mathcal {G}}(W)$, then there is also a directed path between the corresponding pair of nodes of graph ${\mathcal {G}}(M)$. Therefore, the strong connectivity of ${\mathcal {G}}(W)$ implies the strong connectivity of ${\mathcal {G}}(M)$.

• (1) Consider the (1, 2) block (or called submatrix) of the block (or called partitioned) matrix W. Suppose $p_{lj}>0$ for some $l\in \{1,\dots ,m\}$ and $j\in \{1,\dots ,k\}$. It follows from (C.1) and the symmetry of W that

  $$\begin{aligned} w_{l,m+j}=w_{m+j,l}=p_{lj}>0. \end{aligned}$$

  So, there is a bidirectional edge connecting nodes $W_{l}$ and $W_{m+j}$ of graph ${\mathcal {G}}(W)$. Meanwhile, it follows from (C.2), the symmetry of M and

  $$\begin{aligned} p_{lj}>0\ \text{ and } \ q_{jj}>0, \end{aligned}$$

  that

  $$\begin{aligned} m_{l,m+j}=m_{m+j,l}=\sum \limits _{r=1}^{k}p_{lr}q_{jr}\ge p_{lj}q_{jj}>0. \end{aligned}$$

  Hence, there is also a bidirectional edge connecting nodes $M_{l}$ and $M_{m+j}$ of graph ${\mathcal {G}}(M)$.

• (2) Consider the (2, 2) block of W. Suppose $q_{sj}>0$ for some $s,\,j\in \{1,\dots ,k\}$, then

  $$\begin{aligned} w_{m+s,m+j}=w_{m+j,m+s}=q_{sj}+q_{js}\ge q_{sj}>0. \end{aligned}$$

  So, there is a bidirectional edge connecting nodes $W_{m+s}$ and $W_{m+j}$ of ${\mathcal {G}}(W)$. Since at least one host group visits patch j, there exists some $i\in \{1,\dots ,m\}$ such that $p_{ij}>0$, which means that

  $$\begin{aligned} m_{i,m+s}=m_{m+s,i}=\sum \limits _{r=1}^{k}p_{ir}q_{sr}\ge p_{ij}q_{sj}>0. \end{aligned}$$

  So, the nodes $M_{i}$ and $M_{m+s}$ of ${\mathcal {G}}(M)$ are connected by a bidirectional edge. Moreover, it follows from (C.2), the symmetry of M and

  $$\begin{aligned} p_{ij}>0\;\; \text{ and } \;\; q_{jj}>0, \end{aligned}$$

  that

  $$\begin{aligned} m_{i,m+j}=m_{m+j,i}=\sum \limits _{r=1}^{k}p_{ir}q_{jr}\ge p_{ij}q_{jj}>0. \end{aligned}$$

  So, the nodes $M_{i}$ and $M_{m+j}$ of ${\mathcal {G}}(M)$ are also connected by a bidirectional edge. Thus, there is a bidirectional path passing nodes $M_{m+s}$ and $M_{m+j}$ of ${\mathcal {G}}(M)$.

• (3) Consider the (3, 2) block of W. Suppose $q_{cj}>0$ for some $c\in \{k+1,\dots ,n\}$ and $j\in \{1,\dots ,k\}$, then

  $$\begin{aligned} w_{m+c,m+j}=w_{m+j,m+c}=q_{cj}>0. \end{aligned}$$

  So, there is a bidirectional edge connecting nodes $W_{m+c}$ and $W_{m+j}$ of graph ${\mathcal {G}}(W)$. Similarly, there exists some $i\in \{1,\dots ,m\}$ such that $p_{ij}>0$, which implies that

  $$\begin{aligned} m_{i,m+c}=m_{m+c,i}=\sum \limits _{r=1}^{k}p_{ir}q_{cr}\ge p_{ij}q_{cj}>0. \end{aligned}$$

  So, the nodes $M_{i}$ and $M_{m+c}$ of graph ${\mathcal {G}}(M)$ are connected by a bidirectional edge. Moreover, it again follows from (C.2), the symmetry of M and

  $$\begin{aligned} p_{ij}>0\ \text{ and } \ q_{jj}>0, \end{aligned}$$

  that

  $$\begin{aligned} m_{i,m+j}=m_{m+j,i}=\sum \limits _{r=1}^{k}p_{ir}q_{jr}\ge p_{ij}q_{jj}>0. \end{aligned}$$

  There is a bidirectional edge connecting nodes $M_{i}$ and $M_{m+j}$ of graph ${\mathcal {G}}(M)$. Thus, the nodes $M_{m+c}$ and $M_{m+j}$ of graph ${\mathcal {G}}(M)$ are connected by a bidirectional path.

In conclusion, if the directed graph ${\mathcal {G}}(W)$ is strongly connected, then the directed graph ${\mathcal {G}}(M)$ is also strongly connected. So, the matrix M is irreducible. $\square$

Appendix D: Proof of Theorem 3.13

Proof

Let ${\varvec{f}}=(f_{1},\dots ,f_{m+n})$ be the vector field generated by (2.2) and $\phi _t$ the associated semiflow. We rewrite the model system (2.2) as ${\varvec{x}}'={\varvec{f}}({\varvec{x}})$, where

$$\begin{aligned} \begin{aligned} {\varvec{x}}=(x_{1},\dots ,x_{m+n})=(I_{1}^{h},\,\dots ,\,I_{m}^{h},\,I_{1}^{v},\,\dots ,\,I_{n}^{v}). \end{aligned} \end{aligned}$$

By Proposition 2.2, it suffices to consider system (2.2) in the positively invariant set $\Gamma$. We complete the proof by verifying the conditions of Corollary 3.2 in Zhao and Jing (1996).

• (1) Direct calculation yields the Jacobian matrix of system (2.2) at ${\varvec{x}}$, denoted by

  $$\begin{aligned} D{\varvec{f}}({\varvec{x}})=\left( \frac{\partial f_{s}}{\partial x_{r}}\right) _{(m+n)\times (m+n)}, \end{aligned}$$

  where

  $$\begin{aligned} \frac{\partial f_{s}}{\partial x_{r}}= {\left\{ \begin{array}{ll} -b_{s}\sum \limits _{k\in \Omega _{v}^{0}}a_{k}\dfrac{\sum _{j\in \Omega _{v}}q_{jk}I_{j}^{v}}{\sum _{l\in \Omega _{h}}p_{lk}H_{l}}\,p_{sk}- \left( \gamma _{s}+\mu _{s}^{h}\right) , &{} 1\le s=r\le m, \\ b_{s}\left( H_{s}-I_{s}^{h}\right) \sum \limits _{k\in \Omega _{v}^{0}}a_{k}\dfrac{p_{sk}q_{r-m,k}}{\sum _{l\in \Omega _{h}}p_{lk}H_{l}}, &{} 1\le s\le m,\;m+1\le r\le m+n, \\ c_{r}\left( V_{s-m}-I_{s-m}^{v}\right) \sum \limits _{k\in \Omega _{v}^{0}}a_{k}\dfrac{q_{s-m,k}p_{rk}}{\sum _{l\in \Omega _{h}}p_{lk}H_{l}}, &{} m+1\le s\le m+n,\;1\le r\le m, \\ -\sum \limits _{k\in \Omega _{v}^{0}}a_{k}\dfrac{\sum _{i\in \Omega _{h}}c_{i}p_{ik}I_{i}^{h}}{\sum _{l\in \Omega _{h}}p_{lk}H_{l}}\,q_{s-m,k}-\mu _{s-m}^{v}, &{} m+1\le s=r\le m+n,\\ 0, &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

  Clearly, the matrix $D\varvec{f}(\varvec{x})$ is quasi-positive (or called essentially nonnegative) on $\Gamma$. So, system (2.2) is cooperative on $\Gamma$. The strong connectivity of the host-vector network implies that $D\varvec{f}(\varvec{0})=F-V$ is irreducible. It follows that $D\varvec{f}(\varvec{x})$ is irreducible in $\mathring{\Gamma }$, the interior of $\Gamma$. Moreover, any nonzero solution starting at the boundary of $\Gamma$ will immediately enter and stay in $\mathring{\Gamma }$.

• (2) Clearly, ${\varvec{f}}({\varvec{0}})={\varvec{0}}$, and $f_{i}({\varvec{x}})\ge 0$ for all ${\varvec{x}}\in \Gamma$ with $x_i=0$, $i=1,\dots ,m+n$. Meanwhile, $f_{i}(\varvec{x})=-(\gamma _i+\mu _i^h)H_i<0$ for all ${\varvec{x}}\in \Gamma$ with $x_i=H_i$, $i=1,\dots ,m$, and $f_{i}(\varvec{x})=-\mu _{i-m}^vV_{i-m}<0$ for all ${\varvec{x}}\in \Gamma$ with $x_i=V_{i-m}$, $i=m+1,\dots ,m+n$.

• (3) For any $\xi \in (0,1)$ and ${\varvec{x}}\in \Gamma$ with ${\varvec{x}}\gg \varvec{0}$, we have

  $$\begin{aligned} \begin{aligned} f_{i}(\xi {\varvec{x}})-\xi f_{i}({\varvec{x}}) =\xi \,(1-\xi )\,b_{i}\sum _{k\in \Omega _{v}^{0}}a_{k}\frac{\sum _{j\in \Omega _{v}}q_{jk}I_{j}^{v}}{\sum _{l\in \Omega _{h}}p_{lk}H_{l}}\,p_{ik}\,I_{i}^{h}>0, \quad i\in \Omega _{h}, \end{aligned} \end{aligned}$$

  and

  $$\begin{aligned} \begin{aligned} f_{m+j}(\xi {\varvec{x}})-\xi f_{m+j}({\varvec{x}}) =\xi \,(1-\xi )\, \sum _{k\in \Omega _{v}^{0}}a_{k}\frac{\sum _{i\in \Omega _{h}}c_{i}p_{ik}I_{i}^{h}}{\sum _{l\in \Omega _{h}}p_{lk}H_{l}}\,q_{jk}\, I_{j}^{v}>0, \quad j\in \Omega _{v}. \end{aligned} \end{aligned}$$

  Hence, ${\varvec{f}}$ is strictly sublinear on $\Gamma$.

It follows from Theorem 2 in van den Driessche and Watmough (2002) or Theorem A.1 in Diekmann et al. (2010) that

$$\begin{aligned} s(D{\varvec{f}}(\varvec{0}))=s(F-V)>(=,<)\ 0\ \Leftrightarrow \ \mathcal {R}_0>(=,<)\ 1. \end{aligned}$$

By Corollary 3.2 in Zhao and Jing (1996), the global asymptotic stability of system (2.2) is proved. Moreover, the strong monotonicity of $\phi _t$ implies that the unique endemic equilibrium satisfies $\varvec{0}\ll E^*\ll (H_1,\dots ,H_m,V_1,\dots ,V_n)$. $\square$

Appendix E: Proof of Theorem 4.2

Proof

According to (3.1) and (3.2a), we have

$$\begin{aligned} \begin{aligned}&{\mathscr {A}}{\mathscr {D}}^{-1}{\mathscr {B}}{\mathscr {C}}^{-1}=(\alpha _{ij})_{m\times m} \\&\quad =\mathop {\textrm{diag}}\{b_1H_1,\ldots ,b_mH_m\} \\&\quad \cdot \left( \frac{c_j}{\gamma _j+\mu _j^h} \cdot \sum \limits _{s\in \Omega _v} \frac{V_s}{\mu _s^v} \left( \sum \limits _{k\in \Omega _v^0} a_k \, \frac{p_{ik}q_{sk}}{\sum _{l\in \Omega _h}p_{lk}H_l}\right) \left( \sum \limits _{r\in \Omega _v^0} a_r \, \frac{p_{jr}q_{sr}}{\sum _{l\in \Omega _h}p_{lr}H_l}\right) \right) _{m\times m}. \end{aligned} \end{aligned}$$

Define

$$\begin{aligned} \begin{aligned} {\tilde{A}}&=\left( \frac{c_j}{\gamma _j+\mu _j^h} \cdot \sum \limits _{s\in \Omega _v} \frac{V_s}{\mu _s^v} \left( \sum \limits _{k\in \Omega _v^0} a_k \, \frac{p_{ik}q_{sk}}{\sum _{l\in \Omega _h}p_{lk}H_l}\right) \left( \sum \limits _{r\in \Omega _v^0} a_r \, \frac{p_{jr}q_{sr}}{\sum _{l\in \Omega _h}p_{lr}H_l}\right) \right) _{m\times m}\\&\quad \cdot \mathop {\textrm{diag}}\{b_1H_1,\ldots ,b_mH_m\}\\&=\left( \frac{b_j c_j H_j}{\gamma _j+\mu _j^h} \cdot \sum \limits _{s\in \Omega _v} \frac{V_s}{\mu _s^v} \left( \sum \limits _{k\in \Omega _v^0} a_k \, \frac{p_{ik}q_{sk}}{\sum _{l\in \Omega _h}p_{lk}H_l}\right) \left( \sum \limits _{r\in \Omega _v^0} a_r \, \frac{p_{jr}q_{sr}}{\sum _{l\in \Omega _h}p_{lr}H_l}\right) \right) _{m\times m}\\&=\left( h_j \sum \limits _{s\in \Omega _v} v_s \left( \sum \limits _{k\in \Omega _v^0}\sum \limits _{r\in \Omega _v^0}\left( \frac{a_k a_r b_j c_j V}{\mu _s^v(\gamma _j+\mu _j^h)H}\cdot \frac{p_{ik}q_{sk}}{\sum _{l\in \Omega _h}p_{lk}h_l}\cdot \frac{p_{jr}q_{sr}}{\sum _{l\in \Omega _h}p_{lr}h_l}\right) \right) \right) _{m\times m}. \end{aligned} \end{aligned}$$

Clearly, the matrices ${\tilde{A}}$ and ${\mathscr {A}}{\mathscr {D}}^{-1}{\mathscr {B}}{\mathscr {C}}^{-1}$ have the same spectral radius. Denote

$$\begin{aligned} {\tilde{L}}=\left( h_j \sum \limits _{s\in \Omega _v} v_s \left( \sum \limits _{k\in \Omega _v^0}\frac{p_{ik}q_{sk}}{\sum _{l\in \Omega _h}p_{lk}h_l}\right) \left( \sum \limits _{r\in \Omega _v^0}\frac{p_{jr}q_{sr}}{\sum _{l\in \Omega _h}p_{lr}h_l}\right) \right) _{m\times m}. \end{aligned}$$

So,

$$\begin{aligned} \min \limits _{\begin{array}{c} {j\in \Omega _h}\\ {s,k,r\in \Omega _v} \end{array}} \left( {\hat{\mathcal {R}}}_{jjskr}\right) ^2 {\tilde{L}}\le {\tilde{A}} \le \max \limits _{\begin{array}{c} {j\in \Omega _h}\\ {s,k,r\in \Omega _v} \end{array}} \left( {\hat{\mathcal {R}}}_{jjskr}\right) ^2 {\tilde{L}}, \end{aligned}$$

which implies that

$$\begin{aligned}{} & {} \min \limits _{\begin{array}{c} {j\in \Omega _h}\\ {s,k,r\in \Omega _v} \end{array}} {\hat{\mathcal {R}}}_{jjskr} \sqrt{\rho \left( {\tilde{L}}\right) }\le \sqrt{\rho \left( {\tilde{A}}\right) }=\sqrt{\rho ({\mathscr {A}}{\mathscr {D}}^{-1}{\mathscr {B}}{\mathscr {C}}^{-1})}=\mathcal {R}_0\\{} & {} \quad \le \max \limits _{\begin{array}{c} {j\in \Omega _h}\\ {s,k,r\in \Omega _v} \end{array}} {\hat{\mathcal {R}}}_{jjskr} \sqrt{\rho \left( {\tilde{L}}\right) }. \end{aligned}$$

Notice that ${\hat{L}}^{\textrm{T}}={\tilde{L}}$, so it follows from the estimates of $\rho ({\tilde{L}})$ in the proof of Theorem 4.1 that this theorem is proved. $\square$

Appendix F: Proof of Theorem 4.9

Proof

The proof of Theorem 4.2 indicates that $\mathcal {R}_0=\sqrt{\rho ({\tilde{A}})}$ where

$$\begin{aligned} \begin{aligned} {\tilde{A}}&=\left( H_j^2 \sum \limits _{s\in \Omega _v}\sum \limits _{k\in \Omega _v^0} \sum \limits _{r\in \Omega _v^0}\left( \frac{a_ka_rb_jc_jV_s}{\mu _s^v(\gamma _j+\mu _j^h)H_j} \cdot \frac{p_{ik}q_{sk}}{\sum _{l\in \Omega _h}p_{lk}H_l} \cdot \frac{p_{jr}q_{sr}}{\sum _{l\in \Omega _h}p_{lr}H_l} \right) \right) _{m\times m}. \end{aligned} \end{aligned}$$

Denote

$$\begin{aligned} U=\left( H_j^2 \sum \limits _{s\in \Omega _v}\left( \sum \limits _{k\in \Omega _v^0}\frac{p_{ik}q_{sk}}{\sum _{l\in \Omega _h}p_{lk}H_l}\right) \left( \sum \limits _{r\in \Omega _v^0}\frac{p_{jr}q_{sr}}{\sum _{l\in \Omega _h}p_{lr}H_l}\right) \right) _{m\times m}, \end{aligned}$$

then

$$\begin{aligned} \min \limits _{\begin{array}{c} {j\in \Omega _h}\\ {s,k,r\in \Omega _v} \end{array}} \mathcal {R}_{jjskr}\,\sqrt{\rho (U)} \le \sqrt{\rho \left( {\tilde{A}}\right) } =\mathcal {R}_{0} \le \max \limits _{\begin{array}{c} {j\in \Omega _h}\\ {s,k,r\in \Omega _v} \end{array}} \mathcal {R}_{jjskr}\,\sqrt{\rho (U)}. \end{aligned}$$

Define ${\hat{S}}=\mathop {\textrm{diag}}\{H_1,\ldots ,H_m\}$. A similarity transformation finds ${\hat{S}}U{\hat{S}}^{-1}=L$ and hence $\rho (U)=\rho (L)$. The proof is complete by using the estimates on $\rho (L)$ in Theorem 4.7. $\square$

Appendix G: Proof of Theorem 4.12

Proof

It follows from (4.11b) that ${\mathscr {B}}{\mathscr {C}}^{-1}{\mathscr {A}}{\mathscr {D}}^{-1} =(\beta _{ij})_{n\times n}$ where

$$\begin{aligned} \begin{aligned} \beta _{ij}&=\sum \limits _{k\in \Omega _{h}} \left( \frac{a_i\,a_j\,b_k\,c_k V_i}{\mu _{j}^{v}\left( \gamma _{k}+\mu _{k}^{h}\right) H_{k}} \cdot \frac{p_{ki}\,p_{kj}\,H_{k}^{2}}{\sum _{l\in \Omega _{h}}p_{li}H_{l} \cdot \sum _{l\in \Omega _{h}}p_{lj}H_{l}}\right) . \end{aligned} \end{aligned}$$

Define

$$\begin{aligned} {\check{L}}=\left( {\check{l}}_{ij}\right) _{n\times n}= \left( \sum \limits _{k\in \Omega _{h}}\frac{p_{ki}\,p_{kj}\,H_{k}^{2}}{\sum _{l\in \Omega _{h}}p_{li}H_{l} \cdot \sum _{l\in \Omega _{h}}p_{lj}H_{l}}\right) _{n\times n}. \end{aligned}$$

Clearly,

$$\begin{aligned} \begin{aligned} \min \limits _{i,j,k}{\tilde{\mathcal {R}}}_{ijk}\,\sqrt{\rho \left( {\check{L}}\right) }\le \rho ({\mathscr {B}}{\mathscr {C}}^{-1}{\mathscr {A}}{\mathscr {D}}^{-1})=\mathcal {R}_{0}\le \max \limits _{i,j,k}{\tilde{\mathcal {R}}}_{ijk}\,\sqrt{\rho \left( {\check{L}}\right) }. \end{aligned} \end{aligned}$$

It follows from Corollary 8.1.29 in Horn and Johnson (2013) that

$$\begin{aligned} \begin{aligned} \sum _{i\in \Omega _v}{\check{l}}_{ij}&=\sum _{i\in \Omega _v} \sum \limits _{k\in \Omega _{h}}\left( \frac{p_{ki}H_{k}}{\sum _{l\in \Omega _{h}}p_{li}H_{l}} \cdot \frac{p_{kj}H_{k}}{\sum _{l\in \Omega _{h}}p_{lj}H_{l}}\right) \\&\le \sum _{i\in \Omega _v} \sum \limits _{k\in \Omega _{h}}\frac{p_{ki}H_{k}}{\sum _{l\in \Omega _{h}}p_{li}H_{l}} =\sum _{i\in \Omega _v}\frac{\sum _{k\in \Omega _{h}}p_{ki}H_{k}}{\sum _{l\in \Omega _{h}}p_{li}H_{l}} =n, \quad \forall \; j\in \Omega _{v}, \end{aligned} \end{aligned}$$

implies that $\rho ({\check{L}})\le n$. So the upper bound of $\mathcal {R}_0$ is proved.

On the other hand, since ${\check{L}}$ is a real symmetric matrix, the Rayleigh quotient theorem (Horn and Johnson 2013) gives

$$\begin{aligned} \rho \left( {\check{L}}\right) =\max \left\{ \sum \limits _{i,j\in \Omega _{v}}{\check{l}}_{ij}\, {\check{x}}_{i}\,{\check{x}}_{j} \ \bigg |\ ({\check{x}}_1,\,\dots ,\,{\check{x}}_n)\in {\mathbb {R}}^n\ \text{ and } \ \sum _{i\in \Omega _{v}}{\check{x}}_{i}^{2}=1\right\} . \end{aligned}$$

Choosing ${\check{x}}_{i}=1/\sqrt{n}$ for all $i\in \Omega _{v}$ and applying the Cauchy–Schwarz inequality yield

$$\begin{aligned} \begin{aligned} \rho \left( {\check{L}}\right)&\ge \sum \limits _{i,j\in \Omega _{v}}{\check{l}}_{ij}\,{\check{x}}_{i}\,{\check{x}}_{j} =\frac{1}{mn}\sum _{k\in \Omega _h}1^2\cdot \sum \limits _{k\in \Omega _{h}} \left( \sum \limits _{i\in \Omega _{v}}\frac{p_{ki}H_{k}}{\sum _{l\in \Omega _{h}}p_{li}H_{l}}\right) ^{2}\\&\ge \dfrac{1}{mn} \left( \sum \limits _{k\in \Omega _{h}}\left( 1\cdot \sum \limits _{i\in \Omega _{v}} \frac{p_{ki}H_{k}}{\sum _{l\in \Omega _{h}}p_{li}H_{l}}\right) \right) ^{2} =\dfrac{1}{mn} \left( \sum \limits _{i\in \Omega _{v}}\frac{\sum _{k\in \Omega _{h}}p_{ki}H_{k}}{\sum _{l\in \Omega _{h}}p_{li}H_{l}}\right) ^{2} =\dfrac{n}{m}. \end{aligned} \end{aligned}$$

So, we have $\rho \left( {\check{L}}\right) \ge n/m$ and the proof is complete. $\square$

Appendix H: Proof of Theorem 4.16

Proof

Using the next generation matrix method (Diekmann et al. 1990; van den Driessche and Watmough 2002), the basic reproduction numbers of models (4.13) and (4.14) are

$$\begin{aligned} \begin{aligned} \mathcal {R}_{1}=\sqrt{\rho \left( {\mathscr {B}}_{1}{\mathscr {C}}_{1}^{-1}{\mathscr {A}}_{1}{\mathscr {D}}_{1}^{-1}\right) } \ \text{ and } \ \mathcal {R}_{2}=\sqrt{\rho \left( {\mathscr {B}}_{2}{\mathscr {C}}_{2}^{-1}{\mathscr {A}}_{2}{\mathscr {D}}_{2}^{-1}\right) }, \end{aligned} \end{aligned}$$

respectively, where

$$\begin{aligned} \begin{aligned} {\mathscr {B}}_{1}{\mathscr {C}}_{1}^{-1}{\mathscr {A}}_{1}{\mathscr {D}}_{1}^{-1}&= ({\tilde{\beta }}_{ij})_{2\times 2}=\left( \frac{a_ia_jV_i}{\mu _j^v\Psi _i\Psi _j}\sum _{k\in \Omega } \frac{b_kc_k(p_{ki}^fp_{kj}^fH_k^f+p_{ki}^up_{kj}^uH_k^u)}{\gamma _k+\mu _k^h}\right) _{2\times 2}, \\ {\mathscr {B}}_{2}{\mathscr {C}}_{2}^{-1}{\mathscr {A}}_{2}{\mathscr {D}}_{2}^{-1}&= (\beta _{ij})_{2\times 2}=\left( \frac{a_ia_jV_i}{\mu _j^v\Psi _i\Psi _j}\sum _{k\in \Omega } \frac{b_kc_kp_{ki}p_{kj}H_k}{\gamma _k+\mu _k^h}\right) _{2\times 2}. \end{aligned} \end{aligned}$$

Clearly,

$$\begin{aligned} \begin{aligned} (\mathcal {R}_{1})^2=\frac{C_{1}+\sqrt{C_{1}^{2}-4D_{1}}}{2}\ \text{ and } \ (\mathcal {R}_{2})^{2}=\frac{C_{2}+\sqrt{C_{2}^{2}-4D_{2}}}{2}, \end{aligned} \end{aligned}$$

where $C_i$ and $D_i$ are the trace and determinant of matrix ${\mathscr {B}}_{i}{\mathscr {C}}_{i}^{-1}{\mathscr {A}}_{i}{\mathscr {D}}_{i}^{-1}$, respectively.

The inequality $\mathcal {R}_{1}\ge \mathcal {R}_{2}$ is equivalent to

$$\begin{aligned} C_{1}-C_{2}\ge \sqrt{C_{2}^{2}-4D_{2}}-\sqrt{C_{1}^{2}-4D_{1}}. \end{aligned}$$

According to Theorem 3.9 in Gao (2019) or Theorem 3.3 in Chen and Gao (2020), it suffices to show that

$$\begin{aligned} C_1-C_2\ge 0\ \text{ and } \ \left( C_{1}-C_{2}\right) \left( C_{2}D_{1}-C_{1}D_{2}\right) \ge \left( D_{1}-D_{2}\right) ^{2}. \end{aligned}$$

A straightforward but tedious algebraic calculation gives

$$\begin{aligned} \begin{aligned} C_1-C_2&=\sum _{i\in \Omega }\frac{a_i^2V_i}{\mu _i^v\Psi _i^2} \sum _{k\in \Omega }\frac{b_kc_k(p_{ki}^f-p_{ki}^u)^2H_k^fH_k^u}{(\gamma _k+\mu _k^h)H_k}\ge 0, \end{aligned} \end{aligned}$$

with equality if and only if $P^f=P^u$, and

$$\begin{aligned} \begin{aligned}&\left( C_{1}-C_{2}\right) \left( C_{2}D_{1}-C_{1}D_{2}\right) -\left( D_{1}-D_{2}\right) ^{2} =\left( \frac{K_1K_2a_1a_2}{H_1H_2\Psi _1\Psi _2}\right) ^2\cdot \frac{V_1V_2}{\mu _1^v\mu _2^v}\ge 0, \end{aligned} \end{aligned}$$

with equality if and only if $K_1=0$ or $K_2=0$, i.e., $\mathcal {R}_1^{(1)}=\mathcal {R}_1^{(2)}$ or $P^f=P^u$, where

$$\begin{aligned} \begin{aligned} K_1=(\mathcal {R}_1^{(1)})^2-(\mathcal {R}_1^{(2)})^2\ \ \text{ and } \ \ K_2=\sum _{\begin{array}{c} {i,j\in \Omega }\\ {i\ne j} \end{array}} \frac{b_ic_i}{\gamma _i+\mu _i^h}H_i^fH_i^u(p_{ii}^f-p_{ii}^u)^2H_j. \end{aligned} \end{aligned}$$

Consequently, $\mathcal {R}_{1}\ge \mathcal {R}_{2}$ with equality if and only if $\mathcal {R}_1^{(1)}=\mathcal {R}_1^{(2)}$ or $P^f=P^u$. $\square$