Extinction scenarios in evolutionary processes: a multinomial Wright–Fisher approach

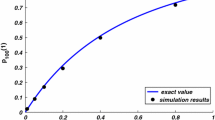
Abstract

We study a discrete-time multi-type Wright–Fisher population process. The mean-field dynamics of the stochastic process is induced by a general replicator difference equation. We prove several results regarding the asymptotic behavior of the model, focusing on the impact of the mean-field dynamics on it. One of the results is a limit theorem that describes sufficient conditions for an almost certain path to extinction, first eliminating the type which is the least fit at the mean-field equilibrium. The effect is explained by the metastability of the stochastic system, which under the conditions of the theorem spends almost all time before the extinction event in a neighborhood of the equilibrium. In addition to the limit theorems, we propose a maximization principle for a general deterministic replicator dynamics and study its implications for the stochastic model.

Appendices

Appendices

1.1 Appendix A. Absorption states and stochastic equilibria

In this appendix we explore the connection between basic geometric properties of the vector field ${\varvec{\Gamma }}$ and the structure of closed communication classes of the Markov chain $\textbf{X}^{(N)}.$ In other words, we study the configuration of absorbing states and identify possible supports of stationary distributions according to the properties of ${\varvec{\Gamma }}$. We remark that the results of this section are included for the sake of completeness and are not used anywhere else in the remainder of the paper. We have made the section self-contained and included the necessary background on the Markov chain theory.

The main result of the appendix is stated in Theorem 7.3 where a geometric characterization of recurrent classes is described. The general structure of recurrent classes of $\textbf{X}^{(N)}$ in this theorem holds universally for the Wright–Fisher model (7) with any update function ${\varvec{\Gamma }}.$ Thus, in Appendix A we deviate from assumption (10) that we have used throughout the paper and to which we will return in the subsequent Appendix B, and adopt instead the following general one:

Assumption 7.1

$\textbf{X}^{(N)}$ is a Markov chain on $\Delta _M$ with transition kernel defined by (7) and an arbitrary update rule ${\varvec{\Gamma }}:\Delta _M\rightarrow \Delta _M.$

Recall (5) and (13). The discussion in this section is largely based on the fact that

$$\begin{aligned} P_N(\textbf{x},\textbf{y})>0 \quad \Longleftrightarrow {{\mathcal {C}}}(\textbf{y})\subset {{\mathcal {C}}}\big ({\varvec{\Gamma }}(\textbf{x})\big )\quad \Longleftrightarrow \quad P_N(\textbf{x},\textbf{z})>0~\text{ for } \text{ all }~\textbf{z}\in \Delta _{[{{\mathcal {C}}}(\textbf{y})],M}. \nonumber \\ \end{aligned}$$

(64)

This simple observation allows one to relate the geometry of zero patterns in the vector field to communication properties, and hence asymptotic behavior, of $\textbf{X}^{(N)}.$

From the point of view of the model’s adequacy in potential applications, (64) is a direct consequence of the fundamental assumption of the Wright–Fisher model that particles in the population update their phenotypes independently of each other and follow the same stochastic protocol. Mathematically, this assumption is expressed in identity (45), whose right-hand side is a sum of independent and identically distributed random indicators. To appreciate this feature of the Wright–Fisher model, we remark that while (64) holds true for an arbitrary model (7), that feature does not hold true, in general, for two most natural generalization of the Wright–Fisher model, namely the Cannings exchangeable model (Ewens 2012) and the pure-drift Generalized Wright–Fisher process of Der et al. (2011).

Recall that two states $\textbf{x},\textbf{y}\in \Delta _{M,N}$ of the finite-state Markov chain $\textbf{X}^{(N)}$ are said to communicate if there exist $i,j\in {{\mathbb {N}}}$ such that $P_N^i(\textbf{x},\textbf{y})>0$ and $P_N^j(\textbf{y},\textbf{x})>0.$ If $\textbf{x}$ and $\textbf{y}$ communicate, we write $\textbf{x}\leftrightarrow \textbf{y}.$ The binary relation $\leftrightarrow$ partitions the state space $\Delta _{M,N}$ into a finite number of disjoint equivalence classes, namely $\textbf{x},\textbf{y}$ belong to the same class if and only if $\textbf{x}\leftrightarrow \textbf{y}.$ A state $\textbf{x}\in \Delta _{M,N}$ is called absorbing if $P_N(\textbf{x},\textbf{x})=1,$ recurrent if $\textbf{X}^{(N)}$ starting at $\textbf{x}$ returns to $\textbf{x}$ infinitely often with probability one, and transient if, with probability one, $\textbf{X}^{(N)}$ starting at $\textbf{x}$ revisits $\textbf{x}$ only a finite number of times. It turns out that each communication class consists of either (1) exactly one absorbing state; or (2) recurrent non-absorbing states only; or (3) transient states only. No other behavior is possible due to zero–one laws enforced by the Markov property (Lawler 2006). A communication class is called closed or recurrent if it belongs to the first or second category, and transient if it belongs to the third one. The chain is called irreducible if there is only one (hence, recurrent) communication class, and aperiodic if $P_N^j(\textbf{x},\textbf{y})>0$ for some $j\in {{\mathbb {N}}}$ and all $\textbf{x},\textbf{y}\in \Delta _{M,N}.$ If $C_1,\ldots ,C_r$ are disjoint recurrent classes of $\textbf{X}^{(N)},$ then the general form of its stationary distribution is $\pi (\textbf{x})=\sum _{i=1}^r \alpha _i \pi _i(\textbf{x})$ where $\pi _i$ is the unique stationary distribution supported on $C_i$ (that is $\pi _i(\textbf{x})>0$ if and only if $\textbf{x}\in C_i$) and $\alpha _i$ are arbitrary non-negative numbers adding up to one. If the chain is irreducible, then the stationary distribution is unique and is strictly positive on the whole state space $\Delta _{M,N}.$ An irreducible finite-state Markov chain is aperiodic if and only if $\pi (\textbf{x})=\lim _{k\rightarrow \infty } P_N^k(\textbf{y},\textbf{x})$ for any $\textbf{x},\textbf{y}\in \Delta _{M,N},$ where $\pi$ is the unique stationary distribution of the chain (Lawler 2006).

Let ${{\mathcal {A}}}_N \subset \Delta _M$ denote the set of absorbing states of the Markov chain $\textbf{X}^{(N)}.$ It readily follows from (7) that ${{\mathcal {A}}}_N\subset V_M,$ and a vertex $\textbf{e}_j\in V_M$ is an absorbing (fixation) state if and only if ${\varvec{\Gamma }}(\textbf{e}_j)=\textbf{e}_j.$ In particular, ${{\mathcal {A}}}_N$ depends only on the update rule ${\varvec{\Gamma }}$ and is independent of the population size N. We summarize this observation as follows:

$$\begin{aligned} {{\mathcal {A}}}_N=\big \{\textbf{e}_j\in V_M:{\varvec{\Gamma }}(\textbf{e}_j)=\textbf{e}_j\big \}\qquad \qquad \forall \, N\in {{\mathbb {N}}}. \end{aligned}$$

(65)

The following lemma asserts that if $\textbf{e}_j$ is an absorbing state of $\textbf{X}^{(N)},$ then the type j cannot be mixed into any stochastic equilibrium of the model, namely any other than $\textbf{e}_j$ state $\textbf{x}\in \Delta _{M,N}$ with $x(j)>0$ is transient.

Lemma 7.2

Let Assumption 7.1 hold. If $\textbf{x}\in \Delta _{M,N}$ is a recurrent state of the Markov chain $\textbf{X}^{(N)}$ and $x(j)>0,$ then $\textbf{e}_j$ is a recurrent state belonging to the same closed communication class as $\textbf{x}.$

Proof

By (65), a state $\textbf{x}\in \Delta _{M,N}$ cannot be absorbing if $\textbf{x}\ne \textbf{e}_j$ and $x(j)>0.$ If $\textbf{x}$ is recurrent and non-absorbing, then there is a state $\textbf{y}\in \Delta _{M,N}$ that belongs to the same closed communication class as $\textbf{x}$ and such that $P_N(\textbf{y},\textbf{x})>0.$ In view of (7) this implies that $\Gamma _j(\textbf{y})>0$ and hence $P_N(\textbf{y},\textbf{e}_j)>0.$ Since the state $\textbf{y}$ is recurrent, $\textbf{e}_j$ must belong to the same communication class as $\textbf{y}$ and $\textbf{x},$ and in particular is recurrent. The proof is complete. $\square$

Recall (5). The same argument as in the above lemma shows that if an interior point $\textbf{x}$ of a simplex $\Delta _{[J],N}$ is recurrent for $\textbf{X}^{(N)},$ then the whole simplex $\Delta _{[J],N}$ belongs to the (recurrent) closed communication class of $\textbf{x}.$ One can rephrase this observation as follows:

Theorem 7.3

Let Assumption 7.1 hold. Then, any recurrent class of the Markov chain $\textbf{X}^{(N)}$ has the form of a simplicial complex $\bigcup _\ell \Delta _{[J_\ell ],N},$ where $J_\ell$ are (possibly overlapping) subsets (possibly singletons) of $S_M.$

With applications in mind, we collect some straightforward implications of this proposition in the next corollary.

Corollary 7.4

Let Assumption 7.1 hold. Then:

• (i) If there is a stationary distribution $\pi$ of $\textbf{X}^{(N)}$ and $J\subset S_M$ such that $\pi (\textbf{x})>0$ for some interior point $\textbf{x}\in \Delta _{[J],N}^\circ ,$ then $\pi (\textbf{y})>0$ for all $\textbf{y}\in \Delta _{[J],N}.$ Furthermore, the following holds in this case unless $\Gamma (\textbf{y})\cdot \textbf{y}=0$ (that is, $\textbf{y}$ and ${\varvec{\Gamma }}(\textbf{y})$ are orthogonal) for all $\textbf{y}\in \Delta _{[J],N}:$

  • (a) Let C be the (closed) communication class to which the above $\textbf{x}$ (and hence the entire $\Delta _{[J],N}$) belongs. Then the Markov chain $\textbf{X}^{(N)}$ restricted to C is aperiodic.

  • (b) Let T be the first hitting time of C,  namely $T=\inf \{k\in {{\mathbb {Z}}}_+:\textbf{X}^{(N)}_k\in C\}.$ As usual, we use here the convention that $\inf \emptyset =+\infty .$ Then

    $$\begin{aligned} \pi (\textbf{y})=\lim _{k\rightarrow \infty } P(\textbf{X}^{(N)}_k=\textbf{y}\mid \textbf{X}^{(N)}_0=\textbf{z},T<\infty ) \end{aligned}$$

    for all $\textbf{y}\in C$ and $\textbf{z}\in \Delta _{M,N}.$ In particular, $\pi (\textbf{y})=\lim _{k\rightarrow \infty }P_N^k(\textbf{z},\textbf{y})$ whenever $\textbf{y},\textbf{z}\in C.$

• (ii) A stationary distribution $\pi$ of $\textbf{X}^{(N)}$ such that $\pi (\textbf{x})>0$ for some interior point $\textbf{x}\in \Delta _{M,N}^\circ$ exists if and only if $\textbf{X}^{(N)}$ is irreducible and aperiodic, in which case the stationary distribution is unique and $\pi (\textbf{y})=\lim _{k\rightarrow \infty } P^k_N(\textbf{x},\textbf{y})>0$ for any $\textbf{x},\textbf{y}\in \Delta _{M,N}.$

• (iii) Let $B=\big \{\exists ~k\in {{\mathbb {N}}}: \textbf{X}^{(N)}_k\in \partial \big (\Delta _{M,N}\big )~\text{ for } \text{ all }~m\ge k\big \}$ be the event that the trajectory of $\textbf{X}^{(N)}$ reach eventually the boundary of the simplex and stays there forever. Then either the Markov chain $\textbf{X}^{(N)}$ is irreducible and aperiodic or $P(B)=1$ for any state $\textbf{X}^{(N)}_0.$

• (iv) If ${\varvec{\Gamma }}(\textbf{e}_j)=\textbf{e}_j$ for some $j\in S_M,$ then $\lim _{k\rightarrow \infty } X^{(N)}_k(j)\in \{0,1\},$ a. s., for any initial distribution of $\textbf{X}^{(N)}.$

We will only prove the claim in (a) of part (i), since the rest of the corollary is an immediate result of a direct combination of Theorem 7.3 and general properties of finite-state Markov chains reviewed in the beginning of the section.

Proof of Corollary 7.4-(i)-a

Suppose that ${\varvec{\Gamma }}(\textbf{y})\cdot \textbf{y}>0$ for some $\textbf{y}\in \Delta _{[J],N}.$ Let $\textbf{z}$ be the projection of $\textbf{y}$ into $\Delta _{[I],M},$ where $I:=\{j\in J:y(j)\Gamma _j(\textbf{y})>0\}.$ That is,

$$\begin{aligned} z(i)= \left\{ \begin{array}{ll} y(i)&{}\text{ if }~y(i)\Gamma _i(\textbf{y})>0, \\ 0&{}\text{ otherwise }. \end{array} \right. \end{aligned}$$

Then $\textbf{z}\in \Delta _{[I],M}^\circ$ and $P_N(\textbf{z},\textbf{z})>0.$ Since $\textbf{z}\in \Delta _{[J],N},$ by Theorem 7.3$\textbf{z}$ belongs to the same closed communication class as $\textbf{x}.$ The asserted aperiodicity of $\textbf{X}^{(N)}$ restricted to C is a direct consequence of the existence of the 1-step communication loop at $\textbf{z}$ (Lawler 2006). $\square$

Example 6

(Harper and Fryer 2016) If $\Gamma _j(\textbf{x})=x(j)^\alpha f(\textbf{x})$ for some $j\in S_M,$ function $f:\Delta _M\rightarrow {{\mathbb {R}}}_+$ such that $f(\textbf{e}_j)=1,$ and a constant $\alpha >0,$ then ${\varvec{\Gamma }}(\textbf{e}_j)=\textbf{e}_j.$ By part (iv) of Corollary 7.4, this fact alone suffices to conclude that $\lim _{k\rightarrow \infty } X^{(N)}_k(j)\in \{0,1\},$ a. s., for this specific type j.

A simple sufficient condition for the Markov chain $\textbf{X}^{(N)}$ to be irreducible and aperiodic is that ${\varvec{\Gamma }}(\Delta _M)\subset \Delta _M^\circ ,$ in which case $P_N(\textbf{x},\textbf{y})>0$ for any $\textbf{x},\textbf{y}\in \Delta _{M,N}.$ If ${\varvec{\Gamma }}\big (\Delta _{M,N}^\circ \big )\subset \Delta _{M,N}^\circ$ but ${\varvec{\Gamma }}(\textbf{e}_j)=\textbf{e}_j$ for all $j\in S_M,$ the model can be viewed as a multivariate analog of what is termed in Chalub and Souza (2017) as a Kimura class of Markov chains. The latter describes evolution dynamics of a population that initially consists of two phenotypes, each one eventually either vanishes or takes over the entire population.

1.2 Appendix B. Permanence of the mean-field dynamics

In this appendix, we focus on Wright–Fisher models with a permanent mean-field dynamics ${\varvec{\Gamma }}.$ The permanence means that the boundary of the state space $\partial (\Delta _M)$ is a repeller for the mean-field dynamics, implying that all types under the mean-field dynamics will ultimately survive (Garay and Hofbauer 2003; Hofbauer and Sigmund 1998; Hutson and Schmitt 1992; Kang and Chesson 2010). This condition is particularly relevant to the stochastic Wright–Fisher model because, as stated in Appendix A, all absorbing states (possibly an empty set) of the Markov chain $\textbf{X}^{(N)}$ lie within the boundary set $\partial (\Delta _M).$ Of course, in the absence of mutations, any vertex of $\Delta _M$ is an absorbing state for the Markov chain $\textbf{X}^{(N)},$ and the latter is going to eventually become fixed on one of the absorbing states with probability one (see Appendix A for formal details). However, we showed in Sect. 4 that a permanent mean-field dynamics induces metastability and a prolonged coexistence of types.

Definition 4

(Hofbauer and Sigmund 1998) ${\varvec{\Gamma }}$ is permanent if there exists $\delta >0$ such that

$$\begin{aligned} \liminf _{k\rightarrow \infty } \psi _k(i)>\delta \qquad \forall \,i\in S_M,{{\varvec{\psi }}}_0\in \Delta _M^\circ . \end{aligned}$$

See Garay and Hofbauer (2003), Schreiber et al. (2018) and references therein for sufficient conditions for the permanence. It turns out that under reasonable additional assumptions, ${\varvec{\Gamma }}$ is permanent for the fitness defined in either (11) or (12). More precisely, we have (for a more general version of the theorem, see Garay and Hofbauer (2003, Theorem 11.4) and Hofbauer and Sigmund (2003, Theorem 5):

Theorem 3

(Garay and Hofbauer 2003) Let $\textbf{A}$ be an $M\times M$ matrix which satisfies the following condition: There exists $\textbf{y}\in \Delta _M^\circ$ such that

$$\begin{aligned} \textbf{y}^T\textbf{A} \textbf{z}> \textbf{z}^T\textbf{A}{} \textbf{z} \end{aligned}$$

for all $\textbf{z}\in \partial (\Delta _M)$ solving the fixed-point equation $\textbf{z}=\frac{1}{\textbf{z}^T\textbf{A}{} \textbf{z}}\big (\textbf{z}\circ \textbf{A}{} \textbf{z}\big ).$

Then:

• (i) There exists $\omega _0>0$ such that ${\varvec{\Gamma }}$ given by (10) and (11) is permanent for all $\omega \in (0,\omega _0).$

• (ii) ${\varvec{\Gamma }}$ given by (10) and (12) is permanent for all $\eta >0.$

Recall Definitions 1 and 2. The setting of the theorem provides a natural within our context example of a non-constant complete Lyapunov function.

Example 7

Suppose that ${\varvec{\Gamma }}$ is a replicator function defined in (10). If $\textbf{A}$ is an $M\times M$ matrix that satisfies the conditions of Theorem 3 and ${{\varvec{\varphi }}}$ in (10) is defined by either (11) with small enough $\omega >0$ or by (12), then ${{\mathcal {R}}}({\varvec{\Gamma }}) \subset K\bigcup \partial (\Delta _M),$ where K is a compact subset of $\Delta _M^\circ .$ In particular, the complete Lyapunov function h constructed in Theorem 2 (p. 14) is strictly increasing on the non-empty open set $\Delta _M^\circ \backslash K.$ Notice that while the average $\textbf{x}\cdot {{\varvec{\varphi }}}(\textbf{x})$ may not be a complete Lyapunov function for ${\varvec{\Gamma }},$ the average $h(\textbf{x})$ of the reproductive fitness $\widetilde{{\varvec{\varphi }}}(\textbf{x}):=h(\textbf{x}){{\varvec{\varphi }}}(\textbf{x})$ is.

In Sect. 4.3 we considered a stochastic Wright–Fisher model with a permanent mean-field map ${\varvec{\Gamma }}.$ This model has a global attractor, consisting of a unique equilibrium point. A sufficient condition for such a dynamics is given by the following theorem (Losert and Akin 1983). Recall (20).

Theorem 4

(Losert and Akin 1983) Let Assumption 4.4 hold. Then the following holds true:

• (a) Recall ${{\varvec{\psi }}}_k$ from (3). If ${{\varvec{\psi }}}_0\in \Delta _M^\circ ,$ then $\lim _{k\rightarrow \infty } {{\varvec{\psi }}}_k={{\varvec{\chi _{eq}}}}.$

• (b) ${\varvec{\Gamma }}$ is a diffeomorphism.

Note that the weak selection condition (cf. Antal et al. 2009; Boenkost et al. 2019; Imhof and Nowak 2006) imposed in part (i) of Theorem 3 is not required in the conditions of Theorem 4.

The evolutionary games with $\textbf{A}=\textbf{A}^T$ are called partnership games (Hofbauer 2011). We refer to Hummert et al. (2018), Huttegger et al. (2014), Traulsen and Reed (2012) for applications of partnership games in evolutionary biology. Condition (32) implies the existence of a unique evolutionary stable equilibrium for the evolutionary game defined by the payoff matrix $\textbf{A}.$ For a symmetric reversible matrix $\textbf{A}$ this condition holds if and only if $\textbf{A}$ has exactly one positive eigenvalue (Kingman 1961; Mandel 1959). Condition (33) ensures that the equilibrium is an interior point. Note that since the equilibrium is unique, the conditions of Theorem 3 are automatically satisfied, that is ${{\varvec{\psi }}}_k$ is permanent. Finally, under the conditions of Theorem 4, the average payoff $\textbf{x}^T\textbf{A}{} \textbf{x}$ is a Lyapunov function (Kingman 1961; Mandel 1959):

$$\begin{aligned} {{\varvec{\psi }}}_k^T\textbf{A}{{\varvec{\psi }}}_k<{{\varvec{\psi }}}_{k+1}^T\textbf{A}{{\varvec{\psi }}}_{k+1}<{{\varvec{\chi _{eq}}}}^T \textbf{A}{{\varvec{\chi _{eq}}}}\qquad \qquad \forall \,k\in {{\mathbb {Z}}}_+, \end{aligned}$$

as long as ${{\varvec{\psi }}}_0\in \Delta _M^\circ$ and ${{\varvec{\psi }}}_0\ne {{\varvec{\chi _{eq}}}}.$