Substrate inhibition can produce coexistence and limit cycles in the chemostat model with allelopathy

Abstract

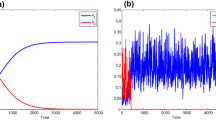
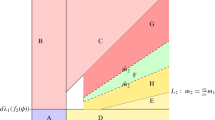
In this work, we consider a model of two microbial species in a chemostat in which one of the competitors can produce a toxin (allelopathic agent) against the other competitor, and is itself inhibited by the substrate. The existence and stability conditions of all steady states of the reduced model in the plane are determined according to the operating parameters. With Michaelis-Menten or Monod growth functions, it is well known that the model can have a unique positive equilibrium which is unstable as long as it exists. By including both monotone and non-monotone growth functions (which is the case when there is substrate inhibition), it is shown that a new positive equilibrium point exists which can be stable according to the operating parameters of the system. This general model exhibits a rich behavior with the coexistence of two microbial species, the multi-stability, the occurrence of stable limit cycles through super-critical Hopf bifurcations and the saddle-node bifurcation of limit cycles. Moreover, the operating diagram describes some asymptotic behavior of this model by varying the operating parameters and illustrates the effect of the inhibition on the emergence of the coexistence region of the species.

A Proofs

1.1 A.1 Proof of Proposition 2

Equilibria of (8) are the solutions of the set of Eq. (9).

• We first note that if $x= 0$ and $y= 0$, we obtain the washout equilibrium $E_0=(0,0)$ which always exists.

• If $y = 0$ and $x>0$, then from the first equation of (9), we have $f_1\left( S^{0}-x_1\right) =D$, or equivalently $S^{0}-x_1=\lambda _1$, where $\lambda _1$ is given by (4). Thus, $x_1=S^{0}-\lambda _1$. This equilibrium exists if and only if $x_1>0$; that is, $\lambda _1<S^{0}$.

• If $y>0$ and $x=0$, then from the second equation of (9), we have

  $$\begin{aligned} (1-k)f_2\left( S^{0}-(1+c)y_2\right) =D, \end{aligned}$$

  where $c=\frac{k}{1-k}$. From hypothesis (H2), equation $(1-k)f_2\left( S\right) =D$ has two positive solutions $S^1=\lambda _2$ and $S^2=\mu _2$ (with $\lambda _2\le \mu _2$) or no solution and we then put $\lambda _2=+\infty$ and $\mu _2=+\infty$. It follows that

  $$\begin{aligned} y_2^1=(S^{0}-\lambda _2)(1-k) \ \ \ \ \hbox {and} \ \ \ \ y_2^2=(S^{0}-\mu _2)(1-k). \end{aligned}$$

  (16)

  Thus, one can conclude that equilibrium ${E}_2^1$ exists if and only if $y_2^1>0$; that is, $\lambda _2<S^{0}$, and ${E}_2^2$ exists if and only if $y_2^2>0$; that is, $\mu _2<S^{0}$.

• If $y>0$ and $x>0$, then from the second equation of (9), we have

  $$\begin{aligned} S^{0}-x_{c_1}-(1+c)y_{c_1}=\lambda _2 \ \ \ \ \hbox {and} \ \ \ \ S^{0}-x_{c_2}-(1+c)y_{c_2}=\mu _2, \end{aligned}$$

  and from the first equation, we get

  $$\begin{aligned} y_{c_1}=\dfrac{1-k}{ k}f^{-1}\left( \frac{D}{f_1(\lambda _2)}\right) \ \ \ \ \hbox {and} \ \ \ \ y_{c_2}=\dfrac{1-k}{ k}f^{-1}\left( \frac{D}{f_1(\mu _2)}\right) . \end{aligned}$$

  Therefore $y_{c_j}$ and $x_{c_j}$ are given by (10) and (11). Hence, a positive equilibrium $E_c^j$, $j=1,2$, of system (8), if it exists, is unique. Let us study conditions of existence of $E_c^j$. Using the fact that f is decreasing and $f(0)=1$ (hypothesis (H3)) we have

  $$\begin{aligned} y_{c_j}>0\Longleftrightarrow & {} D<f_{1}(S^{j}) \Longleftrightarrow \lambda _1<S^{j} \end{aligned}$$

  (17)

  and

  $$\begin{aligned} x_{c_j}>0\Longleftrightarrow & {} S^0-S^{j}-(1+c)y_{c_j}>0 \nonumber \\\Longleftrightarrow & {} S^0>S^{j}+\dfrac{1}{ k}f^{-1}\left( \frac{D}{f_1(S^{j})}\right) \nonumber \\\Longleftrightarrow & {} S^0>F_j(D). \end{aligned}$$

  (18)

  From (17) and (18), we conclude finally that $E_c^j$ exists if and only if $\lambda _1<S^{0}$ and $S^0>F_j(D)$. $\square$

1.2 A.2 Proof of Proposition 3

• At washout equilibrium $E_0$, the matrix M defined by (12) is

  $$\begin{aligned}M_0= \left[ \begin{array}{cc} f_1(S^0)-D &{} 0\\ 0 &{} (1-k)f_2(S^0)-D \end{array} \right] . \end{aligned}$$

  The eigenvalues of $M_0$ are: $f_1(S^0)-D$ and $(1-k)f_2(S^0)-D$. Then, equilibrium $E_0$ is LES if and only if $f_1(S^0)<D$ and $(1-k)f_2(S^0)<D$.

• Suppose that equilibrium $E_1$ exists; that is, $\lambda _1\!<\!S^{0}$. At $E_1$ the matrix M defined by (12) is

  $$\begin{aligned}M_1= \left[ \begin{array}{cc} -(S^{0}-\lambda _1)f_1'(\lambda _1) &{} A\\ 0 &{} (1-k)f_2(\lambda _1)-D \end{array} \right] , \end{aligned}$$

  where $A=(cf'(0)f_1(\lambda _1)-(1+c)f_1'(\lambda _1))(S^{0}-\lambda _1)$. The eigenvalues of $M_1$ are: $-(S^{0}-\lambda _1)f_1'(\lambda _1)<0$ and $(1-k)f_2(\lambda _1)-D$. Therefore, $E_1$ is LES if and only if $(1-k)f_2(\lambda _1)<D$, or equivalently, $\lambda _1<\lambda _2$ or $\lambda _1>\mu _2$.

• Suppose that equilibria $E_2^j$, $j\!=\!1,2$, exist; that is, $\lambda _2\!<\!S^{0}$ and $\mu _2\!<\!S^{0}$. At $E_2^j$ the matrix M defined by (12) is

  $$\begin{aligned}M_2= \left[ \begin{array}{cc} f(k(S^{0}-S^j))f_1(S^j)-D &{} 0\\ -(1-k)y^j_2f_2'(S^j) &{} -y^j_2f_2'(S^j) \end{array} \right] . \end{aligned}$$

  The eigenvalues of $M_2$ are: $-y^j_2f_2'(S^j)$ and $f(k(S^{0}-S^j))f_1(S^j)-D$. At $E_2^1$, we have $-y^j_2f_2'(S^j)<0$ because $f'_2(S^1)=f'_2(\lambda _2)>0$. Therefore, $E_2^1$ is LES if and only if $f(k(S^{0}-\lambda _2))f_1(\lambda _2)<D$. At $E_2^2$, we have $-y^j_2f_2'(S^j)>0$ because $f'_2(S^2)=f'_2(\mu _2)<0$. Thus, $E_2^2$ is unstable.

• At $E_c^j$, the matrix M defined by (12) takes the form

  $$\begin{aligned}M_c= \left[ \begin{array}{cc} m_{11} &{} m_{12} \\ m_{21} &{} m_{22} \\ \end{array} \right] , \end{aligned}$$

  where

  $$\begin{aligned} m_{11}= & {} -f\left( cy_{c_j}\right) f'_1\left( S^{j}\right) x_{c_j}, \\ m_{12}= & {} cf'\left( cy_{c_j}\right) f_1\left( S^{j}\right) x_{c_j}-(1+c)f\left( cy_{c_j}\right) f'_1\left( S^{j}\right) x_{c_j}, \\ m_{21}= & {} -(1-k) f'_2\left( S^{j}\right) y_{c_j}\quad \text {and}\quad m_{22}=- f'_2\left( S^{j}\right) y_{c_j}. \end{aligned}$$

  At $E_c^1$, we have

  $$\begin{aligned} \det (M_c)=k f'_2(S^{1})f'( cy_{c_1}) f_1( S^{1})x_{c_1}y_{c_1} <0 \end{aligned}$$

  because $f'_2(S^{1})=f'_2(\lambda _2)>0$. Thus, $E_c^1$ is unstable. At $E_c^2$, we have

  $$\begin{aligned} \det (M_c)=k f'_2(S^{2})f'(cy_{c_2}) f_1( S^{2})x_{c_2}y_{c_2}>0 \end{aligned}$$

  because $f'_2(S^{2})=f'_2(\mu _2)<0$. Therefore, $E_c^2$ is LES if and only if

  $$\begin{aligned} tr(M_c)=-f( cy_{c_2}) f'_1(\mu _2)x_{c_2}- f'_2(\mu _2)y_{c_2}<0, \end{aligned}$$

  or equivalently,

  $$\begin{aligned} Df'_1(\mu _2)x_{c_2}+f_1(\mu _2) f'_2(\mu _2)y_{c_2}>0. \end{aligned}$$

  $\square$

1.3 A.3 Proof of Lemma 1

Using definitions (11) of $x_{c_2}$ and $y_{c_2}$, one has

$$\begin{aligned} \begin{array}{r c lclcl} F_3(D,S^0)>0 &{} \Longleftrightarrow &{} Df'_1(\mu _2)x_{c_2}\!\left( D,S^0\right) +f_1(\mu _2) f'_2(\mu _2)y_{c_2}\!(D)>0 \\ &{} \Longleftrightarrow &{} Df'_1(\mu _2)\left[ S^0\!-\!\mu _2\!-\!(1\!+\!c)y_{c_2}\!(D)\right] \!+\!f_1(\mu _2) f'_2(\mu _2)y_{c_2}\!>0\\ &{} \Longleftrightarrow &{} S^0>\mu _2(D)+(1\!+\!c)y_{c_2}\!(D)-\dfrac{f_1(\mu _2) f'_2(\mu _2)y_{c_2}\!(D)}{Df'_1(\mu _2)}\\ &{} \Longleftrightarrow &{} S^0>\mu _2(D)+(1\!+\!c)y_{c_2}\!(D)\left[ 1-\dfrac{(1-k)f_1(\mu _2)f'_2(\mu _2)}{Df'_1(\mu _2)}\right] \\ &{} \Longleftrightarrow &{} S^0>F_5(D). \end{array} \end{aligned}$$

$\square$

1.4 A.4 Proof of Theorem 3.1

The proof uses ideas in Sobieszek et al. (2020). The characteristic polynomial at $E_c^2$ takes the form

$$\begin{aligned} F(\lambda )=\lambda ^2+B\lambda +C. \end{aligned}$$

The fact that $C\ne 0$ means that the only way that $E_c^2$ is destabilized is for the two complex conjugate eigenvalues $\lambda _j(D)=\alpha (D)\pm i\beta (D)$, $j = 1,2$, to cross the imaginary axis (because of the continuity of coefficients of F with respect to the parameters), which is the case when

$$\begin{aligned} F_3(D,S^0)=Df'_1(\mu _2)x_{c_2}\!\left( D,S^0\right) +f_1(\mu _2) f'_2(\mu _2)y_{c_2}\!(D)=0,\ \text {i.e.} \ S^{0}=F_5(D). \end{aligned}$$

To have a simple Hopf bifurcation, we need the transversality condition to be verified, i.e. the pair of complex conjugate eigenvalues cross the imaginary axis with non-zero speed. This is guaranteed because the derivative of $F_3$ with respect to $S^0$ is not equal to zero when $F_3(D,S^0)=0$.

Here, $\partial _{S^0} F_3(D,S^0)=Df'_1(\mu _2) \partial _{S^0} x_{c_2}(D,S^0)=Df'_1(\mu _2)>0,$ where $x_{c_2}$ is given by (11). $\square$