Estimation of under-reporting in epidemics using approximations

Abstract

Under-reporting in epidemics, when it is ignored, leads to under-estimation of the infection rate and therefore of the reproduction number. In the case of stochastic models with temporal data, a usual approach for dealing with such issues is to apply data augmentation techniques through Bayesian methodology. Departing from earlier literature approaches implemented using reversible jump Markov chain Monte Carlo (RJMCMC) techniques, we make use of approximations to obtain faster estimation with simple MCMC. Comparisons among the methods developed here, and with the RJMCMC approach, are carried out and highlight that approximation-based methodology offers useful alternative inference tools for large epidemics, with a good trade-off between time cost and accuracy.

Appendix

1.1 A.1 Heuristic justification of the adjustment on p

Considering Eq. (20), we may refer to the following approximation. For a relatively non-informative prior for p, and so also for ${\hat{p}}$, the posterior density of ${\hat{p}}$ is that given by the likelihood function $L(\cdot )$. Regarding the posterior distributions of ${\hat{p}}$ and p as being modelled by the random variables ${\hat{P}}$ and P respectively, we can define the variable X as

$$\begin{aligned} X = P - {\hat{P}} \text{ and } \text{ let } \sigma ^2 = p^2(1-p)/K_r. \end{aligned}$$

Treating $\sigma ^2$ as a constant, we have $X \sim \mathcal {N}(0, \sigma ^2).$ Therefore the multiplicative term $\phi ({\hat{p}} - p)L(\beta ,\gamma ,{\hat{p}};\,\pmb {s_r}, \pmb {r_r})$, in (20), is the product of the density of X and ${\hat{P}}$. Hence, integrating over ${\hat{p}}$ this gives

$$\begin{aligned} \int _0^1 \phi ({\hat{p}} - p)L(\beta ,\gamma ,{\hat{p}};\,\pmb {s_r}, \pmb {r_r})\ d{\hat{p}} \end{aligned}$$

which by definition is the convolution of X and ${\hat{P}}$ and, since X and ${\hat{P}}$ are independent, the density of $P = {\hat{P}} + X$. This result suggests that the means of ${\hat{P}}$ and P are the same and the variance of ${\hat{P}}$ should be increased by the variance of X to obtain the variance of P. In practice the quantity $\sigma ^2 = p^2(1-p)/K_r$ can be estimated by using any reasonable estimate of p. If we use ${\hat{p}}$ to estimate $\sigma ^2$, the uncertainty about p can be estimated by adding to the posterior variance of ${\hat{p}}$ the quantity ${\hat{p}}^2(1-\hat{p})/K_r$.

1.2 A.2 Pseudo-code for Methods 1–3

1.2.1 A.2.1 Method 1

MCMC algorithm using Method 1

• 1. Start with initial values for $\beta ,\gamma ,p$ and $\pmb {s_r}$.

• 2. Update the infection times of the reported cases by selecting one individual at random, propose an infection time based on the distribution of the infectious period and accept it with probability A in (19), given the parameters $\beta ,\gamma$ and p.

• 3. Update the model parameters:

  • (i) Update $\beta$ according to its full posterior conditional distribution in (17), using the current values of $p,\gamma$ and $\pmb {s_r}$.

  • (ii) Update $\gamma$ using its full posterior conditional distribution in (18) and the current values of $p,\beta$ and $\pmb {s_r}$.

  • (iii) Update p using random walk with acceptance probability

    $$\begin{aligned} A_p = \min \left( \frac{L(\beta ,\gamma , p^{new};\,\pmb {s_r}, \pmb {r_r})}{L(\beta ,\gamma , p^{old};\,\pmb {s_r}, \pmb {r_r})}, 1\right) \end{aligned}$$

    using current $\gamma ,\beta$ and $\pmb {s_r}$.

• (iv) Steps 2 and 3 are repeated until convergence.

1.2.2 A.2.2 Method 2

Algorithm for correction on p

• 1. Start with initial values for $\beta ,\gamma ,{\hat{p}},p$ and $\pmb {s_r}$.

• 2. Update the infection times of the reported cases, $\pmb {s_r}$, using Metropolis–Hastings algorithm, given the current values of parameters $\beta ,\gamma ,{\hat{p}}$ and p.

• 3. Update the model parameters:

  • (i) Update $\beta$ according to its full posterior conditional distribution in (17) with p replaced by ${\hat{p}}$, using the current values of $p,{\hat{p}},\gamma$ and $\pmb {s_r}$.

  • (ii) Update $\gamma$ using its full posterior conditional distribution in (18) and the current values of $p,{\hat{p}},\beta$ and $\pmb {s_r}$.

  • (iii) Update ${\hat{p}}$ following a random walk scheme with acceptance probability

    $$\begin{aligned} Acc_{{\hat{p}}} = \min \left( \frac{\phi ({\hat{p}}^{new} - p)L(\beta ,\gamma ,{\hat{p}}^{new};\,\pmb {s_r}, \pmb {r_r})}{\phi (\hat{p}^{old} - p) L(\beta ,\gamma ,{\hat{p}}^{old};\,\pmb {s_r}, \pmb {r_r})}, 1\right) \end{aligned}$$

    using the current values of $p,\gamma ,\beta$ and $\pmb {s_r}$.

  • (iv) Update p using random walk with acceptance probability

    $$\begin{aligned} Acc_p = \min \left( \frac{\pi _p(p^{new}) \phi ({\hat{p}} - p^{new})}{\pi _p(p^{old})\phi ({\hat{p}} - p^{old})}, 1\right) \end{aligned}$$

    using ${\hat{p}},\gamma ,\beta$ and $\pmb {s_r}$. Note that this update is actually independent of $\beta ,\gamma$ and $\pmb {s_r}$.

• 4. Steps 2 and 3 are repeated until convergence.

1.2.3 A.2.3 Method 3

Algorithm for approximate Gibbs sampling

• 1. Start with initial values of $\beta ,\gamma ,p$ and $\pmb {s_r}$.

• 2. Update the infection times of the reported cases, $\pmb {s_r}$, using Metropolis–Hastings algorithm, given the current values of parameters $\beta ,\gamma$ and p.

• 3. Update the model parameters:

  • (i) Update $\beta$ according to its full posterior conditional distribution in (17) using the current values of $p,\gamma$ and $\pmb {s_r}$.

  • (ii) Update $\gamma$ using its full posterior conditional distribution in (18) and the current values of $p,\beta$ and $\pmb {s_r}$.

  • (iii) Solve Eq. (13) and sample the final size K from (14) using current $\beta ,\gamma$ and $\pmb {s_r}$; conditional on the fact that $K \ge K_r$.

  • (iv) Sample the probability of reporting p using (23) using the current final size K.

• 4. Steps 2 and 3 are repeated until convergence.

1.3 A.3 Reversible jump MCMC algorithm

An individual (say k) will always have one of the following states:

• 0: Susceptible;

  i.e $k \in \mathcal {S}$

• 1: Removed and reported;

  i.e $k \in \mathcal {R}_r$

• 2: Removed but not reported;

  i.e $k \in \mathcal {R}_u$.

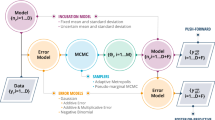
Below are the possible algorithm transitions presented schematically:

The algorithm is now describe in details as follows:

• Choose an individual at random (let us say k).

• If the state of k is 1 (meaning that the individual was removed and reported), we propose the new infection time $s_k$ using $(s_k - r_k) \sim \text {Exp}(\gamma )$ and $s_k$ is accepted with probability :

  $$\begin{aligned} A_{1\rightarrow 1} = \min \left\{ 1, \frac{L(\beta , \gamma ; \pmb {s}^{(new)}, \pmb {r})}{L(\beta , \gamma ; \pmb {s}^{(old)}, \pmb {r})}*\frac{\exp \{-\gamma (r_k - s_k')\}}{\exp \{-\gamma (r_k - s_k)\}}\right\} \end{aligned}$$

  where $s_k'$ is the current infection time of the individual k. There is no change in state.

• If the state of k is 0 (susceptible individual) we propose a removal time $r_k$ uniformly in $(T_0, T)$ (the interval $(T_0, T)$ is the time window in which the epidemic has occurred) and an infection time $s_k$ in $(T_0, r_k)$ and add the pair with probability

  $$\begin{aligned} A_{0\rightarrow 2} = \min \left\{ 1, \frac{(T-T_0)(r_k - T_0)}{2}\frac{L(\beta , \gamma , p; \pmb {s}^{(new)}, \pmb {r}^{(new)})}{L(\beta , \gamma , p; \pmb {s}^{(old)}, \pmb {r}^{(old)})}\right\} . \end{aligned}$$

  If this move is accepted, the state of the individual k becomes 2 (which represents individuals that are removed but not reported), i.e

  $$\begin{aligned} |S| = |S| - 1 \quad \text { and } \quad |\mathcal {R}_u| = |\mathcal {R}_u| + 1. \end{aligned}$$

• If state of k is 2 we either propose, with probability 1 / 2, to update the pair of infection and removal times, or delete the pair of infection and removal times:

  • Update the pair of infection and removal times of k (with $T_0 \le s_k < r_k \le T$) with probability

    $$\begin{aligned} A_{2\rightarrow 2} = \min \left\{ 1, \frac{L(\beta , \gamma , p; \pmb {s}^{(new)}, \pmb {r})}{L(\beta , \gamma , p; \pmb {s}^{(old)}, \pmb {r})} \frac{r_k - T_0}{r_k' - T_0}\right\} \end{aligned}$$

    where $r_k'$ is the removal time of individual k before the new proposed one $r_k$. The state remains the same.

  • Delete the pair of infection and removal times with probability

    $$\begin{aligned} A_{2\rightarrow 0} = \min \left\{ 1, \frac{L(\beta , \gamma , p; \pmb {s}^{(new)}, \pmb {r})}{L(\beta , \gamma , p; \pmb {s}^{(old)}, \pmb {r})} \frac{2}{(T - T_0)(r_k - T_0)}\right\} . \end{aligned}$$

    The state of the individual k becomes 0 if the deletion is accepted, i.e

    $$\begin{aligned} |\mathcal {R}_u| = |\mathcal {R}_u| - 1 \qquad \text { and } \qquad |\mathcal {S}| = |\mathcal {S}| + 1. \end{aligned}$$

1.4 A.4 Auto-correlation functions

See Figs. 5 and 6.

Fig. 5

Auto-correlation function for parameter $\gamma$ (data from Sect. 4). a ACF plot for $\gamma$, Method 1. b ACF plot for $\gamma$, Method 2. c ACF plot for $\gamma$, Method 3. d ACF plot for $\gamma$, Method 4

Fig. 6

Auto-correlation function for parameter K (data from Sect. 4). a ACF plot for K, Method 1. b ACF plot for K, Method 2. c ACF plot for K, Method 3. d ACF plot for K, Method 4