Abstract
Large deviations of conservative interacting particle systems, such as the zero range process, about their hydrodynamic limit and their respective rate functions lead to the analysis of the skeleton equation; a degenerate parabolic-hyperbolic PDE with irregular drift. We develop a robust well-posedness theory for such PDEs in energy-critical spaces based on concepts of renormalized solutions and the equation’s kinetic form. We establish these properties by proving that renormalized solutions are equivalent to classical weak solutions, extending concepts of (DiPerna and Lions in Invent. Math. 98(3):511–547, 1989; Ambrosio in Invent. Math. 158(2):227–260, 2004) to the nonlinear setting.
The relevance of the results toward large deviations in interacting particle systems is demonstrated by applications to the identification of l.s.c. envelopes of restricted rate functions, to zero noise large deviations for conservative SPDE, and to the \(\Gamma \)-convergence of rate functions. The first of these solves a long-standing open problem in the large deviations for zero range processes. The second makes rigorous an informal link between the non-equilibrium statistical mechanics approaches of macroscopic fluctuation theory and fluctuating hydrodynamics.
Similar content being viewed by others
1 Introduction
Large deviations of conservative interacting particle systems, such as the zero range process, about their hydrodynamic limit are described by the rate function
where \(\Phi \) is a monotone nonlinearity. This motivates the analysis of the corresponding skeleton equation, a parabolic-hyperbolic PDE
with irregular drift \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\), posed on the \(d\)-dimensional torus \(\mathbb{T}^{d}\). A primary result of this work is the well-posedness and stability of (2).
These results make important contributions to the understanding of large deviations in non-equilibrium conservative fluctuating systems, including applications to the large deviations of the zero range process (Theorem 39 below), to large deviations of conservative SPDE (Theorem 29 below), which rigorously establishes the link between the non-equilibrium statistical mechanics theories of fluctuating hydrodynamics and macroscopic fluctuation theory, and to the \(\Gamma \)-convergence of the large deviations rate functions (Theorem 33 below).
The results extend to the nonlinear setting concepts of renormalized solutions for PDE with irregular coefficients, introduced by DiPerna and Lions [1] (see also Ambrosio [2], Le Bris and Lions [3], Crippa and De Lellis [4], De Lellis [5], Figalli [6], and Jabin [7, 8]) and combine these with the concept of kinetic solutions introduced by Lions, Perthame, and Tadmor [9] and Perthame [10] (see also, Chen and Perthame [11], Karlsen and Riseboro [12], Bendahmane and Karlsen [13], and De Lellis, Otto, and Westdickenberg [14]).
To appreciate the difficulty in proving well-posedness and stability for (2) let us consider the model case given by the porous media equation \(\Phi (\rho )=\rho ^{m}\), for some \(m\in [1,\infty )\). Scaling arguments (see Sect. 2.1 below) demonstrate that (2) is critical for controls \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\) and initial conditions in \(L^{1}(\mathbb{T}^{d})\), and is supercritical for initial conditions in \(L^{r}(\mathbb{T}^{d})\), for every \(r\in (1,\infty )\). Hence, even in the case of independent particles \(\Phi (\rho )=\rho \), the skeleton equation (2) with \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\) is not of semilinear nature, since also on small scales the diffusive operator does not dominate the convective, irregular term. Consequently, the well-posedness and stability of solutions to (2) are challenging problems.
In this paper, we obtain a new a-priori estimate, which leads to the existence of weak solutions (see Definition 11 below) and optimal regularity estimates. In contrast to linear Fokker–Planck equations (see, for example, Le Bris and Lions [3, 15] and Figalli [6], who also treat \(L^{p}\)-drifts \(g\) under an additional (semi) boundedness assumption on the divergence \(\nabla \cdot g\)), the supercriticality of (2) in \(L^{r}(\mathbb{T}^{d})\) for \(r\in (1,\infty )\) makes it impossible to exploit \(L^{r}(\mathbb{T}^{d})\)-based estimates. Our estimates are based on entropy-entropy dissipation, which requires the nonnegativity of the initial data and yields that, for some \(c\in (0,\infty )\),
with \(\Psi _{\Phi}'(\xi )=\log (\Phi (\xi ))\). We therefore define the energy space for the initial data to be
The proof of uniqueness is significantly more complicated due to the lower integrability of the solution provided by (3). For this reason, previous techniques such as Otto [16] do not apply. Indeed, the arguments of [16] were based on \(L^{r}(\mathbb{T}^{d})\)-estimates, for \(r\in (1,\infty )\).
We instead introduce the concept of a renormalized kinetic solution (see Definition 3 below) to recover uniqueness, which introduces several new difficulties. Foremost, it is not obvious that weak solutions are renormalized kinetic solutions, a difficulty that should be expected from the first-order, linear case. In DiPerna and Lions [1] and Ambrosio [2], this equivalence is shown for drifts \(g\) with spatial regularity in \(W^{1,p}\) (respectively, \(BV\)) and spatially bounded divergence—conditions that are almost optimal due to the counterexample of Depauw [17]. In treating (2) it is therefore necessary to exploit the degenerate regularity implied by (3), and to estimate additional commutator errors appearing in the nonlinear terms using the regularity of \(\Phi ^{\frac{1}{2}}(\rho )\) instead of \(\rho \) itself. Furthermore, even on the renormalized level, standard techniques for uniqueness (see, for example, [11]) are not applicable, since the estimate (3) does not imply the decay of entropy and parabolic defect measures at infinity.
The three main theorems below are obtained under general assumptions that apply, in particular, to the porous media nonlinearity \(\Phi (\xi )=\xi ^{m}\) for every \(m\in [1,\infty )\). The first main result is the well-posedness and stability of (2).
Theorem 1
Theorem 8, Theorem 14, Proposition 20, Proposition 21 below
Let \(\Phi \) satisfy Assumptions 6, 10, and 15below. Then,
-
(1)
For every \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\) and \(\rho _{0} \in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\) there exists a unique weak solution to (2). Moreover, if \(\rho ^{1}\), \(\rho ^{2}\) are weak solutions to (2) with initial data \(\rho _{0}^{1},\rho _{0}^{2}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\) and the same control \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\),
$$ \lVert \rho ^{1}-\rho ^{2} \rVert _{L^{\infty}([0,T];L^{1}(\mathbb{T}^{d}))} \leq \lVert \rho _{0}^{1}-\rho _{0}^{2} \rVert _{L^{1}(\mathbb{T}^{d})}. $$ -
(2)
Let \(\rho ^{n}_{0},\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\) and \(g_{n},g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\) satisfy \(\rho ^{n}_{0}\rightharpoonup \rho _{0}\) and \(g_{n} \rightharpoonup g\) weakly in \(L^{1}(\mathbb{T}^{d})\) and \(L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\) respectively. Then, the corresponding weak solutions \(\rho _{n}\) and \(\rho \) satisfy
$$ \rho _{n}\to \rho \;\;\textrm{strongly in}\;\;L^{1}(\mathbb{T}^{d}\times [0,T]). $$
Having established the well-posedness and stability of the skeleton equation, we next describe the consequences of our results for the non-equilibrium large deviations of interacting particle systems.
The hydrodynamic limit of the empirical density field \(\mu ^{n}\) of the zero range process on the torus with mean local jump rate \(\Phi \) is the solution to the nonlinear diffusion equation
see, for example, Ferrari, Presutti, and Vares [18] and Kipnis and Landim [19]. The particle system will exhibit large fluctuations about this limit which, though infrequent, can have catastrophic effects, such as earthquakes or mechanical failure (see, for example, [20–22]). It is thus important to understand and simulate such rare events. On an exponential scale, the (im)probability of a large fluctuation is described in terms of a large deviations principle with rate function \(I\).
The general approach to large deviations in interacting particle systems, introduced in the seminal works [23, 24], relies on two ingredients to be verified in a case by case manner: first, the so-called superexponential estimates, second, the identification of the lower semicontinuous (l.s.c.) envelope of the rate function restricted to smooth and strictly positive fluctuations, see [19, Chap. 10]. This can be a challenging problem, see, for example, Bodineau, Gallagher, Saint-Raymond, and Simonella, [25, Theorem 3], and the second ingredient is required, since, in a first step, the large deviations lower bound can be established only for nice enough fluctuations. More precisely, one first restricts to the space \(\mathcal {S}\) of positive fluctuations \(\rho \) so that
for some strictly positive \(\rho _{0}\in C^{\infty}(\mathbb{T}^{d})\) and \(H\in C^{3,1}(\mathbb{T}^{d}\times [0,T])\). The extension to a full large deviations result requires the identification of the l.s.c. envelope of the rate function (1) restricted to \(\mathcal {S}\). For the symmetric simple exclusion process, this envelope can be identified, due to the convexity of the rate function [19, Chap. 10, Lemma 5.5]; a property not available for the zero range process. For this reason, for the zero range process, so far, only a restricted large deviations estimate is known, in the sense that the lower bound is known only for nice enough fluctuations, see [26, Theorem 1, and the discussion on p. 66]. The identification of the l.s.c. envelope has remained an open problem for over twenty years since then, and is resolved in the present work on the torus.
Theorem 2
Theorem 39 below
Let \(\Phi \) satisfy Assumptions 6, 10, and 15below. Then, the rate function (1) is equal to the lower semicontinuous envelope of its restriction to the space \(\mathcal {S}\).
Since the assumptions on \(\Phi \) in this theorem include the case of degenerate \(\Phi '\), e.g. \(\Phi (\rho )=\rho ^{m}\) for every \(m\in [1,\infty )\), its applicability goes much beyond the fluctuations of the zero range process. We next demonstrate this by its application to the large deviations for degenerate stochastic PDEs with conservative noise, and their relation to the fluctuations of interacting particle systems.
Macroscopic fluctuation theory (MFT) introduces a general framework for non-equilibrium diffusive systems (see, for example, Bertini, De Sole, Gabrielli, Jona Lasinio, and Landim [27], Derrida [28]), thus extending Onsager-like near to equilibrium theories for non-equilibrium thermodynamics. MFT, which is based on a constitutive formula for large fluctuations around thermodynamic variables, like density and current, can be justified by fluctuating hydrodynamics (see, for example, Hohenberg and Halperin [29], Landau, and Lifshitz [30], Spohn [31], Bouchet, Gawȩdzki, and Nardini [32]). The latter postulates a conservative, singular stochastic PDE describing fluctuations in systems out of equilibrium. The fundamental ansatz of MFT can then be obtained, informally, from fluctuating hydrodynamics as the zero noise large deviations principle for this stochastic PDE. In addition to this conceptual relevance, the relation between zero noise large deviations for conservative stochastic PDE and MFT may serve as the basis for the development of importance sampling techniques to numerically simulate rare events in systems far from equilibrium (see, for example, E, Ren, and Vanden-Eijnden [20], Grafke and Vanden-Eijnden [21], Vanden-Eijnden and Weare [22]). We provide a rigorous link between the zero-noise large deviations of conservative stochastic PDE and the large deviations rate functions appearing in interacting particle systems, including zero range processes, the latter being an example for MFT.
The rate function (1) is informally connected to the small-noise large deviations (\(\varepsilon \to 0\), \(K\to \infty \)) of the stochastic PDE
where \(\xi ^{K}\) is an \(\mathbb{R}^{d}\)-valued spatially correlated noise, converging to space-time white noise \(\xi \) as \(K\rightarrow \infty \), see, for example, Dirr, Stamatakis, and Zimmer [33] and Giacomin, Lebowitz, and Presutti [34, Sect. 4]. In particular, in the ultraviolet limit \(K\to \infty \), this observation links the case of independently diffusing particles to the Dean–Kawasaki equation
which has been considered, for example, by Dean [35], Kawasaki [36], Donev, Fai, and Vanden-Eijnden [37], Donev and Vanden-Eijnden [38], Konarovskyi and von Renesse [39, 40], and Lehmann, Konarovskyi, and von Renesse [41].
This relationship, however, had to remain informal because (5) has only recently been shown to be well-posed by the authors in [42]. In addition, the ultraviolet limit \(K\to \infty \) of (5) is supercritical in the language of singular stochastic PDE and regularity structures (see, for example, Hairer [43], Gubinelli, Imkeller, and Perkowski [44]), and therefore falls outside the scope of the theory. For a discussion of this issue and the appearance of ultraviolet divergences in fluctuating hydrodynamics see [27, p. 595]. Furthermore, it has been observed in [41] that a renormalization is necessary in order to obtain function-valued solutions to (6). These renormalization terms destroy the relationship between the stochastic PDE and the zero range process, since they appear in the rate function for (6) and thereby lead to incorrect predictions of rare events for the particle process. We refer to Hairer and Weber [45] for a discussion of related aspects in the context of the (singular) stochastic quantization equation.
To address the issue of renormalization, the main result of this work identifies a joint scaling regime  such that possible renormalization constants vanish, and such that the solutions \(\rho ^{\varepsilon ,K(\varepsilon )}\) constructed in [42] correctly simulate the rare events in the particle system by satisfying a large deviations principle with rate function (1) (see (110) for the precise definition) in the strong \(L^{1}_{t,x}\)-topology.
such that possible renormalization constants vanish, and such that the solutions \(\rho ^{\varepsilon ,K(\varepsilon )}\) constructed in [42] correctly simulate the rare events in the particle system by satisfying a large deviations principle with rate function (1) (see (110) for the precise definition) in the strong \(L^{1}_{t,x}\)-topology.
Theorem 3
Theorem 29 below
Let \(\Phi \) satisfy Assumptions 6, 10, and 15below. Then, in the \(\varepsilon \rightarrow 0\) scaling regime
the solutions \(\rho ^{\varepsilon ,K(\varepsilon )}\) solving (5) satisfy a large deviations principle with rate function (1) uniformly with respect to weakly \(L^{1}(\mathbb{T}^{d})\)-compact subsets of \(\operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\).
A simplified version of these techniques prove that, for every fixed \(K\in \mathbb{N}\), the solutions to (5) satisfy a small-noise large deviations principle with rate function
for \(P_{K}g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\) the Fourier projection of \(g\) onto the Fourier modes of the noise \(\xi ^{K}\). The final result of this work is the \(\Gamma \)-convergence of these rate functions, as \(K\rightarrow \infty \), to the rate function (1).
Theorem 4
Theorem 33 below
Let \(\Phi \) satisfy Assumptions 6, 10, and 15below. Then, as \(K\rightarrow \infty \), in the sense of \(\Gamma \)-convergence,
1.1 Comments on the literature
The well-posedness of (degenerate) nonlinear parabolic-hyperbolic PDEs: for a detailed overview of the available methods for the well-posedness of (degenerate) PDEs of porous medium type, that is (2) with \(g=0\), we refer to Vázquez [46]. In particular, this includes several approaches to the uniqueness of solutions, for example, based on \(H^{-1}\)-monotonicity [46, Sect. 6.7], going back to Brezis [47], on the well-posedness of weak solutions [46, Sect. 5.3], due to Gilding [48] and Gilding and Peletier [49], on the accretivity in \(L^{1}\) and mild solutions [46, Sect. 10.2], due to Bénilan [50] and Crandall [51], and on the \(L^{1}\)-contraction by duality arguments [46, Sect. 6.2], going back to Bénilan, Crandall, and Pierre [52].
For non-trivial \(g\), equation (2) is a combination of a porous-medium type operator and a scalar conservation law. Since both of these are formally \(L^{1}\)-accretive, the literature on such PDEs concentrates on \(L^{1}\)-based approaches. The abstract theory of accretive operators in Banach spaces, by Bénilan [50], Crandall [51], and Crandall and Liggett [53] can, in principle, be used to prove the well-posedness of limit solutions of implicit Euler schemes. Besides being restricted to regular coefficients in time, since this general theory does not offer a characterization of said limit solutions in terms of the PDE, it cannot offer a solution to the uniqueness and stability problems addressed in this work.
In the context of hyperbolic-parabolic PDEs with regular coefficients, the notion of entropy solutions goes back to Vol’pert and Hudjaev [54], proving the existence and partial uniqueness of \(BV\)-solutions. This was extended by Alt and Luckhaus [55] and Otto [16] to the doubly nonlinear setting. The uniqueness of entropy solutions was first shown by Carrillo [56, 57]. Notably, these works do not touch the issue of irregular coefficients, and they rely on the notion of weak solutions, that is, solutions satisfying \(\nabla \Phi (\rho )\in L_{t,x}^{2}\), a property that cannot be expected in the case of the irregular coefficients of the present work due to the supercriticality of the equation, see Sects. 2.1 and 2.2 below.
A kinetic approach to spatially homogeneous, parabolic-hyperbolic PDEs has been developed by Chen and Perthame [11], for \(\Phi '\ge 0\) and for the flux \(\Phi ^{\frac{1}{2}}\) and \(\Phi \) locally Lipschitz continuous, which was complemented by a renormalized entropy solutions approach by Bendahmane and Karlsen [13]. For simplicity, in the following discussion, we use the terms kinetic solutions and renormalized entropy solutions synonymously.
Parabolic-hyperbolic PDEs with inhomogeneous, regular coefficients have been treated in Karlsen and Ohlberger [58], Chen and Karlsen [59], and Dalibard [60, 61], and the references therein. The case of less regular coefficients has been first considered by Karlsen and Risebro [12], which when applied to the setting of the present paper proves the uniqueness of (bounded) entropy solutions, assuming that \(g \in L^{1}_{t}W^{1,1}_{x} \cap L^{\infty}_{t} C^{0}_{x}\) with bounded divergence and that \(\Phi ^{\frac{1}{2}}\) is locally Lipschitz continuous. In this sense, this work partially generalized [1] to the case of nonlinear fluxes. This was subsequently extended by Wang, Wang, and Li [62] and Barbu and Röckner [63], still in the setting analogous to [1], and locally Lipschitz flux \(\Phi ^{\frac{1}{2}}\).
All of the above works are conceptually different from the present paper in several regards: (I) In the present work, we treat fluxes that are only \(L^{2}_{t,x}\)-integrable, thus going far beyond the classical setting of [1]. In addition, we only assume  -Hölder continuity of the flux in the function variable. (II) The contributions [11–13, 62] work entirely on the level of kinetic solutions. This does not imply the uniqueness of weak solutions. In fact, deducing this would require to prove that all weak solutions are kinetic solutions, which would precisely lead to the nonlinear commutator errors controlled in Sect. 4. We emphasize that passing through the concept of weak solutions is essential in the present work, in order to establish the stability of solutions with respect to the control in Proposition 21 and Theorem 28. (III) In addition, compared to the existing theory of kinetic solutions, e.g. [11], a new treatment of the entropy dissipation measure, as developed in Sect. 2.3 and specifically (15), is necessary, since the decay condition [11, Definition 2.2 (iv)] is not satisfied.
-Hölder continuity of the flux in the function variable. (II) The contributions [11–13, 62] work entirely on the level of kinetic solutions. This does not imply the uniqueness of weak solutions. In fact, deducing this would require to prove that all weak solutions are kinetic solutions, which would precisely lead to the nonlinear commutator errors controlled in Sect. 4. We emphasize that passing through the concept of weak solutions is essential in the present work, in order to establish the stability of solutions with respect to the control in Proposition 21 and Theorem 28. (III) In addition, compared to the existing theory of kinetic solutions, e.g. [11], a new treatment of the entropy dissipation measure, as developed in Sect. 2.3 and specifically (15), is necessary, since the decay condition [11, Definition 2.2 (iv)] is not satisfied.
Duality arguments: We will now discuss the (in-)applicability of the duality argument from [52] to the parabolic-hyperbolic PDEs with irregular coefficients considered in this work. Following [46], in a nutshell, the duality method is based on the following identity, for the difference of two solutions \(\rho ^{1}\) and \(\rho ^{2}\),
with \(a(t,x):= \frac{\Phi (\rho ^{1})-\Phi (\rho ^{2})}{\rho ^{1}-\rho ^{2}}\), \(b(t,x):= \frac{\Phi ^{\frac{1}{2}}(\rho ^{1})-\Phi ^{\frac{1}{2}}(\rho ^{2})}{\rho ^{1}-\rho ^{2}}\), and on choosing the test function \(\varphi \) as a sufficiently regular approximation of the linear dual equation, for smooth forcing \(\theta \),
This method fails in the context of (2) for several reasons: (I) The possible degeneracy of the diffusion in (2) and, thus, of \(a\) in (8) renders the regularity required on \(\varphi \) or approximations thereof problematic. In fact, even employing the improved argument for nonnegative solutions from [64] requires the use of maximum principles, which in turn require \(g\) to have bounded divergence, and sufficient regularity for the dual equation requires \(g\) bounded. (II) The duality method also requires sufficient integrability for the class of solutions considered. Precisely, see [46, Sect. 6.2], it requires \(\rho ,\Phi (\rho )\in L_{t,x}^{2}\). Due to the irregularity of the drift \(g\in L_{t,x}^{2}\), such a higher integrability cannot be expected in the setting of the present work. See also the discussion on \(L^{p}\)-estimates and the entropy-dissipation estimate in Sect. 2.2. (III) Aside from these two issues, the duality argument relies on choosing a test function that solves a linear dual equation (8). However, for linear Kolmogorov equations with irregular coefficients it is well-known that the critical integrability of \(g\in L_{t}^{p}L_{x}^{q}\) is given by the Ladyzhenskaya–Prodi–Serrin (LPS) condition, \(p,q\ge 2\), \(\frac{d}{p}+\frac{2}{q}\le 1\), see, for example [65, 66]. Again, this is not satisfied in the present work.
Linear Fokker–Planck equations with irregular coefficients: their well-posedness and stability of solutions have received considerable attention. We refer to Bogachev, Krylov, Röckner, and Shaposhnikov [67] for a detailed account of the literature, and to DiPerna and Lions [1], Ambrosio [2], De Lellis [5], Le Bris and Lions [3, 15], Boccardo, Orsina, and Porretta [68], Jabin [7, 8], and Porretta [69] for approaches relying on renormalization.
Fluctuations of the zero range process: fluctuations have been analyzed, for example, by Benois, Kipnis, and Landim in [26]. We also refer to Kipnis and Landim [19], Evans and Hanney [70], and the references therein for a detailed account of the theory. Equilibrium large deviations for the zero-range process with long jumps and reservoirs have been analyzed by Bernardin, Gonçalves, Oviedo-Jiménez, and Scotta [71]. For large deviations results in mean-field interacting particle systems we refer to the works by Barré, Bernardin, Chétrite, Chopra, and Mariani [72], Dawson and Gärtner [73, 74], and Gvalani and Schlichting [75].
Large deviations for conservative stochastic PDE: large deviations principles for conservative SPDEs have previously been considered in the works [76] by Mariani and [77] by Bellettini, Bertini, Mariani, and Novaga. We here compare the methods and results when applied in the framework of conservative SPDE (5). We emphasize, however, that the scope of the works [76, 77] goes beyond this by including the case of asymptotically vanishing dissipation, which heuristically corresponds to asymmetric simple exclusion processes. In this sense, the present work extends the first order large deviations obtained in [76, 77] in two directions: first, the rate functions are identified on the space of function-valued solutions. Second, this is achieved under significantly more general conditions on the coefficients, which include nonlinear dissipation \(\Phi \) and degenerate noise \(\sigma \). Since we allow for unbounded initial data and \(\sigma \), the methods developed here handle possible concentration and vacuum effects. Heuristically, this corresponds to potentially degenerate zero range processes, as compared to regularized exclusion processes in [76, 77].
In [76, 77] the rate function could be identified only after passing to a measure-valued formulation for which the skeleton equation is linear, and the corresponding rate function is convex. This significantly simplifies the identification, for example, since the linear structure is nicely compatible with mollification—a fact which is not true in the nonlinear setting, and the control of the resulting nonlinear commutators is a key technical step in the present work. The linearization also comes at the cost of working on much larger spaces, and on the level of function-valued large deviations no explicit representation of the rate function has been obtained, compare [76, Corollary 1]. This issue is fully resolved in the present work. We present an approach that entirely avoids passing to measure-valued solutions, and therefore establishes an LDP with an explicit rate function for the function-valued solutions that is consistent with the LDP for the particle system.
The second main generalization of [76, 77] lies in the assumptions on the coefficients. In [76] it is assumed that \(\sigma \) is \(\mathrm{C}^{2}\)-smooth with \(\sigma (0)=\sigma (1)=0\) and that \(0\leq \rho _{0}\leq 1\). As a consequence, solutions \(\rho \) also take values in the interval \([0,1]\), which rules out concentration and vacuum phenomena. As demonstrated in [78], this significantly simplifies the analysis of the large deviations, since the solutions are bounded and satisfy standard \(L^{p}\)-based regularity estimates. In addition, simple exclusion processes and zero range processes heuristically correspond to singular diffusion coefficients \(\sigma (\rho )=\sqrt{\rho (1-\rho )}\) and \(\sigma (\rho )=\sqrt{\rho}\) respectively, thus violating the \(C^{2}\)-smoothness assumption in [76, 77]. The results of the present work include also these singular cases.
Stochastic PDE with conservative noise: such equations have been considered in the framework of stochastic scalar conservation laws by Lions, Perthame, and Souganidis [79–81], Friz and Gess [82], Gess and Souganidis [83, 84]. Most recently, based on the equation’s kinetic formulation, the authors [42] treated a general class of parabolic-hyperbolic stochastic PDE with nonlinear conservative and multiplicative noise, including the Dean–Kawasaki and nonlinear Dawson–Watanabe equations. Earlier works studying stochastic PDEs with conservative noise include Gess and Souganidis [85], Fehrman and Gess [86], and Dareiotis and Gess [87]. Approaches to their numerics have been developed by Gess, Perthame, and Souganidis [88] and Hoel, Karlsen, Risebro, and Storrosten [89, 90]. Related results on the level of stochastic Hamilton-Jacobi equations have been developed by Lions and Souganidis [91–94] (see Souganidis [95] for a recent account on the theory), with extensions by Friz, Gassiat, Lions, and Souganidis [96]. A detailed analysis of fine properties of solutions has been given by Gassiat and Gess [97], Gassiat, Gess, Lions, and Souganidis [98], and Lions and Souganidis [99].
Large deviation estimates for singular stochastic PDE: such estimates have been derived by Faris and Jona-Lasinio [100], Jona-Lasinio and Mitter [101], Cerrai and Freidlin [102], and Hairer and Weber [45] in the context of stochastic Allen–Cahn equations. In particular, we emphasize that in [45] it is observed that renormalization constants may enter the rate function in the setting of singular stochastic PDE. The results treated in these works are quite different from the present paper, since, due to the additive noise structure of the stochastic Allen–Cahn equation, the treatment of the corresponding skeleton equation does not pose a major difficulty.
The weak convergence approach to large deviation principles: the weak convergence approach goes back to Budhiraja, Dupuis, and Maroulas [103], and it has been used to derive large deviation estimates for singular SPDE by Cerrai and Debussche [104]. Further applications to stochastic PDE with multiplicative noise, depending only on the values of the solution, have been given by Brzeźniak, Goldys, and Jegaraj [105] and Dong, Wu, Zhang, and Zhang [106].
The Dean–Kawasaki equation: the Dean–Kawasaki equation was introduced in Dean [35], Kawasaki [36], and analyzed in Donev, Fai, and Vanden-Eijnden [37], Donev and Vanden-Eijnden [38], Konarovskyi and von Renesse [39, 40], Lehmann, Konarovskyi, and von Renesse [41] and in the references therein. For an informal treatment of the link of macroscopic fluctuation theory (MFT) to fluctuating hydrodynamics in the context of the Dean–Kawasaki equation see Bouchet, Gawȩdzki, and Nardini [32]. The general MFT has received considerable attention, with a comprehensive overview given by Bertini, De Sole, Gabrielli, Jona-Lasinio, and Landim in [27].
1.2 Overview
We introduce the assumptions on the nonlinearity \(\Phi \) at the beginning of each section, and observe now that every assumption is satisfied by the model example \(\Phi (\xi )=\xi ^{m}\), for every \(m\in [1,\infty )\). In Sect. 2, we present an informal analysis of the skeleton equation broken down as follows. In Sect. 2.1, we argue by scaling that the skeleton equation (2) is energy critical for \(L^{1}(\mathbb{T}^{d})\) and is energy supercritical for \(L^{r}(\mathbb{T}^{d})\), if \(r\in (1,\infty )\). We obtain formal a-priori estimates for the solution of (2) in Sect. 2.2 and thereby identify the correct energy space (4) for the initial data. Based on these estimates, in Sect. 2.3 we define a renormalized kinetic solution (see Definition 3 below).
In Sect. 3, we prove the uniqueness of renormalized kinetic solutions (see Theorem 8 below). In Sect. 4, we prove in Theorem 14 the equivalence of renormalized kinetic solutions and weak solutions (see Definition 11 below). In Sect. 5, we prove the existence of renormalized kinetic solutions (see Proposition 20 below), and obtain in Proposition 21 the strong continuity of the solutions with respect to weak convergence of the controls. In Sect. 6, we prove the uniform large deviations principle, which relies on the weak approach to large deviations developed in [103]. In Sect. 7, in Theorem 33, we prove the \(\Gamma \)-convergence of the large deviations rate functions (7) to the rate function (1). In Sect. 8, we characterize the l.s.c. envelope of the restricted rate function.
2 The skeleton equation
The equation defining the large deviations rate function of the zero range process (1) is the so-called skeleton equation. In Sects. 3, 4, and 5 we will prove the existence and uniqueness of solutions to the equation, for \(\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\) and for \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\),
We first argue formally in Sect. 2.1 below that equation (9) is energy critical for \(L^{1}(\mathbb{T}^{d})\) and energy supercritical for \(L^{r}(\mathbb{T}^{d})\), if \(r\in (1,\infty )\). This argument suggests that no standard \(L^{p}\)-theory can be applied, and indeed in Sect. 2.2 below we derive an energy estimate for solutions with initial data in the space \(\operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\) defined in (4). This estimate will be the basis for Definition 3 below, where we present the definition of a renormalized kinetic solution.
We observe in particular that the formal estimates obtained in Sect. 2.2 are significantly weaker than are required to apply standard techniques based on the entropy or kinetic formulation of the equation (see [11, Sect. 2]). This can be seen on the level of the parabolic defect measure (see (15) below), which is neither globally integrable nor decaying at infinity. The proof of uniqueness therefore requires new techniques to control errors at infinity, and the proof of existence is based on a compactness argument that requires optimal estimates for the solution.
2.1 Energy criticality
In this section, we will argue formally that the skeleton equation (9) is energy critical for initial data \(\rho _{0}\in L^{1}(\mathbb{T}^{d})\) and controls \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\). We will consider the case of the porous media equation \(\Phi (\xi )=\xi ^{m}\), for some \(m\in [1,\infty )\), set on the whole space \(\mathbb{R}^{d}\times [0,\infty )\). Precisely, for \(m,p,q\in [1,\infty )\), \(T\in (0,\infty )\), and \(g\in L^{p}([0,T];L^{q}(\mathbb{R}^{d}))^{d}\), suppose that \(\rho \) solves
We will “zoom in” in the sense that, for positive real numbers \(\lambda ,\eta ,\tau \rightarrow 0\) we consider the rescaling
It follows that \(\tilde{\rho}\) solves the equation
for \(\tilde{g}\) defined by
We are interested in understanding the effect of this scaling on the balance between the parabolic and hyperbolic terms. We preserve the diffusion by fixing \(\frac{\tau}{\eta ^{2}\lambda ^{m-1}}=1\), and for \(r\in [1,\infty )\) we preserve the \(L^{r}(\mathbb{R}^{d})\)-norm of the initial data by fixing \(\lambda =\eta ^{\frac{d}{r}}\). It then follows from (10) that
To ensure that this norm does not diverge as \(\eta \rightarrow 0\), we require that
If \(p=q=2\), we conclude that  and therefore that \(r=1\). Conversely, since the lefthand side of this equality is largest for \(r=1\), and since the case \(r=1\) yields the inequality
and therefore that \(r=1\). Conversely, since the lefthand side of this equality is largest for \(r=1\), and since the case \(r=1\) yields the inequality
we conclude that \(p=q=2\) is critical for \(L^{1}(\mathbb{T}^{d})\) and supercritical for \(L^{r}(\mathbb{R}^{d})\), for every \(r\in (1,\infty )\).
2.2 A-priori estimates
In this section, we will motivate the definition of a renormalized kinetic solution of the skeleton equation (see Definition 3 below). This definition is the foundation of the existence and uniqueness theory to follow. We will first derive a formal energy estimate for the solution, and thereby identify the correct energy space for the initial data.
We will restrict attention to nonnegative initial data, which is a necessary assumption for the following estimates to be true (see Remark 1 below). Let \(T\in (0,\infty )\), let \(\rho _{0}\colon \mathbb{T}^{d}\rightarrow [0,\infty )\) be nonnegative, let \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\), and let \(\rho \) denote the solution
Let \(\psi \colon [0,\infty )\rightarrow \mathbb{R}\) and let \(\Psi (\xi )=\int _{0}^{\xi}\psi (\xi ')\, \mathrm {d} \xi '\). After testing the equation with the composition \(\psi (\rho )\),
The nonnegativity of \(\rho \), Hölder’s inequality, and Young’s inequality prove that
To close the estimate we require that \(\Phi (\xi )\psi '(\xi )^{2}\leq \Phi '(\xi )\psi '(\xi )\) and hence that \(\psi '(\xi )\leq \frac{\Phi '(\xi )}{\Phi (\xi )}\). We therefore fix \(\psi _{\Phi}(\xi )=\log (\Phi (\xi ))\) and define \(\Psi _{\Phi}(\xi )= \int _{0}^{\xi}\log (\Phi (\xi '))\, \mathrm {d} \xi '\) to conclude that
The formal estimate then follows from the identity \(2\nabla \Phi ^{\frac{1}{2}}(\rho )= \frac{\Phi '(\rho )}{\Phi ^{\frac{1}{2}}(\rho )}\nabla \rho \).
Remark 1
Estimate (11) is in general false for signed initial data, which can be seen for the heat equation. Since \(\rho (x,t)=x\) solves the heat equation with linear initial data, and since \(x^{\frac{1}{2}}\notin L^{2}([0,T];H^{1}_{\textrm{loc}}(\mathbb{R}))\), we conclude after localizing this argument to the torus.
Remark 2
We observe that estimate (11) is based on the physical entropy of the initial data in the case that \(\Phi (\xi )=\xi ^{m}\), for some \(m\in (0,\infty )\). In this case,
from which it follows from the preservation of the \(L^{1}_{x}\)-norm that the physical entropy is a nondecreasing function of time.
2.3 Renormalized kinetic solutions
In this section, we will define renormalized kinetic solutions to the skeleton equation (9). Based on estimate (11), we first rewrite the equation in the form
On this level, the criticality of the equation can be seen by analyzing the integrability of the products
which are formally \(L^{1}_{t,x}\)-integrable. Indeed, even in one dimension, embedding theorems do not readily yield an improvement because they do not improve the integrability in time.
The borderline integrability of the products (12) and the lack of regularity for the solution make classical techniques untenable and suggest the necessity of a generalized solution theory. We therefore pass to the equation’s kinetic formulation. The kinetic function \(\overline{\chi}\colon \mathbb{R}^{2}\rightarrow \mathbb{R}\) is defined by \(\overline{\chi}(s,\xi )=\mathbf{1}_{\{0<\xi <s\}}-\mathbf{1}_{\{s< \xi <0\}}\), and the kinetic function \(\chi \) of \(\rho \) is defined by
The identities
show formally that the kinetic function \(\chi \) of \(\rho \) satisfies the equation
in \(\mathbb{T}^{d}\times \mathbb{R}\times (0,T)\), where \(\chi (\cdot ,0)= \overline{\chi}(\rho _{0})\) and where \(p\) is the parabolic defect measure on \(\mathbb{T}^{d}\times \mathbb{R}\times (0,T)\) defined by
In view of Sect. 2.2, this measure will be neither finite nor decaying at infinity. We then formally rewrite (14) in the conservative form
and apply the distributional identities (13) to formally derive equation (18) below. Finally, we observe that in the following definition of a renormalized kinetic solution, the formal estimates of Sect. 2.2 are implicit in (17). In particular, while we prove the uniqueness of solutions for nonnegative initial data in \(L^{1}(\mathbb{T}^{d})\), the proof of existence and, in particular, estimate (17) will require that we consider initial data with finite entropy in the sense of (3).
Definition 3
Let \(T\in (0,\infty )\), let \(\Phi \in \mathrm{C}[0,\infty )\cap \mathrm{C}^{1}_{\textrm{loc}}((0, \infty ))\), and let \(\rho _{0}\in L^{1}(\mathbb{T}^{d})\) be nonnegative. A nonnegative function \(\rho \in L^{\infty}([0,T],L^{1}(\mathbb{T}^{d}))\) is a renormalized kinetic solution of (16) with initial data \(\rho _{0}\) if \(\rho \) satisfies the following two properties.
-
(a)
We have that
$$ \Phi ^{\frac{1}{2}}(\rho )\in L^{2}([0,T];H^{1}(\mathbb{T}^{d})).$$(17) -
(b)
For every \(\psi \in \mathrm{C}^{\infty}_{c}(\mathbb{T}^{d}\times (0,\infty ))\) with \(\psi (x,0)=0\), the kinetic function \(\chi \) of \(\rho \) satisfies that, for every \(t\in [0,T]\),
$$\begin{aligned} & \int _{\mathbb{T}^{d}}\int _{\mathbb{R}} \chi (t)\psi = \int _{\mathbb{R}} \int _{\mathbb{T}^{d}}\overline{\chi}(\rho _{0},\xi )\psi + \int _{0}^{t} \int _{\mathbb{R}}\int _{\mathbb{T}^{d}} \Phi '(\xi )\chi \Delta _{x}\psi \\ &\;- \int _{0}^{t}\int _{\mathbb{R}}\int _{\mathbb{T}^{d}}p\partial _{\xi }\psi + 2\int _{0}^{t}\int _{\mathbb{T}^{d}} (\partial _{\xi}\psi )(x,\rho ) \frac{\Phi (\rho )}{\Phi '(\rho )}\nabla _{x}\Phi ^{\frac{1}{2}}( \rho )\cdot g \\ &\;+ \int _{0}^{t}\int _{\mathbb{T}^{d}} \Phi ^{\frac{1}{2}}( \rho )g\cdot (\nabla _{x}\psi )(x,\rho ). \end{aligned}$$(18)
Remark 4
We observe that the equality in equation (18) is satisfied due to the optimal regularity (17), which requires the nonnegativity of the initial data (see Remark 1). In general, we would only expect to obtain an inequality due to the presence of a nonnegative entropy defect measure (see [11, Sect. 2]).
The following lemma proves that renormalized kinetic solutions in the sense of Definition 3 satisfy an integration by parts formula on the level of their kinetic functions.
Lemma 5
Let \(\Phi \in \mathrm{C}([0,\infty ))\cap \mathrm{C}^{1}_{\textrm{loc}}((0, \infty ))\) be nondecreasing, let \(\rho \colon \mathbb{T}^{d}\rightarrow \mathbb{R}\) be measurable, let \(\chi \) be the kinetic function of \(\rho \), and assume that \(\Phi ^{\frac{1}{2}}(\rho )\in H^{1}(\mathbb{T}^{d})\). Then, for every \(\psi \in \mathrm{C}^{\infty}_{c}(\mathbb{T}^{d}\times \mathbb{R})\),
Proof
The proof is a small modification of [11, Appendix A] and follows from the change of variables formula and the fact that \(\Phi \) is nondecreasing. □
3 Uniqueness of renormalized kinetic solutions
In this section, we will prove the uniqueness of renormalized kinetic solutions in the sense of Definition 3 for nonlinearities \(\Phi \) that satisfy Assumption 6 below. The proof of uniqueness is significantly complicated by the fact that the parabolic defect measure is neither globally integrable nor decaying at infinity with respect to the velocity variable \(\xi \in \mathbb{R}\). It is for this reason that we introduce a cutoff in velocity. Lemma 7 below is used to control the error terms that arise when removing this cutoff function. We then prove the uniqueness of renormalized kinetic in Theorem 8 below, the starting point for which is based on the techniques of [11, Theorem 1.1, Sect. 4].
Assumption 6
Let \(\Phi \in \mathrm{C}([0,\infty ))\cap \mathrm{C}^{1}_{\textrm{loc}}((0, \infty ))\) satisfy \(\Phi (0)=0\) and \(\Phi '(\xi )>0\) for every \(\xi \in (0,\infty )\). Assume that
and that there exists \(c\in (0,\infty )\) such that, for every \(M\in (0,\infty )\),
Lemma 7
Let \((X,\mathcal{S},\mu )\) be a measure space, let \(K\in \mathbb{N}\), let \(\{f_{k}\colon X\rightarrow \mathbb{R}\}_{k\in \{1,2,\ldots ,K\}} \subseteq L^{1}(X)\), and for every \(k\in \{1,2,\ldots ,K\}\) let \(\{B_{n,k}\subseteq X\}_{n\in \mathbb{N}}\subseteq \mathcal{S}\) be disjoint subsets. Then,
Proof
The proof of this claim is a straightforward consequence of the fact that, for a sequence of positive numbers \(a_{n}\), if \(\sum _{n=1}^{\infty }a_{n}<\infty \) then \(\liminf _{n\rightarrow \infty} (na_{n}) =0\). □
Theorem 8
Let \(T\in (0,\infty )\), let \(\Phi \in \mathrm{C}([0,\infty ))\cap \mathrm{C}^{1}_{\textrm{loc}}((0, \infty ))\) satisfy Assumption 6, let \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\), and let \(\rho _{0}^{1},\rho _{0}^{2}\in L^{1}(\mathbb{T}^{d})\) be nonnegative. If \(\rho ^{1}\), \(\rho ^{2}\) are solutions of (9) in the sense of Definition 3with control \(g\) and with initial data \(\rho _{0}^{1}\), \(\rho _{0}^{2}\), then
Proof
In order to simplify the notation, we will write the proof in the porous media and fast diffusion case \(\Phi (\xi )=\xi ^{m}\), for some \(m\in (0,\infty )\), and observe in the proof were the more general conditions of Assumption 6 are needed. For the kinetic function \(\chi ^{i}\) of \(\rho ^{i}\), we will write \(\chi ^{i}_{t}(x,\xi )=\chi (x,\xi ,t)\) and we will make similar conventions for the defect measure \(p^{i}_{t}\) and all other time-dependent functions or measures appearing in the proof. For every \(\varepsilon \in (0,1)\) let \(\kappa ^{\varepsilon }\) be a standard convolution kernel on \(\mathbb{T}^{d}\) of scale \(\varepsilon \), for every \(\delta \in (0,1)\) let \(\kappa ^{\delta }\) be a standard convolution kernel on ℝ of scale \(\delta \), and for every \(\varepsilon ,\delta \in (0,1)\) let \(\kappa ^{\varepsilon ,\delta }(x,y,\xi ,\eta )=\kappa ^{\varepsilon }(x-y)\kappa ^{\delta }( \xi -\eta )\). Let \(\chi ^{i,\varepsilon ,\delta }_{t}=(\chi ^{i}_{t}*\kappa ^{\varepsilon ,\delta })\) and let \(\operatorname {sgn}^{\delta}(\eta ) = (\operatorname {sgn}*\kappa ^{\delta })(\eta )=(\operatorname {sgn}*\kappa ^{ \varepsilon ,\delta })(y,\eta )\), where in what follows the convolution kernel \(\kappa ^{\varepsilon ,\delta }\) will play the role of the test function in Definition 3. It is also necessary to introduce a cutoff in the velocity variable. For this, for every \(M\in (0,\infty )\), let \(\zeta ^{M}:[0,\infty )\rightarrow [0,1]\) satisfy \(\zeta ^{M}=0\) on \([0,M^{-1}]\cup [M+1,\infty )\) and \(\zeta ^{M} = 1\) on \([2M^{-1},M]\) and let \(\zeta ^{M}\) linearly interpolate between the values \(\{0,1\}\) on \([M^{-1},2M^{-1}]\) and \([M,M+1]\). We will now begin with the proof of uniqueness.
In what follows, when necessary we will write \((x,\xi )\in \mathbb{T}^{d}\times \mathbb{R}\) for the variables inside the convolutions, and we will write \((y,\eta )\in \mathbb{T}^{d}\times \mathbb{R}\) for the outer integration variables. The fact that the kinetic function is \(\{0,1\}\)-valued proves that
Let \(\overline{\kappa}^{\varepsilon ,\delta }_{i}\) be defined by
and observe from the equation satisfied by \(\rho ^{i}\) that, as distributions on \(\mathbb{T}^{d}\times \mathbb{R}\times (0,T)\),
It then follows from Lemma 5 and the symmetry of the convolution kernel that
We define
We will analyze the terms involving the \(\operatorname {sgn}\) function and the mixed term separately. For every \(i\in \{1,2\}\) let
In what follows, we will let \(t\in [0,T]\), \(M\in (0,\infty )\), \(\varepsilon \in (0,1)\), and \(\delta \in (0,(2M)^{-1})\) be arbitrary. In particular, this choice of \(\delta \) guarantees that
In the argument, we will first let \(\varepsilon \rightarrow 0\), then \(\delta \rightarrow 0\), and then \(M\rightarrow \infty \) which is consistent with this choice.
The sign terms. We will first analyze the \(\operatorname {sgn}\) terms (23), and we will first consider the case \(i=1\). It follows from (21) that, as distributions on \((0,T)\),
The symmetry of the convolution kernel and the distributional equality \(\partial _{\xi} \operatorname {sgn}=2\delta _{0}\) prove that
The case \(i=2\) is identical and this completes the initial analysis of the \(\operatorname {sgn}\) terms.
The mixed term. As distributions on \((0,T)\),
It follows from (21) that
Since the integration by parts formula of Lemma 5 proves that
and since we have the distributional equality \(\partial _{\xi}\chi ^{2}=\delta _{0}(\xi )-\delta _{0}(\xi -\rho ^{2})\),
We obtain an identical formula for \(\mathbb{I}^{\varepsilon ,\delta ,M}_{t,2,\textrm{mix}}\) after swapping the roles of \(i\in \{1,2\}\), and this completes the initial analysis of the mixed term.
The full derivative. We will decompose the full derivative of (22) defined by (23), (25), (26), and (27) into the four terms
defined by the parabolic term
the hyperbolic term
the term involving the control
and the term defined by the cutoff
The four terms on the righthand side of (28) will be handled separately.
The parabolic terms. After adding and subtracting \(2(\rho ^{1}\rho ^{2})^{\frac{1-m}{2}}\) and using that
the parabolic term defined in (29) satisfies
The definition of the parabolic defect measures, Hölder’s inequality, and Young’s inequality prove that
and it therefore follows from (33) that
It then follows from a direct computation using (24), where in the general case we would use here the local  -Hölder continuity of \(\Phi '\) and the local boundedness of \(\Phi '\) and \(\Phi \) away from zero and infinity on compact subsets of \((0,\infty )\), that for some \(c\in (0,\infty )\) depending on \(M\),
-Hölder continuity of \(\Phi '\) and the local boundedness of \(\Phi '\) and \(\Phi \) away from zero and infinity on compact subsets of \((0,\infty )\), that for some \(c\in (0,\infty )\) depending on \(M\),
and therefore, for some \(c\in (0,\infty )\) depending on \(M\),
The boundedness of \(\delta \kappa ^{\delta}\) in \(\delta \in (0,1)\), the supports of \(\kappa ^{\delta }\) and \(\zeta ^{M}\), Hölder’s inequality, and Young’s inequality prove that, for some \(c\in (0,\infty )\) depending on \(M\),
The \(H^{1}_{x}\)-regularity of \((\rho ^{i})^{\frac{m}{2}}\) and the dominated convergence theorem then prove that
which completes the analysis of the parabolic terms.
The hyperbolic terms. A similar analysis relying on the supports of \(\kappa ^{\delta }\) and \(\zeta ^{M}\), the local Lipschitz continuity of \(\Phi \) and therefore \(\Phi ^{\frac{1}{2}}\) on \((0,\infty )\), (24), and the boundedness of \(\delta \kappa ^{\delta }\) in \(\delta \in (0,1)\) proves that the hyperbolic terms (30) satisfy, for some \(c\in (0,\infty )\) depending on \(M\in (0,\infty )\),
Hölder’s inequality and Young’s inequality then prove that
and the \(L^{2}_{t,x}\)-integrability of \(g\), the \(H^{1}_{x}\)-regularity of \((\rho ^{i})^{\frac{m}{2}}\), and the dominated convergence theorem prove that
which completes the analysis of the hyperbolic terms.
The control terms. It follows from (24) and the choice of \(\delta \) and \(M\) that there exists \(c\in (0,\infty )\) depending on \(M\) such that
and therefore the control terms (31) satisfy
The \(L^{2}_{t,x}\)-integrability of \(g\) and \(H^{1}_{x}\)-regularity of \((\rho ^{i})^{\frac{m}{2}}\) then prove that
and, therefore,
which completes the analysis of the control terms.
The cutoff in velocity. It follows from the definition of the parabolic defect measures and \(|2\chi ^{i,\varepsilon ,\delta }-\operatorname {sgn}^{\delta}|\leq 1\) that, for \(\overline{\kappa}_{i,t}^{\delta }(y,\eta ) = \kappa ^{\delta }(\rho ^{i}(y,t)- \eta )\), after passing to the limit \(\varepsilon \rightarrow 0\) in (32) we have that
It is at this point that we would use assumption (19) in the general case to bound \(\Phi (\Phi ')^{-1}\). It then follows from the boundedness of \(|\eta \partial _{\eta}\zeta ^{M}|\) for \(\eta \in (0,1)\), the support of \(\partial _{\eta}\zeta ^{M}\), Hölder’s inequality, and Young’s inequality that, for \(c\in (0,\infty )\) independent of \(M\in (0,\infty )\),
which completes the analysis of the cutoff in velocity.
The conclusion. Returning to (20), it follows from (34), (35), (36), and (37) that, for \(c\in (0,\infty )\) independent of \(M\in (0,\infty )\),
For the final term on the righthand side of (38), the dominated convergence theorem proves that
For the second term on the righthand side of (38), a straightforward application of Lemma 7 applied to the functions
proves that
Returning to (38), we conclude from (39) and (40) that, after taking \(M\rightarrow \infty \),
which completes the proof. □
Proposition 9
Let \(T\in (0,\infty )\), let \(\Phi \) satisfy Assumption 6, let \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\), let \(\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\), and let \(\rho \in L^{1}(\mathbb{T}^{d}\times [0,T])\) be a renormalized kinetic solution of (9) in the sense of Definition 3. Then \(\rho \) has a representative in \(\mathrm{C}([0,T];L^{1}(\mathbb{T}^{d}))\).
Proof
The proof is a deterministic and simplified version of the proof of the analogous fact in [42, Theorem 5.29]. We therefore only outline the main details. In [42, Equation (5.65)], we first identify weakly right- and left-continuous representatives \(\chi ^{\pm}\) of the kinetic function \(\chi \) of \(\rho \) using the equation and properties of the kinetic measure. We then use the equation and the uniqueness proof of Theorem 8 in [42, Equations (5.66), (5.67), and (5.68)] to prove that the \(\chi ^{\pm}\) are kinetic functions in the sense that \(\chi ^{+}(x,\xi ,t)=\mathbf{1}_{\{0<\xi <\rho ^{+}(x,t)\}}\) and \(\chi ^{-}(x,\xi ,t)=\mathbf{1}_{\{0<\xi <\rho ^{-}(x,t)\}}\) for representatives \(\rho ^{\pm}\) of \(\rho \) in \(L^{1}(\mathbb{T}^{d}\times [0,T])\). Finally, using the definition of the parabolic defect measure and the optimal regularity estimate (17), we prove in [42, Equation (5.70)] that \(\rho ^{+}=\rho ^{-}\) is strongly \(L^{1}(\mathbb{T}^{d})\)-continuous in time, which completes the proof. □
4 Equivalence of renormalized kinetic solutions and weak solutions
In this section, we will prove in Theorem 14 that, for nonlinearities \(\Phi \) satisfying the additional Assumption 10, renormalized kinetic solutions (see Definition 3) are equivalent to classical weak solutions (see Definition 11 below). Assumption 10 is broken into two cases, and for the model example \(\Phi (\xi )=\xi ^{m}\) an explicit computation proves that case (i) applies to \(m\in [1,2]\) and case (ii) applies to \(m\in [2,\infty )\). The equivalence of renormalized kinetic solutions and classical weak solutions is used in Proposition 21 below to prove that a weakly convergent sequence of controls induces a strongly convergent sequence of solutions. This fact is not obvious for renormalized kinetic solutions, since the fourth term on the righthand side of (18) will contain what is in general the product between a weakly convergent gradient and weakly convergent control.
Assumption 10
Let \(\Phi \in \mathrm{C}([0,\infty ))\cap \mathrm{C}^{1}_{\textrm{loc}}((0, \infty ))\) satisfy Assumption 6. Assume that \(\Phi \) satisfies one of the following two conditions.
-
(i)
We have that \(\Phi ^{\frac{1}{2}}\colon [0,\infty )\rightarrow [0,\infty )\) is concave, and there exists \(c\in (0,\infty )\) and \(p\in [2,\infty )\) such that, for every \(\xi \in (0,\infty )\),
$$ \Big(\frac{\Phi ^{\frac{1}{2}}(\xi )}{\Phi '(\xi )}\Big)^{p}\leq c \left (\xi +1\right ).$$(41) -
(ii)
We have that \(\Phi ^{\frac{1}{2}}\colon [0,\infty )\rightarrow [0,\infty )\) is convex, there exists \(c\in (0,\infty )\) such that
$$ \sup _{\{\xi \geq 1\}}|\frac{\Phi (\xi +1)}{\Phi (\xi )}|\leq c,$$(42)and for every \(M\in (0,1)\) there exists \(c\in (0,\infty )\) depending on \(M\) such that
$$ \sup _{\{\xi \geq M\}} |\frac{\Phi ^{\frac{1}{2}}(\xi )}{\Phi '(\xi )}|\leq c.$$(43)
Definition 11
Let \(T\in (0,\infty )\), let \(\Phi \in \mathrm{C}([0,\infty ))\cap \mathrm{C}^{1}_{\textrm{loc}}((0, \infty ))\), let \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\), and let \(\rho _{0}\in L^{1}(\mathbb{T}^{d})\) be nonnegative. A weak solution of (9) with initial data \(\rho _{0}\) is a continuous \(L^{1}(\mathbb{T}^{d})\)-valued function \(\rho \in L^{\infty}([0,T];L^{1}(\mathbb{T}^{d}))\) that satisfies the following two properties.
-
(i)
We have \(\Phi ^{\frac{1}{2}}(\rho )\in L^{2}([0,T];H^{1}(\mathbb{T}^{d}))\).
-
(ii)
We have that, for every \(t\in [0,T]\), for every \(\psi \in \mathrm{C}^{\infty}(\mathbb{T}^{d})\),
$$\begin{aligned} \int _{\mathbb{T}^{d}}\rho (x,t)\psi (x)\, \mathrm {d} x& =-\int _{0}^{t}\int _{\mathbb{T}^{d}}2 \Phi ^{\frac{1}{2}}(\rho )\nabla \Phi ^{\frac{1}{2}}(\rho )\cdot \nabla \psi \, \mathrm {d} x\, \mathrm {d} t\\ & \quad +\int _{0}^{t}\int _{\mathbb{T}^{d}}g\Phi ^{\frac{1}{2}}(\rho ) \cdot \nabla \psi \, \mathrm {d} x\, \mathrm {d} t+\int _{\mathbb{T}^{d}}\rho _{0}(x)\psi (x)\, \mathrm {d} x. \end{aligned}$$
It is essentially clear that a renormalized kinetic solution is a weak solution. In order to prove the converse statement, let \(\rho \) be a weak solution in the sense of Definition 11, let \(\psi \in \mathrm{C}^{\infty}_{c}(\mathbb{T}^{d}\times (0,\infty ))\), and let \(\partial _{\xi}\Psi (x,\xi )=\psi (x,\xi )\). The composition \(\Psi (x,\rho ^{\varepsilon })\), for the spatial convolution \(\rho ^{\varepsilon }= \rho *\kappa ^{\varepsilon }\), is then a distributional solution of the equation
Both terms on the righthand side of (44) will be treated identically using only the \(L^{2}_{t,x}\)-integrability of \(g\) and \(\nabla \Phi ^{\frac{1}{2}}(\rho )\) respectively. We therefore let \(F\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\) and observe that, after integrating by parts in space,
The \(L^{1}_{t,x}\)-integrability of the product \(\Phi ^{\frac{1}{2}}(\rho )F\) and boundedness of \(\nabla _{x}\psi \) make it relatively straightforward to pass to the \(\varepsilon \rightarrow 0\) limit in the first term on the righthand side of (45). The second term is more difficult even if \(\rho \) is \(H^{1}_{x}\)-valued, due to the fact that the unboundedness of \(\Phi ^{\frac{1}{2}}(\rho )\) means that \((\Phi ^{\frac{1}{2}}(\rho )F*\kappa ^{\varepsilon })\) is not converging \(L^{2}_{t,x}\)-strongly to its limit \(\Phi ^{\frac{1}{2}}(\rho )F\). In fact, since our analysis holds in an arbitrary dimension, this limit effectively holds only \(L^{1}_{t,x}\)-strongly and not better.
In order to improve this convergence, we observe that the compact support of the test function \(\psi \) yields an \(L^{\infty}_{t,x}\)-bound for the convolution \(\rho ^{\varepsilon }\). The goal of our analysis is to transfer the \(L^{\infty}_{t,x}\)-bound for the convolution to an \(L^{\infty}_{t,x}\)-bound for \(\rho \) itself, and by doing so to establish the \(L^{2}_{t,x}\)-strong convergence of the convolutions \((\Phi ^{\frac{1}{2}}(\rho )F*\kappa ^{\varepsilon })\) away from the vanishing set that \(\rho \) is large. The argument is complicated by the fact that \(\rho \) itself is not regular, and we must therefore exploit the regularity of \(\Phi ^{\frac{1}{2}}(\rho )\). For this reason, we separate the analysis into two cases, depending on whether \(\Phi ^{\frac{1}{2}}\) is concave or convex.
Proposition 12
Let \(T\in (0,\infty )\), let \(\Phi \) satisfy Assumption 6and (i) of Assumption 10, let \(\rho \in L^{\infty}([0,T];L^{1}(\mathbb{T}^{d}))\), let \(\Phi ^{\frac{1}{2}}(\rho )\in L^{2}([0,T];H^{1}(\mathbb{T}^{d}))\), let \(F\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\), let \(\psi \in \mathrm{C}^{\infty}_{c}(\mathbb{T}^{d}\times (0,\infty ))\), and let \(\kappa ^{\varepsilon }\) be standard convolution kernel of scale \(\varepsilon \) on \(\mathbb{T}^{d}\). Then, for \(\rho ^{\varepsilon }= \rho *\kappa ^{\varepsilon }\), for every \(t\in [0,T]\),
Proof
To simplify the notation, we will write the proof in the case \(\Phi (\xi )=\xi ^{m}\), for \(m\in [1,2]\), and indicate where the general version of (i) in Assumption 10 is used. Let \(M\in (0,\infty )\) satisfy \(\operatorname{Supp}(\psi )\subseteq (\mathbb{T}^{d}\times [M^{-1},M])\), let
and let \(A_{0}=(\mathbb{T}^{d}\times [0,T])\setminus A_{1}\). We then form the decomposition
We will first prove that the first term on the righthand side of (46) vanishes as \(\varepsilon \rightarrow 0\). In effect, this is what transfers the \(L^{\infty}\)-bound for \(\rho ^{\varepsilon }\) to \(\rho \) in the \(\varepsilon \rightarrow 0\) limit.
The first term of (46). We aim to show that
Hölder’s inequality proves that
We will first prove that the final term on the righthand side of (48) remains bounded. For every \(x\in \mathbb{T}^{d}\) and \(k\in \mathbb{N}\), for the indicator function \(\mathbf{1}_{k,k+1}\) of \(A_{k}\setminus A_{k+1}\), let
Since the map \(\xi \mapsto \xi ^{\frac{m}{2}}\) is concave, or more generally since \(\Phi ^{\frac{1}{2}}\) is concave, Jensen’s inequality proves that
Therefore, for every \((y,t)\in \operatorname{Supp}(\mathbf{1}_{k,k+1}\psi (\cdot +x,\rho ^{\varepsilon }(\cdot +x, \cdot )))\),
It follows from (49) and (50) that
and it follows from the change of variables formula, the fact that \(\Phi \) is increasing, the definition of \(A_{k}\), and (51) that there exists \(c\in (0,\infty )\) depending on the \(L^{\infty}\)-norm of \(\psi \) such that
It remains to estimate the measure of the sets \(B^{\varepsilon }_{k,x}\). It follows from Chebyshev’s inequality, Jensen’s inequality, and the fundamental theorem of calculus that
for \(\kappa ^{\varepsilon }\mathbf{1}_{k,k+1}=\kappa ^{\varepsilon }(y+x-y')\mathbf{1}_{k,k+1}(y,t)\) in the final line. Since the triangle inequality proves that \(|y-y'|\leq |x|+\varepsilon \) on the support of the convolution kernel, it follows from (53) that
Returning to (52), it follows from (54) that, for \(c\in (0,\infty )\) depending on \(M\),
Returning to (52), it follows from the support of the convolution kernel and (55) that
Returning to (48), it follows from (56) that there exists \(c\in (0,\infty )\) such that
Since for \(c_{0}=\int _{\mathbb{T}^{d}}|\nabla \kappa (x)|\) the functions \(\{c_{0}^{-1}|\varepsilon \nabla \kappa ^{\varepsilon }|\}_{\varepsilon \in (0,1)}\) are a Dirac sequence on \(\mathbb{T}^{d}\) and since \(\psi \in \mathrm{C}^{\infty}_{c}(\mathbb{T}^{d}\times (0,\infty ))\), it follows from the definition of \(A_{1}\) and the dominated convergence theorem that
which in combination with (57) proves that
which completes the proof of (47).
The second term of (46). We will prove that the second term on the righthand side of (46) satisfies
After integrating by parts,
For the first term on the righthand side of (46), the \(L^{1}\)-strong convergence of \((\rho ^{\frac{m}{2}} F*\kappa ^{\varepsilon })\) to \(\rho ^{\frac{m}{2}} F\), the boundedness of \(\nabla _{x}\psi \), the triangle inequality, and the dominated convergence theorem prove that
It remains to treat the second term. In order to treat the potential degeneracy of \(\rho \), it is necessary to replace the convolution of \(\nabla \rho \) with an appropriate convolution of \(\nabla \rho ^{\frac{m}{2}}\). For this, we make a preliminary calculation. In the general case, we let \((\Phi ^{\frac{1}{2}})^{-1}\) denote the function inverse to \(\Phi ^{\frac{1}{2}}\), and use the equality
together with assumption (41) to deduce that \((\Phi ^{\frac{1}{2}})^{-1}\) is locally Lipschitz continuous on \((0,\infty )\). The chain rule, the \(H^{1}_{x}\)-regularity of \(\Phi ^{\frac{1}{2}}(\rho )\), and (61) then prove that
In the case \(\Phi (\xi )=\xi ^{m}\), equality (62) shows that the second term on the righthand side of (46) satisfies
The first convolution will be decomposed in terms of \(A_{0}\) and \(A_{1}\). We will first prove that
In the general case, we will use Hölder’s inequality and the nonnegativity of \(\rho \) to conclude that there exists \(c\in (0,\infty )\) such that, for \(p\in [2,\infty )\) as in (41),
which in the particular case \(\Phi (\xi )=\xi ^{m}\), for \(m\in [1,2]\), proves that there exists \(c\in (0,\infty )\) such that (64) is bounded for \(p=\frac{2}{2-m}\) or any \(p\in [2,\infty )\) if \(m=2\) by
Since \(\rho ^{\varepsilon }(x,t)\) is bounded on the support of \(\psi (x,\rho ^{\varepsilon }(x,t))\), it follows from Hölder’s inequality and the boundedness of \(\rho \) on the set \(A_{0}\) that there exists \(c\in (0,\infty )\) depending on \(M\) such that (65) is bounded by
A calculation identical to (60) using the definition of \(A_{1}\) proves that
In combination (66) and (67) complete the proof of (64). It remains to treat the term involving the integral over \(A_{0}\), which is
Since \(m\in [1,2]\) implies that \(\rho ^{1-\frac{m}{2}}\) and \(\rho \) are bounded on the support of \(\mathbf{1}_{A_{0}}\), where in general we will use (41) to conclude that both \(\Phi ^{\frac{1}{2}}(\rho )(\Phi '(\rho ))^{-1}\) and \(\rho \) are bounded on \(A_{0}\), it follows from the strong \(L^{2}\)-convergence of
the strong \(L^{2}\)-convergence of \((\rho ^{1-\frac{m}{2}}\nabla \rho ^{\frac{m}{2}}\mathbf{1}_{A_{0}}* \kappa ^{\varepsilon })\), the triangle inequality, and Hölder’s inequality that
In combination (60), (63), (64), and (68) complete the proof of (59). In combination, (46), (47), and (59) complete the proof. □
Proposition 13
Let \(T\in (0,\infty )\), let \(\Phi \) satisfy Assumption 6and (ii) of Assumption 10, let \(\rho \in L^{\infty}([0,T];L^{1}(\mathbb{T}^{d}))\), let \(\Phi ^{\frac{1}{2}}(\rho )\in L^{2}([0,T];H^{1}(\mathbb{T}^{d}))\), let \(F\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\), let \(\psi \in \mathrm{C}^{\infty}_{c}(\mathbb{T}^{d}\times (0,\infty ))\), and let \(\kappa ^{\varepsilon }\) be standard convolution kernel of scale \(\varepsilon \) on \(\mathbb{T}^{d}\). Then, for \(\rho ^{\varepsilon }= \rho *\kappa ^{\varepsilon }\), for every \(t\in [0,T]\),
Proof
The proof is similar to Proposition 12, and to simplify the notation we will write the proof in the case \(\Phi (\xi )=\xi ^{m}\), for \(m\in [2,\infty )\), and indicate where the general version of (ii) in Assumption 10 is used. However, in order to exploit the convexity of the nonlinearity, it is necessary to change the definition of the sets \(A_{k}\). Let \(M\in (0,\infty )\) satisfy \(\operatorname{Supp}(\psi )\subseteq (\mathbb{T}^{d}\times [M^{-1},M])\), let
and let \(A_{0}=(\mathbb{T}^{d}\times [0,T])\setminus A_{1}\). We then form the decomposition
As in the proof of Proposition 13, we will first effectively transfer the \(L^{\infty}\)-bound for \(\rho ^{\varepsilon }\) to \(\rho \) by proving that the first term on the righthand side of (69) vanishes as \(\varepsilon \rightarrow 0\).
The first term on (69). We aim to show that
Hölder’s inequality proves that
We will first prove that the final term on the righthand side of (71) remains bounded. Following the identical derivation in Proposition 12, we have that, for \(\mathbf{1}_{k,k+1}\) the indicator function of the set \(A_{k}\setminus A_{k+1}\),
For every \(x\in \mathbb{T}^{d}\) and \(k\in \mathbb{N}\) let
Since it follows by definition of the sets \(B^{\varepsilon }_{k,x}\) and \(A_{k}\) that
it follows from (72) and (73) that, for \(c\in (0,\infty )\) depending on \(\psi \),
It remains to estimate the measure of the sets \(B^{\varepsilon }_{k,x}\). Chebyshev’s inequality and Jensen’s inequality prove that
At this step, in the general case since the convexity proves that the derivative of the inverse of \(\Phi ^{\frac{1}{2}}\) is non-increasing, it follows from the nonnegativity of \(\rho \) that
It then follows from the fundamental theorem of calculus, the nonnegativity of \(\rho \), the fact that \((\Phi ^{\frac{1}{2}})^{-1}(0)=0\), and (76) that
Returning to (75) and applying (77) to \(\Phi (\xi )=\xi ^{m}\), it follows from the definition of the sets \(A_{k}\) and \(m\in [2,\infty )\) that, for \(\kappa ^{\varepsilon }\mathbf{1}_{k,k+1}=\kappa ^{\varepsilon }(y+x-y')\mathbf{1}_{k,k+1}(y,t)\),
It follows from Jensen’s inequality and the fundamental theorem of calculus that
Since on the support of the convolution kernel we have \(|y-y'|\leq |x|+\varepsilon \), it follows from (78) and (79) that there exists \(c\in (0,\infty )\) such that
Returning to (74), where in the general case assumption (42) is used here to control the growth of \(\Phi (M+k+1)\Phi (M+k)^{-1}\), it follows from (80) that, for \(c\in (0,\infty )\) depending on \(M\in (0,\infty )\), for every \(x\in \mathbb{T}^{d}\),
Since \(|x|\leq \varepsilon \) on the support of the convolution kernel, it follows from (74) and (81) that, for every \(\varepsilon \in (0,1)\),
Then, returning to (71), it follows from (82) that
A repetition of the argument leading to (58) proves that
which with (83) completes the proof of (70).
The second term of (69). We will now prove that
We first observe after integrating by parts that this term satisfies
The first term on the rightand side of (84) is treated identically to the case of (60) and satisfies
We will now treat the second term on the righthand side of (84). Since the solution is not in general \(H^{1}_{x}\)-regular, we introduce a cutoff in the velocity variable to isolate the potential singularities of \(\nabla \rho \) on the set \(\{\rho \simeq 0\}\). Let \(\phi \colon \mathbb{R}\rightarrow [0,1]\) be defined by
let \(\phi ^{\eta}(\xi )=\phi (\frac{\xi}{\eta})\) for every \(\eta \in (0,1)\), and observe that
The integration by parts formula of Lemma 5 proves that the final term of (85) satisfies, for every \((x,t)\in \mathbb{T}^{d}\times [0,T]\),
It then follows from (85) and (86) that
The two terms on the righthand side of (87) will be treated separately.
We will first prove that the first term on the righthand side of (87) satisfies
In the general case, we use the support of \(\phi ^{\eta}\) and assumption (43) to conclude that \(\Phi ^{\frac{1}{2}}(\rho )(\Phi '(\rho ))^{-1}(1-\phi ^{\eta}(\rho ))\) is bounded by a constant depending on \(\eta \), that \(\Phi ^{\frac{1}{2}}(\rho )\) is bounded on \(A_{0}\), and that assumption (19) implies that \(\lim _{\xi \rightarrow 0^{+}}\Phi (\xi )(\Phi '(\xi ))^{-1}=0\). Returning to (88) for the case \(\Phi (\xi )=\xi ^{m}\), these considerations and the dominated convergence theorem prove that
which completes the proof of (88).
It remains to treat the second term of (87), for which we will prove that
We commute the convolution on \(\rho ^{\frac{m}{2}}\) using the decomposition
The first two terms on the righthand side of (91) are treated almost identically. We first observe using the definition of the convolution kernel and the fundamental theorem of calculus that, for \(c\in (0,\infty )\) depending on \(\psi \),
Since it follows from the support of \(\phi ^{\eta}\) that \(\int _{\mathbb{R}}\phi ^{\eta}(\xi )\chi (z,\xi ,t)\, \mathrm {d} \xi\leq 2\eta \), it follows from (92), Hölder’s inequality, and the supports of the convolution kernels that
The second term on the righthand side of (91) is treated identically, and it follows from (93) that both the first and second terms on the righthand side of (91) vanish as \(\eta ,\varepsilon \rightarrow 0\). It remains to treat the third term on the righthand side of (91).
Let \(\overline{\phi}^{\eta}(\xi )=\int _{0}^{\xi}\phi ^{\eta}(\xi ') \, \mathrm {d} \xi '\). Since \(\chi = \mathbf{1}_{\{0<\xi <\rho \}}\) the third term on the righthand side of (91) satisfies, after integrating in \(\xi \),
Since in the general case we have that
it follows from the \(H^{1}_{x}\)-regularity of \(\Phi ^{\frac{1}{2}}(\rho )\) applied to the specific case \(\rho ^{\frac{m}{2}}\) and (61) that (94) satisfies, after integrating by parts in the convolution,
In the general case, we use the fact that \(0\leq \overline{\phi}^{\eta}\leq 2\eta \) and assumption (19) to conclude that, for some \(c\in (0,\infty )\) independent of \(\eta \in (0,1)\),
In the case \(\Phi (\xi )=\xi ^{m}\), these considerations and Hölder’s inequality prove that there exists \(c\in (0,\infty )\) independent of \(\varepsilon ,\eta \in (0,1)\) such that (95) satisfies
which vanishes in the \(\eta \rightarrow 0\) limit. In combination (91), (93), and (96) complete the proof of (90). In combination (87), (89), and (90) complete the proof. □
Theorem 14
Let \(T\in (0,\infty )\), let \(\Phi \) satisfy Assumptions 6and 10, let \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\), let \(\rho _{0}\in L^{1}(\mathbb{T}^{d})\), and let \(\rho \in L^{\infty}([0,T];L^{1}(\mathbb{T}^{d}))\). Then, \(\rho \) is a renormalized kinetic solution in the sense of Definition 3with control \(g\) and initial data \(\rho _{0}\) if and only if \(\rho \) is a weak solution in the sense of Definition 11.
Proof
It is straightforward to see that Definition 3 implies Definition 11. We will therefore only prove that Definition 11 implies Definition 3. Assume that \(\rho \) is a weak solution and let \(\chi \) denote the kinetic function of \(\rho \) and let \(p\) denote the parabolic defect measure. For every \(\varepsilon \in (0,1)\) let \(\kappa ^{\varepsilon }\colon \mathbb{T}^{d}\rightarrow \mathbb{R}\) be a standard symmetric convolution kernel of scale \(\varepsilon \in (0,1)\) and let \(\rho ^{\varepsilon }=(\rho * \kappa ^{\varepsilon })\). Let \(\psi \in \mathrm{C}^{\infty}_{c}(\mathbb{T}^{d}\times \mathbb{R})\) and let \(\Psi (x,\xi )=\int _{0}^{\xi}\psi (x,\xi ')\, \mathrm {d} \xi '\). It follows that \(\rho ^{\varepsilon }\in W^{1,1}([0,T];L^{1}(\mathbb{T}^{d}))\) with derivative
and that \(\Psi (\rho ^{\varepsilon })\in W^{1,1}([0,T];L^{1}(\mathbb{T}^{d}))\) with derivative given by (46). Therefore, for every \(t\in [0,T]\),
We pass to the limit \(\varepsilon \rightarrow 0\) using Proposition 12 and Proposition 13, depending on which case of Assumption 10 is satisfied, with \(F=\nabla \Phi ^{\frac{1}{2}}(\rho )\) and \(F=g\) respectively. This completes the proof. □
5 Existence of weak solutions
In this section, we will prove that there exists a weak solution to the skeleton equation
for controls \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\) and initial data \(\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\) in the sense of Definition 11. The existence of renormalized kinetic solutions (see Definition 3) is then a consequence of Theorem 14. However, we emphasize that these methods can also be used to prove the existence of renormalized kinetic solutions in the sense of Definition 3 directly, but we omit these details since this more general result will not be used here.
5.1 Preliminaries
In this section, we introduce in Assumption 15 conditions on \(\Phi \) that will be used to guarantee the regularity and compactness of approximate solutions. This assumption is satisfied by every fast diffusion and porous media nonlinearity. Lemma 16 and Lemma 17 collect two important consequences of Assumption 15.
Assumption 15
Let \(\Phi \in \mathrm{C}([0,\infty ))\cap \mathrm{C}^{1}_{\textrm{loc}}((0, \infty )))\) satisfy \(\Phi (0)=0\) with \(\Phi '(\xi )>0\) for every \(\xi \in (0,\infty )\). Assume that \(\Phi \) satisfies the following four properties.
-
(i)
There exists \(m\in [1,\infty )\) and \(c\in (0,\infty )\) such that
$$ \Phi (\xi )\leq c(1+\xi ^{m})\;\;\textrm{for every}\;\;\xi \in [0, \infty ). $$ -
(ii)
Either there exists \(c\in (0,\infty )\) and
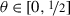 such that $$ \frac{\Phi '(\xi )}{\Phi ^{\frac{1}{2}}(\xi )}\leq c\xi ^{-\theta}\; \;\textrm{for every}\;\;\xi \in (0,\infty ), $$
such that $$ \frac{\Phi '(\xi )}{\Phi ^{\frac{1}{2}}(\xi )}\leq c\xi ^{-\theta}\; \;\textrm{for every}\;\;\xi \in (0,\infty ), $$or there exists \(c\in (0,\infty )\) and \(q\in [1,\infty )\) such that
$$ |\xi -\xi '|^{q}\leq c |\Phi ^{\frac{1}{2}}(\xi )-\Phi ^{\frac{1}{2}}(\xi ')|^{2}\;\; \textrm{for every}\;\;\xi ,\xi '\in [0,\infty ). $$ -
(iii)
There exists \(c\in (0,\infty )\) such that
$$ \Phi '(\xi )\leq c(1+\xi +\Phi (\xi ))\;\;\textrm{for every}\;\;\xi \in (0,\infty ). $$ -
(iv)
We have that \(\log (\Phi )\) is locally integrable on \([0,\infty )\).
Lemma 16
Let \(\Phi \in \mathrm{C}([0,\infty ))\cap \mathrm{C}^{1}_{\textrm{loc}}((0, \infty ))\) satisfy Assumption 15. If a nonnegative \(\rho \in L^{\infty}([0,T];L^{1}(\mathbb{T}^{d}))\) satisfies \(\nabla \Phi ^{\frac{1}{2}}(\rho )\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\), then for every \(\varepsilon \in (0,1)\) there exists \(c\in (0,\infty )\) such that
Proof
The lemma relies on part (i) of Assumption 15 and is a straightforward consequence of the Sobolev embedding theorem and an interpolation estimate. The details can be found in [42, Lemma 5.4]. □
Lemma 17
Let \(\Phi \in \mathrm{C}([0,\infty ))\cap \mathrm{C}^{1}_{\textrm{loc}}((0, \infty ))\) satisfy Assumption 15and let \(\{\rho _{n}\}_{n\in \mathbb{N}}\) be a sequence that satisfies, for some \(c\in (0,\infty )\) and  independent of \(n\),
independent of \(n\),
Then,
and
Proof
The proof is a consequence of part (ii) of Assumption 15, the Aubin–Lions–Simon Lemma [107–109], the compact embedding of the fractional Sobolev space \(W^{\beta ,1}(\mathbb{T}^{d})\) into \(L^{1}(\mathbb{T}^{d})\), the continuous embedding of \(L^{1}(\mathbb{T}^{d})\) into \(H^{-s}(\mathbb{T}^{d})\) for every  , and [42, Lemma 5.11]. □
, and [42, Lemma 5.11]. □
5.2 Regularity and existence of solutions
In this section, we will construct a solution to (97) in Proposition 20 based on the entropy dissipation estimate of Proposition 19. The estimate will be obtained for initial data with finite entropy in the sense of Definition 18, and the proof relies on testing the equation with \(\log (\Phi (\rho ))\) which uses essentially the nonnegativity of the initial data. The existence of solutions is then a consequence of Lemma 17.
Definition 18
Let \(\Phi \) satisfy Assumption 15 and let \(\Psi _{\Phi}(\xi )=\int _{0}^{\xi}\log (\Phi (\xi '))\, \mathrm {d} \xi '\). For every \(R\in (0,\infty )\) let
and let
Proposition 19
Let \(T\in (0,\infty )\), let \(\Phi \) satisfy Assumptions 6, 10, and 15, let \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\), and let \(\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\). Then, if \(\rho \) is a weak solution of (97) in the sense of Definition 11, for some \(c\in (0,\infty )\),
Proof
The nonnegativity of \(\rho \), the \(H^{1}_{x}\)-regularity of \(\Phi ^{\frac{1}{2}}(\rho )\), and an approximation argument by convolution prove that, for \(\Psi _{\Phi ,\delta }(\xi ) = 2\int _{0}^{\xi}\log (\delta +\Phi ^{ \frac{1}{2}}(\xi '))\, \mathrm {d} \xi '\), we have that the composition \(\Psi _{\Phi ,\delta }(\rho )\) satisfies, for every \(t\in [0,T]\),
It then follows from Hölder’s inequality, Young’s inequality, and \(\xi (\xi +\delta )^{-1}\leq 1\) for \(\xi \in [0,\infty )\) that
We pass to the limit \(\delta \rightarrow 0\) using the monotone convergence theorem, which completes the proof. □
Proposition 20
Let \(T\in (0,\infty )\), let \(\Phi \) satisfy Assumptions 6, 10, and 15, let \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\), and let \(\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\). Then, there exists a nonnegative weak solution \(\rho \in L^{\infty}([0,T];L^{1}(\mathbb{T}^{d}))\) of (97) in the sense of Definition 11which satisfies, for every \(t\in [0,T]\),
and which satisfies the estimate of Proposition 19.
Proof
The proof is based on constructing smooth solutions to a sequence of approximating equations
for \(\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\), for \(\eta _{2}\in (0,1)\), and for \(\Phi ^{\frac{1}{2},\eta _{1}}\) for \(\eta _{1}\in (0,1)\) a sequence of smooth, bounded approximations of \(\Phi ^{\frac{1}{2}}\) that satisfy \(\Phi ^{\frac{1}{2},\eta _{1}}(0)=0\), that satisfy, for some \(c\in (0,\infty )\) independent of \(\eta _{1}\),
and, for some \(c\in (0,\infty )\) depending on \(\eta _{1}\),
and that satisfy, for every compact set \(A\subseteq [0,\infty )\),
It is straightforward to prove the existence of continuous \(L^{1}\)-valued solutions to (99) taking values in \(L^{2}([0,T];H^{1}(\mathbb{T}^{d}))\). The reason for considering such specific approximations of \(\Phi ^{\frac{1}{2}}\) is that, using the properties of these approximations, a repetition of Proposition 19 proves that the approximating solutions satisfy estimate (98) uniformly in \(\eta _{1}\). The claim then follows by an application of Lemma 17. □
5.3 Weak-strong continuity
We conclude this section with the proof that a weakly convergent sequence of controls induces a strongly convergent sequence of solutions. This fact will be important in the proof of the large deviations principle below.
Proposition 21
Let \(T\in (0,\infty )\), let \(\Phi \) satisfy Assumptions 6, 10, and 15, let \(\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\), and let \(g_{n}\rightharpoonup g\) weakly in \(L^{2}([0,T]\times \mathbb{T}^{d})^{d}\). Then, for the solutions \(\rho _{n}\) and \(\rho \) of (97) in the sense of Definition 11with initial data \(\rho _{0}\) and with controls \(g_{n}\) and \(g\) respectively, as \(n\rightarrow \infty \),
Proof
The proof is essentially a repetition of Proposition 20 using the fact that the weak convergence of the \(g_{n}\) implies that they are uniformly \(L^{2}_{t,x}\)-bounded, and therefore that the solutions \(\rho _{n}\) are relatively compact in \(L^{1}(\mathbb{T}^{d}\times [0,T])\) by Lemma 17. The claim then follows from the uniqueness of the limit, which follows from Theorem 8 and Theorem 14. □
6 The uniform large deviations principle for conservative SPDE
In this section, we identify a scaling limit for which the solutions of the equation
for correlated noise \(\xi ^{K}\) defined in Sect. 6.1, satisfy a uniform large deviations principle with respect to initial data in weakly compact subsets of \(L^{1}(\mathbb{T}^{d})\) with bounded entropy.
6.1 The noise and well-posedness of (100)
We will prove the LDP for certain spectral approximations of space-time white noise. However, our methods apply without any essential changes to noise of a general type, such as that in Remark 30 below.
Definition 22
Let \((\Omega ,\mathcal {F},\mathbb{P})\) be a probability space, let \(\{\mathcal {F}_{t}\}_{t\in [0,\infty )}\) be a filtration on \((\Omega ,\mathcal {F})\), and let \(\{B^{k},W^{k}\}_{k\in \mathbb{N}_{0}}\) be independent, \(\mathcal {F}_{t}\)-adapted, \(d\)-dimensional Brownian motions. For every \(K\in \mathbb{N}\) we define the noise
for the sum over elements \(k\in \mathbb{Z}^{d}\) with \(|k|\leq K\).
We will understand (100), for \(\xi ^{K}\) as in Definition 22, in its Itô form
for \(N_{K} = \#\{k\in \mathbb{Z}^{d}\colon |k|\leq K\}\). To prove the large deviations result, we will also consider the controlled equation
where \(P_{K}g\) denotes the Fourier projection of a random control onto the span of \(\{\sqrt{2}\sin (k\cdot x),\sqrt{2}\cos (k\cdot x)\}_{\{|k|\leq K \}}\). We now summarize the well-posedness theory for (101) and (102). The essential observation of Theorem 23 is that the ℙ-a.s. \(L^{1}_{x}\)-contraction implies the existence of a measurable solution map, where we view the Brownian motions \((B^{k},W^{k})_{k\in \mathbb{N}_{0}}\) as taking values in the space \(\mathrm{C}([0,\infty );\mathbb{R}^{\infty})\) where \(\mathbb{R}^{\infty}\) is equipped with the metric topology of coordinate-wise convergence.
Theorem 23
Let \(\Phi \in \mathrm{C}([0,\infty ))\cap \mathrm{C}^{1}_{\textrm{loc}}((0, \infty ))\) satisfy Assumptions 6, 10, and 15and let \(\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\). Then, there exists a unique stochastic kinetic solution \(\rho ^{\varepsilon ,K}\in L^{\infty}(\Omega \times [0,T];L^{1}(\mathbb{T}^{d}))\) of (101) with initial condition \(\rho _{0}\) in the sense of [42, Definition 3.4]. If \(\rho _{1}\), \(\rho _{2}\) are two solutions to (101) with initial data \(\rho _{0}^{1},\rho _{0}^{2}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\), then, ℙ-a.s.,
Furthermore, there exists a measurable map
such that, for every \(\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\), ℙ-a.s.,
where \(\rho ^{\varepsilon ,K}\) is the unique solution of (101) in the sense of [42, Definition 3.4].
Proof
The existence of an \(\mathcal {F}_{t}\)-measurable solution and the almost sure \(L^{1}\)-contraction estimate (103) is shown in [42, Theorem 4.7, Theorem 5.29, Corollary 5.31]. It follows from the measurability that, for every \(\rho \in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\), there exists a measurable function \(S^{\varepsilon ,K}_{\rho}\colon \mathrm{C}([0,\infty );\mathbb{R}^{\infty}) \rightarrow L^{1}(\mathbb{T}^{d}\times [0,T])\) such that, ℙ-a.s.,
Since it follows from Proposition 27 below that \(\operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\) equipped with strong \(L^{1}(\mathbb{T}^{d})\)-topology is separable, let \(\{\rho _{n}\}_{n\in \mathbb{N}}\) be a countable dense subset of \(\operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\). It follows from (103) and the countability of the set \(\mathbb{N}\times \mathbb{N}\) that, on a measurable subset of full probability, for every \(n,m\in \mathbb{N}\),
It follows from the density of the \(\{\rho _{n}\}_{n\in \mathbb{N}}\) with respect to the strong \(L^{1}(\mathbb{T}^{d})\)-norm and (105) that there almost surely exists a strongly continuous function \(\overline{S}^{\varepsilon ,K}_{\overline{B}}\colon \operatorname {Ent}_{\Phi}(\mathbb{T}^{d}) \rightarrow L^{1}(\mathbb{T}^{d}\times [0,T])\) such that, for every \(n\in \mathbb{N}\), on a subset of full probability independent of \(n\),
It then follows from (105), (106), and a simplified version of [42, Theorem 5.29, Corollary 5.31] that, for every \(\rho \in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\), on a subset of full probability depending on \(\rho \),
We define \(S^{\varepsilon ,K}\colon \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\times \mathrm{C}([0,T]; \mathbb{R}^{\infty})\rightarrow L^{\infty}([0,T];L^{1}(\mathbb{T}^{d}))\) by the rule
from which it follows from (104) that, for every \(\rho \in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\),
and from (107) that, for almost every realization of \(\overline{B}\),
In combination (108), (109), and the separability of \(\operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\) prove that \(S^{\varepsilon ,K}\) is measurable, which with (104) and (107) completes the proof. □
Proposition 24
Let \(T\in (0,\infty )\) and let \(\Phi \in \mathrm{C}([0,\infty ))\cap \mathrm{C}^{1}_{\textrm{loc}}((0, \infty ))\) satisfy Assumptions 6, 10, and 15. For every \(\varepsilon \in (0,1)\) and \(K\in \mathbb{N}\) let
be defined in Theorem 23. Then, for every \(L^{2}(\mathbb{T}^{d})^{d}\)-valued \(\mathcal {F}_{t}\)-predictable process \(g\) and for every \(\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\), we have for \(g_{k}(\omega ,s)=\langle g(\omega ,s),\sqrt{2}\cos (k\cdot x)\rangle _{L^{2}( \mathbb{T}^{d})}\) and \(g'_{k}(\omega ,s)=\langle g(\omega ,s),\sqrt{2}\sin (k\cdot x)\rangle _{L^{2}( \mathbb{T}^{d})}\) that
is the unique solution of (102) in the sense of [42, Definition 3.4].
Proof
The proof is a consequence of Theorem 23 and the Girsanov theorem (see, for example, [103, Theorem 10]). □
Proposition 25
Let \(\Phi \in \mathrm{C}([0,\infty ))\cap \mathrm{C}^{1}_{\textrm{loc}}((0, \infty ))\) satisfy Assumptions 6, 10, 15, let \(g\) be an \(L^{2}(\mathbb{T}^{d})^{d}\)-valued \(\mathcal {F}_{t}\)-predictable process, and let \(\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\). Assume that \(\varepsilon \in (0,1)\) and \(K\in \mathbb{N}\) satisfy \(\varepsilon K^{d+2}\leq 1\), and let \(\rho ^{\varepsilon ,K}\) be the unique solution of (102) in the sense of Proposition 24. Then, for \(c\in (0,\infty )\) independent of \(\varepsilon \) and \(K\),
Proof
The proof is a consequence of [42, Proposition 5.18, Corollary 5.31]. □
Proposition 26
Let \(\Phi \in \mathrm{C}([0,\infty ))\cap \mathrm{C}^{1}_{\textrm{loc}}((0, \infty ))\) satisfy Assumptions 6, 10, 15, let \(g\) be an \(L^{2}(\mathbb{T}^{d})^{d}\)-valued \(\mathcal {F}_{t}\)-predictable process, let \(\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\), and let \(\{K(\varepsilon )\}_{\varepsilon \in (0,1)}\) be a sequence that satisfies \(\varepsilon K(\varepsilon )^{d+2}\rightarrow 0\) and \(K(\varepsilon )\rightarrow \infty \) as \(\varepsilon \rightarrow 0\). Then the laws of the solutions \(\{\rho ^{\varepsilon ,K(\varepsilon )}\}_{\varepsilon \in (0,1)}\) of (102) with initial data \(\rho _{0}\) and control \(g\) are tight on \(L^{1}(\mathbb{T}^{d}\times [0,T])\).
Proof
The proof is a consequence of Lemma 17, Proposition 25, and [42, Proposition 5.26]. □
6.2 The uniform large deviations principle
We will now use the well-posedness results of Theorem 23 and Proposition 24, the estimates of Proposition 25, and the convergence of Theorem 28 below to establish a large deviations principle for the solutions of (100) along the scaling limit identified in Proposition 26. The LDP is a consequence of the weak approach to large deviations established in [103], as well as Dupuis and Ellis [110] and Budhiraja and Dupuis [111]. Precisely, we will show that the solutions satisfy a large deviations principle with rate function \(I_{\rho _{0}}\) defined by
for the skeleton equation understood in the sense of Definition 11. In fact, relying on the methods of [103, Theorem 6] and Budhiraja, Dupuis, and Salins [112, Theorem 4.3], we will prove the stronger statement that the solutions to (100) satisfy a large deviations principle uniformly with respect to weakly \(L^{1}_{x}\)-compact subsets of the initial data with bounded entropy.
The proof of the LDP relies on establishing two facts. First, we require the compactness of the family of solutions to the skeleton equation with \(L^{2}_{t,x}\)-bounded controls. This is a straightforward consequence of Lemma 17 and Proposition 19. Second, in the scaling regime that \(\varepsilon K(\varepsilon )^{d+2}\rightarrow 0\), we require that the solutions to the controlled equation (102) converge to the solution of the skeleton equation. We prove this statement in Theorem 28, and using these two statements we prove the uniform LDP in Theorem 29.
Proposition 27
Let \(\Phi \) satisfy Assumptions 6, 10, and 15, let \(R\in (0,\infty )\), and let \(\operatorname {Ent}_{\Phi ,R}(\mathbb{T}^{d})\) be defined in Definition 18. Then, \(\operatorname {Ent}_{\Phi ,R}(\mathbb{T}^{d})\) equipped with the strong \(L^{1}(\mathbb{T}^{d})\)-topology is a complete separable metric space.
Proof
The completeness is a consequence of the completeness of \(L^{1}(\mathbb{T}^{d})\) and Fatou’s lemma. The separability follows from the convexity of \(\Psi _{\Phi}\) and Assumption 15, which implies for each \(R\in (0,\infty )\) that \(L^{2}(\mathbb{T}^{d})\cap \operatorname {Ent}_{\Phi ,R}(\mathbb{T}^{d})\) is dense in \(\operatorname {Ent}_{\Phi ,R}(\mathbb{T}^{d})\). Since \(L^{2}(\mathbb{T}^{d})\cap \operatorname {Ent}_{\Phi ,R}(\mathbb{T}^{d})\) is separable as a closed, convex subset of the separable, reflexive, strictly convex Banach space \(L^{2}(\mathbb{T}^{d})\), this completes the proof. □
Theorem 28
Let \(\Phi \) satisfy Assumptions 6, 10, 15, let \(\varepsilon \in (0,1)\), let \(g^{\varepsilon }\) and \(g\) be \(L^{2}(\mathbb{T}^{d})^{d}\)-valued \(\mathcal {F}_{t}\)-predictable processes that satisfy
and that satisfy \(g^{\varepsilon }\rightharpoonup g\) in distribution on \(L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\) equipped with the weak topology, let \(\rho ^{\varepsilon }_{0},\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\) be such that
and let \(\{K(\varepsilon )\}_{\varepsilon \in (0,1)}\) be such that \(\varepsilon K(\varepsilon )^{d+2}\rightarrow 0\) and \(K(\varepsilon )\rightarrow \infty \) as \(\varepsilon \rightarrow 0\). Then the solutions \(\rho ^{\varepsilon }=\rho ^{\varepsilon ,K(\varepsilon )}\) of (102) with initial data \(\rho ^{\varepsilon }_{0}\) and control \(g^{\varepsilon }\) satisfy, as \(\varepsilon \rightarrow 0\),
for \(\rho \) the unique solution of (97) with control \(g\) and initial data \(\rho _{0}\).
Proof
We will first consider nonnegative initial data \(\rho ^{\varepsilon }_{0}\) and \(\rho _{0}\) that are uniformly bounded in \(L^{2}(\mathbb{T}^{d})\). It follows from Lemma 17, Proposition 19, and [42, Proposition 5.26] that the laws of the solutions \(\rho ^{\varepsilon }\) are tight on \(L^{1}(\mathbb{T}^{d}\times [0,T])\), and it follows from Lemma 16 and Proposition 19 that the laws of \(\Phi ^{\frac{1}{2}}(\rho ^{\varepsilon })\) are tight in the topology of weak convergence on \(L^{2}([0,T];H^{1}(\mathbb{T}^{d}))\). Finally, due to the \(L^{2}_{x}\)-integrability of the data, there exists a sequence of finite nonnegative kinetic measures \(\{q^{\varepsilon }\}_{\varepsilon \in (0,1)}\) in the sense of [42, Definitions 3.1, 3.4] that are uniformly bounded in expectation in the sense that
such that the kinetic function \(\chi ^{\varepsilon }\) of \(\rho ^{\varepsilon }\) satisfies ℙ-a.s. the equation, for every \(t\in [0,T]\) and \(\psi \in \mathrm{C}^{\infty}_{c}(\mathbb{T}^{d}\times (0,\infty ))\),
for \(M_{K(\varepsilon )}=\sum _{|k|\leq K(\varepsilon )}k^{2}\simeq K(\varepsilon )^{d+2}\) and for \(P_{K(\varepsilon )}g^{\varepsilon }\) the Fourier projection of \(g^{\varepsilon }\). See [42, Sect. 3] for a full derivation of this equation, where we observe that the fourth and final terms on the righthand side of (111) are integrable due to the compact support of \(\psi \) on \((0,\infty )\).
The essential difficulty in passing to the \(\varepsilon \rightarrow 0\) limit appears in the final term of (111), which as \(\varepsilon \rightarrow 0\) contains the product of weakly convergent sequences \(\nabla \Phi ^{\frac{1}{2}}(\rho ^{\varepsilon })\) and \(g^{\varepsilon }\). We observe, however, that this term does not appear in the weak formulation of the skeleton equation. We will therefore quantify the maximal contribution of this term with the measures \(p^{\varepsilon }\) below, and derive the weak formulation of the skeleton equation by choosing an appropriate sequence of test functions \(\psi \) that approach one in the velocity variable. More precisely, let \(p^{\varepsilon }\) denote the nonnegative, almost surely finite measure defined by
and observe that
Following the methods of [42, Theorem 5.29], we characterize the limiting behavior of the solutions \(\rho ^{\varepsilon }\) by establishing the tightness of the random variables
for \(|q^{\varepsilon }| = q^{\varepsilon }(\mathbb{T}^{d}\times \mathbb{R}\times [0,T])\), in the product metric topology of the state space
for \(L^{1}=L^{1}(\mathbb{T}^{d}\times [0,T])\) equipped with the strong topology and \(L^{2}=L^{2}(\mathbb{T}^{d}\times [0,T])\) and \(L^{2}_{t}H^{1}_{x}=L^{2}([0,T];H^{1}(\mathbb{T}^{d}))\) equipped with the weak topologies. Again following the methods of [42, Theorem 5.29], Prokhorov’s theorem (see, for example, Billingsley [113, Chap. 1, Theorem 5.1]) and the Skorokhod representation theorem (see, for example, [113, Chap. 1, Theorem 6.7]) then reduce the proposition to the following simpler statement: if along a subsequence \(\varepsilon \rightarrow 0\) the random variables \(X^{\varepsilon }\) converge ℙ-a.s. to a random variable
for random nonnegative measures \(\tilde{p}, \tilde{q}\in \mathcal{M}(\mathbb{T}^{d}\times \mathbb{R}\times [0,T])\), for random \(\alpha ,\beta \in \mathbb{R}\), and for Brownian motions \((\tilde{W}^{k},\tilde{B}^{k})_{k\in \mathbb{N}_{0}}\), then
To prove (112), we will recover the classical weak formulation of the skeleton equation by passing to the limit along the subsequence \(\varepsilon \rightarrow 0\) in each of the terms on the righthand side of (111).
The test function. Our aim is to eliminate the equation’s dependence on the velocity variable. Let \(\phi _{\delta }\colon [0,\infty )\rightarrow [0,1]\) be a smooth function that satisfies, for some \(c\in (0,\infty )\) independent of  ,
,
with
and let \(\eta \in \mathrm{C}^{\infty}(\mathbb{T}^{d})\) be arbitrary. We will consider test functions of the form \(\psi _{\delta }(x,\xi )=\phi _{\delta }(\xi )\eta (x)\) and pass first to the limit \(\varepsilon \rightarrow 0\) and then \(\delta \rightarrow 0\) to recover the weak formulation of the skeleton equation.
The initial data. Since the initial data \(\rho ^{\varepsilon }_{0}\) is converging only weakly to \(\rho _{0}\), which is not compatible with the nonlinear dependence of the kinetic function, we introduce the decomposition
It follows from the support of \(\phi _{\delta }\) and the boundedness of \(\eta \), the kinetic function, and the torus that, for some \(c\in (0,\infty )\) independent of \(\varepsilon ,\delta \in (0,1)\),
Therefore, using the weak convergence of \(\rho ^{\varepsilon }_{0}\), for \(c\in (0,\infty )\) independent of \(\delta \),
The bulk terms. The scaling limit \(\varepsilon K(\varepsilon )^{d+2}\rightarrow 0\), the estimates of Proposition 25, and the compact support of \(\psi \) prove that, ℙ-a.s.,
and that, ℙ-a.s.,
For the martingale term, the Burkholder–Davis–Gundy inequality (see, for example, [114, Chap. 4, Theorem 4.1]) and the compact support of \(\psi _{\delta }\) prove that there exists \(c\in (0,\infty )\) such that, for every \(\varepsilon ,\delta \in (0,1)\),
and, therefore, using \(\varepsilon K(\varepsilon )^{d+2}\rightarrow 0\) and the uniform \(H^{1}_{x}\)-regularity of \(\Phi ^{\frac{1}{2}}(\rho ^{\varepsilon })\), along a further subsequence \(\varepsilon \rightarrow 0\), ℙ-a.s.,
The conclusion. The remaining terms are treated using the ℙ-a.s. strong convergence of \(\rho ^{\varepsilon }\) to \(\rho \), the weak convergence of \(P_{K(\varepsilon )}g^{\varepsilon }\rightharpoonup g\) and \(\nabla \Phi ^{\frac{1}{2}}(\rho ^{\varepsilon })\rightharpoonup \nabla \Phi ^{ \frac{1}{2}}(\rho )\), and the weak convergence of \(q^{\varepsilon }\) to \(\alpha \tilde{q}\) and \(p^{\varepsilon }\) to \(\beta \tilde{p}\). This proves with (113), (114), (115), and (116) that, ℙ-a.s. for almost every \(t\in [0,T]\), after passing along a subsequence \(\varepsilon \rightarrow 0\) in (111), the kinetic function \(\chi \) of \(\rho \) satisfies, for \(c\in (0,\infty )\) independent of \(\delta \in (0,1)\),
It follows from [42, Definition 3.4, Proposition 4.6], the support of \(\phi _{\delta }\), the boundedness of \(\eta \), and the finiteness of \(\beta \tilde{q}\) that
and it follows from the finiteness of \(\tilde{p}\), the support of \(\phi _{\delta }\), the boundedness of \(\eta \), assumption (19), and the dominated convergence theorem that
Finally, it follows from the support of \(\phi _{\delta }\) that, ℙ-a.s. for every \(t\in [0,T]\),
Since by assumption \(\Phi (0)=0\) and \(\Phi \) is strictly increasing, we have that \(\rho =0\) if and only if \(\Phi ^{\frac{1}{2}}(\rho )=0\) and we have by Stampacchia’s lemma (see, for example, Evans [115, Chap. 5, Exercises 17,18]) that \(\nabla \Phi ^{\frac{1}{2}}(\rho )=0\) almost everywhere on the set \(\Phi ^{\frac{1}{2}}(\rho )=0\). Therefore,
Similarly it follows from \(\{\rho =0\}=\{\Phi ^{\frac{1}{2}}(\rho )=0\}\) that, ℙ-a.s. for every \(t\in [0,T]\),
and from the support of \(\phi _{\delta }\) and the kinetic function that, ℙ-a.s. for every \(t\in [0,T]\),
Returning to (117), it follows from (118), (119), (120), (121), and (122) that, after passing to a subsequence \(\delta \rightarrow 0\), ℙ-a.s. for almost every \(t\in [0,T]\),
It then follows from a simplified version of Proposition 9 that \(\rho \) has an \(L^{1}\)-continuous representative. We conclude that \(\rho \) is ℙ-a.s. a weak solution of the skeleton equation with control \(g\) in the sense of Definition 11, which by Theorem 8 and Theorem 14 is unique. This completes the proof of (112), and the proof of the proposition for \(L^{2}_{x}\)-integrable initial data. The case that \(\rho ^{\varepsilon }_{0}\) and \(\rho _{0}\) are bounded in \(\operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\) then follows by approximating the \(\rho ^{\varepsilon }_{0}\) by \((\rho ^{\varepsilon }_{0}\wedge n)\in L^{2}(\mathbb{T}^{d})\), the almost sure \(L^{1}_{x}\)-contraction property of [42, Theorem 4.7], the \(L^{1}_{x}\)-contraction property of Theorem 8, and the triangle inequality. This completes the proof. □
Theorem 29
Let \(\Phi \) satisfy Assumptions 6, 10, and 15and let \(\{K(\varepsilon )\}_{\varepsilon \in (0,1)}\) satisfy \(\varepsilon K(\varepsilon )^{d+2}\rightarrow 0\) and \(K(\varepsilon )\rightarrow \infty \) as \(\varepsilon \rightarrow 0\). Then, the rate functions \(I_{\rho _{0}}\) defined in (110) are good rate functions with compact level sets on compact sets, and for every \(\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\) the solutions \(\{\rho ^{\varepsilon }(\rho _{0})\}_{\varepsilon \in (0,1)}\) of (100) satisfy a large deviations principle with rate function \(I_{\rho _{0}}\) on \(L^{1}(\mathbb{T}^{d}\times [0,T])\). Furthermore, for every \(R\in (0,\infty )\), the solutions satisfy a uniform large deviations principle on \(L^{1}(\mathbb{T}^{d}\times [0,T])\) with respect to weakly \(L^{1}(\mathbb{T}^{d})\)-compact subsets of \(\operatorname {Ent}_{\Phi ,R}(\mathbb{T}^{d})\).
Proof
The proof relies on an application of the weak approach to large deviations [103, Theorem 6], the equivalence of uniform Laplace and large deviations principles with respect to compact subsets of the initial data [112, Theorem 4.3], Lemma 17, Proposition 19, and Theorem 28. To apply the framework of [103, Theorem 6], it is necessary to prove the compactness of the solution set of the skeleton equation with uniformly bounded initial data and uniformly bounded controls, and to prove the convergence in distribution of the controlled SPDE (102) to the skeleton equation. The compactness is an immediate consequence of Lemma 17 and Proposition 19, and the required convergence of the controlled SPDE to the skeleton equation is exactly Theorem 28. This completes the proof. □
Remark 30
We emphasize that these techniques apply for general noise of the form \(\xi ^{\delta }= \sum _{k=1}^{\infty }f^{\delta }_{k}\, \mathrm {d} B^{k}_{t}\) provided \(\sum _{k=1}^{\infty }(f^{\delta }_{k})^{2}\) and \(\sum _{k=1}^{\infty} |\nabla f^{\delta }_{k}|^{2}\) are continuous on \(\mathbb{T}^{d}\) and provided that \(\xi ^{\delta }\) is probabilistically stationary in the sense that the quadratic variation \(\sum _{k=1}^{\infty }(f^{\delta }_{k})^{2}\) is constant on \(\mathbb{T}^{d}\). This includes, with no changes to the arguments, spatial smoothings \(\xi ^{\delta }= (\xi *\kappa ^{\delta })\) of space-time white noise for which the solutions satisfy the uniform large deviations principle in the scaling regime \(\varepsilon \delta (\varepsilon )^{-(d+2)}\rightarrow 0\).
7 \(\Gamma \)-Convergence of rate functions
In this section, we will first show that, for every \(K\in \mathbb{N}\), the solutions to the equation
satisfy a small-noise large deviations principle with rate function
for \(P_{K}g\) the Fourier projection of \(g\) onto the span of \(\{\sqrt{2}\sin (k\cdot x),\sqrt{2}\cos (k\cdot x)\}_{\{|k|\leq K \}}\). Then, in Lemma 32 and Theorem 33 we prove that the rate functions (124) converge as \(K\rightarrow \infty \) in the sense of \(\Gamma \)-convergence to the rate function (110).
Proposition 31
Let \(K\in \mathbb{N}\) and let \(\Phi \) satisfy Assumptions 6, 10, and 15, and let \(\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\). Then, the rate functions \(I^{K}_{\rho _{0}}\) defined in (124) are good rate functions with compact level sets on compact sets, and for every \(\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\) the solutions \(\{\rho ^{\varepsilon ,K}(\rho _{0})\}_{\varepsilon \in (0,1)}\) of (123) satisfy a large deviations principle with rate function \(I^{K}_{\rho _{0}}\) on \(L^{1}(\mathbb{T}^{d}\times [0,T])\). Furthermore, for every \(R\in (0,\infty )\), the solutions satisfy a uniform large deviations principle on \(L^{1}(\mathbb{T}^{d}\times [0,T])\) with respect to weakly \(L^{1}(\mathbb{T}^{d})\)-compact subsets of \(\operatorname {Ent}_{\Phi ,R}(\mathbb{T}^{d})\).
Proof
The proof is identical to the proof of Theorem 29 and is obtained by repeating the same argument in the scaling regime that \(K\in \mathbb{N}\) is fixed. □
Lemma 32
Let \(\Phi \) satisfy Assumptions 6, 10, and 15, let \(\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\), let \(I_{\rho _{0}}\) be defined in (110), and let \(I^{K}_{\rho _{0}}\) be defined in (124). Then, for every \(K\in \mathbb{N}\), the infimums appearing in (110) and (124) are attained. Furthermore, for every \(\rho \in L^{1}(\mathbb{T}^{d}\times [0,T])\) satisfying \(I_{\rho _{0}}(\rho )<\infty \) (alternately, \(I^{K}_{\rho _{0}}(\rho )<\infty \) for \(K\in \mathbb{N}\)), there exists a unique \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\) satisfying
Proof
The fact that the infimums appearing in (110) and (124) are achieved is an immediate consequence of Theorem 14, Lemma 17, and Proposition 19, since Definition 11 is stable with respect to weak convergence of the control. For the second statement, suppose that \(\rho \in L^{1}(\mathbb{T}^{d}\times [0,T])\) satisfies \(I_{\rho _{0}}(\rho )<\infty \) (alternately, \(I^{K}_{\rho _{0}}(\rho )<\infty \) for \(K\in \mathbb{N}\)). Then, by the above, the set
is a non-empty, weakly closed, convex subset of \(L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\). The fact that the set is weakly closed implies the existence of a minimizer. The convexity of the set implies that if \(g_{1}\) and \(g_{2}\) are two distinct minimizers then \(g_{3} = \frac{1}{2}(g_{1}+g_{2})\) is also a minimizer, and the uniform convexity of the \(L^{2}_{t,x}\)-norm proves that \(\lVert g_{3} \rVert _{L^{2}}<\lVert g_{1} \rVert _{L^{2}}\), which completes the proof. □
Theorem 33
Let \(\Phi \) satisfy Assumptions 6, 10, and 15, let \(\rho _{0}\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\), let \(I_{\rho _{0}}\) be defined in (110), and let \(I^{K}_{\rho _{0}}\) be defined in (124). Then, as \(K\rightarrow \infty \), in the sense of \(\Gamma \)-convergence,
Proof
Let \(\rho \in L^{1}(\mathbb{T}^{d}\times [0,T])\). In order to establish the \(\Gamma \)-convergence, it is necessary to prove the following two properties. First, for every sequence \(\{\rho _{K_{n}}\}_{n\in \mathbb{N}}\) satisfying as \(n\rightarrow \infty \) that \(K_{n}\rightarrow \infty \) and \(\rho _{K_{n}}\rightarrow \rho \) strongly in \(L^{1}(\mathbb{T}^{d}\times [0,T])\) we have that
Second, there exists a sequence \(\{\rho _{K_{n}}\}_{n\in \mathbb{N}}\) satisfying as \(n\rightarrow \infty \) that \(K_{n}\rightarrow \infty \) and that \(\rho _{K_{n}}\rightarrow \rho \) strongly in \(L^{1}(\mathbb{T}^{d}\times [0,T])\) such that
Proof of (125). Let \(\rho \in L^{1}(\mathbb{T}^{d}\times [0,T])\) and suppose that \(\{\rho _{K_{n}}\}_{n\in \mathbb{N}}\) satisfies as \(n\rightarrow \infty \) that \(K_{n}\rightarrow \infty \) and that
If \(\liminf _{n\rightarrow \infty}I^{K_{n}}(\rho _{K_{n}})=\infty \) then (125) is satisfied. If not, fix a subsequence \(\{K_{m}\}_{m\in \mathbb{N}}\) which satisfies for every \(m\in \mathbb{N}\) that
and that
By Lemma 32, for every \(m\in \mathbb{N}\) fix the unique \(g_{m}\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\) satisfying
It follows from (127) and (128) that there exists \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\) such that, after passing to a further subsequence \(\{K_{m'}\}_{m'\in \mathbb{N}}\), as \(m'\rightarrow \infty \),
Since by assumption, as \(m'\rightarrow \infty \),
it follows from Theorem 14, Theorem 20, and Proposition 21 that \(\rho \) is a solution of (97) in the sense of Definition 11. The weak lower-semicontinuity of the \(L^{2}\)-norm, the definition of \(I_{\rho _{0}}\), and (127) prove that
which completes the proof of (125).
The proof of (126). Let \(\rho \in L^{1}(\mathbb{T}^{d}\times [0,T])\). If \(I_{\rho _{0}}(\rho )=\infty \), then (126) is satisfied. If not, Lemma 32 implies that there exists a unique \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\) such that
For every \(K\in \mathbb{N}\) let \(\rho _{K}\in L^{1}(\mathbb{T}^{d}\times [0,T])\) denote the unique solution of the equation
Since, as \(K\rightarrow 0\),
the methods of Proposition 21 prove that there exists \(\tilde{\rho}\in L^{1}(\mathbb{T}^{d}\times [0,T])\) such that, as \(K\rightarrow \infty \),
and such that \(\tilde{\rho}\) solves (97) in the sense of Definition 3. Since Theorem 8 and Theorem 14 prove that the solution is unique,
Therefore, it follows from (131) and (132) that, as \(K\rightarrow \infty \),
and the definition of the \(\{I^{K}_{\rho _{0}}\}_{K\in \mathbb{N}}\), (129), and (130) prove that
In combination (133) and (134) prove (126), which completes the proof. □
8 The lower semicontinuous envelope of the restricted rate function
As outlined in the introduction, the general approach to large deviations in interacting particle systems introduced in [23, 24] relies on a separate derivation of large deviations lower and upper bounds. As a consequence of these arguments, both estimates lead to possibly different rate functions. The proof of a large deviations principle relies on establishing their identity, which proves to be a challenging problem. In particular, this requires the characterization of the l.s.c. envelope of the lower-bound rate function restricted to smooth fluctuations, which in the case of the zero range process has remained an open problem since [26]. The proof of this is the main point of this section.
More precisely, let \(I^{0}\colon L^{1}(\mathbb{T}^{d}\times [0,T])\rightarrow [0,\infty ]\) be defined by
if \(\rho \in \mathrm{C}([0,T];L^{1}(\mathbb{T}^{d}))\) with \(\rho (\cdot ,0)\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\), and \(I^{0}(\rho )=\infty \) otherwise. It has been demonstrated in [26, Theorem 1 and p.99] that, for the space \(\mathcal {S}\) of smooth fluctuations defined in Definition 38 below, the application of the approach of [23, 24] to the zero range process yields a large deviations lower bound with rate function \(I^{\textrm{lo}}\colon L^{1}(\mathbb{T}^{d}\times [0,T])\rightarrow [0, \infty ]\) defined by
That is, \(I^{\textrm{lo}}\) is the l.s.c. envelope of \(I^{0}\) restricted to smooth fluctuations \(\rho \in \mathcal {S}\).
In contrast, the results of [26, Theorem 1], together with subsequent contributions [116–118] in related settings, suggest the large deviations upper bound with rate function \(I^{\mathrm{up}}\colon L^{1}(\mathbb{T}^{d}\times [0,T])\rightarrow [0, \infty ]\) defined by
for \(\rho \in \mathrm{C}([0,T];L^{1}(\mathbb{T}^{d}))\) with finite entropy-dissipation. That is, \(I^{\mathrm{up}}(\rho )=\infty \) if \(\rho \notin \mathrm{C}([0,T];L^{1}(\mathbb{T}^{d}))\) or if \(\nabla \Phi ^{\frac{1}{2}}(\rho )\notin L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\).
An essential difficulty and open problem since [26] is to identify the resulting rate functions \(I^{\textrm{lo}}\) and \(I^{\mathrm{up}}\), with a key difficulty being the characterization of the l.s.c. envelope appearing in (136). This (or the latter) problem is solved in the present section by Theorem 39 below.
An important realization is that in the proof of Theorem 39 it is instrumental to work with an alternate characterization of the rate function. Precisely, we introduce the rate function
if \(\rho \in \mathrm{C}([0,T];L^{1}(\mathbb{T}^{d}))\) and \(\rho (\cdot ,0)\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\), and we define \(I(\rho )=\infty \) otherwise. In particular, since the equation in (138) is interpreted in the sense of Definition 11 with initial data \(\rho (\cdot ,0)\), this means that \(I(\rho )=\infty \) if \(\rho \) fails to satisfy the entropy dissipation estimate
which using [42, Lemma 5.4] and part (i) of Assumption 15 is equivalent to \(\nabla \Phi ^{\frac{1}{2}}(\rho )\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\). Furthermore, we recall by Proposition 9 that solutions to the skeleton equation are always \(L^{1}(\mathbb{T}^{d})\)-continuous in time, where by convention we always identify \(\rho \in L^{1}(\mathbb{T}^{d}\times [0,T])\) with its unique strongly \(L^{1}(\mathbb{T}^{d})\)-continuous representative when it exists.
We show that on the space of functions \(\rho \in \mathrm{C}([0,T];L^{1}(\mathbb{T}^{d}))\) satisfying the entropy dissipation estimate (139), we have that the rate functions (135), (137), and (138) are equal and given by
where the supremum is taken over smooth functions \(\psi \in \mathrm{C}^{\infty}_{c}(\mathbb{T}^{d}\times [0,T))\), and the space \(H^{1}_{\Phi (\rho )}\) is defined in Definition 34 below. We show the equivalence of the final three expressions appearing in (140) in Lemma 36, and we prove that \(I=I^{\mathrm{up}}\) in Proposition 37.
Definition 34
Let \(\Phi \in \mathrm{C}([0,\infty ))\cap \mathrm{C}^{1}_{\textrm{loc}}((0, \infty ))\) and \(\rho \in L^{\infty}([0,T];L^{1}(\mathbb{T}^{d}))\) satisfy (139). We first introduce the equivalence relation ∼ on \(\mathrm{C}^{\infty}(\mathbb{T}^{d}\times [0,T])\) by
Let \(H^{1}_{\Phi (\rho )}\) be the Hilbert space defined by the completion of the set of equivalence classes \(\mathrm{C}^{\infty}(\mathbb{T}^{d}\times [0,T])/\sim \) with respect to the positive definite inner product
Remark 35
In the setting of Definition 34, let \(L^{2}_{\Phi (\rho )}(\mathbb{T}^{d}\times [0,T])^{d}\) denote the Sobolev space of measurable vector fields \(v\colon \mathbb{T}^{d}\times [0,T]\rightarrow \mathbb{R}^{d}\) satisfying \(\int _{0}^{T}\int _{\mathbb{T}^{d}}\Phi (\rho )|v|^{2}<\infty \), which is the Hilbert space of equivalence classes of vector fields with respect to the inner product
It is an immediate consequence of Definition 34 that the Hilbert space \(H^{1}_{\Phi (\rho )}\) is canonically isomorphic to a closed subspace of \(L^{2}_{\Phi (\rho )}(\mathbb{T}^{d}\times [0,T])^{d}\). For every \(H\in H^{1}_{\Phi (\rho )}\) we will write \(\nabla H\) for the vector field identified by this isomorphism, where for \(H\in L^{2}([0,T];H^{1}(\mathbb{T}^{d}))\) the generalized gradient \(\nabla H\) is equal to the standard weak gradient of \(H\).
Lemma 36
Let \(\Phi \in \mathrm{C}([0,\infty ))\cap \mathrm{C}^{1}_{\textrm{loc}}((0, \infty ))\) and let \(\rho \in \mathrm{C}([0,T];L^{1}(\mathbb{T}^{d}))\) satisfy (139). Then, for the supremum taken over \(\psi \in \mathrm{C}^{\infty}_{c}(\mathbb{T}^{d}\times [0,T))\),
Proof
It is a consequence of the definitions that the lefthand side of (141) is infinite if and only if the righthand side is infinite. In the case that both sides of (141) are finite, it follows from the definitions that the linear functional
extends by density to a unique continuous linear functional on \(H^{1}_{\Phi (\rho )}\). The Riesz Representation Theorem proves that, for a unique \(H_{\rho}\in H^{1}_{\Phi (\rho )}\), for every \(\psi \in \mathrm{C}^{\infty}_{c}(\mathbb{T}^{d}\times (0,T))\),
from which it follows by the density of smooth functions in \(H^{1}_{\Phi (\rho )}\) and the definitions that both sides of (141) are equal to
which completes the proof. □
Proposition 37
Let \(\Phi \in \mathrm{C}([0,\infty ))\cap \mathrm{C}^{1}_{\textrm{loc}}((0, \infty ))\) and let \(\rho \in \mathrm{C}([0,T];L^{1}(\mathbb{T}^{d}))\). Then, \(I(\rho ) = I^{\mathrm{up}}(\rho )\), for the rate functions defined in (137) and (138).
Proof
If \(\rho \) fails to satisfy (139) then both rate functions are infinite by definition. It remains only to consider the case that \(\rho \) satisfies (139). We will first show that if
then \(I(\rho )=\infty \). Proceeding by contradiction, if \(I(\rho )<\infty \) then there exists a control \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\) such that
in the sense of Definition 11. It follows from an approximation argument and the Lebesgue differentiation theorem that \(\rho \) satisfies (144) in the sense of Definition 11 if and only if \(\Phi ^{\frac{1}{2}}(\rho )\in L^{2}([0,T];H^{1}(\mathbb{T}^{d}))\) and, for every \(\psi \in \mathrm{C}^{\infty}_{c}(\mathbb{T}^{d}\times [0,T))\),
which implies using (139), Hölder’s inequality, and Young’s inequality that
which contradicts (143). It remains to consider the case that (143) is finite. A repetition of the argument appearing in Lemma 36 and (142) proves that, in this case, there exists \(H_{\rho}\in H^{1}_{\Phi (\rho )}\) such that
and such that
This proves that \(I(\rho )\leq \frac{1}{2} \lVert \Phi ^{\frac{1}{2}}(\rho )\nabla H_{\rho} \rVert ^{2}_{L^{2}}= \frac{1}{2}\lVert H_{\rho} \rVert ^{2}_{H^{1}_{\Phi (\rho )}}\). To prove the reverse inequality, consider the control set
which is equivalent to the set
for the dual space \(H^{-1}_{\Phi (\rho )}\) of \(H^{1}_{\Phi (\rho )}\). Since \(\nabla H_{\rho}\) is an admissible test function, we have for every \(g\in \textrm{Cont}_{\rho}\) that
It then follows from Hölder’s inequality that, for every \(g\in \textrm{Cont}_{\rho}\),
and therefore that \(I(\rho ) = \frac{1}{2}\lVert H_{\rho} \rVert ^{2}_{H^{1}_{\Phi (\rho )}}\) which with (145) completes the proof. □
Definition 38
Let \(\Phi \in \mathrm{C}([0,\infty ))\cap \mathrm{C}^{1}_{\textrm{loc}}((0, \infty ))\) satisfy Assumptions 6, 10, and 15. Let \(\mathcal{S}\subseteq \mathrm{C}([0,T];L^{1}(\mathbb{T}^{d}))\) denote the subset of all strictly positive and bounded \(\rho \) such that there exist a strictly positive \(\rho _{0}\in \mathrm{C}^{\infty}(\mathbb{T}^{d})\) and an \(H\in \mathrm{C}^{3,1}(\mathbb{T}^{d}\times [0,T])\) such that
in the sense of Definition 11 with control \(g=\Phi ^{\frac{1}{2}}(\rho )\nabla H\).
Theorem 39
Let \(\Phi \in \mathrm{C}([0,\infty ))\cap \mathrm{C}^{3}_{\textrm{loc}}((0, \infty ))\) satisfy Assumptions 6, 10, and 15. Then, for the rate functions defined in (136) and (138),
That is, \(I\) is the l.s.c. envelope of \(I^{0}\) restricted to smooth fluctuations \(\mathcal {S}\) and \(I=I^{\mathrm{lo}}=I^{\mathrm{up}}\).
Proof
It follows from Proposition 37 and Definition 38 that \(I=I^{0}=I^{\mathrm{up}}\) on \(\mathcal {S}\). It is therefore sufficient to show that \(I\) is equal to the l.s.c. envelope of its restriction to \(\mathcal {S}\). Since \(I\) is itself l.s.c. it follows that \(I\leq \overline{I_{|\mathcal {S}}}(\rho )\). It remains to show the opposite inequality. To do this, it is necessary to show that for any \(\rho \) satisfying \(I(\rho )<\infty \) there exists a sequence \(\rho _{n}\in \mathcal{S}\) such that, as \(n\rightarrow \infty \),
Using Lemma 32, let \(g\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\) be the unique control satisfying
We will now construct the smooth approximation. This occurs in three steps: we first introduce a smoothing of the control \(g\) and then a smoothing and perturbation of the initial data \(\rho (\cdot ,0)\in \operatorname {Ent}_{\Phi}(\mathbb{T}^{d})\) so that it becomes strictly positive. Finally, we introduce a cutoff that effectively “turns off” the control when it forces the solution near zero or infinity. This guarantees that the approximate solutions remain strictly bounded away from zero and infinity—and therefore restricts the solution to a region in which the nonlinearity \(\Phi \) is uniformly elliptic—and allows for the application of standard parabolic and elliptic regularity estimates to prove the regularity of the control in the sense of Definition 38.
Step 1: The smooth approximation. Extend \(g\) to \(\mathbb{T}^{d}\times \mathbb{R}\) by defining \(g=0\) on the complement of \(\mathbb{T}^{d}\times [0,T]\), for every \(\varepsilon \in (0,1)\) let \(\kappa _{d+1}^{\varepsilon }\) be a standard convolution kernel on \(\mathbb{T}^{d}\times \mathbb{R}\) of scale \(\varepsilon \), and for every \(n\in \mathbb{N}\) let \(g_{n}\) be the smooth control defined by  . For every \(\varepsilon \in (0,1)\) let \(\kappa ^{\varepsilon }_{d}\) be a smooth convolution kernel on \(\mathbb{T}^{d}\) and for every \(n\in \mathbb{N}\) let \(\rho _{0,n}\) be the smooth, bounded, and strictly positive initial data defined by
. For every \(\varepsilon \in (0,1)\) let \(\kappa ^{\varepsilon }_{d}\) be a smooth convolution kernel on \(\mathbb{T}^{d}\) and for every \(n\in \mathbb{N}\) let \(\rho _{0,n}\) be the smooth, bounded, and strictly positive initial data defined by  . Finally, for every \(n\in \mathbb{N}\) let \(\psi _{n}\colon [0,\infty )\rightarrow [0,1]\) be a smooth function that satisfies \(\psi _{n} = 0\) on
. Finally, for every \(n\in \mathbb{N}\) let \(\psi _{n}\colon [0,\infty )\rightarrow [0,1]\) be a smooth function that satisfies \(\psi _{n} = 0\) on  and \(\psi _{n} = 1\) on
and \(\psi _{n} = 1\) on  .
.
A small adaptation of the proofs of Theorem 8, Proposition 9, and Theorem 14 in this simplified setting prove that, for every \(n\in \mathbb{N}\), there exists a unique solution \(\rho _{n}\in \mathrm{C}([0,T];L^{1}(\mathbb{T}^{d}))\) of the equation
in the sense of Definition 11 with control \(\psi _{n}(\rho _{n})g_{n}\). We will first show that the \(\rho _{n}\) correspond to smooth fluctuations in the sense of Definition 38. The comparison principle, the definition of \(\psi _{n}\), and the definition of \(\rho _{0,n}\) prove that

Since we have that \(\psi _{n}\), \(g_{n}\), and \(\rho _{0,n}\) are smooth and bounded, that \(\Phi \in \mathrm{C}^{3}_{\textrm{loc}}((0,\infty ))\) with \(\Phi '\) strictly positive on compact subsets of \((0,\infty )\), and that \(\rho _{n}\) is bounded and bounded away from zero, it follows from interior Schauder estimates (see, for example, Ladyz̆henskaya, Solonnikov, and Ural’ceva [119]) that \(\rho _{n}\in \mathrm{C}^{3,2}(\mathbb{T}^{d}\times [0,T])\). We view the \(\rho _{n}\) as satisfying the equation
with the control \(\tilde{g}_{n} = \psi _{n}(\rho _{n})g_{n}\). In view of Remark 35, the positivity and boundedness of \(\rho _{n}\) away from zero and infinity and the positivity of \(\Phi \) on \((0,\infty )\) prove that elements of \(H^{1}_{\Phi (\rho _{n})}\) can be identified with a unique element of the Sobolev space \(L^{2}([0,T];H^{1}(\mathbb{T}^{d}))\) that has zero spatial mean on almost every time slice. It then follows from the proof of Proposition 37 that, for every \(n\in \mathbb{N}\), there exists \(H_{n}\in L^{2}([0,T];H^{1}(\mathbb{T}^{d}))\) such that
Hence, we have for every \(n\in \mathbb{N}\) that \(H_{n}\) is a solution to the uniformly elliptic equation
from which we have from  , the local \(\mathrm{C}^{3}\)-regularity and positivity of \(\Phi \) on \((0,\infty )\), the \(\mathrm{C}^{3,2}\)-regularity of \(\rho _{n}\), and interior elliptic regularity estimates (see, for example, [119]) that \(H_{n}\in \mathrm{C}^{3,1}(\mathbb{T}^{d}\times [0,T])\). This completes the proof that \(\rho _{n}\in \mathcal{S}\) for every \(n\in \mathbb{N}\).
, the local \(\mathrm{C}^{3}\)-regularity and positivity of \(\Phi \) on \((0,\infty )\), the \(\mathrm{C}^{3,2}\)-regularity of \(\rho _{n}\), and interior elliptic regularity estimates (see, for example, [119]) that \(H_{n}\in \mathrm{C}^{3,1}(\mathbb{T}^{d}\times [0,T])\). This completes the proof that \(\rho _{n}\in \mathcal{S}\) for every \(n\in \mathbb{N}\).
Step 2: The strong convergence of the smooth approximations. It remains to prove that, along a subsequence as \(n\rightarrow \infty \),
A small adaptation of Proposition 20 in this simplifed setting proves that, for every \(n\in \mathbb{N}\), for every \(t\in [0,T]\), we have that \(\lVert \rho _{n}(\cdot ,t) \rVert _{L^{1}(\mathbb{T}^{d})}=\lVert \rho _{0,n} \rVert _{L^{1}( \mathbb{T}^{d})}\), and the estimates proven in Proposition 19 and the definitions of \(\rho _{0,n}\), \(g_{n}\), and \(\psi _{n}\) prove that there exists \(c\in (0,\infty )\) independent of \(n\in \mathbb{N}\) such that
We have furthermore from the equation and the Sobolev embedding theorem that, for \(c\in (0,\infty )\) independent of \(n\in \mathbb{N}\),

which in view of (146) is uniformly bounded in \(n\in \mathbb{N}\).
The uniform \(L^{1}(\mathbb{T}^{d})\)-boundedness of the \(\rho _{n}\) and estimates (146), (147), and Lemma 17 prove that the \(\rho _{n}\) are relatively compact in \(L^{1}(\mathbb{T}^{d}\times [0,T])\). Therefore, after passing to a subsequence still denoted \(n\rightarrow \infty \), there exists \(\tilde{\rho}\in L^{1}(\mathbb{T}^{d}\times [0,T])\) such that
and such that, as \(n\rightarrow \infty \),
and strongly in \(L^{2}(\mathbb{T}^{d}\times [0,T])\). Furthermore, by definition of the \(\rho _{0,n}\), as \(n\rightarrow \infty \),
Since \(g_{n}\) is a convolution of \(g\), we have that \(g_{n}\rightarrow g\) strongly in \(L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\) as \(n\rightarrow \infty \). It then follows from the almost sure convergence of (148), the support and boundedness of \(\psi _{n}\), (149), and Hölder’s inequality that, as \(n\rightarrow \infty \),
It follows similarly from the almost sure convergence of (148), the continuity of \(\Phi \) and \(\Phi (0)=0\), the fact that \(g_{n}\rightarrow g\) strongly as \(n\rightarrow \infty \), (149), and the support and boundedness of \(\psi _{n}\) that, as \(n\rightarrow \infty \),
In combination, it follows from (151), (152), and \(\Phi (0)=0\) that, as \(n\rightarrow \infty \),
Since (149) and the weak lower semicontinuity of the Sobolev norm prove that \(\tilde{\rho}\) satisfies estimate (146), it follows from Definition 11, (148), (150), and (153) that \(\tilde{\rho}\) is a solution of the equation
in the sense of Definition 11. We therefore conclude using Theorem 8 and Theorem 14 that \(\tilde{\rho}=\rho \) and that the \(\rho _{n}\) converge strongly to \(\rho \) along the subsequence \(n\rightarrow \infty \).
Step 3: Convergence of the rate functions. It remains only to show that, along the subsequence \(n\rightarrow \infty \), we have that
By Lemma 32 let \(h_{n}\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\) be the unique function satisfying, using the definitions of the rate function, \(\psi _{n}\), and \(g_{n}\),
After passing to a subsequence \(n\rightarrow \infty \), for some \(h\in L^{2}(\mathbb{T}^{d}\times [0,T])^{d}\),
from which it follows from (154) that \(\lVert h \rVert _{L^{2}}\leq \lVert g \rVert _{L^{2}}\). Since Proposition 21 proves that \(\rho \) solves
we have by definition of the rate function that \(\lVert h \rVert _{L^{2}}\geq \lVert g \rVert _{L^{2}}\) and therefore that \(\lVert h \rVert _{L^{2}}= \lVert g \rVert _{L^{2}}\). Lemma 32 proves that \(h=g\), which implies that
and therefore, as \(n\rightarrow \infty \),
which completes the proof that \(\overline{I_{|\mathcal {S}}}(\rho )\leq I\) and therefore that \(I^{\textrm{lo}}=\overline{I_{|\mathcal {S}}}(\rho )=I\). Proposition 37 then proves \(I^{\mathrm{up}}=I^{\textrm{lo}}=I\), which completes the proof. □
References
DiPerna, R.J., Lions, P.-L.: Ordinary differential equations, transport theory and Sobolev spaces. Invent. Math. 98(3), 511–547 (1989)
Ambrosio, L.: Transport equation and Cauchy problem for BV vector fields. Invent. Math. 158(2), 227–260 (2004)
Le Bris, C., Lions, P.-L.: Existence and uniqueness of solutions to Fokker–Planck type equations with irregular coefficients. Commun. Partial Differ. Equ. 33(7), 1272–1317 (2008)
Crippa, G., De Lellis, C.: Estimates and regularity results for the DiPerna-Lions flow. J. Reine Angew. Math. 616, 15–46 (2008)
De Lellis, C.: Ordinary differential equations with rough coefficients and the renormalization theorem of Ambrosio [after Ambrosio, DiPerna, Lions]. Sémin. Bourbaki 2006/2007, 972–175203 (2008)
Figalli, A.: Existence and uniqueness of martingale solutions for SDEs with rough or degenerate coefficients. J. Funct. Anal. 254(1), 109–153 (2008)
Jabin, P.-E.: Differential equations with singular fields. J. Math. Pures Appl. (9) 94(6), 597–621 (2010)
Jabin, P.-E.: Critical non-Sobolev regularity for continuity equations with rough velocity fields. J. Differ. Equ. 260(5), 4739–4757 (2016)
Lions, P.-L., Perthame, B., Tadmor, E.: A kinetic formulation of multidimensional scalar conservation laws and related equations. J. Am. Math. Soc. 7(1), 169–191 (1994)
Perthame, B.: Uniqueness and error estimates in first order quasilinear conservation laws via the kinetic entropy defect measure. J. Math. Pures Appl. (9) 77(10), 1055–1064 (1998)
Chen, G.-Q., Perthame, B.: Well-posedness for non-isotropic degenerate parabolic-hyperbolic equations. Ann. Inst. Henri Poincaré, Anal. Non Linéaire 20(4), 645–668 (2003)
Karlsen, K.H., Risebro, N.H.: On the uniqueness and stability of entropy solutions of nonlinear degenerate parabolic equations with rough coefficients. Discrete Contin. Dyn. Syst. 9(5), 1081–1104 (2003)
Bendahmane, M., Karlsen, K.H.: Renormalized entropy solutions for quasi-linear anisotropic degenerate parabolic equations. SIAM J. Math. Anal. 36(2), 405–422 (2004)
De Lellis, C., Otto, F., Westdickenberg, M.: Structure of entropy solutions for multi-dimensional scalar conservation laws. Arch. Ration. Mech. Anal. 170(2), 137–184 (2003)
Le Bris, C., Lions, P.-L.: Renormalized solutions of some transport equations with partially \(W^{1,1}\)-velocities and applications. Ann. Mat. Pura Appl. 183(1), 97–130 (2004)
Otto, F.: \(L^{1}\)-Contraction and uniqueness for quasilinear elliptic–parabolic equations. J. Differ. Equ. 131(1), 20–38 (1996)
Depauw, N.: Non unicité des solutions bornées pour un champ de vecteurs BV en dehors d’un hyperplan. C. R. Math. Acad. Sci. Paris 337(4), 249–252 (2003)
Ferrari, P.A., Presutti, E., Vares, M.E.: Local equilibrium for a one dimensional zero range process. Stoch. Process. Appl. 26, 31–45 (1987)
Kipnis, C., Landim, C.: Scaling Limits of Interacting Particle Systems. Springer, New York (1999)
E, W., Ren, W., Vanden-Eijnden, E.: Simplified and improved string method for computing the minimum energy paths in barrier-crossing events. J. Chem. Phys. 126(16), 164103 (2007)
Grafke, T., Vanden-Eijnden, E.: Numerical computation of rare events via large deviation theory. Chaos 29(6), 063118 (2019)
Vanden-Eijnden, E., Weare, J.: Rare event simulation of small noise diffusions. Commun. Pure Appl. Math. 65(12), 1770–1803 (2012)
Donsker, M.D., Varadhan, S.R.S.: Large deviations from a hydrodynamic scaling limit. Commun. Pure Appl. Math. 42(3), 243–270 (1989)
Kipnis, C., Olla, S., Varadhan, S.R.S.: Hydrodynamics and large deviation for simple exclusion processes. Commun. Pure Appl. Math. 42(2), 115–137 (1989)
Bodineau, T., Gallagher, I., Saint-Raymond, L., Simonella, S.: Statistical dynamics of a hard sphere gas: fluctuating Boltzmann equation and large deviations (2020). arXiv:2008.10403
Benois, O., Kipnis, C., Landim, C.: Large deviations from the hydrodynamical limit of mean zero asymmetric zero range processes. Stoch. Process. Appl. 55(1), 65–89 (1995)
Bertini, L., De Sole, A., Gabrielli, D., Jona-Lasinio, G., Landim, C.: Macroscopic fluctuation theory. Rev. Mod. Phys. 87(2), 593 (2015)
Derrida, B.: Non-equilibrium steady states: fluctuations and large deviations of the density and of the current. J. Stat. Mech. Theory Exp. 2007(07), 07023 (2007)
Hohenberg, P.C., Halperin, B.I.: Theory of dynamic critical phenomena. Rev. Mod. Phys. 49(3), 435–479 (1977)
Landau, L.D., Lifschitz, E.M.: Lehrbuch der Theoretischen Physik (“Landau–Lifschitz”). Band VI, 5th edn., p. 683. Akademie Verlag, Berlin (1991)
Spohn, H.: Large Scale Dynamics of Interacting Particles. Springer, Berlin (2012)
Bouchet, F., Gawȩdzki, K., Nardini, C.: Perturbative calculation of quasi-potential in non-equilibrium diffusions: a mean-field example. J. Stat. Phys. 163(5), 1157–1210 (2016)
Dirr, N., Stamatakis, M., Zimmer, J.: Entropic and gradient flow formulations for nonlinear diffusion. J. Math. Phys. 57(8), 081505 (2016)
Giacomin, G., Lebowitz, J.L., Presutti, E.: Deterministic and stochastic hydrodynamic equations arising from simple microscopic model systems. In: Stochastic Partial Differential Equations: Six Perspectives. Math. Surveys Monogr., vol. 64, pp. 107–152. Am. Math. Soc., Providence (1999)
Dean, D.: Langevin equation for the density of a system of interacting Langevin processes. J. Phys. A, Math. Gen. 29(24), 613 (1996)
Kawasaki, K.: Stochastic model of slow dynamics in supercooled liquids and dense colloidal suspensions. Phys. A, Stat. Mech. Appl. 208(1), 35–64 (1994)
Donev, A., Fai, T.G., Vanden-Eijnden, E.: A reversible mesoscopic model of diffusion in liquids: from giant fluctuations to Fick’s law. J. Stat. Mech. Theory Exp. 2014(4), 04004 (2014)
Donev, A., Vanden-Eijnden, E.: Dynamic density functional theory with hydrodynamic interactions and fluctuations. J. Chem. Phys. 140(23), 234115 (2014)
Renesse, M.-K.: Modified massive Arratia flow and Wasserstein diffusion. Commun. Pure Appl. Math. 72(4), 764–800 (2019)
Konarovskyi, V., von Renesse, M.: Reversible coalescing-fragmentating Wasserstein dynamics on the real line (2017). arXiv:1709.02839
Konarovskyi, V.: Dean-Kawasaki dynamics: ill-posedness vs. triviality. Electron. Commun. Probab. 24, 8–9 (2019)
Fehrman, B., Gess, B.: Well-posedness of the Dean–Kawasaki and nonlinear Dawson–Watanabe equation with correlated noise (2021). arXiv:2108.08858
Hairer, M.: A theory of regularity structures. Invent. Math. 198(2), 269–504 (2014)
Gubinelli, M., Imkeller, P., Perkowski, N.: Paraproducts, rough paths and controlled distributions, 1–30 (2012). arXiv:1210.2684
Hairer, M., Weber, H.: Large deviations for white-noise driven, nonlinear stochastic PDEs in two and three dimensions. Ann. Fac. Sci. Toulouse Math. Sér. 6 24(1), 55–92 (2015)
Vázquez, J.L.: The Porous Medium Equation. Oxford Mathematical Monographs. Clarendon, Oxford (2007)
Brezis, H.: Monotonicity methods in Hilbert spaces and some applications to nonlinear partial differential equations. In: Contributions to Nonlinear Functional Analysis, pp. 101–156. Elsevier, Amsterdam (1971)
Gilding, B.H.: A nonlinear degenerate parabolic equation. Ann. Sc. Norm. Super. Pisa, Cl. Sci. (4) 4(3), 393–432 (1977)
Gilding, B.H., Peletier, L.A.: The Cauchy problem for an equation in the theory of infiltration. Arch. Ration. Mech. Anal. 61(2), 127–140 (1976)
Benilan, P.: Opérateurs \(m\)-accrétifs hémicontinus dans un espace de Banach quelconque. C. R. Hebd. Séances Acad. Sci., Sér. A, Sci. Math. 278, 1029–1032 (1974)
Crandall, M.G.: An introduction to evolution governed by accretive operators. In: Cesari, L., Hale, J.K., LaSalle, J.P. (eds.) Dynamical Systems, pp. 131–165. Academic Press, San Diego (1976)
Bénilan, P., Crandall, M.G., Pierre, M.: Solutions of the porous medium equation in \(\mathbb{R}^{N}\) under optimal conditions on initial values. Indiana Univ. Math. J. 33(1), 51–87 (1984)
Crandall, M.G., Liggett, T.M.: Generation of semi-groups of nonlinear transformations on general Banach spaces. Am. J. Math. 93, 265–298 (1971)
Vol’pert, A.I., Hudjaev, S.I.: The Cauchy problem for second order quasilinear degenerate parabolic equations. Mat. Sb. (N.S.) 78(120), 374–396 (1969)
Alt, H.W., Luckhaus, S.: Quasilinear elliptic-parabolic differential equations. Math. Z. 183(3), 311–341 (1983)
Carrillo, J.: On the uniqueness of the solution of the evolution dam problem. Nonlinear Anal., Theory Methods Appl. 22(5), 573–607 (1994)
Carrillo, J.: Entropy solutions for nonlinear degenerate problems. Arch. Ration. Mech. Anal. 147(4), 269–361 (1999)
Karlsen, K.H., Ohlberger, M.: A note on the uniqueness of entropy solutions of nonlinear degenerate parabolic equations. J. Math. Anal. Appl. 275(1), 439–458 (2002)
Chen, G.-Q., Karlsen, K.H.: Quasilinear anisotropic degenerate parabolic equations with time-space dependent diffusion coefficients. Commun. Pure Appl. Anal. 4(2), 241–266 (2005)
Dalibard, A.-L.: Kinetic formulation for heterogeneous scalar conservation laws. Ann. Inst. Henri Poincaré, Anal. Non Linéaire 23(4), 475–498 (2006)
Dalibard, A.-L.: Kinetic formulation for a parabolic conservation law. Application to homogenization. SIAM J. Math. Anal. 39(3), 891–915 (2007)
Wang, Z., Wang, L., Li, Y.: Renormalized entropy solutions for degenerate parabolic-hyperbolic equations with time-space dependent coefficients. Commun. Pure Appl. Anal. 12(3), 1163–1182 (2013)
Barbu, V., Röckner, M.: Solutions for nonlinear Fokker-Planck equations with measures as initial data and McKean-Vlasov equations. J. Funct. Anal. 280(7), 108926–35 (2021)
Diaz, J.I., Kersner, R.: On a nonlinear degenerate parabolic equation in infiltration or evaporation through a porous medium. J. Differ. Equ. 69(3), 368–403 (1987)
Krylov, N.V., Röckner, M.: Strong solutions of stochastic equations with singular time dependent drift. Probab. Theory Relat. Fields 131(2), 154–196 (2005)
Beck, L., Flandoli, F., Gubinelli, M., Maurelli, M.: Stochastic ODEs and stochastic linear PDEs with critical drift: regularity, duality and uniqueness (2014). arXiv:1401.1530
Bogachev, V.I., Krylov, N.V., Röckner, M., Shaposhnikov, S.V.: Fokker-Planck-Kolmogorov Equations. Mathematical Surveys and Monographs, vol. 207. Am. Math. Soc., Providence (2015)
Boccardo, L., Orsina, L., Porretta, A.: Some noncoercive parabolic equations with lower order termsin divergence form. J. Evol. Equ. 3(3), 407–418 (2003)
Porretta, A.: Weak solutions to Fokker–Planck equations and mean field games. Arch. Ration. Mech. Anal. 216(1), 1–62 (2015)
Evans, M.R., Hanney, T.: Nonequilibrium statistical mechanics of the zero-range process and related models. J. Phys. A 38(19), 195–240 (2005)
Bernardin, C., Gonçalves, P., Oviedo-Jiménez, B., Scotta, S.: Non-equilibrium stationary properties of the boundary driven zero-range process with long jumps (2022). arXiv:2201.07573
Barré, J., Bernardin, C., Chétrite, R., Chopra, Y., Mariani, M.: Gamma convergence approach for the large deviations of the density in systems of interacting diffusion processes (2019). arXiv:1910.04026
Dawson, D.A., Gärtner, J.: Large deviations, free energy functional and quasi-potential for a mean field model of interacting diffusions. Mem. Am. Math. Soc. 78(398), 94 (1989)
Dawson, D.A., Gärtner, J.: Large deviations from the McKean-Vlasov limit for weakly interacting diffusions. Stochastics 20(4), 247–308 (1987)
Gvalani, R., Schlichting, A.: Barriers of the McKean–Vlasov energy via a mountain pass theorem in the space of probability measures. J. Funct. Anal. 279(11), 108720 (2020)
Mariani, M.: Large deviations principles for stochastic scalar conservation laws. Probab. Theory Relat. Fields 147(3–4), 607–648 (2010)
Bellettini, G., Bertini, L., Mariani, M., Novaga, M.: \(\Gamma \)-Entropy cost for scalar conservation laws. Arch. Ration. Mech. Anal. 195(1), 261–309 (2010)
Dirr, N., Fehrman, B., Gess, B.: Conservative stochastic PDE and fluctuations of the symmetric simple exclusion process (2020). arXiv:2012.02126
Lions, P.-L., Perthame, B., Souganidis, P.: Stochastic averaging lemmas for kinetic equations. In: Séminaire Laurent Schwartz — EDP et Applications, pp. 1–17 (2011)
Lions, P.-L., Perthame, B., Souganidis, P.E.: Scalar conservation laws with rough (stochastic) fluxes. Stoch. Partial Differ. Equ., Anal. Computat. 1(4), 664–686 (2013)
Lions, P.-L., Perthame, B., Souganidis, P.E.: Scalar conservation laws with rough (stochastic) fluxes: the spatially dependent case. Stoch. Partial Differ. Equ., Anal. Computat. 2(4), 517–538 (2014)
Friz, P.K., Gess, B.: Stochastic scalar conservation laws driven by rough paths. Ann. Inst. Henri Poincaré, Anal. Non Linéaire 33(4), 933–963 (2016)
Gess, B., Souganidis, P.E.: Scalar conservation laws with multiple rough fluxes. Commun. Math. Sci. 13(6), 1569–1597 (2015)
Gess, B., Souganidis, P.E.: Long-time behavior, invariant measures, and regularizing effects for stochastic scalar conservation laws. Commun. Pure Appl. Math. 70(8), 1562–1597 (2017)
Gess, B., Souganidis, P.E.: Stochastic non-isotropic degenerate parabolic–hyperbolic equations. Stoch. Process. Appl. 127(9), 2961–3004 (2017)
Fehrman, B., Gess, B.: Well-posedness of nonlinear diffusion equations with nonlinear, conservative noise. Arch. Ration. Mech. Anal. 233(1), 249–322 (2019)
Dareiotis, K., Gess, B.: Nonlinear diffusion equations with nonlinear gradient noise. Electron. J. Probab. 25, 35–43 (2020)
Gess, B., Perthame, B., Souganidis, P.E.: Semi-discretization for stochastic scalar conservation laws with multiple rough fluxes. SIAM J. Numer. Anal. 54(4), 2187–2209 (2016)
Hoel, H., Karlsen, K.H., Risebro, N.H., Storrosten, E.B.: Path-dependent convex conservation laws. J. Differ. Equ. 265(6), 2708–2744 (2018)
Hoel, H., Karlsen, K.H., Risebro, N.H., Storrosten, E.B.: Numerical methods for conservation laws with rough flux. Stoch. Partial Differ. Equ., Anal. Computat. 8(1), 186–261 (2020)
Lions, P.-L., Souganidis, P.E.: Fully nonlinear stochastic partial differential equations. C. R. Acad. Sci. Paris Sér. I Math. 326(9), 1085–1092 (1998)
Lions, P.-L., Souganidis, P.E.: Fully nonlinear stochastic partial differential equations: non-smooth equations and applications. C. R. Acad. Sci. Paris Sér. I Math. 327(8), 735–741 (1998)
Lions, P.-L., Souganidis, P.E.: Fully nonlinear stochastic PDE with semilinear stochastic dependence. C. R. Acad. Sci. Paris Sér. I Math. 331(8), 617–624 (2000)
Lions, P.-L., Souganidis, P.E.: Uniqueness of weak solutions of fully nonlinear stochastic partial differential equations. C. R. Acad. Sci. Paris Sér. I Math. 331(10), 783–790 (2000)
Souganidis, P.E.: Pathwise solutions for fully nonlinear first- and second-order partial differential equations with multiplicative rough time dependence. In: Singular Random Dynamics. Lecture Notes in Math., vol. 2253, pp. 75–220. Springer, Berlin (2019)
Friz, P.K., Gassiat, P., Lions, P.-L., Souganidis, P.E.: Eikonal equations and pathwise solutions to fully non-linear SPDEs. Stoch. Partial Differ. Equ., Anal. Computat. 5(2), 256–277 (2017)
Gassiat, P., Gess, B.: Regularization by noise for stochastic Hamilton–Jacobi equations. Probab. Theory Relat. Fields 173(3–4), 1063–1098 (2019)
Gassiat, P., Gess, B., Lions, P.-L., Souganidis, P.E.: Speed of propagation for Hamilton-Jacobi equations with multiplicative rough time dependence and convex Hamiltonians. Probab. Theory Relat. Fields 176(1–2), 421–448 (2020)
Lions, P.-L., Souganidis, P.E.: New regularity results for Hamilton-Jacobi equations and long time behavior of pathwise (stochastic) viscosity solutions. Res. Math. Sci. 7(3), 17–18 (2020)
Faris, W.G., Jona-Lasinio, G.: Large fluctuations for a nonlinear heat equation with noise. J. Phys. A, Math. Gen. 15(10), 3025–3055 (1982)
Jona-Lasinio, G., Mitter, P.K.: Large deviation estimates in the stochastic quantization of \(\phi ^{4}_{2}\). Commun. Math. Phys. 130(1), 111–121 (1990)
Cerrai, S., Freidlin, M.: Approximation of quasi-potentials and exit problems for multidimensional RDE’s with noise. Trans. Am. Math. Soc. 363(7), 3853–3892 (2011)
Budhiraja, A., Dupuis, P., Maroulas, V.: Large deviations for infinite dimensional stochastic dynamical systems. Ann. Probab. 36(4), 1390–1420 (2008)
Cerrai, S., Debussche, A.: Large deviations for the dynamic \(\Phi ^{2n}_{d}\) model. Appl. Math. Optim. 80(1), 81–102 (2019)
Brzeźniak, Z., Goldys, B., Jegaraj, T.: Large deviations and transitions between equilibria for stochastic Landau-Lifshitz-Gilbert equation. Arch. Ration. Mech. Anal. 226(2), 497–558 (2017)
Dong, Z., Wu, J.-L., Zhang, R., Zhang, T.: Large deviation principles for first-order scalar conservation laws with stochastic forcing. Ann. Appl. Probab. 30(1), 324–367 (2020)
Aubin, J.-P.: Un théorème de compacité. C. R. Acad. Sci. Paris 256, 5042–5044 (1963)
Lions, J.-L.: Quelques Méthodes de Résolution des Problèmes aux Limites Non Linéaires p. 554. Dunod; Gauthier-Villars, Paris (1969)
Simon, J.: Compact sets in the space \(L^{p}(0,T;B)\). Ann. Mat. Pura Appl. (4) 146, 65–96 (1987)
Dupuis, P., Ellis, R.: A Weak Convergence Approach to the Theory of Large Deviations. Wiley Series in Probability and Statistics: Probability and Statistics, p. 479. Wiley, New York (1997)
Budhiraja, A., Dupuis, P.: Analysis and Approximation of Rare Events. Probability Theory and Stochastic Modelling, vol. 94, p. 574. Springer, Berlin (2019)
Budhiraja, A., Dupuis, P., Salins, M.: Uniform large deviation principles for Banach space valued stochastic evolution equations. Trans. Am. Math. Soc. 372(12), 8363–8421 (2019)
Billingsley, P.: Convergence of Probability Measures, 2nd edn. Wiley Series in Probability and Statistics: Probability and Statistics, p. 277. Wiley, New York (1999)
Revuz, D., Yor, M.: Continuous Martingales and Brownian Motion, 3rd edn. Grundlehren der mathematischen Wissenschaften, vol. 293, p. 602. Springer, Berlin (1999)
Evans, L.C.: Partial Differential Equations, 2nd edn. Graduate Studies in Mathematics, vol. 19, p. 749. Am. Math. Soc., Providence (2010)
Quastel, J., Yau, H.-T.: Lattice gases, large deviations, and the incompressible Navier-Stokes equations. Ann. Math. (2) 148(1), 51–108 (1998)
Quastel, J., Rezakhanlou, F., Varadhan, S.R.S.: Large deviations for the symmetric simple exclusion process in dimensions \(d\geq 3\). Probab. Theory Relat. Fields 113(1), 1–84 (1999)
Landim, C., Tsunoda, K.: Hydrostatics and dynamical large deviations for a reaction-diffusion model. Ann. Inst. Henri Poincaré Probab. Stat. 54(1), 51–74 (2018)
Ladyz̆henskaya, O.A., Solonnikov, V.A., Ural’ceva, N.N.: Linear and Quasilinear Equations of Parabolic Type. Transl. Math. Monographs, vol. 23. Am. Math. Soc., Providence (1967)
Funding
The first author acknowledges financial support from the Engineering and Physical Sciences Research Council through the EPSRC Early Career Fellowship EP/V027824/1. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – SFB 1283/2 2021 – 317210226.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fehrman, B., Gess, B. Non-equilibrium large deviations and parabolic-hyperbolic PDE with irregular drift. Invent. math. 234, 573–636 (2023). https://doi.org/10.1007/s00222-023-01207-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-023-01207-3



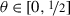 such that
such that