Abstract
Small-amplitude, traveling, space periodic solutions –called Stokes waves– of the 2 dimensional gravity water waves equations in deep water are linearly unstable with respect to long-wave perturbations, as predicted by Benjamin and Feir in 1967. We completely describe the behavior of the four eigenvalues close to zero of the linearized equations at the Stokes wave, as the Floquet exponent is turned on. We prove in particular the conjecture that a pair of non-purely imaginary eigenvalues depicts a closed figure “8”, parameterized by the Floquet exponent, in full agreement with numerical simulations. Our new spectral approach to the Benjamin-Feir instability phenomenon uses a symplectic version of Kato’s theory of similarity transformation to reduce the problem to determine the eigenvalues of a \( 4 \times 4 \) complex Hamiltonian and reversible matrix. Applying a procedure inspired by KAM theory, we block-diagonalize such matrix into a pair of \(2 \times 2 \) Hamiltonian and reversible matrices, thus obtaining the full description of its eigenvalues.
Similar content being viewed by others
1 Introduction
Since the pioneering work of Stokes [47] in 1847, a huge literature has established the existence of steady space periodic traveling waves, namely solutions which look stationary in a moving frame. Such solutions are called Stokes waves. A problem of fundamental importance in fluid mechanics regards their stability/instability subject to long space periodic perturbations. In 1967 Benjamin and Feir [6, 7] discovered, with heuristic arguments, that a long-wave perturbation of a small amplitude space periodic Stokes wave is unstable; see also the the independent results by Lighthill [30] and Zakharov [50, 52] and the survey [53] for an historical overview. This phenomenon is nowadays called “Benjamin-Feir” –or modulational– instability, and it is supported by an enormous amount of physical observations and numerical simulations, see e.g. [1, 18, 19, 35] and references therein.
It took almost thirty years to get the first rigorous proof of the Benjamin-Feir instability for the water waves equations in two dimensions, obtained by Bridges-Mielke [12] in finite depth, and fifty-five years for the infinite depth case, proved last year by Nguyen-Strauss [43].
The problem is mathematically formulated as follows. Consider the pure gravity water waves equations for a bidimensional fluid in deep water and a \(2\pi \)-periodic Stokes wave solution with amplitude \(0< \epsilon \ll 1\). The linearized water waves equations at the Stokes waves are, in the inertial reference frame moving with the speed \( c_{\epsilon } \) of the Stokes wave, a linear time independent system of the form \( h_t = {\mathcal {L}}_{\epsilon } h \) where \( {\mathcal {L}}_{\epsilon } \) is a linear operator with \( 2 \pi \)-periodic coefficients, see (2.13)Footnote 1. The operator \( {\mathcal {L}}_{\epsilon } \) possesses the eigenvalue 0 with algebraic multiplicity four due to symmetries of the water waves equations (that we describe in the next section). The problem is to prove that \( h_t = {\mathcal {L}}_{\epsilon } h \) has solutions of the form \(h(t,x) = \text {Re}\left( e^{\lambda t} e^{\mathrm {i}\,\mu x} v(x)\right) \) where v(x) is a \(2\pi \)-periodic function, \(\mu \) in \( {\mathbb {R}}\) (called Floquet exponent) and \(\lambda \) has positive real part, thus h(t, x) grows exponentially in time. By Bloch-Floquet theory, such \(\lambda \) is an eigenvalue of the operator \( {\mathcal {L}}_{\mu ,\epsilon } := e^{-\mathrm {i}\,\mu x } \,{\mathcal {L}}_{\epsilon } \, e^{\mathrm {i}\,\mu x } \) acting on \(2\pi \)-periodic functions.
The main result of this paper provides the full description of the four eigenvalues close to zero of the operator \( {\mathcal {L}}_{\mu ,\epsilon } \) when \( \epsilon \) and \( \mu \) are small enough, see Theorem 2.3, thus concluding the analysis started in 1967 by Benjamin-Feir. We first state the following result which focuses on the Benjamin-Feir unstable eigenvalues.
Along the paper we denote by \(r(\epsilon ^{m_1} \mu ^{n_1}, \ldots , \epsilon ^{m_p} \mu ^{n_p})\) a real analytic function fulfilling for some \(C >0\) and \(\epsilon , \mu \) sufficiently small, the estimate \(| r(\epsilon ^{m_1} \mu ^{n_1}, \ldots , \epsilon ^{m_p} \mu ^{n_p}) | \le C \sum _{j=1}^p |\epsilon |^{m_j} |\mu |^{n_j} \).
Theorem 1.1
There exist \( \epsilon _1, \mu _0 > 0 \) and an analytic function \({{\underline{\mu }}}: [0,\epsilon _1)\rightarrow [0,\mu _0)\), of the form \( \underline{\mu }(\epsilon ) = 2\sqrt{2} \epsilon (1+r(\epsilon )) \), such that, for any \( \epsilon \in [0, \epsilon _1) \), the operator \({\mathcal {L}}_{\mu ,\epsilon }\) has two eigenvalues \(\lambda ^\pm _1 (\mu ,\epsilon )\) of the form
The function \( 8\epsilon ^2\big (1+r_0(\epsilon ,\mu )\big )-\mu ^2\big (1+r_0'(\epsilon ,\mu ) ) \) is \(>0\), respectively \(<0\), provided \(0<\mu < {\underline{\mu }}(\epsilon )\), respectively \(\mu > {\underline{\mu }}(\epsilon )\).
Let us make some comments on the result.
1. According to (1.1), for values of the Floquet parameter \( 0<\mu < {{\underline{\mu }}} (\epsilon ) \) the eigenvalues \(\lambda ^\pm _1 (\mu , \epsilon ) \) have opposite non-zero real part. As \( \mu \) tends to \( {{\underline{\mu }}} (\epsilon )\), the two eigenvalues \(\lambda ^\pm _1 (\mu ,\epsilon ) \) collide on the imaginary axis far from 0 (in the upper semiplane \( \text {Im} (\lambda ) > 0 \)), along which they keep moving for \( \mu > {{\underline{\mu }}} (\epsilon ) \), see Fig. 1. For \( \mu < 0 \) the operator \( {{\mathcal {L}}}_{\mu ,\epsilon } \) possesses the symmetric eigenvalues \( \overline{\lambda _1^{\pm } (-\mu ,\epsilon )} \) in the semiplane \( \text {Im} (\lambda ) < 0 \).
2. Theorem 1.1 proves the long-standing conjecture that the unstable eigenvalues \(\lambda ^\pm _1 (\mu ,\epsilon )\) depict a complete figure “8” as \(\mu \) varies in the interval \([ - {{\underline{\mu }}}(\epsilon ) , {{\underline{\mu }}}(\epsilon )]\), see Fig. 1. For \( \mu \in [0, {{\underline{\mu }}}(\epsilon )]\) we obtain the upper part of the figure “8”, which is well approximated by the curves \(\mu \mapsto (\pm \frac{\mu }{8}\sqrt{8\epsilon ^2 -\mu ^2}, \frac{1}{2} \mu )\), in accordance with the numerical simulations by Deconinck-Oliveras [19]. For \( \mu \in [{{\underline{\mu }}}(\epsilon ), \mu _0 ]\) the purely imaginary eigenvalues are approximated by \( \mathrm {i}\,\frac{\mu }{2} ( 1 \pm \frac{1}{4}\sqrt{\mu ^2 - 8\epsilon ^2})\). The higher order corrections of the eigenvalues \( \lambda _1^\pm (\mu ,\epsilon ) \) in (1.1), provided by the analytic functions \( r_0(\epsilon ,\mu ), r_0'(\epsilon ,\mu ) \), are explicitly computable. Theorem 1.1 is the first rigorous proof of the “Benjamin-Feir figure 8”, not only for the water waves equations, but also in any model exhibiting modulational instability, that we quote at the end of this introduction (for the focusing 1d NLS equation Deconinck-Upsal [20] showed the presence of a figure “8” for elliptic solutions, exploiting the integrable structure of the equation).
Traces of the eigenvalues \(\lambda ^\pm _1 (\mu ,\epsilon )\) in the complex \(\lambda \)-plane at fixed \(|\epsilon | \ll 1 \) as \(\mu \) varies. For \( \mu \in (0, {\underline{\mu }}(\epsilon )) \) the eigenvalues fill the portion of the 8 in \( \{ \text {Im} (\lambda ) > 0 \} \) and for \( \mu \in ( - {\underline{\mu }}(\epsilon ),0 ) \) the symmetric portion in \( \{ \text {Im} (\lambda ) < 0 \} \)
3. Nguyen-Strauss result in [43] describes the portion of unstable eigenvalues very close to the origin, namely the cross amid the “8”. Formula (1.1) prolongs these local branches of eigenvalues far from the bifurcation, until they collide again on the imaginary axis. Note that as \( 0<\mu \ll \epsilon \) the eigenvalues \( \lambda ^\pm _1 (\mu , \epsilon ) \) in (1.1) have the same asymptotic expansion given in Theorem 1.1 of [43].
4. The eigenvalues (1.1) are not analytic in \((\mu , \epsilon )\) close to the value \(({\underline{\mu }}(\epsilon ),\epsilon )\) where \( \lambda ^\pm _1 (\mu , \epsilon ) \) collide at the top of the figure “8” far from 0 (clearly they are continuous). In previous approaches the eigenvalues are a priori supposed to be analytic in \((\mu , \epsilon )\), and that restricts their validity to suitable regimes. We remark that (1.1) are the eigenvalues of the \( 2 \times 2 \) matrix \({ \mathtt U}\) given in Theorem 2.3, which is analytic in \((\mu , \epsilon )\).
5. In Theorem 2.3 we actually prove the expansion of the unstable eigenvalues of \( {\mathcal {L}}_{\mu ,\epsilon } \) for any value of the parameters \((\mu ,\epsilon )\) in a rectangle \( [0,\mu _0) \times [0,\epsilon _0 )\). The analytic curve \( {{\underline{\mu }}}(\epsilon ) = 2\sqrt{2} \epsilon (1+r(\epsilon )) \), tangent at \( \epsilon = 0 \) to the straight line \( \mu = 2\sqrt{2} \epsilon \) divides such rectangle in the “unstable” region where there exist eigenvalues of \( {{\mathcal {L}}}_{\mu ,\epsilon }\) with non-trivial real part, from the “stable” one where all the eigenvalues of \( {{\mathcal {L}}}_{\mu ,\epsilon }\) are purely imaginary, see Fig. 2.
The blue line is the analytic curve defined implicitly by \(8\epsilon ^2\big (1+r_0(\epsilon ,\mu )\big )-\mu ^2\big (1+r_0'(\epsilon ,\mu ) ) = 0\). For values of \(\mu \) below this curve, the two eigenvalues \(\lambda ^\pm _1(\mu ,\epsilon )\) have opposite real part. For \(\mu \) above the curve, \(\lambda ^\pm _1(\mu ,\epsilon )\) are purely imaginary
6. For larger values of the Floquet parameter \( \mu \), due to Hamiltonian reasons, the eigenvalues will remain on the imaginary axis until the Floquet exponent \( \mu \) reaches values close to the next “collision” between two other eigenvalues of \( {\mathcal L}_{0,\mu } \). For water waves in infinite depth this value is close to \( \mu = 1 / 4 \) and corresponds to eigenvalues close to \( \mathrm {i}\,3 / 4 \). These unstable eigenvalues depict ellipse-shaped curves, called islands, that have been described numerically in [19] and supported by formal expansions in \( \epsilon \) in [18], see also [1].
7. In Theorem 1.1 we have described just the two unstable eigenvalues of \({\mathcal {L}}_{\mu ,\epsilon }\) close to zero. There are also two larger purely imaginary eigenvalues of order \( {\mathcal {O}}(\sqrt{\mu }) \), see Theorem 2.3. We remark that our approach describes all the eigenvalues of \( {{\mathcal {L}}}_{\mu ,\epsilon } \) close to 0 (which are 4).
Any rigorous proof of the Benjamin-Feir instability has to face the difficulty that the perturbed eigenvalues bifurcate from the defective eigenvalue zero. Both Bridges-Mielke [12] (see also the preprint by Hur-Yang [28] in finite depth) and Nguyen-Strauss [43], reduce the spectral problem to a finite dimensional one, here a \(4\times 4\) matrix, and, in a suitable regime of values of \( (\mu , \epsilon )\), prove the existence of eigenvalues with non-zero real part. The paper [12], dealing with water waves in finite depth, bases its analysis on spatial dynamics and a Hamiltonian center manifold reduction, as [28]. Such approach fails in infinite depth (we quote however [29] for an analogue in infinite depth which carries most of the properties of a center manifold). The proof in [43] is based on a Lyapunov-Schmidt decomposition and applies also to the infinite depth case.
Our approach is completely different. Postponing its detailed description after the statement of Theorem 2.3, we only anticipate some of its main ingredients. The first one is Kato’s theory of similarity transformations [34, II-§4]. This method is perfectly suited to study splitting of multiple isolated eigenvalues, for which regular perturbation theory might fail. It has been used, in a similar context, in the study of infinite dimensional integrable systems [5, 33, 36, 40].
In this paper we implement Kato’s theory for the complex operators \({\mathcal {L}}_{\mu ,\epsilon }\) which have an Hamiltonian and reversible structure, inherited by the Hamiltonian [17, 51] and reversible [4, 8, 11] nature of the water waves equations. We show how Kato’s theory can be used to prolong, in an analytic way, a symplectic and reversible basis of the generalized eigenspace of the unperturbed operator \( {{\mathcal {L}}}_{0,0} \) into a (\(\mu ,\epsilon \))-dependent symplectic and reversible basis of the corresponding invariant subspace of \( {{\mathcal {L}}}_{\mu ,\epsilon } \). Thus the restriction of the canonical complex symplectic form to this subspace, is represented, in this symplectic basis, by the constant symplectic matrix \( {\mathtt J}_4 \) defined in (3.23), which is independent of \( (\mu ,\epsilon )\). This feature simplifies considerably perturbation theory.
In this way the spectral problem is reduced to determine the eigenvalues of a \(4 \times 4\) matrix, which depends analytically in \( \mu , \epsilon \) and it is Hamiltonian and reversible. These properties imply strong algebraic features on the matrix entries, for which we provide detailed expansions. Next, inspired by KAM ideas, instead of looking for zeros of the characteristic polynomial of the reduced matrix (as in the periodic Evans function approach [14, 28] or in [26, 43]), we conjugate it to a block-diagonal matrix whose \( 2 \times 2 \) diagonal blocks are Hamiltonian and reversible. One of these two blocks has the eigenvalues given by (1.1), proving the Benjamin-Feir instability figure “8” phenomenon.
Let us mention that modulational instability has been studied also for a variety of approximate water waves models, such as KdV, gKdV, NLS and the Whitham equation by, for instance, Whitham [49], Segur, Henderson, Carter and Hammack [46], Gallay and Haragus [24], Haragus and Kapitula [25], Bronski and Johnson [14], Johnson [32], Hur and Johnson [26], Bronski, Hur and Johnson [13], Hur and Pandey [27], Leisman, Bronski, Johnson and Marangell [37]. Also in these approximate models numerical simulations predict a figure “8” similar to that in Fig. 1 for the bifurcation of the unstable eigenvalues close to zero. However, in none of these approximate models (except for the integrable NLS in [20]) the complete picture of the Benjamin-Feir instability has been rigorously proved so far. We expect that the approach developed in this paper could be applicable for such equations as well, and also to include the effects of surface tension in water waves equations (see e.g. [1]).
To conclude this introduction, we mention the nonlinear modulational instability result of Jin, Liao, and Lin [31] for several approximate water waves models and the preprint by Chen and Su [16] for Stokes waves in deep water. For nonlinear instability results of traveling solitary water waves decaying at infinity on \( {\mathbb {R}}\) (not periodic) we quote [45] and reference therein.
2 The full water waves Benjamin-Feir spectrum
In order to give the complete statement of our spectral result, we begin with recapitulating some well known facts about the pure gravity water waves equations.
The water waves equations and the Stokes waves. We consider the Euler equations for a 2-dimensional incompressible, inviscid, irrotational fluid under the action of gravity. The fluid fills the region \( { {\mathcal {D}}}_\eta := \left\{ (x,y)\in {\mathbb {T}}\times {\mathbb {R}}\,{:}\, y< \eta (t,x)\right\} \), \( {\mathbb {T}}:={\mathbb {R}}/2\pi {\mathbb {Z}}\), with infinite depth and space periodic boundary conditions. The irrotational velocity field is the gradient of a harmonic scalar potential \(\Phi =\Phi (t,x,y) \) determined by its trace \( \psi (t,x)=\Phi (t,x,\eta (t,x)) \) at the free surface \( y = \eta (t, x ) \). Actually \(\Phi \) is the unique solution of the elliptic equation
The time evolution of the fluid is determined by two boundary conditions at the free surface. The first is that the fluid particles remain, along the evolution, on the free surface (kinematic boundary condition), and the second one is that the pressure of the fluid is equal, at the free surface, to the constant atmospheric pressure (dynamic boundary condition). Then, as shown by Zakharov [51] and Craig-Sulem [17], the time evolution of the fluid is determined by the following equations for the unknowns \( (\eta (t,x), \psi (t,x)) \),
where \(g > 0 \) is the gravity constant and \(G(\eta )\) denotes the Dirichlet-Neumann operator \( [G(\eta )\psi ](x) := \Phi _y(x,\eta (x)) - \Phi _x(x,\eta (x)) \eta _x(x)\). It results that \( G(\eta ) [\psi ] \) has zero average.
With no loss of generality we set the gravity constant \(g=1\). The equations (2.1) are the Hamiltonian system
where \( \nabla \) denote the \( L^2\)-gradient, and the Hamiltonian \({\mathcal {H}}(\eta ,\psi ){:=} \frac{1}{2} \int _{{\mathbb {T}}}\left( \psi \,G(\eta )\psi +\eta ^2 \right) \mathrm {d}x \) is the sum of the kinetic and potential energy of the fluid. The associated symplectic 2-form is

In addition of being Hamiltonian, the water waves system (2.1) possesses other important symmetries. First of all it is time reversible with respect to the involution
or equivalently the water waves vector field \( X(\eta , \psi ) \) anticommutes with \( \rho \), i.e. \( X \circ \rho = - \rho \circ X \). This property follows noting that the Dirichlet-Neumann operator satisfies (see e.g. [8])
Noteworthy solutions of (2.1) are the so-called traveling Stokes waves, namely solutions of the form \(\eta (t,x)=\breve{\eta }(x-ct)\) and \(\psi (t,x)=\breve{\psi }(x-ct)\) for some real c and \(2\pi \)-periodic functions \((\breve{\eta } (x), \breve{\psi } (x)) \). In a reference frame in translational motion with constant speed c, the water waves equations (2.1) then become
and the Stokes waves \((\breve{\eta }, \breve{\psi })\) are equilibrium steady solutions of (2.6).
The rigorous existence proof of the bifurcation of small amplitude Stokes waves for pure gravity water waves goes back to the works of Levi-Civita [38], Nekrasov [41], and Struik [48]. We denote by \(B(r):= \{ x \in {\mathbb {R}}:\ |x| < r\}\) the real ball with center 0 and radius r.
Theorem 2.1
(Stokes waves) There exist \(\epsilon _0 >0\) and a unique family of real analytic solutions \((\eta _\epsilon (x), \psi _\epsilon (x), c_\epsilon )\), parameterized by the amplitude \(|\epsilon | \le \epsilon _0\), of
such that \( \eta _\epsilon (x), \psi _\epsilon (x) \) are \(2\pi \)-periodic; \(\eta _\epsilon (x) \) is even and \(\psi _\epsilon (x) \) is odd. They have the expansion
More precisely for any \( \sigma \ge 0 \) and \( s > \frac{5}{2} \), there exists \( \epsilon _0>0 \) such that the map \(\epsilon \mapsto (\eta _\epsilon , \psi _\epsilon , c_\epsilon )\) is analytic from \(B(\epsilon _0) \rightarrow H^{\sigma ,s} ({\mathbb {T}})\times H^{\sigma ,s}({\mathbb {T}})\times {\mathbb {R}}\), where \( H^{\sigma ,s}({\mathbb {T}}) \) is the space of \( 2 \pi \)-periodic analytic functions \( u(x) = \sum _{k \in {\mathbb {Z}}} u_k e^{\mathrm {i}\,k x} \) with \( \Vert u \Vert _{\sigma ,s}^2 := \sum _{k \in {\mathbb {Z}}} |u_k|^2 \langle k \rangle ^{2s} e^{2 \sigma |k|} < + \infty \).
The existence of solutions of (2.7) can nowadays be deduced by the analytic Crandall-Rabinowitz bifurcation theorem from a simple eigenvalue, see e.g. [15]. Since Lewy [39] it is known that \(C^1\) traveling waves are actually real analytic, see also Nicholls-Reitich [42]. The expansion (2.8) is given for example in [43, Proposition 2.2]. The analyticity result of Theorem 2.1 is explicitely proved in [10]. We also mention that more general time quasi-periodic traveling Stokes waves have been recently proved for (2.1) in [9] in finite depth (actually for any constant vorticity), in [22] in infinite depth, and in [8] for gravity-capillary water waves with constant vorticity in any depth.
Linearization at the Stokes waves. In order to determine the stability/instability of the Stokes waves given by Theorem 2.1, we linearize the water waves equations (2.6) with \( c = c_\epsilon \) at \((\eta _\epsilon (x), \psi _\epsilon (x))\). In the sequel we follow closely [43], but, as in [4, 9], we emphasize the Hamiltonian and reversible structures of the linearized equations, since these properties play a crucial role in our proof of the instability result.
By using the shape derivative formula for the differential \( \mathrm {d}_\eta G(\eta )[{{\hat{\eta }}} ]\) of the Dirichlet-Neumann operator (see e.g. formula (3.4) in [43]), one obtains the autonomous real linear system

where
The functions (V, B) are the horizontal and vertical components of the velocity field \( (\Phi _x, \Phi _y) \) at the free surface. Moreover \(\epsilon \mapsto (V,B)\) is analytic as a map \(B(\epsilon _0) \rightarrow H^{\sigma , s-1}({\mathbb {T}})\times H^{\sigma ,s-1}({\mathbb {T}})\).
The real system (2.9) is Hamiltonian, i.e. of the form \( {\mathcal {J}}{\mathcal {A}} \) for a symmetric operator \( {\mathcal {A}} = \mathcal A^\top \), where \({\mathcal {A}}^\top \) is the transposed operator with respect the standard real scalar product of \(L^2({\mathbb {T}}, {\mathbb {R}})\times L^2({\mathbb {T}}, {\mathbb {R}})\).
Moreover, since \( \eta _\epsilon \) is even in x and \( \psi _\epsilon \) is odd in x, then the functions (V, B) are respectively even and odd in x. Using also (2.5), the linear operator in (2.9) is reversible, i.e. it anti-commutes with the involution \( \rho \) in (2.4).
Under the time-independent “good unknown of Alinhac” linear transformation
the system (2.9) assumes the simpler form
Note that, since the transformation Z is symplectic, i.e. \( Z^\top {\mathcal {J}}Z = {\mathcal {J}}\), and reversibility preserving, i.e. \( Z \circ \rho = \rho \circ Z \), the linear system (2.11) is Hamiltonian and reversible as (2.9).
Next, following Levi-Civita [38], we perform a conformal change of variables to flatten the water surface. By [43, Prop. 3.3], or [11, section 2.4], there exists a diffeomorphism of \({\mathbb {T}}\), \( x\mapsto x+{\mathfrak {p}}(x)\), with a small \(2\pi \)-periodic function \({\mathfrak {p}}(x)\), such that, by defining the associated composition operator \( ({\mathfrak {P}}u)(x) := u(x+{\mathfrak {p}}(x))\), the Dirichlet-Neumann operator writes as
where \( {{\mathcal {H}}} \) is the Hilbert transform. The function \({\mathfrak {p}}(x)\) is determined as a fixed point of \({\mathfrak {p}} = {\mathcal {H}}[\eta _\epsilon \circ (\text {Id} + {\mathfrak {p}})]\), see e.g. [43, Proposition 3.3.] or [11, formula (2.125)]. By the analyticity of the map \(\epsilon \rightarrow \eta _\epsilon \in H^{\sigma ,s}\), \(\sigma >0\), \(s > 1/2\), the analytic implicit function theoremFootnote 2 implies the existence of a solution \(\epsilon \mapsto {\mathfrak {p}}(x):={\mathfrak {p}}_\epsilon (x) \) analytic as a map \(B(\epsilon _0) \rightarrow H^{s}({\mathbb {T}})\). Moreover, since \(\eta _\epsilon \) is even, the function \({\mathfrak {p}}(x)\) is odd.
Under the symplectic and reversibility-preserving map
(\( {\mathcal {P}} \) preserves the symplectic 2-form in (2.3) by inspection, and commutes with \( \rho \) being \( {\mathfrak {p}}(x) \) odd), the system (2.11) transforms into the linear system \( h_t = {\mathcal {L}}_\epsilon h \) where \( {\mathcal {L}}_\epsilon \) is the Hamiltonian and reversible real operator
where
The functions \(p_\epsilon (x) \) and \(a_\epsilon (x) \) are even in x and, by the expansion (2.8) of the Stokes wave, it results [43, Lemma 3.7]
In addition, by the analiticity results of the functions \( V, B, {\mathfrak {p}}(x) \) given above, the functions \(p_\epsilon \) and \(a_\epsilon \) are analytic in \(\epsilon \) as maps \(B(\epsilon _0)\rightarrow H^{s} ({\mathbb {T}})\).
Bloch-Floquet expansion. The operator \({\mathcal {L}}_\epsilon \) in (2.13) has \(2\pi \)-periodic coefficients, so its spectrum on \(L^2({\mathbb {R}}, {\mathbb {C}}^2)\) is most conveniently described by Bloch-Floquet theory (see e.g. [32] and references therein). This theory guarantees that
This reduces the problem to study the spectrum of \({\mathcal {L}}_{\mu , \epsilon }\) acting on \(L^2({\mathbb {T}}, {\mathbb {C}}^2)\) for different values of \(\mu \). In particular, if \(\lambda \) is an eigenvalue of \({\mathcal {L}}_{\mu ,\epsilon }\) with eigenvector v(x), then \(h (t,x) = e^{\lambda t} e^{\mathrm {i}\,\mu x} v(x)\) solves \(h_t = {\mathcal {L}}_{\epsilon } h\). We remark that:
1. If \(A = \mathrm {Op}(a) \) is a pseudo-differential operator with symbol \( a(x, \xi ) \), which is \(2\pi \) periodic in the x-variable, then \( A_\mu := e^{- \mathrm {i}\,\mu x}A e^{ \mathrm {i}\,\mu x} = \mathrm {Op} (a(x, \xi + \mu )) \) is a pseudo-differential operator with symbol \( a(x, \xi + \mu ) \) (which can be proved e.g. following Lemma 3.5 of [43]).
2. If A is a real operator then \( \overline{ A_\mu } = A_{- \mu } \). As a consequence the spectrum
Then we can study \( \sigma (A_{\mu }) \) just for \( \mu > 0 \). Furthermore \(\sigma (A_{\mu })\) is a 1-periodic set with respect to \(\mu \), so one can restrict to \(\mu \in [0, \frac{1}{2})\).
By the previous remarks the Floquet operator associated with the real operator \({\mathcal {L}}_\epsilon \) in (2.13) is the complex Hamiltonian and reversible operator (see Definition 2.2 below)
We regard \( {\mathcal {L}}_{\mu ,\epsilon } \) as an operator with domain \(H^1({\mathbb {T}}):= H^1({\mathbb {T}},{\mathbb {C}}^2)\) and range \(L^2({\mathbb {T}}):=L^2({\mathbb {T}},{\mathbb {C}}^2)\), equipped with the complex scalar product
We also denote \( \Vert f \Vert ^2 = (f,f) \).
The complex operator \({\mathcal {L}}_{\mu ,\epsilon }\) in (2.18) is Hamiltonian and Reversible, according to the following definition.
Definition 2.2
(Complex Hamiltonian/Reversible operator) A complex operator \({\mathcal {L}}: H^1({\mathbb {T}},{\mathbb {C}}^2) \rightarrow L^2({\mathbb {T}},{\mathbb {C}}^2) \) is
- (i):
-
Hamiltonian, if \({\mathcal {L}}= {\mathcal {J}}{\mathcal {B}}\) where \( {\mathcal {B}}\) is a self-adjoint operator, namely \( {\mathcal {B}}= {\mathcal {B}}^* \), where \({\mathcal {B}}^*\) (with domain \(H^1({\mathbb {T}})\)) is the adjoint with respect to the complex scalar product (2.19) of \(L^2({\mathbb {T}})\).
- (ii):
-
Reversible, if
$$\begin{aligned} {\mathcal {L}}\circ {{\overline{\rho }}}=- {{\overline{\rho }}}\circ {\mathcal {L}}\, , \end{aligned}$$(2.20)where \({{\overline{\rho }}}\) is the complex involution (cfr. (2.4))
$$\begin{aligned} {{\overline{\rho }}}\begin{bmatrix}\eta (x) \\ \psi (x) \end{bmatrix} := \begin{bmatrix}{{\overline{\eta }}}(-x) \\ -{{\overline{\psi }}}(-x) \end{bmatrix} \, . \end{aligned}$$(2.21)
The property (2.20) for \( {\mathcal {L}}_{\mu ,\epsilon } \) follows because \( {\mathcal {L}}_\epsilon \) is a real operator which is reversible with respect to the involution \( \rho \) in (2.4). Equivalently, since \({\mathcal {J}}\circ {{\overline{\rho }}}= -{{\overline{\rho }}}\circ {\mathcal {J}}\), a complex Hamiltonian operator \( {\mathcal {L}}= {\mathcal {J}}{\mathcal {B}}\) is reversible, if the self-adjoint operator \({\mathcal {B}}\) is reversibility-preserving, i.e.
We shall deeply exploit these algebraic properties in the proof of Theorem 2.3.
In addition \((\mu , \epsilon ) \rightarrow {\mathcal {L}}_{\mu ,\epsilon } \in {\mathcal {L}}(H^1({\mathbb {T}}), L^2({\mathbb {T}}))\) is analytic, since the functions \(\epsilon \mapsto a_\epsilon \), \(p_\epsilon \) defined in (2.15), (2.16) are analytic as maps \(B(\epsilon _0) \rightarrow H^1({\mathbb {T}})\) and \({{\mathcal {L}}}_{\mu ,\epsilon }\) is linear in \(\mu \). Indeed the Fourier multiplier operator \(|D+\mu | \) can be written, for any \( \mu \in [-\frac{1}{2}, \frac{1}{2}) \), as \(|D+\mu | = |D| + \mu {{\,\mathrm{sgn}\,}}(D)+ |\mu | \, \Pi _0 \) and thus (see [43, Section 5.1])
where \({{\,\mathrm{sgn}\,}}(D)\) is the Fourier multiplier operator, acting on \(2\pi \)-periodic functions, with symbol
and \(\Pi _0\) is the projector operator on the zero mode, \(\Pi _0f(x) := \frac{1}{2\pi } \int _{\mathbb {T}}f(x)\mathrm {d}x. \)
Our aim is to prove the existence of eigenvalues of \( {\mathcal {L}}_{\mu ,\epsilon } \) with non zero real part. We remark that the Hamiltonian structure of \({\mathcal {L}}_{\mu ,\epsilon }\) implies that eigenvalues with non zero real part may arise only from multiple eigenvalues of \({\mathcal {L}}_{\mu ,0}\), because if \(\lambda \) is an eigenvalue of \({\mathcal {L}}_{\mu ,\epsilon }\) then also \(-{{\overline{\lambda }}}\) is. In particular simple purely imaginary eigenvalues of \({\mathcal {L}}_{\mu ,0}\) remain on the imaginary axis under perturbation. We now carefully describe the spectrum of \({\mathcal {L}}_{\mu ,0}\).
The spectrum of \({\mathcal {L}}_{\mu ,0}\). The spectrum of the Fourier multiplier matrix operator
consists of the purely imaginary eigenvalues \(\{\lambda _k^\pm (\mu )\;,\; k\in {\mathbb {Z}}\} \), where
It is easily verified (see e.g. [2]) that the eigenvalues \(\lambda _k^\pm (\mu )\) in (2.26) may “collide” only for \(\mu =0\) or \(\mu =\frac{1}{4}\). For \(\mu =0\) the real operator \({\mathcal {L}}_{0,0}\) possesses the eigenvalue 0 with algebraic multiplicity 4,
and geometric multiplicity 3. A real basis of the Kernel of \({\mathcal {L}}_{0,0}\) is
together with the generalized eigenvector
Furthermore 0 is an isolated eigenvalue for \({\mathcal {L}}_{0,0}\), namely the spectrum \(\sigma \left( {\mathcal {L}}_{0,0}\right) \) decomposes in two separated parts
and
Note that \( \sigma ''({\mathcal {L}}_{0,0})\) is contained in \(\{ \lambda \in \mathrm {i}\,{\mathbb {R}}\, : \, |\lambda | \ge 2-\sqrt{2}\}\).
We shall also use that, as proved in Theorem 4.1 in [43], the operator \( {{\mathcal {L}}}_{0,\epsilon } \) possesses, for any sufficiently small \(\epsilon \ne 0\), the eigenvalue 0 with a four dimensional generalized Kernel, spanned by \( \epsilon \)-dependent vectors \( U_1, {{\tilde{U}}}_2, U_3, U_4 \) satisfying, for some real constant \( \alpha _\epsilon \),
By Kato’s perturbation theory (see Lemma 3.1 below) for any \(\mu , \epsilon \ne 0\) sufficiently small, the perturbed spectrum \(\sigma \left( {\mathcal {L}}_{\mu ,\epsilon }\right) \) admits a disjoint decomposition as
where \( \sigma '\left( {\mathcal {L}}_{\mu ,\epsilon }\right) \) consists of 4 eigenvalues close to 0. We denote by \({\mathcal {V}}_{\mu , \epsilon }\) the spectral subspace associated with \(\sigma '\left( {\mathcal {L}}_{\mu ,\epsilon }\right) \), which has dimension 4 and it is invariant by \({\mathcal {L}}_{\mu , \epsilon }\). Our goal is to prove that, for \( \epsilon \) small, for values of the Floquet exponent \( \mu \) in an interval of order \( \epsilon \), the \(4\times 4\) matrix which represents the operator \( {\mathcal {L}}_{\mu ,\epsilon } : {\mathcal {V}}_{\mu ,\epsilon } \rightarrow {\mathcal {V}}_{\mu ,\epsilon } \) possesses a pair of eigenvalues close to zero with opposite non zero real parts.
Before stating our main result, let us introduce a notation we shall use through all the paper:
-
Notation: we denote by \({\mathcal {O}}(\mu ^{m_1}\epsilon ^{n_1},\dots ,\mu ^{m_p}\epsilon ^{n_p})\), \( m_j, n_j \in {\mathbb {N}}\), analytic functions of \((\mu ,\epsilon )\) with values in a Banach space X which satisfy, for some \( C > 0 \), the bound \(\Vert {\mathcal {O}}(\mu ^{m_j}\epsilon ^{n_j})\Vert _X \le C \sum _{j = 1}^p |\mu |^{m_j}|\epsilon |^{n_j}\) for small values of \((\mu , \epsilon )\). We denote \(r_k (\mu ^{m_1}\epsilon ^{n_1},\dots ,\mu ^{m_p}\epsilon ^{n_p}) \) scalar functions \({\mathcal {O}}(\mu ^{m_1}\epsilon ^{n_1},\dots ,\mu ^{m_p}\epsilon ^{n_p})\) which are also real analytic.
Our complete spectral result is the following:
Theorem 2.3
(Complete Benjamin-Feir spectrum) There exist \( \epsilon _0, \mu _0>0 \) such that, for any \( 0\le \mu < \mu _0 \) and \( 0\le \epsilon < \epsilon _0 \), the operator \( {\mathcal {L}}_{\mu ,\epsilon } : {\mathcal {V}}_{\mu ,\epsilon } \rightarrow {\mathcal {V}}_{\mu ,\epsilon } \) can be represented by a \(4\times 4\) matrix of the form

where \( \mathtt {U} \) and \( \mathtt {S} \) are \( 2 \times 2 \) matrices of the form
where in each of the two matrices the diagonal entries are identical. The eigenvalues of the matrix \( \mathtt {U} \) are given by
Note that if \(8\epsilon ^2 (1+r_0(\epsilon ,\mu ))-\mu ^2 (1+r_0'(\epsilon ,\mu )) > 0 \), respectively \(<0\), the eigenvalues \(\lambda ^\pm _1(\mu ,\epsilon )\) have a nontrivial real part, respectively are purely imaginary.
The eigenvalues of the matrix \( \mathtt {S} \) are a pair of purely imaginary eigenvalues of the form
For \( \epsilon = 0\) the eigenvalues \( \lambda _1^\pm (\mu ,0), \lambda _0^\pm (\mu ,0) \) coincide with those in (2.26).
We conclude this section describing in detail our approach.
Ideas and scheme of proof. We first write the operator \({\mathcal {L}}_{\mu ,\epsilon } = \mathrm {i}\,\mu + {{\mathscr {L}}}_{\mu ,\epsilon } \) as in (3.1) and we aim to construct a basis of \({\mathcal {V}}_{\mu ,\epsilon }\) to represent \({{\mathscr {L}}}_{\mu ,\epsilon }\vert _{{\mathcal {V}}_{\mu ,\epsilon }}\) as a convenient \( 4\times 4\) matrix. The unperturbed operator \( {{\mathscr {L}}}_{0,0}\vert _{{\mathcal {V}}_{0,0}}\) possesses 0 as isolated eigenvalue with algebraic multiplicity 4 and generalized kernel \({\mathcal {V}}_{0,0}\) spanned by the vectors \(\{f_1^\pm , f_0^\pm \}\) in (2.27), (2.28).
Exploiting Kato’s theory of similarity transformations for separated eigenvalues we prolong the unperturbed symplectic basis \(\{f_1^\pm , f_0^\pm \}\) of \({\mathcal {V}}_{0,0}\) into a symplectic basis of \({\mathcal {V}}_{\mu ,\epsilon }\) (cfr. Definition 3.6), depending analytically on \(\mu , \epsilon \). In Lemma 3.1 we construct the transformation operator \(U_{\mu ,\epsilon }\), see (3.10), which is invertible and analytic in \(\mu ,\epsilon \), and maps isomorphically \({\mathcal {V}}_{0,0}\) into \({\mathcal {V}}_{\mu ,\epsilon }\). Furthermore, since \( {{\mathscr {L}}}_{\mu ,\epsilon }\) is Hamiltonian and reversible, we prove in Lemma 3.2 that the operator \(U_{\mu ,\epsilon }\) is symplectic and reversibility preserving. This implies that the vectors \( f^\sigma _k(\mu ,\epsilon ) := U_{\mu ,\epsilon }f_k^\sigma \), \( k = 0,1\), \(\sigma = \pm \), form a symplectic and reversible basis of \({\mathcal {V}}_{\mu ,\epsilon } \), according to Definition 3.6.
This construction has the following interpretation in the setting of complex symplectic structures, cfr. [3, 21]. The complex symplectic form (3.18) restricted to the symplectic subspace \( {\mathcal {V}}_{\mu ,\epsilon } \) is represented, in the \( (\mu , \epsilon )\)-dependent symplectic basis \( f^\sigma _k(\mu ,\epsilon )\), by the constant antisymmetric matrix \( \mathtt {J}_4 \) defined in (3.23), for any value of \( (\mu , \epsilon )\). In this sense \( U_{\mu ,\epsilon } \) is acting as a “Darboux transformation”. Consequently, the Hamiltonian and reversible operator \( {{\mathscr {L}}}_{\mu ,\epsilon }\vert _{{\mathcal {V}}_{\mu ,\epsilon }}\) is represented, in the symplectic basis \( f^\sigma _k(\mu ,\epsilon )\), by a \(4\times 4\) matrix of the form \(\mathtt {J}_4 \mathtt {B}_{\mu ,\epsilon }\) with \(\mathtt {B}_{\mu ,\epsilon }\) selfadjoint, see Lemma 3.10. This property simplifies considerably the perturbation theory of the spectrum (we refer to [44] for a discussion, in a different context, of the difficulties raised by parameter-dependent symplectic forms).
We then modify the basis \(\{ f^\sigma _k(\mu ,\epsilon )\} \) to construct a new symplectic and reversible basis \(\{g_k^\sigma (\mu ,\epsilon )\} \) of \({\mathcal {V}}_{\mu ,\epsilon }\), still depending analytically on \(\mu ,\epsilon \), with the additional property that \(g_1^-(0,\epsilon )\) has zero space average; this property plays a crucial role in the expansion obtained in Lemma 4.7, necessary to exhibit the Benjamin-Feir instability phenomenon, see Remark 4.8. By construction, the eigenvalues of the \(4\times 4\) matrix \(\mathtt {L}_{\mu ,\epsilon }\), representing the action of the operator \( {{\mathscr {L}}}_{\mu ,\epsilon }\) on the basis \( \{g_k^\sigma (\mu ,\epsilon )\} \), coincide with the portion of the spectrum \(\sigma '({{\mathscr {L}}}_{\mu ,\epsilon })\) close to zero, defined in (2.31). In Proposition 4.4 we prove that the \(4\times 4\) Hamiltonian and reversible matrix \(\mathtt {L}_{\mu ,\epsilon }\) has the form
where  and \(E = E^*\), \(G = G^*\) and F are \(2 \times 2\) matrices having the expansions (4.13)-(4.15). To compute these expansions –from which the Benjamin-Feir instability will emerge– we use two ingredients. First we Taylor expand \((\mu , \epsilon ) \mapsto U_{\mu ,\epsilon }\) in Lemma A.1. The Taylor expansion of \(U_{\mu ,\epsilon }\) is not a symplectic operator, but this is no longer important to compute the expansions (4.13)-(4.15) of the matrix \(\mathtt {L}_{\mu ,\epsilon }\). We used that \(U_{\mu ,\epsilon }\) is symplectic to prove the Hamiltonian structure (2.35) of \(\mathtt {L}_{\mu ,\epsilon }\). The second ingredient is a careful analysis of \( \mathtt {L}_{0,\epsilon }\) and \(\partial _\mu \mathtt {L}_{\mu ,\epsilon }\vert _{\mu = 0}\). In particular we prove that the (2, 2)-entry of the matrix E in (4.13) does not have any term \({\mathcal {O}}( \epsilon ^m )\) nor \( {\mathcal {O}}( \mu \epsilon ^m ) \) for any \( m \in {\mathbb {N}}\). These terms would be dangerous because they might change the sign of the entry (2, 2) of the matrix E in (4.13) which instead is always negative. This is crucial to prove the Benjamin-Feir instability, as we explain below. We show the absence of terms \({\mathcal {O}}(\epsilon ^m)\), \( m \in {\mathbb {N}}\), fully exploiting the structural information (2.30) concerning the four dimensional generalized Kernel of the operator \({\mathcal {L}}_{0,\epsilon }\) for any \(\epsilon >0\), see Lemma 4.6. The absence of terms \({\mathcal {O}}(\mu \epsilon ^m)\), \( m \in {\mathbb {N}}\), is due to the properties of the basis \(\{ g_k^\sigma (\mu ,\epsilon )\}\) (see Remark 4.8) and it is the motivation for modifying the original basis \(\{ f^\sigma _k(\mu ,\epsilon )\}\).
and \(E = E^*\), \(G = G^*\) and F are \(2 \times 2\) matrices having the expansions (4.13)-(4.15). To compute these expansions –from which the Benjamin-Feir instability will emerge– we use two ingredients. First we Taylor expand \((\mu , \epsilon ) \mapsto U_{\mu ,\epsilon }\) in Lemma A.1. The Taylor expansion of \(U_{\mu ,\epsilon }\) is not a symplectic operator, but this is no longer important to compute the expansions (4.13)-(4.15) of the matrix \(\mathtt {L}_{\mu ,\epsilon }\). We used that \(U_{\mu ,\epsilon }\) is symplectic to prove the Hamiltonian structure (2.35) of \(\mathtt {L}_{\mu ,\epsilon }\). The second ingredient is a careful analysis of \( \mathtt {L}_{0,\epsilon }\) and \(\partial _\mu \mathtt {L}_{\mu ,\epsilon }\vert _{\mu = 0}\). In particular we prove that the (2, 2)-entry of the matrix E in (4.13) does not have any term \({\mathcal {O}}( \epsilon ^m )\) nor \( {\mathcal {O}}( \mu \epsilon ^m ) \) for any \( m \in {\mathbb {N}}\). These terms would be dangerous because they might change the sign of the entry (2, 2) of the matrix E in (4.13) which instead is always negative. This is crucial to prove the Benjamin-Feir instability, as we explain below. We show the absence of terms \({\mathcal {O}}(\epsilon ^m)\), \( m \in {\mathbb {N}}\), fully exploiting the structural information (2.30) concerning the four dimensional generalized Kernel of the operator \({\mathcal {L}}_{0,\epsilon }\) for any \(\epsilon >0\), see Lemma 4.6. The absence of terms \({\mathcal {O}}(\mu \epsilon ^m)\), \( m \in {\mathbb {N}}\), is due to the properties of the basis \(\{ g_k^\sigma (\mu ,\epsilon )\}\) (see Remark 4.8) and it is the motivation for modifying the original basis \(\{ f^\sigma _k(\mu ,\epsilon )\}\).
Thanks to this analysis, the \(2 \times 2\) matrix
possesses two eigenvalues with non-zero real part –we say that it exhibits the Benjamin-Feir phenomenon– as long as the two off-diagonal elements have the same sign, which happens for \( 0< \mu < {{\overline{\mu }}} (\epsilon ) \) with \( {{\overline{\mu }}} (\epsilon ) \sim 2 \sqrt{2} \epsilon \). On the other hand the \( 2 \times 2 \) matrix \(\mathtt {J}_2 G\) has purely imaginary eigenvalues for \( \mu > 0 \) of order \({\mathcal {O}}(\sqrt{\mu })\). In order to prove that the complete \( 4 \times 4 \) matrix \( \mathtt {L}_{\mu ,\epsilon } \) in (2.35) possesses Benjamin-Feir unstable eigenvalues as well, our aim is to eliminate the coupling term \( \mathtt {J}_2 F \). This is done in Sect. 5 by a block diagonalization procedure, inspired by KAM theory. This is a singular perturbation problem because the spectrum of the matrices \(\mathtt {J}_2 E \) and \(\mathtt {J}_2 G\) tends to 0 as \( \mu \rightarrow 0 \). We construct a symplectic and reversibility preserving block-diagonalization transformation in three steps:
1. First step of block-diagonalization (Sect.5.1). Note that the spectral gap between the 2 block matrices \( \mathtt {J}_2 E \) and \( \mathtt {J}_2 G \) is of order \( {\mathcal {O}}(\sqrt{\mu } )\), whereas the entry \( F_{11} \) of the matrix F has size \( {\mathcal {O}}(\epsilon ^3) \). In Sect. 5.1 we perform a symplectic and reversibility-preserving change of coordinates removing \(F_{11}\) and conjugating \( \mathtt {L}_{\mu ,\epsilon }\) to a new Hamiltonian and reversible matrix \(\mathtt {L}^{(1)}_{\mu ,\epsilon }\) whose block-off-diagonal matrix \(\mathtt {J}_2 F^{(1)}\) has size \({\mathcal {O}}(\mu \epsilon , \mu ^3)\) and \(\mathtt {J}_2 E^{(1)} \) has the same form (2.36), and therefore possesses Benjamin-Feir unstable eigenvalues as well. This transformation is inspired by the Jordan normal form of \( \mathtt {L}_{0,\epsilon }\).
2. Second step of block-diagonalization (Sect.5.2). We next perform a step of block-diagonalization to decrease further the size of the off-diagonal blocks: by applying a procedure inspired by KAM theory we obtain (at least) a \( {\mathcal {O}}( \mu ^2 ) \) factor in each entries of \( F^{(2)} \) in (5.14) (by contrast note the presence of \( {\mathcal {O}}(\mu \epsilon ) \) entries in \(F^{(1)}\)). To achieve this, we construct a linear change of variables that conjugates the matrix \(\mathtt {L}^{(1)}_{\mu ,\epsilon }\) to the new Hamiltonian and reversible matrix \( \mathtt {L}_{\mu ,\epsilon }^{(2)} \) in (5.13), where the new off-diagonal matrix \(\mathtt {J}_2 F^{(2)}\) is much smaller than \(\mathtt {J}_2 F^{(1)}\). The delicate point, for which we perform Step 2 separately than Step 3, is to estimate the new block-diagonal matrices after the conjugation, and prove that \(\mathtt {J}_2 E^{(2)}\) has still the form (2.36) – thus possessing Benjamin-Feir unstable eigenvalues. Let us elaborate on this. In order to reduce the size of \(\mathtt {J}_2 F^{(1)} \), we conjugate \(\mathtt {L}_{\mu ,\epsilon }^{(1)}\) by the symplectic matrix \(\exp (S^{(1)})\), where \(S^{(1)}\) is a Hamiltonian matrix with the same form of \( \mathtt {J}_2 F^{(1)} \), see (5.12). The transformed matrix \(\mathtt {L}_{\mu ,\epsilon }^{(2)} = \exp (S^{(1)}) \mathtt {L}_{\mu ,\epsilon }^{(1)}\exp (-S^{(1)}) \) has the Lie expansionFootnote 3

The first line in the right hand side of (2.37) is the original block-diagonal matrix, the second line of (2.37) is a purely off-diagonal matrix and the third line is the sum of two block-diagonal matrices and “h.o.t.” collects terms of much smaller size. We determine \(S^{(1)}\) in such a way that the second line of (2.37) vanishes (this equation would be referred to as the “homological equation” in the context of KAM theory). In this way the remaining off-diagonal matrices (appearing in the h.o.t. remainder) are much smaller in size. We then compute the block-diagonal corrections in the third line of (2.37) and show that the new block-diagonal matrix \( \mathtt {J}_2 E^{(2)} \) has again the form (2.36) (clearly with different remainders, but of the same order) and thus displays Benjamin-Feir instability. This last step is delicate because \(S^{(1)} = {\mathcal {O}}(\epsilon , \mu ^2)\) and \(\mathtt {J}_2 F^{(1)} = {\mathcal {O}}( \mu \epsilon , \mu ^3 )\) and so the matrix in the third line of (2.37) could a priori have elements of size \({\mathcal {O}}(\mu \epsilon ^2)\). Adding a term of size \({\mathcal {O}}(\mu \epsilon ^2)\) to the (1,2)-entry of the matrix \(\mathtt {J}_2 E^{(1)}\), which has the form \( -\frac{\mu ^2}{8}(1+r_5(\epsilon ,\mu )) \) as in (2.36), could make it positive. In such a case the eigenvalues of \(\mathtt {J}_2 E^{(2)}\) would be purely imaginary, and the Benjamin-Feir instability would disappear. Actually, estimating individually each components, we show that no contribution of size \({\mathcal {O}}(\mu \epsilon ^2)\) appears in the (1,2)-entry.
One further comment is needed. We solve the required homological equation without diagonalizing \(\mathtt {J}_2 E^{(1)}\) and \(\mathtt {J}_2 G^{(1)}\) (as done typically in KAM theory). Note that diagonalization is not even possible at \(\mu \sim 2 \sqrt{2}\epsilon \) where \(\mathtt {J}_2 E^{(1)}\) becomes a Jordan block (here its eigenvalues fail to be analytic). We use a direct linear algebra argument that enables to preserve the analyticity in \(\mu , \epsilon \) of the transformed \(4\times 4\) matrix \(\mathtt {L}^{(2)}_{\mu ,\epsilon }\).
3. Complete block-diagonalization (Sect. 5.3). As a last step in Lemma 5.8 we perform, by means of a standard implicit function theorem, a symplectic and reversibility preserving transformation that block-diagonalize \(\mathtt {L}^{(2)}_{\mu ,\epsilon }\) completely. The invertibility properties and estimates required to apply the implicit function theorem rely on the solution of the homological equation obtained in Step 2. The off-diagonal matrix \(\mathtt {J}_2 F^{(2)}\) is small enough to directly prove that the block-diagonal matrix \( \mathtt {J}_2 E^{(3)} \) has the same form of \( \mathtt {J}_2 E^{(2)} \), thus possesses Benjamin-Feir unstable eigenvalues (without distinguishing the entries as we do in Step 2).
In conclusion, the original matrix \(\mathtt {L}_{\mu ,\epsilon }\) in (2.35) has been conjugated to the Hamiltonian and reversible matrix (2.32). This proves Theorem 2.3 and Theorem 1.1.
3 Perturbative approach to the separated eigenvalues
In this section we apply Kato’s similarity transformation theory [34, I-§4-6, II-§4] to study the splitting of the eigenvalues of \( {\mathcal {L}}_{\mu ,\epsilon } \) close to 0 for small values of \( \mu \) and \( \epsilon \). First of all it is convenient to decompose the operator \( {\mathcal {L}}_{\mu ,\epsilon }\) in (2.18) as
where, using also (2.23),
The operator \({{\mathscr {L}}}_{\mu ,\epsilon }\) is still Hamiltonian, having the form

with  selfadjoint, and it is also reversible, namely it satisfies, by (2.20),
selfadjoint, and it is also reversible, namely it satisfies, by (2.20),
whereas  is reversibility-preserving, i.e. fulfills (2.22). Note also that
is reversibility-preserving, i.e. fulfills (2.22). Note also that  is a real operator.
is a real operator.
The scalar operator \( \mathrm {i}\,\mu \equiv \mathrm {i}\,\mu \, \text {Id}\) just translates the spectrum of \( {{\mathscr {L}}}_{\mu ,\epsilon }\) along the imaginary axis of the quantity \( \mathrm {i}\,\mu \), that is, in view of (3.1),
Thus in the sequel we focus on studying the spectrum of \( {{\mathscr {L}}}_{\mu ,\epsilon }\).
Note also that \({{\mathscr {L}}}_{0,\epsilon } = {\mathcal {L}}_{0,\epsilon }\) for any \(\epsilon \ge 0\). In particular \({{\mathscr {L}}}_{0,0}\) has zero as isolated eigenvalue with algebraic multiplicity 4, geometric multiplicity 3 and generalized kernel spanned by the vectors \(\{f^+_1, f^-_1, f^+_0, f^-_0\}\) in (2.27), (2.28). Furthermore its spectrum is separated as in (2.29). For any \(\epsilon \ne 0\) small, \({{\mathscr {L}}}_{0,\epsilon }\) has zero as isolated eigenvalue with geometric multiplicity 2, and two generalized eigenvectors satisfying (2.30).
We also remark that, in view of (2.23), the operator \({{\mathscr {L}}}_{\mu ,\epsilon }\) is linear in \(\mu \). We remind that \( {{\mathscr {L}}}_{\mu ,\epsilon } : Y \subset X \rightarrow X \) has domain \(Y:=H^1({\mathbb {T}}):=H^1({\mathbb {T}},{\mathbb {C}}^2)\) and range \(X:=L^2({\mathbb {T}}):=L^2({\mathbb {T}},{\mathbb {C}}^2)\).
In the next lemma we construct the transformation operators which map isomorphically the unperturbed spectral subspace into the perturbed ones.
Lemma 3.1
Let \(\Gamma \) be a closed, counterclockwise-oriented curve around 0 in the complex plane separating \(\sigma '\left( {{\mathscr {L}}}_{0,0}\right) =\{0\}\) and the other part of the spectrum \(\sigma ''\left( {{\mathscr {L}}}_{0,0}\right) \) in (2.29). There exist \(\epsilon _0, \mu _0>0\) such that for any \((\mu , \epsilon ) \in B(\mu _0)\times B(\epsilon _0)\) the following statements hold:
-
1.
The curve \(\Gamma \) belongs to the resolvent set of the operator \({{\mathscr {L}}}_{\mu ,\epsilon } : Y \subset X \rightarrow X \) defined in (3.2).
-
2.
The operators
$$\begin{aligned} P_{\mu ,\epsilon } := -\frac{1}{2\pi \mathrm {i}\,}\oint _\Gamma ({{\mathscr {L}}}_{\mu ,\epsilon }-\lambda )^{-1} \mathrm {d}\lambda : X \rightarrow Y \end{aligned}$$(3.5)are well defined projectors commuting with \({{\mathscr {L}}}_{\mu ,\epsilon }\), i.e.
$$\begin{aligned} P_{\mu ,\epsilon }^2 = P_{\mu ,\epsilon } \, , \quad P_{\mu ,\epsilon }{{\mathscr {L}}}_{\mu ,\epsilon } = {{\mathscr {L}}}_{\mu ,\epsilon } P_{\mu ,\epsilon } \, . \end{aligned}$$(3.6)The map \((\mu , \epsilon )\mapsto P_{\mu ,\epsilon }\) is analytic from \(B({\mu _0})\times B({\epsilon _0})\) to \( {\mathcal {L}}(X, Y)\).
-
3.
The domain Y of the operator \({{\mathscr {L}}}_{\mu ,\epsilon }\) decomposes as the direct sum
$$\begin{aligned} Y= {\mathcal {V}}_{\mu ,\epsilon } \oplus \text {Ker}(P_{\mu ,\epsilon }) \, , \quad {\mathcal {V}}_{\mu ,\epsilon }:=\text {Rg}(P_{\mu ,\epsilon })=\text {Ker}(\mathrm {Id}-P_{\mu ,\epsilon }) \, , \end{aligned}$$(3.7)of the closed subspaces \({\mathcal {V}}_{\mu ,\epsilon } \), \( \text {Ker}(P_{\mu ,\epsilon }) \) of Y, which are invariant under \({{\mathscr {L}}}_{\mu ,\epsilon }\),
$$\begin{aligned} {{\mathscr {L}}}_{\mu ,\epsilon } : {\mathcal {V}}_{\mu ,\epsilon } \rightarrow {\mathcal {V}}_{\mu ,\epsilon } \, , \qquad {{\mathscr {L}}}_{\mu ,\epsilon } : \text {Ker}(P_{\mu ,\epsilon }) \rightarrow \text {Ker}(P_{\mu ,\epsilon }) \, . \end{aligned}$$Moreover
$$\begin{aligned} \begin{aligned}&\sigma ({{\mathscr {L}}}_{\mu ,\epsilon })\cap \{ z \in {\mathbb {C}} \text{ inside } \Gamma \} = \sigma ({{\mathscr {L}}}_{\mu ,\epsilon }\vert _{{{\mathcal {V}}}_{\mu ,\epsilon }} ) = \sigma '({{\mathscr {L}}}_{\mu , \epsilon }) , \\&\sigma ({{\mathscr {L}}}_{\mu ,\epsilon })\cap \{ z \in {\mathbb {C}} \text{ outside } \Gamma \} = \sigma ({{\mathscr {L}}}_{\mu ,\epsilon }\vert _{Ker(P_{\mu ,\epsilon })} ) = \sigma ''( {{\mathscr {L}}}_{\mu , \epsilon }) \ , \end{aligned} \end{aligned}$$(3.8)proving the “semicontinuity property” (2.31) of separated parts of the spectrum.
-
4.
The projectors \(P_{\mu ,\epsilon }\) are similar one to each other: the transformation operatorsFootnote 4
$$\begin{aligned} U_{\mu ,\epsilon } := \big ( \mathrm {Id}-(P_{\mu ,\epsilon }-P_{0,0})^2 \big )^{-1/2} \big [ P_{\mu ,\epsilon }P_{0,0} + (\mathrm {Id}- P_{\mu ,\epsilon })(\mathrm {Id}-P_{0,0}) \big ] \end{aligned}$$(3.10)are bounded and invertible in Y and in X, with inverse
$$\begin{aligned} U_{\mu ,\epsilon }^{-1} = \big [ P_{0,0} P_{\mu ,\epsilon }+(\mathrm {Id}-P_{0,0}) (\mathrm {Id}- P_{\mu ,\epsilon }) \big ] \big ( \mathrm {Id}-(P_{\mu ,\epsilon }-P_{0,0})^2 \big )^{-1/2} \, , \end{aligned}$$(3.11)and
$$\begin{aligned} U_{\mu ,\epsilon } P_{0,0}U_{\mu ,\epsilon }^{-1} = P_{\mu ,\epsilon } \, , \qquad U_{\mu ,\epsilon }^{-1} P_{\mu ,\epsilon } U_{\mu ,\epsilon } = P_{0,0} \, . \end{aligned}$$(3.12)The map \((\mu , \epsilon )\mapsto U_{\mu ,\epsilon }\) is analytic from \(B(\mu _0)\times B(\epsilon _0)\) to \({\mathcal {L}}(Y)\).
-
5.
The subspaces \({\mathcal {V}}_{\mu ,\epsilon }=\text {Rg}(P_{\mu ,\epsilon })\) are isomorphic one to each other: \( {\mathcal {V}}_{\mu ,\epsilon }= U_{\mu ,\epsilon }{\mathcal {V}}_{0,0}. \) In particular \(\dim {\mathcal {V}}_{\mu ,\epsilon } = \dim {\mathcal {V}}_{0,0}=4 \), for any \((\mu , \epsilon ) \in B(\mu _0)\times B(\epsilon _0)\).
Proof
-
1.
For any \( \lambda \in {\mathbb {C}}\) we decompose
 where \({{\mathscr {L}}}_{0,0} = \begin{bmatrix} \partial _x &{} |D| \\ -1 &{} \partial _x \end{bmatrix}\) and
where \({{\mathscr {L}}}_{0,0} = \begin{bmatrix} \partial _x &{} |D| \\ -1 &{} \partial _x \end{bmatrix}\) and  (3.13)
(3.13)having used also (2.23) and setting \(g(D) := {{\,\mathrm{sgn}\,}}(D) + \Pi _0\). For any \(\lambda \in \Gamma \), the operator \({{\mathscr {L}}}_{0,0}-\lambda \) is invertible and its inverse is the Fourier multiplier matrix operator
$$\begin{aligned} ({{\mathscr {L}}}_{0,0}-\lambda )^{-1} = \text {Op}\left( \frac{1}{(\mathrm {i}\,k-\lambda )^2 + |k|} \begin{bmatrix} \mathrm {i}\,k - \lambda &{} -|k| \\ 1 &{} \mathrm {i}\,k - \lambda \end{bmatrix} \right) : X \rightarrow Y \, . \end{aligned}$$Hence, for \(|\epsilon |<\epsilon _0\) and \(|\mu |<\mu _0\) small enough, uniformly on the compact set \(\Gamma \), the operator
 is bounded, with small operatorial norm. Then \({{\mathscr {L}}}_{\mu ,\epsilon }-\lambda \) is invertible by Neumann series and
is bounded, with small operatorial norm. Then \({{\mathscr {L}}}_{\mu ,\epsilon }-\lambda \) is invertible by Neumann series and  (3.14)
(3.14)This proves that \(\Gamma \) belongs to the resolvent set of \({{\mathscr {L}}}_{\mu ,\epsilon }\).
-
2.
By the previous point the operator \( P_{\mu ,\epsilon } \) is well defined and bounded \( X \rightarrow Y \). It clearly commutes with \({{\mathscr {L}}}_{\mu ,\epsilon }\). The projection property \(P_{\mu ,\epsilon }^2= P_{\mu ,\epsilon }\) is a classical result based on complex integration, see [34], and we omit it. The map
 is analytic. Since the map \(T \mapsto (\text {Id} + T)^{-1}\) is analytic in \({\mathcal {L}}(Y)\) (for \(\Vert T \Vert _{{\mathcal {L}}(Y)} < 1\)) the operators \(({{\mathscr {L}}}_{\mu ,\epsilon }-\lambda )^{-1} \) in (3.14) and \(P_{\mu ,\epsilon }\) in \( {\mathcal {L}}(X,Y) \) are analytic as well with respect to \((\mu ,\epsilon )\).
is analytic. Since the map \(T \mapsto (\text {Id} + T)^{-1}\) is analytic in \({\mathcal {L}}(Y)\) (for \(\Vert T \Vert _{{\mathcal {L}}(Y)} < 1\)) the operators \(({{\mathscr {L}}}_{\mu ,\epsilon }-\lambda )^{-1} \) in (3.14) and \(P_{\mu ,\epsilon }\) in \( {\mathcal {L}}(X,Y) \) are analytic as well with respect to \((\mu ,\epsilon )\). -
3.
The decomposition (3.7) is a consequence of \(P_{\mu ,\epsilon }\) being a continuous projector in \({\mathcal {L}}(Y)\). The invariance of the subspaces follows since \(P_{\mu ,\epsilon }\) and \({{\mathscr {L}}}_{\mu ,\epsilon }\) commute. To prove (3.8) define for an arbitrary \(\lambda _0 \not \in \Gamma \) the operator
$$\begin{aligned} R_{\mu ,\epsilon }(\lambda _0) := - \frac{1}{2\pi \mathrm {i}\,} \oint _\Gamma \frac{1}{\lambda - \lambda _0} \left( {\mathcal {L}}_{\mu ,\epsilon } - \lambda \right) ^{-1} \, \mathrm {d}\lambda \ :\ X \rightarrow Y \ . \end{aligned}$$If \(\lambda _0\) is outside \(\Gamma \), one has \(R_{\mu ,\epsilon }(\lambda _0) ( {{\mathscr {L}}}_{\mu ,\epsilon } - \lambda _0) = ({{\mathscr {L}}}_{\mu ,\epsilon }- \lambda _0)R_{\mu ,\epsilon }(\lambda _0) = P_{\mu ,\epsilon }\) and thus \(\lambda _0 \not \in \sigma ({{\mathscr {L}}}_{\mu ,\epsilon }\vert _{{\mathcal {V}}_{\mu ,\epsilon }})\). For \(\lambda _0\) inside \(\Gamma \), \(R_{\mu ,\epsilon }(\lambda _0) ( {{\mathscr {L}}}_{\mu ,\epsilon } - \lambda _0) = ({{\mathscr {L}}}_{\mu ,\epsilon }- \lambda _0)R_{\mu ,\epsilon }(\lambda _0) = P_{\mu ,\epsilon }- \text {Id}\) and thus \(\lambda _0 \not \in \sigma ({{\mathscr {L}}}_{\mu ,\epsilon }\vert _{Ker(P_{\mu ,\epsilon })})\). Then (3.8) follows.
-
4.
By (3.5), the resolvent identity \( A^{-1} - B^{-1} = A^{-1} (B-A) B^{-1} \) and (3.13), we write
$$\begin{aligned} P_{\mu ,\epsilon } - P_{0,0} = \frac{1}{2\pi \mathrm {i}\,}\oint _\Gamma ({{\mathscr {L}}}_{\mu ,\epsilon }-\lambda )^{-1} {{\mathcal {R}}}_{\mu ,\epsilon } ({{\mathscr {L}}}_{0,0}-\lambda )^{-1} \mathrm {d}\lambda \, . \end{aligned}$$Then \( \Vert P_{\mu ,\epsilon } - P_{0,0} \Vert _{{{\mathcal {L}}}(Y)}<1 \) for \( |\epsilon | < \epsilon _0 \), \( |\mu | < \mu _0 \) small enough and the operators \( U_{\mu ,\epsilon } \) in (3.10) are well defined in \( {\mathcal {L}}(Y)\) (actually \( U_{\mu ,\epsilon } \) are also in \( {\mathcal {L}}(X)\)). The invertibility of \(U_{\mu ,\epsilon }\) and formula (3.12) are proved in [34], Chapter I, Section 4.6, for the pairs of projectors \( Q = P_{\mu ,\epsilon } \) and \( P = P_{0,0} \). The analyticity of \((\mu ,\epsilon ) \mapsto U_{\mu ,\epsilon }\in {\mathcal {L}}(Y)\) follows by the analyticity \((\mu ,\epsilon ) \mapsto P_{\mu ,\epsilon } \in {\mathcal {L}}(Y)\) and of the map \(T \mapsto (\text {Id} - T)^{-\frac{1}{2}}\) in \({\mathcal {L}}(Y)\) for \(\Vert T\Vert _{{\mathcal {L}}(Y)} < 1\).
-
5.
It follows from the conjugation formula (3.12).\(\square \)
The Hamiltonian and reversible nature of the operator \( {{\mathscr {L}}}_{\mu ,\epsilon } \), see (3.3) and (3.4), imply additional algebraic properties for spectral projectors \(P_{\mu ,\epsilon }\) and the transformation operators \(U_{\mu ,\epsilon } \).
Lemma 3.2
For any \((\mu , \epsilon ) \in B(\mu _0)\times B(\epsilon _0)\), the following holds true:
-
(i)
The projectors \(P_{\mu ,\epsilon }\) defined in (3.5) are (complex) skew-Hamiltonian, namely \( {\mathcal {J}}P_{\mu ,\epsilon } \) are skew-Hermitian
$$\begin{aligned} {\mathcal {J}}P_{\mu ,\epsilon }=P_{\mu ,\epsilon }^*{\mathcal {J}}\, , \end{aligned}$$(3.15)and reversibility preserving, i.e. \( {{\overline{\rho }}}P_{\mu ,\epsilon } = P_{\mu ,\epsilon } {{\overline{\rho }}}\).
-
(ii)
The transformation operators \( U_{\mu ,\epsilon } \) in (3.10) are symplectic, namely
$$\begin{aligned} U_{\mu ,\epsilon }^* {\mathcal {J}}U_{\mu ,\epsilon }= {\mathcal {J}}\, , \end{aligned}$$and reversibility preserving.
-
(iii)
\(P_{0,\epsilon }\) and \(U_{0,\epsilon }\) are real operators, i.e. \(\overline{P_{0,\epsilon }}=P_{0,\epsilon }\) and \(\overline{U_{0,\epsilon }}=U_{0,\epsilon }\).
Remark 3.3
The term (complex) skew-Hamiltonian is used in [23, Section 6] for matrices.
Proof
Let \(\gamma :[0,1] \rightarrow {\mathbb {C}}\) be a counter-clockwise oriented parametrization of \(\Gamma \).
- (i):
-
Since \({{\mathscr {L}}}_{\mu ,\epsilon }\) is Hamiltonian, it results \( {{\mathscr {L}}}_{\mu ,\epsilon } {\mathcal {J}}= - {\mathcal {J}}{{\mathscr {L}}}_{\mu ,\epsilon }^* \) on Y. Then, for any scalar \( \lambda \) in the resolvent set of \( {{\mathscr {L}}}_{\mu ,\epsilon } \), the number \( - \lambda \) belongs to the resolvent of \({{\mathscr {L}}}_{\mu ,\epsilon }^* \) and
$$\begin{aligned} {\mathcal {J}}({{\mathscr {L}}}_{\mu ,\epsilon } -\lambda )^{-1} = - ({{\mathscr {L}}}_{\mu ,\epsilon }^*+\lambda )^{-1} {\mathcal {J}}\, . \end{aligned}$$(3.16)Taking the adjoint of (3.5), we have
$$\begin{aligned} P_{\mu ,\epsilon }^* = \frac{1}{2\pi \mathrm {i}\,} \int _0^1 \left( {\mathcal {L}}_{\mu ,\epsilon }^* -{{\overline{\gamma }}}(t)\right) ^{-1} \dot{{\overline{\gamma }}}(t)\mathrm {d}t = \frac{1}{2\pi \mathrm {i}\,} \oint _\Gamma \left( {\mathcal {L}}_{\mu ,\epsilon }^* +\lambda \right) ^{-1} \mathrm {d}\lambda \, , \end{aligned}$$(3.17)because the path \(-{{\overline{\gamma }}} (t) \) winds around the origin clockwise. We conclude that
$$\begin{aligned} {{\mathcal {J}}}P_{\mu ,\epsilon }{\mathop {=}\limits ^{(3.5)}}&-\frac{1}{2\pi \mathrm {i}\,} \oint _\Gamma {\mathcal {J}}\left( {{\mathscr {L}}}_{\mu ,\epsilon } -\lambda \right) ^{-1} \mathrm {d}\lambda \\ {\mathop {=}\limits ^{(3.16)}}&\frac{1}{2\pi \mathrm {i}\,} \oint _\Gamma \left( {{{\mathscr {L}}}}_{\mu ,\epsilon }^* +\lambda \right) ^{-1}{\mathcal {J}}\mathrm {d}\lambda \ {\mathop {=}\limits ^{(3.17)}} P_{\mu ,\epsilon }^* {\mathcal {J}}\, . \end{aligned}$$Let us now prove that \(P_{\mu ,\epsilon }\) is reversibility preserving. By (3.4) one has \( ({{\mathscr {L}}}_{\mu ,\epsilon } - \lambda ) {{\overline{\rho }}} = {{\overline{\rho }}} ( - {{\mathscr {L}}}_{\mu ,\epsilon } - \overline{\lambda })\) and, for any scalar \( \lambda \) in the resolvent set of \( {{\mathscr {L}}}_{\mu ,\epsilon } \), we have \( {{\overline{\rho }}} ({{\mathscr {L}}}_{\mu ,\epsilon } - \lambda )^{-1} = - ( {{\mathscr {L}}}_{\mu ,\epsilon } + {{\overline{\lambda }}} )^{-1} {{\overline{\rho }}} \), using also that \( ({{\overline{\rho }}})^{-1} = {{\overline{\rho }}} \). Thus, recalling (3.5) and (2.21), we have
$$\begin{aligned} {{\overline{\rho }}} P_{\mu ,\epsilon }&=\frac{1}{2\pi \mathrm {i}\,} \int _0^1 -\left( {{\mathscr {L}}}_{\mu ,\epsilon } +\overline{\gamma }(t)\right) ^{-1}\dot{{{\overline{\gamma }}}}(t) \mathrm {d}t \, \overline{\rho }\\&=-\frac{1}{2\pi \mathrm {i}\,} \oint _\Gamma ({{\mathscr {L}}}_{\mu ,\epsilon } - \lambda )^{-1}\mathrm {d}\lambda \, {{\overline{\rho }}} = P_{\mu ,\epsilon } \overline{\rho }\, , \end{aligned}$$because the path \(-{{\overline{\gamma }}} (t) \) winds around the origin clockwise.
- (ii):
-
If an operator A is skew-Hamiltonian then \(A^k\), \(k\in {\mathbb {N}}\), is skew-Hamiltonian as well. As a consequence, being the projectors \(P_{\mu ,\epsilon }\), \(P_{0,0}\) and their difference skew-Hamiltonian, the operator \(\big ( \mathrm {Id}-(P_{\mu ,\epsilon }-P_{0,0})^2 \big )^{-1/2}\) defined as in (3.9) is skew Hamiltonian as well. Hence, by (3.10) we get
$$\begin{aligned} {\mathcal {J}}U_{\mu , \epsilon }&=\left[ \big ( \mathrm {Id}-(P_{\mu ,\epsilon }-P_{0,0})^2 \big )^{-1/2} \right] ^* \\&\quad \times \big [ P_{0,0}P_{\mu ,\epsilon } +(\mathrm {Id}-P_{0,0}) (\mathrm {Id}- P_{\mu ,\epsilon })\big ]^* \ {\mathcal {J}}{\mathop {=}\limits ^{(3.11)}}\ \ U_{\mu ,\epsilon }^{-*} {\mathcal {J}}\end{aligned}$$and therefore \( U_{\mu ,\epsilon }^{*} {\mathcal {J}}U_{\mu , \epsilon } = {\mathcal {J}}\). Finally the operator \(U_{\mu ,\epsilon }\) defined in (3.10) is reversibility-preserving just as \({{\overline{\rho }}}\) commutes with \(P_{\mu ,\epsilon }\) and \(P_{0,0}\).
- (iii):
-
By (3.5) and since \({{\mathscr {L}}}_{0,\epsilon }\) is a real operator, we have
$$\begin{aligned} \overline{P_{0,\epsilon }} = \frac{1}{2\pi \mathrm {i}\,} \int _0^1 \left( {{\mathscr {L}}}_{0,\epsilon } -\overline{\gamma }(t)\right) ^{-1}\dot{{{\overline{\gamma }}}}(t) \mathrm {d}t = - \frac{1}{2\pi \mathrm {i}\,} \oint _\Gamma \left( {{\mathscr {L}}}_{0,\epsilon } - \lambda \right) ^{-1} \mathrm {d}\lambda = P_{0,\epsilon } \end{aligned}$$because the path \({{\overline{\gamma }}} (t) \) winds around the origin clockwise, proving that the operator \(P_{0,\epsilon }\) is real. Then the operator \(U_{0,\epsilon }\) defined in (3.10) is real as well.\(\square \)
By the previous lemma, the linear involution \({{\overline{\rho }}}\) commutes with the spectral projectors \(P_{\mu ,\epsilon }\) and then \({{\overline{\rho }}}\) leaves invariant the subspaces \( {\mathcal {V}}_{\mu ,\epsilon } = \text {Rg}(P_{\mu ,\epsilon }) \).
Let us discuss the implications of the previous lemma in the setting of complex symplectic structures, presented for example in [3, 21]. The infinite dimensional complex space \( L^2 ({\mathbb {T}}, {\mathbb {C}}^2) \), with scalar product (2.19), is equipped with the complex symplectic form

which is sesquilinear, skew-Hermitian and non-degenerate, cfr. Definition 1 in [21]. The skew-Hamiltonian property (3.15) of the projector \( P_{\mu ,\epsilon } \) implies the following lemma.
Lemma 3.4
For any \( (\mu ,\epsilon )\), the linear subspace \( {\mathcal {V}}_{\mu ,\epsilon } = \text {Rg}(P_{\mu ,\epsilon }) \) is a complex symplectic subspace of \(L^2 ({\mathbb {T}}, {\mathbb {C}}^2) \), namely the symplectic form  in (3.18), restricted to \( {\mathcal {V}}_{\mu ,\epsilon } \), is non-degenerate.
in (3.18), restricted to \( {\mathcal {V}}_{\mu ,\epsilon } \), is non-degenerate.
Proof
Let \( {{\tilde{f}}} \in {\mathcal {V}}_{\mu ,\epsilon } \), thus \({{\tilde{f}}} = P_{\mu ,\epsilon } {{\tilde{f}}}\). Suppose that  for any \( {{\tilde{g}}} = P_{\mu ,\epsilon } g \in {\mathcal {V}}_{\mu ,\epsilon } \), \( g \in L^2 ({\mathbb {T}}, {\mathbb {C}}^2) \). Thus
for any \( {{\tilde{g}}} = P_{\mu ,\epsilon } g \in {\mathcal {V}}_{\mu ,\epsilon } \), \( g \in L^2 ({\mathbb {T}}, {\mathbb {C}}^2) \). Thus

We deduce that \( {\mathcal {J}}{{\tilde{f}}} = 0 \) and then \( {{\tilde{f}}} = 0 \). \(\square \)
Remark 3.5
In view of Lemma 3.2-(ii) the transformation operator \( U_{\mu ,\epsilon } \) is symplectic, namely preserves the symplectic form (3.18), i.e.  , for any \( f, g \in L^2 ({\mathbb {T}}, {\mathbb {C}}^2) \).
, for any \( f, g \in L^2 ({\mathbb {T}}, {\mathbb {C}}^2) \).
Symplectic and reversible basis of \({\mathcal {V}}_{\mu ,\epsilon }\). It is convenient to represent the Hamiltonian and reversible operator \( {{\mathscr {L}}}_{\mu ,\epsilon } : {\mathcal {V}}_{\mu ,\epsilon } \rightarrow {\mathcal {V}}_{\mu ,\epsilon } \) in a basis which is symplectic and reversible, according to the following definition.
Definition 3.6
(Symplectic and reversible basis) A basis \(\mathtt {F}:=\{\mathtt {f}^+_1,\,\mathtt {f}^-_1,\,\mathtt {f}^+_0,\mathtt {f}^-_0 \}\) of \({\mathcal {V}}_{\mu ,\epsilon }\) is
-
symplectic if, for any \( k, k' = 0,1 \),
$$\begin{aligned} \begin{aligned}&\left( {\mathcal {J}}\mathtt {f}_k^-\,,\,\mathtt {f}_k^+\right) = 1 \, , \ \ \big ( {\mathcal {J}}\mathtt {f}_k^\sigma , \mathtt {f}_k^\sigma \big ) = 0 \, , \ \forall \sigma = \pm \, ; \\&\quad \text {if} \ k \ne k' \ \text {then} \ \big ( {\mathcal {J}}\mathtt {f}_k^\sigma , \mathtt {f}_{k'}^{\sigma '} \big ) = 0 \, , \ \forall \sigma , \sigma ' = \pm \, . \end{aligned} \end{aligned}$$(3.19) -
reversible if
$$\begin{aligned} \begin{aligned}&{{\overline{\rho }}} \mathtt {f}^+_1 = \mathtt {f}^+_1 , \quad {{\overline{\rho }}} \mathtt {f}^-_1 = - \mathtt {f}^-_1 , \quad {{\overline{\rho }}} \mathtt {f}^+_0 = \mathtt {f}^+_0 , \quad {{\overline{\rho }}} \mathtt {f}^-_0 = - \mathtt {f}^-_0, \\&\text {i.e. } {{\overline{\rho }}}\mathtt {f}_k^\sigma = \sigma \mathtt {f}_k^\sigma \, , \ \forall \sigma = \pm , k = 0,1 \, . \end{aligned} \end{aligned}$$(3.20)
Remark 3.7
By Remark 3.5, the operator \(U_{\mu ,\epsilon }\) maps a symplectic basis in a symplectic basis.
In the next lemma we outline a property of a reversible basis. We use the following notation along the paper: we denote by even(x) a real \(2\pi \)-periodic function which is even in x, and by odd(x) a real \(2\pi \)-periodic function which is odd in x.
Lemma 3.8
The real and imaginary parts of the elements of a reversible basis \(\mathtt {F}=\{\mathtt {f}^\pm _k \}\), \(k=0,1\), enjoy the following parity properties
Proof
By the definition of the involution \({{\overline{\rho }}}\) in (2.21), we get
The properties of \(\mathtt {f}_k^-\) follow similarly. \(\square \)
We now expand a vector of \( {\mathcal {V}}_{\mu ,\epsilon } \) along a symplectic basis.
Lemma 3.9
Let \(\mathtt {F}= \{ \mathtt {f}_{1}^+, \mathtt {f}_{1}^-, \mathtt {f}_{0}^+, \mathtt {f}_{0 }^- \} \) be a symplectic basis of \( {\mathcal {V}}_{\mu ,\epsilon } \). Then any \(\mathtt {f}\) in \( {\mathcal {V}}_{\mu ,\epsilon }\) has the expansion
Proof
We decompose \( \mathtt {f}= \alpha _{1}^+ \mathtt {f}_{1}^+ + \alpha _{1}^- \mathtt {f}_{1}^- +\alpha _{0}^+ \mathtt {f}_{0}^+ + \alpha _{0}^- \mathtt {f}_{0}^- \) for suitable coefficients \( \alpha _k^\sigma \in {\mathbb {C}}\). By applying \({\mathcal {J}}\), taking the \(L^2\) scalar products with the vectors \( \{ \mathtt {f}_k^\sigma \}_{\sigma = \pm , k=0,1}\), using (3.19) and noting that \( \left( {\mathcal {J}}\mathtt {f}_k^+\,,\,\mathtt {f}_k^-\right) = - 1 \), we get the expression of the coefficients \(\alpha _k^\sigma \) as in (3.22). \(\square \)
We now represent \({{\mathscr {L}}}_{\mu ,\epsilon } :{\mathcal {V}}_{\mu ,\epsilon }\rightarrow {\mathcal {V}}_{\mu ,\epsilon } \) with respect to a symplectic and reversible basis.
Lemma 3.10
The \( 4 \times 4 \) matrix that represents the Hamiltonian and reversible operator  with respect to a symplectic and reversible basis \(\mathtt {F}=\{\mathtt {f}_1^+,\mathtt {f}_1^-,\mathtt {f}_0^+,\mathtt {f}_0^-\} \) of \({\mathcal {V}}_{\mu ,\epsilon }\) is
with respect to a symplectic and reversible basis \(\mathtt {F}=\{\mathtt {f}_1^+,\mathtt {f}_1^-,\mathtt {f}_0^+,\mathtt {f}_0^-\} \) of \({\mathcal {V}}_{\mu ,\epsilon }\) is

is the self-adjoint matrix

The entries of the matrix \(\mathtt {B}_{\mu ,\epsilon }\) are alternatively real or purely imaginary: for any \( \sigma = \pm \), \( k = 0, 1 \),

Proof
Lemma 3.9 implies that

Then the matrix representing the operator \({{\mathscr {L}}}_{\mu ,\epsilon } :{\mathcal {V}}_{\mu ,\epsilon }\rightarrow {\mathcal {V}}_{\mu ,\epsilon } \) with respect to the basis \(\mathtt {F}\) is given by \(\mathtt {J}_4 \mathtt {B}_{\mu ,\epsilon }\) with \(\mathtt {B}_{\mu ,\epsilon }\) in (3.24). The matrix \(\mathtt {B}_{\mu ,\epsilon }\) is selfadjoint because  is a selfadjoint operator. We now prove (3.25). By recalling (2.21) and (2.19) it results
is a selfadjoint operator. We now prove (3.25). By recalling (2.21) and (2.19) it results
Then, by (3.26), since  is reversibility-preserving and (3.20), we get
is reversibility-preserving and (3.20), we get

which proves (3.25). \(\square \)
Remark 3.11
The complex symplectic form  in (3.18) restricted to the symplectic subspace \({\mathcal {V}}_{\mu ,\epsilon }\) is represented, in any symplectic basis (cfr. (3.19)), by the matrix \(\mathtt {J}_4\) in (3.23), acting in \({\mathbb {C}}^4\) with the standard complex scalar product.
in (3.18) restricted to the symplectic subspace \({\mathcal {V}}_{\mu ,\epsilon }\) is represented, in any symplectic basis (cfr. (3.19)), by the matrix \(\mathtt {J}_4\) in (3.23), acting in \({\mathbb {C}}^4\) with the standard complex scalar product.
Hamiltonian and reversible matrices. It is convenient to give a name to the matrices of the form obtained in Lemma 3.10.
Definition 3.12
A \( 2n \times 2n \), \( n = 1,2, \) matrix of the form \(\mathtt {L}=\mathtt {J}_{2n} \mathtt {B}\) is
-
1.
Hamiltonian if \( \mathtt {B}\) is a self-adjoint matrix, i.e. \(\mathtt {B}=\mathtt {B}^*\);
-
2.
Reversible if \(\mathtt {B}\) is reversibility-preserving, i.e. \(\rho _{2n}\circ \mathtt {B}= \mathtt {B}\circ \rho _{2n} \), where
$$\begin{aligned} \rho _4 := \begin{pmatrix}\rho _2 &{} 0 \\ 0 &{} \rho _2\end{pmatrix}, \qquad \rho _2 := \begin{pmatrix} {\mathfrak {c}} &{} 0 \\ 0 &{} - {\mathfrak {c}} \end{pmatrix}, \end{aligned}$$(3.27)and \({\mathfrak {c}}: z \mapsto {{\overline{z}}} \) is the conjugation of the complex plane. Equivalently, \(\rho _{2n} \circ \mathtt {L}= - \mathtt {L}\circ \rho _{2n}\).
In the sequel we shall mainly deal with \( 4 \times 4 \) Hamiltonian and reversible matrices. The transformations preserving the Hamiltonian structure are called symplectic, and satisfy
If Y is symplectic then \(Y^*\) and \(Y^{-1}\) are symplectic as well. A Hamiltonian matrix \(\mathtt {L}=\mathtt {J}_4 \mathtt {B}\), with \(\mathtt {B}=\mathtt {B}^*\), is conjugated through Y in the new Hamiltonian matrix
Note that the matrix \( \rho _4 \) in (3.27) represents the action of the involution \({{\overline{\rho }}} : {{\mathcal {V}}}_{\mu ,\epsilon } \rightarrow {{\mathcal {V}}}_{\mu ,\epsilon } \) defined in (2.21) in a reversible basis (cfr. (3.20)). A \( 4\times 4\) matrix \(\mathtt {B}=(\mathtt {B}_{ij})_{i,j=1,\dots ,4}\) is reversibility-preserving if and only if its entries are alternatively real and purely imaginary, namely \(\mathtt {B}_{ij}\) is real when \(i+j\) is even and purely imaginary otherwise, as in (3.25). A \(4\times 4\) complex matrix \(\mathtt {L}=(\mathtt {L}_{ij})_{i,j=1, \ldots , 4}\) is reversible if and only if \(\mathtt {L}_{ij}\) is purely imaginary when \(i+j\) is even and real otherwise.
In the sequel we shall use that the flow of a Hamiltonian reversibility-preserving matrix is symplectic and reversibility-preserving.
Lemma 3.13
Let \(\Sigma \) be a self-adjoint and reversible matrix, then \(\exp (\tau \mathtt {J}_4 \Sigma )\), \( \tau \in {\mathbb {R}} \), is a reversibility-preserving symplectic matrix.
Proof
The flow \(\varphi (\tau ) := \exp (\tau \mathtt {J}_4 \Sigma )\) solves \( \frac{d}{d\tau } \varphi (\tau ) := \mathtt {J}_4 \Sigma \varphi (\tau ) \), with \(\varphi (0) = \mathrm {Id}\). Then \( \psi (\tau ) := \varphi (\tau )^* \mathtt {J}_4 \varphi (\tau ) -\mathtt {J}_4\) satisfies \(\psi (0)=0\) and \(\frac{d}{d\tau } \psi (\tau )= \varphi (\tau )^*\mathtt {J}_4^*\mathtt {J}_4 \varphi (\tau )+ \varphi (\tau )^* \mathtt {J}_4\mathtt {J}_4 \varphi (\tau ) = 0 \, . \) Then \( \psi (\tau ) = 0 \) for any \( \tau \) and \(\varphi (\tau ) \) is symplectic.
The matrix \(\exp (\tau \mathtt {J}_4 \Sigma ) = \sum _{n \ge 0} \frac{1}{n!} ( \tau \mathtt {J}_4 \Sigma )^n \) is reversibility-preserving since each \((\mathtt {J}_4 \Sigma )^n\), \( n \ge 0 \), is reversibility-preserving. \(\square \)
4 Matrix representation of \( {{\mathscr {L}}}_{\mu ,\epsilon }\) on \( {\mathcal {V}}_{\mu ,\epsilon }\)
In this section we use the transformation operators \(U_{\mu ,\epsilon }\) obtained in the previous section to construct a symplectic and reversible basis of \({\mathcal {V}}_{\mu ,\epsilon }\) and, in Proposition 4.4, we compute the \(4\times 4\) Hamiltonian and reversible matrix representing \( {{\mathscr {L}}}_{\mu ,\epsilon }:{\mathcal {V}}_{\mu ,\epsilon } \rightarrow {\mathcal {V}}_{\mu ,\epsilon }\) on such basis.
First basis of \({\mathcal {V}}_{\mu ,\epsilon }\). In view of Lemma 3.1, the first basis of \({\mathcal {V}}_{\mu ,\epsilon }\) that we consider is

obtained applying the transformation operators \( U_{\mu ,\epsilon } \) in (3.10) to the vectors
which form a basis of \( {\mathcal {V}}_{0,0} =\mathrm {Rg} (P_{0,0}) \), cfr. (2.27)-(2.28). Note that the real valued vectors \( \{ f_1^\pm , f_0^\pm \} \) are orthonormal with respect to the scalar product (2.19), and satisfy
thus forming a symplectic and reversible basis for \( {\mathcal {V}}_{0,0} \), according to Definition 3.6.
In view of Remarks 3.5 and 3.7, the symplectic operators \( U_{\mu ,\epsilon } \) transform, for any \( (\mu , \epsilon ) \) small, the symplectic basis (4.2) of \( {\mathcal {V}}_{0,0} \), into the symplectic basis (4.1):
Lemma 4.1
The basis \( {{\mathcal{{F}}}} \) of \({\mathcal {V}}_{\mu ,\epsilon }\) defined in (4.1), is symplectic and reversible, i.e. satisfies (3.19) and (3.20). Each map \((\mu , \epsilon ) \mapsto f^\sigma _k(\mu , \epsilon )\) is analytic as a map \(B(\mu _0)\times B(\epsilon _0) \rightarrow H^1({\mathbb {T}})\).
Proof
Since by Lemma 3.2-(ii) the maps \( U_{\mu ,\epsilon } \) are symplectic and reversibility-preserving the transformed vectors \( f_{1}^+(\mu ,\epsilon ),\dots ,f_{0}^-(\mu ,\epsilon ) \) are symplectic orthogonals and reversible as well as the unperturbed ones \( f_1^+,\dots , f_0^- \). The analyticity of \(f^\sigma _k(\mu , \epsilon )\) follows from the analyticity property of \(U_{\mu , \epsilon }\) proved in Lemma 3.1. \(\square \)
In the next lemma we provide a suitable expansion of the vectors \( f_k^\sigma (\mu ,\epsilon ) \) in \( (\mu , \epsilon ) \). We denote by \(even_0(x)\) a real, even, \(2\pi \)-periodic function with zero space average. In the sequel \({\mathcal {O}}(\mu ^{m} \epsilon ^{n}) \small \begin{bmatrix}even(x) \\ odd(x) \end{bmatrix}\) denotes an analytic map in \((\mu , \epsilon )\) with values in \( H^1({\mathbb {T}}, {\mathbb {C}}^2) \), whose first component is even(x) and the second one odd(x); similar meaning for \({\mathcal {O}}(\mu ^{m} \epsilon ^{n}) \small \begin{bmatrix}odd(x) \\ even(x) \end{bmatrix}\), etc...
Lemma 4.2
(Expansion of the basis  ) For small values of \((\mu , \epsilon )\) the basis
) For small values of \((\mu , \epsilon )\) the basis  in (4.1) has the following expansion
in (4.1) has the following expansion
where the remainders \({\mathcal {O}}()\) are vectors in \(H^1({\mathbb {T}})\). For \(\mu =0\) the basis \(\{f_k^\pm (0,\epsilon ), k=0,1 \} \) is real and
Proof
The long calculations are given in Appendix A. \(\square \)
Second basis of \({\mathcal {V}}_{\mu ,\epsilon }\). We now construct from the basis  in (4.1) another symplectic and reversible basis of \({\mathcal {V}}_{\mu ,\epsilon }\) with an additional property. Note that the second component of the vector \(f_1^-(0,\epsilon )\) is an even function whose space average is not necessarily zero, cfr. (4.8). Thus we introduce the new symplectic and reversible basis of \({\mathcal {V}}_{\mu ,\epsilon }\)
in (4.1) another symplectic and reversible basis of \({\mathcal {V}}_{\mu ,\epsilon }\) with an additional property. Note that the second component of the vector \(f_1^-(0,\epsilon )\) is an even function whose space average is not necessarily zero, cfr. (4.8). Thus we introduce the new symplectic and reversible basis of \({\mathcal {V}}_{\mu ,\epsilon }\)
defined by
with
Note that \(n(\mu ,\epsilon )\) is real, because, in view of (3.26) and Lemma 4.1,
This new basis has the property that \(g_1^-(0,\epsilon )\) has zero average, see (4.21). We shall exploit this feature crucially in Lemma 4.7, see remark 4.8.
Lemma 4.3
The basis \({\mathcal {G}}\) in (4.9) is symplectic and reversible, i.e. it satisfies (3.19) and (3.20). Each map \((\mu , \epsilon ) \mapsto g^\sigma _k(\mu , \epsilon )\) is analytic as a map \(B(\mu _0)\times B(\epsilon _0) \rightarrow H^1({\mathbb {T}}, {\mathbb {C}}^2)\).
Proof
The vectors \(g_k^\pm (\mu ,\epsilon ) \), \(k=0,1\) satisfy (3.19) and (3.20) because \(f_k^\pm (\mu ,\epsilon ) \), \(k=0,1\) satisfy the same properties as well, and \(n(\mu ,\epsilon )\) is real. The analyticity of \(g^\sigma _k(\mu , \epsilon )\) follows from the corresponding property of the basis  . \(\square \)
. \(\square \)
We now state the main result of this section.
Proposition 4.4
The matrix that represents the Hamiltonian and reversible operator \( {{\mathscr {L}}}_{\mu ,\epsilon } : {\mathcal {V}}_{\mu ,\epsilon } \rightarrow {\mathcal {V}}_{\mu ,\epsilon } \) in the symplectic and reversible basis \({\mathcal {G}}\) of \({\mathcal {V}}_{\mu ,\epsilon }\) defined in (4.9), is a Hamiltonian matrix \(\mathtt {L}_{\mu ,\epsilon }=\mathtt {J}_4 \mathtt {B}_{\mu ,\epsilon }\), where \(\mathtt {B}_{\mu ,\epsilon } \) is a self-adjoint and reversibility preserving (i.e. satisfying (3.25)) \( 4 \times 4\) matrix of the form
where E, F, G are the \( 2 \times 2 \) matrices
The rest of this section is devoted to the proof of Proposition 4.4. The first step is to provide the following expansion in \((\mu ,\epsilon )\) of the basis \({\mathcal {G}}\).
Lemma 4.5
(Expansion of the basis \({\mathcal {G}}\)) For small values of \((\mu ,\epsilon ) \), the basis \( {{\mathcal {G}}}\) defined in (4.9) has the following expansion
In particular, at \(\mu =0\), the basis \( \{ g^\sigma _k (0,\epsilon ), \sigma = \pm , k =0 ,1 \} \) is real,
and, for any \(\epsilon \),
Proof
First note that, by (4.8), \( \small f_0^-(0,\epsilon ) = \begin{bmatrix}0 \\ 1 \end{bmatrix} \), and thus \(g_1^-(0,\epsilon ) \) in (4.9) reduces to
which satisfies (4.21), recalling also that the first component of \( f_1^-(0,\epsilon ) \) is odd. In order to prove (4.16)-(4.19) we note that \(n(\mu ,\epsilon )\) in (4.10) is real by (4.11), and satisfies, by (4.5), (4.7),
Hence, in view of (4.4)-(4.7), the vectors \( g^\sigma _k (\mu ,\epsilon ) \) satisfy the expansion (4.16)-(4.19). Finally at \(\mu =0\) the vectors \(g^\pm _k(0,\epsilon )\), \(k = 0,1\), are real being real linear combinations of real vectors. \(\square \)
We start now the proof of Proposition 4.4. It is useful to decompose  in (3.3) as
in (3.3) as

where  ,
,  ,
,  are the self-adjoint and reversibility preserving operators
are the self-adjoint and reversibility preserving operators



Note that the operators  ,
,  are linear in \( \mu \). In order to prove (4.12)- (4.15) we exploit the representation Lemma 3.10 and compute perturbatively the \( 4 \times 4 \) matrices, associated, as in (3.24), to the self-adjoint and reversibility preserving operators
are linear in \( \mu \). In order to prove (4.12)- (4.15) we exploit the representation Lemma 3.10 and compute perturbatively the \( 4 \times 4 \) matrices, associated, as in (3.24), to the self-adjoint and reversibility preserving operators  ,
,  and
and  , in the basis \({\mathcal {G}} \).
, in the basis \({\mathcal {G}} \).
Lemma 4.6
(Expansion of \(\mathtt {B}_\epsilon \)) The self-adjoint and reversibility preserving matrix \(\mathtt {B}_\epsilon := \mathtt {B}_\epsilon (\mu )\) associated, as in (3.24), with the self-adjoint and reversibility preserving operator  , defined in (4.22), with respect to the basis \({\mathcal {G}} \) of \( {{\mathcal {V}}}_{\mu ,\epsilon } \) in (4.9), expands as
, defined in (4.22), with respect to the basis \({\mathcal {G}} \) of \( {{\mathcal {V}}}_{\mu ,\epsilon } \) in (4.9), expands as

Proof
We expand the matrix \( \mathtt {B}_\epsilon (\mu ) \) as
To simplify notation, during this proof we often identify a matrix with its matrix elements.
The matrix \(\mathtt {B}_\epsilon (0)\). The main result of this long paragraph is to prove that the matrix \(\mathtt {B}_\epsilon (0)\) has the expansion (4.30). The matrix \(\mathtt {B}_\epsilon (0)\) is real, because the operator  is real and the basis \( \{ g_k^\pm (0,\epsilon ) \}_{k=0,1}\) is real. Consequently, by (3.25), its matrix elements \((\mathtt {B}_\epsilon (0))_{i,j}\) are real whenever \(i+j\) is even and vanish for \(i+j\) odd. In addition \(g^-_0(0,\epsilon ) = \small \begin{bmatrix}0 \\ 1 \end{bmatrix}\) by (4.20), and, by (4.22), we get
is real and the basis \( \{ g_k^\pm (0,\epsilon ) \}_{k=0,1}\) is real. Consequently, by (3.25), its matrix elements \((\mathtt {B}_\epsilon (0))_{i,j}\) are real whenever \(i+j\) is even and vanish for \(i+j\) odd. In addition \(g^-_0(0,\epsilon ) = \small \begin{bmatrix}0 \\ 1 \end{bmatrix}\) by (4.20), and, by (4.22), we get  , for any \( \epsilon \). We deduce that the self-adjoint matrix \( \mathtt {B}_\epsilon (0) \) has the form
, for any \( \epsilon \). We deduce that the self-adjoint matrix \( \mathtt {B}_\epsilon (0) \) has the form

with \({\mathtt {a}}\), \({\mathtt {b}}\), \({\mathtt {c}}\), \(\alpha \) real numbers depending on \(\epsilon \). We claim that \( {\mathtt {b}}= 0 \) for any \( \epsilon \). As a first step we prove that
Indeed, by Theorem 4.1 in [43], the operator \( {{\mathscr {L}}}_{0,\epsilon } \equiv {{\mathcal {L}}}_{0,\epsilon }\) possesses, for any sufficiently small \(\epsilon \ne 0\), the eigenvalue 0 with a four dimensional generalized Kernel \( {\mathcal {W}}_\epsilon := \text {span} \{ U_1, {{\tilde{U}}}_2, U_3, U_4 \} \), spanned by \( \epsilon \)-dependent vectors \( U_1, \tilde{U}_2, U_3, U_4 \) satisfying (2.30). Note that \( U_1, {{\tilde{U}}}_2 \) are eigenvectors, and \( U_3, U_4\) generalized eigenvectors, of \( {{\mathscr {L}}}_{0,\epsilon }\) with eigenvalue 0. By Lemma 3.1 it results that \( {\mathcal {W}}_\epsilon = {{\mathcal {V}}}_{0,\epsilon } = \text {Rg}(P_{0,\epsilon } )\) and by (2.30) we have \( {{\mathscr {L}}}_{0,\epsilon }^2 = 0 \) on \( {\mathcal {V}}_{0,\epsilon } \). Thus the matrix

which represents \( {{\mathscr {L}}}_{0,\epsilon }:{\mathcal {V}}_{0,\epsilon }\rightarrow {\mathcal {V}}_{0,\epsilon }\), satisfies \( \mathtt {L}^2_\epsilon (0) = 0 \), namely

This implies (4.28). We now prove that the matrix \(\mathtt {B}_\epsilon (0)\) defined in (4.27) expands as

We expand the operator  in (4.22) as
in (4.22) as

where the remainder term \({\mathcal {O}}(\epsilon ^3) \in {\mathcal {L}}(Y, X)\) and, by (2.15)-(2.16),
\( \bullet \) Expansion of \({\mathtt {a}}=\epsilon ^2+r(\epsilon ^3)\). By (4.16) we split the real function \(g_1^+(0,\epsilon )\) as
where both \(g_{1_2}^+\) and \({\mathcal {O}}(\epsilon ^3)\) are vectors in \(H^1({\mathbb {T}})\). Since  , and both
, and both  ,
,  are self-adjoint real operators, it results
are self-adjoint real operators, it results

By (4.31) one has

Then the \(\epsilon ^2\)-term of \({\mathtt {a}}\) is  and, by (4.34), (4.35), (4.33), a direct computation gives \({\mathtt {a}}= \epsilon ^2 +r(\epsilon ^3)\) as stated in (4.30).
and, by (4.34), (4.35), (4.33), a direct computation gives \({\mathtt {a}}= \epsilon ^2 +r(\epsilon ^3)\) as stated in (4.30).
In particular, for \(\epsilon \ne 0\) sufficiently small, one has \({\mathtt {a}}\ne 0\) and the second alternative in (4.28) is ruled out, implying \({\mathtt {b}}= 0\).
\( \bullet \) Expansion of \({\mathtt {c}}=1+r(\epsilon ^3)\). By (4.18) we split the real-valued function \(g_0^+(0,\epsilon )\) as
Since, by (2.27) and (4.31),  , and both
, and both  ,
,  are self-adjoint real operators,
are self-adjoint real operators,

where we also used \(\Vert f_0^+\Vert = 1\) and \( (f_0^+ , g_{0_1}^+ )= (f_0^+, g_{0_2}^+ ) =0\). By (4.31), (4.32) one has

Then the \(\epsilon ^2\)-term of \({\mathtt {c}}\) is  and, by (4.36)-(4.38), we conclude that \({\mathtt {c}}= 1 +r(\epsilon ^3)\) as stated in (4.30).
and, by (4.36)-(4.38), we conclude that \({\mathtt {c}}= 1 +r(\epsilon ^3)\) as stated in (4.30).
\( \bullet \) Expansion of \(\alpha ={\mathcal {O}}(\epsilon ^3)\). By (4.33), (4.36) and since  are self-adjoint and real we have
are self-adjoint and real we have

Recalling that  and
and  , we arrive at
, we arrive at

using that, by (4.33), (4.35), (4.36) (4.38), all the scalar products in the formula vanish.
We have proved the expansion (4.30).
Linear terms in \( \mu \). We now compute the terms of \(\mathtt {B}_\epsilon (\mu )\) that are linear in \(\mu \). It results

We now prove that

The matrix \( \mathtt {L}_\epsilon (0) \) in (4.29) where \({\mathtt {b}}=0\), represents the action of the operator \({\mathcal {L}}_{0,\epsilon }:{\mathcal {V}}_{0,\epsilon }\rightarrow {\mathcal {V}}_{0,\epsilon }\) in the basis \( \{ g^{\sigma }_k (0,\epsilon ) \} \) and then we deduce that \( {\mathcal {L}}_{0,\epsilon } g_1^-(0,\epsilon ) = 0 \), \( {\mathcal {L}}_{0,\epsilon } g_0^-(0,\epsilon ) = 0 \). Thus also  ,
,  , for every \(\epsilon \), and the second and the fourth column of the matrix X in (4.40) are zero. In order to compute the other two columns we use the expansion of the derivatives, where denoting with a dot the derivative w.r.t. \(\mu \),
, for every \(\epsilon \), and the second and the fourth column of the matrix X in (4.40) are zero. In order to compute the other two columns we use the expansion of the derivatives, where denoting with a dot the derivative w.r.t. \(\mu \),
that follow by (4.16)-(4.19). In view of (4.3), (4.16)-(4.19), (4.29) and since  , we have
, we have

The other two columns of the matrix X in (4.39) have the expansion (4.40), by (4.41) and (4.42).
Quadratic terms in \( \mu \). By denoting with a double dot the double derivative w.r.t. \(\mu \), we have

We claim that \(Y = 0 \). Indeed, its first, second and fourth column are zero, since  for \(f_k^\sigma \in \{ f_1^+,f_1^-,f_0^- \} \). The third column is also zero by noting that
for \(f_k^\sigma \in \{ f_1^+,f_1^-,f_0^- \} \). The third column is also zero by noting that  and
and
We claim that

Indeed, by (4.41), we have \(\dot{g}^+_0(0,0)=\dot{g}^-_0(0,0)= 0\). Therefore the last two columns of Z, and by self-adjointness the last two rows, are zero. By (4.41), \(\dot{g}^+_1(0,0) = \frac{\mathrm {i}\,}{4}\small \begin{bmatrix}\sin (x) \\ \cos (x) \end{bmatrix}\) and \(\dot{g}^-_1(0,0) = \frac{\mathrm {i}\,}{4} \small \begin{bmatrix}\cos (x) \\ -\sin (x) \end{bmatrix}\), so that  and
and  , and we obtain the matrix (4.44) computing the scalar products.
, and we obtain the matrix (4.44) computing the scalar products.
In conclusion (4.26), (4.39), (4.40), (4.43), the fact that \(Y=0\) and (4.44) imply (4.25), using also the selfadjointness of \(\mathtt {B}_\epsilon \) and (3.25). \(\square \)
We now consider  .
.
Lemma 4.7
(Expansion of \(\mathtt {B}^\flat \)) The self-adjoint and reversibility-preserving matrix \(\mathtt {B}^\flat \) associated, as in (3.24), to the self-adjoint and reversibility-preserving operator  , defined in (4.23), with respect to the basis \({\mathcal {G}}\) of \( {{\mathcal {V}}}_{\mu ,\epsilon } \) in (4.9), admits the expansion
, defined in (4.23), with respect to the basis \({\mathcal {G}}\) of \( {{\mathcal {V}}}_{\mu ,\epsilon } \) in (4.9), admits the expansion

Proof
We have to compute the expansion of the matrix entries 
 . The operator
. The operator  in (4.23) is linear in \(\mu \) and by (4.16), (4.17), (4.21) and the identities \( {{\,\mathrm{sgn}\,}}(D) \sin (kx) = - \mathrm {i}\,\cos (kx) \) and \( {{\,\mathrm{sgn}\,}}(D)\cos (kx) = \mathrm {i}\,\sin (kx) \) for any \( k \in {\mathbb {N}}\), we have
in (4.23) is linear in \(\mu \) and by (4.16), (4.17), (4.21) and the identities \( {{\,\mathrm{sgn}\,}}(D) \sin (kx) = - \mathrm {i}\,\cos (kx) \) and \( {{\,\mathrm{sgn}\,}}(D)\cos (kx) = \mathrm {i}\,\sin (kx) \) for any \( k \in {\mathbb {N}}\), we have

Note that \(\mu \small \begin{bmatrix} 0 &{} 0 \\ 0 &{} \Pi _0 \end{bmatrix}g^-_1(\mu ,\epsilon ) = {\mathcal {O}}(\mu ^3\epsilon , \mu ^2\epsilon ^2)\) thanks to the property (4.21) of the basis \({\mathcal {G}}\).
In addition, by (4.18)-(4.19), we get that

Taking the scalar products of the above expansions of  with the functions \(g^{\sigma '}_{k'}(\mu ,\epsilon ) \) expanded as in (4.16)-(4.19) we deduce (4.45). \(\square \)
with the functions \(g^{\sigma '}_{k'}(\mu ,\epsilon ) \) expanded as in (4.16)-(4.19) we deduce (4.45). \(\square \)
Remark 4.8
The (2, 2) entry in the matrix \( \mathtt {B}^\flat \) in (4.45) has no terms \( {\mathcal {O}}(\mu \epsilon ^k ) \), thanks to property (4.21). This property is fundamental in order to verify that the (2, 2) entry of the matrix E in (4.13) starts with \( - \frac{\mu ^2}{8} \) and therefore it is negative for \( \mu \) small. Such property does not hold for the first basis  defined in (4.1), and this motivates the use of the second basis \({{\mathcal {G}}}\).
defined in (4.1), and this motivates the use of the second basis \({{\mathcal {G}}}\).
Finally we consider  .
.
Lemma 4.9
(Expansion of \(\mathtt {B}^\sharp \)) The self-adjoint and reversibility-preserving matrix \(\mathtt {B}^\sharp \) associated, as in (3.24), to the self-adjoint and reversibility-preserving operators  , defined in (4.24), with respect to the basis \({\mathcal {G}}\) of \( {{\mathcal {V}}}_{\mu ,\epsilon } \) in (4.9), admits the expansion
, defined in (4.24), with respect to the basis \({\mathcal {G}}\) of \( {{\mathcal {V}}}_{\mu ,\epsilon } \) in (4.9), admits the expansion

Proof
Since  and \(p_\epsilon ={\mathcal {O}}(\epsilon )\) by (2.15), we have the expansion
and \(p_\epsilon ={\mathcal {O}}(\epsilon )\) by (2.15), we have the expansion

We claim that the matrix entries  , \( k, k' = 0,1 \) are zero. Indeed they are real by (3.25), and also purely imaginary, since the operator
, \( k, k' = 0,1 \) are zero. Indeed they are real by (3.25), and also purely imaginary, since the operator  is purely imaginaryFootnote 5 and the basis \( \{ g_k^\pm (0,\epsilon ) \}_{k=0,1}\) is real. Hence \(\mathtt {B}^\sharp \) has the form
is purely imaginaryFootnote 5 and the basis \( \{ g_k^\pm (0,\epsilon ) \}_{k=0,1}\) is real. Hence \(\mathtt {B}^\sharp \) has the form

and \(\alpha \), \( \beta \), \( \gamma \), \( \delta \) are real numbers. As  in \({\mathcal {L}}(Y)\), we get immediately that \( \gamma =r( \mu \epsilon ) \) and \( \delta = r(\mu \epsilon ) \). Next we compute the expansion of \(\beta \) and \(\eta \). We split the operator
in \({\mathcal {L}}(Y)\), we get immediately that \( \gamma =r( \mu \epsilon ) \) and \( \delta = r(\mu \epsilon ) \). Next we compute the expansion of \(\beta \) and \(\eta \). We split the operator  in (4.24) as
in (4.24) as

with \(p_1(x)\) in (4.32) and \({\mathcal {O}}(\mu \epsilon ^2) \in {\mathcal {L}}(Y)\). By (4.49) and the expansion (4.16)-(4.19), \(g_1^+(0,\epsilon ) = f_1^+ + {\mathcal {O}}(\epsilon )\), \(g_1^-(0,\epsilon )=f_1^-+{\mathcal {O}}(\epsilon )\), \(g_0^+(0,\epsilon )=f_0^+ +{\mathcal {O}}(\epsilon )\), \(g_0^-(0,\epsilon ) = \small \begin{bmatrix}0 \\ 1 \end{bmatrix}\) we obtain

Computing  ,
,  and the various scalar products with the vectors \(f^\sigma _k\) in (4.2), we get \( \beta =r(\mu \epsilon ^2) \), \( \eta = r(\mu \epsilon ^2) \). Using also (4.47) and (4.48), one gets (4.46). \(\square \)
and the various scalar products with the vectors \(f^\sigma _k\) in (4.2), we get \( \beta =r(\mu \epsilon ^2) \), \( \eta = r(\mu \epsilon ^2) \). Using also (4.47) and (4.48), one gets (4.46). \(\square \)
5 Block-decoupling
The \( 4 \times 4 \) Hamiltonian and reversible matrix \(\mathtt {L}_{\mu ,\epsilon } = \mathtt {J}_4 \mathtt {B}_{\mu ,\epsilon } \) obtained in Proposition 4.4, has the form
where E, G, F are the \( 2 \times 2 \) matrices in (4.13)-(4.15). In particular \(\mathtt {J}_2 E\) has the form
and therefore possesses two eigenvalues with non-zero real part (“Benjamin-Feir” eigenvalues), as long as its two off-diagonal entries have the same sign, see the discussion below (2.36). In order to prove that also the full \( 4 \times 4 \) matrix \( \mathtt {L}_{\mu ,\epsilon } \) in (5.1) possesses Benjamin-Feir unstable eigenvalues, we aim to eliminate the coupling term \( \mathtt {J}_2 F \) by a change of variables. More precisely in this section we conjugate the matrix \(\mathtt {L}_{\mu ,\epsilon }\) in (5.1) to the Hamiltonian and reversible block-diagonal matrix \(\mathtt {L}_{\mu ,\epsilon }^{(3)}\) in (5.35),
where \(\mathtt {J}_2 E^{(3)}\) is a \(2 \times 2\) matrix with the same form as (5.2) (clearly with different remainders, but of the same order). The spectrum of the \( 4 \times 4 \) matrix \( \mathtt {L}_{\mu ,\epsilon }^{(3)}\), which coincides with that of \( \mathtt {L}_{\mu ,\epsilon } \), contains the Benjamin-Feir unstable eigenvalues of the \( 2 \times 2 \) matrix \(\mathtt {J}_2 E^{(3)} \) (it turns out that the two eigenvalues of \( \mathtt {J}_2 G^{(3)}\) are purely imaginary). This will prove Theorem 2.3.
The block-diagonalization of \( \mathtt {L}_{\mu ,\epsilon } \) is achieved in three steps, in Lemma 5.1, Lemma 5.2, and finally Lemma 5.8. Motivations and goals of each step were described at the end of Sect. 2.
5.1 First step of Block-decoupling
We write the matrices E, F, G in (4.12) as
where the real numbers \( E_{ij}, F_{ij}, G_{ij} \), \( i , j = 1,2 \), have the expansion given in (4.13)-(4.15).
Lemma 5.1
Conjugating the Hamiltonian and reversible matrix \(\mathtt {L}_{\mu ,\epsilon } = \mathtt {J}_4 \mathtt {B}_{\mu ,\epsilon } \) obtained in Proposition 4.4 through the symplectic and reversibility-preserving \( 4 \times 4 \)-matrix
where \( m = r(\epsilon ^3, \mu \epsilon ^2, \mu ^2\epsilon , \mu ^3 ) \) is a real number, we obtain the Hamiltonian and reversible matrix
where \( \mathtt {B}_{\mu ,\epsilon }^{(1)} \) is a self-adjoint and reversibility-preserving \( 4 \times 4\) matrix
where the \( 2 \times 2 \) matrices \(E^{(1)} \), \( G^{(1)} \) have the same expansion (4.13)-(4.14) of E, G and
Note that the entry \( F^{(1)}_{11} \) is 0, the other entries of \( F^{(1)}\) have the same size as for F in (4.15).
Proof
The matrix Y is symplectic, i.e. (3.28) holds, and since m is real, it is reversibility preserving, i.e. satisfies (3.25). By (3.29),
where, by (5.4) and (5.3), the self-adjoint matrices \(E^{(1)}, G^{(1)} \) are
Similarly, the off-diagonal \( 2 \times 2 \) matrix \(F^{(1)} \) is
where we have used that the first entry of this matrix is \(F_{11} + m G_{11} = 0 \), by the definition of m in (5.4). By (5.8)-(5.10) and (4.13)-(4.15) we deduce the expansion of \( \mathtt {B}_{\mu ,\epsilon }^{(1)} \) in (5.7), (5.6) and consequently that of (5.5). \(\square \)
5.2 Second step of block-decoupling
We now perform a further step of block decoupling, obtaining the new Hamiltonian and reversible matrix \( \mathtt {L}_{\mu ,\epsilon }^{(2)} \) in (5.13) where the \(2 \times 2 \) matrix \( \mathtt {J}_2 E^{(2)} \) has still the Benjamin-Feir unstable eigenvalues and the size of the new coupling matrix \(\mathtt {J}_2 F^{(2)}\) is much smaller than \(\mathtt {J}_2 F^{(1)}\). In particular note that the entries of \( F^{(2)} \) in (5.14) have size \( {\mathcal {O}}(\mu ^2 \epsilon ^3, \mu ^3 \epsilon ^2, \mu ^5 \epsilon , \mu ^7) \) whereas those of \( F^{(1)} \) in (5.7) are \( {\mathcal {O}}(\mu \epsilon ^3, \mu ^3)\).
Lemma 5.2
(Step of block-decoupling) There exists a \(2\times 2\) reversibility-preserving matrix X, analytic in \( (\mu , \epsilon ) \), of the form
such that, by conjugating the Hamiltonian and reversible matrix \(\mathtt {L}_{\mu ,\epsilon }^{(1)}\), defined in (5.5), with the symplectic and reversibility-preserving \(4\times 4\) matrix
we get the Hamiltonian and reversible matrix
where the \( 2 \times 2 \) self-adjoint and reversibility-preserving matrices \(E^{(2)} \), \( G^{(2)} \) have the same expansion of \( E^{(1)} \), \( G^{(1)} \), namely of E, G, given in (4.13)-(4.14), and
Remark 5.3
The new matrix \( \mathtt {L}_{\mu ,\epsilon }^{(2)} \) in (5.13) is still analytic in \( (\mu , \epsilon )\), as \( \mathtt {L}_{\mu ,\epsilon }^{(1)}\). This is not obvious a priori, since the spectrum of the matrices \( \mathtt {J}_2 E^{(1)} \) and \( \mathtt {J}_2 G^{(1)} \) is shrinking to zero as \( (\mu , \epsilon ) \rightarrow 0 \).
The rest of the section is devoted to the proof of Lemma 5.2. We denote for simplicity \( S = S^{(1)} \).
The matrix \(\text {exp}(S)\) is symplectic and reversibility preserving because the matrix S in (5.12) is Hamiltonian and reversibility preserving, cfr. Lemma 3.13. Note that S is reversibility preserving since X has the form (5.11).
We now expand in Lie series the Hamiltonian and reversible matrix \( \mathtt {L}_{\mu ,\epsilon }^{(2)} = \exp (S)\mathtt {L}_{\mu ,\epsilon }^{(1)} \exp (-S) \).
We split \(\mathtt {L}_{\mu ,\epsilon }^{(1)}\) into its \(2\times 2\)-diagonal and off-diagonal Hamiltonian and reversible matrices
In order to construct a transformation which eliminates the main part of the off-diagonal part \( R^{(1)} \), we conjugate \(\mathtt {L}_{\mu ,\epsilon }^{(1)}\) by a symplectic matrix \(\exp (S)\) generated as the flow of a Hamiltonian matrix S with the same form of \( R^{(1)} \). By a Lie expansion we obtain
where \(\text {ad}_A(B) := [A,B] := AB - BA \) denotes the commutator between linear operators A, B.
We look for a \( 4 \times 4 \) matrix S as in (5.12) which solves the homological equation
which, recalling (5.15), amounts to eliminate the off-diagonal part
Note that the equation \( \mathtt {J}_2F^{(1)}+\mathtt {J}_2\Sigma D_0 - D_1\mathtt {J}_2\Sigma = 0 \) implies also \( \mathtt {J}_2{[F^{(1)}]}^*+\mathtt {J}_2\Sigma ^*D_1-D_0\mathtt {J}_2\Sigma ^* = 0 \) and viceversa. Thus, writing \( \Sigma =\mathtt {J}_2 X \), namely \( X = - \mathtt {J}_2 \Sigma \), the Eq. (5.17) is equivalent to solve the “Sylvester” equation
Recalling (5.15), (5.11) and (5.3), it amounts to solve the \(4\times 4\) real linear system

Recall that, by (5.7), \(F_{11}=0\).
We solve this system using the following result, verified by a direct calculus.
Lemma 5.4
The determinant of the matrix
where a, b, c, d, e are real numbers, is
If \( \det A \ne 0 \) then A is invertible and
As the Sylvester matrix  in (5.19) has the form (5.20) with (cfr. (4.13), (4.14))
in (5.19) has the form (5.20) with (cfr. (4.13), (4.14))
we use (5.21) to compute

Moreover, by (5.22), we have

Therefore, for any \(\mu \ne 0\), there exists a unique solution  of the linear system (5.19), namely a unique matrix X which solves the Sylvester Eq. (5.18).
of the linear system (5.19), namely a unique matrix X which solves the Sylvester Eq. (5.18).
Lemma 5.5
The matrix solution X of the Sylvester Eq. (5.18) is analytic in \((\mu , \epsilon ) \) and admits an expansion as in (5.11).
Proof
The expansion (5.11) of the coefficients  follows, for any \(\mu \ne 0 \) small, by (5.25) and the expansions of \( F_{ij} \) in (5.7). In particular each \(x_{ij}\) admits an analytic extension at \(\mu = 0\) and the resulting matrix X still solves (5.18) at \(\mu = 0\) (note that, for \(\mu = 0\), one has \(F^{(1)}= 0\) and the Sylvester equation does not have a unique solution). \(\square \)
follows, for any \(\mu \ne 0 \) small, by (5.25) and the expansions of \( F_{ij} \) in (5.7). In particular each \(x_{ij}\) admits an analytic extension at \(\mu = 0\) and the resulting matrix X still solves (5.18) at \(\mu = 0\) (note that, for \(\mu = 0\), one has \(F^{(1)}= 0\) and the Sylvester equation does not have a unique solution). \(\square \)
Since the matrix S solves the homological equation \(\left[ S\,,\, D^{(1)} \right] + R^{(1)} =0\) we deduce by (5.16) that
The matrix \(\frac{1}{2} \left[ S\,,\, R^{(1)} \right] \) is, by (5.12), (5.15), the block-diagonal Hamiltonian and reversible matrix
where, since \( \Sigma = \mathtt {J}_2 X \),
denoting \( \text {Sym}(A) := \frac{1}{2} (A+ A^* )\).
Lemma 5.6
The self-adjoint and reversibility-preserving matrices \( {{\tilde{E}}}, {{\tilde{G}}} \) in (5.28) have the form
Proof
For simplicity set \(F=F^{(1)}\). By (5.11), (5.7) and since \(F_{11} = 0\) (cfr. (5.7)), one has
and, adding its symmetric (cfr. (5.28)), the expansion of \({{\tilde{E}}}\) in (5.29) follows. For \({{\tilde{G}}}\) one has
and the expansion of \({{\tilde{G}}} \) in (5.29) follows by symmetrizing. \(\square \)
We now show that the last term in (5.26) is very small.
Lemma 5.7
The \( 4 \times 4 \) Hamiltonian and reversibility matrix
where the \( 2 \times 2 \) self-adjoint and reversible matrices \({{\widehat{E}}} = \small \begin{pmatrix} {{\widehat{E}}}_{11} &{} \mathrm {i}\,{{\widehat{E}}}_{12} \\ -\mathrm {i}\,{{\widehat{E}}}_{12} &{} \widehat{E}_{22}\end{pmatrix}\), \( {{\widehat{G}}} = \small \begin{pmatrix} {{\widehat{G}}}_{11} &{} \mathrm {i}\,{{\widehat{G}}}_{12} \\ -\mathrm {i}\,{{\widehat{G}}}_{12} &{} {{\widehat{G}}}_{22}\end{pmatrix}\) have entries
and the \(2\times 2\) reversible matrix \( F^{(2)}\) admits an expansion as in (5.14).
Proof
Since S and \( R^{(1)} \) are Hamiltonian and reversibility-preserving then \( \text {ad}_S R^{(1)} = [S, R^{(1)} ] \) is Hamiltonian and reversibility-preserving as well. Thus each \( \exp (\tau S) \, \text {ad}_S^2( R^{(1)} ) \, \exp (-\tau S)\) is Hamiltonian and reversibility-preserving, and formula (5.30) holds. In order to estimate its entries we first compute \(\text {ad}_S^2( R^{(1)} )\). Using the form of S in (5.12) and \([S, R^{(1)} ]\) in (5.27) one gets
and \({{\tilde{E}}}\), \({{\tilde{G}}}\) are defined in (5.28). In order to estimate \({{\tilde{F}}}\), we write \( \small {{\tilde{G}}} = \begin{pmatrix} {{\tilde{G}}}_{11} &{} \mathrm {i}\,{{\tilde{G}}}_{12} \\ -\mathrm {i}\,\tilde{G}_{12} &{} {{\tilde{G}}}_{22}\end{pmatrix}\), \( \small {{\tilde{E}}} = \begin{pmatrix} {{\tilde{E}}}_{11} &{} \mathrm {i}\,{{\tilde{E}}}_{12} \\ -\mathrm {i}\,\tilde{E}_{12} &{} {{\tilde{E}}}_{22}\end{pmatrix}\) and, by (5.29), (5.11) and \(\Sigma = \mathtt {J}_2 X\), we obtain
Thus the matrix \({{\tilde{F}}}\) in (5.32) has an expansion as in (5.14). Then, for any \( \tau \in [0,1]\), the matrix \(\exp (\tau S) \, \text {ad}_S^2( R^{(1)} ) \, \exp (-\tau S) = \text {ad}_S^2( R^{(1)} ) (1 + {\mathcal {O}}(\mu ,\epsilon ))\). In particular the matrix \(F^{(2)}\) in (5.30) has the same expansion of \(\tilde{F}\), whereas the matrices \({{\widehat{E}}}\), \({{\widehat{G}}}\) have entries at least as in (5.31). \(\square \)
Proof of Lemma 5.2
It follows by Lemmata 5.6 and 5.7. The matrix \(E^{(2)} := E^{(1)} + {{\tilde{E}}} + {\widehat{E}}\) has the same expansion of \(E^{(1)}\) in (4.13). The same holds for \(G^{(2)}\).
5.3 Complete block-decoupling and proof of the main results
We now block-diagonalize the \( 4\times 4\) Hamiltonian and reversible matrix \(\mathtt {L}_{\mu ,\epsilon }^{(2)}\) in (5.13). First we split it into its \(2\times 2\)-diagonal and off-diagonal Hamiltonian and reversible matrices
Lemma 5.8
There exist a \(4\times 4\) reversibility-preserving Hamiltonian matrix \(S^{(2)}:=S^{(2)}(\mu ,\epsilon )\) of the form (5.12), analytic in \((\mu , \epsilon )\), of size \({\mathcal {O}}(\epsilon ^3, \mu \epsilon ^2, \mu ^3\epsilon ,\mu ^5)\), and a \(4\times 4\) block-diagonal reversible Hamiltonian matrix \(P:=P(\mu ,\epsilon )\), analytic in \((\mu , \epsilon )\), of size \(\mu ^2{\mathcal {O}}(\epsilon ^4,\mu ^4\epsilon ^3,\mu ^6\epsilon ^2,\mu ^8\epsilon ,\mu ^{10}) \), such that
In particular
where \(E^{(3)}\) and \(G^{(3)}\) are selfadjoint and reversibility-preserving matrices of the form (4.13)-(4.14).
Proof
We set for brevity \( S = S^{(2)} \). The Eq. (5.34) is equivalent to the system
where \(\Pi _D\) is the projector onto the block-diagonal matrices and \(\Pi _\varnothing \) onto the block-off-diagonal ones. The second equation in (5.36) is equivalent, by a Lie expansion, and since \( [S, R^{(2)}] \) is block-diagonal, to
The “nonlinear homological equation” (5.37), i.e. \( [S,D^{(2)}] = -\frac{1}{\mu }R^{(2)} -\mu {\mathcal {R}}(S)\), is equivalent to solve the \(4\times 4\) real linear system

associated, as in (5.19), to (5.37). The vector \( \mu \vec {v}(\mu ,\epsilon ) \) is associated with \( - \frac{1}{\mu } R^{(2)} \) with \(R^{(2)} \) in (5.33). The vector \( \mu ^2 \vec {g}(\mu ,\epsilon ,\vec {x}) \) is associated with the matrix \( -\mu {\mathcal {R}}(S) \), which is a Hamiltonian and reversible block-off-diagonal matrix (i.e of the form (5.15)), of size \({\mathcal {R}}(S)={\mathcal {O}}(\mu )\) since \(\Pi _\varnothing \text {ad}^2_S(D^{(2)}) = 0\). The function \( \vec {g}(\mu ,\epsilon ,\vec {x}) \) is quadratic in \( \vec {x} \). In view of (5.14) one has
System (5.38) is equivalent to  and, writing
and, writing  (cfr. (5.25)), to
(cfr. (5.25)), to

By the implicit function theorem this equation admits a unique small solution \(\vec {x}=\vec {x}(\mu ,\epsilon )\), analytic in \( (\mu , \epsilon ) \), with size \({\mathcal {O}}(\epsilon ^3,\mu \epsilon ^2,\mu ^3\epsilon ,\mu ^5) \) as \( \vec {v} \) in (5.39). The claimed estimate of P follows by the the first equation of (5.36) and the estimate for S and of \( R^{(2)} \) obtained by (5.14). \(\square \)
Proof of Theorems 2.3 and 1.1
By Lemma 5.8 and recalling (3.1) the operator \( {\mathcal {L}}_{\mu ,\epsilon } : {\mathcal {V}}_{\mu ,\epsilon } \rightarrow {\mathcal {V}}_{\mu ,\epsilon } \) is represented by the \(4\times 4\) Hamiltonian and reversible matrix
where the matrices \(E^{(3)}\) and \(G^{(3)}\) expand as in (4.13)-(4.14). Consequently the matrices \(\mathtt {U}\) and \(\mathtt {S}\) have an expansion as in (2.33), (2.34). Theorem 2.3 is proved. The unstable eigenvalues in Theorem 1.1 arise from the block \(\mathtt {U}\). Its bottom-left entry vanishes for \( \frac{\mu ^2}{8} (1+r'_1(\mu ,\epsilon )) = \epsilon ^2 (1+r''_1(\mu ,\epsilon )) \), which, by taking square roots, amounts to solve \( \mu = 2\sqrt{2} \epsilon (1+r(\mu ,\epsilon )) \). By the implicit function theorem, it admits a unique analytic solution \({\underline{\mu }}(\epsilon ) = 2\sqrt{2} \epsilon (1+ r(\epsilon )). \) The proof of Theorem 1.1 is complete. \(\square \)
Notes
We use that the composition operator \( p \mapsto \eta (x + p(x) ) \) induced by an analytic function \( \eta (x) \) is analytic on \( H^s ({\mathbb {T}} )\) for \(s>1/2\).
recall that \(\exp (S) L \exp (-S)\,{=}\,\sum _{n \ge 0} \frac{1}{n!} \text {ad}_S^n(L)\), where \(\text {ad}_S^0(L)\,{:=}\,L\), and, for \(n \,{\ge }\, 1\), \(\text {ad}_S^n(L)=[S, \text {ad}_S^{n-1}(L)]\).
The operator \((\mathrm {Id}-R)^{-\frac{1}{2}} \) is defined, for any operator R satisfying \(\Vert R\Vert _{{{\mathcal {L}}}(Y)}<1 \), by the power series
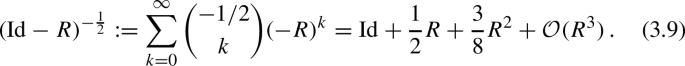
An operator \({\mathcal {A}}\) is purely imaginary if \(\overline{{\mathcal {A}}}=-{\mathcal {A}}\). A purely imaginary operator sends real functions into purely imaginary ones.
References
Akers, B.: Modulational instabilities of periodic traveling waves in deep water. Phys. D 300, 26–33 (2015)
Akers, B., Nicholls, D.: Spectral stability of deep two-dimensional gravity water waves: repeated eigenvalues. SIAM J. App. Math. 72(2), 689–711 (2012)
Arnold, V.I.: The complex Lagrangian Grassmanian. Func. Anal. Appl. 34, 208–210 (2000)
Baldi, P., Berti, M., Haus, E., Montalto, R.: Time quasi-periodic gravity water waves in finite depth. Inv. Math. 214(2), 739–911 (2018)
Bambusi, D., Maspero, A.: Birkhoff coordinates for the Toda Lattice in the limit of infinitely many particles with an application to FPU. J. Funct. Anal. 270(5), 1818–1887 (2016)
Benjamin, T.: Instability of periodic wave trains in nonlinear dispersive systems. Proceedings of the Royal Society of London, A 299(1456), 59–75 (1967)
Benjamin, T., Feir, J.: The disintegration of wave trains on deep water. Part 1. Theory. J. Fluid Mech. 27(3), 417–430 (1967)
Berti, M., Franzoi, L., Maspero, A.: Traveling quasi-periodic water waves with constant vorticity. Archive for Rational Mechanics 240, 99–202 (2021)
Berti, M., Franzoi, L., Maspero, A.: Pure gravity traveling quasi-periodic water waves with constant vorticity, arXiv:2101.12006, (2021), to appear on Communications in Pure and Applied Mathematics
Berti, M., Maspero, A., Ventura, P.: On the analyticity of the Dirichlet-Neumann operator and Stokes waves, to arXiv:2201.04675, to appear on Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl
Berti, M., Montalto, R.: Quasi-periodic standing wave solutions of gravity-capillary water waves, 263, MEMO 1273, Memoires AMS, ISSN 0065-9266, (2020)
Bridges, T., Mielke, A.: A proof of the Benjamin-Feir instability. Arch. Rational Mech. Anal. 133(2), 145–198 (1995)
Bronski, J., Hur, V., Johnson, M.: Modulational Instability in Equations of KdV Type. In: Tobisch E. (eds) New Approaches to Nonlinear Waves. Lecture Notes in Physics, vol. 908. Springer, (2016)
Bronski, J., Johnson, M.: The modulational instability for a generalized Korteweg-de Vries equation. Arch. Ration. Mech. Anal. 197(2), 357–400 (2010)
Buffoni, B., Toland, J.: Analytic theory of global bifurcation. Princeton series in applied mathematics. pp. 169. Princeton University Press, Princeton, NJ (2003)
Chen, G., Su, Q.: Nonlinear modulational instabililty of the Stokes waves in 2d full water waves. arXiv:2012.15071
Craig, W., Sulem, C.: Numerical simulation of gravity waves. J. Comput. Phys. 108(1), 73–83 (1993)
Creedon, R., Deconinck, B., Trichtchenko, O.: High-Frequency Instabilities of Stokes Waves. J. Fluid Mech. 937, A24 (2022). https://doi.org/10.1017/jfm.2021.1119
Deconinck, B., Oliveras, K.: The instability of periodic surface gravity waves. J. Fluid Mech. 675, 141–167 (2011)
Deconinck, B., Upsal, J.: The Orbital Stability of Elliptic Solutions of the Focusing Nonlinear Schrödinger Equation. SIAM J. Math. Anal. 52(1), 1–41 (2020)
Everitt, W.N., Markus, L.: Complex symplectic geometry with applications to ordinary differential operators. Trans. Amer. Math. Soc. 351, 4905–4945 (1999)
Feola, R., Giuliani, F.: Quasi-periodic traveling waves on an infinitely deep fluid under gravity. arXiv:2005.08280, to appear on Memoirs of the American Mathematical Society
Faßbender, H., Mackey, S., Mackey, N., Xu, H.: Hamiltonian square roots of skew-Hamiltonian matrices. Linear Algebra Appl. 287(1), 125–159 (1999)
Gallay, T., Haragus, M.: Stability of small periodic waves for the nonlinear Schrödinger equation. J. Differential Equations 234, 544–581 (2007)
Haragus, M., Kapitula, T.: On the spectra of periodic waves for infinite-dimensional Hamiltonian systems. Phys. D 237, 2649–2671 (2008)
Hur, V., Johnson, M.: Modulational instability in the Whitham equation for water waves. Stud. Appl. Math. 134(1), 120–143 (2015)
Hur, V., Pandey, A.: Modulational instability in nonlinear nonlocal equations of regularized long wave type. Phys. D 325, 98–112 (2016)
Hur, V., Yang, Z.: Unstable Stokes waves. arXiv:2010.10766
Iooss, G., Kirrmann, P.: Capillary gravity waves on the free surface of an inviscid fluid of infinite depth. Arch. Rat. Mech. Anal. 136, 1–19 (1996)
Lighthill, M.J.: Contribution to the theory of waves in nonlinear dispersive systems. IMA J. Appl. Math. 1(3), 269–306 (1965)
Jin, J., Liao, S., Lin, Z.: Nonlinear modulational instability of dispersive PDE models. Arch. Ration. Mech. Anal. 231(3), 1487–1530 (2019)
Johnson, M.: Stability of small periodic waves in fractional KdV type equations. SIAM J. Math. Anal. 45, 2529–3228 (2013)
Kappeler, T.: Fibration of the phase space for the Korteweg-de Vries equation. Annales de l’institut Fourier 41(3), 539–575 (1991)
Kato, T.: Perturbation theory for linear operators. Die Grundlehren der mathematischen wissenschaften, Vol. 132, pp. 592 Band 132 Springer-Verlag, New York (1966)
Korotkevich, A.O., Dyachenko, A.I., Zakharov, V.E.: Numerical simulation of surface waves instability on a homogeneous grid. Physica D: Nonlinear Phenomena, Volumes 321–322, 51–66 (2016)
Kuksin, S., Perelman, G.: Vey theorem in infinite dimensions and its application to KdV. Discrete Cont. Dyn. Syst. 27(1), 1–24 (2010)
Leisman, K., Bronski, J., Johnson, M., Marangell, R.: Stability of Traveling Wave Solutions of Nonlinear Dispersive Equations of NLS Type. Arch. Rational Mech. Anal. 240, 927–969 (2021)
Levi-Civita, T.: Détermination rigoureuse des ondes permanentes d’ ampleur finie. Math. Ann. 93, 264–314 (1925)
Lewy, H.: A note on harmonic functions and a hydrodynamical application. Proc. Amer. Math. Soc. 3, 111–113 (1952)
Maspero, A.: Tame majorant analyticity for the Birkhoff map of the defocusing Nonlinear Schrödinger equation on the circle. Nonlinearity 31(5), 1981–2030 (2018)
Nekrasov, A.: On steady waves. Izv. Ivanovo-Voznesenk. Politekhn. 3, (1921)
Nicholls, D., Reitich, F.: On analyticity of travelling water waves. Proc. R. Soc. A 461, 1283–130 (2005)
Nguyen, H., Strauss, W.: Proof of modulational instability of Stokes waves in deep water. To appear in Comm. Pure Appl. Math., (2020). https://doi.org/10.1002/cpa.22073
Olver, P.J.: Hamiltonian perturbation theory and water waves. Cont. Math., Amer. Math. Society. 28, 231–249 (1984)
Rousset, F., Tzvetkov, N.: Transverse instability of the line solitary water-waves. Invent. Math. 184, 257–388 (2011)
Segur, H., Henderson, D., Carter, J., Hammack, J.: Stabilizing the Benjamin-Feir instability. J. Fluid Mech. 539, 229–271 (2005)
Stokes, G.: On the theory of oscillatory waves. Trans. Cambridge Phil. Soc. 8, 441–455 (1847)
Struik, D.: Détermination rigoureuse des ondes irrotationelles périodiques dans un canal á profondeur finie. Math. Ann. 95, 595–634 (1926)
Whitham, G.B.: Linear and Nonlinear Waves. J. Wiley-Sons, New York (1974)
Zakharov, V.: The instability of waves in nonlinear dispersive media. J. Exp. Teor. Phys. 24(4), 740–744 (1967)
Zakharov, V.: Stability of periodic waves of finite amplitude on the surface of a deep fluid. Zhurnal Prikladnoi Mekhaniki i Teckhnicheskoi Fiziki 9(2), 86–94 (1969)
Zakharov, V., Kharitonov, V.: Instability of monochromatic waves on the surface of a liquid of arbitrary depth. J. Appl. Mech. Tech. Phys. 11, 747–751 (1970)
Zakharov, V., Ostrovsky, L.: Modulation instability: the beginning. Phys. D 238(5), 540–548 (2009)
Acknowledgements
We thank Bernard Deconinck, Walter Strauss, Huy Nguyen and Vera Hur for several useful discussions that introduced us to the fascinating problem of Benjamin-Feir instability. We also thank David Nicholls, John Toland, Pavel Plotnikov and Erik Wahlén for pointing us some references.
Funding
Open access funding provided by Scuola Internazionale Superiore di Studi Avanzati - SISSA within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A Proof of lemma 4.2
A Proof of lemma 4.2
We provide the expansion of the basis \(f_k^\pm (\mu ,\epsilon ) = U_{\mu ,\epsilon }f_k^\pm \), \(k=0,1\), in (4.1), where \(f_k^\pm \) defined in (4.2) belong to the subspace \({\mathcal {V}}_{0,0}:=\text {Rg}(P_{0,0})\). We first Taylor-expand the transformation operators \(U_{\mu ,\epsilon }\) defined in (3.10). We denote \(\partial _\epsilon \) with an apex and \(\partial _\mu \) with a dot.
Lemma A.1
The first jets of \(U_{\mu ,\epsilon }P_{0,0}\) are
where
and
The operators \({{\mathscr {L}}}_{0,0}'\) and \({\dot{{\mathscr {L}}}}_{0,0}\) are
with \(a_1(x)=p_1(x)=-2\cos (x)\), cfr. (2.15)-(2.16). The operator \({\dot{{\mathscr {L}}}}_{0,0}'\) is
Proof
By (3.10) and (3.9) one has the Taylor expansion in \({\mathcal {L}}(Y)\)
where \({\mathcal {O}}(P_{\mu ,\epsilon }-P_{0,0})^4 = {\mathcal {O}}(\epsilon ^4,\epsilon ^3\mu ,\epsilon ^2\mu ^2,\epsilon \mu ^3,\mu ^4) \in {\mathcal {L}}(Y)\). Consequently one derives (A.1), (A.2), using also the identity \(\dot{P}_{0,0} P_{0,0}' P_{0,0} + P_{0,0}' \dot{P}_{0,0} P_{0,0} = - P_{0,0} \dot{P}_{0,0}' P_{0,0}\), which follows differentiating \(P_{\mu ,\epsilon }^2 = P_{\mu ,\epsilon }\). Differentiating (3.5) one gets (A.3)–(A.5c). Formulas (A.6)-(A.7) follow by (3.2). \(\square \)
By the previous lemma we have the Taylor expansion
In order to compute the vectors \(P_{0,0}' f_k^\sigma \) and \(\dot{P}_{0,0} f_k^\sigma \) using (A.3) and (A.4), it is useful to know the action of \(({{\mathscr {L}}}_{0,0} - \lambda )^{-1}\) on the vectors
Lemma A.2
The space \( H^1({\mathbb {T}}) \) decomposes as \( H^1({\mathbb {T}}) = {\mathcal {V}}_{0,0} \oplus {\mathcal {U}}\oplus {\mathcal {W}}_{H^1} \), with \({\mathcal {W}}_{H^1}:= \overline{\bigoplus \limits _{k=2}^\infty {\mathcal {W}}_k}^{H^1}\!\!\!\!\!\!\! \), where the subspaces \({\mathcal {V}}_{0,0}, {\mathcal {U}}\) and \( {\mathcal {W}}_k \), defined below, are invariant under \({{\mathscr {L}}}_{0,0} \) and the following properties hold:
-
(i)
\( {\mathcal {V}}_{0,0} = \text {span} \{ f^+_1, f^-_1, f^+_0, f^-_0\}\) is the generalized kernel of \({{\mathscr {L}}}_{0,0}\). For any \( \lambda \ne 0 \) the operator \( {{\mathscr {L}}}_{0,0}-\lambda : {\mathcal {V}}_{0,0} \rightarrow {\mathcal {V}}_{0,0} \) is invertible and
$$\begin{aligned} \begin{aligned}&({{\mathscr {L}}}_{0,0}-\lambda )^{-1}f_1^+ = -\frac{1}{\lambda }f_1^+ \, , \quad ({{\mathscr {L}}}_{0,0}-\lambda )^{-1}f_1^- = -\frac{1}{\lambda }f_1^-,\\&\quad ({{\mathscr {L}}}_{0,0}-\lambda )^{-1}f_0^- = -\frac{1}{\lambda }f_0^- \, , \end{aligned} \end{aligned}$$(A.10)$$\begin{aligned} ({{\mathscr {L}}}_{0,0}-\lambda )^{-1}f_0^+ = -\frac{1}{\lambda }f_0^+ + \frac{1}{\lambda ^2} f_0^- \, . \end{aligned}$$(A.11) -
(ii)
\({\mathcal {U}}:= \text {span}\left\{ f_{-1}^+, f_{-1}^- \right\} \). For any \( \lambda \ne \pm 2 \mathrm {i}\,\) the operator \( {{\mathscr {L}}}_{0,0}-\lambda : {\mathcal {U}}\rightarrow {\mathcal {U}}\) is invertible and
$$\begin{aligned} \begin{aligned} ({{\mathscr {L}}}_{0,0}-\lambda )^{-1} f_{-1}^+&= \frac{1}{\lambda ^2+4}\left( -\lambda f_{-1}^+ + 2 f_{-1}^-\right) ,\\ ({{\mathscr {L}}}_{0,0}-\lambda )^{-1} f_{-1}^-&= \frac{1}{\lambda ^2+4}\left( -2 f_{-1}^+ - \lambda f_{-1}^-\right) \,. \end{aligned} \end{aligned}$$(A.12) -
(iii)
Each subspace \({\mathcal {W}}_k:= \text {span}\left\{ f_k^+, \ f_k^-, f_{-k}^+, \ f_{-k}^- \right\} \) is invariant under \( {{\mathscr {L}}}_{0,0} \). Let \({\mathcal {W}}_{L^2}:=\overline{\bigoplus \limits _{k=2}^\infty {\mathcal {W}}_k}^{L^2}\!\!\!\!\!\!\). For any \(|\lambda | < \frac{1}{2}\), the operator \( {{\mathscr {L}}}_{0,0}-\lambda : {\mathcal {W}}_{H^1} \rightarrow {\mathcal {W}}_{L^2} \) is invertible and, for any \(f \in {\mathcal {W}}_{L^2} \),
$$\begin{aligned} ({{\mathscr {L}}}_{0,0}-\lambda )^{-1} f = (\partial _x^2 + |D|)^{-1} \begin{bmatrix} \partial _x &{} - |D| \\ 1 &{} \partial _x\end{bmatrix} f + \lambda \varphi _f(\lambda , x) \, , \end{aligned}$$(A.13)for some analytic function \(\lambda \mapsto \varphi _f(\lambda , \cdot ) \in H^1({\mathbb {T}}, {\mathbb {C}}^2)\).
Proof
By inspection the spaces \({\mathcal {V}}_{0,0}\), \({\mathcal {U}}\) and \( {\mathcal {W}}_k\) are invariant under \( {{\mathscr {L}}}_{0,0}\) and, by Fourier series, they decompose \(H^1({\mathbb {T}}, {\mathbb {C}}^2)\).
- (i):
-
Formulas (A.10)-(A.11) follow using that \(f_1^+, f_1^-, f_0^-\) are in the kernel of \({{\mathscr {L}}}_{0,0}\), and \({{\mathscr {L}}}_{0,0}f_0^+ =-f_0^- \).
- (ii):
-
Formula (A.12) follows using that \({{\mathscr {L}}}_{0,0} f^+_{-1} = -2 f^{-}_{-1}\) and \({{\mathscr {L}}}_{0,0} f^-_{-1} = 2 f^{+}_{-1}\).
- (iii):
-
Let \({\mathcal {W}}{:=} {\mathcal {W}}_{H^1}\). The operator
 is invertible for any \( \lambda {\notin } \{ \pm \mathrm {i}\, \sqrt{|k|} \pm \mathrm {i}\,k, k \ge 2, k \in {{\mathbb {N}}} \}\) and
is invertible for any \( \lambda {\notin } \{ \pm \mathrm {i}\, \sqrt{|k|} \pm \mathrm {i}\,k, k \ge 2, k \in {{\mathbb {N}}} \}\) and  . In particular, by Neumann series, for any \( \lambda \) such that
. In particular, by Neumann series, for any \( \lambda \) such that 
 , e.g. for any \( |\lambda | < 1/ 2 \),
, e.g. for any \( |\lambda | < 1/ 2 \), 
Formula (A.13) follows with

We shall also use the following formulas, obtained by (A.6) and (4.2):
We finally compute \(P_{0,0}' f_k^\sigma \) and \(\dot{P}_{0,0}f_k^\sigma \).
Lemma A.3
One has
Proof
We first compute \(P_{0,0}'f_1^+\). By (A.3), (A.10) and (A.14) we deduce
We note that \( \small \begin{bmatrix}2\sin (2x) \\ 0 \end{bmatrix} \) belongs to \( {\mathcal {W}}\), being equal to \( f_{-2}^- - f_2^- \) (recall (A.9)). By (A.13) there is an analytic function \(\lambda \mapsto \varphi (\lambda , \cdot ) \in H^1({\mathbb {T}}, {\mathbb {C}}^2)\) so that
using the residue Theorem. Similarly one computes \(P_{0,0}'f_1^-\). By (A.3), (A.10) and (A.14), one has \(P_{0,0}'f_0^-=0\). Next we compute \(P_{0,0}'f_0^+\). By (A.3), (A.10), (A.11) and (A.14) we get
where in the last step we used the residue theorem. We compute now \(\dot{P}_{0,0} f^+_1\). First we have \( \dot{P}_{0,0}f_1^+ =\ \frac{\mathrm {i}\,}{2\pi \mathrm {i}\,} \oint _\Gamma \frac{1}{\lambda }({{\mathscr {L}}}_{0,0}-\lambda )^{-1} \small \begin{bmatrix}\cos (x) \\ 0 \end{bmatrix} \mathrm {d}\lambda \) and then, writing \( \small \begin{bmatrix}\cos (x) \\ 0 \end{bmatrix} =\frac{1}{2} (f_1^+ + f_{-1}^+ )\) and using (A.12), we conclude
using again the residue theorem. The computations of \(\dot{P}_{0,0}f^-_1\), \(\dot{P}_{0,0} f_0^+\), \(\dot{P}_{0,0} f_0^-\) are analogous. \(\square \)
So far we have obtained the linear terms of the expansions (4.4), (4.5), (4.6), (4.7). We now provide further information about the expansion of the basis at \(\mu =0\).
Lemma A.4
The basis \(\{f_k^\sigma (0,\epsilon ), \, k = 0,1 , \sigma = \pm \}\) is real. For any \(\epsilon \) it results \(f_0^-(0,\epsilon ) \equiv f_0^- \). The property (4.8) holds.
Proof
The reality of the basis \(f_k^\sigma (0,\epsilon )\) is a consequence of Lemma 3.2-(iii). Since, recalling (3.2), \( {{\mathscr {L}}}_{0,\epsilon } f_0^{-} = 0 \) for any \( \epsilon \) (cfr. (2.30)), we deduce \(({{\mathscr {L}}}_{0,\epsilon }-\lambda )^{-1}f_0^-= -\frac{1}{\lambda }f_0^- \) and then, using also the residue theorem,
In particular \(P_{0,\epsilon }f_0^- = P_{0,0} f_0^-\), for any \( \epsilon \) and we get, by (3.10), \(f_0^-(0,\epsilon ) = U_{0,\epsilon } f_0^- = f_0^-\), for any \( \epsilon \).
Let us prove property (4.8). In view of (3.21) and since the basis is real, we know that \( \small f_k^+ (0,\epsilon ) =\begin{bmatrix}even(x) \\ odd(x) \end{bmatrix} \), \( \small f_k^- (0,\epsilon ) =\begin{bmatrix}odd(x) \\ even(x) \end{bmatrix} \), for any \( k=0,1 \). By Lemma 4.1 the basis \(\{f_k^\sigma (0,\epsilon )\}\) is symplectic (cfr. (3.19)) and, since \({\mathcal {J}}f_0^-(0,\epsilon ) = {\mathcal {J}}f_0^- = \small \begin{bmatrix}1 \\ 0 \end{bmatrix}\), for any \(\epsilon \), we get
Thus the first component of both \(f_1^+(0,\epsilon )\) and \(f_0^+(0,\epsilon )- \small \begin{bmatrix}1 \\ 0 \end{bmatrix}\) has zero average, proving (4.8). \(\square \)
We now provide further information about the expansion of the basis at \(\epsilon =0\).
Lemma A.5
For any small \(\mu \), we have \(f_0^+(\mu ,0) \equiv f_0^+ \) and \(f_0^-(\mu ,0) \equiv f_0^- \). Moreover the vectors \(f_1^+(\mu ,0)\) and \(f_1^-(\mu ,0)\) have both components with zero space average.
Proof
The operator \({{\mathscr {L}}}_{\mu ,0} = \small \begin{bmatrix} \partial _x &{} |D+\mu |\\ -1 &{} \partial _x \end{bmatrix}\) leaves invariant the subspace \({\mathcal {Z}}:=\text {span}\{f_0^+,\,f_0^-\}\) since \( {{\mathscr {L}}}_{\mu ,0} f_0^+ = -f_0^- \) and \( {{\mathscr {L}}}_{\mu ,0} f_0^- = \mu f_0^+ \). The operator  has the two eigenvalues \(\pm \mathrm {i}\,\sqrt{\mu }\), which, for small \(\mu \), lie inside the loop \(\Gamma \) around 0 in (3.5). Then, by (3.8), we have \({\mathcal {Z}} \subseteq {{\mathcal {V}}}_{\mu ,0} = \text {Rg}(P_{\mu ,0}) \) and
has the two eigenvalues \(\pm \mathrm {i}\,\sqrt{\mu }\), which, for small \(\mu \), lie inside the loop \(\Gamma \) around 0 in (3.5). Then, by (3.8), we have \({\mathcal {Z}} \subseteq {{\mathcal {V}}}_{\mu ,0} = \text {Rg}(P_{\mu ,0}) \) and
The basis \(\{f_k^\sigma (\mu ,0) \}\) is symplectic. Then, since \( \small {\mathcal {J}}f_0^+ = \begin{bmatrix}0 \\ -1 \end{bmatrix} \) and \(\small {\mathcal {J}}f_0^- = \begin{bmatrix}1 \\ 0 \end{bmatrix} \), we have
namely both the components of \(f_1^\pm (\mu ,0)\) have zero average. \(\square \)
We finally consider the \(\mu \epsilon \) term in the expansion (A.8) of the vectors \(f_k^\sigma (\mu ,\epsilon ) \), \( k = 0,1 \), \( \sigma = \pm \).
Lemma A.6
The derivatives \( (\partial _{\mu } \partial _\epsilon f_k^\sigma )(0,0) = \left( \dot{P}_{0,0}'- \frac{1}{2} P_{0,0}\dot{P}_{0,0}' \right) f_k^\sigma \) satisfy
Proof
We decompose the Fourier multiplier operator \({\dot{{\mathscr {L}}}}_{0,0}\) in (A.6) as
and, accordingly, we write \(\dot{P}_{0,0}' = (\mathrm{A.5a})^{(I)} + (\mathrm{A.5a})^{(II)} + (\mathrm{A.5b})^{(I)} + (\mathrm{A.5b})^{(II)} + (\mathrm{A.5c}) \) defining
Note that the operators \((\mathrm{A.5a})^{(I)}\), \((\mathrm{A.5b})^{(I)}\) and (A.5c) are purely imaginary because \({\dot{{\mathscr {L}}}}_{0,0}^{(I)}\) is purely imaginary, \({{\mathscr {L}}}_{0,0}' \) in (A.6) is real and \(\dot{{\mathscr {L}}}_{0,0}'\) in (A.7) is purely imaginary (argue as in Lemma 3.2-(iii)). Then, applied to the real vectors \(f^\sigma _k\), \(k = 0,1\), \(\sigma = \pm \), give purely imaginary vectors.
We first compute \((\partial _{\mu } \partial _\epsilon f_1^+)(0,0)\). Using (A.10) and (A.14) we get
because, by Lemma A.2, \( ({{\mathscr {L}}}_{0,0}-\lambda )^{-1} \small \begin{bmatrix}\sin (2x) \\ 0 \end{bmatrix} \in {\mathcal {W}}\) and therefore it is a vector with zero average, so in the kernel of \(\dot{{\mathscr {L}}}_{0,0}^{(II)}\). In addition \((\mathrm{A.5b})^{(II)}f_1^+ = 0\) since \( {\dot{{\mathscr {L}}}}_{0,0}^{(II)} ({{\mathscr {L}}}_{0,0}-\lambda )^{-1} f_1^+ = 0\). All together \(\dot{P}_{0,0}' f_1^+ \) is a purely imaginary vector. Since \(P_{0,0}\) is a real operator, also \( (\dot{P}_{0,0}'- \frac{1}{2} P_{0,0}\dot{P}_{0,0}' ) f_1^+ \) is purely imaginary, and Lemma 3.8 implies that \((\partial _{\mu } \partial _\epsilon f_1^+)(0,0) \) has the claimed structure in (A.16). In the same way one proves the structure for \((\partial _{\mu } \partial _\epsilon f_1^-)(0,0)\).
Next we prove that \((\partial _{\mu } \partial _\epsilon f_0^+)(0,0)\), in addition to being purely imaginary, has zero average. We have, by (A.11) and (A.14)
and since the operators \(({{\mathscr {L}}}_{0,0}-\lambda )^{-1}\) and \(\dot{{\mathscr {L}}}_{0,0}^{(I)}\) are both Fourier multipliers, hence they preserve the absence of average of the vectors, then \((\mathrm{A.5a})^{(I)} f_0^+\) has zero average. In addition \((\mathrm{A.5a})^{(II)}\)
Next \( (\mathrm{A.5b})^{(I)} f_0^+ = 0\) since \(\dot{{\mathscr {L}}}_{0,0}^{(I)} f_0^\pm = 0\), cfr. (2.24). Using also that \( {\dot{{\mathscr {L}}}}_{0,0}^{(II)} f_0^+ = 0\) and \( \dot{{\mathscr {L}}}_{0,0}^{(II)} f_0^- = f_0^+ \),
using (A.12) and the residue theorem. Finally, by (A.11) and (A.7) where \( p_1 (x) = - 2 \cos (x) \),
is a vector with zero average. We conclude that \(\dot{P}_{0,0}' f_0^+\) is an imaginary vector with zero average, as well as \((\partial _\mu \partial _\epsilon f_0^+)(0,0)\) since \(P_{0,0}\) sends zero average functions in zero average functions. Finally, by Lemma 3.8, \((\partial _\mu \partial _\epsilon f_0^+)(0,0)\) has the claimed structure in (A.16).
We finally consider \((\partial _{\mu } \partial _\epsilon f_0^-)(0,0)\). By (A.10) and \({{\mathscr {L}}}_{0,0}'f_0^-=0\) (cfr. (A.14)), it results, for \(M=I, II,\)
Next by (A.10) and \({\dot{{\mathscr {L}}}}_{0,0}^{(I)} f_0^- = 0\) we get \((\mathrm{A.5b})^{(I)}f_0^- = 0\). Then, since \( {\dot{{\mathscr {L}}}}_{0,0}^{(II)} f_0^- = f_0^+\),
which is the only real term of \( (\partial _\mu \partial _\epsilon f_0^-)(0,0)\) in (A.16). Finally by (A.10) and (A.7)
by (A.10), (A.12) and the residue theorem. In conclusion \(\dot{P}_{0,0}' f_0^- = \frac{1}{2}\small \begin{bmatrix}\sin (x) \\ \cos (x) \end{bmatrix} - \frac{ \mathrm {i}\,}{2} \begin{bmatrix}\cos (x) \\ -\sin (x) \end{bmatrix} \in {\mathcal {U}}\) and, since \(P_{0,0}\vert _{{\mathcal {U}}} = 0\), we find that \(\left( \dot{P}_{0,0}'- \frac{1}{2} P_{0,0}\dot{P}_{0,0}' \right) f_0^- = \frac{1}{2} \small \begin{bmatrix}\sin (x) \\ \cos (x) \end{bmatrix} - \frac{ \mathrm {i}\,}{2} \begin{bmatrix}\cos (x) \\ \sin (x) \end{bmatrix} \). \(\square \)
This completes the proof of Lemma 4.2.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Berti, M., Maspero, A. & Ventura, P. Full description of Benjamin-Feir instability of stokes waves in deep water. Invent. math. 230, 651–711 (2022). https://doi.org/10.1007/s00222-022-01130-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-022-01130-z




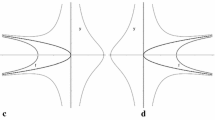


 where
where 
 is bounded, with small operatorial norm. Then
is bounded, with small operatorial norm. Then 
 is analytic. Since the map
is analytic. Since the map 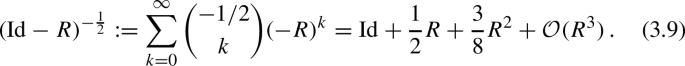
 is invertible for any
is invertible for any  . In particular, by Neumann series, for any
. In particular, by Neumann series, for any 
 , e.g. for any
, e.g. for any 
