Abstract
We prove the existence of smooth solutions to the Gross–Pitaevskii equation on \(\mathbb {R}^3\) that feature arbitrarily complex quantum vortex reconnections. We can track the evolution of the vortices during the whole process. This permits to describe the reconnection events in detail and verify that this scenario exhibits the properties observed in experiments and numerics, such as the \(t^{1/2}\) and change of parity laws. We are mostly interested in solutions tending to 1 at infinity, which have finite Ginzburg–Landau energy and physically correspond to the presence of a background chemical potential, but we also consider the cases of Schwartz initial data and of the Gross–Pitaevskii equation on the torus. In the proof, the Gross–Pitaevskii equation operates in a nearly linear regime, so the result applies to a wide range of nonlinear Schrödinger equations. Indeed, an essential ingredient in the proofs is the development of novel global approximation theorems for the Schrödinger equation on \(\mathbb {R}^n\). Specifically, we prove a qualitative approximation result that applies for solutions defined on very general spacetime sets and also a quantitative result for solutions on product sets in spacetime \(D\times \mathbb {R}\). This hinges on frequency-dependent estimates for the Helmholtz–Yukawa equation that are of independent interest.
Similar content being viewed by others
1 Introduction
The Gross–Pitaevskii equation,
models the evolution of a Bose–Einstein condensate (sometimes called a superfluid). This is an important instance of a nonlinear Schrödinger equation, which has the peculiarity that, instead of looking for solutions that decay at infinity, one is often interested in functions that tend to 1 as \(|x|\rightarrow \infty \). From a physical point of view, this is related to the consideration of a chemical potential (or background condensate) at infinity, which is given by the trivial solution \(u=1\) in \(\mathbb {R}^3\). Mathematically, one can relate the Gross–Pitaevskii equation with the Ginzburg–Landau functional
so one picks solutions that tend to 1 fast enough at infinity to have finite Ginzburg–Landau energy. In fact, the solution \(u=1\) that corresponds to the background potential is the global minimizer of the Ginzburg–Landau energy.
Note that we have not introduced a small parameter in the equation: this is the non-dimensional form of the equation, which is customarily used in the numerical simulations and heuristic analysis carried out in the physics literature [26, 32]. It is worth recalling that the Gross–Pitaevskii equation describes (in a suitable sense) the interaction of N bosons in a cubic box of side length L in the thermodynamic limit \(N\rightarrow \infty \), \(L\rightarrow \infty \). For more details on the physical interpretation of the Gross–Pitaevskii equation and its rigorous derivation as the asymptotic limit of a dilute gas of bosons, see [29].
1.1 Reconnection of quantum vortices for the Gross–Pitaevskii equation
A hot topic in condensed matter physics is the study of the evolution of quantum vortices [3]. Recall that the quantum vortices of the superfluid at time t are defined as the connected components of the set
so, as u is complex valued, they are typically given by closed curves in space. A central aspect is the analysis of the vortex reconnection, that is, the process through which two quantum vortices cross, each of them breaking into two parts and exchanging part of itself for part of the other (see Fig. 1, top). This may lead to a change of topology of the quantum vortices. Among the extensive literature on this topic, an outstanding contribution is the first experimental measurement of vortex reconnection in superfluid helium [7]. In this paper it was observed that the distance between the vortices behaves as \(C|t-T|^{1/2}\) near the reconnection time T. Further numerical [26, 37] and theoretical [32] studies have analyzed quantum vortex reconnections (of very different global properties) in detail, showing that the above separation rate is in fact universal (this is nowadays called the \(t^{1/2}\) law). Another intriguing numerical observation [26] is that the parity of the number of quantum vortices changes at reconnection time, meaning that an even number of vortices reconnect into an odd number of quantum vortices and viceversa.
Top: Visual description of the reconnection phenomenon. Here a quantum vortex in the shape of a trefoil knot reconnects into two linked unknots. Bottom: Numerical simulation of a solution to the Gross–Pitaevskii equation that exhibits a cascade of reconnections that transform a K6-2 knot into an unknot. Courtesy of Irvine, Kauffman and Kleckner [26]
As an aside, let us recall that the Gross–Pitaevskii equation, and other nonlinear Schrödinger equations, are somehow connected with the 3D Euler equation [5, 6]. This provides some heuristic relation between the quantum vortices of a Bose–Einstein condensate and vortex filaments in an incompressible fluid [21, 22, 24, 27]. However, in this paper we will not pursue this line of ideas.
Our motivation for this paper is to prove the reconnection of quantum vortices in smooth solutions to the Gross–Pitaevskii equation. More precisely, in view of the experimental and numerical evidence, there are two issues that we want to analyze in this context. Firstly, we aim to show that, just as in the physics literature, in the reconnections we construct the distance between vortices near the reconnection time obeys the \(t^{1/2}\) law. Secondly, we aim to track the vortex reconnection process at all times, both locally and globally, even if the topology of the initial and final vortices are completely different. This is motivated by the numerical evidence [26] that, when looked at from a global point of view, vortex reconnection can occur so that the topology (i.e., the knot and link type) of the vortices changes wildly.
Our main result shows that, given any finite initial and final configurations of quantum vortices (which do not need to be topologically equivalent) and any conceivable way of reconnecting them (that is, of transforming one into the other), there is a smooth initial datum \(u_0\) whose associated solution realizes this specific vortex reconnection scenario.
To make this statement precise, one can describe the initial and final vortex configurations by links \(\Gamma _0, \Gamma _1\subset \mathbb {R}^3\). By a link we denote a finite union of closed pairwise disjoint curves without self-intersections, contained in \(\mathbb {R}^3\), and of class \(C^\infty \) (we do not fix an orientation for these curves). Notice that \(\Gamma _0\) and \(\Gamma _1\) do not necessarily have the same number of connected components, and that these components need not be homeomorphic. To describe a way of transforming the link \(\Gamma _0\) into \(\Gamma _1\) in time T, we introduce the notion of a pseudo-Seifert surface. By this we will mean a smooth, two-dimensional, bounded, orientable surface \(\Sigma \subset \mathbb {R}^4\) whose boundary is
As an additional technical assumption, we will assume that the surface is in generic position, meaning that the fourth (“time”) coordinate of \(\mathbb {R}^4\) is a Morse function on \(\Sigma \) that does not have any critical points on the boundary \(\partial \Sigma \). This kind of pseudo-Seifert surfaces can be used to describe any reconnection cascade like the ones numerically studied in [26] (see Fig. 1, bottom for an illustrative example). As a matter of fact, we show in Sect. 6 that pseudo-Seifert surfaces provide a universal mechanism of describing the reconnection process for the initial and final links \(\Gamma _0,\Gamma _1\).
The theorem can then be stated as follows. To state this result, let us begin by introducing some notation. Given a spacetime subset \(\Omega \subset \mathbb {R}^{n+1}\) (here, \(n=3\)), let us denote by
its intersection with the time t slice. Furthermore, we use the notation
for the dilation on \(\mathbb {R}^3\) with ratio \(\eta >0\).
Theorem 1.1
Consider two links \(\Gamma _0,\Gamma _1\subset \mathbb {R}^3\) and a pseudo-Seifert surface \(\Sigma \subset \mathbb {R}^4\) connecting \(\Gamma _0\) and \(\Gamma _1\) in time \(T>0\). Then, there is a global smooth solution u(x, t) to the Gross–Pitaevskii equation on \(\mathbb {R}^{3}\), tending to 1 at infinity, which realizes the vortex reconnection pattern described by \(\Sigma \) up to a diffeomorphism. Specifically, for any \(\varepsilon >0\) and any \(k>0\), one has:
-
(i)
The function u tends to 1 exponentially fast at infinity. More precisely, \(1-u\in C^\infty _{\mathrm {loc}}(\mathbb {R}, {{\mathcal {S}}}(\mathbb {R}^3))\), where \({{\mathcal {S}}}(\mathbb {R}^3)\) is the Schwartz space.
-
(ii)
One can track the evolution of the quantum vortices during the prescribed reconnection process at all times. More precisely, there is some \(\eta >0\) and a diffeomorphism \(\Psi \) of \(\mathbb {R}^4\) with \(\Vert \Psi -\mathrm{id}\Vert _{C^k(\mathbb {R}^4)}<\varepsilon \) such that \(\Lambda _{\eta }[\Psi (\Sigma )_t]\) is a union of connected components of \(Z_u(\eta ^2 t)\) for all \(t\in [0,T]\).
-
(iii)
In particular, there is a smooth one-parameter family of diffeomorphisms \(\{\Phi ^t\}_{t\in \mathbb {R}}\) of \(\mathbb {R}^3\) with \(\Vert \Phi ^t-\mathrm{id}\Vert _{C^k(\mathbb {R}^3)}<\varepsilon \) and a finite union of closed intervals \({{\mathcal {I}}}\subset (0,T)\) of total length less than \(\varepsilon \) such that \(\Lambda _\eta [\Phi ^t(\Sigma _t)]\) is a union of connected components of the set \(Z_u(\eta ^2 t)\) for all \(t\in [0,T]\backslash {{\mathcal {I}}}\).
-
(iv)
The separation distance obeys the \(t^{1/2}\) law and the parity of the number of quantum vortices of \(\Phi ^t(\Sigma _t)\) changes at each reconnection time, in the sense described above.
Remark 1.2
The parameter \(\eta >0\) is small, which means that the reconnection process takes place in a small space region of size of order \(\eta \) during a very short time scale \(\eta ^2 T\). To understand the effect of this rescaling, it is convenient to rescale the spacetime variables as \(x=:\eta y\) and \(t=:\eta ^2\tau \), so that the Gross-Pitaevskii equation takes the form
where \(v(y,\tau ):=u(\eta y,\eta ^2 \tau )\). It is then obvious that when \(\eta \ll 1\), the Gross–Pitaevskii equation in the rescaled coordinates \((y,\tau )\) can be analyzed as a perturbation of the linear Schrödinger equation. Physically this means that, in this spacetime scale, the wave function behaves essentially as a solution to the free Schrödinger equation, so the interatomic interactions become negligible. Note that, after the time scale \(\eta ^2T\), our method of proof does not provide any information of the evolution of the solution u(x, t) of the Gross–Pitaevskii equation; in particular, the contribution of the nonlinear term becomes significant.
Before presenting the main ideas of the proof of this theorem, it is worth comparing it with our previous result with Lucà on vortex reconnection for the 3D Navier–Stokes equation [15]. From the point of view of what we prove, the main difference is that the Navier–Stokes result shows that one can take a finite number of “observation times” \(T_0<T_1<\dots < T_N\) such that the vortex structures present at the fluid at time \(T_k\) are not topologically equivalent to those at time \(T_{k\pm 1}\), which shows in an indirect way that at least one reconnection event must have taken place. In constrast, in the above theorem one can control the evolution of the quantum vortices during the whole reconnection process, and in particular one can describe in detail how the reconnection occurs. This is key to verify that these reconnection scenarios possess the properties that are observed in the physics literature, such as the aforementioned \(t^{1/2}\) and change of parity laws. We discuss in Sect. 6 other relevant physical properties that are also featured.
From the point of view of the strategy of the proof, the result about the Navier–Stokes equation involves two ideas. Firstly, one comes up with a (rather sophisticated) construction of a family of Beltrami fields (that is, eigenfunctions of the curl operator) of arbitrarily high frequency that present vortex lines of “robustly distinct” topologies. This step is time-independent. The time-dependent part of the argument hinges on the idea of transition to lower frequencies: acting in the linear regime, the diffusive part of the equation guarantees that a high-frequency Beltrami field can represent the leading part of the solution at time \(T_0\) while a Beltrami field of a still high but much lower frequency may dominate at a fixed later time \(T_1\).
It is obvious that this heat-equation-type argument will not work for the Gross–Pitaevskii equation even in the linear regime, which is controlled by the Schrödinger equation. Our strategy is completely different. Still, from an analytic point of view, an important simplification is that the rescalings with parameter \(\eta \) that appear in the statement enable us to construct solutions that tend to 1 as \(|x|\rightarrow \infty \) for which, for practical purposes, the Gross–Pitaevskii equation operates in a linear regime. This paves the way to using, in an essential part of the argument, a remarkable global approximation property of the linear Schrödinger equation
with \(x\in \mathbb {R}^n\) and \(n\geqslant 2\), which to the best of our knowledge has never been observed before.
1.2 Global approximation theorems for the Schrödinger equation
Roughly speaking, this property ensures that a function that satisfies the Schrödinger equation on a spacetime set with certain mild topological properties can be approximated, in a suitable norm, by a global solution of the form \(e^{it\Delta } u_0\), with \(u_0\) a Schwartz function.
All the spacetime sets we take in this paper are assumed to have a smooth boundary unless otherwise stated. Furthermore, we will use the notation
A non-quantitative global approximation theorem can then be stated as follows, where the relation \(\Omega '\subset \subset \Omega \) means that the closure of the set \(\Omega '\) is contained in \(\Omega \).
Theorem 1.3
Let v satisfy the Schrödinger equation (1.4) in a bounded open set with smooth boundary \(\Omega \subset \mathbb {R}^{n+1}\) and take a smaller set \(\Omega {'}\subset \subset \Omega \). Suppose that \(v\in L^2H^s(\Omega )\) for some \(s\in \mathbb {R}\) and that the set \(\mathbb {R}^n\backslash \Omega _t\) is connected for all \(t\in \mathbb {R}\). Then, for any \(\varepsilon >0\), there is a Schwartz function \(w_0\in {{\mathcal {S}}}(\mathbb {R}^n)\) such that \(w:= e^{it\Delta } w_0\) approximates v as
Remark 1.4
As will be clear from the proof, the choice of the norm \(L^2H^s(\Omega )\) in Theorem 1.3 is completely inessential. Instead, we could have taken \(H^s(\Omega )\) for any real s or the Hölder norm \(C^s(\Omega )\) for any \(s\geqslant 0\), for instance.
If the set \(\Omega \) where the “local solution” v is defined is of the form
where \(D\subset \mathbb {R}^n\) is a bounded open set with smooth boundary, the above qualitative approximation result can be promoted to a quantitative statement. The local solution v must additionally satisfy a certain decay condition for large times (which is obviously satisfied in nontrivial examples). In order to state the quantitative result in a convenient form, here and in what follows we denote by
the time Fourier transform of a function (or tempered distribution) v(x, t) defined on \(\Omega \). Also, we use the Japanese bracket
Theorem 1.5
Let \(\Omega := D\times \mathbb {R}\), where \(D\subset \mathbb {R}^n\) is a bounded open set with smooth boundary whose complement \(\mathbb {R}^n\backslash D\) is connected. Suppose that \(v\in L^2(\Omega )\) satisfies the Schrödinger equation (1.4) in \(\Omega \) and its time Fourier transform is bounded as
for some \(\sigma >0\) and all \(\tau _0\geqslant 0\). Then, for each \(\varepsilon \in (0,1)\) and any \(T>0\):
-
(i)
There is a Schwartz initial datum \(w_0\in {{\mathcal {S}}}(\mathbb {R}^n)\) such that the solution to the Schrödinger equation \(w:= e^{it\Delta } w_0\) approximates v on \(\Omega _T:=D\times (-T,T)\) as
$$\begin{aligned} \Vert v-w\Vert _{L^2(\Omega _T)}\leqslant \varepsilon M \end{aligned}$$and \(w_0\) is bounded as
$$\begin{aligned} \Vert w_0\Vert _{L^2(\mathbb {R}^n)}\leqslant e^{e^{e^{e^{C\varepsilon ^{-1/\sigma }}}}} M \,. \end{aligned}$$ -
(ii)
Given any smaller set \(D'\subset \subset D\), one can take an initial datum \(w_0\in {{\mathcal {S}}}(\mathbb {R}^n)\) such that \(w:= e^{it\Delta } w_0\) approximates v on \(\Omega '_T:=D'\times (-T,T)\) as
$$\begin{aligned} \Vert v-w\Vert _{L^2(\Omega '_T)}\leqslant \varepsilon M \end{aligned}$$and \(w_0\) satisfies the sharper bound
$$\begin{aligned} \Vert w_0\Vert _{L^2(\mathbb {R}^n)}\leqslant e^{e^{C\varepsilon ^{-1/\sigma }}} M \,. \end{aligned}$$
Here the constant C depends on T and on the geometry of the domains.
Remark 1.6
In the context of global approximation theorems for second order elliptic PDEs, quantitative bounds analogous to those obtained in Theorem 1.5 are known to be optimal in their \(\varepsilon \) dependence, up to the precise constants of the estimate [34, Section 5].
Let us recall that global approximation theorems are classical in the case of elliptic and hypoelliptic operators [9, 19, 28, 30], starting with the work of Runge in complex analysis. These results have been recently extended to the related setting of parabolic operators [14]. The case of dispersive equations, however, is substantially different and presents new key technical subtleties. The way we solve these difficulties in the above non-quantitative approximation result hinges on a careful analysis of integrals defined by Bessel functions with real and complex arguments.
A quantitative approximation theorem for elliptic equations was first established by Salo and Rüland in [34]. Specifically, they show that a function v satisfying a nice linear elliptic equation (e.g., the Laplace equation) on a smooth bounded domain \(\Omega \) can be approximated in \(L^2\) by solutions to the elliptic equation on a larger domain \(\Omega _1\) whose \(L^2\) norm is controlled in terms of the \(H^1(\Omega )\) norm of v and the geometry of the domains. The gist of the proof is a stability argument, which boils down to a three-sphere estimate: if the \(L^2\) norm of a solution to the elliptic equation is of order 1 over the ball \(B_2\) and small over the ball \(B_{1/2}\), then the \(L^2\) norm of the solution on the ball \(B_1\) is small too. Here \(B_r\) denotes the open ball centered at the origin of radius r. Although one has effective Carleman estimates for the Schrödinger equation [20, 25], this kind of three-sphere inequalities do not hold for the Schrödinger equation. Indeed, just as in the case of the heat equation [16], one can construct counterexamples using that, for each \(\alpha >1\), a Tychonov-type argument shows the existence of smooth solutions to the Schrödinger equation on \(\mathbb {R}^n\times \mathbb {R}\) that are bounded as
if \(t>0\) and vanish for \(t\leqslant 0\) (see e.g. [35, Exercise 2.24]). Hence the question of which spacetime domains possess some kind of quantitative approximation property for the Schrödinger equation remains open.
The proof of our quantitative approximation theorem exploits the connection, via the time Fourier transform, between solutions to the Schrödinger equation on \(D\times \mathbb {R}\) and solutions to the Helmholtz–Yukawa equation on D (that is, the equation
where the constant \(\tau \) can be positive or negative). The first part of the proof, which is of considerable interest in itself (Theorem 2.4), consists of a quantitative approximation theorem for the Helmholtz–Yukawa equation with frequency-dependent control of a suitable norm of the global solution on the whole space \(\mathbb {R}^n\). The norm we control in this elliptic approximation theorem is a natural one: it essentially reduces to the Agmon–Hörmander seminorm when \(\tau <0\) and is a suitable generalization thereof for \(\tau >0\). One should note that, unlike the Rüland–Salo quantitative approximation [34], where the approximating solution is only assumed to be defined on a larger but still bounded domain, here we strive to estimate solutions that are defined on the whole space \(\mathbb {R}^n\), and also to keep track of the dependence of the constants on the “frequency” \(\tau \). The second part of the proof of Theorem 1.5 is again based on careful manipulations of Bessel functions, which are in particular employed to replace (modulo small errors) an initial datum that grows exponentially fast at infinity by a Schwartz one.
1.3 Organization of the paper
In Sect. 2 we start by proving a quantitative global approximation theorem for the Helmholtz–Yukawa equation with constants that depend on the frequency. In Sect. 3 we provide a lemma on non-quantitative approximation for the Schrödinger equation that permits to approximate a solution on a general bounded spacetime set \(\Omega \) as in Theorem 1.3 by a solution on a larger spacetime cylinder. The proofs of Theorems 1.3 and 1.5 are presented in Sect. 4. Global approximation theorems are crucially used in the proof of our result on vortex reconnection (Theorem 1.1), which is given in Sect. 5. In Sect. 6 we discuss how this scenario of vortex reconnection presents the key features observed in the physics literature. In particular, we note that when one considers solutions to the Gross–Pitaevskii equation that fall off at infinity, which physically corresponds to the more flexible case of laser beams, we can prove a somewhat stronger result. The case of the Gross–Pitaevskii equation on the torus is considered too. The paper concludes with a short Appendix where we present some calculations with Bessel functions.
2 Frequency-Dependent Global Approximation for the Helmholtz–Yukawa Equation
Our objective in this section is to obtain a global approximation result for the Helmholtz–Yukawa equation. In addition to its intrinsic interest, this is a key ingredient in the proof of Theorem 1.5. There are two aspects that we need to pay attention to. Firstly, we need to control the dependence on the frequency \(\tau \). Secondly, we aim to control natural norms of the global solution over the whole space \(\mathbb {R}^n\). Since some functions (such as the fundamental solutions we consider) take a slightly different form when \(n=2\), for the ease of notation, we will hereafter assume that \(n\geqslant 3\). The case \(n=2\) only involves minor modifications and can be tackled using the same arguments.
We will first prove several auxiliary lemmas. We start with a stability lemma where the key point is the explicit dependence of the stability constants on \(\tau \). Here and in what follows, we will use the notation
for the positive and negative parts of the real number \(\tau \). Also, for the ease of notation, given an open set D, we often denote the \(L^2(D)\) norm of a function f by \(\Vert f\Vert _D\). Throughout, \(B_R\) denotes the open ball centered at the origin of radius R.
Lemma 2.1
Suppose that the function \(\psi \in H^1(D)\) satisfies the elliptic equation
in a smooth bounded domain D, where \(\tau \) is a real constant. If \(D'\) is another smooth domain whose closure is contained in D, then the following global stability estimate holds:
Likewise, if \(D'\subset \subset D''\subset \subset D\) is a bounded domain with a smooth boundary, we have the interior stability inequality
Here C, \(\mu \) and \(\theta \) are positive constants that do not depend on \(\tau \).
Proof
The key ingredient of these stability inequalities is to control the dependence on \(\tau \) of the 3-sphere estimate
We will shortly show that this inequality holds for concentric balls of radii \(R_1<R_2<R_3\) contained in D for some \(\theta >0\) depending on the radii but not on \(\tau \). One this 3-sphere inequality has been established, a standard argument of propagation of smallness [2] yields the interior stability result (2.2), and also the stability estimate up to the boundary (2.1).
To derive the basic estimate (2.1), we notice that when \(\tau <0\), the estimate (2.3) was proved by Donnelly–Fefferman [13]. If \(\tau >0\), we use that \(\psi (x,t):= e^{\tau t} \varphi (x)\) satisfies the heat equation
on \(D\times \mathbb {R}\). A result of Escauriaza–Vessella [16] then shows
for some positive constants C, c, which translates into
This readily implies
thereby completing the proof of the 3-sphere inequality (2.3). \(\square \)
In the following lemma we compute a fundamental solution for the operator \(\Delta -\tau \) with the sharp decay at infinity:
Proposition 2.2
Suppose that \(n\geqslant 3\). The function
satisfies the distributional equation
on \(\mathbb {R}^n\). Here \(Y_\nu \) and \(K_\nu \) denote the Bessel function and the modified Bessel function of the second kind, respectively, and the normalization constants depend on the dimension. Furthermore, \(G_\tau \) can be written as
where \(H_\tau \) is bounded as
Proof
A straightforward computation in spherical coordinates shows that \(G_\tau (x)\) satisfies the equation
on \(\mathbb {R}^n\backslash \{0\}\). In view of the asymptotic behavior of the Bessel functions at 0, the dimensional constants can be chosen so that
so it is standard that it satisfies the distributional equation (2.5).
To estimate \(G_\tau \), recall that the Bessel functions \(Y_\nu \) and \(K_\nu \) are bounded for \(r>0\) as
Plugging these estimates into the expression for \(G_\tau \) results in (2.6). \(\square \)
We shall also need frequency-dependent estimates for the convolution of the fundamental solution with a compactly supported function:
Lemma 2.3
Let \(w:= G_\tau * f\) with a function f supported on a bounded domain \(Y\subset \mathbb {R}^n\). Given any bounded domain \(B\subset \mathbb {R}^n\), one has
where the constant C depends on n, B and Y but not on \(\tau \).
Proof
The bound (2.6) implies that
so we readily obtain, for all \(x\in B\),
Standard estimates for Riesz potentials then yield
To estimate the second derivatives of w, we use the equation \(\Delta w= \tau w+ f\), obtaining
The estimate for \(\Vert w\Vert _{H^1(B)}\) then follows by interpolation. \(\square \)
The norm that we will employ to control the growth of solutions to the Helmholtz–Yukawa equation at infinity (with \(\tau \ne 0\)) is

To motivate the choice of this norm, recall that the natural norm to control solutions to the Helmholtz equation
on \(\mathbb {R}^n\) is the Agmon–Hörmander seminorm [19, 33]
Indeed, a solution to the Helmholtz equation with sharp decay can be written as the Fourier transform of a measure on the sphere with an \(L^2\) density,
and the norm \(\Vert f\Vert _{L^2(\mathbb {S}^{n-1})}\) turns out to be equivalent to (2.7) [19, Theorem 7.1.28]. Since we are also concerned with solutions to the Yukawa equation (that is, the Helmholtz equation with a negative sign), one can replace the definition (2.7) as above (which is also sharp when \(\tau >0\)). It is standard [23] that the only solution to the equation
on \(\mathbb {R}^n\) whose associated seminorm  is zero is the trivial solution \(\varphi =0\). For technical reasons, we also define the weighted \(L^\infty \) norm
is zero is the trivial solution \(\varphi =0\). For technical reasons, we also define the weighted \(L^\infty \) norm

Obviously this is a stronger norm, as

for any function \(\varphi \).
The main result of this section, which builds upon ideas of Rüland–Salo [34], is the following global approximation theorem for the Helmholtz–Yukawa equation. It should be stressed that the reason for which the statement is more technically involved than one would have liked is that we want to control both the case of large \(|\tau |\) (which works just fine) and the case of small \(|\tau |\). While the latter case does not present any essential difficulties, it is awkward to write estimates that are uniform in \(\tau \). This is due to the fact that the triple norm obviously collapses in the case \(\tau =0\) (i.e., because harmonic functions do not decay on average at infinity). This leads to the introduction of a constant \(\tau _1\) to write estimates that we can conveniently invoke in later sections. Still, the information that one can prove in the case of small \(|\tau |\) (and in particular in the case of harmonic functions) is more precise than what we state here, so the interested reader should take a look at Step 4 of the proof.
Theorem 2.4
Let \(\varphi \in H^1(D)\) satisfy the equation
in a bounded domain \(D\subset \mathbb {R}^n\). Let us fix some \(\tau _1>0\). Assume that the complement \(\mathbb {R}^n\backslash D\) is connected and set
Then, for each \(\varepsilon \in (0,1)\), one can find a solution of the equation \(\Delta \psi -\tau \psi =0\) on \(\mathbb {R}^n\) such that:
-
(i)
If \(|\tau |>\tau _1\), \(\psi \) approximates \(\varphi \) in the whole domain
$$\begin{aligned} \Vert \varphi -\psi \Vert _{L^2(D)}\leqslant \varepsilon \Vert \varphi \Vert _{L^2(D)}^{1/2}\Vert \varphi \Vert _{H^1(D)}^{1/2} \end{aligned}$$and is bounded as

-
(ii)
Given a smaller subset \(D'\subset \subset D\), if \(|\tau |>\tau _1\), \(\psi \) approximates \(\varphi \) on \(D'\) as
$$\begin{aligned} \Vert \varphi -\psi \Vert _{L^2(D')}\leqslant \varepsilon \Vert \varphi \Vert _{L^2(D')}^{1/2}\Vert \varphi \Vert _{H^1(D')}^{1/2} \end{aligned}$$and is bounded as

-
(iii)
If \(|\tau |\leqslant \tau _1\), \(\psi \) approximates \(\varphi \) on the whole domain as
$$\begin{aligned} \Vert \varphi -\psi \Vert _{L^2(D)}\leqslant \varepsilon \Vert \varphi \Vert _{L^2(D)}^{1/2}\Vert \varphi \Vert _{H^1(D)}^{1/2} \end{aligned}$$and is bounded as
$$\begin{aligned} |\psi (x)|\leqslant (N_{\varepsilon ,1}\langle x\rangle )^{N_{\varepsilon ,1}}e^{{\tau _+^{1/2}}|x|}\Vert \varphi \Vert _{L^2(D)}\,. \end{aligned}$$Furthermore,
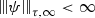 for all \(\tau \ne 0\).
for all \(\tau \ne 0\). -
(iv)
Given a smaller subset \(D'\subset \subset D\), if \(|\tau |\leqslant \tau _1\), \(\psi \) approximates \(\varphi \) on \(D'\) as
$$\begin{aligned} \Vert \varphi -\psi \Vert _{L^2(D')}\leqslant \varepsilon \Vert \varphi \Vert _{L^2(D')}^{1/2}\Vert \varphi \Vert _{H^1(D')}^{1/2} \end{aligned}$$and is bounded as
$$\begin{aligned} |\psi (x)|\leqslant (\widetilde{N}_{\varepsilon ,1}\langle x\rangle )^{\widetilde{N}_{\varepsilon ,1}}e^{{\tau _+^{1/2}}|x|}\Vert \varphi \Vert _{L^2(D)}\,. \end{aligned}$$Furthermore,
 for all \(\tau \ne 0\).
for all \(\tau \ne 0\).
The constants only depend on the domains D and \(D'\) and on \(\tau _1\).
Proof
Let us start by assuming that \(|\tau |>\tau _1\) and proving the estimates up to the boundary, which correspond to the first item of the statement. The estimates in the smaller domain \(D'\) will be tackled in Step 3, while uniform estimates for \(|\tau |\leqslant \tau _1\) will be presented in Step 4.
Step 1: Approximation by solutions with localized sources Let us consider a ball B containing the closure of D and fix a bounded open set \( Y \subset \subset \mathbb {R}^n\backslash {\overline{B}}\). Let us define the space of solutions
Consider the linear operator \(L^2(Y)\rightarrow {{\mathcal {X}}}\) defined by
and denote by \({{\mathcal {K}}}\) its kernel. We are interested in the orthogonal complement
so we denote by \({{\mathcal {P}}}: L^2(Y)\rightarrow {{\mathcal {K}}}^\perp \) the orthogonal projection. Let us call \(A: {{\mathcal {K}}}^\perp \rightarrow {{\mathcal {X}}}\) the restriction of the linear map (2.10) to this set. If \(\phi \) is any function in \(L^2(D)\) and \(f\in L^2(Y)\), it is clear that
so the adjoint \(A^*: {{\mathcal {X}}}\rightarrow {{\mathcal {K}}}^\perp \) of A must be given by
Furthermore, for \(\phi \in L^2(D)\), if \(g\in {{\mathcal {K}}}\) one obviously has
so one can drop the projector in the above expression for \(A^*\) and simply write
The map \(A^*A\) is a positive, compact, self-adjoint operator on \({{\mathcal {K}}}^\perp \). Furthermore, the range of A is dense on \({{\mathcal {X}}}\) by standard non-quantitative global approximation theorems for elliptic equations [9]. It then follows that there are positive constants \(\alpha _j\) and orthonormal bases \(\{f_j\}_{j=1}^\infty \) of \({{\mathcal {K}}}^\perp \) and \(\{\phi _j\}_{j=1}^\infty \) of \({{\mathcal {X}}}\) such that
Given a solution \(\varphi \in {{\mathcal {X}}}\), let us consider its decomposition
and, for any \(\alpha >0\), define the element of \({{\mathcal {K}}}^\perp \)
Note that obviously
As \(\alpha \rightarrow 0\), it is clear that AF defines an approximation of \(\varphi \). To control how accurate this approximation is, let
denote the error, which is supported on D. It is obviously bounded as
In order to derive better bounds, let us consider the function \(w:=G_\tau * E\), which satisfies the equation
Its \(L^2\) norm on Y is obviously given by
We now estimate
In passing to the second equality we have used that \(E=\Delta w-\tau w\) is orthogonal to \(AF= \varphi -E\). To pass to the third equality we integrate by parts and use that \(\Delta \varphi -\tau \varphi =0\). For the last estimate we use the trace inequality.
To control the norm \(\Vert w\Vert _{H^{\frac{1}{2}}(\partial D)}\), we can use the trace inequality and take a domain \(B'\) containing \({\overline{D}}\cup Y\) to write
For the last inequality we have simply interpolated the \(H^1\) norm of w. As \(w= G_\tau * E\), the \(H^2\) norm of w can be estimated using Lemma 2.3 and the rough bound (2.12) as
For the \(L^2(B'\backslash D)\) norm of w we use a finer argument that employs the stability estimate stated in Lemma 2.1. The starting point is that w satisfies the equation \(\Delta w-\tau w=0\) on \(B'\backslash \overline{D}\) and that its \(L^2\) norm on the subset \(Y\subset B'\backslash D\) is small by (2.13). Hence one can write
Here we have also used the bounds for the \(H^1\) norm of \(w= G_\tau *E\) derived in Lemma 2.3.
Putting all the estimates together, we have shown that for any \(\alpha >0\) one can take a function \(F\in L^2(Y)\) such that \(w:= G_\tau *F\) is bounded as in (2.11) and approximates \(\varphi \) in D as
with \(\mu '>0\). Equivalently, for any \(\varepsilon >0\) one can choose F as above such that \(w:= G_\tau *F\) approximates \(\varphi \) as
and is bounded as
Step 2: Approximation by a global solution with controlled behavior at infinity Let us start by choosing a slightly smaller ball \(B'' \subset \subset B\). Since \(w:= G_\tau *F\) satisfies the equation
on B, it is then a straightforward consequence of Lemma 2.3 that
for any nonnegative s. For convenience, let us fix a ball \(B''\) as above and denote its radius by \(R''\).
Consider an orthonormal basis of spherical harmonics on the unit sphere \(\mathbb {S}^{n-1}\) of dimension \((n-1)\), which we denote by \(Y_{lm}\). Hence \(Y_{lm}\) is an eigenfunction of the spherical Laplacian satisfying
l is a nonnegative integer and m ranges from 1 to the multiplicity
of the corresponding eigenvalue of the spherical Laplacian.
The expansion of w in spherical harmonics,
converges in any \( H^s(B'')\) norm, with the coefficients being given by
Using the notation
it is clear from (2.18) and the expression for the spherical eigenvalues (Eq. (2.19)) that
Hence, for any \(s>1\) there is a positive constant \(C_s\) such that
which ensures that
Here we have employed the bound (2.17) for \(\Vert F\Vert _Y\). It then follows that, for any \(\varepsilon >0\), there are large constants c and s, depending on \(\varepsilon \) but not on \(\tau \), such that if one sets
and
one has
Let us now pass to the study of the function \(w_{lm}\). As \(w_{lm}\) satisfies the ODE
and is bounded at \(r=0\), one can write it in terms of a modified Bessel function of the first kind as
where \(A_{lm}\) is a \(\tau \)-dependent constant.
We need to obtain an estimate for the coefficient \(A_{lm}\). It is clear that
If \({R''}\) denotes the radius of the ball \(B''\), the key point is then to estimate the function
where we can assume that \(\nu \geqslant 1/2\) and \(\alpha \in \mathbb {R}^+\cup i\mathbb {R}^+\). Suitable upper and lower bounds have been computed in Lemma A.1 in Appendix A, showing in particular that
for all \(\alpha \in \mathbb {R}^+\cup i\mathbb {R}^+\). This lower bound translates into the upper bound
The large time asymptotics of Bessel functions [17, 8.451.1 and 8.451.5],
shows that

Note that the error terms \(O_l(({\tau ^{1/2}}r)^{-1})\) are not bounded uniformly in l, but this does not have any effect on our argument.
To estimate \(\psi \) pointwise, we can resort to the uniform estimate [4]
where C does not depend on \(\nu \geqslant 1\) and
This bound, which obviously applies to the Bessel function \(I_\nu (z)\) too because of the relation
readily shows that \(\psi \) also satisfies the pointwise bound

Here we have used the well-known bound
Putting together the bounds for \(A_{lm}\), \(\Vert w_{lm}\Vert \), \(l_0\) and \(\Vert F\Vert _Y\), this results in the bound provided in the first item of the statement.
Step 3: The interior approximation result We are left with the task of proving the quantitative approximation result with sharper bounds on the smaller domain \(D'\), which corresponds to the second assertion of the statement.
The proof goes as before with minor modifications. To derive an analog of Step 1, all the objects are defined with \(D'\) playing the role of D; e.g., one sets
All the arguments remain valid without any further modifications until one reaches the estimate (2.15). There one can now employ the interior estimate in Lemma 2.1, which results in
for some \(\theta \in (0,1)\). Since \(\Vert w\Vert _Y\leqslant \alpha \Vert E\Vert _{D'}\), one can argue as before to obtain
This easily leads to the estimate
Using the same reasoning as before with
instead of (2.20), one arrives at the desired result.
Step 4: The case of small \(|\tau |\) In the case of harmonic functions (\(\tau =0\)), a minor variation of the proof shows that a harmonic function on D can be approximated on this domain by a harmonic polynomial of degree at most \( e^{C/\varepsilon }\) whose coefficients are bounded in absolute value by \(e^{e^{C/\varepsilon }}\). If the approximation is performed on a smaller domain \(D'\), the degree of the polynomial is bounded by \(C\varepsilon ^{-C}\) and its coefficients are bounded by \(C\varepsilon ^{-\varepsilon ^{-C}}\). This translates into the bounds specified in the statement. Likewise, in the case of small \(|\tau |\), one can reuse the bounds for Bessel functions employed in the previous steps of the proof to show that the bounds of the points (iii) and (iv) hold uniformly in this case. \(\square \)
3 A Lemma on Non-quantitative Approximation by Solutions of the Schrödinger Equation on a Spacetime Cylinder
In this section we prove a lemma on approximation for the Schrödinger equation that will be instrumental in our proof of Theorem 1.3.
Before presenting this result, let us introduce some notation. If \(L^2_c(\mathbb {R}^{n+1})\) denotes the space of \(L^2\) functions on the spacetime with compact support, we can define the operators \({{\mathcal {T}}}\) and \({{\mathcal {T}}}^*\) as the maps \(L^2_c(\mathbb {R}^{n+1})\rightarrow L^\infty L^2(\mathbb {R}^{n+1})\) given by
where
is the fundamental solution of the Schrödinger equation. To put it differently,
Of course, the action of \({{\mathcal {T}}}\) and \({{\mathcal {T}}}^*\) is well defined on more general distributions, which in this paper will always be of compact support. In the following proposition we recall some elementary properties of \({{\mathcal {T}}}\) and \({{\mathcal {T}}}^*\):
Proposition 3.1
Given any \(f,h\in L^2_c(\mathbb {R}^{n+1})\), the following statements hold:
-
(i)
For any \(t_0\) below the support of f, \({{\mathcal {T}}}f\) is the solution to the Cauchy problem
$$\begin{aligned} (i\partial _t+\Delta ) {{\mathcal {T}}}f=if\,,\qquad {{\mathcal {T}}}f|_{t=t_0}=0\,. \end{aligned}$$ -
(ii)
For any \(t_0\) above the support of h, \({{\mathcal {T}}}^*h\) is the solution to the Cauchy problem
$$\begin{aligned} (i\partial _t+\Delta ) {{\mathcal {T}}}^*h=-ih\,,\qquad {{\mathcal {T}}}^*h|_{t=t_0}=0\,. \end{aligned}$$ -
(iii)
\(\displaystyle \int _{\mathbb {R}^{n+1}} {{\mathcal {T}}}f(x,t)\, \overline{h(x,t)}\, dx\, dt=\int _{\mathbb {R}^{n+1}} f(x,t)\, \overline{{{\mathcal {T}}}^*h(x,t)}\, dx\, dt\).
-
(iv)
\({{\mathcal {T}}}\) and \({{\mathcal {T}}}^*\) commute with spacetime derivatives. That is, if \(f,g\in C^\infty _c(\mathbb {R}^{n+1})\),
$$\begin{aligned} D^\alpha ({{\mathcal {T}}}f)= {{\mathcal {T}}}(D^\alpha f)\quad \text {and}\quad D^\alpha ({{\mathcal {T}}}^*g)= {{\mathcal {T}}}^*(D^\alpha g) \end{aligned}$$for any multiindex \(\alpha \).
Proof
The first three statements follow by a straightforward computation. In order to see that \(D^\alpha ({{\mathcal {T}}}f)= {{\mathcal {T}}}(D^\alpha f)\), the easiest way is to differentiate the equation satisfied by \({{\mathcal {T}}}f\). This way we arrive at
for any \(t_0\) below the support of f, which means that indeed \(D^\alpha {{\mathcal {T}}}f= {{\mathcal {T}}}(D^\alpha f)\). The proof that \(D^\alpha ({{\mathcal {T}}}^*g)= {{\mathcal {T}}}^*(D^\alpha g)\) is analogous. \(\square \)
To state the approximation result, it is also convenient to define the notion of admissible set:
Definition 3.2
Let \(\Omega \subset \mathbb {R}^{n+1}\) be an open set in spacetime whose closure is contained in the spacetime cylinder \({{\mathcal {C}}}:=B_R\times \mathbb {R}\). We say that the set \(S\subset \mathbb {R}^{n+1}\) is \((\Omega ,R)\)-admissible if:
-
(i)
S is a spacetime cylinder of the form \(B\times (T_1,T_2)\) contained in \(\mathbb {R}^{n+1}\backslash {\overline{{{\mathcal {C}}}}}\), where \(B\subset \mathbb {R}^n\) is a ball.
-
(ii)
The projection of S on the time axis contains that of \(\Omega \), that is,
$$\begin{aligned} \{t: (x,t)\in \Omega \text { for some } x\in \mathbb {R}^n\}\subset \subset (T_1,T_2)\,. \end{aligned}$$
We are now ready to state and prove the main result of this section:
Lemma 3.3
Let \(\Omega \subset \subset B_R\times \mathbb {R}\) be a bounded domain in spacetime with smooth boundary such that the complement \(\mathbb {R}^n\backslash \Omega _t\) is connected for all t. Fix any \((\Omega ,R)\)-admissible set \(S\subset \mathbb {R}^{n+1}\) and a smaller domain \(\Omega '\subset \subset \Omega \). For some real s, consider a function \(v\in L^2H^s(\Omega )\) that satisfies the Schrödinger equation
in the distributional sense on \(\Omega \). Then, for any \(\varepsilon >0\), there is a function \(f\in C^\infty _c(S)\) such that \({{\mathcal {T}}}f\) approximates v in \(\Omega '\) as
Remark 3.4
A cursory look at the proof reveals that the proposition remains valid for solutions v in many other functional spaces, e.g. in \(H^s(\Omega )\) or \(C^k(\Omega )\).
Proof
Since the bounded spacetime set \(\Omega \subset \mathbb {R}^{n+1}\) has a smooth boundary, we can extend \(v|_\Omega \) to a compactly supported function on \(\mathbb {R}^{n+1}\) of class \(L^2H^s(\mathbb {R}^{n+1})\) by multiplying by a smooth cutoff function. We assume that this cutoff function is 1 in a small neighborhood U of the closure of \(\Omega '\) and vanishes on the complement of \(\Omega \). We will still denote this extension by v. Since \(\Omega _t^c\) is connected for all t, we can safely assume (taking a larger open set \(\Omega '\subset \subset \Omega \) if necessary), that \(\mathbb {R}^n\backslash \Omega '_t\) is also connected for all t.
Let us consider an approximation of the identity \(F_\eta (x,t):= \eta ^{-n-1} F(x/\eta ,t/\eta )\) defined by a function \(F\in C^\infty _c(\mathbb {R}^{n+1})\) such that its support is contained in the unit ball \(B_1\) and \(\int _{\mathbb {R}^{n+1}} F(x,t)\, dx\, dt=1\). Setting \(v^\eta := F_\eta * v\), since \(i\partial _t v+ \Delta v=0\) outside \(\Omega \backslash U\) and \({\text {supp}}F_\eta \subset B_\eta \), it follows that
whenever the distance from the point (x, t) to the set \(\Omega \backslash U\) is greater than \(\eta \).
In particular, for small enough \(\eta \), \(v^\eta \) is a smooth function, whose support is contained in a neighborhood of \(\Omega \) of width \(\eta \), which satisfies the equation
in an open neighborhood \(\Omega ''\supset \supset \Omega ' \) and whose difference
is as small as one wishes.
As \(v^\eta (x,t_0)=0\) for all x and any negative enough negative time \(t_0\), by defining the smooth, compactly supported function
Proposition ensures that one can write
Note that, by definition,
is contained in a set of the form \(\Omega ^\eta \backslash \overline{\Omega ''}\), where \(\Omega ^\eta \) is the support of \(v^\eta \) (and is therefore contained in an \(\eta \)-neighborhood of \(\Omega \)). Note that
We claim that, given any \(\varepsilon >0\) and any positive integer k, there is a function g in \(C^\infty _c(S)\) such that the function \({{\mathcal {T}}}g\) approximates \(v^\eta \) on the set \(\Omega ' \) in the \(H^k\) norm as
To prove this, consider the space of smooth functions
which we consider as a subset of the Banach space \(H^k({\Omega '} )\). As the proof involves a duality argument, let us recall [11] that, as the boundary of \(\Omega '\) is smooth, the dual space of \(H^k (\Omega ')\) is the space
The duality pairing between \(u\in H^k(\Omega ')\) and \(\phi \in H^{-k}_{\overline{\Omega '}}\) is defined as
where U is any function in \(H^{k}_{\mathrm {loc}}(\mathbb {R}^{n+1})\) such that \(U|_{\Omega '}=u\) and where the angle bracket on the RHS henceforth stands for the standard duality pairing on \(\mathbb {R}^{n+1}\) (between elements of \(H^k\) and \(H^{-k}\) or between Schwartz functions and tempered distributions). The above pairing is obviously independent of the choice of U.
Since
in \(\mathbb {R}^{n+1}\) by Proposition , in particular \((i\partial _t +\Delta ) {{\mathcal {T}}}g=0\) in the cylinder \(B_R\times \mathbb {R}\). Now suppose that there exists an element in the dual space \(\phi \in H^{-k}_{\overline{\Omega '}}\) such that
for all \(u\in {{\mathcal {V}}}\). By the definition of \(\phi \) and Proposition , it then follows that, for all \(g\in C^\infty _c(S)\),
which implies that \({{\mathcal {T}}}^*\phi \equiv 0\) in the interior of S, where \({{\mathcal {T}}}^*\phi \) denotes the distribution
Then \({{\mathcal {T}}}^*\phi \) satisfies the Schrödinger equation
and in particular
in the complement of the set \(\overline{\Omega '} \).
Let us now recall the unique continuation property of the Schrödinger equation (see e.g. [36]): \(\square \)
Theorem 3.5
(Unique continuation property). Let \(W\subset \mathbb {R}^{n+1}\) be an open set in spacetime such that \(W_t\) is connected for all \(t\in {\mathbb {R}}\). If a function satisfies the equation \(i\partial _t h+\Delta h=0\) in W and \(h=0\) in some nonempty open set V contained in W, then \(h(x,t)=0\) for all \((x,t)\in W\) such that the intersection \(V_t\cap W\) is nonempty.
It then follows from the fact that \({{\mathcal {T}}}^*\phi \equiv 0\) on S and the connectedness of \(\mathbb {R}^n\backslash \Omega '_t\) for all t that \({{\mathcal {T}}}^*\phi (x,t)=0\) for all t such that
and all \(x \in \mathbb {R}^n\) such that \((x,t)\not \in \overline{\Omega '} \). By the time projection condition that appears in Definition 3.2 and the fact that \(S'\subset \mathbb {R}^{n+1}\backslash \overline{\Omega '}\), this implies that \({{\mathcal {T}}}^*\phi =0\) on \(S'\), which in turn means that
As a consequence of the Hahn–Banach theorem, \(v^\eta \) can then be approximated by an element \(u\in {{\mathcal {V}}}\) as in (3.5), as we wanted to conclude.
There is a slight technical point about the application of the unique continuation theorem to \({{\mathcal {T}}}^*\phi \) that we have omitted. In [36] this result is proved, for more general Schrödinger-type equations, under the assumption that \({{\mathcal {T}}}^*\phi \in L^2_{\mathrm {loc}}\), which does not hold in our case because \(\phi \) is only in \(H^{-k}\). However, this regularity assumption is not essential in the case of the usual Schrödinger equation, as one can apply the argument to the mollified function
with a small enough parameter \(\eta '\) and \(F_{\eta '}\) as in the beginning of the proof. The details are just as above. Lemma 3.3 then follows. \(\square \)
4 Global Approximation Theorems for the Schrödinger Equation
The quantitative and non-quantitative global approximation theorems for the Schrödinger equation that we stated in the Introduction are proved in this section. We start with the quantitative result, which will readily give the non-quantitative one when combined with Lemma 3.3:
Proof of Theorem 1.5
Let us begin with the case of approximation in the whole cylinder \(\Omega =D\times \mathbb {R}\), which corresponds to the first part of the statement. For the sake of clarity, we will divide the proof in several steps.
Step 1: Approximation by a global solution of the Schrödinger equation that grows at spatial infinity As \(v\in L^2(\Omega )\) satisfies the Schrödinger equation in \(\Omega \), its time Fourier transform \({\widehat{v}}(x, \tau )\) must satisfy the Helmholtz–Yukawa equation
on D. Theorem 2.4 ensures that for every \(\varepsilon '>0\) there is a function \({{\widehat{\psi }}}(x,\tau )\) that satisfies the equation
on \(\mathbb {R}^n\) and approximates \({\widehat{v}}(x,\tau )\) as
Furthermore, \({{\widehat{\psi }}}(x,\tau )\) is bounded as

if \(|\tau |>\tau _1\) (where \(\tau _1\) is some fixed constant) and as
if \(|\tau |\leqslant \tau _1\). The quantity \(N_{\varepsilon ,\tau }\) was defined in (2.9) and we are taking
for some constant \(K>1+1/(2\sigma )\). Let us also recall from the proof of Theorem 2.4 that \({{\widehat{\psi }}}(x,\tau )\) is of the form
where \(Y_{lm}\) are normalized spherical harmonics, and that one has effective bounds (depending on \(\tau \) and \(\varepsilon \)) for the constants \(A_{lm}(\tau )\) and \(l_\tau \).
Equation (4.1), the approximation estimate (4.2) and the hypothesis
imply that one can take
with c a large constant independent of \(\varepsilon \), so that the function
satisfies the Schrödinger equation
on \(\mathbb {R}^{n+1}\) and approximates v as
It follows from the formula (4.6) and the bounds derived in Theorem 2.4 that \(v_1\) is a smooth function satisfying the pointwise bound
with
Step 2: Approximation via compactly supported initial data Let us now set
where \(\delta >0\) is a small positive constant to be determined later, and set
Note that \(u_\delta \) is obviously in the Schwartz space \({{\mathcal {S}}}(\mathbb {R}^n)\) by the bounds (4.3)-(4.4). Therefore, using the formula (4.6) and the integral formulation
one can write
where
Let us integrate over the angular variables first. Denoting the unit sphere by \(\mathbb {S}^{n-1}\), let us now record the expression for the Fourier transform of a spherical harmonic [10]:
Using this formula and introducing spherical coordinates
the function \({{\mathcal {B}}}_{lm}(x,t,\tau ;\delta )\) can be readily written as
where we have set, for \(r>0\),
We can now use the formula [17, 6.633.4] to compute the integral in closed form:
Plugging these formulas in the expression (4.8) and using the identity between Bessel functions (2.25), we readily find that
In view of the formula for \(v_1(x,t)\), the above limit can be rewritten as
uniformly for (x, t) in any compact spacetime subset.
To estimate the difference \(v_1-e^{it\Delta } u_\delta \) on \(\Omega _T=D\times (-T,T)\), it suffices to notice that the dependence on the parameter \(\delta \) (which only appears in the function \({{\mathcal {M}}}_{lm}(r,t,\tau ;\delta )\)) can be controlled using that
Therefore, using the bounds for Bessel functions as in Theorem 2.4 and the bounds for the constants \(\tau _\varepsilon \) and \(A_{lm}(\tau )\), after some straightforward manipulations one obtains that there is some \(\delta _T>0\), depending on T, such that
Here we have set
One can therefore take some positive \(\delta _\varepsilon \) of the form
such that
The \(L^2\) norm of the initial datum \(u_\delta \) can now be computed using the pointwise bound (4.7):
Note that the constants in \(N_\varepsilon \) may vary from line to line. The first assertion of Theorem 1.5 then follows.
Step 3: The interior approximation estimate The proof is exactly the same but one uses interior estimates for the function \({{\widehat{\psi }}}(x,\tau )\), which result in the sharper bound for \(v_1\)
Substituting this bound in the integral for the \(L^2\) norm of the initial datum \(u_\delta \), this yields
which completes the proof of the theorem. \(\square \)
The following result is a straightforward variation of Theorem 1.5 where we impose additional regularity on the local solution to control more derivatives of the functions involved. This is needed in the proof of Theorem 1.3. For concreteness, we only consider the interior case, which suffices for our purposes:
Lemma 4.1
Let \(\Omega := D\times \mathbb {R}\), where \(D\subset \mathbb {R}^n\) is a bounded set with smooth boundary whose complement \(\mathbb {R}^n\backslash D\) is connected. Take \(k\geqslant 1\) and fix some smaller set \(D'\subset \subset D\). Assume that \(v\in L^2H^k(\Omega )\) satisfies the Schrödinger equation (1.4) in \(\Omega \) and its time Fourier transform is bounded as
for some \(\sigma >0\) and all \(\tau _0\geqslant 0\). Then, for each \(\varepsilon \in (0,1)\) and any \(T>0\), one can take an initial datum \(u_0\in {{\mathcal {S}}}(\mathbb {R}^n)\) such that \(u:= e^{it\Delta } u_0\) approximates v on \(\Omega '_T:=D'\times (-T,T)\) as
and \(u_0\) is bounded as
The constant C depends on k, T and on the geometry of the domains.
Proof
The proof is just as in Theorem 1.5 modulo minor changes. Indeed, with the faster convergence rate that we have required on the integral (4.12) and the obvious estimate
the function \(v_1\), defined as above, is readily shown to approximate v as
One can define \(u_\delta \) as in the proof of Theorem (1.5) so that the approximation holds in \(L^2H^k\). Indeed, it is not hard to see that a statement just like (4.9) also holds when one takes spatial derivatives on both sides of the equation. To obtain bounds, it suffices to replace the estimate (4.11) by
The claim readily follows. \(\square \)
The non-quantitative approximation theorem stated in the Introduction is now an easy consequence of the results that we have already established:
Proof of Theorem 1.3
Assume that the set \(\Omega \) is contained in \(B_{R/2}\times (-R,R)\) and take an \((\Omega ,R)\)-admissible set S (see Definition 3.2). By Lemma 3.3, there is a function \(f\in C^\infty _c(S)\) such that the function \(u:={{\mathcal {T}}}f\) approximates v as
Note that, by definition, this function satisfies the Schrödinger equation
in \(B_R\times \mathbb {R}\). Furthermore, it follows from the fact that f is compactly supported and the expression of the fundamental solution G(x, t) that u is bounded as
Denoting by \(\widehat{u}(x,\tau )\) the Fourier transform of u(x, t) with respect to time, it then follows from the mapping properties of the Fourier transform that for all \(n\geqslant 2\) and all \(N\geqslant 1\) one has
where the constant depends on N. In view of this decay property of the time Fourier transform of u, the condition (4.12) holds for any positive integer k, so Lemma 4.1 ensures that there exists an initial datum \(w_0\in {{\mathcal {S}}}(\mathbb {R}^n)\) such that \(w:= e^{it\Delta }w_0\) approximates u as
The theorem is then proved. \(\square \)
5 Vortex Reconnection for the Gross–Pitaevskii Equation
In this section we provide the proof of the result on vortex reconnection for the Gross–Pitaevskii equation (Theorem 1.1). For convenience, we will divide the proof in three steps:
Step 1: Construction of a local solution using noncharacteristic hypersurfaces in spacetime. Let \(\Sigma \subset \mathbb {R}^4\) be a pseudo-Seifert surface connecting the curves \(\Gamma _0,\Gamma _1\subset \mathbb {R}^3\) in time T, as defined in the Introduction. The existence of these surfaces is standard because all closed curves in \(\mathbb {R}^4\) are isotopic. (It should be noticed, however, that in general one cannot choose \(\Sigma \) as a knot cobordism, that is, homeomorphic to \(\Gamma _0\times (0,1)\).) One can also extend \(\Sigma \) so that it is defined for times slightly smaller than 0 and slightly larger than T.
Moreover, if necessary one can deform the curves \(\Gamma _0,\Gamma _1\) with a smooth diffeomorphism arbitrarily close to the identity in the \(C^k\) norm to ensure that the curves \(\Gamma _0,\Gamma _1\) and the surface \(\Sigma \) are real analytic, and that \(\Sigma \) is in general position with respect to the time axis in the sense that the set of points
is finite. Here \(e_4:= (0,0,0,1)\) is the time direction and \(N_{(x,t)}\Sigma \) is the normal plane of \(\Sigma \) at the point (x, t). We will label all the points of this form as
Equivalently, this means that, after deforming \(\Sigma \) by a small diffeomorphism if necessary, the coordinate t is a Morse function on \(\Sigma \), so the claim is a straightforward consequence of the density of Morse functions [18, Theorem 6.1.2]. It is also standard that we can assume all the critical points \(X_j\) of the function \(t|_\Sigma \) correspond to different critical values, meaning that \(t_k\ne t_j\) for all \(1\leqslant j\ne k\leqslant J\). For future reference, let us denote the set of these critical times by
Observe that an equivalent characterization of this set is
We now claim that there exists a vector field a(x, t) on \(\mathbb {R}^4\) such that, for every point \((x,t)\in \Sigma \), the vector
is not parallel to the time direction, \(e_4\) (in particular, nonzero). Here \((\tau _1,\tau _2)\) is any oriented orthonormal basis of the tangent space \(T_{(x,t)}\Sigma \) and the product of three vectors \(V_1\wedge V_2\wedge V_3\) in \(\mathbb {R}^4\) is defined as 0 if the vectors are linearly dependent and as the only vector, modulo a multiplicative factor that is inessential for our present purpose, that is orthogonal to \(V_1\), \(V_2\) and \(V_3\). (The multiplicative factor is of course determined by the norms of \(V_j\) and the orientation of \(\mathbb {R}^4\).)
To show the existence of the vector field a(x, t), let us recall that the normal bundle of \(\Sigma \) in \(\mathbb {R}^4\) is trivial [31], so there are analytic vector fields \(N_1(x,t)\) and \(N_2(x,t)\) on \(\mathbb {R}^4\) such that
One can then write the vector field a as
where \(f_1,f_2\) are analytic real-valued functions on \(\mathbb {R}^4\) to be determined. Since obviously the vector W(x, t) must be normal to the surface \(\Sigma \) at the point (x, t) and \(e_4\) is only normal at the finite number of points specified in (5.1), it is clear that the only conditions that the functions \(f_1,f_2\) must satisfy are
for \(1\leqslant j\leqslant J\) to ensure that \(W(x_j,t_j)\) is not parallel to \(e_4\) at these points and
for all \((x,t)\in \Sigma \) to make sure that W(x, t) is always nonzero. The existence of the functions \(f_1,f_2\) is then apparent.
Now that we have the vector field a(x, t), we can next define an analytic hypersurface S in \(\mathbb {R}^4\) as
where \(s_0>0\) is small enough. It follows from the construction that the normal direction N of S, which is proportional to the vector field W defined in (5.3) modulo an error of size \(O(s_0)\), is never parallel to the time direction, \(e_4\). Furthermore, it is clear from the definition of S that it is diffeomorphic to the product \(\Sigma \times (-s_0,s_0)\), so one can take a real-valued analytic function \(\phi :S\rightarrow \mathbb {R}\) on the hypersurface S such that
and its gradient is transverse to \(\Sigma \), i.e., that its intrinsic gradient (or covariant derivative) \(\nabla _S\phi \) does not vanish on \(\Sigma \).
Consider the Cauchy problem
where N is a unit normal vector to the hypersurface S in \(\mathbb {R}^4\) and \(\nabla _{x,t} v\) denotes the spacetime gradient of v. The hypersurface S is non-characteristic for the Schrödinger equation because N is never parallel to the time direction. Hence the Cauchy–Kowalewskaya theorem ensures that there exists a real analytic solution v to the problem (5.5) defined in a neighborhood \(V\subset \mathbb {R}^4\) of S.
An important observation is that
provided that we take a small enough neighborhood V. In order to see this, let us denote the real and imaginary parts of v by
and notice that the Cauchy conditions we have imposed can be rewritten as
Therefore \(v_2\) only vanishes on S, while \((v_1|_S)^{-1}(1)=\Sigma \). Furthermore, the gradients of \(v_1\) and \(v_2\) are transverse on \(\Sigma =v_1^{-1}(1)\cap v_2^{-1}(0)\), that is,
This is clear because \(N\cdot \nabla _{x,t}v_1|_S=0\), which ensures that
which is transverse to \(\Sigma \) by the definition of \(\phi \), while \(\nabla _{x,t}v_2|_S=N\).
Step 2: Robust geometric properties of the local solution. By Eq. (3.45.6), it is clear that
for all t, where we recall that \(\Sigma _{t_0}:=\{(x,t)\in \Sigma : t=t_0\}\) is the intersection of \(\Sigma \) with the time \(t_0\) slice. As t is a Morse function on \(\Sigma \) by construction, the reconnection times \(t_j\) must be critical values of the function \(t|_\Sigma \) because the constant time slice and the surface \(\Sigma \) stop being transverse (that is, the vector \(e_4\) belongs to the normal plane at the critical point \(X_j:=(x_j,t_j)\in \Sigma \)). Besides, as the critical level \(\{t= t_j\}\cap \Sigma \) must be a curve (i.e., of dimension 1), it follows that the critical point \(X_j\) must be a saddle point, that is, of Morse index 1. The Morse lemma then ensures that there are smooth local coordinates \((y_1,y_2)\) on a small neighborhood of \(X_j\) in \(\Sigma \) such that, in that neighborhood,
Furthermore, with \(X:=(x,t)\in \mathbb {R}^4\), there are two linearly independent vectors \(V_1,V_2\) on \(\mathbb {R}^4\) such that
Since the distance between the two sheets of the hyperbola (5.7) is
when measured with respect to the metric \(dy_1^2+dy_2^2\), it follows from (5.8) that the distance \(d_j(t)\) between the corresponding two components of the set \(Z_{1-v}(t)\) near the reconnection time \(t_j\) is bounded as
It is also a standard consequence of Morse theory for functions on a surface whose critical points have all distinct critical values that the parity of the number of components of a level set changes as one crosses a critical value.
The above geometric construction is robust under suitable perturbations of the function v. More precisely, Thom’s transversality theorem [1, Theorem 20.2] ensures that, given any \(k\geqslant 1\) and \(\delta >0\), there exists some \(\varepsilon >0\) such that:
-
(i)
The level set of value 1 of any function w with
$$\begin{aligned} \Vert w-v\Vert _{C^k(V)}<\delta \end{aligned}$$(5.10)satisfies
$$\begin{aligned} w^{-1}(1)\cap V= \Psi (\Sigma )\,, \end{aligned}$$(5.11)where \(\Psi \) is a smooth diffeomorphism of \(\mathbb {R}^4\) with \(\Vert \Psi -\mathrm{id}\Vert _{C^k(\mathbb {R}^{n+1})}<\varepsilon \).
-
(ii)
There is a finite union of closed intervals \({{\mathcal {I}}}\subset (0,T)\) containing the set \({{\mathcal {P}}}\) (cf. (5.2)) of total length less than \(\varepsilon \) and a continuous one-parameter family of diffeomorphisms \(\{\Phi ^t\}_{t\in \mathbb {R}}\) of \(\mathbb {R}^3\) with \(\sup _{t\in \mathbb {R}}\Vert \Phi ^t-\mathrm{id}\Vert _{C^k(\mathbb {R}^3)}<\varepsilon \) such that \(\Phi ^t(\Sigma _t)= Z_{1-w}(t)\cap V\) for all \(t\in [0,T]\backslash {{\mathcal {I}}}\).
-
(iii)
The distance \(d_j(t)\) between the two components of the set \(Z_{1-w}(t)\cap V\) near a critical point \(X_j'\) of index 1 of the Morse function \(t|_{\Phi (\Sigma )}\) is bounded as in Eq. (5.9).
-
(iv)
The parity of the number of components of \(Z_{1-w}(t)\cap V\) is different at each time \(t= t_j-\delta '\) and \(t_j+\delta '\), for any small enough \(\delta '>0\).
Remark 5.1
By an easy transversality argument, one can provide a more exhaustive description of the zero set \(Z_{1-w}(t)\) as follows. For \(t\in [0,T]\backslash {{\mathcal {I}}}\), item (ii) means that \(Z_{1-w}(t)\cap V\) is a small deformation of the smooth embedded curve \(\Sigma _t\) that corresponds to the intersection of the spacetime surface \(\Sigma \) with the time slice \(\mathbb {R}^3\times \{t\}\). The times \(t_0\in {{\mathcal {P}}}\) are those at which the curve \(\Sigma _{t_0}\) self-intersects, so that \(\Sigma _{t_0}\) is then a smooth immersed curve. What happens is that there is another finite set \({{\mathcal {P}}}'\), at a distance at most \(\varepsilon \) of \({{\mathcal {P}}}\) and of the same cardinality, such that for all \(t_0'\in {{\mathcal {P}}}'\), \(Z_{1-w}(t_0')\cap V\) is also a smooth immersed curve, while for \(t\in {{\mathcal {I}}}\) slightly above or below a critical time \(t_0'\in {{\mathcal {P}}}'\) as above, the zero set \(Z_{1-w}(t)\cap V\) is a smooth embedded curve with the same structure as before.
Step 3: Construction of the solution to the Gross–Pitaevskii equation. Theorem 1.3 and Remark 1.4 guarantee that there exists a Schwartz function \(w_0\in {{\mathcal {S}}}(\mathbb {R}^n)\) such that \(w:=e^{it\Delta }w_0\) approximates the above function v as
where \(k\geqslant 1\) can be chosen at will.
Let us now consider the rescaled Gross–Pitaevskii equation
on \(\mathbb {R}^3\) with initial datum
where \(\delta >0\) is a small constant. In view of Duhamel’s formula
it is standard (see e.g. [35]) that, for all small enough \(\delta \), there exists a global solution \(\widetilde{u}\) to this equation with
which is bounded as
for any \(T>0\). The constant C depends on T and \(w_0\) but not on \(\delta \). It then follows from our application of Thom’s isotopy theorem (5.10) in Step 2 that the zero set \(\widetilde{u}^{-1}(0)\) satisfies (5.11) for some smooth diffeomorphism \(\Psi \) of \(\mathbb {R}^4\) with \(\Vert \Psi -\mathrm{id}\Vert _{C^k(\mathbb {R}^4)}<\varepsilon \), and that the zero set \(Z_{\widetilde{u}}(t)\) is of the form described in item (ii) of Step 2. Also by Step 2, \(\widetilde{u}\) satisfies the \(t^{1/2}\) law and the change of parity property.
Notice that the function
satisfies the Gross–Pitaevskii equation
and tends to 1 as
Since u is just an (anisotropic) rescaling of \(\widetilde{u}\), we infer that the zero set of u is of the form described in the statement of the theorem.
6 Comparison with Experimental Observations and Solutions with Other Conditions at Infinity
6.1 Comparison with experimental results
A remarkable feature of the strategy that we have employed to prove the existence of solutions to the Gross–Pitaevskii equation featuring vortex reconnection is that it presents the same qualitative properties that are observed in the physics literature:
6.1.1 The \(t^{1/2}\) law
As we discussed in the Introduction, in the reconnection scenarios that we construct, the distance between reconnecting vortices near the reconnection time T behaves as \(|t-T|^{1/2}\). This is in perfect agreement with the \(t^{1/2}\) law for the separation velocities that have measured in the laboratory [7], observed numerically [37] and heuristically explained in [32].
6.1.2 Change of parity of the components at reconnection
We also stressed that the parity of the number of reconnecting quantum vortices is numerically observed to change at each reconnection time [26], as depicted in Fig. 1. The reconnection scenarios we construct also feature this property as an indirect consequence of Morse theory for functions on surfaces.
6.1.3 Birth and death of quantum vortices
Numerical simulations also show that quantum vortices can be created or destroyed [26], as also shown in Fig. 1 (bottom). This is a degenerate case of vortex reconnection that appears, in our scenarios, whenever the Morse function \(t|_\Sigma \) has any local extrema.
6.1.4 Pseudo-Seifert surfaces as a universal scenario of vortex reconnection
The time evolution of a quantum vortex (which is generically, at each time, a smooth curve in \(\mathbb {R}^3\)) automatically defines a surface \(\Sigma \) in spacetime \(\mathbb {R}^4\). Generically, this surface is smooth by Sard’s theorem and the time coordinate is a Morse function on \(\Sigma \). Therefore, the description of vortex reconnection we use in the construction of the scenarios is, in a way, universal.
6.1.5 Physical limitations of the result
There are two interesting aspects of vortex reconnection that our result does not capture. The first one is that, although we know it is finite, we cannot estimate the number of vortices at each time (i.e., of connected components of the zero set \(Z_u(t)\)). Hence a heuristic explanation of the freedom in prescribing reconnections that we show is that there can be an enormous number of vortices in interaction. Another limitation is that we cannot estimate the probability of a certain reconnection scenario. Intuitively, this is because we only employ the linear regime of the equation, while to ascertain which transition is most energy-efficient globally one should also understand nonlinear effects.
6.2 Solutions to NLS that decay at infinity: the case of laser beams
It is folk wisdom in physics that, in the Gross–Pitaevskii equation, if one replaces the asymptotic condition \(u(x,t)\rightarrow 1\) as \(|x|\rightarrow \infty \) by a decay condition (e.g., that u be square integrable), it should be easier to show that there is a wealth of reconnections. In the language of physics, this is because the condition \(u\rightarrow 1\) is associated with the existence of a chemical potential at infinity. In constrast, the decay condition \(u\rightarrow 0\) corresponds to the more flexible case of optical vortices, which describes laser beams [12].
We shall next mention how the strategy that we have developed applies to the case of laser beams (and to many other nonlinear Schrödinger equations). Remarkably, we do find that in this setting the argument leads to a stronger reconnection theorem, in that the diffeomorphism that appears in the statement can be arbitrarily close to the identity:
Theorem 6.1
Consider two links \(\Gamma _0,\Gamma _1\subset \mathbb {R}^3\) and a pseudo-Seifert surface \(\Sigma \subset \mathbb {R}^4\) connecting \(\Gamma _0\) and \(\Gamma _1\) in time \(T>0\). For any \(\varepsilon >0\) and any \(k>0\), there is a Schwartz initial datum \(u_0\in {{\mathcal {S}}}(\mathbb {R}^3)\) such that the corresponding solution to the Gross–Pitaevskii equation \(u\in C^\infty _{\mathrm {loc}}(\mathbb {R}, {{\mathcal {S}}}(\mathbb {R}^3))\) realizes the vortex reconnection pattern described by \(\Sigma \) up to a small deformation. More precisely, for any fixed \(\varepsilon >0\) and \(k>0\), the properties (ii)–(iv) of Theorem 1.1 hold with \(\eta :=1\).
Proof
The proof goes just as in Theorem 1.1. Indeed, Steps 1 and 2 apply directly in this setting, the only difference being that the level sets \(v^{-1}(1)\) and \(Z_{1-v}(t)\) (and similarly for w) have to be replaced by \(v^{-1}(0)\) and \(Z_v(t)\), and that the condition \(\phi ^{-1}(1)=\Sigma \) (Eq. (5.4)) must be replaced by
In Step 3, one similarly considers the rescaled modified Gross–Pitaevskii equation
on \(\mathbb {R}^3\) with initial datum
where \(\delta >0\) is a small constant. Another easy argument using Duhamel’s formula then yields that for all small enough \(\delta \) there exists a global solution \(\widetilde{u}\in C^\infty _{\mathrm {loc}}(\mathbb {R},{{\mathcal {S}}}(\mathbb {R}^3))\) to this equation, which is bounded as
The results about the robustness of the geometric properties of v proved in Step 2 obviously apply to \(\widetilde{u}\). If we now note that the function
satisfies the Gross–Pitaevskii equation
and has the same zero set as \(\widetilde{u}\), the result then follows. \(\square \)
Remark 6.2
It is clear from the proof that Theorem 6.1 holds verbatim if one replaces the Gross–Pitaevskii equation by a NLS equation of the form
provided that the nonlinearity \(V(u,{\overline{u}})\) is subcritical, a smooth enough function of u and \({\overline{u}}\), and of order o(|u|) for \(|u|\ll 1\). In particular, the result obviously holds for the linear Schrödinger equation.
6.3 The periodic case: the Gross–Pitaevskii equation on \(\mathbb {T}^3\)
To conclude, we shall next sketch how the above results can be extended to the case of the Gross–Pitaevskii equation
when the spatial variable takes values in the 3-torus \(\mathbb {T}^3:= (\mathbb {R}/2\pi \mathbb {Z})^3\).
For the ease of notation, we regard the unit ball \(B_1\subset \mathbb {R}^3\) as a subset of \(\mathbb {T}^3\) with the obvious identification. The dilation \(\Lambda _\eta \), introduced in (1.3), can then be understood as a map from \(B_1\subset \mathbb {T}^3\) into itself provided that \(\eta <1\).
Theorem 6.3
Consider two links \(\Gamma _0,\Gamma _1\) contained in the unit ball \(B_1\subset \mathbb {R}^3\) and a pseudo-Seifert surface \(\Sigma \) connecting \(\Gamma _0\) and \(\Gamma _1\) in time \(T>0\). We assume that \(\Sigma \) is contained in the spacetime cylinder \(B_1\times \mathbb {R}\). For any \(\varepsilon >0\) and any \(k>0\), there is an initial datum \(u_0\in C^\infty (\mathbb {T}^3)\) such that the corresponding solution to the Gross–Pitaevskii equation \(u\in C^\infty _{\mathrm {loc}}(\mathbb {T}^3\times \mathbb {R})\) realizes the vortex reconnection pattern described by \(\Sigma \) up to a diffeomorphism. Specifically:
-
(i)
The evolution of the vortex set \(Z_u(t)\) is known for all times during the reconnection process: there is some \(\eta >0\) and a diffeomorphism \(\Psi \) of \(\mathbb {T}^3\times \mathbb {R}\) with \(\Vert \Psi -\mathrm{id}\Vert _{C^k(\mathbb {T}^3\times \mathbb {R})}<\varepsilon \) such that \(\Lambda _{\eta }[\Psi (\Sigma )_t]\) is a union of connected components of \(Z_u(\eta ^2 t)\) for all \(t\in [0,T]\).
-
(ii)
In particular, there is a smooth one-parameter family of diffeomorphisms \(\{\Phi ^t\}_{t\in \mathbb {R}}\) of \(\mathbb {T}^3\) with \(\Vert \Phi ^t-\mathrm{id}\Vert _{C^k(\mathbb {T}^3)}<\varepsilon \) and a finite union of closed intervals \({{\mathcal {I}}}\subset (0,T)\) of total length less than \(\varepsilon \) such that \(\Lambda _\eta [\Phi ^t(\Sigma _t)]\) is a union of connected components of the set \(Z_u(\eta ^2 t)\) for all \(t\in [0,T]\backslash {{\mathcal {I}}}\).
-
(iii)
The separation distance obeys the \(t^{1/2}\) law and the parity of the number of quantum vortices of \(\Phi ^t(\Sigma _t)\) changes at each reconnection time.
Proof
By Remark 6.2, there is a Schwartz initial datum \(v_0\in {{\mathcal {S}}}(\mathbb {R}^3)\) such that the solution to the Schrödinger equation on \(\mathbb {R}^3\) \(v:=e^{it\Delta }v_0\) realizes the reconnection pattern defined by \(\Sigma \) up to a small deformation and satisfies the properties described in Theorem 6.1. We can assume that this reconnection takes place in the bounded spacetime domain \(B_1\times (0,T)\).
Note that v can be written in terms of the Fourier transform of \(v_0\) as
As \({\widehat{v}}_0\) is a Schwartz function, it is standard that, for (x, t) in the bounded set \(B_1\times (0,T)\), the above integral can be approximated by a Riemann sum of the form
as
where k and \(\varepsilon >0\) are fixed but arbitrary and J is a large positive integer. One possible way of choosing the points \(\xi _j\) is by taking a cube of side J centered at the origin, dividing it into \(J^6\) cubes of side \(J^{-1}\) and letting \(\xi _j\) be any point in the \(j^{\mathrm {th}}\) cube. For a large enough J, it is clear that the approximation bound (6.2) will hold. It is also apparent that one can pick all the points \(\xi _j\) rational, i.e., \(\xi _j\in \mathbb Q^3\). Observe that the approximation estimate and the stability under small perturbations of reconnection scenarios that we constructed in Theorem 6.1 ensures that \(v_1\) features reconnections that are diffeomorphic to, and a small deformation of, those described by the pseudo-Seifert surface \(\Sigma \).
Let N be the height of the point \((\xi _1,\xi _2,\dots , \xi _{J^6})\in {\mathbb {Q}}^{3J^6}\), that is, the least common denominator of its coordinates in reduced form, and define
By the way we have picked N it is clear that w(x, t) defines a function in \(C^\infty _{\mathrm {loc}}(\mathbb {T}^3\times \mathbb {R})\) that satisfies the Schrödinger equation on the 3-torus:
The zero set of w is simply the image of the zero set of \(v_1|_{(-\pi N,\pi N)^3\times \mathbb {R}}\) under the map
In view of the properties of \(v_1= w\circ \Theta _N\), this immediately implies that w features reconnections contained in the set \(B_{1/N}\times (0,T/N^2)\) that are diffeomorphic to the scenario described by \(\Sigma \) and satisfy the properties of the statement. This fact is robust under small perturbations.
It is now easy to promote this solution of the linear Schrödinger equation on \(\mathbb {T}^3\) to a global smooth solution of the modified Gross–Pitaevskii equation
on \(\mathbb {T}^3\) that is close to w using Duhamel’s formula and Bourgain’s dispersive estimates on the torus [8]. This can be transformed into a solution to the Gross–Pitaevskii equation using the formula (6.1) just as in Theorem 6.1. This completes the proof of the theorem with \(\eta :=1/N\). \(\square \)
References
Abraham, R., Robbin, J.: Transversal Mappings and Flows. Benjamin, New York (1967)
Alessandrini, G., Rondi, L., Rosset, E., Vessella, S.: The stability for the Cauchy problem for elliptic equations. Inverse Probl. 25, 123004 (2009)
Aranson, I.S., Kramer, L.: The world of the complex Ginzburg–Landau equation. Rev. Mod. Phys. 74, 99–143 (2002)
Balodis, P., Córdoba, A.: The convergence of multidimensional Fourier–Bessel series. J. Anal. Math. 77, 269–286 (1999)
Banica, V., Vega, L.: Scattering for 1D cubic NLS and singular vortex dynamics. J. Eur. Math. Soc. 14, 209–253 (2012)
Banica, V., Vega, L.: The initial value problem for the binormal flow with rough data. Ann. Sci. Éc. Norm. Supér. 48, 1423–1455 (2015)
Bewley, G.P., Paoletti, M.S., Sreenivasan, K.R., Lathrop, D.P.: Characterization of reconnecting vortices in superfluid helium. Proc. Natl. Acad. Sci. 105, 13707–13710 (2008)
Bourgain, J.: Global Solutions of Nonlinear Schrödinger Equations. AMS, Providence (1999)
Browder, F.E.: Approximation by solutions of partial differential equations. Am. J. Math. 84, 134–160 (1962)
Canzani, Y., Sarnak, P.: Topology and nesting of the zero set components of monochromatic random waves. Commun. Pure Appl. Math. 72, 343–374 (2019)
Chandler-Wilde, S.N., Hewett, D.P., Moiola, A.: Sobolev spaces on non-Lipschitz subsets of \({\mathbb{R}}^n\) with application to boundary integral equations on fractal screens. Integral Equ. Oper. Theor. 87, 179–224 (2017)
Dennis, M.R., King, R.P., Jack, B., O’Holleran, K., Padgett, M.J.: Isolated optical vortex knots. Nat. Phys. 6, 118–121 (2010)
Donnelly, H., Fefferman, C.: Nodal sets of eigenfunctions on Riemannian manifolds. Invent. Math. 93, 161–183 (1988)
Enciso, A., García-Ferrero, M.A., Peralta-Salas, D.: Approximation theorems for parabolic equations and movement of local hot spots. Duke Math. J. 168, 897–939 (2019)
Enciso, A., Lucà, R., Peralta-Salas, D.: Vortex reconnection in the three dimensional Navier–Stokes equations. Adv. Math. 309, 452–486 (2017)
Escauriaza, L., Vessella, S.: Optimal three cylinder inequalities for solutions to parabolic equations with Lipschitz leading coefficients. Contemp. Math. 333, 79–87 (2003)
Gradshteyn, I.S., Ryzhik, I.M.: Table of Integrals, Series, and Products. Academic, Amsterdam (2015)
Hirsch, M.W.: Differential Topology. Springer, New York (1994)
Hörmander, L.: The Analysis of Linear Partial Differential Operators I. Springer, Berlin (2003)
Isakov, V.: Carleman type estimates in an anisotropic case and applications. J. Differ. Equ. 105, 217–238 (1993)
Jerrard, R.L., Seis, C.: On the vortex filament conjecture for Euler flows. Arch. Ration. Mech. Anal. 224, 135–172 (2017)
Jerrard, R.L., Soner, H.M.: Dynamics of Ginzburg–Landau vortices. Arch. Ration. Mech. Anal. 142, 99–125 (1998)
Kato, T.: Growth properties of solutions of the reduced wave equation with a variable coefficient. Commun. Pure Appl. Math. 12, 403–425 (1959)
Kenig, C.E., Ponce, G., Vega, L.: On the interaction of nearly parallel vortex filaments. Commun. Math. Phys. 243, 471–483 (2003)
Kenig, C.E., Sogge, C.D.: A note on unique continuation for Schrödinger’s operator. Proc. Am. Math. Soc. 103, 543–546 (1988)
Kleckner, D., Kauffman, L.H., Irvine, W.T.M.: How superfluid vortex knots untie. Nat. Phys. 12, 650–655 (2016)
Lannes, D.: The Water Waves Problem. AMS, Providence (2013)
Lax, P.D.: A stability theorem for solutions of abstract differential equations, and its application to the study of the local behavior of solutions of elliptic equations. Commun. Pure Appl. Math. 9, 747–766 (1956)
Lieb, E.H., Seiringer, R., Solovej, J.P., Yngvason, J.: The Mathematics of the Bose Gas and Its Condensation. Birkhäuser, Basel (2005)
Malgrange, B.: Existence et approximation des solutions des équations aux dérivées partielles et des équations de convolution. Ann. Inst. Fourier 6, 271–355 (1955–1956)
Massey, W.S.: On the normal bundle of a sphere imbedded in Euclidean space. Proc. Am. Math. Soc. 10, 959–964 (1959)
Nazarenko, S., West, R.: Analytical solution for nonlinear Schrödinger vortex reconnection. J. Low Temp. Phys. 132, 1–10 (2003)
Perthame, B., Vega, L.: Energy concentration and Sommerfeld condition for Helmholtz equation with variable index at infinity. Geom. Funct. Anal. 17, 1685–1707 (2008)
Rüland, A., Salo, M.: Quantitative Runge approximation and inverse problems. Int. Math. Res. Not. 20, 6216–6234 (2019)
Tao, T.: Nonlinear Dispersive Equations. AMS, Providence (2006)
Tataru, D.: Carleman estimates, unique continuation and applications. https://math.berkeley.edu/ tataru/papers/ucpnotes.ps
Villois, A., Proment, D., Krstulovic, G.: Universal and nonuniversal aspects of vortex reconnections in superfluids. Phys. Rev. Fluids 2, 044701 (2017)
Acknowledgements
The authors are indebted to Luis Escauriaza for explanations concerning three-sphere inequalities for the Schrödinger equation, including the counterexample that we can construct using a Tychonov-type argument. A.E. is supported by the ERC Consolidator Grant 862342. D.P.-S. is supported by the grants MTM PID2019-106715GB-C21 (MICINN) and Europa Excelencia EUR2019-103821 (MCIU). This work is supported in part by the ICMAT–Severo Ochoa grant CEX2019-000904-S.
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by K. Nakanishi
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A. Uniform lower bounds for the integral of a Bessel function
Appendix A. Uniform lower bounds for the integral of a Bessel function
Notice that the function \({{\mathcal {I}}}_\nu (\alpha )\), introduced in (2.24), can be written as
where we define \(Z_\nu (z):= J_\nu (z)\) if \(\alpha \in i\mathbb {R}^+\) and \(Z_\nu (z):= I_\nu (z)\) if \(\alpha \in \mathbb {R}^+\). Hence a first observation that is useful when computing lower bounds for the function \({{\mathcal {I}}}_\nu (\alpha )\) is that \(|\alpha |^2 {{\mathcal {I}}}_\nu (\alpha )\) is an increasing function of \(|\alpha |\).
We will write \(F\approx G\) if there is a positive constant (which does not depend on \(\nu \) or \(\alpha \)), such that
Likewise, \(F\lesssim G\) means that \(F\leqslant CG\) with C as above, and \(F\ll G\) means that \(F\leqslant \delta G\) for a certain small constant \(\delta \), again independent of \(\nu \) or \(\alpha \).
Lemma A.1
With \(\alpha \in \mathbb {R}^+\cup i\mathbb {R}^+\) and \(\nu \geqslant \frac{1}{2}\), the function \({{\mathcal {I}}}_\nu (\alpha )\) satisfies the lower bound
Proof
We need to analyze the different cases separately:
Case 1: \(|\alpha |\lesssim 1\) and \(\nu \lesssim 1\) The asymptotics for Bessel functions near zero [17, 8.440 and 8.445], \(I_\nu (z)= C z^\nu +O(z^{\nu +1})\), together with the fact that \(I_\nu (z)\) is obviously of order 1 if \(\nu \) and |z| are, immediately yield that
in this region of the parameter space.
Case 2: \(|\alpha |\gg 1\) and \(\nu \lesssim 1\) The usual large time asymptotics for Bessel functions of fixed order [17, 8.451.1 and 8.451.5],
ensure that
if \(\alpha \in \mathbb {R}^+\), while for \(\alpha \in i\mathbb {R}^+\)
Case 3: \(|\alpha |\lesssim 1\) and \(\nu \gg 1\) The asymptotic expansions for Bessel functions of large order [17, 8.452.1],
ensure that
Case 4: \(|\alpha |\gg 1\) and \(\nu \gg 1\) Since \(|\alpha |^2\, {{\mathcal {I}}}_\nu (\alpha )\) is an increasing function of \(|\alpha |\), from Case 3 we immediately get that
Putting all the cases together we arrive at the bounds in the statement. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Enciso, A., Peralta-Salas, D. Approximation Theorems for the Schrödinger Equation and Quantum Vortex Reconnection. Commun. Math. Phys. 387, 1111–1149 (2021). https://doi.org/10.1007/s00220-021-04177-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-021-04177-w








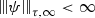 for all
for all  for all
for all