Skip to main content
SpringerLink
Log in

Stability and Instability of Extreme Reissner-Nordström Black Hole Spacetimes for Linear Scalar Perturbations I

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

Abstract

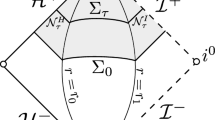
We study the problem of stability and instability of extreme Reissner-Nordström spacetimes for linear scalar perturbations. Specifically, we consider solutions to the linear wave equation \({\square_{g}\psi=0}\) on a suitable globally hyperbolic subset of such a spacetime, arising from regular initial data prescribed on a Cauchy hypersurface Σ0 crossing the future event horizon \({\mathcal{H}^{+}}\) . We obtain boundedness, decay and non-decay results. Our estimates hold up to and including the horizon \({\mathcal{H}^{+}}\) . The fundamental new aspect of this problem is the degeneracy of the redshift on \({\mathcal{H}^{+}}\) . Several new analytical features of degenerate horizons are also presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. Alinhac, S.: Geometric analysis of hyperbolic differential equations: An introduction, The London Mathematical Society, Lecture Note Series 374, Cambridge: Cambridge Univ. Press, 2010

  2. Andersson, L., Blue, P.: Hidden symmetries and decay for the wave equation on the Kerr spacetime. http://arxiv.org/abs/0908.2265v2 [math.Ap], 2009

  3. Aretakis, S.: Stability and Instability Of Extreme Reissner-Nordström Black Hole Spacetimes for Linear Scalar Perturbations II. Preprint

  4. Aretakis, S.: The Price Law for Self-Gravitating Scalar Fields On Extreme Black Hole Spacetimes. Preprint

  5. Bičák J.: Gravitational collapse with charge and small asymmetries I: scalar perturbations. Gen. Rel. Grav. 3(4), 331–349 (1972)

    Article  ADS  Google Scholar 

  6. Blue P., Soffer A.: Semilinear wave equations on the Schwarzschild manifold. I. Local decay estimates. Adv. Diff. Eqs. 8(5), 595–614 (2003)

    MathSciNet  MATH  Google Scholar 

  7. Blue P., Sterbenz J.: Uniform decay of local energy and the semi-linear wave equation on Schwarzschild space. Commun. Math. Phys. 268(2), 481–504 (2006)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  8. Blue P., Soffer A.: Phase space analysis on some black hole manifolds. J. Func. Anal. 256(1), 1–90 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  9. Blue, P., Soffer, A.: Improved decay rates with small regularity loss for the wave equation about a Schwarzschild black hole. http://arxiv.org/abs/math/0612168v1 [math.Ap], 2006

  10. Christodoulou, D., Klainerman, S.: The Global Nonlinear Stability of the Minkowski Space. Princeton, NJ: Princeton University Press, 1994

  11. Christodoulou D.: On the global initial value problem and the issue of singularities. Class. Quant. Grav. 16(12A), A23–A35 (1999)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  12. Christodoulou D.: The instability of naked singularities in the gravitational collapse of a scalar field. Ann. of Math. 149(1), 183–217 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  13. Christodoulou D.: The Action Principle and Partial Differential Equations. Princeton University Press, Princeton, NJ (2000)

    MATH  Google Scholar 

  14. Christodoulou, D.: The Formation of Black Holes in General Relativity. Zurich: European Mathematical Society Publishing House, 2009

  15. Chruściel P.T., Tod K.P.: The classification of static electro-vacuum space-times containing an asymptotically flat spacelike hypersurface with compact interior. Commun. Math. Phys. 271, 577–589 (2007)

    Article  ADS  MATH  Google Scholar 

  16. Chruściel, P.T., Nguyen, L.: A uniqueness theorem for degenerate Kerr-Newman black holes. http://arxiv.org/abs/1002.1737v1 [gr-qc], 2010

  17. Dafermos M.: Stability and instability of the Cauchy horizon for the spherically symmetric Einstein-Maxwell-scalar field equations. Ann. of Math. 158(3), 875–928 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  18. Dafermos M.: The interior of charged black holes and the problem of uniqueness in general relativity. Comm. Pure App. Math. 58(4), 445–504 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  19. Dafermos M., Rodnianski I.: A proof of Price’ s law for the collapse of a self-gravitating scalar field. Invent. Math. 162, 381–457 (2005)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  20. Dafermos M., Rodnianski I.: The redshift effect and radiation decay on black hole spacetimes. Comm. Pure Appl. Math. 62, 859–919 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  21. Dafermos, M., Rodnianski, I.: The wave equation on Schwarzschild-de Sitter spacetimes. http://arxiv.org/abs/0709.2766v1 [gr-qc], 2007

  22. Dafermos, M., Rodnianski, I.: A note on energy currents and decay for the wave equation on a Schwarzschild background. http://arxiv.org/abs/0710.0171v1 [math.Ap], 2007

  23. Dafermos, M., Rodnianski, I.: A proof of the uniform boundedness of solutions to the wave equation on slowly rotating Kerr backgrounds. http://arxiv.org/abs/0805.4309v2 [gr-qc], 2008

  24. Dafermos, M., Rodnianski, I.: Lectures on Black Holes and Linear Waves. http://arxiv.org/abs/0811.0354v1 [gr-qc], 2008

  25. Dafermos, M.: The evolution problem in general relativity, Current developments in mathematics 2008, Somerville, MA: Int. Press, 2009, pp. 1-66

  26. Dafermos, M., Rodnianski, I.: A new physical-space approach to decay for the wave equation with applications to black hole spacetimes. http://arxiv.org/abs/0910.4957v1 [math.Ap], 2009, Submitted to proc. ICMP, prague, Aug, 2009

  27. Dafermos, M., Rodnianski, I.: Decay for solutions of the wave equation on Kerr exterior spacetimes I−II: The cases \({\left|a\right|\ll M}\) or axisymmetry. http://arxiv.org/abs/1010.5132v1 [gr-qc], 2010

  28. Dafermos, M., Rodnianski, I.: The black holes stability problem for linear scalar perturbations. http://arxiv.org/abs/1010.5137v1 [gr-qc], 2010

  29. Donninger, R., Schlag, W., Soffer, A.: On pointwise decay of linear waves on a Schwarzschild black hole background. http://arxiv.org/abs/0911.3179v1 [math.Ap], 2009

  30. Finster F., Kamran N., Smoller J., Yau S.T.: Decay of solutions of the wave equations in the Kerr geometry. Commun. Math. Phys. 264(2), 221–255 (2008)

    Google Scholar 

  31. Graves J.C., Brill D.R.: Oscillatory Character of Reissner-Nordström Metric for an Ideal Charged Wormhole. Phys. Rev. 120, 1507–1513 (1960)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  32. Hawking, S.W., Ellis, G.F.R.: The large scale structure of spacetime, Cambridge Monographs on Mathematicals Physics, No. 1, London-New York: Cambridge University Press, 1973

  33. Klainerman S.: Uniform decay estimates and the Lorentz invariance of the classical wave equation. Commun. Pure Appl. Math. 38, 321–332 (1985)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  34. Kronthaler, J.: Decay rates for spherical scalar waves in a Schwarzschild geometry. http://arxiv.org/abs/0709.3703v1 [gr-qc], 2007

  35. Lindblad H., Rodnianski I.: The global stability of Minkowski spacetime in harmonic gauge. Ann. of Math. 171(3), 1401–1477 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  36. Luk J.: Improved decay for solutions to the linear wave equation on a Schwarzschild black hole. Ann. H. Poincareé 11, 805–880 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  37. Marolf, D.: The danger of extremes. http://arxiv.org/abs/1005.2999v2 [gr-qc], 2010

  38. Marzuola J., Metcalfe J., Tataru D., Tohaneanu M.: Strichartz estimates on Schwarzschild black hole backgrounds. Commun. Math. Phys. 293(1), 37–83 (2010)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  39. Morawetz C.S.: The limiting amplitude principle. Comm. Pure Appl. Math. 15, 349–361 (1962)

    Article  MathSciNet  MATH  Google Scholar 

  40. Morawetz C.S.: Time Decay for Nonlinear Klein-Gordon Equation. Proc. Roy. Soc. London 306, 291–296 (1968)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  41. Nordström G.: On the Energy of the Gravitational Field in Einstein’s Theory. Verhandl. Koninkl. Ned. Akad. Wetenschap., Afdel. Natuurk., Amsterdam 26, 1201–1208 (1918)

    MATH  Google Scholar 

  42. Price R.: Nonspherical perturbations of relativistic gravitational collapse. I. Scalar and gravitational perturbations. Phys. Rev. D 5(3), 2419–2438 (1972)

    Article  MathSciNet  ADS  Google Scholar 

  43. Poisson E.: A Relativist’s Toolkit: The Mathematics of Black-Hole Mechanics. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  44. Regge T., Wheeler J.: Stability of a Schwarzschild singularity. Phys. Rev. 108, 1063–1069 (1957)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  45. Reissner H.: Über die Eigengravitation des elektrischen Feldes nach der Einstein’schen Theorie. Annalen der Physik 50, 106–120 (1916)

    Article  ADS  Google Scholar 

  46. Rodnianski, I., Speck, J.: The Stability of the Irrotational Euler-Einstein System with a Positive Cosmological Constant. http://arxiv.org/abs/0911.5501v2 [math-ph], 2010

  47. Schlue, V.: Linear waves on higher dimensional Schwarzschild black holes. Rayleigh Smith Knight Essay 2010, University of Cambridge, January 2010

  48. Sogge C.: Lectures on nonlinear wave equations. International Press, Boston (1995)

    MATH  Google Scholar 

  49. Tataru, D., Tohaneanu, M.: Local energy estimate on Kerr black hole backgrounds. http://arxiv.org/abs/0810.5766v2 [math.Ap], 2008

  50. Tataru, D.: Local decay of waves on asymptotically flat stationary space-times. http://arxiv.org/abs/0910.5290v2 [math.Ap], 2010

  51. Taylor M.E.: Partial Differential Equations I. Springer, New York (1996)

    Google Scholar 

  52. Twainy, F.: The Time Decay of Solutions to the Scalar Wave Equation in Schwarzschild Background. Thesis. San Diego: University of California, 1989

  53. Wald R.M.: Note on the stability of the Schwarzschild metric. J. Math. Phys. 20, 1056–1058 (1979)

    Article  MathSciNet  ADS  Google Scholar 

  54. Wald, R.M.: General Relativity. The University of Chicago Press, 1984

  55. Wald R., Kay B.: Linear stability of Schwarzschild under perturbations which are nonvanishing on the bifurcation 2-sphere. Classical Quantum Gravity 4(4), 893–898 (1987)

    Article  MathSciNet  ADS  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, Wilberforce Road, Cambridge, CB3 0WB, United Kingdom

    Stefanos Aretakis

Authors
  1. Stefanos Aretakis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Stefanos Aretakis.

Additional information

Communicated by P.T. Chruściel

Rights and permissions

Reprints and permissions

About this article

Cite this article

Aretakis, S. Stability and Instability of Extreme Reissner-Nordström Black Hole Spacetimes for Linear Scalar Perturbations I. Commun. Math. Phys. 307, 17–63 (2011). https://doi.org/10.1007/s00220-011-1254-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00220-011-1254-5

Keywords

Search

Navigation