Abstract
The higher-order guaranteed lower eigenvalue bounds of the Laplacian in the recent work by Carstensen et al. (Numer Math 149(2):273–304, 2021) require a parameter \(C_{\text {st},1}\) that is found not robust as the polynomial degree p increases. This is related to the \(H^1\) stability bound of the \(L^{2}\) projection onto polynomials of degree at most p and its growth \(C_{\textrm{st, 1}}\propto (p+1)^{1/2}\) as \(p \rightarrow \infty \). A similar estimate for the Galerkin projection holds with a p-robust constant \(C_{\text {st},2}\) and \(C_{\text {st},2} \le 2\) for right-isosceles triangles. This paper utilizes the new inequality with the constant \(C_{\text {st},2}\) to design a modified hybrid high-order eigensolver that directly computes guaranteed lower eigenvalue bounds under the idealized hypothesis of exact solve of the generalized algebraic eigenvalue problem and a mild explicit condition on the maximal mesh-size in the simplicial mesh. A key advance is a p-robust parameter selection. The analysis of the new method with a different fine-tuned volume stabilization allows for a priori quasi-best approximation and improved \(L^{2}\) error estimates as well as a stabilization-free reliable and efficient a posteriori error control. The associated adaptive mesh-refining algorithm performs superior in computer benchmarks with striking numerical evidence for optimal higher empirical convergence rates.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper proposes and analyzes a new hybrid high-order (HHO) eigensolver for the direct computation of guaranteed lower eigenvalue bounds (GLB) for the Laplacian.
1.1 Three categories of GLB
The min-max principle enables guaranteed upper eigenvalue bounds but prevents a direct computation of a GLB by a conforming approximation in a Rayleigh quotient. So GLB shall be based on nonconforming finite element methods (FEM), on modified mass and/or stiffness matrices (with reduced integration or fine-tuned stabilization terms), or on further post-processing. The last decade has seen a few GLB we group in three categories (i)–(iii).
-
(i)
The a posteriori error analysis for symmetric second-order elliptic eigenvalue problems started with [35, 43, 54] under the (unverified) hypothesis of a sufficiently small mesh-size. With additional a priori information on spectral gaps, the latest a posteriori post-processings [13,14,15] provide GLB.
-
(ii)
Classical nonconforming FEM [20, 22, 45] and mixed FEM [39] allow for the GLB \(\lambda _h/(1+\delta \lambda _h)\le \lambda \) with the discrete eigenvalue \(\lambda _h\) and a known parameter \(\delta \propto h_{\max }^2\) in terms of the maximal mesh-size \(h_{\max }\). On the positive side, the GLB provides unconditional information on the exact eigenvalue \(\lambda \) from the computed discrete eigenvalue \(\lambda _h\). On the negative side, the global parameter \(h_{\max }\) can spoil a very accurate approximation \(\lambda _h\) in this GLB and is of lowest-order only. A fine-tuned stabilization of the classical nonconforming FEM in [23], however, provides a first (but low-order) remedy of the third category.
-
(iii)
Higher-order hybrid discontinuous Galerkin (HDG) or HHO discretizations [19, 25] can compute direct GLB \(\lambda _h\le \lambda \) under the sufficient condition (e.g., in [19] for the HHO method and the Laplacian)
$$\begin{aligned} \sigma _1^2\beta +\kappa ^2 h_{\max }^2\min \{\lambda ,\lambda _h\}\le \alpha \end{aligned}$$(1.1)with (universal or computed) constants \(\sigma _1, \kappa \) and known parameters \(0<\alpha<1, 0<\beta <\infty \) (selected in the discrete scheme). If the exact Dirichlet eigenvalue \(\lambda \) of number \(j \in \mathbb {N}_0\) of the Laplace operator and the corresponding discrete eigenvalue \(\lambda _h\) satisfy (1.1), then \(\lambda _h \le \lambda \) is a GLB. The two-fold use of (1.1) is a priori or a posteriori. First, given an upper bound \(\mu \ge \lambda > 0\) of \(\lambda \) (e.g., by some conforming approximation or post-processing), (1.1) provides an upper bound \(h_{\max }^2 \le (\alpha - \sigma _1^2\beta )/(\kappa ^2\mu )\) for the maximal initial mesh-size. This condition is sufficient for (1.1) and guarantees a priori that \(\lambda _h \le \lambda \). Second, (1.1) may be checked a posteriori for any computed value \(\lambda _h\). Then \(\sigma _1^2\beta +\kappa ^2 h_{\max }^2 \lambda _h \le \alpha \) implies (1.1) and so, \(\lambda _h \le \lambda \).
This paper presents a new HHO eigensolver of the third category.
1.2 Motivation and outline of Sect. 2
The constants \(\sigma _1^2 :=C_\text {st,1}^2 - 1\) and \(\kappa :=C_P C_\text {st,1}\) in (1.1) depend on the Poincaré constant \(C_P \le 1/\pi \) and a stability constant \(C_\text {st,1}\). The latter has to be contrasted with the constant \(C_{\textrm{st, 2}}\), where \(C_{\textrm{st, 1}}\) and \(C_{\textrm{st, 2}}\) are the best possible constants in the stability estimates
in a given simplex \(T \subset \mathbb {R}^n\) with the (component-wise) \(L^{2}\) projection \(\Pi _m\) and the Galerkin projection \(G_m\) onto polynomials of total degree at most \(m\in {\mathbb {N}}_0\). The two constants \(C_\text {st,1}\) and \(C_\text {st,2}\) are independent of the diameter \(h_T :=\text {diam}(T)\) of T, but might depend on the shape of T and the polynomial degree p. Figure 1 illustrates the behaviour of \(C_{\textrm{st, 1}}\) and \(C_{\textrm{st, 2}}\) for different triangular shapes and various polynomial degrees p. Section 2 investigates the p-robustness of \(C_{\textrm{st, 2}}\) and reveals that \(C_{\textrm{st, 2}}\le C_{\textrm{st,1}}\propto \sqrt{p+1}\) tends to infinity as \(p\rightarrow \infty \), while we conjecture \(C_{\textrm{st,2}}\le \sqrt{2}\) for triangles T with maximum interior angle \(\omega \le \pi /2\). Notice that a large constant \(C_\text {st,1}\) leads to a large \(\sigma _1\) in (1.1) and so, \(\alpha < 1\) enforces small \(\beta \) and restricts the GLB to very fine meshes. The main motivation of this work arises from the convenient bound \(C_{\textrm{st, 2}}\le \sqrt{2}\): Can we design a discretization method of the third category (iii) based on \(\sigma _2 :=C_P C_\text {st,2}\le \sqrt{2}/\pi \) in (1.1)?
1.3 A modified HHO method and outline of Sect. 3
This paper provides an affirmative answer with a new fine-tuned stabilization in a modified HHO scheme in Sect. 3 and a new criterion
sufficient for the GLB \(\lambda _h\le \lambda \). One advantage of (1.4) over (1.1) is the straight-forward and p-robust parameter selection \(\beta :=\alpha /\sigma _2^2\). It turns out that \(\sigma _2 \le \kappa \) and so (1.4) improves on (1.1) in the sense that \(\sigma _2^2 h_{\max }^2\lambda \le \alpha \) holds on much coarser triangulations for higher polynomial degrees p.
Given a bounded polyhedral Lipschitz domain \(\Omega \subset \mathbb {R}^n\), let \(V :=H^1_0(\Omega )\) denote the Sobolev space endowed with the energy scalar product \(a(u,v) :=(\nabla u, \nabla v)_{L^2(\Omega )}\) and the \(L^{2}\) scalar product \(b(u,v) :=(u,v)_{L^2(\Omega )}\) for all \(u,v \in V\). This paper considers the model problem that seeks an eigenpair \((\lambda , u) \in \mathbb {R}_+ \times (V{\setminus }\{0\})\) such that
The HHO methodology has been introduced in [31, 32] and is related to HDG and nonconforming virtual element methods [27]. Given a regular triangulation \(\mathcal {T}\) into simplices, the ansatz space \(V_h = P_{p+1}(\mathcal {T}) \times P_p(\mathcal {F}(\Omega ))\) consists of piecewise polynomials of (total) degree at most \(p+1\) attached to the simplices and piecewise polynomials of degree at most p attached to the interior faces. Two reconstruction operators link the two components of \(v_h \in V_h\): The potential reconstruction \(\mathcal {R}v_h \in P_{p+1}(\mathcal {T})\) provides a discrete approximation to v in the space of piecewise polynomials \(P_{p+1}(\mathcal {T})\) of degree at most \(p+1\). The gradient reconstruction \(\mathcal {G}v_h \in \text {RT}_p^\text {pw}(\mathcal {T})\) approximates the gradient \(\nabla v\) in the space of piecewise Raviart-Thomas functions \(\text {RT}_p^\text {pw}(\mathcal {T})\) [1, 30]. Let \(S v_h :=v_\mathcal {T}- \mathcal {R}v_h \in P_{p+1}(\mathcal {T})\) for any \(v_h = (v_\mathcal {T}, v_\mathcal {F}) \in V_h\) denote the additional cell-based stabilization. Given positive parameters \(0< \alpha < 1\) and \(0< \beta < \infty \), the bilinear forms \(a_h: V_h \times V_h \rightarrow \mathbb {R}\) and \(b_h: V_h \times V_h \rightarrow \mathbb {R}\) read
The discrete eigenvalue problem seeks \((\lambda _h,u_h)\in \mathbb {R}^+\times (V_h\setminus \{0\})\) with
The definitions of \(\mathcal {R}\), \(\mathcal {G}\), and further details follow in Sect. 3 below.
1.4 GLB with p-robust parameters and outline of Sect. 4
The discrete bilinear form \(a_h\) from [19] with parameter \(C_\textrm{st, 1}\propto \sqrt{p+1}\) utilizes the different stabilization \(\beta (\nabla _\text {pw}S u_h, \nabla _\text {pw}S v_h)_{L^2(\Omega )}\) instead of \(\beta (h_\mathcal {T}^{-2} S u_h, S v_h)_{L^2(\Omega )}\) in (1.6). The two stabilizations are locally equivalent, but the innovative difference is that the parameter selection in the new scheme circumvents an inverse inequality, and rather builds it into the scheme. Section 4 verifies the sufficient condition (1.4) for exact GLB under the assumption of exact solve.
1.5 A priori error analysis of the new scheme and outline of Sect. 5
A quasi-best approximation for the source problem [38] allows for quasi-best approximation results in Theorem 5.1 for a simple eigenvalue \(\lambda \), namely
with a positive constant \(C_{1}\) and the minimum \(0 < s \le 1\) of the index of elliptic regularity and one; the HHO interpolation \(\text {I}: V \rightarrow V_h\) is recalled in Sect. 3.3 below. Compared to earlier results in [12, 19], (1.9) provides an additional positive power s of \(h_{\max }\) in the \(L^{2}\) error. This is important as it eventually enables the absorption of higher-order terms in the a posteriori error analysis.
1.6 Stabilization-free a posteriori error analysis and outline of Sect. 6
Let \(p_h :=\Pi _p \mathcal {G}u_h \in P_p(\mathcal {T};\mathbb {R}^n)\) denote the \(L^{2}\) projection of the gradient reconstruction \(\mathcal {G}u_h \in \text {RT}_p^\text {pw}(\mathcal {T})\) onto the space of vector-valued piecewise polynomials \(P_p(\mathcal {T};\mathbb {R}^n)\). For any \(T \in \mathcal {T}\) of volume |T|, define
with the normal jump \([p_h \cdot \nu _F]_F\) and the tangential jump \([p_h \times \nu _F]_F\) of \(p_h\) across a side F of T. Theorem 6.1 asserts reliability and efficiency of the error estimator \(\eta ^2 :=\sum _{T \in \mathcal {T}} \eta ^2(T)\) for sufficiently small mesh-sizes \(h_{\max }\) in the sense that
1.7 Adaptive mesh-refining algorithm and outline of Sect. 7
Three 2D computer experiments in Sect. 7 provide striking numerical evidence that the criterion (1.4) indeed leads to confirmed lower eigenvalue bounds. The adaptive mesh-refining algorithm driven by the refinement indicator \(\eta \) from (1.10) recovers the optimal convergence rates of the eigenvalue error \(\lambda - \lambda _h\) in all numerical benchmarks with singular eigenfunctions. This is the first time that p-robust higher-order GLB of the third category are displayed.
1.8 General notation
Standard notation for Lebesgue and Sobolev function spaces applies throughout this paper. In particular, \((\bullet ,\bullet )_{L^2(\omega )}\) denotes the \(L^{2}\) scalar product and \(H(\text {div},\omega )\) is the space of Sobolev functions with weak divergence in \(L^2(\omega )\) for a domain \(\omega \subset \mathbb {R}^n\). Recall the abbreviation \(V :=H^1_0(\Omega )\) for the space of Sobolev functions, endowed with the energy scalar product \(a(u,v) :=(\nabla u, \nabla v)_{L^2(\Omega )}\) and the \(L^{2}\) scalar product \(b(u,v) :=(u,v)_{L^2(\Omega )}\) for all \(u,v \in V\).
For a subset \(M \subset \mathbb {R}^n\) of diameter \(h_M\), let \(P_p(M)\) denote the space of polynomials of maximal (total) degree p regarded as functions defined in M. Given a simplex \(T \subset \mathbb {R}^n\), the space of Raviart–Thomas finite element functions reads
The Galerkin projection \(G :=G_{p+1}: H^1(T) \rightarrow P_{p+1}(T)\) maps \(f \in H^1(T)\) to the unique solution Gf to \(\Pi _0 G f = \Pi _0 f\) and
with the convention \(H^1(T) :=H^1(\text {int}(T))\) for the interior \(\text {int}(T) = T^\circ \) of T. The Poincaré constant \(C_P\) bounds \(\Vert (1-\Pi _0)f\Vert _{L^2(T)}\le C_Ph_T\Vert \nabla f\Vert _{L^2(T)}\) for all \(f\in H^1(T)\). In 2D, \(C_P \le 1/j_{1,1} = 0.260980\) with the first positive root of the Bessel function \(J_1\) [44] and \(C_P \le 1/\pi \) in any space dimension [5, 49]. The context-sensitive notation \(|\bullet |\) may denote the absolute value of a scalar, the Euclidean norm of a vector, the length of a side, or the volume of a simplex. The notation \(A \lesssim B\) abbreviates \(A \le CB\) for a generic constant C independent of the mesh-size and \(A \approx B\) abbreviates \(A \lesssim B \lesssim A\). Throughout this paper, \(C_1, \dots , C_{14}\) denote positive constants independent of the mesh-size.
2 Stability estimates
This section discusses the behaviour of the constants \(C_\textrm{st, 1}, C_{\textrm{st, 2}}\) from (1.2)–(1.3) as \(p\rightarrow \infty \) and the computation of \(\sigma _2:=C_PC_\textrm{st, 2}\) with the Poincaré constant \(C_P\) in (1.4) that arises from the stability estimates in Lemma 2.2 below.
2.1 Stability constants and estimates
The following theorem asserts that \(C_{\textrm{st, 2}}\) is p-robust (and small in general, see Fig. 1) whereas \(C_\textrm{st, 1}\rightarrow \infty \) as \(p\rightarrow \infty \).
Theorem 2.1
For any simplex T, there exist positive constants \(1 \le C_\textrm{st, 2}\le C_{\textrm{st, 1}}\) independent of the diameter \(h_T\) such that (1.2)–(1.3) hold. In \(n=2,3\) space dimensions, \( C_{\textrm{st, 1}}\approx \sqrt{p+1}\) and \( C_{\textrm{st, 2}}\approx 1 \) as \(p\rightarrow \infty \).
Proof
The existence of the constants \(1 \le C_{\textrm{st, 1}} \le C_\textrm{st, 2}\) follows from [25, Theorem 3.1]; cf. Appendix A for further details. The technical proof of the p-robustness of \(C_\text {st,2}\) involves a linear bounded operator \(R^{\text {curl}}: H^{-1}(T;\mathbb {R}^{3}) \rightarrow L^2(T;\mathbb {R}^3)\) from [28, 42, 46] and is carried out in Appendix B. The robustness holds for \(n = 2\) with a simpler and hence omitted proof.
The remaining parts of this proof concern the growth of \(C_\textrm{st, 1}\). Let \(X:=H^1(T)/\mathbb {R}\) denote the Hilbert space with inner product \((\nabla \bullet , \nabla \bullet )_{L^2(T)}\) and note that \(\text {ker}(\nabla (1-\Pi _{p+1}))=\text {ker}((1-\Pi _p)\nabla )=P_{p+1}(T)\). Since \(\Vert (1-\Pi _p)\nabla \phi \Vert _{L^2(T)}\le {\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| \phi \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }\) for every \(\phi \in X\), the definition of the operator norm of the oblique projection \(1-\Pi _{p+1}\in L(X)\) provides
Kato’s oblique projection lemma [52] for the Hilbert space X leads to \(\Vert \Pi _{p+1}\Vert =\Vert 1-\Pi _{p+1}\Vert \,\le \, C_{\textrm{st, 1}}\) and \((1-\Pi _{p+1})G= 0\) in X for the Galerkin projection G shows
for any \(f\in X\). Since \({\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| (1-G)f \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }\le C_{\textrm{st, 2}} \Vert (1-\Pi _p)\nabla f\Vert _{L^2(T)}\) from (1.3), this proves \(\Vert \Pi _{p+1}\Vert \le C_{\textrm{st, 1}}\le C_{\textrm{st, 2}}\Vert \Pi _{p+1}\Vert \). The growth \(\Vert \Pi _{p+1}\Vert \approx \sqrt{p+1}\) is known for tensor-product domains and also holds for simplices in \(n=2,3\) dimensions; see [55] and [47, Sec. 5] for \(\Vert \Pi _{p+1}\Vert \lesssim \sqrt{p+1}\) and Appendix C for the proof of \(\sqrt{p+1}\lesssim \Vert \Pi _{p+1}\Vert \). \(\square \)
The Poincaré inequality with the Poincaré constant \(C_P\) and (1.3) with \(C_{\textrm{st, 2}}\approx 1\) lead to a p-robust stability estimate with \(\sigma _2:=C_PC_\textrm{st, 2}\).
Lemma 2.2
(p-robust stability) Any \(f\in H^1(T)\), T a simplex, and \(p\in \mathbb {N}_0\) satisfy
\(\square \)
2.2 Numerical comparison and conjecture
The following theorem considers the computation of guaranteed upper bounds of \(C_{\textrm{st, 2}}\) in \(n=2,3 \) space dimensions for a control of \(\sigma _2\) in (2.1).
Given \(v \in H^1(T;\mathbb {R}^n)\) and \(w \in H^1(T;\mathbb {R}^{2n-3})\), let \(\text {curl}\,v :=\partial _1 v_2 - \partial _2 v_1\) and \(\text {Curl}\,w :=(\partial _2 w, -\partial _1 w)^t\) for \(n = 2\) and \(\text {curl}\,v :=(\partial _2 v_3 - \partial _3 v_2, \partial _3 v_1 - \partial _1 v_3, \partial _1 v_2 - \partial _2 v_1)^t\) and \(\text {Curl}\,w :=\text {curl}\,w\) for \(n = 3\). For any \(g \in H^{-1}(T;\mathbb {R}^{2n-3})\) in the dual space of \(H^1_0(T;\mathbb {R}^{2n-3})\) endowed with the operator norm \({\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| \bullet \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }_{*}\), let \((-\Delta )^{-1} g \in H^1_0(T;\mathbb {R}^{2n-3})\) denote the weak solution to \(-\Delta v = g\) in T componentwise with \({\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| g \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }_* = {\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| (-\Delta )^{-1} g \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }\).
The gradients \(\nabla P_{p+1}(T)\) of polynomials \(P_{p+1}(T)\) of degree at most \(p+1\) form a subspace of \(P_p(T;\mathbb {R}^n)\) and give rise to the \(L^{2}\) orthogonal decomposition \(P_p(T;\mathbb {R}^n) = Q_p \oplus \nabla P_{p+1}(T)\) with \(Q_p \perp \nabla P_{p+1}(T)\) in \(L^2(T;\mathbb {R}^n)\). Let \(\text {P}: P_p(T;\mathbb {R}^n) \rightarrow \nabla P_{p+1}(T)\) denote the \(L^{2}\) orthogonal projection onto \(\nabla P_{p+1}(T) \subset P_p(T;\mathbb {R}^n)\). The bilinear forms \(\mathfrak {a}: Q_p \times Q_p \rightarrow \mathbb {R}\) and \(\mathfrak {b}: Q_p \times Q_p \rightarrow \mathbb {R}\) are defined, for any \(q_p,r_p \in Q_p\), by
Theorem 2.3
(Stability constant) The maximal eigenvalue
of the eigenvalue problem
leads to the upper bound \(C_\text {st,2} \le \max \{1,m_p C_n\}\) for \(C_{2}= 1\) and \(C_{3}= 2/\sqrt{3}\).
Notice that (2.4) is a finite-dimensional eigenvalue problem and \((-\Delta )^{-1}q_p\) in \(\mathfrak {b}(q_p,r_p)\) can be approximated by, e.g., a conforming FEM. Numerical experiments below even suggest that the bound \(C_\textrm{st, 2}=m_p\) is exact in \(n=2\) dimensions.
Proof
If \(p = 0\), \(\nabla P_1(T) = P_0(T;\mathbb {R}^n)\) implies \(\nabla G f = \Pi _0 \nabla f\) for all \(f \in H^1(T)\), whence \(C_\text {st,2} = 1\). The remaining parts of the proof therefore assume \(p \ge 1\). Given \(f \in H^1(T)\), assume without loss of generality that \(\nabla f \perp \nabla P_{p+1}(T)\) in \(L^2(T;\mathbb {R}^n)\) (otherwise substitute \(g :=f - Gf\) and observe that \(\Vert (1 - \Pi _p) \nabla f\Vert _{L^2(T)} = \Vert (1 - \Pi _p)\nabla g\Vert _{L^2(T)}\)). Throughout this proof, abbreviate \(q_p :=\Pi _p \nabla f \in P_p(T;\mathbb {R}^n)\). A Helmholtz decomposition leads to \(q_p = \nabla a + \text {Curl}\,b\) with \(a \in H^1(T)\) and \(b \in H^1_0(T;\mathbb {R}^{2n-3})\). For any \(v \in H^1_0(T;\mathbb {R}^{2n-3})\), the \(L^{2}\) orthogonality \(\text {Curl}\,v \perp \nabla a\) in \(L^2(T;\mathbb {R}^n)\), an integration by parts, and a Cauchy inequality prove
In 2D, \(\Vert \text {Curl}\,v\Vert _{L^2(\Omega )} = {\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| v \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }\) and in 3D, \(\Vert \text {Curl}\,v\Vert _{L^2(\Omega )} \le 2 {\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| v \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }/\sqrt{3}\). (The proof solely involves elementary algebra and is therefore omitted.) Hence, (2.5) implies
(Notice that \({\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| q_p \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }_* = \Vert \text {Curl}\,b\Vert _{L^2(T)} = {\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| b \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }\) in 2D). Since \(\nabla P_{p+1}(T) \subset P_p(T;\mathbb {R}^n)\), the best approximation of \(q_p\) in \(\nabla P_{p+1}(T)\) satisfies the \(L^{2}\) orthogonality \(q_p \perp \nabla P_{p+1}(T)\). This and the Pythagoras theorem provide
On the other hand, the constant \(m_p\) from (2.3) satisfies
Hence, (2.6) implies
The Pythagoras identity \({\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| f - a \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }^2 + \Vert \text {Curl}\,b\Vert _{L^2(T)}^2 = \Vert \nabla f - q_k\Vert _{L^2(T)}^{2}\), a triangle inequality, the estimate \(2(\nabla a, \nabla (f - a))_{L^2(T)} \le \delta {\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| a \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }^2 + {\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| f-a \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }^2/\delta \), and (2.7) show, for all positive parameters \(\delta > 0\), that
If \(m_pC_n > 1\), then \(\delta :=m_p^2 C_n^2 - 1\) leads to \(\max \{1+\delta , (1+1/\delta )(m_p^2C_n^2-1)\} = m_p^2C_n^2\). If \(m_pC_n \le 1\), then \(\inf _{\delta > 0} \max \{1+\delta , (1+1/\delta )(m_p^2C_n^2-1)\} = 1\). This concludes the proof of \(C_{\text {st,2}} \le \max \{1,m_pC_n\}\). Notice that \({\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| \text {curl}\,q_p \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }_*^2 = {\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| (-\Delta )^{-1} \text {curl}\,q_p \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }^2 = b(q_p,q_p)\) and the orthogonal decomposition \(P_p(T;\mathbb {R}^n) = Q_p \oplus \nabla P_{p+1}(T)\) with \(\text {curl}\, \nabla P_{p+1}(T) \equiv 0\) reveal
with the bilinear forms \(\mathfrak {a}\) and \(\mathfrak {b}\) from (2.2). The min-max principle [4, Sec. 8] and (2.9) show that \(m_p^2\) is the maximal eigenvalue of (2.4). This concludes the proof. \(\square \)
Example 2.4
(Numerical example) Table 1 displays the computed maximal eigenvalue \(m_p^2\ge C_{\textrm{st,2}}^2\) of the eigenvalue problem (2.4) for the right-isosceles triangle T. The right-hand side is approximated by the Courant FEM of polynomial degree 10 on a uniform triangulation of T with 50721 degrees of freedom. The lower bounds
for \(C_{\textrm{st,2}}\) and \(C_{\textrm{st,1}}\) from (1.2) are computable Rayleigh quotients and displayed in Fig. 1. Computer experiments provide numerical evidence for the convergence of the lower bounds of \(C_{\textrm{st,2}}\) to \(m_p\) as \(N\rightarrow \infty \) and, hence, for \(C_\textrm{st,2}=m_p\). The lower bound of \(C_{\textrm{st, 1}}\propto \sqrt{p+1}\) displays the expected growth.
Undisplayed numerical experiments suggest that a small minimal interior angle does not affect the asymptotic bound of \(C_{\textrm{st,2}}\), but leads to increased growth of \(C_{\textrm{st,1}}\) as \(p\rightarrow \infty \). We observed \(C_{\textrm{st, 2}}=m_p\) and the convergence \(C_{\textrm{st, 2}}^2\rightarrow 2\) as \(p\rightarrow \infty \) for different isosceles and various right triangles, whereas an interior angle \(\omega >\pi /2\) has a mild influence on the maximal value of \(C_{\textrm{st, 2}}\) as shown for isosceles triangles in Fig. 2.
(Recall that the constants \(C_{\textrm{st, 1}}\) and \(C_{\textrm{st, 2}}\) are invariant under scaling.) This leads to our following conjecture in accordance with Fig. 1 for any \(p\in {\mathbb {N}}_0\).
Conjecture 2.5
For triangles T with maximal interior angle \(\omega \le \pi /2\), \(C_{\textrm{st,2}} \le \sqrt{2}\).
3 The modified HHO method
This section introduces the HHO method and the discrete eigenvalue problem.
3.1 Triangulation
Let \(\mathcal {T}\) be a regular triangulation of \(\Omega \) into simplices in the sense of Ciarlet such that \(\cup _{T \in \mathcal {T}} T = \overline{\Omega }\). Given a simplex \(T \in \mathcal {T}\) of positive volume \(|T| > 0\), let \(\mathcal {F}(T)\) denote the set of the \(n+1\) hyperfaces of T, called sides of T. Define the set of all sides \(\mathcal {F}= \cup _{T \in \mathcal {T}} \mathcal {F}(T)\) and the set of interior sides \(\mathcal {F}(\Omega ) = \mathcal {F}{\setminus }\{F \in \mathcal {F}:F\subset \partial \Omega \}\) in \(\mathcal {T}\). For any interior side \(F \in \mathcal {F}(\Omega )\), there exist exactly two simplices \(T_+, T_- \in \mathcal {T}\) such that \(\partial T_+ \cap \partial T_- = F\). The orientation of the outer normal unit \(\nu _F = \nu _{T_+}|_F = -\nu _{T_-}|_F\) along F is fixed and \(\omega _F :=\text {int}(T_+ \cup T_-)\) denotes the side patch of F. Let \([v]_F :=(v|_{T_+})|_F - (v|_{T_-})|_F \in L^1(F)\) denote the jump of \(v \in L^1(\omega _F)\) with \(v \in W^{1,1}(T_\pm )\) across F. For any boundary side \(F \in \mathcal {F}(\partial \Omega ) :=\mathcal {F}{\setminus }\mathcal {F}(\Omega )\), there exists a unique \(T \in \mathcal {T}\) with \(F \in \mathcal {F}(T)\). Then \(\omega _F :=\text {int}(T)\), \(\nu _F :=\nu _T\) is the exterior unit vector of \(F \in \mathcal {F}(T)\), and \([v]_F :=v|_F\). The triangulation \(\mathcal {T}\) gives rise to the space \(H^1(\mathcal {T}) :=\{v \in L^2(\Omega ): v|_T \in H^1(T)\}\) of piecewise Sobolev functions. The differential operators \(\text {div}_\text {pw}\), \(\nabla _\text {pw}\), and \(\Delta _\text {pw}\) denote the piecewise applications of \(\text {div}\), \(\nabla \), and \(\Delta \) without explicit reference to the triangulation \(\mathcal {T}\).
3.2 Discrete spaces
Let \(P_p(\mathcal {T})\), \(P_p(\mathcal {F})\), and \(\text {RT}^\text {pw}_p(\mathcal {T})\) denote the space of piecewise functions with restrictions to \(T \in \mathcal {T}\) or \(F \in \mathcal {F}\) in \(P_p(T)\), \(P_p(F)\), and \(\text {RT}_p(T)\). The local mesh-sizes give rise to the piecewise constant function \(h_\mathcal {T}\in P_0(\mathcal {T})\) with \(h_\mathcal {T}|_T \equiv h_T = \text {diam}(T)\) in \(T \in \mathcal {T}\) and \(h_{\max } :=\Vert h_\mathcal {T}\Vert _{L^\infty (\Omega )}\) abbreviates the maximal mesh-size of \(\mathcal {T}\). The \(L^{2}\) projections \(\Pi _p: L^1(\Omega ) \rightarrow P_p(\mathcal {T})\), \(\Pi _\mathcal {F}^p: L^1(\cup \mathcal {F}) \rightarrow P_p(\mathcal {F})\), and \(\Pi _{\text {RT}}: L^1(\Omega ;\mathbb {R}^n) \rightarrow \text {RT}_p^\text {pw}(\mathcal {T})\) onto \(P_p(\mathcal {T})\), \(P_p(\mathcal {F})\), and \(\text {RT}_p^\text {pw}(\mathcal {T})\) are computed cell-wise. For vector-valued functions \(\tau \in L^1(\Omega ;\mathbb {R}^n)\), the \(L^{2}\) projection \(\Pi _p\) onto \(P_p(\mathcal {T};\mathbb {R}^n) = P_p(\mathcal {T})^n\) applies componentwise. The Pythagoras theorem implies the stability of \(L^{2}\) projections, for any \(\tau \in L^2(\Omega ;\mathbb {R}^n)\) and \(v \in L^2(\Omega )\),
The Galerkin projection Gf of \(f \in H^1(\mathcal {T})\) is computed cell-wise by (1.12) with
The inclusion \(\nabla _\text {pw}P_{p+1}(\mathcal {T}) \subset P_p(\mathcal {T};\mathbb {R}^n) \subset \text {RT}_p^\text {pw}(\mathcal {T})\) leads, for any \(f \in H^1(\mathcal {T})\), to
3.3 HHO methodology
Let \(V_h :=P_{p+1}(\mathcal {T}) \times P_p(\mathcal {F}(\Omega ))\) denote the ansatz space of the HHO method for \(p\in {\mathbb {N}}_0\). The interior sides \(\mathcal {F}(\Omega )\) give rise to the subspace \(P_p(\mathcal {F}(\Omega ))\) of all \((v_F)_{F \in \mathcal {F}} \in P_p(\mathcal {F})\) with the convention \(v_F \equiv 0\) on any boundary side \(F \in \mathcal {F}(\partial \Omega )\) for homogenous boundary conditions. In other words, the notation \(v_h \in V_h\) means \(v_h = (v_\mathcal {T},v_\mathcal {F}) = \big ((v_T)_{T \in \mathcal {T}},(v_F)_{F \in \mathcal {F}}\big )\) for some \(v_\mathcal {T}\in P_{p+1}(\mathcal {T})\) and \(v_\mathcal {F}\in P_p(\mathcal {F}(\Omega ))\) with the identification \(v_T = v_\mathcal {T}|_T \in P_{p+1}(T)\) and \(v_F = v_\mathcal {F}|_F \in P_p(F)\). Given \(v_h = (v_\mathcal {T},v_\mathcal {F}) \in V_h\), the norm \(\Vert v_h\Vert _h\) of \(v_h\) in \(V_h\) from [32, Eq. (28)] or [31, Eq. (41)] reads
The interpolation \(\text {I}: V \rightarrow V_h\) maps \(v\mapsto \text {I}v :=(\Pi _{p+1} v, \Pi _\mathcal {F}^p v) \in V_h\).
Potential reconstruction. The potential reconstruction \(\mathcal {R}v_h \in P_{p+1}(\mathcal {T})\) of \(v_h = (v_\mathcal {T},v_\mathcal {F}) \in V_h\) satisfies, for all discrete test functions \(\varphi _h \in P_{p+1}(\mathcal {T})\), that
The bilinear form \((\nabla _\text {pw}\bullet , \nabla _\text {pw}\bullet )_{L^2(\Omega )}\) on the left-hand side of (3.5) defines a scalar product and the right-hand side of (3.5) is a linear functional in the quotient space \(P_{p+1}(\mathcal {T})/P_0(\mathcal {T})\). The Riesz representation \(\mathcal {R}v_h \in P_{p+1}(\mathcal {T})\) of this linear functional in \(P_{p+1}(\mathcal {T})/P_0(\mathcal {T})\) is selected by
The unique solution \(\mathcal {R}v_h \in P_{p+1}(\mathcal {T})\) to (3.5)–(3.6) defines the potential reconstruction operator \(\mathcal {R}: V_h \rightarrow P_{p+1}(\mathcal {T})\).
Gradient reconstruction. The gradient reconstruction \(\mathcal {G}v_h \in \text {RT}_p^\text {pw}(\mathcal {T})\) of \(v_h = (v_\mathcal {T},v_\mathcal {F}) \in V_h\) satisfies, for all discrete test functions \(\phi _h \in \text {RT}_p^\text {pw}(\mathcal {T})\), that
In other words, \(\mathcal {G}v_h\) is the Riesz representation of the linear functional on the right-hand side of (3.7) in the Hilbert space \(\text {RT}_p^\text {pw}(\mathcal {T})\) endowed with the \(L^{2}\) scalar product. Since \(\nabla _\text {pw}P_{p+1}(\mathcal {T}) \subset \text {RT}_p^\text {pw}(\mathcal {T})\), (3.7) implies the \(L^{2}\) orthogonality \(\mathcal {G}v_h - \mathcal {R}v_h \perp \nabla _\text {pw}P_{p+1}(\mathcal {T})\). The following lemma recalls the commutativity of \(\mathcal {G}\) and \(\mathcal {R}\) [1, 31,32,33]. The Galerkin projection G is defined in (1.12).
Lemma 3.1
(Commutativity) Any \(v \in V\) satisfies \(\mathcal {G}\text {I}v = \Pi _{\text {RT}} \nabla v\) and \(\mathcal {R}\text {I}v = G v\). \(\square \)
3.4 Discrete eigenvalue problem
Given positive constants \(0< \alpha < 1\) and \(0< \beta < \infty \), recall \(a_h\) and \(b_h\) from (1.6)–(1.7). Notice, for any \(u_h, v_h \in V_h\), that
The discrete problem seeks a discrete eigenpair \((\lambda _h, u_h) \in \mathbb {R}_+ \times V_h{\setminus }\{0\}\) such that
Lemma 3.2
(Discrete norm) The bilinear form \(a_h: V_h \times V_h \rightarrow \mathbb {R}\) is a scalar product in \(V_h\). The induced norm \(\Vert \bullet \Vert _{a,h} :=a_h(\bullet ,\bullet )^{1/2} \approx \Vert \bullet \Vert _h\) is equivalent to the discrete norm \(\Vert \bullet \Vert _h\) from (3.4).
Proof
The equivalence \(\Vert \bullet \Vert _{a,h} \approx \Vert v_h\Vert _h\) for all \(v_h \in V_h\) is proven in [19, Lemma 3.5] for the stabilization \(\beta (\nabla _\text {pw}S u_h, \nabla _\text {pw}S v_h)_{L^2(\Omega )}\) instead of \(\beta (h_\mathcal {T}^{-2} S u_h, S v_h)_{L^2(\Omega )}\) in the definition (1.6) of \(a_h\). Since the two stabilizations are locally equivalent, this leads to the assertion. \(\square \)
The discrete eigenvalue problem (3.9) gives rise to the symmetric generalized algebraic eigenvalue problem
The application of the Schur complement as in [19, Section 3.3] leads to the algebraic eigenvalue problem \((A_{\mathcal {T}\mathcal {T}} - A_{\mathcal {T}\mathcal {F}}A_{\mathcal {F}\mathcal {F}}^{-1}A_{\mathcal {F}\mathcal {T}}) x_\mathcal {T}= \lambda _h B_{\mathcal {T}\mathcal {T}} x_\mathcal {T}\). Hence, (3.10) provides \(N :=\dim P_{p+1}(\mathcal {T})=|\mathcal {T}|\bigl ({\begin{matrix} p+1+n\\ n \end{matrix}}\bigr )\) positive discrete eigenvalues \(0< \lambda _h(1) \le \lambda _h(2) \le \dots \le \lambda _h(N) < \infty \); all other eigenvalues \(\lambda _h(j) :=\infty \) for \(j > N\) are infinity.
4 Lower eigenvalue bounds
This section establishes the sufficient conditions on the parameters \(\alpha , \beta \) in (1.4) such that the HHO method from (3.9) provides direct GLB. Let \(\lambda \) (resp. \(\lambda _h\)) denote the j-th continuous (resp. discrete) eigenvalue of (1.5) (resp. (3.9)) for fixed \(j \in \mathbb {N}\). Recall \(0< \alpha < 1\), \(0< \beta < \infty \), and the constant \(\sigma _2\) from (2.1).
Theorem 4.1
(GLB) If \(\sigma _2^2\max \{\beta , h_{\max }^2\min \{\lambda _h,\lambda \}\} \le \alpha \), then \(\lambda _h \le \lambda \).
Remark 4.2
(GLB for \(j > N\)) The number \(j\in {\mathbb {N}}\) in the theorem can be larger than the dimension N. Then \(\alpha <\sigma _2^2\lambda h_{\max }^2\) follows. In other words \(\lambda (N+1)>\alpha \sigma _2^{-2}h_{\max }^{-2}\) is an a priori bound for the exact eigenvalue \(\lambda (N+1)\) for free.
Proof of Theorem 4.1
The proof applies the key arguments from [19, Theorem 4.1], but then reflects a different stabilization. This enables a different sufficient condition in the theorem with a more appropriate precise arrangement of the constants. (In fact, G in (1.3)–(2.1) is replaced by \(\Pi _{p+1}\) in [19], whence \(C_{\text {st,2}}\) in this paper is not larger than \(C_{\text {st},1}\) in [19] and \(\kappa \) from [19] is bounded by \(\sigma _2\) from (2.1).) Besides those differences, the first steps in the proof are very analogous and adopted for brevity.
Observe carefully that, in the beginning, \(\sigma _2^2 h_{\max }^2\min \{\lambda _h,\lambda \} \le \alpha \) does not immediately imply that \(0<\lambda _h\le \infty \) is finite.
Step 1: Reduction to \(h_{\max }^2 \sigma _2^2 \lambda < 1\). If \(h_{\max }^2 \sigma _2^2 \lambda \ge 1\), then \(h_{\max }^2 \sigma _2^2 \lambda _h \le \alpha < 1 \le h_{\max }^2 \sigma _2^2 \lambda \), whence \(\lambda _h\) is finite and \(\lambda _h \le \lambda \). The remaining parts of this proof therefore assume \(h_{\max }^2 \sigma _2^2 \lambda < 1\).
Step 2: The first j exact and pairwise orthonormal eigenfunctions \(\phi _1, \dots , \phi _j \in V\) of (1.5) satisfy that \(\Pi _{p+1} \phi _1, \dots , \Pi _{p+1} \phi _j \in P_{p+1}(\mathcal {T})\) are linear independent. The proof follows the lines of Step 2 in the proof of [19, Theorem 4.1] (with \(\delta :=\sigma _2 h_{\max }\)).
Step 3: There exists \(\phi \in \text {span}\{\phi _1,\dots ,\phi _j\}\) with \(\Vert \phi \Vert _{L^2(\Omega )} = 1\), \(\Vert \nabla \phi \Vert ^2_{L^2(\Omega )} \le \lambda \), and
The proof follows the lines of Step 3 in the proof of [19, Theorem 4.1] and considers the \(\min \)-\(\max \) principle for the algebraic eigenvalue problem (3.10) with the j-dimensional subspace spanned by \(\text {I}\phi _1, \dots , \text {I}\phi _j \in V_h\). It is the linear independence of \(\Pi _{p+1} \phi _1, \dots , \Pi _{p+1} \phi _j \in P_{p+1}(\mathcal {T})\) that guarantees \(j \le N = \dim P_{p+1}(\mathcal {T})\) and that the algebraic eigenvalue problem (3.10) has at least j finite eigenvalues; whence \(\lambda _h=\lambda _h(j)<\infty \). The bound of \(\lambda _h\) in the \(\min \)-\(\max \) principle by some maximizer \(v_h:=\text {I}\phi \) of the Rayleigh quotient in \( \text {span}\{\text {I}\phi _1, \dots , \text {I}\phi _j \} \subset V_h\) is rewritten as
for \(\phi \in \text {span}\{\phi _1,\dots ,\phi _j\}\) with \(\Vert \phi \Vert _{L^2(\Omega )} = 1\) and \(\Vert \nabla \phi \Vert ^2_{L^2(\Omega )} \le \lambda \). It follows from Step 2 that \( b_h(\text {I}\phi , \text {I}\phi ) =\Vert \Pi _{p+1}\phi \Vert _{L^2(\Omega )}^2 >0\) cannot vanish.
This and the Pythagoras theorem \(\Vert \Pi _{p+1} \phi \Vert _{L^2(\Omega )}^2 =1 - \Vert (1 - \Pi _{p+1})\phi \Vert _{L^2(\Omega )}^2>0 \) (recall \(1=\Vert \phi \Vert ^2_{L^2(\Omega )} \)) conclude the proof of (4.1).
Step 4: First lower bound for \(\lambda - \lambda _h\) under the assumption \(\beta \sigma _2^2 \le \alpha \).
The commutativity \(\mathcal {G}\text {I}\phi = \Pi _{\text {RT}} \nabla \phi \) from Lemma 3.1.a and \((1 - \alpha ) \mathcal {G}u_h + \alpha \Pi _p \mathcal {G}u_h = (1 - \alpha )(1 - \Pi _p)\mathcal {G}u_h + \Pi _p \mathcal {G}u_h\) for \(u_h = \text {I}\phi \) prove that \(a_h(\text {I}\phi , \text {I}\phi )\) in (3.8) is equal to
The identity \(\Vert (1 - \Pi _p) \Pi _{\text {RT}} \nabla \phi \Vert _{L^2(\Omega )} = \Vert \Pi _\text {RT}(1 - \Pi _p) \nabla \phi \Vert _{L^2(\Omega )}\) follows from the inclusion \(P_p(\mathcal {T};\mathbb {R}^n) \subset \text {RT}_p^\text {pw}(\mathcal {T})\) and \(\Pi _p \Pi _{\text {RT}} \nabla \phi = \Pi _p \nabla \phi = \Pi _\text {RT}\Pi _p \phi \). This, (4.2), and \(\Vert \Pi _\text {RT}(1 - \Pi _p) \nabla \phi \Vert _{L^2(\Omega )} \le \Vert (1 - \Pi _p) \nabla \phi \Vert _{L^2(\Omega )}\) from (3.1) lead to
The Pythagoras theorem and \(\Vert \nabla \phi \Vert _{L^2(\Omega )}^2 \le \lambda \) prove
Recall \(S \text {I}\phi = \Pi _{p+1} \phi - \mathcal {R}\text {I}\phi = \Pi _{p+1} \phi - G \phi \) from Lemma 3.1.b. The piecewise mesh-size function \(h_\mathcal {T}\) does not interfere with the projection \(\Pi _{p+1}\) and so the Pythagoras theorem reads
The combination of (4.1) with (4.3)–(4.5) results in
This, the stability estimate (2.1), and \(h_{\max }^{-1} \le h_\mathcal {T}^{-1}\) in \(\Omega \) imply
Recall \(\Vert (1 - \Pi _{p+1}) \phi \Vert _{L^2(\Omega )}^2 \,\le \Vert (1 - G) \phi \Vert _{L^2(\Omega )}^2 \le \sigma _2^2 h_{\max }^2\Vert (1 - \Pi _p)\nabla \phi \Vert _{L^2(\Omega )}^2\) from the best approximation property of \(\Pi _{p+1}\) and (2.1) as well as \(\alpha - \beta \sigma _2^2 \ge 0\) from the assumptions. Consequently, the left-hand side of (4.6) is greater than or equal to \(\Vert (1 - \Pi _{p+1})\phi \Vert _{L^2(\Omega )}^2\) times
In conclusion, \(0\le \Vert (1 - \Pi _{p+1}) \phi \Vert _{L^2(\Omega )}<1 \) (from the end of Step 3) and
Step 5: Finish of the proof. After the reduction to \(h_{\max }^2 \sigma _2^2 \lambda < 1\), the above Steps 2–4 of the proof have utilized \(\beta \sigma _2^2 \le \alpha \), but they carefully avoided any assumption on \(\lambda \) and \(\lambda _h\), although it is supposed that \(\sigma _2^2 h_{\max }^2\min \{\lambda _h,\lambda \} \le \alpha \). In case that \(\sigma _2^2 h_{\max }^2\lambda _h \le \alpha \), the assertion \(0\le \lambda - \lambda _h\) follows immediately from (4.7). In the remaining case \(\sigma _2^2 h_{\max }^2\lambda \le \alpha \), the pre-factor in the left-hand side of (4.7) has the lower bound \(\lambda - \lambda _h \le \alpha \sigma _2^{-2} h_{\max }^{-2} - \lambda _h\). Therefore (4.7) implies
Recall that \(0\le \Vert (1 - \Pi _{p+1}) \phi \Vert _{L^2(\Omega )}<1\) from Step 4 to see that the last displayed estimate is impossible unless \(0 \le \lambda - \lambda _h\). \(\square \)
5 A priori error analysis
The Babuška-Osborn theory [4] for the spectral approximation of compact selfadjoint operators leads to a priori convergence rates for the approximation of \(\lambda \) and of u in the energy norm [12, 19]. This section establishes the quasi-best approximation estimate (1.9) for a simple eigenvalue \(\lambda \), that eventually allows for the absorption of higher-order terms in the a posteriori error analysis of Sect. 6.
Throughout the remaining parts of this paper, suppose that \(\beta \le \alpha /\sigma _2^2\) with \(\sigma _2\) from (2.1). Let \(\lambda :=\lambda (j)\) be a simple eigenvalue of (1.5) with the corresponding eigenfunction \(u :=u(j) \in V\). Let \((\lambda _h,u_h) :=(\lambda _h(j), u_h(j))\) denote the j-th discrete eigenpair of (3.9) with \(u_h = (u_\mathcal {T},u_\mathcal {F}) \in V_h\), \(\Vert u\Vert _{L^2(\Omega )} = 1 = \Vert u_\mathcal {T}\Vert _{L^2(\Omega )}\), and \((u,u_\mathcal {T})_{L^2(\Omega )} \ge 0\). Recall that \(0 < s \le 1\) denotes the minimum of the index of elliptic regularity and one.
Theorem 5.1
(A priori) If \(h_{\max }\) is sufficiently small, then (1.9) holds. The constant \(C_{1}\) exclusively depends on p, n, \(\Omega \), and the shape regularity of \(\mathcal {T}\).
The following lemmas precede the proof of Theorem 5.1. The first one recalls the enriching operator from [38] and adds the estimate (5.1). Recall the induced discrete norm \(\Vert \bullet \Vert _{a,h} :=a_h(\bullet ,\bullet )^{1/2}\) from Lemma 3.2.
Lemma 5.2
(Enriching operator) There exists a linear bounded operator \(\text {J}: V_h \rightarrow V\) that is a right-inverse of \(\text {I}\), i.e., \(v_h=\text {I}\text {J} v_h=(\Pi _{p+1}\text {J}v_h, \Pi _\mathcal {F}^p\text {J}v_h)\) for all \(v_h \in V_{h}\), and stable in the sense that \(\Vert \nabla \text {J} v_{h}\Vert _{L^2(\Omega )} \le \Vert \text {J}\Vert \Vert v_{h}\Vert _{a,h}\) with \(\Vert \text {J}\Vert \lesssim 1\). Any \(v \in V\) satisfies
The constants \(\Vert \text {J}\Vert \) and \(C_{4}\) solely depend on p, n, and the shape regularity of \(\mathcal {T}\).
Proof
The construction of the enriching operator \(\text {J}:V_h\rightarrow V\) in spirit of [53] involves standard averaging and bubble-function techniques from [54] and is explained in [38, Section 4.3] for a related HHO method without the proof of (5.1). Notice that \(\text {J}\) from [38] (called stabilized bubble smoother \(E_\text {H}\) therein) only satisfies \(\text {J} v_h - v_\mathcal {T}\perp P_{p-1}(\mathcal {T})\) for any given \(v_h=(v_\mathcal {T}, v_\mathcal {F})\in V_h\). However, a straight-forward modification of [38, Eq. (4.16)] (in the notation of [38], \(\mathcal {B}_K v_\mathcal {M} \in P_{p+1}(K)\) should be defined by equation (4.16) therein for all \(q \in P_{p+1}(K)\)) immediately provides a right-inverse \(\text {J}\) of \(\text {I}\). The arguments from [38, Propositions 4.5 and 4.7] apply and lead to the stability of \(\text {J}\) with respect to the equivalent discrete norm \(\Vert \bullet \Vert _h\approx \Vert \bullet \Vert _{a,h}\) from Lemma 3.2.
It remains to prove (5.1) which is well-known for the Crouzeix-Raviart finite element method with an appropriate interpolation \(\text {I}\) and the conforming companion \(\text {J}\) from [21, Proposition 2.3] for \(n=2\) and from [24, Section 5.8] for \(n=3\). Given any \(v_h\in V_h\), let \(\mathcal {A} v_h \in S^{p+1}_0(\mathcal {T}):=P_{p+1}(\mathcal {T})\cap H^1_0(\Omega )\) denote the nodal average of \(\mathcal {R}v_h\), cf. [38, Eq. (4.24)]. With [38, Eq. (4.18)] and with the above modification in [38, Eq. (4.16)], the bubble smoother \(\mathcal B:L^2(\Omega )\times L^2(\bigcup \mathcal {F})\rightarrow H^1_0(\Omega )\) from [38, Proposition 4.6] satisfies, for \((v_{\mathcal {M}},v_\Sigma )\in L^2(\Omega )\times L^2(\bigcup \mathcal {F})\), the stability estimate
with the \(L^{2}\) projection \(\Pi _F^p\) onto \(P_p(F)\) for all faces \(F \in \mathcal {F}\). A triangle inequality, the stability of \(\Pi _F^p\) on a face F, and a discrete trace inequality show \(\Vert \Pi _F^p (v_F - \mathcal {A} v_h)\Vert _{L^2(F)} \le \Vert \Pi _F^p (v_F - (\mathcal {R}v_h)|_T)\Vert _{L^2(F)} + h_F^{-1/2}\Vert \mathcal {R}v_h - \mathcal {A} v_h\Vert _{L^2(T)}\) for all \(F \in \mathcal {F}(T)\) and \(T \in \mathcal {T}\). This, a triangle inequality for \(\text {J}:=\mathcal {A}+\mathcal {B}(1-\mathcal {A})\), (5.2), and the second inequality on [38, p. 2180] result in
Given \(v \in V\), the stability of the \(L^{2}\) projections \(\Pi _{p+1}\) and \(\Pi _F^p\) from (3.1) prove \(\Vert \Pi _{p+1}(v - \mathcal {R}\text {I}v)\Vert _{L^2(T)} \le \Vert v - \mathcal {R}\text {I}v\Vert _{L^2(T)}\) and \(\Vert \Pi _F^p (v - \mathcal {R}(\text {I}v)|_T)\Vert _{L^2(F)} \le \Vert v - (\mathcal {R}\text {I}v)|_T\Vert _{L^2(F)}\) for all \(T \in \mathcal {T}\) and \(F \in \mathcal {F}(T)\). Given an interior side \(F = T_+ \cap T_- \in \mathcal {F}(\Omega )\) for \(T_\pm \in \mathcal {T}\), the triangle inequality shows
For boundary sides \(F \in \mathcal {F}(\partial \Omega )\), it holds \(\Vert [\mathcal {R}\text {I}v]_F\Vert _{L^2(F)} = \Vert v - \mathcal {R}\text {I}v\Vert _{L^2(F)}\). The choice \(v_h :=\text {I}v\) in (5.3), the aforementioned inequalities, the trace inequality, and the piecewise application of the Poincaré inequality imply \(\Vert \nabla _\text {pw}(\mathcal {R}\text {I}v - \text {J} \text {I}v)\Vert _{L^2(\Omega )} \lesssim \Vert \nabla _\text {pw}(v - \mathcal {R}\text {I}v)\Vert _{L^2(\Omega )}\). This, the triangle inequality
and the \(L^{2}\) orthogonality \(\nabla _\text {pw}(v - \mathcal {R}\text {I}v) \perp \nabla _\text {pw}P_{p+1}(\mathcal {T})\) conclude the proof of (5.1). \(\square \)
The second lemma proves quasi-best approximation estimates for a source problem.
Lemma 5.3
(Best-approximation) Given \(f \in L^2(\Omega )\), let \(\widetilde{u} \in V\) solve \(-\Delta \widetilde{u} = f\) in \(\Omega \). The solution \(\widetilde{u}_h = (\widetilde{u}_\mathcal {T}, \widetilde{u}_\mathcal {F}) \in V_h\) to
and the data oscillation \(\text {osc}(f,\mathcal {T}) :=\Vert h_\mathcal {T}(1 - \Pi _{p+1})f\Vert _{L^2(\Omega )}\) satisfy
with the constant \(C_{5}:=\max \{\Vert \text {J}\Vert + (\alpha ^2/(1-\alpha )+ \beta C_P^2)^{1/2}, \Vert \text {J}\Vert C_P\}\).
Proof
Throughout this proof, abbreviate \(\widetilde{e}_h :=\text {I}\widetilde{u} - \widetilde{u}_h \in V_h\). Since \(\Pi _{p+1}u - \widetilde{u}_\mathcal {T}=\Pi _{p+1}\text {J}\widetilde{e}_h\in P_{p+1}(\mathcal {T})\) by Lemma 5.2, the discrete problem (5.4) shows
The commutativity \(\Pi _{\text {RT}} \nabla v = \mathcal {G}\text {I}v\) for \(v\in V\) from Lemma 3.1 enters this proof in two ways. First, it verifies \(\Pi _p \mathcal {G}\text {I}\widetilde{u} = \Pi _p \nabla \widetilde{u}\) with \(v:=\widetilde{u}\) so that (3.8) reads
Second, for \(v:=\text {J}\widetilde{e}_h\), the resulting \(L^{2}\) orthogonality \(\nabla \text {J} \widetilde{e}_h - \mathcal {G}\widetilde{e}_h \perp \text {RT}_p^\text {pw}(\mathcal {T})\) to the piecewise Raviart-Thomas functions \(\text {RT}_p^\text {pw}(\mathcal {T})\) provides
Since \(\widetilde{u}\in V\) solves \(-\Delta \widetilde{u} = f\) in \(\Omega \), this and (5.6)–(5.7) verify
The choice \(\phi :=\widetilde{u}\) in (4.5) implies \(\Vert h_\mathcal {T}^{-1} S\text {I}\widetilde{u}\Vert _{L^2(\Omega )} \le \Vert h_\mathcal {T}^{-1}(\widetilde{u} - G \widetilde{u})\Vert _{L^2(\Omega )}\) with the Galerkin projection G from (1.12). Hence, the Poincaré inequality shows
A Cauchy and a piecewise application of the Poincaré inequality reveal
The combination of (5.8)–(5.10) with a Cauchy inequality provides
This, (3.2)–(3.3), the stability \(\Vert \nabla \text {J} \widetilde{e}_h\Vert _{L^2(\Omega )} \le \Vert \text {J}\Vert \Vert \widetilde{e}_h\Vert _{a,h}\) from Lemma 5.2, a Cauchy inequality, and \((1-\alpha )\Vert \mathcal {G}\widetilde{e}_h\Vert _{L^2(\Omega )}^2 + \beta \Vert h_\mathcal {T}^{-1}S \widetilde{e}_h\Vert _{L^2(\Omega )}^{2} \le \Vert \widetilde{e}_h\Vert _{a,h}^2\) from (1.6) conclude the proof. \(\square \)
The final lemma links (3.9) to (5.4). Recall the simple eigenpair \((\lambda , u)\) of (1.5) and the associated discrete eigenpair \((\lambda _h,u_h)\) of (3.9) with \(u_h = (u_\mathcal {T}, u_\mathcal {F}) \in V_h\) and \((u, u_\mathcal {T})_{L^2(\Omega )}\ge 0\).
Lemma 5.4
(Upper bound for \(\Vert u - u_\mathcal {T}\Vert _{L^2(\Omega )}\)) If \(h_{\max }\) is sufficiently small, then \(\widetilde{u}_h = (\widetilde{u}_\mathcal {T}, \widetilde{u}_\mathcal {F}) \in V_h\) from Lemma 5.3 with \(f :=\lambda u\) satisfies
with the constant \(C_{6} :=\sqrt{2}(1 + \max _{k \in \{1,\dots ,N\}{\setminus }\{j\}} |\lambda /(\lambda _h(k) - \lambda )|) < \infty \).
Proof
This follows as in [21, Lem. 2.4] with straight-forward modifications and is hence omitted. \(\square \)
Proof of Theorem 5.1
The proof of (1.9) is split into three steps.
Step 1 provides the \(L^{2}\) error estimate
Recall \(\widetilde{u}_h = (\widetilde{u}_\mathcal {T},\widetilde{u}_\mathcal {F})\in V_h\) from Lemma 5.3 with \(f :=\lambda u\). Lemma 5.4, a triangle inequality, and (2.1) with \(\Vert (1-\Pi _{p+1})u\Vert _{L^2(\Omega )}\le \Vert (1-G)u\Vert _{L^2(\Omega )}\) lead to
Convergence rates for the error \(\Vert \Pi _{p+1} u - \widetilde{u}_\mathcal {T}\Vert _{L^2(\Omega )}\) in HHO methods for a source problem are established in [31, 32, 38]. This proof follows [21, 38] and utilizes the operator \(\text {J}: V_h \rightarrow V\) from Lemma 5.2. Abbreviate \(\widetilde{e}_h = (\widetilde{e}_\mathcal {T},\widetilde{e}_\mathcal {F}) :=\text {I}u - \widetilde{u}_h\in V_h\) and let \(z \in V\) solve \(-\Delta z = \widetilde{e}_\mathcal {T}\) in \(\Omega \), i.e., \(z\in V\) satisfies
Let \(z_C \in S_0^{1}(\mathcal {T}):=P_{1}(\mathcal {T})\cap V\) denote the Scott-Zhang interpolation [50] of z and observe that \((1-\Pi _p)\nabla z_C\equiv 0\) vanishes. Lemma 3.1 implies \(S\text {I}z_C\equiv 0\) and therefore, the identity \(a_h(\text {I}z_C,\widetilde{u}_h) = (\nabla z_C, \mathcal {G}\widetilde{u}_h)\) follows from (3.8) with \(\mathcal {G}\text {I}z_C=\nabla z_C\). Lemma 3.1 and \(\text {I}\text {J}=1\) verify \(\Pi _{\text {RT}} \nabla \text {J} \text {I}u = \mathcal {G}\text {I}u=\Pi _\text {RT}\nabla u\) and \(\Pi _\text {RT}\nabla \text {J} \widetilde{u}_h = \mathcal {G}\widetilde{u}_h\). This, \(\nabla z_C\in P_0(\mathcal {T};\mathbb {R}^n) \subset \text {RT}_p^{\text {pw}}(\mathcal {T})\), and the symmetry of \(a_h\) show
with \(a(u, z_C) = \lambda (u, z_C)_{L^2(\Omega )} = a_h(\widetilde{u}_h, \text {I}z_C)\) from (1.5) and (5.4) in the last step. Hence, (5.13)–(5.14), a Cauchy inequality, and \(\Vert \nabla \text {J} \widetilde{e}_h\Vert _{L^2(\Omega )} \le \Vert \text {J}\Vert \Vert \widetilde{e}_h\Vert _{a,h}\) from Lemma 5.2 confirm
The stability estimate (2.1) proves \(\text {osc}(\lambda u,\mathcal {T}) \le \lambda \sigma _2 \Vert h_{\mathcal {T}}^2(1 - \Pi _p) \nabla u\Vert _{L^2(\Omega )}\). This, Lemma 5.3, and (3.3) provide
The elliptic regularity theory establishes \(z \in V \cap H^{1+s}(\Omega )\) for \(0 < s \le 1\) on the polyhedral Lipschitz domain \(\Omega \) and the approximation property of the Scott-Zhang interpolation \(z_C\) [50] provides the constants \(C_{7},C_{8}\) depending exclusively on the domain \(\Omega \) such that
Since \(\Pi _{p+1}J\widetilde{e}_h=\widetilde{e}_\mathcal {T}=\Pi _{p+1} u - \widetilde{u}_\mathcal {T}\), the combination of (5.15)–(5.16) verifies
with \(C_{9}:=\Vert \text {J}\Vert C_{5}C_{7}C_{8}(1+\lambda \sigma _2h_{\max }^2)\). This and (5.12) conclude the proof of (5.11) with \(C_{10}:=C_{6}(\sigma _2 h_\textrm{max}^{1-s}+C_{9})\) and Step 1.
Step 2 discusses the remaining term \( |\lambda -\lambda _h|+ \Vert \text {I}u-u_h\Vert ^2_{a,h}\) on the left-hand side of (1.9).
Abbreviate \(e_h :=\text {I}u - u_h \in V_h\). Elementary algebra with the normalization \(\Vert u\Vert _{L^2(\Omega )} = 1 = \Vert u_\mathcal {T}\Vert _{L^2(\Omega )}\) reveals \(2\lambda = \lambda \Vert u - u_\mathcal {T}\Vert _{L^2(\Omega )}^2 + 2\lambda (u,u_\mathcal {T})_{L^2(\Omega )}\). This and \(\Vert e_h\Vert _{a,h}^2 - \lambda _h = \Vert \text {I}u\Vert _{a,h}^2 - 2a_h(\text {I}u, u_h)\) result in
Step 2.1 bounds \(\Vert \text {I}u\Vert _{a,h}^2 - \lambda \). The commutativity \(\Pi _\text {RT}\nabla u = \mathcal {G}\text {I}u\) from Lemma 3.1 and (3.8) with \(\Pi _p \Pi _{\text {RT}} \nabla u = \Pi _p \nabla u\) show
This and \(\lambda = \Vert \nabla u\Vert _{L^2(\Omega )}^2\) prove
Thus, \(0<\alpha <1\) and (5.9) with \(\widetilde{u}\) replaced by u imply
Step 2.2 controls \(\lambda (u, u_\mathcal {T})_{L^2(\Omega )} - a_h(\text {I}u, u_h)\).
The weak problem (1.5) and \(\Pi _{p+1}\text {J} u_h=u_\mathcal {T}\) reveal
Lemma 3.1 provides \(\Pi _\text {RT}\nabla \text {J} u_h = \mathcal {G}u_h\) and \(\mathcal {G}\text {I}u = \Pi _{\text {RT}} \nabla u\). This and (3.8) lead to
This and (5.19) show
Therefore, the Cauchy inequality and \(P_p(\mathcal {T};\mathbb {R}^n) \subset \text {RT}_p^\text {pw}(\mathcal {T};\mathbb {R}^n)\) imply
In the following, we control the terms on the right-hand side of (5.20). The split \(u_h=\text {I}u-e_h\), \(\Vert h_\mathcal {T}^{-1} S\text {I}u\Vert _{L^2(\Omega )}\ge 0\), and a Cauchy inequality provide
from (5.9) with \(\widetilde{u}\) replaced by u and a Young inequality with arbitrary \(t>0\) in the last step. Notice that \(\Pi _p \nabla \text {J}\text {I}u = \mathcal {G} \text {I}u = \Pi _p \nabla u\) by Lemma 3.1. Hence, a triangle inequality and \(\Vert \nabla (u - \text {J}\text {I}u)\Vert _{L^2(\Omega )} \le C_{4}\Vert \nabla _\text {pw}(u - G u)\Vert _{L^2(\Omega )}\) from a combination of (5.1) with (3.2)–(3.3) verify
This, (2.1), a triangle inequality with the split \(u_h=\text {I}u-e_h\), and the stability \(\Vert \nabla \text {J} e_h\Vert _{L^2(\Omega )} \le \Vert \text {J}\Vert \Vert e_h\Vert _{a,h}\) from Lemma 5.2 provide
The combination of (5.22)–(5.23) with (2.1) and a Young inequality with \(t>0\) reveal
Then (5.20)–(5.21), (5.23)–(5.24) with the choice \(t:=2(1+\lambda \sigma _2^2h_\textrm{max}^2)\Vert \text {J}\Vert +2C_P\), and \(\beta \Vert h_\mathcal {T}^{-1}Se_h\Vert _{L^2(\Omega )}^2\le \Vert e_h\Vert _{a,h}^2\) from (1.6) lead to
with \(C_{11}:=(1+\lambda \sigma _2^2h_{\textrm{max}}^2)(1+C_{4} + \Vert \text {J}\Vert t/2) + \beta C_Pt/2\).
Step 3 finishes the proof. Theorem 4.1 guarantees \(\lambda _h \le \lambda \) for sufficiently small mesh-sizes \(h_{\max } \le (\alpha /(\lambda \sigma _2^2))^{1/2}\). This, the combination of (5.17)–(5.18), and (5.25) with the \(L^{2}\) error estimate (5.11) from Step 1 result in
Thus, (5.11) and (3.2) conclude the proof of (1.9) with \(C_{1} :=2(\lambda C_{10}^{{2}} h_\textrm{max}^{2\,s} +\beta C_P^2 + 2C_{11})+C_{10}^2\). \(\square \)
Theorem 5.1 implies the following convergence rates and recovers [12, 19] for the eigenvalues and eigenfunctions error in the \(H^1\) seminorm.
Corollary 5.5
(Convergence) If \(u \in V \cap H^{1+t}(\Omega )\) for \(s \le t \le p+1\), then
Proof
This follows immediately from Theorem 5.1, the stability (1.3), and standard approximation properties of piecewise polynomials [11, Lemma 4.3.8]. \(\square \)
The techniques of this section also apply to the HHO method of [19] and lead to the optimal rate \(s + t\) for the \(L^{2}\) error towards a simple eigenvalue therein.
6 A posteriori error analysis
The two assumptions (A1)–(A2) below concern some \(q \in H^1(\mathcal {T};\mathbb {R}^n)\) and lead to a stabilization-free a posteriori error control of \(\Vert \nabla u - q\Vert _{L^2(\Omega )}\) in two or three space dimensions. Let \(\text {RT}_0(\mathcal {T}):=\text {RT}_0^\text {pw}(\mathcal {T})\cap H(\text {div})\) denote the lowest-order conforming Raviart-Thomas space, set \(S^m_0(\mathcal {T}):=P_m(\mathcal {T})\cap H^1_0(\Omega )\) for \(m\in {\mathbb {N}}\), and suppose
-
(A1)
\((q, \nabla v_C)_{L^2(\Omega )} = \lambda _h(u_\mathcal {T}, v_C)_{L^2(\Omega )}\) for all \(v_C \in S_{0}^{1}(\mathcal {T})\),
-
(A2)
\((q, q_\text {RT})_{L^2(\Omega )} = 0\) for all \(q_\text {RT}\in \text {RT}_0(\mathcal {T})\) with \(\text {div}\, q_\text {RT}= 0\).
Theorem 6.1
(A posteriori) Any \(q \in H^1(\mathcal {T};\mathbb {R}^n)\) with (A1)–(A2) and \(\eta \) from (1.10) with \(p_h\) replaced by q satisfy
The constant \(C_{12}\) only depends on p, n, \(\Omega \), and the shape regularity of \(\mathcal {T}\).
Proof
This is an extension of [8] to eigenvalue problems. For the convenience of the reader, the main arguments are briefly outlined below. Let \(\psi \in V\) solve \(- \Delta \psi = -\text {div}\,q \in H^{-1}(\Omega )\) so that the Pythagoras theorem allows for the split
Upper bound for \(\Vert \nabla (u - \psi )\Vert _{L^2(\Omega )}\). Abbreviate \(\varrho :=u - \psi \in V\) and let \(\varrho _C \in S^1_0(\mathcal {T})\) denote the Scott-Zhang interpolation of \(\varrho \) [50]. Then (A1), \((\nabla \psi , \nabla \varrho )_{L^2(\Omega )} = (q, \nabla \varrho )_{L^2(\Omega )}\), and (1.5) lead to
The last two \(L^{2}\) scalar products on the right-hand side of (6.3) arise in the explicit residual-based a posteriori error estimation of standard conforming FEM for the Poisson model problem, cf., e.g., [2, Section 2.2] or [37, Chapter 34], and are controlled by
This, (6.3), a Cauchy inequality, and a Friedrichs inequality result in
Upper bound for \(\Vert \nabla \psi - q\Vert _{L^2(\Omega )}\). The function \(\phi :=\nabla \psi - q \in L^2(\Omega ;\mathbb {R}^n)\) is divergence-free \(\text {div}\,\phi = 0\) and orthogonal to the divergence-free Raviart-Thomas functions \(q_{\text {RT}}\in \text {RT}_0(\mathcal {T})\) from (A2). The Helmholtz decomposition on a simply connected domain \(\Omega \) immediately implies \(\text {Curl}\,\beta = \phi \) for some \(\beta \in H^1(\Omega ;\mathbb {R}^{2n-3})\), but in this paper, the domain \(\Omega \) does not need to be simply connected. However, the extra condition (A2) ensures the existence of some orthogonal correction \(\phi _{\text {RT}}\in \text {RT}_0(\mathcal {T})\) with \(\text {div}\,\phi _{\text {RT}}=0\) such that the integrals \(\int _{\Gamma _j} (\phi -\phi _{\text {RT}})\cdot \nu \text {d} s=0\) over the \(J\in {\mathbb {N}}\) connectivity components \(\Gamma _j\) for \(j=1,...,J\) of \(\partial \Omega \) vanish, cf. [8, Lemma 2] for further details. Thus classical theorems [40] imply the existence of \(\beta \in H^1(\Omega ;\mathbb {R}^{2n-3})\) such that \(\text {Curl}\,\beta = \phi -\phi _{\text {RT}}\) and \(\Vert \nabla \beta \Vert _{L^2(\Omega )}\lesssim \Vert \phi \Vert _{L^2(\Omega )}\). Since the Scott-Zhang interpolation \(\beta _C \in S^1_0(\mathcal {T};\mathbb {R}^{2n-3})\) of \(\beta \) satisfies \(\text {Curl}\,\beta _C \in \text {RT}_0(\mathcal {T})\) and \(\text {div}\, \text {Curl}\,\beta _C = 0\), (A2) shows
A piecewise integration by parts, the trace inequality, the approximation property of the Scott-Zhang interpolation [50], and the Cauchy inequality lead to
The combination of (6.2) with (6.4)–(6.5) concludes the proof of (6.1). \(\square \)
One key observation is that \(q :=p_h :=\Pi _p \mathcal {G}u_h\) satisfies (A1)–(A2) as shown in the proof of Theorem 6.2 below. This leads to reliable a posteriori error control for \(\Vert \nabla u - p_h\Vert _{L^2(\Omega )}\). Theorem 6.1 can also be applied to the HHO scheme of [12], where \(q :=\nabla _\text {pw}\mathcal {R}u_h\) satisfies (A1)–(A2) for \(p \ge 1\). The lowest-order case \(p=0\) therein can be treated separately as in [8].
Theorem 6.2
(Reliability and efficiency) For sufficiently small mesh-sizes \(h_{\max }\), \(p_h :=\Pi _p \mathcal {G}u_h \in P_p(\mathcal {T};\mathbb {R}^n)\) and \(\eta \) from (1.10) satisfy (1.11). The constants \(C_\text {eff}\) and \(C_\text {rel}\) exclusively depend on p, n, \(\Omega \), and the shape regularity of \(\mathcal {T}\).
Proof
The first part of the proof verifies that \(p_h = \Pi _p \mathcal {G}u_h\) satisfies (A1)–(A2).
Proof of (A1). Any \(v_C \in S^1_0(\mathcal {T})\) satisfies \(\nabla v_C = \mathcal {G}\text {I}v_C \in P_0(\mathcal {T})\) and \(v_C = \mathcal {R}\text {I}v_C\). Thus \(S \text {I}v_C = 0\) and so,
Proof of (A2). Given \(q_\text {RT}\in \text {RT}_0(\mathcal {T}) \subset H(\text {div},\Omega )\) with \(\text {div}\, q_\text {RT}= 0\), the normal jump \([q_\text {RT}\cdot \nu _F]_F\) vanishes on any interior side \(F \in \mathcal {F}(\Omega )\). Since divergence-free functions in \(\text {RT}_0(\mathcal {T})\) are piecewise constant, the definition of \(\mathcal {G}\) from (3.7) shows \((p_h,q_\text {RT})_{L^2(\Omega )} = (\mathcal {G}u_h,q_\text {RT})_{L^2(\Omega )} = 0\) and concludes the proof of (A2).
Proof of reliability. Since \(q = p_h\) satisfies (A1)–(A2), Theorem 6.1 asserts
The normalization \(\Vert u\Vert _{L^2(\Omega )} = 1 = \Vert u_\mathcal {T}\Vert _{L^2(\Omega )}\), elementary algebra, and the combination of the a priori estimate (1.9) with (3.2) reveal
with the elliptic regularity of \(u \in V \cap H^{1+s}(\Omega )\) for the parameter \(0 < s \le 1\) and \(C_{13}:=\max \{|\lambda -\lambda _h|, \lambda \lambda _h\}C_{1}\). The inequalities (1.3) and \(p_h\in P_p(\mathcal {T}; \mathbb {R}^n)\) prove
For sufficiently small mesh-sizes \(h_{\max }\), \(C_{14}:=C_{12}C_{13}h_\textrm{max}^{2\,s}C_{\textrm{st,2}}^2<1\) and (6.6)–(6.8) lead to
Under the additional assumption \(h_{\max } \le (\alpha /(\lambda \sigma _2^2))^{1/2}\), the quasi-best approximation (1.9) and (6.8)–(6.9) conclude the proof of
with \(C_{\textrm{rel}}:=(1+C_{1}C_\textrm{st, 2}^2)C_{12} (1-C_{14})^{-1}\).
Proof of efficiency. The proof of \(\eta ^2 \lesssim \Vert \nabla u - p_h\Vert _{L^2(\Omega )}^2\) utilizes bubble-function techniques from [54]. Similar arguments are employed in [29] for the Crouzeix-Raviart FEM and, e.g., in [2, 8, 33, 37] for the source problem. The efficiency \(\sum _{F \in \mathcal {F}} h_F\Vert [p_h \times \nu _F]_F\Vert _{L^2(F)}^2 \lesssim \Vert \nabla u - p_h\Vert ^2_{L^2(\Omega )}\) follows from the arguments in the proof of [8, Lemma 7] for the Poisson model problem; hence further details are omitted. The focus is therefore on the proof of the efficiency of
Given \(F \in \mathcal {F}(\Omega )\), let \(b_F \in S^n(\mathcal {T})\) denote the face-bubble function with \(0 \le b_F \le 1\) in \(\Omega \) and \(\text {supp}(b_F) = \overline{\omega _F}\) [54, Section 3.1]. Define \(\varrho \in S^{p+n}_0(\mathcal {T})\) such that \(\varrho |_F = b_F[p_h\cdot \nu _F]_F \in P_{p+n}(F)\), \(\text {supp}(\varrho ) = \overline{\omega _F}\), and \(\varrho \) vanishes at all Lagrange points [11] in \(\overline{\Omega }\setminus F\). Inverse estimates [54, Ineq. (3.2)] and an integration by parts prove, for any \(F \in \mathcal {F}(\Omega )\), that
This, \((\nabla u, \nabla \varrho )_{L^2(\omega _F)} = \lambda (u,\varrho )_{L^2(\Omega )},\) and a Cauchy inequality imply
This, the inverse estimate \(\Vert \nabla \varrho \Vert _{L^2(\omega _F)} \lesssim h_F^{-1}\Vert \varrho \Vert _{L^2(\omega _F)}\) [11, Lemma 4.5.3], and \(\Vert \varrho \Vert _{L^2(\omega _F)}^2 \approx h_F\Vert \varrho \Vert _{L^2(F)}^2 \le h_F\Vert [p_h\cdot \nu _F]_F\Vert _{L^2(F)}^2\) [54, Ineq. (3.5)] show
Let \(b_T \in P_{n+1}(T) \cap W^{1,\infty }_0(T)\) denote the volume-bubble function in \(T\in \mathcal {T}\) with \(0 \le b_T \le 1\) and \(b_T = 0\) on \(\partial T\) [54, Section 3.1]. Abbreviate \(v_{p+1} :=\text {div}\, p_h + \lambda _h u_T \in P_{p+1}(T)\) and define \(\varphi :=b_T v_{p+1} \in S^{p+n+2}_0(T):=P_{p+n+2}(T)\cap H^1_0(T)\subset V\). Inverse estimates [54, Ineq. (3.1)] and an integration by parts imply
Since (the extension by zero of) \(\varphi \) belongs to V, (1.5) provides \((\nabla \varphi , \nabla u)_{L^2(T)} = \lambda (u, \varphi )_{L^2(T)}\). This, (6.12), and a Cauchy inequality lead to
Hence \(\Vert \varphi \Vert _{L^2(T)} = \Vert b_T v_{p+1}\Vert _{L^2(T)} \le \Vert v_{p+1}\Vert _{L^2(T)}\) from \(0 \le b_T \le 1\) in T and the inverse estimate \(\Vert \nabla \varphi \Vert _{L^2(T)} \le h_T^{-1}\Vert \varphi \Vert _{L^2(T)}\) [11, Lemma 4.5.3] reveal
The local estimate \(h_T\Vert \text {curl}\,p_h\Vert _{L^2(T)} \lesssim \Vert \nabla u - p_h\Vert _{L^2(T)}\) follows from similar arguments as above and details are omitted. The combination of this with the local estimates (6.11) and (6.13) results in \(\eta ^2 \lesssim \Vert \nabla u - p_h\Vert _{L^2(\Omega )}^2 + \Vert h_\mathcal {T}(\lambda u - \lambda _h u_\mathcal {T})\Vert _{L^2(\Omega )}^2\). This and the control over \(\Vert \lambda u - \lambda _h u_\mathcal {T}\Vert _{L^2(\Omega )}\) in (6.7)–(6.8) lead to the efficiency \(\eta ^2 \lesssim \Vert \nabla u - p_h\Vert _{L^2(\Omega )}^2\). \(\square \)
7 Numerical examples
The section presents three numerical benchmarks for the approximation of Dirichlet eigenvalues of the Laplacian on nonconvex domains \(\Omega \subset \mathbb {R}^2\).
7.1 Parameter selection
For right-isosceles triangles, recall \(C_\text {st,2} \le \sqrt{2}\) from Example 2.4 and \(C_P = 1/(\sqrt{2}\pi )\) from [44]. Throughout this section, let \(\alpha = 0.5\) and \(\beta :=\alpha /\sigma _2^2 = 4.934802\) with \(\sigma _2^2 = C_P^2 C_{\text {st,2}}^2 = 1/\pi ^2 = 0.101321\). The computable (a posteriori) condition \(\sigma _2^2 \max \{\beta , h_{\max }^2 \lambda _h(j)\} \le \alpha \) from Theorem 4.1 leads to \(\text {GLB}(j) :=\lambda _h(j) \le \lambda (j)\). Since the parameters are chosen before-hand, the condition \(h_{\max }^2 \lambda _h \le \alpha /\sigma _2^2 = 4.934802\) may not be satisfied on a coarse mesh with large \(h_{\max }\) and j. In this case, \(\text {GLB}(j) :=0\) (which is a guaranteed lower eigenvalue bound), so only GLB are displayed in this section.
7.2 Numerical realization
The algebraic eigenvalue problem (3.10) is realized with the iterative solver eigs from the MATLAB standard library in an extension of the data structures and short MATLAB programs in [3, 17]; the termination and round-off errors are expected to be very small and neglected for simplicity.
Polynomial degrees \(p = 0, \dots , 4\) in the numerical benchmarks of Sect. 7
The a posteriori estimate from Theorem 6.1 motivates the refinement indicator \(\eta ^2(T)\) from (1.10) with \(\eta ^2 = \sum _{T \in \mathcal {T}} \eta ^2(T)\). The standard adaptive algorithm [18, Algorithm 2.2] is modified in that, if \(h_{\max }^2 \lambda _h \le \alpha /\sigma _2^2\) is not satisfied, the mesh is uniformly refined. It runs with the initial triangulations from Fig. 3, the default bulk parameter \(\theta = 0.5\), and polynomial degrees p displayed in Fig. 4.
The uniform and adaptive mesh-refinements lead to convergence history plots of the eigenvalue error \(\lambda (j) - \text {GLB}(j)\) and the a posteriori estimate \(\eta ^2\) plotted against the number of degrees of freedom of \(V_h\) (ndof) in log-log plots below; dashed (resp. solid) lines represent uniform (resp. adaptive) mesh-refinements.
7.3 L-shaped domain
The first example concerns the principle Dirichlet eigenvalue on the domain \(\Omega :=(-1,1)^2\setminus ([0,1)\times [0,-1))\) with a re-entering corner at (0, 0) and the reference value \(\lambda (1) = 9.6397238440219410\) from [9]. This leads to the suboptimal convergence rate 2/3 for \(\lambda (1) - \text {GLB}(1)\) and \(\eta ^2\) (for all p) on uniform triangulations in Fig. 5. The adaptive mesh-refining algorithm refines towards the origin as displayed in Fig. 6 and recovers the optimal convergence rates \(p+1\) for \(\lambda (1) - \text {GLB}(1)\) and \(\eta ^2\).
Adaptive triangulations of the L-shaped domain in Sect. 7.3 into 1034 triangles for \(p = 0\) (left) and into 1138 triangles for \(p = 3\) (right) for the approximation to \(\lambda (1)\)
7.4 Isospectral domain
Adaptive triangulations of the isospectral domain in Sect. 7.4 into 1342 triangles for \(p = 0\) (left) and into 1311 triangles for \(p = 3\) (right) for the approximation to \(\lambda (1)\)
The isospectral drums are pairs of non-isometric domains with identical spectrum of the Laplace operator. This subsection considers the domain \(\Omega \) shown in Fig. 3b from [41]; the reference values \(\lambda (1) = 2.53794399980\) and \(\lambda (25) = 29.5697729132\) are from [9] and [34]. Figure 7 shows the suboptimal convergence rate 2/3 for \(\lambda (1) - \text {GLB}(1)\) and \(\eta ^2\) for the approximation of the principle eigenvalue \(\lambda (1)\) on uniformly refined triangulations. The adaptive mesh-refining algorithm refines towards four singular corners (for \(p = 3\)) as depicted in Fig. 9 and recovers the optimal convergence rates \(p+1\) for \(\lambda (1) - \text {GLB}(1)\) and \(\eta ^2\). Figure 8 displays the empirical convergence rate 1 for both \(\lambda (25) - \text {GLB}(25)\) and \(\eta ^2\) in case \(p = 0\), while it is the expected rate 2/3 for \(p\ge 1\) in the presence of a typical corner singularity in the eigenfunction. We conjecture that the singular contribution to the corresponding eigenfunction in this particular example has a very small coefficient and the reduced asymptotic convergence rate 2/3 is therefore barely visible unless a very high accuracy is reached (e.g., absolute error in the eigenvalues much smaller than \(5\times 10^{-4}\)). The adaptive mesh-refining algorithm refines towards four re-entering corners and recovers the optimal convergence rates \(p+1\) for \(\lambda (25) - \text {GLB}(25)\) and \(\eta ^2\). There are two reasons for the plateau observed in the convergence history plot of \(\lambda (25)-\text {GLB}(25)\) in Fig. 8a. First, a larger pre-asymptotic range is expected and observed for the approximation of larger eigenvalues. Second, the condition \(h_{\max }^2 \lambda _h \le \alpha \) is not satisfied for the first triangulations, whence \(\text {GLB}\) is set to zero. An asymptotic behaviour is observed beyond 30,000 degrees of freedom for all displayed polynomial degrees \(p = 0, \dots , 4\).
7.5 Dumbbell-slit domain
The final example approximates the principle Dirichlet eigenvalue \(\lambda (1)\) on the domain \(\Omega :=(-3,2) \times (-1,1) {\setminus } ((-3,-2]\times \{0\} \cup [-1,1] \times [-3/4,1))\) displayed in Fig. 3c. This is a modification of the numerical example in [23, Section 4.2]. The reference value \(\lambda (1) = 8.367702430882\) stems from an adaptive computation with the polynomial degree \(p = 5\). The adaptive algorithm refines towards the reentrant corners at \((-1,-3/4)\) and \((-2,0)\) as displayed in Fig. 10, while the triangles in the subdomain \((1,2) \times (-1,1)\) remain unchanged for \(p \ge 1\). Hence, there may be no reduction of the maximal mesh-size \(h_{\max }\). Figure 11 displays suboptimal convergence rate 0.5 for the errors \(\lambda (1) - \text {GLB}(1)\) and \(\eta ^2\) for \(p = 0,\dots ,4\). The adaptive mesh-refining recovers the optimal convergence rates \(p+1\).
Adaptive triangulations of the dumbbell-slit domain in Sect. 7.5 into 1588 triangles for \(p = 0\) (left) and into 1505 triangles for \(p = 3\) (right) for the approximation to \(\lambda (1)\)
7.6 Conclusions
The computer experiments provide empirical evidence for optimal convergence rates of the adaptive mesh-refining algorithm. The ad hoc choice \(\alpha = 1/2\) is robust in all computer experiments. For \(\beta = \alpha /\sigma _2^2\), the computable condition \(\sigma _2^2 h_{\max }^2 \lambda _h(j) \le \alpha \) leads to confirmed lower eigenvalue bounds and holds on triangulations into right-isosceles triangles, whenever the maximal mesh-size \(h_{\max }\) satisfies \( \lambda _hh_{\max }^2 \le \alpha \pi ^2\). In all displayed numerical benchmarks, \(\lambda _h\) is a lower eigenvalue bound of \(\lambda \) even for \(\lambda _hh_{\max }^2 > \alpha \pi ^2\). The computed (but otherwise undisplayed) efficiency indices \(7 {\times } 10^{-2} \le I :=|\lambda - \lambda _h|\eta ^{-2} \le 4 {\times } 10^{-3}\) range in the numerical examples from \(7\times 10^{-2}\) to \(4 {\times } 10^{-3}\) for an asymptotic range \(2 {\times } 10^4\le \text {ndof} \le 10^5\); the quotient I decreases for larger polynomial degree p. The overall numerical experience provides convincing evidence for the efficiency and reliability of the stabilization-free a posteriori error estimates of this paper. Higher polynomial degrees p lead to significantly more accurate lower bounds and clearly outperform lowest-order discretizations.
References
Abbas, M., Ern, A., Pignet, N.: Hybrid high-order methods for finite deformations of hyperelastic materials. Comput. Mech. 62(4), 909–928 (2018)
Ainsworth, M., Oden, J.T.: A Posteriori Error Estimation in Finite Element Analysis. Wiley, New York (2000)
Alberty, J., Carstensen, C., Funken, S.A.: Remarks around 50 lines of Matlab: short finite element implementation. Numer. Algorithms 20(2–3), 117–137 (1999)
Babuška, I., Osborn, J.: Eigenvalue problems. In: Handbook of Numerical Analysis, vol. II, pp. 641–787. North-Holland, Amsterdam (1991)
Bebendorf, M.: A note on the Poincaré inequality for convex domains. Z. Anal. Anwendungen 22(4), 751–756 (2003)
Bernardi, C., Maday, Y.: Polynomial interpolation results in Sobolev spaces. J. Comput. Appl. Math. 43(1–2), 53–80 (1992)
Bernardi, C., Maday, Y.: Spectral methods. In: Handbook of Numerical Analysis, vol. 5, pp. 209–485. Elsevier (1997)
Bertrand, F., Carstensen, C., Gräßle, B., Tran, N.T.: Stabilization-free HHO a posteriori error control. Numer. Math. 154(3–4), 369–408 (2023)
Betcke, T., Trefethen, L.N.: Reviving the method of particular solutions. SIAM Rev. 47(3), 469–491 (2005)
Boffi, D., Brezzi, F., Fortin, M.: Mixed Finite Element Methods and Applications, vol. 44. Springer, Heidelberg (2013)
Brenner, S.C., Scott, L.R.: The Mathematical Theory of Finite Element Methods, vol. 15, 3rd edn. Springer, New York (2008)
Calo, V., Cicuttin, M., Deng, Q., Ern, A.: Spectral approximation of elliptic operators by the hybrid high-order method. Math. Comput. 88(318), 1559–1586 (2019)
Cancès, E., Dusson, G., Maday, Y., Stamm, B., Vohralík, M.: Guaranteed a posteriori bounds for eigenvalues and eigenvectors: multiplicities and clusters. Math. Comput. 89(326), 2563–2611 (2020)
Cancès, E., Dusson, G., Maday, Y., Stamm, B., Vohralík, M.: Guaranteed and robust a posteriori bounds for Laplace eigenvalues and eigenvectors: a unified framework. Numer. Math. 140(4), 1033–1079 (2018)
Cancès, E., Dusson, G., Maday, Y., Stamm, B., Vohralík, M.: Guaranteed and robust a posteriori bounds for Laplace eigenvalues and eigenvectors: conforming approximations. SIAM J. Numer. Anal. 55(5), 2228–2254 (2017)
Canuto, C., Quarteroni, A.: Approximation results for orthogonal polynomials in Sobolev spaces. Math. Compd. 38(157), 67–86 (1982)
Carstensen, C., Brenner, S.C.: Finite element methods. In: Stein, E., de Borst, R., Hughes, T.J.R. (eds.) Encyclopedia of Computational Mechanics, 2nd edn., pp. 1–47. Wiley, New York (2017)
Carstensen, C., Feischl, M., Page, M., Praetorius, D.: Axioms of adaptivity. Comput. Math. Appl. 67(6), 1195–1253 (2014)
Carstensen, C., Ern, A., Puttkammer, S.: Guaranteed lower bounds on eigenvalues of elliptic operators with a hybrid high-order method. Numer. Math. 149(2), 273–304 (2021)
Carstensen, C., Gallistl, D.: Guaranteed lower eigenvalue bounds for the biharmonic equation. Numer. Math. 126(1), 33–51 (2014)
Carstensen, C., Gallistl, D., Schedensack, M.: Adaptive nonconforming Crouzeix–Raviart FEM for eigenvalue problems. Math. Compd. 84(293), 1061–1087 (2015)
Carstensen, C., Gedicke, J.: Guaranteed lower bounds for eigenvalues. Math. Compd. 83(290), 2605–2629 (2014)
Carstensen, C., Puttkammer, S.: Direct guaranteed lower eigenvalue bounds with optimal a priori convergence rates for the bi-Laplacian. SIAM J. Numer. Anal. 61(2), 812–836 (2023)
Carstensen, C., Puttkammer, S.: How to prove the discrete reliability for nonconforming finite element methods. J. Comput. Math. 38(1), 142–175 (2020)
Carstensen, C., Zhai, Q., Zhang, R.: A skeletal finite element method can compute lower eigenvalue bounds. SIAM J. Numer. Anal. 58(1), 109–124 (2020)
Chaumont-Frelet, T., Ern, A., Vohralík, M.: Polynomial-degree-robust \(H({\rm curl})\)-stability of discrete minimization in a tetrahedron. C. R. Math. Acad. Sci. Paris 358(9–10), 1101–1110 (2020)
Cockburn, B., Di Pietro, D.A., Ern, A.: Bridging the hybrid high-order and hybridizable dG methods. ESAIM Math. Model. Numer. Anal. 50(3), 635–650 (2016)
Costabel, M., McIntosh, A.: On BogovskiÄĭ and regularized Poincaré integral operators for de Rham complexes on Lipschitz domains. Math. Z. 265(2), 297–320 (2010)
Dari, E.A., Durán, R.G., Padra, C.: A posteriori error estimates for non-conforming approximation of eigenvalue problems. Appl. Numer. Math. 62(5), 580–591 (2012)
Di Pietro, D.A., Droniou, J., Manzini, G.: Discontinuous skeletal gradient discretisation methods on polytopal meshes. J. Comput. Phys. 355, 397–425 (2018)
Di Pietro, D.A., Ern, A.: A hybrid high-order locking-free method for linear elasticity on general meshes. Comput. Methods Appl. Mech. Eng. 283, 1–21 (2015)
Di Pietro, D.A., Ern, A., Lemaire, S.: An arbitrary-order and compact-stencil discretization of diffusion on general meshes based on local reconstruction operators. Comput. Methods Appl. Math. 14(4), 461–472 (2014)
Di Pietro, D.A., Tittarelli, R.: An introduction to hybrid high-order methods. In: Numerical Methods for PDEs, vol. 15, pp. 75–128. Springer, Cham (2018)
Driscoll, T.A.: Eigenmodes of isospectral drums. SIAM Rev. 39(1), 1–17 (1997)
Durán, R.G., Padra, C., Rodríguez, R.: A posteriori error estimates for the finite element approximation of eigenvalue problems. Math. Models Methods Appl. Sci. 13(8), 1219–1229 (2003)
Ern, A., Guermond, J.-L.: Finite Elements I-Approximation and Interpolation, vol. 72. Springer, New York (2021)
Ern, A., Guermond, J.-L.: Finite Elements II-Galerkin Approximation, Elliptic and Mixed PDEs, vol. 73. Springer, New York (2021)
Ern, A., Zanotti, P.: A quasi-optimal variant of the hybrid high-order method for elliptic partial differential equations with \(H^{-1}\) loads. IMA J. Numer. Anal. 40(4), 2163–2188 (2020)
Gallistl, D.: Mixed methods and lower eigenvalue bounds. Math. Compd. 92(342), 1491–1509 (2023)
Girault, V., Raviart, P.-A.: Finite Element Methods for Navier–Stokes Equations. Theory and Algorithms, vol. 5. Springer, Berlin (1986)
Gordon, C., Webb, D., Wolpert, S.: Isospectral plane domains and surfaces via Riemannian orbifolds. Invent. Math. 110(1), 1–22 (1992)
Hiptmair, R.: Discrete Compactness for p-Version of Tetrahedral Edge Elements. arXiv:0901.0761 (2009)
Larson, M.G.: A posteriori and a priori error analysis for finite element approximations of self-adjoint elliptic eigenvalue problems. SIAM J. Numer. Anal. 38(2), 608–625 (2000)
Laugesen, R.S., Siudeja, B.A.: Minimizing Neumann fundamental tones of triangles: an optimal Poincaré inequality. J. Differ. Equ. 249(1), 118–135 (2010)
Liu, X.: A framework of verified eigenvalue bounds for self-adjoint differential operators. Appl. Math. Comput. 267, 341–355 (2015)
Melenk, J.M., Rojik, C.: On commuting \(p\)-version projection-based interpolation on tetrahedra. Math. Compd. 89(321), 45–87 (2020)
Melenk, J.M., Wurzer, T.: On the stability of the boundary trace of the polynomial L2-projection on triangles and tetrahedra (extended version). arXiv:1302.7189 (2013)
Monk, P.: Finite Element Methods for Maxwell’s Equations. Oxford University Press, New York (2003)
Payne, L.E., Weinberger, H.F.: An optimal Poincaré inequality for convex domains. Arch. Ration. Mech. Anal. 5, 286–292 (1960)
Scott, L.R., Zhang, S.: Finite element interpolation of nonsmooth functions satisfying boundary conditions. Math. Compd. 54(190), 483–493 (1990)
Sherwin, S.J., Karniadakis, G.E.: A new triangular and tetrahedral basis for high-order (hp) finite element methods. Int. J. Numer. Methods Eng. 38(22), 3775–3802 (1995)
Szyld, D.B.: The many proofs of an identity on the norm of oblique projections. Numer. Algorithm 42(3–4), 309–323 (2006)
Veeser, A., Zanotti, P.: Quasi-optimal nonconforming methods for symmetric elliptic problems. II—Overconsistency and classical nonconforming elements. SIAM J. Numer. Anal. 57(1), 266–292 (2019)
Verfürth, R.: A Review of A Posteriori Error Estimation and Adaptive Mesh-Refinement Techniques. Wiley, Chichester (1996)
Wurzer, T.: Stability of the trace of the polynomial L2-projection on triangles. In: Technical Report 36, Institute for Analysis and Scientific Computing, Vienna (2010)
Acknowledgements
The authors gratefully thank Prof. Markus Melenk (Vienna University of Technology) for the discussion about the \(H^1\) stability of the \(L^{2}\) projection that eventually led to the proof of (C) and Prof. Alexandre Ern (CERMICS, ENPC) for his alternative proof of the p-robustness of \(C_{\text {st,2}}\) in (B).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work has been supported by the German Research Foundation (DFG) in the Priority Program 1748 Reliable simulation techniques in solid mechanics: Development of non-standard discretization methods, mechanical and mathematical analysis CA 151/22-2 and under Germany’s Excellence Strategy - The Berlin Mathematics Research Center MATH+ (EXC-2046/1, project ID: 390685689) as well as by the European Union’s Horizon 2020 research and innovation programme (project DAFNE grant agreement No. 891734 and project RandomMultiScales grant agreement No. 865751).
Appendix: On p-robustness of constants in refined \(H^1\) stability estimates
Appendix: On p-robustness of constants in refined \(H^1\) stability estimates
This appendix provides details of the proof of Theorem 2.1 in the paper with focus on the constants \(C_{\text {st,1}}, C_\text {st,2}\) and their dependence on the polynomial degree \(p \in \mathbb {N}_0\) in three space dimensions.
1.1 Overview
Let \({\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| \bullet \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| } :=\Vert \nabla \bullet \Vert _{L^2(T)}\) abbreviate the seminorm in the Sobolev space \(H^1(T):=H^1(\text {int}(T))\) and let \(\Pi _p\) denote the \(L^{2}\) projection onto the space \(P_p(T)\) of polynomials of total degree at most \(p \in \mathbb {N}_0\) for a fixed tetrahedron \(T \subset \mathbb {R}^3\). For any Sobolev function \(f \in H^1(T)\), the Galerkin projection \(G f \in P_{p+1}(T)\) is the unique polynomial of degree at most \(p+1\) with the prescribed integral mean \(\Pi _0 G f = \Pi _0 f\) and the orthogonality \(\nabla (f - Gf) \perp \nabla P_{p+1}(T)\) in \(L^2(T;\mathbb {R}^3)\). The constants \(C_\text {st,1}\) and \(C_\text {st,2}\) are the best possible constants in the stability estimates
Theorem 2.1 asserts the following properties of \(C_\text {st,1}\) and \(C_\text {st,2}\).
-
(A)
There exist positive constants \(1 \le C_\text {st,2} \le C_\text {st,1} < \infty \) that satisfy (1)–(2). The constants \(C_\text {st,1}\) and \(C_\text {st,2}\) are independent of the diameter \(h_T\) of T.
-
(B)
\(C_\text {st,2}\) is p robust, i.e., \(C_\text {st,2}\) is uniformly bounded for all \(p \in \mathbb {N}_0\).
-
(C)
\(C_\text {st,1} \approx \sqrt{p+1}\) is not p robust.
The proof of \(\Vert \Pi _{p+1}\Vert \le C_{\textrm{st, 1}}\le C_{\textrm{st, 2}} \Vert \Pi _{p+1}\Vert \lesssim \sqrt{p+1}\) is already explained in the paper and \(\sqrt{p+1}\lesssim \Vert \Pi _{p+1}\Vert \) is established below in C.
1.2 A. Proof of existence
The two assumptions (H1)–(H2) from [25, Theorem 3.1] imply the existence of the constant \(C_\text {st,1} < \infty \) in [19, Theorem 2.3]. The \(L^{2}\) orthogonality \(\nabla (1 - G) f \perp \nabla P_{p+1}(T)\) implies \({\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| (1 - G) f \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| } \le \Vert \nabla (1 - \Pi _{p+1}) f\Vert _{L^2(T)}\) for all \(f \in H^1(T)\), whence \(C_{\text {st,1}} \le C_\text {st,2} < \infty \). The best approximation property of the \(L^{2}\) projection \(\Pi _p\) proves \(\Vert (1 - \Pi _p) \nabla f\Vert _{L^2(T)} \le {\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| (1 - G) f \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }\) and, therefore, \(1 \le C_\text {st,1}\). Notice that (A) holds in any space dimension. \(\square \)
1.3 B. Proof of p robustness of \(C_{\textrm{st, 2}}\)
Let \(\text {N}_p(T) :=P_p(T;\mathbb {R}^3) \oplus (P_p^\text {hom}(T;\mathbb {R}^3) \times x) = P_p(T;\mathbb {R}^3) \oplus \{q \in P_{p+1}^{\text {hom}}(T;\mathbb {R}^3): x \cdot q(x) = 0 \text { for all } x \in T\}\) denote the first-kind Nédélec finite element space with the space \(P_p^\text {hom}(T;\mathbb {R}^3)\) of homogenous polynomials of (total) degree p. Since \(P_p(T;\mathbb {R}^3) \subset \text {N}_p(T)\), the \(L^{2}\) projection \(\Pi _\text {N}\) onto \(\text {N}_p(T)\) satisfies \(\Vert (1 - \Pi _\text {N}) \nabla f\Vert _{L^2(T)} \le \Vert (1 - \Pi _p) \nabla f\Vert _{L^2(T)}\) for all \(f \in H^1(T)\). Hence, the existence of a constant C(T) independent of p and \(\text {diam}(T)\) such that
implies (B). Given any \(f \in H^1(T)\), abbreviate \(q_\text {N} :=\Pi _\text {N} \nabla f \in \text {N}_p(T)\) and observe \(r_\text {RT}:=\text {curl}\,q_\text {N} \in \text {RT}_p(T)\) with \(\text {div}\,r_\text {RT}= 0\), e.g., from [36, Lemma 15.10], [10, Eq. (2.3.62)], or [48, Lemma 5.40]. It goes back to [28] to define a Bogovskiǐ-type integral operator as a pseudo-differential operator of order \(-1\) of a Hörmander class \(S^{-1}_{1,0}(\mathbb {R}^n)\) that leads to right-inverses for differential operators. In particular, there exists a bounded linear operator \(R^{\text {curl}}: H^{-1}(T;\mathbb {R}^3) \rightarrow L^2(T;\mathbb {R}^3)\) such that \(R_\text {N} :=R^{\text {curl}} r_\text {RT}\in \text {N}_p(T)\) satisfies \(\text {curl}\, R_\text {N} = r_\text {RT}\). Since \(R_\text {N} - q_\text {N} \in \text {N}_p(T)\) is curl-free by design, \(R_\text {N} - q_\text {N} = \nabla \psi \) is the gradient of some function \(\psi \in H^1(T)\) in the tetrahedron T. The structure of \(\text {N}_p(T)\) enforces \(\psi \in P_{p+1}(T)\) (cf. [36, Lemma 15.10] and [48, Lemma 5.28] for the proof). Recall that \(\nabla G f\) is the best-approximation of \(\nabla f\) in \(\nabla P_{p+1}(T)\) and deduce (from \(\nabla P_{p+1}(T) \subset P_p(T;\mathbb {R}^3) \subset N_p(T)\)) that it is also the best-approximation of \(q_\text {N} = \Pi _\text {N} \nabla f\). Hence,
The operator norm \(\Vert R^{\text {curl}}\Vert \) of \(R^{\text {curl}}\) allows for \(\Vert R_\text {N}\Vert _{L^2(T)} \le \Vert R^\text {curl}\Vert {\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| r_\text {RT} \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }_*\) with the norm \({\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| \bullet \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }_*\) in the dual space \(H^{-1}(T;\mathbb {R}^3)\) of \(H^1_0(T;\mathbb {R}^3)\) (endowed with the \(H^1\) seminorm \({\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| \bullet \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }\)), i.e.,
Recall \(r_\text {RT}= \text {curl}\,q_\text {N}\). An integration by parts and \(\text {curl}\,\nabla f = 0 \in L^2(T)\) provide
for any \(v \in H^1_0(T;\mathbb {R}^3)\). This, a Cauchy inequality, and the estimate \(\Vert \text {Curl}\,v\Vert _{L^2(T)} \le 2{\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| v \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }/\sqrt{3}\) reveal \({\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| r_\text {RT} \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }_* \le 2\Vert (1 - \Pi _\text {N})\nabla f\Vert _{L^2(T)}/\sqrt{3}\). Hence (4) implies
This and the Pythagoras theorem result in
This proves (3) with \(C(T) :=\sqrt{1 + 4\Vert R^{\text {curl}}\Vert ^2/3}\) and, therefore, (B). More details on \(\Vert R^{\text {curl}}\Vert \) and further applications can be found in [28, Section 3], [42, Section 2], and [46, Lemma 6.4].
An alternative proof of (3) involves the main result of [26] and was kindly provided by A. Ern in private communications from 03/08/2022. For \(v :=\nabla f \in H(\text {curl}, T)\) with \(\text {curl}\, v = 0\), let \(v_h^*\) (resp. \(w_h^*\)) denote the minimizer of \(\Vert v - v_h\Vert _{L^2(\Omega )}\) among \(v_h \in \mathcal {K} :=\{v_h \in N_p(T): \text {curl}\,v = 0\}\) (resp. \(\Vert v - w_h\Vert _{L^2(\Omega )}\) among \(w_h \in N_p(T)\)). The \(L^{2}\) orthogonality \(w_h^* - v_h^* \perp \mathcal {K}\) from the Euler-Lagrange equations associated with these minimization problems implies that the difference \(w_h^* - v_h^*\) minimizes the functional \(\Vert z_h\Vert _{L^2(T)}\) among all \(z_h \in w_h^* + \mathcal {K}\). Invoking the results of [28], it is known from [26, Theorem 2] that
with a p-robust constant \(\widetilde{C}(T) > 0\). Since \(\text {curl}(w_h^* - v) = \text {curl} w_h^*\), we infer \(\Vert w_h^* - v_h^*\Vert _{L^2(T)} \le \widetilde{C}(T)\Vert v - w_h^*\Vert _{L^2(T)}\). This and a triangle inequality imply
This is (3) with \(C(T) :=1 + \widetilde{C}(T)\) because \(w_h^* = \Pi _\text {N} \nabla f\) by design and \(v_h^* = \nabla G f\) from \(\mathcal {K} = \nabla P_{p+1}(T)\). \(\square \)
1.4 C. Lower growth \(\sqrt{p+1}\lesssim \Vert \Pi _{p+1}\Vert \)
While a compactness argument in [25, Theorem 3.1] leads to the existence of \(C_\text {st,1},\,{ thedependenceof}C_\text {st,1}{} { onthepolynomialdegree}p{ remainedobscuredandonlyanupperboundfor}p = 0\) was given. The proof of Theorem 2.1 in the paper establishes
An upper bound \(\Vert \Pi _{p+1}\Vert \lesssim \sqrt{p+1}{} { ofthegrowthofthe}H^1{ stabilityconstantofthe}L^{2}{} \) projection is known from [47, Sec. 5] and [55]. The remaining parts of this appendix therefore consider the reverse direction \(\sqrt{p+1}\lesssim \Vert \Pi _{p+1}\Vert { foratetrahedronanddepartwithamotivatingclassicalresultin}1{ D}.{ Forsimplicity},\,{ thefollowingpresentationappliesanindexshiftanddiscusses}\Vert \Pi _p\Vert \approx \sqrt{p}{} { forarbitrary}p\ge 1\).
1.4.1 Lower bound in 1D
In one space dimension, \(\Vert \Pi _p\Vert \approx \sqrt{p}{} \) is established, e.g., in [16, Theorem 2.4] and [6, Remark 3.5]. Let \(L_k{ for}k \in \mathbb {N}_0{ denotetheLegendrepolynomialsinthereferenceinterval}I:=(-1,1).{ Then}L_k{ satisfies},\,{ forall}k \in \mathbb {N}_0\),
with the convention \(L_{-1} \equiv 0{ in}I\), cf., e.g., [7, Eqns (3.11), (3.12), (5.3)]. The pairwise \(L^{2}{} { orthogonalityof}L_k\) and (5)–(6) lead to
whence \(\Vert \nabla \Pi _{p} \widehat{L}_{p}\Vert _{L^2(I)}\approx \sqrt{p}\Vert \nabla \widehat{L}_{p}\Vert _{L^2(I)}{} { forall}p \ge 1.{ Thisproves}\sqrt{p} \lesssim \Vert \Pi _p\Vert { in}1{ D}.{ Asimilarresultholdsforthe}L^{2}{} { projection}\widetilde{\Pi }_{p}:L^2(D)\rightarrow Q_{p}(D) \cong P_{p}(I)^n\) onto the space of tensor-product polynomials on the \(n\)-cube \(D:=I^n=(-1,+1)^n\) [16]. For simplicity and because the arguments carry over to triangles as well, the following proof considers simplices in \(n=3\) dimensions only.
Proof of \(\sqrt{p}\lesssim \Vert \Pi _p\Vert \) for \(n=3.{ Let}p\in {\mathbb {N}}{} { bearbitraryandlet}F:Q\rightarrow T\) denote the coordinate transformation
from the cube \(Q:=(-1,1)^3{ ontothereferencetetrahedron}T :=\text {conv}\{(-1,-1,-1),(1,-1,-1), (-1, 1, -1), (-1, -1, 1)\}{} { withtheJacobian}J_F{ and}\text {det} J_F=(1-\eta _2)(1-\eta _3)^2/8\), see, e.g., [51] and [47, Section 3] for a derivation. An integration by substitution leads, for any \(f \in L^1(Q)\), to
Define \(\varphi (\eta _2,\eta _3):=(1-\eta _2)(1-\eta _3),\,U_p(\eta _1, \eta _2,\eta _3):=\varphi (\eta _2,\eta _3)^{p-1}\widehat{L}_p(\eta _1),\,{ and}\widetilde{U}_p:=U_p\circ F^{-1}\in L^2(T){ for}p \ge 1.{ Thechainrule}\nabla \widetilde{U}_p = J_F^{-\top }\nabla U_p\circ F^{-1}{} \) for the gradient and (5) provides \((\nabla \widetilde{U}_p)\circ F = \varphi (\eta _2, \eta _3)^{p-2} M(\eta _1, \eta _2) G(\eta _1)\) with
A Cauchy inequality in \(\mathbb {R}^3\) proves
This, the integration by substitution formula (7), \(R_p:=\int _{-1}^1\int _{-1}^1(1-\eta _2)^{2p-3}(1-\eta _3)^{2p-2}\text {d}{(\eta _2,\eta _3)}\in {\mathbb {R}},\,{ and}|\eta _j|\le 1{ for}j=1,2,3{ and}(\eta _1,\eta _2, \eta _3)\in Q\) show
The pairwise \(L^{2}{} \) orthogonality of Legendre polynomials and (5)–(6) verify
for \(p\ge 1\). This, (6), and (8) provide the bound \(2p{\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| \widetilde{U}_p \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }^2\le 39 R_p{ for}p\ge 1.{ Itremainstocontrol}\nabla \Pi _p \tilde{U}_p\) from below. Recall from [51] that the polynomials \(\widetilde{\psi }_{j,k,\ell }:=\psi _{j,k,\ell }\circ F^{-1}\in P_{j+k+\ell }(T){ for}j,k,\ell \in {\mathbb {N}}_0\) with
are \(L^2(T){ orthogonalandthat}(\widetilde{\psi }_{j,k,\ell }\ |\ 0\le j+k+\ell \le p){ formsabasisof}P_p(T)\). The pairwise orthogonality of the Legendre polynomials, (5), and (7) imply that
vanishes for all \(k,\ell \in {\mathbb {N}}{} { and}j\le p\). Consequently,
This, the chain rule for partial derivatives, and (6)–(7) show
The term \(2p(p-1)(2p+1)^{-2}\ge 0{ ismonotonicallyincreasingin}p\ge 1{ andboundedfrombelowby}4/25{ for}p\ge 2\). Thus, (9) and \(2p{\left| \hspace{-1.0625pt}\left| \hspace{-1.0625pt}\left| \widetilde{U}_p \right| \hspace{-1.0625pt}\right| \hspace{-1.0625pt}\right| }^2\le 39 R_p\) provide
for all \(p\ge 2,\,{ whence}\sqrt{p} \lesssim \Vert \Pi _p\Vert { onthereferencetetrahedron}T.{ Thisandascalingargumentwithanaffinetransformationconcludestheproofforageneraltetrahedron}. \square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Carstensen, C., Gräßle, B. & Tran, N.T. Adaptive hybrid high-order method for guaranteed lower eigenvalue bounds. Numer. Math. (2024). https://doi.org/10.1007/s00211-024-01407-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00211-024-01407-w




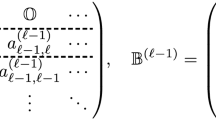

 , the right-isosceles triangle
, the right-isosceles triangle  ,
, 










