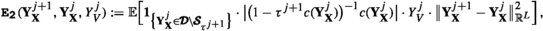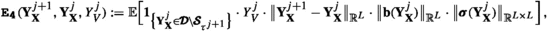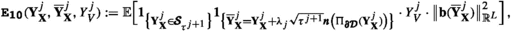A posteriori error analysis and adaptivity for high-dimensional elliptic and parabolic boundary value problems

Abstract

We derive a posteriori error estimates for the (stopped) weak Euler method to discretize SDE systems which emerge from the probabilistic reformulation of elliptic and parabolic (initial) boundary value problems. The a posteriori estimate exploits the use of a scaled random walk to represent noise, and distinguishes between realizations in the interior of the domain and those close to the boundary. We verify an optimal rate of (weak) convergence for the a posteriori error estimate on deterministic meshes. Based on this estimate, we then set up an adaptive method which automatically selects local deterministic mesh sizes, and prove its optimal convergence in terms of given tolerances. Provided with this theoretical backup, and since corresponding Monte-Carlo based realizations are simple to implement, these methods may serve to efficiently approximate solutions of high-dimensional (initial-)boundary value problems.

1 Introduction

Let $\pmb {{\mathcal {D}}}\subset {\mathbb {R}}^{L}$ be a bounded domain, and $L\in {\mathbb {N}}$. In the first part of this work, we derive an a posteriori error estimate and an adaptive time-stepping strategy based on it, for a discretization which is based on the probabilistic representation of the elliptic partial differential equation (PDE) with Dirichlet condition

$$\begin{aligned} \frac{1}{2}\textrm{Tr}\Bigl (\pmb {\sigma }({\textbf{x}}) \pmb {\sigma }^{\top }({\textbf{x}}) D_{{\textbf{x}}}^{2}u({\textbf{x}})\Bigr )+ \bigl \langle {\textbf{b}}({\textbf{x}}), D_{{\textbf{x}}}u(\textbf{x})\bigr \rangle _{{\mathbb {R}}^{L}}+ c({\textbf{x}})u({\textbf{x}})+g({\textbf{x}})= & {} 0 \quad \text {for all } \;\, \textbf{x}\in \pmb {{\mathcal {D}}}, \nonumber \\ u({\textbf{x}})= & {} \phi ({\textbf{x}}) \quad \text {for all} \;\, {\textbf{x}}\in \pmb {\partial }\pmb {{\mathcal {D}}},\nonumber \\ \end{aligned}$$

(1.1)

where ${\textbf{b}}:\overline{\pmb {{\mathcal {D}}}}\rightarrow {\mathbb {R}}^{L}$, $\pmb {\sigma }:\overline{\pmb {{\mathcal {D}}}}\rightarrow {\mathbb {R}}^{L\times L}$, $c:\overline{\pmb {{\mathcal {D}}}}\rightarrow {\mathbb {R}}^{-}_{0}$, $g:\overline{\pmb {{\mathcal {D}}}}\rightarrow {\mathbb {R}}$ and $\phi :\overline{\pmb {{\mathcal {D}}}}\rightarrow {\mathbb {R}}$ are given. For proper settings of data such as stated in Sect. 3.1, there exists a unique classical solution $u:\overline{\pmb {{\mathcal {D}}}}\rightarrow {\mathbb {R}}$ of problem (1.1), given by the probabilistic representation

$$\begin{aligned} u({\textbf{x}})={\mathbb {E}}\Big [\phi \bigl ({\textbf{X}}^{{\textbf{x}}}_{\pmb {\tau }^{{\textbf{x}}}}\bigr )V_{\pmb {\tau }^{{\textbf{x}}}}^{{\textbf{x}}}+Z_{\pmb {\tau }^{{\textbf{x}}}}^{{\textbf{x}}}\Big ]\qquad \text {for all} \;\, {\textbf{x}}\in \pmb {{\mathcal {D}}}, \end{aligned}$$

(1.2)

see e.g. [40, p. 366], where

• (1) $\textbf{X}^{{\textbf{x}}} \equiv \{ \textbf{X}^{{\textbf{x}}}_{t};\, t \ge 0\}$ denotes the ${{\mathbb {R}}}^L$-valued solution of the stochastic differential equation (SDE)

  $$\begin{aligned} {\mathrm d}{{\textbf{X}}}_t = {\textbf{b}}({\textbf{X}}_{t}){\mathrm d}t + \pmb {\sigma }({\textbf{X}}_{t}){\mathrm d}{{\textbf{W}}}_{t} \quad \text {for all} \;\, t >0, \qquad {{\textbf{X}}}_{0} = {{\textbf{x}}} \in \pmb {{\mathcal {D}}}\subset {\mathbb {R}}^L\,, \end{aligned}$$

  (1.3)

  starting in ${\textbf{x}}\in \pmb {{\mathcal {D}}}$, where $\textbf{W} \equiv \{ \textbf{W}_t;\, t\ge 0\}$ is an ${{\mathbb {R}}}^L$-valued Wiener process on a filtered probability space $(\Omega , {{\mathcal {F}}}, \{{{\mathcal {F}}}_t \}_{t \ge 0}, {{\mathbb {P}}})$, and the first exit time of ${\textbf{X}}^{{\textbf{x}}}$ from $\pmb {{\mathcal {D}}}$ is

  $$\begin{aligned} \pmb {\tau }^{{\textbf{x}}}:=\inf \big \{ t>0:\; {\textbf{X}}^{{\textbf{x}}}_{t} \notin \pmb {{\mathcal {D}}}\big \}. \end{aligned}$$

  (1.4)

• (2) $V^{{\textbf{x}}}\equiv \{V_{t}^{{\textbf{x}}}\,;\,t\ge 0\}$ resp. $Z^{{\textbf{x}}}\equiv \{Z_{t}^{{\textbf{x}}}\,;\,t \ge 0\}$ denote the ${\mathbb {R}}$-valued solutions of the random ordinary differential equations (ODE)

  $$\begin{aligned} {\mathrm d}V_{t}= & {} c({{\textbf{X}}}^{{\textbf{x}}}_{t})V_{t} {\mathrm d}t\quad \text {for all} \;\, t >0, \qquad V_{0} = 1, \quad \text {and} \end{aligned}$$

  (1.5)
  $$\begin{aligned} {\mathrm d}Z_{t}= & {} g({{\textbf{X}}}^{{\textbf{x}}}_{t})V_{t} {\mathrm d}t \quad \text {for all} \;\, t >0, \qquad Z_{0} = 0. \end{aligned}$$

  (1.6)

To numerically solve (1.1), deterministic schemes based on finite differences, finite volumes, or finite elements are well-known, which are complemented by rigorous a priori and a posteriori error analysis. However, these methods all suffer from the ‘curse of dimensionality’, which restricts their implementations to small values $1\le L\le 4$ in practice. To simulate the boundary value problem (1.1) for $L\gg 4$, other (deterministic) mesh-based methods are available, such as sparse grids, or methods that rely on tensor-structured data and (structure-inheriting) compatible operators; see also Sect. 2 for more details.

In this work the probabilistic interpretation of (1.1) is taken to approximate $u({\textbf{x}})$, ${\textbf{x}}\in \pmb {{\mathcal {D}}}$, for high-dimensional problems, i.e., $L\gg 4$, and free from (restrictive) constraints on data in (1.1): specifically, the first goal is an a posteriori error analysis for discretization Scheme 2 (see Sect. 3.3) based on [40, p. 365 ff., Sec. 6.3] to bound the approximation error for $u({\textbf{x}})$, ${\textbf{x}}\in \pmb {{\mathcal {D}}}$ in terms of the computed solution $\{{\textbf{Y}}_{{\textbf{X}}}^{j}\}_{j\ge 0}$. A distinct feature of Scheme 2 is the use of a scaled random walk instead of unbounded Wiener increments to rigorously derive the a posteriori error bound (1.7) below.

To our knowledge, the first a posteriori (weak) error analysis for the Euler method with Wiener increments (unbounded) (4.29) to solve the Kolmogorov PDE on $\pmb {{\mathcal {D}}}={\mathbb {R}}^{L}$ goes back to [48], whose application is restricted to low dimensions L. These techniques are later extended to the related (parabolic) boundary value problem in [20], where ‘stopping’ is realized when corresponding iterates have come ‘close’ to $\pmb {\partial {\mathcal {D}}}$ rather than onto $\pmb {\partial {\mathcal {D}}}$; however, the a posteriori error analysis still suffers from same restrictions; see Sect. 2.

In this work, for ${\textbf{x}}\in \pmb {{\mathcal {D}}}$ fixed, and a given mesh $\{t_{j}\}_{j\ge 0}\subset [0,\infty )$ with local mesh sizes $\{\tau ^{j+1}\}_{j\ge 0}$, we verify the following a posteriori (weak) error estimate for iterates $\{({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j},Y_{Z}^{j})\}_{j=0}^{J^{*}}$ from Scheme 2

$$\begin{aligned} \Bigl \vert u({\textbf{x}}) - {\mathbb {E}}\bigl [\phi (\textbf{Y}_{{\textbf{X}}}^{J^{*}})Y_{V}^{J^{*}}+Y_{Z}^{J^{*}}\bigr ] \Bigr \vert \le \pmb {C}(\phi ,g)\cdot \sum \limits _{j=0}^{\infty } \tau ^{j+1} \big \{{{\mathfrak {G}}}_{1}^{(j)} + {{\mathfrak {G}}}_{2}^{(j)}+ {{\mathfrak {G}}}_{3}^{(j)} \big \},\nonumber \\ \end{aligned}$$

(1.7)

with $\pmb {C}(\phi ,g)>0$, (computable) a posteriori error estimators $\{{\mathfrak {G}}_{\ell }^{(\cdot )}\}_{\ell =1}^{3}$ in terms of the discrete solution, and $J^{*}\equiv J^{*}({\textbf{x}}) \in {\mathbb {N}}_{0}$ the stopping index. Main achievements in our work are then

• (i) its construction, which is based on Taylor’s formula (rather than Itô’s formula) to properly address the use of scaled random walk; see Theorem 4.1. At time $t_{j}$, the functional ${{\mathfrak {G}}}_{1}^{(j)}$ is assembled from those states that realize in the interior of $\pmb {{\mathcal {D}}}$, while the remaining two are assembled from those in a ${\mathcal {O}}(\sqrt{\tau ^{j+1}})-$neighborhood of the boundary, addressing possible bouncing back/stopping.

• (ii) Stability results in Sect. 3.3 concerning ‘discrete stopping’ ensure that the sum in (1.7) is in fact finite, and, besides the ‘stopping’-mechanism in Scheme 2, they are the key to verify optimal first order of convergence for (1.7) on families of (time-)meshes with maximum mesh size $\tau ^{max}>0$, when $\tau ^{max} \searrow 0$; see Theorem 4.6.

• (iii) Estimate (1.7) will be used in Sect. 5 to construct an adaptive time stepping algorithm (see Algorithm 5.1) for which we prove local, as well as global termination, and optimal convergence behaviour in terms of the tolerance (${\texttt {Tol}}>0$); see Sect. 5.

ad (i). The derivation of (1.7) in Sect. 4.1 conceptually follows the guideline of [35, Thm. 3.1], where an a posteriori (weak) error estimate is presented for the (semi-implicit) Euler method, which uses (unbounded) Wiener increments; in fact, ${\mathfrak {G}}_{1}^{(\cdot )}$ in (1.7) is conceptually close to the estimator in [35, (3.1)]; see also item 3. Remark 4.1. While [35] considered the Kolmogorov PDE (see (1.8)) on the whole space $\pmb {{\mathcal {D}}}={\mathbb {R}}^{L}$, we here consider bounded domains $\pmb {{\mathcal {D}}}\subset {\mathbb {R}}^{L}$, which requires the proper numerical approximation of the stopping time $\pmb {\tau }^{{\textbf{x}}}$ in (1.4) when $\textbf{X}^{{\textbf{x}}}$ crosses the boundary $\pmb {\partial {\mathcal {D}}}$. To this end, the weak Euler method in Scheme 2 in combination with the corresponding ‘stopping’-mechanism enables a successive (local) construction of iterates $\{{\textbf{Y}}_{{\textbf{X}}}^{j}\}_{j\ge 0}$ up to the boundary $\pmb {\partial {\mathcal {D}}}$, where all of them lie in $\overline{\pmb {{\mathcal {D}}}}$: in this respect, we denote by $\pmb {{\mathcal {S}}}_{\tau ^{j+1}}\subset \overline{\pmb {{\mathcal {D}}}}$, $j\ge 0$, the set of points which are close to $\pmb {\partial {\mathcal {D}}}$. We characterize this ‘boundary strip’ via the verification:

• If $\textrm{d}({\textbf{Y}}_{{\textbf{X}}}^{j},\pmb {\partial {\mathcal {D}}}):=\inf \{\Vert {\textbf{Y}}_{{\textbf{X}}}^{j} - {\textbf{v}}\Vert _{{\mathbb {R}}^{L}}\,|\, {\textbf{v}}\in \pmb {\partial {\mathcal {D}}}\}\ge \lambda _{j}\sqrt{\tau ^{j+1}}$, then ${\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}}$, and hence ${\textbf{Y}}_{{\textbf{X}}}^{j+1}\in \overline{\pmb {{\mathcal {D}}}}$,

• If $0<\textrm{d}({\textbf{Y}}_{{\textbf{X}}}^{j},\pmb {\partial {\mathcal {D}}})< \lambda _{j}\sqrt{\tau ^{j+1}}$, then ${\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}$,

for a suitable number $\lambda _{j}>0$; see Sect. 3.3 for a proper choice. Once ${\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}$, it is either projected onto $\pmb {\partial {\mathcal {D}}}$ and the procedure stops or is ‘bounced back’ to the interior of $\pmb {{\mathcal {D}}}$ (with some probability). This different treatment of realizations of ${\textbf{Y}}_{{\textbf{X}}}^{j}$ via Scheme 2 is reflected in the error estimators $\{{\mathfrak {G}}_{\ell }^{(\cdot )}\}_{\ell =1}^{3}$ in (1.7) (see Fig. 1): those which contribute to the functional ${\mathfrak {G}}_{1}^{(j)}$ take positions in $\pmb {{\mathcal {D}}}{\setminus } \pmb {{\mathcal {S}}}_{\tau ^{j+1}}$; in contrast, ${\mathfrak {G}}_{3}^{(j)}$ accounts for those in the boundary strip $\pmb {{\mathcal {S}}}_{\tau ^{j+1}}$, while ${\mathfrak {G}}_{2}^{(j)}$ assembles the subset of those realizations, which bounce back to the interior of $\pmb {{\mathcal {D}}}$.

Fig. 1

Realizations which A contribute to ${\mathfrak {G}}_{1}^{(j)}$, B to ${\mathfrak {G}}_{2}^{(j)}$, and C to ${\mathfrak {G}}_{3}^{(j)}$

We illustrate the role of the different estimators $\{{\mathfrak {G}}_{\ell }^{(\cdot )}\}_{\ell =1}^{3}$ in (1.7) for a prototype PDE (1.1).

Example 1.1

Let $L\in {\mathbb {N}}$ and $\pmb {{\mathcal {D}}}=\big \{{\textbf{x}}\in {\mathbb {R}}^{L}\,:\,\Vert {\textbf{x}}\Vert _{{\mathbb {R}}^{L}}<1\big \}$. Consider (1.1) with ${\textbf{b}}({\textbf{x}})\equiv {\textbf{0}}$, $\pmb {\sigma }({\textbf{x}})\equiv \sqrt{\frac{2}{L}}\cdot {\mathbb {I}}$, where ${\mathbb {I}}$ denotes the $L-$dimensional identity matrix, $c({\textbf{x}})\equiv 0$. Then, $\{{\mathfrak {G}}_{\ell }^{(j)}\}_{\ell =1}^{3}$ in Theorem 4.1 are $(j\ge 0)$¹:

$$\begin{aligned} {\mathfrak {G}}_{1}^{(j)}&= \frac{1}{2}\cdot {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}}\cdot \big \Vert {\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j}\big \Vert _{{\mathbb {R}}^{L}}^{2} \Big ] \,,\\ {\mathfrak {G}}_{2}^{(j)}&=\frac{1}{2}\cdot {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \cdot \big \Vert {\textbf{Y}}_{{\textbf{X}}}^{j+1}-\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}\big \Vert _{{\mathbb {R}}^{L}}^{2} \Big ] \,,\\ {\mathfrak {G}}_{3}^{(j)}&=2\cdot {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} \Big ]\,. \end{aligned}$$

${\mathfrak {G}}_{1}^{(j)}$ accounts for incremental changes within the interior $\pmb {{\mathcal {D}}}{\setminus } \pmb {{\mathcal {S}}}_{\tau ^{j+1}}$. The terms in ${\mathfrak {G}}_{3}^{(j)}$ account for those iterates that have already entered $\pmb {{\mathcal {S}}}_{\tau ^{j+1}}$, and where the event of a ‘projection’ resp. ‘bouncing back’ is about to happen next. The terms in ${\mathfrak {G}}_{2}^{(j)}$ account for those realizations in $\pmb {{\mathcal {S}}}_{\tau ^{j+1}}$ which will be ‘bounced back’.

ad (ii). Once the a posteriori error estimate has been established in Theorem 4.1, we analyze its convergence behavior along sequences of shrinking meshes with maximum mesh size $\tau ^{max}>0$. The result in Theorem 4.6 shows an optimal rate of convergence, and thus recovers the well-known a priori estimate for iterates $\{({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j},Y_{Z}^{j})\}_{j=0}^{J^{*}}$ of Scheme 2; see [40, p. 369, Thm. 3.4]. In fact, the presence of the estimator $\{{\mathfrak {G}}_{2}^{(j)}\}_{j\ge 0}$ is crucial to validate order 1; in fact, if it would be removed from the estimator, and an immediate projection onto $\pmb {\partial {\mathcal {D}}}$ of an iterate in the boundary strip would occur, only a convergence order $\frac{1}{2}$ of the reduced a posteriori error estimate may be expected; this conclusion may be drawn from the a priori error analysis in [40, p. 370, Rem. 3.5] where this selective ‘bouncing back/projection’-mechanism was conceived. Further crucial tools in the proof of Theorem 4.6 are stability results in Sect. 3.3 for the boundedness of visits in the boundary strips $\big \{\pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}_{j\ge 0}$, and the discrete stopping time (see Lemmata 3.3 and 3.4), which generalize related stability results in [40, p. 367, Lem. 3.2] and [40, p. 367, Lem. 3.2] to non-uniform time steps; see also Remark 3.1 for further details.

ad (iii). In Sect. 5, the a posteriori error estimate (1.7) is used to construct an adaptive method (see Algorithm 5.1) which automatically selects deterministic (local) step sizes $\tau ^{j+1}=t_{j+1}-t_{j}$ in every iteration step. For this purpose, given some tolerance ${\texttt {Tol}}>0$ and $j\ge 0$, we check via iterated refinement/coarsening of the current step size $\tau ^{j+1}$ whether the partial sum $\sum \nolimits _{k=0}^{j} \tau ^{k+1} \big \{{{\mathfrak {G}}}_{1}^{(k)} + {{\mathfrak {G}}}_{2}^{(k)}+ {{\mathfrak {G}}}_{3}^{(k)} \big \}$ is below (a multiple of) a pre-assigned tolerance ${\texttt {Tol}}>0$; see (5.1). If compared to [35, Algorithm 4.1], the main difficulty for the boundary value problem (1.1) here is to set up a thresholding criterion that properly addresses the ‘discrete stopping’, for which the stability results in Lemmata 3.3 and 3.4 hold; see also the discussion in the beginning of Sect. 5.1. Theorem 5.2 then validates computation of each new time step $\tau ^{j+1}$ in Algorithm 5.1 after finitely many iterations (i.e., in ${\mathcal {O}}\bigl (\log ({\texttt {Tol}}^{-1})\bigr )$), at most ${\mathbb {E}}\big [J^{*}\big ]={{\mathcal {O}}}(\texttt{Tol}^{-1})$ many steps to (globally) terminate, and a weak error convergence order ${\mathcal {O}}({\texttt {Tol}})$.

The following example from [10] illustrates efficient local mesh refinement—coarsening by the adaptive Algorithm 5.1 for $L\gg 1$.

Fig. 2

Example 1.2 for $L=2$: temporal evolution of positions of samples in $\overline{\pmb {{\mathcal {D}}}}$: samples in the interior of $\pmb {{\mathcal {D}}}$; samples in the corresponding boundary strips; ${\square }$ samples on $\pmb {\partial {\mathcal {D}}}$

Example 1.2

(see [10]) Let $L=10$ and $\pmb {{\mathcal {D}}}:=\big \{{\textbf{x}}\in {\mathbb {R}}^{L}\,:\,\Vert {\textbf{x}}\Vert _{{\mathbb {R}}^{L}}<1\big \}$. Consider (1.1) with $\pmb {\sigma }({\textbf{x}})={\mathbb {I}}$, ${\textbf{b}}({\textbf{x}})\equiv {\textbf{0}}$, $c({\textbf{x}})\equiv 0$, $g({\textbf{x}})\equiv 1$ and $\phi ({\textbf{x}})\equiv 0$. Fix ${\textbf{x}}={\textbf{0}}$. We use Algorithm 5.1 (with ${\texttt {Tol}}=0.005$, ${\texttt {M}}=10^{4}$) to get the approximation ${\texttt {u}}^{({\texttt {M}})}({\textbf{x}})$ of the solution $u({\textbf{x}})=\frac{1}{L}\bigl (1-\Vert {\textbf{x}} \Vert ^{2}_{{\mathbb {R}}^{L}}\bigr )$. Here,

$$\begin{aligned} {\texttt {u}}^{({\texttt {M}})}({\textbf{x}}):={\mathbb {E}}_{{\texttt {M}}}\bigl [\phi (\textbf{Y}_{{\textbf{X}}}^{J^{*}})Y_{V}^{J^{*}}+Y_{Z}^{J^{*}}\bigr ]:=\frac{1}{{\texttt {M}}}\sum \limits _{m=1}^{{\texttt {M}}}\phi \bigl (\textbf{Y}_{{\textbf{X}}}^{J^{*},m}\bigr )Y_{V}^{J^{*},m}+Y_{Z}^{J^{*},m} \quad ({\textbf{x}}\in \pmb {{\mathcal {D}}}) \end{aligned}$$

denotes the empirical mean to approximate ${\mathbb {E}}\bigl [\phi (\textbf{Y}_{{\textbf{X}}}^{J^{*}})Y_{V}^{J^{*}}+Y_{Z}^{J^{*}}\bigr ]$. The initial refinement and gradual coarsening of the step sizes (‘U’-profile) in Fig. 3A is a typical consequence of Algorihm 5.1 allowing for an interaction between informations from the (empirical) error estimators $\{{\mathfrak {G}}_{\ell }^{(\cdot ),({\texttt {M}})}\}_{\ell =1}^{3}$ and a minor weightening of ‘outlier-samples’ according to the shape of the distribution of the stopping time $t_{J^{*}}$; see Fig. 3B, Fig. 2, and also the detailed classification of related dynamics in the beginning of Sect. 6. In a comparative consideration of Fig. 3A, B, and C, first samples enter the boundary strips at time $\approx 0.025$ and hence (possibly) get projected onto $\pmb {\partial {\mathcal {D}}}$, which is why we observe a refinement of step sizes up to this time. Within the time interval [0.025, 0.125], most of the samples hit $\pmb {\partial {\mathcal {D}}}$ which involves fine step sizes in this region to reach a certain level of accuracy regulated by the choice of ${\texttt {Tol}}$. Those samples, which have not been stopped before time 0.125 may be considered as ‘outlier-samples’ which most likely spoil the approximation. The mechanism in Algorithm 5.1 automatically allows a gradual coarsening of related step sizes for the generation of these leftover samples, which increases the width of their boundary strips, and hence forces their immediate projection onto $\pmb {\partial {\mathcal {D}}}$, i.e., a stopping of Algorithm 5.1. Moreover, Algorithm 5.1 is efficient to reach the same accuracy (Error $\approx 0.002$, ${\texttt {Tol}}=0.005$, ${\texttt {M}}=10^{4}$, ${\textbf{x}}={\textbf{0}}$); the needed number of steps to terminate in Algorithm 5.1 resp. the empirical mean of the stopping index $J^{*}$ is $\max \limits _{m=1,\ldots ,{\texttt {M}}} J^{*}(\omega _{m})=642$ (CPU time: 243 sec) resp.  ${\mathbb {E}}_{{\texttt {M}}}[J^{*}]\approx 362$—opposed to $\max \limits _{m=1,\ldots ,{\texttt {M}}} J^{*}(\omega _{m})=3757$ (CPU time: 800 s) resp. ${\mathbb {E}}_{{\texttt {M}}}[J^{*}]\approx 957$ for Scheme 2 on a uniform mesh. Hence, automatic mesh size selection which leans on where current states realize (i.e., in the interior, where only ${\mathfrak {G}}_{1}^{(\cdot )}$ is active or close to the boundary, where ${\mathfrak {G}}_{2}^{(\cdot )}$ and ${\mathfrak {G}}_{3}^{(\cdot )}$ adjust proper scaling) highly increases the efficiency of Scheme 2.

Fig. 3

A Semi-Log plot of the (adaptive) step sizes generated via Algorithm 5.1. B Shape of the distribution of $t_{J^{*}}$ illustrated via a histogram plot. C Temporal evolution of (sample-)iterates in the interior of $\pmb {{\mathcal {D}}}$. D Convergence rate (error) Log-log plot via Algorithm 5.1 (${\texttt {M}}=10^5$, ${\textbf{x}}={\textbf{0}}$)

The second part of this work focuses on the parabolic PDE with proper terminal and Dirichlet boundary data,

$$\begin{aligned} \partial _t u(t, \textbf{x}) + \frac{1}{2}\textrm{Tr}\Bigl (\pmb {\sigma }({\textbf{x}})\pmb {\sigma }^{\top }({\textbf{x}}) D_{{\textbf{x}}}^{2}u(t,{\textbf{x}})\Bigr )+\big \langle {\textbf{b}}(\textbf{x}), D_{{\textbf{x}}}u(t,\textbf{x})\big \rangle _{{\mathbb {R}}^{L}}+ g(t,{\textbf{x}})= & {} 0 \qquad \text {for all} \;\, (t,\textbf{x}) \in [0,T) \times \pmb {{\mathcal {D}}}, \nonumber \\ u(T,\textbf{x})= & {} \phi (T,\textbf{x}) \qquad \text {for all} \;\, \textbf{x} \in \overline{\pmb {{\mathcal {D}}}}\,,\nonumber \\ u(t,{\textbf{x}})= & {} \phi (t,{\textbf{x}}) \qquad \text {for all} \;\, (t,{\textbf{x}})\in [0,T)\times \pmb {\partial }\pmb {{\mathcal {D}}},\nonumber \\ \end{aligned}$$

(1.8)

where additionally $T>0$, and $g:[0,T]\times \overline{\pmb {{\mathcal {D}}}}\rightarrow {\mathbb {R}}$, $\phi :[0,T]\times \overline{\pmb {{\mathcal {D}}}}\rightarrow {\mathbb {R}}$. Under proper settings of data stated in Sect. 3.2, there exists a unique classical solution $u:[0,T]\times \overline{\pmb {{\mathcal {D}}}}\rightarrow {\mathbb {R}}$ of problem (1.8), which has the following probabilistic representation; see e.g. [40, p. 340]:

$$\begin{aligned} u(t,{\textbf{x}})={\mathbb {E}}\Big [\phi \bigl (\pmb {\tau }^{t,{\textbf{x}}},{\textbf{X}}^{t,{\textbf{x}}}_{\pmb {\tau }^{t,{\textbf{x}}}}\bigr )+Z_{\pmb {\tau }^{t,{\textbf{x}}}}\Big ]\qquad \text {for all} \;\, (t,{\textbf{x}})\in [0,T)\times \pmb {{\mathcal {D}}}, \end{aligned}$$

(1.9)

where

• (1) $\textbf{X}^{t,{\textbf{x}}} \equiv \{ \textbf{X}^{t,{\textbf{x}}}_{s};\, s \in [t,T]\}$ denotes the ${{\mathbb {R}}}^L$-valued solution of the SDE

  $$\begin{aligned} {\mathrm d}{{\textbf{X}}}_s = {\textbf{b}}( {{\textbf{X}}}_s) {\mathrm d}s + \pmb {\sigma }({\textbf{X}}_{s}) {\mathrm d}{{\textbf{W}}}_{s} \quad \text {for all} \;\, s \in (t,T], \qquad {{\textbf{X}}}_{t} = {{\textbf{x}}} \in \pmb {{\mathcal {D}}}\subset {\mathbb {R}}^L\,,\nonumber \\ \end{aligned}$$

  (1.10)

  starting at time $t\in [0,T)$ in ${\textbf{x}}\in \pmb {{\mathcal {D}}}$, and the first exit time of ${\textbf{X}}^{t,{\textbf{x}}}$ from $\pmb {{\mathcal {D}}}$ is

  $$\begin{aligned} \pmb {\tau }^{t,{\textbf{x}}}:=\inf \big \{ s>t:\; {\textbf{X}}^{t,{\textbf{x}}}_{s} \notin \pmb {{\mathcal {D}}}\text { or } s\notin (t,T)\big \}. \end{aligned}$$

  (1.11)

• (2) $Z\equiv \{Z_{s};\,s\in [t,T]\}$ denotes the ${\mathbb {R}}$-valued solution of the (random) (ODE)

  $$\begin{aligned} {\mathrm d}Z_{s} = g(s,{{\textbf{X}}}^{t,{\textbf{x}}}_{s}) {\mathrm d}s \quad \text {for all} \;\, s \in (t,T], \qquad Z_{t} = 0. \end{aligned}$$

  (1.12)

If compared to deterministic numerical methods—see also Sect. 2.2—, a conceptional advantage of probabilistic numerical methods which approximate (1.8) is that only one (temporal) discretization parameter is needed. Consequently, main structural tools which led to a posteriori error estimate (1.7) for (1.1) now may easily be adopted to approximate (1.9), and evenly so for the later construction of an adaptive method; for $(t,{\textbf{x}})\in [0,T)\times \pmb {{\mathcal {D}}}$ fixed, the a posteriori error estimate on a given mesh $\{t_{j}\}_{j=0}^{J}\subset [t,T]$ with local mesh sizes $\{\tau ^{j+1}\}_{j=0}^{J-1}$ for iterates $\{({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{Z}^{j})\}_{j=0}^{J^{*}}$ from Scheme 3 to approximate (1.9) takes again the form

$$\begin{aligned}{} & {} \Bigl \vert u(t,{\textbf{x}}) - {\mathbb {E}}\bigl [\phi (t_{J^{*}},\textbf{Y}_{{\textbf{X}}}^{J^{*}})+Y_{Z}^{J^{*}}\bigr ] \Bigr \vert \nonumber \\{} & {} \quad \le \pmb {{\mathfrak {C}}}(\phi ,g) \cdot \sum \limits _{j=0}^{J-1} \tau ^{j+1} \big \{{{\mathfrak {H}}}_{1}^{(j)} + {{\mathfrak {H}}}_{2}^{(j)}+ {{\mathfrak {H}}}_{3}^{(j)} \big \}, \end{aligned}$$

(1.13)

with $\pmb {{\mathfrak {C}}}(\phi ,g)>0$, $J\equiv J(t,{\textbf{x}})\in {\mathbb {N}}$, (computable) a posteriori error estimators $\{{\mathfrak {H}}_{\ell }^{(\cdot )}\}_{\ell =1}^{3}$, and $0\le J^{*}\equiv J^{*}(t,{\textbf{x}})\le J$ the stopping index; see Theorem 4.7.

The following example details $\{{\mathfrak {H}}_{\ell }^{(\cdot )}\}_{\ell =1}^{3}$ in (1.13) for a prototype PDE (1.8).

Example 1.3

Let $L\in {\mathbb {N}}$ and $\pmb {{\mathcal {D}}}=\big \{{\textbf{x}}\in {\mathbb {R}}^{L}\,:\,\Vert {\textbf{x}}\Vert _{{\mathbb {R}}^{L}}<1\big \}$. Consider (1.8) with ${\textbf{b}}({\textbf{x}})\equiv {\textbf{0}}$, $\pmb {\sigma }({\textbf{x}})\equiv \sqrt{\frac{2}{L}}\cdot {\mathbb {I}}$, $g(t,{\textbf{x}})\equiv 0$, and $\phi$ smooth. Then,

$$\begin{aligned} {\mathfrak {H}}_{1}^{(j)}&= {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}}\cdot \big \Vert {\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j}\big \Vert _{{\mathbb {R}}^{L}}^{2} \Big ] +2\cdot {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}}\Big ] \cdot \tau ^{j+1}\,,\\ {\mathfrak {H}}_{2}^{(j)}&= {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \cdot \big \Vert {\textbf{Y}}_{{\textbf{X}}}^{j+1}-\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}\big \Vert _{{\mathbb {R}}^{L}}^{2} \Big ] \\&\quad +2\cdot {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \Big ]\cdot \tau ^{j+1} \,,\\ {\mathfrak {H}}_{3}^{(j)}&= 2\cdot {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} \Big ]\,. \end{aligned}$$

The three estimators take similar roles as in Example 1.1 for (1.1).

The following items (i)–(iii) comment on the construction of (1.13), its convergence analysis, and use to construct an adaptive method.

• (i) If compared to Scheme 2 for the elliptic problem (1.1), Scheme 3 (see Sect. 3.4) exploits an additional observance of ‘stopping’ when there is no projection onto $\pmb {\partial {\mathcal {D}}}$ before the terminal time $T>0$, but is similar elsewise. Consequently, the form of (1.13) is close to (1.7).

• (ii) If compared to (1.7), the convergence analysis of (1.13) along sequences of shrinking meshes with a maximum mesh size simplifies since the stopping time $\pmb {\tau }^{t,{\textbf{x}}}$ in (1.11) is ${\mathbb {P}}-$a.s. bounded by the terminal time $T>0$, which, in particular, avoids a related stability result concerning ‘discrete-stopping’. In fact, only Lemma 3.5 is needed, which is an analogue of Lemma 3.3 in the elliptic setting.

• (iii) Similar to Algorithm 5.1 in Sect. 5, we construct an adaptive time-stepping algorithm (see Algorithm 5.3) based on (1.13), for which we prove (again) local and global termination, as well as optimal convergence in terms of a given tolerance ${\texttt {Tol}}>0$. The (successive) step size selection procedure in Algorithm 5.3 proceeds in the same way as in Algorithm 5.1: given ${\texttt {Tol}}>0$ and $j\ge 0$, the current step size $\tau ^{j+1}$ is (automatically) generated (via iterated refinement/coarsening), such that the partial sum $\sum \nolimits _{k=0}^{j} \tau ^{k+1} \big \{{{\mathfrak {H}}}_{1}^{(k)} + {{\mathfrak {H}}}_{2}^{(k)}+ {{\mathfrak {H}}}_{3}^{(k)} \big \}$ is below ${\texttt {Tol}}$ times a specified ‘temporal weight’, which grows with $t_{j}$, but is bounded by means of the stability result in Lemma 3.5. In the fully practical implementation of Algorithm 5.3 (as well as Algorithm 5.1), where arising expectations are approximated by Monte-Carlo method, the ‘temporal weight’ gradually forces those leftover samples, which have not been projected onto $\pmb {\partial {\mathcal {D}}}$ with the majority of samples, to a projection. These ‘forced’ projections are obtained by enlarging corresponding boundary strips through a gradual coarsening of the step sizes (see Examples 1.2 and 1.4, and also Fig. 2). We refer to Sects. 5 and 6 for further details.

The following example from [33, Experiment 7.1] illustrates local mesh refinement-coarsening by Algorithm 5.3.

Example 1.4

(see [33, Experiment 7.1]) Let $T=1$, and $\pmb {{\mathcal {D}}}:=\big \{{\textbf{x}}=(x_{1},x_{2})^{\top }\in {\mathbb {R}}^{2}\,:\,\Vert {\textbf{x}}\Vert _{{\mathbb {R}}^{2}}<1\big \}$. Consider (1.8) with

$$\begin{aligned} \pmb {\sigma }({\textbf{x}})&\equiv \left[ \begin{array}{rr} 1 &{} 0 \\ 0 &{} 2 \\ \end{array} \right] \,, \;{\textbf{b}}({\textbf{x}})=\left[ \begin{array}{r} -x_{2} \\ x_{1} \\ \end{array} \right] \,,\; \\ g(t,{\textbf{x}})&=5\bigl (1-e^{-(T-t)}\bigr )-\bigl (25-x_{1}^{2}-x_{2}^{2}\bigr )e^{-(T-t)}\,,\\ \phi (t,{\textbf{x}})&=\bigl (25-x_{1}^{2}-x_{2}^{2}\bigr )\bigl (1-e^{-(T-t)}\bigr )\,. \end{aligned}$$

The corresponding solution is given by $u(t,{\textbf{x}})=\bigl (25-x_{1}^{2}-x_{2}^{2}\bigr )\bigl (1-e^{-(T-t)}\bigr )$. We fix $(t,{\textbf{x}})=(0,{\textbf{0}})$, and use Algorithm 5.3 (with ${\texttt {Tol}}=0.01$, ${\texttt {M}}=10^{4}$) to approximate $u(t,{\textbf{x}})$ by ${\texttt {u}}^{({\texttt {M}})}(t,{\textbf{x}})$. Illustrated in Fig. 4 below, the methodology of Algorithm 5.3 allowing for interactions between $\{{\mathfrak {H}}_{\ell }^{(\cdot ),({\texttt {M}}) }\}_{\ell =1}^{3}$ and a less weightening of ‘outlier-samples’ is conceptually similar to Algorithm 5.1: we observe a refinement of step sizes (within [0, 0.05]) till first samples hit $\pmb {\partial {\mathcal {D}}}$; fine step sizes are needed within [0.05, 0.4], where most samples are projected onto $\pmb {\partial {\mathcal {D}}}$; afterwards, we observe a gradual coarsening of the step sizes (within [0.4, 1]) to force ‘outlier-samples’ to hit $\pmb {\partial {\mathcal {D}}}$ resp. to proceed to the terminal time T as fast as possible. Furthermore, Algorithm 5.3 is (also) efficient to reach the same accuracy (Error $\approx 0.015$, ${\texttt {Tol}}=0.02$, ${\texttt {M}}=10^{4}$, $(t,{\textbf{x}})=(0,{\textbf{0}})$); the needed number of steps to terminate in Algorithm 5.3 resp. the empirical mean of the stopping index $J^{*}$ is $\max \limits _{m=1,\ldots ,{\texttt {M}}} J^{*}(\omega _{m})=709$ (CPU time: 297 sec) resp.  ${\mathbb {E}}_{{\texttt {M}}}[J^{*}]\approx 129$—as opposed to $\max \limits _{m=1,\ldots ,{\texttt {M}}} J^{*}(\omega _{m})=8000$ (CPU time: 1500 s) resp. ${\mathbb {E}}_{{\texttt {M}}}[J^{*}]\approx 1607$ for Scheme 3 on a uniform mesh.

Fig. 4

A Semi-Log plot of the (adaptive) step sizes generated via Algorithm 5.3. B Shape of the distribution of $t_{J^{*}}$ illustrated via a histogram plot. C Temporal evolution of (sample-)iterates in the interior of $\pmb {{\mathcal {D}}}$. D Convergence rate (error) Log-log plot via Algorithm 5.3 (${\texttt {M}}=10^5$, $(t,{\textbf{x}})=(0,{\textbf{0}})$)

The remainder of this paper is organized as follows: Sect. 2 provides a survey of existing (adaptive) methods for the approximation of the elliptic, as well as the parabolic PDE. Section 3 collects the assumptions needed for the data in (1.1) resp. (1.8), recalls a priori bounds for the solution of (1.1) resp. (1.8) and presents Schemes 1 to 3, as well as corresponding stability results. The a posteriori error estimates (1.7) and (1.13) are derived in Sect. 4, where also its optimal convergence orders are shown. The related adaptive methods are proposed and analyzed in Sect. 5. Section 6 presents computational studies.

2 A short review of a posteriori error analysis and adaptivity

Deterministic methods to solve PDE’s (1.1) and (1.8) usually employ meshes to resolve the state space, and their implementation usually is complicated. In contrast, probabilistic methods are meshless, comparatively easier to implement, and still are applicable in high dimensions L. Their efficiency increases rapidly with the recent emergence of modern (parallel) GPU architectures; see [30]. The main goal in this section is to survey some existing representative directions in the a posteriori error analysis and adaptive numerical methods for the (initial-)boundary value problems (1.1) and (1.8).

2.1 Probabilistic methods to discretize high-dimensional PDE’s

In the literature, there exist different numerical methods for (1.2) or (1.9), which may be seen as examples of more general ‘stopped diffusion’ problems. Most of them use the explicit Euler method, i.e., (3.1) where ‘$\pmb {\xi }_{j+1}\sqrt{\tau ^{j+1}}$’ is replaced by the Wiener increments ‘${\textbf{W}}_{t_{j+1}}-{\textbf{W}}_{t_{j}}$’; see (4.29). The main difficulty then is to accurately compute the (discrete) stopping time (1.4) resp. (1.11), when the related (discrete) solution path leaves the domain $\pmb {{\mathcal {D}}}$. This problem becomes even more prominent when the related first exit time $\pmb {{\tilde{\tau }}}$ of the (abstract) continuified Euler process $\pmb {{\mathcal {Y}}}^{{\textbf{X}}}$ (see (4.30)) is compared in this context on an interval $[t_{j},t_{j+1}]$—where trajectories may exit $\pmb {{\mathcal {D}}}$ even though all discrete (explicit) Euler iterates lie in $\pmb {{\mathcal {D}}}$; see Fig. 5a below. An a priori error analysis therefore cuts the convergence rate from 1 to $\frac{1}{2}$; see [27, Thm. 2.3]. To recover optimal order, more simulations are needed close to the boundary to accurately capture discrete stopping. First works in this direction are [27, 28], which prove optimal convergence order 1. To use the method in [28], the exit probability of $\pmb {{\mathcal {Y}}}^{{\textbf{X}}}$ leaving the domain, i.e., the probability that $\pmb {{\tilde{\tau }}}$ lies in a time interval specified by two (consecutive) grid points needs be available explicitly, which is only known for certain domains (e.g. when $\pmb {{\mathcal {D}}}$ is a half-space; see e.g. [28]). For general underlying domains $\pmb {{\mathcal {D}}}$, this approach needs be combined with local transformations of $\pmb {\partial {\mathcal {D}}}$ to be successful.

In order to avoid local charts close to $\pmb {\partial {\mathcal {D}}}$, the ‘boundary shifting method’ is presented in [29] which shrinks the domain $\pmb {{\mathcal {D}}}$ to generate more frequent exits. If compared to the ‘Brownian bridge method’ above, an explicit formula for exit probabilities of $\pmb {{\mathcal {Y}}}^{{\textbf{X}}}$ is not required anymore, which broadens the applicability of the method to more general domains. The corresponding error analysis guarantees order $o(\sqrt{\Delta t})$, while computations evidence order 1. For further, different strategies to ensure accurate ‘stopping’, we also refer to [10, 36,37,38].

The methods that we discussed so far were supplemented by a priori error analysis; to our knowledge, the only work that addresses a posteriori error analysis in this setting is [20]. For $g\equiv 0$ in (1.8), and based on an (asymptotic) weak a posteriori error expansion with computable leading order term, a time-stepping method is proposed which generates global stochastic (adaptive) meshes to approximate (1.9). However, these (random) mesh generations are only based on the computable part of the underlying error expansion, and adaptivity here thus remains heuristic. The corresponding derivation uses computable exit probabilities (similar to [27, 28]), and is elsewise similar to the procedure in [41, 48]: the derivation rests on the weak error expansion via PDE (1.8), which practically involves numerical approximations of derivatives of the (unknown) solution u of (1.8), whose simulation is only feasible in small dimensions L. The computational experiments in this work indicate a convergence order 1, but no theoretical results are known that support these observations.

The methods above are primarily addressing the (efficient) approximation (1.8) rather than (1.1). We here mention the works [8, 9, 11] which computationally study the approximation of (1.1) by extending the ideas from [28]: there, $\pmb {\tau }^{{\textbf{x}}}$ in (1.4) is (accurately) approximated by sampling from a distribution, which is constructed by means of the related exit probability. Computational studies with the corresponding method evidence an improved convergence order 1 as well.

These schemes all use the (explicit) Euler method with unbounded Wiener increments. From a practical viewpoint however, the weak Euler method in (3.1) is an alternative option, as it uses bounded random variables in every iteration step (see Scheme 1 below) to avoid overshootings outside the domain by controlling the steps up to the boundary; in particular the work [39] verifies first order convergence for (3.1) in an associated scheme (very close to Scheme 2 resp. 3), which—except for a projection onto $\pmb {\partial {\mathcal {D}}}$ resp. bouncing back to the inside of $\pmb { {\mathcal {D}}}$—does not require further adjustments of its iterates close to $\pmb {\partial {\mathcal {D}}}$. We use this simple, fully practical method (3.1) within Schemes 2 and 3 in Sect. 4 to provide computable right-hand sides in an a posteriori error analysis, which may then be used to set up an adaptive time-stepping strategy based on it in Sect. 5.²

2.2 Deterministic adaptive methods in low dimension—AFEM

Adaptive finite element methods (AFEM) base an automatic adjustment of a given mesh ${{\mathcal {T}}}_0$ covering $\pmb {{{\mathcal {D}}}} \subset {{\mathbb {R}}}^L$ on an a posteriori error estimator $\eta ^2(u_{{{\mathcal {T}}}_0}, {{\mathcal {T}}}_0) \equiv \eta ^2 = \sum _{T^{m,0} \in {{\mathcal {T}}}_0} \eta ^2_{T^{m,0}}$ for the computed approximation $u_{{{\mathcal {T}}}_0}: \overline{\pmb {{{\mathcal {D}}}}} \rightarrow {{\mathbb {R}}}$ for (1.1) on ${{\mathcal {T}}}_0$. FEM is a general deterministic Galerkin method for (1.1) posed on an arbitrary low-dimensional domain $\pmb {{{\mathcal {D}}}}$; in practice, its use then leads to large coupled algebraic systems to be inverted by means of advanced iterative solvers, where its performance crucially hinges on the ellipticity of (1.1). AFEM extends these concepts, by trying to optimally distribute nodal mesh points across $\pmb {{{\mathcal {D}}}}$, guided by local $\{\eta _{T^{m,0}};\, T^{m,0} \in {{\mathcal {T}}}_0\}$ where $\eta _{T} \equiv \eta _T(u_{{{\mathcal {T}}}_0}\bigl \vert _{T^{m,0}}, T^{m,0})$, while aiming for optimal accuracy under fixed computational costs; it is an iterative method which repeatedly refines meshes locally and thus generates a family of nested $\{ {{\mathcal {T}}}_{{\ell }} \}_{\ell =1}^{\ell ^*}$—until the related approximate $u_{{{{\mathcal {T}}}_{{{\ell ^*}}}}}: \overline{\pmb {{{\mathcal {D}}}}} \rightarrow {{\mathbb {R}}}$ of (1.1) fulfills a certain threshold criterion.

Existing AFEM mainly uses Hilbert space methods to derive an (residual-based) a posteriori estimator $\eta (u_{{{\mathcal {T}}}_{{\ell }}}, {{\mathcal {T}}}_{{\ell }})$ to upperly bound the error $u-u_{{{\mathcal {T}}}_{{\ell }}}$ in the ‘energy norm’, with an unknown factor (e.g., Poincare’s constant reflecting stability properties of (1.1), and another one which accounts for admitted triangulations; see [21, 42]). For AFEM, this estimate then suggests the following loop

$$\begin{aligned} {\texttt {Solve}} \ \longrightarrow \ {\texttt {Estimate}} \longrightarrow \ {\texttt {Mark}} \ \longrightarrow \ {\texttt {Refine}} \end{aligned}$$

(2.1)

to automatically generate a sequence of (increasingly more) specific, (locally) refined meshes $\{ {{\mathcal {T}}}_{h^{\ell }}\}_{\ell }$, starting from a coarse mesh ${{\mathcal {T}}}_{0}$, which all cover ${{\mathcal {D}}}$: for a given ${{\mathcal {T}}}_{{\ell }}$, we

(1):

(‘Solve’) first compute $u_{{{\mathcal {T}}}_{{\ell }}}$ with the help of direct or indirect solvers (e.g., PCG, multigrid method, GMRES, or BICG) that solves a large linear system. Then

(2):

(‘Estimate’) the estimator $\eta (u_{{{\mathcal {T}}}_{{\ell }}}, {{\mathcal {T}}}_{{\ell }})$ is computed to decide whether or not $u_{{{\mathcal {T}}}_{{\ell }}}$ is sufficiently accurate, and/or ${{\mathcal {T}}}_{{\ell }}$ should be refined or not. Based on the estimator alone is

(3):

(‘Mark’) ‘Dörfler’s marking strategy’ (see (2.2) below), which selects those elements $\widetilde{{\mathcal {T}}}_{{\ell }}:= \{ T^{m,\ell } \in {{\mathcal {T}}}_{{\ell }}\}$ which are up to refinement.

(4):

(‘Refine’) Only mesh refinement is admitted to obtain the new nested mesh ${{\mathcal {T}}}_{{\ell +1}}$—via the ‘newest bisection method’ that splits the marked elements in (3).

It remained open until [19] to show that tuple $\{ (u_{{{\mathcal {T}}}_{{\ell }}}, {{\mathcal {T}}}_{{\ell }})\}_{\ell }$ obtained from (1) to (4) meet a pre-assigned error tolerance within finite steps $\ell ^{*}$: next to the assumption of a sufficiently fine initial ${{\mathcal {T}}}_{0}$ and the ‘one interior node’-condition in (4), the convergence proof for AFEM in [19] for Poisson’s problem rests on ‘Dörfler’s strategy marking’:

$$\begin{aligned} \text{ Find } \text{ a } \text{ subset } \widetilde{{\mathcal {T}}}_{{\ell }} \subset {{\mathcal {T}}}_{{\ell }}: \qquad \qquad \eta (u_{{{\mathcal {T}}}_{{\ell }}}, \widetilde{{\mathcal {T}}}_{{\ell }}) \ge \theta \eta (u_{{{\mathcal {T}}}_{{\ell }}}, {{\mathcal {T}}}_{{\ell }}) \end{aligned}$$

(2.2)

for a fixed $0< \theta < 1$, which ensures that sufficiently many elements from ${{\mathcal {T}}}_{{\ell }} \equiv \{ T^{m,\ell }\}_m$ are chosen that constitute a fixed proportion of the global error estimator [42]. The work [19] initiated a whole series of works to broaden convergence results for more general AFEM of sort (2.1), s.t. the relevant contraction property remains valid, which is

$$\begin{aligned} \exists \, \beta \in (0,1):\qquad \qquad \int _{\pmb {{{\mathcal {D}}}}} \vert \nabla (u-u_{{{\mathcal {T}}}_{{\ell }}})\vert ^2\, \textrm{d}x \le C \beta ^{\ell } \qquad (\ell \in {{\mathbb {N}}}), \end{aligned}$$

with a generic constant $C \equiv C(\pmb {{{\mathcal {D}}}})>0$ that depends on $\pmb {{{\mathcal {D}}}}$ and admitted mesh geometries: to e.g. remove in [14] the (too costly) ‘one interior node’-condition in (4), next to required sufficiently fine initial ${{\mathcal {T}}}_0$, the concept of ‘total error’ was central. Another direction generalizes the convergence property of AFEM to nonsymmetric linear-elliptic, and even quasi-linear problems; see e.g. [5, 22]. Next to the contraction property, ‘mesh optimality’ is a crucial property for AFEM to have, which bounds the number of degrees of freedom $N_{\ell ^*} = \sharp {{\mathcal {T}}}_{\ell ^*}$ in the terminating mesh ${{\mathcal {T}}}_{{\ell ^*}}$: the first work in this direction is [7], which shows optimal convergence rates (in terms of $N_{\ell ^*}$; for the Poisson problem) for a certain AFEM which included a crucial coasening step; this step was later removed by a modified approach in [47]. For a further discussion of ‘mesh optimality’ for AFEM we refer to [43], and [13] where sufficient criteria are identified which ensure optimal convergence rates for a general AFEM; and to e.g. [5, 22] for more general (PDEs). We remark that the proof of ‘mesh optimality’ usually requires $\theta \in (0, \theta ^*)$ in (2.2), for $\theta ^*$ sufficiently small to bound the number of marked elements in step (3)—whose value is not explicit for actual simulations. We refer to [18] for a further discussion.

These concepts are applied in [16, 23, 31] to construct adaptive methods based on the implicit Euler method for the heat equation, as a special example of the evolutionary PDE (1.8): for every $n \ge 0$, to (iteratively) find the new time step $\tau _n$, and then the spatial mesh ${{\mathcal {T}}}_n$ to cover $\pmb {{{\mathcal {D}}}}$, different error indicators are identified which subsequently (and thus independently) address these goals. These indicators are space-time localizations of computable terms in the a posteriori error estimate [50], see also [31, Thm. 3.1], whose derivation is based on the concept of weak (variational) solution for (1.8), to bound the error in the global Bochner norm $L^2(0,T; {{\mathbb {H}}}^1_0) \cap W^{1,2}(0,T; {{\mathbb {H}}}^{-1})$. As a consequence, given $n \ge 0$, and $\tau _n$, the construction of a mesh ${{\mathcal {T}}}_n$ to approximate the solution of

$$\begin{aligned} \frac{1}{\tau _n} u^n + {{\mathcal {L}}} u^n = \frac{1}{\tau _n} u^{n-1} + g, \end{aligned}$$

where ${\mathcal {L}}=-\Delta$, via the convergent AFEM strategy (2.1) is then possible. However, the subtle interplay of different spatial and temporal scales and the decoupled treatment of related error occuring in each time step makes the construction of an efficient adaptive method for (1.8) more challenging in this parabolic case (see also [23]): also, we have to make sure that

• (i) $\tau _n$ may iteratively be constructed via a finite sequence $\{\tau _{n,\ell }\}_{\ell \ge 0}^{\ell ^*_n}$, and that

• (ii) The final time T is reached after finitely many steps, i.e., there exists $N \in {{\mathbb {N}}}$ (deterministic): $\tau _N \ge T$

to conclude convergence of the adaptive method. The adaptive method in [16] satisfies (i) but lacks (ii); a first convergent method is given in [31], where each time-step starts with a possible coarsening of $(\tau _{n-1}, {{\mathcal {T}}}_{n-1})$, and only refinements afterwards; a uniform energy estimate for iterates is now employed to determine a (uniform) minimum admissible time step for each n to meet the error tolerance, and thus show termination of the adaptive method, i.e., property (ii)—although with nonoptimal complexity bounds.

2.3 Deterministic methods to discretize high-dimensional PDE’s—tensor sparsity

For $\pmb {{{\mathcal {D}}}} = (0,1)^L$, mesh-based methods (such as FEM used in Sect. 2.2) to e.g. solve PDE (1.1) suffer the curse of dimensionality: for N the number of points on a uniform mesh per dimension, the number of related nodal basis functions is ${{\mathcal {O}}}(N^L)$, which grows exponentially with the dimension L. Sparse grids on hypercubes $\pmb {{{\mathcal {D}}}} = (0,1)^L$ drastically cut down this complexity of a full mesh to ${{\mathcal {O}}}(N \vert \log (N)\vert ^{L-1} )$ many grid points: they discard those elements of a hierarchical basis in tensor product form which have small support, such that no loss of approximation power for sufficiently smooth solutions of PDE (1.1) occurs, see e.g. [12]; for the heat equation in (1.8) and rough initial data in tensor form, graded time meshes properly address this requirement for sparse spatial grids in [44]. As e.g. detailed in [12, 45], the efficient use of sparse grids for high dimensions L requires a restricted data setting $({\textbf{b}},\pmb {\sigma },c,g,\phi , \pmb {{\mathcal {D}}})$: for non-constant elliptic operators ${\mathcal {L}}$ including convection, or a domain that is not of tensor structure, as well as non-constant (Dirichlet-) boundary data partly non-trivial extensions are necessary, and those setups of data typically lower accuracy, and reachable L; see the discussion in [49]. Also, a theoretical backup for local adaptive mesh adjustments (see [12, 45]) that preserve optimal complexity as L increases is less developed.

To approach even larger dimensions L based on tensor product representations for approximate solutions of PDE (1.1) with ‘Laplacian like operator’, the construction of a proper (sub-)set of basis functions will be part in the low rank approximation method itself; see e.g. [4] for a recent survey. We also mention [25, 46], where its complexity is compared with sparse grids, and smoothness of the function was again found to be crucial for the efficiency of the low rank approximation. According to [1], its efficiency crucially hinges on the differential operator in PDE (1.1) to ‘have a simple tensor product structure’, and that (L-dependent) ranks, whose optimal value is not evident in general [2] should be chosen properly; see also [4, Sect. 5.3]. In fact, related theoretical discussions in [17] for the high-dimensional PDE (1.1) with constant, symmetric elliptic operators ${\mathcal {L}}\equiv -\textrm{div} (\pmb {A} \nabla u)$ with $\pmb {A}\in {\mathbb {R}}^{L\times L}_{{\texttt {diag}}}$ conclude the transfer of tensor-sparsity from data to solutions, which motivates low-rank tensor format approximations for the solution of PDE (1.1) in those cases; but such a structural transfer may get lost in the case of stronger couplings [3] for general $\pmb {A} \in {{\mathbb {R}}}^{L \times L}_\texttt{spd}$, demanding higher ranks for a proper approximation.

While current research on deterministic methods for large L mainly focuses on the efficient use of ‘tensor-sparsity respecting data’ to fight the ‘curse of dimensionality’, we base the construction of easily implementable, adaptive methods to solve PDEs (1.1) resp. (1.8) on their probabilistic reformulations (1.2) resp. (1.9): general domains $\pmb {{\mathcal {D}}} \subset {{\mathbb {R}}}^L$, and elliptic differential operators ${{\mathcal {L}}} \equiv {{\mathcal {L}}}(\textbf{x})$ in (1.1) resp. (1.8) are admitted, which appear in physical applications in particular, for which convergence with optimal rates for the related adaptive Algorithms 5.1 and 5.3 that base on a posteriori error estimators will provide a theoretical backup.

3 Assumptions and tools

Section 3.1 lists basic requirements on data ${\textbf{b}},\pmb {\sigma },c,g,\phi$ in (1.1), which guarantee the existence of a unique classical solution $u:\overline{\pmb {{\mathcal {D}}}}\rightarrow {\mathbb {R}}$ of (1.1); see e.g. [24, Ch. 6]. Moreover, we recall bounds for $\{D_{{\textbf{x}}}^{\ell }u\}_{\ell =1}^{4}$ of (1.1). In almost the same manner, Sect. 3.2 presents assumptions on data ${\textbf{b}},g,\phi$ in (1.8), which ensure the existence of a unique classical solution u of (1.8); see e.g. [32, p. 320, Thm. 5.2]. Moreover, we recall bounds for $\{D_{{\textbf{x}}}^{\ell }u\}_{\ell =1}^{4}$ of (1.8).

For a sufficiently smooth $\mathbf {\varphi }\in {\mathcal {C}}({{\mathbb {R}}}^L; {{\mathbb {R}}}^{n})$, corresponding (matrix) operator norms are given as $(\, n,L\in {\mathbb {N}}$, ${\textbf{x}}\in {\mathbb {R}}^{L}\,)$

$$\begin{aligned}&\Vert D^{\ell }\mathbf {\varphi }({\textbf{x}})\Vert _{{\mathcal {L}}\big (\underbrace{{\mathbb {R}}^{L}\times \ldots \times {\mathbb {R}}^{L}}_{\ell -\text {times}};{\mathbb {R}}^{n}\big )}:=\sup \limits _{\Vert {\textbf{v}}_{i} \Vert _{{\mathbb {R}}^{L}}=1}\Vert D^{\ell }\mathbf {\varphi }({\textbf{x}})({\textbf{v}}_{1},\ldots ,{\textbf{v}}_{\ell })\Vert _{{\mathbb {R}}^{n}}\qquad (\ell \in {\mathbb {N}})\, , \end{aligned}$$

where $\Vert \cdot \Vert _{{\mathbb {R}}^{n}}$ denotes the (Euclidean) vector norm of a ${\mathbb {R}}^{n}$-valued vector. If $n=L$, we write ${\mathcal {L}}^{\ell }\equiv {\mathcal {L}}\big ({\mathbb {R}}^{L}\times \ldots \times {\mathbb {R}}^{L};{\mathbb {R}}^{L}\big )$. If $n=1$, $D\equiv D_{{\textbf{x}}}$ denotes the gradient and $D^{2}\equiv D^{2}_{{\textbf{x}}}$ the Hessian matrix of $\mathbf {\varphi }$, and we also write ${\mathcal {L}}^{\ell }\equiv {\mathcal {L}}\big ({\mathbb {R}}^{L}\times \ldots \times {\mathbb {R}}^{L};{\mathbb {R}}\big )$. Moreover, $\Vert D_{{\textbf{x}}}\mathbf {\varphi }({\textbf{x}})\Vert _{{\mathcal {L}}^{1}}=\Vert D_{{\textbf{x}}}\mathbf {\varphi }({\textbf{x}})\Vert _{{\mathbb {R}}^{L}}$, $\Vert D^{2}_{{\textbf{x}}}\mathbf {\varphi }({\textbf{x}})\Vert _{{\mathcal {L}}^{2}}=\Vert D^{2}_{{\textbf{x}}}\mathbf {\varphi }({\textbf{x}})\Vert _{{\mathbb {R}}^{L\times L}}$, where $\Vert \cdot \Vert _{{\mathbb {R}}^{L\times L}}$ denotes the spectral (matrix) norm.

For $k\in {\mathbb {N}}$ and $\beta \in (0,1)$, we denote by ${\mathcal {C}}^{k+\beta }(\overline{\pmb {{\mathcal {D}}}};{\mathbb {R}})$ the Banach space consisting of continuous functions v in $\pmb {{\mathcal {D}}}$, with continuous derivatives up to order k in $\overline{\pmb {{\mathcal {D}}}}$, such that

$$\begin{aligned} \Vert v\Vert _{\pmb {{\mathcal {D}}}}^{(k+\beta )}:=\sum \limits _{j=0}^{k} \sum \limits _{|\pmb {j^{\prime }}|=j} \sup \limits _{{\textbf{x}}\in \pmb {{\mathcal {D}}}} |\partial _{{\textbf{x}}}^{\pmb {j^{\prime }}} v({\textbf{x}})|+ \sum \limits _{|\pmb {j^{\prime }}|=k}\sup \limits _{{\textbf{x}},{\textbf{y}}\in \pmb {{\mathcal {D}}},\;{\textbf{x}}\ne {\textbf{y}}} \frac{|\partial _{{\textbf{x}}}^{\pmb {j^{\prime }}} v({\textbf{x}})-\partial _{{\textbf{x}}}^{\pmb {j^{\prime }}} v({\textbf{y}})|}{\Vert {\textbf{x}}-{\textbf{y}}\Vert _{{\mathbb {R}}^{L}}^{\beta }}<\infty \,, \end{aligned}$$

or rather

$$\begin{aligned} \Vert v\Vert _{\pmb {{\mathcal {D}}}}^{(k,\beta )}:=\sum \limits _{j=0}^{k} \sup \limits _{|\pmb {j^{\prime }}|=j}\, \sup \limits _{{\textbf{x}}\in \pmb {{\mathcal {D}}}} |\partial _{{\textbf{x}}}^{\pmb {j^{\prime }}} v({\textbf{x}})|+ \sup \limits _{|\pmb {j^{\prime }}|=k}\,\sup \limits _{{\textbf{x}},{\textbf{y}}\in \pmb {{\mathcal {D}}},\;{\textbf{x}}\ne {\textbf{y}}} \frac{|\partial _{{\textbf{x}}}^{\pmb {j^{\prime }}} v({\textbf{x}})-\partial _{{\textbf{x}}}^{\pmb {j^{\prime }}} v({\textbf{y}})|}{\Vert {\textbf{x}}-{\textbf{y}}\Vert _{{\mathbb {R}}^{L}}^{\beta }}<\infty \,, \end{aligned}$$

where the above summation is taken over all multi-index $\pmb {j^{\prime }}$ of length $|\pmb {j^{\prime }}|$.

In a similar manner, we denote by ${\mathcal {C}}^{\nicefrac {(k+\beta )}{2},k+\beta }([0,T]\times \overline{\pmb {{\mathcal {D}}}};{\mathbb {R}})$ the Banach space consisting of continuous functions w in $[0,T)\times \pmb {{\mathcal {D}}}$, with continuous derivatives up to order k in $[0,T]\times \overline{\pmb {{\mathcal {D}}}}$, such that

$$\begin{aligned} \Vert w\Vert _{[0,T)\times \pmb {{\mathcal {D}}}}^{(k+\beta )}&:=\sum \limits _{j=0}^{k} \sum \limits _{\begin{array}{c} 2r+|\pmb {j^{\prime }}|=j \\ r\in {\mathbb {N}}_{0} \end{array}} \sup \limits _{(t,{\textbf{x}})\in [0,T)\times \pmb {{\mathcal {D}}}} |\partial _{t}^{r}\partial _{{\textbf{x}}}^{\pmb {j^{\prime }}} w(t,{\textbf{x}})|\\&\quad + \sum \limits _{\begin{array}{c} 2r+|\pmb {j^{\prime }}|=k \\ r\in {\mathbb {N}}_{0} \end{array}}\sup \limits _{\begin{array}{c} (t,{\textbf{x}}),(t,{\textbf{y}})\in [0,T]\times \overline{\pmb {{\mathcal {D}}}} \\ {\textbf{x}}\ne {\textbf{y}} \end{array}} \frac{|\partial _{t}^{r}\partial _{{\textbf{x}}}^{\pmb {j^{\prime }}} w(t,{\textbf{x}})-\partial _{t}^{r}\partial _{{\textbf{x}}}^{\pmb {j^{\prime }}} w(t,{\textbf{y}}) }{\Vert {\textbf{x}}-{\textbf{y}}\Vert _{{\mathbb {R}}^{L}}^{\beta }}\\&\quad + \sum \limits _{\begin{array}{c} 2r+|\pmb {j^{\prime }}|=k \\ r\in {\mathbb {N}}_{0} \end{array}}\sup \limits _{\begin{array}{c} (t,{\textbf{x}}),(s,{\textbf{x}})\in [0,T]\times \overline{\pmb {{\mathcal {D}}}} \\ t\ne s \end{array}} \frac{|\partial _{t}^{r}\partial _{{\textbf{x}}}^{\pmb {j^{\prime }}} w(t,{\textbf{x}})-\partial _{t}^{r}\partial _{{\textbf{x}}}^{\pmb {j^{\prime }}} w(s,{\textbf{x}}) }{|t-s|^{\beta }}<\infty \,, \end{aligned}$$

see also [32, p. 2 ff.] for further details.

3.1 The elliptic PDE (1.1): assumptions and bounds for $\{D_{{\textbf{x}}}^{\ell }u\}_{\ell =1}^{4}$

We give assumptions, under which there exists a unique classical solution $u\in {\mathcal {C}}^{4+\beta }\bigl ( \overline{\pmb {{\mathcal {D}}}};{\mathbb {R}}\bigr )$ $(0<\beta <1)$ of PDE (1.1); see [24, Ch. 6].

(A0):

$\pmb {{\mathcal {D}}}$ is bounded, and the boundary $\pmb {\partial {\mathcal {D}}}$ is of class ${\mathcal {C}}^{4+\beta }$.

(A1):

${\textbf{b}}:\overline{\pmb {{\mathcal {D}}}}\rightarrow {\mathbb {R}}^{L}$, with $b_{i}(\cdot )\in {\mathcal {C}}^{2+\beta }(\overline{\pmb {{\mathcal {D}}}};{\mathbb {R}}),\; i=1,\ldots ,L$ .

(A2):

$\pmb {\sigma }:\overline{\pmb {{\mathcal {D}}}}\rightarrow {\mathbb {R}}^{L\times L}$, with $\sigma _{ij}(\cdot )\in {\mathcal {C}}^{2+\beta }(\overline{\pmb {{\mathcal {D}}}};{\mathbb {R}}),\; i,j=1,\ldots ,L$. Moreover, there exists a constant $\lambda _{\pmb {\sigma }}>0$, s.t.

$$\begin{aligned} \big \langle {\textbf{y}},\pmb {\sigma }({\textbf{z}}) \pmb {\sigma }^{\top }({\textbf{z}}){\textbf{y}} \big \rangle _{{\mathbb {R}}^{L}}\ge \lambda _{\pmb {\sigma }}\Vert {\textbf{y}}\Vert _{{\mathbb {R}}^{L}}^{2} \quad \text {for all} \;\, {\textbf{z}}\in \overline{\pmb {{\mathcal {D}}}},\; {\textbf{y}}\in {\mathbb {R}}^{L}. \end{aligned}$$

(A3):

$c\in {\mathcal {C}}^{2+\beta }(\overline{\pmb {{\mathcal {D}}}};{\mathbb {R}}^{-}_{0})$, $g \in {\mathcal {C}}^{2+\beta }(\overline{\pmb {{\mathcal {D}}}};{\mathbb {R}})$ and $\phi \in {\mathcal {C}}^{4+\beta }\bigl (\overline{\pmb {{\mathcal {D}}}};{\mathbb {R}}\bigr )$.

In the next section, we need extra asssumptions (cf. Remark 3.1). Hence, we assume

(A1$^{*}$):

$\langle {\textbf{z}},{\textbf{b}}({\textbf{z}})\rangle _{{\mathbb {R}}^{L}}\ge 0 \quad \text {for all} \;\, {\textbf{z}}\in \pmb {{\mathcal {D}}}$.

(A1$^{**}$):

There exists a constant $C_{{\textbf{b}},\pmb {\sigma },L}>0$, s.t.

$$\begin{aligned} 2\langle {\textbf{z}},{\textbf{b}}({\textbf{z}})\rangle _{{\mathbb {R}}^{L}}+L\lambda _{\pmb {\sigma }}\ge C_{{\textbf{b}},\pmb {\sigma },L} \quad \text {for all} \;\, {\textbf{z}}\in \pmb {{\mathcal {D}}}. \end{aligned}$$

Lemma 3.1

Assume (A0) – (A3) in (1.1). Then, for $\ell =1,2,3,4$,

$$\begin{aligned} \pmb {C}_{D^{\ell }}(\phi ,g):=\sup _{ \textbf{z} \in \pmb {{\mathcal {D}}}} \Vert D^{\ell }_\textbf{x} u(\textbf{z})\Vert _{{\mathcal {L}}^{\ell }} \le \pmb {C}(\phi ,g)\,, \end{aligned}$$

where

$$\begin{aligned} \pmb {C}(\phi ,g):=\pmb {\textsf{C} }\bigg \{ \Vert g \Vert _{\pmb {{\mathcal {D}}}}^{(2,\beta )} + \Vert \phi \Vert _{\pmb {{\mathcal {D}}}}^{(4,\beta )} + \sup \limits _{{\textbf{z}}\in \pmb {\partial {\mathcal {D}}}}|\phi ({\textbf{z}})|\bigg \}, \end{aligned}$$

for some constant $\pmb {\textsf{C} }>0$ depending on the data in (1.1), the dimension L and the domain $\pmb {{\mathcal {D}}}$.

The proof of Lemma 3.1 is an immediate consequence of [24, p. 142, Prob. 6.2 and p. 36, Thm. 3.7].

3.2 The parabolic PDE (1.8): assumptions and bounds for $\{D_{{\textbf{x}}}^{\ell }u\}_{\ell =1}^{4}$

We give assumptions, under which there exists a unique classical solution $u\in {\mathcal {C}}^{\nicefrac {(2+\beta )}{2}+1,4+\beta }\bigl ([0,T]\times \overline{\pmb {{\mathcal {D}}}};{\mathbb {R}}\bigr )$ $(0<\beta <1)$ of PDE (1.8); see [32, p. 320, Thm. 5.2].

(B0):

$\pmb {{\mathcal {D}}}$ is bounded, and the boundary $\pmb {\partial {\mathcal {D}}}$ is of class ${\mathcal {C}}^{4+\beta }$.

(B1):

${\textbf{b}}:\overline{\pmb {{\mathcal {D}}}}\rightarrow {\mathbb {R}}^{L}$, with $b_{i}(\cdot )\in {\mathcal {C}}^{2+\beta }(\overline{\pmb {{\mathcal {D}}}};{\mathbb {R}}) \quad i=1,\ldots ,L$ .

(B2):

$\pmb {\sigma }:\overline{\pmb {{\mathcal {D}}}}\rightarrow {\mathbb {R}}^{L\times L}$, with $\sigma _{ij}(\cdot )\in {\mathcal {C}}^{2+\beta }(\overline{\pmb {{\mathcal {D}}}};{\mathbb {R}}),\; i,j=1,\ldots ,L$. Moreover, there exists a constant $\lambda _{\pmb {\sigma }}>0$, s.t.

$$\begin{aligned} \big \langle {\textbf{y}},\pmb {\sigma }({\textbf{z}}) \pmb {\sigma }^{\top }({\textbf{z}}){\textbf{y}} \big \rangle _{{\mathbb {R}}^{L}}\ge \lambda _{\pmb {\sigma }}\Vert {\textbf{y}}\Vert _{{\mathbb {R}}^{L}}^{2} \quad \text {for all} \;\, {\textbf{z}}\in \overline{\pmb {{\mathcal {D}}}},\; {\textbf{y}}\in {\mathbb {R}}^{L}. \end{aligned}$$

(B3):

$g \in {\mathcal {C}}^{\nicefrac {(2+\beta )}{2},2+\beta }([0,T]\times \overline{\pmb {{\mathcal {D}}}};{\mathbb {R}})$ and $\phi \in {\mathcal {C}}^{\nicefrac {(2+\beta )}{2}+1,4+\beta }\bigl ([0,T]\times \overline{\pmb {{\mathcal {D}}}};{\mathbb {R}}\bigr )$, with $(j=0,1)$

$$\begin{aligned}&\partial _{t}^{j+1} \phi (t, \textbf{x}) + \big \langle {\textbf{b}}( \textbf{x}), D_{{\textbf{x}}}\bigl (\partial _{t}^{j}\phi (t,\textbf{x})\bigr )\big \rangle _{{\mathbb {R}}^{L}}\\&\qquad + \frac{1}{2}\textrm{Tr}\Bigl (\pmb {\sigma }({\textbf{x}})\pmb {\sigma }^{\top }({\textbf{x}}) D_{{\textbf{x}}}^{2}\bigl (\partial _{t}^{j}\phi (t,{\textbf{x}})\bigr )\Bigr ) +\partial _{t}^{j} g(t,{\textbf{x}})= 0 \\&\quad \; \text {for all} \;\, (t,\textbf{x}) \in \{T\} \times \pmb {\partial {\mathcal {D}}}\,. \end{aligned}$$

Lemma 3.2

Assume (B0) – (B3) in (1.8). Then, for $\ell =1,2,3,4$,

$$\begin{aligned} \sup _{ (t,\textbf{z}) \in [0,T)\times \pmb {{\mathcal {D}}}} \Vert D^{\ell }_\textbf{x} u(t,\textbf{z})\Vert _{{\mathcal {L}}^{\ell }} \le \pmb {{\mathfrak {C}}}(\phi ,g)\,, \end{aligned}$$

where

$$\begin{aligned} \pmb {{\mathfrak {C}}}(\phi ,g):=\pmb {\textsf{C} }\Big \{ \Vert g \Vert _{[0,T)\times \pmb {{\mathcal {D}}}}^{(2+\beta )} + \Vert \phi (T,\cdot )\Vert _{\pmb {{\mathcal {D}}}}^{(4+\beta )} + \Vert \phi \Vert _{[0,T)\times \pmb {\partial {\mathcal {D}}}}^{(4+\beta )} \Big \}, \end{aligned}$$

for some constant $\pmb {\textsf{C} }>0$ depending on the data in (1.8), the dimension L and the domain $\pmb {{\mathcal {D}}}$.

The proof of Lemma 3.2 is an immediate consequence of [32, p. 320, Thm. 5.2].

3.3 Discretization for the elliptic PDE (1.1): scheme and stability

Scheme 2 below will be used to approximate (1.2) from (1.1). For this purpose, we fix ${\textbf{x}}\in \pmb {{\mathcal {D}}}$ and let $\{t_{j}\}_{j\ge 0}\subset [0,\infty )$ be a mesh with local mesh sizes $\{\tau ^{j+1}\}_{j\ge 0}$.

Scheme 1

Let $j\ge 0$. For given $({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j},Y_{Z}^{j})$ at time $t_{j}$, find the ${\mathbb {R}}^{L}$-valued random variable $\textbf{Y}_{{\textbf{X}}}^{j+1}$ from

$$\begin{aligned} \textbf{Y}_{{\textbf{X}}}^{j+1} = \textbf{Y}_{{\textbf{X}}}^j + {\textbf{b}}(\textbf{Y}_{{\textbf{X}}}^{j}) {\tau }^{j+1} + \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\xi }_{j+1}\sqrt{\tau ^{j+1}} , \qquad \textbf{Y}_{{\textbf{X}}}^0 = \textbf{x}\,, \end{aligned}$$

(3.1)

where $\pmb {\xi }_{j+1}=\bigl (\xi _{j+1}^{(1)},\ldots ,\xi _{j+1}^{(L)}\bigr )^{\top }$ is a ${\mathbb {R}}^{L}$-valued random vector, whose entries are independent two-point distributed random variables, taking values $\pm 1$ with probability $\frac{1}{2}$ each, as well as the ${\mathbb {R}}$-valued random variables $Y_{V}^{j+1}$, $Y_{Z}^{j+1}$ from

$$\begin{aligned} Y_{V}^{j+1}= & {} Y_{V}^{j} + {\tau }^{j+1} c({\textbf{Y}}_{{\textbf{X}}}^{j})Y_{V}^{j+1} , \qquad Y_{V}^0 = 1\,, \qquad \text {and} \end{aligned}$$

(3.2)

$$\begin{aligned} Y_{Z}^{j+1}= & {} Y_{Z}^{j} + {\tau }^{j+1} g({\textbf{Y}}_{{\textbf{X}}}^{j})Y_{V}^{j} , \qquad Y_{Z}^0 = 0\,, \end{aligned}$$

(3.3)

to approximate solution $\textbf{X}_{t_{j+1}}$ from (1.3), $V_{t_{j+1}}$ from (1.5), and $Z_{t_{j+1}}$ from (1.6) at time $t_{j+1} = t_{j} + \tau ^{j+1}$.

The iterates $\{Y_{V}^{j}\}_{j\ge 0}$ from (3.2) are computed via the implicit Euler method in order to ensure $0<Y_{V}^{j}\le 1$ ($j\ge 0$) without additonal smallness assumptions of the corresponding step sizes $\{\tau ^{j+1}\}_{j\ge 0}$.

Scheme 2 below is closely based on [40, p. 365 ff., Sec. 6.3] and uses Scheme 1 to approximate (1.2) by ‘${\mathbb {E}}\bigl [\phi (\textbf{Y}_{{\textbf{X}}}^{J^{*}})Y_{V}^{J^{*}}+Y_{Z}^{J^{*}}\bigr ]$’, where $J^{*}=J^{*}(\omega )$ is the smallest number such that ${\textbf{Y}}_{{\textbf{X}}}^{J^{*}}\in \pmb {\partial {\mathcal {D}}}$. Recalling the characterization of the boundary strip $\pmb {{\mathcal {S}}}_{\tau ^{j+1}}$ in Sect. 1 (see also Fig. 5b), we observe that $\lambda _{j}>0$ has to be chosen such that $\lambda _{j} \sqrt{\tau ^{j+1}} \ge \Vert {\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j}\Vert _{{\mathbb {R}}^{L}}$, i.e., as (computable) upper bound of the distance between two iterates. Hence, choosing

$$\begin{aligned} \lambda _{j}:=\Vert {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \Vert _{{\mathbb {R}}^{L}} \sqrt{\tau ^{j+1}} + \sqrt{L} \Vert \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j}) \Vert _{{\mathbb {R}}^{L\times L}}, \end{aligned}$$

(3.4)

is suitable.

Consequently, we identify ${\textbf{Y}}_{{\textbf{X}}}^{j} \in \pmb {{\mathcal {D}}}$ as being ‘close’ to resp. ‘away’ from $\pmb {\partial {\mathcal {D}}}$, when ${\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}$ resp. ${\textbf{Y}}_{{\textbf{X}}}^{j}\notin \pmb {{\mathcal {S}}}_{\tau ^{j+1}}$. For the following, we denote by $\Pi _{\pmb {\partial {\mathcal {D}}}}:\overline{\pmb {{\mathcal {D}}}}\rightarrow \pmb {\partial {\mathcal {D}}}$ the projection onto the boundary $\pmb {\partial {\mathcal {D}}}$, and by $\pmb {n}\bigl ( \Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{z}})\bigr )$ the unit internal normal to $\pmb {\partial {\mathcal {D}}}$ at $\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{z}})$; see Fig. 5b.

Scheme 2

Let $j\ge 0$. Let $({\textbf{Y}}_{{\textbf{X}}}^{j}$, $Y_{V}^{j}$, $Y_{Z}^{j})$ be given, and ${\textbf{Y}}_{{\textbf{X}}}^{k} \in \pmb {{\mathcal {D}}}$, for $k =0,\ldots ,j$.

(1):

(‘ ${\texttt {Localization}}$’) If ${\textbf{Y}}_{{\textbf{X}}}^{j}\notin \pmb {{\mathcal {S}}}_{\tau ^{j+1}}$, set $\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}:={\textbf{Y}}_{{\textbf{X}}}^{j}$.

(a):

If ${\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}$, go to (4).

(b):

If ${\textbf{Y}}_{{\textbf{X}}}^{j}\notin \pmb {{\mathcal {D}}}$, set $J^{*}:=j$, $t_{J^{*}}:=t_{j}$, ${\textbf{Y}}_{{\textbf{X}}}^{J^{*}}:=\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j})$, $Y_{V}^{J^{*}}:=Y_{V}^{j}$, $Y_{Z}^{J^{*}}:=Y_{Z}^{j}$, and STOP.

(2):

(‘ ${\texttt {Localization}}$’) If ${\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}$, then either $\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}=\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j})$ with probability

$$\begin{aligned} p_{j}:= & {} {\mathbb {P}}\big [\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}=\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j})\,|{\textbf{Y}}_{{\textbf{X}}}^{j}\big ]\nonumber \\= & {} \frac{ \lambda _{j}\sqrt{\tau ^{j+1}}}{\big \Vert {\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )-\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j})\big \Vert _{{\mathbb {R}}^{L}}}, \end{aligned}$$

(3.5)

or $\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )$ with probability $1-p_{j}$.

(3):

(‘${\texttt {Projection}}$’) If $\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}=\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j})$, set $J^{*}:=j$, $t_{J^{*}}:=t_{j}$, ${\textbf{Y}}_{{\textbf{X}}}^{J^{*}}:=\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j})$, $Y_{V}^{J^{*}}:=Y_{V}^{j}$, $Y_{Z}^{J^{*}}:=Y_{Z}^{j}$, and STOP.

(4):

(‘ ${\texttt {Solve}}$’) Set ${\textbf{Y}}_{{\textbf{X}}}^{j}:=\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}$. Compute ${\textbf{Y}}_{{\textbf{X}}}^{j+1}$, $Y_{V}^{j+1}$ and $Y_{Z}^{j+1}$ via Scheme 1, set $t_{j+1}:=t_{j}+\tau ^{j+1}$.

(5):

Put $j:=j+1$, and return to (1).

For $j>J^{*}$, we set $({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j},Y_{Z}^{j})=({\textbf{Y}}_{{\textbf{X}}}^{J^{*}},Y_{V}^{J^{*}},Y_{Z}^{J^{*}})$.

Note that $p_{j}>\frac{1}{2}$ in Step (2) of Scheme 2, since $\textrm{d}({\textbf{Y}}_{{\textbf{X}}}^{j},\pmb {\partial {\mathcal {D}}})=\big \Vert {\textbf{Y}}_{{\textbf{X}}}^{j}-\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j})\big \Vert _{{\mathbb {R}}^{L}} < \lambda _{j}\sqrt{\tau ^{j+1}}$, and ${\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )\notin \pmb {{\mathcal {S}}}_{\tau ^{j+1}}$.

Fig. 5

a Exit of the continuified Euler process $\pmb {{\mathcal {Y}}}^{{\textbf{X}}}$ in (4.30). b Projection resp. bouncing back mechanism in Scheme 2

The following lemma estimates the number of iterates $\{{\textbf{Y}}_{{\textbf{X}}}^{j}\}_{j\ge 0}$ from Scheme 2 in the boundary strips; it may be considered as a generalization of [40, p. 367, Lem. 3.2] for non-uniform time steps.

Lemma 3.3

Assume (A0)–(A3). Fix ${\textbf{x}}\in \pmb {{\mathcal {D}}}$. Let $\{t_{j}\}_{j\ge 0}\subset [0,\infty )$ be a mesh with local mesh sizes $\{\tau ^{j+1}\}_{j\ge 0}$. Let $\{{\textbf{Y}}_{{\textbf{X}}}^{j}\}_{j\ge 0}$ be from Scheme 2. Then

$$\begin{aligned} \sum \limits _{j=0}^{\infty } {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Big ]<2. \end{aligned}$$

Proof

Let $j\in {\mathbb {N}}$. Since the probability $p_{j}$ in (3.5) is greater than $\frac{1}{2}$, we obtain

$$\begin{aligned} {\mathbb {P}}[J^{*}=j]&={\mathbb {E}}\Big [ {\mathbb {E}}\big [{\textbf{1}}_{\{J^{*}=j\}}\,|\,{\textbf{Y}}_{{\textbf{X}}}^{j}\big ]\Big ]={\mathbb {E}}\bigg [ {\mathbb {E}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{ \overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}=\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \big \}}\,|\,{\textbf{Y}}_{{\textbf{X}}}^{j}\Big ]\bigg ]\\&={\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}}\cdot p_{j}\big ]>\frac{1}{2}{\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}}\big ] \,. \end{aligned}$$

Consequently, we have

$$\begin{aligned} \sum \limits _{j=0}^{\infty } {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Big ]<2\sum \limits _{j=0}^{\infty } {\mathbb {P}}[J^{*}=j]=2\,. \end{aligned}$$

$\square$

The following lemma yields boundedness of the expected discrete stopping time

$$\begin{aligned} t_{J^{*}}:=\min \big \{t_{j}:\,{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {\partial {\mathcal {D}}},\;j\ge 0\big \}, \end{aligned}$$

which approximates (1.4).

Lemma 3.4

Assume (A0) – (A3). Fix ${\textbf{x}}\in \pmb {{\mathcal {D}}}$. Let $\{t_{j}\}_{j\ge 0}\subset [0,\infty )$ be a mesh with local mesh sizes $\{\tau ^{j+1}\}_{j\ge 0}$ and maximum mesh size $\tau ^{max}:=\max _{j}\tau ^{j+1}$. Let $\{{\textbf{Y}}_{{\textbf{X}}}^{j}\}_{j\ge 0}$ be from Scheme 2. For $\tau ^{max}$ either sufficiently small, or for general $\tau ^{max}>0$ if (A1) is complemented by (A1$^{*}$) or (A1$^{**}$), we have

$$\begin{aligned} {\mathbb {E}}[t_{J^{*}}]\le C , \end{aligned}$$

where $C>0$ depends on the dimension L, the domain $\pmb {{\mathcal {D}}}$ and the data in (1.1), but is independent of ${\textbf{x}}\in \pmb {{\mathcal {D}}}$.

Proof

Step 1: (Derivation of a ‘discrete Dynkin-formula’) We derive a ‘discrete Dynkin-formula’ adapted to our setting. Let $f\in {\mathcal {C}}({\mathbb {R}}^{L})$ and $k\in {\mathbb {N}}$. A first calculation yields

$$\begin{aligned} {\mathbb {E}}\big [f\bigl ({\textbf{Y}}_{{\textbf{X}}}^{J^{*}\wedge k }\bigr )-f({\textbf{x}})\big ]&={\mathbb {E}}\bigg [ \sum \limits _{j=0}^{J^{*} \wedge k -1} \big \{ f({\textbf{Y}}_{{\textbf{X}}}^{j+1})-f({\textbf{Y}}_{{\textbf{X}}}^{j})\big \}\bigg ]\nonumber \\&={\mathbb {E}}\bigg [ \sum \limits _{j=0}^{J^{*} \wedge k -1} \big \{ f({\textbf{Y}}_{{\textbf{X}}}^{j+1})-f(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})+f(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}) -f({\textbf{Y}}_{{\textbf{X}}}^{j})\big \}\bigg ] \nonumber \\&= \underbrace{{\mathbb {E}}\bigg [ \sum \limits _{j=0}^{k -1} {\textbf{1}}_{\{J^{*}>j \}} \cdot \big \{ f({\textbf{Y}}_{{\textbf{X}}}^{j+1})-f(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\big \}\bigg ]}_{=:\pmb {T_{1}}}\nonumber \\&\quad + \underbrace{{\mathbb {E}}\bigg [ \sum \limits _{j=0}^{k -1} {\textbf{1}}_{\{J^{*} >j \}} \cdot \big \{ f(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})-f({\textbf{Y}}_{{\textbf{X}}}^{j})\big \}\bigg ]}_{=:\pmb {T_{2}}}\,. \end{aligned}$$

(3.6)

(a) (Investigation of $\pmb {T_{1}}$) According to the procedure in Scheme 2, we have

$$\begin{aligned} \pmb {T_{1}}= \pmb {T_{1,1}} + \pmb {T_{1,2}}, \end{aligned}$$

(3.7)

where

$$\begin{aligned} \pmb {T_{1,1}}&:={\mathbb {E}}\bigg [ \sum \limits _{j=0}^{k -1} {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \cdot \big \{ f({\textbf{Y}}_{{\textbf{X}}}^{j+1})-f({\textbf{Y}}_{{\textbf{X}}}^{j})\big \}\bigg ]\,,\\ \pmb {T_{1,2}}&:={\mathbb {E}}\bigg [ \sum \limits _{j=0}^{k-1} {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \cdot \big \{ f({\textbf{Y}}_{{\textbf{X}}}^{j+1})-f(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\big \}\bigg ]\,. \end{aligned}$$

(b) (Investigation of $\pmb {T_{1,1}}$) Taylor’s formula yields

$$\begin{aligned} \pmb {T_{1,1}}=\pmb {T_{1,1,1}}+\pmb {T_{1,1,2}}, \end{aligned}$$

(3.8)

where

$$\begin{aligned} \pmb {T_{1,1,1}}&:={\mathbb {E}}\bigg [ \sum \limits _{j=0}^{k-1} {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \cdot \big \langle D_{{\textbf{x}}}f({\textbf{Y}}_{{\textbf{X}}}^{j}),{\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j}\big \rangle _{{\mathbb {R}}^{L}}\bigg ]\,,\\ \pmb {T_{1,1,2}}&:=\frac{1}{2}{\mathbb {E}}\bigg [ \sum \limits _{j=0}^{ k -1} {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \cdot \textrm{Tr}\Bigl (D_{{\textbf{x}}}^{2}f(\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j})\bigl ({\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j}\bigr )\bigl ({\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j}\bigr )^{\top }\Bigr )\bigg ]\,, \end{aligned}$$

for some $\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j}$ between ${\textbf{Y}}_{{\textbf{X}}}^{j+1}$ and ${\textbf{Y}}_{{\textbf{X}}}^{j}$, i.e., $\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+\theta \bigl ({\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j} \bigr )$ with $\theta \in (0,1)$. We use (3.1) to represent the increment ‘${\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j}$’ in $\pmb {T_{1,1,1}}$, as well as the tower property and independency arguments to get

$$\begin{aligned} \pmb {T_{1,1,1}}&={\mathbb {E}}\bigg [\sum \limits _{j=0}^{ k -1} {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \cdot \big \langle D_{{\textbf{x}}}f({\textbf{Y}}_{{\textbf{X}}}^{j}),{\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\big \rangle _{{\mathbb {R}}^{L}}\cdot \tau ^{j+1}\bigg ]\nonumber \\&\quad + \sum \limits _{j=0}^{ k-1} \underbrace{{\mathbb {E}}\Big [ {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \cdot \big \langle D_{{\textbf{x}}}f({\textbf{Y}}_{{\textbf{X}}}^{j}),\pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\xi }_{j+1}\big \rangle _{{\mathbb {R}}^{L}}\cdot \sqrt{\tau ^{j+1}}\bigg ]}_{=0}\nonumber \\&={\mathbb {E}}\bigg [\sum \limits _{j=0}^{ k -1} {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \cdot \big \langle D_{{\textbf{x}}}f({\textbf{Y}}_{{\textbf{X}}}^{j}),{\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\big \rangle _{{\mathbb {R}}^{L}}\cdot \tau ^{j+1}\bigg ]\,. \end{aligned}$$

(3.9)

Similar arguments as in (3.9), i.e., representing the increment ‘${\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j}$’ in $\pmb {T_{1,1,2}}$ via (3.1) and using standard calculations, as well as independency arguments lead to

$$\begin{aligned} \pmb {T_{1,1,2}}&=\frac{1}{2}{\mathbb {E}}\bigg [\sum \limits _{j=0}^{k -1} {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \cdot \textrm{Tr}\Bigl (D_{{\textbf{x}}}^{2}f({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\sigma }^{\top }({\textbf{Y}}_{{\textbf{X}}}^{j})\Bigl )\cdot \tau ^{j+1}\bigg ]+\pmb {T_{1,1,2,1}}\,, \end{aligned}$$

(3.10)

where

$$\begin{aligned} \pmb {T_{1,1,2,1}}&=\frac{1}{2}{\mathbb {E}}\bigg [\sum \limits _{j=0}^{k -1} {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \cdot \textrm{Tr}\Bigl (D_{{\textbf{x}}}^{2}f(\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j}){\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j}){\textbf{b}}^{\top }({\textbf{Y}}_{{\textbf{X}}}^{j})\Bigl )\cdot \bigl (\tau ^{j+1}\bigr )^{2}\bigg ]\\&\quad + \frac{1}{2}{\mathbb {E}}\bigg [\sum \limits _{j=0}^{ k -1} {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \\&\quad \cdot \textrm{Tr}\Bigl (\Big \{D_{{\textbf{x}}}^{2}f(\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j})-D_{{\textbf{x}}}^{2}f({\textbf{Y}}_{{\textbf{X}}}^{j})\Big \}{\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\bigl (\pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j}) \pmb {\xi }_{j+1}\bigr )^{\top }\Bigl )\cdot \bigl (\tau ^{j+1}\bigr )^{\frac{3}{2}}\bigg ]\\&\quad + \frac{1}{2}{\mathbb {E}}\bigg [\sum \limits _{j=0}^{ k -1} {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \\&\quad \cdot \textrm{Tr}\Bigl (\Big \{D_{{\textbf{x}}}^{2}f(\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j})-D_{{\textbf{x}}}^{2}f({\textbf{Y}}_{{\textbf{X}}}^{j})\Big \}\pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j}) \pmb {\xi }_{j+1}{\textbf{b}}^{\top }({\textbf{Y}}_{{\textbf{X}}}^{j})\Bigl )\cdot \bigl (\tau ^{j+1}\bigr )^{\frac{3}{2}}\bigg ]\\&\quad + \frac{1}{2}{\mathbb {E}}\bigg [\sum \limits _{j=0}^{ k -1} {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \\&\quad \cdot \textrm{Tr}\Bigl (\Big \{D_{{\textbf{x}}}^{2}f(\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j})-D_{{\textbf{x}}}^{2}f({\textbf{Y}}_{{\textbf{X}}}^{j})\Big \}\pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j}) \pmb {\xi }_{j+1}\bigl (\pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j} \pmb {\xi }_{j+1}\bigr )^{\top }\Bigl )\cdot \tau ^{j+1}\bigg ]\,. \end{aligned}$$

Plugging (3.9) and (3.10) into (3.8) yields

$$\begin{aligned} \pmb {T_{1,1}}&={\mathbb {E}}\bigg [\sum \limits _{j=0}^{ k -1} {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \cdot \big \langle D_{{\textbf{x}}}f({\textbf{Y}}_{{\textbf{X}}}^{j}),{\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\big \rangle _{{\mathbb {R}}^{L}}\cdot \tau ^{j+1}\bigg ] \nonumber \\&\quad + \frac{1}{2}{\mathbb {E}}\bigg [\sum \limits _{j=0}^{k -1} {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \cdot \textrm{Tr}\Bigl (D_{{\textbf{x}}}^{2}f({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\sigma }^{\top }({\textbf{Y}}_{{\textbf{X}}}^{j})\Bigl )\cdot \tau ^{j+1}\bigg ]+\pmb {T_{1,1,2,1}}\,. \end{aligned}$$

(3.11)

c) (Investigation of $\pmb {T_{1,2}}$) Since the investigation of $\pmb {T_{1,2}}$ is similar to $\pmb {T_{1,1}}$, we obtain

$$\begin{aligned} \pmb {T_{1,2}}&={\mathbb {E}}\bigg [\sum \limits _{j=0}^{ k -1} {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}}\nonumber \\&\quad \cdot \big \langle D_{{\textbf{x}}}f(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}),{\textbf{b}}(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\big \rangle _{{\mathbb {R}}^{L}}\cdot \tau ^{j+1}\bigg ] \nonumber \\&\quad + \frac{1}{2}{\mathbb {E}}\bigg [\sum \limits _{j=0}^{k -1} {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}}\nonumber \\&\quad \cdot \textrm{Tr}\Bigl (D_{{\textbf{x}}}^{2}f(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\pmb {\sigma }(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\pmb {\sigma }^{\top }(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\Bigl )\cdot \tau ^{j+1}\bigg ] \nonumber \\&\quad +\overline{\pmb {T_{1,1,2,1}}}\,, \end{aligned}$$

(3.12)

where $\overline{\pmb {T_{1,1,2,1}}}$ has the same representation as $\pmb {T_{1,1,2,1}}$, where every ${\textbf{Y}}_{{\textbf{X}}}^{j}$ in the trace terms is replaced by $\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}$, and ${\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}{\setminus } \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}}$ is replaced by ${\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}}$.

d) (Investigation of $\pmb {T_{2}}$) According to the procedure in Scheme 2, we obtain

$$\begin{aligned} \pmb {T_{2}}={\mathbb {E}}\bigg [ \sum \limits _{j=0}^{k -1} {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \cdot \big \{ f(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})-f({\textbf{Y}}_{{\textbf{X}}}^{j})\big \}\bigg ].\nonumber \\ \end{aligned}$$

(3.13)

e) We insert (3.11) and (3.12) into (3.7), and plug the resulting expression as well as (3.13) into (3.6) to obtain

$$\begin{aligned}&{\mathbb {E}}\big [f\bigl ({\textbf{Y}}_{{\textbf{X}}}^{J^{*}\wedge k }\bigr )\big ]=f({\textbf{x}})+{\mathbb {E}}\bigg [\sum \limits _{j=0}^{ k -1} {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \cdot \big \langle D_{{\textbf{x}}}f({\textbf{Y}}_{{\textbf{X}}}^{j}),{\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\big \rangle _{{\mathbb {R}}^{L}}\cdot \tau ^{j+1}\bigg ] \nonumber \\&\quad + \frac{1}{2}{\mathbb {E}}\bigg [\sum \limits _{j=0}^{k -1} {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \cdot \textrm{Tr}\Bigl (D_{{\textbf{x}}}^{2}f({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\sigma }^{\top }({\textbf{Y}}_{{\textbf{X}}}^{j})\Bigl )\cdot \tau ^{j+1}\bigg ]+\pmb {T_{1,1,2,1}}\nonumber \\&\quad +{\mathbb {E}}\bigg [\sum \limits _{j=0}^{ k -1} {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \cdot \big \langle D_{{\textbf{x}}}f(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}),{\textbf{b}}(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\big \rangle _{{\mathbb {R}}^{L}}\cdot \tau ^{j+1}\bigg ] \nonumber \\&\quad + \frac{1}{2}{\mathbb {E}}\bigg [\sum \limits _{j=0}^{k -1} {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}}\nonumber \\&\quad \cdot \textrm{Tr}\Bigl (D_{{\textbf{x}}}^{2}f(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\pmb {\sigma }(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\pmb {\sigma }^{\top }(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\Bigl )\cdot \tau ^{j+1}\bigg ] \nonumber \\&\quad +\overline{\pmb {T_{1,1,2,1}}} + {\mathbb {E}}\bigg [ \sum \limits _{j=0}^{k -1} {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \cdot \big \{ f(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})-f({\textbf{Y}}_{{\textbf{X}}}^{j})\big \}\bigg ]\,. \end{aligned}$$

(3.14)

Step 2: (Proof of the statement for $\tau ^{max}$ sufficiently small) Let $n\in {\mathbb {N}}$. Choose a ${\textbf{B}}\in {\mathbb {R}}^{L}$ such that $\min \limits _{{\textbf{z}}\in \overline{\pmb {{\mathcal {D}}}}}\Vert {\textbf{z}}+{\textbf{B}}\Vert _{{\mathbb {R}}^{L}}^{2n}\ge 1$. Set $A^{2}:=\max \limits _{{\textbf{z}}\in \overline{\pmb {{\mathcal {D}}}}}\Vert {\textbf{z}}+{\textbf{B}}\Vert _{{\mathbb {R}}^{L}}^{2n}$ and consider (3.14) with

$$\begin{aligned} f({\textbf{z}})&=A^{2}-\Vert {\textbf{z}}+{\textbf{B}}\Vert _{{\mathbb {R}}^{L}}^{2n} \qquad ({\textbf{z}}\in \pmb {{\mathcal {D}}})\,,\\ \partial _{x_{i}}f({\textbf{z}})&=-2n \Vert {\textbf{z}}+{\textbf{B}}\Vert _{{\mathbb {R}}^{L}}^{2(n-1)}(z_{i}+B_{i})\qquad i=1,\ldots ,L\,,\\ \partial _{x_{i}}\partial _{x_{j}}f({\textbf{z}})&=-4n(n-1) \Vert {\textbf{z}}+{\textbf{B}}\Vert _{{\mathbb {R}}^{L}}^{2(n-2)}(z_{i}+B_{i})(z_{j}+B_{j})\\&\quad -2n\Vert {\textbf{z}}+{\textbf{B}}\Vert _{{\mathbb {R}}^{L}}^{2(n-1)}\delta _{ij}\qquad i,j=1,\ldots ,L\,. \end{aligned}$$

We refer to [40, p. 367, Lemma 3.2] for a similar choice of a function f in a related setting. By applying (A2) four times, we consequently obtain for $k\in {\mathbb {N}}$

We choose $n\in {\mathbb {N}}$ large enough such that

$$\begin{aligned} 2\big \langle {\textbf{z}}+{\textbf{B}},{\textbf{b}}({\textbf{z}})\big \rangle _{{\mathbb {R}}^{L}}+(2n-2+L)\lambda _{\pmb {\sigma }}\ge 1 \quad \text {for all} \;\, {\textbf{z}}\in \pmb {{\mathcal {D}}}. \end{aligned}$$

Since $f({\textbf{z}})\ge 0$, ${\textbf{z}}\in \overline{\pmb {{\mathcal {D}}}}$, $\Vert {\textbf{Y}}_{{\textbf{X}}}^{j}+{\textbf{B}}\Vert _{{\mathbb {R}}^{L}}^{2(n-1)}\ge 1$, $\Vert \overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}+{\textbf{B}}\Vert _{{\mathbb {R}}^{L}}^{2(n-1)}\ge 1$, and $\sum \nolimits _{j=0}^{k-1} {\mathbb {E}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}}\Big ]<2$ due to Lemma 3.3, we further get

$$\begin{aligned} 0&\le f({\textbf{x}})-n \cdot {\mathbb {E}}\bigg [ \sum \nolimits _{j=0}^{k-1} \Big \{{\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}}\\&\quad +{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}}\Big \}\cdot \tau ^{j+1} \bigg ]\\&\quad + \pmb {T_{1,1,1,2}}+\overline{\pmb {T_{1,1,1,2}}}+2A^{2}\\&= f({\textbf{x}})-n \cdot {\mathbb {E}}\bigg [ \sum \limits _{j=0}^{k -1} {\textbf{1}}_{\{J^{*} >j \}}\cdot \tau ^{j+1} \bigg ] + \pmb {T_{1,1,1,2}}+\overline{\pmb {T_{1,1,1,2}}}+2A^{2}\\&= f({\textbf{x}})-n \cdot {\mathbb {E}}[t_{J^{*}\wedge k}]+\pmb {T_{1,1,1,2}}+\overline{\pmb {T_{1,1,1,2}}}+2A^{2}\,. \end{aligned}$$

By means of standard calculations and Taylor’s formula one can show that

$$\begin{aligned} \pmb {T_{1,1,1,2}}+\overline{\pmb {T_{1,1,1,2}}}\le {\mathfrak {C}}(n)\tau ^{max}{\mathbb {E}}[t_{J^{*}\wedge k}], \end{aligned}$$

where ${\mathfrak {C}}(n)>0$. For $\tau ^{max}$ sufficiently small, i.e., $\tau ^{max}\le \frac{n}{{\mathfrak {C}}(n)}$, we thus have

$$\begin{aligned} {\mathbb {E}}[t_{J^{*}\wedge k}]\le \frac{f({\textbf{x}})+2A^{2}}{n-{\mathfrak {C}}(n)\tau ^{max}}, \end{aligned}$$

Letting $k\rightarrow \infty$ yields the assertion.

Step 3: (Proof of the statement under (A1$^{*}$)) Set $A^{max}:=\max \limits _{{\textbf{z}}\in \overline{\pmb {{\mathcal {D}}}}}\Vert {\textbf{z}} \Vert _{{\mathbb {R}}^{L}}^{2}$ and consider (3.14) with

$$\begin{aligned} f({\textbf{z}})=A^{max}-\Vert {\textbf{z}}\Vert _{{\mathbb {R}}^{L}}^{2} \qquad ({\textbf{z}}\in \pmb {{\mathcal {D}}}). \end{aligned}$$

Applying (A2) and (A1$^{*}$) and using the fact that $\pmb {T_{1,1,1,2}}+\overline{\pmb {T_{1,1,1,2}}}\le 0$, we obtain for $k\in {\mathbb {N}}$

$$\begin{aligned} {\mathbb {E}}\big [f\bigl ({\textbf{Y}}_{{\textbf{X}}}^{J^{*}\wedge k }\bigr )\big ]\le f({\textbf{x}})-\lambda _{\pmb {\sigma }}L \cdot {\mathbb {E}}[t_{J^{*}\wedge k}]+2A^{max}\,. \end{aligned}$$

(3.15)

Since $f({\textbf{z}})\ge 0$, ${\textbf{z}}\in \overline{\pmb {{\mathcal {D}}}}$, we obtain

$$\begin{aligned} {\mathbb {E}}[t_{J^{*}\wedge k}]\le \frac{3A^{max}-\Vert {\textbf{x}}\Vert _{{\mathbb {R}}^{L}}^{2}}{\lambda _{\pmb {\sigma }}L }. \end{aligned}$$

Hence, letting $k\rightarrow \infty$ yields the assertion.

Step 4: (Proof of the statement under (A1$^{**}$)) The assertion immediately follows from (3.15) and (A1$^{**}$). $\square$

Remark 3.1

1. Lemma 3.4 generalizes [40, p. 367, Lem. 3.2] to non-uniform time steps. There, (uniform) time steps are chosen ‘small enough’ to ensure the statement from Lemma 3.4 without postulating additional assumptions such as (A1$^{*}$) or (A1$^{**}$).

2. For (A1$^{*}$) or (A1$^{**}$), Lemma 3.4 holds for general mesh sizes, which is needed to establish optimal convergence of the adaptive Algorithm 5.1; see Theorem 5.2. Examples 1.2 and 6.2 satisfy (A1$^{*}$).

3. For the usual Euler method in (4.29), it is possible to derive a similar result as in Lemma 3.4only under (A0)–(A3) thanks to Dynkin’s-formula.

4. The constant $C>0$ can be explicitly identified under assumption (A1$^{*}$) resp. (A1$^{**}$). In the first case

$$\begin{aligned} {\mathbb {E}}[t_{J^{*}}]\le \frac{1}{\lambda _{\pmb {\sigma }}L}\Big (3 \max \limits _{{\textbf{z}}\in \overline{\pmb {{\mathcal {D}}}}} \Vert {\textbf{z}} \Vert _{{\mathbb {R}}^{L}}^{2}-\Vert {\textbf{x}}\Vert _{{\mathbb {R}}^{L}}^{2}\Big )\le \frac{1}{\lambda _{\pmb {\sigma }}L}\cdot 3\max \limits _{{\textbf{z}}\in \overline{\pmb {{\mathcal {D}}}}} \Vert {\textbf{z}} \Vert _{{\mathbb {R}}^{L}}^{2}=:C, \end{aligned}$$

while in the second

$$\begin{aligned} {\mathbb {E}}[t_{J^{*}}]\le \frac{1}{C_{{\textbf{b}},\pmb {\sigma },L}}\Big (3\max \limits _{{\textbf{z}}\in \overline{\pmb {{\mathcal {D}}}}} \Vert {\textbf{z}} \Vert _{{\mathbb {R}}^{L}}^{2}-\Vert {\textbf{x}}\Vert _{{\mathbb {R}}^{L}}^{2}\Big )\le \frac{1}{C_{{\textbf{b}},\pmb {\sigma },L}}\cdot 3\max \limits _{{\textbf{z}}\in \overline{\pmb {{\mathcal {D}}}}} \Vert {\textbf{z}} \Vert _{{\mathbb {R}}^{L}}^{2}=:C. \end{aligned}$$

3.4 Discretization for the parabolic PDE (1.8): scheme and stability

Fix $(t,{\textbf{x}})\in [0,T)\times \pmb {{\mathcal {D}}}$ in (1.9) and let $\{t_{j}\}_{j=0}^{J}\subset [t,T]$ be a mesh with local step sizes $\{\tau ^{j+1}\}_{j=0}^{J-1}$, where $J\equiv J(t,{\textbf{x}})\in {\mathbb {N}}$. We use (3.1) and (3.3) with $Y_{V}^{j}\equiv 1$, and where ‘$g({\textbf{Y}}_{{\textbf{X}}}^{j})$’ is replaced by ‘$g(t_{j},{\textbf{Y}}_{{\textbf{X}}}^{j})$’ to approximate (1.10) and (1.12). In the following, we state Scheme 3, which is closely based on [40, p. 353 ff., Subsec. 6.2.1], and which can be seen as an analog to Scheme 2 in the elliptic setting to approximate (1.9) by ‘${\mathbb {E}}\bigl [\phi (t_{J^{*}},\textbf{Y}_{{\textbf{X}}}^{J^{*}})+Y_{Z}^{J^{*}}\bigr ]$’.

Scheme 3

Let $j\ge 0$. Let (${\textbf{Y}}_{{\textbf{X}}}^{j}$, $Y_{Z}^{j}$) be given with ${\textbf{Y}}_{{\textbf{X}}}^{k} \in \pmb {{\mathcal {D}}}$, $k =0,\ldots ,j$.

(1):

Proceed as in (1)–(4) in Scheme 2.

(2):

(‘ ${\texttt {Stop}}$’) If $j+1=J$, set $J^{*}:=j+1$, $t_{J^{*}}:=t_{J}$, ${\textbf{Y}}_{{\textbf{X}}}^{J^{*}}:={\textbf{Y}}_{{\textbf{X}}}^{J}$, $Y_{Z}^{J^{*}}:=Y_{Z}^{J}$, and STOP.

For $j>J^{*}$, we set $({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j},Y_{Z}^{j})=({\textbf{Y}}_{{\textbf{X}}}^{J^{*}},Y_{V}^{J^{*}},Y_{Z}^{J^{*}})$.

Similar to Lemma 3.3, the following lemma can be considered as a generalization of [40, p. 356, Lem. 2.2] to non-uniform time steps, which estimates the number of iterates $\{{\textbf{Y}}_{{\textbf{X}}}^{j}\}_{j=0}^{J}$ from Scheme 3 in the boundary strips.

Lemma 3.5

Assume (B0)–(B3). Fix $(t,{\textbf{x}})\in [0,T)\times \pmb {{\mathcal {D}}}$. Let $J\equiv J(t,{\textbf{x}})\in {\mathbb {N}}$ and $\{t_{j}\}_{j=0}^{J}\subset [t,T]$ be a mesh with local mesh sizes $\{\tau ^{j+1}\}_{j=0}^{J-1}$. Let $\{{\textbf{Y}}_{{\textbf{X}}}^{j}\}_{j=0}^{J}$ be from Scheme 3. Then

$$\begin{aligned} \sum \limits _{j=0}^{J-1} {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Big ]<2. \end{aligned}$$

4 A posteriori weak error analysis

In Sect. 4.1, we derive an a posteriori error estimate for iterates $\{({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j},Y_{Z}^{j})\}_{j\ge 0}$ of Scheme 2 within the approximative framework of the elliptic PDE (1.1); see Theorem 4.1. It is shown in Theorem 4.6 that the resulting error estimators converge with optimal order 1 on a mesh with maximum mesh size $\tau ^{max}>0$; the relevant tools for its verification are Theorem 4.1 and Lemmata 3.3 and 3.4. Corresponding results for the parabolic PDE (1.8), cf. Theorem 4.7 and Theorem 4.8 are derived in Sect. 4.2. In Sect. 4.3, we derive an a posteriori error estimate for the (usual) Euler scheme and discuss related difficulties.

4.1 A posteriori weak error estimation: derivation and optimality for the elliptic PDE (1.1)

The following result bounds the approximation error $\Bigl \vert u({\textbf{x}}) - {\mathbb {E}}\bigl [\phi (\textbf{Y}_{{\textbf{X}}}^{J^{*}})Y_{V}^{J^{*}}+Y_{Z}^{J^{*}}\bigr ] \Bigr \vert$ in terms of computable a posteriori error estimators $\{{\mathfrak {G}}_{\ell }^{(\cdot )}\}_{\ell =1}^{3}$.

Theorem 4.1

Assume (A0) – (A3) in Sect. 3.1. Fix ${\textbf{x}}\in \pmb {{\mathcal {D}}}$. Let $\{t_{j}\}_{j\ge 0}\subset [0,\infty )$ be a mesh with local step sizes $\{\tau ^{j+1}\}_{j\ge 0}$. Let $\{({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j},Y_{Z}^{j})\}_{j\ge 0}$ solve Scheme 2. Then we have

$$\begin{aligned} \Bigl \vert u({\textbf{x}}) - {\mathbb {E}}\bigl [\phi (\textbf{Y}_{{\textbf{X}}}^{J^{*}})Y_{V}^{J^{*}}+Y_{Z}^{J^{*}}\bigr ] \Bigr \vert \le \pmb {C}(\phi ,g)\cdot \sum \limits _{j=0}^{\infty } \tau ^{j+1} \big \{{{\mathfrak {G}}}_{1}^{(j)} + {{\mathfrak {G}}}_{2}^{(j)}+ {{\mathfrak {G}}}_{3}^{(j)} \big \}\,, \end{aligned}$$

(4.1)

where $\pmb {C}(\phi ,g)>0$ is the constant from Lemma 3.1, and the a posteriori error estimators $\{{\mathfrak {G}}_{\ell }^{(j)}\}_{\ell =1}^{3}$, are given by

$$\begin{aligned} {\mathfrak {G}}_{1}^{(j)}&:= \pmb {\texttt {E} _\texttt {1} }({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j})\cdot \tau ^{j+1} + \frac{1}{2}\cdot \pmb {\texttt {E} _\texttt {2} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j}) + \frac{1}{2} \cdot \pmb {\texttt {E} _\texttt {3} }({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j})\cdot \tau ^{j+1}\\&\quad + \sqrt{L}\cdot \pmb {\texttt {E} _\texttt {4} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j}) \cdot \bigl (\tau ^{j+1}\bigr )^{\frac{1}{2}} + \frac{1}{4} L\cdot \pmb {\texttt {E} _\texttt {5} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j})\\&\quad + \frac{1}{2} L\cdot \pmb {\texttt {E} _\texttt {6} }({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j})\cdot \tau ^{j+1} + \pmb {\texttt {E} _\texttt {7} }({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j+1},Y_{V}^{j}) \,, \\ {\mathfrak {G}}_{2}^{(j)}&:= \pmb {\texttt {E} _\texttt {8} }({\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j},Y_{V}^{j})\cdot \tau ^{j+1} + \frac{1}{2}\cdot \pmb {\texttt {E} _\texttt {9} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j},Y_{V}^{j})\\&\quad + \frac{1}{2} \cdot \pmb {\texttt {E} _\texttt {10} }({\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j},Y_{V}^{j})\cdot \tau ^{j+1} + \sqrt{L}\cdot \pmb {\texttt {E} _\texttt {11} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j},Y_{V}^{j}) \cdot \bigl (\tau ^{j+1}\bigr )^{\frac{1}{2}}\\&\quad + \frac{1}{4} L\cdot \pmb {\texttt {E} _\texttt {12} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j},Y_{V}^{j}) + \frac{1}{2} L\cdot \pmb {\texttt {E} _\texttt {13} }({\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j},Y_{V}^{j})\cdot \tau ^{j+1} \\&\quad +\pmb {\texttt {E} _\texttt {14} }({\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j},Y_{V}^{j+1},Y_{V}^{j}) \,,\\ {\mathfrak {G}}_{3}^{(j)}&:=2 \cdot \pmb {\texttt {E} _\texttt {15} }\bigl ({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j}\bigr )\,, \end{aligned}$$

with computable terms

• 1.
• 2.
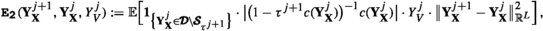
• 3.
• 4.
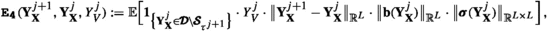
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
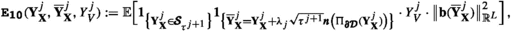
• 11.
• 12.
• 13.
• 14.
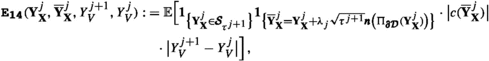
• 15.

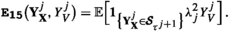
Remark 4.1

1. For ${\textbf{b}}({\textbf{x}})\equiv {\textbf{0}}$, $\pmb {\sigma }({\textbf{x}})\equiv \sqrt{2}\cdot {\mathbb {I}}$, where ${\mathbb {I}}$ denotes the $L-$dimensional identity matrix, which are data requirements in (1.1) for well-known elliptic PDE’s such as the Poisson equation or Helmholtz equation, the particular error estimators $\{{\mathfrak {G}}_{\ell }^{(\cdot )}\}_{\ell =1}^{3}$ simplify considerably. For Poisson’s equation, where additionally $c({\textbf{x}})\equiv 0$ is required in (1.1), only $\pmb {{\texttt {E}}_{\texttt {5}}}(\cdot ),\pmb {{\texttt {E}}_{\texttt {12}}}(\cdot )$ and $\pmb {{\texttt {E}}_{\texttt {15}}}(\cdot )$ constitute $\{{\mathfrak {G}}_{\ell }^{(\cdot )}\}_{\ell =1}^{3}$; cf.  Example 1.1.

2. The derivation of the a posteriori error estimate (4.1) crucially depends on the use of the weak Euler method (3.1) and the associated procedure in Scheme 2. Note that the right-hand side of (4.1) is ‘computable’, i.e., in practice, the terms $\{\pmb {{\texttt {E}}_{{\ell }}}\bigl (\cdot )\}_{\pmb {{{\ell }}}=1,\ldots ,15}$ may be approximated by Monte-Carlo method, which typically provides a basis for an efficient error approximation (see Sect. 6 for further details). In contrast, we present an a posteriori error analysis via the explicit Euler method (4.29) in Sect. 4.3, whose derivation is (also) close to [35, Thm. 3.1], and discuss upcoming difficulties, where, in particular, the computation of terms in a posteriori form involved there is not straightforward; cf. Remark 4.3.

3. The terms $\{\pmb {{\texttt {E}}_{{\ell }}}\bigl (\cdot )\}_{\pmb {{{\ell }}}=1,\ldots ,7}$ in ${\mathfrak {G}}_{1}^{(\cdot )}$ capture dynamics away from $\pmb {\partial {\mathcal {D}}}$ and may be related to the terms in the error estimator in [35, (3.1)]. The additional terms $\{\pmb {{\texttt {E}}_{{\ell }}}\bigl (\cdot )\}_{\pmb {{{\ell }}}=8,\ldots ,15}$ in ${\mathfrak {G}}_{2}^{(\cdot )}$ and ${\mathfrak {G}}_{3}^{(\cdot )}$ address stopping dynamics near the boundary, which, however, do not appear in the framework of [35, Thm. 3.1].

The proof of Theorem 4.1 consists of several steps: Lemma 4.2 represents the error on the left-hand side of (4.1) with the help of the (unknown) solution u of (1.1). Lemmata 4.3, 4.4 and 4.5 estimate the expressions ‘$\pmb {I_{j}}$’, ‘$\pmb {II_{j}}$’ and ‘$\pmb {III_{j}}$’ emerging from Lemma 4.2 and given in (4.2), (4.3) and (4.4), respectively. The derivation of the a posteriori error estimate (4.1) then follows by combining these lemmata.

Lemma 4.2

Assume (A0) – (A3). Fix ${\textbf{x}}\in \pmb {{\mathcal {D}}}$. Let $\{t_{j}\}_{j\ge 0}\subset [0,\infty )$ be a mesh with local step sizes $\{\tau ^{j+1}\}_{j\ge 0}$. Let $\{({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j},Y_{Z}^{j})\}_{j\ge 0}$ solve Scheme 2. Then we have

$$\begin{aligned} \Bigl \vert u({\textbf{x}}) - {\mathbb {E}}\bigl [\phi (\textbf{Y}_{{\textbf{X}}}^{J^{*}})Y_{V}^{J^{*}}+Y_{Z}^{J^{*}}\bigr ] \Bigr \vert \le \sum \limits _{j=0}^{\infty } \big \{\pmb {I_{j}} + \pmb {II_{j}} + \pmb {III_{j}} \big \}\,, \end{aligned}$$

where

$$\begin{aligned} \pmb {I_{j}}&:=\Big |{\mathbb {E}}\Bigl [ {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \big \{u({\textbf{Y}}_{{\textbf{X}}}^{j+1})Y_{V}^{j+1}-u({\textbf{Y}}_{{\textbf{X}}}^{j})Y_{V}^{j}+Y_{Z}^{j+1} -Y_{Z}^{j} \big \} \Big ] \Big |\,, \end{aligned}$$

(4.2)

$$\begin{aligned} \pmb {II_{j}}&:= \Big |{\mathbb {E}}\Bigl [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \nonumber \\&\quad \cdot \big \{u({\textbf{Y}}_{{\textbf{X}}}^{j+1})Y_{V}^{j+1}-u(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})Y_{V}^{j}+Y_{Z}^{j+1} -Y_{Z}^{j} \big \} \Big ] \Big |\,, \end{aligned}$$

(4.3)

$$\begin{aligned} \pmb {III_{j}}&:=\Big |{\mathbb {E}}\Bigl [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} \big \{ u(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})Y_{V}^{j}-u({\textbf{Y}}_{{\textbf{X}}}^{j})Y_{V}^{j}\big \} \Bigr ] \Big |\,. \end{aligned}$$

(4.4)

Proof

Considering PDE (1.1) and observing that $Y_{V}^{0}=1$, $Y_{Z}^{0}=0$, a first calculation leads to

$$\begin{aligned}&\Bigl \vert u({\textbf{x}}) - {\mathbb {E}}\bigl [\phi (\textbf{Y}_{{\textbf{X}}}^{J^{*}})Y_{V}^{J^{*}}+Y_{Z}^{J^{*}}\bigr ] \Bigr \vert = \Bigl |u({\textbf{x}})Y_{V}^{0}+Y_{Z}^{0}- {\mathbb {E}}\bigl [ u(\textbf{Y}_{{\textbf{X}}}^{J^{*}})Y_{V}^{J^{*}}+Y_{Z}^{J^{*}}\bigr ] \Bigr \vert \nonumber \\&\quad = \Bigg |{\mathbb {E}}\biggl [ \sum \limits _{j=0}^{J^{*}-1} u({\textbf{Y}}_{{\textbf{X}}}^{j+1})Y_{V}^{j+1}+Y_{Z}^{j+1}-u({\textbf{Y}}_{{\textbf{X}}}^{j})Y_{V}^{j}-Y_{Z}^{j}\biggr ] \Bigg |\nonumber \\&\quad = \bigg |\sum \limits _{j=0}^{\infty } {\mathbb {E}}\bigl [ \underbrace{u(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})Y_{V}^{j}+Y_{Z}^{j}-u({\textbf{Y}}_{{\textbf{X}}}^{j})Y_{V}^{j}-Y_{Z}^{j}}_{=:\pmb {d}_{j}}\nonumber \\&\quad + \underbrace{u({\textbf{Y}}_{{\textbf{X}}}^{j+1})Y_{V}^{j+1}+Y_{Z}^{j+1} - u(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})Y_{V}^{j}-Y_{Z}^{j}}_{=:\pmb {d}_{j}^{\prime }} \bigr ] \bigg |\,. \end{aligned}$$

(4.5)

Since $\pmb {d}_{j}\equiv 0$ on the event $\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\notin \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}$, $\pmb {d}_{j}^{\prime }\equiv 0$ on the event $\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}\cap \big \{ \overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}=\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \big \}$, $\pmb {d}_{j}^{\prime }\equiv 0$ on the event $\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\notin \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}\cap \big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\notin \pmb {{\mathcal {D}}} \big \}$ and $\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}\cap \big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\notin \pmb {{\mathcal {D}}} \big \}=\emptyset$, the assertion follows from (4.5). $\square$

Lemma 4.3

Assume (A0) – (A3). Fix ${\textbf{x}}\in \pmb {{\mathcal {D}}}$. Let $\{t_{j}\}_{j\ge 0}\subset [0,\infty )$ be a mesh with local step sizes $\{\tau ^{j+1}\}_{j\ge 0}$. Let $\{({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j},Y_{Z}^{j})\}_{j\ge 0}$ solve Scheme 2. Then, for every $j\ge 0$, we have

$$\begin{aligned} \pmb {I_{j}}&\le \pmb {C}(\phi ,g)\cdot {\mathfrak {G}}_{1}^{(j)} \cdot \tau ^{j+1}\,, \end{aligned}$$

where $\pmb {I_{j}}$ is given in (4.2), and $\pmb {C}(\phi ,g)>0$ is from Lemma 3.1.

Proof

In the following, we write $A_{j}:=\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}{\setminus }\pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}$ to simplify the notation. In a first step, we rewrite $\pmb {I_{j}}$ by making use of (3.2) and (3.3) in Scheme 1.

$$\begin{aligned} \pmb {I_{j}}&=\Big |{\mathbb {E}}\Big [ {\textbf{1}}_{A_{j}}\cdot \Big \{ u({\textbf{Y}}_{{\textbf{X}}}^{j+1})Y_{V}^{j+1}-u({\textbf{Y}}_{{\textbf{X}}}^{j+1})Y_{V}^{j}\nonumber \\&\quad + u({\textbf{Y}}_{{\textbf{X}}}^{j+1})Y_{V}^{j}-u({\textbf{Y}}_{{\textbf{X}}}^{j})Y_{V}^{j} + g({\textbf{Y}}_{{\textbf{X}}}^{j})Y_{V}^{j}\cdot \tau ^{j+1}\Big \}\Big ] \Big |\nonumber \\&= \Big |{\mathbb {E}}\Big [ {\textbf{1}}_{A_{j}}\cdot \Big \{ u({\textbf{Y}}_{{\textbf{X}}}^{j+1})\bigl (1-\tau ^{j+1}c({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )^{-1}c({\textbf{Y}}_{{\textbf{X}}}^{j})Y_{V}^{j}\cdot \tau ^{j+1} \nonumber \\&\quad + \bigl [ u({\textbf{Y}}_{{\textbf{X}}}^{j+1}) - u({\textbf{Y}}_{{\textbf{X}}}^{j})\bigr ]Y_{V}^{j} + g({\textbf{Y}}_{{\textbf{X}}}^{j})Y_{V}^{j}\cdot \tau ^{j+1}\Big \}\Big ] \Big |\,. \end{aligned}$$

(4.6)

Step 1: (Employing PDE (1.1)) We use Taylor’s formula to deduce from (4.6)

$$\begin{aligned} \pmb {I_{j}}&=\Big |{\mathbb {E}}\Big [ {\textbf{1}}_{A_{j}}\cdot Y_{V}^{j}\cdot \Big \{ \bigl [u({\textbf{Y}}_{{\textbf{X}}}^{j+1})-u({\textbf{Y}}_{{\textbf{X}}}^{j})\bigr ]\bigl (1-\tau ^{j+1}c({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )^{-1}c({\textbf{Y}}_{{\textbf{X}}}^{j})\cdot \tau ^{j+1} \nonumber \\&\quad + u({\textbf{Y}}_{{\textbf{X}}}^{j})\bigl (1-\tau ^{j+1}c({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )^{-1}c({\textbf{Y}}_{{\textbf{X}}}^{j})\cdot \tau ^{j+1} + g({\textbf{Y}}_{{\textbf{X}}}^{j})\cdot \tau ^{j+1} \nonumber \\&\quad + \big \langle D_{{\textbf{x}}}u({\textbf{Y}}_{{\textbf{X}}}^{j}),{\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j}\big \rangle _{{\mathbb {R}}^{L}}\nonumber \\&\quad +\frac{1}{2}\textrm{Tr}\Bigl (D_{{\textbf{x}}}^{2}u(\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j})({\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j})({\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j})^{\top } \Bigr ) \Big \}\Big ] \Big |\,, \end{aligned}$$

(4.7)

for some $\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j}$ between ${\textbf{Y}}_{{\textbf{X}}}^{j+1}$ and ${\textbf{Y}}_{{\textbf{X}}}^{j}$, i.e., $\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+\theta \bigl ({\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j} \bigr )$ with $\theta \in (0,1)$. Now, we use the identity in (1.1) to restate $g({\textbf{Y}}_{{\textbf{X}}}^{j})\cdot \tau ^{j+1}$ in (4.7)

$$\begin{aligned} \pmb {I_{j}}&=\Big |{\mathbb {E}}\Big [ {\textbf{1}}_{A_{j}}\cdot Y_{V}^{j}\cdot \Big \{ \bigl [u({\textbf{Y}}_{{\textbf{X}}}^{j+1})-u({\textbf{Y}}_{{\textbf{X}}}^{j})\bigr ]\bigl (1-\tau ^{j+1}c({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )^{-1}c({\textbf{Y}}_{{\textbf{X}}}^{j})\cdot \tau ^{j+1} \nonumber \\&\quad + u({\textbf{Y}}_{{\textbf{X}}}^{j})\bigl (1-\tau ^{j+1}c({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )^{-1}c({\textbf{Y}}_{{\textbf{X}}}^{j})\cdot \tau ^{j+1}-u({\textbf{Y}}_{{\textbf{X}}}^{j})c({\textbf{Y}}_{{\textbf{X}}}^{j})\cdot \tau ^{j+1} \nonumber \\&\quad - \langle {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j}), D_{{\textbf{x}}}u({\textbf{Y}}_{{\textbf{X}}}^{j})\rangle _{{\mathbb {R}}^{L}}\cdot \tau ^{j+1} - \frac{1}{2}\textrm{Tr}\Bigl (\pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\sigma }^{\top }({\textbf{Y}}_{{\textbf{X}}}^{j}) D_{{\textbf{x}}}^{2}u({\textbf{Y}}_{{\textbf{X}}}^{j})\Bigr )\cdot \tau ^{j+1} \nonumber \\&\quad + \big \langle D_{{\textbf{x}}}u({\textbf{Y}}_{{\textbf{X}}}^{j}),{\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j}\big \rangle _{{\mathbb {R}}^{L}}\nonumber \\&\quad +\frac{1}{2}\textrm{Tr}\Bigl (D_{{\textbf{x}}}^{2}u(\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j})({\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j})({\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j})^{\top } \Bigr ) \Big \}\Big ] \Big |\,. \end{aligned}$$

(4.8)

Next, we use (3.1) to represent ${\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j}$ in (4.8), and standard calculations,

$$\begin{aligned} \pmb {I_{j}}&\le \pmb {K_{1}}+\pmb {K_{2}}+\pmb {K_{3}}+\pmb {K_{4}}+\pmb {K_{5}}\,, \end{aligned}$$

(4.9)

where

$$\begin{aligned} \pmb {K_{1}}&:=\Big |{\mathbb {E}}\Big [ {\textbf{1}}_{A_{j}}\cdot \bigl (1-\tau ^{j+1}c({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )^{-1}c({\textbf{Y}}_{{\textbf{X}}}^{j})Y_{V}^{j}\cdot \big \{ u({\textbf{Y}}_{{\textbf{X}}}^{j+1})-u({\textbf{Y}}_{{\textbf{X}}}^{j}) \big \} \Big ] \Big |\cdot \tau ^{j+1}, \\ \pmb {K_{2}}&:=\frac{1}{2}\Big |{\mathbb {E}}\Big [ {\textbf{1}}_{A_{j}} \cdot Y_{V}^{j}\cdot \textrm{Tr}\Bigl (D_{{\textbf{x}}}^{2}u(\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j}) {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j}) {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})^{\top } \Bigr )\Big ] \Big |\cdot \bigl (\tau ^{j+1}\bigr )^{2}, \\ \pmb {K_{3}}:&=\frac{1}{2}\Big |{\mathbb {E}}\Big [ {\textbf{1}}_{A_{j}} \cdot Y_{V}^{j}\cdot \textrm{Tr}\Bigl (D_{{\textbf{x}}}^{2}u(\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j}) \Big \{ {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\bigl ( \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j}) \pmb {\xi }_{j+1} \bigr )^{\top } \\&\quad + \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\xi }_{j+1} {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})^{\top }\Big \}\Bigr )\Big ] \Big |\cdot \bigl (\tau ^{j+1}\bigr )^{\frac{3}{2}}, \\ \pmb {K_{4}}:&=\frac{1}{2}\Big |{\mathbb {E}}\Big [ {\textbf{1}}_{A_{j}} \cdot Y_{V}^{j}\cdot \Big \{ \textrm{Tr}\Bigl (D_{{\textbf{x}}}^{2}u(\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j})\pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j}) \pmb {\xi }_{j+1} \bigl (\pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j}) \pmb {\xi }_{j+1} \bigr )^{\top } \Bigr )\\&\quad -\textrm{Tr}\Bigl (D_{{\textbf{x}}}^{2}u({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\sigma }^{\top }({\textbf{Y}}_{{\textbf{X}}}^{j}) \Bigr )\Big \}\Big ] \Big |\cdot \tau ^{j+1}\,, \\ \pmb {K_{5}}&:=\Big |{\mathbb {E}}\Big [ {\textbf{1}}_{A_{j}}\cdot u({\textbf{Y}}_{{\textbf{X}}}^{j}) c({\textbf{Y}}_{{\textbf{X}}}^{j})\cdot \big \{ Y_{V}^{j+1}-Y_{V}^{j} \big \} \Big ] \Big |\cdot \tau ^{j+1}\,. \end{aligned}$$

Step 2: (Estimation of $\pmb {K_{1}},\pmb {K_{2}},\pmb {K_{3}},\pmb {K_{4}},\pmb {K_{5}}$) We estimate the terms in (4.9) independently.

(a) (Estimation of $\pmb {K_{1}}$) We use Taylor’s formula to get

$$\begin{aligned} \pmb {K_{1}}&=\Big |{\mathbb {E}}\Big [ {\textbf{1}}_{A_{j}}\cdot \bigl (1-\tau ^{j+1}c({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )^{-1}c({\textbf{Y}}_{{\textbf{X}}}^{j})Y_{V}^{j}\cdot \Big \{ \big \langle D_{{\textbf{x}}}u({\textbf{Y}}_{{\textbf{X}}}^{j}),{\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j}\big \rangle _{{\mathbb {R}}^{L}} \\&\quad +\frac{1}{2}\textrm{Tr}\Bigl (D_{{\textbf{x}}}^{2}u(\hat{\hat{{\textbf{Y}}}}_{{\textbf{X}}}^{j})({\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j})({\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j})^{\top } \Bigr ) \Big \} \Big ] \Big |\cdot \tau ^{j+1}\,, \end{aligned}$$

for some $\hat{\hat{{\textbf{Y}}}}_{{\textbf{X}}}^{j}$ between ${\textbf{Y}}_{{\textbf{X}}}^{j+1}$ and ${\textbf{Y}}_{{\textbf{X}}}^{j}$. Using again (3.1) for ${\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j}$, independency, the fact that $Y_{V}^{j}>0$ (this follows from the generation of $Y_{V}^{j}$ via the implicit Euler method (3.2)), Lemma 3.1 and standard arguments lead to

$$\begin{aligned} \pmb {K_{1}}\le \pmb {C}(\phi ,g)\cdot \pmb {{\texttt {E}}_{\texttt {1}}}({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j})\cdot \bigl (\tau ^{j+1}\bigr )^{2} + \frac{1}{2}\pmb {C}(\phi ,g)\cdot \pmb {{\texttt {E}}_{\texttt {2}}}({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j})\cdot \tau ^{j+1}\,. \end{aligned}$$

(4.10)

(b) (Estimation of $\pmb {K_{2}}$) Lemma 3.1 and standard arguments immediately lead to

$$\begin{aligned} \pmb {K_{2}}\le \frac{1}{2} \pmb {C}(\phi ,g)\cdot \pmb {{\texttt {E}}_{\texttt {3}}}({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j})\cdot \bigl (\tau ^{j+1}\bigr )^{2}. \end{aligned}$$

(4.11)

(c) (Estimation of $\pmb {K_{3}}$) We add and substract $D^{2}_{{\textbf{x}}}u({\textbf{Y}}_{{\textbf{X}}}^{j})$, use independency and Lemma 3.1 to obtain

$$\begin{aligned} \pmb {K_{3}}&=\frac{1}{2}\Big |{\mathbb {E}}\Big [ {\textbf{1}}_{A_{j}} \cdot Y_{V}^{j}\cdot \textrm{Tr}\Bigl ( \Big \{D_{{\textbf{x}}}^{2}u(\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j})-D^{2}_{{\textbf{x}}}u({\textbf{Y}}_{{\textbf{X}}}^{j}) \Big \}\nonumber \\&\quad \; \Big \{ {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\bigl ( \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\xi }_{j+1} \bigr )^{\top } +\pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j}) \pmb {\xi }_{j+1} {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})^{\top }\Big \}\Bigr )\Big ] \Big |\cdot \bigl (\tau ^{j+1}\bigr )^{\frac{3}{2}} \nonumber \\&\le {\mathbb {E}}\Big [ {\textbf{1}}_{A_{j}} \cdot Y_{V}^{j} \cdot \Vert D_{{\textbf{x}}}^{2}u(\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j})-D^{2}_{{\textbf{x}}}u({\textbf{Y}}_{{\textbf{X}}}^{j}) \Vert _{{\mathbb {R}}^{L\times L}} \Vert {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \Vert _{{\mathbb {R}}^{L}} \cdot \Vert \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\xi }_{j+1} \Vert _{{\mathbb {R}}^{L}} \Big ] \nonumber \\&\quad \cdot \bigl (\tau ^{j+1}\bigr )^{\frac{3}{2}} \nonumber \\&\le \pmb {C}(\phi ,g)\cdot {\mathbb {E}}\Big [ {\textbf{1}}_{A_{j}} \cdot Y_{V}^{j} \cdot \Vert \hat{{\textbf{Y}}}_{{\textbf{X}}}^{j} - {\textbf{Y}}_{{\textbf{X}}}^{j} \Vert _{{\mathbb {R}}^{L}} \Vert {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \Vert _{{\mathbb {R}}^{L}}\cdot \Vert \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\xi }_{j+1} \Vert _{{\mathbb {R}}^{L}} \Big ] \cdot \bigl (\tau ^{j+1}\bigr )^{\frac{3}{2}} \,, \end{aligned}$$

(4.12)

where we estimate $\Vert D_{{\textbf{x}}}^{2}u(\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j})-D^{2}_{{\textbf{x}}}u({\textbf{Y}}_{{\textbf{X}}}^{j}) \Vert _{{\mathbb {R}}^{L\times L}}\le \pmb {C}(\phi ,g)\cdot \Vert \hat{{\textbf{Y}}}_{{\textbf{X}}}^{j} - {\textbf{Y}}_{{\textbf{X}}}^{j} \Vert _{{\mathbb {R}}^{L}}$. In order to estimate the term $\Vert \hat{{\textbf{Y}}}_{{\textbf{X}}}^{j} - {\textbf{Y}}_{{\textbf{X}}}^{j} \Vert _{{\mathbb {R}}^{L}}$ in (4.12), we recall that $\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j}$ is a point between ${\textbf{Y}}_{{\textbf{X}}}^{j}$ and ${\textbf{Y}}_{{\textbf{X}}}^{j}$, i.e., $\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j}-{\textbf{Y}}_{{\textbf{X}}}^{j}=\theta \bigl ( {\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j}\bigr )$ with $\theta \in (0,1)$; thus we have

$$\begin{aligned} \Vert \hat{{\textbf{Y}}}_{{\textbf{X}}}^{j} - {\textbf{Y}}_{{\textbf{X}}}^{j} \Vert _{{\mathbb {R}}^{L}}\le \Vert {\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j}\Vert _{{\mathbb {R}}^{L}}. \end{aligned}$$

(4.13)

Plugging (4.13) into (4.12) and using $\Vert \pmb {\xi }_{j+1}\Vert _{{\mathbb {R}}^{L}}=\sqrt{L}$ then leads to

$$\begin{aligned} \pmb {K_{3}}&\le \pmb {C}(\phi ,g)\sqrt{L}\cdot \pmb {{\texttt {E}}_{\texttt {4}}}({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j}) \cdot \bigl (\tau ^{j+1}\bigr )^{\frac{3}{2}} \,. \end{aligned}$$

(4.14)

d) (Estimation of $\pmb {K_{4}}$) We start with a straightforward rewriting of $\pmb {K_{4}}$.

$$\begin{aligned} \pmb {K_{4}}&=\frac{1}{2}\Big |{\mathbb {E}}\Big [ {\textbf{1}}_{A_{j}} \cdot Y_{V}^{j} \cdot \Big \{ \big \langle \big \{D_{{\textbf{x}}}^{2}u(\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j}) - D_{{\textbf{x}}}^{2}u({\textbf{Y}}_{{\textbf{X}}}^{j}) \big \} \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j}) \pmb {\xi }_{j+1}, \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j}) \pmb {\xi }_{j+1} \big \rangle _{{\mathbb {R}}^{L}} \\&\quad + \big \langle D_{{\textbf{x}}}^{2}u({\textbf{Y}}_{{\textbf{X}}}^{j}) \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j}) \pmb {\xi }_{j+1}, \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\xi }_{j+1} \big \rangle _{{\mathbb {R}}^{L}} \\&\quad -\textrm{Tr}\Bigl (D_{{\textbf{x}}}^{2}u({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\sigma }^{\top }({\textbf{Y}}_{{\textbf{X}}}^{j})\Bigr )\Big \}\Big ] \Big |\cdot \tau ^{j+1}\,. \end{aligned}$$

By the independence of $\xi _{j+1}^{(i)}$ and $\xi _{j+1}^{(k)}$ (note that $\pmb {\xi }_{j+1}=(\xi _{j+1}^{(1)},\ldots ,\xi _{j+1}^{(L)})^{\top }$), and Lemma 3.1, we deduce

$$\begin{aligned} \pmb {K_{4}}&\le \pmb {K_{4,1}} \,, \end{aligned}$$

(4.15)

where

$$\begin{aligned} \pmb {K_{4,1}}&:=\frac{1}{2}\Big |{\mathbb {E}}\Big [ {\textbf{1}}_{A_{j}}\cdot Y_{V}^{j} \cdot \Big \{ \big \langle \big \{D_{{\textbf{x}}}^{2}u(\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j}) - D_{{\textbf{x}}}^{2}u({\textbf{Y}}_{{\textbf{X}}}^{j}) \big \} \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j}) \pmb {\xi }_{j+1}, \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j}) \pmb {\xi }_{j+1} \big \rangle _{{\mathbb {R}}^{L}} \Big ] \Big |\cdot \tau ^{j+1}\\&= \frac{1}{2}\Big |{\mathbb {E}}\Big [ {\textbf{1}}_{A_{j}}\cdot Y_{V}^{j}\cdot \big \langle D_{{\textbf{x}}}^{3}u({\textbf{Y}}_{{\textbf{X}}}^{j}) \big \{ \hat{{\textbf{Y}}}_{{\textbf{X}}}^{j} -{\textbf{Y}}_{{\textbf{X}}}^{j} \big \}\pmb {Z}_{j},\pmb {Z}_{j} \big \rangle _{{\mathbb {R}}^{L}} \Big ] \Big |\cdot \tau ^{j+1} \\&\quad + \frac{1}{4}\Big |{\mathbb {E}}\Big [ {\textbf{1}}_{A_{j}} \cdot Y_{V}^{j}\cdot \big \langle D_{{\textbf{x}}}^{4}u(\hat{\hat{{\textbf{Y}}}}_{{\textbf{X}}}^{j}) \big \{ \hat{{\textbf{Y}}}_{{\textbf{X}}}^{j} -{\textbf{Y}}_{{\textbf{X}}}^{j} \big \}\big \{ \hat{{\textbf{Y}}}_{{\textbf{X}}}^{j} -{\textbf{Y}}_{{\textbf{X}}}^{j} \big \}\pmb {Z}_{j},\pmb {Z}_{j} \big \rangle _{{\mathbb {R}}^{L}} \Big ] \Big |\cdot \tau ^{j+1}\,, \end{aligned}$$

by Taylor’s formula, where $\pmb {Z}_{j}:= \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j}) \pmb {\xi }_{j+1}$, and, for some $\hat{\hat{{\textbf{Y}}}}_{{\textbf{X}}}^{j}$ between ${\textbf{Y}}_{{\textbf{X}}}^{j}$ and $\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j}$. Next, by Lemma 3.1, (4.13), since $\Vert \pmb {\xi }_{j+1}\Vert _{{\mathbb {R}}^{L}}^{2}=L$, we estimate

$$\begin{aligned} \pmb {K_{4,1}}&\le \pmb {K_{4,1,1}} + \frac{1}{4}\pmb {C}(\phi ,g) L\cdot \pmb {{\texttt {E}}_{\texttt {5}}}({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j}) \cdot \tau ^{j+1}\,, \end{aligned}$$

(4.16)

where

$$\begin{aligned} \pmb {K_{4,1,1}}:=\frac{1}{2}\Big |{\mathbb {E}}\Big [ {\textbf{1}}_{A_{j}}\cdot Y_{V}^{j}\cdot \big \langle D_{{\textbf{x}}}^{3}u({\textbf{Y}}_{{\textbf{X}}}^{j}) \big \{ \hat{{\textbf{Y}}}_{{\textbf{X}}}^{j} -{\textbf{Y}}_{{\textbf{X}}}^{j} \big \} \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\xi }_{j+1}, \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j}) \pmb {\xi }_{j+1} \big \rangle _{{\mathbb {R}}^{L}} \Big ] \Big |\cdot \tau ^{j+1}. \end{aligned}$$

In order to estimate $\pmb {K_{4,1,1}}$, we again use the representation $\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j}-{\textbf{Y}}_{{\textbf{X}}}^{j}=\theta \bigl ( {\textbf{Y}}_{{\textbf{X}}}^{j+1}-{\textbf{Y}}_{{\textbf{X}}}^{j}\bigr )$ with $\theta \in (0,1)$, and (3.1) to represent ${\textbf{Y}}_{{\textbf{X}}}^{j+1} -{\textbf{Y}}_{{\textbf{X}}}^{j}$,

$$\begin{aligned} \pmb {K_{4,1,1}}\le \frac{1}{2} \pmb {C}(\phi ,g) L \cdot \pmb {{\texttt {E}}_{\texttt {6}}}({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j}) \cdot \bigl (\tau ^{j+1}\bigr )^{2}. \end{aligned}$$

(4.17)

We combine (4.17) with (4.16) and plug the resulting expression into (4.15) to obtain

$$\begin{aligned} \pmb {K_{4}}&\le \frac{1}{4}\pmb {C}(\phi ,g) L\cdot \pmb {{\texttt {E}}_{\texttt {5}}}({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j}) \cdot \tau ^{j+1} + \frac{1}{2} \pmb {C}(\phi ,g) L \cdot \pmb {{\texttt {E}}_{\texttt {6}}}({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j}) \cdot \bigl (\tau ^{j+1}\bigr )^{2} \,. \end{aligned}$$

(4.18)

e) (Estimation of $\pmb {K_{5}}$) Lemma 3.1 and standard arguments immediately lead to

$$\begin{aligned} \pmb {K_{5}}\le \pmb {C}(\phi ,g)\cdot \pmb {{\texttt {E}}_{\texttt {7}}}({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j+1},Y_{V}^{j})\cdot \tau ^{j+1}. \end{aligned}$$

(4.19)

Step 3: Finally, combining (4.10), (4.11), (4.14), (4.18) and (4.19) with (4.9) proves the assertion. $\square$

The following lemma estimates $\pmb {II_{j}}$ from (4.3). Its proof is very similar to the proof of Lemma 4.3 and will thus be omitted; see also [34] for more details.

Lemma 4.4

Assume (A0) – (A3). Fix ${\textbf{x}}\in \pmb {{\mathcal {D}}}$. Let $\{t_{j}\}_{j\ge 0}\subset [0,\infty )$ be a mesh with local step sizes $\{\tau ^{j+1}\}_{j\ge 0}$. Let $\{({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j},Y_{Z}^{j})\}_{j\ge 0}$ solve Scheme 2. Then, for every $j\ge 0$, we have

$$\begin{aligned} \pmb {II_{j}}&\le \pmb {C}(\phi ,g) \cdot {\mathfrak {G}}_{2}^{(j)} \cdot \tau ^{j+1}\,, \end{aligned}$$

where $\pmb {II_{j}}$ is given in (4.3), and $\pmb {C}(\phi ,g)>0$ is from Lemma 3.1.

The next lemma estimates $\pmb {III_{j}}$ from (4.4).

Lemma 4.5

Assume (A0) – (A3). Fix ${\textbf{x}}\in \pmb {{\mathcal {D}}}$. Let $\{t_{j}\}_{j\ge 0}\subset [0,\infty )$ be a mesh with local step sizes $\{\tau ^{j+1}\}_{j\ge 0}$. Let $\{({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j},Y_{Z}^{j})\}_{j\ge 0}$ solve Scheme 2. Then, for every $j\ge 0$, we have

$$\begin{aligned} \pmb {III_{j}}\le \pmb {C}(\phi ,g) \cdot {\mathfrak {G}}_{3}^{(j)}\cdot \tau ^{j+1}\,, \end{aligned}$$

where $\pmb {III_{j}}$ is given in (4.4), and $\pmb {C}(\phi ,g)>0$ is from Lemma 3.1.

Proof

We take the conditional expectation w.r.t. ${\textbf{Y}}_{{\textbf{X}}}^{j}$ and use measureability arguments to obtain in a first calculation

$$\begin{aligned} \pmb {III_{j}}&=\Bigg |{\mathbb {E}}\bigg [{\mathbb {E}}\Bigl [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}}Y_{V}^{j}\Big \{ u({\textbf{Y}}_{{\textbf{X}}}^{j})- {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}=\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \big \}} u\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j})\bigr )\\&\quad -{\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}}\pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}}u\bigl ( {\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}}\pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )\bigr ) \Big \}\,\Big |\,{\textbf{Y}}_{{\textbf{X}}}^{j}\Bigr ] \bigg ] \Bigg |\\&=\bigg |{\mathbb {E}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}}Y_{V}^{j}\Big \{ u({\textbf{Y}}_{{\textbf{X}}}^{j}) - p_{j}\cdot u\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j})\bigr ) \\&\quad - (1-p_{j})\cdot u\bigl ( {\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}}\pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )\bigr )\big \} \Big ] \bigg |\,, \end{aligned}$$

where $p_{j}$ is given in (3.5). We apply the mean value theorem twice to get

$$\begin{aligned} \pmb {III_{j}}&=\Bigg |{\mathbb {E}}\Bigg [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}}Y_{V}^{j}\bigg \{ u({\textbf{Y}}_{{\textbf{X}}}^{j})-u\bigl ( {\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}}\pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )\bigr ) \nonumber \\&\quad + \frac{u\bigl ( {\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}}\pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )-u\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j})\bigr )\bigr )}{\big \Vert {\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )-\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j})\big \Vert _{{\mathbb {R}}^{L}}} \cdot \lambda _{j}\sqrt{\tau ^{j+1}} \bigg \} \Bigg ] \Bigg |\nonumber \\&\le {\mathbb {E}}\Bigg [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \big |Y_{V}^{j} \big |\Bigg |-\Big \langle D_{{\textbf{x}}}u(\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j}),\pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )\Big \rangle _{{\mathbb {R}}^{L}} \cdot \lambda _{j}\sqrt{\tau ^{j+1}} \nonumber \\&\quad + \frac{\Big \langle D_{{\textbf{x}}}u(\hat{\hat{{\textbf{Y}}}}_{{\textbf{X}}}^{j}), {\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )-\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) }{\big \Vert {\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )-\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j})\big \Vert _{{\mathbb {R}}^{L}}} \cdot \lambda _{j}\sqrt{\tau ^{j+1}}\Bigg |\,\Bigg ]\,, \end{aligned}$$

(4.20)

for some points $\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j}$, $\hat{\hat{{\textbf{Y}}}}_{{\textbf{X}}}^{j}$ between ${\textbf{Y}}_{{\textbf{X}}}^{j}$ and ${\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}}\pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )$, and between $\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j})$ and ${\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}}\pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )$, respectively.

Next, we define $\varphi \bigl ({\textbf{z}},\pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )\bigr ):=\big \langle D_{{\textbf{x}}}u({\textbf{z}}),\pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )\big \rangle _{{\mathbb {R}}^{L}}$, ${\textbf{z}}\in \pmb {{\mathcal {D}}}$. Since

$$\begin{aligned} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )=\frac{{\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )-\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j})}{\big \Vert {\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )-\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j})\big \Vert _{{\mathbb {R}}^{L}}}, \end{aligned}$$

we can rewrite (4.20) as follows,

$$\begin{aligned} \pmb {III_{j}}&\le {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \lambda _{j}\big |Y_{V}^{j} \big |\Big |\varphi \bigl (\hat{\hat{{\textbf{Y}}}}_{{\textbf{X}}}^{j},\pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \bigr ) - \varphi \bigl (\hat{{\textbf{Y}}}_{{\textbf{X}}}^{j},\pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \bigr )\Big |\, \Big ] \cdot \sqrt{\tau ^{j+1}} \nonumber \\&\le \sup \limits _{{\textbf{z}}\in \pmb {{\mathcal {D}}}} \sup \limits _{\Vert {\textbf{v}}\Vert _{{\mathbb {R}}^{L}}=1} \Vert D_{{\textbf{z}}}\varphi ({\textbf{z}},{\textbf{v}})\Vert _{{\mathbb {R}}^{L}}\cdot {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \lambda _{j}\big |Y_{V}^{j} \big |\Vert \hat{{\textbf{Y}}}_{{\textbf{X}}}^{j} - \hat{\hat{{\textbf{Y}}}}_{{\textbf{X}}}^{j} \Vert _{{\mathbb {R}}^{L}} \Big ] \cdot \sqrt{\tau ^{j+1}}\,. \end{aligned}$$

(4.21)

Since $\Vert \hat{{\textbf{Y}}}_{{\textbf{X}}}^{j} - \hat{\hat{{\textbf{Y}}}}_{{\textbf{X}}}^{j} \Vert _{{\mathbb {R}}^{L}}\le 2\lambda _{j} \sqrt{\tau ^{j+1}}$ ${\mathbb {P}}-$a.s., and $Y_{V}^{j}> 0$, $j\ge 0$, and for all ${\textbf{v}}\in {\mathbb {R}}^{L}$ with $\Vert {\textbf{v}} \Vert _{{\mathbb {R}}^{L}}=1$

$$\begin{aligned} \Vert D_{{\textbf{z}}}\varphi ({\textbf{z}},{\textbf{v}})\Vert _{{\mathbb {R}}^{L}}= \sqrt{\sum \limits _{i=1}^{L} \big |\langle D_{{\textbf{z}}} \partial _{z_{i}} u({\textbf{z}}),{\textbf{v}}\rangle _{{\mathbb {R}}^{L}}\big |^{2}}\le \pmb {C}(\phi ,g), \end{aligned}$$

the assertion then follows from (4.21). $\square$

Next, we show convergence with optimal (weak) order 1 of the a posteriori error estimate (4.1) on a mesh with maximum mesh size $\tau ^{max}>0$. Theorems 4.1 and 4.6 then imply the a priori estimate [40, p. 369, Thm. 3.4], in particular.

Theorem 4.6

Assume (A0) – (A3). Fix ${\textbf{x}}\in \pmb {{\mathcal {D}}}$. Let $\{({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j},Y_{Z}^{j})\}_{j\ge 0}$ solve Scheme 2 on a mesh $\{t_{j}\}_{j\ge 0}\subset [0,\infty )$ with local mesh sizes $\{\tau ^{j+1}\}_{j\ge 0}$ and maximum mesh size $\tau ^{max}=\max _{j}\tau ^{j+1}>0$.

(i):

If $\tau ^{max}$ is sufficiently small, there exists $\pmb {C}>0$, independent of $\tau ^{max}$, such that

$$\begin{aligned} \pmb {C}(\phi ,g)\cdot \sum \limits _{j=0}^{\infty } \tau ^{j+1} \big \{{{\mathfrak {G}}}_{1}^{(j)} + {{\mathfrak {G}}}_{2}^{(j)}+ {{\mathfrak {G}}}_{3}^{(j)} \big \} \le \pmb {C}\cdot \tau ^{max} . \end{aligned}$$

(ii):

If (A1$^{*}$) or (A1$^{**}$) holds in addition, there exists $\pmb {C}>0$, independent of $\tau ^{max}$, such that

$$\begin{aligned} \pmb {C}(\phi ,g)\cdot \sum \limits _{j=0}^{\infty } \tau ^{j+1} \big \{{{\mathfrak {G}}}_{1}^{(j)} + {{\mathfrak {G}}}_{2}^{(j)}+ {{\mathfrak {G}}}_{3}^{(j)} \big \} \le \pmb {C}\cdot \tau ^{max} . \end{aligned}$$

Proof

In the following, $\pmb {C}>0$ is a constant, which might differ from line to line, but is always independent of $\tau ^{max}$.

Step 1: We independently bound $\{\pmb {{\texttt {E}}_{\texttt {k}}}(\cdot )\}_{k=1,\ldots ,14}$ appearing in the error estimators $\{{\mathfrak {G}}_{\ell }^{(j)}\}_{j\ge 0}$, $\ell =1,2$, in (4.1).

a) Bounds for $\{\pmb {{\texttt {E}}_{\texttt {k}}}(\cdot )\}_{k=1,\ldots ,7}$ in ${\mathfrak {G}}_{1}^{(j)}$: Due to (A0) – (A3), we have

$$\begin{aligned} \max \limits _{{\textbf{y}}\in \overline{\pmb {{\mathcal {D}}}}}\Vert {\textbf{b}}({\textbf{y}})\Vert _{{\mathbb {R}}^{L}}\le \pmb {C}\,,\quad \max \limits _{{\textbf{y}}\in \overline{\pmb {{\mathcal {D}}}}}\Vert \pmb {\sigma }({\textbf{y}})\Vert _{{\mathbb {R}}^{L\times L}}\le \pmb {C},\quad \max \limits _{{\textbf{y}}\in \overline{\pmb {{\mathcal {D}}}}}|c({\textbf{y}})|\le \pmb {C}\,, \end{aligned}$$

for some constant $\pmb {C}>0$. Moreover, since $c\le 0$, we have $0<Y_{V}^{j}\le 1$ for every $j\ge 0$. Let $j\ge 0$. We immediately obtain

$$\begin{aligned} \pmb {{\texttt {E}}_{\texttt {k}}}({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j})\le \pmb {C}\cdot {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}}\Big ] \qquad \pmb {{\texttt {k}}}=1,3,6\,. \end{aligned}$$

By means of (3.3) and standard arguments used before, we further get

$$\begin{aligned} \pmb {{\texttt {E}}_{\texttt {k}}}({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j})\le \pmb {C}\cdot {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}}\Big ] \cdot \tau ^{j+1} \qquad \pmb {{\texttt {k}}}=2,5\,. \end{aligned}$$

and

$$\begin{aligned} \pmb {{\texttt {E}}_{\texttt {4}}}({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j})\le \pmb {C}\cdot {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}}\Big ] \cdot \bigl (\tau ^{j+1}\bigr )^{\frac{1}{2}}\,. \end{aligned}$$

Moreover, due to (3.2), we obtain

$$\begin{aligned} \pmb {{\texttt {E}}_{\texttt {7}}}({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j+1},Y_{V}^{j})\le \pmb {C}\cdot {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}}\Big ] \cdot \tau ^{j+1}\,. \end{aligned}$$

Consequently, by considering the representation of ${\mathfrak {G}}_{1}^{(j)}$ in Theorem 4.1, we obtain

$$\begin{aligned} {\mathfrak {G}}_{1}^{(j)}\le \pmb {C}\cdot {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}}\Big ] \cdot \tau ^{j+1}. \end{aligned}$$

(4.22)

b) Bounds for $\{\pmb {{\texttt {E}}_{\texttt {k}}}(\cdot )\}_{k=8,\ldots ,14}$ in ${\mathfrak {G}}_{2}^{(j)}$: Similar to a), we obtain

$$\begin{aligned} {\mathfrak {G}}_{2}^{(j)}\le \pmb {C}\cdot {\mathbb {E}}\Bigl [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}}\Big ]\cdot \tau ^{j+1}. \end{aligned}$$

(4.23)

Step 2: Let $j\ge 0$. By means of the representation of $\lambda _{j}$ in (3.4), and the fact that $0<Y_{V}^{j}\le 1$, we get

$$\begin{aligned} {\mathfrak {G}}_{3}^{(j)}&\le \pmb {C}\cdot {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Big ] \,. \end{aligned}$$

(4.24)

Step 3: We plug (4.22), (4.23) and (4.24) into (4.1), and use $\tau ^{j+1}\le \tau ^{max}$, to get

$$\begin{aligned}&\sum \limits _{j=0}^{\infty } \tau ^{j+1} \big \{{{\mathfrak {G}}}_{1}^{(j)} + {{\mathfrak {G}}}_{2}^{(j)}+ {{\mathfrak {G}}}_{3}^{(j)} \big \}\nonumber \\&\quad \le \pmb {C}\cdot \tau ^{max}\cdot \sum \limits _{j=0}^{\infty } \tau ^{j+1}{\mathbb {E}}\Big [ {\textbf{1}}_{\big \{ {\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}}\nonumber \\&\qquad + {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \Big ] \nonumber \\&\qquad + \pmb {C}\cdot \tau ^{max}\cdot \sum \limits _{j=0}^{\infty } {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Big ] \nonumber \\&\quad = \pmb {C}\cdot \tau ^{max}\cdot \Bigg \{\sum \limits _{j=0}^{\infty } \tau ^{j+1}{\mathbb {E}}\Big [ {\textbf{1}}_{\{J^{*}>j\}}\Big ] +\sum \limits _{j=0}^{\infty } {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Big ]\Bigg \}\,. \end{aligned}$$

(4.25)

Due to Lemma 3.3, we have

$$\begin{aligned} \sum \limits _{j=0}^{\infty } {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Big ]<2, \end{aligned}$$

(4.26)

and due to Lemma 3.4, we obtain in both cases (i) and (ii)

$$\begin{aligned} \sum \limits _{j=0}^{\infty } \tau ^{j+1}{\mathbb {E}}\Big [ {\textbf{1}}_{\{J^{*}>j\}} \Big ]={\mathbb {E}}[t_{J^{*}}]\le C\, \end{aligned}$$

(4.27)

for some constant $C>0$ independent of $j\ge 0$ and $\tau ^{max}$.

Step 4: We plug (4.26) and (4.27) into (4.25), which proves assertions (i) and (ii). $\square$

4.2 A posteriori weak error estimation: derivation and optimality for the parabolic PDE (1.8)

Close to Theorems 4.1 and 4.6 for the elliptic PDE (1.1), we derive corresponding results for PDE (1.8); see Theorems 4.7 and  4.8 below. Since its derivation is similar to the one that lead to Theorem 4.1 elsewise, we present the upcoming results without proof and refer to [34] for a detailed derivation.

Theorem 4.7

Assume (B0)–(B3) in Sect. 3.2. Fix $(t,{\textbf{x}})\in [0,T)\times \pmb {{\mathcal {D}}}$. Let $J\equiv J(t,{\textbf{x}})\in {\mathbb {N}}$ and $\{t_{j}\}_{j=0}^{J}\subset [t,T]$ be a mesh with local step sizes $\{\tau ^{j+1}\}_{j=0}^{J-1}$. Let $\{({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{Z}^{j})\}_{j=0}^{J}$ solve Scheme 3. Then we have

$$\begin{aligned} \Bigl \vert u(t,{\textbf{x}}) - {\mathbb {E}}\bigl [\phi (t_{J^{*}},\textbf{Y}_{{\textbf{X}}}^{J^{*}})+Y_{Z}^{J^{*}}\bigr ] \Bigr \vert \le \pmb {{\mathfrak {C}}}(\phi ,g)\cdot \sum \limits _{j=0}^{J-1} \tau ^{j+1} \big \{{{\mathfrak {H}}}_{1}^{(j)} + {{\mathfrak {H}}}_{2}^{(j)}+ {{\mathfrak {H}}}_{3}^{(j)} \big \}\,, \end{aligned}$$

(4.28)

where the a posteriori error estimators $\{{\mathfrak {H}}_{\ell }^{(j)}\}_{\ell =1}^{3}$, are given by

$$\begin{aligned} {\mathfrak {H}}_{1}^{(j)}&:= \pmb {\texttt {E} _\texttt {1} }({\textbf{Y}}_{{\textbf{X}}}^{j}) \cdot \tau ^{j+1} + \frac{3}{2} \cdot \pmb {\texttt {E} _\texttt {2} }({\textbf{Y}}_{{\textbf{X}}}^{j}) \cdot \tau ^{j+1} + \frac{1}{2}\cdot \pmb {\texttt {E} _\texttt {3} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j})\\&\quad +\pmb {\texttt {E} _\texttt {4} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j})+ \pmb {\texttt {E} _\texttt {5} }({\textbf{Y}}_{{\textbf{X}}}^{j}) \cdot \tau ^{j+1} \\&\quad + \Big \{\frac{1}{2}C_{D^{2}{\textbf{b}}} + \frac{1}{4}L C_{D^{2}\pmb {\sigma }\pmb {\sigma }^{\top }}\Big \} \cdot \pmb {\texttt {E} _\texttt {6} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j})\\&\quad +L \cdot \pmb {\texttt {E} _\texttt {7} }({\textbf{Y}}_{{\textbf{X}}}^{j}) \cdot \tau ^{j+1}+ \frac{1}{2}L\cdot \pmb {\texttt {E} _\texttt {8} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j})\\&\quad + \frac{1}{2}L \cdot \pmb {\texttt {E} _\texttt {9} }({\textbf{Y}}_{{\textbf{X}}}^{j})\cdot \tau ^{j+1} + \frac{1}{2}L\cdot \pmb {\texttt {E} _\texttt {10} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j}) + \frac{1}{2}L \cdot \pmb {\texttt {E} _\texttt {11} }({\textbf{Y}}_{{\textbf{X}}}^{j})\cdot \tau ^{j+1}\\&\quad +\sqrt{L} \cdot \pmb {\texttt {E} _\texttt {12} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j})\cdot \sqrt{\tau ^{j+1}} + \big |\pmb {\texttt {E} _\texttt {13} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},t_{j})\big |+ \pmb {\texttt {E} _\texttt {14} }({\textbf{Y}}_{{\textbf{X}}}^{j})\cdot \tau ^{j+1}\\ {\mathfrak {H}}_{2}^{(j)}&:= \pmb {\texttt {E} _\texttt {15} }({\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}) \cdot \tau ^{j+1} + \frac{3}{2} \cdot \pmb {\texttt {E} _\texttt {16} }({\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}) \cdot \tau ^{j+1} \\&\quad + \frac{1}{2}\cdot \pmb {\texttt {E} _\texttt {17} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})+\pmb {\texttt {E} _\texttt {18} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\\&\quad + \pmb {\texttt {E} _\texttt {19} }({\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}) \cdot \tau ^{j+1} +\Big \{\frac{1}{2}C_{D^{2}{\textbf{b}}} + \frac{1}{4}L C_{D^{2}\pmb {\sigma }\pmb {\sigma }^{\top }}\Big \} \cdot \pmb {\texttt {E} _\texttt {20} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}) \\&\quad +L \cdot \pmb {\texttt {E} _\texttt {21} }({\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}) \cdot \tau ^{j+1} + \frac{1}{2}L\cdot \pmb {\texttt {E} _\texttt {22} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\\&\quad + \frac{1}{2}L \cdot \pmb {\texttt {E} _\texttt {23} }({\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\cdot \tau ^{j+1} \\&\quad + \frac{1}{2}L\cdot \pmb {\texttt {E} _\texttt {24} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}) + \frac{1}{2}L \cdot \pmb {\texttt {E} _\texttt {25} }({\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\cdot \tau ^{j+1}\\&\quad +\sqrt{L} \cdot \pmb {\texttt {E} _\texttt {26} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\cdot \sqrt{\tau ^{j+1}}\\&\quad + \big |\pmb {\texttt {E} _\texttt {27} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j},t_{j})\big |+ \pmb {\texttt {E} _\texttt {28} }({\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\cdot \tau ^{j+1}\\ {\mathfrak {H}}_{3}^{(j)}&:=2\cdot \pmb {\texttt {E} _\texttt {29} }\bigl ({\textbf{Y}}_{{\textbf{X}}}^{j}\bigr )\,, \end{aligned}$$

where $C_{D^{2}{\textbf{b}}}:=\sup \limits _{{\textbf{y}}\in \overline{\pmb {{\mathcal {D}}}}}\Vert D^{2}{\textbf{b}}({\textbf{y}})\Vert _{{\mathcal {L}}^{2}}$, $C_{D^{2}\pmb {\sigma }\pmb {\sigma }^{\top }}:=\sup \limits _{{\textbf{y}}\in \overline{\pmb {{\mathcal {D}}}}} \sup \limits _{\Vert {\textbf{v}}_{i}\Vert _{{\mathbb {R}}^{L}}} \Vert D^{2} \pmb {\sigma }({\textbf{y}})\pmb {\sigma }^{\top }({\textbf{y}})({\textbf{v}}_{1},{\textbf{v}}_{2})\Vert _{{\mathbb {R}}^{L \times L}}$, and $\pmb {{\mathfrak {C}}}(\phi ,g)\ge 1$ is the constant from Lemma 3.2, and with computable terms

• 1. $\begin{aligned} \pmb {\texttt {E} _\texttt {1} }({\textbf{Y}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}{\setminus }\pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Vert {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L}}\Big ]\,, \end{aligned}$

• 2. $\begin{aligned} \pmb {\texttt {E} _\texttt {2} }({\textbf{Y}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}{\setminus }\pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Vert {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L}}^{2}\Big ]\,, \end{aligned}$

• 3. $\begin{aligned} \pmb {\texttt {E} _\texttt {3} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}{\setminus }\pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Vert {\textbf{Y}}_{{\textbf{X}}}^{j+1} - {\textbf{Y}}_{{\textbf{X}}}^{j} \Vert _{{\mathbb {R}}^{L}}^{2} \Vert {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L}}\Big ]\,, \end{aligned}$

• 4. $\begin{aligned} \pmb {\texttt {E} _\texttt {4} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}{\setminus }\pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Vert {\textbf{Y}}_{{\textbf{X}}}^{j+1} - {\textbf{Y}}_{{\textbf{X}}}^{j} \Vert _{{\mathbb {R}}^{L}} \Vert {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j+1}) -{\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L}}\Big ]\,, \end{aligned}$

• 5. $\begin{aligned} \pmb {\texttt {E} _\texttt {5} }({\textbf{Y}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}{\setminus }\pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Vert D{\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \cdot {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L}}\Big ]\,, \end{aligned}$

• 6. $\begin{aligned} \pmb {\texttt {E} _\texttt {6} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j}):= {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}{\setminus }\pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Vert {\textbf{Y}}_{{\textbf{X}}}^{j+1} - {\textbf{Y}}_{{\textbf{X}}}^{j} \Vert _{{\mathbb {R}}^{L}}^{2} \Big ]\,, \end{aligned}$

• 7. $\begin{aligned} \pmb {\texttt {E} _\texttt {7} }({\textbf{Y}}_{{\textbf{X}}}^{j}):= {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}{\setminus }\pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Vert {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \Vert _{{\mathbb {R}}^{L}} \Vert \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j}) \Vert _{{\mathbb {R}}^{L\times L}}^{2} \Big ]\,, \end{aligned}$

• 8. $\begin{aligned} \pmb {\texttt {E} _\texttt {8} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j}):= {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}{\setminus }\pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Vert {\textbf{Y}}_{{\textbf{X}}}^{j+1} - {\textbf{Y}}_{{\textbf{X}}}^{j} \Vert _{{\mathbb {R}}^{L}}^{2} \Vert \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j}) \Vert _{{\mathbb {R}}^{L\times L}}^{2} \Big ]\,, \end{aligned}$

• 9. $\begin{aligned} \pmb {\texttt {E} _\texttt {9} }({\textbf{Y}}_{{\textbf{X}}}^{j}):= {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}{\setminus }\pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Vert \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j}) \Vert _{{\mathbb {R}}^{L\times L}}^{2} \Big ]\,, \end{aligned}$

• 10. $\begin{aligned} \pmb {\texttt {E} _\texttt {10} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j})&:= {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}{\setminus }\pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Vert {\textbf{Y}}_{{\textbf{X}}}^{j+1} - {\textbf{Y}}_{{\textbf{X}}}^{j} \Vert _{{\mathbb {R}}^{L}} \\&\qquad \qquad \cdot \Vert \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j+1})\pmb {\sigma }^{\top }({\textbf{Y}}_{{\textbf{X}}}^{j+1})-\pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\sigma }^{\top }({\textbf{Y}}_{{\textbf{X}}}^{j}) \Vert _{{\mathbb {R}}^{L\times L}} \Big ]\,, \end{aligned}$

• 11. $\tiny \begin{aligned} \pmb {\texttt {E} _\texttt {11} }({\textbf{Y}}_{{\textbf{X}}}^{j})&:= {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}{\setminus }\pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Vert D\pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j})\pmb {\sigma }^{\top }({\textbf{Y}}_{{\textbf{X}}}^{j}) \cdot {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L\times L}} \Big ]\,, \end{aligned}$

• 12. $\tiny \begin{aligned} \pmb {\texttt {E} _\texttt {12} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j}):= {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}{\setminus }\pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Vert {\textbf{Y}}_{{\textbf{X}}}^{j+1} - {\textbf{Y}}_{{\textbf{X}}}^{j} \Vert _{{\mathbb {R}}^{L}} \Vert {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L}} \Vert \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L\times L}} \Big ]\,, \end{aligned}$

• 13. $\begin{aligned} \pmb {\texttt {E} _\texttt {13} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},t_{j}):={\mathbb {E}}\Bigl [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}{\setminus }\pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \bigl ( g(t_{j},{\textbf{Y}}_{{\textbf{X}}}^{j+1})-g(t_{j},{\textbf{Y}}_{{\textbf{X}}}^{j})\bigr ) \Big ]\,, \end{aligned}$

• 14. $\begin{aligned} \pmb {\texttt {E} _\texttt {14} }({\textbf{Y}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}{\setminus }\pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \Big ]\,, \end{aligned}$

• 15. $\tiny \begin{aligned} \pmb {\texttt {E} _\texttt {15} }({\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Bigl [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \Vert {\textbf{b}}(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L}} \Big ]\,, \end{aligned}$

• 16. $\tiny \begin{aligned}&\pmb {\texttt {E} _\texttt {16} }({\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Bigl [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \Vert {\textbf{b}}(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L}}^{2} \Big ]\,, \end{aligned}$

• 17. $\tiny \begin{aligned} \pmb {\texttt {E} _\texttt {17} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Bigl [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}}&\Vert {\textbf{Y}}_{{\textbf{X}}}^{j+1} - \overline{{\textbf{Y}}}_{{\textbf{X}}}^{j} \Vert _{{\mathbb {R}}^{L}}^{2}\cdot \Vert {\textbf{b}}(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L}}\Big ]\,, \end{aligned}$

• 18. $\tiny \begin{aligned} \pmb {\texttt {E} _\texttt {18} }&({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\\&:={\mathbb {E}}\Bigl [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \Vert {\textbf{Y}}_{{\textbf{X}}}^{j+1} - \overline{{\textbf{Y}}}_{{\textbf{X}}}^{j} \Vert _{{\mathbb {R}}^{L}} \Vert {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j+1}) -{\textbf{b}}(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L}} \Big ]\,, \end{aligned}$

• 19. $\tiny \begin{aligned} \pmb {\texttt {E} _\texttt {19} }({\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Bigl [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \Vert D{\textbf{b}}(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}) \cdot {\textbf{b}}(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L}} \Big ]\,, \end{aligned}$

• 20. $\tiny \begin{aligned} \pmb {\texttt {E} _\texttt {20} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Bigl [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \Vert {\textbf{Y}}_{{\textbf{X}}}^{j+1} - \overline{{\textbf{Y}}}_{{\textbf{X}}}^{j} \Vert _{{\mathbb {R}}^{L}}^{2}\Big ] \,, \end{aligned}$

• 21. $\tiny \begin{aligned} \pmb {\texttt {E} _\texttt {21} }({\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}):= {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \Vert {\textbf{b}}(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}) \Vert _{{\mathbb {R}}^{L}} \Vert \pmb {\sigma }(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}) \Vert _{{\mathbb {R}}^{L\times L}}^{2} \Big ]\,, \end{aligned}$

• 22. $\tiny \begin{aligned} \pmb {\texttt {E} _\texttt {22} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Bigl [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}}&\Vert {\textbf{Y}}_{{\textbf{X}}}^{j+1} - \overline{{\textbf{Y}}}_{{\textbf{X}}}^{j} \Vert _{{\mathbb {R}}^{L}}^{2}\cdot \Vert \pmb {\sigma }(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L\times L}}^{2}\Big ]\,, \end{aligned}$

• 23. $\tiny \begin{aligned} \pmb {\texttt {E} _\texttt {23} }({\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Bigl [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \Vert \pmb {\sigma }(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L\times L}}^{2}\Big ]\,, \end{aligned}$

• 24. $\tiny \begin{aligned} \pmb {\texttt {E} _\texttt {24} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})&:= {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \Vert {\textbf{Y}}_{{\textbf{X}}}^{j+1} - \overline{{\textbf{Y}}}_{{\textbf{X}}}^{j} \Vert _{{\mathbb {R}}^{L}} \\&\quad \cdot \Vert \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j+1})\pmb {\sigma }^{\top }({\textbf{Y}}_{{\textbf{X}}}^{j+1})-\pmb {\sigma }(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\pmb {\sigma }^{\top }(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L\times L}} \Big ]\,, \end{aligned}$

• 25. $\begin{aligned} \pmb {\texttt {E} _\texttt {25} }({\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})&:= {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \\&\quad \cdot \Vert D\pmb {\sigma }(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\pmb {\sigma }^{\top }(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\cdot {\textbf{b}}(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L\times L}} \Big ]\,, \end{aligned}$

• 26. $\tiny \begin{aligned} \pmb {\texttt {E} _\texttt {26} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}):=&{\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \Vert {\textbf{Y}}_{{\textbf{X}}}^{j+1} - \overline{{\textbf{Y}}}_{{\textbf{X}}}^{j} \Vert _{{\mathbb {R}}^{L}} \\&\cdot \Vert {\textbf{b}}(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}) \Vert _{{\mathbb {R}}^{L}} \Vert \pmb {\sigma }(\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}) \Vert _{{\mathbb {R}}^{L\times L}} \Big ]\,, \end{aligned}$

• 27. $\tiny \begin{aligned} \pmb {\texttt {E} _\texttt {27} }({\textbf{Y}}_{{\textbf{X}}}^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j},t_{j}):={\mathbb {E}}\Bigl [&{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \\&\cdot \bigl ( g(t_{j},{\textbf{Y}}_{{\textbf{X}}}^{j+1})-g(t_{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j})\bigr ) \Big ] \,, \end{aligned}$

• 28. $\begin{aligned} \pmb {\texttt {E} _\texttt {28} }({\textbf{Y}}_{{\textbf{X}}}^{j},\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Bigl [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}}\big \}} {\textbf{1}}_{\big \{\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}={\textbf{Y}}_{{\textbf{X}}}^{j}+ \lambda _{j}\sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr ) \big \}} \Big ] \,, \end{aligned}$

• 29. $\begin{aligned} \pmb {\texttt {E} _\texttt {29} }\bigl ({\textbf{Y}}_{{\textbf{X}}}^{j}\bigr )={\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1}} \big \}} \lambda _{j}^{2}\Big ]\,. \end{aligned}$

Remark 4.2

1. For ${\textbf{b}}({\textbf{x}})\equiv {\textbf{0}}$, $g(t,{\textbf{x}})\equiv 0$ and $\pmb {\sigma }({\textbf{x}})\equiv \sqrt{2a}\cdot {\mathbb {I}}$, where $a>0$, which are data requirements in (1.8) for the (homogeneous) heat equation, the particular error estimators $\{{\mathfrak {H}}_{\ell }\}_{\ell =1}^{3}$ simplify considerably: only $\pmb {{\texttt {E}}_{\texttt {6}}}(\cdot ),\pmb {{\texttt {E}}_{\texttt {8}}}(\cdot ),\pmb {{\texttt {E}}_{\texttt {14}}}(\cdot ),\pmb {{\texttt {E}}_{\texttt {20}}}(\cdot ),\pmb {{\texttt {E}}_{\texttt {22}}}(\cdot ),\pmb {{\texttt {E}}_{\texttt {28}}}(\cdot )$ and $\pmb {{\texttt {E}}_{\texttt {29}}}(\cdot )$ constitute $\{{\mathfrak {H}}_{\ell }^{(\cdot )}\}_{\ell =1}^{3}$; cf. Example 1.3.

2. An a posteriori error estimate for a more general PDE (1.8) with $c(t,{\textbf{x}})\ne 0$ (cf. also(1.1)), and/or ${\textbf{b}}\equiv {\textbf{b}}(t,{\textbf{x}})$, $\pmb {\sigma }\equiv \pmb {\sigma }(t,{\textbf{x}})$ is possible, but its corresponding derivation would be more complicated.

3. The terms $\{\pmb {{\texttt {E}}_{{\ell }}}\bigl (\cdot )\}_{\pmb {{{\ell }}}=1,\ldots ,14}$ in ${\mathfrak {H}}_{1}^{(\cdot )}$ capture dynamics away from $\pmb {\partial {\mathcal {D}}}$ and may be related to the terms in the error estimator in [35, (3.1)]. The additional terms $\{\pmb {{\texttt {E}}_{{\ell }}}\bigl (\cdot )\}_{\pmb {{{\ell }}}=15,\ldots ,29}$ in ${\mathfrak {H}}_{2}^{(\cdot )}$ and ${\mathfrak {H}}_{3}^{(\cdot )}$ address stopping dynamics near the boundary, which, however, do not appear in the framework of [35, Thm. 3.1]; cf. also 3. in Remark 4.1.

The following theorem states convergence with optimal (weak) order 1 of (4.28); its proof is similar to the one in Theorem 4.6 and can be found in [34].

Theorem 4.8

Assume (B0)–(B3) in Sect. 3.2. Fix $(t,{\textbf{x}})\in [0,T)\times \pmb {{\mathcal {D}}}$. Let $J\equiv J(t,{\textbf{x}})\in {\mathbb {N}}$ and let $\{({\textbf{Y}}_{{\textbf{X}}}^{j},Y_{Z}^{j})\}_{j=0}^{J}$ solve Scheme 3 on a mesh $\{t_{j}\}_{j=0}^{J}\subset [t,T]$ with local mesh sizes $\{\tau ^{j+1}\}_{j=0}^{J-1}$ and maximum mesh size $\tau ^{max}=\max _{j}\tau ^{j+1}$. Then, there exists $\pmb {C}\equiv \pmb {C}(\phi ,g,T)>0$, such that

$$\begin{aligned} \pmb {{\mathfrak {C}}}(\phi ,g)\cdot \sum \limits _{j=0}^{J-1} \tau ^{j+1} \big \{{{\mathfrak {H}}}_{1}^{(j)} + {{\mathfrak {H}}}_{2}^{(j)}+ {{\mathfrak {H}}}_{3}^{(j)} \big \} \le \pmb {C}\cdot \tau ^{max}. \end{aligned}$$

4.3 A posteriori error analysis for the Euler method

Consider the Euler method

$$\begin{aligned} {\textbf{Y}}_{{\textbf{X}}}^{j+1} = \textbf{Y}_{{\textbf{X}}}^{j} + {\textbf{b}}(\textbf{Y}_{{\textbf{X}}}^{j}) \tau ^{j+1} + \pmb {\sigma }(\textbf{Y}_{{\textbf{X}}}^{j})\bigl ({\textbf{W}}_{t_{j+1}}-{\textbf{W}}_{t_{j}}\bigr ) \qquad (j\ge 0) , \quad {\textbf{Y}}_{{\textbf{X}}}^{0}={\textbf{x}},\nonumber \\ \end{aligned}$$

(4.29)

to approximate (1.8). The interpolating continuified Euler process $\pmb {{\mathcal {Y}}}^{{\textbf{X}}}\equiv \big \{ \pmb {{\mathcal {Y}}}_{t}^{{\textbf{X}}}\,;t\ge 0\big \}$ of the $\{{\textbf{Y}}_{{\textbf{X}}}^{j}\}_{j\ge 0}$ is given by

$$\begin{aligned} \pmb {{\mathcal {Y}}}_{t}^{{\textbf{X}}} = \textbf{Y}_{{\textbf{X}}}^j + {\textbf{b}}(\textbf{Y}_{{\textbf{X}}}^{j}) (t-t_{j}) + \pmb {\sigma }({\textbf{Y}}_{{\textbf{X}}}^{j})\bigl ({\textbf{W}}_{t}-{\textbf{W}}_{t_{j}}\bigr ) \qquad t\in [t_{j},t_{j+1}] \qquad (j\ge 0).\nonumber \\ \end{aligned}$$

(4.30)

We consider the parabolic PDE (1.8) with $\pmb {\sigma }({\textbf{x}})\equiv {\mathbb {I}}$, $g\equiv 0$ for simplicity; cf. also Example 1.3. For the following, we fix $(t,{\textbf{x}})\in [0,T)\times \pmb {{\mathcal {D}}}$ in (1.9) and let $\{t_{j}\}_{j=0}^{J}\subset [t,T]$ be a mesh with local step sizes $\{\tau ^{j+1}\}_{j=0}^{J-1}$, where $J\equiv J(t,{\textbf{x}})\in {\mathbb {N}}$. We denote by

$$\begin{aligned} \pmb {{\tilde{\tau }}}:=\inf \big \{s>t:\,\pmb {{\mathcal {Y}}}_{s}^{{\textbf{X}},t,{\textbf{x}}}\in \pmb {\partial {\mathcal {D}}} \text { or } s\notin (t,T)\big \}\ \end{aligned}$$

(4.31)

the first exit time of $\pmb {{\mathcal {Y}}}^{{\textbf{X}},t,{\textbf{x}}} \equiv \big \{\pmb {{\mathcal {Y}}}^{{\textbf{X}},t,{\textbf{x}}}_{s}\,;\,s\in [t,T]\big \}$, which starts at time $t\in [0,T]$ in ${\textbf{x}}\in \pmb {{\mathcal {D}}}$. Motivated by [26, p. 181], the expression

$$\begin{aligned} \sum \limits _{j=0}^{J-1}{\mathbb {E}}\Big [ {\textbf{1}}_{\{\pmb {{\tilde{\tau }}}\in (t_{j},t_{j+1}]\}}\phi (t_{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j+1})\Big ] \end{aligned}$$

(4.32)

is now used to approximate (1.9). In this respect, (4.32) first localizes $\pmb {{\tilde{\tau }}}$ in $(t_{j},t_{j+1}]$, and if it is assured, proceeds via the approximation $\pmb {{\tilde{\tau }}}\approx t_{j+1}$. The following theorem presents a related a posteriori error estimate for (4.29), (4.31). From its representation it is not difficult to obtain first order of convergence for (4.33) on families of (time-) meshes with maximum mesh size $\tau ^{max}>0$. We refer to [34] for more details.

Theorem 4.9

Assume (B0)–(B3) in Sect. 3.2. Fix $(t,{\textbf{x}})\in [0,T)\times \pmb {{\mathcal {D}}}$. Let $J\equiv J(t,{\textbf{x}})\in {\mathbb {N}}$, and $\{t_{j}\}_{j=0}^{J}\subset [t,T]$ be a mesh with local step sizes $\{\tau ^{j+1}\}_{j=0}^{J-1}$. Let $\{\pmb {{\mathcal {Y}}}_{t_{j}}^{{\textbf{X}},t,{\textbf{x}}}\}_{j=0}^{J}$ solve (4.30). Then, for $\pmb {{\mathfrak {C}}}(\phi ,g)\ge 1$ from Lemma 3.2,

$$\begin{aligned} \biggl \vert u(t,{\textbf{x}}) - \sum \limits _{j=0}^{J-1}{\mathbb {E}}\Big [ {\textbf{1}}_{\{\pmb {{\tilde{\tau }}}\in (t_{j},t_{j+1}]\}}\phi (t_{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j+1})\Big ] \biggr \vert \le \pmb {{\mathfrak {C}}}(\phi ,g)\cdot \sum \limits _{j=0}^{J-1} \tau ^{j+1} \big \{\tilde{{\mathfrak {H}}}_{1}^{(j)} + \tilde{{\mathfrak {H}}}_{2}^{(j)}\big \}\,, \end{aligned}$$

(4.33)

where the a posteriori error estimators $\{\tilde{{\mathfrak {H}}}_{\ell }^{(j)}\}_{\ell =1}^{2}$ are given by

$$\begin{aligned} \tilde{{\mathfrak {H}}}_{1}^{(j)}&:= \frac{1}{2} \cdot \pmb {{\tilde{\texttt {E} }}_\texttt {1} }({\textbf{Y}}_{{\textbf{X}}}^{j}) \cdot \tau ^{j+1}+ \frac{1}{4}L \cdot \pmb {{\tilde{\texttt {E} }}_\texttt {2} }({\textbf{Y}}_{{\textbf{X}}}^{j}) \cdot \tau ^{j+1} +\frac{1}{2}L\cdot \pmb {{\tilde{\texttt {E} }}_\texttt {3} }({\textbf{Y}}_{{\textbf{X}}}^{j}) \cdot \tau ^{j+1} \\&\quad + \Big \{ C_{D^{2}{\textbf{b}}} \cdot \sqrt{\pmb {\tilde{\texttt {E} }_\texttt {4} }({\textbf{Y}}_{{\textbf{X}}}^{j})}+\frac{1}{2}L C_{D^{3}{\textbf{b}}}+LC_{D^{2}{\textbf{b}}}\Big \} \\&\quad \cdot \sqrt{\frac{1}{15} \pmb {{\tilde{\texttt {E} }}_\texttt {4} }({\textbf{Y}}_{{\textbf{X}}}^{j})\cdot \tau ^{j+1} + \frac{L}{8}\cdot \pmb {{\tilde{\texttt {E} }}_\texttt {5} }({\textbf{Y}}_{{\textbf{X}}}^{j})}\cdot \bigl (\tau ^{j+1}\bigr )^{\frac{3}{2}}\,,\\ \tilde{{\mathfrak {H}}}_{2}^{(j)}&:= \pmb {{\tilde{\texttt {E} }}_\texttt {6} }({\textbf{Y}}_{{\textbf{X}}}^{j})\,, \end{aligned}$$

where $C_{D^{2}{\textbf{b}}}:=\sup \limits _{{\textbf{y}}\in \overline{\pmb {{\mathcal {D}}}}}\Vert D^{2}{\textbf{b}}({\textbf{y}})\Vert _{{\mathcal {L}}^{2}}$, $C_{D^{3}{\textbf{b}}}:=\sup \limits _{{\textbf{y}}\in \overline{\pmb {{\mathcal {D}}}}}\Vert D^{3}{\textbf{b}}({\textbf{y}})\Vert _{{\mathcal {L}}^{3}}$, and with computable terms

• 1. $\begin{aligned} \pmb {{\tilde{\texttt {E} }}_\texttt {1} }({\textbf{Y}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Big [{\textbf{1}}_{\{ t_{j}<\pmb {{\tilde{\tau }}}\}} \Vert D{\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\cdot {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L}}\Big ]\,, \end{aligned}$

• 2. $\begin{aligned} \pmb {{\tilde{\texttt {E} }}_\texttt {2} }({\textbf{Y}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Big [{\textbf{1}}_{\{ t_{j}<\pmb {{\tilde{\tau }}}\}} \Vert D^{2}{\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\Vert _{{\mathcal {L}}^{2}} \Big ]\,, \end{aligned}$

• 3. $\begin{aligned} \pmb {{\tilde{\texttt {E} }}_\texttt {3} }({\textbf{Y}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Big [{\textbf{1}}_{\{ t_{j}<\pmb {{\tilde{\tau }}}\}} \Vert D{\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\Vert _{{\mathcal {L}}^{1}} \Big ]\,, \end{aligned}$

• 4. $\begin{aligned} \pmb {{\tilde{\texttt {E} }}_\texttt {4} }({\textbf{Y}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Big [{\textbf{1}}_{\{ t_{j}<\pmb {{\tilde{\tau }}}\}} \Vert {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L}}^{2}\Big ]\,, \end{aligned}$

• 5. $\begin{aligned} \pmb {{\tilde{\texttt {E} }}_\texttt {5} }({\textbf{Y}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Big [{\textbf{1}}_{\{ t_{j}<\pmb {{\tilde{\tau }}}\}} \Big ]\,, \end{aligned}$

• 6. $\begin{aligned} \pmb {{\tilde{\texttt {E} }}_\texttt {6} }({\textbf{Y}}_{{\textbf{X}}}^{j}):={\mathbb {E}}\Big [{\textbf{1}}_{\{\pmb {{\tilde{\tau }}}\in (t_{j},t_{j+1}]\}}\bigl (C_{\partial \phi }+ C_{D\phi }\Vert {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j})\Vert _{{\mathbb {R}}^{L}}+\tfrac{1}{2}LC_{D^{2}\phi }\bigr )\Big ]\,, \end{aligned}$

where

$$\begin{aligned} C_{\partial \phi }&:=\sup \limits _{(s,{\textbf{y}})\in [0,T]\times \overline{\pmb {{\mathcal {D}}}}}|\partial \phi (s,{\textbf{y}})|\,,\qquad C_{D\phi }:=\sup \limits _{(s,{\textbf{y}})\in [0,T]\times \overline{\pmb {{\mathcal {D}}}}}\Vert D\phi (s,{\textbf{y}})\Vert _{{\mathbb {R}}^{L}}\,,\\ C_{D^{2}\phi }&:=\sup \limits _{(s,{\textbf{y}})\in [0,T]\times \overline{\pmb {{\mathcal {D}}}}}\Vert D^{2}\phi (s,{\textbf{y}})\Vert _{{\mathbb {R}}^{L\times L}}\,. \end{aligned}$$

Proof

(Sketch of the proof of Theorem 4.9) We add and substract the term ${\mathbb {E}}\big [\phi (\pmb {{\tilde{\tau }}},\pmb {{\mathcal {Y}}}^{{\textbf{X}},t,{\textbf{x}}}_{\pmb {{\tilde{\tau }}}})\bigr ]$ in the expression on the left-hand side of (4.33) to get

$$\begin{aligned}&\biggl \vert u(t,{\textbf{x}}) - \sum \limits _{j=0}^{J-1}{\mathbb {E}}\Big [ {\textbf{1}}_{\{\pmb {{\tilde{\tau }}}\in (t_{j},t_{j+1}]\}}\phi (t_{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j+1})\Big ] \biggr \vert \\&\quad \le \underbrace{\Bigl \vert u(t,{\textbf{x}}) - {\mathbb {E}}\big [\phi (\pmb {{\tilde{\tau }}},\pmb {{\mathcal {Y}}}^{{\textbf{X}},t,{\textbf{x}}}_{\pmb {{\tilde{\tau }}}})\bigr ] \Bigr |}_{=:\pmb {\tilde{I}}}\\&\qquad + \underbrace{\biggl |{\mathbb {E}}\big [\phi (\pmb {{\tilde{\tau }}},\pmb {{\mathcal {Y}}}^{{\textbf{X}},t,{\textbf{x}}}_{\pmb {{\tilde{\tau }}}})\bigr ] - \sum \limits _{j=0}^{J-1}{\mathbb {E}}\Big [ {\textbf{1}}_{\{\pmb {{\tilde{\tau }}}\in (t_{j},t_{j+1}]\}}\phi (t_{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j+1})\Big ] \biggr \vert }_{=:\pmb {\tilde{II}}}\,. \end{aligned}$$

a) Estimation of $\pmb {\tilde{I}}$: The estimation of $\pmb {\tilde{I}}$ is similar to [35, Thm. 3.1], where an a posteriori error estimate on $[0,T]\times {\mathbb {R}}^{L}$ is presented, and conceptually uses the same tools due to the Wiener process involved in (4.29) resp. (4.30). By means of the fact that ${\mathbb {E}}\big [\phi (\pmb {{\tilde{\tau }}},\pmb {{\mathcal {Y}}}^{{\textbf{X}},t,{\textbf{x}}}_{\pmb {{\tilde{\tau }}}})\bigr ]={\mathbb {E}}\big [u(\pmb {{\tilde{\tau }}},\pmb {{\mathcal {Y}}}^{{\textbf{X}},t,{\textbf{x}}}_{\pmb {{\tilde{\tau }}}})\bigr ]$, Itô’s formula, the identity in the first line of (1.8), Lemma 3.2, as well as Malliavin calculus techniques, we obtain

$$\begin{aligned} \pmb {\tilde{I}}\le \pmb {{\mathfrak {C}}}(\phi ,g)\cdot \sum \limits _{j=0}^{J-1} \tau ^{j+1} \tilde{{\mathfrak {H}}}_{1}^{(j)} \,. \end{aligned}$$

b) Estimation of $\pmb {\tilde{II}}$: Using Itô’s formula immediately leads to

$$\begin{aligned} \pmb {\tilde{II}}&=\biggl |\sum \limits _{j=0}^{J-1}{\mathbb {E}}\Big [ {\textbf{1}}_{\{\pmb {{\tilde{\tau }}}\in (t_{j},t_{j+1}]\}}\Bigl (\phi (t_{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j+1})-\phi (\pmb {{\tilde{\tau }}},\pmb {{\mathcal {Y}}}^{{\textbf{X}},t,{\textbf{x}}}_{\pmb {{\tilde{\tau }}}})\Bigr )\Big ] \biggr |\\&\le \sum \limits _{j=0}^{J-1} \biggl |{\mathbb {E}}\Big [ {\textbf{1}}_{\{\pmb {{\tilde{\tau }}}\in (t_{j},t_{j+1}]\}} \int _{{\tilde{\tau }}}^{t_{j+1}} \partial _{s} \phi (s,\pmb {{\mathcal {Y}}}^{{\textbf{X}},t,{\textbf{x}}}_{s})+\big \langle {\textbf{b}}({\textbf{Y}}_{{\textbf{X}}}^{j}),D_{{\textbf{x}}}\phi (s,\pmb {{\mathcal {Y}}}^{{\textbf{X}},t,{\textbf{x}}}_{s})\big \rangle _{{\mathbb {R}}^{L}}\\&\quad +\frac{1}{2}\textrm{Tr}\bigl (D_{{\textbf{x}}}^{2}\phi (s,\pmb {{\mathcal {Y}}}^{{\textbf{X}},t,{\textbf{x}}}_{s})\bigr )\textrm{d}s\Big ] \\&\quad + {\mathbb {E}}\Big [ {\textbf{1}}_{\{\pmb {{\tilde{\tau }}}\in (t_{j},t_{j+1}]\}} \int _{{\tilde{\tau }}}^{t_{j+1}} \big \langle D_{{\textbf{x}}}\phi (s,\pmb {{\mathcal {Y}}}^{{\textbf{X}},t,{\textbf{x}}}_{s}),\textrm{d}{\textbf{W}}_{s}\big \rangle _{{\mathbb {R}}^{L}} \Big ] \bigg |\,. \end{aligned}$$

Since ${\textbf{1}}_{\{\pmb {{\tilde{\tau }}}\in (t_{j},t_{j+1}]\}}=1-{\textbf{1}}_{\{\pmb {{\tilde{\tau }}}\le t_{j}\}}-{\textbf{1}}_{\{\pmb {{\tilde{\tau }}}>t_{j+1}\}}$, and due to arguments from probability theory, we get

$$\begin{aligned} {\mathbb {E}}\Big [ {\textbf{1}}_{\{\pmb {{\tilde{\tau }}}\in (t_{j},t_{j+1}]\}} \int _{{\tilde{\tau }}}^{t_{j+1}} \big \langle D_{{\textbf{x}}}\phi (s,\pmb {{\mathcal {Y}}}^{{\textbf{X}},t,{\textbf{x}}}_{s}),\textrm{d}{\textbf{W}}_{s}\big \rangle _{{\mathbb {R}}^{L}} \Big ]=0. \end{aligned}$$

Thus, we conclude

$$\begin{aligned} \pmb {\tilde{II}}\le \pmb {{\mathfrak {C}}}(\phi ,g)\cdot \sum \limits _{j=0}^{J-1} \tau ^{j+1} \tilde{{\mathfrak {H}}}_{2}^{(j)} \,. \end{aligned}$$

$\square$

Remark 4.3

The terms in $\tilde{{\mathfrak {H}}}_{1}^{(\cdot )}$ address effects inside $\pmb {{\mathcal {D}}}$, and due to their derivation, are very similar to those in [35, Thm. 3.1]. In contrast, $\tilde{{\mathfrak {H}}}_{2}^{(\cdot )}$ captures effects concerning ‘stopping’. In the framework of Example 1.3 for instance, we have

$$\begin{aligned} \tilde{{\mathfrak {H}}}_{1}^{(j)}\equiv 0\,,\quad \tilde{{\mathfrak {H}}}_{2}^{(j)}=\bigl (C_{\partial \phi }+ \tfrac{1}{2}LC_{D^{2}\phi }\bigr )\cdot {\mathbb {E}}\Big [{\textbf{1}}_{\{\pmb {{\tilde{\tau }}}\in (t_{j},t_{j+1}]\}}\Big ]\,. \end{aligned}$$

The practical application of the a posteriori error estimate (4.33) is restricted by terms $\pmb {{\tilde{\texttt {E}}}_{\texttt {1}}}(\cdot ),\ldots ,\pmb {{\tilde{\texttt {E}}}_{\texttt {6}}}(\cdot )$ in $\tilde{{\mathfrak {H}}}_{1}^{(\cdot )}$ and $\tilde{{\mathfrak {H}}}_{2}^{(\cdot )}$, and even of (4.32) itself, which involves the abstract stopping time $\pmb {{\tilde{\tau }}}$. A possibility to tackle this problem might be the use of concepts from [28] (cf. Sect. 2.1), which, however, requires (additional) approximations.

5 Adaptive weak Euler methods: algorithm and convergence

The Theorems 4.1 resp. 4.7 provide a posteriori error estimates for the approximation of (1.2) resp. (1.9). In this section, we use these results to set up adaptive methods that automatically steer successive local mesh size selection to meet a pre-assigned tolerance ${\texttt {Tol}}>0$ of the overall errors.

5.1 Adaptive weak Euler method for the elliptic PDE (1.1)

The algorithm below combines Scheme 2 with an automatic step size selection procedure, which is based on the a posteriori error estimate in Sect. 4.1. In every step indexed by $j\in {\mathbb {N}}_{0}$, we first check the ‘safeguard’ criterion I (see Algorithm 5.1 below), which holds if the computation of ${\textbf{Y}}_{{\textbf{X}}}^{j}$ through II (2) b) and II (3) in the previous step took place with a step size being ‘too large’. Next, we check via II if ${\textbf{Y}}_{{\textbf{X}}}^{j}$ is ‘close’ to the boundary $\pmb {\partial {\mathcal {D}}}$ and then may possibly be projected onto $\pmb {\partial {\mathcal {D}}}$; and if not, we compute the subsequent iterates ${\textbf{Y}}_{{\textbf{X}}}^{j+1},Y_{V}^{j+1},Y_{Z}^{j+1}$ with the help of step size $\tau ^{j+1}$. With this information at hand, we compute the a posteriori error estimators $\{{\mathfrak {G}}_{\ell }^{(j)}\}_{\ell =1}^{3}$—for which we assume that the error estimators can be computed exactly— and check for a given tolerance $\texttt{Tol}>0$, if the criterion in III which also incorporates the already computed $\{{\mathfrak {G}}_{\ell }^{(k)}\}_{k=0}^{j-1}$, $(\ell =1,2,3)$, and which is

$$\begin{aligned}&\sum \limits _{k=0}^{j} \tau ^{k+1} \big \{{{\mathfrak {G}}}_{1}^{(k)} + {{\mathfrak {G}}}_{2}^{(k)}+ {{\mathfrak {G}}}_{3}^{(k)} \big \} \nonumber \\&\quad \overset{!}{\le } {\texttt {Tol}}\cdot \biggl ( 1+ a_{j}\cdot \sum \limits _{k=0}^{j} \bigg \{\tau ^{k+1}{\mathbb {E}}\big [{\textbf{1}}_{\{ J^{*}>k\}} \big ]+ {\mathbb {E}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{k}\in \pmb {{\mathcal {S}}}_{\tau ^{k+1}}\big \}} \Big ]\bigg \} \biggr )\,, \end{aligned}$$

(5.1)

is met or not to decide whether to coarsen or refine the current mesh size $\tau ^{j+1}$. Different to the local criterion in [35, Algorithm 4.1], criterion (5.1) involves the error estimators $\{{\mathfrak {G}}_{\ell }^{(k)}\}_{\ell =1}^{3}$ with $k\le j$ in summarized form, and aims for ${\texttt {Tol}}$ times a ‘temporal weight’ as corresponding upper bound to properly address stopping in (5.2) in Theorem 5.2. Hence, a summation also appears on the right-hand side of (5.1) to address accumulated errors; see Theorem 5.2 below. Furthermore, $\{a_{j}\}_{j\ge 0}$ is a sequence of additional ‘weights’ with $1\le a_{j-1}\le a_{j}\le \textsf{C}$ for some $\textsf{C} > 0$, which may be given by the user; see Sect. 6 for a detailed explanation. A suitable choice may be $a_{j}:=\min \bigl (1+L\cdot t_{j},1+L\cdot (C+k)\bigr )$, for some $k\in {\mathbb {N}}$, where $C>0$ is the constant from Lemma 3.4. We also refer to Sect. 6 for a Monte-Carlo version of Algorithm 5.1 below.

Algorithm 5.1

Fix ${\texttt {Tol}}>0$ and $\tau ^{1}\ge {\texttt {Tol}}$. Let $(\tau ^j,t_{j},{\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j},Y_{Z}^{j})$ and $a_{j}$ be given for some $j\ge 0$. Define $\tau ^{j+1,0}:=\tau ^{j}$.

I:

(‘${\texttt {Safeguard}}$’) If ${\textbf{Y}}_{{\textbf{X}}}^{j}\notin \pmb {{\mathcal {D}}}$, set $J^{*}:=j$, $t_{J^{*}}:=t_{j}$, ${\textbf{Y}}_{{\textbf{X}}}^{J^{*}}:=\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j})$, $Y_{V}^{J^{*}}:=Y_{V}^{j}$, $Y_{Z}^{J^{*}}:=Y_{Z}^{j}$, and STOP.

—For $\ell =0,1,2,\ldots$ do:

II:

(1):

(‘${\texttt {Localization}}$’) If ${\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1,\ell }}$, set $\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}:={\textbf{Y}}_{{\textbf{X}}}^{j}$ and go to II (3).

(2):

(‘${\texttt {Localization}}$’) If ${\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1,\ell }}$, draw a Bernoulli distributed random variable ${\texttt {U}}$ with parameter $p_{j}$ given in (3.5).

a):

(‘${\texttt {Projection}}$’) If ${\texttt {U}}=1$, set $J^{*}:=j$, $t_{J^{*}}:=t_{j}$, ${\textbf{Y}}_{{\textbf{X}}}^{J^{*}}:=\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j})$, $Y_{V}^{J^{*}}:=Y_{V}^{j}$, $Y_{Z}^{J^{*}}:=Y_{Z}^{j}$, and go to III.

b):

(‘${\texttt {Bouncing \text { }} back}$’) If ${\texttt {U}}=0$, set $\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}:={\textbf{Y}}_{{\textbf{X}}}^{j}+\lambda _{j} \sqrt{\tau ^{j+1,\ell }} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j}) \bigr )$ and go to II (3).

(3):

(‘${\texttt {Solve}}$’) Set ${\textbf{Y}}_{{\textbf{X}}}^{j}:=\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j}$. Compute ${\textbf{Y}}_{{\textbf{X}}}^{j+1}$, $Y_{V}^{j+1}$ and $Y_{Z}^{j+1}$ via Scheme 1 with step size $\tau ^{j+1,\ell }$.

III:

(‘${\texttt {Computation}}$’) Compute $\{{\mathfrak {G}}_{i}^{(j,\ell )}\}_{i=1}^{3}$, i.e., $\{{\mathfrak {G}}_{i}^{(j)}\}_{i=1}^{3}$ with step size $\tau ^{j+1,\ell }$, set

$$\begin{aligned} \pmb {{\mathfrak {G}}}^{(j,\ell )}&:=\sum \limits _{k=0}^{j-1} \tau ^{k+1} \big \{{{\mathfrak {G}}}_{1}^{(k)} + {{\mathfrak {G}}}_{2}^{(k)}+ {{\mathfrak {G}}}_{3}^{(k)} \big \} + \tau ^{j+1,\ell } \big \{{{\mathfrak {G}}}_{1}^{(j,\ell )} + {{\mathfrak {G}}}_{2}^{(j,\ell )}+ {{\mathfrak {G}}}_{3}^{(j,\ell )} \big \}\,,\\ {\texttt {I}}_{j,\ell }&:=\sum \limits _{k=0}^{j-1} \bigg \{\tau ^{k+1}{\mathbb {E}}\big [{\textbf{1}}_{\{ J^{*}>k\}} \big ]+ {\mathbb {E}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{k}\in \pmb {{\mathcal {S}}}_{\tau ^{k+1}}\big \}} \Big ]\bigg \}\\&\quad + \tau ^{j+1,\ell }{\mathbb {E}}\big [{\textbf{1}}_{\{ J^{*}>k\}} \big ]+ {\mathbb {E}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1,\ell }}\big \}} \Big ]\,, \end{aligned}$$

and decide:

(1):

If $\pmb {{\mathfrak {G}}}^{(j,\ell )}>{\texttt {Tol}}\cdot \bigl (1+a_{j}\cdot {\texttt {I}}_{j,\ell } \bigr )$, set $\tau ^{j+1,\ell +1}:=\frac{\tau ^{j+1,\ell }}{2}$, and $\ell \hookrightarrow \ell +1$.

(2):

If $\frac{{\texttt {Tol}}}{2}\cdot \bigl (1+a_{j}\cdot {\texttt {I}}_{j,\ell } \bigr ) \le \pmb {{\mathfrak {G}}}^{(j,\ell )}\le {\texttt {Tol}}\cdot \bigl (1+a_{j}\cdot {\texttt {I}}_{j,\ell } \bigr )$, and

a):

if ${\texttt {U}}=1$, STOP.

b):

if ${\texttt {U}}=0$, set $\tau ^{j+1}:=\tau ^{j+1,\ell }$, $t_{j+1}:=t_{j}+\tau ^{j+1}$, and $j \hookrightarrow j+1$.

(3):

If $\pmb {{\mathfrak {G}}}^{(j,\ell )}< \frac{{\texttt {Tol}}}{2}\cdot \bigl (1+a_{j}\cdot {\texttt {I}}_{j,\ell } \bigr )$, and

a):

if ${\texttt {U}}=1$, STOP.

b):

if ${\texttt {U}}=0$, set $\tau ^{j+1}:=\tau ^{j+1,\ell }$, $t_{j+1}:=t_{j}+\tau ^{j+1}$. Then set $\tau ^{j+1}:=2\tau ^{j+1}$ and $j \hookrightarrow j+1$.

After the admissible step size $\tau ^{j+1}$ has been generated through the (finite) sequence $\{\tau ^{j+1,\ell }\}_{\ell \ge 0}$ of refinements III (1) which precedes a single potential coarsening step III (3), the new local error (up to time $t_{j+1}$) is bounded by (5.1).

The following theorem validates termination and convergence (w.r.t. ‘${\texttt {Tol}}$’) of Algorithm 5.1; its proof is similar to [35, Thm. 4.2], and exploits the stability results in Lemmata 3.3 and 3.4.

Theorem 5.2

Let $\texttt {Tol} >0$. Suppose (A0) – (A3) in Sect. 3.1. Further suppose that the step sizes $\{\tau ^{j+1}\}_{j\ge 0}$ are sufficiently small according to Lemma 3.4, or either (A1$^{*}$) or (A1$^{**}$) are valid. Fix ${\textbf{x}}\in \pmb {{\mathcal {D}}}$. Then, Algorithm 5.1 generates each local step size $\tau ^{j+1}$ after ${\mathcal {O}}\bigl (\log (\texttt {Tol} ^{-1})\bigr )$ many iterations and terminates after ${\mathbb {E}}\big [J^{*}\big ]={\mathcal {O}}\bigl (\texttt {Tol} ^{-1}\bigr )$ time steps. Furthermore, the $4-$tuple $\big \{(\tau ^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},Y_{V}^{j},Y_{Z}^{j})\big \}_{j\ge 0}$ satisfies

$$\begin{aligned} \Bigl \vert u({\textbf{x}}) - {\mathbb {E}}\bigl [\phi (\textbf{Y}_{{\textbf{X}}}^{J^{*}})Y_{V}^{J^{*}}+Y_{Z}^{J^{*}}\bigr ] \Bigr \vert \le {\textbf {C}}\cdot \texttt {Tol} , \end{aligned}$$

(5.2)

where ${\textbf {C}}>0$ depends on $\pmb {C}(\phi ,g)>0$ from Lemma 3.1, $C>0$ from Lemma 3.4, and the upper bound of $\max \limits _{j\ge 0} a_{j}$.

In the following proof, let $\pmb {C}\ge 1$ be a constant which might differ from line to line, but is always independent of $\tau ^{j+1}$ and $j\ge 0$.

Proof

a) Termination for each $j\ge 0$: Fix $j\ge 0$, $\ell \ge 0$, and use (4.22), (4.23) and (4.24) to deduce

$$\begin{aligned} \tau ^{j+1,\ell }\big \{{\mathfrak {G}}_{1}^{(j,\ell )}+{\mathfrak {G}}_{2}^{(j,\ell )}+ {\mathfrak {G}}_{3}^{(j,\ell )} \big \}\le & {} \pmb {C} \tau ^{j+1,\ell }\bigg \{ \tau ^{j+1,\ell } {\mathbb {E}}\big [{\textbf{1}}_{\{J^{*}>j \}} \big ]\nonumber \\{} & {} + {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1,\ell }} \big \}} \Big ]\bigg \} . \end{aligned}$$

(5.3)

Hence, we generate a finite sequence $\{\tau ^{j+1,\ell }\}_{\ell =1}^{\ell _{j+1}^{*}}$ with $\tau ^{j+1,\ell }=\frac{\tau ^{j+1,0}}{2^{\ell }}$, $\ell =0,\ldots ,\ell _{j+1}^{*}$, according to the refinement mechanism III (1) in Algorithm 5.1 until either III (2), or III (3) is met. In view of (5.3), as well as

$$\begin{aligned} \pmb {{\mathfrak {G}}}^{(j,\ell )}&\le {\texttt {Tol}}\cdot \bigg \{1+a_{j-1}\cdot \sum \limits _{k=0}^{j-1} \tau ^{k+1}{\mathbb {E}}\big [{\textbf{1}}_{\{ J^{*}>k\}} \big ]+ {\mathbb {E}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{k}\in \pmb {{\mathcal {S}}}_{\tau ^{k+1}}\big \}} \Big ]\bigg \} \nonumber \\&\quad + \pmb {C} \tau ^{j+1,\ell }\bigg \{ \tau ^{j+1,\ell } {\mathbb {E}}\big [{\textbf{1}}_{\{J^{*}>j \}} \big ] + {\mathbb {E}}\Big [ {\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1,\ell }} \big \}} \Big ]\bigg \} \nonumber \\&\overset{!}{\le }{\texttt {Tol}}\cdot \bigl (1+a_{j}\cdot {\texttt {I}}_{j,\ell }\bigr )\,, \end{aligned}$$

(5.4)

and the fact that $a_{j}\ge 1$ and $a_{j}-a_{j-1}\ge 0$, we find out that $\ell =\Big \lceil \nicefrac {\log \Bigl (\tfrac{ \tau ^{j+1,0} \pmb {C}}{{\texttt {Tol}}} \Bigr )}{\log (2)} \Big \rceil$ is the smallest number such that

$$\begin{aligned} \pmb {C}\cdot \tau ^{j+1,\ell }=\pmb {C} \cdot \frac{\tau ^{j+1,0}}{2^{\ell }} {\mathop {\le }\limits ^{!}}{\texttt {Tol}}, \end{aligned}$$

which, however, implies (5.4). Consequently,

$$\begin{aligned} 0\le \ell _{j+1}^{*}\le \Bigg \lceil \frac{\log \Bigl (\tfrac{ \tau ^{j+1,0} \pmb {C}}{{\texttt {Tol}}} \Bigr )}{\log (2)} \Bigg \rceil \,, \end{aligned}$$

(5.5)

which yields a maximum of ${\mathcal {O}}\bigl (\log ({\texttt {Tol}}^{-1})\bigr )$ (refinement) steps to accept the local step size $\tau ^{j+1}:=\tau ^{j+1,\ell _{j+1}^{*}}=\frac{\tau ^{j+1,0}}{2^{\ell _{j+1}^{*}}}$.

(b) Global termination We show by induction that

$$\begin{aligned} \tau ^{j+1}\ge \frac{{\texttt {Tol}}}{2\pmb {C}} \qquad (j\ge 0). \end{aligned}$$

(5.6)

This means that all step sizes are bounded from below by $\frac{{\texttt {Tol}}}{2\pmb {C}}$, which, in particular, can be considered as the smallest step size that Algorithm 5.1 is able to generate.

The base case follows by the choice of the initial mesh size $\tau ^{1}\ge {\texttt {Tol}}$. Now suppose that we have generated ${\textbf{Y}}_{{\textbf{X}}}^{j}$, $Y_{V}^{j}$ and $Y_{Z}^{j}$ with step size $\tau ^{j}\ge \frac{{\texttt {Tol}}}{2\pmb {C}}$ and no ‘stopping’ has been detected before. In order to successfully compute ${\textbf{Y}}_{{\textbf{X}}}^{j+1}$ (and $Y_{V}^{j}$, $Y_{Z}^{j+1}$), we set $\tau ^{j+1,0}:=\tau ^{j}$ (if III (2) occurred in the generation of $\tau ^{j}$), or $\tau ^{j+1,0}:=2\tau ^{j}$ (if III (3) occurred in the generation of $\tau ^{j}$). In all cases, $\tau ^{j+1,0}\ge \frac{{\texttt {Tol}}}{2\pmb {C}}$. Via a), we generate a finite sequence $\{\tau ^{j+1,\ell }\}_{\ell =0}^{\ell _{j+1}^{*}}$ until either III (2), or III (3) is met, and then generate ${\textbf{Y}}_{{\textbf{X}}}^{j+1}$ (and $Y_{V}^{j}$, $Y_{Z}^{j+1}$) with step size $\tau ^{j+1}:=\tau ^{j+1,\ell ^{*}_{j+1}}=\frac{\tau ^{j+1,0}}{2^{\ell ^{*}_{j+1}}}$. Since $\lceil x \rceil \le 1+x$, $x\in {\mathbb {R}}$, we conclude by means of (5.5) that

$$\begin{aligned} \tau ^{j+1}:=\tau ^{j+1,\ell ^{*}_{j+1}}=\frac{\tau ^{j+1,0}}{2^{\ell ^{*}_{j+1}}} \ge \frac{{\texttt {Tol}}}{2\pmb {C}}. \end{aligned}$$

Having (5.6) at hand, we conclude that

$$\begin{aligned} {\mathbb {E}}[t_{J^{*}}]=\sum \limits _{j=0}^{\infty } \tau ^{j+1}{\mathbb {E}}\big [ {\textbf{1}}_{\{ J^{*}>j\}} \big ]\ge {\mathbb {E}}\big [J^{*}\big ]\cdot \frac{{\texttt {Tol}}}{2\pmb {C}}. \end{aligned}$$

By Lemma 3.4, we may infer ${\mathbb {E}}\big [J^{*}\big ]={\mathcal {O}}\bigl ({\texttt {Tol}}^{-1}\bigr )$.

(c) Convergence rate Let $j \ge 0$. We (upper) bound the right-hand side of (5.1) (independent of j). By means of the boundedness of $a_{j}\le \textsf{C}$, and Lemmata 3.3 and 3.4, we immediately obtain

$$\begin{aligned}&{\texttt {Tol}}\cdot \biggl ( 1+ a_{j}\cdot \sum \limits _{k=0}^{j} \bigg \{\tau ^{k+1}{\mathbb {E}}\big [{\textbf{1}}_{\{ J^{*}>k\}} \big ]+ {\mathbb {E}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{k}\in \pmb {{\mathcal {S}}}_{\tau ^{k+1}}\big \}} \Big ]\bigg \} \biggr )\nonumber \\&\quad \le {\texttt {Tol}}\cdot \biggl ( 1+ \textsf{C} \cdot \sum \limits _{k=0}^{\infty } \bigg \{\tau ^{k+1}{\mathbb {E}}\big [{\textbf{1}}_{\{ J^{*}>k\}} \big ]+ {\mathbb {E}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{k}\in \pmb {{\mathcal {S}}}_{\tau ^{k+1}}\big \}} \Big ]\bigg \} \biggr ) \nonumber \\&\quad \le {\texttt {Tol}}\cdot \biggl ( 1+ \textsf{C} \cdot \biggl ( {\mathbb {E}}[t_{J^{*}}]+ \sum \limits _{k=0}^{\infty }{\mathbb {E}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{k}\in \pmb {{\mathcal {S}}}_{\tau ^{k+1}}\big \}} \Big ]\biggr ) \biggr ) \nonumber \\&\quad \le {\texttt {Tol}}\cdot \biggl ( 1+ \textsf{C} \cdot \bigl ( C+ 2 \bigr ) \biggr )\,, \end{aligned}$$

(5.7)

where $C>0$ is from Lemma 3.4. Now, (5.2) immediately follows from the a posteriori error estimate (4.1), the tolerance criterion in Algorithm 5.1 (cf. (5.1)), and (5.7). $\square$

5.2 Adaptive weak Euler method for the parabolic PDE (1.8)

By following a similar guideline in the setup of Algorithm 5.1, we present an adaptive algorithm (see Algorithm 5.3 below) for the (pointwise, i.e., for $(t,{\textbf{x}})\in [0,T)\times \pmb {{\mathcal {D}}}$ fixed) approximation of PDE (1.8). Similar to Theorem 5.2 in Sect. 5.1, Theorem 5.4 validates termination and convergence of the adaptive method. For a detailed discussion and verification of the upcoming reults, we refer to [34].

Algorithm 5.3

Fix ${\texttt {Tol}}>0$ and $\tau ^{1}\ge {\texttt {Tol}}$. Let $(\tau ^j,t_{j}, {\textbf{Y}}_{{\textbf{X}}}^{j},Y_{Z}^{j})$ and $a_{j}=1+L\cdot t_{j}$ be given for some $j\ge 0$. Define $\tau ^{j+1,0}:=\tau ^{j}$.

I:

Proceed as in Step I in Algorithm 5.1.

— For $\ell =0,1,2,\ldots$ do:

II:

Proceed as in Step II in Algorithm 5.1.

III:

(‘${\texttt {Computation}}$’)  Compute $\{{\mathfrak {H}}_{i}^{(j,\ell )}\}_{i=1}^{3}$, i.e., $\{{\mathfrak {H}}_{i}^{(j)}\}_{i=1}^{3}$ with step size $\tau ^{j+1,\ell }$, set

$$\begin{aligned} \pmb {{\mathfrak {H}}}^{(j,\ell )}&:=\sum \limits _{k=0}^{j-1} \tau ^{k+1} \big \{{{\mathfrak {H}}}_{1}^{(k)} + {{\mathfrak {H}}}_{2}^{(k)}+ {{\mathfrak {H}}}_{3}^{(k)} \big \} + \tau ^{j+1,\ell } \big \{{{\mathfrak {H}}}_{1}^{(j,\ell )} + {{\mathfrak {H}}}_{2}^{(j,\ell )}+ {{\mathfrak {H}}}_{3}^{(j,\ell )} \big \}\,,\\ {\texttt {I}}_{j,\ell }&:=\sum \limits _{k=0}^{j-1} \bigg \{\tau ^{k+1}{\mathbb {E}}\big [{\textbf{1}}_{\{ J^{*}>k\}} \big ]+ {\mathbb {E}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{k}\in \pmb {{\mathcal {S}}}_{\tau ^{k+1}}\big \}} \Big ]\bigg \}\\&\quad + \tau ^{j+1,\ell }{\mathbb {E}}\big [{\textbf{1}}_{\{ J^{*}>k\}} \big ]+ {\mathbb {E}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1,\ell }}\big \}} \Big ]\,, \end{aligned}$$

and proceed according to III (1) – (3) in Algorithm 5.1.

STOP, if $t_{j}\ge T$ for some j and set $J:=j$, $J^{*}:=J$, $t_{J^{*}}=t_{J}$, ${\textbf{Y}}_{{\textbf{X}}}^{J^{*}}:={\textbf{Y}}_{{\textbf{X}}}^{J}$, $Y_{Z}^{J^{*}}:=Y_{Z}^{J}$.

Similar to Theorem 5.2, the following theorem states termination and convergence (w.r.t. ‘${\texttt {Tol}}$’) of Algorithm 5.3. Its proof simplifies due to the a priori knowledge of the terminal time $T>0$, and will thus be omitted.

Theorem 5.4

Let $\texttt {Tol} >0$. Suppose (B0)–(B3) in Sect. 3.2. Fix $(t,{\textbf{x}})\in [0,T)\times \pmb {{\mathcal {D}}}$. Then, Algorithm 5.3 generates each local step size $\tau ^{j+1}$ after ${\mathcal {O}}\bigl (\log (\texttt {Tol} ^{-1})\bigr )$ many iterations and terminates after ${\mathcal {O}}\bigl (\texttt {Tol} ^{-1}\bigr )$ time steps. Furthermore, the $3-$tuple $\big \{(\tau ^{j+1},{\textbf{Y}}_{{\textbf{X}}}^{j},Y_{Z}^{j})\big \}_{j\ge 0}$ satisfies

$$\begin{aligned} \Bigl \vert u(t,{\textbf{x}}) - {\mathbb {E}}\bigl [\phi (t_{J^{*}},\textbf{Y}_{{\textbf{X}}}^{J^{*}})+Y_{Z}^{J^{*}}\bigr ] \Bigr \vert \le {\textbf {C}}\cdot \texttt {Tol} , \end{aligned}$$

where ${\textbf {C}}>0$ depends on $\pmb {{\mathfrak {C}}}(\phi ,g)\ge 1$ from Lemma 3.2, and $T>0$.

6 Monte-Carlo simulations for adaptive weak Euler methods

All simulations are conducted via MATLAB (version: 2017a and 2019a).

In the practical implementation of Algorithm 5.1 (and also for Algorithm 5.3), we replace all expectations $\pmb {{\texttt {E}}_{{\ell }}}(\cdot )$, $\pmb {{{\ell }}}=1,\ldots ,15$ contained in $\big \{{\mathfrak {G}}_{\ell }^{(\cdot )}\big \}_{\ell =1}^{3}$ (in Algorithm 5.1) by their empirical means $\pmb {{\texttt {E}}_{{\ell }}}^{({\texttt {M}})}(\cdot )$, $\pmb {{{\ell }}}=1,\ldots ,15$, and write $\big \{{\mathfrak {G}}_{\ell }^{(\cdot ),({\texttt {M}})}\big \}_{\ell =1}^{3}$ for the related (empirical) error estimators. Moreover, in every simulation concerning (1.1), we chose $a_{j}:=\min \bigl (1+L\cdot t_{j},1+L\cdot C\bigr )$ (with $C>0$ from Lemma 3.4) as additional ‘weight’ in Algorithm 5.1. For all experiments reported in this section, by repeating the simulations for varying ${\texttt {M}}$, we found ${\texttt {M}}\in \{10^{4},10^{5}\}$ to be large enough to ensure a stable (computational) convergence study.

For the sake of practicality, we formulate an implementable Monte-Carlo version of Algorithm 5.1. A Monte-Carlo version of Algorithm 5.3 can be stated in a similar manner.

Algorithm 6.1

(Monte-Carlo version of Algorithm 5.1) Fix ${\texttt {Tol}}>0$, ${\texttt {M}}\in {\mathbb {N}}$ and $\tau ^{1}\ge {\texttt {Tol}}$. Let $\big \{\bigl (\tau ^{j},t_{j}, {\textbf{Y}}_{{\textbf{X}}}^{j,m},Y_{V}^{j,m},Y_{Z}^{j,m}\bigr )\bigr \}_{m=1}^{{\texttt {M}}}$ be given for some $j\ge 0$, let $a_{j}$ be given for some $j\ge 0$ and let ${\mathcal {M}}_{j}$ be the set of all sample indices $m=1,\ldots ,{\texttt {M}}$, for which no exit of $\{{\textbf{Y}}_{{\textbf{X}}}^{i,m}\}_{i=0}^{j}$ from $\pmb {{\mathcal {D}}}$ has been detected. Define $\tau ^{j+1,0}:=\tau ^{j}$.

For $m\in {\mathcal {M}}_{j}$ do:

I:

(‘${\texttt {Safeguard}}$’) If ${\textbf{Y}}_{{\textbf{X}}}^{j,m}\notin \pmb {{\mathcal {D}}}$, set $J^{*,m}:=j$, $t_{J^{*,m}}:=t_{j}$, ${\textbf{Y}}_{{\textbf{X}}}^{J^{*,m},m}:=\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j,m})$, $Y_{V}^{J^{*,m},m}:=Y_{V}^{j,m}$, $Y_{Z}^{J^{*,m},m}:=Y_{Z}^{j,m}$, and set ${\mathcal {M}}_{j}:={\mathcal {M}}_{j}\setminus \{m\}$.

end-for

For $\ell =0,1,2,\ldots$ do: Set $\tilde{{\mathcal {M}}}_{j}:={\mathcal {M}}_{j}$.

For $m\in {\mathcal {M}}_{j}$ do:

II:

(1):

(‘${\texttt {Localization}}$’) If ${\textbf{Y}}_{{\textbf{X}}}^{j,m}\in \pmb {{\mathcal {D}}}\setminus \pmb {{\mathcal {S}}}_{\tau ^{j+1,\ell }}$, set $\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j,m}:={\textbf{Y}}_{{\textbf{X}}}^{j,m}$ and go to II (3).

(2):

(‘${\texttt {Localization}}$’) If ${\textbf{Y}}_{{\textbf{X}}}^{j,m}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1,\ell }}$, draw a Bernoulli distributed random variable ${\texttt {U}}^{m}$ with parameter $p_{j}^{m}$ given in (3.5).

a):

(‘${\texttt {Projection}}$’) If ${\texttt {U}}^{m}=1$, set $J^{*,m}:=j$, $t_{J^{*,m}}:=t_{j}$, ${\textbf{Y}}_{{\textbf{X}}}^{J^{*,m},m}:=\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j,m})$, $Y_{V}^{J^{*,m},m}:=Y_{V}^{j,m}$, $Y_{Z}^{J^{*,m},m}:=Y_{Z}^{j,m}$, and set $\tilde{{\mathcal {M}}}_{j}:=\tilde{{\mathcal {M}}}_{j}\setminus \{m\}$.

b):

(‘${\texttt {Bouncing back}}$’) If ${\texttt {U}}^{m}=0$, set $\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j,m}:={\textbf{Y}}_{{\textbf{X}}}^{j,m}+\lambda _{j}^{m} \sqrt{\tau ^{j+1}} \pmb {n}\bigl (\Pi _{\pmb {\partial {\mathcal {D}}}}({\textbf{Y}}_{{\textbf{X}}}^{j,m}) \bigr )$ and go to II (3).

(3):

(‘${\texttt {Solve}}$’) Set ${\textbf{Y}}_{{\textbf{X}}}^{j,m}:=\overline{{\textbf{Y}}}_{{\textbf{X}}}^{j,m}$. Compute ${\textbf{Y}}_{{\textbf{X}}}^{j+1,m}$, $Y_{V}^{j+1,m}$ and $Y_{Z}^{j+1,m}$ via Scheme 1 with step size $\tau ^{j+1,\ell }$.

end-for

III:

(‘${\texttt {Computation}}$’) Compute $\{{\mathfrak {G}}_{i}^{(j,\ell ),({\texttt {M}})}\}_{i=1}^{3}$, i.e., $\{{\mathfrak {G}}_{i}^{(j),({\texttt {M}})}\}_{i=1}^{3}$ with step size $\tau ^{j+1,\ell }$, set

$$\begin{aligned} \pmb {{\mathfrak {G}}}^{(j,\ell ),({\texttt {M}})}&:=\sum \limits _{k=0}^{j-1} \tau ^{k+1} \big \{{{\mathfrak {G}}}_{1}^{(k),({\texttt {M}})} + {{\mathfrak {G}}}_{2}^{(k),({\texttt {M}})}+ {{\mathfrak {G}}}_{3}^{(k),({\texttt {M}})} \big \} \\&\quad + \tau ^{j+1,\ell } \big \{{{\mathfrak {G}}}_{1}^{(j,\ell ),({\texttt {M}})} + {{\mathfrak {G}}}_{2}^{(j,\ell ),({\texttt {M}})}+ {{\mathfrak {G}}}_{3}^{(j,\ell ),({\texttt {M}})} \big \}\,,\\ {\texttt {I}}_{j,\ell }^{({\texttt {M}})}&:=\sum \limits _{k=0}^{j-1} \bigg \{\tau ^{k+1}{\mathbb {E}}_{{\texttt {M}}}\big [{\textbf{1}}_{\{ J^{*}>k\}} \big ]+ {\mathbb {E}}_{{\texttt {M}}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{k}\in \pmb {{\mathcal {S}}}_{\tau ^{k+1}}\big \}} \Big ]\bigg \}\\&\quad + \tau ^{j+1,\ell }{\mathbb {E}}_{{\texttt {M}}}\big [{\textbf{1}}_{\{ J^{*}>k\}} \big ]+ {\mathbb {E}}_{{\texttt {M}}}\Big [{\textbf{1}}_{\big \{{\textbf{Y}}_{{\textbf{X}}}^{j}\in \pmb {{\mathcal {S}}}_{\tau ^{j+1,\ell }}\big \}} \Big ]\,, \end{aligned}$$

and decide:

(1):

If $\pmb {{\mathfrak {G}}}^{(j,\ell ),({\texttt {M}})}>{\texttt {Tol}}\cdot \bigl (1+a_{j}\cdot {\texttt {I}}_{j,\ell }^{({\texttt {M}})} \bigr )$, set $\tau ^{j+1,\ell +1}:=\frac{\tau ^{j+1,\ell }}{2}$, and $\ell \hookrightarrow \ell +1$.

(2):

If $\frac{{\texttt {Tol}}}{2}\cdot \bigl (1+a_{j}\cdot {\texttt {I}}_{j,\ell }^{({\texttt {M}})} \bigr ) \le \pmb {{\mathfrak {G}}}^{(j,\ell ),({\texttt {M}})}\le {\texttt {Tol}}\cdot \bigl (1+a_{j}\cdot {\texttt {I}}_{j,\ell }^{({\texttt {M}})} \bigr )$, set $\tau ^{j+1}:=\tau ^{j+1,\ell }$, $t_{j+1}:=t_{j}+\tau ^{j+1}$, ${\mathcal {M}}_{j+1}:=\tilde{{\mathcal {M}}}_{j}$, end-for and $j \hookrightarrow j+1$.

(3):

If $\pmb {{\mathfrak {G}}}^{(j,\ell ),({\texttt {M}})}< \frac{{\texttt {Tol}}}{2}\cdot \bigl (1+a_{j}\cdot {\texttt {I}}_{j,\ell }^{({\texttt {M}})} \bigr )$, set $\tau ^{j+1}:=\tau ^{j+1,\ell }$, $t_{j+1}:=t_{j}+\tau ^{j+1}$, ${\mathcal {M}}_{j+1}:=\tilde{{\mathcal {M}}}_{j}$. Then, set $\tau ^{j+1}:=2\tau ^{j+1}$, end-for and $j \hookrightarrow j+1$.

STOP, if ${\mathcal {M}}_{j}=\emptyset$.

Note that the set ‘${\mathcal {M}}_{j}$’ which contains the indices of ‘active’ samples in $\pmb {{\mathcal {D}}}$ shrinks as time progresses.

As seen in Examples 1.2 and 1.4 (and also in (most of) the examples below), the plots of the step sizes generated via Algorithms 5.1 and 5.3 conceptually have the same structure (‘U’-profile). This related dynamics can be classified into three phases (cf. Fig. 2):

• Initial phase In this stage, no stopping dynamics takes place, and step sizes are refined until first samples enter the boundary strips.

• Bulk phase Here, the step sizes attain smallest values and remain constant over a certain period of time. In this period, the majority of samples are projected onto the boundary $\pmb {\partial {\mathcal {D}}}$, where the smallness of the step sizes guarantee accuracy of those projections.

• End phase In this phase, the leftover samples, i.e., the ‘outlier-samples’, are gradually forced to be projected onto $\pmb {\partial {\mathcal {D}}}$ by a gradual coarsening of the step sizes. Besides the guidance of refinement/coarsening through the error estimators, the ‘temporal weight’ in (5.1) is mainly responsible for this additional dynamics towards the end.

So far, the data requirements of Examples 1.2 and 1.4 coincide with the assumptions in Sect. 3. In the following two subsections, we (mostly) consider data setups for simulations of (1.1) and (1.8), which go beyond the scope of our theoretical backup. Even in these cases, where e.g. $\pmb {{\mathcal {D}}}$ has a reentrant corner (see Example 6.3), or boundary and terminal data are incompatible (see Examples 6.4 and 6.5), Algorithms 5.1 and 5.3 still yield promising results.

6.1 Simulations for the elliptic PDE (1.1)

The following example with a quadratic inhomogeneity g and a quartic boundary condition $\phi$ is taken from [9, Problem 4.2.2b]. The discussion in [6, Subsec. 5.5, Fig. 9] states sub-optimal practical performance of Scheme 2, if run on a fixed mesh; see Fig. 6C below. In contrast to this, the results in Example 6.2 below show that complementary ‘time adaptivity’ (see Algorithm 5.1) recovers optimal convergence.

Example 6.2

(see [9, Problem 4.2.2b]) Let $L=32$ and $\pmb {{\mathcal {D}}}:=\big \{{\textbf{x}}\in {\mathbb {R}}^{L}\,:\,\Vert {\textbf{x}}\Vert _{{\mathbb {R}}^{L}}<1\big \}$. Consider (1.1) with $\pmb {\sigma }({\textbf{x}})={\mathbb {I}}$, ${\textbf{b}}({\textbf{x}})\equiv {\textbf{0}}$, $c({\textbf{x}})\equiv 0$ and

$$\begin{aligned} g({\textbf{x}})=-\sum \limits _{i=1}^{L}i\cdot x_{i}^{2}\,,\qquad \phi ({\textbf{x}})=\frac{1}{6}\sum \limits _{i=1}^{L}i\cdot x_{i}^{4} \qquad ({\textbf{x}}\in \pmb {{\mathcal {D}}})\,. \end{aligned}$$

For ${\texttt {M}}=10^5$ fixed, we investigate the convergence rate for the approximation ${\texttt {u}}^{({\texttt {M}})}({\textbf{x}})$ of the solution $u({\textbf{x}})=\phi ({\textbf{x}})$ at ${\textbf{x}}=(\nicefrac {5}{100},\ldots ,\nicefrac {5}{100})^{\top }$. Figure 6B illustrates optimal order of convergence 1 with respect to ${\texttt {Tol}}$—as opposed to sub-optimal order $\frac{1}{2}$ (as also found in [6, Subsec. 5.5, Fig. 9]) on uniform-meshes; see Fig. 6C. It seems that time adaptivity in this respect preserves the theoretically stated first order convergence even for ‘complicated’ functions g and $\phi$ involved in (1.1). Figure 6D illustrates the time efficiency to reach the same accuracy of Algorithm 5.1 over Scheme 2 on a uniform mesh.

Fig. 6

A Semi-Log plot of the (adaptive) step sizes generated via Algorithm 5.1 (with ${\texttt {Tol}}=0.01$). B Convergence rate (error) Log-log plot via Algorithm 5.1. C Convergence rate (error) Log-log plot via Scheme 2 on uniform meshes with step size h. D Semi-Log plot of computational times: adaptive vs. uniform

The next example from [6, Example 1] considers a data setup for (1.1) in a $3-$dimensional, non-convex domain $\pmb {{\mathcal {D}}}$ with a reentrant corner. Computational studies in [6, Example 1] with the original method [39] on uniform meshes (again) state a suboptimal performance when approximating the solution at a point close to the corner. Although this experimental framework violates our assumptions, we see that Algorithm 5.1 even in this case performs very well, and achieves the desired order of convergence; see Fig. 7D.

Example 6.3

(see [6, Example 1]) Let $\pmb {{\mathcal {D}}}:=\big \{{\textbf{x}}=(x_{1},x_{2},x_{3})^{\top }\in {\mathbb {R}}^{3}:\,\Vert {\textbf{x}}\Vert _{{\mathbb {R}}^{3}}<1\big \}{\setminus } \big \{{\textbf{x}}=(x_{1},x_{2},x_{3})^{\top }\,:\, x_{1}\ge 0.67\,,\;x_{2}\ge 0.67\,,\;x_{3}\ge 0.67 \big \}$. Consider (1.1) with

$$\begin{aligned} \pmb {\sigma }({\textbf{x}})&=\begin{bmatrix} \sqrt{1+|x_{3} |} &{} 0 &{} 0 \\ \frac{1}{2} \sqrt{1+|x_{1} |} &{} \sqrt{\frac{3}{4}} \sqrt{1+|x_{1} |} &{} 0 \\ 0 &{} \frac{1}{2} \sqrt{1+|x_{2} |} &{} \sqrt{\frac{3}{4}}\sqrt{1+|x_{2} |} \\ \end{bmatrix} \,, \quad {\textbf{b}}({\textbf{x}})=\begin{bmatrix} x_{2} \\ x_{3} \\ x_{1} \\ \end{bmatrix} \,, \quad c({\textbf{x}})\equiv 0\,, \\ g({\textbf{x}})&=-\Bigl ( x_{2}^{2}x_{3} + x_{3}^{2} x_{1} + x_{1}^{2} x_{2}\\&\quad + \frac{1}{2}\Bigl ( x_{3} \sqrt{1+|x_{1} |} \sqrt{1+|x_{3} |} + x_{1} \sqrt{\frac{3}{4}} \sqrt{1+|x_{1} |} \sqrt{1+|x_{2} |}\Bigr ) \Bigr )\,,\\ \phi ({\textbf{x}})&=x_{1} x_{2} x_{3}\,. \end{aligned}$$

The corresponding solution is given by $u({\textbf{x}})=x_{1} x_{2} x_{3}$. We fix ${\textbf{x}}=(0.57,0.57,0.57)^{\top }$, and use Algorithm 5.1 (with ${\texttt {Tol}}=0.01$, ${\texttt {M}}=10^{5}$) to approximate $u({\textbf{x}})$ (see Fig. 7B and C for resulting features). As stated in [6, Example 1], the suboptimal performance there is due the frequent overshoots of the inner corner of $\pmb {{\mathcal {D}}}$, where an ‘ad-hoc’ value $\lambda _{j}\equiv 2$ in (3.4) is used within the related method (on uniform meshes) to characterize the boundary strips. In contrast, the (automatic) choice of adaptive step sizes in combination with the flexible choice of $\lambda _{j}$ according to (3.4) accurately identifies particular boundary strips, i.e., leads to proper projections onto $\pmb {\partial {\mathcal {D}}}$, and yields a first order convergent approximation. Furthermore, Algorithm 5.1 is efficient to reach the same accuracy (Error $\approx 0.002$); the needed number of steps to terminate is $\max \limits _{m=1,\ldots ,{\texttt {M}}} J^{*}(\omega _{m})=842$ (CPU time: 3786 s)—opposed to $\max \limits _{m=1,\ldots ,{\texttt {M}}} J^{*}(\omega _{m})=2123$ (CPU time: 6000 sec) for Scheme 2 (with $\lambda _{j}\equiv 2$) on a uniform mesh.

Fig. 7

A Representation of $\overline{\pmb {{\mathcal {D}}}}$. B Semi-Log plot of the (adaptive) step sizes generated via Algorithm 5.3. C Shape of the distribution of $t_{J^{*}}$ illustrated via a histogram plot. D Convergence rate (error) Log-log plot via Algorithm 5.3 (${\texttt {M}}=5\cdot 10^5$, ${\textbf{x}}=(0.57,0.57,0.57)^{\top }$)

6.2 Simulations for the parabolic PDE (1.8)

The following example from [15] (‘time-reversed’ here in our setting) considers incompatible terminal and boundary data in (1.8), and hence violates assumption (B3) in Sect. 3.2. We observe encouraging results with Algorithm 5.3 also in this case, where different structures of step size plots (‘L’-profiles) occur, depending on the point in space and time at which the solution is approximated; see Fig. 8D below.

Example 6.4

[see [15, Subsec. 3.2]] Let $T=1$, and $\pmb {{\mathcal {D}}}:=(0,1)^{2}$. Consider (1.8) with $\pmb {\sigma }({\textbf{x}})\equiv \sqrt{0.4}\cdot {\mathbb {I}}$, ${\textbf{b}}({\textbf{x}})\equiv {\textbf{0}}$, $g(t,{\textbf{x}})\equiv 0$, and

$$\begin{aligned} \phi (t,{\textbf{x}})={\left\{ \begin{array}{ll} \sin \bigl (\frac{5\pi }{4}x_{1}+\frac{3\pi }{4}\bigr )\sin \bigl (\frac{5\pi }{4}x_{2}+\frac{3\pi }{4}\bigr )\,, &{} t=T \\ 0\,, &{} t<T\,. \end{array}\right. } \end{aligned}$$

For ${\texttt {M}}=10^{4}$ and ${\texttt {Tol}}=10^{-4}$ fixed, Fig. 8 below displays step size plots for the approximation of $u(0.98,{\textbf{x}})$ at two different values for ${\textbf{x}}$: one in the spatio-temporal incompatibility region (cf. $(\textrm{B})$), and one in the interior of $\pmb {{\mathcal {D}}}$ (cf. $(\textrm{C})$). In both step size plots, we observe a ‘L’-profile structure—opposed to a ‘U’-structure as before, which is due to the temporal dynamics involved here, since ‘not enough’ samples are projected onto $\pmb {\partial {\mathcal {D}}}$ within the short time interval [0.98, 1]. Consequently, a gradual coarsening, i.e., the ‘end phase’ does not occur—opposed to Fig. 9B and C, where for ${\texttt {Tol}}=0.01$ fixed, related step size plots are shown at a different time $t=0$, at which the incompatibility has dissolved. Moreover, the reversed ‘L’-profile structure of the step size plot in Fig. 9B results from the position of the (spatial) point (close to $\pmb {\partial {\mathcal {D}}}$) at which u is approximated, and the choice of ${\texttt {Tol}}$: here, samples are already located in the boundary strips at the beginning, which is why the ‘initial phase’ does not take place. Furthermore, in order to make up for the incompatibility effect, more time steps, i.e., $\max \limits _{m=1,\ldots ,{\texttt {M}}}J^{*}(\omega _{m})=154$, are needed in Fig. 8B as opposed to $\max \limits _{m=1,\ldots ,{\texttt {M}}}J^{*}(\omega _{m})=42$ in Fig. 8C. On the contrary, at time $t=0$, more time steps, i.e., $\max \limits _{m=1,\ldots ,{\texttt {M}}}J^{*}(\omega _{m})=128$, are needed for an approximation at the point in the interior of $\pmb {{\mathcal {D}}}$ (cf. Fig. 9C) as opposed to $\max \limits _{m=1,\ldots ,{\texttt {M}}}J^{*}(\omega _{m})=57$ for an approximation at the point close to $\pmb {\partial {\mathcal {D}}}$ (cf. Fig. 9B).

Fig. 8

A Solution in $\pmb {{\mathcal {D}}}$ at $t=0.98$. Semi-Log plots of (adaptive) step sizes for $t=0.98$ and B ${\textbf{x}}=(0.05,0.6)^{\top }$, C ${\textbf{x}}=(0.6,0.6)^{\top }$. D Convergence rate (error) Log-log plot via Algorithm 5.3 (${\texttt {M}}=5\cdot 10^5$, $t=0.98,{\textbf{x}}=(0.05,0.6)^{\top }$)

Fig. 9

A Solution in $\pmb {{\mathcal {D}}}$ at $t=0$. Semi-Log plots of (adaptive) step sizes for $t=0$ and B ${\textbf{x}}=(0.05,0.6)^{\top }$, C ${\textbf{x}}=(0.6,0.6)^{\top }$

Example 6.5 below is from [44, Subsec. 6.2] (again, ‘time-reversed’ here) and similarly to Example 6.4, exhibits an incompatibility of boundary and terminal data at times close to $T>0$, but in a high-dimensional domain $\pmb {{\mathcal {D}}}$. Within the framework of this example—also complementing phenomena of Algorithm 5.3 in Example 6.4, we continue the investigation of different aspects of Algorithm 5.3 concerning the choice of ${\texttt {M}}$ and ${\texttt {Tol}}$ with respect to the absolute error.

Example 6.5

[see [44, Subsec. 6.2]] Let $T=1$, and $\pmb {{\mathcal {D}}}:=(0,1)^{10}$. Consider (1.8) with $\pmb {\sigma }({\textbf{x}})\equiv \sqrt{2}\cdot {\mathbb {I}}$, ${\textbf{b}}({\textbf{x}})\equiv {\textbf{0}}$, $g(t,{\textbf{x}})\equiv 0$, and

$$\begin{aligned} \phi (t,{\textbf{x}})={\left\{ \begin{array}{ll} 1\,, &{} t=T \\ 0\,, &{} t<T\,. \end{array}\right. } \end{aligned}$$

We fix ${\textbf{x}}=(0.05,0.5,\ldots ,0.5)^{\top }\in \pmb {{\mathcal {D}}}$. Tables 1, 2, 3 and 4 display errors in relation to ${\texttt {Tol}}$ and ${\texttt {M}}$ for the approximation of $u(t,{\textbf{x}})$ at different times t. As we can see in the tables below, the approximation via Algorithm 5.3 at times close to T, i.e., where the incompatibility effect is present, needs much more Monte-Carlo samples ${\texttt {M}}$ and very small values for ${\texttt {Tol}}$ to aim for a ‘small’ corresponding error, as opposed to the approximation at times ‘away’ from T, where the incompatibility effect dissolves.

Table 1 $t=0.99$

Table 2 $t=0.95$

Table 3 $t=0.9$

Table 4 $t=0.7$