Skip to main content
SpringerLink
Log in

Mixed and hybrid Petrov–Galerkin finite element discretization for optimal control of the wave equation

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Abstract

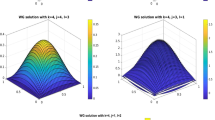
A mixed finite element discretization of an optimal control problem for the linear wave equation with homogeneous Dirichlet boundary condition is considered. For the temporal discretization, a Petrov–Galerkin scheme is utilized and the Raviart–Thomas finite elements for spatial discretization is used. A priori error analysis is proved for this numerical scheme. A hybridized formulation is proposed and if the Arnold–Brezzi post-processing method is applied, better convergence rates with respect to space are observed. The interchangeability of discretization and optimization holds both for mixed and hybrid formulations. Numerical experiments illustrating the theoretical results are presented using the lowest-order Raviart–Thomas elements.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Anselmann, M., Bause, M., Becher, S., Matthies, G.: Galerkin-collocation approximation in time for the wave equation and its post-processing. ESAIM Math. Model. Numer. Anal. 54, 2099–2123 (2020)

  2. Apel, T., Flaig, T.G.: Crank-Nicolson Schemes for optimal control problems with evolution equations. SIAM J. Numer. Anal. 50, 1484–1512 (2012)

    Article  MathSciNet  Google Scholar 

  3. Arnold, D., Brezzi, F.: Mixed and nonconforming finite element methods: implementation, post-processing and error estimates. RAIRO Model. Math. Anal. Numer. 19, 7–32 (1985)

    Article  MathSciNet  Google Scholar 

  4. Bahriawati, C., Carstensen, C.: Three Matlab implementations of the lowest-order Raviart–Thomas MFEM with a posteriori error control. Comput. Methods Appl. Math. 5, 333–361 (2005)

    Article  MathSciNet  Google Scholar 

  5. Bangerth, W., Rannacher, R.: Adaptive finite element techniques for the acoustic wave equation. J. Comput. Acoustics 1, 1–17 (1999)

    MATH  Google Scholar 

  6. Baker, G.A.: Error estimates for finite element methods for second order hyperbolic equations. SIAM J. Numer. Anal. 13, 564–576 (1976)

    Article  MathSciNet  Google Scholar 

  7. Barzilai, J., Borwein, J.: Two-point step size gradient method. IMA J. Numer. Anal. 8, 141–148 (1988)

    Article  MathSciNet  Google Scholar 

  8. Bause, M., Köcher, U., Radu, F.A., Schieweck, F.: Post-processed Galerkin approximation of improved order for wave equations. Math. Comput. 89, 595–627 (2020)

    Article  MathSciNet  Google Scholar 

  9. Bècache, E., Joly, P., Tsogka, C.: An analysis of new mixed finite elements for the approximation of wave propagation problems. SIAM J. Numer. Anal. 37, 1053–1084 (2000)

    Article  MathSciNet  Google Scholar 

  10. Brandts, J.H.: Superconvergence and a posteriori error estimation for triangular mixed finite elements. Numer. Math. 68, 311–324 (1994)

    Article  MathSciNet  Google Scholar 

  11. Brezzi, F., Fortin, M.: Mixed and Hybrid Finite Element Methods. Springer, New York (1991)

    Book  Google Scholar 

  12. Chen, Y., Lu, Z.: Error estimates for parabolic optimal control problem by fully discrete mixed finite element methods. Finite Elem. Anal. Des. 46, 957–965 (2010)

    Article  MathSciNet  Google Scholar 

  13. Cowsar, L.C., Dupont, T.F., Wheeler, M.F.: A priori estimates for mixed finite element methods for the wave equations. Comput. Methods Appl. Mech. Eng. 8, 205–222 (1990)

    Article  MathSciNet  Google Scholar 

  14. Cowsar, L.C., Dupont, T.F., Wheeler, M.F.: A priori estimates for mixed finite element approximations of second-order hyperbolic equations with absorbing boundary conditions. SIAM J. Numer. Anal. 33, 492–504 (1996)

    Article  MathSciNet  Google Scholar 

  15. Dai, Y.H., Fletcher, R.: Projected Barzilai–Borwein methods for large-scale box constrained quadratic programming. Numer. Math. 100, 21–47 (2005)

    Article  MathSciNet  Google Scholar 

  16. Dörfler, W., Findeisen, S., Wieners, C., Ziegler, D.: Parallel adaptive discontinuous Galerkin discretizations in space and time for linear elastic and acoustic waves. In: Langer, U., Steinbach, O. (eds.) Space-Time Methods: Applications to Partial Differential Equations. De Gruyter, Berlin (2019)

    MATH  Google Scholar 

  17. Egger, H., Radu, B.: Super-convergence and post-processing for mixed finite element approximations of the wave equation. B. Numer. Math. 140, 427–447 (2018)

    Article  MathSciNet  Google Scholar 

  18. Ern, A., Guermond, J.-L.: Theory and Practice of Finite Elements. Springer, New York (2004)

    Book  Google Scholar 

  19. Ernesti, J., Wieners, C.: Space-time discontinuous Petrov–Galerkin methods for linear wave equations in heterogeneous media. Comput. Methods Appl. Math. 19, 465–481 (2019)

    Article  MathSciNet  Google Scholar 

  20. Hinze, M.: A variational discretization concept in control constrained optimization: the linear-quadratic case. Comput. Optim. Appl. 30, 45–61 (2005)

    Article  MathSciNet  Google Scholar 

  21. Hou, T.: Error estimates and superconvergence of semidiscrete mixed methods for optimal control problems governed by hyperbolic equations. Numer. Anal. Appl. 5, 348–362 (2012)

    Article  Google Scholar 

  22. Jenkins, E.W., Rivière, B., Wheeler, M.F.: A priori error estimates for mixed finite element approximations fo the acoustic wave equation. SIAM J. Numer. Anal. 40, 1698–1715 (2002)

    Article  MathSciNet  Google Scholar 

  23. Kröner, A., Kunisch, K., Vexler, B.: Semismooth Newton methods for optimal control of the wave equation with control constraints. SIAM J. Control Optim. 49, 830–858 (2011)

    Article  MathSciNet  Google Scholar 

  24. Lehoucq, R.B., Sorensen, D.C., Yang, C.: ARPACK USERS GUIDE: Solution of Large Scale Eigenvalue Problems by Implicitly Restarted Arnoldi Methods. SIAM, Philadelphia, PA (1998)

    Book  Google Scholar 

  25. Meidner, D., Vexler, B.: A priori error estimates for the space-time finite element discretization of parabolic optimal control problems. Part I: Problems without control constraints. SIAM J. Control Optim. 47, 1150–1177 (2008)

  26. Meidner, D., Vexler, B.: A priori error analysis of the Petrov–Galerkin Crank–Nicholson Scheme for parabolic optimal control problems. SIAM J. Control. Optim. 49, 2183–2211 (2011)

    Article  MathSciNet  Google Scholar 

  27. Makridakis, Ch.G.: On mixed finite element methods for linear elastodynamics. Numer. Math. 61, 235–260 (1992)

    Article  MathSciNet  Google Scholar 

  28. Pazy, A.: Semigroups of Linear Operators and Applications to Partial Differential Equations. Springer, New York (1983)

    Book  Google Scholar 

  29. Peralta, G.: Error estimates for mixed and hybrid FEM for elliptic optimal control problems with penalizations, submitted

  30. Quarteroni, A., Valli, A.: Numerical Approximations of Partial Differential Equations. Springer, Heidelberg (2008)

    MATH  Google Scholar 

  31. Raviart, P.A., Thomas, J.M.: A mixed finite element method for second order elliptic problems. Lect. Notes Math 606, 292–315 (1977)

    Article  MathSciNet  Google Scholar 

  32. Sellitto, A., Cimmelli, V.A., Jou, D.: Mesoscopic Theories of Heat Transport in Nanosystems. Spinger, New York (2016)

    Book  Google Scholar 

  33. Tröltzsch, F.: Optimal Control of Partial Differential Equations: Theory. American Mathematical Society, Providence, Rhode Island, Methods and Applications (2010)

    MATH  Google Scholar 

  34. Xing, X., Chen, Y.: Error estimates of mixed methods for optimal control problems governed by parabolic equations. Int. J. Numer. Method Eng. 75, 735–754 (2008)

    Article  MathSciNet  Google Scholar 

  35. Xing, X., Chen, Y., Yi, N.: Error estimates of mixed finite element methods for quadratic control problems. J Comput. Appl. Math. 233, 1812–1820 (2010)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors are grateful to the reviewers for the careful reading and valuable suggestions that led to the improvement of the paper.

Author information

Authors and Affiliations

  1. Department of Mathematics and Computer Science, University of the Philippines Baguio, Governor Pack Road, 2600, Baguio, Philippines

    Gilbert Peralta

  2. Institute for Mathematics and Scientific Computing, University of Graz, Heinrichstrasse 36, 8010, Graz, Austria

    Karl Kunisch

  3. RICAM Institute, Austrian Academy of Sciences, Altenbergerstrasse 69, 4040, Linz, Austria

    Karl Kunisch

Authors
  1. Gilbert Peralta
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Karl Kunisch
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Gilbert Peralta.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Peralta, G., Kunisch, K. Mixed and hybrid Petrov–Galerkin finite element discretization for optimal control of the wave equation. Numer. Math. 150, 591–627 (2022). https://doi.org/10.1007/s00211-021-01258-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-021-01258-9

Mathematics Subject Classification

Search

Navigation