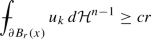Nondegeneracy for stable solutions to the one-phase free boundary problem

Abstract

We prove the nondegeneracy condition for stable solutions to the one-phase free boundary problem. The proof is by a De Giorgi iteration, where we need the Sobolev inequality of Michael and Simon and, consequently, an integral estimate for the mean curvature of the free boundary. We then apply the nondegeneracy estimate to obtain local curvature bounds for stable free boundaries in dimension n, provided the Bernstein-type theorem for stable, entire solutions in the same dimension is valid. In particular, we obtain this curvature estimate in $n=2$ dimensions.

Appendix A: Auxiliary results

We recall the notion of a viscosity solution of (1) (see [6]). First we define viscosity super- and subsolutions.

Definition A.1

A viscosity supersolution of (1) in a domain $D\subseteq {\mathbb {R}}^n$ is a non-negative function $w\in C(D)$ such that $\Delta w \le 0$ in $D^+(w)$ and for every $x_0\in F(w)$ with a tangent ball B from the positive side ($x_0\in \partial B$ and $B\subset D^+(w)$), there is $\alpha \le 1$ such that

$$\begin{aligned} u(x) = \alpha \langle x-x_0, \nu \rangle ^+ + o(|x-x_0|) \end{aligned}$$

as $x\rightarrow x_0$ non-tangentially in B, with $\nu$ the inner normal to $\partial B$ at $x_0$.

Definition A.2

A viscosity subsolution of (1) in a domain $D\subseteq {\mathbb {R}}^n$ is a non-negative function $w\in C(D)$ such that $\Delta w \ge 0$ in $D^+(w)$ and for every $x_0\in F(w)$ with a tangent ball B in the zero set ($x_0\in \partial B$ and $B\subset \{w=0\}$), there is $\alpha \ge 1$ such that

$$\begin{aligned} u(x) = \alpha \langle x-x_0, \nu \rangle ^+ + o(|x-x_0|) \end{aligned}$$

as $x\rightarrow x_0$ non-tangentially in $B^c$, with $\nu$ the outer normal to $\partial B$ at $x_0$.

A viscosity solution in D is a function that is both a supersolution and a subsolution in the sense above.

The class of viscosity solutions is particularly well suited for taking uniform limits. We quote the following result

Lemma A.3

[18, Lemma 4.4] Let $u_k\in C(D)$ be a sequence of viscosity solutions of (1) in D such that $u_k\rightarrow u$ uniformly and u is Lipschitz continuous. Then u is also a viscosity supersolution of (1) in D. If, in addition, $\overline{D^{+}(u_k)} \rightarrow \overline{D^{+}(u)}$ locally in the Hausdorff distance, then u is a viscosity subsolution, as well.

As a corollary, we have the following well known result (see [6, Lemma 1.21] or [18, Proposition 4.2] for the proof) describing uniform limits of Lipschitz continuous and non-degenerate viscosity solutions.

Proposition A.4

Let $D\subseteq {\mathbb {R}}^n$ be a domain and $\{u_k\} \subset C(D)$ be a sequence of viscosity solutions of (1) in D which satisfies

• (Uniform Lipschitz continuity) There exists a constant C, such that

  $$\begin{aligned} \Vert \nabla u_k\Vert _{L^{\infty }(D)} \le C; \end{aligned}$$

• (Uniform non-degeneracy) There exists a constant c, such that

  

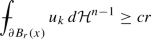
  for every $B_r(x) \subseteq D$, centered at a free boundary point $x\in F(u_k)$.

Then any limit $u \in C(\overline{D})$ of a uniformly convergent on compacts subsequence $u_k \rightarrow u$ satisfies

• (1) $\overline{D^+(u_k)} \rightarrow \overline{D^+(u)}$ and $F(u_k) \rightarrow F(u)$ locally in the Hausdorff distance;

• (2) $1_{\{u_k>0\}} \rightarrow 1_{\{u>0\}}$ in $L^1_{\text {loc}}(D)$;

Moreover, u is a Lipschitz continuous, non-degenerate viscosity solution of (1).

In the next proposition we establish the fact that globally defined viscosity solutions of the one-phase FBP have a gradient bounded by 1.

Proposition A.5

Let $u:{\mathbb {R}}^n\rightarrow [0,\infty )$ be an entire viscosity solution of the one-phase FBP (1), with $F(u)\ne \emptyset$, and let $\Omega :=\{x\in {\mathbb {R}}^n: u(x)>0\}$ denote the positive phase of u. Then

$$\begin{aligned} |\nabla u(x)| \le 1 \quad \text {for all } x\in \Omega . \end{aligned}$$

Furthermore, if $|\nabla u(x_0)| = 1$ for some $x_0\in \Omega$, then $|\nabla u (x)|\equiv 1$ in the connected component ${\mathcal {C}}$ of $\Omega$, containing $x_0$, so that $u|_{{\mathcal {C}}}(x) = (x-p)\cdot e$ for some $p\in {\mathbb {R}}^n$ and unit vector $e\in {\mathbb {R}}^n$.

Proof

We sketch out the argument from [26, Proposition 2.1], written for a closely related problem.

First, we show that there is a dimensional constant $C>0$ such that

$$\begin{aligned} |\nabla u|\le C \quad \text {in } \Omega . \end{aligned}$$

Pick any $x\in \Omega$. By rescaling and recentering, we may assume that $x=0$ and $d(x, F(u))=1$. By applying the Harnack inequality plus gradient estimates to u in $B_1$, it suffices to show that $u(0)\le C_0$. Let $p\in F(u)\cap \partial B_1$ and note that $B_1$ is a ball touching F(u) from the positive side.

By the Harnack inequality, we know that $u\ge cu(0)$ in $B_{1/2}$. Consider the harmonic function h in the annulus $B_1{\setminus } B_{1/2}$, having boundary values $h=cu(0)$ on $\partial B_{1/2}$ and $h=0$ on $\partial B_1$. Then $h_\nu (p) = c_0 u(0)$, where $\nu$ denotes the inner unit normal to $\partial B_1$ at p. On the other hand, the maximum principle implies $h\le u$ in $B_1{\setminus } B_{1/2}$, so that the Hopf Lemma, in conjunction with the viscosity supersolution property, yields the desired bound

$$\begin{aligned} 1 \ge u_\nu (p) \ge h_\nu (p) = c_0 u(0). \end{aligned}$$

Therefore, the supremum $L:=\sup _{\Omega } |\nabla u|\le C$ is positive and finite. Let $x_k\in \Omega$ be a sequence of points such that $|\nabla u(x_k)| \rightarrow L$ as $k\rightarrow \infty$. Define the following rescales of u

$$\begin{aligned} v_k(x):=d_k^{-1} u(x_k + d_k x), \quad \text {where } d_k:=d(x_k, F(u)). \end{aligned}$$

Then the $v_k$ satisfy: $\Vert \nabla v_k\Vert _{L^\infty }\le L$, the distance $d(0,F(v_k))=1$ and $|\nabla v_k(0)|=|\nabla u(x_k)| \rightarrow L$ as $k\rightarrow \infty$. Thus, the sequence of uniformly Lipschitz continuous, viscosity solutions $\{v_k\}$ subconverges uniformly on compact subsets of ${\mathbb {R}}^n$ to the globally defined, Lipschitz continuous function v, which is harmonic in its positive phase $\tilde{\Omega }:=\{v>0\}$, satisfies $\Vert \nabla v\Vert _{L^\infty }\le L$, and which is a viscosity supersolution on account of Lemma A.3. Furthermore, since $v_k\rightarrow v$ uniformly on $\overline{B_1}$ and $v_k-v$ is harmonic in $B_1$, we have

$$\begin{aligned} |\nabla v(0) - \nabla v_k(0)| \le C \Vert v_k - v\Vert _{C(B_1)} \rightarrow 0 \quad \text {as } k\rightarrow \infty , \end{aligned}$$

so that $|\nabla v(0)|=L$.

However, since $\Delta |\nabla v|^2 =2|\nabla ^2 v|^2 \ge 0$ in $\tilde{\Omega }$, we know that $|\nabla v|^2$ is subharmonic in $\tilde{\Omega }$, so that the strong maximum principle implies that $|\nabla v|\equiv L$ in the connected component ${\mathcal {C}}$ of $\tilde{\Omega }$ containing 0. Therefore, $2|\nabla ^2 v|^2 = \Delta |\nabla v|^2 = 0$ in ${\mathcal {C}}$, so that v is a linear function in ${\mathcal {C}}$ with slope $L>0$. This means that the component ${\mathcal {C}}$ is actually a half-space and for some $p\in {\mathbb {R}}^n$, and unit vector $e\in {\mathbb {R}}^n$, we have

$$\begin{aligned} v(x) = L(x-p)\cdot e \quad \text {for all } x\in {\mathcal {C}}. \end{aligned}$$

We now infer that $L\le 1$ from the fact that v is a viscosity supersolution to (1).

To establish the remaining part of the proposition (regarding the possibility of $|\nabla u(x_0)|=1$), we use the verbatim argument from the paragraph above. $\square$

We end the appendix with the following lemma.

Lemma A.4

Let u be a classical solution to (1) in $B_1\subset {\mathbb {R}}^n$ which is Lipschitz continuous and nondegenerate (with universal constants) in $B_1$. Assume that $0\in F(u)$ and that the second fundamental form A of F(u) is bounded

$$\begin{aligned} |A(p)| \le C \quad \text {for all } p\in F(u), \end{aligned}$$

by some absolute constant $C>0$. Then there exists a constant $c\in (0,1)$ such that, in a suitable Euclidean coordinate system, the connected component ${\mathcal {C}}$ of $B_c^+(u)$, whose boundary contains 0, is the supergraph:

$$\begin{aligned} {\mathcal {C}}= \{x=(x',x_n)\in B_{c}: x_n> f(x')\}, \end{aligned}$$

(47)

for some $f:B_{c}'\rightarrow {\mathbb {R}}$ with $\Vert f\Vert _{C^2(B_c')}\le 1/c$.

Proof

Since the curvature of F(u) is bounded by an absolute constant, there is a small absolute constant $c>0$, such that the component F of $F(u)\cap B_{c}$ containing 0, is given by a graph

$$\begin{aligned} F = \{(x',x_n)\in B_{c}: x_n= f(x')\}, \end{aligned}$$

with $\Vert f\Vert _{C^2(B_c')}\le 1/c$. Let us show that, by possibly reducing the constant c, the connected component ${\mathcal {C}}$ of $B_c^+(u)$ bordering the origin, is the supergraph (47).

Assume that this last statement is false. Then there exist a sequence $c_k\rightarrow 0$ and a sequence of counterexamples $\{u_k\}$ such that the component ${\mathcal {C}}_k$ of $B_{c_k}^+(u_k)$ bordering 0 has at least two free boundary connected components: the connected component $F_k$ of 0 in $F(u_k)\cap B_{c_k}$, and another component $\tilde{F}_k$. Choose $\tilde{F_k}$ to be the closest such component to $F_k$ and set $d_k:=\text {dist}(F_k,\tilde{F}_k)\le c_k$. Consider now the rescaled solutions

$$\begin{aligned} v_k(x):=d_k^{-1} [u_k{\mathcal {C}}_k](d_k x) \quad \text {in } B_{d_k^{-1}c_k}\supseteq B_1, \end{aligned}$$

and denote by $G_k:=d_k^{-1}F_k$, $\tilde{G}_k:=d_k^{-1}\tilde{F}_k$. We have that

$$\begin{aligned} \text {dist}(G_k, \tilde{G}_k) = 1, \end{aligned}$$

(48)

while the curvature

$$\begin{aligned} |A_{G_k}|\le d_k \sup |A_{F(u_k)}| \le c_k C \rightarrow 0. \end{aligned}$$

Now, according to Proposition A.4 the uniformly Lipschitz continuous and nondegenerate $v_k$ converge to the limit $v=x_n^+$ uniformly on compacts, with $G_k$ converging to a subset $G\subseteq \{x_n=0\}$. On the other hand, by the Hausdorff convergence of the free boundaries, (48) suggests that F(v) also has a component sitting at a unit distance away from G. This yields a contradiction and the proof of the lemma is complete. $\square$