Convergence, financial development, and policy analysis

Abstract

We study the relationship among inflation, economic growth, and financial development in a Schumpeterian overlapping generations model with credit constraints. In the baseline case, money is super-neutral. When the financial development exceeds some critical level, the economy catches up and then converges to the growth rate of the world technology frontier. Otherwise, the economy converges to a poverty trap with a growth rate lower than the frontier and with inflation decreasing with the level of financial development. We then study efficient allocation and identify the sources of inefficiency in a market equilibrium. We show that a particular combination of monetary and fiscal policies can make a market equilibrium attain the efficient allocation.

Appendices

Appendix

Proofs

Proof of Proposition 1

We first study the steady state. Using Eqs. (18), (19), (20), and (21) and setting $z_{t}=z,$ we derive a system of four steady-state equations

$$\begin{aligned} R_{f}= & {} \frac{1+z}{1+g}F^{\prime }(n)\psi , \end{aligned}$$

(A.1)

$$\begin{aligned} a= & {} \frac{\left( 1+g\right) F(n)}{g+F\left( n\right) }, \end{aligned}$$

(A.2)

$$\begin{aligned} n= & {} \frac{\left( 1-\alpha \right) \zeta a}{1+g}\left\{ \lambda +\frac{ \left( 1-\lambda \right) }{1+\beta +\gamma }\left[ \beta -\frac{\gamma }{ R_{f}/\left( 1+z\right) -1}\right] \right\} , \end{aligned}$$

(A.3)

and $\varPi =\left( 1+z\right) /\left( 1+g\right)$ to determine four steady-state variables $R_{f},$a,  n,  and $\varPi .$

From these equations, we show that n is determined by the equation

$$\begin{aligned} n=\frac{\left( 1-\alpha \right) \zeta F(n)}{g+F(n)}\left\{ \lambda +\frac{ \left( 1-\lambda \right) }{1+\beta +\gamma }\left[ \beta -\frac{\gamma }{ F^{\prime }(n)\psi /\left( 1+g\right) -1}\right] \right\} . \end{aligned}$$

Equivalently, it follows from $n=\varPhi \left( \mu \right)$ and $F=\varPhi ^{-1}$ that $\mu$ is determined by the equation

$$\begin{aligned} \varPhi ^{\prime }\left( \mu \right) =\frac{\psi }{R_{f}/\varPi }, \end{aligned}$$

(A.4)

where

$$\begin{aligned} \frac{R_{f}}{\varPi }=\left( 1+g\right) \left\{ 1+\frac{\gamma }{\beta -\left[ \frac{\varPhi \left( \mu \right) \left( g+\mu \right) }{\left( 1-\alpha \right) \zeta \mu }-\lambda \right] \frac{1+\beta +\gamma }{1-\lambda }}\right\} \end{aligned}$$

and $\varPi =\left( 1+z\right) /\left( 1+g\right) .$ Since $\varPhi ^{\prime \prime }>0,$$\varPhi ^{\prime }>0$, and $\varPhi \left( 0\right) =0,$ we can check that $\varPhi \left( \mu \right) \left( g+\mu \right) /\mu$ decreases with $\mu .$ Thus, the real interest rate $R_{f}/\varPi$ is decreasing in $\mu$ and $\varPhi ^{\prime }\left( \mu \right)$ is increasing in $\mu$. Given conditions (22) and (23), it follows from the intermediate value theorem that there is a unique solution $\mu ^{*}\in \left( 0,1\right)$ to (A.4).¹⁰ The associated R&D investment is given by $n^{*}=\varPhi \left( \mu ^{*}\right)$ and hence $R_{f}^{*}$ and $a^{*}$ are determined by (A.1) and (A.2). We also assume that the condition

$$\begin{aligned} \frac{R_{f}^{*}}{1+z}>1+\frac{\gamma }{\beta } \end{aligned}$$

(A.5)

is satisfied so that (12) holds along the balanced growth path. We will verify later that this condition is indeed satisfied in the proof of Proposition 2.

Using (A.3) and (15), we can rewrite the credit constraint (6) along a balanced growth path as

$$\begin{aligned} n\left( \frac{\beta R_{f}}{\varPi }-\kappa \right) \le \frac{\beta R_{f}}{\varPi } \frac{\lambda \left( 1-\alpha \right) \zeta a}{1+g}. \end{aligned}$$

The critical value of $\kappa$ such that the credit constraint just binds in the steady-state equilibrium is given by

$$\begin{aligned} \kappa ^{*}=\frac{\beta R_{f}^{*}}{\varPi }\left[ 1-\frac{\lambda \left( 1-\alpha \right) \zeta a^{*}}{n^{*}\left( 1+g\right) }\right] . \end{aligned}$$

(A.6)

When $\kappa >\kappa ^{*},$ the credit constraint does not bind. It follows from (A.4) that money supply does not affect the equilibrium innovation rate $\mu ^{*}.$ An increase in the money growth rate raises the nominal interest rate one for one and hence does not affect savings. Thus, the supply of funds for innovation does not depend on monetary policy.

Next we study local dynamics. By defining $r_{t}\equiv R_{ft}/\left( 1+z_{t+1}\right)$ and eliminating $R_{ft}/\varPi _{t+1},$ we can reduce the equilibrium system (18), (19), (20), and (21) to three equations

$$\begin{aligned} a_{t+1}= & {} F\left( n_{t}\right) +\frac{1-F\left( n_{t}\right) }{1+g}a_{t}, \end{aligned}$$

(A.7)

$$\begin{aligned} r_{t}-1= & {} F^{\prime }(n_{t})\psi \frac{a_{t}}{a_{t+1}\left( 1+g\right) } \frac{r_{t+1}-1}{r_{t+1}}, \end{aligned}$$

(A.8)

$$\begin{aligned} n_{t}= & {} \frac{\left( 1-\alpha \right) \zeta a_{t}}{1+g}\left[ \lambda + \frac{\left( 1-\lambda \right) }{1+\beta +\gamma }\left( \beta -\frac{\gamma }{r_{t}-1}\right) \right] , \end{aligned}$$

(A.9)

for three variables $a_{t},n_{t},$ and $r_{t}.$ Assume that $z_{t}$ is constant over time.

Log-linearizing the above equations around the steady state yields

$$\begin{aligned} \hat{a}_{t+1}= & {} \frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }\hat{n}_{t}+\frac{1-F\left( n\right) }{1+g}\hat{a}_{t}, \nonumber \\ \hat{r}_{t}= & {} \frac{(r-1)}{r}\left[ \frac{F^{\prime \prime }(n)n}{F^{\prime }(n)}\hat{n}_{t}-\frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }\hat{n }_{t}+\frac{g+F\left( n\right) }{1+g}\hat{a}_{t}\right] +\frac{1}{r}\hat{r} _{t+1}, \nonumber \\ \hat{n}_{t}= & {} \hat{a}_{t}+\frac{\frac{\left( 1-\lambda \right) }{1+\beta +\gamma }\gamma \frac{r}{(r-1)^{2}}}{\lambda +\frac{\left( 1-\lambda \right) }{1+\beta +\gamma }\left( \beta -\frac{\gamma }{r-1}\right) }\hat{r} _{t}\equiv \hat{a}_{t}+\vartheta \hat{r}_{t}, \end{aligned}$$

(A.10)

where a variable without time subscript denotes the steady-state value and a variable with a hat denotes the log deviation from the steady state. It follows from condition (A.5) that $\vartheta >0.$

Eliminating $\hat{n}_{t}$ yields a system of two linear difference equations

$$\begin{aligned} \left[ \begin{array}{c} \hat{a}_{t+1} \\ \hat{r}_{t+1} \end{array} \right] =J\left[ \begin{array}{c} \hat{a}_{t} \\ \hat{r}_{t} \end{array} \right] , \end{aligned}$$

(A.11)

where

$$\begin{aligned} J\equiv \left[ \begin{array}{cc} \frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }+\frac{1-F\left( n\right) }{1+g} &{} \vartheta \frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) } \\ (1-r)\left[ 1-\frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }-\frac{ 1-F\left( n\right) }{1+g}+\frac{F^{\prime \prime }(n)n}{F^{\prime }(n)} \right] &{} r+(r-1)\vartheta \left[ \frac{g}{1+g}\frac{nF^{\prime }(n)}{ F\left( n\right) }-\frac{F^{\prime \prime }(n)n}{F^{\prime }(n)}\right] \end{array} \right] . \end{aligned}$$

We now study the eigenvalues of J to determine the local stability of the equilibrium system. Consider the quadratic characteristic equation

$$\begin{aligned} G\left( \nu \right) =\left| J-\nu I\right| =0. \end{aligned}$$

After a tedious calculation, we obtain

$$\begin{aligned} G(0)= & {} \left[ \frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }+\frac{ 1-F\left( n\right) }{1+g}\right] r-\frac{1-F\left( n\right) }{1+g} (r-1)\vartheta \frac{F^{\prime \prime }(n)n}{F^{\prime }(n)} \nonumber \\&+\,\vartheta \frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }(r-1), \end{aligned}$$

(A.12)

and

$$\begin{aligned} G(1)= & {} \left[ \frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }+\frac{ 1-F\left( n\right) }{1+g}-1\right] (r-1)\left[ 1-\frac{F^{\prime \prime }(n)n }{F^{\prime }(n)}\right] \nonumber \\&+\,\vartheta \frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) } (r-1)\vartheta \frac{F^{\prime \prime }(n)n}{F^{\prime }(n)}. \end{aligned}$$

(A.13)

Under conditions (24), (A.5), $F^{\prime }>0,$ and $F^{\prime \prime }<0$, we can check that $G\left( 0\right) >0$ and $G\left( 1\right) <0.$ It follows from the intermediate value theorem that there exists an eigenvalue $\nu _{1}\in \left( 0,1\right)$ such that $G\left( \nu _{1}\right) =0.$ Since $\lim {}_{x\rightarrow \infty }G(x)=\infty ,$ it follows from the intermediate value theorem that there exists another eigenvalue $\nu _{2}>1$ such that $G\left( \nu _{2}\right) =0.$ We conclude that the steady state is a saddle point.

Finally, we study transition dynamics. We set $z_{t}=z$ for all t for simplicity. Then, we can write the log-linearized equilibrium solution as

$$\begin{aligned} \hat{a}_{t+1}=\phi _{a}\hat{a}_{t},\text { }\hat{r}_{t}=\hat{R}_{ft}=\phi _{r} \hat{a}_{t},\text { }\hat{n}_{t}=\phi _{n}\hat{a}_{t},\text { }\hat{r} _{ft}=\phi _{rr}\hat{a}_{t},\text { and }\hat{\varPi }_{t+1}=\phi _{\varPi }\hat{a} _{t}, \end{aligned}$$

where $r_{ft}\equiv R_{ft}/\varPi _{t+1}$ denotes the real interest rate. We want to determine the signs of all the coefficients. We first use the phase diagram in Fig. 6 to determine the signs of $\phi _{a}$ and $\phi _{r}$. By (A.11), the locus $\hat{a}_{t+1}=\hat{a}_{t}$ represents the equation

$$\begin{aligned} \hat{r}_{t}=\frac{1-\frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }- \frac{1-F\left( n\right) }{1+g}}{\vartheta \frac{g}{1+g}\frac{nF^{\prime }(n) }{F\left( n\right) }}\hat{a}_{t}, \end{aligned}$$

(A.14)

which has a positive slope by condition (24). The locus $\hat{r} _{t+1}=\hat{r}_{t}$ represents the equation

$$\begin{aligned} r_{t}=\frac{1-\frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }-\frac{ 1-F\left( n\right) }{1+g}+\frac{F^{\prime \prime }(n)n}{F^{\prime }(n)}}{ 1+\vartheta [\frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }- \frac{F^{\prime \prime }(n)n}{F^{\prime }(n)}]}\hat{a}_{t}. \end{aligned}$$

(A.15)

Since $F^{\prime \prime }<0$ and $F^{\prime }>0,$ the slope of this line may be either positive or negative. The left panel of Fig. 6 shows the plot of the case in which the locus $\hat{r}_{t+1}=\hat{r}_{t}$ is negative. We can see that, if $\hat{a}_{1}<0$, namely if the initial value $a_{1}$ is below the steady state, the interest rate $\hat{r}_{t}$ declines but $a_{t}$ increases over time to their steady-state values along the saddle path. We now turn to case in which the slope of the locus $\hat{r}_{t+1}=\hat{r}_{t}$ is positive, illustrated in the right panel of Fig. 6. We can show that the slope of the locus $\hat{a}_{t+1}=\hat{a}_{t}$ is greater than the slope of the locus $\hat{r}_{t+1}=\hat{r}_{t}$. We can see that, if the initial value $a_{1}$ is below the steady state, $r_{t}$ and $a_{t}$ both increase over time, approaching their steady-state values.

Fig. 6

Phase diagram for the case with perfect credit market

In summary, we have shown that $\phi _{a}\in \left( 0,1\right)$ and $\phi _{r}$ can be either positive or negative. Up to the first-order approximation, the productivity growth satisfies

$$\begin{aligned} \log A_{t+1}-\log A_{t}=\hat{a}_{t+1}-\hat{a}_{t}+\log (1+g)=(\phi _{a}-1) \hat{a}_{t}+\log (1+g). \end{aligned}$$

Thus, when $a_{1}$ is slightly below the steady state, the productivity growth is positive and decreases to the steady state. By $\hat{n}_{t}=\hat{a} _{t}+\vartheta \hat{r}_{t}$, we have $\phi _{n}=1+\vartheta \phi _{r}$. If $\phi _{r}>0$, then we have $\phi _{n}>0$ since $\vartheta >0$. In the case of $\phi _{r}<0$ as in the left panel of Fig. 6, we see that the saddle path is flatter than the locus $r_{t+1}=r_{t}$. Namely, we must have

$$\begin{aligned} \phi _{r}>\frac{1-\frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }- \frac{1-F\left( n\right) }{1+g}+\frac{F^{\prime \prime }(n)n}{F^{\prime }(n)} }{1+\vartheta \left[ \frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }- \frac{F^{\prime \prime }(n)n}{F^{\prime }(n)}\right] }. \end{aligned}$$

This implies that

$$\begin{aligned} \phi _{n}= & {} 1+\vartheta \phi _{r}>1+\vartheta \frac{1-\frac{g}{1+g}\frac{ nF^{\prime }(n)}{F\left( n\right) }-\frac{1-F\left( n\right) }{1+g}+\frac{ F^{\prime \prime }(n)n}{F^{\prime }(n)}}{1+\vartheta \left[ \frac{g}{1+g} \frac{nF^{\prime }(n)}{F\left( n\right) }-\frac{F^{\prime \prime }(n)n}{F^{\prime }(n)}\right] } \\= & {} \frac{1+\vartheta \frac{g+F\left( n\right) }{1+g}}{1+\vartheta \left[ \frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }-\frac{F^{\prime \prime }(n)n}{F^{\prime }(n)}\right] }>0, \end{aligned}$$

where the inequality follows from $F^{\prime }>0,$$F^{\prime \prime }<0,$ and $\vartheta >0$. Thus, as $a_{t}$ increases to the steady state, $n_{t}$ will do so too. Since $\mu _{t}=F\left( n_{t}\right)$ and $F^{\prime }>0,$$\mu _{t}$ also increases to the steady state.

Log-linearizing equation (18) yields

$$\begin{aligned} \widehat{r}_{ft}=\frac{nF^{\prime \prime }(n)}{F^{^{\prime }}(n)}\hat{n}_{t}= \frac{nF^{\prime \prime }(n)}{F^{^{\prime }}(n)}\phi _{n}\hat{a}_{t}\equiv \phi _{rr}\hat{a}_{t}. \end{aligned}$$

It follows from $F^{\prime \prime }<0,$$F^{\prime }>0,$ and $\phi _{n}>0$ that $\phi _{rr}<0$. Thus, as $a_{t}$ increases to the steady state, the real interest rate $r_{ft}$ decreases to the steady state. Finally, log-linearizing equation (20) given $z_{t}=z$ for all t yields

$$\begin{aligned} \hat{\varPi }_{t+1}= & {} \hat{a}_{t}-\hat{a}_{t+1}-\frac{1}{r-1}(\hat{r}_{t}-\hat{r }_{t+1})=(1-\phi _{a})\hat{a}_{t}-\frac{1}{r-1}(1-\phi _{a})\phi _{r}\hat{a}_{t} \\= & {} (1-\phi _{a})\left( 1-\frac{1}{r-1}\phi _{r}\right) \hat{a}_{t}\equiv \phi _{\varPi }\hat{a}_{t}. \end{aligned}$$

If $\phi _{r}<0$, then we have $\phi _{\varPi }>0$. If $\phi _{r}>0$, we use the equation

$$\begin{aligned} \hat{\varPi }_{t+1}=\hat{r}_{t}-\widehat{r}_{ft}=\left( \phi _{r}-\phi _{rr}\right) \hat{a}_{t}\equiv \phi _{\varPi }\hat{a}_{t} \end{aligned}$$

to deduce $\phi _{\varPi }>0$. In both cases, $\varPi _{t}$ increases with $a_{t}$ to the steady state. $\square$

Proof of Proposition 2

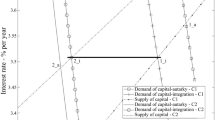
The equilibrium system consists of Eqs. (19), (20), (21), and (25). First, we study the steady state, in which the equilibrium system becomes (A.2), (A.3), and the following equation

$$\begin{aligned} \underset{\text {supply}}{\underbrace{\lambda +\frac{1-\lambda }{1+\beta +\gamma }\left[ \beta -\frac{\gamma }{R_{f}/\left( 1+z\right) -1}\right] } \text { }}=\underset{\text {limit}}{\underbrace{\frac{\lambda \beta R_{f}/\varPi }{\beta R_{f}/\varPi -\kappa }}}, \end{aligned}$$

(A.16)

where $\varPi =\left( 1+z\right) /\left( 1+g\right) .$ The expression on the left-hand side of equation (A.16) is increasing in $R_{f}$ and the expression on the right-hand side is decreasing in $R_{f}.$ When $R_{f}/\left( 1+z\right) =1+\gamma /\beta ,$ the credit supply takes the value $\lambda$, which is below the borrowing limit when $\beta R_{f}/\varPi -\kappa >0.$ When $R_{f}\rightarrow \infty ,$ the credit supply approaches $\lambda +\frac{\left( 1-\lambda \right) \beta }{1+\beta +\gamma }$, which is higher than the credit limit $\lambda .$ Thus, by the intermediate value theorem there is a unique solution for $R_{f}$ to equation (A.16) such that

$$\begin{aligned} \frac{R_{f}}{1+z}>\max \left\{ 1+\frac{\gamma }{\beta },\frac{\kappa \varPi }{ \beta \left( 1+z\right) }\right\} . \end{aligned}$$

(A.17)

Let $R_{f}^{**}$ denote the solution. Using Eqs. (A.3), ( A.2), and (A.16), we derive that

$$\begin{aligned} n=\frac{\lambda \left( 1-\alpha \right) \zeta F\left( n\right) }{g+F\left( n\right) }\frac{\beta R_{f}^{**}/\varPi }{\beta R_{f}^{**}/\varPi -\kappa }. \end{aligned}$$

We can equivalently rewrite this equation in terms of $\mu$ as

$$\begin{aligned} \varPhi \left( \mu \right) \left( g+\mu \right) =\frac{\left( 1-\alpha \right) \zeta \lambda \beta R_{f}^{**}/\varPi }{\beta R_{f}^{**}/\varPi -\kappa }\mu . \end{aligned}$$

(A.18)

Notice that there is a trivial solution $\mu =0$ to the above equation since $\varPhi \left( 0\right) =0$. We rule out this solution by the following condition:

$$\begin{aligned} \varPhi ^{\prime }\left( 0\right) g<\frac{\left( 1-\alpha \right) \zeta \lambda \beta R_{f}^{**}/\varPi }{\beta R_{f}^{**}/\varPi -\kappa }<\varPhi \left( 1\right) \left( g+1\right) . \end{aligned}$$

(A.19)

Then, it follows from the intermediate value theorem that there is a unique solution, denoted by $\mu ^{**}\in \left( 0,1\right) ,$ to Eq. (A.18). The corresponding R&D investment level is denoted by $n^{**}=\varPhi \left( \mu ^{**}\right) >0.$

Define the critical values $\kappa ^{**}$ and $\bar{\kappa }$ for $\kappa$ such that

$$\begin{aligned}&\varPhi ^{\prime }\left( 0\right) g=\frac{\left( 1-\alpha \right) \zeta \lambda \beta R_{f}^{**}/\varPi }{\beta R_{f}^{**}/\varPi -\kappa ^{**}},\\&\frac{\left( 1-\alpha \right) \zeta \lambda \beta R_{f}^{**}/\varPi }{ \beta R_{f}^{**}/\varPi -\bar{\kappa }}=\varPhi \left( 1\right) \left( g+1\right) . \end{aligned}$$

where $R_{f}^{**}$ is the solution to Eq. (A.16) and is a function of $\kappa .$ We can verify that the expression

$$\begin{aligned} \frac{R_{f}^{**}/\varPi }{R_{f}^{**}/\varPi -\kappa } \end{aligned}$$

increases with $\kappa$ along the supply curve in Fig. 3. Thus, the values $\kappa ^{**}$ and $\bar{\kappa }$ are unique. When $\kappa ^{**}<\kappa <\bar{\kappa },$ condition (A.19) holds.

From Fig. 3, we can see that the unconstrained equilibrium interest rate under perfect credit market is higher than that under binding credit constraint. Thus, (A.17) and hence (22) and (A.5) must hold for the unconstrained equilibrium. If $\kappa ^{**}<\kappa <\min \left\{ \kappa ^{*},\bar{\kappa }\right\} ,$ then the unconstraint equilibrium derived in Proposition 1 violates the credit constraint and condition (A.19) is satisfied. For (26) to hold, we need

$$\begin{aligned} \psi F^{\prime }\left( n^{**}\right) >\frac{R_{f}^{**}}{\varPi } . \end{aligned}$$

Since (A.1) holds at $n^{*}$ and $R_{f}^{*}$ and since $n^{**}<n^{*}$ and $R_{f}^{**}<R_{f}^{*},$ the above condition follows from the concavity of F. The rest of the proof follows from the analysis in the main text using Fig. 3. In particular, an increase in $\kappa$ raises the nominal interest rate $R_{f}^{**}$ and hence raises $n^{**}$ by combining Eqs. (A.3) and (A.2). It also raises the corresponding $a^{**}$ by (A.2). But there is no growth effect because the economy still grows at the rate g on the balanced growth path.

Next we study the local stability. As in the proof of Proposition 1, we rewrite the equilibrium system (19), (20), (21), and (25) as

$$\begin{aligned}&a_{t+1}=F\left( n_{t}\right) +\frac{1-F\left( n_{t}\right) }{1+g}a_{t},\end{aligned}$$

(A.20)

$$\begin{aligned}&r_{t}-1=\frac{R_{ft}}{\varPi _{t+1}}\frac{(r_{t+1}-1)}{r_{t+1}}\frac{a_{t}}{ a_{t+1}\left( 1+g\right) }, \end{aligned}$$

(A.21)

$$\begin{aligned}&n_{t}=\frac{\left( 1-\alpha \right) \zeta a_{t}}{1+g}\left[ \lambda +\frac{ \left( 1-\lambda \right) }{1+\beta +\gamma }\left( \beta -\frac{\gamma }{ r_{t}-1}\right) \right] , \end{aligned}$$

(A.22)

$$\begin{aligned}&\left\{ \lambda +\frac{\left( 1-\lambda \right) }{1+\beta +\gamma }\left[ \beta -\frac{\gamma }{r_{t}-1}\right] \right\} =\frac{\beta R_{ft}/\varPi _{t+1} }{\beta R_{ft}/\varPi _{t+1}-\kappa }\lambda . \end{aligned}$$

(A.23)

Define $r_{ft}\equiv R_{ft}/\varPi _{t+1}.$ Log-linearizing this system yields

$$\begin{aligned} \hat{a}_{t+1}= & {} \frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }\hat{n }_{t}+\frac{1-F\left( n\right) }{1+g}\hat{a}_{t}, \nonumber \\ \frac{r}{r-1}\hat{r}_{t}= & {} \hat{r}_{ft}+\frac{1}{r-1}\hat{r}_{t+1}+\hat{a} _{t}-\hat{a}_{t+1}, \nonumber \\ \hat{n}_{t}= & {} \hat{a}_{t}+\vartheta \hat{r}_{t}, \nonumber \\ \hat{r}_{ft}= & {} -\frac{\vartheta (\beta R_{f}/\varPi -\kappa )}{\kappa }\hat{r} _{t}\equiv -\varrho \hat{r}_{t}, \end{aligned}$$

(A.24)

where $\vartheta$ is given in (A.10). Notice that $\varrho ,\vartheta >0$ by condition (A.17).

Simplifying yields a system of two equations for $\hat{a}_{t}$ and $\hat{r}_{t}$:

$$\begin{aligned} \left[ \begin{array}{c} \hat{a}_{t+1} \\ \hat{r}_{t+1} \end{array} \right]= & {} \left[ \begin{array}{cc} \frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }+\frac{1-F\left( n\right) }{1+g} &{} \vartheta \frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) } \\ (1-r)\left[ 1-\frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }-\frac{ 1-F\left( n\right) }{1+g}\right] &{} r+(r-1)[\vartheta \frac{g}{1+g}\frac{ nF^{\prime }(n)}{F\left( n\right) }+\varrho ] \end{array} \right] \left[ \begin{array}{c} \hat{a}_{t} \\ \hat{r}_{t} \end{array} \right] \nonumber \\\equiv & {} J\left[ \begin{array}{c} \hat{a}_{t} \\ \hat{r}_{t} \end{array} \right] \end{aligned}$$

(A.25)

Consider the quadratic characteristic equation $G\left( \nu \right) \equiv \left| J-\nu I\right| =0.$ We can check that $G\left( 0\right) >0$ and $G\left( 1\right) <0$ by condition (27). Moreover, $\lim _{x\rightarrow \infty }G\left( x\right) =\infty$ As in the proof of Proposition 1, we deduce that there is an eigenvalue inside the unit circle and an eigenvalue outside the unit circle. Thus, the steady state is a saddle point.

Fig. 7

Phase diagram for the case with not too tight credit constraint

Finally, we study transition dynamics using the phase diagram in Fig. 7. The locus $a_{t+1}=a_{t}$ represents the line

$$\begin{aligned} \hat{r}_{t}=\frac{1-\frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }- \frac{1-F\left( n\right) }{1+g}}{\vartheta \frac{g}{1+g}\frac{nF^{\prime }(n) }{F\left( n\right) }}\hat{a}_{t}, \end{aligned}$$

and the locus $r_{t+1}=r_{t}$ represents the line

$$\begin{aligned} \hat{r}_{t}=\frac{1-\frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }- \frac{1-F\left( n\right) }{1+g}}{1+\vartheta \frac{g}{1+g}\frac{nF^{\prime }(n)}{F\left( n\right) }+\varrho }\hat{a}_{t}. \end{aligned}$$

Notice that both lines have a positive slope and the locus $\hat{r}_{t+1}= \hat{r}_{t}$ is flatter than the locus $\hat{a}_{t+1}=\hat{a}_{t}$. Thus, if the initial value $\hat{a}_{1}<0$, then both $\hat{r}_{t}$ and $\hat{a}_{t}$ will increase over time to their steady-state values.

We now examine the dynamics of other variables. As in the proof of Proposition 1, we only need to study the signs of coefficients $\phi _{rr},$$\phi _{n},$ and $\phi _{\varPi }.$ Since $R_{ft}=r_{t}(1+z)$ and z is constant, $R_{ft}$ increases over time as $a_{t}$ increases over time given initial $\hat{a}_{1}<0$. Since $\hat{n}_{t}=\hat{a}_{t}+\vartheta \hat{r} _{t}\equiv \phi _{n}\hat{a}_{t}$ and $\phi _{n}>0$, as both $\hat{a}_{t}$ and $\hat{r}_{t}$ increase overtime, so does $\hat{n}_{t}.$ Since

$$\begin{aligned} \hat{r}_{ft}=-\frac{\vartheta (\beta R_{f}/\varPi -\kappa )}{\kappa }\hat{r} _{t}\equiv -\varrho \hat{r}_{t}=-\varrho \phi _{r}\hat{a}_{t}\equiv \phi _{rr}\hat{a}_{t}, \end{aligned}$$

we have $\phi _{rr}<0.$ Thus, the real interest rate $R_{ft}/\varPi _{t+1}$ decreases with $a_{t}$ to the steady state. The growth rate of the economy up to the first-order approximation is given by

$$\begin{aligned} \log A_{t+1}-\log A_{t}=\hat{a}_{t+1}-\hat{a}_{t}+\log (1+g)=(\phi _{a}-1) \hat{a}_{t}+\log (1+g). \end{aligned}$$

It follows from $\phi _{a}\in \left( 0,1\right)$ that the growth rate of the economy declines as $a_{t}$ increases. It follows from

$$\begin{aligned} \hat{\varPi }_{t+1}=\hat{r}_{t}-\hat{r}_{ft}=(\phi _{r}-\phi _{rr})\hat{a} _{t}\equiv \phi _{\varPi }\hat{a}_{t}, \end{aligned}$$

$\phi _{r}>0,$ and $\phi _{rr}<0$ that the inflation rate $\varPi _{t}$ increases with $a_{t}$ to the steady state. $\square$

Proof of Proposition 3

The equilibrium system still consists of Eqs. (19), (20), (21), and (25). We first study the steady state which is characterized by Eqs. (A.3), (A.2), (A.16), and

$$\begin{aligned} \varPi =\frac{1+z}{1+g}\text { }\underset{t\rightarrow \infty }{\lim }\frac{a_{t} }{a_{t+1}}. \end{aligned}$$

(A.26)

Notice that $a_{t}$ may not converge to a positive constant when $0<\kappa <\kappa ^{**}$. As in the proof of Proposition 2, Eq. (A.18) still holds. But when $\kappa \in \left( 0,\kappa ^{**}\right) ,$ the first inequality in assumption (A.19) is violated so that the following inequality holds in the steady state:

$$\begin{aligned} \varPhi ^{\prime }\left( 0\right) g>\frac{\left( 1-\alpha \right) \zeta \lambda \beta R_{f}/\varPi }{\beta R_{f}/\varPi -\kappa }. \end{aligned}$$

(A.27)

Thus, the only solution to Eq. (A.18) is $\mu ^{p}=0.$ As a result, we have $n^{p}=a^{p}=0$ in the steady state.

The following algebra shows that the productivity growth will converge to a rate between 0 and $1+g$ for $\kappa <\kappa ^{**}:$

$$\begin{aligned} \underset{t\rightarrow \infty }{\lim }\frac{A_{t+1}}{A_{t}}= & {} \left( 1+g\right) \underset{t\rightarrow \infty }{\lim }\frac{a_{t+1}}{a_{t}} =\left( 1+g\right) \underset{t\rightarrow \infty }{\lim }\left( \frac{\mu _{t}}{a_{t}}+\frac{1-\mu _{t}}{1+g}\right) \\= & {} \left( 1+g\right) \underset{t\rightarrow \infty }{\lim }\frac{F\left( n_{t}\right) }{a_{t}}+1=\left( 1+g\right) \underset{a\rightarrow 0}{\lim } \frac{F\left( n\right) }{a}+1 \\= & {} \left( 1+g\right) F^{\prime }\left( 0\right) \frac{\partial n}{\partial a} |_{a\rightarrow 0}+1=F^{\prime }\left( 0\right) \frac{\left( 1-\alpha \right) \zeta \lambda \beta R_{f}/\varPi }{\beta R_{f}/\varPi -\kappa }+1 \\< & {} F^{\prime }\left( 0\right) \varPhi ^{\prime }\left( 0\right) g+1=g+1, \end{aligned}$$

where we have used Eqs. (A.3) and (A.16) and $\mu _{t}\rightarrow 0$ to derive the second last equality. The last inequality holds because (A.27) holds. By (A.26) and the above expression for $\underset{t\rightarrow \infty }{\lim }\frac{a_{t+1}}{a_{t}},$ the steady-state inflation rate satisfies

$$\begin{aligned} \varPi =\frac{1+z}{F^{\prime }\left( 0\right) \frac{\left( 1-\alpha \right) \zeta \lambda \beta R_{f}/\varPi }{\beta R_{f}/\varPi -\kappa }+1}>\frac{1+z}{1+g}. \end{aligned}$$

(A.28)

The poverty trap steady state is characterized by a system of two equations (A.16) and (A.28) for two variables $R_{f}$ and $\varPi$.

We modify Fig. 3 to show the existence of a unique solution denoted by $\varPi ^{p}$ and $R_{f}^{p}.$ Now the horizontal axis shows the real interest rate $R_{f}/\varPi$ instead of the nominal interest rate $R_{f}.$ The borrowing-limit curve still describes the expression on the right-hand side of equation (A.16) as a decreasing function of $R_{f}/\varPi$. The supply curve describes the expression on the left-hand side of (A.16), which is written as a function $R_{f}/\varPi$:

$$\begin{aligned}&\lambda +\frac{1-\lambda }{1+\beta +\gamma }\left[ \beta -\frac{\gamma }{ \frac{R_{f}}{\varPi }\frac{\varPi }{1+z}-1}\right] \\&\quad =\lambda +\frac{1-\lambda }{ 1+\beta +\gamma }\left[ \beta -\frac{\gamma }{\frac{R_{f}}{\varPi }\left( F^{\prime }\left( 0\right) \frac{\left( 1-\alpha \right) \zeta \lambda \beta R_{f}/\varPi }{\beta R_{f}/\varPi -\kappa }+1\right) ^{-1}-1}\right] , \end{aligned}$$

where we have used (A.28) to substitute for $\varPi .$ We can check that the above expression increases with $R_{f}/\varPi .$ As in the proof of Proposition 2, there is a unique intersection point between the borrowing-limit and supply curves such that (A.17) holds, which determines the equilibrium real interest rate $R_{f}/\varPi$. Then $\varPi ^{p}$ and $R_{f}^{p}$ are determined.

It follows from (A.28) that $\varPi ^{p}>\left( 1+z\right) /\left( 1+g\right)$ and $\varPi ^{p}$ decreases with $\kappa$ as $\frac{\lambda \beta R_{f}/\varPi }{\beta R_{f}/\varPi -\kappa }$ increases with $\kappa$ (see Fig. 3). Similarly, $\underset{t\rightarrow \infty }{\lim }A_{t+1}/A_{t}$ increases with $\kappa .$

Next we study the local stability of the poverty trap steady state. The equilibrium system is still given by Eqs. (A.20) through (A.23). Since the steady-state values of $n_{t}$ and $a_{t}$ are zero, we cannot use log-linearization. Instead we use linearization in levels to derive

$$\begin{aligned} F\left( n_{t}\right) =F(0)+F^{\prime }(0)n_{t}=F^{\prime }(0)n_{t}. \end{aligned}$$

Substituting this equation into (19) yields

$$\begin{aligned} a_{t+1}=F^{\prime }(0)n_{t}+\frac{1-F^{\prime }(0)n_{t}}{1+g}a_{t}. \end{aligned}$$

(A.29)

Combining Eqs. (21) and (25) yields

$$\begin{aligned} n_{t}=\frac{\left( 1-\alpha \right) \zeta a_{t}}{1+g}\frac{\lambda \beta R_{ft}/\varPi _{t+1}}{\beta R_{ft}/\varPi _{t+1}-\kappa }. \end{aligned}$$

Linearizing around the steady state yields

$$\begin{aligned} n_{t}=\frac{\left( 1-\alpha \right) \zeta }{1+g}\frac{\lambda \beta R_{f}/\varPi }{\beta R_{f}/\varPi -\kappa }a_{t}. \end{aligned}$$

(A.30)

Substituting this equation into (A.29), we obtain the approximate law of motion for $a_{t}$:

$$\begin{aligned} a_{t+1}=\left\{ F^{\prime }(0)\frac{\left( 1-\alpha \right) \zeta }{1+g} \frac{\lambda \beta R_{f}/\varPi }{\beta R_{f}/\varPi -\kappa }+\frac{1}{1+g} \right\} a_{t}-\frac{F^{\prime }(0)}{1+g}\frac{\left( 1-\alpha \right) \zeta }{1+g}\frac{\lambda \beta R_{f}/\varPi }{\beta R_{f}/\varPi -\kappa }a_{t}^{2}. \end{aligned}$$

(A.31)

We have shown earlier that

$$\begin{aligned} 0<F^{\prime }(0)\frac{\left( 1-\alpha \right) \zeta }{1+g}\frac{\lambda \beta R_{f}/\varPi }{\beta R_{f}/\varPi -\kappa }+\frac{1}{1+g}<1, \end{aligned}$$

when $\kappa \in \left( 0,\kappa ^{**}\right) .$ It follows from (A.31) that $a_{t}$ decreases monotonically to the steady state $a^{p}=0$ whenever it starts at any small $a_{1}>0.$ Thus, the steady state is a saddle point. It follows from (A.30) that $n_{t}$ also decreases monotonically to the steady state $n^{p}=0.$ Since $\mu _{t}=F\left( n_{t}\right) ,$$\mu _{t}$ also decreases monotonically to the steady state $\mu ^{p}=0.$

We can derive the approximate productivity growth rate around the steady state

$$\begin{aligned} \frac{A_{t+1}}{A_{t}}-1= & {} \frac{a_{t+1}}{a_{t}}(1+g)-1 \nonumber \\= & {} F^{\prime }(0)\left( 1-\alpha \right) \zeta \frac{\lambda \beta R_{f}/\varPi }{\beta R_{f}/\varPi -\kappa }\nonumber \\&-F^{\prime }(0)\frac{\left( 1-\alpha \right) \zeta }{1+g}\frac{\lambda \beta R_{f}/\varPi }{\beta R_{f}/\varPi -\kappa }a_{t}, \end{aligned}$$

(A.32)

where the second equality follows from substitution of (A.31). Since $F^{\prime }\left( 0\right) >0$ and $\frac{\lambda \beta R_{f}/\varPi }{\beta R_{f}/\varPi -\kappa }>0,$ the productivity growth rate increases to the steady state when $a_{t}$ decreases to the steady state.

We log-linearize equation (A.21) to derive

$$\begin{aligned} \frac{r}{r-1}\hat{r}_{t}=\hat{r}_{ft}+\frac{1}{r-1}\hat{r}_{t+1}+\hat{x}_{t}, \end{aligned}$$

(A.33)

where we define $r_{ft}=R_{ft}/\varPi _{t+1}$ and

$$\begin{aligned} x_{t}\equiv \frac{a_{t}}{a_{t+1}}=\frac{1}{F^{\prime }(0)\frac{\left( 1-\alpha \right) \zeta }{1+g}\left[ \frac{\beta R_{f}/\varPi }{\beta R_{f}/\varPi -\kappa }\lambda \right] +\frac{1}{1+g}-\frac{F^{\prime }(0)}{1+g}\frac{ \left( 1-\alpha \right) \zeta }{1+g}\frac{\lambda \beta R_{f}/\varPi }{\beta R_{f}/\varPi -\kappa }a_{t}}. \end{aligned}$$

Here the second equality follows from Eq. (A.31). We then obtain the log-linearized equation

$$\begin{aligned} \hat{x}_{t}=\frac{F^{\prime }(0)\frac{\left( 1-\alpha \right) \zeta }{1+g} \frac{\lambda \beta R_{f}/\varPi }{\beta R_{f}/\varPi -\kappa }}{F^{\prime }(0)\left( 1-\alpha \right) \zeta \frac{\lambda \beta R_{f}/\varPi }{\beta R_{f}/\varPi -\kappa }+1}a_{t}\equiv \phi _{x}a_{t}. \end{aligned}$$

Substituting (A.24) into (A.33) yields

$$\begin{aligned} \hat{r}_{t}=\frac{1}{r+(r-1)\varrho }\hat{r}_{t+1}+\frac{r-1}{r+(r-1)\varrho }\hat{x}_{t}. \end{aligned}$$

(A.34)

We now drop the quadratic term in (A.31) and write the first-order approximation to the law of motion as $a_{t+1}=\phi _{a}a_{t},$ where $\phi _{a}\in \left( 0,1\right) .$ Since $r=R_{f}/\left( 1+z\right) >1$ and $\varrho >0$ by (A.17), we iterate (A.34) forward to derive

$$\begin{aligned} \hat{r}_{t}=\frac{\left( r-1\right) \phi _{x}}{r+(r-1)\varrho -\phi _{a}} a_{t}. \end{aligned}$$

Thus, as $a_{t}$ decreases to the steady state, $\hat{r}_{t}$ also decreases to the steady state and so does $R_{ft}.$ It follows from (A.24) and $\varrho >0$ that the real interest rate $r_{ft}=R_{ft}/\varPi _{t+1}$ increases to the steady state when $\hat{r}_{t}$ or $R_{ft}$ decreases to the steady state. Finally, since

$$\begin{aligned} \hat{\varPi }_{t+1}=\hat{r}_{t}-\hat{r}_{ft}=(1+\varrho )\hat{r}_{t}, \end{aligned}$$

the inflation rate $\varPi _{t}$ decreases to the steady state when $\hat{r} _{t}$ decreases to the steady state. $\square$

Proof of Proposition 4

Let $\beta ^{t}\varLambda _{t}$ and $\beta ^{t}\varLambda _{t}q_{t}$ be the Lagrange multipliers associated with (32) and (13), respectively. The variable $q_{t}$ represents the shadow value of the technology $A_{t+1}.$ The first-order conditions are given by

$$\begin{aligned} \omega u^{\prime }\left( c_{t}^{e}\right)= & {} u^{\prime }\left( c_{t}^{o}\right) ~=u^{\prime }\left( c_{t}^{y}\right) =\varLambda _{t}, \\ \varLambda _{t}= & {} \beta \varLambda _{t+1}\left( \frac{1}{\alpha }-1\right) \left[ \alpha ^{ \frac{1}{1-\alpha }}\bar{A}_{t+1}-\left( \frac{\alpha }{\chi }\right) ^{ \frac{1}{1-\alpha }}\chi A_{t}\right] \frac{F^{\prime }\left( N_{t}/\bar{A}_{t+1}\right) }{\bar{A}_{t+1}} \\&+\varLambda _{t}q_{t}[\bar{A}_{t+1}-A_{t}]\frac{F^{\prime }\left( N_{t}/\bar{A}_{t+1}\right) }{\bar{A}_{t+1}}, \\ \varLambda _{t}q_{t}= & {} \beta (1-\mu _{t+1})\varLambda _{t+1}q_{t+1}+\beta ^{2}\varLambda _{t+2}(1-\mu _{t+1})\left( \frac{1}{\alpha }-1\right) \left( \frac{\alpha }{ \chi }\right) ^{\frac{1}{1-\alpha }}\chi . \end{aligned}$$

In the steady state, we have

$$\begin{aligned} q=\frac{\beta }{1+g}(1-\mu )q+\left( \frac{\beta }{1+g}\right) ^{2}(1-\mu )\left( \frac{1}{\alpha }-1\right) \left( \frac{\alpha }{\chi }\right) ^{\frac{1}{1-\alpha } }\chi , \end{aligned}$$

and

$$\begin{aligned} \frac{1}{F^{\prime }\left( n\right) }=\beta \frac{1}{1+g}\left( \frac{1}{\alpha } -1\right) \left[ \alpha ^{\frac{1}{1-\alpha }}-\left( \frac{\alpha }{\chi }\right) ^{\frac{1}{1-\alpha }}\chi \frac{a}{1+g}\right] +q\left[ 1-\frac{a}{1+g} \right] . \end{aligned}$$

Equation (13) implies

$$\begin{aligned} a=\frac{F\left( n\right) (1+g)}{g+F\left( n\right) }. \end{aligned}$$

(A.35)

Using the above three equations, we can derive

$$\begin{aligned} \frac{1}{F^{\prime }\left( n\right) }= & {} \frac{\beta }{1+g}\left( \frac{1}{\alpha } -1\right) \left[ \alpha ^{\frac{1}{1-\alpha }}-\left( \frac{\alpha }{\chi }\right) ^{\frac{1}{1-\alpha }}\chi \right] \\&+\frac{\beta }{1+g-\beta (1-F\left( n\right) )}(\frac{1}{\alpha }-1)\left( \frac{\alpha }{\chi }\right) ^{\frac{1}{1-\alpha }}\chi \frac{g}{g+F\left( n\right) }. \end{aligned}$$

This equation is equivalent to Eq. (34). We can easily check that the expression on the left-hand side of the equation is an increasing function of $\mu$ and the expression on the right-hand side is a decreasing function of $\mu$. Given Assumption 1, it follows from the intermediate value theorem that there is a unique solution, denoted by $\mu _\mathrm{FB}\in \left( 0,1\right) ,$ to the above equation. Then, we obtain the efficient investment level $n_{F}=\varPhi \left( \mu _\mathrm{FB}\right)$. Plugging it into (A.35) gives $a_\mathrm{FB}.$ The efficient consumption and production allocation is derived in the main text. $\square$

Proof of Proposition 5

Suppose that there is no fiscal policy. When money increments are transferred to entrepreneurs instead of savers, the saver’s consumption and portfolio choices are given by

$$\begin{aligned} c_{t}^{y}= & {} \frac{(1-\lambda )w_{t}}{1+\beta +\gamma }, \end{aligned}$$

(A.36)

$$\begin{aligned} c_{t+1}^{o}= & {} \frac{\beta }{1+\beta +\gamma }\frac{R_{ft}}{\varPi _{t+1}} (1-\lambda )w_{t}, \end{aligned}$$

(A.37)

$$\begin{aligned} \frac{M_{t}}{P_{t}}= & {} \frac{\gamma }{1+\beta +\gamma }\frac{R_{ft}}{R_{ft}-1 }(1-\lambda )w_{t}, \end{aligned}$$

(A.38)

$$\begin{aligned} \frac{S_{t}}{P_{t}}= & {} \frac{1}{1+\beta +\gamma }\frac{\beta R_{ft}-\beta -\gamma }{R_{ft}-1}(1-\lambda )w_{t}, \end{aligned}$$

(A.39)

where we assume that

$$\begin{aligned} R_{ft}>1+\frac{\gamma }{\beta }, \end{aligned}$$

so that savings and money demand are positive. Notice that the demand for money and savings depends on the nominal interest rate instead of the real interest rate. The monetary transfer is given by

$$\begin{aligned} \frac{M_{t}-M_{t-1}}{P_{t}}=\frac{z_{t}}{z_{t}+1}\frac{M_{t}}{P_{t}}=\frac{ z_{t}}{z_{t}+1}\frac{\gamma }{1+\beta +\gamma }\frac{R_{ft}}{R_{ft}-1} (1-\lambda )w_{t}, \end{aligned}$$

where the second equality follows from (A.38).

The competitive equilibrium for a given interest rate sequence $\left\{ R_{ft}\right\}$ under perfect credit markets can be summarized by a system of four difference equations, (18), (19), (20), and

$$\begin{aligned} n_{t}=\frac{\left( 1-\alpha \right) \zeta a_{t}}{1+g}\left[ \lambda +\frac{ z_{t}}{1+z_{t}}\frac{(1-\lambda )}{1+\beta +\gamma }\frac{\gamma R_{ft}}{ R_{ft}-1}+\frac{\left( 1-\lambda \right) }{1+\beta +\gamma }\frac{\beta R_{ft}-\beta -\gamma }{R_{ft}-1}\right] . \end{aligned}$$

(A.40)

for four sequences $\{z_{t}\},\left\{ a_{t}\right\} ,\{\varPi _{t+1}\},$ and $\{n_{t}\}$ such that (6) and $R_{ft}>1+\gamma /\beta$ are satisfied. Equation (A.40) says that R&D investment is financed by the entrepreneur’s wage income, monetary transfer, and external credit.

In the steady state, the system becomes three equations (A.1), (A.2), and

$$\begin{aligned} n=\frac{\left( 1-\alpha \right) \zeta a}{1+g}\left[ \lambda +\frac{z}{1+z} \frac{(1-\lambda )}{1+\beta +\gamma }\frac{\gamma R_{f}}{R_{f}-1}+\frac{ \left( 1-\lambda \right) }{1+\beta +\gamma }\frac{\beta R_{f}-\beta -\gamma }{R_{f}-1}\right] , \end{aligned}$$

(A.41)

for three unknowns n, z, and a, when the nominal interest rate $R_{f}$ is set by the monetary authority. Given the efficient innovation rate $\mu _\mathrm{FB}$, we have $n_\mathrm{FB}=\varPhi \left( \mu _\mathrm{FB}\right) ,$ and

$$\begin{aligned} a_\mathrm{FB}=\frac{\left( 1+g\right) F(n_\mathrm{FB})}{g+F\left( n_\mathrm{FB}\right) }. \end{aligned}$$

We now show that the monetary authority can set a specific nominal interest rate such that the efficient innovation can be implemented in a market equilibrium with a perfect credit market on the balanced growth path. Specifically, using the steady-state system, we can derive one equation for one unknown $R_{f}$:

$$\begin{aligned} n_\mathrm{FB}=\frac{\left( 1-\alpha \right) \zeta a_\mathrm{FB}}{1+g}\left[ \lambda +\frac{ (1-\lambda )}{1+\beta +\gamma }\frac{\left( \gamma +\beta \right) \left( R_{f}-1\right) -\gamma \psi F^{\prime }\left( n_\mathrm{FB}\right) /\left( 1+g\right) }{R_{f}-1}\right] \!, \end{aligned}$$

The expression on the right-hand side of the equation is an increasing function of $R_{f}$. Under Assumption 2, this function takes a value lower than $n_\mathrm{FB}$ at $R_{f}=1+\gamma /\beta$ and a value higher than $n_\mathrm{FB}$ when $R_{f}\rightarrow \infty$. It follows from the intermediate value theorem that there exists a unique solution, denoted by $\bar{R}_{f}>1+\gamma /\beta$, to the above equation. Given $R_{f}=\bar{R} _{f},$ we can also easily show that $n=n_\mathrm{FB}$ is the only equilibrium solution.

Once $\bar{R}_{f}$ is determined, we can solve for the money growth rate z using (A.1):

$$\begin{aligned} 1+z=\frac{\bar{R}_{f}\left( 1+g\right) }{F^{\prime }\left( n_\mathrm{FB}\right) \psi }. \end{aligned}$$

Other equilibrium variables can also be easily determined.

Finally, we show that there exists a cutoff $\kappa _{0}$ such that when $\kappa \ge \kappa _{0}$ the credit constraint does not bind in the market equilibrium described above. The credit constraint is given by

$$\begin{aligned} \left( \frac{\beta R_{ft}}{\varPi _{t+1}}-\kappa \right) N_{t}\le \frac{\beta R_{ft}}{\varPi _{t+1}}\left[ \lambda w_{t}+\frac{z_{t}}{1+z_{t}}\frac{\gamma \left( 1-\lambda \right) }{1+\beta +\gamma }\frac{R_{ft}}{R_{ft}-1}w_{t} \right] , \end{aligned}$$

where the second term in the square bracket is the monetary transfer. In the steady state, this constraint becomes

$$\begin{aligned} \left( \frac{\beta R_{f}}{\varPi }-\kappa \right) n\le \frac{\beta R_{f}}{\varPi } \frac{\left( 1-\alpha \right) \zeta a}{1+g}\left[ \lambda +\frac{z}{1+z} \frac{1-\lambda }{1+\beta +\gamma }\frac{\gamma R_{f}}{R_{f}-1}\right] , \end{aligned}$$

where we have used Eq. (15). The desired cutoff $\kappa _{0}$ is defined by the following equation

$$\begin{aligned} n_\mathrm{FB}=\frac{\beta \bar{R}_{f}\left( 1+g\right) /\left( 1+z\right) }{\beta \bar{R}_{f}\left( 1+g\right) /\left( 1+z\right) -\kappa _{0}}\frac{\left( 1-\alpha \right) \zeta a_\mathrm{FB}}{1+g}\left[ \lambda +\frac{z}{1+z}\frac{ 1-\lambda }{1+\beta +\gamma }\frac{\gamma \bar{R}_{f}}{\bar{R}_{f}-1}\right] . \end{aligned}$$

The proof is completed. $\square$

Proof of Proposition 6

First, we show that for any given $\mu _{t-1}$ the efficient GDP is higher than the market GDP because of the monopoly distortion. To show this result, we observe that the efficient GDP $Y_{t}^{e}$ is given by (31). By ( 17), the equilibrium GDP in the market economy is given by

$$\begin{aligned} Y_{t}= & {} w_{t}+\mu _{t-1}\psi \bar{A}_{t} \\= & {} \left( 1-\alpha \right) \left( \frac{\alpha }{\chi }\right) ^{\frac{ \alpha }{1-\alpha }}\left[ \mu _{t-1}\bar{A}_{t}+(1-\mu _{t-1})A_{t-1}\right] +\left( \chi -1\right) \mu _{t-1}\left( \frac{\alpha }{\chi }\right) ^{\frac{ 1}{1-\alpha }}\bar{A}_{t}, \end{aligned}$$

where we have substituted Eqs. (13) and (15) and the expressions for $\zeta$ and $\psi .$ We can easily verify that $Y_{t}^{e}>Y_{t}.$

To achieve the efficient GDP, the government can subsidize the final good firm’s input expenditure. Let $\tau _{xt}(i)$ be the subsidy to input i in period t. Then the final good producer’s problem is given by

$$\begin{aligned} \max ~ L_{t}^{1-\alpha }\int _{0}^{1}A_{t}\left( i\right) ^{1-\alpha }x_{t}\left( i\right) ^{\alpha }\mathrm{d}i-\int _{0}^{1}\tau _{xt}(i)p_{t}(i)x_{t}(i)\mathrm{d}i-w_{t}L_{t}. \end{aligned}$$

This leads to

$$\begin{aligned} x_{t}(i)=\left( \frac{\tau _{xt}(i)p_{t}\left( i\right) }{\alpha }\right) ^{ \frac{1}{\alpha -1}}A_{t}\left( i\right) . \end{aligned}$$

(A.42)

Since $p_{t}\left( i\right) =\chi$, it follows from (30) and ( A.42) that setting

$$\begin{aligned} \tau _{xt}(i)=\tau _{xt}^{0}(i)\equiv \left\{ \begin{array}{ll} \frac{1}{\chi } &{} \quad \text {if an innovation occurs} \\ 1 &{} \quad \text {otherwise} \end{array} \right. \end{aligned}$$

achieves the efficient intermediate input level and final GDP $Y_{t}^{e}$.

In this case, a successful innovator produces intermediate good $x_{t}\left( i\right) =\alpha ^{\frac{1}{1-\alpha }}\bar{A}_{t}$ and earns monopoly profits

$$\begin{aligned} p_{t}\left( i\right) x_{t}\left( i\right) -x_{t}\left( i\right) =\chi \alpha ^{\frac{1}{1-\alpha }}\bar{A}_{t}-\alpha ^{\frac{1}{1-\alpha }}\bar{A} _{t}=\psi ^{*}\bar{A}_{t}, \end{aligned}$$

where $\psi ^{*}\equiv \alpha ^{\frac{1}{1-\alpha }}(\chi -1)>\psi$. Since the final good firm earns zero profit, the real wage under the government policies is given by

$$\begin{aligned} w_{t}=\left( 1-\alpha \right) \left[ \alpha ^{\frac{\alpha }{1-\alpha }}\mu _{t-1}\bar{A}_{t}+(1-\mu _{t-1})\left( \frac{\alpha }{\chi }\right) ^{\frac{ \alpha }{1-\alpha }}A_{t-1}\right] . \end{aligned}$$

(A.43)

The total subsidy is given by

$$\begin{aligned} \int _{0}^{1}\left( 1-\tau _{xt}\left( i\right) \right) p_{t}\left( i\right) x_{t}\left( i\right) \mathrm{d}i=\alpha ^{\frac{1}{1-\alpha }}\mu _{t-1}\bar{A} _{t}(\chi -1). \end{aligned}$$

Let $w_{Dt}=w_{t}-T_{w}\bar{A}_{t}$ denote the after-tax wage. Since money increments are transferred to entrepreneurs instead of savers, we rederive the saver’s decision rules as

$$\begin{aligned} c_{t}^{y}= & {} \frac{(1-\lambda )w_{Dt}}{1+\beta +\gamma }, \end{aligned}$$

(A.44)

$$\begin{aligned} c_{t+1}^{o}= & {} \frac{\beta }{1+\beta +\gamma }\frac{R_{ft}}{\varPi _{t+1}} (1-\lambda )w_{Dt}, \end{aligned}$$

(A.45)

$$\begin{aligned} \frac{M_{t}}{P_{t}}= & {} \frac{\gamma }{1+\beta +\gamma }\frac{R_{ft}}{R_{ft}-1 }(1-\lambda )w_{Dt}, \end{aligned}$$

(A.46)

$$\begin{aligned} \frac{S_{t}}{P_{t}}= & {} \frac{1}{1+\beta +\gamma }\frac{\beta R_{ft}-\beta -\gamma }{R_{ft}-1}(1-\lambda )w_{Dt}, \end{aligned}$$

(A.47)

where we assume that

$$\begin{aligned} R_{ft}>1+\frac{\gamma }{\beta }, \end{aligned}$$

so that savings and money demand are positive.

The entrepreneur’s budget constraint (4) when young becomes

$$\begin{aligned} N_{t}=\frac{B_{t}}{P_{t}}+\lambda w_{Dt}+\tau _{et}, \end{aligned}$$

(A.48)

where $\tau _{et}$ is the monetary transfer

$$\begin{aligned} \tau _{et}=\frac{M_{t}-M_{t-1}}{P_{t}}. \end{aligned}$$

(A.49)

The entrepreneur’s problem is to maximize his expected consumption when old:

$$\begin{aligned} \max ~(1+\tau _{N})F\left( N_{t}/\bar{A}_{t+1}\right) \psi ^{*}\bar{A}_{t+1}-T_{N}\bar{A}_{t+1}-R_{ft}\frac{P_{t}}{P_{t+1}}[N_{t}-\lambda w_{Dt}-\tau _{t}^{e}]. \end{aligned}$$

Suppose that the credit constraint is slack. The first-order condition implies that

$$\begin{aligned} (1+\tau _{N})F^{\prime }(n_{t})\psi ^{*}=R_{ft}\frac{P_{t}}{P_{t+1}}. \end{aligned}$$

(A.50)

By the market-clearing condition for loans and Eqs. (A.46), (A.47), (A.48), and (A.49), we derive that

$$\begin{aligned} N_{t}=\lambda w_{Dt}+\frac{z_{t}}{1+z_{t}}\frac{(1-\lambda )\gamma }{1+\beta +\gamma }\frac{R_{ft}}{R_{ft}-1}w_{Dt}+\frac{1-\lambda }{1+\beta +\gamma } \frac{\beta R_{ft}-\beta -\gamma }{R_{ft}-1}w_{Dt}. \end{aligned}$$

(A.51)

The three terms on the right-hand side of this equation give three sources of funds for the R&D investment: internal funds (wage), government monetary transfers, and external debt.

In the steady state, equation (A.2) still holds and (A.50) becomes

$$\begin{aligned} (1+\tau _{N})F^{\prime }(n)\psi ^{*}=\frac{R_{f}}{\varPi }, \end{aligned}$$

(A.52)

where $\varPi =\left( 1+z\right) /\left( 1+g\right) .$ Using (15) and (A.2), we rewrite (A.51) as

$$\begin{aligned} n=\eta \left[ \lambda +\frac{z}{1+z}\frac{(1-\lambda )}{1+\beta +\gamma } \frac{\gamma R_{f}}{R_{f}-1}+\frac{1-\lambda }{1+\beta +\gamma }\frac{\beta R_{f}-\beta -\gamma }{R_{f}-1}\right] , \end{aligned}$$

(A.53)

where it follows from (A.43) that

$$\begin{aligned} \eta \equiv \frac{w_{Dt}}{\bar{A}_{t+1}}=\left( 1-\alpha \right) \left[ \frac{\alpha ^{\frac{\alpha }{1-\alpha }}\mu }{1+g}+(1-\mu )\left( \frac{ \alpha }{\chi }\right) ^{\frac{\alpha }{1-\alpha }}\frac{a}{\left( 1+g\right) ^{2}}\right] -\frac{T_{w}}{1+g} \end{aligned}$$

(A.54)

is constant along a balanced growth path. The variable $\eta$ represents the normalized after-tax wage on the balanced growth path.

By (A.48) and (A.49), the credit constraint (5) becomes

$$\begin{aligned} N_{t}\le \frac{\beta R_{ft}/\varPi _{t+1}}{\beta R_{ft}/\varPi _{t+1}-\kappa } \left[ \lambda w_{Dt}+\frac{z_{t}}{1+z_{t}}\frac{\gamma \left( 1-\lambda \right) }{1+\beta +\gamma }\frac{R_{ft}}{R_{ft}-1}w_{Dt}\right] . \end{aligned}$$

(A.55)

In the steady state, this constraint becomes

$$\begin{aligned} n\le \frac{\eta \beta R_{f}/\varPi }{\beta R_{f}/\varPi -\kappa }\left[ \lambda + \frac{z}{1+z}\frac{1-\lambda }{1+\beta +\gamma }\frac{\gamma R_{f}}{R_{f}-1} \right] , \end{aligned}$$

(A.56)

where we have used Eq. (A.54).

Since we do not consider government spending and government debt, the following government budget constraint must be satisfied:

$$\begin{aligned} \tau _{N}F\left( N_{t-1}/\bar{A}_{t}\right) \psi ^{*}\bar{A}_{t}+\alpha ^{\frac{1}{1-\alpha }}\mu _{t-1}\bar{A}_{t}(\chi -1)+\tau _{et}=T_{N}\bar{A} _{t}+T_{w}\bar{A}_{t}+\frac{M_{t}-M_{t-1}}{P_{t}}, \end{aligned}$$

where the second term represents the total subsidy to intermediate inputs. By (A.49), this constraint along a balanced growth path becomes

$$\begin{aligned} \tau _{N}F\left( n\right) \psi ^{*}+\alpha ^{\frac{1}{1-\alpha }}\mu (\chi -1)=T_{N}+T_{w}. \end{aligned}$$

(A.57)

The steady-state competitive equilibrium under fiscal and monetary policy instruments $\{R_{f},\tau _{x}\left( i\right) , T_{w},\tau _{N} , T_{N}\}$ consists of four equations (A.2), (A.52), (A.53), and $\varPi =\left( 1+z\right) /\left( 1+g\right)$ for four variables n, a, z, and $\varPi$ such that (A.56) and (A.57) hold.¹¹

We use (33) and $\omega =1$ to derive the efficient consumption for the young saver

$$\begin{aligned} c_{t}^{y}=\frac{1}{3}\left( Y_{t}^{e}-N_{t}\right) . \end{aligned}$$

To implement this efficient consumption in a market equilibrium, we use (A.44) to set the labor income tax as

$$\begin{aligned} T_{w}\bar{A}_{t}=w_{t}-\frac{1+\beta +\gamma }{3(1-\lambda )}\left( Y_{t}^{e}-N_{t}\right) . \end{aligned}$$

Using Eqs. (15) and (31), we derive that

$$\begin{aligned} T_{w}= & {} \left[ 1-\frac{1+\beta +\gamma }{3(1-\lambda )}\right] \left( 1-\alpha \right) \left[ \alpha ^{\frac{\alpha }{1-\alpha }}\mu +(1-\mu )\left( \frac{\alpha }{\chi }\right) ^{\frac{\alpha }{1-\alpha }}\frac{a}{ \left( 1+g\right) }\right] \\&+\frac{1+\beta +\gamma }{3(1-\lambda )}\left( 1+g\right) n, \nonumber \end{aligned}$$

(A.58)

on the balanced growth path. We set $T_{N}$ such that the government budget constraint (A.57) is satisfied.

It remains to choose $\tau _{N}$ and $R_{f}$ such that the competitive equilibrium implies efficient production and innovation such that $a=a_\mathrm{FB} ,$$n=n_\mathrm{FB},$ and $\mu =F\left( n_\mathrm{FB}\right)$. We maintain the following assumption similar to Assumption 2 such that the efficient R&D investment cannot be self-financed by the entrepreneur’s wage income and monetary transfers and external credit are needed.

Assumption 3

Parameter values are such that $0<\gamma <1-\beta$ and

$$\begin{aligned} \lambda \eta _\mathrm{FB}<n_\mathrm{FB}<\eta _\mathrm{FB}\left[ \lambda +\frac{\left( 1-\lambda \right) \left( \beta +\gamma \right) }{1+\beta +\gamma }\right] , \end{aligned}$$

where $\eta _\mathrm{FB}$ is defined in (A.54) and where $T_{w}$ is defined in (A.58) with $\mu =\mu _\mathrm{FB}$ and $a=a_\mathrm{FB}$.

We now set policy variables $R_{f}^{0},$$\tau _{N}^{0},$$T_{N}^{0},$ and $T_{w}^{0}$ such that they satisfy

$$\begin{aligned} n_\mathrm{FB}= & {} \eta _\mathrm{FB}\left[ \lambda +\frac{1-\lambda }{1+\beta +\gamma }\frac{ \beta \left( \gamma +\beta \right) \left( R_{f}^{0}-1\right) -\gamma }{\beta \left( R_{f}^{0}-1\right) }\right] , \end{aligned}$$

(A.59)

$$\begin{aligned} \tau _{N}^{0}= & {} \frac{\left( 1+g\right) /\beta }{F^{\prime }(n_\mathrm{FB})\psi ^{*}}-1,\end{aligned}$$

(A.60)

$$\begin{aligned} T_{N}^{0}= & {} \tau _{N}^{0}F\left( n_\mathrm{FB}\right) \psi ^{*}+\alpha ^{\frac{1}{ 1-\alpha }}F\left( n_\mathrm{FB}\right) (\chi -1)-T_{w}^{0},\nonumber \\ T_{w}^{0}= & {} \left[ 1-\frac{1+\beta +\gamma }{3(1-\lambda )}\right] \left( 1-\alpha \right) \left[ \alpha ^{\frac{\alpha }{1-\alpha }}\mu _\mathrm{FB}+(1-\mu )\left( \frac{\alpha }{\chi }\right) ^{\frac{\alpha }{1-\alpha }}\frac{a_\mathrm{FB} }{\left( 1+g\right) }\right] \nonumber \\&+\frac{1+\beta +\gamma }{3(1-\lambda )}\left( 1+g\right) n_\mathrm{FB}. \end{aligned}$$

(A.61)

As in the proof of Proposition 5, we use the intermediate value theorem to show that under Assumption 3 there exists a unique solution for $R_{f}^{0}>1+\gamma /\beta$ to equation (A.59).

Define the cutoff $\kappa ^{0}$ by the equation

$$\begin{aligned} n_\mathrm{FB}=\frac{\left( 1+g\right) \eta _\mathrm{FB}}{1+g-\kappa ^{0}}\left[ \lambda + \frac{\beta R_{f}^{0}-1}{\beta R_{f}^{0}}\frac{1-\lambda }{1+\beta +\gamma } \frac{\gamma \left( 1+g\right) }{1+g-\beta }\right] . \end{aligned}$$

(A.62)

Then, when $\kappa \ge \kappa ^{0}$ the credit constraint does not bind on the balanced growth path.

Given the above monetary and fiscal policy variables, the steady-state system (A.2), (A.52), (A.53), and $\varPi =\left( 1+z\right) /\left( 1+g\right)$ becomes

$$\begin{aligned} a= & {} \frac{F\left( n\right) (1+g)}{g+F\left( n\right) }\text {, \ }\varPi =\frac{1+z }{1+g}\text {, \ }\frac{F^{\prime }\left( n\right) }{F^{\prime }\left( n_\mathrm{FB}\right) }=\frac{R_{f}^{0}}{\varPi }\frac{\beta }{1+g},\\ n= & {} \eta \left[ \lambda +\frac{z}{1+z}\frac{(1-\lambda )}{1+\beta +\gamma } \frac{\gamma R_{f}^{0}}{R_{f}^{0}-1}+\frac{1-\lambda }{1+\beta +\gamma } \frac{\beta R_{f}^{0}-\beta -\gamma }{R_{f}^{0}-1}\right] , \end{aligned}$$

for four variables $n, a, \mu ,$ and z.

We can simplify this system to one equation for n:

$$\begin{aligned} \frac{n}{\eta }=\lambda +\left[ 1-\frac{F^{\prime }\left( n\right) }{\beta R_{f}^{0}F^{\prime }\left( n_\mathrm{FB}\right) }\right] \frac{(1-\lambda )}{ 1+\beta +\gamma }\frac{\gamma R_{f}^{0}}{R_{f}^{0}-1}+\frac{1-\lambda }{ 1+\beta +\gamma }\frac{\beta R_{f}^{0}-\beta -\gamma }{R_{f}^{0}-1}, \end{aligned}$$

(A.63)

where

$$\begin{aligned} \eta =\frac{1+\beta +\gamma }{3(1-\lambda )}\left[ \left( 1-\alpha \right) \left[ \frac{\alpha ^{\frac{\alpha }{1-\alpha }}F\left( n\right) }{1+g} +(1-F\left( n\right) )\frac{\left( \frac{\alpha }{\chi }\right) ^{\frac{ \alpha }{1-\alpha }}F\left( n\right) }{\left( 1+g\right) \left( g+F\left( n\right) \right) }\right] -\left( 1+g\right) n\right] . \end{aligned}$$

We can check that $n=n_\mathrm{FB}$ is a solution to equation (A.63). We next show that this is only solution. Since $F\left( n\right)$ is concave and $F\left( 0\right) =0,$ we can show that $F\left( n\right) /n$ decreases with n. Thus, $\eta /n$ decreases with n or $n/\eta$ increases with n. We also know that the expression on the right-hand side of (A.63) increases with n. Two monotonic curves can only have one intersection point if there is any. Thus, there is a unique solution $n=n_\mathrm{FB}$ to equation (A.63).

We can then verify that the solution to the above system is given by

$$\begin{aligned} a=a_\mathrm{FB},~ n=n_\mathrm{FB},~ z=\beta R_{f}^{0}-1,~\varPi = \frac{\beta R_{f}^{0}}{1+g}. \end{aligned}$$

Since the market real interest rate $R_{f}^{0}/\varPi =\beta \left( 1+g\right)$ is the same as the efficient rate in (35), the old saver consumption satisfies $c_{t+1}^{o}=c_{t}^{y}\left( 1+g\right) .$ Thus, $c_{t}^{o}=c_{t}^{y}$ on the balanced growth path. We then attain consumption efficiency by (33) with $\omega =1$. Since the above system has a unique solution, the preceding solution is the only steady-state equilibrium that attains the efficient innovation, production, and consumption allocation. $\square$

Data description

For Fig. 1, we follow Levine et al. (2000) and AHM (2005) and consider cross-sectional data on 71 countries over the period 1960–1995. As in their papers, we use private credit, defined as the value of credits by financial intermediaries to the private sector, divided by GDP, as our preferred measure of financial development. We construct this measure using the updated 2017 version of the Financial Development and Structure Database. We have also used other measures of financial development and the pattern in Fig. 1 does not change. We construct the average per capita GDP growth rates using the Penn World Table and construct the average inflation rates and the average (broad) money growth rates using the World Bank WDI database. We delete outliers with average inflation rates higher than 40%, but the pattern in Fig. 1 still holds for the full sample. The outliers are Argentina, Bolivia, Brazil, Chile, Israel, Peru, and Uruguay. The non-convergence countries used in Panel D of Fig. 1 are identified according to Table II of AHM (2005).