1 Introduction

In order to increase the effect of high explosives, the introduction of reactive particles is frequently used. Aluminized high explosives have higher total energy than pure high explosives, and the effects are most distinct in the far field, where both longer pressure duration and higher pressure impulse are observed [1,2,3]. A review on enhanced explosives is given in [4]. When such high explosives are used in enclosed structures, multiple shock reflection occur, and high levels of quasi-static pressure are observed [5]. The goal of the present paper is to investigate shock propagation, interaction, and spontaneous ignition of aluminium particle clouds in a shock tube environment numerically and evaluate different combustion models. The problem of interest is based on the experimental results of Omang and Hauge [6]. As discussed in [6], the term "ignition" is used to describe reaction onset of aluminium particle clouds exposed to sufficient heating.

The number of published experimental shock tube studies on spontaneous ignition of aluminium particles is rather sparse. Additionally, the use of published experimental data for code validations is not straightforward since it requires a number of parameters to be given. The work presented by Benkiewicz and Hayashi [7] is a numerical study of shock-ignited aluminium particles. The work is based on [8] and [9], although they have chosen their own parameters. The aluminium particle diameter is relatively small (5 \(\upmu \)m). Effects of particle agglomeration have been neglected, although this effect may be important for the chosen particle diameter size [10]. The particles are found to be mainly heated by the reflected shock, and the ignition delay time is found to be between 80 and 100 \(\upmu \)s. The ignition delay is the time measured from when the shock reflects at the end wall until ignition is observed. With the chosen ignition temperature of 1350 K, they find that the shock Mach number must be as high as \(M_\text {s} = 3\), in order for ignition to take place.

Another numerical study of shock-ignited aluminium particles is presented by Balakrishnan et al. [11]. Their study is based on the experiments by Boiko et al. [9], using a two-phase numerical method. The particle cloud is assumed to be 5 cm in radius, and the aluminium particle flakes have a size of 4–6 \(\upmu \)m. The initial cloud mass density range is chosen to be 50–200 \(\times \) \(10^3\) \(\text {kg/m}^3\). They find that an increase in the initial cloud mass density also gives an increased aluminium particle burning time. Similarly, an increase in the shock Mach number leads to a reduced ignition delay time, as the particle heating is found to be more efficient.

In [12], the importance of the particle heating rate is discussed as a mean to understand low-temperature ignition of aluminium particles. The definition of heating rate is divided into low-speed heating, for 8–10 degrees per second, and high-speed heating, for 20 degrees per second or more.

The subject of particle heating rate is further discussed in [13, 14]. Here, the physical mechanism of the particle heating and combustion is divided in two. The first mechanism is relevant for dilute particle suspensions, where the heating is relatively slow, and combustion of the particles may be treated individually. The second mechanism is described for denser particle suspension, where there is a delay due to particle heating and self-heating, followed by a particle reaction of a more explosive-like character. The differences in the nature of these two mechanisms suggests that reaction models developed for single particle combustion are not necessarily correct for rapidly heated particle clouds [13].

For our numerical simulations, we use a numerical code based on smoothed particle hydrodynamics (SPH) methodology [15]. The code includes several extensions to the original SPH method and is called multi-phase regularized smoothed hydrodynamics (MP-RSPH) [16]. In the present paper, we wish to extend our numerical description to include dense gas–particle mixtures, as well as particle ignition and combustion. This is accomplished by introducing additional terms to the equations of motion. The numerical results are compared to the published experimental results. In previous work, a multi-phase model was developed and tested for two-phase gas–particle problems [16]. The study focused on inert particles, and the formulation was limited to relatively low volume fractions in the particle–gas mixture.

In the present study, the numerical simulations are based on our experimental study of shock interacting with aluminium particle clouds in a shock tube [6]. A set of numerical combustion models are evaluated, and results from two different empirical burn rate expressions are compared. The experiments are conducted with aluminium particles deposited on a horizontal splitter plate mounted to the shock tube end wall. Since the shock tube is closed, the shock wave propagates across the particle ridge twice. The key findings from the experimental work were that the cloud of accelerated reactive aluminium particles can be ignited at relatively low gas temperatures. The results indicated a gas temperature down to approximately 635 K. The results showed an ignition delay time decreasing with increasing shock strength. Although the aluminium cloud burn time results showed a significant scatter, the burn time was observed to decrease with increasing gas temperature.

2 Multi-phase regularized smoothed particle hydrodynamics

MP-RSPH is based on the fundamentals of the smoothed particle hydrodynamics (SPH) method. The SPH method was originally developed for studies of astrophysical problems [17, 18], but the field of use has over the last 45 years been extended to cover a broader range of problems, for example, magneto-hydrodynamics [19], liquids [20, 21], solids [22], fragmentation [23], impact [24], breaking ocean waves [25], and shock waves [26,27,28]. Several thorough reviews on SPH are available, see, for instance, [15, 29,30,31].

In SPH, the grid structure known from finite difference methods [32] is replaced by sets of interpolation particles. The numerical description is Lagrangian, since the particles move with the fluid flow. A smoothing length, h, is defined as a characteristic particle size, with kernel function defined to give the weighted contribution from each particle. The choice of a kernel function with compact support is preferred, as it limits the number of particles interacting [33]. Additional properties assigned to the particles include mass, density, pressure, energy, and velocity. For a more fundamental introduction to SPH, the reader is referred to an early review paper by Monaghan [15].

In the current work, we use the in-house code MP-RSPH. In MP-RSPH, we have extended the SPH methodology to include extra features such as spatial resolution refinement, particle regularization, axial and spherical symmetry properties, and a multi-phase description.

The variable spatial resolution is similar to the adaptive mesh refinement used in finite difference methods [34]. In MP-RSPH, regions are automatically assigned smoothing lengths according to changes in the locally calculated property gradients. This spatial refinement feature is introduced to reduce the number of simulation particles and consequently increase computational speed. The resolution refinements only allow a factor two in the smoothing length refinement steps.

Additionally, a particle regularization process is applied at regular time intervals. The automated regularization procedure is typically invoked every 40 time steps. The gain of running such a feature is an optimized resolution and an increased accuracy. Further description and details are found in [35]. MP-RSPH also allows for spherical and axial symmetry constraints to be imposed [36]. This feature is not used in the present work.

The present paper focuses on the new physics added, giving a description of the additional terms not previously discussed. For dense particle distributions, the effect of particle–particle collisions has been shown to be important. For the given experimental conditions, the maximum particle–particle collision term is of the same order of magnitude as the maximum particle-to-gas acceleration term and many orders of magnitude larger than the maximum radiation term. The particle–particle collision term is also found to serve as a stabilizer of the numerical code, preventing the occurrences of close SPH–particle pairs. The particle–particle collision term is therefore included in the present work, whereas the processes of particle lifting and particle agglomeration have been neglected, and the particles are assumed to be in suspension and homogeneously distributed, at the time of shock arrival. This assumption is made, as we are not interested in a detailed study of the individual particles behaviour, but rather look at a statistical representation of the aluminium particle cloud as a whole. The experimental results [6] show, in fact, that the particles are in relatively uniform suspension at the time of particle ignition.

2.1 Source terms

MP-RSPH includes a multi-phase description which will be further discussed in the present paper. In the case of a two-phase problem, the numerical description is built from two separate sets of equations of motion. The first phase represents the gas phase, whereas the second phase describes a set of solid particles. The relative gas and particle void fractions \(\theta _{\text {g}}\) and \(\theta _{\text {d}}\) satisfy,

$$\begin{aligned} \theta _{\text {g}}+\theta _{\text {d}}=1. \end{aligned}$$
(1)

Furthermore, the mass density per unit volume \({\hat{\rho }}\) is defined as \({\hat{\rho }} = \theta \rho \) for both phases, where \(\rho \) is the total mass density. The two sets of equations of motion are coupled through their source terms. For inert particles, the contributing source terms are assumed to be drag force and heat transfer between the two phases. For reactive particles, additional source terms such as radiation and mass exchange between the two phases must be added. A thorough description of the multi-phase code for inert particles was given in Omang and Trulsen [16], where the choice of parameters was studied in detail. Based on comparison with experimental studies, the choice of drag coefficient was found to be the most important parameter, followed by the Nusselt number and the dynamic viscosity. Based on this study, the Ingebo drag term [37], Knudsen Nusselt number [38], and Chapman and Cowling dynamic viscosity [39] are chosen for the numerical simulation presented here.

2.1.1 Radiative heat transfer

A separate radiative heat transfer term is added to the energy equation for the gas,

$$\begin{aligned} \frac{\text {d} e_{a}}{\text {d}t}\Big |_{\text {rad}}\;=\sum _{j} \frac{m_{j}}{{\hat{\rho }}_{{j}}\hat{\rho _{{a}}}}\epsilon \sigma (T_{{j}}^4-T_{a}^4)W_{{ja}}, \end{aligned}$$
(2)

and for the solid particles as,

$$\begin{aligned} \frac{\text {d}e_{{i}}}{\text {d}t}\Big |_{\text {rad}}\;= -\sum _b \frac{m_{b}}{{\hat{\rho }}_{{i}}\hat{\rho _{{b}}}}\epsilon \sigma (T_{{i}}^4-T_{{b}}^4)W_{{ib}}. \end{aligned}$$
(3)

The subscripts a and b are used to represent the gas particles, whereas the subscripts i and j are used for the solid particles. Mass, pressure, temperature, and energy are given as m, P, T, e, whereas \(W_{{ja}}\) is the interpolation kernel [33]. The \(\sigma \) symbol is used for Boltzmann’s constant, and \(\epsilon \) is the emissivity. Based on [8], the emissivity is set to \(\epsilon = 0.9\).

2.1.2 Mass exchange between phases

The mass exchange between the two phases gives additional terms to the energy equation. For the gas, the mass exchange expression is given as,

$$\begin{aligned} \frac{\text {d} e_{{a}}}{\text {d}t}\Big |_{\text {mass}}\;=\sum _{j} m_{j}\frac{{J}}{{\hat{\rho }}_{{j}}\hat{\rho _{{a}}}}(e_{{j}}-e_{{a}})W_{{ja}}, \end{aligned}$$
(4)

and for the solid particles

$$\begin{aligned} \frac{\text {d} e_{{i}}}{\text {d}t}\Big |_{\text {mass}}\;=-\sum _{b} m_{b}\frac{{J}}{{\hat{\rho }}_{{i}}\hat{\rho _{{b}}}}(e_{{i}}-e_{{b}})W_{{ib}}, \end{aligned}$$
(5)

where J is defined as the burn rate. Similar expressions for gas and solid particles are added to the momentum equation of motion,

$$\begin{aligned} \frac{\text {d}{\textbf{v}}_{{a}}}{\text {d}t}\Big |_{\text {mass}}\,= & {} \,\sum _{j} m_{j}\frac{J}{{\hat{\rho }}_{a}\hat{\rho _{{j}}}} {\textbf{v}}_{{ja}}W_{{ja}}, \end{aligned}$$
(6)
$$\begin{aligned} \frac{\text {d}{\textbf{v}}_{{i}}}{\text {d}t}\Big |_{\text {mass}} \,= & {} \,-\sum _{b} m_{b}\frac{J}{{\hat{\rho }}_{i}\hat{\rho _{{b}}}} {\textbf{v}}_{{ib}}W_{{ib}}, \end{aligned}$$
(7)

where \({\textbf{v}}\) is the velocity.

2.1.3 Particle–particle collision term

For dilute gas–particle mixtures, the particle–particle collision term may be ignored due to low particle–particle collision probability. For denser mixtures, however, the collision probability is increased and a collision term is included in the solid particle momentum equation. The form of the collision term chosen is similar to the gas-pressure term,

$$\begin{aligned} \frac{\text {d}{\textbf{v}}_{{i}}}{\text {d}t}\Big |_{\text {pp}} \, =\, -\sum _{b} m_{b} \left( \frac{P_{i}\theta _{i}}{{\hat{\rho }}_{i}^2}+\frac{P_{j}\theta _{j}}{{\hat{\rho }}_{j}^2} \right) \nabla _{i} W_{ij}. \end{aligned}$$
(8)

2.1.4 Burn rate

In the present work, three different burn rate models are evaluated. The diffusive combustion term, \(J_{\text {diff}}\) [40], is given by,

$$\begin{aligned} J_{\text {diff}}=\left\{ \begin{array}{ll} 0, &{}\quad \text{ for } \quad T<T_{\text {ign}} \\ \frac{3\theta _{j}\hat{\rho _{j}}}{\tau _{b}}(1+0.276\sqrt{\text {Re}}),&{}\quad \text {for}\quad T>T_{\text {ign}}\\ \end{array}, \right. \end{aligned}$$
(9)

where Re is the Reynolds number,

$$\begin{aligned} \text {Re}=\frac{\rho _\text {g}\theta _\text {g} d_\text {d} |v_\text {g}-v_\text {d}|}{\mu } \end{aligned}$$
(10)

(\(\mu \) is the dynamic viscosity, and \(d_\text {d}\) is the particle diameter). The kinetic combustion term, \(J_\text {kin}\) [41], is written as,

$$\begin{aligned} J_{\text {kin}}=\pi d_\text {d}^2n_\text {p}Z_{\text {hyb}}\exp \left( -\frac{E_\text {a1}}{R_\text {g}T_\text {d}}\right) , \end{aligned}$$
(11)

with the universal gas constant, \(R_\text {g}\), and the activation energy, \(E_{\text {a1}}\). The particle number density is given as \(n_\text {p}\), and the pre-exponential factor, \(Z_\text {hyb}\), is given in Table 3. The third combustion term is a combination of the two models, called the total burn rate model, \(J_{\text {tot}}\),

$$\begin{aligned} J_\text {tot}=\left( \frac{1}{J_\text {kin}}+\frac{1}{J_\text {diff}}\right) ^{-1}. \end{aligned}$$
(12)

The total burn rate model is constructed to give a more gradual and smoother ignition process [41]. The particle burn time, \(\tau _\text {b}\), is based on empirical data. Two different particle burn time expressions are considered. The first one is the K &V expression given by Khasainov and Veyssiere [40],

$$\begin{aligned} \tau _\text {b1}=K d^2\phi ^{-0.9}, \end{aligned}$$
(13)

where K is the burn rate parameter and \(\phi \) is the volume fraction of all the oxidizing species. In the present simulations, the assumption \(\sum \phi = 1\) was made. The second empirical expression, O &H, is based on our experiments (Omang and Hauge [6]),

$$\begin{aligned} \tau _\text {b2}=c_\text {2}\exp {\left( \frac{E_\text {a2}}{R_\text {g}T_\text {5}}\right) }, \end{aligned}$$
(14)

where parameters \(c_\text {2}\) and \(E_\text {a2}\) were obtained through an Arrhenius curve fit based on the entire experimental data set. The burn rate only depends on the gas temperature, and the parameters are listed in Table 3.

The three different burn models are illustrated in Fig. 1 with the total model \(J_\text {tot}\) (blue), the kinetic model \(J_\text {kin}\) (red), and diffusive model \(J_\text {diff}\) K &V (green) curves. The choice of parameters is further discussed in Sect. 4.3.1. In Fig. 1, the velocity difference \(|v_\text {g}-v_\text {d}|\) is set to 400 m/s. The small area delimited by the three curves, above the total model but below the kinetic and diffusive models, illustrates the difference between the three models. In lack of well-described experimental data, a generic numerical study of the combustion models was presented in [42]. The key findings were that the models were quite sensitive to the choice of parameters. The burn rate model \(J_\text {diff}\) was found to give a much more efficient burning process than the smoother \(J_\text {tot}\) model.

Fig. 1
figure 1

Burn rate profiles plotted as a function of temperature for the diffusive \(J_\text {diff}\) K &V (green), kinetic \(J_\text {kin}\) (red), and total \(J_\text {tot}\) (blue) burn models, assuming \( |v_\text {g}-v_\text {d} |= 400\) m/s. The parameters were corrected to match the estimated ignition temperature, as discussed in Sect. 4.3.2

Full size image

3 Problem formulation

The main goal of the present study is to investigate shock propagation, shock–particle cloud interaction, particle cloud heating, and spontaneous ignition of aluminium particle clouds numerically. The work is based on the experimental work presented in Omang and Hauge [6].

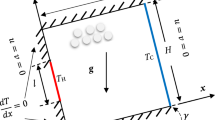
The experiments are conducted in a 5.78-m-long high-pressure shock tube with inner dimensions 83\(\times \)83 mm. The driver section is 1.38 m long, and the driven tube is 4.4 m long. The window section is the end section of the tube, with an observable length of approximately 100 mm. Inside the window section, a 90-mm-long splitter plate is mounted to the end wall, with the horizontal side facing upwards. The splitter plate has a 12-degree angle on the lower side. The aluminium particles studied are deposited on the splitter plate. The particle ridge covers the distance from 10 mm to 90 mm, along the centreline. A 3D-printed form of dimensions \(80.0\times 3.0\times 1.5\) mm is used to shape the aluminium ridge. The same amount of aluminium, sufficient to fill the entire form, 340 mg, is used for all the experiments. The aluminium particles have an average diameter of 40 \(\upmu \)m.

Outside the window section, two high-speed video cameras are mounted onto a beam splitter. This set-up allows both a compact schlieren set-up and a dark film camera to be operated simultaneously, but with a time interlay. While the schlieren images reveal the transition from a regular shock reflection into a Mach reflection on the lower splitter plate side, a plane shock front is observed on the upper side. The particle cloud reveals itself as a slight broadening of the shock front due to the slowing down of the shock in the encounter with the cloud. The dark camera exposures show essentially particle burning in a homogeneous cloud. The formation of the particle cloud is caused by the shock and post-shock conditions of the gas, as well as vibrations in the shock tube and splitter plate induced by the creation of the shock. These facts suggest that a one-dimensional simulation model would be suitable for the present problem. The shock position and Mach number can be determined from the schlieren images, whereas the ignition and burning of the aluminium particles are observed from the dark camera captures. Pressure sensors are mounted flush with the shock tube ceiling. The pressure sensor positions are given in Table 1.

Table 1 Pressure sensor positions
Full size table

The shock tube regions are defined relative to the shock, with the driver section defined as region 4. The undisturbed gas ahead of the shock is defined as region 1, and the region between the shock front and the contact surface (also called the contact discontinuity) is defined as region 2. Region 3 is the region behind the contact surface. When the shock reflects at the end wall, the area behind the reflected shock is defined as region 5. In the experiments, shocks are generated for Mach numbers in the range \(M_\text {s}\) = 1.50\(-\)2.36, and the estimated gas temperature, \(T_\text {5}\), in the reflected shock region was found to be in the range from 490 to 950 K [6].

The filling of the driver section is accomplished with an air-cooled compressor, which is cooling and compressing the gas. The pressure in the driver section is measured using pressure sensor S1, whereas the initial temperature or density must be estimated, since the thermal response of the temperature sensor was too slow to respond to the temperature development. The effect of changing the initial driver temperature \(T_\text {4}\) was evaluated in a parameter study for each experiment using the pressure sensor positions to construct numerical sensors for comparison.

4 Results

In order to investigate shock-induced ignition of aluminium particle clouds in greater detail, a numerical study is presented in a step-wise manner, starting with a simple test description and adding additional physics gradually. The first numerical test is a single-phase simulation of a plain shock tube without particles introduced. The next test is to introduce inert particles and investigate how the particles are heated, their temperature development, and what the velocity profile looks like. Based on these results, the final set of tests includes the combustion process, comparing numerical results obtained with the different combustion models to the experimental data.

4.1 Single-phase shock simulations

The numerical results to be presented in the following are compared with the experimental results in [6]. The numerical model does not include effects such as energy losses associated with membrane ruptures. For the comparison with the experimental results, it is therefore necessary to modify the experimental initial conditions in order to reproduce the experimentally observed Mach numbers. In Table 2, the numerical initial conditions chosen for the relevant experiments are given. The results for the numerical tests 1 to 4 are all based on experiment 6.

Table 2 Initial conditions based on the experimental data
Full size table

Our first test case represents a simplification of the original experiment, assuming an ideal shock tube without splitter plate and particles. The shock is formed when the membrane ruptures at \(x = 1.38\) m and propagates along the driven tube, until it reaches the end wall. Based on results from the numerical simulations, the shock position and its contact surface are plotted in the x–t diagram in Fig. 2. The dashed black curve illustrates the shock position, whereas the red curve illustrates the contact surface. The initial shock is reflected at the end wall, and the shock direction is reversed. The contact surface position is determined until it interacts with the reflected shock. At this point, a rather complex phenomenon is observed where the reflected shock and contact surface interact, delaying the reflected shock for several milliseconds. The reflected shock then picks up speed again and continues to propagate back along the tube until it is reflected at the driver end wall, reversing the shock propagation direction for a second time. The green circles plotted in Fig. 2 illustrate results from the experiments and fit well with the dashed shock position curve. The size of the small coloured blue box close to the window section end wall illustrates the time period and region where combustion is observed and is based on the experimental results.

In Fig. 3, pressure histories of the experimental pressure sensors (black) are compared with the numerical results of test 1 (red), test 2 (green), and test 3 (blue) plotted in the given order. The exact time of the membrane rupture is not known. The simulations and experiments are therefore calibrated such that the shock time-of-arrival at pressure sensor S2 coincides. With this calibration, the shock time-of-arrival compares well with the numerical result for all the sensors, indicating that our simulations represent the shock velocity well. Also, the pressure levels after the first pressure rise show good agreement for all the pressure sensors. The pressure histories are plotted for a longer time span than the burning process, which was observed to end before 10 ms in Fig. 2.

Fig. 2
figure 2

An x–t diagram for the initial and reflected shock trajectories (dashed lines). The contact surface is plotted in red. The green symbols represent the experimental results of the pressure sensors, and the size of the blue box illustrates the estimated burning period in time and space

Full size image

For sensors S2 and S3, the experimental data show small additional pressure peaks for \(t = 32.7\) and 33.6 ms, respectively. These small peaks are assumed to be formed due partial shock reflection at the membrane remnants, see [6]. These effects are not accounted for in the numerical simulations.

Fig. 3
figure 3

Pressure histories for the pressure sensors. The black lines show the experimental results, whereas the red lines show the results from a single-phase numerical simulation. The green lines illustrate results from an inert two-phase numerical simulation, whereas the blue colour shows results from simulations including ignition and particle burning. The green line is completely covered by the blue curve

Full size image

For sensors S4 and S5, outside the window section, discrepancies between the two curves are observed for the time interval 8–10 ms. The numerical simulations then again catch up with the experimental results. For this time interval, large density steps are observed, as the reflected shock collides with the contact surface. This clearly is a challenging problem numerically, similar to the problem discussed in, for instance, [43]. The numerical problem is found to be present for incident shock Mach numbers above 2. Although the simulations are not an exact representation of the real experiments, the overall agreement of the two curves is good, providing additional physical insight into the experiments.

4.2 Two-phase shock simulations with inert particles

In test 2, we include inert particles in the simulations, performing a two-phase one-dimensional numerical simulation. The particles (\(d = 40\,\upmu \)m) are assumed to be evenly distributed initially, as a 80-mm-long particle cloud. The actual volume fraction \(\theta _\text {d}\) is somewhat uncertain, but was set to \(\theta _\text {d} = 0.001\). The initial conditions are again given inTable 2. In Fig. 3, the green colour represents the inert two-phase numerical simulation. The difference is not expected to be visible for the sensors outside the window section S1–S7, where there are no particles distributed, and the three curves cover each other almost completely. For the sensor at the end wall, S8, a slightly higher pressure level is observed.

The temperatures of the two phases are essential to the ignition process. Test 2 is useful in providing data on the temperature development for both species. The overall maximum temperature of gas and particles is therefore plotted as a function of time in Fig. 4, using black and green colours, respectively. Although the figure does not contain spatial information, different features can be recognized. Initially, the gas temperature is low, also in the driver section, but increases abruptly as the shock is formed at the membrane. The particles, on the other hand, are at rest under ambient conditions in the window section. The next gas temperature rise is due to the shock reflection at the end wall. The region behind the shock with post-shock conditions contains warm gas, which again interacts with the reflected shock. The heating of the particles is observed to start prior to the first shock reflection, as the shock interacts with the particles before reaching the end wall. Since the particles are heavy relatively to the gas, the temperature rise is less instantaneous. Although the initial heating rate is slower, at \(t= 15.3\) ms the particle temperature rises above the gas temperature curve. This trend is observed for the remainder of the simulation. The red dotted line is the experimentally determined time of ignition. As the simulations illustrate, the ignition occurs as the fourth temperature rise is observed in the maximum gas temperature curve. At this point in time, the contact surface is interacting with the reflected shock causing both the gas and particle temperature to rise.

Fig. 4
figure 4

Maximum gas and particle temperatures as a function of time. The results are obtained with an inert two-phase numerical simulation. The red dotted line shows the ignition point determined from the experimental results

Full size image

Temperature measurements are difficult in a shock tube environment due to the slow response of temperature sensors. Since the aluminium particle ignition temperature is dependent on the shock strength, the particle ignition temperature is estimated from the inert particle simulations. For the present case, the aluminium particle ignition temperature is determined from where the ignition line intersects with the numerical simulation of the maximum particle temperature in Fig. 4. In the present case, the particle ignition temperature is estimated to be \(T_\text {ign} = 718\) K.

Fig. 5
figure 5

The figure shows the maximum relative velocity and temperature as a function of time. The red line shows the ignition point determined from the experimental results

Full size image

The results from numerical simulations with inert particles are well suited in order to investigate the maximum relative velocity between the two phases in closer details. In Fig. 5a, we plot the absolute maximum relative velocity as a function of time for test 2. The first relative velocity peak is due to the shock arrival at the particle cloud. The second velocity peak is due to the interaction of the reflected shock with the contact surface. For this second peak, the relative velocity is as high as 200 m/s. The time of ignition as determined from the experiments coincides with this second relative velocity peak.

Table 3 Initial parameters chosen for the numerical simulations
Full size table

A similar plot of the maximum relative temperature is presented in Fig. 5b. Also in this case, two distinct peaks are observed. The first peak is the shock arrival at the particle cloud. The maximum relative temperature is clearly high, as the post-shock gas is warm relative to the cold particles initially at rest. The second peak is observed when the reflected shock interacts with the contact surface. In this complicated reflection region, the maximum relative temperature is quite high. The experimentally determined ignition, plotted with a red vertical line, illustrates that the ignition takes place when the second rise of the maximum relative temperature is observed. That is, the experimentally determined time of ignition coincides with the second peak of both maximum relative velocity and maximum relative temperature between gas and particles. The same behaviour is observed for the other analysed experiments in [6], in which ignition takes place.

4.3 Two-phase shock simulation with reactive particles

MP-RSPH is written in a module based manner, so that ignition and combustion are easily introduced in the numerical simulations. In this section, particle ignition and burning are included, and the three different burn models are compared. In the experiments [6], an image processing procedure was applied to the dark film images to determine pixel intensity curves for each experiment. These curves were further used to determine the ignition delay and aluminium particle burn time.

In Sect. 4.3.1 (test 3), numerical simulations based on published burn rate parameters are presented for the three combustion models, whereas in Sect. 4.3.2 (test 4) the burn rate parameters are corrected and the results using \(J_\text {tot}\), \(J_\text {kin}\), and \(J_\text {diff}\) for K &V and O &H are presented. In Sect. 4.3.3, the differences in particle mass loss for the three burn models are discussed.

4.3.1 Comparing combustion models

In the results from the inert particle simulations, test 3, the estimated particle ignition temperature was set to \(T_\text {ign} = 718\) K. Using the burn rate expressions from (9)–(12), with parameters as listed in Table 3 taken from [7, 44], scaled particle burning numbers from three different numerical simulation are presented in Fig. 6. The scaled pixel intensity curve based on the experiments is plotted in black. The purple curve represents the total burn rate expression, whereas the orange colour represents the kinetic burn rate description. The results from the K &V diffusive burn rate are illustrated in green. Clearly, compared to the experimental data, the diffusive burn rate model gives the best fit, although for the parameters chosen, the burn time is too long.

4.3.2 Comparing burn time rates

The pressure histories with reactive particles included (test 4) are presented in Fig. 3 using blue colour. The blue curves are difficult to distinguish from the red and green curves, as they almost cover each other completely. The blue curve is, however, observable slightly above the single-phase pressure profile at the end-wall sensor S8.

Test 4 is also based on the ignition temperature estimated from the inert numerical simulations. In this test, however, the combustion model parameters are manually adjusted to make sure that 25\(\%\) rise of the maximum value coincides with the experimentally obtained ignition temperature of 718 K (black circle), as illustrated in Fig. 1. The green, red, and blue lines represent the corrected diffusive (K &V), kinetic, and total burn models, respectively, with the parameters given in Table 3. Both diffusive models are assumed to contribute only if the particle temperature rises above the ignition temperature.

Fig. 6
figure 6

Scaled particle burning intensity for test 3 where the curves \(J_{\text {kin}}\) (orange), K &V \(J_{\text {diff}}\) (green), and \(J_{\text {tot}}\) (purple) are plotted. The black curve represents the scaled pixel intensity from the experimental data. The coloured curves are based on parameters found in [7, 44]

Full size image

The pixel intensity curves for the total (blue), kinetic (orange), and the two diffusive models are presented in Fig. 7a. As the figure illustrates, both the kinetic and total models give a poor representation of the experimental data. The green curve represents the results using the burn rate K &V given in (13), while the red curve is based on our empirical burn rate expression O &H given in (14). The experimentally obtained curve is almost completely covered by the two simulations. As the figure illustrates, both models based on the diffusive burn rate model give good representation of the burning intensity. When comparing Figs. 6 and 7a, it is, however, clear that the green curve in Fig. 7a gives a much better result than the green curve in Fig. 6, illustrating that the choice of parameters for the K &V model must be done with care.

Fig. 7
figure 7

Scaled particle burning intensity for test a 4, b 5, c 6, and d 7, where \(J_{\text {tot}}\) is the blue curve, \(J_\text {kin}\) is the orange curve, and \(J_{\text {diff}}\) is plotted for \(\tau _{\text {b2}}\) (red curve) and \(\tau _{\text {b1}}\) (green curve). The black curve represents the scaled pixel intensity from the experimental data

Full size image

The same numerical simulations were repeated for tests 5–7, plotted in Fig. 7b–d, representing experiments 28, 29, and 30 in [6], with the initial conditions for the simulations given in Tables 2 and 3. The black curves show the experiments, whereas the blue and orange curves represent the total and kinetic models, respectively. The two diffusive burn rates, O &H and K &V, are plotted in red and green. For all three simulations, the shapes of the diffusive numerical curves are similar, and the agreement with the scaled pixel intensity results is good, taking the stochastic nature of the results into account. As demonstrated for tests 3 and 4, however, adjusting the parameters for the K &V diffusive burn rate \(J_\text {diff}(\tau _\text {b1})\) for each experiment is essential to the results obtained. The burn rate parameter K thus seems to be dependent on temperature. Choosing the O &H burn rate \(J_\text {diff}(\tau _\text {b2})\) instead, only the particle ignition temperature must be estimated. When experimental data are available, the particle ignition temperature may be estimated from numerical simulations of the inert particle cloud.

In lack of experimental data, the ignition temperature may also be estimated from the maximum gas and particle temperature curves. For all numerical tests presented here, the point of ignition was identified to take place at the fourth step in the gas temperature profile, as illustrated in Fig. 4, where the red vertical line is plotted. The estimated particle ignition temperature is found to be located within this step.

4.3.3 Scaled particle mass loss

Figure 8 illustrates the scaled mass loss as a function of time for the different burn rate models, using the corrected parameters in test 4, experiment 6. The orange and blue curves show the results for the kinetic and total burn rate models, respectively. The green colour represents the K &V diffusive burn model, whereas the red curve represents the O &H diffusive burn rate based on our experiments. The two diffusive model curves coincide. As discussed in [42], the choice of burn rate model is important for the particle burning efficiency. Clearly, both diffusive burn models are far more efficient than the kinetic and total burn models.

5 Discussion

Fig. 8
figure 8

Scaled total particle mass as a function of time using the diffusive \(J_\text {diff}(\tau _\text {b2})\) (red), \(J_\text {diff}(\tau _\text {b1})\) (green), total \(J_\text {tot}\) (blue), and \(J_\text {kin}\) (orange) burn rate models. The red and green curves coincide

Full size image

Based on numerical simulations of a selection of experiments, we find that the maximum gas and particle temperatures are important for the understanding of the heating of particles. The heating process is a step-wise process governed by the shock and post-shock conditions, as well as the contact surface interaction with the reflected shock. When the results from the inert numerical simulations are combined with the experimentally determined time of ignition, the particle ignition temperature can be estimated. In lack of experimental data, this curve may also be used to estimate the ignition temperature, which is identified at the fourth step in the maximum gas temperature curve. The estimated ignition temperature is further used as an ignition switch to activate the burning process in the numerical simulations. Choosing the O &H burn rate expression, the burning process is well described by the numerical simulations. With the K &V burn rate expression, however, caution must be taken to determine the proper burn rate constant in accordance with each experiments, as the expression is sensitive to small changes. The burn rate constant was determined based on a curve fit matching of the curve rise time to the estimated ignition temperature shown in Fig. 1. The curve fitting procedure is necessary for each experiment.

In the early work by Pokhil et al. [12], heating rate is discussed as a means to explain particle ignition in the low-temperature regime, with high speed heating suggested for 20 degrees per second or more. As the maximum particle temperature curve illustrates (Fig. 4), the heating rate of the particles far exceeds their suggested criteria.

6 Summary

In the present paper, numerical simulations are performed to evaluate the importance of the choice of physical parameters necessary to study two-phase shock–particle interactions of reactive particles. Due to the passage of both the initial and reflected shocks, the particles are sufficiently heated and eventually ignited, given that the shock is strong enough. The simulations are performed systematically with increasing degree of complexity to improve the understanding of the importance of the relevant parameters. For dense particle distribution, particle–particle collisions have to be taken into account. This is accomplished with the addition of a numerical term, similar to the expression used for numerical particle–particle collisions in the gas. The numerical burn rate equation is quite sensitive to the choice of parameters, and even small changes are shown to have a large impact on the results obtained. The difference in particle burning intensities of Figs. 6 and 7a illustrates that.

Numerical simulations of two-phase situations, such as the interaction of gas with micro-sized solid particles, are complex problems, especially when ignition and burning of the reactive particles are considered. In the present work, the simulations are therefore made as simple as possible, while focusing on the underlying physics. The aluminium particles are treated as a cloud, and the behaviour of individual particles is not studied. Particle methods, such as MP-RSPH, are well suited for studies of such problems, as the numerical particles only represent a statistical representation of the cloud, and not the individual particle behaviour.

In the presentation of the experimental work [6], the combustion process was discussed in greater detail, distinguishing between the kinetic combustion of nanoparticles and the diffusive combustion process usually observed for larger micro-sized particles. It was concluded that the results indicated a diffusive combustion process. The present numerical simulations comparing the three combustion models support this conclusion, since the diffusive models give by far the best fit to the experimental data.

When the K &V burn rate constant is adjusted for each experiment, both the K &V and O &H models agree well with experimental results. For future work, however, the O &H burn rate model seems to be preferred, since it does not require detailed adjustments for each experimental data set.