Skip to main content
SpringerLink
Log in

Mach stem evolution in a confined multi-room

  • Original Article
  • Published:
Shock Waves Aims and scope Submit manuscript

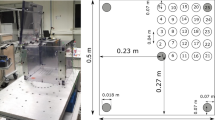
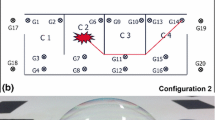
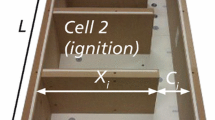
Abstract

It is well established that detonation in a confined environment can lead to the formation of a Mach stem along the walls or after diffraction on an obstacle. As the formation of this kind of reflection can produce higher levels of overpressure, it is important to study and understand its formation and propagation for safety purposes in the event of an accidental or intentional detonation. This paper reports an experimental approach to the propagation of a Mach stem formed by the diffraction of a shock wave around an obstacle and compares the height of the triple point with an empirical model from Kinney and Graham. In predictive models, the Mach stem is formed by a charge detonating above the ground, which is why its evolution is different from a Mach stem formed after diffraction. The shock waves were generated by the detonation of a stoichiometric hemispherical charge of propane-oxygen. The visualization was coupled with 30 pressure sensors to record pressure history data in order to determine the influence of the Mach stem on wall overpressure inside a small-scale model, representing two rooms in a building separated by an open door.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Ben-Dor, G.: Shock Wave Reflection Phenomena. Springer, Berlin (2007). https://doi.org/10.1007/978-3-540-71382-1

    Book  MATH  Google Scholar 

  2. Kinney, G.F., Graham, K.J.: Explosive Shocks in Air. Springer, Berlin (1985). https://doi.org/10.1007/978-3-642-86682-1

    Book  Google Scholar 

  3. Kisters, T., Kuder, J.: Experimental characterization of a near-field HOB-detonation. 22th International Symposium on Military Aspects of Blast and Shock, Bourges, France, 04–09 November (2012)

  4. Leete, K.M., Gee, K.L., Neilsen, T.B., Truscott, T.T.: Mach stem formation in outdoor measurements of acoustic shocks. J. Acoust. Soc. Am. 138, 522–527 (2015). https://doi.org/10.1121/1.4937745

    Article  Google Scholar 

  5. Needham, C.E.: Blast Waves: Shock Wave and High Pressure Phenomena. Springer, Berlin (2018). https://doi.org/10.1007/978-3-319-65382-2

    Book  Google Scholar 

  6. Boutillier, J., Ehrhardt, L., De Mezzo, S., Deck, C., Magnan, P., Naz, P., Willinger, R.: Evaluation of the existing triple point path models with new experimental data: proposal of an original empirical formulation. Shock Waves 28, 243–252 (2018). https://doi.org/10.1007/s00193-017-0743-7

  7. Xiao, W., Andrae, M., Gebbeken, N.: Development of a new empirical formula for prediction of triple point path. Shock Waves 30, 677–686 (2020). https://doi.org/10.1007/s00193-020-00968-7

    Article  Google Scholar 

  8. U.S. Department of the Army, Unified Facilities Criteria (UFC), Structures to Resist the Effects of Accidental Explosions. UFC-3-340-02. Washington (2008)

  9. Whitham, G.B.: A new approach to problems of shock dynamics, part 1: two dimensional problems. J. Fluid Mech. 2, 145–171 (1957). https://doi.org/10.1017/S002211205700004X

    Article  MathSciNet  MATH  Google Scholar 

  10. Parks, E.K.: Supersonic flow in a shock tube of divergent cross-section. UTIA Report No. 18, University of Toronto, Canada (1952)

  11. Skews, B.W.: The shape of a diffracting shock wave. J. Fluid Mech. 11, 297–304 (1967). https://doi.org/10.1017/S0022112067000825

    Article  Google Scholar 

  12. Koroteeva, E.Y., Znamenskaya, I.A., Glazyrin, F.N., Sysoev, N.N.: Numerical and experimental study of shock waves emanating from an open-ended rectangular tube. Shock Waves 26, 269–277 (2016). https://doi.org/10.1007/s00193-016-0650-3

  13. Hargather, M.J., Settles, G.S.: Optical measurement and scaling of blasts from gram-range explosive charges. Shock Waves 17, 215–223 (2007). https://doi.org/10.1007/s00193-007-0108-8

    Article  Google Scholar 

  14. Igra, O., Wang, L., Falcovitz, J., Heilig, W.: Shock wave propagation in a branched duct. Shock Waves 8, 375–381 (1998). https://doi.org/10.1007/s001930050130

    Article  MATH  Google Scholar 

  15. Gault, K., Sochet, I., Hakenholz, L., Collignon, A.: Influence of the explosion center on shock wave propagation in a confined room. Shock Waves 30, 473–481 (2020). https://doi.org/10.1007/s00193-020-00946-z

    Article  Google Scholar 

  16. Rigby, S.E., Akintaro, O.I., Fuller, B.J., Tyas, A., Curry, R.J., Langdon, G.S., Pope, D.J.: Predicting the response of plates subjected to near-field explosions using an energy equivalent impulse. Int. J. Impact Eng. 128, 24–36 (2019). https://doi.org/10.1016/j.ijimpeng.2019.01.014

    Article  Google Scholar 

  17. Edri, I., Savir, Z., Feldgun, V.R., Karinski, Y.S., Yankelevsky, D.Z.: On blast pressure analysis due to a partially confined explosion, I: experimental studies. Int. J. Protect. Struct. 2, 1–20 (2011). https://doi.org/10.1260/2041-4196.2.1.1

    Article  Google Scholar 

  18. Bazhenova, T., Gvozdeva, L., Zhilin, Yu.: Change in the shape of the diffracting shock wave at a convex corner. Acta Astronautica 6, 401–412 (1978). https://doi.org/10.1016/0094-5765(79)90107-3

    Article  Google Scholar 

  19. Bazhenova, T., Gvozdeva, L., Nettleton, M.: Unsteady interactions of shock wave. Prog. Aerosp. Sci. 21, 249–331 (1984). https://doi.org/10.1016/0376-0421(84)90007-1

    Article  Google Scholar 

  20. Tracker (Video Analysis and Modeling Tool). https://physlets.org/tracker/

  21. Eveillard, S.: Propagation d’une onde de choc en présence d’une Barrière de Protection. University of Orléans, France, Thesis (2013)

  22. Sauvan, P.E., Sochet, I., Trélat, S.: Analysis of reflected blast wave pressure profiles in a confined room. Shock Waves 22, 253–264 (2012). https://doi.org/10.1007/s00193-012-0363-1

    Article  Google Scholar 

Download references

Acknowledgements

This work was funded by DGA Techniques Navales under contract No. 15-86-0027.

Author information

Authors and Affiliations

  1. PRISME EA 4229, INSA Centre Val de Loire, Bourges, France

    G. Ruscade & I. Sochet

  2. DGA Techniques Navales, Toulon, France

    K. Djafer

Authors
  1. G. Ruscade
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. I. Sochet
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. K. Djafer
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to I. Sochet.

Additional information

Communicated by M. Hargather.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ruscade, G., Sochet, I. & Djafer, K. Mach stem evolution in a confined multi-room. Shock Waves 32, 395–404 (2022). https://doi.org/10.1007/s00193-022-01083-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00193-022-01083-5

Keywords

Search

Navigation