Characterizing growth instability: new evidence on unit roots and structural breaks in countries’ long run trajectories

Abstract

In this paper we investigate whether long run time series of income per capita are better described by a trend-stationary model with few structural changes or by unit root processes in which permanent stochastic shocks are responsible for the observed growth discontinuities. For a group of advanced and developing countries in the Maddison database, we employ a unit root test that allows for an unspecified number of breaks under the alternative hypothesis (up to some ex ante determined maximum). Monte Carlo simulations studying the finite sample properties of the test are reported and discussed. When compared with previous findings in the literature, our results show less evidence against the unit root hypothesis. We find even fewer rejections when relaxing the assumption of Gaussian shocks. Our results are broadly consistent with the implications of evolutionary macro models which posit frequent growth shifts and fat-tailed distribution of aggregate shocks.

1 Introduction

Among empirical growth economists a consensus has begun to emerge concerning the unstable nature of economic growth. It is now widely recognized that the vast majority of growth experiences, even when considering now-rich countries, do not comply with a simple steady-state growth model (Ben-David and Papell 1995; Papell and Prodan 2014). Growth experiences are remarkably heterogeneous. Considering aggregate income data, it is common to observe several growth discontinuities of different kinds such as accelerations, collapses, sudden stops or level jumps (Easterly et al. 1993; Pritchett et al. 2000; Hausmann et al. 2005; Lamperti and Mattei 2018b). Nevertheless, there is clearly less consensus when it comes to characterizing growth instability with econometric models.

A major issue is whether growth paths are better described by a trend-stationary model with relatively few structural breaks or by unit root processes in which permanent stochastic shocks are responsible for continuous changes. From an observational point of view, stationary models (or I(0) models) describe relatively stable growth dynamics with few changes in trend (e.g. growth accelerations or decelerations) or in levels (e.g. jumps or sudden falls). On the contrary, unit root processes (or integrated I(1) models) show an open trajectory depicted by random shocks with levels and trend continuously shifting at potentially any point in time. As pointed out by Perron et al. (2006), one should not restrict the analysis to these two limiting cases as there are several interesting instances in between. The key question is therefore: do the data reveal frequent and large growth discontinuities or do structural changes occur at most occasionally? From this standpoint, testing for unit roots, rather than discerning definitively between stationary vis-à-vis integrated models, allows for inferences to be drawn on where we stand between these two alternatives.

Addressing this question has strong empirical and theoretical implications for practitioners working in the field of economic growth, by allowing researchers to inform new generations of growth models and to discern among existing ones, including for instance a comparison between endogenous growth and evolutionary models. Moreover, information on the presence of unit roots and structural breaks has clear relevance in many empirical applications such as convergence tests or the identification of growth episodes. We discuss these implications extensively in Section 2.

This paper contributes to the literature by investigating the presence of unit roots and structural breaks in long run time series of per capita GDP. Methodologically, we build upon the test in Kapetanios (2005) and add novel features to the literature, mainly along three dimensions: (i) we treat the number of breaks (not only their location) as unknown; (ii) we exploit the sequential approach of Bai (1997) to extend the number of breaks to four and, consequently, we include in the analysis also a group of developing countries with more volatile series; and (iii) we implement a robust search algorithm that resembles the practices for the identification of growth episodes adopted in the empirical literature.

Our results provide less support for trend stationarity than previous contributions. In a sample of 34 countries we find 17 rejections of the unit root null hypothesis. Interestingly, developing countries exhibit only four rejections, thus, showing a more complex and unstable dynamics than advanced ones. Moreover, even less evidence against the unit root hypothesis is found when we relax the assumption of Gaussian innovations by using bootstrapped critical values. This points to the general conclusion according to which the dismissal of the unit root hypothesis in GDP series may be premature. In particular, more attention should be devoted to investigating the role of the various search algorithms implemented in unit root tests, as well as of the assumptions on the distribution of the shocks, in driving the evidence against integrated models. From a theoretical perspective, we conjecture a relationship to evolutionary growth models which point at remarkably heterogeneous growth trajectories with frequent discontinuities and non-Gaussian distributions of shocks.

The remainder of this work proceeds as follows: Section 2 discusses the theoretical and empirical implications of our analysis; Section 3 presents a literature review of existing tests and their applications; Section 4 describes the methodology; Section 5 shows some Monte Carlo experiments to assess power and size properties of the test in finite samples; Section 6 presents the empirical strategy while in Section 7 we introduce and discuss the results; Section 8 concludes.

2 Unit roots and structural breaks: theoretical and empirical implications for economic growth

Figure 1 reports simulated time series for different models: a trend-stationary model with no breaks; a trend stationary model with a level break at t = 70 and a slope break at t = 140; and an integrated (unit root) model. The difference between stationary and unit root models is immediately apparent. In the former, stochastic shocks are mean-reverting and do not alter the long-run trajectory of the time series. Deviations from steady growth may only occur when we exogenously impose structural changes in the main parameters. I(1) models, in contrast, depict an unstable growth pattern characterized by frequent shifts resulting from the accumulation of stochastic shocks. Thus, structural changes occurs continuously in these class of models.

Fig. 1

Notes: The I(0) model (red line) is: y_t = 0.04 + 0.04t + 0.3y_t− 1 + e_t; The I(0) model (green line) with breaks is: y_t = 0.04 + 0.04t + 0.3y_t− 1 − DU(70) − 0.03DT(140)e_t; The I(1) model (blue line) is: y_t = 0.04 + y_t− 1 + e_t,; For each model we have: $e_{t} \sim \mathcal {N} (0,1)$

A comparison between stationary and unit roots models

As stated in the Introduction, unit root tests allow us to draw inferences on how frequent structural changes are. This provides relevant implications for applied macroeconomists studying economic growth. In fact, a better characterization of growth instability using empirical data may provide important stylized facts for growth models since the ability to account for the frequency and nature of growth discontinuities is a key element for discriminating among different models. As an illustrative example, let us focus on the dynamics of GDP per capita in three major classes of theoretical growth models (i.e. Neoclassical, Endogenous growth and Evolutionary). The standard Solow model implicitly suggests a log-linear trend with level shifts in response to changes in policy parameters (affecting e.g. physical and human capital accumulation). Deviations from the trend are transitory, with the speed of reversion to the trend depending on the so-called speed of convergence (i.e. a measure of how fast countries converge to their equilibrium trend).¹ The emergence of level effects is also a characteristic of semi-endogenous growth models with decreasing returns to scale in the research sector (Jones 1995, 2005). In these models, public policies (e.g. R&D subsidies) only affect the level of GDP per capita but not its growth rate. This is a fundamental difference with respect to endogenous growth models in which parameter shocks regulating the accumulation of physical and human capital (Romer 1986; Lucas 1988) or R&D expenditures (Grossman and Helpman 1991; Aghion and Howitt 1992) cause shifts in the equilibrium growth rate of the economy.² On the contrary, evolutionary models emphasize out-of-equilibrium dynamics and can hardly be reconciled with a trend-stationary data generating process.³ Frequent growth discontinuities are emergent properties resulting from non-linearities and from the aggregation of endogenous stochastic innovations at the microeconomic level. In addition, the complex interactions and the correlating mechanisms among agents tend to generate fat-tailed shocks at all levels of aggregation. Hence, evolutionary models are probably better approximated by path-dependent I(1) processes with fat-tailed stochastic errors. Policy shocks still play a crucial role but their effect is far from being deterministic, depending on the specific realization of events associated with the arrival of innovations and to their “disruptive” consequences on the economic system.⁴ These properties characterize both early models (Nelson and Winter 1982; Silverberg and Verspagen 1994, 1995; Dosi et al. 1994) and second generation ones with a stronger focus on empirical validation (Dosi et al. 2010, 2015, 2019, 2020; Lamperti et al. 2018a). Yet, evolutionary models have not, as yet, been adopted to replicate the observed dynamics of growth episodes.⁵ In this respect, our empirical analysis may encourage new studies using evolutionary growth models to explicitly address such new evidence. Finally, albeit not primarily concerned with long run growth, Real Business Cycle and DSGE models often generate I(1) time series when technology shocks are highly persistent. Nevertheless, differently from evolutionary models, it has been shown that the propagation mechanisms in these models do not lead to fat-tailed distributions of macroeconomic shocks (Ascari et al. 2015). In Table 1 we summarize the implications from different growth models in terms of structural breaks and unit roots.

Table 1 Implications of growth models in terms of unit roots and structural breaks

The practical relevance of distinguishing models with stochastic trends from stationary alternatives also extends to empirical applications. First, economists are interested in studying empirical patterns of cross-country convergence/divergence, i.e. understanding whether poor countries are catching up with rich ones or whether they are falling behind. It has been shown that knowledge of the time series properties of income per capita should inform statistical tests for convergence. When a series presents frequent trend and level shifts (as with I(1) models), standard convergence tests based on cross-sectional or panel growth regressions (see Mankiw et al. 1992; Islam 1995, for early contributions) may lead to misleading results (Pritchett et al. 2000; Lee et al. 1997). These are, in fact, grounded on a trend-stationary characterization of the growth process and are intended to estimate the rate at which each country converges to its own steady growth rate. Alternatively, time series tests that estimate cointegration relations among countries are well suited to deal with unit root processes (Bernard and Durlauf 1995; Pesaran 2007). A recent literature focuses instead on the identification of specific growth episodes and their determinants. For instance, a key question concerns the drivers of sustained growth episodes as opposed to short-lived expansions. The search for growth episodes is generally carried out either by formal tests for structural breaks (Jones and Olken 2008; Kerekes 2007; Berg et al. 2012) or by imposing filters based on subjective economic criteria (Hausmann et al. 2005, 2006; Aizenman and Spiegel 2010; Bluhm et al.2016).⁶ Nevertheless, the search is often not informed by evidence from unit root tests and the economic filters adopted generally reflect time-invariant and deterministic characteristics which are not suited to capturing the stochastic nature of structural shifts observed in integrated models. Accounting for unit roots may allow for the design of better filtering criteria and may inform the decision to use the series in levels or first-differences. Finally, when using formal statistical tests for structural breaks, it is recommended to use new techniques which are consistent under both I(0) and I(1) models (Kejriwal and Perron 2010; Perron and Yabu 2009; Harvey et al. 2009).

3 Unit root tests with structural breaks and long-run growth: a review of the literature

Stemming from Nelson and Plosser (1982), researchers have started to pay attention to the possible presence of stochastic trends in macroeconomic data. This interest was originally motivated by the fact that in I(1) type processes the distinction between secular movements and business cycles becomes blurred as the trend component itself displays fluctuations. Nevertheless, when a time series exhibits a unit root, it is equally complicated to distinguish growth episodes occurring at medium run frequencies from the secular stochastic trend. As a consequence, the identification of unit roots and structural breaks has gained increasing relevance also in the field of growth empirics (see e.g. Papell and Prodan2014; Kejriwal and Lopez 2013).

Following Perron (1989), it is now common practice to incorporate structural breaks in unit root tests, with evidence suggesting that omitting dummies for structural change in Dickey-Fuller regressions results in a failure to reject the unit root null hypothesis (Perron 1989). Drawing on Zivot and Andrews (1992) and Christiano (1992) these tests now also feature a data-dependent algorithm to determine the location of the structural shifts under the alternative hypothesis. However, a major drawback of such an approach concerns the assumption of a fixed number of breaks, typically determined ex ante.⁷ This creates a gap with the empirical literature in which data-driven procedures are used, not only to identify break dates, but also to select the number of relevant structural changes. To deal with this issue, Kapetanios (2005) presents a test of the unit root hypothesis against I(0) alternatives with an unspecified number of breaks (up to some exogenously given maximum). The test, nevertheless, features a search algorithm based on the minimization of t-statistics which has been shown to perform poorly in identifying the correct number of shifts and their dates (Vogelsang and Perron 1998; Lee and Strazicich 2001). Recent contributions in the field have addressed specific aspects such as the possibility of I(1) models with breaks (Carrion-i Silvestre et al. 2009; Harvey et al. 2013), extensions to spatial panel models (Baltagi et al. 2016; Sengupta et al. 2017) and the consistency of trend break locations (Yang et al. 2017).⁸

Unit roots and structural break tests have been applied to a wide range of macroeconomic time series including inflation and interest rates (Clemente et al. 2017), unemployment (García-Cintado et al. 2015; Cheng et al. 2014), exchange rates (Månsson and Sjölander 2014), and commodity and oil prices (Gadea et al. 2017; Winkelried 2018). Relatively few empirical applications of unit root tests have focused on countries’ long-run growth paths, although a number of studies test for the presence of unit roots in historical time series of real GDP per capita, generally for a few advanced countries.⁹ (Ben-David and Papell 1995) apply the test of Zivot and Andrews (1992), allowing for a break in both the trend and the constant, in a sample of OECD countries and reject the unit root hypothesis for 7 out of 16 series. In a follow up paper, Ben-David et al. (2003) show that by incorporating an additional break it is possible to reject the null for 12 out of 16 countries. Extending previous analysis, Papell and Prodan (2014) consider various models with different break forms for a sample of 19 OECD countries and 7 Asian economies. Their results report, respectively, 15 rejections for the OECD group and 6 rejections for the Asian one. An alternative framework is proposed by Kejriwal and Lopez (2013). They present an econometric procedure that uses in a sequential manner various tests allowing for up to two structural breaks under both the null and the alternative. In contrast to existing results, their approach indicates no evidence against the unit root hypothesis. For the sake of comparison, results from these studies are summarized in Table 5. Finally, Zerbo and Darné (2018) conducts a similar analysis using shorter time series for developing countries, also finding no evidence against the unit root model.

4 Methodology

Our methodology builds upon and extends (Kapetanios 2005). We consider the following null hypothesis:

$$ y_{t}=\mu + y_{t-1} + {\Psi}^{*} (L) v_{t}, $$

(1)

where: Ψ^∗(L) = A^∗(L)^− 1B(L); A^∗(L) and B(L) are lag polynomials respectively of order p and q with all the roots outside the unit circle and v is a zero-mean sequence of iid random variables.

The alternative model considered takes the form:

$$ y_{t}= \mu + \upbeta t + {\Psi} (L) \big[\sum\limits_{i=1}^{m} \theta_{i} DU(T_{i})_{t} + \sum\limits_{i=1}^{m} \gamma_{i} DT(T_{i})_{t} + v_{t} \big] $$

(2)

where: Ψ(L) = A(L)^− 1B(L); A(L) = (1 − αL)A^∗(L). The intercept and trend break dummies are and with being the indicator function and T_i a generic break date. Notice that, according to the so-called innovation outlier specification, changes in the trend or in the constant evolve as any other shock. For instance, while the immediate impact of a generic variation in the constant is 𝜃_i, the corresponding long-run effect will be Ψ(1)𝜃_i.

Both the null and the alternative model can be nested in a general DF-type of regression:

$$ y_{t}=\mu+ \upbeta t + \alpha y_{t-1} + \sum\limits_{i=1}^{m} \theta_{i} DU(T_{i})_{t} + \sum\limits_{i=1}^{m} \gamma_{i} DT(T_{i})_{t} + \sum\limits_{j=1}^{k} c_{j}{\Delta} y_{t-j} + \epsilon_{t} $$

(3)

In our analysis, the number of breaks (m), the lag-truncation parameter (k) and the break dates (T₁,...,T_m) are treated as unknown. Therefore, for a given number of breaks m, the null and the alternative hypothesis are defined as:

$$ H_{0}: \alpha=1, \theta_{i}=\gamma_{i}=0 \quad \forall i \in [1,m] $$

$$ H_{1}: \alpha < 1 $$

Let us now focus on some methodological considerations. First, we are using the most general model that includes for each break both the intercept and the trend shift dummy. As discussed by Sen (2003), when the form of the breaks is unknown, the preferred strategy is to adopt a general specification allowing for changing intercept and trend in order to minimize power distortions.¹⁰ Second, structural breaks are allowed only under the alternative hypothesis whereas the null model is described by an I(1) process without exogenous shifts in its deterministic components. Such asymmetric treatment of breaks characterizes several unit root tests proposed in the literature (Zivot and Andrews 1992; Banerjee et al. 1992; Lumsdaine and Papell 1997; Perron 1997). However, Vogelsang and Perron (1998) and Lee and Strazicich (2001) show that size distortions arise when structural breaks are present under the null as a result of the nuisance parameter associated with the trend function. Although it has been pointed out that serious distortions only emerge in the presence of large shifts and may not be particularly relevant in practice (Vogelsang and Perron 1998; Perron et al. 2006), several works have directly addressed the issue (Lee and Strazicich 2003; Narayan and Popp 2010, Narayan and Popp; Harris et al. 2009; Carrion-i Silvestre et al. 2009; Harvey et al. 2013). In this paper, however, we do not include breaks in the null model since we are interested in discriminating among a pure I(1) specification and alternative models with a small number of exogenous shifts. From an economic point of view, this amounts to testing the hypothesis that growth episodes are generated by frequent stochastic events rather than by a few exogenous structural changes. Hence, the results from the test proposed here have to be interpreted in a conservative way since rejections may occur when the data follows an integrated process with few breaks. As will be reported subsequently, despite the evidence in favor of I(1) models tending to be negatively biased, our results still suggest fewer rejections than in previous works.

As for other tests in the literature, we implement a data-driven procedure to estimate the break locations. Also, following Kapetanios (2005), we allow for an unspecified number of breaks under the alternative hypothesis, up to some maximum M. This represents a major improvement with respect to early tests found in the literature which assumed a fixed number of breaks (Zivot and Andrews 1992; Lumsdaine and Papell 1997). As stressed by Kejriwal and Lopez (2013), it is desirable to select the model with the appropriate number of breaks before proceeding with the unit root test as the imposition of extraneous dummy variables leads to considerable power losses. In this respect, the paper provides a first step in incorporating in the unit root test a methodology for the identification of structural shifts that is broadly in tune with the one actually used by practitioners in the field of growth empirics when looking for growth episodes (Kerekes 2007; Jones and Olken 2008; Berg et al. 2012; Kar et al. 2013).

The search algorithm used to choose m and (T₁,...,T_m) is grounded in the sequential (one-by-one) break estimation approach proposed by Bai (1997). With respect to Kapetanios (2005) we introduce two innovations. First, we select the number of breaks and their location by minimizing the sum of squared residuals instead of the test statistic for α = 1.¹¹ Second, as the sequential procedure leads to limiting distributions of locations that diverge from the ones obtained via simultaneous estimation, we implement the repartition procedure suggested by Bai (1997) to correct for this bias. The algorithm can be described by the following steps:

• Step 1. Sequential estimation: For each m ∈ [1,M] and holding k = K fixed, where M and K refer to exogenously determined upper bounds respectively for the number of breaks and the truncation-lag parameter, obtain the break locations sequentially by minimizing the sum of squared residuals from Eq. 3 conditional on past breaks estimation. Thus, a generic break date is estimated as:

  $$ \hat{T}_{m} = \text{argmin}_{T_{m}} S (\hat{T}_{1},..., \hat{T}_{m-1}, T_{m}), $$

  (4)

  where:

  $$ \begin{array}{@{}rcl@{}} S(\hat{T}_{1},..., \hat{T}_{m-1}, T_{m}) &=& \sum\limits_{t=k+2}^{T} \left( y_{t} - \hat{\mu} - \hat{\upbeta} t - \hat{\alpha} y_{t-1} - \sum\limits_{i=1}^{m-1} \hat{\theta}_{i} DU(\hat{T}_{i})_{t} - \hat{\theta}_{m} DU(T_{m})_{t}\right.\\ &&\left.-\sum\limits_{i=1}^{m-1} \hat{\gamma}_{i} DT(\hat{T}_{i})_{t} - \hat{\gamma}_{m} DT(T_{m})_{t} - \sum\limits_{j=1}^{K} \hat{c}_{j}{\Delta} y_{t-j} \right)^{2} \end{array} $$

  (5)

• Step 2. Repartition procedure: For each m ∈ [2,M] and the associated partition $(\hat {T}_{1},..., \hat {T}_{m})$, each break date is re-estimated by fitting a one-shift model in the data interval defined by $[\hat {T}_{i-1}; \hat {T}_{i+1}]$.¹² The new estimates $(T^{*}_{1},..., T^{*}_{m})$ are consistent and share the same asymptotic distributions as those obtained by global maximization (Bai 1997).¹³ The intuition underlying the repartition procedure is rather simple: it entails fine tuning by re-estimating separately each break date in the data segment defined by the preceding break (or the initial observation for the first break point) and the subsequent shift (or the final observation for the last break point). Notice that the whole search scheme is carried out imposing a trimming parameter h, expressed as a share of the sample size, to ensure a minimum length for each segment between breaks.

• Step3. Model selection: As we are left with M + 1 possible partitions (including also the case with no breaks), the model with the appropriate number of breaks (m^∗) is chosen using the BIC criteria. The truncation-lag parameter k^∗ is then selected using the general-to-specific approach advocated by Ng and Perron (1995), i.e. starting from the upper bound (K) we remove one lag at the time until the last lag in an autoregression of order k^∗ is significant while the last lag in an autoregression of order k^∗ + 1 is not significant.

Concerning model selection, different approaches have been proposed in the econometric literature. Kapetanios (2005) proposes to select the optimal partition by minimizing the t-statistic for α. As for selecting breaks locations, such an approach is unlikely to deliver satisfactory results since the imposition of more dummies will generally overestimate the true number of shifts.¹⁴ The recommended strategy by Bai and Perron (2003) is to test for the presence of an additional shift in all the segments between break dates.¹⁵ This supF(l|l + 1) test allows one to discriminate between l and l + 1 breaks, and when used sequentially can be used to choose the model with the correct number of structural changes. Simulation evidence in Bai and Perron (2006) shows that both the sequential procedure and the BIC criteria perform better than other approaches. The former has the advantage of taking into account heterogeneity across segments and of being robust when serial correlation is present. Nevertheless, the sequential testing method presents serious power losses in small samples as it is typically carried out with ever fewer observations (Antoshin et al. 2008). Therefore, for this specific application, the BIC criteria appears to be more suited.¹⁶ A general issue with the BIC criteria concerns its poor performance under the null (i.e. when breaks are not present) when serial correlation is not accounted for. In our case, however, such a problem is addressed by directly controlling for serial correlation via the inclusion of k lags in the regression.

Finally, having selected $(T^{*}_{1},..., T^{*}_{m})$, m^∗ and k^∗, we fit the corresponding regression and use as test statistics both the standard t-statistic (t_α) for the null of α = 1 and the Wald statistic (F_T) for the joint null: $\alpha =1; \theta _{1}=...=\theta _{m^{*}}=\gamma _{1}=...=\gamma _{m^{*}}=0$.¹⁷

5 Finite sample size, power and break selection properties

In this section we present the critical values and explore the finite sample size and power properties of our testing strategy via Monte Carlo simulations.¹⁸ Table 2 reports finite sample critical values for different M, h and T.¹⁹ Following Kapetanios (2005), to generate critical values, we compute the distributions of the test statistics (t_α and F_T) under the null via Monte Carlo simulations of standard random walks (10,000 replications).²⁰ Then, we compute the thresholds for different levels of confidence.

Table 2 Finite sample critical values for t_α and F_T

Table 3 Size and power results under different parametrizations

Let us now present simulation results to investigate size and power properties of the test. The experimental design follows that of Vogelsang and Perron (1998) and Sen (2003). The simulated model takes the general form:

$$ [1-(\alpha+\rho)L+\rho L^{2}]y_{t}= (1+\lambda L)[\sum\limits_{i=1}^{A} \theta_{i} DU(T_{i})_{t} + \sum\limits_{i=1}^{B} \gamma_{i} DT(T_{i})_{t}+ e_{t}], $$

(6)

where $e_{t} \sim \mathcal {N} (0,1)$. For each experiment we run 1000 replications of length T = 200 and report the rejection rate at the 5% level using the appropriate critical values for M = 4 and h = 0.1. The following combinations of ρ and λ are tested: {(0,0);(0.5,0);(− 0.5,0);(0,0.5);(0,− 0.5)}. In the size simulations we impose α = 1 and A = B = 0, while for the power simulations we experiment for α ∈{0.9;0.8;0.7;0.6;0.5} introducing different number of breaks of different forms and magnitudes.²¹ Results are reported in Table 3. Let us now emphasize some key features emerging from simulations:

• 1. The size of t_α and F_T is reasonably close to the nominal value. A well-known exception is the case with a negative moving average component in which both the test statistics are slightly over-sized.²²

• 2. In the absence of breaks, F_T displays uniformly higher power than t_α across all the experiments.

• 3. When the number of structural changes increases, some loss in power has to be expected, ceteris paribus, as a result of the introduction of additional dummies (see Kapetanios 2005, for a discussion of this issue).

• 4. Convergence to 100% power occurs fast as the magnitude of the breaks increases. As documented by Sen (2003), F_T converges faster than the standard t-statistic since it incorporates information on the presence of breaks. Notice that the power gains associated with increasing break magnitudes (holding constant the variance of shocks) are symmetrical to those associated with lower variance (holding constant the size of the breaks).

• 5. The power generally increases monotonically as we move away from the null (i.e. as α decreases). Nevertheless, in the presence of a negative autoregressive term, the power of F_T may slightly decrease between α = 0.9 and α = 0.6.

• 6. For α = 0.9, F_T has a higher power than t_α in almost all the experiments, i.e. it is better suited to investigate cases with the autoregressive parameter close to unity.

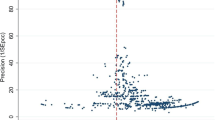
We also study the effects of changing the length of the time series (cf. Figure 2).²³ As expected, for shorter time series the test has lower power. Nevertheless, it is reassuring that for sufficiently large breaks F_T do not display strong power losses.

Fig. 2

The effect on power of different time series lengths

Let us now compare the power performance of t_α and F_T with the standard Kapetanios test. Results are reported in Fig. 3 for M ∈{2;3;4} and different parameter values of the simulated model. Some important aspects stand out from the simulations. First, as pointed out by Ohara (1999), the power of all the statistics falls dramatically when M is lower than the true number of breaks. Second, for t_α and the Kapetanios test statistic a less pronounced reduction in power also appears when increasing M, given the number of true breaks. The performance of F_T, on the contrary, remains largely unaffected by this second effect. Most importantly, the Kapetanios test exhibits higher power than both t_α and F_T in a limited set of instances when no breaks are present under the null. Generally, F_T tends to outperform the other statistics, especially when the upper bound M increases (cf. the panels with M = 4 in Fig. 3).

Fig. 3

General power comparison - F_T, t_α, the Kapetanios statistic (min-t_α)

In Figs. 4 and 5 we show that our search scheme leads to a more precise estimation of the number of breaks and their locations, as compared to the standard approach based on the minimization of the t-statistic.²⁴ Figure 4 assumes the number of breaks to be known (equal to 4) and plots the distributions of the estimated break dates under different degrees of serial correlation. We report a substantial improvement with the distributions of break locations becoming more symmetric and centered around the true dates, in particular for the first two breaks. Figure 5 compares the selected number of structural shifts under both procedures. Once again, the minimization of the t-statistic performs poorly as it tends to always select a number of breaks equal to the upper bound M, resulting in a general overestimation, while using the BIC criteria entails a higher probability to choose the correct number of breaks.

Fig. 4

Distribution of break dates - Two step minimization of SSR (left panels) vis-à-vis sequential minimization of t_α (right panels)

Fig. 5

Frequency of selected number of breaks - BIC criteria (left panels) vis-à-vis sequential minimiziation of t_α (right panels)

Overall, according to our simulation exercises, the testing procedure proposed here turns out to yield gains in terms of both power performance and the precision of breaks estimation. In particular, one should expect a generally higher power for F_T than for t_α.²⁵ However, since the Wald statistic may exhibit non-monotonic power in the few specific instances described above, in the empirical application we also report results using t_α.

6 The empirical strategy

We investigate the presence of unit roots and structural breaks in income per capita series. Table 4 summarizes the results from previous studies. Data are taken from the last release of the Maddison database (Bolt et al. 2018).²⁶ To preserve the robustness of our analysis we focus exclusively on time series with at least 100 consecutive observations, leaving us with a sample of 34 countries (20 OECD and 14 developing).²⁷

Table 4 Rejection rates and break dates from other studies using Maddison data

Concerning the choice of M, as documented in Section 5, a parsimonious specification of M may improve the power of the test when the true number of shifts is less than or equal to the specified maximum. However, large power losses exist when the number of breaks is greater than the maximum allowed. Therefore, we report results for both M = 3 and M = 4 and find no evidence of power losses.²⁸ Indeed, it is reassuring that the number of rejections does not fall when allowing for an additional break. In all tests the trimming parameter is set to h = 0.1.

In contrast to previous studies which rely on asymptotic critical values (Lumsdaine and Papell 1997; Kejriwal and Lopez 2013; Papell and Prodan 2014), for each country in the sample (and each M) we obtain series-specific critical values to take into account the idiosyncratic characteristics of each time series.²⁹ The key intuition is that under the null the first differences of the series can be described by a stationary ARMA process with no breaks. Following Christiano (1992) and Zivot and Andrews (1992), for each series we take first differences and estimate a battery of ARMA(p,q) models. To determine the appropriate number of lags p and q we use the BIC criteria. After selecting the appropriate null model, the distribution of both t_α and F_T as well as the associated critical values are approximated via Monte Carlo simulations (with 5000 replications). In the simulations we allow for two alternative assumptions regarding the nature of the stochastic disturbances: (i) Normal shocks with zero mean and standard deviation estimated from the residuals; (ii) Randomly drawn shocks (with replacement) from the distribution of residuals. Hence, critical values are computed both assuming the Gaussianity of the shocks and via bootstrapping (cf. Table 9 in the Appendix B). The latter technique has the advantage of restraining from parametric assumptions but may lead to spurious results in small samples, in particular when the criteria used for model selection fail to identify serial correlation in the error term. As a consequence, results are reported for both approaches in Table 5.

Table 5 Results from the unit root tests and estimated break dates for M = 3 and M = 4

7 Discussion of results

For OECD countries, our methodology rejects the null of the unit root in only 13 of 20 instances under the assumption of Gaussian shocks (cf Table 5). Consistently with the power simulations reported in Section 5, we find a higher number of rejections when using the Wald statistic. Although our results do not contrast strongly with the previous literature (cf. Table 4), we find additional failures to reject the null (i.e. Canada, Denmark, Sweden, Switzerland). These differences reflect the different break search methodology adopted and, possibly, the use of series-specific critical values vis-à-vis asymptotic ones. Somewhat consistently with Kejriwal and Lopez (2013), relying on the minimization of the SSR rather than the t-statistics produces less evidence against the unit root hypothesis.³⁰

This paper also presents new evidence for developing countries. In particular, we find only 4 rejections in a sample of 14 developing economies. Intuitively, those countries tend to experience more erratic growth processes with persistent and frequent (possibly more than four) shifts in both level and trend. This is in line with several contributions emphasizing the ubiquitous presence of growth discontinuities in poor- and middle-income countries (Pritchett et al. 2000; Hausmann et al. 2005; Lamperti and Mattei 2018b). Yet, it should be noticed that results may be affected by the shorter time series (the average number of observations for developing countries is 147) or by higher variance. Although we can partially correct these biases when using series-specific critical values, it is not possible to unambiguously disentangle their magnitude.

Another relevant contribution of our work regards the possibility of departing from the assumption of Gaussian shocks by deriving bootstrapped critical values. Rejection levels using bootstrapped critical values are reported in brackets in Table 5. Interestingly, this leads to considerably less evidence against the unit root hypothesis. In Fig. 6, the empirical distribution of the residuals under the null is contrasted with the best Normal fit. Departures from Normality appear to exist in some countries in terms of skewness and, most importantly, excess kurtosis.³¹ This seems to suggest that the assumption of Gaussianity may bias the results in favour of trend-stationary models. One may conjecture, instead, that GDP time series may be well described by I(1) models with fat-tailed innovations. Such a characterization is consistent with empirical findings which identify Laplacian distributions of aggregate growth shocks (Castaldi and Dosi 2009; Fagiolo et al. 2008). Fat-tailed distributions of shocks entail a growth process driven by large and lumpy events. They typically emerge when some of the assumptions of the central limit theorem are violated. In particular, it has been pointed out that the presence of dynamic increasing returns and strong correlating mechanisms (e.g. competition, network externalities) at the firm level may lead to a non-trivial aggregation of microeconomic shocks, which in turn may lead to the emergence of fat tails in macroeconomic data (Bottazzi and Secchi 2006; Dosi 2007; Fagiolo et al. 2008). An I(1) characterization of the GDP per capita series with non-Gaussian innovations is common to many evolutionary growth models.³² These models generally describe the growth process as a result of complex interactions across individuals and organizations which, in turn, lead to path dependency and irreversibility of shocks as well as to the emergence of fat-tailed distributions at all levels of aggregation. The lack of evidence against I(1) processes may be interpreted as pointing towards a strong degree of “complexity” and inter-relatedness across economic units, thus, providing support for evolutionary models. For instance, Dosi et al. (2019) present a multi-country agent-based model in which firms interact both domestically and in international markets following idiosyncratic learning trajectories. Simulation results show that countries endogenously differentiate and cluster into two groups of winners and losers exhibiting extremely erratic paths with fat-tailed distributions of growth rates. As stated in Section 2, RBC and DSGE models may also be consistent with I(1) aggregate time series even though they can hardly generate fat-tailed distributions of growth rates.

Fig. 6

Residuals from the selected I(1) model - empirical density (in green) vs. Normal fit

Figure 7 reports the estimated structural breaks for each time series. Break dates are estimated under the I(0) alternative and, therefore, they have a meaningful interpretation when the unit root null is rejected. Nevertheless, it should be noticed that break locations for all countries tend to capture major historical events such as wars, booms and crisis. In this respect, the endogenous identification of relevant episodes provides a further validation of the search algorithm proposed here. Moreover, consistent with previous contributions, there is no evidence of a single steady state model as each country displays at least one structural break. In Table 6 we report estimates of break dummy coefficients for the series which appear to be stationary. Most countries with I(0) time series tend to exhibit significant changes in both their intercepts and trends. As an illustrative example consider the case of France whose experience is representative of those of many OECD countries. Our break selection procedure suggests two major crashes associated with the two world wars, which are both accompanied by subsequent periods of growth acceleration. The phase of strong catching up in the aftermath of World War two is then followed by a period of relative stagnation (i.e. a negative trend shift) at the end of the 1970s following the oil crisis (Perron 1989). The presence of (relatively few) changes in growth rates within-country, possibly associated also to level shifts, is a feature of endogenous growth models exhibiting “strong” scale effects. Less evidence is found supporting pure Neoclassical and semi-endogenous models which predict only level effects. This is broadly consistent with the results of Papell and Prodan (2014), who find growth effects in the majority of the time series considered.³³

Fig. 7

Time series of income per capita and estimated break dates

Table 6 Estimates of structural break dummies

The evidence presented here has some relevant implications for applied work in the field of growth empirics. First, the presence of unit roots in many GDP series affects significantly the identification of specific kinds of growth episodes. Several empirical papers disregard prior unit root testing when looking for structural changes in the data. The choice of a level versus first-difference specification is crucial for the appropriate implementation of structural breaks search procedures, however. Our results indicate that for most GDP time series, especially in developing countries, the first-difference variant has to be preferred. Moreover, the results call into question the widespread practice of using simple economic filters, based on invariant criteria (e.g. a jump in growth rates of a given amount lasting for some years), to identify growth shifts. In fact, the evidence in favour of I(1) models hints at extremely frequent growth discontinuities which hardly obey deterministic and recurrent characteristics.

To corroborate our results we performed robustness checks. First, we ran the test assuming a fixed number of structural changes in order to identify possible power losses arising due to the selection of the appropriate number of breaks. Results are reported in Appendix A (cf. Table 7). Although showing general consistency with the baseline case, they indicate even fewer rejections, thus, excluding the possibility that our results are being driven by power losses due to the selection procedure adopted. As a second robustness check, we run the test imposing a smaller trimming parameter (h = 0.05, cf. Table 8) in order to allow for more consecutive break dates. This results in three extra rejections for OECD countries while the coefficient of New Zealand becomes statistically insignificant. Hence, allowing for shorter growth segments provides only limited additional evidence against the unit root hypothesis.

8 Conclusion

In this paper we test the unit root hypothesis in long-run income time series against the alternative of stationary models with multiple structural breaks. Our approach extends the test in Kapetanios (2005) by introducing a more robust search procedure which provides substantial improvements in terms of power and breaks identification (cf. the evidence in Section 5).

As argued in Section 2, distinguishing I(1) models from stationary alternatives has relevant theoretical and empirical implications in the field of economic growth. The tension between integrated and trend stationary models (with breaks) can be summarized by the following question: how frequently do countries experience structural breaks in their GDP per capita series? In the limit, unit root models are stationary processes in which both the intercept and the trend change permanently at any point in time. Hence, if structural breaks occur particularly often, the distinction between I(1) and I(0) specifications becomes extremely blurred. In this perspective, testing for unit roots amounts to testing for the frequency of structural changes. The procedure introduced in this paper has the aim of distinguishing between models with several permanent changes in mean and trend and alternatives with relatively few variations. Our results are more favorable to the first alternative.

Even in advanced countries we find less evidence against I(1) processes in comparison to previous studies that tend to find a relatively large number of rejections (Ben-David et al. 2003; Papell and Prodan 2014), with our results being more in line with new results pointing at a resurgence of the unit root hypothesis in GDP data (Kejriwal and Lopez 2013; Zerbo and Darné 2018). Another contribution of this paper is the inclusion of developing countries in the analysis. However, even by allowing for up to four breaks, we fail to reject the null of a unit root in most of the countries considered. Such results suggest the presence of strong growth discontinuities in backward economies which make their growth paths hardly distinguishable from a random walk. Finally, the number of rejections fall when using bootstrapped critical values instead of Gaussian shocks, possibly hinting at the presence of I(1) models with fat-tailed innovations.

In Section 7, such results have been interpreted as providing support to evolutionary growth models which stress path dependency, nonlinearities and the non-trivial aggregation of microeconomic shocks. At the macroeconomic level, these characteristics typically lead to the emergence of series exhibiting several growth shifts, similar to I(1) models.

From the point of view of growth empirics, we emphasize the importance of unit root testing prior to (or jointly with) structural break identification. Indeed, if countries exhibit growth trajectories similar to random walks, the practice of fitting structural change models on the series in levels may lead to spurious and inconsistent results.

Our results also suggest some future lines of research. First, it becomes crucial to move towards testing methodologies that are robust to the presence of fat-tailed shocks. Quantile autoregressions (QAR) are a natural candidate in this respect, as they allow for the investigation of persistence properties of a time series at different quantiles of the conditional distribution (Koenker and Xiao 2004, 2006). Recently, structural break tests have been developed in the framework of QAR (Qu 2008; Oka and Qu 2011). Incorporating unit root tests in this setting would clearly be a key achievement. Second, there is a lot to learn from the growth dynamics of developing countries. The unstable and complex patterns shown by this group of economies call for further research efforts. As a matter of fact, most empirical papers investigating growth episodes in less developed countries tend to adopt a deterministic characterization of growth discontinuities, relying on constant and recurrent criteria (e.g. 2% acceleration in growth rates for a minimum number of years) to define episodes. The evidence presented here partially challenges this approach since we have shown that for developing countries, growth shifts are extremely frequent and exhibit random characteristics in terms of form and magnitude. Unfortunately, long run time series are available only for a limited sample of economies while both unit root and structural break tests suffer from finite sample biases. As a first attempt to address the issue, Antoshin et al. (2008) present a methodology for structural break testing suited for short time series. More generally, improving the small sample performance of unit root tests would allow one to perform a similar investigation using post-war data for a larger set of economies.

Appendices

Appendix A: Robustness checks

Table 7 Results from unit roots tests imposing a fixed number of breaks for M = 3 and M = 4

Table 8 Results from unit roots tests imposing h = 0.05 for M = 3 and M = 4

Appendix B: Series-specific critical values

Table 9 Series-specific critical values for M = 3 and M = 4 – derived using the Monte Carlo method under both Gaussian shocks and bootstrapping