1 Introduction

Model-based hydrodynamic leveling is an efficient and flexible method to connect islands and offshore tide gauges with the height system on land (Slobbe et al. 2018a). The technique uses mean water level (MWL) differences between tide gauges provided by a regional, high-resolution hydrodynamic model. The averaging period can be chosen freely. For instance, Slobbe et al. (2018a) obtained the best results when averaging the water levels over the summer months of their 19-year simulation period. Afrasteh et al. (2021) showed that combining model-based hydrodynamic leveling data with data of the Unified European Leveling Network (UELN) may improve the quality of the European Vertical Reference Frame (EVRF). Assuming the model-based MWLs can be obtained with a uniform variance of 4.5 cm\(^2\) (corresponding to a standard deviation of 3 cm for each hydrodynamic leveling connection), the median of the propagated height standard deviations improved by \(38\%\) compared to the spirit leveling-only solution. If the model(s) provide the MWLs with a uniform variance of 12.5 cm\(^2\) (corresponding to a standard deviation of 5 cm for each hydrodynamic leveling connection), the reported improvement is still \(29\%\). Although promising, a more realistic impact assessment is yet to be done as a proof is lacking that hydrodynamic models can indeed provide the MWL at the tide gauge locations with an accuracy of a few centimeters. Apart from that, Afrasteh et al. (2021) assumed that the noise variance–covariance (VC) matrix of the model-derived MWLs is a diagonal matrix. The goal of this paper is to develop a more realistic correlated error model and to confirm whether previous noise assumptions were sensible.

Obtaining the full noise VC matrix is not straightforward. Indeed, this would be the case if model output includes full noise VC matrices or when an ensemble of model outputs is available or can be generated. However, the first is typically not the case, and the latter is not feasible given the size of the model in terms of grid nodes and the intended simulation period (in the order of decades). Moreover, in both cases proper noise models need to be available for all forcing datasets as well as the open boundary conditions. Therefore, inspired by the successful approach of Ditmar et al. (2011) and Farahani et al. (2016), among others, our approach will be to develop an empirical noise model for the model-derived MWLs based on the differences between observation- and model-derived MWLs.

A successful implementation places at least four requirements on the observed water level data. First, the distribution of the observation sites should result in a representative sample of the coastal MWL model errors. Second, the observed time series must be long compared to the averaging period so that multiple noise realizations can be calculated over the water level averaging period we aim for (i.e., one or more summer periods). Third, the sampling interval must be sufficiently high to average high-frequency water level variations. Finally, the water levels must be expressed in the same height system. The adjective ‘coastal’ in the first requirement has been added as we want to establish the hydrodynamic leveling connections between tide gauges located in coastal waters (i.e., the waters up to a few km from the coast). Given the higher variability of the physical processes that play a role in these waters (Kantha and Clayson 2000; Iglesias et al. 2020), the model performance in the coastal waters is expected to be poorer than in the deep and shelf waters. The third requirement relates to the possible use of satellite radar altimeter data, which have a much lower temporal resolution than tide gauge records.

Considering the first three criteria, tide gauge records are an appropriate data source to develop an empirical noise model. Although compared to other parts of the Earth there are many tide gauges available in our target area (the European sea waters in the broad sense and the north-east Atlantic region including the North Sea in the narrow sense), we have to make compromises when deriving a noise model. The main limiting factor is that most tide gauges are not deployed to build long and stable time series. Therefore, in addition to gaps, long time series often show abrupt jumps. Moreover, it is not always clear when and with what accuracy a tide gauge is connected to the mainland height system, nor with what frequency the connections are verified. Therefore, beyond the usual and pragmatic assumptions of time stationarity and spatial isotropy, we need to shorten the timespan over which we average the water levels.

The main objective of this study is to develop and analyze an empirical noise model for model-derived coastal summer mean water levels (SMWLs) and use that to obtain a more realistic quality impact of combining hydrodynamic leveling and UELN data in realizing the European Vertical Reference System (EVRS). The motivation to use the summer MWLs rather than the MWLs averaged over the entire simulation period follows from the results of Slobbe et al. (2018a); by only averaging over the summer months we ignore storm surge periods and get more accurate MWL differences. Note that we consider any SMWL signal not captured by the hydrodynamic models to be part of the noise. The analysis of the obtained noise model includes an assessment of the spatiotemporal performance level with which state-of-the-art hydrodynamic models are able to represent the SMWL. In doing so, we consider three hydrodynamic models for the Northeast Atlantic Ocean, including the North Sea and Wadden Sea; the Forecasting Ocean Assimilation Model 7 km Atlantic Margin model (AMM7) (Tonani and Ascione 2021), the DCSMv6-ZUNOv4 (Zijl et al. 2013, 2015), and the 3D DCSM-FM (Zijl et al. 2020). To gain insight into the differences in model performance in the coastal waters versus the deep and shelf waters, we will develop empirical noise models for the latter two based on TOPEX/Jason satellite radar altimeter data and compare them with the one for the coastal waters. This analysis will be conducted for the DCSMv6-ZUNOv4 model only. We will also assess the contribution of errors in the vertical referencing of the tide gauges to the observation-derived SMWLs. Note that throughout the paper, the term ‘SMWL’ refers to the average water level calculated over all May to September months of one or more years. Moreover, when we refer to a noise model for, e.g., 3D DCSM-FM, we refer to a specific reanalysis conducted with this model.

Indeed, comparing observation- and model-derived (mean) water levels is routinely done in assessing model performance and presented in many publications (e.g., Woodworth et al. 2013; Filmer et al. 2018). These include our area of interest (e.g., Holt et al. 2005; Slobbe et al. 2013; Zijl et al. 2013; Slobbe et al. 2018a; Hermans et al. 2020). The combination of the following two aspects makes the present analysis different. First, based on the results of Slobbe et al. (2018a) we are interested in the model performance in terms of ‘summer’ MWL. Second, our analysis goes beyond typical comparison studies as we will particularly assess the magnitude of the noise correlations.

The paper is organized as follows. Sect. 2 describes the methodology used to generate the noise models, the metrics used to assess the model performance, and the experiment conducted to obtain a more realistic quality impact of combining hydrodynamic leveling and UELN data in realizing the EVRS. Sect. 3 introduces the data sets used in this paper. In Sect. 4, we present, analyze, and discuss all results. Finally, we conclude by summarizing the main findings of the paper in Sect. 5.

2 Methodology

2.1 Noise model generation

2.1.1 Preliminaries

A hydrodynamic leveling connection comprises the geopotential difference (\(\Delta {W}\)) between two UELN height benchmarks (HBMs), each connected to a tide gauge. It can be written as

$$\begin{aligned} \Delta {W}^{{\tiny \textrm{HBM}}_y}_{{\tiny \textrm{HBM}}_x}&= \Delta {W}^{{\tiny \textrm{TGZ}}_x}_{{\tiny \textrm{HBM}}_x} + \Delta {W}^{\overline{{\tiny \textrm{SMWL}}}_x}_{{\tiny \textrm{TGZ}}_x} + \Delta {W}^{\widetilde{{\tiny \textrm{SMWL}}}_y}_{\widetilde{{\tiny \textrm{SMWL}}}_x}\nonumber \\&\quad + \Delta {W}^{{\tiny \textrm{TGZ}}_y}_{\overline{{\tiny \textrm{SMWL}}}_y} + \Delta {W}^{{\tiny \textrm{HBM}}_y}_{{\tiny \textrm{TGZ}}_y}, \end{aligned}$$
(1)

where x and y refer to a tide gauge, TGZ stands for tide gauge zero, and \(\overline{{\tiny \textrm{SMWL}}}\) and \(\widetilde{{\tiny \textrm{SMWL}}}\) are the observation- and model-derived SMWLs, respectively. We usually refer to the HBM to which the TGZ is connected as the ‘tide gauge benchmark’ (TGBM). However, not all TGBMs are part of the UELN. If not, \(\Delta {W}^{{\tiny \textrm{TGZ}}_.}_{{\tiny \textrm{HBM}}_.} = \Delta {W}^{{\tiny \textrm{TGZ}}_.}_{{\tiny \textrm{TGBM}}_.} + \Delta {W}^{{\tiny \textrm{TGBM}}_.}_{{\tiny \textrm{HBM}}_.}\). Note further that in Eq. (1) any time variability is ignored. As pointed out in Afrasteh et al. (2021) both the observation- and model-derived tide gauge records need to be reduced to the reference epoch adopted in the EVRF (epoch 2000.0). The same applies to the leveling data acquired to connect the HBM to the TGZ. To simplify the present discussion, we assume this reduction has been done. Another premise is that in establishing the hydrodynamic leveling connections, the timespan over which we compute both the observation- and model-derived SMWLs is the same for all tide gauges. By doing this, we reduce potential time-dependent, large-scale errors in the modeled water levels, and it greatly simplifies the problem as the noise model is just 1-dimensional.

The uncertainties associated with the five independent terms in Eq. (1) together determine the precision of the hydrodynamic leveling data. By far the largest contributor is, however, the middle term \(\Delta {W}^{\widetilde{{\tiny \textrm{SMWL}}}_y}_{\widetilde{{\tiny \textrm{SMWL}}}_x}\), which is expected to be at the cm level. Indeed, supposing the connections between the HBMs and TGZs are established by spirit leveling conducted with a precision of 0.5 mm/km (corresponding to the precision of first-order leveling (Bossler 1984)) and that we only use tide gauges within 10 km from the UELN height benchmarks, the contributions of the first and last term are below 2 mm in terms of standard deviation. Similarly, the uncertainty of the MWL computed over one month of sea level observations is already \(< 1\) mm in length units based on a 10-min sampling and assuming white noise with a standard deviation of 5 cm.

Considering now a set of hydrodynamic leveling connections, the full noise VC matrix \(Q_{{\tiny \textrm{hl}}}\) is obtained by

$$\begin{aligned} Q_{{\tiny \textrm{hl}}} = Q_{{\tiny \textrm{1}}} + Q_{{\tiny \textrm{2}}} + A_{{\tiny \textrm{hl}}} Q_{\widetilde{{\tiny \textrm{SMWL}}}} A_{\hbox {\tiny {hl}}}^{\textrm{T}} + Q_{{\tiny \textrm{4}}} + Q_{{\tiny \textrm{5}}}, \end{aligned}$$
(2)

where \(Q_{{\tiny \textrm{1}}}\), \(Q_{{\tiny \textrm{2}}}\), \(Q_{{\tiny \textrm{4}}}\), and \(Q_{{\tiny \textrm{5}}}\) are the diagonal noise VC matrices associated with \(\Delta {W}^{{\tiny \textrm{TGZ}}_x}_{{\tiny \textrm{HBM}}_x}\), \(\Delta {W}^{\overline{{\tiny \textrm{SMWL}}}_x}_{{\tiny \textrm{TGZ}}_x}\), \(\Delta {W}^{{\tiny \textrm{TGZ}}_y}_{\overline{{\tiny \textrm{SMWL}}}_y}\), and \(\Delta {W}^{{\tiny \textrm{HBM}}_y}_{{\tiny \textrm{TGZ}}_y}\), respectively; \(A_{{\tiny \textrm{hl}}}\) is the design matrix of the hydrodynamic leveling dataset; and \(Q_{\widetilde{{\tiny \textrm{SMWL}}}}\) the full noise VC matrix of the model-derived SMWLs. Estimating \(Q_{\widetilde{{\tiny \textrm{SMWL}}}}\) is one of the main goals of this paper and a critical step in the development of model-based hydrodynamic leveling.

2.1.2 Overall approach to generate a noise model of the model-derived SMWLs in coastal waters

As motivated in Sect. 1, \(Q_{\widetilde{{\tiny \textrm{SMWL}}}}\) will be computed from an empirical noise model derived from the differences between observation- and model-based SMWLs at a set of N coastal tide gauges within the model domain. The criteria applied to select the tide gauges are discussed in Sect. 3.2. The overall approach to compute the noise model from these data comprises four steps:

Step 1: Compute the \(T_{{\tiny \textrm{avg}}}\)-SMWL time series. We refer to the SMWL averaged over interval \(T_{{\tiny \textrm{avg}}}\) as the \(T_{{\tiny \textrm{avg}}}\)-SMWL. In dealing with tide gauge data, \(T_{{\tiny \textrm{avg}}}\) is one, two, or three summer periods. Given the time span of 22 years over which model-derived water levels are available (\(T_{{\tiny \textrm{sim}}}\)), a larger number of summer periods for \(T_{{\tiny \textrm{avg}}}\) will not provide sufficient realizations of the noise per tide gauge. The \(T_{{\tiny \textrm{avg}}}\)-SMWL time series are computed by averaging the monthly MWLs over all May to September months in each consecutive time interval of \(T_{{\tiny \textrm{avg}}}\) years. To increase the data availability, we permit for one missing monthly MWL per ‘summer’ period. The model-derived monthly MWLs are in all cases calculated as the arithmetic mean of the modeled water levels. To account for ‘small’ data gaps in the observed water level time series (total time for which no data are available should be \(<10\) days per month), the observation-derived monthly MWLs are estimated along with the tides. For this, we used the UTide Matlab functions (Codiga 2020). The automated decision tree method, which is based on the equilibrium tide and the conventional Rayleigh criterion, has been applied to select the constituents to be included in the harmonic analysis (Codiga 2011).

Step 2: Generate noise realizations. The next step in our approach is to generate a set of noise realizations. For each tide gauge, they are obtained by taking the difference between the observation- and model-derived \(T_{{\tiny \textrm{avg}}}\)-SMWL time series of step 1. If the simulation period is \(T_{{\tiny \textrm{sim}}}\), the number of differences assuming no data gaps equals \(\lfloor T_{{\tiny \textrm{sim}}}/T_{{\tiny \textrm{avg}}} \rfloor \). We consider these differences as realizations of the noise in the model-derived \(T_{{\tiny \textrm{avg}}}\)-SMWL. In case no difference could be computed due to data gaps in the observation-derived SMWL time series, the difference is set to NaN. Note that all monthly MWL differences are excluded from the analysis if the difference between the observation- and model-derived monthly MWLs exceeds the median plus/minus three times the standard deviation (estimated as \(1.4826\ \times \) the median absolute deviation (MAD) (Cook and Weisberg 1982; Rousseeuw and Croux 1993)). About 1% of the months were excluded this way. We also removed for each \(T_{{\tiny \textrm{avg}}}\) period the mean difference over all tide gauges. Based on a bootstrapping approach (Mooney and Duval 1993), we then generate K sets of noise realizations at all N tide gauges.

Step 3: Compute empirical covariance functions. For each set, consisting of N differences, we compute an empirical covariance function \({\hat{C}}\) (e.g., Wackernagel 2003) using:

$$\begin{aligned} {\hat{C}}(D_{{\tiny \textrm{sea}}}) = \frac{1}{M(D_{{\tiny \textrm{sea}}})} \sum _{M(D_{{\tiny \textrm{sea}}})} \left( Z(s_i) - {\overline{Z}} \right) \left( Z(s_j) - {\overline{Z}} \right) , \end{aligned}$$
(3)

where \(D_{{\tiny \textrm{sea}}}\) is the sea distance, \(M(D_{{\tiny \textrm{sea}}})\) the set of tide gauges separated by sea distances within a given interval (see Sect. 2.1.5 for the way these intervals are defined), Z(s) is the difference between the observation- and model-derived SMWLs at location s, and \({\overline{Z}}\) the average difference. The sea distance is, loosely spoken, the shortest distance to travel between two points over sea (see Sect. 2.1.4 for the method applied to compute these distances). It is used as the distance metric to account for the presence of land. In computing \({\hat{C}}(D_{{\tiny \textrm{sea}}})\), it is assumed that the covariance function is isotropic.

Step 4: Fit an analytical noise model. The last step involves the fitting of an analytical model through the average empirical covariances. This is the subject of Sect. 2.1.6. Note that in computing the average empirical covariance function, the averaging is applied to the empirical correlograms obtained as \({\hat{C}}(D_{{\tiny \textrm{sea}}})/{\hat{C}}(0)\). To obtain the average empirical covariance function, we scale the average empirical correlogram by the variance computed as squared MAD of the differences between the observation- and model-derived SMWLs at all tide gauges scaled by 1.4826. To build \(Q_{\widetilde{{\tiny \textrm{SMWL}}}}\), the analytical model has to be evaluated for the sea distances among the tide gauges involved in establishing the hydrodynamic leveling connections.

2.1.3 Overall approach to generate a noise model of the model-derived SMWLs in deep and shelf waters

The noise models for the deep and shelf waters will be calculated from satellite radar altimeter data (see Sect. 3.3 for a description of the data). The limited temporal resolution (about 10 days) requires a different strategy than described in Sect. 2.1.2. In short, the period over which a reliable average water level can be calculated is much longer. In this study, we used the full data period of 1997–2019. The following procedure is applied using the instantaneous water levels as input.

Step 1: Compute difference time series. We interpolated the modeled instantaneous water levels at the altimeter data locations (see Fig. 1) and subtracted them from the observed ones. After that, we binned the differences resulting in one difference time series per 6.5 km in along-track direction. In the binning, we fitted a function through the data accounting for a slope in latitude and longitude directions as well as a linear trend over time and an annual and semi-annual cycle. To reduce the observations to the mean position of all data points in a bin, we used the estimated slope parameters.

Step 2: Compute the average difference over all May to September months and edit the dataset. From each time series, we selected the data points acquired in the months May to September and computed the average. All points for which the difference exceeds the median of all differences plus five times the standard deviation are excluded as an ‘outlier’. Here again, the standard deviation is estimated as \(1.4826 \times \) the MAD.

Step 3: Compute the ‘sea distance matrix’. The sea distance matrix describes the sea distances among all bins. See Sect. 2.1.4 for further details.

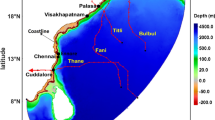
Step 4: Split the dataset into deep and shelf waters. The separation between the deep and shelf waters is determined based on the 200 m depth contour line shown in Fig. 1.

Step 5: Compute the empirical covariance function. After determining the ‘optimal’ lag distances using the method described in Sect. 2.1.5, we compute the empirical covariance functions using Eq. (3).

2.1.4 Computing the sea distance

To compute the sea distances among all observation locations (i.e., tide gauges or altimeter data points), we discretized the region using a uniform grid with a spacing of 0.05 degrees. Using the grid nodes classified as ‘sea’ based on GMT’s grdlandmask (Wessel et al. 2019), we form a graph of which the vertices are connected in east-west and north-south directions. Using Matlab’s graphshortestpath function, we calculate the Dijkstra shortest path (Dijkstra 1959) between nodes closest to the observation locations. Adding up the distance between the observation locations and the nearest vertices to the shortest path will end up in the sea distance. Note that we did not establish diagonal connections between vertices as all hydrodynamic models being considered in this study use rectangular grids.

2.1.5 Defining the lag distances

Usually, lags (also referred to as ‘distance bins/classes’) for which the empirical covariances are calculated have a uniform spacing. The maximum lag distance is half the distance between the two data points furthest from each other, and the lag tolerance (i.e., half the interval within which a distance must be to belong to a particular lag) is half the lag spacing. Given that in particular the number of tide gauges is limited, we use a non-uniform spacing and lag tolerance in which the lags are chosen so that approximately the same number of pairs are available for each lag distance. The maximum lag distance is set to 2100 km, which is approximately 65% of the sea distance between the two tide gauges furthest from each other. In using a non-uniform spacing and lag tolerance, we ensure that we have provided sufficient data points for computing the covariance value for each lag. The only exception to this is lag zero, for which the lag tolerance is set to zero. The latter means that the number of points available for this lag equals the number of tide gauges/altimeter data points.

2.1.6 The analytical covariance model

Many models of covariance functions have been proposed. For some examples, we refer to, e.g., Christakos (2012); Hristopulos (2020). In this study, we use a composite model that is the superposition of the ‘nugget effect’ and I J-Bessel models (see Hristopulos 2020, Sect. 4.2.2). The nugget effect describes a possible discontinuity at the origin. If present, it points to random errors in the observation- and model-derived SMWLs and signal at short spatial scales that cannot be resolved from the data or by the hydrodynamic model. The J-Bessel model is chosen because it admits negative values and provides a good fit of the empirical covariance functions. The composite model is defined as:

$$\begin{aligned} C(h) = {\left\{ \begin{array}{ll} c_0 + \sigma ^{2}_{x} &{} \text {if } h=0\\ \frac{\sigma ^{2}_{x}}{I}\ \sum _{i=1}^{I} 2^{\nu }\ \Gamma (\nu +1)\ h^{-\nu }\ J_{\nu }(h),\\ \text {with } \nu \ge d/2-1 &{} \text {if } 0 < h \le h_{{\tiny \textrm{max}}}, \end{array}\right. } \end{aligned}$$
(4)

where h is the dimensionless lag defined as \(D_{{\tiny \textrm{sea}}}/\xi _i\), \(\xi _i\) the characteristic length, \(c_0\) is the nugget effect (i.e., the magnitude of the discontinuity at the origin, \(\sigma ^{2}_{x}\) is the variance by which the J-Bessel models are scaled, \(\Gamma \) denotes the Gamma function (Hristopulos 2020, Eq. 4.17), \(J_{\nu }(\cdot )\) is the Bessel function of the first kind of order \(\nu \) (Watson 1995), d denotes the number of spatial dimensions (\(d=2\) in our case), and \(h_{{\tiny \textrm{max}}}\) is the dimensionless maximum lag (i.e., \(2100\ \hbox {km}/\xi _i\)). Note that in this study the maximum value for I is equal to two. The parameters \(c_0\), \(\xi _i\), \(\nu \), and \(\sigma ^{2}_{x}\) are estimated by applying Matlab’s global optimization solver GlobalSearch. The algorithm minimizes the sum of the squared differences between the empirical covariance function values and the analytical model such that \(1E-4 \le c_0 \le 1E{-}2\), \(1E2 \le \xi _1 \le 2E2\), \(2E2 \le \xi _2 \le 5E2\), \(0 \le \nu \le .25\), \(1E-5 \le \sigma ^{2}_{x} \le 1E-3\), and \(c_0+\sigma ^{2}_{x}\) equals the empirical covariance at \(h=0\). In case \(I=1\), we use \(1E2 \le \xi _1 \le 5E2\). Moreover, we apply the constraint that the resulting noise VC matrix (obtained by evaluating the model at the sea distances among the involved tide gauges) should be positive definite. In doing so, we set the objective function to infinite in case the minimum eigenvalue is smaller than machine epsilon (i.e., \(2.2204E-16\)). The last constraint is a technical solution to account for the fact that our distance metric is non-Euclidean. Without this constraint, there would be no guarantee that the fitted model provides a positive definite noise VC matrix ( Hristopulos 2020, pp. 114).

2.2 Metrics used to assess the spatiotemporal model performance

Many metrics are available to assess a model’s spatial and temporal performance (e.g., Bennett et al. 2013). Here, the temporal model performance is assessed for the subregions shown in Fig. 1 by the cumulative distribution functions of both the mean absolute error (MAE) and the Kling-Gupta efficiency (KGE) metric (Gupta et al. 2009) computed for all tide gauges within the sub-area. The spatial performance is assessed using both the MAE and the spatial efficiency (SPAEF) metric (Koch et al. 2018).

Part of the differences between observation- and model-derived SMWLs are explained by time-dependent but space-independent model biases (e.g., Jahanmard et al. 2021). Indeed, for the application at hand these errors do not matter as we use the differences in model-derived SMWLs between two tide gauges. To eliminate the contribution of these errors to the model performance, we apply a time-dependent bias correction calculated from a subset of tide gauges spanning the model domain for which a full time series is available (see Fig. 1). For the same reason, we use slightly modified formulations for the KGE and SPAEF metrics. The modified formulation for the Kling-Gupta efficiency metric, referred to as mKGE, is

$$\begin{aligned} \hbox {mKGE} = 1-\sqrt{(\alpha _Q - 1)^2 + (\beta _Q - 1)^2 + \gamma _Q^2}, \end{aligned}$$
(5)

where \(\alpha _Q\) is the Pearson correlation coefficient between the observation- and model-derived SMWL time series (only used in case it is significantly different from zero at the 0.05 significance level), \(\beta _Q\) is the relative variability based on the ratio of standard deviation in model-derived and observation-derived SMWL values, and \(\gamma _Q\) is the difference between the averages of the model-derived and observation-derived SMWL time series normalized by the standard deviation of the observation-derived SMWL data. In the original formulation, \(\gamma _Q\) is the ratio of the averages. The modified spatial efficiency metric, referred to as mSPAEF, is

$$\begin{aligned} \hbox {mSPAEF} = 1-\sqrt{(\alpha - 1)^2 + (\beta - 1)^2 + (\gamma - 1)^2} \end{aligned}$$
(6)

where \(\alpha \) is the Pearson correlation coefficient between the observation- and model-derived SMWL pattern, \(\beta \) is the ratio of standard deviation in model-derived and observation-derived SMWL values, and \(\gamma \) is the histogram intersection for the histogram of the observation-derived pattern and the histogram of the model-derived pattern. In the original formulation, \(\beta \) is the ratio of the standard deviation over the mean. To suppress the impact of outliers on the computed standard deviations, we estimate these as \(1.4826 \times \) the MAD. For both the mKGE and mSPAEF metrics, the ideal value equals 1, while a value far below 0 indicates the model lacks any performance.

2.3 Re-assessing the expected quality impact of combining hydrodynamic leveling and UELN data in realizing the EVRS

To obtain a more realistic expectation of the quality impact of combining hydrodynamic leveling and UELN data in realizing the EVRS, we conducted an experiment that has a similar setup as Experiments I and II of Afrasteh et al. (2021). The experiment assumes four hydrodynamic models are available, each covering part of the European sea waters. The four domains comprise the Mediterranean Sea, the Black Sea, the Baltic Sea, and the north-east Atlantic region including the North Sea. Connections between tide gauges are established only in case both are located in the same sea basin. It is further assumed that each of the four hydrodynamic models describes the coastal SMWLs with a precision consistent with the obtained noise model. That is, we assume our noise model derived for a hydrodynamic model covering the north-east Atlantic region including the North Sea also applies to the other basins. This assumption is considered to be reasonable in case (i) the models have comparable resolutions, (ii) the underlying bathymetries have similar quality, and iii) the models are forced using the same datasets. Note that in case the sea distance between two tide gauges is larger than the maximum lag distance for which we computed the empirical covariance functions, the covariance is set to zero. The full noise VC matrix \(Q_{\widetilde{{\tiny \textrm{SMWL}}}}\) obtained this way is used to compute \(Q_{{\tiny \textrm{hl}}}\) (Eq. 2). Here, we ignored the contributions of \(Q_{{\tiny \textrm{1}}}\), \(Q_{{\tiny \textrm{2}}}\), \(Q_{{\tiny \textrm{4}}}\), and \(Q_{{\tiny \textrm{5}}}\) (see Sect. 2.1.1). Using the heuristic search method described in Afrasteh et al. (2021, Sect. 2.3), we identified the set of hydrodynamic leveling connections that provide the lowest median of the propagated height standard deviations. The benchmark solution is the spirit-leveling only solution (see Afrasteh et al. 2021, Sect. 5.1.1). To assess the impact of including noise correlations, we also repeat the experiment by setting the off-diagonal elements in \(Q_{\widetilde{{\tiny \textrm{SMWL}}}}\) to zero.

Table 1 Summary of the main characteristics of the hydrodynamic models used in this study as well as a brief of the setup applied to generate the reanalyses
Full size table

3 Data

3.1 Model-derived water level time series

In this study, three reanalysis products generated by three different hydrodynamic models have been used; the Atlantic—European North West Shelf—Ocean Physics Reanalysis (Tonani and Ascione 2021), a reanalysis obtained using the coupled two-domain DCSMv6-ZUNOv4 model (Zijl et al. 2013, 2015; Slobbe et al. 2018a), and one generated using the 3D Dutch Continental Shelf Model—Flexible Mesh (3D DCSM-FM) (Zijl et al. 2020).

The first reanalysis is produced using the Forecasting Ocean Assimilation Model 7 km Atlantic Margin model (FOAM AMM7) which uses version 3.6 of the Nucleus for European Modelling of the Ocean (NEMO) ocean model code (Madec et al. 2016) and the 3DVar NEMOVar system to assimilate observations (Mogensen et al. 2012). The data are publicly available at the Copernicus Marine Service (https://doi.org/10.48670/moi-00059). We refer to this dataset as the ‘AMM7’ dataset. Note that in this dataset all the grid points east of \(10^\circ \) E were masked (Renshaw et al. 2021).

The DCSMv6-ZUNOv4 dataset is obtained using the Dutch Continental Shelf Model version 6 (DCSMv6) and the Zuidelijk Noordzee model version 4 (ZUNOv4) in the outer and inner domain (Fig. 1 in Slobbe et al. 2018a), respectively. The DCSMv6-ZUNOv4 is a 2D model; the baroclinic forcing has been added using the method described by Slobbe et al. (2013). This model has also been used by Slobbe et al. (2018a). In this study, we redid the simulation to incorporate the updated salinity and temperature data from the earlier mentioned AMM7 dataset. Since the salinity and temperature data east of \(10^\circ \) E were masked in this dataset, we applied the same masking to the DCSMv6-ZUNOv4 derived water levels. The WAQUA software package, on which the DCSMv6-ZUNOv4 model is based, provides the opportunity to generate output at user-defined locations and epochs. In this study, we used this option to compute water levels at locations/epochs satellite radar altimeter data are available.

The 3D DCSM-FM reanalysis is obtained using the Delft3D Flexible Mesh software framework that allows for the use of unstructured grids. For this study, we have used software version 2.17.05.72090. Note that the model is still under development. One known issue in the model is an apparent strong vertical circulation between the bottom and the pycnocline in the deep ocean originating from instabilities close to the open boundaries. This results in a less accurate representation of the MWL in deep ocean waters.

The three models/reanalyses differ in many ways. A detailed discussion of this goes beyond the scope of this paper. We refer to Table 1 for a summary of the main characteristics of the models as well as a brief overview of the setup applied when generating the reanalyses. Further details can be found in the cited references. For all products, we used/generated the water levels from 1997 to 2019.

3.2 Tide gauge records

We collected about 200 high-resolution, coastal water level time series for the period 1997–2019. The time series were acquired by different national authorities in the countries Belgium, Denmark, France, Germany, Ireland, the Netherlands, Norway, Sweden, and Great Britain. All time series have been visually inspected for outliers and use the national height datum as the vertical reference for the water levels. For any meta-information regarding the national height datums, we refer to http://crs.bkg.bund.de/crseu/crs/eu-national.php.

A tide gauge record is used to generate a noise model for a particular hydrodynamic model if: (i) the tide gauge is located inside the model domain, (ii) the tide gauge is outside the tidal flat areas, and (iii) the tide gauge is east from \(10^\circ \) longitude (only in case of the AMM7 and DCSMv6-ZUNOv4 models). After excluding the tide gauge stations that do not meet these criteria, we applied a data editing step in which we excluded all records for which the median difference between the observation- and model-derived monthly MWL time series exceeded the median of the medians plus/minus three times the standard deviation (estimated as mentioned before). Figure 1 shows the tide gauges available to generate a noise model per hydrodynamic model. For the AMM7, DCSMv6-ZUNOv4, and the 3D DCSM-FM models, there are 123, 150, and, 171 stations available, respectively. As can be inferred from Fig. 2, these numbers refer to the total number of tide gauges for which we have at least one summer of water levels available.

Fig. 1
figure 1

Map showing the tide gauge locations, altimeter data (grey dots), and the subregions used when assessing the temporal model performance. Here, BNN covers the Bay of Biscay, the North Atlantic Ocean and the Norwegian Sea; BCII covers the Bristol Channel, Celtic Sea, Irish Sea and St. George’s Channel, and the Inner Seas off the West Coast of Scotland; EC stands for English Channel; KS is the Kattegat–Skagerrak Seas: NS stands for North Sea; and WS for Wadden Sea. Tide gauges plotted with a triangle symbol are measured using GNSS. The ones with a black circle around show the tide gauges used to correct the bias in the model-derived SMWL (See Sect. 2.2). All tide gauges east from the dashed black line are only available for the 3D DCSM-FM model. The red line is the 200 m depth contour separating the model domain in the deep and shelf waters (Sect. 2.1.3)

Full size image
Fig. 2
figure 2

Number of available tide gauges per sub-area over time

Full size image

The most important preprocessing step for the tide gauge data is to unify the height datums. In this study, we will refer all observed water levels to the EGG2015 quasi-geoid model (Denker 2015) in the mean-tide system (\(\zeta _{{\tiny \textrm{EGG2015}}}\)). These water levels, referred to as \(\chi _{{\tiny \textrm{EGG2015}}}\) are obtained as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \chi _{{\tiny \textrm{EGG2015}}} = \chi _{{\tiny \textrm{NHD}}} + (h^{{\tiny \textrm{HBM}}}_{{\tiny \textrm{GNSS}}} - H^{{\tiny \textrm{HBM}}}_{{\tiny \textrm{NHD}}}) - \zeta _{{\tiny \textrm{EGG2015}}} &{} \text {if GNSS is available} \\ \chi _{{\tiny \textrm{EGG2015}}} = \chi _{{\tiny \textrm{NHD}}} + h^{{\tiny \textrm{HRS}}} - \zeta _{{\tiny \textrm{EGG2015}}} &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$
(7)

where \(\chi _{{\tiny \textrm{NHD}}}\) is the water level expressed relative to the national height datum (NHD), \(h^{{\tiny \textrm{HBM}}}_{{\tiny \textrm{GNSS}}}\) is the ellipsoidal height of a nearby HBM obtained using GNSS, \(H^{{\tiny \textrm{HBM}}}_{{\tiny \textrm{NHD}}}\) is the physical height (e.g., orthometric or normal height) of the HBM, and \(h^{{\tiny \textrm{HRS}}}\) is the ellipsoidal height of the national height reference surface (HRS). Where applicable, all heights have been transformed to the mean-tide system. For the GNSS data, we used Petit and Luzum (2011, Eq. 7.14a). For the physical heights and EGG2015 height anomalies, we used the equations provided by Mäkinen and Ihde (2008). Table 2 shows per country the information about the used HRS and the source of the GNSS data. Regarding the GNSS data, we always used the most recent GNSS solution available. To get an idea about the uncertainty of the second method (i.e., second row Eq. (7)), we will analyze in Sect. 4.3 the differences between \((h^{{\tiny \textrm{HBM}}}_{{\tiny \textrm{GNSS}}} - H^{{\tiny \textrm{HBM}}}_{{\tiny \textrm{NHD}}})\) and \(h^{{\tiny \textrm{HRS}}}\).

Table 2 Height reference surface and source of GNSS data per country
Full size table

3.3 Satellite radar altimetry time series

Satellite radar altimetry data, acquired by the TOPEX/Poseidon and Jason satellite altimeters, were obtained through the Radar Altimeter Database System (RADS, http://rads.tudelft.nl/rads/rads.shtml). All data from 1997 to 2019 were combined (except the data from the interleaved orbits). Note that RADS hardly contains data in the first five km from the coast. The following geophysical and range corrections were applied (Scharroo et al. 2016): ionosphere (smoothed dual-frequency altimeter observations), dry troposphere (ECMWF), wet troposphere (radiometer, ECMWF), solid tide (Cartwright and Edden 1973; Cartwright and Taylor 1971), pole tide (Wahr 1985), load tide (FES2014), and sea state bias (CLS). We also applied the reference frame offset and ‘slope correction’ discussed by Sandwell and Smith (2014). The latter is negligibly small, except over the shelf edge where it reaches a few centimeters. Finally, we transformed the data to the GRS80 ellipsoid and subtracted the EGG2015 quasi-geoid model in the mean-tide system. All observations for which the differences compared to the DCSMv6-ZUNOv4 derived water levels exceeds the median plus/minus five times the standard deviation (estimated as mentioned before) are flagged as outliers.

3.4 Spirit leveling data

The spirit leveling data used to re-assess the expected quality impact of combining hydrodynamic leveling and UELN data in realizing the EVRS are identical to the data used by Afrasteh et al. (2021). The data include (i) the locations of all UELN height markers, (ii) a list describing which height markers are connected (except for the countries Ukraine, Russia, and Belarus), (iii) the a priori variances of the geopotential differences for the available connections, and (iv) the variances obtained by variance component estimation (except for Great Britain, Ukraine, Russia, and Belarus). As described by Afrasteh et al. (2021), we reconstructed the missing leveling connections in Ukraine, Russia, and Belarus. In all experiments conducted in this study, we used the variances that the BKG obtained by variance component estimation. For Great Britain, the a priori variances were used.

4 Results and discussion

4.1 Noise models for the model-derived coastal SMWL

The average empirical noise covariance functions for the model-derived coastal MWLs computed over one summer period (i.e., the 1-SMWLs (\(T_{{\tiny \textrm{avg}}}=1\))) are shown in Fig. 3. Each of the empirical covariance functions is computed based on 10, 000 bootstrap ensembles and for 31 lag distances, ranging between sea distances of 0 and 2100 km. Note that the maximum sea distance between two tide gauges is 3300 km. As also shown in Fig. 3, the number of pairs available per lag is except for the first and last lags typically larger than 210 (3D DCSM-FM), 165 (DCSMv6-ZUNOv4), and 100 (AMM7). For the 3D DCSM-FM model, we also computed the empirical noise covariance functions associated with the 2-SMWLs and 3-SMWLs (see Fig. 4).

Fig. 3
figure 3

The empirical noise covariance functions for the 3D DCSM-FM (top panel), DCSMv6-ZUNOv4 (middle panel) and AMM7 (bottom panel) models. The red circles indicate the ensemble means. The bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme ensemble values not considered outliers, i.e., 99.3 percent coverage. The blue lines show the fitted analytical models presented in Eq. (4) and used in Sect. 4.5 (for 3D DCSM-FM only). Note that for 3D DCSM-FM we included two J-Bessel models in the composite model, while for the other hydrodynamic models we included one. The green dots for each plot indicate the number of pairs available per lag

Full size image
Fig. 4
figure 4

The averaged empirical noise covariance functions associated with the 3D DCSM-FM derived SMWLs computed over one, two or three summers

Full size image

The empirical noise covariance functions show the following:

  • The model noise is spatially correlated. All functions show positive covariances for sea distances up to 250 km. For larger distances, they fluctuate around zero for the 3D DCSM-FM. For the DCSMv6-ZUNOv4 and AMM7 models, the covariances for larger distances are mostly negative.

  • For all models, there is a relatively large discontinuity in the empirical covariance function at zero sea distance (i.e., nugget effect). The estimated nugget effect is lowest for the 3D DCSM-FM (12.1 cm\(^2\)) and highest for the DCSMv6-ZUNOv4 (16.3 cm\(^2\)). The variance (i.e., covariance at zero sea distance) for these two models is 15.3 cm\(^2\) and 21.7 cm\(^2\), respectively. For the AMM7 model, the estimated nugget effect and variance are 15.3 cm\(^2\) and 21.5 cm\(^2\), respectively.

  • Noise covariances have higher magnitudes for the AMM7 and DCSMv6-ZUNOv4 models compared to the 3D DCSM-FM model. Moreover, the first zero-crossing occurs for larger sea distances.

  • Averaging the MWLs over two or three summer periods (i.e., the 2-SMWLs and 3-SMWLs), hardly changes the shape of the noise covariance functions. The largest change is in the variance, which decreases from 15.3 to 14.1 cm\(^2\) and 12.7 cm\(^2\), and the estimated nugget effect that decreases from 12.1 to 11.0 cm\(^2\) and 10.0 cm\(^2\), respectively.

Note that contrary to the empirical covariance functions for the DCSMv6-ZUNOv4 and AMM7 models, the one for the 3D DCSM-FM model is also based on tide gauges in the Kattegat–Skagerrak. A detailed analysis (not shown in this paper) indicates that the exclusion of the Kattegat–Skagerrak mainly affects the empirical covariances for sea distances \(>1000\) km.

Also, note that the computed error bars are likely too small. Indeed, in our approach any time correlation of the ‘noise’ is ignored. Since we also consider SMWL signals not captured by the model as noise, any such time-varying signal will result in noise realizations that are not independent. This, in turn, results in over-optimistic error bars.

The empirical covariance functions provide, albeit limited, insight into the performance of the different models in representing the coastal 1-SMWL. At the same time, we should again realize that a contribution has been introduced by the uncertainty in the vertical referencing of the tide gauges and in the applied height datum unification. This uncertainty will partly contribute to the observed nugget effect (see further Sect. 4.3), but also partly explains the observed spatial correlations (quasi-geoid errors are spatially correlated). However, this uncertainty is not expected to explain the total nugget effect. As noted by Hristopulos (2020), the nugget effect describes: (i) independent measurement errors that are due to the measurement process; (ii) purely random fluctuations endogenous to the system, and (iii) sub-resolution variability, i.e., fluctuations with characteristic length scales that are below the resolution limit of the observations. In our case, the latter also points to the fact that hydrodynamic models are not always able to resolve the local SMWL variability at specific tide gauge locations. This is not surprising when we consider that many tide gauges are located in harbors, estuaries or other locations with complex bathymetry, or near flood defense structures. Solving the local hydrodynamics requires ultra-high resolutions, not only of the model, but also of the required forcing data. Moreover, where rivers flow into the sea, the models must be extended far into the rivers.

The comparison between the three models reflects the advances in modeling. Although the 3D DCSM-FM model should be considered as a preliminary model (see Sect. 3.1), we see significant improvements over the other two models. The variance and nugget effect are lower, implying that the model is better able to represent local processes. Moreover, the spatial error covariances are also lower. In comparison with the AMM7 model, the first could have been expected given the much higher resolution of the 3D DCSM-FM. With regard to the DCSMv6-ZUNOv4 model, the improved performance can partly be attributed to the resolution (for waters outside the North Sea and Wadden Sea), the fact that DCSMv6-ZUNOv4 is a 2D model (see Sect. 3.1) and differences in forcing data (see Table 1). In Sect. 4.2, we present the results of the spatiotemporal performance assessment to further analyze these differences.

Fig. 5
figure 5

The cumulative distribution functions for both the MAE (dashed lines) and mKGE (solid lines) metrics per hydrodynamic model for all tide gauges located in the subregion

Full size image

4.2 Spatiotemporal model performance in representing the coastal 1-SMWL

For the analyses presented in this section, we used 120 tide gauges that are included in all models. The only exception is the temporal model performance assessment conducted for the KS region; the tide gauges being used there are only available for 3D DCSM-FM (see Sect. 3.1 and Fig. 1).

The metrics aimed to assess the temporal model performance are summarized in Fig. 5. Each panel shows the cumulative distribution functions for both the MAE and mKGE metrics for all tide gauges per subregion (see Fig. 1). Fig. 6 summarizes the assessment of the spatial model performance using both the MAE and mSPAEF metrics. The figures show the following:

  • The performance of each model depends on the subregion. This can be observed by comparing both the MAE and mKGE cumulative distribution functions for the different subregions shown in Fig. 5.

  • In all subregions, there are a number of tide gauges at which the models apparently lack the skills to represent the coastal 1-SMWLs (mKGE \(<< 0\)). Note that these tide gauges may differ per model. Expressed in percentages, we observe that in the worst case (subregion BNN) only 20% of all tide gauges have a mKGE \(> 0\), while in the best case (subregion KS) this percentage is about 80%.

  • In BNN and WS, the 3D DCSM-FM model clearly outperforms the other models. In BCII, the AMM7 model shows the best performance. In the NS and EC, the performance level is comparable for the different models.

  • The best performance for the 3D DCSM-FM model is obtained in the KS region.

  • The spatial performance assessment shows strong variability over time. In terms of MAE, we observe for all models an improved performance between 2004–2011. The largest improvement is observed for 3D DCSM-FM (from 4.25 cm in 1998 to \(\sim 3\) cm in 2008). For all models, the performance degrades toward the end of the timespan considered in this study. In terms of the mSPAEF, this behavior is also observed, though it is less pronounced.

  • Both in terms of MAE and mSPAEF, the 3D DCSM-FM model outperforms the other models over almost the entire timespan.

Fig. 6
figure 6

The MAE (top panel) and the mSPAEF (bottom panel) metrics used to assess the spatial model performance for each of the three considered hydrodynamic models

Full size image

It should be noted that a poor temporal performance in terms of MAE and mKGE may be caused by biases in the observation- and/or model-derived 1-SMWL time series. Indeed, such a bias would show up one-to-one in the MAE values and would affect \(\gamma _Q\) (see Eq. 5). A detailed analysis, not shown here, indeed shows that \(\gamma _Q\) has the largest variability and is mainly causing the lower mKGE values observed in Fig. 5.

Before interpreting the temporal performance, it is important to remember that although the size of the model domains suggests otherwise, the models may have been primarily developed for specific waters such as the Dutch waters in case of the 3D DCSM-FM and the DCSMv6-ZUNOv4 models. The importance of a good model performance elsewhere is proportional to the extent to which it influences the performance in these target waters. Both target application(s) and area largely explain the differences in the design of the models and the forcing data used in the reanalyses (see Table 1). These in turn explain the differences in performance in the different subregions. With this in mind, the higher performance of the 3D DCSM-FM in the WS is not a surprise; this model has a much higher spatial resolution (3D DCSM-FM vs. AMM7) and it is a 3D model (3D DCSM-FM vs. DCSMv6-ZUNOv4). Likewise for the higher performance of AMM7 in the BCII. Contrary to 3D DCSM-FM and DCSMv6-ZUNOv4, the AMM7 reanalysis is a British product. It goes beyond the scope of this paper to fully explain the observed performances. The take-home message from the results is that if one would have the resources to combine the good elements (such as the bathymetry in certain areas, schematization, and parametrization) of all models into a new model, further improvements are possible. At the same time, one has to keep in mind that for the application at hand it is not required to have a good performance at all tide gauge locations. Afrasteh et al. (2021) showed that adding already a small number of hydrodynamic leveling connections to the UELN dataset has a significant impact on the quality of the EVRS. Our results show that in each subregions at least some tide gauges are available where the model has the necessary skills.

The spatial performance is somewhat difficult to explain. This mainly concerns the deterioration observed from the year 2011 onward. The improvement in the first period is in line with the improvement in the quality of the forcing data / open boundary conditions caused by the increased amount and quality of available observations to generate them (e.g., Hersbach et al. 2020). The deteriorated performance starting in 2011 does not fit into this picture. We would like to emphasize that time variations in the distribution of the number of tide gauges over the various subregions (Fig. 2) are not the explanation. When we repeat the analysis using only all tide gauges for which a full time series is available, we see the same pattern. Possible explanations for the deteriorated performance starting in 2011 include: (i) errors in the forcing data/boundary conditions, and (ii) model errors (e.g., missing large-scale, slow (multi-decadal) dynamic processes in the model physics). Regarding the latter, remember that all three models were originally developed to make short-term operational forecasts.

4.3 Assessment of the contribution of errors in the vertical referencing of the tide gauges to the observation-derived SMWLs

At 45 tide gauges (see Fig. 1), we computed the differences between \((h^{{\tiny \textrm{HBM}}}_{{\tiny \textrm{GNSS}}} - H^{{\tiny \textrm{HBM}}}_{{\tiny \textrm{NHD}}})\) and \(h^{{\tiny \textrm{HRS}}}\) (see Eq. 7). A map and histogram of the differences are shown in Fig. 7. The results show the following:

  • The median of the differences is 0.0 cm, while the standard deviation (estimated as before) is 2.7 cm.

  • The French tide gauges Concarneau and L’Herbaudière behave as outliers (absolute difference \(>5\) cm). For Concarneau, the last leveling seems to be conducted in April 2003 SONEL Leveling (2007), while GNSS was installed in November 2007 SONEL GPS (2003). The distance between the GNSS antenna and the tide gauge is about 1 km. We lack any details about how and when the GNSS has been connected to the TGBM. L’Herbaudière is quite a new station (data since June 2014). No further meta-information for this tide gauge is available.

  • We do neither observe much regional variability, nor strong spatial patterns.

Assuming that GNSS provides heights with an uncertainty between 0.5–1 cm and that we have connected both the tide gauge as well as the GNSS to the TGBM using precise leveling with an uncertainty of just a few mm, the expected uncertainty of the ellipsoidal height of the SMWL is about 1 cm. If this height is obtained by adding \(h^{{\tiny \textrm{HRS}}}\), the uncertainty is between 1 and 2 cm. This gives an expected uncertainty of the differences between 1.4 and 2.2 cm. The observed standard deviation of 2.7 cm is slightly larger. Possible explanations include: (i) vertical land motion between the time GNSS data were acquired and the reference epoch of \(h^{{\tiny \textrm{HRS}}}\) (typically, this enters via the corrector surface/innovation function added to the gravimetric (quasi-)geoid), and (ii) a lower quality of the \(h^{{\tiny \textrm{HRS}}}\) along the coast (many countries including the Netherlands suffer from a gap in gravity data along the coast (Farahani et al. 2017)).

The estimated uncertainty (standard deviation) of the EGG2015 quasi-geoid is 1.9 cm (Denker et al. 2018). This makes the expected uncertainty of the SMWLs expressed relative to EGG2015 2.1 cm in case GNSS is exploited and between 2.1 and 2.8 cm otherwise. Consequently, a significant part of the observed variance (see Sect. 4.1) may be explained by uncertainties associated with the vertical referencing of the tide gauges/SMWLs. For example, in case of the 3D DCSM-FM the contribution is between approximately \(30\%\) and \(50\%\) for the 1-SMWLs. In terms of nugget effect, the contribution is between 35 and 65%. Indeed, part of these errors will be correlated. Denker et al. (2018) refer to a covariance function being derived for the computed height anomalies, which has a half-length of about 40 km and zeros at about 80, 220, 370 km, and so on. They stated that “over longer distances, e.g., beyond the second and third zero of the covariance function, the height anomalies are nearly uncorrelated.” Since we lack the full VC matrix of the EGG2015, we cannot assess/remove the contribution of EGG2015 to the observed error correlations (remember that we use a different distance metric). In the remainder, we will remove a contribution of \(2.15^2\) (\(1.9^2+1^2\)) from the observed variance. Indeed, the vertical referencing to EGG2015 is only required to obtain a noise model. It is not required when computing hydrodynamic leveling connections.

Fig. 7
figure 7

Map and histogram of the differences between \((h^{{\tiny \textrm{HBM}}}_{{\tiny \textrm{GNSS}}} - H^{{\tiny \textrm{HBM}}}_{{\tiny \textrm{NHD}}})\) and \(h^{{\tiny \textrm{HRS}}}\) for tide gauges equipped with GNSS receivers

Full size image

4.4 The coastal water noise model versus the altimeter-derived deep and shelf water noise models

The empirical noise covariance functions for the DCSMv6-ZUNOv4 derived deep and shallow water 22-SMWLs are shown in Fig. 8. As a reference, we included the average empirical noise covariance function for the DCSMv6-ZUNOv4 derived coastal 1-SMWLs shown in Fig. 3 (middle panel). Note that 3856 points are in deep water, whereas 2294 points are in the shelf waters. Hence, for both empirical covariance functions the number of pairs available per lag is always larger than 1000. Also note that \(95\%\) of all altimeter time series comprise more than 345 data points. The empirical noise covariance functions show the following:

  • The empirical noise covariance function for the deep waters is significantly different from the one for the shelf waters. The former shows larger covariance values for both short and long sea distances. The latter shows much less fluctuations. It does show, though, some small, large-scale pattern with positive covariances up to a lag distance of about 1000 km and negative covariances for larger distances.

  • Both functions show a small jump at \(\sim 190\) km (shelf waters) and \(\sim 220\) km (deep waters). A detailed analysis revealed that up to this distance the covariances are mainly calculated in the along-track direction. From these distances, the covariances are partly determined by pairs in the across-track direction.

  • Both functions also differ significantly from the empirical noise covariance function of the coastal 1-SMWL. Contrary to the latter, there seems to be no nugget effect. The pattern over short distances is also different.

Fig. 8
figure 8

The empirical noise covariance function for deep, shelf waters computed using differences between satellite altimetry data and DCSMv6-ZUNOv4 averaged over period 1997–2019. As a reference, we included the empirical noise covariance function for the coastal 1-SMWL computed for DCSMv6-ZUNOv4 (Fig. 3, middle panel)

Full size image

Some caution is required in interpreting the above results. The averaging period is different (1–3 summers for the coastal waters and 22 summers for the deep and shelf waters). Furthermore, this comparison has only been conducted for the DCSMv6-ZUNOv4 model. Since this is a 2D model, we cannot expect to get the best performance in deep waters where baroclinic processes dominate the SMWL variability (Slobbe et al. 2013). At the same time, the results do not contradict expectations based on oceanographic arguments; along the coast, processes have a higher variability compared to the shelf and in deep water. This may have an impact on the empirical noise covariance function, notably at short spatial scales. The results of this experiment are a first confirmation that this is indeed the case. It shows that a noise model for the coastal SMWL cannot be calculated from altimeter data in the shelf and deep waters. Whether or not a dedicated coastal altimetry data product can help in this respect remains to be studied.

4.5 The expected quality impact of combining hydrodynamic leveling and UELN data on the EVRF revisited

The experiment described in Sect. 2.3 is conducted using the best-performing 3D DCSM-FM fitted noise model for the coastal 1-SMWLs and 3-SMWLs. Moreover, we quantified the effect of ignoring error covariances for the SMWLs, i.e., using the diagonal elements of the noise VC matrix only. The results, summarized in Table 3 and Fig. 9, show:

  • Adding all 182 connections reduces the median propagated standard deviation of all adjusted heights from 13.8 to 10.6 mm (one summer averaging period) and to 10.3 mm (three summers averaging period). This corresponds to an improvement of \(23\%\) and \(25\%\), respectively.

  • Ignoring the noise covariances leads to an overestimation of the improvement by \(7\%\) (one summer averaging period) and \(8\%\) (three summers averaging period), i.e., by using only the diagonal elements of the full noise VC matrix the obtained improvements are \(30\%\) and \(33\%\), respectively.

  • The improvement differs strongly per country; values range from 1 (Slovakia) to \(>50\%\) (Great Britain).

  • Including noise correlations leads to a higher overall improvement for the first 9 (three summers averaging period) or 10 connections (one summer averaging period). For larger numbers of connections, the overall improvement is too optimistic if we ignore the noise correlations.

Table 3 The median propagated standard deviation (SD) of the adjusted heights in millimeters (per country and in total)
Full size table
Fig. 9
figure 9

Overall quality improvement of the EVRF (expressed as the percentage with which the median propagated height standard deviation decreases compared to the spirit-leveling only solution) obtained by adding hydrodynamic leveling data as a function of the number of added connections. The solid lines correspond to scenarios in which the full noise VC matrix for the SMWL was used computed using the 3D DCSM-FM noise models associated with the coastal 1-SMWLs and 3-SMWLs. The dashed lines correspond to scenarios in which the covariances were ignored

Full size image

Ignoring the noise covariances, the precision with which we can derive the 1-SMWL differences is 4.6 cm in terms of standard deviation. This is close to the 5 cm that Afrasteh et al. (2021) used in Experiment II, which has the same setup as the experiment conducted in this paper. The results obtained here are therefore almost identical (\(30\%\) vs. \(29\%\)) to the previously published results. What is new is the insight we get when comparing the results obtained with and without including the noise covariances. Indeed, ignoring the noise covariances results in a too optimistic quality impact (i.e., overall improvement is overestimated up to \(8\%\)). Only for the first few connections that we add, the overall improvement is larger. Apparently there are two conflicting effects. The first has to do with the fact that we use model-derived SMWL differences in hydrodynamic leveling. As noise in the SMWLs is correlated, some of the errors will be eliminated once we calculate the differences. This has a positive impact on the overall improvement. On the other hand, correlations among the hydrodynamic leveling connections result in less ‘information’ being added when the number of added connections increases. This is the second effect.

The choice of the composite analytical model fitted through the empirical covariance function has limited impact on the total quality impact. This follows from an experiment in which we used a composite analytical model defined by the superposition of the nugget effect and Cardinal Sine (see Hristopulos 2020, Sect. 4.2.2) models (not shown). Similar to the J-Bessel model, the Cardinal Sine model admits negative covariances. Compared to the use of the J-Bessel model, the total quality impact increases from \(23\%\) to \(25\%\) for the coastal 1-SMWLs. The quality of the fit through the empirical covariance function, however, is slightly lower.

Note that in presenting and discussing these results, we focused on the impact of our developed noise model. For a discussion of these results in a broader sense, we refer to Afrasteh et al. (2021).

5 Summary and conclusion

A recent study by Afrasteh et al. (2021) showed that combining model-based hydrodynamic leveling data with data of the Unified European Leveling Network (UELN) may improve the quality of the European Vertical Reference Frame (EVRF) significantly. Assuming a variance of 4.5 cm\(^2\) for the model-derived SMWL differences (corresponding to a 3 cm standard deviation for the hydrodynamic leveling connections), the observed reduction in the median standard deviation of the adjusted heights was \(38\%\). In case the variance is 12.5 cm\(^2\) (corresponding to a 5 cm standard deviation for the hydrodynamic leveling connections), this improvement is still \(29\%\). Although promising, evidence so far has been lacking that hydrodynamic models can indeed represent the SMWL differences with this precision. In addition, the assumption of uncorrelated noise is not realistic. This study builds on our previous work by developing and analyzing a noise model for the model-derived coastal SMWLs and using it to obtain a more realistic quality impact of combining hydrodynamic leveling and UELN data in realizing the European Vertical Reference System (EVRS).

To develop the noise model, we used an empirical approach based on calculating an average empirical covariance function from the differences between tide gauge- and model-derived SMWLs. Three models have been used: the 3D DCSM-FM model, the DCSMv6-ZUNOv4 model and the AMM7 model. A reanalysis was performed for the first two models over the period 1997–2019. For AMM7, we used the output for the same timespan from a publicly available reanalysis. Given the differences in coverage, we had 171, 150, and 123 tide gauges available for 3D DCSM-FM, DCSMv6-ZUNOv4, and AMM7, respectively. In order to have multiple realizations of the noise, an averaging period of 1 summer was chosen. The impact of an averaging period of 2 and 3 summers was examined for the 3D DCSM-FM model.

First, we presented the empirical noise covariance functions for the different models. The functions show that the noise is indeed spatially correlated, although the correlations are different per model. Furthermore, they all show a relatively large discontinuity at the origin (i.e., nugget effect). This points to random errors in the observation- and model-derived SMWLs and signals at short spatial scales that cannot be resolved from the data or by the hydrodynamic model. The nugget effect is lowest for the 3D DCSM-FM (12.1 cm\(^2\)) and highest for the DCSMv6-ZUNOv4 (16.3 cm\(^2\)). The variance values for these models are 15.3 cm\(^2\) and 21.7 cm\(^2\), respectively. The empirical noise covariance functions obtained from an averaging period of two and three years do not really differ from those associated with an averaging period of one year. The biggest change is in the variance and nugget effect; the variance drops to 14.1 cm\(^2\) and 12.7 cm\(^2\), and the nugget effect to 11.0 cm\(^2\) and 10.0 cm\(^2\).

Second, we assessed both the spatial and temporal performance with which the considered hydrodynamic models are able to represent the coastal 1-SMWL. In both assessments, two different metrics have been used. The results show that for all three models, the performance varies over space and time. Regarding temporal performance, there is no model that performs best everywhere; different models score better in different subregions. In some subregions, we see no difference in performance. Also in all subregions there are more or less tide gauges where models do not show good agreement with the observations. In most cases, the poor agreement is caused by biases in the observation- and/or model-derived 1-year SMWL time series. Regarding spatial performance, all models showed an improved performance in the period 2004–2011. Here, we saw the best performance for 3D DCSM-FM over almost the entire period. It was beyond the scope of this study to explain the differences in performance. In any case, it is not important for hydrodynamic leveling that the models always and everywhere have a good performance; we can omit tide gauges/time periods where/in which the model has poorer performance. At the same time, the fact that the models have a different performance in different regions indicates that further improvements are possible. That is, one could combine the good elements of all models in one, new model.

Errors in the vertical referencing of the tide gauges contribute to the obtained noise covariance functions. In this study, we looked at their contribution to the variance. An analysis of the differences between the ellipsoidal heights of the local height reference surface (HRS) obtained from GNSS/leveling and the HRS that is officially used results in an uncertainty of 2.7 cm in terms of standard deviation. This is slightly higher than the expected uncertainty (between 1.4 and 2.2 cm). Possible explanations are: (i) vertical land motion between the time GNSS data were acquired and the reference epoch of the HRS, and (ii) a lower quality of the HRS along the coast. Given the 1.9 cm uncertainty of EGG2015, we estimate that for 3D DCSM-FM ultimately between 30 and \(50\%\) (lower for the other models) of the variance is explained by the uncertainty in the vertical referencing of the tide gauge/SMWLs.

Next, we presented the empirical noise covariance functions for the deep and shelf waters in the target area calculated from TOPEX/Jason satellite altimetry data. As only the WAQUA software package, on which the DCSMv6-ZUNOv4 model is based, provided the opportunity to generate output at user-defined locations and epochs, the deep and shelf water empirical covariance functions are only calculated for this model. Both functions are not only significantly different from each other, but also from the function computed for coastal SMWLs. This is in line with oceanographic expectations, namely that the dynamics along the coast are more complex than in deep and shelf waters. Hence, altimeter data have limited value in obtaining a noise model for the coastal SMWLs. It remains to be studied, however, whether a dedicated coastal altimetry data product is useful in this respect.

Finally, we looked at the impact of the improved noise model on the quality of the EVRF. We used the noise model obtained for the 3D DCSM-FM assuming that a comparable performance can also be obtained in other European waters. This assumption is considered to be reasonable in case (i) the models have comparable resolutions, (ii) the underlying bathymetries have similar quality, and (iii) the models are forced using the same datasets. The setup of the experiment was identical to Experiments I and II of Afrasteh et al. (2021), except for the assumption made in that study that the noise VC matrix of the model-derived MWLs was diagonal. The results show that using 1-SMWLs, the expected improvement in the median standard deviation of the adjusted heights is \(23\%\). In the case of averaging over three summers, the improvement is \(25\%\). Ignoring error correlations results in an overestimation of the total quality impact by \(7\%\) (one summer averaging period) and \(8\%\) (three summers averaging period).

Developing a noise model for model-derived coastal SMWLs is indeed challenging. Compared to other parts of the world, European waters contain many tide gauges. At the same time, many of these tide gauges are not deployed to build long and stable time series; they include gaps and/or sudden jumps and sometimes exhibit spurious signals in the low frequencies that are probably best explained as measuring (or measurement correction) errors. In many cases, we also lack information about the vertical referencing and its control over time. This is crucial information, given that some tide gauges are located in areas with vertical ground movement. Ideally, one should at least correct for the latter. However, since in most cases the necessary information is missing, this correction is often neglected. In any case, we can expect that almost everywhere the model errors are significantly larger than the vertical land motion. A significant contributor to the computed empirical noise covariance functions are errors in the vertical referencing of the tide gauges/SMWLs. Removing this requires at least a full noise VC matrix for the (quasi-)geoid model used. If all the tide gauges are properly connected to a nearby UELN height marker, an iterative approach is possible in which the vertical referencing is improved based on new realizations of the EVRS. However, given the small impact of taking the noise covariances into account as demonstrated in this study, the question is whether it is worth doing so.

In any case, the results of this research encourage further development of model-based hydrodynamic leveling. Indeed, we have shown that today’s hydrodynamic models have the accuracy to improve the quality of the EVRF up to \(25\%\). Our future work will be to demonstrate the quality impact of including model-based hydrodynamic leveling data in realizing the EVRS using real data.