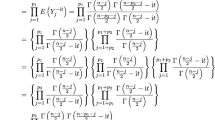Bayesian multi-way balanced nested MANOVA models with random effects and a large number of the main factor levels

Abstract

This article considers the balanced nested multi-way multivariate analysis of variance (MANOVA) models with random effects and a large number of main factor levels under certain prior assumptions. Two different parametrizations for the MANOVA models with random effects and the corresponding explicit asymptotics are established. The asymptotic approximations are then compared with those obtained from the classical large-sample approximation and Markov chain Monte Carlo method via a balanced nested two-way MANOVA model with random effects. Simulation results demonstrate that our approach is superior to the classical approximation method on estimating the posterior standard deviations of variance component parameters.

Appendix

Proof of Lemma 1:

Recall that the conditional mean function ${\varvec{g}}_{a}=(E[T'|{\varvec{\phi }},{\varvec{y}}],E[R_{0v}'|T,{\varvec{y}}],E[R_{1v}'|T,{\varvec{y}}],E[R_{2v}'|T,{\varvec{\beta }},{\varvec{y}}], E[{\varvec{\beta }}'|T,R_{2v},{\varvec{y}}])'.$ From the Eq. (4), we obtain

$$\begin{aligned} \begin{aligned} {\varvec{v}}_{ij}|{\varvec{v}}_i,{\varvec{\phi }},{\varvec{y}}&{\mathop {\sim }\limits ^{\text {ind}}}N_p({W_{1}^*}^{-1}[P_{0}\bar{\varvec{y}}_{ij}+Q_{1}{\varvec{v}}_{i}],{W_{1}^*}^{-1}),\ j=1,\ldots ,b,\ i=1,\ldots ,a,\\ {\varvec{v}}_{i}|{\varvec{\phi }},{\varvec{y}}&{\mathop {\sim }\limits ^{\text {ind}}}N_p({W_{2}^*}^{-1}[P_{1}\bar{\varvec{y}}_{i}+Q_{2}{\varvec{\beta }}],{W_{2}^*}^{-1}),\ i=1,\ldots ,a, \end{aligned} \end{aligned}$$

where $P_0=cQ_0, P_1=bcQ_1{W_{1}^*}^{-1}Q_0$, $Q_k=R^{-1}_k,k=0,1,2,$ and $W_k^*=P_{k-1}+Q_k$, $k=1,2$. Note that, for example, $T_0=\frac{1}{abc}\sum _{i,j,k}({\varvec{v}}_{ij}-{\varvec{y}}_{ijk})({\varvec{v}}_{ij}-{\varvec{y}}_{ijk})' =\frac{1}{ab}\sum _{i,j}({\varvec{v}}_{ij}-\bar{\varvec{y}}_{ij})({\varvec{v}}_{ij}-\bar{\varvec{y}}_{ij})'+S_0$, $E[T_{0}|{\varvec{\phi }},{\varvec{y}}]=E[E[T_{0}|\{{\varvec{v}}_{i}\text {'s}\},{\varvec{\phi }},{\varvec{y}}]|{\varvec{\phi }},{\varvec{y}}]$, and

$$\begin{aligned} \begin{aligned} E[T_{0}|\{{\varvec{v}}_{i}\text {'s}\},{\varvec{\phi }},{\varvec{y}}]=&\frac{1}{ab}\sum _{i,j}\big [\text {Cov}[({\varvec{v}}_{ij}-\bar{\varvec{y}}_{ij})|{\varvec{v}}_{i},{\varvec{\phi }},{\varvec{y}}]\\&+E[({\varvec{v}}_{ij}-\bar{\varvec{y}}_{ij})|{\varvec{v}}_{i},{\varvec{\phi }},{\varvec{y}}]E[({\varvec{v}}_{ij}-\bar{\varvec{y}}_{ij})'|{\varvec{v}}_{i},{\varvec{\phi }},{\varvec{y}}]\big ]+S_0\\ =&{W_1^*}^{-1}+{W_1^*}^{-1}Q_1\big [\frac{1}{ab}\sum _{i,j}({\varvec{v}}_{i}-\bar{\varvec{y}}_{ij})({\varvec{v}}_{i}-\bar{\varvec{y}}_{ij})'\big ]Q_1{W_1^*}^{-1}+S_0\\ =&{W_1^*}^{-1}+{W_1^*}^{-1}Q_1[S_1+\frac{1}{a}\sum _{i}({\varvec{v}}_{i}-\bar{\varvec{y}}_{i})({\varvec{v}}_{i}-\bar{\varvec{y}}_{i})']Q_1{W_1^*}^{-1}+S_0.\\ \end{aligned} \end{aligned}$$

Then, under the settings in Lemma 1, the components of ${\varvec{g}}_a$ can be calculated through the following conditional mean functions.

$$\begin{aligned} \begin{aligned} E[T_{0}|{\varvec{\phi }},{\varvec{y}}]&={W_1^*}^{-1}+{W_1^*}^{-1}Q_1[S_1+E[T_{20}|{\varvec{\phi }},{\varvec{y}}]]Q_1{W_1^*}^{-1}+S_0,\\ E[T_{1}|{\varvec{\phi }},{\varvec{y}}]&={W_1^*}^{-1}+{W_1^*}^{-1}P_0[S_1+E[T_{20}|{\varvec{\phi }},{\varvec{y}}]]P_0{W_1^*}^{-1},\\ E[T_{2}|{\varvec{\phi }},{\varvec{y}}]&={W_2^*}^{-1}+{W_2^*}^{-1}[P_1S_2P_1+Q_2({\varvec{\beta }}-\bar{\varvec{y}})({\varvec{\beta }}-\bar{\varvec{y}})'Q_2]{W_2^*}^{-1},\\ E[T_{3}|{\varvec{\phi }},{\varvec{y}}]&={W_2^*}^{-1}[P_1\bar{\varvec{y}}+Q_2{\varvec{\beta }}],\\ E[R_k|T,{\varvec{y}}]&=T_k,\ k=0,1,\ E[R_2|T,{\varvec{\beta }},{\varvec{y}}]=T_2,\ E[{\varvec{\beta }}|T,R_2,{\varvec{y}}]=T_3, \end{aligned}\nonumber \\ \end{aligned}$$

(A.1)

where $T_{20}=\frac{1}{a}\sum _{i}({\varvec{v}}_i-\bar{\varvec{y}}_i)({\varvec{v}}_i-\bar{\varvec{y}}_i)'$ and $E[T_{20}|{\varvec{\phi }},{\varvec{y}}]={W_2^*}^{-1}+{W_2^*}^{-1}Q_2[S_2+({\varvec{\beta }}-\bar{\varvec{y}})({\varvec{\beta }}-\bar{\varvec{y}})']Q_2{W_2^*}^{-1}$. Some algebra implies (8) provided that $b, c>1$ and $\varvec{\mu }_{R_{k}}>0,\ k=0,1,2$. $\square$

Proof of Theorem 1:

To prove the asymptotic normality of the posterior distribution for $\varTheta _a$, it suffices, by the Proposition 1, to verify (i) the first part of the assumption (A1), the existence of fixed points of ${\varvec{g}}_a$ and ${\varvec{g}}$, and ${\varvec{\mu }}_{\varTheta _{a}}{\mathop {\longrightarrow }\limits ^{a\rightarrow \infty }} {\varvec{\mu }}_{\varTheta }$; (ii) the second part of the assumption (A1), $\varSigma _D>0$; (iii) the assumption (A2), the asymptotic normality for each conditional; (iv) $\varSigma >0$; (v) the regularity condition(s), ${\varvec{g}}_a$ is continuously differentiable and $\dot{{\varvec{g}}}_a({\varvec{t}}){\mathop {\longrightarrow }\limits ^{a\rightarrow \infty }}\dot{{\varvec{g}}}({\varvec{t}})$ (in the neighborhood of ${\varvec{\mu }}_{\varTheta _{a}}$). Note that we have shown that (i) holds in Lemma 1, and (iv) $\varSigma >0$ implies (ii) holds.

As to the (v), the regularity condition(s), by Eq. (A.1), it is sufficient to check if each component of ${\varvec{g}}_a$, or simply ${\varvec{g}}_{1a}=E[T|{\varvec{\phi }},{\varvec{y}}]$, is continuously differentiable and all its partial derivatives converge since $\dot{{\varvec{g}}}_{2a}$,...,$\dot{{\varvec{g}}}_{5a}$ are just some constant vectors. From Eq. (A.1) or, more concisely, Eq. (A.4), the conditional mean functions of ${T_k}'s$ can be expressed as a linear combinations of the products of some positive definite matrices, inverses of positive definite matrices, or vectors where each of which matrix or vector is a linear combinations of $\{R_k's,{\varvec{\beta }}\}$. It is easy to see that if all the such matrices or vectors are continuously differentiable and their partial derivatives converge. Hence the conditions hold.

Recall that $\varTheta _a=(\varTheta '_{1a},\ldots ,\varTheta '_{5a})'=(T',R_{0v}',R_{1v}',R_{2v}',{\varvec{\beta }}')'$, $R=(R'_{0v},R'_{1v},R'_{2v})'$, and ${\varvec{\phi }}=(R',{\varvec{\beta }}')'$. We then break the proof into two parts: (a) prove the asymptotic normality for each conditional, which is the (iii); (b) simplify $\varSigma$ and derive the relationship among $\varSigma _T$, $\varSigma _{T{\varvec{\phi }}}$, and $\varSigma _{\varvec{\phi }}$; (c) calculate $\varSigma _{\varvec{\phi }}$ explicitly. We defer the proof of (iv) $\varSigma >0$ to Theorem 3.

(a) The conditionally asymptotic normality of $\varTheta _{1a}$ (or T), $T=(T'_{0v},T'_{1v},T'_{2v},T'_3)'$, $T_{rv}=\text {vech}(T_r),\ r=0,1,2$:

Let ${\varvec{a}}=({\varvec{a}}'_0,{\varvec{a}}'_1,{\varvec{a}}'_2,{\varvec{a}}'_{3})'$, where ${\varvec{a}}_0, {\varvec{a}}_1, {\varvec{a}}_2$ are $p_1$-dimensional column vectors and ${\varvec{a}}_3$ is a p-dimensional column vector. $p_1=\frac{p(p+1)}{2}$. Then, by the Eq. (6),

$$\begin{aligned} {\varvec{a}}'T= & {} \frac{1}{a}\sum _{i=1}^{a}\bigg \{\frac{1}{bc}\sum _{j,k} {\varvec{a}}'_0\text {vech}[({\varvec{v}}_{ij}-\bar{\varvec{y}}_{ij})({\varvec{v}}_{ij}-\bar{\varvec{y}}_{ij})']\\&+\frac{1}{b}\sum _{j,k} {\varvec{a}}'_1\text {vech}[({\varvec{v}}_{ij}-{\varvec{v}}_{i})({\varvec{v}}_{ij}-{\varvec{v}}_{i})']\\&+{\varvec{a}}'_{2}\text {vech}[({\varvec{v}}_{i}-\bar{\varvec{y}})({\varvec{v}}_{i}-\bar{\varvec{y}})']+{\varvec{a}}'_{3}{\varvec{v}}_{i}\bigg \}+{\varvec{a}}'_0S_{0v} \\= & {} \frac{1}{a}\sum _{{i}=1}^{a}H_{i}+\frac{1}{ab}\sum _{i,j}{\varvec{a}}'_0\text {vech}[\bar{\varvec{y}}_{ij}\bar{\varvec{y}}'_{ij}]+ {\varvec{a}}'_{2}\text {vech}[\bar{\varvec{y}}\bar{\varvec{y}}']+{\varvec{a}}'_0S_{0v}, \end{aligned}$$

where $H_{i}$ can be expressed as $(\mathbf {v}_{i}' B_T\mathbf {v}_{i}+\mathbf {v}_{i}'\mathbf {b}_{i})$, a combination of a quadratic form and a linear combination of $\mathbf {v}_{i}=({\varvec{v}}'_{i1},\ldots ,{\varvec{v}}'_{ib},{\varvec{v}}'_{i})',\ i=1,\ldots ,a$, and all the coefficients of function of $\mathbf {v}_{i}$, $H_{i}$, are uniformly bounded. Moreover, from the Eq. (4), it is easily to see that $\mathbf {v}_{i}$’s given ${\varvec{\phi }}$ and ${\varvec{y}}$ are conditionally independent, normally distributed, i.e.

$$\begin{aligned} \begin{aligned} \mathbf {v}_{i}|{\varvec{\phi }},{\varvec{y}}{\mathop {\sim }\limits ^{\text {ind}}}N_{p(b+1)}(Q^{-1}_{\mathbf {v}_{i}}E_{\mathbf {v}_{i}},Q^{-1}_{\mathbf {v}_{i}}),\ \end{aligned} \end{aligned}$$

where $Q_{\mathbf {v}_{i}}=\begin{pmatrix}I_b\otimes (P_0+Q_1)&{} -\mathbf {1}_b\otimes Q_1\\ newmathbf{1}'_b\otimes Q_1&{} P_1+Q_2\end{pmatrix}$, $E_{\mathbf {v}_{i}}=(\bar{\varvec{y}}'_{i1}P_0,\ldots ,\bar{\varvec{y}}'_{ib}P_0,{\varvec{\beta }}'Q_2)'$, and $\mathbf {1}_b$ is a b-dimensional column vector of all ones. Hence, we have $E|H_{i}-E(H_{i})|^{2+\delta }$ = O(1) for some $\delta > 0$. Thus, the asymptotic normality of T given ${\varvec{\phi }}$ and ${\varvec{y}}$ as a tends to infinity follows by the Liapounov criterion and the Cramér-Wold device.

The conditionally asymptotic normality of $\varTheta _{ia},\ i=2,\ldots ,5$ ($R_{0v}$,$R_{1v}$,$R_{2v}$,$\varvec{\beta }$):

Recall that each conditional distribution of $R_k$ follows an inverse Wishart distribution and the conditional distribution of ${\varvec{\beta }}$ is normally distributed. We then use the following lemma to derive the conditionally asymptotic normality of each $R_{kv}$.

Lemma A.1

Suppose $R\sim \mathrm{IW}_p(m_n,\varPsi _n)$, $\frac{m_n}{n}{\mathop {\longrightarrow }\limits ^{n\rightarrow \infty }} m>0$, and $\frac{\varPsi _n}{n}{\mathop {\longrightarrow }\limits ^{n\rightarrow \infty }} \varPsi \ge 0$. Then $\sqrt{n}(R_{v}-E(R_{v})){\mathop {\longrightarrow }\limits ^{\mathcal {L}}}N_{p_1}(\mathbf {0},\frac{2}{m^3}{{\varPsi }^{\otimes 2h}}).$

Note that, from Jelenkowska (1995) or Press (2005), we have

$$\begin{aligned} \begin{aligned} \lim _{{n}\rightarrow \infty }n\mathrm{{Cov}}(R_v)&=\lim _{{n}\rightarrow \infty }n\mathrm{{Cov}}(L_p\mathrm{{vec}}(R))\\&= \lim _{{n}\rightarrow \infty }nL_p\frac{(m_n-p+1)I_{p^2}+(m_n-p-1)K_p}{(m_n-p)(m_n-p-1)^2(m_n-p-3)}{{\varPsi _n}^{\otimes 2}}L'_p\\&= L_p\frac{2}{m^3}N_p{{\varPsi }^{\otimes 2}}L'_p=\frac{2}{m^3}L_pN_p{{\varPsi }^{\otimes 2}}N_pL'_p=\frac{2}{m^3}{{\varPsi }^{\otimes 2h}}. \end{aligned} \end{aligned}$$

The proof of Lemma A.1 is similar to that shown in Anderson (2003) for the Wishart distribution case and hence is omitted.

Thus, the asymptotic normalities for conditional $R_{0v}$, $R_{1v}$, $R_{2v}$, and ${\varvec{\beta }}$ are as follows.

$$\begin{aligned}&\sqrt{a}(R_{0v}-E(R_{0v}|T,{\varvec{y}})|_{\varTheta _a={\varvec{\mu }}_{\varTheta _a}}){\mathop {\longrightarrow }\limits ^{\mathcal {L}}}N_{p_1}(\mathbf {0},\frac{2}{bc}{{{\varvec{\mu }}_{T_0}}^{\otimes 2h}}),\nonumber \\&\sqrt{a}(R_{1v}-E(R_{1v}|T,{\varvec{y}})|_{\varTheta _a={\varvec{\mu }}_{\varTheta _a}}){\mathop {\longrightarrow }\limits ^{\mathcal {L}}}N_{p_1}(\mathbf {0},\frac{2}{b}{{{\varvec{\mu }}_{T_1}}^{\otimes 2h}}),\nonumber \\&\sqrt{a}(R_{2v}-E(R_{2v}|T,{\varvec{\beta }},{\varvec{y}})|_{\varTheta _a={\varvec{\mu }}_{\varTheta _a}}){\mathop {\longrightarrow }\limits ^{\mathcal {L}}}N_{p_1}(\mathbf {0},2{{{\varvec{\mu }}_{T_2}}^{\otimes 2h}}),\nonumber \\&\sqrt{a}({\varvec{\beta }}-E({\varvec{\beta }}|T,R_{2},{\varvec{y}})|_{\varTheta _a={\varvec{\mu }}_{\varTheta _a}}){\mathop {\longrightarrow }\limits ^{\mathcal {L}}}N_p(\mathbf {0},{\varvec{\mu }}_{R_2}). \end{aligned}$$

(A.2)

(b) From the Proposition 1, we have $\varSigma =V^{-1}\varSigma _D$, where, from the Eqs. (8) and (A.2),

$$\begin{aligned} \varSigma _D= & {} \mathrm {blkdiag}\{\varSigma _1,\ldots ,\varSigma _5\},\\= & {} \mathrm {blkdiag}\{\lim _{{\textit{a}}\rightarrow \infty }{\textit{a}}\cdot \mathrm{{Cov}}(T|{\varvec{\phi }},{\varvec{y}})\big |_{{\varvec{\phi }}={\varvec{\mu }}_{{\varvec{\phi }}}}, \frac{2}{bc}{{{\varvec{\mu }}_{R_0}}^{\otimes 2h}},\frac{2}{b}{{{\varvec{\mu }}_{R_{1}}}^{\otimes 2h}},2{{{\varvec{\mu }}_{R_2}}^{\otimes 2h}},{\varvec{\mu }}_{R_{2}}\}, \end{aligned}$$

the matrix V is a $5\times 5$ block matrix, $\{V_{ij}\}_{1\le i,j\le 5}$, and

$$\begin{aligned} \begin{aligned} V&=\lim _{a\rightarrow \infty }\begin{pmatrix} I_{p_2}&{}-\frac{\partial E(T|{\varvec{\phi }},{\varvec{y}})}{\partial R_{0v}'}&{}-\frac{\partial E(T|{\varvec{\phi }},{\varvec{y}})}{\partial R_{1v}'}&{}-\frac{\partial E(T|{\varvec{\phi }},{\varvec{y}})}{\partial R_{2v}'}&{}-\frac{\partial E(T|{\varvec{\phi }},{\varvec{y}})}{\partial {\varvec{\beta }}'}\\ -\frac{\partial E(R_{0v}|T,{\varvec{y}})}{\partial T'}&{}I_{p_1}&{}-\frac{\partial E(R_{0v}|T,{\varvec{y}})}{\partial R_{1v}'}&{}-\frac{\partial E(R_{0v}|T,{\varvec{y}})}{\partial R_{2v}'}&{}-\frac{\partial E(R_{0v}|T,{\varvec{y}})}{\partial {\varvec{\beta }}'}\\ -\frac{\partial E(R_{1v}|T,{\varvec{y}})}{\partial T'}&{}-\frac{\partial E(R_{1v}|T,{\varvec{y}})}{\partial R_{0v}'}&{}I_{p_1}&{}-\frac{\partial E(R_{1v}|T,{\varvec{y}})}{\partial R_{2v}'}&{}-\frac{\partial E(R_{1v}|T,{\varvec{y}})}{\partial {\varvec{\beta }}'}\\ -\frac{\partial E(R_{2v}|T,{\varvec{\beta }},{\varvec{y}})}{\partial T'}&{}-\frac{\partial E(R_{2v}|T,{\varvec{\beta }},{\varvec{y}})}{\partial R_{0v}'}&{}-\frac{\partial E(R_{2v}|T,{\varvec{\beta }},{\varvec{y}})}{\partial R_{1v}'}&{}I_{p_1}&{}-\frac{\partial E(R_{2v}|T,{\varvec{\beta }},{\varvec{y}})}{\partial {\varvec{\beta }}'}\\ -\frac{\partial E({\varvec{\beta }}|T,R_{2v},{\varvec{y}})}{\partial T'}&{}-\frac{\partial E({\varvec{\beta }}|T,R_{2v},{\varvec{y}})}{\partial R_{0v}'}&{}-\frac{\partial E({\varvec{\beta }}|T,R_{2v},{\varvec{y}})}{\partial R_{1v}'}&{}-\frac{\partial E({\varvec{\beta }}|T,R_{2v},{\varvec{y}})}{\partial R_{2v}'}&{}I_{p}\\ \end{pmatrix}\Bigg |_{\varTheta _a={\varvec{\mu }}_{\varTheta _a}}. \end{aligned} \end{aligned}$$

By the Eq. (A.1), the block sub-matrices of V, $V_{ij}$’s, are given as follows:

$$\begin{aligned} A\equiv & {} -[V_{12}\ V_{13}\ V_{14}\ V_{15}]=\lim _{a\rightarrow \infty }\frac{\partial E(T|{\varvec{\phi }},{\varvec{y}})}{\partial {\varvec{\phi }}'}\bigg |_{{\varvec{\phi }}={\varvec{\mu }}_{{\varvec{\phi }}}},\\ {[}V'_{21}\ V'_{31}\ V'_{41}\ V'_{51}]'= & {} -I_{p_2},\ V_{23}=V_{24}=V_{34}=V_{32}=V_{42}=V_{43}=\mathbf {O}_{p_1},\\ V_{25}= & {} V_{35}=V_{45}=V'_{52}=V'_{53}=V'_{54}=\mathbf {O}_{p_1,p}.\\ \end{aligned}$$

Thus, the asymptotic covariance of $\varTheta _a=(T',R_{0v}',R_{1v}',R_{2v}',{\varvec{\beta }}')'$, $\varSigma$, can be simplified to a 2$\times$2 block matrix (from a 5$\times$5 block matrix), which is the asymptotic covariance of $(T',{\varvec{\phi }}')'$, and owing to the symmetry of $\varSigma$, we have

$$\begin{aligned} \varSigma&=V^{-1}\varSigma _D=\begin{pmatrix} I_{p_2} &{} -A \\ -I_{p_2} &{} I_{p_2} \end{pmatrix}^{-1}\begin{pmatrix} \varSigma _1 &{} \mathbf {O}_{p_2} \\ \mathbf {O}_{p_2} &{} \varSigma ^*_2 \end{pmatrix}\nonumber \\&=\begin{pmatrix} (I_{p_2}-A)^{-1}\varSigma _1 &{} (I_{p_2}-A)^{-1}A\varSigma ^*_2 \\ (I_{p_2}-A)^{-1}\varSigma _1 &{} (I_{p_2}-A)^{-1}\varSigma ^*_2 \end{pmatrix}=\begin{pmatrix} \varSigma _T &{} \varSigma _{T{\varvec{\phi }}} \\ \varSigma '_{T{\varvec{\phi }}} &{} \varSigma _{{\varvec{\phi }}} \end{pmatrix},\nonumber \\ \varSigma _T&=\varSigma _{T{\varvec{\phi }}} =\varSigma '_{T{\varvec{\phi }}}=(I_{p_2}-A)^{-1}\varSigma _1=\varSigma _{{\varvec{\phi }}}-\varSigma ^*_2,\nonumber \\ \varSigma _{{\varvec{\phi }}}&=(I_{p_2}-A)^{-1}\varSigma ^*_2,\ \varSigma ^*_{2}=\mathrm{{blkdiag}} \{\varSigma _2,\ldots , \varSigma _5\}. \end{aligned}$$

(A.3)

(c) To simplify the calculation of A and $\varSigma _{\varvec{\phi }}$, define $\varLambda _0=R_0$, $\varLambda _{1}=cR_1+R_0$, $\varLambda _{2}=bcR_2+\varLambda _{1}$, and $\varLambda =(\varLambda '_{0v},\varLambda '_{1v},\varLambda '_{2v},{\varvec{\beta }}')'$. Then we have

$$\begin{aligned} \begin{aligned} R_0&=\varLambda _{0},\ R_1=\frac{\varLambda _{1}-\varLambda _{0}}{c},\ R_2=\frac{\varLambda _{2}-\varLambda _{1}}{bc},\ Q_0=\varLambda ^{-1}_0,\ Q_1=[\frac{\varLambda _{1}-\varLambda _{0}}{c}]^{-1},\ Q_2=[\frac{\varLambda _{2}-\varLambda _{1}}{bc}]^{-1},\\ P_0&=c\varLambda ^{-1}_0,\ P_1=bcQ_1{W_{1}^*}^{-1}Q_0=bc\varLambda _{1}^{-1},\\ {W_1^*}^{-1}&=(cR^{-1}_0+R^{-1}_1)^{-1}=R_0[cR_1+R_0]^{-1}R_1(=R_1[cR_1+R_0]^{-1}R_0)=\varLambda _{0}\varLambda _{1}^{-1}[\frac{\varLambda _{1}-\varLambda _{0}}{c}],\\ {W_2^*}^{-1}&=(P_1+R^{-1}_2)^{-1}=P_1^{-1}[P^{-1}_1+R_2]^{-1}R_2(=R_2[P^{-1}_1+R_2]^{-1}P_1^{-1})=\varLambda _{1}\varLambda _{2}^{-1}\frac{\varLambda _{2}-\varLambda _{1}}{bc}. \end{aligned} \end{aligned}$$

The conditional mean functions of $T_i$’s given $\varLambda$ and ${\varvec{y}}$ are

$$\begin{aligned} \begin{aligned} E[T_{0}|\varLambda ,{\varvec{y}}]&=\varLambda _{0}\varLambda _{1}^{-1}\left[ \frac{\varLambda _{1}-\varLambda _{0}}{c}\right] +\varLambda _{0}\varLambda _{1}^{-1}\left[ S_1+\varLambda _{1}\varLambda _{2}^{-1}\frac{\varLambda _{2}-\varLambda _{1}}{bc}\right] \varLambda _{1}^{-1}\varLambda _{0}\\&\quad +\varLambda _{0}\varLambda _{2}^{-1}[S_2+({\varvec{\beta }}-\bar{\varvec{y}})({\varvec{\beta }}-\bar{\varvec{y}})']\varLambda _{2}^{-1}\varLambda _{0}+S_0,\\ E[T_{1}|\varLambda ,{\varvec{y}}]&=\varLambda _{0}\varLambda _{1}^{-1}\left[ \frac{\varLambda _{1}-\varLambda _{0}}{c}\right] +[I_{p_1}-\varLambda _{0}\varLambda _{1}^{-1}][S_1+\varLambda _{1}\varLambda _{2}^{-1}\frac{\varLambda _{2}-\varLambda _{1}}{bc}][I_{p_1}-\varLambda _{1}^{-1}\varLambda _{0}]\\&\quad +[I_{p_1}-\varLambda _{0}\varLambda _{1}^{-1}]\varLambda _{1}\varLambda _{2}^{-1}[S_2+({\varvec{\beta }}-\bar{\varvec{y}})({\varvec{\beta }}-\bar{\varvec{y}})']\varLambda _{2}^{-1}\varLambda _{1}[I_{p_1}-\varLambda _{1}^{-1}\varLambda _{0}],\\ E[T_{2}|\varLambda ,{\varvec{y}}]&=\varLambda _{1}\varLambda _{2}^{-1}\frac{\varLambda _{2}-\varLambda _{1}}{bc}+[I_{p_1}-\varLambda _{1}\varLambda _{2}^{-1}]S_2[I_{p_1}-\varLambda _{2}^{-1}\varLambda _{1}]\\&\quad +\varLambda _{0}\varLambda _{2}^{-1}({\varvec{\beta }}-\bar{\varvec{y}})({\varvec{\beta }}-\bar{\varvec{y}})'\varLambda _{2}^{-1}\varLambda _{0},\\ E[T_{3}|\varLambda ,{\varvec{y}}]&=[I_{p_1}-\varLambda _{1}\varLambda _{2}^{-1}]\bar{\varvec{y}}+\varLambda _{1}\varLambda _{2}^{-1}{\varvec{\beta }}, \end{aligned}\nonumber \\ \end{aligned}$$

(A.4)

and

$$\begin{aligned} A=\lim _{{a}\rightarrow \infty }\frac{\partial E(T|\varLambda ,{\varvec{y}})}{\partial \varLambda '}\frac{\partial \varLambda }{\partial {\varvec{\phi }}'}\big |_{\varLambda ={\varvec{\mu }}_{\varLambda }}=A^*\cdot \frac{\partial \varLambda }{\partial {\varvec{\phi }}'}, \end{aligned}$$

where $A^*$ is a $4\times 4$ block matrix, $A^*=\lim _{{a}\rightarrow \infty }\frac{\partial E(T|\varLambda ,{\varvec{y}})}{\partial \varLambda '}\big |_{\varLambda ={\varvec{\mu }}_{\varLambda }}$,

$$\begin{aligned} \begin{aligned} {\varvec{\mu }}_{\varLambda }&=({\varvec{\mu }}'_{\varLambda _{0v}},{\varvec{\mu }}'_{\varLambda _{1v}},{\varvec{\mu }}'_{\varLambda _{2v}},{\varvec{\mu }}'_{{\varvec{\beta }}})',\ {\varvec{\mu }}_{\varLambda _{0}}=\frac{c}{c_1}S_0,\ {\varvec{\mu }}_{\varLambda _{1}}=\frac{bc}{b_1}S_1,\ {\varvec{\mu }}_{\varLambda _{2}}=bcS_2,\\ \end{aligned}\nonumber \\ \end{aligned}$$

(A.5)

$\frac{\partial \varLambda }{\partial {\varvec{\phi }}'}=\text {blkdiag}\{L_1^*,I_p\}$, $L_1^*$ is a lower block triangular matrix, and

$$\begin{aligned} L_1^*=\begin{pmatrix}I_{p_1} &{} \mathbf {O}_{p_1} &{} \mathbf {O}_{p_1} \\ I_{p_1} &{} cI_{p_1} &{} \mathbf {O}_{p_1} \\ I_{p_1} &{} cI_{p_1} &{} bcI_{p_1} \end{pmatrix}. \end{aligned}$$

To calculate the matrices $A^*$ and hence $\varSigma$, we introduce the first-order matrix differential operator and the following lemma.

Definition A.1

(Magnus and Neudecker 1980, 1999)

• (a) (matrix differentials) Let F(X) be a differentiable $m\times p$ matrix function of an $n\times q$ matrix of real variables X. Define the first differential $\text {d}F(X)$ to be the matrix of differentials $\{\text {d} F(X)\}_{ij},\ i=1,\ldots ,m,\ j=1,\ldots ,p.$

• (b) The duplication matrix $D_p$ is the $p^2\times \frac{p(p+1)}{2}$ matrix such that $D_p \text {vech}(C)=\mathrm{{vec}}(C)$ and $C^{\otimes 2l}\equiv L_pC^{\otimes 2}D_p$ for any $p\times p$ matrix C.

Lemma A.2

(Magnus and Neudecker 1980, 1999)

• (a) $\text {d}(XY)=(\text {d}X)Y+X(\text {d}Y)$; $\text {d}X^{-1}=-X^{-1}(\text {d}X)X^{-1}$ for any nonsingular matrix X;

• (b) $\mathrm{{vec}}(ABC)=(C'\otimes A)\mathrm{{vec}}(B)$ for any A, B, C matrices of appropriate sizes;

• (c) $N'_p=N_p$; $D_pL_pN_p=N_p$; $N_pD_p=D_p$; $N_p{{C}^{\otimes 2}}={{C}^{\otimes 2}}N_p=N_p{{C}^{\otimes 2}}N_p$ for any square matrix C;

• (d) $(L_pN_p{{C}^{\otimes 2}}N_pL'_p)^{-1}=D'_p{{(C^{-1})}^{\otimes 2}}D_p$ for any nonsingular matrix C.

In the following, we calculate the (1, 1)th and (1, 2)th blocks of $A^*$. Calculations for other (i, j)th blocks of $A^*$ just follow the same techniques.

By the Eq. (A.4) and Lemma A.2 (a), the first differential of $E[T_{0}|\varLambda ,{\varvec{y}}]$ with respect to $\varLambda _{0}$ evaluated at ${\varvec{\mu }}_\varLambda$ is

$$\begin{aligned} \begin{aligned} \text {d}E[T_{0}|\varLambda ,{\varvec{y}}]|_{\varLambda ={\varvec{\mu }}_\varLambda }=&\text {d}\bigg [\frac{1}{c}\varLambda _{0}+\varLambda _{0}\left[ -\frac{1}{c}\varLambda ^{-1}_{1}+\varLambda ^{-1}_{1}S_1\varLambda ^{-1}_{1}+\frac{1}{bc}\varLambda ^{-1}_{1}\right] \varLambda _{0}\\&+\varLambda _{0}[-\frac{1}{bc}\varLambda ^{-1}_{2}+\varLambda ^{-1}_{2}[S_2+({\varvec{\beta }}-\bar{\varvec{y}})({\varvec{\beta }}-\bar{\varvec{y}})']\varLambda ^{-1}_{2}]\varLambda _{0}+S_0\bigg ]\bigg |_{\varLambda ={\varvec{\mu }}_\varLambda }\\ =&\frac{1}{c}(\text {d}\varLambda _{0})+\text {d}\left[ \varLambda _{0}\left[ -\frac{1}{c}\varLambda ^{-1}_{1}+\varLambda ^{-1}_{1}S_1\varLambda ^{-1}_{1}+\frac{1}{bc}\varLambda ^{-1}_{1}\right] \Bigg |_{\varLambda ={\varvec{\mu }}_\varLambda }\varLambda _{0}\right] \\&+\text {d}\left. \left[ \varLambda _{0}\left[ \left. -\frac{1}{bc}\varLambda ^{-1}_{2}+\varLambda ^{-1}_{2}[S_2+({\varvec{\beta }}-\bar{\varvec{y}})({\varvec{\beta }}-\bar{\varvec{y}})'\right] \varLambda ^{-1}_{2}\right] \right| _{\varLambda ={\varvec{\mu }}_\varLambda }\varLambda _{0}\right] \\ =&\frac{1}{c}(\text {d}\varLambda _{0}).\\ \end{aligned} \end{aligned}$$

Thus,

$$\begin{aligned} \begin{aligned} \text {d}E[T_{0v}|\varLambda ,{\varvec{y}}]|_{\varLambda ={\varvec{\mu }}_\varLambda }=&\text {vech}\bigg [\text {d}E[T_{0}|\varLambda ,{\varvec{y}}]|_{\varLambda ={\varvec{\mu }}_\varLambda }\bigg ] =\text {vech}\bigg [\frac{1}{c}(\text {d}\varLambda _{0})\bigg ]= \frac{1}{c}\text {d}\varLambda _{0v}, \end{aligned} \end{aligned}$$

and the (1, 1)th block of $A^*$, $\{A^*\}_{11}=\lim _{{a}\rightarrow \infty }\frac{\partial E(T|\varLambda ,{\varvec{y}})}{\partial \varLambda _{0v}'}\bigg |_{\varLambda ={\varvec{\mu }}_{\varLambda }}=\frac{1}{c}I_{p_1}.$

Next, the first differential of $E[T_{0}|{\varvec{\phi }},{\varvec{y}}]$ with respect to $\varLambda _{1}$ evaluated at ${\varvec{\mu }}_\varLambda$ is

$$\begin{aligned} \begin{aligned} \text {d}E[T_{0}|\varLambda ,{\varvec{y}}]|_{\varLambda ={\varvec{\mu }}_\varLambda }=&\text {d}\bigg [\frac{1}{c}[\varLambda _{0}-\varLambda _{0}\varLambda ^{-1}_{1}\varLambda _{0}]+\varLambda _{0}\varLambda ^{-1}_{1}S_1\varLambda ^{-1}_{1}\varLambda _{0}+\frac{1}{bc}\varLambda _{0}[\varLambda ^{-1}_{1}-\varLambda ^{-1}_{2}]\varLambda _{0}\\&+\varLambda _{0}\varLambda ^{-1}_{2}[S_2+({\varvec{\beta }}-\bar{\varvec{y}})({\varvec{\beta }}-\bar{\varvec{y}})']\varLambda ^{-1}_{2}\varLambda _{0}+S_0\bigg ]\bigg |_{\varLambda ={\varvec{\mu }}_\varLambda }\\ =&\bigg [\frac{1}{c}\varLambda _{0}\varLambda ^{-1}_{1}(\text {d}\varLambda _{1})\varLambda ^{-1}_{1}\varLambda _{0}-[\varLambda _{0}\varLambda ^{-1}_{1}(\text {d}\varLambda _{1})\varLambda ^{-1}_{1}S_1\varLambda ^{-1}_{1}\varLambda _{0}\\&+\varLambda _{0}\varLambda ^{-1}_{1}S_1\varLambda ^{-1}_{1}(\text {d}\varLambda _{1})\varLambda ^{-1}_{1}\varLambda _{0}]-\frac{1}{bc}\varLambda _{0}\varLambda ^{-1}_{1}(\text {d}\varLambda _{1})\varLambda ^{-1}_{1}\varLambda _{0}\bigg ]\bigg |_{\varLambda ={\varvec{\mu }}_\varLambda }\\ =&\bigg [ \frac{1}{c}A_{01}(\text {d}\varLambda _{1})A'_{01}-\frac{2b_1}{bc}A_{01}(\text {d}\varLambda _{1})A'_{01}-\frac{1}{bc}A_{01}(\text {d}\varLambda _{1})A'_{01}\bigg ]\\ =&\bigg [-\frac{b_1}{bc}A_{01}(\text {d}\varLambda _{1})A'_{01}\bigg ],\ \end{aligned} \end{aligned}$$

where $A_{01}={\varvec{\mu }}_{\varLambda _{0}}{\varvec{\mu }}_{\varLambda _{1}}^{-1}=\frac{b_1}{bc}S_0S_1^{-1}$. By Lemma A.2 (b),

$$\begin{aligned} \begin{aligned} \text {d}E[T_{0v}|\varLambda ,{\varvec{y}}]|_{\varLambda ={\varvec{\mu }}_\varLambda }=&\text {vech}\bigg [\text {d}E[T_{0}|\varLambda ,{\varvec{y}}]|_{\varLambda ={\varvec{\mu }}_\varLambda }\bigg ] =-\frac{b_1}{bc}L_p\text {vec}\bigg [A_{01}(\text {d}\varLambda _{1})A'_{01}\bigg ]\\ =&-\frac{b_1}{bc}L_p{{A_{01}}^{\otimes 2}}\text {vec}(\text {d}\varLambda _{1})=-\frac{b_1}{bc}L_p{{A_{01}}^{\otimes 2}}D_p\text {d}\varLambda _{1v}=-\frac{b_1}{bc}{{A_{01}}^{\otimes 2l}}\text {d}\varLambda _{1v}.\\ \end{aligned} \end{aligned}$$

The (1,2) block of $A^*$, $\{A^*\}_{12}=\lim _{{a}\rightarrow \infty }\frac{\partial E(T|\varLambda ,{\varvec{y}})}{\partial \varLambda _{1v}'}\bigg |_{\varLambda ={\varvec{\mu }}_{\varLambda }}=-\frac{b_1}{bc}{{A_{01}}^{\otimes 2l}}$. Hence, we obtain $A^*=\mathrm {blkdiag}\{A_1^*,I_p-{\varvec{\mu }}_{R_2}S_2^{-1}\}$ and $A_1^*=$

$$\begin{aligned} \begin{aligned} \begin{pmatrix} \frac{1}{c}I_{p_1} &{} -\frac{b_1}{bc}{{A_{01}}^{\otimes 2l}} &{} -\frac{1}{bc}{{A_{02}}^{\otimes 2l}}\\ -\frac{1}{c}I_{p_1}&{} \frac{1}{c}(I_{p_1}-\frac{b_1}{b}{{(I_{p_1}-A_{01})}^{\otimes 2l}}) &{} -\frac{1}{bc}{{(A_{02}-A_{12})}^{\otimes 2l}}\\ \mathbf {O}_{p_1} &{} -\frac{1}{bc}I_{p_1} &{} \frac{1}{bc}(I_{p_1}-{{(I_{p_1}-A_{12})}^{\otimes 2l}})\\ \end{pmatrix}, \end{aligned} \end{aligned}$$

where $A_{12}={\varvec{\mu }}_{\varLambda _{1}}{\varvec{\mu }}_{\varLambda _{2}}^{-1}=\frac{1}{b_1}S_1S_2^{-1}$, and $A_{02}={\varvec{\mu }}_{\varLambda _{0}}{\varvec{\mu }}_{\varLambda _{2}}^{-1}=\frac{1}{bc_1}S_0S_2^{-1}$. Note that the calculation of $A^*$ is based on the following formulas:

$$\begin{aligned} \begin{aligned} {\varvec{\mu }}^{-1}_{\varLambda _{1}}&=\frac{1}{c}{\varvec{\mu }}^{-1}_{R_1}(I_{p_1}-A_{01}),\ {\varvec{\mu }}^{-1}_{\varLambda _{2}}=\frac{1}{c}{\varvec{\mu }}^{-1}_{R_1}(A_{12}-A_{02}),\ {\varvec{\mu }}^{-1}_{\varLambda _{2}}=\frac{1}{bc}{\varvec{\mu }}^{-1}_{R_2}(I_{p_1}-A_{12}),\\ \end{aligned} \end{aligned}$$

and for $i<j$, by Lemma A.2 (c) and (d),

$$\begin{aligned} \begin{aligned} {\varvec{\mu }}_{\varLambda _i}^{\otimes 2h}{{\varvec{\mu }}_{\varLambda _j}^{\otimes 2h}}^{-1} =&L_pN_p{\varvec{\mu }}^{\otimes 2}_{\varLambda _i}N_pL'_p(L_pN_p{\varvec{\mu }}^{\otimes 2}_{\varLambda _j}N_pL'_p)^{-1} =L_pN_p{\varvec{\mu }}^{\otimes 2}_{\varLambda _i}N_pL'_pD'_p({\varvec{\mu }}^{-1}_{\varLambda _j})^{\otimes 2}D_p\\ =&L_pN_p{\varvec{\mu }}^{\otimes 2}_{\varLambda _i}N_p({\varvec{\mu }}^{-1}_{\varLambda _j})^{\otimes 2}D_p = L_p({\varvec{\mu }}_{\varLambda _i}{\varvec{\mu }}^{-1}_{\varLambda _j})^{\otimes 2}D_p={A_{ij}}^{\otimes 2l}. \end{aligned} \end{aligned}$$

Thus, after some calculations,

$$\begin{aligned} \begin{aligned} \varSigma _{\varvec{\phi }}^{-1}&={\varSigma _2^*}^{-1}(I_{p_2}-A)=\mathrm {blkdiag}\{Q_A,S_2^{-1}\},\ A=\mathrm {blkdiag}\{A_1,I_p-{\varvec{\mu }}_{R_2}S_2^{-1}\},\ A_1=A_1^*L^*,\\ Q_A&=(\mathrm {blkdiag}\{\varSigma _2,\varSigma _3,\varSigma _4\})^{-1}(I_{3p_1}-A_1)\\&=\frac{1}{2}\begin{pmatrix} bc_1{{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{0}}}^{-1}+b_1{{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{1}}}^{-1}+{{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{2}}}^{-1}&{} b_1c{{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{1}}}^{-1}+c{{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{2}}}^{-1}&{} bc{{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{2}}}^{-1}\\ b_1c{{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{1}}}^{-1}+c{{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{2}}}^{-1}&{} b_1c^2{{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{1}}}^{-1}+c^2{{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{2}}}^{-1}&{} bc^2{{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{2}}}^{-1}\\ bc{{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{2}}}^{-1} &{} bc^2{{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{2}}}^{-1}&{}b^2c^2{{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{2}}}^{-1} \end{pmatrix}. \end{aligned}\nonumber \\ \end{aligned}$$

(A.6)

Or simply

$$\begin{aligned} Q_A=\frac{1}{2}{L_1^*}'\mathrm {blkdiag}\{bc_1{{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{0}}}^{-1}, b_1{{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{1}}}^{-1},{{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{2}}}^{-1}\}L_1^*.\end{aligned}$$

Some algebra results in (9).

Proof of Theorem 2:

The proofs of the existence and the convergence of the explicit fixed point (the first part of (A1) in Proposition 1), the asymptotic normality of the posterior distribution of $\varTheta _a$, the assumption (A2), and the positive definiteness of $\varSigma _s$ are similar to those in Lemma 1 and Theorem 1. We omit them to save space. Next, similar to the Eq. (A.3) in the centering case, $\varSigma _s$ after some algebra can be expressed as

$$\begin{aligned} \begin{aligned} \varSigma _s=&\begin{pmatrix} I_{p_2} &{} -A_s \\ -B_s &{} I_{p_2} \end{pmatrix}^{-1}\begin{pmatrix} \varSigma _{1s} &{} \mathbf {O}_{p_2} \\ \mathbf {O}_{p_2} &{} \varSigma ^*_{2s} \end{pmatrix}\\ =&\begin{pmatrix} (I_{p_2}-A_sB_s)^{-1}\varSigma _{1s} &{} A_s(I_{p_2}-B_s A_s)^{-1}\varSigma ^*_{2s} \\ B_s(I_{p_2}-A_s B_s )^{-1}\varSigma _{1s} &{} (I_{p_2}-B_s A_s)^{-1}\varSigma ^*_{2s} \end{pmatrix}=\begin{pmatrix} \varSigma _{T_s} &{} \varSigma _{T_s{\varvec{\phi }}} \\ \varSigma '_{T_s{\varvec{\phi }}} &{} \varSigma _{\varvec{\phi }}\end{pmatrix},\\ \end{aligned}\nonumber \\ \end{aligned}$$

(A.7)

where $\varSigma ^{*}_{2s}=\mathrm {blkdiag}\{\varSigma _2,\varSigma _3,\varSigma _4,\varSigma _{5s}\},\ \varSigma _{5s}=\frac{1}{bc}{\varvec{\mu }}_{R_0}$, and

$$\begin{aligned} B_s =I_{p_2}+\begin{pmatrix} \mathbf {O}_{p_1,3p_1} &{}-L_p(\bar{\varvec{y}}\otimes I_p+I_p\otimes \bar{\varvec{y}})\\ \mathbf {O}_{2p_1+p,3p_1}&{} \mathbf {O}_{2p_1+p,p}\end{pmatrix}. \end{aligned}$$

Hence $(I_{p_2}-B_s A_s)^{-1}\varSigma ^*_{2s}=\varSigma _{\varvec{\phi }}$ implies $A_s=B_s^{-1}(I_{p_2}-\varSigma ^*_{2s}\varSigma _{\varvec{\phi }}^{-1})$. Thus, $\varSigma _{T_s{\varvec{\phi }}}=A_s(I_{p_2}-B_s A_s)^{-1}\varSigma ^*_{2s}=B_s^{-1}(\varSigma _{\varvec{\phi }}-\varSigma _{2s}^*)$ and $\varSigma _{T_s}=B_s^{-1}(\varSigma _{\varvec{\phi }}-\varSigma _{2s}^*)B_s^{-1'}$ as shown in Theorem 2.

Proof of Corollary 1

From the proofs of Theorems 1 and 2 (see the Eqs. (A.6) and (A.7)), the derivatives of mean functions for the standard and centering cases, $\dot{{\varvec{g}}}_s$ and $\dot{{\varvec{g}}}_c$, are

$$\begin{aligned} \begin{aligned} \dot{{\varvec{g}}}_s=\begin{pmatrix}\mathbf {O}_{p_2} &{} A_s\\ B_s &{} \mathbf {O}_{p_2}\end{pmatrix},\ \dot{{\varvec{g}}}_c=\begin{pmatrix}\mathbf {O}_{p_2} &{} A\\ I_{p_2} &{} \mathbf {O}_{p_2}\end{pmatrix}. \end{aligned} \end{aligned}$$

Note that these two derivatives can be partitioned as $\begin{pmatrix} \mathbf {O}_{p_2} &{} E \\ F &{} \mathbf {O}_{p_2} \end{pmatrix}$. By Lemma A.3 in Su and Johnson (2006), $\rho _s=\rho (\dot{{\varvec{g}}}_s)$ and $\rho _c=\rho (\dot{{\varvec{g}}}_c)$ are less than one. Second, the characteristic polynomials of $\dot{{\varvec{g}}}_c$ and $\dot{{\varvec{g}}}_s$ are $p_{\dot{{\varvec{g}}}_c}(\lambda )$=det($\lambda ^2I_{p_2}-A$) and $p_{\dot{{\varvec{g}}}_s}(\lambda )$=det($\lambda ^2I_{p_2}-B_sA_s$), respectively. Here

$$\begin{aligned} \begin{aligned} A&=\begin{pmatrix}A_1 &{} \mathbf {O}_{p_2}\\ \mathbf {O}_{p_2} &{} I_{p_2}-\frac{1}{bc}\varvec{\mu }_{R_{0}}S_2^{-1}\end{pmatrix},\ B_sA_s=\begin{pmatrix}A_1 &{} \mathbf {O}_{p_2}\\ \mathbf {O}_{p_2} &{} I_{p_2}-\varvec{\mu }_{R_{2}}S_2^{-1}\end{pmatrix}, \end{aligned} \end{aligned}$$

and $A_1 =A_1^*L^*=$

$$\begin{aligned} -\begin{pmatrix}-\frac{1}{c}I+\frac{1}{bc}[b_1{{A_{01}}^{\otimes 2l}}+{{A_{02}}^{\otimes 2l}}]&{} \frac{1}{b}[b_1{{A_{01}}^{\otimes 2l}}+{{A_{02}}^{\otimes 2l}}]&{} {{A_{02}}^{\otimes 2l}}\\ \frac{1}{bc}[b_1{{(I-A_{01})}^{\otimes 2l}}+{{(A_{12}-A_{02})}^{\otimes 2l}}]&{} \frac{1}{b}[b_1{{(I-A_{01})}^{\otimes 2l}}+{{(A_{12}-A_{02})}^{\otimes 2l}}]-I&{}{{(I-A_{12})}^{\otimes 2l}}\\ \frac{1}{bc}{{(I-A_{12})}^{\otimes 2l}} &{} \frac{1}{b}{{(I-A_{12})}^{\otimes 2l}} &{} {{(I-A_{12})}^{\otimes 2l}}-I \end{pmatrix}. \end{aligned}$$

Thus,

$$\begin{aligned} \rho _s= & {} \max \bigg \{\sqrt{\rho (A_1)}, \sqrt{\rho (I_p-\frac{1}{bc}\varvec{\mu }_{R_{0}}S_2^{-1})}\bigg \},\\ \rho _c= & {} \max \bigg \{\sqrt{\rho (A_1)}, \sqrt{\rho (I_p-\varvec{\mu }_{R_{2}}S_2^{-1})}\bigg \}. \end{aligned}$$

Next, any eigenvalue of $I_p-\frac{1}{bc}\varvec{\mu }_{R_{0}}S_2^{-1}$, $\lambda (I_p-\frac{1}{bc}\varvec{\mu }_{R_{0}}S_2^{-1}) =\lambda (S_2^{-1/2}(\varvec{\mu }_{R_{2}}+\frac{1}{b}\varvec{\mu }_{R_{1}})S_2^{-1/2})>0$ and $0< \rho (I_p-\frac{1}{bc}\varvec{\mu }_{R_{0}}S_2^{-1})=1-\lambda _{\text {min}}(\frac{1}{bc}\varvec{\mu }_{R_{0}}S_2^{-1}) < 1$ provided $0< \rho _s < 1$. Similarly, $\lambda (I_p-\varvec{\mu }_{R_{2}}S_2^{-1})) =\lambda (S_2^{-1/2}(\frac{1}{b}\varvec{\mu }_{R_{1}}+\frac{1}{bc}\varvec{\mu }_{R_{2}})S_2^{-1/2})>0$ and $0< \rho (I_p-\varvec{\mu }_{R_{2}}S_2^{-1})=1-\lambda _{\text {min}}(\varvec{\mu }_{R_{0}}S_2^{-1}) < 1$ provided $0< \rho _c < 1$. Note that

$$\begin{aligned} S_2^{-1/2}{\varvec{\mu }}_{R_2}S_2^{-1/2}= S_2^{-1/2}\frac{1}{bc}{\varvec{\mu }}_{R_0}S_2^{-1/2}+S_2^{-1/2}({\varvec{\mu }}_{R_2}-\frac{1}{bc}{\varvec{\mu }}_{R_0})S_2^{-1/2}. \end{aligned}$$

By Weyl’s Theorem for symmetric matrices (Horn and Johnson 2012), ${\varvec{\mu }}_{R_2}-\frac{1}{bc}{\varvec{\mu }}_{R_0}\ge (\le ) 0$ implies $\lambda _{\text {min}}(S_2^{-1/2}\frac{1}{bc}{\varvec{\mu }}_{R_0}S_2^{-1/2})\le (\ge )\ \lambda _{\text {min}}(S_2^{-1/2}{\varvec{\mu }}_{R_2}S_2^{-1/2})$. Thus, $\rho _c\le (\ge ) \rho _s$ provided $\lambda _{\text {min}}(S_2^{-1/2}\frac{1}{bc}\varvec{\mu }_{R_{0}}S_2^{-1/2})\le (\ge )\ \lambda _{\text {min}}(S_2^{-1/2}\varvec{\mu }_{R_{2}}S_2^{-1/2})$ or simply $\lambda _{\text {min}}(\frac{1}{bc}\varvec{\mu }_{R_{0}}S_2^{-1})\le (\ge )\ \lambda _{\text {min}}(\varvec{\mu }_{R_{2}}S_2^{-1})$. Furthermore, $\rho (A_1)\rightarrow 0$ as both b and c tend to infinity, $\rho (I_p-{\varvec{\mu }}_{R_2}S_2^{-1}) \rightarrow 0$ as b tends to infinity, and $\rho (I_p-\frac{1}{bc}{\varvec{\mu }}_{R_0}S_2^{-1})\rightarrow 1$ as b or $c\rightarrow \infty$. Thus, $\rho _c\rightarrow 0$ as both b and $c\rightarrow \infty$, and $\rho _s\rightarrow 1$ as b or $c\rightarrow \infty$. $\square$

Proof of Theorem 3:

Similar to the proof of Theorem 1, we first show the unique fixed point for ${\varvec{g}}_n$ and then break the rest proof into three parts: (a) derive the asymptotic normality of conditional distribution of $R_{kv},\ k=0,\ldots ,r$, and ${\varvec{\beta }}$; (b) compute $\varSigma$ by simplifying $\varSigma$ and derive the relationship between $\varSigma _T$, $\varSigma _{T{\varvec{\phi }}}$, and $\varSigma _{\varvec{\phi }}$; (c) calculate $\varSigma$ explicitly; and (d) show that $\varSigma >0$. We omit the proof of the asymptotic normality of the conditional T and the verification of the regularity condition(s) since it is similar to arguments used in the proof of Theorem 1.

First, for simplicity, we define some notations used in the following. Let

$$\begin{aligned}\begin{aligned}&Q_k=R^{-1}_k,\ k=0,\ldots ,r,\\&W_1=W_1^*=n_rQ_0+Q_1,\ P_0=n_rQ_0,\\&W_k=n_{r-k+1}Q_{k-1}+Q_k,\ W_k^*=W_k-n_{r-k+1}Q_{k-1}W_{k-1}^{*^{-1}}Q_{k-1},\ P_{k-1}=W_{k}^*-Q_{k},\\&T_{k0}=\frac{1}{n_0\ldots n_{r-k}}\sum _{{i_0...i_{r-k}}}({\varvec{v}}_{i_0...i_{r-k}}-\bar{\varvec{y}}_{i_0...i_{r-k}})({\varvec{v}}_{i_0...i_{r-k}}-\bar{\varvec{y}}_{i_0...i_{r-k}})',\ k=2,\ldots ,r.\\ \end{aligned}\end{aligned}$$

From the Eq. (11), we have

$$\begin{aligned} \begin{aligned} {\varvec{v}}_{i_0...i_{r-k}}|{\varvec{v}}_{i_0...i_{{r-k-1}}},{\varvec{\phi }},{\varvec{y}}&\sim N({W_{k}^*}^{-1}[P_{k-1}\bar{\varvec{y}}_{i_0...i_{r-k}}+Q_{k}{\varvec{v}}_{i_0...i_{r-k-1}}],{W_{k}^*}^{-1}),\ k=1,\ldots ,r-1,\\ {\varvec{v}}_{i_0}|{\varvec{\phi }},{\varvec{y}}&\sim N({W_{r}^*}^{-1}[P_{r-1}\bar{\varvec{y}}_{i_0}+Q_r{\varvec{\beta }}],{W_{k}^*}^{-1}).\\ \end{aligned} \end{aligned}$$

(A.8)

Then, the components of ${\varvec{g}}_n$ can be derived through the following conditional mean functions.

$$\begin{aligned} E[T_{0}|{\varvec{\phi }},{\varvec{y}}]= & {} W^{-1}+W^{-1}Q_1[S_1+E[T_{20}|{\varvec{\phi }},{\varvec{y}}]]Q_1W^{-1}+S_0,\nonumber \\ E[T_k|{\varvec{\phi }},{\varvec{y}}]= & {} {W_k^*}^{-1}+{W_k^*}^{-1}P_{k-1}[S_k+E[T_{k+1,0}|{\varvec{\phi }},{\varvec{y}}]]P_{k-1}{W_k^*}^{-1},\ k=1,\ldots ,r-1,\nonumber \\ E[T_{r}|{\varvec{\phi }},{\varvec{y}}]= & {} {W_r^*}^{-1}+{W_r^*}^{-1}[P_{r-1}S_rP_{r-1}+Q_r({\varvec{\beta }}-\bar{\varvec{y}})({\varvec{\beta }}-\bar{\varvec{y}})'Q_r]{W_r^*}^{-1},\nonumber \\ E[T_{r+1}|{\varvec{\phi }},y]= & {} {W_r^*}^{-1}[P_{r-1}\bar{\varvec{y}}+Q_r{\varvec{\beta }}],\nonumber \\ E[R_k|T,{\varvec{y}}]= & {} T_k,\quad k=0,\ldots r-1,\nonumber \\ E[R_r|T,{\varvec{\beta }},{\varvec{y}}]= & {} T_r+(T_{r+1}-\bar{\varvec{y}})(\bar{\varvec{y}}-{\varvec{\beta }})'+(\bar{\varvec{y}}-{\varvec{\beta }})(T_{r+1}-\bar{\varvec{y}})'+({\varvec{\beta }}-\bar{\varvec{y}})({\varvec{\beta }}-\bar{\varvec{y}})',\nonumber \\ E[{\varvec{\beta }}|T,R_r,{\varvec{y}}]= & {} T_{r+1}, \end{aligned}$$

(A.9)

where

$$\begin{aligned} \begin{aligned} E[T_{k0}|{\varvec{\phi }},{\varvec{y}}]&={W_k^*}^{-1}+{W_k^*}^{-1}Q_k[S_k+E[T_{k+1,0}|{\varvec{\phi }},{\varvec{y}}]]Q_k{W_k^*}^{-1},\ k=2,\ldots ,r-1,\\ E[T_{r0}|{\varvec{\phi }},{\varvec{\beta }},{\varvec{y}}]&={W_r^*}^{-1}+{W_r^*}^{-1}Q_r[S_r+({\varvec{\beta }}-\bar{\varvec{y}})({\varvec{\beta }}-\bar{\varvec{y}})']Q_r{W_r^*}^{-1}. \end{aligned} \end{aligned}$$

Next, we solve the unique fixed point of ${\varvec{g}}_n$ iteratively. Let

$U_k({\varvec{\phi }}) =E[T_{k0}|{\varvec{\phi }},{\varvec{y}}]$, a function of ${\varvec{\phi }}$. First, solve

$$\begin{aligned} \begin{aligned} E[T_0|{\varvec{\phi }},{\varvec{y}}]&=W^{-1}+W^{-1}Q_1[S_1+U_2({\varvec{\phi }})]Q_1W^{-1}+S_0,\ E[R_0|T,{\varvec{y}}]=T_0,\\ E[T_1|{\varvec{\phi }},{\varvec{y}}]&=W^{-1}+W^{-1}P_0[S_1+U_2({\varvec{\phi }})]P_0W^{-1},\ E[R_1|T,{\varvec{y}}]=T_1.\ \end{aligned} \end{aligned}$$

The solution is

$$\begin{aligned} {\varvec{\mu }}_{R_0}={\varvec{\mu }}_{T_0}=\frac{n_r}{n_r-1}S_0,\ {\varvec{\mu }}_{R_1}={\varvec{\mu }}_{T_1}=U_2({\varvec{\phi }})+S_1-\frac{1}{n_r-1}S_0. \end{aligned}$$

Then, by iteratively solving the following equations and plugging the solution into the next step,

$$\begin{aligned} \begin{aligned} E[T_{k0}|{\varvec{\phi }},{\varvec{y}}]&={W_k^*}^{-1}+{W_k^*}^{-1}Q_{k}[S_k+U_{k+1}({\varvec{\phi }})]Q_{k}{W_k^*}^{-1},\\ {\varvec{\mu }}_{R_{k-1}}&=U_{k}({\varvec{\phi }})+S_{k-1}-\frac{1}{n_{r-k+2}-1}S_{k-2},\\ E[T_{k}|{\varvec{\phi }},{\varvec{y}}]&={W_k^*}^{-1}+{W_k^*}^{-1}P_{k-1}[S_k+U_{k+1}({\varvec{\phi }})]P_{k-1}{W_k^*}^{-1},\\ E[R_k|T,{\varvec{y}}]&=T_k,\ k=2,\ldots ,r-1, \end{aligned} \end{aligned}$$

we obtain

$$\begin{aligned} \begin{aligned} {\varvec{\mu }}_{R_{k-1}}&={\varvec{\mu }}_{T_{k-1}}=\frac{n_{r-k+1}}{n_{r-k+1}-1}S_{k-1}-\frac{1}{n_{r-k+2}-1}S_{k-2},\ {\varvec{\mu }}_{U_{k}({\varvec{\phi }})}=\frac{1}{n_{r-k}}S_{k}, \\ {\varvec{\mu }}_{R_{k}}&={\varvec{\mu }}_{T_{k}}=U_{k+1}({\varvec{\phi }})+S_{k}-\frac{1}{n_{r-k+1}-1}S_{k-1},\ k=2,\ldots ,r-1.\\ \end{aligned} \end{aligned}$$

The last step is to solve

$$\begin{aligned} \begin{aligned} E[T_{r0}|{\varvec{\phi }},{\varvec{y}}]&={W_r^*}^{-1}+{W_r^*}^{-1}Q_r[S_r+({\varvec{\beta }}-\bar{\varvec{y}})({\varvec{\beta }}-\bar{\varvec{y}})']Q_r{W_r^*}^{-1},\\ {\varvec{\mu }}_{R_{r-1}}&=U_{r}({\varvec{\phi }})+S_{r-1}-\frac{1}{n_{2}-1}S_{r-2},\\ E[T_{r}|{\varvec{\phi }},{\varvec{y}}]&={W_r^*}^{-1}+{W_r^*}^{-1}[P_{r-1}S_rP_{r-1}+Q_r({\varvec{\beta }}-\bar{\varvec{y}})({\varvec{\beta }}-\bar{\varvec{y}})'Q_r]{W_r^*}^{-1},\\ E[R_r|T,{\varvec{\beta }},{\varvec{y}}]&=T_r,\ E[T_{r+1}|{\varvec{\phi }},{\varvec{y}}]={W_r^*}^{-1}[P_{r-1}\bar{\varvec{y}}+Q_r{\varvec{\beta }}],\ E[{\varvec{\beta }}|T,R_r,{\varvec{y}}]=T_{r+1}. \end{aligned} \end{aligned}$$

This implies

$$\begin{aligned} \begin{aligned} {\varvec{\mu }}_{R_{r-1}}&={\varvec{\mu }}_{T_{r-1}}=\frac{n_{1}}{n_{1}-1}S_{r-1}-\frac{1}{n_{2}-1}S_{r-2},\ {\varvec{\mu }}_{U_r}=\frac{1}{n_1-1}S_{r-1},\\ {\varvec{\mu }}_{R_{r}}&={\varvec{\mu }}_{T_{r}}=S_r-\frac{1}{n_1-1}S_{r-1},\ {\varvec{\mu }}_{{\varvec{\beta }}}={\varvec{\mu }}_{T_{r+1}}=\bar{\varvec{y}}. \end{aligned} \end{aligned}$$

In each step, we require $n_k>1$ and ${\varvec{\mu }}_{R_k}>0$, $i=1,\ldots ,r$, to have a unique solution.

(a) The asymptotic normalities for conditional $R_{0v},\ldots , R_{rv}$, and ${\varvec{\beta }}$ are as follows.

$$\begin{aligned} \begin{aligned} \sqrt{n_0}&[R_{kv}-E(R_{kv}|T,{\varvec{y}})]|_{\varTheta _n={\varvec{\mu }}_{\varTheta _n}}){\mathop {\longrightarrow }\limits ^{\mathcal {L}}}N_{p_1}(\mathbf {0},\frac{2{{{\varvec{\mu }}_{T_k}}^{\otimes 2h}}}{n_1\ldots n_{r-k}}),\ k=0,\ldots ,r-1,\\ \sqrt{n_0}&[R_{rv}-E(R_{rv}|T,{\varvec{\beta }},{\varvec{y}})]|_{\varTheta _n={\varvec{\mu }}_{\varTheta _n}}){\mathop {\longrightarrow }\limits ^{\mathcal {L}}}N_{p_1}(\mathbf {0},2{{{\varvec{\mu }}_{T_r}}^{\otimes 2h}}),\\ \sqrt{n_0}&[{\varvec{\beta }}-E({\varvec{\beta }}|T,R_{r},{\varvec{y}})|_{\varTheta _n={\varvec{\mu }}_{\varTheta _n}}]{\mathop {\longrightarrow }\limits ^{\mathcal {L}}}N_p(\mathbf {0},{\varvec{\mu }}_{R_r}).\\ \end{aligned}\nonumber \\ \end{aligned}$$

(A.10)

(b) Note that conditioning on T and ${\varvec{\beta }}$, $R_k$’s are independent, and

$$\begin{aligned} \begin{aligned} \lim _{{n_0}\rightarrow \infty }&\frac{\partial E({\varvec{\phi }}|T,{\varvec{y}})}{\partial T'}\Big |_{T={\varvec{\mu }}_T}=I_{(r+1)p_1+p},\ \lim _{{n_0}\rightarrow \infty }\frac{\partial E(R|T,{\varvec{\beta }},{\varvec{y}})}{\partial {\varvec{\beta }}'}\Big |_{T={\varvec{\mu }}_T,\ {\varvec{\beta }}={\varvec{\mu }}_{\varvec{\beta }}}=\mathbf {O}_{(r+1)p_1,p},\\ \lim _{{n_0}\rightarrow \infty }&\frac{\partial E({\varvec{\beta }}|T,R,{\varvec{y}})}{\partial R'}\Big |_{T={\varvec{\mu }}_T,\ R={\varvec{\mu }}_R}=\mathbf {O}_{p,(r+1)p_1}. \end{aligned} \end{aligned}$$

The asymptotic covariance can then be simplified to a 2$\times$2 block matrix (from an (r+3)$\times$(r+3) block matrix), $(T',{\varvec{\phi }}')'=(\varTheta '_{1n},\varTheta '_{2n})'$, and expressed as

$$\begin{aligned} \begin{aligned} \varSigma =&\begin{pmatrix} (I_{(r+1)p_1+p}-A)^{-1}\varSigma _1 &{}(I_{(r+1)p_1+p}-A)^{-1}A\varSigma ^*_2 \\ (I_{(r+1)p_1+p}-A)^{-1}\varSigma _1 &{} (I_{(r+1)p_1+p}-A)^{-1}\varSigma ^*_2\end{pmatrix}=\begin{pmatrix} \varSigma _T &{} \varSigma _{T{\varvec{\phi }}} \\ \varSigma '_{T{\varvec{\phi }}} &{} \varSigma _{{\varvec{\phi }}} \end{pmatrix},\\ \varSigma _T=&\varSigma _{T{\varvec{\phi }}} =\varSigma '_{T{\varvec{\phi }}}=(I_{(r+1)p_1+p}-A)^{-1} \varSigma _1=\varSigma _{{\varvec{\phi }}}-\varSigma ^*_2,\\ \varSigma _{{\varvec{\phi }}}=&(I_{(r+1)p_1+p}-A)^{-1}\varSigma ^*_2,\\ \end{aligned}\nonumber \\ \end{aligned}$$

(A.11)

where, from the Eqs. (16) and (A.10),

$$\begin{aligned} \begin{aligned} \varSigma _1&=\lim _{n_0\rightarrow \infty }n_0\cdot \text {Cov}(T|{{\varvec{\phi }}},{\varvec{y}})\big |_{{\varvec{\phi }}={\varvec{\mu }}_{{\varvec{\phi }}}},\\ \varSigma ^*_2&=\mathrm {blkdiag}\{\varSigma _2,\ldots ,\varSigma _{r+3}\}=\mathrm {blkdiag}\{\frac{2}{n_1\ldots n_r}{{{\varvec{\mu }}_{R_0}}^{\otimes 2h}}, \ldots ,\frac{2}{n_1}{{{\varvec{\mu }}_{R_{r-1}}}^{\otimes 2h}},2{{{\varvec{\mu }}_{R_r}}^{\otimes 2h}},{\varvec{\mu }}_{R_r}\},\\ A&=\varSigma _1\varSigma ^{*-1}_2=\lim _{{n_0}\rightarrow \infty }\frac{\partial E(T|{\varvec{\phi }},{\varvec{y}})}{\partial {\varvec{\phi }}'}\Big |_{{\varvec{\phi }}={\varvec{\mu }}_{\varvec{\phi }}}. \end{aligned} \end{aligned}$$

(c) To simplify the calculation of A and $\varSigma _{\varvec{\phi }}$, define $\varLambda _{0}=R_0,\ \varLambda _k=n_{r-k+1}\cdots n_rR_k+\varLambda _{k-1}$. We have $R_k=\frac{1}{n_{r-k+1}\ldots n_r}(\varLambda _k-\varLambda _{k-1}),\ k=1,\ldots ,r.$ Let $\varLambda =(\varLambda '_{0v},\ldots ,\varLambda '_{rv},{\varvec{\beta }}')'$. From the Eqs. (A.9) and (16), we obtain

$$\begin{aligned} \begin{aligned} {W_k^*}^{-1}&=\varLambda _{k-1}\varLambda ^{-1}_k\bigg [\frac{\varLambda _k-\varLambda _{k-1}}{n_{r-k+1}\cdots n_r}\bigg ] =\bigg [\frac{\varLambda _k-\varLambda _{k-1}}{n_{r-k+1}\cdots n_r}\bigg ]\varLambda ^{-1}_k\varLambda _{k-1},\\ {W_k^*}^{-1}Q_k&=\varLambda _{k-1}\varLambda ^{-1}_k,\ {W_k^*}^{-1}P_{k-1}=I_p-\varLambda _{k-1}\varLambda ^{-1}_k,\ k=1,\ldots ,r.\\ \end{aligned}\nonumber \\ \end{aligned}$$

(A.12)

Note that $\frac{\partial E(T|{\varvec{\phi }},{\varvec{y}})}{\partial {\varvec{\phi }}'}=\frac{\partial E(T|{\varvec{\phi }},{\varvec{y}})}{\partial \varLambda '} \frac{\partial \varLambda }{\partial {\varvec{\phi }}'}$, where $\frac{\partial \varLambda }{\partial R'}=\text {blkdiag}\{L_1^*,I_p\}$, $L_1^*$ is a lower block triangular matrix with its block components

$$\begin{aligned} \{L_1^*\}_{ij}= {\left\{ \begin{array}{ll} I_{p_1}, &{} i\ge 1,\ j=1, \\ n_{r+2-j}\cdots n_rI_{p_1}, &{} i\ge j,\ j\ge 2,\\ \mathbf {O}_{p_1}, &{} i<j. \end{array}\right. } \end{aligned}$$

Also, $E(T|{\varvec{\phi }},{\varvec{y}})=E(T|\varLambda ,{\varvec{y}})$ depends on $\varLambda$ through ${W_k^*}^{-1}$, ${W_k^*}^{-1}Q_k$, and ${\varvec{\beta }}$, which are simple functions of $\varLambda _{k-1}$, $\varLambda _{k}$, and ${\varvec{\beta }}$ only. Some algebra results in $\varSigma _{\varvec{\phi }}^{-1}=\text {blkdiag}\{Q_A,S_r^{-1}\}$ and

$$\begin{aligned} \begin{aligned} Q_A=\frac{1}{2}{L_1^*}'\text {blkdiag}\{n_1\cdots n_{r-1}(n_r-1){{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{0}}}^{-1}, \ldots ,(n_1-1){{\varvec{\mu }}^{\otimes 2h}_{\varLambda _{r-1}}}^{-1},{{\varvec{\mu }}^{\otimes 2h}_{\varLambda _r}}^{-1}\}L_1^*, \end{aligned} \end{aligned}$$

where ${\varvec{\mu }}_{\varLambda _k}=\frac{n_r\cdots n_{r-k}}{n_{r-k}-1}S_k,\ k=0,\ldots ,r-1,\ {\varvec{\mu }}_{\varLambda _r}=n_r\ldots n_1S_r.$ Note that $Q_A$ satisfies the quasi-triangle property (Rizvi 1984). Hence, the inverse of $Q_A$ is a block quasi-tridiagonal matrix. By Theorem 2 in Rizvi and some calculations, we obtain Eq. (17).

(d) From the Eq. (A.11), and the Schur complement condition of positive definiteness, $\varSigma >0$ if and only if $\varSigma _T>0$ and $\varSigma _{\varvec{\phi }}-\varSigma _T\varSigma ^{-1}_T\varSigma _T=\varSigma _2^*>0$. Note that the block diagonal entries of $\varSigma _2^*$ are all positive definite, thus $\varSigma _2^*>0$.

Similarly, $\varSigma _T>0$ if and only if

$$\begin{aligned} \varSigma _T^{(1)}>0,\ \{\varSigma _T\}_{kk}-{B^{(k)}}'{\varSigma _T^{(k-1)}}^{-1}{B^{(k)}}>0,\ k=2,\ldots ,r+1,\ \{\varSigma _T\}_{r+2,r+2}>0,\nonumber \\ \end{aligned}$$

(A.13)

where $\{\varSigma _T\}_{ij}$ denotes the (i, j)th block of $\varSigma _T$, and the first $(r+1)$ leading principal block sub-matrices of $\varSigma _T$ are

$$\begin{aligned} \begin{aligned} \varSigma _T^{(1)}&=\{\varSigma _T\}_{11},\ \varSigma _T^{(k)}=\begin{pmatrix} \varSigma _T^{(k-1)}&{} B^{(k)}\\ {B^{(k)}}' &{} \{\varSigma _T\}_{kk}\end{pmatrix},\ k=2,\ldots ,r+1,\\ {B^{(2)}}&=\{\varSigma _T\}_{12},\ {B^{(k)}}'=(\mathbf {O}_{p_1,(k-2)p_1},\{\varSigma _T\}_{k-1,k}),\ k=3,\ldots ,r+1. \end{aligned}\nonumber \\ \end{aligned}$$

(A.14)

Note that $\{\varSigma _T\}_{r+2,r+2}=S_r-{\varvec{\mu }}_{R_r}=\frac{1}{n_r-1}S_{r-1}>0$. Consider the following lemma.

Lemma A.3

$$\begin{aligned} \begin{aligned} \mathrm{{(a).}}\&\varSigma _T^{(1)}=-\{\varSigma _T\}_{12}=\frac{2}{n_1...n_r(n_r-1)}{{\varvec{\mu }}_{R_0}}^{\otimes 2h}>0;\\&\{\varSigma _T\}_{k,k+1}=\varSigma _{k,k+1}<0,\ k=1,\ldots ,r;\\ \mathrm{{(b).}}\&\{\varSigma _T\}_{kk}+\{\varSigma _T\}_{k-1,k}+\{\varSigma _T\}_{k,k+1}= \frac{2}{n_1...n_{r-k+1}(n_{r-k+2}-1)} \\&\times L_pN_p({\varvec{\mu }}_{R_{k-1}}\otimes S_{k-2}+S_{k-2}\otimes {\varvec{\mu }}_{R_{k-1}})N_pL_p'>0,\ k=2,\ldots ,r+1. \end{aligned} \end{aligned}$$

When $k=r+1$, we set $n_1...n_{r-k+1}=1$.

Proof:

We only show that (b) holds when $k=2,\ldots ,r$ since the proof of (b) when $k=r+1$ is similar to the proof of (b) when $k<r+1$ and the proof of (a) is straightforward. By the Eq. (16), we have ${\varvec{\mu }}_{R_{k-1}}=\frac{n_{r-k+1}}{n_{r-k+1}-1}S_{k-1}-\frac{1}{n_{r-k+2}-1}S_{k-2}$ or

$$\begin{aligned} {{S_{k-1}}^{\otimes 2h}}=\frac{(n_{r-k+1}-1)^2}{n^2_{r-k+1}}\bigg [{\varvec{\mu }}_{R_{k-1}}+\frac{1}{n_{r-k+2}-1}S_{k-2}\bigg ]^{\otimes 2h},\ k=2,\ldots ,r-1. \end{aligned}$$

Thus,

$$\begin{aligned} \begin{aligned} \{\varSigma _T\}_{kk}&+\{\varSigma _T\}_{k-1,k}+\{\varSigma _T\}_{k,k+1}=\varSigma _{kk}-\{\varSigma _2^*\}_{kk}+\varSigma _{k-1,k}+\varSigma _{k,k+1}\\ =&\frac{2}{n_1\ldots n_{r-k}}\bigg [\frac{{{S_{k-2}}^{\otimes 2h}}}{n_{r-k+1}(n_{r-k+2}-1)^3}+ \frac{n_{r-k+1}^2{{S_{k-1}}^{\otimes 2h}}}{(n_{r-k+1}-1)^3}\bigg ]-\frac{2}{n_1\cdots n_{r-k+1}}{{{\varvec{\mu }}_{R_{k-1}}}^{\otimes 2h}}\\&-\frac{2\cdot n_{r-k+2}{{S_{k-2}}^{\otimes 2h}}}{n_1\cdots n_{r-k+1}(n_{r-k+2}-1)^3}-\frac{2\cdot n_{r-k+1}{{S_{k-1}}^{\otimes 2h}}}{n_1\cdots n_{r-k}(n_{r-k+1}-1)^3}\\ =&\frac{2\cdot n_{r-k+1}{{S_{k-1}}^{\otimes 2h}}}{n_1\cdots n_{r-k}(n_{r-k+1}-1)^2} -\frac{2\cdot {{S_{k-2}}^{\otimes 2h}}}{n_1\cdots n_{r-k+1}(n_{r-k+2}-1)^2} -\frac{2}{n_1\cdots n_{r-k+1}}{{{\varvec{\mu }}_{R_{k-1}}}^{\otimes 2h}}\\ =&\frac{2}{n_1\cdots n_{r-k+1}(n_{r-k+2}-1)}L_pN_p({\varvec{\mu }}_{R_{k-1}}\otimes S_{k-2}+S_{k-2}\otimes {\varvec{\mu }}_{R_{k-1}})N_pL_p'>0,\ k=2,\ldots ,r. \end{aligned} \end{aligned}$$

We then prove that the Eq. (A.13) is true by Lemma A.3 and the mathematical induction. Also, for any two square symmetric matrices A and B, $A>B\ (A\ge B)$ denotes $A-B>0\ (A-B\ge 0)$.

For $m=1$, by Lemma A.3 (a)., we have $\varSigma _T^{(1)}>0$. For $m=2$, by the Eq. (A.14) and Lemma A.3 (a), $-{B^{(2)}}'{\varSigma _T^{(1)}}^{-1}{B^{(2)}}=-\{\varSigma _T\}_{12}'{\varSigma _T^{(1)}}^{-1}\{\varSigma _T\}_{12}=\{\varSigma _T\}_{12}$ and $\{\varSigma _T\}_{23}=\varSigma _{23}<0$, and by Lemma A.3 (b), we have

$$\begin{aligned} \begin{aligned} \{\varSigma _T\}_{22}-{B^{(2)}}'{\varSigma _T^{(1)}}^{-1}{B^{(2)}} =\{\varSigma _T\}_{22}+\{\varSigma _T\}_{12}>\{\varSigma _T\}_{22}+\{\varSigma _T\}_{12}+\{\varSigma _T\}_{23}>0. \end{aligned} \end{aligned}$$

Suppose for $m=k$, $2\le k\le r-1$,

$$\begin{aligned} -{B^{(k)}}'{\varSigma _T^{(k-1)}}^{-1}{B^{(k)}}\ge \{\varSigma _T\}_{k-1,k},\ \{\varSigma _T\}_{kk}-{B^{(k)}}'{\varSigma _T^{(k-1)}}^{-1}{B^{(k)}}>0. \end{aligned}$$

For $m=k+1$, by Lemma A.3, $\{\varSigma _T\}_{kk}+\{\varSigma _T\}_{k-1,k}+\{\varSigma _T\}_{k,k+1}>0$ and $-\{\varSigma _T\}_{k,k+1}=-\varSigma _{k,k+1}>0$. This implies

$$\begin{aligned}\begin{aligned} \{\varSigma _T\}_{kk}-{B^{(k)}}'{\varSigma _T^{(k-1)}}^{-1}{B^{(k)}}\ge \{\varSigma _T\}_{kk}+\{\varSigma _T\}_{k-1,k}> -\{\varSigma _T\}_{k,k+1}>0, \end{aligned}\end{aligned}$$

and hence

$$\begin{aligned}\begin{aligned} -{B^{(k+1)}}'{\varSigma _T^{(k)}}^{-1}{B^{(k+1)}}&=-(\mathbf {O}_{p_1,(k-1)p_1},\{\varSigma _T\}_{k,k+1}){\varSigma _T^{(k)}}^{-1}(\mathbf {O}_{p_1,(k-1)p_1},\{\varSigma _T\}_{k,k+1})'\\&=-\{\varSigma _T\}_{k,k+1}[\{\varSigma _T\}_{kk}-{B^{(k)}}'{\varSigma _T^{(k-1)}}^{-1}{B^{(k)}}]^{-1}\{\varSigma _T\}_{k,k+1} \ge \{\varSigma _T\}_{k,k+1}. \end{aligned}\end{aligned}$$

Similarly, by Lemma A.3, $\{\varSigma _T\}_{k+1,k+1}+\{\varSigma _T\}_{k,k+1}+\{\varSigma _T\}_{k+1,k+2}>0$ and $-\{\varSigma _T\}_{k+1,k+2}=-\varSigma _{k+1,k+2}>0$, we have

$$\begin{aligned}&\{\varSigma _T\}_{k+1,k+1}-{B^{(k+1)}}'{\varSigma _T^{(k)}}^{-1}{B^{(k+1)}}\\&\ge \{\varSigma _T\}_{k+1,k+1}+\{\varSigma _T\}_{k,k+1}> -\{\varSigma _T\}_{k+1,k+2}>0. \end{aligned}$$

This completes the proof. $\square$

Proofs of Theorem 4 and Corollary 2:

The proofs of Theorem 4 and Corollary 2 are similar to Theorems 2 and 3, and Corollary 1, respectively. We omit them to save space. $\square$