Abstract
The current literature formally links “OR forms” (named after Osborne and Rubinstein, in A course in game theory. MIT, London, 1994) with “KS forms” (named after Kuhn and Selten by Kline and Luckraz, in Econ Theory Bull 4:85–94, 2016). It also formally links “simple forms” with “AR forms” (the former is less prominent than the latter, and both are from Alós-Ferrer and Ritzberger, in The theory of extensive form games. Springer, Berlin, 2016a). This paper makes three contributions. First, it introduces a fifth game form whose nodes are sets of past choices. Second, it formally links these new “choice-set forms” with OR forms. Third, it formally links KS forms with simple forms. The result is a formal five-way equivalence which provides game theorists with a broad spectrum of alternative game specifications.
Similar content being viewed by others
1 Introduction
1.1 Introducing choice-set forms
The first contribution of this paper is to introduce a new game specification in which nodes are sets of past choices. An example choice-set form appears in Fig. 1. This is similar but not identical to the well-known Osborne-Rubinstein (OR) game specification in which nodes are sequences of past choices. An example OR form also appears in Fig. 1. The new specification has an apparent advantage in the sense that sets are simpler mathematical objects than sequences. Section 7 carefully discusses the advantages and disadvantages of the new specification relative to the OR form, and also relative to the remaining three specifications in this paper.
Selten’s “horse” in each of the five specifications. This paper [a] introduces choice-set forms, [b] links choice-set forms and OR forms, and [c] links KS forms and simple forms. (Shown are the tree, the choices, and the information sets of each of five forms. Not shown are the forms’ players. Preferences are not formulated in this paper.)
1.2 Linking choice-set forms and OR forms
The second contribution of this paper is to build a formal connection between choice-set forms and OR forms. This formal equivalence will require two qualifications, because choice-set forms are slightly less general than OR forms in two regards. First, choice-set forms implicitly impose no absentmindedness in the sense of Piccione and Rubinstein (1997). Second, they implicitly impose no shared alternatives in the sense that two information sets are not allowed to share the same (feasible) alternatives (i.e., choices).
Theorem 3.1 shows that every OR form with no absentmindedness and no shared alternatives is equivalent to a choice-set form. Conversely, Theorem 3.2 shows that every choice-set form is equivalent to an OR form with no absentmindedness and no shared alternatives. Thus the theorems show (given no absentmindedness and no shared alternatives) that there is a logical redundancy at the heart of the OR specification: sets of past choices can unambiguously replace sequences of past choices.
All five specifications are essentially equivalent, even though they are fundamentally different in how they specify nodes and choices. (A minor issue is that only OR forms and KS forms allow absentmindedness. Section 7.1 discusses absentmindedness, shared alternatives, and two other minor issues.)
1.3 Linking OR forms, KS forms, simple forms, and AR forms
Let an “AR form” be a discrete extensive form as defined by Alós-Ferrer and Ritzberger (2016a) (henceforth AR16). An example AR form appears in Fig. 1. Such forms extend the specification of von Neumann and Morgenstern (1944). Incidentally, AR16 also defines non-discrete extensive forms for differential and yet more general games. Such non-discrete forms are beyond the scope of this paper.
The current literatureFootnote 1 does not provide a formal connection between OR forms and AR forms. This may be surprising because some prominent and valuable articlesFootnote 2 have tangentially and informally suggested otherwise. It seems that the misstep was caused by improperly combining the following two (correct) results from AR16. [a] AR16 Example 6.5 (p. 145) essentially says that OR trees constitute a special case of “simple trees”. This accords with Fig. 2’s top line, which shows that OR trees specify nodes as choice sequences while simple trees specify nodes as abstract entities. [b] AR16 Theorems 6.2 and 6.4 (pp. 139 and 147) say that “simple forms” are equivalent to AR forms. This equivalence is repeated here as Theorems 6.1 and 6.2, and is shown between the last two columns of Fig. 2. Together, [a] and [b] might seem to suggest that OR forms are special cases of AR forms. But this logic would be faulty because [a] concerns only trees while [b] concerns entire forms.Footnote 3 Thus the reasoning does not provide a formal link between OR forms and AR forms.
Fortunately, it only remains to link OR forms and simple forms because [b] links simple forms and AR forms. Further, part of this remaining gap is bridged by Kline and Luckraz (2016) (henceforth KL16). They essentially show that OR forms are equivalent to “KS forms”, where the initials K and S correspond to Kuhn (1953) and Selten (1975). This equivalence is repeated here as Theorems 4.1 and 4.2, and is shown between the OR and KS columns of Fig. 2.Footnote 4
Thus it yet remains to link KS forms and simple forms. KS forms and simple forms are similar in that they both specify nodes as abstract entities (as shown in the top row of Fig. 2). However, KS forms and simple forms differ in that KS forms specify their choices as abstract entities, while simple forms specify their choices as sets of nodes (as shown in the second row of Fig. 2).
The third contribution of this paper is to bridge this gap between KS forms and simple forms. This new equivalence appears as Theorems 5.1 and 5.2, and is shown between the KS and simple columns of Fig. 2. With this missing piece in place, it emerges that all five specifications are essentially equivalent. This provides game theorists with a wide spectrum of equivalent specifications.
1.4 Organization
Sections 2, 3, 4, 5, and 6 of this paper move from left to right across the five specifications in Fig. 2. Section 7 considers the minor qualifications in the theorems, and discusses the advantages and disadvantages of each game specification. Finally, the four pairs of equivalence theorems in this paper suggest four equivalences between subcategories of a category of game forms. First steps in this direction are Streufert (2018a, b).
2 Choice-set Forms
The following game specification is new.
Let N be a set of nodesn, and let C be a set of choicesc. By assumption, each node is a set of choices. In other words, each node n satisfies \(n{ \ }{ \subseteq }{ \ }C\). A node can be either a finite set or an infinite set. Let T be the set of finite nodes t. In other words, let \(T = { \lbrace }{ \ }n{ \in }N{ \ }|{ \ }n{ \ }\text {is a finite set}{ \ }{ \rbrace }\). A choice-set tree is a pair (C, N) such that [cs1] N is a nonempty collection of subsets of C,

To understand [cs2]Footnote 5, let a last choice of a finite node t be any choice \(c{ \in }t\) such that  is also a node. In other words, let a last choice of a node be any choice in the node whose removal results in another node. [cs2] requires that each nonempty node has a unique last choice. For example, the pair \(C = { \lbrace }\mathsf {a}{ \rbrace }\) and \(N = { \lbrace }{ \lbrace }\mathsf {a}{ \rbrace }{ \rbrace }\) does not satisfy [cs2] because \(T = N\) and the node \(t = { \lbrace }\mathsf {a}{ \rbrace }\) does not have a last choice. In contrast, the pair \(C = { \lbrace }\mathsf {a}{ \rbrace }\) and \(N = { \lbrace }{ \lbrace }{ \rbrace },{ \lbrace }\mathsf {a}{ \rbrace }{ \rbrace }\) does satisfy [cs2] because \({ \lbrace }\mathsf {a}{ \rbrace }\) is the only nonempty finite node and its last choice is \(\mathsf {a}\). For another example, the pair \(C = { \lbrace }\mathsf {a,b}{ \rbrace }\) and \(N = { \lbrace }{ \lbrace }{ \rbrace },{ \lbrace }\mathsf {a}{ \rbrace },{ \lbrace }\mathsf {b}{ \rbrace },{ \lbrace }\mathsf {a,b}{ \rbrace }{ \rbrace }\) violates [cs2] because both \(\mathsf {a}\) and \(\mathsf {b}\) are last choices of the node \({ \lbrace }\mathsf {a,b}{ \rbrace }\). In contrast, the pair \(C = { \lbrace }\mathsf {a,b}{ \rbrace }\) and \(N = { \lbrace }{{ \lbrace }{ \rbrace },{ \lbrace }\mathsf {b}{ \rbrace },{ \lbrace }\mathsf {a,b}{ \rbrace }}{ \rbrace }\) satisfies [cs2]. Finally, consider the set C of choices and the set N of nodes shown in the top left diagram of Fig. 1. This pair of sets satisfies [cs2] because each of its eight nonempty nodes has a unique last choice.
is also a node. In other words, let a last choice of a node be any choice in the node whose removal results in another node. [cs2] requires that each nonempty node has a unique last choice. For example, the pair \(C = { \lbrace }\mathsf {a}{ \rbrace }\) and \(N = { \lbrace }{ \lbrace }\mathsf {a}{ \rbrace }{ \rbrace }\) does not satisfy [cs2] because \(T = N\) and the node \(t = { \lbrace }\mathsf {a}{ \rbrace }\) does not have a last choice. In contrast, the pair \(C = { \lbrace }\mathsf {a}{ \rbrace }\) and \(N = { \lbrace }{ \lbrace }{ \rbrace },{ \lbrace }\mathsf {a}{ \rbrace }{ \rbrace }\) does satisfy [cs2] because \({ \lbrace }\mathsf {a}{ \rbrace }\) is the only nonempty finite node and its last choice is \(\mathsf {a}\). For another example, the pair \(C = { \lbrace }\mathsf {a,b}{ \rbrace }\) and \(N = { \lbrace }{ \lbrace }{ \rbrace },{ \lbrace }\mathsf {a}{ \rbrace },{ \lbrace }\mathsf {b}{ \rbrace },{ \lbrace }\mathsf {a,b}{ \rbrace }{ \rbrace }\) violates [cs2] because both \(\mathsf {a}\) and \(\mathsf {b}\) are last choices of the node \({ \lbrace }\mathsf {a,b}{ \rbrace }\). In contrast, the pair \(C = { \lbrace }\mathsf {a,b}{ \rbrace }\) and \(N = { \lbrace }{{ \lbrace }{ \rbrace },{ \lbrace }\mathsf {b}{ \rbrace },{ \lbrace }\mathsf {a,b}{ \rbrace }}{ \rbrace }\) satisfies [cs2]. Finally, consider the set C of choices and the set N of nodes shown in the top left diagram of Fig. 1. This pair of sets satisfies [cs2] because each of its eight nonempty nodes has a unique last choice.
To understand [cs3], note that this equation relates the infinite nodes (that is, the members of  ) to the finite nodes (that is, the members of T). By definition, a chain in T is a subcollection \(T^*{ \ }{ \subseteq }{ \ }T\) such that any two distinct nodes t and \(t^{ \prime }\) in \(T^*\) satisfy \(t{ \ }{ \subset }{ \ }t^{ \prime }\) or \(t{ \ }{ \supset }{ \ }t^{ \prime }\). The union of an infinite chain of finite nodes is obviously an infinite set. The \({ \supseteq }\) direction of [cs3] requires that each such union must be a node. For example, the pair \(C = { \mathbb Z}\) and \(N = { \lbrace }{{ \lbrace }{ \rbrace },{ \lbrace }\mathsf {4}{ \rbrace },{ \lbrace }\mathsf {4,5}{ \rbrace },{ \lbrace }\mathsf {4,5,6}{ \rbrace },\ldots }{ \rbrace }\) violates [cs3] because [a] \(T = N\), [b] \(T^* = T\) is an infinite chain in T, and [c] \({ \cup }T^* = { \lbrace }\mathsf {4,5,6,\ldots }{ \rbrace }{ \ }{ \notin }{ \ }N\). In contrast the pair \(C = { \mathbb Z}\) and \(N = { \lbrace }{{ \lbrace }{ \rbrace },{ \lbrace }\mathsf {4}{ \rbrace },{ \lbrace }\mathsf {4,5}{ \rbrace },{ \lbrace }\mathsf {4,5,6}{ \rbrace },\ldots }{ \rbrace }\)\({ \cup }\)\({ \lbrace }{{ \lbrace }\mathsf {4,5,6,}\ldots { \rbrace }}{ \rbrace }\) satisfies [cs3]. Meanwhile, the \({ \subseteq }\) direction of [cs3] requires that every infinite node is the union of an infinite chain of finite nodes. For example, the pair \(C = { \mathbb Z}\) and \(N = { \lbrace }{{ \lbrace }{ \rbrace },{ \lbrace }\mathsf {4}{ \rbrace },{ \lbrace }\mathsf {4,5}{ \rbrace },{ \lbrace }\mathsf {4,5,6}{ \rbrace },\ldots }{ \rbrace }\)\({ \cup }\)\({ \lbrace }{{ \lbrace }\mathsf {4,5,6},\ldots { \rbrace },{ \lbrace }\mathsf {5,6,7},\ldots { \rbrace }}{ \rbrace }\) violates [cs3] because \({ \lbrace }\mathsf {5,6,7,\ldots }{ \rbrace }\) cannot be constructed as the union of an infinite chain of finite nodes. Incidentally, the \({ \subseteq }\) direction of [cs3] implies that every infinite node is countable. It also implies, with the help of [cs1]–[cs2], that \({ \lbrace }{ \rbrace }{ \ }{ \in }{ \ }T\).Footnote 6 Call \({ \lbrace }{ \rbrace }\) the root node.
) to the finite nodes (that is, the members of T). By definition, a chain in T is a subcollection \(T^*{ \ }{ \subseteq }{ \ }T\) such that any two distinct nodes t and \(t^{ \prime }\) in \(T^*\) satisfy \(t{ \ }{ \subset }{ \ }t^{ \prime }\) or \(t{ \ }{ \supset }{ \ }t^{ \prime }\). The union of an infinite chain of finite nodes is obviously an infinite set. The \({ \supseteq }\) direction of [cs3] requires that each such union must be a node. For example, the pair \(C = { \mathbb Z}\) and \(N = { \lbrace }{{ \lbrace }{ \rbrace },{ \lbrace }\mathsf {4}{ \rbrace },{ \lbrace }\mathsf {4,5}{ \rbrace },{ \lbrace }\mathsf {4,5,6}{ \rbrace },\ldots }{ \rbrace }\) violates [cs3] because [a] \(T = N\), [b] \(T^* = T\) is an infinite chain in T, and [c] \({ \cup }T^* = { \lbrace }\mathsf {4,5,6,\ldots }{ \rbrace }{ \ }{ \notin }{ \ }N\). In contrast the pair \(C = { \mathbb Z}\) and \(N = { \lbrace }{{ \lbrace }{ \rbrace },{ \lbrace }\mathsf {4}{ \rbrace },{ \lbrace }\mathsf {4,5}{ \rbrace },{ \lbrace }\mathsf {4,5,6}{ \rbrace },\ldots }{ \rbrace }\)\({ \cup }\)\({ \lbrace }{{ \lbrace }\mathsf {4,5,6,}\ldots { \rbrace }}{ \rbrace }\) satisfies [cs3]. Meanwhile, the \({ \subseteq }\) direction of [cs3] requires that every infinite node is the union of an infinite chain of finite nodes. For example, the pair \(C = { \mathbb Z}\) and \(N = { \lbrace }{{ \lbrace }{ \rbrace },{ \lbrace }\mathsf {4}{ \rbrace },{ \lbrace }\mathsf {4,5}{ \rbrace },{ \lbrace }\mathsf {4,5,6}{ \rbrace },\ldots }{ \rbrace }\)\({ \cup }\)\({ \lbrace }{{ \lbrace }\mathsf {4,5,6},\ldots { \rbrace },{ \lbrace }\mathsf {5,6,7},\ldots { \rbrace }}{ \rbrace }\) violates [cs3] because \({ \lbrace }\mathsf {5,6,7,\ldots }{ \rbrace }\) cannot be constructed as the union of an infinite chain of finite nodes. Incidentally, the \({ \subseteq }\) direction of [cs3] implies that every infinite node is countable. It also implies, with the help of [cs1]–[cs2], that \({ \lbrace }{ \rbrace }{ \ }{ \in }{ \ }T\).Footnote 6 Call \({ \lbrace }{ \rbrace }\) the root node.
Now derive two entities from a choice-set tree (C, N). First, define \((C_t)_{t{ \in }T}\) at each t by \(C_t = { \lbrace }\,c{ \in }C\,|\,c{ \notin }t{ \ }\text {and}{ \ }t{ \cup }{ \lbrace }c{ \rbrace }{ \in }T\,{ \rbrace }\). Thus each \(C_t\) is the set of choices that are feasible at the node t. Second, define \(X = { \lbrace }\,t{ \in }T\,|\,C_t{ \ne }{ \varnothing }\,{ \rbrace }\). Call its members the decision nodes. Then assume
[cs4] considers a collection of sets. Call each of its member sets an information set. Note each \({ \lbrace }t{ \in }X|c{ \in }C_t{ \rbrace }\) is the set of decision nodes from which the choice c is feasible. Routinely, the same set is generated by multiple choices. That set is the information set from which those choices are feasible. [cs4] requires that these constructed information sets cannot intersect. The familiar properties of information sets then follow. In particular, [a] the collection of information sets partitions the decision-node set X,Footnote 7 and [b] two nodes in the same information set have the same set of feasible choices.Footnote 8
For example, consider the choice-set tree defined by \(C = { \lbrace }\mathsf {a,b,e,f}{ \rbrace }\) and \(N = { \lbrace }{{ \lbrace }{ \rbrace },{ \lbrace }\mathsf {a}{ \rbrace },{ \lbrace }\mathsf {b}{ \rbrace },{ \lbrace }\mathsf {a,e}{ \rbrace },{ \lbrace }\mathsf {a,f}{ \rbrace },{ \lbrace }\mathsf {b,e}{ \rbrace }}{ \rbrace }\). Here \(X = { \lbrace }{{ \lbrace }{ \rbrace },{ \lbrace }\mathsf {a}{ \rbrace },{ \lbrace }\mathsf {b}{ \rbrace }}{ \rbrace }\), \(C_{{ \lbrace }{ \rbrace }} = { \lbrace }\mathsf {a,b}{ \rbrace }\), \(C_{{ \lbrace }\mathsf {a}{ \rbrace }} = { \lbrace }\mathsf {e,f}{ \rbrace }\), and \(C_{{ \lbrace }\mathsf {b}{ \rbrace }} = { \lbrace }\mathsf {e}{ \rbrace }\). Thus \({ \lbrace }t{ \in }X|\mathsf {e}{ \in }C_t{ \rbrace } = { \lbrace }{{ \lbrace }\mathsf {a}{ \rbrace },{ \lbrace }\mathsf {b}{ \rbrace }}{ \rbrace }\) and \({ \lbrace }t{ \in }X|\mathsf {f}{ \in }C_t{ \rbrace } = { \lbrace }{ \lbrace }\mathsf {a}{ \rbrace }{ \rbrace }\). These two sets of decision nodes are unequal and intersecting, in violation of [cs4]. In contrast, consider Fig. 1’s choice-set tree (the figure’s dashed line is irrelevant at this point). In other words, consider \(C = { \lbrace }\mathsf {a,b,g,d,e,f}{ \rbrace }\) and \(N = { \lbrace }{{ \lbrace }{ \rbrace },{ \lbrace }\mathsf {a}{ \rbrace },{ \lbrace }\mathsf {a,g}{ \rbrace },}\)\({ \lbrace }\mathsf {b}{ \rbrace },\)\({ \lbrace }\mathsf {a,d}{ \rbrace },\)\({ \lbrace }\mathsf {b,e}{ \rbrace },\)\({ \lbrace }\mathsf {b,f}{ \rbrace },\)\({ \lbrace }\mathsf {a,d,e}{ \rbrace },\)\({ \lbrace }\mathsf {a,d,f}{ \rbrace }{ \rbrace }\). Here \(X = { \lbrace }{{ \lbrace }{ \rbrace },{ \lbrace }\mathsf {a}{ \rbrace },{ \lbrace }\mathsf {b}{ \rbrace },{ \lbrace }\mathsf {a,d}{ \rbrace }}{ \rbrace }\), \(C_{{ \lbrace }{ \rbrace }} = { \lbrace }\mathsf {a,b}{ \rbrace }\), \(C_{{ \lbrace }\mathsf {a}{ \rbrace }} = { \lbrace }\mathsf {g,d}{ \rbrace }\), and \(C_{{ \lbrace }\mathsf {b}{ \rbrace }} = C_{{ \lbrace }\mathsf {a,d}{ \rbrace }} = { \lbrace }\mathsf {e,f}{ \rbrace }\). Thus [i] \({ \lbrace }t{ \in }X|\mathsf {a}{ \in }C_t{ \rbrace }\)\(=\)\({ \lbrace }t{ \in }X|\mathsf {b}{ \in }C_t{ \rbrace }\)\(=\)\({ \lbrace }{ \lbrace }{ \rbrace }{ \rbrace }\), and [ii] \({ \lbrace }t{ \in }X|\mathsf {g}{ \in }C_t{ \rbrace } = { \lbrace }t{ \in }X|\mathsf {d}{ \in }C_t{ \rbrace } = { \lbrace }{ \lbrace }\mathsf {a}{ \rbrace }{ \rbrace }\), and [iii] \({ \lbrace }t{ \in }X|\mathsf {e}{ \in }C_t{ \rbrace }\)\(=\)\({ \lbrace }t{ \in }X|\mathsf {f}{ \in }C_t{ \rbrace }\)\(=\)\({ \lbrace }{{ \lbrace }\mathsf {b}{ \rbrace },{ \lbrace }\mathsf {a,d}{ \rbrace }}{ \rbrace }\) (the figure’s dashed line shows this set [iii]). These three sets of decision nodes are disjoint, as [cs4] requires. They are the form’s (constructed) information sets.
Further, let I be a set of players i, and let \((C_i)_{i{ \in }I}\) assign a set \(C_i\) of choices to each player i. A choice-set form is a pair \(((C_i)_{i{ \in }I},N)\) such that \(({ \cup }_{i{ \in }I}C_i,N)\) is a choice-set tree which satisfies [cs4], and in addition, [cs5]  and [cs6] \(({ \forall }t{ \in }X)({ \exists }i{ \in }I){ \ }C_t{ \ }{ \subseteq }{ \ }C_i\). [cs5] requires that each choice is assigned to exactly one player. Thus [cs6] implies that all a decision node’s choices are assigned to exactly one player. Thus [b] (two paragraphs above) implies that all an information set’s choices are assigned to exactly one player.
and [cs6] \(({ \forall }t{ \in }X)({ \exists }i{ \in }I){ \ }C_t{ \ }{ \subseteq }{ \ }C_i\). [cs5] requires that each choice is assigned to exactly one player. Thus [cs6] implies that all a decision node’s choices are assigned to exactly one player. Thus [b] (two paragraphs above) implies that all an information set’s choices are assigned to exactly one player.
Incidentally, the set of outcomes is  . The set
. The set  consists of the infinite nodes, and the set
consists of the infinite nodes, and the set  consists of the finite nodes that are not decision nodes. Later, preferences can be assigned over
consists of the finite nodes that are not decision nodes. Later, preferences can be assigned over  , or more generally if appropriate assumptions are introduced, over some space of probability distributions over
, or more generally if appropriate assumptions are introduced, over some space of probability distributions over  .
.
3 OR forms
3.1 Definition
An OR form here is identical to a game in Osborne and Rubinstein (1994) (p. 200) without the players’ preferences. This specification is repeated in KL16 (p. 86).Footnote 9
Let C be a set of choicesc, and let \(\bar{N}\) be a set of nodes \(\bar{n}\). By assumption, each node is a sequence of choices. In other words, each node is of the form \(\bar{n}= (c_k)^K_{k=1}\), where \(K{ \ }{ \in }{ \ }{ \lbrace }0,1,2,\ldots { \rbrace }{ \cup }{ \lbrace }{ \infty }{ \rbrace }\). Note that \((c_k)^0_{k=1} = { \lbrace }{ \rbrace }\) is the empty sequence. An OR tree is a pair \((C,\bar{N})\) such that [OR1] \(\bar{N}\) is a nonempty collection of sequences in C, [OR2] \(({ \forall }\,(c_k)^K_{k=1}{ \in }\bar{N},\)\(L{<}K)\)\((c_k)^L_{k=1}{ \ }{ \in }{ \ }\bar{N}\) (where both \(K = { \infty }\) and \(L = 0\) are permitted), and [OR3] \(({ \forall }\,(c_k)^{ \infty }_{k=1}{ \in }C^{ \infty })\)\((c_k)^{ \infty }_{k=1}{ \ }{ \in }{ \ }\bar{N}\) if \(({ \forall }L{<}{ \infty }){ \ }(c_k)^L_{k=1}{ \ }{ \in }{ \ }\bar{N}\) (where \(C^{ \infty }\) is the collection of infinite sequences in C).
This paragraph derives three entities from an OR tree. First, let  be the collection of finite sequences \(\bar{t}\) belonging to \(\bar{N}\). Second, define \((C_{\bar{t}})_{\bar{t}{ \in }\bar{T}}\) at each \(\bar{t}\) by \(C_{\bar{t}} = { \lbrace }\,c{ \in }C\,|\,\bar{t}{ \oplus }(c){ \in }\bar{T}{ \ }{ \rbrace }\), where \(\bar{t}{ \oplus }(c)\) is the concatenation of the finite sequence \(\bar{t}\) with the one-element sequence (c). Thus each \(C_{\bar{t}}\) is the set of choices that are feasible at the node \(\bar{t}\). Third, define \(\bar{X}= { \lbrace }\,\bar{t}{ \in }\bar{T}\,|\,C_{\bar{t}}{ \ne }{ \varnothing }\,{ \rbrace }\). Call \(\bar{X}\) the set of decision nodes.
be the collection of finite sequences \(\bar{t}\) belonging to \(\bar{N}\). Second, define \((C_{\bar{t}})_{\bar{t}{ \in }\bar{T}}\) at each \(\bar{t}\) by \(C_{\bar{t}} = { \lbrace }\,c{ \in }C\,|\,\bar{t}{ \oplus }(c){ \in }\bar{T}{ \ }{ \rbrace }\), where \(\bar{t}{ \oplus }(c)\) is the concatenation of the finite sequence \(\bar{t}\) with the one-element sequence (c). Thus each \(C_{\bar{t}}\) is the set of choices that are feasible at the node \(\bar{t}\). Third, define \(\bar{X}= { \lbrace }\,\bar{t}{ \in }\bar{T}\,|\,C_{\bar{t}}{ \ne }{ \varnothing }\,{ \rbrace }\). Call \(\bar{X}\) the set of decision nodes.
Next let I be a set of playersi, and assign decision nodes to players by a player-assignment function \(\bar{P}\). In brief, assume [OR4] \(\bar{P}{:}\bar{X}{ \rightarrow }I\). Then associate with each player i a collection \(\bar{{ \mathscr {H}}}_i\) of information sets\(\bar{H}\). Assume [OR5] \(({ \forall }i{ \in }I){ \ }\bar{{ \mathscr {H}}}_i\) partitions \(\bar{P}^{-1}(i)\). Thus each player’s information-set collection \(\bar{{ \mathscr {H}}}_i\) partitions the player’s set \(\bar{P}^{-1}(i)\) of decision nodes. Further assume [OR6] \(({ \forall }\bar{H}{ \in }{ \cup }_{i{ \in }I}\bar{{ \mathscr {H}}}_i,\bar{t}{ \in }\bar{H},\bar{t}^{ \prime }{ \in }\bar{H})\)\(C_{\bar{t}} = C_{\bar{t}^{ \prime }}\). This is the usual assumption that two nodes in the same information set must have the same feasible choices. By definition, an OR form\({ \langle }(C,\bar{N}),(\bar{P},(\bar{{ \mathscr {H}}}_i)_{i{ \in }I}){ \rangle }\) is an OR tree \((C,\bar{N})\) together with a player set I, a player-assignment function \(\bar{P}\), and a list \((\bar{{ \mathscr {H}}}_i)_{i{ \in }I}\) of player information-set collections that satisfy [OR4]–[OR6].
Incidentally, the set of outcomes is  . The set
. The set  consists of the infinite sequences, and the set
consists of the infinite sequences, and the set  consists of the nondecision finite sequences. Later, preferences can be defined over
consists of the nondecision finite sequences. Later, preferences can be defined over  , or more generally if appropriate assumptions are introduced, over some space of probability distributions over
, or more generally if appropriate assumptions are introduced, over some space of probability distributions over  .
.
3.2 The equivalence between choice-set forms and OR forms
[OR6] states that two nodes in the same information set have the same alternatives.Footnote 10 As usual, define \(C_{\bar{H}}\) at each \(\bar{H}{ \ }{ \in }{ \ }{ \cup }_{i{ \in }I}\bar{{ \mathscr {H}}}_i\) by \(({ \forall }\bar{t}{ \in }\bar{H}){ \ }C_{\bar{H}} = C_{\bar{t}}\). Thus \(C_{\bar{H}}\) is the set of alternatives at the information set \(\bar{H}\). Say that an OR form has no shared alternatives if and only if \(({ \forall }\bar{H}{ \in }{ \cup }_{i{ \in }I}{ \mathscr {H}}_i,\bar{H}^{ \prime }{ \in }{ \cup }_{i{ \in }I}\bar{{ \mathscr {H}}}_i){ \ }\bar{H}{ \ }{ \ne }{ \ }\bar{H}^{ \prime }\) implies \(C_{\bar{H}}{ \cap }C_{\bar{H}^{ \prime }} = { \varnothing }\). Hence a form has no shared alternatives if and only if each of its information sets has its own alternatives. On the one hand, this condition is vacuous in the sense that one can always introduce enough alternatives so that each information set has its own alternatives. On the other hand, it is natural to repeatedly use the same alternatives in a repeated game.
An OR form has no absentmindedness if and only if  (Piccione and Rubinstein 1997, p. 10). Hence a form has no absentmindedness if and only if none of its information sets contains both a node and a predecessor of that node. No-absentmindedness is regarded as a very weak assumption. It is explicitly incorporated into the game specification of Kuhn (1953) (p. 48, Definition 2(II)), and is defended at length by AR16 (Sect. 4.2.3). Further, it is weaker than perfect recall, and AR16 (p. 150) argues that a game without perfect recall “fails to capture rational behaviour”.
(Piccione and Rubinstein 1997, p. 10). Hence a form has no absentmindedness if and only if none of its information sets contains both a node and a predecessor of that node. No-absentmindedness is regarded as a very weak assumption. It is explicitly incorporated into the game specification of Kuhn (1953) (p. 48, Definition 2(II)), and is defended at length by AR16 (Sect. 4.2.3). Further, it is weaker than perfect recall, and AR16 (p. 150) argues that a game without perfect recall “fails to capture rational behaviour”.
No-absentmindedness plays a pivotal role in this section, as the following proposition demonstrates. In the proposition, the function R takes any sequence \((c_k)^K_{k=1}\) to its range. In particular, if K is finite, R takes \((c_k)^K_{k=1} = (c_1,c_2,\ldots \,c_K)\) to \({ \lbrace }c_1,c_2,\ldots \,c_K{ \rbrace }\). Similarly, if K is infinite, R takes \((c_k)^K_{k=1} = (c_1,c_2,\ldots \,)\) to \({ \lbrace }c_1,c_2,\ldots \,{ \rbrace }\).
Proposition 3.0
Consider an OR form with no shared alternatives, and let \(\bar{N}\) be its collection of nodes. Then the form has no absentmindedness iff \(R|_{\bar{N}}\) is injective. (Proof: Lemma A.5(a\({ \Leftrightarrow }\)c).)
Consider the forward direction of the proposition. This paragraph notes how easy it is to derive injectivity when the form’s information sets are ordered. Consider any node \(\bar{n}\). Since a choice determines its information set because of the no-shared-alternatives assumption, the choices in \(R(\bar{n})\) must be played in the order of their information sets. Hence the set \(R(\bar{n})\) determines the sequence \(\bar{n}\).
An OR form with no absentmindedness. In accord with Proposition 3.0, \(R|_{\bar{N}}\) is injective
But the forward direction of Proposition 3.0 goes further. It shows that \(R|_{\bar{N}}\) is injective even when the form’s information sets are unordered, provided only that no-absentmindedness holds. For example, consider Fig. 3, which replicates the classic example of unordered information sets from Kuhn (1953), Fig. 1; Gilboa (1997), Fig. 2; Ritzberger (1999), Fig. 1; and Ritzberger (2002), Fig. 3.8. Unordered information sets give rise to choices that can be played in different orders. Accordingly, the choices \(\mathsf {a}^\mathsf {1}\) and \(\mathsf {a}^\mathsf {2}\) in Fig. 3 have been played in different orders at the nodes \((\mathsf {1}^\mathsf {*},\mathsf {a}^\mathsf {1},\mathsf {a}^\mathsf {2})\) and \((\mathsf {2}^\mathsf {*},\mathsf {a}^\mathsf {2},\mathsf {a}^\mathsf {1})\). However, the choices in \(R((\mathsf {1}^\mathsf {*},\mathsf {a}^\mathsf {1},\mathsf {a}^\mathsf {2})) = { \lbrace }\mathsf {1}^\mathsf {*},\mathsf {a}^\mathsf {1},\mathsf {a}^\mathsf {2}{ \rbrace }\) can only be played in the order \((\mathsf {1}^\mathsf {*},\mathsf {a}^\mathsf {1},\mathsf {a}^\mathsf {2})\), and the choices in \(R((\mathsf {2}^\mathsf {*},\mathsf {a}^\mathsf {2},\mathsf {a}^\mathsf {1})) = { \lbrace }\mathsf {2}^\mathsf {*},\mathsf {a}^\mathsf {1},\mathsf {a}^\mathsf {2}{ \rbrace }\) can only be played in the order \((\mathsf {2}^\mathsf {*},\mathsf {a}^\mathsf {2},\mathsf {a}^\mathsf {1})\). Intuitively, this happens because the set \({ \lbrace }\mathsf {1}^\mathsf {*},\mathsf {a}^\mathsf {1},\mathsf {a}^\mathsf {2}{ \rbrace }\) contains \(\mathsf {1}^\mathsf {*}\), and because the set \({ \lbrace }\mathsf {2}^\mathsf {*},\mathsf {a}^\mathsf {1},\mathsf {a}^\mathsf {2}{ \rbrace }\) contains \(\mathsf {2}^\mathsf {*}\). This suggests that if a form has two choices whose order is not exogenously determined, then any sequence that lists the two choices must also list another choice (or set of choices) that determines their order. Showing that this can be done, whenever there is no-absentmindedness, is the interesting part of the proposition’s proof.
Meanwhile, the reverse direction of Proposition 3.0 shows that no-absentmindedness is necessary for injectivity. For example, consider Fig. 4, which replicates the classic example of absentmindedness in Piccione and Rubinstein (1997), Fig. 1. Here R takes both the sequence \((\mathsf {a})\) and the sequence \((\mathsf {a,a})\) to the set \({ \lbrace }\mathsf {a}{ \rbrace }\). Thus, \(R|_{\bar{N}}\) is not injective. The proposition’s proof shows that something similar happens whenever no-absentmindedness is violated.
An OR form with absentmindedness. In accord with Proposition 3.0, \(R|_{\bar{N}}\) is not injective (consider \((\mathsf {a})\) and \(\mathsf {(a,a)}\))
Theorem 3.1 uses the forward direction of Proposition 3.0 to show that every OR form with no shared alternatives and no absentmindedness is equivalent to a choice-set form. The reverse direction of Proposition 3.0 shows that Theorem 3.1 cannot be extended to include any OR forms that have absentmindedness.
Theorem 3.1
(choice-set \({ \leftarrow }\) OR) Suppose \({ \langle }(C,\bar{N}),(\bar{P},(\bar{{ \mathscr {H}}}_i)_{i{ \in }I}){ \rangle }\) is an OR form with no shared alternatives and no absentmindedness. Define \(N = { \lbrace }R(\bar{n})|\bar{n}{ \in }\bar{N}{ \rbrace }\). Then (a) (C, N) is a choice-set tree and \(R|_{\bar{N}}\) is a bijection from \(\bar{N}\) onto N. Further, define \((C_i)_{i{ \in }I}\) at each i by \(C_i = { \cup }_{\bar{H}{ \in }\bar{{ \mathscr {H}}}_i}C_{\bar{H}}\) , where \((C_{\bar{H}})_{\bar{H}{ \in }\bar{{ \mathscr {H}}}_i}\) is derived from the OR form. Then (b) \(((C_i)_{i{ \in }I},N)\) is a choice-set form. (Proof A.7.)
Conversely, Theorem 3.2 shows that every choice-set form is equivalent to an OR form with no shared alternatives and no absentmindedness. The theorem’s proof constructs the OR form, and is the longest proof in the paper.
Theorem 3.2
(choice-set \({ \rightarrow }\)OR) Suppose \(((C_i)_{i{ \in }I},N)\) is a choice-set form. Then (a) there is an \(\bar{N}\) such that \(({ \cup }_{i{ \in }I}C_i,\bar{N})\) is an OR tree and \(R|_{\bar{N}}\) is a bijection from \(\bar{N}\) onto N. Further, derive \(\bar{T}\), \((C_{\bar{t}})_{\bar{t}{ \in }\bar{T}}\), and \(\bar{X}\) from this OR tree. Also define \(\bar{P}{:}\bar{X}{ \rightarrow }I\) at each \(\bar{t}{ \ }{ \in }{ \ }\bar{X}\) by setting \(\bar{P}(\bar{t})\) equal to the unique i for which \(C_{\bar{t}}{ \ }{ \subseteq }{ \ }C_i\). Also define \((\bar{{ \mathscr {H}}}_i)_{i{ \in }I}\) at each i by \(\bar{\mathscr {H}}_{i}={ \lbrace }\,{ \lbrace }\bar{t}{ \in }\bar{X}|c{ \in }C_{\bar{t}}{ \rbrace }{ \ne }{ \varnothing }\,|\,c{ \in }C_i\,{ \rbrace }\). Then (b) \({ \langle }({ \cup }_{i{ \in }I}C_i,\bar{N}),\)\((\bar{P},(\bar{{ \mathscr {H}}}_i)_{i{ \in }I}){ \rangle }\) is a well-defined OR form with no shared alternatives and no absentmindedness. (Proof A.8.)
4 KS forms
4.1 Definition
A KS form here is identical to a KS game (KL16, p. 89) without the players’ preferences.Footnote 11 The letters K and S refer to Kuhn (1953) and Selten (1975).
Begin with a set T of nodest, and a set E of edgese. By definition, a pair (T, E) is a directed graph if and only if \(E{ \ }{ \subseteq }{ \ }{ \lbrace }(t,t^{\sharp }){ \in }T^2|t{ \ne }t^{\sharp }{ \rbrace }\) (Bang-Jensen and Gutin 2009, p. 2). Say that one node timmediately precedes another node \(t^{\sharp }\) if and only if t is immediately succeeded by \(t^{\sharp }\) if and only if \((t,t^{\sharp }){ \ }{ \in }{ \ }E\). Further, say that a finite walk from\(t^1\)to\(t^K\) is a sequence \((t^k)^K_{k=1}\) such that \(K{ \in }{ \lbrace }2,3,\ldots { \rbrace }\) and \(({ \forall }k{<}K){ \ }(t^k,t^{k+1}){ \ }{ \in }{ \ }E\) (Bang-Jensen and Gutin 2009, p. 11). Similarly, an infinite walk from\(t^1\) is a sequence \((t^k)^K_{k=1}\) such that \(K = { \infty }\) and \(({ \forall }k{<}K){ \ }(t^k,t^{k+1}){ \ }{ \in }{ \ }E\). By definition, a KS graph-tree is a triple (T, E, r) such that [KS1] (T, E) is a directed graph and \(r{ \ }{ \in }{ \ }T\), and [KS2] for each  there is a unique finite walk from r to \(t^{\sharp }\). Call r the root node of the graph-tree. Further, let \(X = { \lbrace }t{ \in }T|({ \exists }t^{\sharp }{ \in }T)(t,t^{\sharp }){ \in }E{ \rbrace }\) be the set of nodes with at least one successor, and call each \(t{ \ }{ \in }{ \ }X\) a decision node.
there is a unique finite walk from r to \(t^{\sharp }\). Call r the root node of the graph-tree. Further, let \(X = { \lbrace }t{ \in }T|({ \exists }t^{\sharp }{ \in }T)(t,t^{\sharp }){ \in }E{ \rbrace }\) be the set of nodes with at least one successor, and call each \(t{ \ }{ \in }{ \ }X\) a decision node.
Next associate, with each node \(t{ \ }{ \in }{ \ }T\), a set \(C_{t}\) of feasible choicesc. Such a feasible set can be empty. Further, associate, with each node \(t{ \ }{ \in }{ \ }T\), a choice-to-successor function\({ \psi }_{t}{:}C_{t}{ \rightarrow }{ \lbrace }t^{\sharp }{ \in }T|(t,t^{\sharp }){ \in }E{ \rbrace }\), which is a bijection from t’s feasible set \(C_{t}\) of choices c onto the set \({ \lbrace }t^{\sharp }{ \in }T|(t,t^{\sharp }){ \in }E{ \rbrace }\) of nodes \(t^{\sharp }\) that immediately succeed t. For future reference, call this bijectivity assumption [KS3]. [KS3] implies [a] \(t{ \ }{ \in }{ \ }X\) if and only if [b] \(C_t{ \ }{ \ne }{ \ }{ \varnothing }\) if and only if [c] \({ \psi }_t\) is a nonempty function. By definition, a KS augmented-tree\({ \langle }(T,E,r),(C_{t},{ \psi }_{t})_{t{ \in }T}{ \rangle }\) is a KS graph-tree (T, E, r) together with a \((C_t,{ \psi }_t)_{t{ \in }T}\) consisting of feasible sets and choice-to-successor functions that satisfy [KS3].
Now introduce a set I of playersi, and assign decision nodes to players by a player-assignment functionP. Assume [KS4] \(P{:}X{ \rightarrow }I\). Then associate with each player i a collection \({ \mathscr {H}}_i\) of information setsH. Assume [KS5] \(({ \forall }i{ \in }I){ \ }{ \mathscr {H}}_i\) partitions \(P^{-1}(i)\). In other words, assume each player’s information-set collection \({ \mathscr {H}}_i\) partitions the player’s set \(P^{-1}(i)\) of decision nodes. Also assume [KS6] \(({ \forall }i{ \in }I,\)\(H{ \in }{ \mathscr {H}}_i,\)\(t{ \in }H,\)\(t^{ \prime }{ \in }H)\)\(C_t = C_{t^{ \prime }}\). Because of this, let \(C_{H}\) denote the feasible-choice set at the information set H. By definition, a KS form\({ \langle }(T,E,r),(C_t,{ \psi }_t)_{t{ \in }T},(P,({ \mathscr {H}}_i)_{i{ \in }I}){ \rangle }\) is a KS augmented-tree \({ \langle }(T,E,r), (C_{t},{ \psi }_{t})_{t}{ \rangle }\) together with a player set I, a player-assignment function P, and a list \(({ \mathscr {H}}_i)_{i{ \in }I}\) of player information-set collections that satisfy [KS4]–[KS6].
Incidentally, the collection of outcomes is  ,Footnote 12 where \({ \mathscr {W}}_r\) is the collection of (finite and infinite) walks from r, and where \({ \mathscr {W}}_r^X = { \lbrace }\,(t^k)^K_{k=0}{ \in }{ \mathscr {W}}_r\,|\,K{<}{ \infty },\,t^K{ \in }X\,{ \rbrace }\) is the collection of (finite) walks from r to a decision node. The collection
,Footnote 12 where \({ \mathscr {W}}_r\) is the collection of (finite and infinite) walks from r, and where \({ \mathscr {W}}_r^X = { \lbrace }\,(t^k)^K_{k=0}{ \in }{ \mathscr {W}}_r\,|\,K{<}{ \infty },\,t^K{ \in }X\,{ \rbrace }\) is the collection of (finite) walks from r to a decision node. The collection  consists of [i] the infinite walks from r, and [ii] the (finite) walks from r to nondecision nodes. Later, preferences can be defined over
consists of [i] the infinite walks from r, and [ii] the (finite) walks from r to nondecision nodes. Later, preferences can be defined over  , or more generally if appropriate assumptions are introduced, over some space of probability distributions over
, or more generally if appropriate assumptions are introduced, over some space of probability distributions over  .
.
4.2 The Kline/Luckraz equivalence between OR forms and KS forms
Theorem 4.1 requires some additional notation. As in the previous paragraph, consider a KS form and let \({ \mathscr {W}}_r\) be the collection of walks from r. Next let \({ \mathscr {W}}_r^T\)\(=\)\({ \lbrace }\,(t^k)^K_{k=0}{ \in }{ \mathscr {W}}_r\,|\,K{<}{ \infty }\,{ \rbrace }\) be the collection of finite walks from r. Finally, let the node-to-walk function\(w{:}T{ \rightarrow }{ \lbrace }(r){ \rbrace }{ \cup }{ \mathscr {W}}_r^T\) be the bijection mapping [i] \(r{ \ }{ \in }{ \ }T\) to (r) and [ii] each  to [KS2]’s walk from r to \(t^{\sharp }\).
to [KS2]’s walk from r to \(t^{\sharp }\).
Theorem 4.1
(OR \({ \leftarrow }\) KS) Suppose \({ \langle }(T,E,r),(C_{t},{ \psi }_{t})_{t{ \in }T},(P,({ \mathscr {H}}_i)_{i{ \in }I}){ \rangle }\) is a KS form, and derive its \({ \mathscr {W}}_r\). Define \(C = { \cup }_{t{ \in }T}C_{t}\). Also define \({ \alpha }\) and \(\bar{N}\) by letting \({ \alpha }\) be the surjective function, from \({ \lbrace }(r){ \rbrace }{ \cup }{ \mathscr {W}}_r\) onto \(\bar{N}{ \ }{ \subseteq }{ \ }C^{ \infty }\), such that \({ \alpha }((r)) = { \lbrace }{ \rbrace }\) and \(({ \forall }(t^k)^K_{k=0}{ \in }{ \mathscr {W}}_r)\)\({ \alpha }((t^k)^K_{k=0}) = ({ \psi }^{-1}_{t^{k-1}}(t^k))^K_{k=1}\). Then (a) \({ \alpha }\) is a well-defined bijection and \((C,\bar{N})\) is an OR tree. Further, derive \(w{:}T{ \rightarrow }{ \lbrace }(r){ \rbrace }{ \cup }{ \mathscr {W}}_r^T\) from the KS form by the previous paragraph. Also derive \(\bar{T}\) and \(\bar{X}\) from the OR tree \((C,\bar{N})\). Also define \(\bar{P}{:}\bar{X}{ \rightarrow }I\) at each \(\bar{t}{ \ }{ \in }{ \ }\bar{X}\) by \(\bar{P}(\bar{t}) = P{ \circ }w^{-1}{ \circ }{ \alpha }^{-1}(\bar{t})\). Also define \((\bar{{ \mathscr {H}}}_i)_{i{ \in }I}\) at each i by \(\bar{{ \mathscr {H}}}_i = { \lbrace }{ \ }{ \lbrace }{ \alpha }{ \circ }w(t)|t{ \in }H{ \rbrace }{ \ }|\)\(H{ \in }{ \mathscr {H}}_i{ \ }{ \rbrace }\). Then (b) \({ \langle }(C,\bar{N}),(\bar{P},(\bar{{ \mathscr {H}}}_i)_{i{ \in }I}){ \rangle }\) is an OR form. (Corollary of KL16 Lemma 2 and KL16 Theorem 1.)Footnote 13
Theorem 4.2
(OR \({ \rightarrow }\) KS) Suppose \({ \langle }(C,\bar{N}),(\bar{P},(\bar{{ \mathscr {H}}}_i)_{i{ \in }I}){ \rangle }\) is an OR form, and derive its \(\bar{T}\) and \((C_{\bar{t}})_{\bar{t}{ \in }\bar{T}}\). Define \(E = { \lbrace }{ \ }(\bar{t},\bar{t}^{\,\sharp }){ \in }\bar{T}^2{ \ }|{ \ }({ \exists }c{ \in }C){ \ }\bar{t}{ \oplus }(c){=}\bar{t}^{\,\sharp }{ \ }{ \rbrace }\). Then (a) \((\bar{T},E,{ \lbrace }{ \rbrace })\) is a KS graph-tree. Further, define \(({ \psi }_{\bar{t}}{:}C_{\bar{t}}{ \rightarrow }\bar{T})_{\bar{t}{ \in }\bar{T}}\) at each \(\bar{t}\) by \(({ \forall }c{ \in }C_{\bar{t}}){ \ }{ \psi }_{\bar{t}}(c) = \bar{t}{ \oplus }(c)\). Then (b) \({ \langle }(\bar{T},E,{ \lbrace }{ \rbrace }),(C_{\bar{t}},{ \psi }_{\bar{t}})_{\bar{t}{ \in }\bar{T}},(\bar{P},(\bar{{ \mathscr {H}}}_i)_{i{ \in }I}){ \rangle }\) is a KS form. (Corollary of KL16 Theorem 2.)
5 Simple forms
5.1 Definition
A simple form here is virtually identical to a simple extensive form in AR16 (p. 146).Footnote 14 The difference is insignificant.Footnote 15
Let T be a set of nodes t, and let \({ \ge }\) be a binary relation on T. A simple tree (AR16, p. 143) is a pair \((T,{ \ge })\) such that [s1] \((T,{ \ge })\) is a partial ordering (AR16, p. 20) with a maximum, [s2] \(({ \forall }s{ \in }T)\)\({ \lbrace }t{ \in }T|t{ \ge }s{ \rbrace }\) is a finite chain, and [s3] \(({ \forall }t{ \in }T,t^A{ \in }T){ \ }t > t^A\) implies \(({ \exists }t^B{ \in }T){ \ }t > t^B\) and neither \(t^A{ \ }{ \ge }{ \ }t^B\) nor \(t^B{ \ }{ \ge }{ \ }t^A\). Define r = max T, and call r the root node. Say that tprecedes\(t^{\sharp }\) if and only if t is succeeded by \(t^{\sharp }\) if and only if \(t > t^{\sharp }\). Let \(X{ \ }{ \subseteq }{ \ }T\) be the set of nodes t which have at least one successor, and call every such node \(t{ \ }{ \in }{ \ }X\) a decision node. Define  by \(p(t^{\sharp })\) = min\({ \lbrace }t{ \in }T|t{>}t^{\sharp }{ \rbrace }\), and call \(p(t^{\sharp })\) the (immediate) predecessor of the node \(t^{\sharp }\) (AR16, p. 145).
by \(p(t^{\sharp })\) = min\({ \lbrace }t{ \in }T|t{>}t^{\sharp }{ \rbrace }\), and call \(p(t^{\sharp })\) the (immediate) predecessor of the node \(t^{\sharp }\) (AR16, p. 145).
By assumption, a choice \(\hat{c}\) will be a nonempty set of non-root nodes  . In other words, each choice \(\hat{c}\) satisfies
. In other words, each choice \(\hat{c}\) satisfies  . The set of nodes at which a choice \(\hat{c}\) is feasible is \(p(\hat{c}) = { \lbrace }p(t^{\sharp })|t^{\sharp }{ \in }\hat{c}{ \rbrace }\) (AR16, p. 145). Note that this equation is the standard way of defining the image of a set (such as \(\hat{c}\)) under a function (such as p). Accordingly, \(p(\hat{c})\) is the set of nodes \(p(t^{\sharp })\) that immediately precede a node \(t^{\sharp }\) in \(\hat{c}\). Further, let I be the set of players i, and let \((\hat{C}_i)_{i{ \in }I}\) list a collection \(\hat{C}_i\) of choices \(\hat{c}\) for each player i.
. The set of nodes at which a choice \(\hat{c}\) is feasible is \(p(\hat{c}) = { \lbrace }p(t^{\sharp })|t^{\sharp }{ \in }\hat{c}{ \rbrace }\) (AR16, p. 145). Note that this equation is the standard way of defining the image of a set (such as \(\hat{c}\)) under a function (such as p). Accordingly, \(p(\hat{c})\) is the set of nodes \(p(t^{\sharp })\) that immediately precede a node \(t^{\sharp }\) in \(\hat{c}\). Further, let I be the set of players i, and let \((\hat{C}_i)_{i{ \in }I}\) list a collection \(\hat{C}_i\) of choices \(\hat{c}\) for each player i.
At each decision node \(t{ \ }{ \in }{ \ }X\), let \(A_i(t) = { \lbrace }\,\hat{c}{ \in }\hat{C}_i\,|\,t{ \in }p(\hat{c})\,{ \rbrace }\) be the set of feasible choices for player i, and let \(J(t) = { \lbrace }\,i{ \in }I\,|\,A_i(t){ \ne }{ \varnothing }\,{ \rbrace }\) be the set of decision makers. By definition, a simple (extensive) form (p. 146 in AR16, and note 15 here) is a triple \((T,{ \ge },(\hat{C}_i)_{i{ \in }I})\) such that \((T,{ \ge })\) is a simple tree, [s4] each \(\hat{C}_i\) is a collection of nonempty subsets \(\hat{c}\) of  ,
,
[s7] \(({ \forall }\hat{c}{ \in }{ \cup }_{i{ \in }I}\hat{C}_i)(\not \exists { \lbrace }t^{\sharp A},t^{\sharp B}{ \rbrace }{ \subseteq }\hat{c}){ \ }t^{\sharp A} > t^{\sharp B}\), and [s8]  . AR16 (p. 146) explains that [s5] concerns the standard properties of information sets, that [s6] describes how choices determine successors when simultaneous decisions are allowed, and that [s7] prohibits absentmindedness. Among other things, [s3] and [s8] prohibit trivial decisions.
. AR16 (p. 146) explains that [s5] concerns the standard properties of information sets, that [s6] describes how choices determine successors when simultaneous decisions are allowed, and that [s7] prohibits absentmindedness. Among other things, [s3] and [s8] prohibit trivial decisions.
Incidentally, the outcomes of a simple form are the maximal chains of its simple tree (such chains can be finite or infinite). Later, preferences can be defined over the collection of maximal chains, or more generally if appropriate assumptions are introduced, over some space of probability distributions over the collection of maximal chains.
5.2 The equivalence between KS forms and simple forms
The following two theorems are new. In both theorems, part (a) is more straightforward than part (b).
The theorems use some minor conditions, all of which are discussed in Sect. 7.1. First, say that a simple form has no simultaneous decisions if and only if \(({ \forall }t{ \in }X)\)J(x) is a singleton. Second, say that a KS form has no absentmindedness if and only if \(({ \forall }H{ \in }{ \cup }_{i{ \in }I}{ \mathscr {H}}_i,\!\)\(t^A{ \in }H,\!\)\(t^B{ \in }H)\) there is not a walk from \(t^A\) to \(t^B\). Third, say that a KS form has no trivial decisions if and only if \(({ \forall }t{ \in }T){ \ }|C_{t}|{ \ }{ \ne }{ \ }1\).
Theorem 5.1
(KS \({ \leftarrow }\) simple) Suppose \((T,{ \ge },(\hat{C}_i)_{i{ \in }I})\) is a simple form with no simultaneous decisions, and derive its r, p, and X. Define \(E = { \lbrace }(t,t^{\sharp }){ \in }T^2|t{=}p(t^{\sharp }){ \rbrace }\). Then (a) (T, E, r) is a KS graph-tree. Further, define \((C_t)_{t{ \in }T}\) at each t by \(C_t = { \lbrace }{ \ }\hat{c}{ \in }{ \cup }_{i{ \in }I}\hat{C}_i{ \ }|{ \ }t{ \in }p(\hat{c}){ \ }{ \rbrace }\). Also, define \(({ \psi }_t{:}C_t{ \rightarrow }{ \lbrace }t^{\sharp }{ \in }T|(t,t^{\sharp }){ \in }E{ \rbrace })_{t{ \in }T}\) at each t and each \(\hat{c}{ \in }C_t\) by letting \({ \psi }_t(\hat{c})\) be the unique element of \(p^{-1}(t){ \cap }\hat{c}\). Also, define \(P{:}X{ \rightarrow }I\) at each \(t{ \ }{ \in }{ \ }X\) by letting P(t) equal to the unique i for which \(({ \exists }\hat{c}{ \in }\hat{C}_i)\)\(t{ \ }{ \in }{ \ }p(\hat{c})\). Finally, define \(({ \mathscr {H}}_i)_{i{ \in }I}\) at each i by \({ \mathscr {H}}_i = { \lbrace }p(\hat{c})|\hat{c}{ \in }\hat{C}_i{ \rbrace }\). Then (b) \({ \langle }(T,E,r),\)\((C_t,{ \psi }_t)_{t{ \in }T},\)\((P,({ \mathscr {H}}_i)_{i{ \in }I}){ \rangle }\) is a well-defined KS form with no absentmindedness and no trivial decisions. (Proof A.9.)
Theorem 5.2
(KS \({ \rightarrow }\) simple) Suppose \({ \langle }(T,E,r),\!\)\((C_t,{ \psi }_t)_{t{ \in }T},\!\)\((P,({ \mathscr {H}}_i)_{i{ \in }I}){ \rangle }\) is a KS form with no absentmindedness and no trivial decisions. Let > be \({ \lbrace }\,(t,t^{\sharp }){ \in }T^2\,|\!\) there is a walk from t to \(t^{\sharp }{ \rbrace }\), and let \({ \ge }\) be \({ \lbrace }\,(t,t^{\sharp }){ \in }T^2\,|\!\)\(t{=}t^{\sharp }\) or \(t{>}t^{\sharp }\,{ \rbrace }\). Then (a) \((T,{ \ge })\) is a simple tree. Further, define \((\hat{C}_i)_{i{ \in }I}\) at each i by \(\hat{C}_i = { \lbrace }{ \ }{ \lbrace }{ \psi }_t(c)|t{ \in }H{ \rbrace }{ \ }|{ \ }c{ \in }C_{H},{ \ }H{ \in }{ \mathscr {H}}_i{ \ }{ \rbrace }\) where \((C_H)_{H{ \in }{ \mathscr {H}}_i}\) is derived from the KS form. Then (b) \((T,{ \ge },(\hat{C}_i)_{i{ \in }I})\) is a simple form with no simultaneous decisions. (Proof A.10.)
6 AR forms
6.1 Definition
An AR form here is virtually identical to a discrete extensive form in AR16 (p. 138).Footnote 16 The difference is insignificant.Footnote 17
Let \(\dot{N}\) be a nonempty collection of nonempty sets \(\dot{n}\). Define \({ \varOmega } = { \cup }\dot{N}\). Call \(\dot{N}\) the set of nodes\(\dot{n}\), and call \({ \varOmega }\) the space of outcomes\({ \omega }\). Notice that every node \(\dot{n}\) is a subset of \({ \varOmega }\). In other words, every node \(\dot{n}\) is a set of outcomes \({ \omega }\). By definition, the node \(\dot{n}{ \ }{ \in }{ \ }\dot{N}\)precedes the node \(\dot{n}^{\sharp }{ \ }{ \in }{ \ }\dot{N}\) if and only if \(\dot{n}\) is succeeded by \(\dot{n}^{\sharp }\) if and only if \(\dot{n}{ \ }{ \supset }{ \ }\dot{n}^{\sharp }\). Note that \({ \varOmega }\) itself can be a member of \(\dot{N}\). If so, \(\dot{n}= { \varOmega }\) is a node which precedes all other nodes  .
.
By definition, a (discrete) AR tree (AR16, p. 47, Definition 2.4; AR16, p. 112, Definition 5.1; and AR16, p. 135, Definition 6.1) is a pair \((\dot{N},{ \supseteq })\) which satisfies two sets of conditions. First, it satisfies [AR1] \((\dot{N},{ \supseteq })\) is a partially ordered set, [AR2] \({ \varOmega }{ \ }{ \in }{ \ }\dot{N}\), where \({ \varOmega }\) is defined to be \({ \cup }\dot{N}\),Footnote 18 [AR3] \(({ \forall }\dot{N}^*{ \subseteq }\dot{N})\)\(\dot{N}^*\) is a chain if and only if \(({ \exists }{ \omega }{ \in }{ \varOmega })({ \forall }\dot{n}^*{ \in }\dot{N}^*){ \ }{ \omega }{ \ }{ \in }{ \ }\dot{n}^*\), and [AR4] \(({ \forall }{ \omega }{ \in }{ \varOmega },{ \omega }^{ \prime }{ \in }{ \varOmega })\)\({ \omega }{ \ }{ \ne }{ \ }{ \omega }^{ \prime }\) implies  and
and  . Call \({ \varOmega }\) the root node, and let \(\dot{X}= { \lbrace }\,\dot{n}{ \in }\dot{N}\,|\,({ \exists }\dot{n}^{\sharp }{ \in }\dot{N})\)\(\dot{n}{ \supset }\dot{n}^{\sharp }\,{ \rbrace }\) be the set of decision nodes (AR16, p. 69). Second, it satisfies [AR5] each nonempty chain in \(\dot{N}\) has a maximum, and [AR6] \(({ \forall }\dot{n}{ \ne }{ \varOmega })\)\({ \lbrace }\dot{n}^{\flat }{ \in }\dot{N}|\dot{n}^{\flat }{ \supset }\dot{n}{ \rbrace }\) has an infimum in
. Call \({ \varOmega }\) the root node, and let \(\dot{X}= { \lbrace }\,\dot{n}{ \in }\dot{N}\,|\,({ \exists }\dot{n}^{\sharp }{ \in }\dot{N})\)\(\dot{n}{ \supset }\dot{n}^{\sharp }\,{ \rbrace }\) be the set of decision nodes (AR16, p. 69). Second, it satisfies [AR5] each nonempty chain in \(\dot{N}\) has a maximum, and [AR6] \(({ \forall }\dot{n}{ \ne }{ \varOmega })\)\({ \lbrace }\dot{n}^{\flat }{ \in }\dot{N}|\dot{n}^{\flat }{ \supset }\dot{n}{ \rbrace }\) has an infimum in  . Let \(\dot{p}(\dot{n}) = \text {min}{ \lbrace }\dot{n}^{\flat }{ \in }\dot{N}|\)\(\dot{n}^{\flat }{ \supset }\dot{n}{ \rbrace }\) be the (immediate) predecessor of \(\dot{n}\) (AR16, p. 133), and let \(\dot{T}= { \lbrace }{ \varOmega }{ \rbrace }{ \cup }\)\({ \lbrace }\dot{n}{ \in }\dot{N}|\dot{p}(\dot{n}){ \ }\text {exists}{ \rbrace }\). Among other things, [AR6] implies \(\dot{X}{ \ }{ \subseteq }{ \ }\dot{T}\).Footnote 19 Thus \(\dot{N}\) is partitioned by
. Let \(\dot{p}(\dot{n}) = \text {min}{ \lbrace }\dot{n}^{\flat }{ \in }\dot{N}|\)\(\dot{n}^{\flat }{ \supset }\dot{n}{ \rbrace }\) be the (immediate) predecessor of \(\dot{n}\) (AR16, p. 133), and let \(\dot{T}= { \lbrace }{ \varOmega }{ \rbrace }{ \cup }\)\({ \lbrace }\dot{n}{ \in }\dot{N}|\dot{p}(\dot{n}){ \ }\text {exists}{ \rbrace }\). Among other things, [AR6] implies \(\dot{X}{ \ }{ \subseteq }{ \ }\dot{T}\).Footnote 19 Thus \(\dot{N}\) is partitioned by  .
.  is the set of nondecision nodes without immediate predecessors,
is the set of nondecision nodes without immediate predecessors,  is the set of nondecision nodes with immediate predecessors, and \(\dot{X}\) is the set of decision nodes.Footnote 20
is the set of nondecision nodes with immediate predecessors, and \(\dot{X}\) is the set of decision nodes.Footnote 20
Nondecision (i.e., “terminal”) nodes are closely related to outcomes. In particular, nondecision nodes are singleton nodes in the sense that \(({ \forall }\dot{n}{ \in }\dot{N})\)\(\dot{n}{ \ }{ \notin }{ \ }\dot{X}\) if and only if \(({ \exists }{ \omega }{ \in }{ \varOmega })\)\(\dot{n}={ \lbrace }{ \omega }{ \rbrace }\) (AR16, p. 86, Lemma 4.1(b)). This does not imply \(\dot{N}{ \ }{ \supseteq }{ \ }{ \lbrace }{ \lbrace }{ \omega }{ \rbrace }|{ \omega }{ \in }{ \varOmega }{ \rbrace }\).Footnote 21 However, \(\dot{N}{ \ }{ \supseteq }{ \ }{ \lbrace }{ \lbrace }{ \omega }{ \rbrace }|{ \omega }{ \in }{ \varOmega }{ \rbrace }\) does hold when \(\dot{N}\) is finite. Further, there is a compelling sense in which any \(\dot{N}\) can be expanded to \(\dot{N}{ \ }{ \cup }{ \ }{ \lbrace }{ \lbrace }{ \omega }{ \rbrace }|{ \omega }{ \in }{ \varOmega }{ \rbrace }\) without changing its meaning (AR16, p. 50, Proposition 2.11).
Now introduce a set I of playersi, and let \(\dot{C}_i\) denote player i’s set of choices\(\dot{c}\). By assumption, a choice \(\dot{c}\) is a nonempty subset of \({ \varOmega }\). Further, let \(P(\dot{c})\) denote the set of nodes \(\dot{n}\) at which the choice \(\dot{c}\) is feasible, and define it by \(\dot{P}(\dot{c}) = { \lbrace }{ \ }\dot{p}(\dot{t}^{\sharp }){ \ }|{ \ }\dot{t}^{\sharp }{ \in }\dot{T},{ \ }\dot{c}{ \supseteq }\dot{t}^{\sharp },\)\(\text {and}\)\((\not \exists \dot{t}{ \in }\dot{T}){ \ }\dot{c}{ \supseteq }\dot{t}{ \supset }\dot{t}^{\sharp }{ \ }{ \rbrace }\) (AR16, p. 134, Proposition 6.2(b)). This \(\dot{P}\) is not related to the player-assignment functions \(\bar{P}\) and P of OR and KS forms.
At each decision node \(\dot{t}{ \ }{ \in }{ \ }\dot{X}\), let \(A_i(\dot{t}) = { \lbrace }\,\dot{c}{ \in }\dot{C}_i\,|\,\dot{t}{ \in }P(\dot{c})\,{ \rbrace }\) be the set of feasible choices for player i, and let \(J(\dot{t}) = { \lbrace }\,i{ \in }I\,|\,A_i(\dot{t}){ \ne }{ \varnothing }\,{ \rbrace }\) be the set of decision makers. By definition, a (discrete) AR form (p. 138 in A16, and note 17 here) is a triple \((\dot{N},{ \supseteq },(\dot{C}_i)_{i{ \in }I})\) such that \((\dot{N},{ \supseteq })\) is a (discrete) AR tree, [AR7] every \(\dot{c}{ \ }{ \in }{ \ }{ \cup }_{i{ \in }I}\dot{C}_i\) is a nonempty proper subset of \({ \varOmega }\) which is both the union of a subcollection of \(\dot{N}\) and a superset of some member of  ,
,
AR16 (p. 138) explains that [AR8] states the standard properties of information sets, and that [AR9] describes how choices determine successors when simultaneous decisions are allowed.
Incidentally, recall that the space \({ \varOmega }\) of outcomes is primitive (or, virtually the same, that \(\dot{N}\) is primitive and \({ \varOmega }\) is defined as \({ \cup }\dot{N}\)). Thus it is straightforward to define preferences over \({ \varOmega }\). Recent contributions which do so include Alós-Ferrer and Ritzberger (2016b, 2017b, c). More generally, preferences might be defined over some space of probability distributions over \({ \varOmega }\), if appropriate assumptions are introduced.
6.2 The Alós–Ferrer/Ritzberger equivalence between simple forms and AR forms
Theorem 6.1
(simple \({ \leftarrow }\) AR) Suppose \((\dot{N},{ \supseteq },(\dot{C}_i)_{i{ \in }I})\) is a (discrete) AR form, and derive its \({ \varOmega }\), \(\dot{p}\), and \(\dot{T}\). Then (a) \((\dot{T},{ \supseteq })\) is a simple tree. Further, define \((\hat{C}_i)_{i{ \in }I}\) at each i by  . Then (b) \((\dot{T},{ \supseteq },(\hat{C}_i)_{i{ \in }I})\) is a simple form [(a) Corollary of AR16, p. 144, Proposition 6.5(b). (b) Corollary of AR16, p. 139, Theorem 6.2 (DEF\({ \Rightarrow }\)EDP), and AR16, p. 147, Theorem 6.4(b).]
. Then (b) \((\dot{T},{ \supseteq },(\hat{C}_i)_{i{ \in }I})\) is a simple form [(a) Corollary of AR16, p. 144, Proposition 6.5(b). (b) Corollary of AR16, p. 139, Theorem 6.2 (DEF\({ \Rightarrow }\)EDP), and AR16, p. 147, Theorem 6.4(b).]
The order isomorphism in Theorem 6.2 means that there is a bijection \({ \varphi }{:}T{ \rightarrow }\dot{N}\) such that \(({ \forall }t{ \in }T,t^{\sharp }{ \in }T)\)\(t{ \ }{ \ge }{ \ }t^{\sharp }\) if and only if \({ \varphi }(t){ \ }{ \supseteq }{ \ }{ \varphi }(t^{\sharp })\) (AR16, p. 20). In this case, the bijection is \(T{ \ }{ \ni }{ \ }t \mapsto { \lbrace }{ \omega }{ \in }{ \varOmega }|t{ \in }{ \omega }{ \rbrace }{ \ }{ \in }{ \ }\dot{N}\) (AR16, p. 144, note 7).
Theorem 6.2
(simple \({ \rightarrow }\) AR) Suppose \((T,{ \ge },(\hat{C}_i)_{i{ \in }I})\) is a simple form. Let \({ \varOmega }\) be \((T,{ \ge })\)’s collection of maximal chains, and let \(\dot{N}= { \lbrace }{ \ }{ \lbrace }{ \omega }{ \in }{ \varOmega }|t{ \in }{ \omega }{ \rbrace }{ \ }|{ \ }t{ \in }T{ \ }{ \rbrace }\). Then (a) \((\dot{N},{ \supseteq })\) is a (discrete) AR tree which is order-isomorphic to \((T,{ \ge })\). Further, define \((\dot{C}_i)_{i{ \in }I}\) at each i by \(\dot{C}_i = { \lbrace }{ \ }{ \cup }_{t^{\sharp }{ \in }\hat{c}}{ \lbrace }{ \omega }{ \in }{ \varOmega }|t^{\sharp }{ \in }{ \omega }{ \rbrace }{ \ }|{ \ }\hat{c}{ \in }\hat{C}_i{ \ }{ \rbrace }\). Then (b) \((\dot{N},{ \supseteq },(\dot{C})_{i{ \in }I})\) is a (discrete) AR form. [(a) Corollary of AR16, p. 144, Proposition 6.5(a). (b) Corollary of AR16, p. 147, Theorem 6.4(a), and AR16, p. 139, Theorem 6.2 (EDP\({ \Rightarrow }\)DEF).]
7 Advantages and disadvantages
7.1 Four minor features of the five specifications
Theorems 3.1 and 3.2 restrict OR forms by no absentmindedness and no shared alternatives.Footnote 22 Theorems 5.1 and 5.2 restrict KS forms by no absentmindedness and no trivial decisions, and also restrict simple forms by no simultaneous decisions. Absentmindedness, shared alternatives, trivial decisions, and simultaneous decisions are all features of game specifications. Each of these features corresponds to a row in Table 1, and each is discussed in a paragraph below.
Absentmindedness is listed first because it is the only feature whose absence limits the range of social interactions that can be modeled. At the same time, this limitation is very unimportant (Sect. 3.2, second paragraph). Absentmindedness is currently allowed in OR forms and KS forms, and might later be allowed in simple forms by removing [s7]. Absentmindedness is incompatible with choice-set forms (sentence before Theorem 3.1) and AR forms (AR16 Sect. 4.2.3).
OR forms and KS forms allow information sets to share alternatives (i.e., choices), and this can be convenient when defining a repeated game. Yet, disallowing shared alternatives is an innocuous assumption in the sense that one can always introduce enough alternatives so that each information set has its own alternatives. Choice-set forms disallow shared alternatives because \({ \lbrace }t{ \in }X|c{ \in }C_t{ \rbrace }\) (if nonempty) is the unique information set associated with the choice c (recall [cs4]).
Trivial decisions can be convenient for expanding game trees. Trivial decisions are currently allowed in choice-set forms, OR forms, and KS forms. It seems they might later be allowed in simple forms by altering [s3] and [s8], and in AR forms by pursuing AR16, pp. 64–65.
Simultaneous decisions are more convenient than cascading information sets in the sense of AR16, pp. 140–142. Simultaneous decisions are already built into simple forms and AR forms. A similar construction seems possible for choice-set forms, OR forms, and KS forms (as in Osborne and Rubinstein 1994, p. 102).
7.2 General discussion
Although all four features are of minor importance, Table 1 and the preceding paragraph argue that OR forms and KS forms have more of the features than choice-set forms and AR forms. Further, simple forms seem able to gain absentmindedness by removing [s7] and to gain trivial decisions by altering [s3] and [s8]. In this sense, the three middle specifications appear to be slightly more general than the two specifications on the ends.
Now consider these three middle specifications in the context of Fig. 2. The left-right spectrum there is identical to the left-right spectrum in Table 1. KS forms are special because both their nodes and their choices are abstract (see the top two rows of Fig. 2). This allows one to specify both nodes and choices flexibly, as desired. OR forms are less flexible but more efficient notationally since they express nodes in terms of choices. Symmetrically, simple forms are less flexible but more efficient notationally since they express choices in terms of nodes.
At the two ends of the spectrum, choice-set forms and AR forms sacrifice small amounts of generality for even more notational efficiency. In both cases, the extra efficiency is gained by using more set theory. For example, precedence becomes set inclusion: On the left, a choice-set form has t preceding \(t^{\sharp }\) if and only if \(t{ \ }{ \subset }{ \ }t^{\sharp }\), while on the right, an AR form has \(\dot{t}\) preceding \(\dot{t}^{\sharp }\) if and only if \(\dot{t}{ \ }{ \supset }{ \ }\dot{t}^{\sharp }\).
As the last sentence suggests, the two spectrum ends are opposites in some sense. On the spectrum’s left, nodes are expressed in terms of choices (see Fig. 2’s top row). Since that is done in terms of past choices, the notation looks backward more efficiently. For example, it can be relatively easy [a] to find the product of the probabilities of past choices, [b] to sum the rewards and costs from past choices, or [c] to sum the infinite relative likelihoods of past choices (Streufert 2015a, Sects. 3.3, 4.1). In contrast, on the spectrum’s right, nodes and choices are expressed in terms of outcomes (see Fig. 2’s top rows). Since outcomes are in the future, this notation looks forward more efficiently. For example, it can be relatively easy [a] to abstractly analyze preferences over outcomes without even referring to the time horizon (Alós-Ferrer and Ritzberger 2016b), or [b] to connect game forms with the standard statistical foundations of stochastic processes.
Although it is natural to have a favourite game specification, there appears to be no objective sense in which one game specification is best for all purposes. Thus it may be advantageous to be fluent in several specifications, so as to be able to freely choose the specification that best fits the purpose at hand.
Notes
This reference to the literature excludes an earlier multi-paper version of the present paper. Streufert (2015b) links OR forms and choice-set forms, and Streufert (2015c) links choice-set forms and AR forms. That connection between OR forms and AR forms is less straightforward than the one in this paper.
The distinction between tree and form can be subtle. AR16 and the present paper use “tree” to mean nodes and precedence, and use “form” to mean a tree together with choices, information sets, and players. [a] concerns trees. In particular, there is nothing in AR16 Example 6.5 that concerns the choices of the simple specification. (The choices of the OR specification do appear in AR16 Example 6.5, but only because OR nodes are specified in terms of those choices.)
KL16 uses the word “tree” differently than it is used in AR16, the present paper, and much of the literature. In particular, their theorems show the equivalence of “OR-trees” and “KS-trees”, where a “KS-tree” is defined to be a tree augmented with choices. Accordingly, their “KS-tree” is about halfway from a tree to a form (as this paper and much of the literature uses those two terms).
\({ \lbrace }{ \rbrace }\) and \({ \varnothing }\) are alternative notations for the empty set. I use \({ \lbrace }{ \rbrace }\) for a root node, and use \({ \varnothing }\) for all other purposes.
To prove this, note N is nonempty by [cs1]. Thus, either T is nonempty, or
 is nonempty. The latter also implies that T is nonempty by the \({ \subseteq }\) direction of [cs3]. Hence there is a \(t{ \ }{ \in }{ \ }T\). Hence |t| applications of [cs2] imply \({ \lbrace }{ \rbrace }{ \ }{ \in }{ \ }T\).
is nonempty. The latter also implies that T is nonempty by the \({ \subseteq }\) direction of [cs3]. Hence there is a \(t{ \ }{ \in }{ \ }T\). Hence |t| applications of [cs2] imply \({ \lbrace }{ \rbrace }{ \ }{ \in }{ \ }T\).To prove this, first note that each information set is nonempty by inspection (empty sets of the form \({ \lbrace }t{ \in }X|c{ \in }C_t{ \rbrace }\) arise from choices c that are never feasible, and [cs4]’s construction simply discards them). Second, the information sets are disjoint by [cs4] itself. Third, the union of the information sets is a subset of X because each information set is a subset of X by inspection (incidentally \(({ \forall }c{ \in }C)\)\({ \lbrace }t{ \in }X|c{ \in }C_t{ \rbrace } = { \lbrace }t{ \in }T|c{ \in }C_t{ \rbrace }\)). To show the reverse inclusion, take any \(t^*{ \ }{ \in }{ \ }X\). Its \(C_{t^*}\) is nonempty by the definition of X, and so, there exists \(c^*{ \ }{ \in }{ \ }C_{t^*}\) such that \(t^*{ \ }{ \in }{ \ }{ \lbrace }t{ \in }X|c^*{ \in }C_t{ \rbrace }\).
To prove this, suppose both \(t^1\) and \(t^2\) belong to the information set \({ \lbrace }t{ \in }X|c^A{ \in }C_t{ \rbrace }\) and yet \(C_{t^1}{ \ }{ \ne }{ \ }C_{t^2}\). Without loss of generality, the inequality implies that there exists
 . Thus \(t^1{ \ }{ \in }{ \ }{ \lbrace }t{ \in }X|c^B{ \in }C_t{ \rbrace }\) and \(t^2{ \ }{ \notin }{ \ }{ \lbrace }t{ \in }X|c^B{ \in }C_t{ \rbrace }\). Then \({ \lbrace }t{ \in }X|c^A{ \in }C_t{ \rbrace }\) and \({ \lbrace }t{ \in }T|c^B{ \in }C_t{ \rbrace }\) intersect because they both contain \(t^1\), and yet they are unequal because the first contains \(t^2\) and the second does not. This contradicts [cs4].
. Thus \(t^1{ \ }{ \in }{ \ }{ \lbrace }t{ \in }X|c^B{ \in }C_t{ \rbrace }\) and \(t^2{ \ }{ \notin }{ \ }{ \lbrace }t{ \in }X|c^B{ \in }C_t{ \rbrace }\). Then \({ \lbrace }t{ \in }X|c^A{ \in }C_t{ \rbrace }\) and \({ \lbrace }t{ \in }T|c^B{ \in }C_t{ \rbrace }\) intersect because they both contain \(t^1\), and yet they are unequal because the first contains \(t^2\) and the second does not. This contradicts [cs4].Several changes have been made to facilitate comparison across game specifications. First, \(a\,{ \in }\,{ \mathscr {A}}\) and \((a^k)^K_{k{ \in }1}\,{=}\,h\,{ \in }\,{ \mathscr {H}}\) in KL16 become \(c\,{ \in }\,C\) and \((c_k)^K_{k=1}\,{=}\,\bar{n}\,{ \in }\,\bar{N}\) here. Second, OR1 and OR2 there become [OR2] here. Third, \({ \mathscr {H}}_f\) and \({ \mathscr {H}}^D\) become \(\bar{T}\) and \(\bar{X}\). Fourth, \(({ \mathscr {A}}_{h})_{h{ \in }{ \mathscr {H}}_f}\) becomes \((C_{\bar{t}})_{\bar{t}{ \in }\bar{T}}\). Fifth, \(i\,{ \in }\,N\) and \((I_i)_{i{ \in }N}\) become \(i\,{ \in }\,I\) and \((\bar{{ \mathscr {H}}}_i)_{i{ \in }I}\). Sixth, P and \(P_i\) become \(\bar{P}\) and \(\bar{P}^{-1}(i)\).
The terms “alternative”, “action”, and “choice” are fundamentally synonymous (see note 22).
Several changes have been made to facilitate comparison across game specifications. First, \({ \langle }(V,E,r),(A_v,{ \psi }_v)_{v{ \in }V}){ \rangle }\) in KL16 becomes \({ \langle }(T,E,r),(C_t,{ \psi }_t)_{t{ \in }T}{ \rangle }\) here. Second, a “KS-tree” there becomes a “KS augmented-tree” here (this accords with note 4). Third, \(V^D\) becomes X. Fourth, \({ \mathscr {P}}\) and \({ \mathscr {P}}_f\) and \({ \mathscr {P}}^D\) become \({ \lbrace }(r){ \rbrace }{ \cup }{ \mathscr {W}}_r\) and \({ \lbrace }(r){ \rbrace }{ \cup }{ \mathscr {W}}_r^T\) and \({ \lbrace }(r){ \rbrace }{ \cup }{ \mathscr {W}}_r^X\). Fifth, both p and \(w{ \cup }{ \lbrace }(r,(r)){ \rbrace }\) become w. Sixth, \(i\,{ \in }\,N\) and \((I_i)_{i{ \in }N}\) become \(i\,{ \in }\,I\) and \(({ \mathscr {H}}_i)_{i{ \in }I}\). Seventh, \(P_i\) becomes \(P^{-1}(i)\).
This construction fails when \(|T| = 1\), which is a trivial case. (In this case there are no walks.)
More details of my adaptations, of both KL16 and AR16, are available on request.
Some notational changes have been made to facilitate comparison across game specifications. First, \(x_0\) there becomes r here. Second, \(T = (N,{ \ge })\) there becomes \((T,{ \ge })\) here. In other words, [a] N there becomes T here, and [b] T there has no equivalent here.
The difference is that [s4] strengthens the phrase before AR16, p. 146, Definition 6.4 (SF1), by requiring that [1] no choice \(\hat{c}{ \ }{ \in }{ \ }{ \cup }_{i{ \in }I}\hat{C}_i\) contains r, and [2] no choice \(\hat{c}{ \ }{ \in }{ \ }{ \cup }_{i{ \in }I}\hat{C}_i\) equals \({ \varnothing }\). I argue that [1] and [2] are insignificant by considering the set \(p(\hat{c})\) of nodes at which such choices \(\hat{c}\) would be feasible. Regarding [1], suppose \(\hat{c}\) did contain r. Then \(p(\hat{c}) = { \lbrace }p(t)|t{ \in }\hat{c}{ \rbrace }\) would contain p(r), which is ill-defined. Regarding [2], \(p({ \varnothing }) = { \lbrace }p(t^{\sharp })|t^{\sharp }{ \in }{ \varnothing }{ \rbrace }\) is empty, and thus \({ \varnothing }\) is never feasible.
Some notational changes have been made to facilitate comparison across game specifications. First, the set W of plays w in AR16 becomes the set \({ \varOmega }\) of outcomes \({ \omega }\) here. Second,
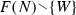 there becomes
there becomes 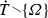 here. Third, a move \(x{ \ }{ \in }{ \ }X\) there becomes a decision node \(\dot{t}{ \ }{ \in }{ \ }\dot{X}\) here. Fourth, \(T = (N,{ \supseteq })\) there becomes \((\dot{N},{ \supseteq })\) here. In other words, [a] N there becomes \(\dot{N}\) here, and [2] T there has no equivalent here ([a] merits emphasis because note 14 in the previous section changed N to T).
here. Third, a move \(x{ \ }{ \in }{ \ }X\) there becomes a decision node \(\dot{t}{ \ }{ \in }{ \ }\dot{X}\) here. Fourth, \(T = (N,{ \supseteq })\) there becomes \((\dot{N},{ \supseteq })\) here. In other words, [a] N there becomes \(\dot{N}\) here, and [2] T there has no equivalent here ([a] merits emphasis because note 14 in the previous section changed N to T).The difference is that [AR7] strengthens the phrase before AR16, p. 138, Definition 6.2 (DEF1), by requiring that [1] no choice \(\dot{c}{ \ }{ \in }{ \ }{ \cup }_{i{ \in }I}\dot{C}_i\) is equal to \({ \varOmega }\), and [2] every choice \(\dot{c}{ \ }{ \in }{ \ }{ \cup }_{i{ \in }I}\dot{C}_i\) is a superset of some
 . I argue that [1] and [2] are insignificant by considering the set \(\dot{P}(\dot{c})\) of nodes at which such choices \(\dot{c}\) would be feasible. Regarding [1], \(\dot{P}({ \varOmega }) = { \lbrace }\dot{p}(\dot{t}^{\sharp })|\dot{t}^{\sharp }{ \in }\dot{T},{ \varOmega }{ \supseteq }\dot{t}^{\sharp },(\not \exists \dot{t}{ \in }\dot{T}){ \varOmega }{ \supseteq }\dot{t}{ \supset }\dot{t}^{\sharp }{ \rbrace }\) equals \({ \lbrace }\dot{p}({ \varOmega }){ \rbrace }\), and \(\dot{p}({ \varOmega })\) is not naturally defined. Regarding [2], suppose that \(\dot{c}{ \ }{ \ne }{ \ }{ \varOmega }\) (by [1]) and that \(\dot{c}\) does not contain any
. I argue that [1] and [2] are insignificant by considering the set \(\dot{P}(\dot{c})\) of nodes at which such choices \(\dot{c}\) would be feasible. Regarding [1], \(\dot{P}({ \varOmega }) = { \lbrace }\dot{p}(\dot{t}^{\sharp })|\dot{t}^{\sharp }{ \in }\dot{T},{ \varOmega }{ \supseteq }\dot{t}^{\sharp },(\not \exists \dot{t}{ \in }\dot{T}){ \varOmega }{ \supseteq }\dot{t}{ \supset }\dot{t}^{\sharp }{ \rbrace }\) equals \({ \lbrace }\dot{p}({ \varOmega }){ \rbrace }\), and \(\dot{p}({ \varOmega })\) is not naturally defined. Regarding [2], suppose that \(\dot{c}{ \ }{ \ne }{ \ }{ \varOmega }\) (by [1]) and that \(\dot{c}\) does not contain any  . Then \(\dot{P}(\dot{c}) = { \lbrace }\dot{p}(\dot{t}^{\sharp })|\dot{t}^{\sharp }{ \in }\dot{T},\dot{c}{ \supseteq }\dot{t}^{\sharp },(\not \exists \dot{t}{ \in }\dot{T})\dot{c}{ \supseteq }\dot{t}{ \supset }\dot{t}^{\sharp }{ \rbrace }\) is empty, and thus there is no node at which \(\dot{c}\) is feasible.
. Then \(\dot{P}(\dot{c}) = { \lbrace }\dot{p}(\dot{t}^{\sharp })|\dot{t}^{\sharp }{ \in }\dot{T},\dot{c}{ \supseteq }\dot{t}^{\sharp },(\not \exists \dot{t}{ \in }\dot{T})\dot{c}{ \supseteq }\dot{t}{ \supset }\dot{t}^{\sharp }{ \rbrace }\) is empty, and thus there is no node at which \(\dot{c}\) is feasible.[AR2] does not appear in AR16, p. 47, Definition 2.4, but does appear in Alós-Ferrer and Ritzberger 2013 , p. 78, Definition 1. The latter is relevant in the present (discrete) context. See, for example, the use of rootedness in AR16, p. 144, Proposition 6.5, first sentence of part (b)’s proof.
[AR6] implies that each non-root node without an immediate predecessor is necessarily a nondecision node (AR16, p. 135, Proposition 6.3, second sentence of proof). In other words,
 . This is equivalent to
. This is equivalent to  . This implies \(\dot{X}{ \ }{ \subseteq }{ \ }\dot{T}\) since \({ \varOmega }{ \ }{ \in }{ \ }\dot{T}\) by definition.
. This implies \(\dot{X}{ \ }{ \subseteq }{ \ }\dot{T}\) since \({ \varOmega }{ \ }{ \in }{ \ }\dot{T}\) by definition.This sentence fails when \(|\dot{N}| = 1\), which is a trivial case. (In such a case \({ \varOmega }\) is a nondecision node.)
For example, \(\dot{N}\not \supseteq { \lbrace }{ \lbrace }{ \omega }{ \rbrace }|{ \omega }{ \in }{ \varOmega }{ \rbrace }\) in the AR16 tree that Theorem 6.2 constructs from any simple tree having infinite maximal chains. This accords with the theorem’s claim that the AR16 tree is order-isomorphic to the simple tree: neither the AR16 tree nor the simple tree has (nondecision) nodes corresponding to the simple tree’s infinite maximal chains.
The terms “alternative”, “action”, and “choice” are fundamentally synonymous. The only distinction is that “action” tends to be used when alternatives can be shared (e.g., Osborne and Rubinstein 1994; KL16), and “choice” tends to be used when they cannot (e.g., von Neumann and Morgenstern 1944 Sect. 9–10; Ritzberger 2002, Sect. 3.2; AR16). This paper uses “choice” because the new concept of choice-set forms implicitly assumes that alternatives cannot be shared, as shown two paragraphs hence.
In the text, a sequence is denoted by \(\bar{n}= (c_k)^K_{k=1}\) for some \(K{ \ }{ \in }{ \ }{ \lbrace }0,1,2,\ldots { \rbrace }{ \cup }{ \lbrace }{ \infty }{ \rbrace }\), and an initial segment is denoted by \((c_k)^L_{k=1}\) for some \(L < K\) [this resembles notation from Osborne and Rubinstein (1994)]. In this appendix, the elements of a sequence \(\bar{n}\) are denoted \(\bar{n}_k\) rather than \(c_k\), the length of a sequence is denoted \(K(\bar{n}){ \ }{ \in }{ \ }{ \lbrace }0,1,2,\ldots { \rbrace }{ \cup }{ \lbrace }{ \infty }{ \rbrace }\), and an initial segment is denoted \(_1\bar{n}_{ \ell } = (\bar{n}_1,\bar{n}_2,\ldots \,\bar{n}_{ \ell })\) for some \({ \ell } < K(\bar{n})\).
References
Alós-Ferrer C, Ritzberger K (2013) Large extensive form games. Econ Theory 52:75–102
Alós-Ferrer C, Ritzberger K (2016a) The theory of extensive form games. Springer, Berlin (referred to as AR16)
Alós-Ferrer C, Ritzberger K (2016b) Equilibrium existence for large perfect information games. J Math Econ 62:5–18
Alós-Ferrer C, Ritzberger K (2017a) Characterizations of perfect recall. Int J Game Theory 46:311–326
Alós-Ferrer C, Ritzberger K (2017b) Characterizing existence of equilibrium for large extensive form games: a necessity result. Econ Theory 63:407–430
Alós-Ferrer C, Ritzberger K (2017c) Does backwards induction imply subgame perfection? Games Econ Behav 103:19–29
Bang-Jensen J, Gutin GZ (2009) Digraphs: theory, algorithms and applications. Springer, Berlin
Gilboa I (1997) A comment on the absent-minded driver paradox. Games Econ Behav 20:25–30
Kline JJ, Luckraz S (2016) Equivalence between graph-based and sequence-based extensive form games. Econ Theory Bull 4:85–94 (referred to as KL16)
Kuhn HW (1953) Extensive games and the problem of information. In: Kuhn HW (ed) Classics in game theory, Princeton (1997), pp 46–68, originally in Contributions to the Theory of Games, ed. by H. W. Kuhn and A. W. Tucker, pp. 193–216, Princeton (1953)
Osborne MJ, Rubinstein A (1994) A course in game theory. MIT, London
Piccione M, Rubinstein A (1997) On the interpretation of decision problems with imperfect recall. Games Econ Behav 20:3–24
Ritzberger K (1999) Recall in extensive form games. Int J Game Theory 28:69–87
Ritzberger K (2002) Foundations of non-cooperative game theory. Oxford University, Oxford
Selten R (1975) Reexamination of the perfectness concept for equilibrium points in extensive games. Int J Game Theory 4:25–55
Streufert PA (2015a) An elementary proof that additive i-likelihood characterizes the supports of consistent assessments. J Math Econ 59:37–46
Streufert PA (2015b) Specifying nodes as sets of choices. Western University, Department of Economics Research Report Series 2015-1, September, p 50
Streufert PA (2015c) Choice-set forms are dual to outcome-set forms. Western University, Department of Economics Research Report Series 2015-3, September, p 55
Streufert PA (2018a) The category of node-and-choice preforms for extensive-form games. Studia Logica (Special Issue: Logics for Social Behaviour) 106:1001–1064
Streufert PA (2018b) The category of node-and-choice forms, with subcategories for choice-sequence forms and choice-set forms. Western University, Department of Economics Research Report Series 2018-6, p 41
von Neumann J, Morgenstern O (1944) Theory of games and economic behavior. Princeton University, Princeton
Acknowledgements
I am very indebted to two anonymous referees, who generously and insightfully addressed a very long preliminary version of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Proofs
Proofs
Lemma A.1
Suppose T is a collection of finite subsets t of C. Then, for any \(s{ \ }{ \subseteq }{ \ }C\), (a) there is an infinite chain \(T^*\) in T such that \({ \cup }T^* = s\) iff (b) there is \((t^m)_{m{ \ge }1}{ \ }{ \in }{ \ }T^{ \infty }\) such that \(({ \forall }m{ \ge }1){ \ }t^m{ \ }{ \subset }{ \ }t^{m+1}\) and \({ \cup }_{m{ \ge }1}t^m = s\).
Proof
The reverse direction is proved by setting \(T^* = { \lbrace }t^m|m{ \ge }1{ \rbrace }\).
To prove the forward direction, take any s and assume \(T^*\) is an infinite chain in T such that \({ \cup }T^*\,{=}\,s\). Define \((t^m)_{m{ \ge }1}\) recursively by \(t^1 =\) min \(T^*\) and \(({ \forall }m{ \ge }2){ \ }t^m =\) min  . Every step in this infinite recursion is well-defined because [a] \(T^*\) is infinite by assumption and [b] every nonempty subcollection of \(T^*\) has a minimum because \(T^*\) is a chain of finite sets by assumption. By inspection, \(({ \forall }m{ \ge }1)\)\(t^m{ \ }{ \subset }{ \ }t^{m+1}\). Thus it remains to show \({ \cup }_{m{ \ge }1}t^m = s\). Note that \({ \cup }_{m{ \ge }1}t^m{ \ }{ \subseteq }{ \ }{ \cup }T^* = s\), where the set inclusion holds by \(({ \forall }m{ \ge }1){ \ }t^m{ \ }{ \in }{ \ }T^*\), and where the equality holds by assumption. Conversely, the next two paragraphs show \(s{ \ }{ \subseteq }{ \ }{ \cup }_{m{ \ge }1}t^m\).
. Every step in this infinite recursion is well-defined because [a] \(T^*\) is infinite by assumption and [b] every nonempty subcollection of \(T^*\) has a minimum because \(T^*\) is a chain of finite sets by assumption. By inspection, \(({ \forall }m{ \ge }1)\)\(t^m{ \ }{ \subset }{ \ }t^{m+1}\). Thus it remains to show \({ \cup }_{m{ \ge }1}t^m = s\). Note that \({ \cup }_{m{ \ge }1}t^m{ \ }{ \subseteq }{ \ }{ \cup }T^* = s\), where the set inclusion holds by \(({ \forall }m{ \ge }1){ \ }t^m{ \ }{ \in }{ \ }T^*\), and where the equality holds by assumption. Conversely, the next two paragraphs show \(s{ \ }{ \subseteq }{ \ }{ \cup }_{m{ \ge }1}t^m\).
This paragraph shows by induction that \(({ \forall }m{ \ge }0){ \ }m{ \ }{ \le }{ \ }|t^{m+1}|\). The initial step (\(m = 0\)) is \(0{ \ }{ \le }{ \ }|t^1|\), which holds trivially. The inductive step (\(m{ \ }{ \ge }{ \ }1\)) is \(m{ \ }={ \ }(m{-}1){+}1\)\({ \le }\)\(|t^{m}|{+}1\)\({ \le }\)\(|t^{m+1}|\), where the first inequality holds by the inductive hypothesis and the second inequality holds by \(t^m{ \ }{ \subset }{ \ }t^{m+1}\).
Finally take any \(c{ \ }{ \in }{ \ }s\). Since \(s = { \cup }T^*\) by assumption, there exists some \(t^*{ \ }{ \in }{ \ }T^*\) such that \(c{ \ }{ \in }{ \ }t^*\). Consider the element \(t^{|t^*|+1}\) in the sequence \((t^m)_{m{ \ge }1}\). Since both \(t^*\) and \(t^{|t^*|+1}\) belong to \(T^*\), and since \(T^*\) is a chain, either \(t^*{ \ }{ \subseteq }{ \ }t^{|t^*|+1}\) or \(t^*{ \ }{ \supset }{ \ }t^{|t^*|+1}\). The latter would imply \(|t^*|{ \ }>{ \ }|t^{|t^*|+1}|\). Since this would contradict the previous paragraph (at \(m = |t^*|\)), it must be that \(t^*{ \ }{ \subseteq }{ \ }t^{|t^*|+1}\). Hence \(c{ \ }{ \in }{ \ }t^*{ \ }{ \subseteq }{ \ }t^{|t^*|+1}{ \ }{ \subseteq }{ \ }{ \cup }_{m{ \ge }1}t^m\).
Lemma A.2
Suppose \((C,\bar{N})\) is an OR tree. Further suppose \(\bar{s}{ \ }{ \in }{ \ }C^{ \infty }\) is such that \(({ \forall }k{ \ge }1)({ \exists }m{ \ge }k){ \ }_1\bar{s}_m{ \ }{ \in }{ \ }\bar{T}\).Footnote 23 Then \(\bar{s}{ \ }{ \in }{ \ }\bar{N}\).
Proof
Because of [OR3], it suffices to show that \(({ \forall }k{ \ge }1){ \ }_1\bar{s}_k{ \ }{ \in }{ \ }\bar{T}\). Toward this end, take any \(k{ \ }{ \ge }{ \ }1\). By assumption, there exists \(m{ \ }{ \ge }{ \ }k\) such that \(_1\bar{s}_m{ \ }{ \in }{ \ }\bar{T}\). Thus by [OR2], \(_1\bar{s}_k{ \ }{ \in }{ \ }\bar{T}\).
Lemma A.3
Consider an OR form with no shared alternatives. Then \({ \cup }_{i{ \in }I}\bar{{ \mathscr {H}}}_i\) = \({ \lbrace }{ \ }{ \lbrace }\bar{t}{ \in }\bar{T}|c{ \in }C_{\bar{t}}{ \rbrace }{ \ne }{ \varnothing }{ \ }|{ \ }c{ \in }C{ \ }{ \rbrace }\).
Proof
Claim 1: Suppose [1]\(\bar{H}{ \ }{ \in }{ \ }\bar{{ \mathscr {H}}}_i\), [2] \(\bar{t}^*{ \ }{ \in }{ \ }\bar{H}\), and [3] \(c^*{ \ }{ \in }{ \ }C_{\bar{t}^*}\). Then\(\bar{H}= { \lbrace }\,\bar{t}{ \in }\bar{T}\,|\! \)\(c^*{ \in }C_{\bar{t}}\,{ \rbrace }\). For \({ \subseteq }\), note [1], [OR4], and [OR5] imply \(\bar{H}{ \ }{ \subseteq }{ \ }\bar{T}\). So take \(\bar{t}^{ \prime }{ \ }{ \in }{ \ }\bar{H}\). Then [2], [3], and [OR6] imply \(c^*{ \ }{ \in }{ \ }C_{\bar{t}^{ \prime }}\). Hence \(\bar{t}^{ \prime }{ \ }{ \in }{ \ }{ \lbrace }\bar{t}{ \in }\bar{T}|c^*{ \in }C_{\bar{t}}{ \rbrace }\). For \({ \supseteq }\), take \(\bar{t}{ \ }{ \in }{ \ }\bar{T}\) such that \(c^*{ \ }{ \in }{ \ }C_{\bar{t}}\). Then [2], [3], and the assumption of no shared alternatives imply \(\bar{t}{ \ }{ \in }{ \ }\bar{H}\).
Main Argument. For \({ \subseteq }\). Suppose \(\bar{H}{ \ }{ \in }{ \ }\bar{{ \mathscr {H}}}_i\). Then [OR4] and [OR5] imply that \({ \varnothing }{ \ }{ \ne }{ \ }\bar{H}{ \ }{ \subseteq }{ \ }\bar{X}\). Hence there exists \(\bar{t}^*{ \ }{ \in }{ \ }\bar{H}{ \ }{ \subseteq }{ \ }\bar{X}\). Since \(\bar{t}^*{ \ }{ \in }{ \ }\bar{X}\), there exists \(c^*{ \ }{ \in }{ \ }C_{\bar{t}^*}\). Since \(\bar{H}\) is nonempty, it suffices to show \(\bar{H}= { \lbrace }\bar{t}{ \in }\bar{T}|c^*{ \in }C_{\bar{t}}{ \rbrace }\). This follows from Claim 1. For \({ \supseteq }\). Take any \(c^*{ \ }{ \in }{ \ }C\) and assume \({ \lbrace }\bar{t}{ \in }\bar{T}|c^*{ \in }C_{\bar{t}}{ \rbrace }{ \ }{ \ne }{ \ }{ \varnothing }\). By nonemptiness, there exists \(\bar{t}^*\) such that \(c^*{ \ }{ \in }{ \ }C_{\bar{t}^*}\). Thus \(\bar{t}^*{ \ }{ \in }{ \ }X\). Thus by [OR4] and [OR5], there exists \(i{ \ }{ \in }{ \ }I\) and \(\bar{H}{ \ }{ \in }{ \ }\bar{{ \mathscr {H}}}_i\) such that \(\bar{t}^*{ \ }{ \in }{ \ }\bar{H}\). Hence \(\bar{H}= { \lbrace }\bar{t}{ \in }\bar{T}|c^*{ \in }C_{\bar{t}}{ \rbrace }\) by Claim 1. \(\square \)
Lemma A.4
Consider an OR form with no shared alternatives. Then (a) there is no absentmindedness iff (b) \(({ \forall }\bar{n}{ \in }\bar{N},\bar{t}{ \in }\bar{T})\)\(|{ \lbrace }k{ \ge }1|\bar{n}_k{ \in }C_{\bar{t}}{ \rbrace }|{ \ }{ \le }{ \ }1\) iff (c) \(({ \forall }\bar{t}{ \in }\bar{T})\)\(|R(\bar{t})| = K(\bar{t})\).
Proof
Not (a)\({ \Rightarrow }\)not (b). Assume absentmindedness. Then there exist \(\bar{H}\,{ \in }\,{ \cup }_{i{ \in }I}\bar{{ \mathscr {H}}}_i\), \(\bar{t}\,{ \in }\,\bar{H}\), and \({ \ell }\,{<}\,K(\bar{t})\) such that \({_1\bar{t}_{{ \ell }}}\,{ \in }\,\bar{H}\). Since \({ \ell }\,{<}\,K(\bar{t})\), \(\bar{t}_{{ \ell }+1}\) is well-defined and satisfies \(\bar{t}_{{ \ell }+1}\,{ \in }\,C_{{_1\bar{t}_{{ \ell }}}}\). Thus since \({_1\bar{t}_{{ \ell }}}\) and \(\bar{t}\) share an information set, [OR6] implies \(\bar{t}_{{ \ell }+1}\,{ \in }\,C_{\bar{t}}\). Thus \(\bar{n}= \bar{t}{ \oplus }(\bar{t}_{{ \ell }+1})\) is well-defined. Then [a] \(|{ \lbrace }k{ \ge }1|\bar{n}_k{ \in }C_{{_1\bar{t}_{{ \ell }}}}{ \rbrace }|\) is at least \(|{ \lbrace }k{ \ge }1|\bar{n}_k{=}\bar{t}_{{ \ell }+1}{ \rbrace }|\) by \(\bar{t}_{{ \ell }+1}{ \ }{ \in }{ \ }C_{{_1\bar{t}_{{ \ell }}}}\); which [b] is at least \(|{ \lbrace }\,{ \ell }{+}1,\,K(\bar{t}){+}1\,{ \rbrace }|\) by the construction of \(\bar{n}\); which [c] equals 2 by \({ \ell }<K(\bar{t})\).
Not (b)\({ \Rightarrow }\)not (c). Let \(\bar{n}\,{ \in }\,\bar{N}\) and \(\bar{t}\,{ \in }\,\bar{T}\) be such that \(|{ \lbrace }k{ \ge }1|\bar{n}_k{ \in }C_{\bar{t}}{ \rbrace }|{ \ }{ \ge }{ \ }2\). Then there are \({ \ell }\) and k such that \({ \ell } < k\) and \({ \lbrace }\bar{n}_{ \ell },\bar{n}_k{ \rbrace }{ \ }{ \subseteq }{ \ }C_{\bar{t}}\). Thus \(\bar{t}\) belongs to both \({ \lbrace }\bar{t}{ \in }\bar{T}|\bar{n}_{ \ell }{ \in }C_{\bar{t}}{ \rbrace }\) and \({ \lbrace }\bar{t}{ \in }\bar{T}|\bar{n}_k{ \in }C_{\bar{t}}{ \rbrace }\). These are information sets by Lemma A.3. Since these two information sets intersect, [OR4] and [OR5] imply that the two are equal. Note that \({_1\bar{n}_{k-1}}\) belongs to the latter. Thus it belongs to the former. In other words, \(\bar{n}_{ \ell }{ \ }{ \in }{ \ }C_{{_1\bar{n}_{k-1}}}\). Thus \(\bar{t}^* = {_1\bar{n}_{k-1}}{ \oplus }(\bar{n}_{ \ell })\) is well-defined. Since \({ \ell } < k\), \(\bar{t}^*_{ \ell }\) is well-defined and equals \(\bar{n}_{ \ell }\). Since \({ \ell } < k\) and both \(\bar{t}^*_{ \ell }\) and \(\bar{t}^*_k\) equal \(\bar{n}_{ \ell }\), \(|R(\bar{t}^*)| < K(\bar{t}^*)\).
Not (c)\({ \Rightarrow }\)not (a). Suppose \(|R(\bar{t})|{ \ }{ \ne }{ \ }K(\bar{t})\). Thus since \(|R(\bar{t})| > K(\bar{t})\) is inconceivable, \(|R(\bar{t})| < K(\bar{t})\). Thus there are indices \(1{ \ }{ \le }{ \ }{ \ell } < k{ \ }{ \le }{ \ }K(\bar{t})\) such that \(\bar{t}_{ \ell } = \bar{t}_k\). Since [a] \(\bar{t}_{ \ell }{ \ }{ \in }{ \ }C_{{_1\bar{t}_{{ \ell }-1}}}\), [b] \(\bar{t}_k{ \ }{ \in }{ \ }C_{{_1\bar{t}_{k-1}}}\), and [c] \(\bar{t}_{ \ell } = \bar{t}_k\), both \({_1\bar{t}_{{ \ell }-1}}\) and \({_1\bar{t}_{k-1}}\) belong to \({ \lbrace }\bar{t}{ \in }\bar{T}|\bar{t}_k{ \in }C_{\bar{t}}{ \rbrace }\). By Lemma A.3, this is an information set. Since \({ \ell } < k\), the last two sentences imply that this information set contains both \({_1\bar{t}_{{ \ell }-1}}\) and its successor \({_1\bar{t}_{k-1}}\). \(\square \)
Lemma A.5
(Establishes Proposition 3.0 and slightly more) Consider an OR form with no shared alternatives. Then (a) there is no absentmindedness iff (b) \(R|_{\bar{T}}\) is injective iff (c) \(R|_{\bar{N}}\) is injective.
Proof
Not (a)\({ \Rightarrow }\)not (b). Suppose there is absentmindedness. Then Lemma A.4 (a\({ \Leftrightarrow }\)c) implies there is a sequence \(\bar{t}\) such that \(|R(\bar{t})|{ \ }{ \ne }{ \ }K(\bar{t})\). Since \(|R(\bar{t})| > K(\bar{t})\) is inconceivable, \(|R(\bar{t})| < K(\bar{t})\). Thus there exist indices \(1{ \ }{ \le }{ \ }{ \ell } < k{ \ }{ \le }{ \ }K(\bar{t})\) such that \(\bar{t}_{ \ell } = \bar{t}_k\). Hence \(R({_1\bar{t}_{k-1}}) = R({_1\bar{t}_{k}})\).
Not (b)\({ \Rightarrow }\)not (c). This is obvious since \(\bar{T}{ \ }{ \subseteq }{ \ }\bar{N}\).
Not (c)\({ \Rightarrow }\)not (a). Assume that \(\bar{n}^1\) and \(\bar{n}^2\) are distinct elements of \(\bar{N}\) such that \(R(\bar{n}^1) = R(\bar{n}^2)\).
On the one hand, suppose there does not exist a \(k{ \ }{ \ge }{ \ }1\) such that \(\bar{n}^1_k{ \ }{ \ne }{ \ }\bar{n}^2_k\). Then \(\bar{n}^1 = {_1^{}\bar{n}_{K(\bar{n}^1)}^{\,2}}\) or \(\bar{n}^2 = {_1^{}\bar{n}_{K(\bar{n}^2)}^{\,1}}\). Without loss of generality, assume the former. Since \(\bar{n}^1{ \ }{ \ne }{ \ }\bar{n}^2\) by assumption, \(\bar{n}^2_{K(\bar{n}^1)+1}\) exists. Thus since \(R(\bar{n}^1) = R(\bar{n}^2)\) by assumption, \(K(\bar{n}^1){ \ }{ \ne }{ \ }0\) and there exists some \({ \ell }{ \ }{ \le }{ \ }K(\bar{n}^1)\) such that \(\bar{n}^1_{ \ell } = \bar{n}^2_{K(\bar{n}^1)+1}\). But the assumption \(\bar{n}^1 = {_1^{}\bar{n}_{K(\bar{n}^1)}^{\,2}}\) implies \(\bar{n}^1_{ \ell } = \bar{n}^2_{ \ell }\), and thus the last sentence implies \(\bar{n}^2_{ \ell } = \bar{n}^2_{K(\bar{n}^1)+1}\). This and \({ \ell }{ \ }{ \le }{ \ }K(\bar{n}^1)\) imply \(|R({_1\bar{n}^2_{K(\bar{n}^1)+1}})| < K({_1\bar{n}^2_{K(\bar{n}^1)+1}})\). This implies absentmindedness by Lemma A.4(a\({ \Leftrightarrow }\)c).
On the other hand, suppose there exists a \(k{ \ }{ \ge }{ \ }1\) such that \(\bar{n}^1_k{ \ }{ \ne }{ \ }\bar{n}^2_k\). Then let \({ \ell }\) be the smallest such k. Then [a] \({_1^{}\bar{n}_{{ \ell }-1}^{\,1}} = {_1^{}\bar{n}_{{ \ell }-1}^{\,2}}\) and [b] \(\bar{n}^1_{ \ell }{ \ }{ \ne }{ \ }\bar{n}^2_{ \ell }\). Since \(\bar{n}^1_{ \ell }{ \ }{ \in }{ \ }C_{{_1^{}\bar{n}_{{ \ell }-1}^{\,1}}}\) and \(\bar{n}^2_{ \ell }{ \ }{ \in }{ \ }C_{{_1^{}\bar{n}_{{ \ell }-1}^{\,2}}}\), [a] implies [c] \({ \lbrace }\bar{n}^1_{ \ell },\bar{n}^2_{ \ell }{ \rbrace }{ \ }{ \subseteq }{ \ }C_{{_1^{}\bar{n}_{{ \ell }-1}^{\,1}}}\). Further, [b] and \(R(\bar{n}^1) = R(\bar{n}^2)\) imply the existence of some \({ \ell }^*{ \ }{ \ne }{ \ }{ \ell }\) such that \(\bar{n}^1_{{ \ell }^*} = \bar{n}^2_{ \ell }\). This and [c] imply \({ \lbrace }\bar{n}^1_{ \ell },\bar{n}^1_{{ \ell }^*}{ \rbrace }{ \ }{ \subseteq }{ \ }C_{{_1^{}\bar{n}_{{ \ell }-1}^{\,1}}}\). This and \({ \ell }^*{ \ }{ \ne }{ \ }{ \ell }\) imply \(|{ \lbrace }k^{ \prime }{ \ge }1|\bar{n}^1_{k^{ \prime }}{ \in }C_{\bar{t}}{ \rbrace }|{ \ }{ \ge }{ \ }2\) for \(\bar{t}= {_1^{}\bar{n}_{{ \ell }-1}^{\,1}}\). This implies absentmindedness by Lemma A.4(a\({ \Leftrightarrow }\)b).
Lemma A.6
Consider an OR form with no shared alternatives and no absentmindedness. Assume \(R(\bar{t}^{\,\flat }){ \ }{ \subseteq }{ \ }R(\bar{t})\). Then \(K(\bar{t}^{\flat }){ \ }{ \le }{ \ }K(\bar{t})\) and \(\bar{t}^{\flat }= {_1\bar{t}_{K(\bar{t}^{\,\flat })}}\).
Proof
Note that \(K(\bar{t}^{\,\flat })\) = \(|R(\bar{t}^{\,\flat })|{ \ }{ \le }{ \ }|R(\bar{t})|\) = \(K(\bar{t})\), where the equalities hold by two applications of Lemma A.4(a\({ \Leftrightarrow }\)c), and where the inequality holds because \(R(\bar{t}^{\,\flat }){ \ }{ \subseteq }{ \ }R(\bar{t})\). This is the first of the lemma’s two conclusions. For the second conclusion, it suffices to show that \({_1^{}\bar{t}_{K(\bar{t}^{\,\flat })}^{\,\flat }} = {_1\bar{t}_{K(\bar{t}^{\,\flat })}}\). For this, it suffices that the next two paragraphs show, by induction on \(k{ \ }{ \in }{ \ }{ \lbrace }1,2,\ldots \,K(\bar{t}^{\,\flat }){ \rbrace }\), that \(({ \forall }k{ \le }K(\bar{t}^{\,\flat }))\)\({_1^{}\bar{t}_{k}^{\,\flat }} = {_1\bar{t}_{k}}\).
For the initial step at \(k=1\), suppose that \(\bar{t}^{\,\flat }_1{ \ }{ \ne }{ \ }\bar{t}_1\). Note [a] \({ \lbrace }\bar{t}^{\,\flat }_1,\bar{t}_1{ \rbrace }{ \ }{ \subseteq }{ \ }C_{{ \lbrace }{ \rbrace }}\). Also, \(R(\bar{t}^{\,\flat }){ \ }{ \subseteq }{ \ }R(\bar{t})\) implies there is [b] \({ \ell } > 1\) such that [c] \(\bar{t}^{\,\flat }_1 = \bar{t}_{ \ell }\). [a] and [c] imply that \({ \lbrace }\bar{t}_{ \ell },\bar{t}_1{ \rbrace }{ \ }{ \subseteq }{ \ }C_{{ \lbrace }{ \rbrace }}\). This and [b] imply that \(|{ \lbrace }k{ \ge }1|\bar{t}_k{ \in }C_{{ \lbrace }{ \rbrace }}{ \rbrace }|{ \ }{ \ge }{ \ }2\). This is inconsistent with no absentmindedness by Lemma A.4(a\({ \Leftrightarrow }\)b).
For the inductive step at \(k{ \ }{ \in }{ \ }{ \lbrace }2,3,\ldots \,K(\bar{t}^{\,\flat }){ \rbrace }\), suppose [1] \({_1^{}\bar{t}_{k-1}^{\,\flat }} = {_1\bar{t}_{k-1}}\) and [2] \(\bar{t}^{\,\flat }_k{ \ }{ \ne }{ \ }\bar{t}_k\). Since \(\bar{t}^{\,\flat }_k{ \ }{ \in }{ \ }C_{{_1^{}\bar{t}_{k-1}^{\,\flat }}}\) and \(\bar{t}_k{ \ }{ \in }{ \ }C_{{_1\bar{t}_{k-1}}}\), [1] implies [3] \({ \lbrace }\bar{t}^{\,\flat }_k,\bar{t}_k{ \rbrace }{ \ }{ \subseteq }{ \ }C_{{_1\bar{t}_{k-1}}}\). Also, since \(R(\bar{t}^{\,\flat }){ \ }{ \subseteq }{ \ }R(\bar{t})\), [2] implies there is [4] \({ \ell }{ \ }{ \ne }{ \ }k\) such that [5] \(\bar{t}^{\,\flat }_k = \bar{t}_{ \ell }\). [3] and [5] imply \({ \lbrace }\bar{t}_{ \ell },\bar{t}_k{ \rbrace }{ \ }{ \subseteq }{ \ }C_{{_1\bar{t}_{k-1}}}\). This and [4] imply \(|{ \lbrace }k^{ \prime }{ \ge }1|\bar{t}_{k^{ \prime }}{ \in }C_{{_1\bar{t}_{k-1}}}{ \rbrace }|{ \ }{ \ge }{ \ }2\). This is inconsistent with no absentmindedness by Lemma A.4(a\({ \Leftrightarrow }\)b). \(\square \)
Proof A.7
(for Theorem 3.1: choice-set \({ \leftarrow }\) OR)(a). Claims 2, 7, and 9 show that (C, N) is a choice-set tree by deriving [cs1], [cs2], and [cs3]. Further, Claim 1 shows that \(R|_{\bar{N}}\) is a bijection from \(\bar{N}\) to N.
- Claim 1: :
-
\(R|_{\bar{N}}\)is a bijection from\(\bar{N}\)ontoN. By the theorem’s definition of N, \(R|_{\bar{N}}\) is surjective. By Proposition 3.0, \(R|_{\bar{N}}\) is injective.
- Claim 2: :
-
[cs1] holds. By [OR1], \(\bar{N}\) is a nonempty collection of sequences in C. Thus by the definition of N, N is a nonempty collection of subsets of C.
- Claim 3: :
-
\(R|_{\bar{T}}\)is a bijection from\(\bar{T}\)ontoT. Because of Claim 1 and the fact that \(\bar{T}{ \ }{ \subseteq }{ \ }\bar{N}\), it suffices to show that \({ \lbrace }R(\bar{t})|\bar{t}{ \in }\bar{T}{ \rbrace } = T\). To show the \({ \subseteq }\) direction, take any \(\bar{t}{ \ }{ \in }{ \ }\bar{T}\). By the definition of N, \(R(\bar{t}){ \ }{ \in }{ \ }N\). Further, \(|R(\bar{t})|{ \ }{ \le }{ \ }K(\bar{t}) < { \infty }\) because \(\bar{t}{ \ }{ \in }{ \ }\bar{T}\). By the last two sentences, \(R(\bar{t}){ \ }{ \in }{ \ }T\). To show the \({ \supseteq }\) direction, take any [a] \(t{ \ }{ \in }{ \ }T\). By the definition of N, there exists \(\bar{n}\) such that [b] \(R(\bar{n}) = t\). It remains to show that \(\bar{n}{ \ }{ \in }{ \ }\bar{T}\). Toward that end, suppose \(\bar{n}{ \ }{ \notin }{ \ }\bar{T}\). Then by [OR2], \(({ \forall }{ \ell }{ \ge }1)\)\(_1\bar{n}_{ \ell }\) would be a well-defined member of \(\bar{T}\). Thus \(({ \forall }{ \ell }{ \ge }1){ \ }|R(\bar{n})|{ \ }{ \ge }{ \ }|R(_1\bar{n}_{ \ell })| = K(_1\bar{n}_{ \ell }) = { \ell }\), where the first equality holds by Lemma A.4(a\({ \Leftrightarrow }\)c), and where the rest holds by inspection. This implies that \(|R(\bar{n})|\) is infinite. Thus [b] implies |t| is infinite. This contradicts [a].
- Claim 4: :
-
\(({ \forall }\bar{t}^{\,\flat }{ \in }\bar{T},c{ \in }C,\bar{t}{ \in }\bar{T})\)\(\bar{t}^{\,\flat }{ \oplus }(c)\,{=}\,\bar{t}\)\({ \Rightarrow }\)\(({ \ }c\,{ \notin }\,R(\bar{t}^{\,\flat })\)and\(R(\bar{t}^{\,\flat }){ \cup }{ \lbrace }c{ \rbrace }\,{=}\,R(\bar{t}){ \ })\). Suppose \(\bar{t}^{\,\flat }{ \oplus }(c) = \bar{t}\). This implies \(R(\bar{t}^{\,\flat }){ \cup }{ \lbrace }c{ \rbrace } = R(\bar{t}^{\,\flat }{ \oplus }(c)) = R(\bar{t})\), which is the second fact to be derived. Also \(|R(\bar{t}^{\,\flat })| +1\)\(=\)\(K(\bar{t}^{\,\flat }) +1\)\(=\)\(K(\bar{t})\)\(=\)\(|R(\bar{t})|\) by Lemma A.4(a\({ \Leftrightarrow }\)c), by \(\bar{t}^{\,\flat }{ \oplus }(c) = \bar{t}\), and by Lemma A.4(a\({ \Leftrightarrow }\)c) again. This and \(\bar{t}^{\,\flat }{ \oplus }(c) = \bar{t}\) yield \(c{ \ }{ \notin }{ \ }R(\bar{t}^{\,\flat })\), which is the first fact to be derived.
- Claim 5: :
-
\(({ \forall }\bar{t}^{\,\flat }{ \in }\bar{T},c{ \in }C,\bar{t}{ \in }\bar{T})\)\(\bar{t}^{\,\flat }{ \oplus }(c)\,{=}\,\bar{t}\)\({ \Leftrightarrow }\)\(({ \ }c\,{ \notin }\,R(\bar{t}^{\,\flat })\)\(\text {and}\)\(R(\bar{t}^{\,\flat }){ \cup }{ \lbrace }c{ \rbrace }\,{=}\,R(\bar{t}){ \ })\). Because of Claim 4, it suffices to show the reverse direction. Toward that end, assume [i] \(c{ \ }{ \notin }{ \ }R(\bar{t}^{\,\flat })\) and [ii] \(R(\bar{t}^{\,\flat }){ \cup }{ \lbrace }c{ \rbrace } = R(\bar{t})\). Note \(K(\bar{t}^{\,\flat })+1 = |R(\bar{t}^{\,\flat })|+1 = |R(\bar{t})| = K(\bar{t})\) by Lemma A.4(a\({ \Leftrightarrow }\)c), by [i] and [ii], and by Lemma A.4(a\({ \Leftrightarrow }\)c) again. So, trivially, \(K(\bar{t}^{\,\flat }) = K(\bar{t}){-}1\). Also, since \(R(\bar{t}^{\,\flat })\)\({ \subseteq }\)\(R(\bar{t}^{\,\flat }){ \cup }{ \lbrace }c{ \rbrace }\)\(= R(\bar{t})\) by [ii], Lemma A.6 implies \(\bar{t}^{\,\flat }= {_1\bar{t}_{K(\bar{t}^{\,\flat })}}\). The last two sentences yield [a] \(\bar{t}^{\,\flat }= {_1\bar{t}_{K(\bar{t})-1}}\). [i] and [ii] yield [b]
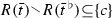 . [a] and [b] yield [c] \(\bar{t}_{K(\bar{t})} = c\). [a] and [c] yield \(\bar{t}^{\,\flat }{ \oplus }(c) = \bar{t}\).
. [a] and [b] yield [c] \(\bar{t}_{K(\bar{t})} = c\). [a] and [c] yield \(\bar{t}^{\,\flat }{ \oplus }(c) = \bar{t}\). - Claim 6: :
-
Take
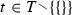 . Then (a)\((R|_{\bar{T}})^{-1}(t)\)is a well-defined sequence in\(\bar{T}\)and (b)\(({ \forall }c{ \in }C)\)\(c = [(R|_{\bar{T}})^{-1}(t)]_{K((R|_{\bar{T}})^{-1}(t))}\)iff\(c{ \in }t\)and
. Then (a)\((R|_{\bar{T}})^{-1}(t)\)is a well-defined sequence in\(\bar{T}\)and (b)\(({ \forall }c{ \in }C)\)\(c = [(R|_{\bar{T}})^{-1}(t)]_{K((R|_{\bar{T}})^{-1}(t))}\)iff\(c{ \in }t\)and . (a) holds by Claim 3. For (b), take \(c{ \ }{ \in }{ \ }C\). I argue \(c = [(R|_{\bar{T}})^{-1}(t)]_{K((R|_{\bar{T}})^{-1}(t))}\) is [1] equivalent to \(({ \exists }\bar{t}^{\,\flat }{ \in }\bar{T}){ \ }\bar{t}^{\,\flat }{ \oplus }(c) = (R|_{\bar{T}})^{-1}(t)\) by inspection; which is [2] equivalent to \(({ \exists }t^{\flat }{ \in }T)\)\((R|_{\bar{T}})^{-1}(t^{\flat }){ \oplus }(c) = (R|_{\bar{T}})^{-1}(t)\) by Claim 3; which is [3] equivalent to \(({ \exists }t^{\flat }{ \in }T)\)\(c{ \ }{ \notin }{ \ }R{ \circ }(R|_{\bar{T}})^{-1}(t^{\flat })\) and \(R{ \circ }(R|_{\bar{T}})^{-1}(t^{\flat }){ \cup }{ \lbrace }c{ \rbrace } = R{ \circ }(R|_{\bar{T}})^{-1}(t)\) by Claim 5 at \(\bar{t}^{\,\flat }\)\(=\)\((R|_{\bar{T}})^{-1}(t^{\flat })\) and \(\bar{t}= (R|_{\bar{T}})^{-1}(t)\); which is [4] equivalent to \(({ \exists }t^{\flat }{ \in }T){ \ }c{ \notin }t^{\flat }\) and \(t^{\flat }{ \cup }{ \lbrace }c{ \rbrace }{=}t\) by manipulation; which is [5] equivalent to \(({ \exists }t^{\flat }{ \in }T){ \ }c{ \in }t\) and
. (a) holds by Claim 3. For (b), take \(c{ \ }{ \in }{ \ }C\). I argue \(c = [(R|_{\bar{T}})^{-1}(t)]_{K((R|_{\bar{T}})^{-1}(t))}\) is [1] equivalent to \(({ \exists }\bar{t}^{\,\flat }{ \in }\bar{T}){ \ }\bar{t}^{\,\flat }{ \oplus }(c) = (R|_{\bar{T}})^{-1}(t)\) by inspection; which is [2] equivalent to \(({ \exists }t^{\flat }{ \in }T)\)\((R|_{\bar{T}})^{-1}(t^{\flat }){ \oplus }(c) = (R|_{\bar{T}})^{-1}(t)\) by Claim 3; which is [3] equivalent to \(({ \exists }t^{\flat }{ \in }T)\)\(c{ \ }{ \notin }{ \ }R{ \circ }(R|_{\bar{T}})^{-1}(t^{\flat })\) and \(R{ \circ }(R|_{\bar{T}})^{-1}(t^{\flat }){ \cup }{ \lbrace }c{ \rbrace } = R{ \circ }(R|_{\bar{T}})^{-1}(t)\) by Claim 5 at \(\bar{t}^{\,\flat }\)\(=\)\((R|_{\bar{T}})^{-1}(t^{\flat })\) and \(\bar{t}= (R|_{\bar{T}})^{-1}(t)\); which is [4] equivalent to \(({ \exists }t^{\flat }{ \in }T){ \ }c{ \notin }t^{\flat }\) and \(t^{\flat }{ \cup }{ \lbrace }c{ \rbrace }{=}t\) by manipulation; which is [5] equivalent to \(({ \exists }t^{\flat }{ \in }T){ \ }c{ \in }t\) and 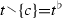 by manipulation; which is [6] equivalent to \(c{ \in }t\) and
by manipulation; which is [6] equivalent to \(c{ \in }t\) and  .
. - Claim 7: :
-
[cs2] holds. Take \(t{ \ }{ \ne }{ \ }{ \lbrace }{ \rbrace }\). It must be shown that t has a unique last choice. Claim 6 establishes that the last elements of the sequence \((R|_{\bar{T}})^{-1}(t)\) are identical to the last choices (Sect. 2) of the set t. Since the sequence \((R|_{\bar{T}})^{-1}(t)\) is nonempty because the set t is nonempty, the sequence has a unique last element. By the previous two sentences, the set t has a unique last choice.
- Claim 8: :
-
 . Take
. Take 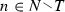 . By the definition of N, there is \(\bar{n}{ \ }{ \in }{ \ }\bar{N}\) such that \(n = R(\bar{n})\). Thus, since \(n{ \ }{ \notin }{ \ }T\), \(R(\bar{n})\) is infinite. This and \(\bar{n}{ \ }{ \in }{ \ }\bar{N}\) imply
. By the definition of N, there is \(\bar{n}{ \ }{ \in }{ \ }\bar{N}\) such that \(n = R(\bar{n})\). Thus, since \(n{ \ }{ \notin }{ \ }T\), \(R(\bar{n})\) is infinite. This and \(\bar{n}{ \ }{ \in }{ \ }\bar{N}\) imply  . Hence, by [OR2], we may define \(T^* = { \lbrace }R(_1\bar{n}_{ \ell })|{ \ell }{ \ge }1{ \rbrace }\). As required, \(\,T^*\,{ \subseteq }\,T\) because [a] R takes \(\bar{N}\) to N and [b] finite sequences have finite ranges. Further, \(T^*\) is an infinite chain because [i] it is a chain by inspection and [ii] \(({ \forall }{ \ell }{ \ge }1){ \ }|R(_1\bar{n}_{ \ell })| = { \ell }\) by Lemma A.4(a\({ \Leftrightarrow }\)c). Finally, n equals \(R(\bar{n})\) by the definition of \(\bar{n}\); which equals \(R({ \cup }{ \lbrace }{_1\bar{n}_{ \ell }}|{ \ell }{ \ge }1{ \rbrace })\) by \(\bar{n}\) being an infinite sequence; which equals \({ \cup }{ \lbrace }R({_1\bar{n}_{ \ell }})|{ \ell }{ \ge }1{ \rbrace }\) by manipulation; which equals \({ \cup }T^*\) by the definition of \(T^*\).
. Hence, by [OR2], we may define \(T^* = { \lbrace }R(_1\bar{n}_{ \ell })|{ \ell }{ \ge }1{ \rbrace }\). As required, \(\,T^*\,{ \subseteq }\,T\) because [a] R takes \(\bar{N}\) to N and [b] finite sequences have finite ranges. Further, \(T^*\) is an infinite chain because [i] it is a chain by inspection and [ii] \(({ \forall }{ \ell }{ \ge }1){ \ }|R(_1\bar{n}_{ \ell })| = { \ell }\) by Lemma A.4(a\({ \Leftrightarrow }\)c). Finally, n equals \(R(\bar{n})\) by the definition of \(\bar{n}\); which equals \(R({ \cup }{ \lbrace }{_1\bar{n}_{ \ell }}|{ \ell }{ \ge }1{ \rbrace })\) by \(\bar{n}\) being an infinite sequence; which equals \({ \cup }{ \lbrace }R({_1\bar{n}_{ \ell }})|{ \ell }{ \ge }1{ \rbrace }\) by manipulation; which equals \({ \cup }T^*\) by the definition of \(T^*\). - Claim 9: :
-
[cs3] holds. Because of Claim 8, it suffices to show that
 . Toward that end, suppose \(T^*\) is an infinite chain in T. Because \(T^*\) is an infinite chain, \({ \cup }T^*\) must be an infinite set. Thus, it remains to show that \({ \cup }T^*{ \ }{ \in }{ \ }N\). By Lemma A.1 at \(s = { \cup }T^*\), there is an infinite sequence \((t^m)_{m{ \ge }1}\) in T such that [a] \(({ \forall }m{ \ge }1){ \ }t^m{ \ }{ \subset }{ \ }t^{m+1}\) and [b] \({ \cup }_{m{ \ge }1}t^m = { \cup }T^*\). Further, by Claim 3, there is an infinite sequence \((\bar{t}^{\,m})_{m{ \ge }1}\) in \(\bar{T}\) such that [c] \(({ \forall }m{ \ge }1){ \ }t^m = R(\bar{t}^{\,m})\). [a] and [c] imply [d] \(({ \forall }m{ \ge }1){ \ }R(\bar{t}^{\,m}){ \ }{ \subset }{ \ }R(\bar{t}^{\,m+1})\). [d] and two applications of Lemma A.4(a\({ \Leftrightarrow }\)c) yield [e] \(({ \forall }m{ \ge }1){ \ }K(\bar{t}^{\,m}) = |R(\bar{t}^{\,m})| < |R(\bar{t}^{\,m+1})| = K(\bar{t}^{\,m+1})\). Also, [d] and Lemma A.6 yield [f] \(({ \forall }m{ \ge }1){ \ }\bar{t}^{\,m} = {_1\bar{t}^{\,m+1}_{K(t^m)}}\). [e] and [f] imply [g] \({ \cup }_{m{ \ge }1}\bar{t}^m{ \ }{ \in }{ \ }C^{ \infty }\) and [h] \(({ \forall }m^{ \prime }{ \ge }1)\)\(_1({ \cup }_{m{ \ge }1}\bar{t}^m)_{m^{ \prime }} =\bar{t}^{m^{ \prime }}\). [h] implies \(({ \forall }k{ \ge }1)({ \exists }m^{ \prime }{ \ge }k)\)\(_1({ \cup }_{m{ \ge }1}\bar{t}^m)_{m^{ \prime }}\)\(=\)\(\bar{t}^{m^{ \prime }}\)\({ \in }{ \ }\bar{T}\). This, [g], and Lemma A.2 at \(\bar{s} = { \cup }_{m{ \ge }1}\bar{t}^m\) imply [i] \({ \cup }_{m{ \ge }1}\bar{t}^m{ \ }{ \in }{ \ }\bar{N}\). So, \({ \cup }T^* = { \cup }_{m{ \ge }1}t^m\) by [b]; which equals \({ \cup }_{m{ \ge }1}R(\bar{t}^m)\) by [c]; which equals \(R({ \cup }_{m{ \ge }1}\bar{t}^m)\) by manipulation; which belongs to \({ \lbrace }R(\bar{n})|\bar{n}{ \in }\bar{N}{ \rbrace }\) by [i]; which equals N by the theorem’s definition of N.
. Toward that end, suppose \(T^*\) is an infinite chain in T. Because \(T^*\) is an infinite chain, \({ \cup }T^*\) must be an infinite set. Thus, it remains to show that \({ \cup }T^*{ \ }{ \in }{ \ }N\). By Lemma A.1 at \(s = { \cup }T^*\), there is an infinite sequence \((t^m)_{m{ \ge }1}\) in T such that [a] \(({ \forall }m{ \ge }1){ \ }t^m{ \ }{ \subset }{ \ }t^{m+1}\) and [b] \({ \cup }_{m{ \ge }1}t^m = { \cup }T^*\). Further, by Claim 3, there is an infinite sequence \((\bar{t}^{\,m})_{m{ \ge }1}\) in \(\bar{T}\) such that [c] \(({ \forall }m{ \ge }1){ \ }t^m = R(\bar{t}^{\,m})\). [a] and [c] imply [d] \(({ \forall }m{ \ge }1){ \ }R(\bar{t}^{\,m}){ \ }{ \subset }{ \ }R(\bar{t}^{\,m+1})\). [d] and two applications of Lemma A.4(a\({ \Leftrightarrow }\)c) yield [e] \(({ \forall }m{ \ge }1){ \ }K(\bar{t}^{\,m}) = |R(\bar{t}^{\,m})| < |R(\bar{t}^{\,m+1})| = K(\bar{t}^{\,m+1})\). Also, [d] and Lemma A.6 yield [f] \(({ \forall }m{ \ge }1){ \ }\bar{t}^{\,m} = {_1\bar{t}^{\,m+1}_{K(t^m)}}\). [e] and [f] imply [g] \({ \cup }_{m{ \ge }1}\bar{t}^m{ \ }{ \in }{ \ }C^{ \infty }\) and [h] \(({ \forall }m^{ \prime }{ \ge }1)\)\(_1({ \cup }_{m{ \ge }1}\bar{t}^m)_{m^{ \prime }} =\bar{t}^{m^{ \prime }}\). [h] implies \(({ \forall }k{ \ge }1)({ \exists }m^{ \prime }{ \ge }k)\)\(_1({ \cup }_{m{ \ge }1}\bar{t}^m)_{m^{ \prime }}\)\(=\)\(\bar{t}^{m^{ \prime }}\)\({ \in }{ \ }\bar{T}\). This, [g], and Lemma A.2 at \(\bar{s} = { \cup }_{m{ \ge }1}\bar{t}^m\) imply [i] \({ \cup }_{m{ \ge }1}\bar{t}^m{ \ }{ \in }{ \ }\bar{N}\). So, \({ \cup }T^* = { \cup }_{m{ \ge }1}t^m\) by [b]; which equals \({ \cup }_{m{ \ge }1}R(\bar{t}^m)\) by [c]; which equals \(R({ \cup }_{m{ \ge }1}\bar{t}^m)\) by manipulation; which belongs to \({ \lbrace }R(\bar{n})|\bar{n}{ \in }\bar{N}{ \rbrace }\) by [i]; which equals N by the theorem’s definition of N.
(b). It must be shown that \(({ \cup }_{i{ \in }I}C_i,N)\) is a choice-set tree, and that \(((C_i)_{i{ \in }I},N)\) satisfies [cs4], [cs5], and [cs6]. This is done by Claims 11, 14, 15, and 16.
- Claim 10: :
-
\({ \cup }N{ \ }{ \subseteq }{ \ }{ \cup }_{i{ \in }I}C_i\). By definition, \(N = { \lbrace }R(\bar{n})|\bar{n}{ \in }\bar{N}{ \rbrace }\). Thus it suffices to show \({ \cup }{ \lbrace }R(\bar{n})|\bar{n}{ \in }\bar{N}{ \rbrace }{ \ }{ \subseteq }{ \ }{ \cup }_{i{ \in }I}C_i\). Toward that end, take any \(\bar{n}{ \ }{ \in }{ \ }\bar{N}\) and any \(c{ \ }{ \in }{ \ }R(\bar{n})\). Then there exists \(k{ \ }{ \ge }{ \ }1\) such that \(c = \bar{n}_k\). Thus [a] \(c{ \ }{ \in }{ \ }C_{{_1\bar{n}_{k-1}}}\). So \({_1\bar{n}_{k-1}}{ \ }{ \in }{ \ }\bar{X}\), which by [OR4] and [OR5] implies there are \(i{ \ }{ \in }{ \ }I\) and [b] \(\bar{H}^*{ \ }{ \in }{ \ }\bar{{ \mathscr {H}}}_i\) such that [c] \({_1\bar{n}_{k-1}}{ \ }{ \in }{ \ }\bar{H}^*\). So, \(c{ \ }{ \in }{ \ }C_{{_1\bar{n}_{k-1}}}\) by [a]; which equals \(C_{\bar{H}^*}\) by [c]; which is a subset of \({ \cup }{ \lbrace }C_{\bar{H}}|\bar{H}{ \in }\bar{{ \mathscr {H}}}_i{ \rbrace }\) by [b]; which equals \(C_i\) by the theorem’s definition of \(C_i\).
- Claim 11: :
-
\(({ \cup }_{i{ \in }I}C_i,N)\)is a choice-set tree. By part (a), (C, N) is a choice-set tree. Equivalently, (C, N) satisfies [cs1]–[cs3]. By inspection, these three conditions are only concerned with the choices in \({ \cup }N\). So, if \(C^{ \prime }\) is any superset of \({ \cup }N\), then \((C^{ \prime },N)\) satisfies [cs1]–[cs3]. Thus, by Claim 10, \(({ \cup }_{i{ \in }I}C_i,N)\) satisfies [cs1]–[cs3].
- Claim 12: :
-
\(({ \forall }\bar{t}{ \in }\bar{T}){ \ }C_{\bar{t}} = C_{R(\bar{t})}\). Take any \(\bar{t}\). I argue \(C_{\bar{t}}\) [a] equals \( { \lbrace }\,c{ \in }C\,|\,\bar{t}{ \oplus }(c){ \in }\bar{T}\,{ \rbrace }\) by the (OR) definition of \(C_{\bar{t}}\); which [b] equals \({ \lbrace }\,c{ \in }C\,|\,({ \exists }\bar{t}^{\sharp }{ \in }\bar{T})\,\bar{t}{ \oplus }(c){=}\bar{t}^{\sharp }\,{ \rbrace }\) by rearrangement; which [c] equals \({ \lbrace }\,c{ \in }C\,|\,({ \exists }\bar{t}^{\sharp }{ \in }\bar{T})\,c{ \notin }R(\bar{t})\) and \(R(\bar{t}){ \cup }{ \lbrace }c{ \rbrace }{=}R(\bar{t}^{\sharp })\,{ \rbrace }\) by Claim 5; which [d] equals \({ \lbrace }\,c{ \in }C\,|\,c{ \notin }R(\bar{t})\) and \(R(\bar{t}){ \cup }{ \lbrace }c{ \rbrace }{ \in }T\,{ \rbrace }\) because \(R|_{\bar{T}}\) is onto T by Claim 3; which [e] equals \(C_{R(\bar{t})}\) by the (choice-set) definition of \(C_{R(\bar{t})}\).
- Claim 13: :
-
\( R|_{\bar{X}}\)is a bijection from\(\bar{X}\)ontoX. By Claim 3 and the fact that \(\bar{X}{ \ }{ \subseteq }{ \ }\bar{T}\), it suffices to show that \({ \lbrace }R(\bar{t})|\bar{t}{ \in }\bar{X}{ \rbrace } = X\). For the \({ \subseteq }\) direction, suppose \(\bar{t}{ \ }{ \in }{ \ }\bar{X}\). Then \(C_{\bar{t}}{ \ }{ \ne }{ \ }{ \varnothing }\). Thus by Claim 12, \(C_{R(\bar{t})}{ \ }{ \ne }{ \ }{ \varnothing }\). Hence \(R(\bar{t}){ \ }{ \in }{ \ }X\). Conversely, suppose \(t{ \ }{ \in }{ \ }X\). By Claim 3, there exists \(\bar{t}{ \ }{ \in }{ \ }\bar{T}\) such that \(R(\bar{t}) = t\). Thus it suffices to show \(\bar{t}{ \ }{ \in }{ \ }\bar{X}\). Since \(R(\bar{t}) = t\) and \(t{ \ }{ \in }{ \ }X\), \(C_{R(\bar{t})}{ \ }{ \ne }{ \ }{ \varnothing }\). Thus by Claim 12, \(C_{\bar{t}}{ \ }{ \ne }{ \ }{ \varnothing }\). Hence \(\bar{t}{ \ }{ \in }{ \ }\bar{X}\).
- Claim 14: :
-
[cs4] holds. Suppose there were \(c^A{ \ }{ \in }{ \ }{ \cup }_iC_i\) and \(c^B{ \ }{ \in }{ \ }{ \cup }_{i{ \in }I}C_i\) such that \({ \lbrace }t{ \in }X|c^A{ \in }C_t{ \rbrace }\) and \({ \lbrace }t{ \in }X|c^B{ \in }C_t{ \rbrace }\) were unequal but intersecting. Then, without loss of generality, assume that \(t^2\) is in both sets and that \(t^1\) is in the former but not the latter. Then \(t^1{ \ }{ \in }{ \ }X\) and \(t^2{ \ }{ \in }{ \ }X\) are such that \({ \lbrace }c^A,c^B{ \rbrace }{ \ }{ \subseteq }{ \ }C_{t^2}\), \(c^A{ \ }{ \in }{ \ }C_{t^1}\), and \(c^B{ \ }{ \notin }{ \ }C_{t^1}\). By Claim 13 and \(\bar{X}{ \ }{ \subseteq }{ \ }\bar{T}\), there exist \(\bar{t}^1\) and \(\bar{t}^2\) in \(\bar{T}\) such that \(R(\bar{t}^1) = t^1\) and \(R(\bar{t}^2) = t^2\). Thus by the second-previous sentence and Claim 12, \({ \lbrace }c^A,c^B{ \rbrace }{ \ }{ \subseteq }{ \ }C_{\bar{t}^2}\), \(c^A{ \ }{ \in }{ \ }C_{\bar{t}^1}\), and \(c^B{ \ }{ \notin }{ \ }C_{\bar{t}^1}\). Thus \(\bar{t}^2\) is in both \({ \lbrace }\bar{t}{ \in }\bar{T}|c^A{ \in }C_{\bar{t}}{ \rbrace }\) and \({ \lbrace }\bar{t}{ \in }\bar{T}|c^B{ \in }C_{\bar{t}}{ \rbrace }\), while \(\bar{t}^1\) is in the former but not the latter. Therefore, since these two sets belong to \({ \cup }_{i{ \in }I}\bar{{ \mathscr {H}}}_i\) by Lemma A.3, \({ \cup }_{i{ \in }I}\bar{{ \mathscr {H}}}_i\) is not pairwise disjoint. This contradicts [OR4] and [OR5].
- Claim 15: :
-
[cs5] holds. Suppose there were \(i{ \ }{ \in }{ \ }I\),
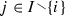 , and \(c{ \ }{ \in }{ \ }C_i{ \cap }C_j\). By the theorem’s definition of \(C_i\), there is \(\bar{H}_i{ \ }{ \in }{ \ }\bar{{ \mathscr {H}}}_i\) such that \(c{ \ }{ \in }{ \ }C_{\bar{H}_i}\). Similarly there is \(\bar{H}_j{ \ }{ \in }{ \ }\bar{{ \mathscr {H}}}_j\) such that \(c{ \ }{ \in }{ \ }C_{\bar{H}_j}\). Note [i] \(c{ \ }{ \in }{ \ }C_{\bar{H}_i}{ \cap }C_{\bar{H}_j}\). Yet, \(\bar{H}_i{ \ }{ \subseteq }{ \ }\bar{P}^{-1}(i)\) and \(\bar{H}_j{ \ }{ \subseteq }{ \ }\bar{P}^{-1}(j)\) by [OR5]. This implies \(\bar{H}_i{ \ }{ \ne }{ \ }\bar{H}_j\) because \(\bar{P}^{-1}(i){ \cap }\bar{P}^{-1}(j) = { \varnothing }\) by [OR4]. Thus [ii] \(C_{\bar{H}_i}{ \cap }C_{\bar{H}_j} = { \varnothing }\) by the assumption of no shared alternatives. [i] and [ii] contradict.
, and \(c{ \ }{ \in }{ \ }C_i{ \cap }C_j\). By the theorem’s definition of \(C_i\), there is \(\bar{H}_i{ \ }{ \in }{ \ }\bar{{ \mathscr {H}}}_i\) such that \(c{ \ }{ \in }{ \ }C_{\bar{H}_i}\). Similarly there is \(\bar{H}_j{ \ }{ \in }{ \ }\bar{{ \mathscr {H}}}_j\) such that \(c{ \ }{ \in }{ \ }C_{\bar{H}_j}\). Note [i] \(c{ \ }{ \in }{ \ }C_{\bar{H}_i}{ \cap }C_{\bar{H}_j}\). Yet, \(\bar{H}_i{ \ }{ \subseteq }{ \ }\bar{P}^{-1}(i)\) and \(\bar{H}_j{ \ }{ \subseteq }{ \ }\bar{P}^{-1}(j)\) by [OR5]. This implies \(\bar{H}_i{ \ }{ \ne }{ \ }\bar{H}_j\) because \(\bar{P}^{-1}(i){ \cap }\bar{P}^{-1}(j) = { \varnothing }\) by [OR4]. Thus [ii] \(C_{\bar{H}_i}{ \cap }C_{\bar{H}_j} = { \varnothing }\) by the assumption of no shared alternatives. [i] and [ii] contradict. - Claim 16: :
-
[cs6] holds. Take any \(t{ \ }{ \in }{ \ }X\). By Claim 13, there exists [1] \(\bar{t}{ \ }{ \in }{ \ }\bar{X}\) such that [2] \(R(\bar{t}) = t\). [1] and [OR4] imply there is i such that \(\bar{t}{ \ }{ \in }{ \ }P^{-1}(i)\). This and [OR5] imply there is [3] \(\bar{H}^*{ \ }{ \in }{ \ }\bar{{ \mathscr {H}}}_i\) such that \(\bar{t}{ \ }{ \in }{ \ }\bar{H}^*\). So by [OR6], [4] \(C_{\bar{t}} = C_{\bar{H}^*}\). Hence \(C_t\) equals \(C_{\bar{t}}\) by [2] and Claim 12; which equals \(C_{\bar{H}^*}\) by [4]; which is a subset of \({ \cup }{ \lbrace }C_{\bar{H}}|\bar{H}{ \in }\bar{{ \mathscr {H}}}_i{ \rbrace }\) by [3]; which equals \(C_i\) by the theorem’s definition of \(C_i\).
Proof A.8
(for Theorem 3.2: choice-set \({ \rightarrow }\) OR)Definition ofC, \(c_*\), and\((T_k)_{k{ \ge }0}\). First, let \(C = { \cup }_{i{ \in }I}C_i\). Second, [cs2] implies the existence of a function  that takes each nonempty \(t{ \ }{ \in }{ \ }T\) to its unique last choice \(c_*(t)\). Third, define \((T_k)_{k{ \ge }0}\) by \(T_k = { \lbrace }\,t{ \in }T\,|\,|t|{=}k\,{ \rbrace }\). Note \(T = { \cup }_{k{ \ge }0}T_k\). Also note \(T_0 = { \lbrace }{ \lbrace }{ \rbrace }{ \rbrace }\) by note 6.
that takes each nonempty \(t{ \ }{ \in }{ \ }T\) to its unique last choice \(c_*(t)\). Third, define \((T_k)_{k{ \ge }0}\) by \(T_k = { \lbrace }\,t{ \in }T\,|\,|t|{=}k\,{ \rbrace }\). Note \(T = { \cup }_{k{ \ge }0}T_k\). Also note \(T_0 = { \lbrace }{ \lbrace }{ \rbrace }{ \rbrace }\) by note 6.
Definition of\((Q_k)_{k{ \ge }0}\). This paragraph recursively defines a sequence \((Q_k)_{k{ \ge }0}\) of surjective functions which map choice sets to choice sequences. More precisely, each \(Q_k\) will map each \(t{ \ }{ \in }{ \ }T_k\) to some finite sequence in C. To begin, define the one-element function \(Q_0{:}T_0{ \rightarrow }Q_0(T_0)\) by \(Q_0({ \lbrace }{ \rbrace }) = { \lbrace }{ \rbrace }\). Note that the codomain of \(Q_0\) has been set equal to its range \(Q_0(T_0) = { \lbrace }{ \lbrace }{ \rbrace }{ \rbrace }\). Then, for any \(k{ \ }{ \ge }{ \ }1\), use \(Q_{k-1}\) to define \(Q_k{:}T_k{ \rightarrow }Q_k(T_k)\) by  . Note that \(Q_k\) is well-defined at each \(t{ \ }{ \in }{ \ }T_k\) because [a]
. Note that \(Q_k\) is well-defined at each \(t{ \ }{ \in }{ \ }T_k\) because [a]  by [cs2] and [b] \(T_{k-1}\) is the domain of the function \(Q_{k-1}\) which was defined in the last step of the recursion. Also note that the codomain of \(Q_k\) has been set equal to its range \(Q_k(T_k)\).
by [cs2] and [b] \(T_{k-1}\) is the domain of the function \(Q_{k-1}\) which was defined in the last step of the recursion. Also note that the codomain of \(Q_k\) has been set equal to its range \(Q_k(T_k)\).
Definition of\(\bar{N}\). Define \(\bar{N}= { \cup }_{k{ \ge }0}Q_k(T_k){ \ }{ \cup }{ \ }{ \lbrace }\,\bar{s}{ \in }C^{ \infty }\,|\,({ \forall }{ \ell }{ \ge }0)\,_1\bar{s}_{ \ell }\,{ \in }\,{ \cup }_{k{ \ge }0}Q_k(T_k)\,{ \rbrace }\), where \(C^{ \infty }\) denotes the set of all infinite sequences in C.
- Claim 1: :
-
[OR1] holds. By inspection, \(\bar{N}\) consists of sequences in C. Further, \(\bar{N}\) is nonempty because [a] \(Q({ \lbrace }{ \rbrace }) = { \lbrace }{ \rbrace }\) is an element of \(Q_0(T_0)\) by the definition of \(Q_0\), and [b] \(Q_0(T_0){ \ }{ \subseteq }{ \ }\bar{N}\) by the definition of \(\bar{N}\).
- Claim 2: :
-
[OR2] holds for\(K = { \infty }\). Suppose \(\bar{s}{ \ }{ \in }{ \ }\bar{N}{ \cap }C^{ \infty }\). Since \(\bar{s}\) is infinite and \({ \cup }_{k{ \ge }0}Q_k(T_k)\) consists of finite sequences, \(\bar{s}{ \ }{ \notin }{ \ }{ \cup }_{k{ \ge }0}Q_k(T_k)\). Thus the \({ \subseteq }\) half of the definition of \(\bar{N}\) implies \(({ \forall }{ \ell }{ \ge }0)\,_1\bar{s}_{ \ell }\,{ \in }\,{ \cup }_{k{ \ge }0}Q_k(T_k)\). This implies \(({ \forall }{ \ell }{ \ge }0)\,_1\bar{s}_{ \ell }\,{ \in }\,\bar{N}\) since \({ \cup }_{k{ \ge }0}Q_k(T_k){ \ }{ \subseteq }{ \ }\bar{N}\) by the \({ \supseteq }\) half of the definition of \(\bar{N}\).
- Claim 2: :
-
[OR3] holds. Suppose \(\bar{s}{ \ }{ \in }{ \ }C^{ \infty }\) satisfies \(({ \forall }{ \ell }{ \ge }0)\,_1\bar{s}_{ \ell }\,{ \in }\,\bar{N}\). Since each \(_1\bar{s}_{ \ell }\) is finite, the \({ \subseteq }\) half of the definition of \(\bar{N}\) implies that \(({ \forall }{ \ell }{ \ge }0)\)\(_1\bar{s}_{ \ell }\,{ \in }\,{ \cup }_{k{ \ge }0}Q_k(T_k)\). Thus the \({ \supseteq }\) half of the definition of \(\bar{N}\) implies \(\bar{s}{ \ }{ \in }{ \ }\bar{N}\).
- Claim 3: :
-
\(\bar{T}= { \cup }_{k{ \ge }0}Q_k(T_k)\). Section 3.1 defines \(\bar{T}\) to be the collection of finite sequences in \(\bar{N}\). Thus the claim holds by inspecting the definition of \(\bar{N}\).
- Claim 4: :
-
\(({ \forall }k{ \ge }0,t{ \in }T_k){ \ }K(Q_k(t)) = k\). This can be shown by induction. The initial step (\(k = 0\)) holds because \(T_0 = { \lbrace }{ \lbrace }{ \rbrace }{ \rbrace }\) by the definition of \(T_0\), and because \(K(Q_0({ \lbrace }{ \rbrace }))\)\(=\)\(K({ \lbrace }{ \rbrace }) = 0\) by the definition of \(Q_0\). The inductive step (\(k{ \ }{ \ge }{ \ }1\)) holds because for any \(t{ \ }{ \in }{ \ }T_k\), \(K(\,Q_k(t)\,)\) equals
 by the definition of \(Q_k\), which equals
by the definition of \(Q_k\), which equals 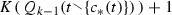 by inspection. This equals \((k{-}1) + 1\) by [a] the inductive hypothesis and [b] the fact that
by inspection. This equals \((k{-}1) + 1\) by [a] the inductive hypothesis and [b] the fact that  by \(t{ \ }{ \in }{ \ }T_k\) and [cs2]. Finally, \((k{-}1) + 1 = k\).
by \(t{ \ }{ \in }{ \ }T_k\) and [cs2]. Finally, \((k{-}1) + 1 = k\). - Claim 5: :
-
\(({ \forall }k{ \ge }0){ \ }Q_k(T_k) = { \lbrace }\,\bar{t}{ \in }\bar{T}\,|\,K(\bar{t}){=}k\,{ \rbrace }\). Fix \(k{ \ }{ \ge }{ \ }0\). The \({ \subseteq }\) direction follows from Claim 4 at k. Conversely, take any [a] \(\bar{t}{ \ }{ \in }{ \ }\bar{T}\) such that [b] \(K(\bar{t}) = k\). By [a] and the \({ \subseteq }\) direction of Claim 3, there are \(k^{ \prime }{ \ }{ \ge }{ \ }0\) and [c] \(t^{ \prime }{ \ }{ \in }{ \ }T_{k^{ \prime }}\) such that [d] \(\bar{t}= Q_{k^{ \prime }}(t^{ \prime })\). Note \(K(\bar{t})\) equals \(K(Q_{k^{ \prime }}(t^{ \prime }))\) by [d]; which equals \(k^{ \prime }\) by [c] and Claim 4 at \(k^{ \prime }\). This and [b] imply \(k = k^{ \prime }\). This, [c], and [d] imply \(\bar{t}{ \ }{ \in }{ \ }Q_k(T_k)\).
- Claim 6: :
-
 . Fix
. Fix  . Note \(\bar{t}{ \ }{ \in }{ \ }Q_{K(\bar{t})}(T_{K(\bar{t})})\) by Claim 5. Thus there is \(t{ \ }{ \in }{ \ }T_{K(\bar{t})}\) such that \(\bar{t}= Q_{K(\bar{t})}(t)\). Since \(\bar{t}{ \ }{ \ne }{ \ }{ \lbrace }{ \rbrace }\) by assumption, \(K(\bar{t}){ \ }{ \ge }{ \ }1\). The last two sentences and the definition of \(Q_{K(\bar{t})}\) imply
. Note \(\bar{t}{ \ }{ \in }{ \ }Q_{K(\bar{t})}(T_{K(\bar{t})})\) by Claim 5. Thus there is \(t{ \ }{ \in }{ \ }T_{K(\bar{t})}\) such that \(\bar{t}= Q_{K(\bar{t})}(t)\). Since \(\bar{t}{ \ }{ \ne }{ \ }{ \lbrace }{ \rbrace }\) by assumption, \(K(\bar{t}){ \ }{ \ge }{ \ }1\). The last two sentences and the definition of \(Q_{K(\bar{t})}\) imply 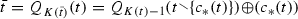 . I argue [a]
. I argue [a]  by the previous sentence; which [b] belongs to \(Q_{K(t)-1}(T_{K(t)-1})\) by \(t{ \ }{ \in }{ \ }T_{K(\bar{t})}\) and [cs2]; which [c] is a subset of \(\bar{T}\) by Claim 3.
by the previous sentence; which [b] belongs to \(Q_{K(t)-1}(T_{K(t)-1})\) by \(t{ \ }{ \in }{ \ }T_{K(\bar{t})}\) and [cs2]; which [c] is a subset of \(\bar{T}\) by Claim 3. - Claim 7: :
-
\(({ \cup }_{i{ \in }I}C_i,\bar{N})\)is an OR tree. Because of Claims 1–3, it suffices to show that [OR2] holds for \(K < { \infty }\). Toward that end, take any \(\bar{n}{ \ }{ \in }{ \ }\bar{N}\) and any \({ \ell }{ \ }{ \ge }{ \ }0\) such that \({ \ell }< K(\bar{n}) < { \infty }\). By \(K(\bar{n}) < { \infty }\) and the definition of \(\bar{T}\), \(\bar{n}{ \ }{ \in }{ \ }\bar{T}\). Thus \({_1\bar{n}_{{ \ell }}}\) belongs to \(\bar{T}\) by \(K(\bar{t}){-}{ \ell }\) applications of Claim 6; which is a subset of \(\bar{N}\) by the definition of \(\bar{T}\).
- Claim 8: :
-
(a)\({ \cup }_{k{ \ge }0}Q_k\,{:}\,T{ \rightarrow }\bar{T}\)is well-defined and (b)\(({ \forall }t{ \in }T)\,({ \cup }_{k{ \ge }0}Q_k)(t) = Q_{|t|}(t)\). Take \(t{ \ }{ \in }{ \ }T\). The definition of \((T_k)_{k{ \ge }0}\) implies [1] \(t{ \ }{ \in }{ \ }T_{|t|}\) and [2] \((T_k)_{k{ \ge }0}\) partitions T. [1] and [2] imply \(({ \cup }_{k{ \ge }0}Q_k)(t)\) is [3] well-defined and [4] equal to \(Q_{|t|}(t)\). Also, \(({ \cup }_{k{ \ge }0}Q_k)(t)\) equals \(Q_{|t|}(t)\) by [4]; which belongs to \(Q_{|t|}(T_{|t|})\) by [1]; which is a subset of \(\bar{T}\) by Claim 3. (a) follows from [3] and the previous sentence. (b) follows from [4].
- Claim 9: :
-
\(({ \forall }k{ \ge }0,t{ \in }T_k){ \ }R(Q_k(t)) = t\). This can be shown by induction. The initial step (\(k = 0\)) holds because \(T_0 = { \lbrace }{ \lbrace }{ \rbrace }{ \rbrace }\) by the definition of \(T_0\) and because \(R(Q_0({ \lbrace }{ \rbrace })) = R({ \lbrace }{ \rbrace }) = { \lbrace }{ \rbrace }\) by the definition of \(Q_0\). To see the inductive step, take any \(k{ \ }{ \ge }{ \ }1\) and any \(t{ \ }{ \in }{ \ }T_k\). Then \(R(\,Q_k(t)\,)\) [a] equals
 by the definition of \(Q_k\), which [b] equals
by the definition of \(Q_k\), which [b] equals  by inspection, which [c] equals
by inspection, which [c] equals  by the inductive hypothesis, which [d] equals t.
by the inductive hypothesis, which [d] equals t. - Claim 10: :
-
\(R|_{\bar{T}}\,{:}\,\bar{T}{ \rightarrow }T\)is the inverse of\({ \cup }_{k{ \ge }0}Q_k\). Claim 9 implies that \(({ \forall }k{ \ge }0)\)\(R|_{Q_k(T_k)} = Q_k^{-1}\) and that it maps from \(Q_k(T_k)\) onto \(T_k\). Claim 5 implies that the members of \({ \lbrace }Q_k(T_k)|k{ \ge }0{ \rbrace }\) are disjoint. The definition of \((T_k)_{k{ \ge }0}\) implies that the members of \({ \lbrace }T_k|k{ \ge }0{ \rbrace }\) are disjoint. The last three sentences imply that \(R|_{{ \cup }_kQ_k(T_k)} = ({ \cup }_{k{ \ge }0}Q_k)^{-1}\) and that it maps from \({ \cup }_{k{ \ge }0}Q_k(T_k)\) onto \({ \cup }_{k{ \ge }0}T_k\). This is equivalent to the claim because [a] \({ \cup }_{k{ \ge }0}Q_k(T_k) = \bar{T}\) by Claim 3 and because [b] \({ \cup }_{k{ \ge }0}T_k = T\) by the definition of \((T_k)_{k{ \ge }0}\).
- Claim 11: :
-
\(({ \forall }k{ \ge }1,t^{\flat }{ \in }T_{k-1},c{ \in }C,t{ \in }T_k){ \ }Q_{k-1}(t^{\flat }){ \oplus }(c) = Q_k(t)\)iff both\(c{ \ }{ \notin }{ \ }t^{\flat }\)and\(t^{\flat }{ \cup }{ \lbrace }c{ \rbrace }=t\). Take any such k, \(t^{\flat }\), c, and t. I argue [a] \(Q_{k-1}(t^{\flat }){ \oplus }(c) = Q_k(t)\) is equivalent to
 by the definition of \(Q_k\); which [b] is equivalent to the combination of
by the definition of \(Q_k\); which [b] is equivalent to the combination of  and \(c{=}c_*(t)\) by rearrangement; which [c] is equivalent to
and \(c{=}c_*(t)\) by rearrangement; which [c] is equivalent to  and \(c{=}c_*(t)\) by applying R to both sides of the first equality and then simplifying it via Claim 10; which [d] is equivalent to
and \(c{=}c_*(t)\) by applying R to both sides of the first equality and then simplifying it via Claim 10; which [d] is equivalent to 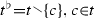 , and \(c{=}c_*(t)\); which [e] is equivalent to
, and \(c{=}c_*(t)\); which [e] is equivalent to  and \(c{ \in }t\) since \(t^{\flat }{ \in }T\) by assumption; which [f] is equivalent to \(c{ \notin }t^{\flat }\) and \(t^{\flat }{ \cup }{ \lbrace }c{ \rbrace }{=}t\) by rearrangement.
and \(c{ \in }t\) since \(t^{\flat }{ \in }T\) by assumption; which [f] is equivalent to \(c{ \notin }t^{\flat }\) and \(t^{\flat }{ \cup }{ \lbrace }c{ \rbrace }{=}t\) by rearrangement. - Claim 12: :
-
\(({ \forall }t^{\flat }{ \in }T,c{ \in }C,t{ \in }T)\)\(({ \cup }_{k{ \ge }0}Q_k)(t^{\flat }){ \oplus }(c) = ({ \cup }_{k{ \ge }0}Q_k)(t)\)iff both\(c{ \ }{ \notin }{ \ }t^{\flat }\)and\(t^{\flat }{ \cup }{ \lbrace }c{ \rbrace } = t\). Take \(t^{\flat }\), c, and t. By Claim 8(b) it suffices to show [a] \(Q_{|t^{\flat }|}(t^{\flat }){ \oplus }(c) = Q_{|t|}(t)\) is equivalent to [b] \(c{ \ }{ \notin }{ \ }t^{\flat }\) and \(t^{\flat }{ \cup }{ \lbrace }c{ \rbrace } = t\) together. For the forward direction, assume [a]. Two applications of Claim 5 imply \(K(Q_{|t^{\flat }|}(t^{\flat })) = |t^{\flat }|\) and \(K(Q_{|t|}(t)) = |t|\). This and [a] imply \(|t|{ \ }{ \ge }{ \ }1\) and \(|t^{\flat }| = |t|{-}1\). Hence [a] and the forward direction of Claim 11 at \(k = |t|\) imply [b]. Conversely, assume [b]. [b] implies \(|t|{ \ }{ \ge }{ \ }1\) and \(|t^{\flat }| = |t|{-}1\). Hence [b] and the reverse direction of Claim 11 at \(k = |t|\) imply [a].
- Claim 13: :
-
\(({ \forall }\bar{t}^{\,\flat }{ \in }\bar{T},c{ \in }C,\bar{t}{ \in }\bar{T})\)\(\bar{t}^{\,\flat }{ \oplus }(c) = \bar{t}\)iff both\(c{ \ }{ \notin }{ \ }R(\bar{t}^{\,\flat })\)and\(R(\bar{t}^{\,\flat }){ \cup }{ \lbrace }c{ \rbrace }\,{=}\,R(\bar{t})\). Take any \(\bar{t}^{\,\flat }\), c, and \(\bar{t}\). By Claim 10, \(\bar{t}^{\,\flat }{ \oplus }(c) = \bar{t}\) is equivalent to \(({ \cup }_{k{ \ge }0}Q_k){ \circ }R(\bar{t}^{\,\flat }){ \oplus }(c) = ({ \cup }_{k{ \ge }0}Q_k){ \circ }R(\bar{t})\). This, in turn, is equivalent to the combination of c\({ \notin }\)\(R(\bar{t}^{\,\flat })\) and \(R(\bar{t}^{\,\flat }){ \cup }{ \lbrace }c{ \rbrace }=R(\bar{t})\) by Claim 12 applied at \(t^{\flat }= R(\bar{t}^{\,\flat })\) and \(t = R(\bar{t})\).
- Claim 14: :
-
\(({ \forall }\bar{t}{ \in }\bar{T}){ \ }C_{\bar{t}} = C_{R(\bar{t})}\). Take any \(\bar{t}\). I argue \(C_{\bar{t}}\) [a] equals \({ \lbrace }\,c{ \in }C\,|\,\bar{t}{ \oplus }(c){ \in }\bar{T}\,{ \rbrace }\) by the (OR) definition of \(C_{\bar{t}}\); which [b] equals \({ \lbrace }\,c{ \in }C\,|\,({ \exists }\bar{t}^{\sharp }{ \in }\bar{T})\,\bar{t}{ \oplus }(c){=}\bar{t}^{\sharp }\,{ \rbrace }\) by rearrangement; which [c] equals \({ \lbrace }\,c{ \in }C\,|\,({ \exists }\bar{t}^{\sharp }{ \in }\bar{T})\,c{ \notin }R(\bar{t})\) and \(R(\bar{t}){ \cup }{ \lbrace }c{ \rbrace }{=}R(\bar{t}^{\sharp })\,{ \rbrace }\) by Claim 13; which equals [d] \({ \lbrace }\,c{ \in }C\,|\,c{ \notin }R(\bar{t})\) and \(R(\bar{t}){ \cup }{ \lbrace }c{ \rbrace }{ \in }T\,{ \rbrace }\) because the \(R|_{\bar{T}}\) is onto T by Claim 10; which [e] equals \(C_{R(\bar{t})}\) by the (choice-set) definition of \(C_{R(\bar{t})}\).
- Claim 15: :
-
\(R|_{\bar{X}}\)is a bijection from\(\bar{X}\)ontoX. Because of \(\bar{X}{ \ }{ \subseteq }{ \ }\bar{T}\) and Claim 10, it suffices to show that \({ \lbrace }R(\bar{t})|\bar{t}{ \in }\bar{X}{ \rbrace } = X\). For the \({ \subseteq }\) direction, suppose \(\bar{t}{ \ }{ \in }{ \ }\bar{X}\). Then \(C_{\bar{t}}{ \ }{ \ne }{ \ }{ \varnothing }\). Thus by Claim 14, \(C_{R(\bar{t})}{ \ }{ \ne }{ \ }{ \varnothing }\). Hence \(R(\bar{t}){ \ }{ \in }{ \ }X\). Conversely, suppose \(t{ \ }{ \in }{ \ }X\). By Claim 10, there exists \(\bar{t}{ \ }{ \in }{ \ }\bar{T}\) such that \(R(\bar{t}) = t\). Thus it suffices to show \(\bar{t}{ \ }{ \in }{ \ }\bar{X}\). Since \(R(\bar{t}) = t\) and \(t{ \ }{ \in }{ \ }X\), \(C_{R(\bar{t})}{ \ }{ \ne }{ \ }{ \varnothing }\). Thus by Claim 14, \(C_{\bar{t}}{ \ }{ \ne }{ \ }{ \varnothing }\). Hence \(\bar{t}{ \ }{ \in }{ \ }\bar{X}\).
- Claim 16: :
-
\(\bar{P}\)is well-defined and [OR4] holds. It suffices to show \(\bar{P}{:}\bar{X}{ \rightarrow }I\) is well-defined. This is equivalent to \(({ \forall }\bar{t}{ \in }\bar{X})({ \exists }!i{ \in }I)\)\(C_{\bar{t}}{ \ }{ \subseteq }{ \ }C_i\). By Claim 14, this is equivalent to \(({ \forall }\bar{t}{ \in }\bar{X})({ \exists }!i{ \in }I)\)\(C_{R(\bar{t})}{ \ }{ \subseteq }{ \ }C_i\). By Claim 15, this is equivalent to \(({ \forall }t{ \in }X)({ \exists }!i{ \in }I)\)\(C_t{ \ }{ \subseteq }{ \ }C_i\). To show this, take \(t{ \ }{ \in }{ \ }X\). [cs6] implies there is an \(i{ \ }{ \in }{ \ }I\) such that \(C_t{ \ }{ \subseteq }{ \ }C_i\). [cs5] implies that this i is unique since [i] \(C_t{ \ }{ \ne }{ \ }{ \varnothing }\) since [ii] \(t{ \ }{ \in }{ \ }X\).
- Claim 17: :
-
\(({ \forall }c{ \in }{ \cup }_{i{ \in }I}C_i){ \ }{ \lbrace }\,R(\bar{t})\,|\,\bar{t}{ \in }\bar{X}, c{ \in }C_{\bar{t}}\,{ \rbrace } = { \lbrace }\,t{ \in }X\,|\,c{ \in }C_t\,{ \rbrace }\). Take any c. For the \({ \subseteq }\) direction, take any \(\bar{t}{ \ }{ \in }{ \ }\bar{X}\) such that \(c{ \ }{ \in }{ \ }C_{\bar{t}}\). Note \(\bar{t}{ \ }{ \in }{ \ }\bar{X}\) and Claim 15 imply \(R(\bar{t}){ \ }{ \in }{ \ }X\). Further, \(c{ \ }{ \in }{ \ }C_{\bar{t}}\) and Claim 14 imply \(c{ \ }{ \in }{ \ }C_{R(\bar{t})}\). The previous two sentences imply \(R(\bar{t}){ \ }{ \in }{ \ }{ \lbrace }\,t{ \in }X\,|\,c{ \in }C_t\,{ \rbrace }\). Conversely, take any \(t{ \ }{ \in }{ \ }X\) such that \(c{ \ }{ \in }{ \ }C_t\). Note \(t{ \ }{ \in }{ \ }X\) and Claim 15 imply the existence of a \(\bar{t}{ \ }{ \in }{ \ }\bar{X}\) such that \(t = R(\bar{t})\). Further, [a] \(c{ \ }{ \in }{ \ }C_t\) by assumption; which [b] equals \(C_{R(\bar{t})}\) by the previous sentence; which [c] equals \(C_{\bar{t}}\) by Claim 14. The previous two sentences imply \(t{ \ }{ \in }{ \ }{ \lbrace }\,R(\bar{t})\,|\,\bar{t}{ \in }\bar{X}, c{ \in }C_{\bar{t}}\,{ \rbrace }\).
- Claim 18: :
-
[OR5] holds. Take \(i{ \ }{ \in }{ \ }I\). It must be shown that \(\bar{{ \mathscr {H}}}_i\) partitions \(\bar{P}^{-1}(i)\). By definition, \(\bar{{ \mathscr {H}}}_i = { \lbrace }\,{ \lbrace }\bar{t}{ \in }\bar{X}|c{ \in }C_{\bar{t}}{ \rbrace }\,{ \ne }\,{ \varnothing }\,|\,c{ \in }C_i{ \ }{ \rbrace }\) and \(\bar{P}^{-1}(i) = { \lbrace }\,\bar{t}{ \in }\bar{X}\,|\,C_{\bar{t}}{ \subseteq }C_i\,{ \rbrace }\). [1] By inspection, each member of \(\bar{{ \mathscr {H}}}_i\) is nonempty. [2] By Claim 10, \({ \lbrace }\,{ \lbrace }\bar{t}{ \in }\bar{X}|c{ \in }C_{\bar{t}}{ \rbrace }\,{ \ne }\,{ \varnothing }\,|\) \(c{ \in }C_i{ \ }{ \rbrace }\) is pairwise disjoint iff \({ \lbrace }\,{ \lbrace }R(\bar{t})\,|\,\bar{t}{ \in }\bar{X}, c{ \in }C_{\bar{t}}{ \rbrace } { \ne }\,{ \varnothing }\,|\,c{ \in }C_i{ \ }{ \rbrace }\) is pairwise disjoint. By Claim 17, this holds iff \({ \lbrace }\,{ \lbrace }t{ \in }X|c{ \in }C_t{ \rbrace } { \ne }\,{ \varnothing }\,|\,c{ \in }C_i{ \ }{ \rbrace }\) is pairwise disjoint. This is implied by [cs4]. [3] It remains to show that \({ \cup }{ \lbrace }\,{ \lbrace }\bar{t}{ \in }\bar{X}|c{ \in }C_{\bar{t}}{ \rbrace }\,{ \ne }\,{ \varnothing }\,|\,c{ \in }C_i{ \ }{ \rbrace }\)\(=\)\({ \lbrace }\,\bar{t}{ \in }\bar{X}\,|\,C_{\bar{t}}{ \subseteq }C_i\,{ \rbrace }\). For the \({ \subseteq }\) direction, take any \(c{ \ }{ \in }{ \ }C_i\) and any \(\bar{t}{ \ }{ \in }{ \ }\bar{X}\) such that \(c{ \ }{ \in }{ \ }C_{\bar{t}}\). It suffices to show that \(C_{\bar{t}}{ \ }{ \subseteq }{ \ }C_i\). Since \(c{ \ }{ \in }{ \ }C_{\bar{t}}{ \cap }C_i\), [cs5] implies that there cannot be a
 such that \(C_{\bar{t}}{ \ }{ \subseteq }{ \ }C_j\). Thus [cs6] implies \(C_{\bar{t}}{ \ }{ \subseteq }{ \ }C_i\). Conversely, take any \(\bar{t}^*{ \ }{ \in }{ \ }\bar{X}\) such that \(C_{\bar{t}^*}{ \ }{ \subseteq }{ \ }C_i\). Then arbitrarily choose any \(c^*{ \ }{ \in }{ \ }C_{\bar{t}^*}\). So \(\bar{t}^*{ \ }{ \in }{ \ }{ \lbrace }\bar{t}{ \in }\bar{X}|c^*{ \in }C_{\bar{t}}{ \rbrace }\) and this set is in the collection \({ \lbrace }\,{ \lbrace }\bar{t}{ \in }\bar{X}|c{ \in }C_{\bar{t}}{ \rbrace }{ \ne }{ \varnothing }\,|\,c{ \in }C_i\,{ \rbrace }\) because \(c^*{ \ }{ \in }{ \ }C_{\bar{t}^*}{ \ }{ \subseteq }{ \ }C_i\).
such that \(C_{\bar{t}}{ \ }{ \subseteq }{ \ }C_j\). Thus [cs6] implies \(C_{\bar{t}}{ \ }{ \subseteq }{ \ }C_i\). Conversely, take any \(\bar{t}^*{ \ }{ \in }{ \ }\bar{X}\) such that \(C_{\bar{t}^*}{ \ }{ \subseteq }{ \ }C_i\). Then arbitrarily choose any \(c^*{ \ }{ \in }{ \ }C_{\bar{t}^*}\). So \(\bar{t}^*{ \ }{ \in }{ \ }{ \lbrace }\bar{t}{ \in }\bar{X}|c^*{ \in }C_{\bar{t}}{ \rbrace }\) and this set is in the collection \({ \lbrace }\,{ \lbrace }\bar{t}{ \in }\bar{X}|c{ \in }C_{\bar{t}}{ \rbrace }{ \ne }{ \varnothing }\,|\,c{ \in }C_i\,{ \rbrace }\) because \(c^*{ \ }{ \in }{ \ }C_{\bar{t}^*}{ \ }{ \subseteq }{ \ }C_i\). - Claim 19: :
-
\({ \langle }({ \cup }_{i{ \in }I}C_i,\bar{N}),(\bar{P},(\bar{{ \mathscr {H}}}_i)_{i{ \in }I}){ \rangle }\)is a well-defined OR form.\(({ \cup }_{i{ \in }I}C_i,\bar{N})\) is an OR tree by Claim 7. \(\bar{P}\) is well-defined and [OR4] holds by Claim 16. [OR5] holds by Claim 18. Thus it remains to show [OR6]. Toward that end, suppose that \(\bar{t}^1\) and \(\bar{t}^2\) belong to the (OR) information set \({ \lbrace }\,\bar{t}{ \in }\bar{X}\,|\,c{ \in }C_{\bar{t}}\,{ \rbrace }\). Then \(R(\bar{t}^1)\) and \(R(\bar{t}^2)\) belong to \({ \lbrace }\,R(\bar{t})\,|\,\bar{t}{ \in }\bar{X}, c{ \in }C_{\bar{t}}\,{ \rbrace }\). Thus Claim 17 implies \(R(\bar{t}^1)\) and \(R(\bar{t}^2)\) belong to the (choice-set) information set \({ \lbrace }\,t{ \in }X\,|\,c{ \in }C_t\,{ \rbrace }\). Thus note 8 (Sect. 2) implies \(C_{R(\bar{t}^1)} = C_{R(\bar{t}^2)}\). Thus Claim 14 implies \(C_{\bar{t}^1} = C_{\bar{t}^2}\).
- Claim 20: :
-
\(({ \forall }c{ \in }{ \cup }_{i{ \in }I}C_i,\bar{H}{ \in }{ \cup }_{i{ \in }I}\bar{{ \mathscr {H}}}_i){ \ }c{ \ }{ \in }{ \ }C_{\bar{H}}\)iff\(\bar{H}= { \lbrace }\,\bar{t}{ \in }\bar{X}\,|\,c{ \in }C_{\bar{t}}\,{ \rbrace }\). Take c and \(\bar{H}\). For the reverse direction, assume \(\bar{H}= { \lbrace }\,\bar{t}{ \in }\bar{X}\,|\,c{ \in }C_{\bar{t}}\,{ \rbrace }\). By inspection, \(({ \forall }\bar{t}{ \in }\bar{H}){ \ }c{ \ }{ \in }{ \ }C_{\bar{t}}\). Hence \(c{ \ }{ \in }{ \ }C_{\bar{H}}\) by the usual definition of \(C_{\bar{H}}\). For the forward direction, suppose \(c{ \ }{ \in }{ \ }C_{\bar{H}}\). Then the definition of \(C_{\bar{H}}\) implies \(({ \forall }\bar{t}{ \in }\bar{H}){ \ }c{ \ }{ \in }{ \ }C_{\bar{t}}\). This implies \(({ \forall }\bar{t}{ \in }\bar{H})\)\(\bar{t}{ \ }{ \in }{ \ }\bar{X}\). By the last two sentences, \(\bar{H}{ \ }{ \subseteq }{ \ }{ \lbrace }\,\bar{t}{ \in }\bar{X}\,|\,c{ \in }C_{\bar{t}}\,{ \rbrace }\). Further, \(\bar{H}\) is an information set by assumption, and \({ \lbrace }\,\bar{t}{ \in }\bar{X}\,|\,c{ \in }C_{\bar{t}}\,{ \rbrace }\) is an information set by the theorem’s definition of \((\bar{{ \mathscr {H}}}_i)_{i{ \in }I}\). Since the information sets partition \(\bar{X}\) by Claim 19, [OR4], and [OR5]; the previous two sentences imply \(\bar{H}= { \lbrace }\,\bar{t}{ \in }\bar{X}\,|\,c{ \in }C_{\bar{t}}\,{ \rbrace }\).
- Claim 21: :
-
\({ \langle }({ \cup }_{i{ \in }I}C_i,\bar{N}),(\bar{P},(\bar{{ \mathscr {H}}}_i)_{i{ \in }I}){ \rangle }\)is an OR form with no shared alternatives. Given Claim 19, it remains to show that there are no shared alternatives. Toward that end, suppose there were \(H^1{ \ }{ \in }{ \ }{ \cup }_{i{ \in }I}\bar{{ \mathscr {H}}}_i\), \(H^2{ \ }{ \in }{ \ }{ \cup }_{i{ \in }I}\bar{{ \mathscr {H}}}_i\), and \(c^*{ \ }{ \in }{ \ }{ \cup }_{i{ \in }I}C_i\) such that \(c^*{ \ }{ \in }{ \ }C_{\bar{H}^1}{ \cap }C_{\bar{H}^2}\). Then by Claim 20, both \(\bar{H}^1\) and \(\bar{H}^2\) would equal \({ \lbrace }\bar{t}{ \in }\bar{X}|c^*{ \in }C_{\bar{t}}{ \rbrace }\). Hence \(\bar{H}^1\) would equal \(\bar{H}^2\).
- Claim 22: :
-
\({ \langle }({ \cup }_{i{ \in }I}C_i,\bar{N}),(\bar{P},(\bar{{ \mathscr {H}}}_i)_{i{ \in }I}){ \rangle }\)is an OR form with no shared alternatives and no absentmindedness. Because of Claim 21, it suffices to show that there is no absentmindedness. This follows from Claim 21, Claim 10, and Lemma A.5(a\({ \Leftrightarrow }\)b).
- Claim 23: :
-
 is an infinite chain inT. Take any such \(\bar{n}\). (1) By Claim 22 and [OR2], \({ \lbrace }{_1\bar{n}_{{ \ell }}}|{ \ell }{ \ge }1{ \rbrace }{ \ }{ \subseteq }{ \ }\bar{T}\). Thus by Claim 10, \({ \lbrace }R({_1\bar{n}_{{ \ell }}})|{ \ell }{ \ge }1{ \rbrace }{ \ }{ \subseteq }{ \ }T\). (2) Note that \(({ \forall }{ \ell }{ \ge }1){ \ }R({_1\bar{n}_{{ \ell }}}){ \ }{ \subseteq }{ \ }R({_1\bar{n}_{{ \ell }+1}})\) simply because each \({_1\bar{n}_{{ \ell }}}{ \ }{ \subseteq }{ \ }{_1\bar{n}_{{ \ell }+1}}\). Hence \({ \lbrace }R({_1\bar{n}_{{ \ell }}})|{ \ell }{ \ge }1{ \rbrace }\) is a chain. (3) Claim 22 and Lemma A.4(a\({ \Leftrightarrow }\)c) imply that \(({ \forall }{ \ell }{ \ge }1)\)\(|R({_1\bar{n}_{{ \ell }}})| = { \ell }\). Hence \({ \lbrace }R({_1\bar{n}_{{ \ell }}})|{ \ell }{ \ge }1{ \rbrace }\) is infinite.
is an infinite chain inT. Take any such \(\bar{n}\). (1) By Claim 22 and [OR2], \({ \lbrace }{_1\bar{n}_{{ \ell }}}|{ \ell }{ \ge }1{ \rbrace }{ \ }{ \subseteq }{ \ }\bar{T}\). Thus by Claim 10, \({ \lbrace }R({_1\bar{n}_{{ \ell }}})|{ \ell }{ \ge }1{ \rbrace }{ \ }{ \subseteq }{ \ }T\). (2) Note that \(({ \forall }{ \ell }{ \ge }1){ \ }R({_1\bar{n}_{{ \ell }}}){ \ }{ \subseteq }{ \ }R({_1\bar{n}_{{ \ell }+1}})\) simply because each \({_1\bar{n}_{{ \ell }}}{ \ }{ \subseteq }{ \ }{_1\bar{n}_{{ \ell }+1}}\). Hence \({ \lbrace }R({_1\bar{n}_{{ \ell }}})|{ \ell }{ \ge }1{ \rbrace }\) is a chain. (3) Claim 22 and Lemma A.4(a\({ \Leftrightarrow }\)c) imply that \(({ \forall }{ \ell }{ \ge }1)\)\(|R({_1\bar{n}_{{ \ell }}})| = { \ell }\). Hence \({ \lbrace }R({_1\bar{n}_{{ \ell }}})|{ \ell }{ \ge }1{ \rbrace }\) is infinite. - Claim 24: :
-
\({ \lbrace }R(\bar{n})|\bar{n}{ \in }\bar{N}{ \rbrace }{ \ }{ \subseteq }{ \ }N\). Claim 10 yields \({ \lbrace }R(\bar{t})|\bar{t}{ \in }\bar{T}{ \rbrace } = T{ \ }{ \subseteq }{ \ }N\). Thus it suffices to show
 . Toward that end, take
. Toward that end, take  . Since \(\bar{n}\) is infinite, \(\bar{n}= { \cup }{ \lbrace }{_1\bar{n}_{{ \ell }}}|{ \ell }{ \ge }1{ \rbrace }\). So [a] \(R(\bar{n}) = R({ \cup }{ \lbrace }{_1\bar{n}_{{ \ell }}}|{ \ell }{ \ge }1{ \rbrace })\); which [b] equals \({ \cup }{ \lbrace }R({_1\bar{n}_{{ \ell }}})|{ \ell }{ \ge }1{ \rbrace }\) by rearrangement; which [c] belongs to N by Claim 23 and the reverse direction of [cs3].
. Since \(\bar{n}\) is infinite, \(\bar{n}= { \cup }{ \lbrace }{_1\bar{n}_{{ \ell }}}|{ \ell }{ \ge }1{ \rbrace }\). So [a] \(R(\bar{n}) = R({ \cup }{ \lbrace }{_1\bar{n}_{{ \ell }}}|{ \ell }{ \ge }1{ \rbrace })\); which [b] equals \({ \cup }{ \lbrace }R({_1\bar{n}_{{ \ell }}})|{ \ell }{ \ge }1{ \rbrace }\) by rearrangement; which [c] belongs to N by Claim 23 and the reverse direction of [cs3]. - Claim 25: :
-
 . Take any
. Take any  . By the forward direction of [cs3], there exists an infinite chain \(T^*{ \ }{ \subseteq }{ \ }T\) such that \({ \cup }T^* = n\). Thus by Lemma A.1, there is an infinite sequence \((t^m)_{m{ \ge }1}\) in T such that [a] \(({ \forall }m{ \ge }1){ \ }t^m{ \ }{ \subset }{ \ }t^{m+1}\) and [b] \({ \cup }_{m{ \ge }1}t^m = { \cup }T^*\). Further, by Claim 10, there is an infinite sequence \((\bar{t}^m)_{m{ \ge }1}\) in \(\bar{T}\) such that [c] \(({ \forall }m{ \ge }1){ \ }t^m = R(\bar{t}^m)\). [a] and [c] imply [d] \(({ \forall }m{ \ge }1)\)\(R(\bar{t}^m){ \ }{ \subset }{ \ }R(\bar{t}^{m+1})\). [d], Claim 22, and two applications of Lemma A.4(a\({ \Leftrightarrow }\)c) yield [e] \(({ \forall }m{ \ge }1){ \ }K(\bar{t}^m) = |R(\bar{t}^m)| < |R(\bar{t}^{m+1})| = K(\bar{t}^{m+1})\). Also, [d], Claim 22, and Lemma A.6 yield that [f] \(({ \forall }m{ \ge }1){ \ }\bar{t}^m = {_1\bar{t}^{m+1}_{K(t^m)}}\). [e] and [f] imply that [g] \({ \cup }_{m{ \ge }1}\bar{t}^m\)\({ \in }\)\(({ \cup }_{i{ \in }I}C_i)^{ \infty }\) and [h] \(({ \forall }m^{ \prime }{ \ge }1)\)\({_1({ \cup }_{m{ \ge }1}\bar{t}^m)_{m^{ \prime }}} = \bar{t}^{m^{ \prime }}\). [h] implies \(({ \forall }k{ \ge }1)({ \exists }m^{ \prime }{ \ge }k)\)\({_1({ \cup }_{m{ \ge }1}\bar{t}^m)_{m^{ \prime }}} = t^{m^{ \prime }}{ \ }{ \in }{ \ }\bar{T}\). This, [g], Claim 22, and Lemma A.2 imply [i] \({ \cup }_{m{ \ge }1}\bar{t}^m{ \ }{ \in }{ \ }\bar{N}\). Therefore, n equals \({ \cup }T^*\) by the definition of \(T^*\); which equals \({ \cup }_{m{ \ge }1}t^m\) by [b]; which equals \({ \cup }_{m{ \ge }1}R(\bar{t}^m)\) by [c]; which equals \(R({ \cup }_{m{ \ge }1}\bar{t}^m)\) by rearrangement; which belongs to \({ \lbrace }R(\bar{n})|\bar{n}{ \in }\bar{N}{ \rbrace }\) by [i].
. By the forward direction of [cs3], there exists an infinite chain \(T^*{ \ }{ \subseteq }{ \ }T\) such that \({ \cup }T^* = n\). Thus by Lemma A.1, there is an infinite sequence \((t^m)_{m{ \ge }1}\) in T such that [a] \(({ \forall }m{ \ge }1){ \ }t^m{ \ }{ \subset }{ \ }t^{m+1}\) and [b] \({ \cup }_{m{ \ge }1}t^m = { \cup }T^*\). Further, by Claim 10, there is an infinite sequence \((\bar{t}^m)_{m{ \ge }1}\) in \(\bar{T}\) such that [c] \(({ \forall }m{ \ge }1){ \ }t^m = R(\bar{t}^m)\). [a] and [c] imply [d] \(({ \forall }m{ \ge }1)\)\(R(\bar{t}^m){ \ }{ \subset }{ \ }R(\bar{t}^{m+1})\). [d], Claim 22, and two applications of Lemma A.4(a\({ \Leftrightarrow }\)c) yield [e] \(({ \forall }m{ \ge }1){ \ }K(\bar{t}^m) = |R(\bar{t}^m)| < |R(\bar{t}^{m+1})| = K(\bar{t}^{m+1})\). Also, [d], Claim 22, and Lemma A.6 yield that [f] \(({ \forall }m{ \ge }1){ \ }\bar{t}^m = {_1\bar{t}^{m+1}_{K(t^m)}}\). [e] and [f] imply that [g] \({ \cup }_{m{ \ge }1}\bar{t}^m\)\({ \in }\)\(({ \cup }_{i{ \in }I}C_i)^{ \infty }\) and [h] \(({ \forall }m^{ \prime }{ \ge }1)\)\({_1({ \cup }_{m{ \ge }1}\bar{t}^m)_{m^{ \prime }}} = \bar{t}^{m^{ \prime }}\). [h] implies \(({ \forall }k{ \ge }1)({ \exists }m^{ \prime }{ \ge }k)\)\({_1({ \cup }_{m{ \ge }1}\bar{t}^m)_{m^{ \prime }}} = t^{m^{ \prime }}{ \ }{ \in }{ \ }\bar{T}\). This, [g], Claim 22, and Lemma A.2 imply [i] \({ \cup }_{m{ \ge }1}\bar{t}^m{ \ }{ \in }{ \ }\bar{N}\). Therefore, n equals \({ \cup }T^*\) by the definition of \(T^*\); which equals \({ \cup }_{m{ \ge }1}t^m\) by [b]; which equals \({ \cup }_{m{ \ge }1}R(\bar{t}^m)\) by [c]; which equals \(R({ \cup }_{m{ \ge }1}\bar{t}^m)\) by rearrangement; which belongs to \({ \lbrace }R(\bar{n})|\bar{n}{ \in }\bar{N}{ \rbrace }\) by [i]. - Claim 26: :
-
\({ \lbrace }R(\bar{n})|\bar{n}{ \in }\bar{N}{ \rbrace } = N\). The \({ \subseteq }\) direction holds by Claim 24. For the converse, take any \(n{ \ }{ \in }{ \ }N\). If \(n{ \ }{ \in }{ \ }T\), the result follows from Claim 10. If \(n{ \ }{ \notin }{ \ }T\), the result follows from Claim 25.
Conclusion. (a) \(({ \cup }_{i{ \in }I}C_i,\bar{N})\) is an OR tree by Claim 7. \(R|_{\bar{N}}\) is injective by Claim 22 and Proposition 3.0. \(R|_{\bar{N}}\) is onto N by Claim 26. (b) \({ \langle }({ \cup }_{i{ \in }I}C_i,\bar{N}),(\bar{P},(\bar{{ \mathscr {H}}}_i)_{i{ \in }I}){ \rangle }\) is an OR form with no shared alternatives and no absentmindedness by Claim 22.
Proof A.9
(for Theorem 5.1: KS \({\leftarrow }\) simple) Part (a) follows from Claim 1(a), and part (b) follows from Claims 10–12.
- Claim 1: :
-
(a) (T, E, r) is a KS graph-tree, (b)\(({ \forall }t{ \in }T,t^{\sharp }{ \in }T)\)\(t > t^{\sharp }\)iff there is a walk fromtto\(t^{\sharp }\), and (c) the decision-node set derived from\((T,{ \ge })\)equals the decision node set derived from (T, E, r). ((c) will be used implicitly to ensure that the symbol X is unambiguous). A simple tree is specified via order theory, while a KS graph-tree is specified via graph theory. The conversion from the former to the latter is relatively straightforward. Details are available on request.
- Claim 2: :
-
\(({ \forall }t{ \in }T,\hat{c}{ \in }{ \cup }_{i{ \in }I}\hat{C}_i){ \ }t{ \ }{ \in }{ \ }p(\hat{c})\)iff\(p^{-1}(t){ \cap }\hat{c}{ \ }{ \ne }{ \ }{ \varnothing }\). Take t and \(\hat{c}\). By manipulation, \(t{ \ }{ \in }{ \ }p(\hat{c})\) iff \(({ \exists }t^{\sharp }{ \in }\hat{c}){ \ }t=p(t^{\sharp })\) iff \(({ \exists }t^{\sharp }{ \in }\hat{c}){ \ }t^{\sharp }{ \in }p^{-1}(t)\) iff \(p^{-1}(t){ \cap }\hat{c}{ \ }{ \ne }{ \ }{ \varnothing }\).
- Claim 3: :
-
 is well-defined and [KS3] holds att. Suppose
is well-defined and [KS3] holds att. Suppose  . Then [a] \(p^{-1}(t){ \ }={ \ }{ \varnothing }\) by the (simple) definition of X. Thus [b] \({ \lbrace }t^{\sharp }{ \in }T|(t,t^{\sharp }){ \in }E{ \rbrace } = { \varnothing }\) by the theorem’s definition of E. Also, [a] implies [c] \(({ \forall }\hat{c}{ \in }{ \cup }_{i{ \in }I}\hat{C}_i){ \ }p^{-1}(t){ \cap }\hat{c}= { \varnothing }\). Hence Claim 2 implies [d] \(({ \forall }\hat{c}{ \in }{ \cup }_{i{ \in }I}\hat{C}_i){ \ }t{ \ }{ \notin }{ \ }p(\hat{c})\). Hence [e] \(C_t = { \varnothing }\) and [f] \({ \psi }_t = { \varnothing }\) by the theorem’s definition of \(C_t\) and \({ \psi }_t\). [KS3] at t follows from [b], [e], and [f].
. Then [a] \(p^{-1}(t){ \ }={ \ }{ \varnothing }\) by the (simple) definition of X. Thus [b] \({ \lbrace }t^{\sharp }{ \in }T|(t,t^{\sharp }){ \in }E{ \rbrace } = { \varnothing }\) by the theorem’s definition of E. Also, [a] implies [c] \(({ \forall }\hat{c}{ \in }{ \cup }_{i{ \in }I}\hat{C}_i){ \ }p^{-1}(t){ \cap }\hat{c}= { \varnothing }\). Hence Claim 2 implies [d] \(({ \forall }\hat{c}{ \in }{ \cup }_{i{ \in }I}\hat{C}_i){ \ }t{ \ }{ \notin }{ \ }p(\hat{c})\). Hence [e] \(C_t = { \varnothing }\) and [f] \({ \psi }_t = { \varnothing }\) by the theorem’s definition of \(C_t\) and \({ \psi }_t\). [KS3] at t follows from [b], [e], and [f]. - Claim 4: :
-
\(({ \forall }t{ \in }X)\)\({ \lbrace }\,{ \lbrace }t^{\sharp }{ \rbrace }\,|\,t^{\sharp }{ \in }p^{-1}(t)\,{ \rbrace }\)\(=\)\({ \lbrace }\,p^{-1}(t){ \cap }\hat{c}\,|\,t{ \in }p(\hat{c}),\,\hat{c}{ \in }{ \cup }_{i{ \in }I}\hat{C}_i\,{ \rbrace }\). Take any \(t{ \ }{ \in }{ \ }X\). Because of no simultaneous decisions, there is an \(i^*{ \ }{ \in }{ \ }I\) such that \(J(t) = { \lbrace }i^*{ \rbrace }\). I argue \({ \lbrace }\,{ \lbrace }t^{\sharp }{ \rbrace }\,|\,t^{\sharp }{ \in }p^{-1}(t)\,{ \rbrace }\) [a] equals \({ \lbrace }\,p^{-1}(t){ \cap }({ \cap }_{i{ \in }J(t)}\hat{c}_i)\,|\!\)\((\hat{c}_i)_{i{ \in }J(t)}{ \in }{ \varPi }_{i{ \in }J(t)}A_i(t)\,{ \rbrace }\) by [s6]; which [b] equals \({ \lbrace }\,p^{-1}(t){ \cap }({ \cap }_{i{ \in }{ \lbrace }i^*{ \rbrace }}\hat{c}_i)\,|\!\)\((\hat{c}_i)_{i{ \in }{ \lbrace }i^*{ \rbrace }}{ \in }{ \varPi }_{i{ \in }{ \lbrace }i^*{ \rbrace }}{ \lbrace }\hat{c}{ \in }\hat{C}_i|t{ \in }p(\hat{c}){ \rbrace }\,{ \rbrace }\) by the definitions of \(i^*\) and \(A_{i^*}\); which [c] equals \({ \lbrace }\,p^{-1}(t){ \cap }\hat{c}\,|\,\hat{c}{ \in }\hat{C}_{i^*},\,t{ \in }p(\hat{c})\,{ \rbrace }\) by rearrangement; which [d] equals \({ \lbrace }\,p^{-1}(t){ \cap }\hat{c}\,|\!\)\(\hat{c}{ \in }{ \cup }_{i{ \in }I}\hat{C}_i,\,t{ \in }p(\hat{c})\,{ \rbrace }\) because the definitions of \(i^*\) and J imply that \(i^*\) is the only \(i{ \ }{ \in }{ \ }I\) for which \(A_i(t) = { \lbrace }\,\hat{c}{ \in }\hat{C}_i\,|\,t{ \in }p(\hat{c}){ \rbrace }\,\) is nonempty.
- Claim 5: :
-
\(({ \forall }t{ \in }X){ \ }{ \psi }_t\)is well-defined. Take \(t{ \ }{ \in }{ \ }X\). Take \(\hat{c}{ \ }{ \in }{ \ }C_t\). Then the definition of \(C_t\) implies \(t{ \ }{ \in }{ \ }p(\hat{c})\) and \(\hat{c}{ \ }{ \in }{ \ }{ \cup }_{i{ \in }I}\hat{C}_i\). Thus the \({ \supseteq }\) direction of Claim 4 implies there is \(t^{\sharp *}\) such that \(p^{-1}(t){ \cap }\hat{c}= { \lbrace }t^{\sharp *}{ \rbrace }\). It remains to show that \(t^{\sharp *}{ \ }{ \in }{ \ }{ \lbrace }t^{\sharp }{ \in }T|(t,t^{\sharp }){ \in }E{ \rbrace }\). I argue \(t^{\sharp *}\) [a] belongs to \(p^{-1}(t)\) by the second-previous sentence; which [b] equals \({ \lbrace }t^{\sharp }{ \in }T|(t,t^{\sharp }){ \in }E{ \rbrace }\) by the theorem’s definition of E.
- Claim 6: :
-
\(({ \forall }t{ \in }X){ \ }{ \psi }_t\)is surjective. Take \(t{ \ }{ \in }{ \ }X\). Take \(t^{\sharp *}{ \ }{ \in }{ \ }{ \lbrace }t^{\sharp }{ \in }T|(t,t^{\sharp }){ \in }E{ \rbrace }\). Then by the definition of E, \(t^{\sharp *}{ \ }{ \in }{ \ }p^{-1}(t)\). Thus, by the \({ \subseteq }\) direction of Claim 4, there exists \(\hat{c}{ \ }{ \in }{ \ }{ \cup }_{i{ \in }I}\hat{C}_i\) such that \(t{ \ }{ \in }{ \ }p(\hat{c})\) and \({ \lbrace }t^{\sharp *}{ \rbrace } = p^{-1}(t){ \cap }\hat{c}\). The two set memberships imply \(\hat{c}{ \ }{ \in }{ \ }C_t\) by the theorem’s definition of \(C_t\), and the equality implies \({ \psi }_t(\hat{c}) = t^{\sharp *}\) by the theorem’s definition of \({ \psi }_t\).
- Claim 7: :
-
\(({ \psi }_t)_{t{ \in }T}\)is well-defined, and [KS3] holds. Given Claims 3–6, it suffices to show that \(({ \forall }t{ \in }X){ \ }{ \psi }_t\) is injective. Suppose not. Then there would be \(t{ \ }{ \in }{ \ }X\), \(\hat{c}{ \ }{ \in }{ \ }C_t\), and \(\hat{c}^{ \prime }{ \ }{ \in }{ \ }C_t\) such that \(\hat{c}{ \ }{ \ne }{ \ }\hat{c}^{ \prime }\) and \({ \psi }_t(\hat{c}) = { \psi }_t(\hat{c}^{ \prime })\). Note that \(\hat{c}{ \ }{ \in }{ \ }C_t\) implies \(t{ \ }{ \in }{ \ }p(\hat{c})\), and similarly, that \(\hat{c}^{ \prime }{ \ }{ \in }{ \ }C_t\) implies \(t{ \ }{ \in }{ \ }p(\hat{c}^{ \prime })\). The two together imply \(p(\hat{c}){ \cap }p(\hat{c}^{ \prime }){ \ }{ \ne }{ \ }{ \varnothing }\). This, \(\hat{c}{ \ }{ \ne }{ \ }\hat{c}^{ \prime }\), and [s5] together imply that \(\hat{c}{ \cap }\hat{c}^{ \prime } = { \varnothing }\). Meanwhile, \({ \psi }_t(\hat{c}) = { \psi }_t(\hat{c}^{ \prime })\) and the definition of \({ \psi }_t\) imply that \(p^{-1}(t){ \cap }\hat{c}\) and \(p^{-1}(t){ \cap }\hat{c}^{ \prime }\) are identical singleton sets. The last two sentences contradict one another.
- Claim 8: :
-
P is well-defined, and [KS4] holds. Take any \(t{ \ }{ \in }{ \ }X\). By the assumption of no simultaneous decisions, J(t) is a singleton. Thus, by the definition of J, there is a unique i for which \(({ \exists }\hat{c}{ \in }\hat{C}_i)\)\(t{ \in }p(\hat{c})\).
- Claim 9: :
-
[KS5] holds. Take any i. Note \(P^{-1}(i)\) equals \({ \lbrace }\,t{ \in }X\,|\,({ \exists }\hat{c}{ \in }\hat{C}_i)t{ \in }p(\hat{c})\,{ \rbrace }\) by the definition of P; which equals \(X\,{ \cap }\,{ \cup }{ \lbrace }p(\hat{c})|\hat{c}{ \in }\hat{C}_i{ \rbrace }\) by rearrangement; which equals \({ \cup }{ \lbrace }p(\hat{c})|\hat{c}{ \in }\hat{C}_i{ \rbrace }\) by the definitions of p and X. Also, \({ \mathscr {H}}_i = { \lbrace }p(\hat{c})|\hat{c}{ \in }\hat{C}_i{ \rbrace }\) by definition. The last two sentences imply \({ \cup }{ \mathscr {H}}_i = P^{-1}(i)\). Hence it remains to show that the members of \({ \mathscr {H}}_i = { \lbrace }p(\hat{c})|\hat{c}{ \in }\hat{C}_i{ \rbrace }\) are nonempty and disjoint. Each \(p(\hat{c})\) is nonempty because [s4] requires that each \(\hat{c}\) is a nonempty subset of
 . To show disjointness, suppose there were \(\hat{c}\,{ \in }\,\hat{C}_i\) and \(\hat{c}^{ \prime }\,{ \in }\,\hat{C}_i\) such that [1] \(p(\hat{c}){ \ }{ \ne }{ \ }p(\hat{c}^{ \prime })\) and [2] \(p(\hat{c}){ \cap }p(\hat{c}^{ \prime }){ \ }{ \ne }{ \ }{ \varnothing }\). [1] implies \(\hat{c}{ \ }{ \ne }{ \ }\hat{c}^{ \prime }\). This, [2], and [s5] imply \(p(\hat{c}) = p(\hat{c}^{ \prime })\), which contradicts [1].
. To show disjointness, suppose there were \(\hat{c}\,{ \in }\,\hat{C}_i\) and \(\hat{c}^{ \prime }\,{ \in }\,\hat{C}_i\) such that [1] \(p(\hat{c}){ \ }{ \ne }{ \ }p(\hat{c}^{ \prime })\) and [2] \(p(\hat{c}){ \cap }p(\hat{c}^{ \prime }){ \ }{ \ne }{ \ }{ \varnothing }\). [1] implies \(\hat{c}{ \ }{ \ne }{ \ }\hat{c}^{ \prime }\). This, [2], and [s5] imply \(p(\hat{c}) = p(\hat{c}^{ \prime })\), which contradicts [1]. - Claim 10: :
-
\({ \langle }(T,E,r),(C_t,{ \psi }_t)_{t{ \in }T},(P,({ \mathscr {H}}_i)_{i{ \in }I}){ \rangle }\)is a well-defined KS form. Claims 5 and 8 show \(({ \psi }_t)_{t{ \in }T}\) and P are well-defined. Claim 1(a) and 7–9 show [KS1]–[KS5]. Thus it remains to show [KS6]. Toward that end, suppose [a] \(H{ \ }{ \in }{ \ }{ \mathscr {H}}_i\), [b] \(t^1{ \in }{ \ }H\), and [c] \(t^2{ \ }{ \in }{ \ }H\). I will show \(C_{t^1}{ \ }{ \ne }{ \ }C_{t^2}\) leads to a contradiction. Toward that end, suppose \(C_{t^1}{ \ }{ \ne }{ \ }C_{t^2}\). Then by the theorem’s definition of \((C_t)_{t{ \in }T}\), \({ \lbrace }\hat{c}{ \in }{ \cup }_{i{ \in }I}\hat{C}_i|t^1{ \in }p(\hat{c}){ \rbrace }\)\({ \ne }\)\({ \lbrace }\hat{c}{ \in }{ \cup }_{i{ \in }I}\hat{C}_i|t^2{ \in }p(\hat{c}){ \rbrace }\). Thus, w.l.o.g., there is [d] \(\hat{c}^*{ \ }{ \in }{ \ }{ \cup }_{i{ \in }I}\hat{C}_i\) such that [e] \(t^1{ \ }{ \in }{ \ }p(\hat{c}^*)\) but [f] \(t^2{ \ }{ \notin }{ \ }p(\hat{c}^*)\). Note [g] \(p(\hat{c}^*)\) belongs to \({ \lbrace }p(\hat{c})|\hat{c}{ \in }{ \cup }_{i{ \in }I}\hat{C}_i{ \rbrace }\) by [d]; which equals \({ \cup }_{i{ \in }I}{ \lbrace }p(\hat{c})|\hat{c}{ \in }\hat{C}_i{ \rbrace }\) by rearrangement; which equals \({ \cup }_{i{ \in }I}{ \mathscr {H}}_i\) by the theorem’s definition of \(({ \mathscr {H}}_i)_{i{ \in }I}\). Since [i] \(t^1\) belongs to both H and \(p(\hat{c}^*)\) by [b] and [e], and [ii] both H and \(p(\hat{c}^*)\) belong to \({ \cup }_{i{ \in }I}{ \mathscr {H}}_i\) by [a] and [g], and [iii] the members of \({ \cup }_{i{ \in }I}{ \mathscr {H}}_i\) are disjoint by Claims 8 and 9, it must be that \(H = p(\hat{c}^*)\). This contradicts [c] and [f].
- Claim 11: :
-
The KS form has no trivial decisions. It suffices to show that \(({ \forall }t{ \in }T)\)\(|C_t|{ \ }{ \ge }{ \ }1\)\({ \Rightarrow }\)\(|C_t|{ \ }{ \ge }{ \ }2\). Toward that end, take \(t{ \ }{ \in }{ \ }T\) and suppose \(\hat{c}{ \ }{ \in }{ \ }C_t\). By the definition of \(C_t\), \(t{ \ }{ \in }{ \ }p(\hat{c})\) and \(\hat{c}{ \ }{ \in }{ \ }{ \cup }_{i{ \in }I}\hat{C}_i\). Thus, by the \({ \supseteq }\) direction of Claim 4, there is \(t^{\sharp }\) such that [a] \({ \lbrace }t^{\sharp }{ \rbrace } = p^{-1}(t){ \cap }\hat{c}\). Meanwhile, [s8] implies there is [b]
 . [a] and [b] imply [c] \(t^{\sharp \prime }{ \ }{ \ne }{ \ }t^{\sharp }\). Further, [b] and the \({ \subseteq }\) direction of Claim 4 imply there is [d] \(\hat{c}^{ \prime }{ \ }{ \in }{ \ }{ \cup }_{i{ \in }I}\hat{C}_i\) such that [e] \(t{ \ }{ \in }{ \ }p(\hat{c}^{ \prime })\) and [f] \({ \lbrace }t^{\sharp \prime }{ \rbrace } = p^{-1}(t){ \cap }\hat{c}^{ \prime }\). [f], [a], and [c] imply \(\hat{c}^{ \prime }{ \ }{ \ne }{ \ }\hat{c}\). Finally, [d] and [e] imply \(\hat{c}^{ \prime }{ \ }{ \in }{ \ }C_t\). So \(\hat{c}\) and \(\hat{c}^{ \prime }\) are distinct members of \(C_t\).
. [a] and [b] imply [c] \(t^{\sharp \prime }{ \ }{ \ne }{ \ }t^{\sharp }\). Further, [b] and the \({ \subseteq }\) direction of Claim 4 imply there is [d] \(\hat{c}^{ \prime }{ \ }{ \in }{ \ }{ \cup }_{i{ \in }I}\hat{C}_i\) such that [e] \(t{ \ }{ \in }{ \ }p(\hat{c}^{ \prime })\) and [f] \({ \lbrace }t^{\sharp \prime }{ \rbrace } = p^{-1}(t){ \cap }\hat{c}^{ \prime }\). [f], [a], and [c] imply \(\hat{c}^{ \prime }{ \ }{ \ne }{ \ }\hat{c}\). Finally, [d] and [e] imply \(\hat{c}^{ \prime }{ \ }{ \in }{ \ }C_t\). So \(\hat{c}\) and \(\hat{c}^{ \prime }\) are distinct members of \(C_t\). - Claim 12: :
-
The KS form has no absentmindedness. Suppose there were a walk \((t^k)^K_{k=1}\) from \(t^1\) to \(t^K\) and an \(H{ \ }{ \in }{ \ }{ \cup }_{i{ \in }I}{ \mathscr {H}}_i\) such that \({ \lbrace }t^1,t^K{ \rbrace }{ \ }{ \subseteq }{ \ }H\). Since \((t^1,t^2){ \ }{ \in }{ \ }E\), Claim 6 implies there is \(\hat{c}{ \ }{ \in }{ \ }C_{t^1}\) such that [a] \({ \psi }_{t^1}(\hat{c}) = t^2\). Further, since \({ \lbrace }t^1,t^K{ \rbrace }{ \ }{ \subseteq }{ \ }H\), Claim 10 and [KS6] imply \(\hat{c}{ \ }{ \in }{ \ }C_{t^K}\). Thus we may define [b] \(t^{K+1} = { \psi }_{t^K}(\hat{c})\). By the definition of \(({ \psi }_t)_{t{ \in }T}\), [a] and [b] imply [c] \( p^{-1}(t^1){ \cap }\hat{c}= { \lbrace }t^2{ \rbrace }\) and [d] \(p^{-1}(t^K){ \cap }\hat{c}= { \lbrace }t^{K+1}{ \rbrace }\). [c] and [d] together imply [e] \({ \lbrace }t^2,t^{K+1}{ \rbrace }{ \ }{ \subseteq }{ \ }\hat{c}\). Further, [b] and Claim 5 imply \((t^K,t^{K+1})\,{ \in }\,E\); which implies \((t^k)^{K+1}_{k=2}\) is a walk; which implies \(({ \forall }k{ \le }K)\)\((t^k,t^{k+1})\,{ \in }\,E\); which by the definition of E implies \(({ \forall }k{ \le }K){ \ }t^k = p(t^{k+1})\); which by the definition of p and the transitivity of > implies \(t^2 > t^{K+1}\). This and [e] contradict [s7].
Proof A.10
(for Theorem 5.2: KS \({ \rightarrow }\) simple) Part (a) follows from Claim 1(a), and part (b) follows from Claim 16.
- Claim 1: :
-
(a) The theorem’s part (a) holds, namely,\((T,{ \ge })\)is a simple tree. (b)requals the root node derived from\((T,{ \ge })\). (c)\(({ \forall }t{ \in }T,t^{\sharp }{ \in }T)\)\((t,t^{\sharp })\,{ \in }\,E\) iff \(t\,{=}\,p(t^{\sharp })\), wherepis derived from\((T,{ \ge })\). (d) The decision-node set derived from (T, E, r) equals the decision-node set derived from\((T,{ \ge })\). [(b) and (d) will be used implicitly to ensure that the symbols r and X are unambiguous.] A KS graph-tree is specified via graph theory while a simple tree is specified via order theory. The conversion from the former to the latter is relatively straightforward. Details are available on request.
- Claim 2: :
-
\(({ \forall }t{ \in }T,c{ \in }C_t)\)(a)
 and (b)\(p({ \psi }_t(c)) = t\). Suppose \(c{ \ }{ \in }{ \ }C_t\). Then [KS3] implies \({ \psi }_t(c){ \ }{ \in }{ \ }{ \lbrace }t^{ \prime }{ \in }T|(t,t^{ \prime }){ \in }E{ \rbrace }\). Hence \((t,{ \psi }_t(c)){ \ }{ \in }{ \ }E\). So \(t = p({ \psi }_t(c))\) by Claim 1(c). So
and (b)\(p({ \psi }_t(c)) = t\). Suppose \(c{ \ }{ \in }{ \ }C_t\). Then [KS3] implies \({ \psi }_t(c){ \ }{ \in }{ \ }{ \lbrace }t^{ \prime }{ \in }T|(t,t^{ \prime }){ \in }E{ \rbrace }\). Hence \((t,{ \psi }_t(c)){ \ }{ \in }{ \ }E\). So \(t = p({ \psi }_t(c))\) by Claim 1(c). So 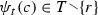 since the domain of p is
since the domain of p is  .
. - Claim 3: :
-
[s4] holds. Suppose \(\hat{c}{ \ }{ \in }{ \ }\hat{C}_i\). By the theorem’s definition of \(\hat{C}_i\), there are [a] \(H{ \ }{ \in }{ \ }{ \mathscr {H}}_i\) and [b] \(c{ \ }{ \in }{ \ }C_H\) such that [c] \(\hat{c}= { \lbrace }{ \psi }_t(c)|t{ \in }H{ \rbrace }\). It suffices to show [i] \(\hat{c}{ \ }{ \ne }{ \ }{ \varnothing }\) and [ii]
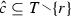 . [i] By [KS5] and [a], H is a member of a partition. So \(H{ \ }{ \ne }{ \ }{ \varnothing }\). So there is \(t{ \ }{ \in }{ \ }H\). So \(c{ \ }{ \in }{ \ }C_t\) by [b]. So \({ \psi }_t(c)\) is well-defined by [KS3]. So \(\hat{c}{ \ }{ \ne }{ \ }{ \varnothing }\) by [c]. [ii] By [c], it suffices to show \(({ \forall }t{ \in }H)\)
. [i] By [KS5] and [a], H is a member of a partition. So \(H{ \ }{ \ne }{ \ }{ \varnothing }\). So there is \(t{ \ }{ \in }{ \ }H\). So \(c{ \ }{ \in }{ \ }C_t\) by [b]. So \({ \psi }_t(c)\) is well-defined by [KS3]. So \(\hat{c}{ \ }{ \ne }{ \ }{ \varnothing }\) by [c]. [ii] By [c], it suffices to show \(({ \forall }t{ \in }H)\) . Toward that end, take \(t{ \ }{ \in }{ \ }H\). So \(c{ \ }{ \in }{ \ }C_t\) by [b]. So
. Toward that end, take \(t{ \ }{ \in }{ \ }H\). So \(c{ \ }{ \in }{ \ }C_t\) by [b]. So 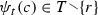 by Claim 2(a).
by Claim 2(a). - Claim 4: :
-
\(({ \forall }i{ \in }I,\hat{c}{ \in }\hat{C}_i,\hat{c}^{ \prime }{ \in }\hat{C}_i)\)\(\hat{c}{ \ }{ \ne }{ \ }\hat{c}^{ \prime }\)\({ \Rightarrow }\)\(\hat{c}{ \cap }\hat{c}^{ \prime } = { \varnothing }\). For the contrapositive, suppose \(t^{\sharp }{ \ }{ \in }{ \ }\hat{c}{ \cap }\hat{c}^{ \prime }\). Then by the definition of \(\hat{C}_i\), there exist \(H{ \ }{ \in }{ \ }{ \mathscr {H}}_i\), \(c{ \ }{ \in }{ \ }C_H\), and \(t{ \ }{ \in }{ \ }H\) such that [a1] \(\hat{c}= { \lbrace }{ \psi }_s(c)|s{ \in }H{ \rbrace }\) and [a2] \({ \psi }_t(c) = t^{\sharp }\), and similarly, there exist \(H^{ \prime }{ \ }{ \in }{ \ }{ \mathscr {H}}_i\), \(c^{ \prime }{ \ }{ \in }{ \ }C_{H^{ \prime }}\), and \(t^{ \prime }{ \ }{ \in }{ \ }H^{ \prime }\) such that [b1] \(\hat{c}^{ \prime } = { \lbrace }{ \psi }_s(c^{ \prime })|s{ \in }H^{ \prime }{ \rbrace }\) and [b2] \({ \psi }_{t^{ \prime }}(c^{ \prime }) = t^{\sharp }\). [a2] and [b2] imply [c] \({ \psi }_t(c) = { \psi }_{t^{ \prime }}(c^{ \prime })\). Thus \(p({ \psi }_t(c)) = p({ \psi }_{t^{ \prime }}(c^{ \prime }))\). Thus by Claim 2(b), [d] \(t = t^{ \prime }\). Thus [e] \(H = H^{ \prime }\) by [KS5]. Further, since \({ \psi }_t\) is injective by [KS3], [c] and [d] imply [f] \(c = c^{ \prime }\). [a1], [b1], [e], and [f] imply \(\hat{c}= \hat{c}^{ \prime }\).
- Claim 5: :
-
\(({ \forall }i{ \in }I,\hat{c}{ \in }\hat{C}_i){ \ }p(\hat{c}){ \ }{ \in }{ \ }{ \mathscr {H}}_i\). Suppose \(\hat{c}{ \ }{ \in }{ \ }\hat{C}_i\). Then by the construction of \(\hat{C}_i\), there are \(H{ \ }{ \in }{ \ }{ \mathscr {H}}_i\) and \(c{ \ }{ \in }{ \ }C_H\) such that \(\hat{c}= { \lbrace }{ \psi }_t(c)|t{ \in }H{ \rbrace }\). I argue \(p(\hat{c})\) [a] equals \({ \lbrace }p(t^{\sharp })|t^{\sharp }{ \in }\hat{c}{ \rbrace }\) by rearrangement; which [b] equals \({ \lbrace }p(t^{\sharp })|t^{\sharp }{ \in }{ \lbrace }{ \psi }_t(c)|t{ \in }H{ \rbrace }{ \rbrace }\) by the previous sentence; which [c] equals \({ \lbrace }p({ \psi }_t(c))|t{ \in }H{ \rbrace }\) by rearrangement; which [d] equals \({ \lbrace }t|t{ \in }H{ \rbrace }\) by Claim 2(b); which equals H.
- Claim 6: :
-
[s5] holds. Because of Claim 4, it suffices to show \(({ \forall }i{ \in }I,\hat{c}{ \in }\hat{C}_i,\hat{c}^{ \prime }{ \in }\hat{C}_i)\)\(p(\hat{c}){ \cap }p(\hat{c}^{ \prime })\)\({ \ne }\)\({ \varnothing }\)\({ \Rightarrow }\)\(p(\hat{c}) = p(\hat{c}^{ \prime })\). Suppose \(\hat{c}{ \ }{ \in }{ \ }\hat{C}_i\), \(\hat{c}^{ \prime }{ \ }{ \in }{ \ }\hat{C}_i\), and \(p(\hat{c}){ \cap }p(\hat{c}^{ \prime }){ \ } { \ne }{ \ }{ \varnothing }\). By two applications of Claim 5, \(p(\hat{c})\) and \(p(\hat{c}^{ \prime })\) belong to \({ \mathscr {H}}_i\). So \(p(\hat{c}) = p(\hat{c}^{ \prime })\) by [KS5].
- Claim 7: :
-
\(({ \forall }i{ \in }I,H{ \in }{ \mathscr {H}}_i,t{ \in }H,c{ \in }C_H)\)\(p^{-1}(t){ \cap }{ \lbrace }{ \psi }_s(c)|s{ \in }H{ \rbrace }\)\(=\)\({ \lbrace }{ \psi }_t(c){ \rbrace }\). Suppose \(H{ \ }{ \in }{ \ }{ \mathscr {H}}_i\), \(t{ \ }{ \in }{ \ }H\), and \(c{ \ }{ \in }{ \ }C_H\). Take any \(t^{\sharp }\) in the intersection. Then there is \(s{ \ }{ \in }{ \ }H\) such that [a] \({ \psi }_s(c) = t^{\sharp }\). Thus by Lemma 2(b), [b] \(p(t^{\sharp }) = s\). But since \(t^{\sharp }{ \ }{ \in }{ \ }p^{-1}(t)\) by assumption, [c] \(p(t^{\sharp }) = t\). [b] and [c] imply \(s = t\) and thus [a] implies \(t^{\sharp }= { \psi }_t(c)\). Conversely, \({ \psi }_t(c){ \ }{ \in }{ \ }p^{-1}(t)\) by [KS3] and Claim 1(c). Also, \({ \psi }_t(c){ \ }{ \in }{ \ }{ \lbrace }{ \psi }_s(c)|s{ \in }H{ \rbrace }\) by \(t{ \ }{ \in }{ \ }H\). Hence \({ \psi }_t(c)\) is in the intersection.
- Claim 8: :
-
\(({ \forall }t{ \in }X,t^{\sharp }{ \in }p^{-1}(t))({ \exists }i{ \in }I,\hat{c}{ \in }\hat{C}_i)\)(a)\(t{ \ }{ \in }{ \ }p(\hat{c})\)and (b)\(p^{-1}{ \cap }\hat{c}= { \lbrace }t^{\sharp }{ \rbrace }\). Suppose [1] \(t{ \ }{ \in }{ \ }X\) and [2] \(t^{\sharp }{ \ }{ \in }{ \ }p^{-1}(t)\). By [1], [KS4], and [KS5], there are \(i{ \ }{ \in }{ \ }I\) and [3] \(H{ \ }{ \in }{ \ }{ \mathscr {H}}_i\) such that [4] \(t{ \ }{ \in }{ \ }H\). By [2], [KS3], and Claim 1(c), there is [5] \(c{ \ }{ \in }{ \ }C_t\) such that [6] \({ \psi }_t(c) = t^{\sharp }\). Further, by [4], [5], [KS6], and the definition of \(C_H\), [7] \(c{ \ }{ \in }{ \ }C_H\). Let \(\hat{c}= { \lbrace }{ \psi }_s(c)|s{ \in }H{ \rbrace }\). Note \(\hat{c}{ \ }{ \in }{ \ }\hat{C}_i\) by [3] and [7]. For (a), note that \(p(\hat{c})\) equals \({ \lbrace }p{ \circ }{ \psi }_s(c)|s{ \in }H{ \rbrace }\) by the definition of \(\hat{c}\); which equals \({ \lbrace }s|s{ \in }H{ \rbrace }\) by Claim 2(b); which equals H. This equality and [4] imply \(t{ \ }{ \in }{ \ }p(\hat{c})\). For (b), note that \(p^{-1}(t){ \cap }\hat{c}\) equals \(p^{-1}(t){ \cap }{ \lbrace }{ \psi }_s(c)|s{ \in }H{ \rbrace }\) by the definition of \(\hat{c}\); which equals \({ \lbrace }{ \psi }_t(c){ \rbrace }\) by Claim 7, [3], [4] and [7]; which equals \({ \lbrace }t^{\sharp }{ \rbrace }\) by [6].
- Claim 9: :
-
\(({ \forall }t{ \in }X) { \ }{ \lbrace }\,{ \lbrace }t^{\sharp }{ \rbrace }\,|\,t^{\sharp }{ \in }p^{-1}(t)\,{ \rbrace } = { \lbrace }\,p^{-1}(t){ \cap }\hat{c}\,|\,t{ \in }p(\hat{c}),\hat{c}{ \in }{ \cup }_{i{ \in }I}\hat{C}_i\,{ \rbrace }.\) The \({ \subseteq }\) direction follows from Claim 8. For the \({ \supseteq }\) direction, suppose [a] \(t{ \ }{ \in }{ \ }p(\hat{c})\) and [b] \(\hat{c}{ \ }{ \in }{ \ }\hat{C}_i\). By [b] and the construction of \(\hat{C}_i\), there exist [c] \(H{ \ }{ \in }{ \ }{ \mathscr {H}}_i\) and [d] \(c{ \ }{ \in }{ \ }C_H\) such that [e] \(\hat{c}= { \lbrace }{ \psi }_s(c)|s{ \in }H{ \rbrace }\). Note \(p(\hat{c})\) equals \({ \lbrace }p{ \circ }{ \psi }_s(c)|s{ \in }H{ \rbrace }\) by [e]; which equals \({ \lbrace }s|s{ \in }H{ \rbrace }\) by Claim 2(b); which equals H. This equality and [a] imply [f] \(t{ \ }{ \in }{ \ }H\). Further, \(p^{-1}(t){ \cap }\hat{c}\) equals \(p^{-1}(t){ \cap }{ \lbrace }{ \psi }_s(c)|s{ \in }H{ \rbrace }\) by [e], which equals \({ \lbrace }{ \psi }_t(c){ \rbrace }\) by Claim 7, [c], [d], and [f]. Thus it suffices to show that \({ \psi }_t(c){ \ }{ \in }{ \ }p^{-1}(t)\). This holds by [KS3] and Claim 1(c).
- Claim 10: :
-
\(({ \forall }t{ \in }X,i{ \in }I,\hat{c}{ \in }\hat{C}_i){ \ }t{ \ }{ \in }{ \ }p(\hat{c}){ \ }{ \Rightarrow }{ \ }P(t) = i\). Suppose \(t{ \ }{ \in }{ \ }X\), [a] \(\hat{c}{ \ }{ \in }{ \ }\hat{C}_i\), and [b] \(t{ \ }{ \in }{ \ }p(\hat{c})\). Claim 5 and [a] imply \(p(\hat{c}){ \ }{ \in }{ \ }{ \mathscr {H}}_i\). This and [b] imply \(t{ \ }{ \in }{ \ }{ \cup }{ \mathscr {H}}_i\). This and [KS5] imply \(t{ \ }{ \in }{ \ }P^{-1}(i)\). This and [KS4] imply \(P(t) = i\).
- Claim 11: :
-
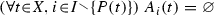 . Suppose \(A_i(t){ \ }{ \ne }{ \ }{ \varnothing }\). Then there exists \(\hat{c}{ \ }{ \in }{ \ }A_i(t)\). By the definition of \(A_i(t)\), \(\hat{c}{ \ }{ \in }{ \ }\hat{C}_i\) and \(t{ \ }{ \in }{ \ }p(\hat{c})\). Thus by Claim 10, \(P(t) = i\).
. Suppose \(A_i(t){ \ }{ \ne }{ \ }{ \varnothing }\). Then there exists \(\hat{c}{ \ }{ \in }{ \ }A_i(t)\). By the definition of \(A_i(t)\), \(\hat{c}{ \ }{ \in }{ \ }\hat{C}_i\) and \(t{ \ }{ \in }{ \ }p(\hat{c})\). Thus by Claim 10, \(P(t) = i\). - Claim 12: :
-
\(({ \forall }t{ \in }X){ \ }J(t) = { \lbrace }P(t){ \rbrace }\). Take \(t{ \ }{ \in }{ \ }X\). Then P(t) is well-defined by [KS4]. Further, by the definition of X, \(p^{-1}(t){ \ }{ \ne }{ \ }{ \varnothing }\). Thus by Claim 9, there is [1] \(\hat{c}{ \ }{ \in }{ \ }{ \cup }_{i{ \in }I}\hat{C}_i\) such that [2] \(t{ \ }{ \in }{ \ }p(\hat{c})\). [1] implies there is \(i^*{ \ }{ \in }{ \ }I\) such that [3] \(\hat{c}{ \ }{ \in }{ \ }\hat{C}_{i^*}\). [2] and [3] imply \(\hat{c}{ \ }{ \in }{ \ }A_{i^*}(t)\). So Claim 11 implies both \(i^* = P(t)\) and \(J(t) = { \lbrace }P(t){ \rbrace }\).
- Claim 13: :
-
[s6] holds. Take \(t{ \ }{ \in }{ \ }X\). \(J(t){ \ }{ \ne }{ \ }{ \varnothing }\) by Claim 12. Also, \({ \lbrace }\,{ \lbrace }t^{\sharp }{ \rbrace }\,|\,t^{\sharp }{ \in }p^{-1}(t)\,{ \rbrace }\) [1] equals \({ \lbrace }\,p^{-1}(t){ \cap }\hat{c}\,|\!\)\(t{ \in }p(\hat{c}),\hat{c}{ \in }{ \cup }_{i{ \in }I}\hat{C}_i\,{ \rbrace }\) by Claim 9; which [2] equals \({ \lbrace }\,p^{-1}(t){ \cap }\hat{c}\!\)\(|\!\)\(t{ \in }p(\hat{c}),\hat{c}{ \in }\hat{C}_{P(t)}\,{ \rbrace }\) by Claim 10; which [3] equals \({ \lbrace }\,p^{-1}(t){ \cap }\hat{c}\!\)\(|\!\)\(\hat{c}{ \in }A_{P(t)}\,{ \rbrace }\) by the definition of \((A_i)_{i{ \in }I}\); which [4] equals \({ \lbrace }\,p^{-1}(t){ \cap }({ \cap }_{i{ \in }J(t)}\hat{c}_i)\,|\!\)\((\hat{c}_i)_{i{ \in }J(t)}{ \in }{ \varPi }_{i{ \in }J(t)}A_i(t)\,{ \rbrace }\) by Claim 12.
- Claim 14: :
-
[s7] holds. Suppose there were [1] \(\hat{c}{ \ }{ \in }{ \ }\hat{C}_i\) and [2] \({ \lbrace }t^{\sharp A},t^{\sharp B}{ \rbrace }{ \ }{ \subseteq }{ \ }\hat{c}\) such that [3] \(t^{\sharp A} > t^{\sharp B}\). [3] and the construction of > imply there is a walk \((t^k)^K_{k=1}\) from \(t^1 = t^{\sharp A}\) to \(t^K = t^{\sharp B}\). [1] and the construction of \(\hat{c}\) imply there are \(H{ \ }{ \in }{ \ }{ \mathscr {H}}_i\) and \(c{ \ }{ \in }{ \ }C_H\) such that \(\hat{c}= { \lbrace }{ \psi }_s(c)|s{ \in }H{ \rbrace }\). This and [2] imply there is [4] \({ \lbrace }t^A,t^B{ \rbrace }{ \ }{ \subseteq }{ \ }H\) such that \({ \psi }_{t^A}(c) = t^{\sharp A}\) and \({ \psi }_{t^B}(c) = t^{\sharp B}\). Thus by Claim 2(b), [5] \(t^A = p(t^{\sharp A})\) and [6] \(t^B = p(t^{\sharp B})\). By Claim 1(c), [5] implies \((t^A,t^{\sharp A}){ \ }{ \in }{ \ }E\) and thus \((t^k)^K_{t=0}\) is a walk from \(t^0 = t^A\) over \(t^1 = t^{\sharp A}\) to \(t^K = t^{\sharp B}\). Note \((t^{K-1},t^{\sharp B}){ \ }{ \in }{ \ }E\). Thus by Claim 1(c), \(t^{K-1} = p(t^{\sharp B})\). This and [6] imply \(t^{K-1} = t^B\). Thus \((t^k)^{K-1}_{k=0}\) is a walk from \(t^0 = t^A\) to \(t^{K-1} = t^B\). This and [4] contradict the assumption that the KS form has no absentmindedness.
- Claim 15: :
-
[s8] holds. Suppose there were \(t{ \ }{ \in }{ \ }X\) and \(\hat{c}{ \ }{ \in }{ \ }\hat{C}_i\) such that \(p^{-1}(t){ \ }{ \subseteq }{ \ }\hat{c}\). By construction, there exists [1] \(H{ \ }{ \in }{ \ }{ \mathscr {H}}_i\) and [2] \(c{ \ }{ \in }{ \ }C_{H}\) such that \(\hat{c}= { \lbrace }{ \psi }_s(c)|s{ \in }H{ \rbrace }\). By the previous two sentences, [3] \(p^{-1}(t){ \ }{ \subseteq }{ \ }{ \lbrace }{ \psi }_s(c)|s{ \in }H{ \rbrace }\). Note that \({ \lbrace }t{ \rbrace }\) equals \(p{ \circ }p^{-1}(t)\) because \(p^{-1}(t){ \ }{ \ne }{ \ }{ \varnothing }\) by \(t{ \ }{ \in }{ \ }X\); which is a subset of \({ \lbrace }p{ \circ }{ \psi }_s(c)|s{ \in }H{ \rbrace }\) by [3]; which equals \({ \lbrace }s|s{ \in }H{ \rbrace }\) by Claim 2(b); which equals H. In other words, [4] \(t{ \ }{ \in }{ \ }H\). Further, \({ \lbrace }{ \psi }_t(c^{ \prime })|c^{ \prime }{ \in }C_t{ \rbrace }\) equals \({ \lbrace }t^{\sharp }{ \in }T|(t,t^{\sharp }){ \in }E{ \rbrace }\) by [KS3]; which equals \(p^{-1}(t)\) by Claim 1(c); which equals \(p^{-1}(t){ \cap }{ \lbrace }{ \psi }_s(c)|s{ \in }H{ \rbrace }\) by [3]; which equals \({ \lbrace }{ \psi }_t(c){ \rbrace }\) by Claim 7, [1], [2], and [4]. In brief, [5] \({ \lbrace }{ \psi }_t(c^{ \prime })|c^{ \prime }{ \in }C_t{ \rbrace } = { \lbrace }{ \psi }_t(c){ \rbrace }\). Since \({ \psi }_t\) is injective by [KS3], [5] implies \(|C_t| = 1\). This contradicts the assumption that the KS form has no trivial decisions.
- Claim 16: :
-
The theorem’s part (b) holds.\((T,{ \ge },(\hat{C}_i)_{i{ \in }I})\) is a simple form by Claims 1(a), 3, 6, 13, 14, and 15. It has no simultaneous decisions by Claim 12.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Streufert, P.A. Equivalences among five game specifications, including a new specification whose nodes are sets of past choices. Int J Game Theory 48, 1–32 (2019). https://doi.org/10.1007/s00182-018-0652-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-018-0652-8









 is nonempty. The latter also implies that T is nonempty by the
is nonempty. The latter also implies that T is nonempty by the  . Thus
. Thus 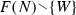 there becomes
there becomes 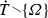 here. Third, a move
here. Third, a move  . I argue that [1] and [2] are insignificant by considering the set
. I argue that [1] and [2] are insignificant by considering the set  . Then
. Then  . This is equivalent to
. This is equivalent to  . This implies
. This implies 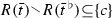 . [a] and [b] yield [c]
. [a] and [b] yield [c] 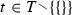 . Then (a)
. Then (a) . (a) holds by Claim 3. For (b), take
. (a) holds by Claim 3. For (b), take 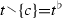 by manipulation; which is [6] equivalent to
by manipulation; which is [6] equivalent to  .
. . Take
. Take 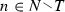 . By the definition of N, there is
. By the definition of N, there is  . Hence, by [OR2], we may define
. Hence, by [OR2], we may define  . Toward that end, suppose
. Toward that end, suppose 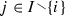 , and
, and  by the definition of
by the definition of 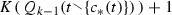 by inspection. This equals
by inspection. This equals  by
by  . Fix
. Fix  . Note
. Note 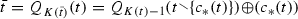 . I argue [a]
. I argue [a]  by the previous sentence; which [b] belongs to
by the previous sentence; which [b] belongs to  by the definition of
by the definition of  by inspection, which [c] equals
by inspection, which [c] equals  by the inductive hypothesis, which [d] equals t.
by the inductive hypothesis, which [d] equals t. by the definition of
by the definition of  and
and  and
and 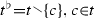 , and
, and  and
and  such that
such that  is an infinite chain inT. Take any such
is an infinite chain inT. Take any such  . Toward that end, take
. Toward that end, take  . Since
. Since  . Take any
. Take any  . By the forward direction of [cs3], there exists an infinite chain
. By the forward direction of [cs3], there exists an infinite chain  is well-defined and [KS3] holds att. Suppose
is well-defined and [KS3] holds att. Suppose  . Then [a]
. Then [a]  . To show disjointness, suppose there were
. To show disjointness, suppose there were  . [a] and [b] imply [c]
. [a] and [b] imply [c]  and (b)
and (b)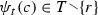 since the domain of p is
since the domain of p is  .
.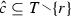 . [i] By [KS5] and [a], H is a member of a partition. So
. [i] By [KS5] and [a], H is a member of a partition. So  . Toward that end, take
. Toward that end, take 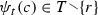 by Claim 2(a).
by Claim 2(a).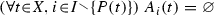 . Suppose
. Suppose