Measuring public inflation perceptions and expectations in the UK

Abstract

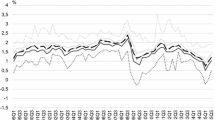
The Bank of England Inflation Attitudes Survey asks individuals about their inflation perceptions and expectations in eight intervals including an indifference limen. This paper studies fitting a mixture normal distribution to such interval data, allowing for multiple modes. Bayesian analysis is useful since ML estimation may fail. A hierarchical prior helps to obtain a weakly informative prior. The No-U-Turn Sampler speeds up posterior simulation. Permutation invariant parameters are free from the label switching problem. The paper estimates the distributions of public inflation perceptions and expectations in the UK during 2001Q1–2017Q4. The estimated means are useful for measuring information rigidity.

Appendix: HMC methods and the NUTS

Understanding an HMC method requires some knowledge of physics. The Boltzmann (Gibbs, canonical) distribution describes the distribution of possible states in a system. Given an energy function E(.) and the absolute temperature T, the pdf of a Boltzmann distribution is $\forall x$,

$$\begin{aligned} f(x) \propto \exp \left( -\frac{E(x)}{kT}\right) \end{aligned}$$

(A.1)

where k is the Boltzmann constant. One can think of any pdf f(.) as the pdf of a Boltzmann distribution with $E(x):=-\ln f(x)$ and $kT=1$.

The Hamiltonian is an energy function that sums the potential and kinetic energies of a state. An HMC method treats $-\ln p(\varvec{\theta }|\varvec{y})$ as the potential energy at position $\varvec{\theta }$ and introduces an auxiliary momentum $\varvec{z}$ drawn randomly from ${\mathrm {N}}(\varvec{0},\varvec{\varSigma })$, whose kinetic energy is $-\ln p(\varvec{z}) \propto \varvec{z}'\varvec{\varSigma }^{-1}\varvec{z}/2$ with mass matrix $\varvec{\varSigma }$. The resulting Hamiltonian is

$$\begin{aligned} H(\varvec{\theta },\varvec{z})&:=-\ln p(\varvec{\theta }|\varvec{y})-\ln p(\varvec{z}) \nonumber \\&=-\ln p(\varvec{\theta },\varvec{z}|\varvec{y}) \end{aligned}$$

(A.2)

An HMC method draws from $p(\varvec{\theta },\varvec{z}|\varvec{y})$, which is a Boltzmann distribution with energy function $H(\varvec{\theta },\varvec{z})$.

The Hamiltonian is constant over (fictitious) time t by the law of conservation of mechanical energy, i.e., $\forall t \in \mathbb {R}$,

$$\begin{aligned} \dot{H}(\varvec{\theta }(t),\varvec{z}(t))=0 \end{aligned}$$

(A.3)

or

$$\begin{aligned} \dot{\varvec{\theta }}(t)H_{\varvec{\theta }}(\varvec{\theta }(t),\varvec{z}(t)) +\dot{\varvec{z}}(t)H_{\varvec{z}}(\varvec{\theta }(t),\varvec{z}(t)) =\varvec{0}\end{aligned}$$

(A.4)

Thus, Hamilton’s equation of motion is $\forall t \in \mathbb {R}$,

$$\begin{aligned} \dot{\varvec{\theta }}(t)&=H_{\varvec{z}}(\varvec{\theta }(t),\varvec{z}(t)) \end{aligned}$$

(A.5)

$$\begin{aligned} \dot{\varvec{z}}(t)&=-H_{\varvec{\theta }}(\varvec{\theta }(t),\varvec{z}(t)) \end{aligned}$$

(A.6)

The Hamiltonian dynamics says that $(\varvec{\theta },\varvec{z})$ moves on a contour of $H(\varvec{\theta },\varvec{z})$, i.e., $p(\varvec{\theta },\varvec{z}|\varvec{y})$.

Conceptually, given $\varvec{\varSigma }$ and an initial value for $\varvec{\theta }$, an HMC method proceeds as follows:

• 1. Draw $\varvec{z}\sim {\mathrm {N}}(\varvec{0},\varvec{\varSigma })$ independently from $\varvec{\theta }$.

• 2. Start from $(\varvec{\theta },\varvec{z})$ and apply Hamilton’s equations of motion for a certain length of (fictitious) time to obtain $(\varvec{\theta }',\varvec{z}')$, whose joint probability density equals that of $(\varvec{\theta },\varvec{z})$.

• 3. Discard $\varvec{z}$ and $\varvec{z}'$, and repeat.

This gives a reversible Markov chain on $(\varvec{\theta },\varvec{z})$, since the Hamiltonian dynamics is reversible; see Neal (2011, p. 116). The degree of serial dependence or speed of convergence depends on the choice of $\varvec{\varSigma }$ and the length of (fictitious) time in the second step. The latter can be fixed or random, but cannot be adaptive if it breaks reversibility.

In practice, an HMC method approximates Hamilton’s equations of motion in discrete steps using the leapfrog method. This requires choosing a step size $\varepsilon$ and the number of steps L. Because of approximation, the Hamiltonian is no longer constant during the leapfrog method, but adding a Metropolis step after the leapfrog method keeps reversibility. Thus, given $\varvec{\varSigma }$ and an initial value for $\varvec{\theta }$, an HMC method proceeds as follows:

• 1. Draw $\varvec{z}\sim {\mathrm {N}}(\varvec{0},\varvec{\varSigma })$ independently from $\varvec{\theta }$.

• 2. Start from $(\varvec{\theta },\varvec{z})$ and apply Hamilton’s equations of motion approximately by the leapfrog method to obtain $(\varvec{\theta }',\varvec{z}')$.

• 3. Accept $(\varvec{\theta }',\varvec{z}')$ with probability $\min \{\exp (-H(\varvec{\theta }',\varvec{z}'))/\exp (-H(\varvec{\theta },\varvec{z})),1\}$.²²

• 4. Discard $\varvec{z}$ and $\varvec{z}'$, and repeat.

The degree of serial dependence or speed of convergence depends on the choice of $\varvec{\varSigma }$, $\varepsilon$, and L. Moreover, the computational cost of each iteration depends on the choice of $\varepsilon$ and L.

The NUTS developed by Hoffman and Gelman (2014) adaptively chooses L while keeping reversibility. Though the algorithm of the NUTS is complicated, it is easy to use with Stan, a modeling language for Bayesian computation with the NUTS (and other methods). Stan tunes $\varvec{\varSigma }$ and $\varepsilon$ adaptively during warm-up. The user only specifies the data, model, and prior. One can call Stan from other popular languages and softwares such as R, Python, MATLAB, Julia, Stata, and Mathematica. The NUTS often has better convergence properties than other popular MCMC methods such as the Gibbs sampler and M–H algorithm.