1 Introduction

Polymer-based composites are widely used in engineering applications due to their potential as lightweight materials, combining low weight with high specific stiffness and strength, accompanied by design freedom for structural parts [1, 2]. For the characterization and modeling of the composite’s material behavior, an understanding of chemo-thermo-mechanical processes within the polymer matrix is a key factor. In this work, the thermoplastic polymer polyamide 6 (PA 6) is considered as potential matrix material. The hydrophilic nature of the amide functional group of the PA 6 monomers leads to an uptake of water into the polymer network when PA 6 is exposed to humid environments. This water uptake can reach 9 wt% in dry weight [3]. Consequences are an increased chain mobility, a shift in the glass transition temperature of PA 6 [4, 5], and a swelling of the polymer as chain molecules are pushed apart due to diffusing water molecules [6].

Depending on operating conditions, also drying processes occur in PA 6. In this context, experimental results of relaxation tests performed on injection molded PA 6, presented by several of the authors in [7], showed an unusual relaxation behavior, indicating drying effects, which is briefly summarized in the following. In [7], PA 6 specimens with a length \(l = 83\,~\textrm{mm}\), a width \(w = 10\,~\textrm{mm}\) and a thickness \(t = 2\,~\textrm{mm}\) were water jet cut from injection molded plates. Directly after molding, the specimens are typically in a dry-as-molded (DAM) state and only take up water due to environmental conditions. As the DAM state was not known, the specimens were stored first in a vacuum oven and afterwards in a desiccator to ensure a DAM state. Before relaxation testing, two PA 6 specimens were preconditioned to ATM-23/50, i.e. at a temperature \(\theta = 23^\circ \text {C}\) and a relative humidity of \(\phi = 50\,\%\text {RH}\), which leads to a mass uptake of 2.5–3 wt% [3]. This was achieved by placing them in a climatic chamber with an accelerated preconditioning program for seven days. Multiple weighing confirmed an equilibrium moisture content that did not change in the following days.

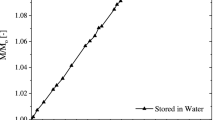
The two specimens were tested in a static relaxation experiment. To this end, the specimens were placed in the testing chamber of a GABO Eplexor® \(500\,~\textrm{N}\) and allowed to settle for one hour. Subsequently, a constant strain \(\varepsilon _0 = 0.1\,\%\) was applied and held constant for six hours. The testing conditions differed, as one specimen was placed in an environmental chamber with humidity control (HC) at \(\phi = 50\,\%\textrm{RH}\), while the other was tested in a chamber without HC at \(\phi \approx 35\,\%\textrm{RH}\). The unusual relaxation behavior is observed when the relaxation modulus  R(t), which connects the applied constant strain \(\varepsilon _0\) to the stress via \({\sigma (t) = R(t) \varepsilon _0}\), is depicted over time for a duration of six hours, c.f. Fig. 1. The relaxation modulus for the specimen tested with HC decreases with increasing time as expected [6]. The specimen tested without HC, however, shows an increasing relaxation modulus over time which is linked to drying of the specimen due to the deviation in ambient humidity level compared to the specimen’s humidity content [7, 8]. The drying process leads to a contraction of the specimen, which is prohibited by the constant applied strain \(\varepsilon _0\). Thus the relaxation modulus R(t) increases. Multiple weighing of the two samples confirmed the suspected drying as the specimen tested with HC did not change it’s mass considerably, whereas the specimen tested without HC lost \(1.115\,\%\) of it’s mass relative to it’s initial mass, c.f. [7, Tab. 5].

Clearly, there is a need to consider these observations in chemo-mechanically coupled models in order to predict the diffusion-deformation behavior of PA 6 in varying operating conditions. Numerous studies have been conducted to this end. An excellent review is given in [9]. In the context of coupled chemo-mechanical modeling approaches, we want to briefly mention models considering non-constant diffusion coefficients [6, 10, 11], changing elastic or viscoelastic properties [6, 12, 13] and a varying glass transition temperature [14]. However, to the best knowledge of the authors, so far no model has been proposed to predict the experimentally observed increase in R(t) during a relaxation experiment due to drying of PA 6. In order to bridge this gap, the goal of this work is the derivation and application of a chemo-mechanical continuum model that couples water diffusion in PA 6 to viscoelastic deformations. The derivation includes a detailed discussion of the balance equations and the constitutive theory which considers both chemical and mechanical contributions to the free energy. The chemical part relies on the Flory–Huggins model [15, 16] for enthalpy and entropy of mixing, while the mechanical part introduces viscoelastic strains [6]. As the previously published approaches mentioned above require cumbersome experimental identification of each dependency on water concentration and result in large numbers of material parameters, our model relies on constant parameters which significantly simplifies the presentation, implementation and application of the model equations. However, we clearly outline limitations of our model. We apply the model to study drying of PA 6 specimens in an uncoupled diffusion simulation and subsequently in a chemo-mechanically coupled simulation of relaxation experiments.

The work is structured as follows: In Sect. 2, the theoretical framework of the model is presented, introducing balance laws and the constitutive theory. In Sect. 3, a Finite-Element implementation of the derived governing equations is presented and applied to predict both the drying of PA 6 specimens without mechanical deformation as well as an increasing relaxation modulus due to drying. Concluding remarks and an outlook are given in Sect. 4.

Fig. 1
figure 1

Relaxation modulus over time for two relaxation experiments conducted on PA 6 at \(80^\circ \,\textrm{C}\). Both specimens were conditioned at a humidity level of \(\phi = 50\,\%\textrm{RH}\) at \(80^\circ \textrm{C}\). One specimen was tested with humidity control (HC) at \(\phi = 50\,\%\textrm{RH}\), while the other specimen was tested without HC and the ambient humidity level was \(\phi \approx 35\,\%\textrm{RH}\). In the first hour of the experiment, both specimens are allowed to settle at \(\varepsilon _0 = 0\,\%\), such that the temperature reaches an equilibrium. Subsequently, the strain is applied and held constant for \(6\,\textrm{h}\)

Full size image

2 Theory

2.1 Basic assumptions

In this section, we present the governing balance equations and the constitutive theory, which we subsequently solve using Finite-Elements in order to model the diffusion of water in polyamide. Two phases have to be considered, polyamide and water, which is commonly achieved by using mixture theory [17]. In mixture theory, each phase is described by an individual set of balance equations, commonly a balance for mass, of linear momentum, energy and entropy. Balance equations for the mixture result by superposition of both sets of equations, i.e., it is assumed, that both phases can occupy the same volume at a given time.

Solving these balance equations for both phases in a Finite-Element context is computationally expensive due to the large number of degrees of freedom. Examples for the successful application of mixture theory to the interaction of polymers and liquids can be found in, e.g., [12, 18]. However, it is often advantageous to simplify the set of governing balance equations if the diffusing phase carries only negligible amounts of mass [19]. This is achieved by assuming that the contribution of the diffusing phase to the balance laws of the mixture is restricted to an individual mass balance that describes the evolution of the diffusing phase’s concentration. This implies, that the mixture of both phases is dominated by the mass of the non-diffusing phase. Possible contributions to the behavior of the mixture can be considered by adding terms in the mixture balance laws for linear momentum, energy and entropy as a function of this concentration. With this approach, the amount of additional degrees of freedoms is limited to a single one, namely, the concentration of water.

In addition, the constitutive theory follows from a single free energy for the mixture, instead of two separate ones for each phase. As the maximum uptake of water in PA 6 is below 10 wt%, we assume that contributions of water concentration to the mixture behavior are limited to a flux of internal energy, similar to the flux of internal energy due to heat flux, which is a common approach in chemo-mechanically coupled models, see, e.g., [20,21,22]. The balance of entropy relies on the Clausius-Duhem assumption for entropy production and flux [23] and no further contributions from the diffusing water are introduced.

As outlined in the introduction, the goal of this work is a comprehensive presentation of the model. To this end, all further assumptions underlying the constitutive theory are summarized below. These assumptions allow us to present a relatively simple model, that relies on few material parameters and no extra experimental work. A discussion and comparison to previous works of these assumptions is given at the end ob this section. The assumptions are:

  • Small strain setting relying on the infinitesimal strain tensor \(\varvec{\varepsilon }= \text {sym}\left( \text {grad}\left( {\varvec{ u}}\right) \right) .\)

  • Isotropic material behavior.

  • Constant material parameters with respect to water concentration.

  • Absence of chemical reactions between water molecules and the PA 6 chains. As reactions are excluded, the model could also be called diffuso-mechanical.

  • Constant mass density of PA 6 denoted by \(\rho \).

  • Negligence of inertia effects due to the time scale of water diffusion processes.

  • Absence of volume forces.

  • Purely volumetric, reversible swelling strain, being linear in the difference between current water concentration and a reference concentration [6, 13].

  • A deviatoric linear viscoelastic model and an elastic behavior in volumetric deformations to describe the mechanical material behavior of PA 6 [6].

  • Isothermal conditions, such that parameter dependencies on temperature are discarded. In addition, heat-storage contribution to the free energy is discarded.

  • Applicability of the Flory–Huggins model [15, 16] for entropy and enthalpy of mixing to describe the chemical part of the free energy.

  • Negligence of the semi-crystalline structure of PA 6.

2.2 Description of the water content

As no separate continuum is introduced for the diffusing water, a definition of water content at any material point within PA 6 is necessary. This allows us to discuss the influence of water, e.g. due to swelling, on PA 6. Various works found different ways to approach this topic which will be briefly summarized here. The goal is to allow the reader to compare differing approaches to each other. A straightforward way to express water content is by using the concentration c, expressed as the ratio of the infinitesimal mass of water \(\text {d}m_\textrm{w} = \rho _\textrm{w}\, \text {d}V\) to the infinitesimal mass of dry polyamide \(\text {d}m_\textrm{p,dry} = \rho _\textrm{p, dry} \,\text {d}V\)

$$\begin{aligned} {c = \frac{\text {d}m_\textrm{w}}{\text {d}m_\textrm{p,dry}} = \frac{\rho _\textrm{w}}{\rho _\textrm{p, dry}}}, \end{aligned}$$
(1)

where \(\rho _\textrm{w}\) is the mass density of water, \(\rho _\textrm{p, dry}\) the mass density of dry PA 6 and \(\text {d}V = \text {d}V_\textrm{w} + \text {d}V_\textrm{p,dry}\) the infinitesimal volume element. In a homogeneous system this results in the mass fraction \(c = m_\textrm{w} / m_\textrm{p,dry}\) [9]. For increasing water content, c increases up to a maximum concentration \(c_\textrm{max}\), which denotes the maximum amount of water, that can be taken up by PA 6. Experiments indicate, that this maximum is at roughly \(c_\textrm{max} = 9 \%\), almost independent of temperature [6, 13]. Based on this observation, a normalized concentration or occupancy \(\tilde{c}\) is frequently introduced by

$$\begin{aligned} \tilde{c} = \frac{c}{c_\textrm{max}} \in \left[ 0,1\right] . \end{aligned}$$
(2)

Another approach to quantify water content in PA 6 is the polymer volume fraction \(\varphi \), expressed as the ratio of a differential polymer volume element \({\text {d}V_\textrm{p,dry}}\) with respect to the differential total volume \(\text {d}V\) [21]

$$\begin{aligned} \varphi = {\frac{\text {d}V_\textrm{p,dry}}{\text {d}V_\textrm{w} + \text {d}V_\textrm{p, dry}}}. \end{aligned}$$
(3)

A fourth way of quantifying water content is the number of molecules of water per volume of dry PA 6, expressed as \(\vartheta \) [21]. To this end, we introduce \(\vartheta _\textrm{max}\) as the maximum number of water particles per volume of PA 6 via

$$\begin{aligned} {\vartheta _\textrm{max} = \frac{\rho _\textrm{p,dry} c_\textrm{max}}{M_\textrm{w}}}, \end{aligned}$$
(4)

where \(M_\textrm{w}\) in \(~\mathrm{kg/mol}\) is the molar mass of water. We want to point out, that both \(c_\textrm{max}\) and \(\vartheta _\textrm{max}\) are material parameters, that describe the maximum amount of water, that PA 6 can take up, where the former specifies the maximum infinitesimal mass fraction, while the latter describes the maximum number of moles per volume. Based on \(\vartheta _\textrm{max}\), a relation between \(\vartheta , c\) and \(\tilde{c}\) can be computed according to

$$\begin{aligned} \vartheta = \frac{{\vartheta _\textrm{max}}}{c_\textrm{max}} c = {\vartheta _\textrm{max}} \tilde{c}. \end{aligned}$$
(5)

We conclude this short summary by relating \(\varphi \) with \(\vartheta \). We need to consider the volumetric expansion of polyamide due to the presence of water molecules. To this end, the volumetric expansion coefficient of water in polyamide, \(\Omega \), needs to be introduced, further outlined below. This implies that the infinitesimal volume of water at a material point can be expressed as \(\text {d}V_\textrm{w} = \Omega \vartheta \text {d}V_\textrm{p,dry}\). Building upon this coefficient, the relation is [21]

$$\begin{aligned} \varphi ={\frac{1}{1 + \frac{\text {d}V_\textrm{w}}{\text {d}V_\textrm{p, dry}}}} = \frac{1}{1 + \Omega \vartheta }. \end{aligned}$$
(6)

In the following, we will make use of the definition for the concentration c and occupancy \(\tilde{c}\). However, using the relations summarized above, readers can express quantities as functions of \(\vartheta \) or \(\varphi \).

2.3 Balance equations

We start by formulating a balance equation for the diffusion of water, expressed for the normalized water concentration \(\tilde{c}\), see Eq. 2. The concentration can change due to a flux of water \({\varvec{ j}}\), into or out of PA 6. In its local form, the mass balance reads [20, 21, 24]

$$\begin{aligned} \dot{\vartheta } = {\vartheta _\textrm{max}} \dot{\tilde{c}} = - \textrm{div }\left( {\varvec{ j}} \right) . \end{aligned}$$
(7)

The local balance of linear momentum for the mixture is introduced as

$$\begin{aligned} \textrm{div }\left( \varvec{\sigma } \right) = \textbf{0}, \end{aligned}$$
(8)

where \(\varvec{\sigma }\) is the Cauchy stress tensor in PA 6. The balance of angular momentum implies the symmetry of the Cauchy stress, i.e. \(\varvec{\sigma }= \varvec{\sigma }^{\intercal }\). The balance of internal energy for the mixture considers, additionally to the heat flux, the change due to water flux across the system boundary by \(\mu {\varvec{ j}}\cdot {\varvec{ n}}\), where \(\mu \) is the chemical potential of water and \({\varvec{ n}}\) the outer normal of PA 6. The local balance of internal energy is then [20, 25]

$$\begin{aligned} \rho \dot{e} = \varvec{\sigma }\cdot \dot{\varvec{\varepsilon }} - \mu \text {div}\left( {\varvec{ j}}\right) - \text {grad}\left( \mu \right) \cdot {\varvec{ j}}- \textrm{div }\left( {\varvec{ q}} \right) + \rho \omega , \end{aligned}$$
(9)

where \(-\textrm{div }\left( {\varvec{ q}} \right) + \rho \omega \) denotes changes in internal energy due to heat flux \({\varvec{ q}}\) and heat source \(\omega \). The non-standard contribution to the flux in internal energy due to water flux is given by \({-\text {div}\left( \mu {\varvec{ j}}\right) = }- \mu \text {div}\left( {\varvec{ j}}\right) - \text {grad}\left( \mu \right) \cdot {\varvec{ j}}\). Inserting the mass balance of the diffusing water from Eq. 7 yields

$$\begin{aligned} \rho \dot{e} = \varvec{\sigma }\cdot \dot{\varvec{\varepsilon }} + \mu {\vartheta _\textrm{max}} \dot{\tilde{c}} - \text {grad}\left( \mu \right) \cdot {\varvec{ j}}- \textrm{div }\left( {\varvec{ q}} \right) + \rho \omega . \end{aligned}$$
(10)

Finally, to complete the necessary balance equations, we introduce the entropy balance and the assumption of a non-negative entropy production in it’s local form for constant temperature \(\theta \) as

$$\begin{aligned} \rho \dot{\eta } \ge - \text {div}\left( \frac{{\varvec{ q}}}{\theta }\right) + \rho \frac{\omega }{\theta }, \end{aligned}$$
(11)

where \(\eta \) is the entropy, \({\varvec{ q}}/ \theta \) the entropy flux and \(\omega / \theta \) entropy supply due to heat sources. We want to point out, that the specific form of the entropy flux \({\varvec{ q}}/\theta \), which neglects a contribution of the diffusing water, is a simplifying assumption. This assumption was introduced in [20, 25] and is commonly used in chemo-mechanically coupled theories, see, e.g., [21, 22].

2.4 Thermodynamically consistent constitutive equations

To arrive at a closed set of governing equations, we rely on the Coleman-Noll procedure [23] to derive a thermodynamically consistent material theory. Therefore, we introduce the free energy via a Legendre transformation

$$\begin{aligned} \psi = e - \theta \eta . \end{aligned}$$
(12)

By inserting Eq. 12 into Eq. 11 and eliminating the heat sources \(\omega \) by means of Eq. 10, we arrive at

$$\begin{aligned} \rho \left( \dot{\psi } + \eta \dot{\theta } \right) - \varvec{\sigma }\cdot \dot{\varvec{\varepsilon }} + \frac{{\varvec{ q}}\cdot \textrm{grad}\left( \theta \right) }{\theta } - \mu {\vartheta _\textrm{max}} \dot{\tilde{c}} + \text {grad}\left( \mu \right) \cdot {\varvec{ j}}\le 0. \end{aligned}$$
(13)

In our theory, the independent variables are the set \(\Lambda = \left( \varvec{\varepsilon }, \theta , \tilde{c}, \underline{\alpha }\right) \), where \(\underline{\alpha }\) is a tuple of internal variables, that later on will be used to model the viscoelastic deformation of polyamide. Based on the equipresence argument, we insert \(\psi = \psi \left( \Lambda \right) \) into Eq. 13 to arrive at

$$\begin{aligned} \left( \rho \frac{\partial \psi }{\partial \varvec{\varepsilon }} - \varvec{\sigma }\right) \cdot \dot{\varvec{\varepsilon }} + \left( \frac{\partial \psi }{\partial \theta } + \eta \right) \rho \dot{\theta } + \left( \rho \frac{\partial \psi }{\partial \tilde{c}} - \mu {\vartheta _\textrm{max}}\right) \dot{\tilde{c}} + \rho \frac{\partial \psi }{\partial \underline{\alpha }} \cdot \dot{\underline{\alpha }} \,+ \textrm{grad}\left( \mu \right) \cdot {\varvec{ j}}+ \frac{1}{\theta } {\varvec{ q}}\cdot \textrm{grad}\left( \theta \right) \le 0. \end{aligned}$$
(14)

This inequality has to hold for all thermodynamic processes \(\Lambda \). We start by considering reversible processes and thus conclude, that the the potential relations

$$\begin{aligned} \varvec{\sigma }= \rho \frac{\partial \psi }{\partial \varvec{\varepsilon }}, \quad \eta = - \frac{\partial \psi }{\partial \theta }, \quad \mu = \frac{\rho }{{\vartheta _\textrm{max}}}\frac{ \partial \psi }{\partial \tilde{c}} \end{aligned}$$
(15)

hold, for both reversible and irreversible processes. The remaining dissipation inequality is

$$\begin{aligned} \rho \frac{\partial \psi }{\partial \underline{\alpha }} \cdot \dot{\underline{\alpha }} \,+ \textrm{grad}\left( \mu \right) \cdot {\varvec{ j}}+ \frac{1}{\theta } {\varvec{ q}}\cdot \textrm{grad}\left( \theta \right) \le 0. \end{aligned}$$
(16)

The dissipation inequality implies restrictions for the choice of heat flux \({\varvec{ q}}\), water flux \({\varvec{ j}}\) and the evolution of internal variables \(\underline{\dot{\alpha }}\). In addition, we conclude from Eq. 15 that we need to specify a free energy that relates the constitutive quantities \(\varvec{\sigma }, \mu \) and \(\eta \) to the process parameters \(\varvec{\varepsilon }, \theta , \tilde{c}\) and \(\underline{\alpha }\). Here we formulate a single free energy for the continuum of polyamide and water, which is additively split in a mechanical and a chemical part via

$$\begin{aligned} \psi (\Lambda ) = \psi _\textrm{m}\left( \varvec{\varepsilon }, \theta , \tilde{c}, \underline{\alpha } \right) + \psi _\textrm{c}(\theta , \tilde{c}), \end{aligned}$$
(17)

where the mechanical part \(\psi _\textrm{m}\) depends on \(\varvec{\varepsilon }, \theta , \tilde{c}\) and \(\underline{\alpha }\), while the chemical part \(\psi _\textrm{c}\) solely depends on \(\theta \) and \(\tilde{c}\). The chemical part of the free energy \(\psi _\textrm{c}\) follows from considering changes in the free enthalpy and the entropy due to mixing of water and PA 6. At this stage we want to mention, that typically this relation is used to describe a change in Gibb’s energy due to mixing, i.e., \(g_\textrm{c}\). However, as pointed out in [26], the chemical part \(\psi _\textrm{c}\) of the free energy and the Gibb’s energy \(g_\textrm{c}\) coincide in our approach, i.e. \(\psi _\textrm{c} = g_\textrm{c}\), as the mechanical part is considered separately in \(\psi _\textrm{m}\).

Commonly in chemo-mechanics, a highly idealized model is used that allows to express the entropy of mixing for ideal gases and assumes a vanishing enthalpy of mixing. This approach has been successfully used to model hydrogen diffusion in metal lattices or Lithium diffusion in silicon anodes, c.f. [22, 27]. However, this highly idealized model is not valid for the mixture of PA 6 and water, considered in this work, as neither water molecules nor PA 6 behave like ideal gases [21, 28].

Instead, to describe the chemical contribution to the free energy, the model of Flory and Huggins [15, 16] is used in this work, which is based on a lattice model as depicted in Fig. 2a. The polymer consists of polymer molecules, which occupy connected lattice points, whereas the rest of the lattice is occupied by water molecules. Flory and Huggins introduced a parameter \(\chi \) (later called Flory–Huggins parameter) that models interactions of the long polymer molecules and the small water molecules and introduces a non vanishing enthalpy of mixing. The larger the Flory–Huggins parameter, the stronger the interaction between both molecules, the larger the enthalpy of mixing. The Flory–Huggins entropy of mixing is in close analogy to the entropy of mixing of ideal gases, but is a function of the partial volume instead of the concentration. The change in free energy is, based on the Flory Huggins model [21, 26],

$$\begin{aligned} \rho \psi _\textrm{c} = \mu _0 {\vartheta _\textrm{max}} \tilde{c} + R \theta {\vartheta _\textrm{max}} \tilde{c} \left( \text {ln}\left( \frac{\Omega {\vartheta _\textrm{max}} \tilde{c}}{1 + \Omega {\vartheta _\textrm{max}} \tilde{c}}\right) + \frac{\chi }{1 + \Omega {\vartheta _\textrm{max}} \tilde{c}} \right) . \end{aligned}$$
(18)

To specify \(\psi _\textrm{m}\), chemical and viscoelastic strains are introduced. Chemical strains \(\varvec{\varepsilon }_\textrm{c}\) are volumetric [21]

$$\begin{aligned} \varvec{\varepsilon }_\textrm{c} = \alpha _\textrm{c} \Delta \tilde{c} {\varvec{ I}}, \end{aligned}$$
(19)

where \(3 \alpha _\textrm{c} = \Omega {\vartheta _\textrm{max}}\) is a dimensionless swelling coefficient [6, 10] and \(\Delta \tilde{c}\) is the difference of the current concentration to a normalized reference concentration \(\tilde{c}_0\), for which no swelling occurs. Viscoelastic strains \(\varvec{\varepsilon }_\mathrm{v, \alpha }\) are introduced as internal variables \(\underline{\alpha }\). A standard linear viscoelastic Maxwell element model is used with \(N_\textrm{MW}\) Maxwell elements in parallel to an equilibrium stiffness \({\mathbb { C}}_0\), c.f. Fig. 2b. To this end, the viscosity tensor \({\mathbb { V}}_\alpha \) for Maxwell element \(\alpha \) as well as it’s inverse, the fluidity tensor \({\mathbb { F}}_\alpha \) are introduced by

$$\begin{aligned} {\mathbb { V}}_\alpha = \tau _\alpha {\mathbb { C}}_\alpha , \quad {\mathbb { F}}_\alpha = \frac{1}{\tau _\alpha } {\mathbb { C}}_{\alpha }^{-1}, \end{aligned}$$
(20)

where \({\mathbb { C}}_\alpha = 2 G_\alpha {\mathbb { P}}_2\) is the stiffness of each element, \(G_\alpha \) the respective shear modulus and \({\mathbb { P}}_2\) the projector on symmetric deviatoric tensors of rank 2. This implies, that all viscous strains are volume preserving. For each Maxwell element, the relaxation time and the inverse of the stiffness are denoted by \(\tau _\alpha \) and \({\mathbb { C}}_\alpha ^{-1}\) respectively [29]. The evolution of the viscous strains follows from

$$\begin{aligned} \dot{\varvec{\varepsilon }}_\mathrm{v,\alpha } = {\mathbb { F}}_\alpha \left[ \varvec{\sigma }_\mathrm{v, \alpha }\right] . \end{aligned}$$
(21)

Building upon the chemical strain and the viscous strains in each Maxwell element, an elastic strain is retrieved for both the equilibrium stiffness and each Maxwell element by

$$\begin{aligned} \varvec{\varepsilon }_\textrm{e,0} = \varvec{\varepsilon }- \varvec{\varepsilon }_\textrm{c}, \quad \varvec{\varepsilon }_\mathrm{e,\alpha } = \varvec{\varepsilon }- \varvec{\varepsilon }_\mathrm{v, \alpha }. \end{aligned}$$
(22)

The stress in each Maxwell element can now be given by

$$\begin{aligned} \varvec{\sigma }_\mathrm{v, \alpha } = {\mathbb { C}}_\alpha \left[ \varvec{\varepsilon }- \varvec{\varepsilon }_{\textrm{v},\alpha }\right] . \end{aligned}$$
(23)

Based on these quantities, the mechanical part of the free energy is considered to be a quadratic function of the elastic strain and expressed as [29]

$$\begin{aligned} \rho \psi _\textrm{m} = \frac{1}{2} (\varvec{\varepsilon }- \varvec{\varepsilon }_\textrm{c}) \cdot {\mathbb { C}}_0 \left[ \varvec{\varepsilon }- \varvec{\varepsilon }_\textrm{c}\right] + \frac{1}{2}\sum _{\alpha =1}^{N_\textrm{MW}} \left( \varvec{\varepsilon }- \varvec{\varepsilon }_{\textrm{v},\alpha }\right) \cdot {\mathbb { C}}_{\alpha }\left[ \varvec{\varepsilon }- \varvec{\varepsilon }_{\textrm{v},\alpha }\right] . \end{aligned}$$
(24)

Here, \({\mathbb { C}}_0 = 3 K_0 {\mathbb { P}}_1 + 2G_0 {\mathbb { P}}_2\) is the isotropic equilibrium stiffness with compression modulus \(K_0\) and shear modulus \(G_0\). \({\mathbb { P}}_1\) is the projector onto spherical tensors of rank 2.

Fig. 2
figure 2

a Schematic of the Flory–Huggins mean-field model to predict both enthalpy and entropy of mixing of a polymer with a solvent. b Schematic of the Maxwell element model used to describe the viscoelastic behavior of PA 6. Next to \(N_\textrm{ME}\) elements a reference stiffness in series with an \(\alpha _\textrm{c}\)-element, representing the isochoric swelling of PA 6, is attached in parallel

Full size image

Based on the potential relations in Eq. 15, the free energy given by Eqs. 18 and 24 results in

$$\begin{aligned} \begin{aligned} \varvec{\sigma }&= {\mathbb { C}}_0 \left[ \varvec{\varepsilon }- {\alpha _\textrm{c}} \Delta \tilde{c} {\varvec{ I}}\right] + \sum _{\alpha }^\mathrm{{N_{MW}}}{{\mathbb { C}}_{\alpha } \left[ \varvec{\varepsilon }- \varvec{\varepsilon }_\mathrm{{v},\alpha } \right] } \\ \mu&= \mu _0 + R \theta \left( \ln \left( \frac{3 {\alpha _\textrm{c}}\tilde{c}}{1 + 3 {\alpha _\textrm{c}} \tilde{c}}\right) + \frac{1}{1 + 3 {\alpha _\textrm{c}} \tilde{c}} + \frac{\chi }{\left( 1 + 3 {\alpha _\textrm{c}} \tilde{c}\right) ^2} \right) - \frac{{\alpha _\textrm{c}}}{{\vartheta _\textrm{max}}} \textrm{tr }( \varvec{\sigma } ). \end{aligned} \end{aligned}$$
(25)

To conclude the constitutive theory, we introduce the water flux which is proportional to the gradient in the chemical potential, with a proportionality factor \(m(\tilde{c}, \theta )\), that is interpreted as the mobility of water in the polymer network. This is summarized as

$$\begin{aligned} {\varvec{ j}}= - m(\tilde{c}, \theta ) \text {grad}\left( \mu \right) , \end{aligned}$$
(26)

with a scalar mobility \(m(\tilde{c}, \theta )\) being linear in \(\tilde{c}\). For increasing \(\tilde{c}\), experiments have shown that diffusion occurs at a faster rate [6, 10]. In [21], a proposal was made to capture this behavior by considering a change in mobility due to an increase of water molecules with a dimensionless function \(\gamma \left( \tilde{c}\right) \). We follow this approach such that the mobility is given by

$$\begin{aligned} m = \frac{D {\vartheta _\textrm{max}}}{R \theta } \gamma \left( \tilde{c}\right) , \quad \text {where}\quad \gamma \left( \tilde{c}\right) = 1 + \gamma _\textrm{S} \tilde{c} \end{aligned}$$
(27)

and the diffusion coefficient is D. This ansatz fulfills the dissipation inequality 16 and leads to an increasing mobility for increasing \(\tilde{c}\). For maximum water content, the mobility is \(1 + \gamma _\textrm{S}\) times its dry value.

2.5 Closed set of governing equations

For the implementation of the coupled set of governing equations it is advantageous to change the independent chemical variable from concentration to chemical potential. This has several reasons:

  • Solving the diffusion equation for \(\tilde{c}\) requires the solution of a partial differential equation (PDE) with a bounded solution variable as \(c \ge 0\). Enforcing this inequality constraint is either numerically costly [30] or impossible in commercial FEM packages.

  • The flux term in the diffusion equations is linear in the gradient of the chemical potential, itself being a function of the displacement gradient. This necessitates to approximate gradients of mechanical stresses on FEM meshes, which makes solutions susceptible to mesh sensitivity and less generally applicable. In addition, this results in the requirement of C2-continuous functions to interpolate the displacement field \({\varvec{ u}}\) as second order gradients have to be computed.

  • An open system, i.e. a system that is exposed to an atmosphere with a given ambient humidity \(\phi \), can not readily be simulated in a concentration based setting. This is due to the fact, that chemical potential and concentration are linked through the hydrostatic stress.

These reasons motivate a change in independent variables from concentration to chemical potential. To achieve this, we differentiate Eq. 25 (2) in time and use the result to express the rate of change in occupancy as a function of the rate of change in chemical potential. Introducing some abbreviations

$$\begin{aligned} \begin{aligned} k_0&= \ln \left( {\frac{3 {\alpha _\textrm{c}} \tilde{c}}{1 + 3 {\alpha _\textrm{c}} \tilde{c}}}\right) + \frac{1}{1 + 3 {\alpha _\textrm{c}} \tilde{c}} + \frac{\chi }{\left( 1 + 3 {\alpha _\textrm{c}} \tilde{c}\right) ^2}, \\ k_1&= \frac{\partial k_0}{\partial \tilde{c}} = \frac{1 - 6 {\alpha _\textrm{c}} (\chi - 1/2)\tilde{c}}{(3 {\alpha _\textrm{c}} \tilde{c} + 1)^3 \tilde{c}} ,\\ k_2&= R \theta k_1 + \frac{{\alpha _\textrm{c}}^2 \text {tr}\left( {\mathbb { C}}_0 \left[ {\varvec{ I}}\right] \right) }{{\vartheta _\textrm{max}}}, \end{aligned} \end{aligned}$$
(28)

allows us to find

$$\begin{aligned} \dot{\tilde{c}} = \frac{\dot{\mu } + {\alpha _\textrm{c}} \text {tr}\left( {\mathbb { C}}_0\left[ \dot{\varvec{\varepsilon }}\right] \right) / {\vartheta _\textrm{max}}}{k_2}. \end{aligned}$$
(29)

Combining the constitutive laws outlined in the previous subsection, the balance of linear momentum, Eq. 8, and inserting Eq. 29 in Eq. 7 allows us to arrive at the closed set of governing equations

$$\begin{aligned} \begin{aligned} \text {div}\left( \varvec{\sigma }{(\varvec{\varepsilon }, \tilde{c}, \varvec{\varepsilon }_{\textrm{v},\alpha })}\right) = \textbf{0}, \quad \frac{{\vartheta _\textrm{max}}}{k_2} \dot{\mu } = \text {div}\left( m \,\text {grad}\left( \mu \right) \right) - \frac{{\alpha _\textrm{c}} \text {tr}\left( {\mathbb { C}}_0 \left[ \dot{\varvec{\varepsilon }}\right] \right) }{k_2}, \end{aligned} \end{aligned}$$
(30)

where the constitutive equations for \(\varvec{\sigma }\) and m are defined in Eq. 25 (1) and Eq. 27. and \(k_2\) is given in Eq. 28. To complete the model, both initial and boundary values have to be specified. We denote initial conditions by a hat and boundary conditions by a bar, i.e. the initial chemical potential is \(\hat{\mu }\) and boundary displacements are given by \(\bar{{\varvec{ u}}}\). Both initial and boundary chemical potentials \(\hat{\mu }\) and \(\bar{\mu }\), when PA 6 is exposed to an atmosphere with a given relative humidity \(\phi \), are computed by [28]

$$\begin{aligned} \mu _{0, \textrm{vapor}} + R \theta \ln {\phi } = {\left\{ \begin{array}{ll} \hat{\mu }, \quad t = 0 \\ \bar{\mu }, \quad t > 0,\end{array}\right. } \end{aligned}$$
(31)

where \(\mu _{0, \textrm{vapor}}\) is the reference chemical potential of water in air. A short summary of the nomenclature for initial and boundary conditions used in all simulations of the subsequent Sect. 3 is given in Table 1. As the concentration is no longer a degree of freedom, no boundary or initial concentration is specified when the model is used. However, an initial concentration \(\hat{c}\) in wt\(\%\) follows from evaluating the initial displacements \(\hat{{\varvec{ u}}}\) and the initial chemical potential \(\hat{\mu }\) by means of Eq. 25 (2). The same holds for concentrations \(\bar{c}\) at the boundary, which follow for known boundary displacements \(\bar{{\varvec{ u}}}\) and boundary chemical potential \(\bar{\mu }\).

Table 1 Nomenclature for initial and boundary conditions
Full size table

2.6 Discussion of the model equations

Before identifying the model and implementing it in a commercial Finite-Element solver to study chemo-mechanically coupled deformation and drying processes in PA 6, we want to comment in the following on several of the assumptions that lead to the closed set of governing equations presented in Eq. 30. By this, the newly derived model can be compared with existing models to identify possible extensions and limitations of the model can be more clearly identified.

Balance equations. By the specific form of the balance of entropy given in Eq. 11, we assume that mass transport does not contribute to entropy flux and supply, which is often done in chemo-mechanically coupled theories [21, 22, 25]. However, instead of introducing the contribution of water to the mixture behavior in the balance of internal energy in Eq. 9, we could also have introduced a non-standard entropy flux due to water flux, as, e.g., done in [12, 18]. However, both approaches lead to identical constitutive relations when thermodynamics are introduced, as noted in [18, 25, 31]. Introducing the diffusing phases contribution in the balance of internal energy allows a clear interpretation of the chemical potential, as noted in [20]. Therefore, we prefer the version proposed in [20, 25].

Dependence on water concentration and temperature. As stated, many material parameters (such as glass transition temperature [14, 32, 33], stiffness [6], Poisson’s ratio [6], diffusion constant [3]) in PA 6 have been experimentally shown to be dependent on the moisture content, as well as temperature. However, we have neglected this in our model entirely, in order to arrive at a comparably simple model, still capturing the essence of the observed relaxation behavior, c.f. Fig. 1. As a side note we want to point out, that introducing non constant material parameters in the potential relations derived in Eq. 15 leads to an increasing complexity of the material laws. This can be studied by imagining the stiffness tensors of the equilibrium spring being a function of water concentration. When this dependency is introduced in the mechanical part of the free energy in Eq. 24 and the chemical potential is derived from it, a non-standard term being quadratic in the elastic strain is added to the chemical potential of water.

Isotropy of the constitutive laws. All material laws are assumed to be isotropic within our work. However, this does not represent all experimental observations, as in injection molded PA 6 specimens, an anisotropy of both stiffness constants as well as extension parameters has been shown [11, 13].

Reaction term. In the mass balance introduced in Eq. 7, no production term is introduced. This limits the derived model to studying water uptake or loss from the medium surrounding PA 6, but does not allow for simulating chemical reactions between PA 6 and water. Introducing a production term between water molecules and PA 6 in Eq. 7 allows to study, e.g., ageing effects [18] due to chemical reactions between both phases.

Extensions to the model. In the view of the authors, the presented model can be extended to consider anisotropic material, as, e.g., observed in [10, 11], to large deformations [21] or nonlinear viscoelastic models [34], without reasonable effort.

Heat contribution. Neglecting heat-storage contributions to the total free energy is inspired by numerous publications in the context of chemo-mechanical processes at constant temperature, see, e.g., [21, 22, 28]. However, considering non isothermal cases, e.g. along the lines of [21, 22], can be considered a valuable extension of the theory.

3 Applications

3.1 Parameter identification

Table 2 Chemical material parameters used in all simulations of this work. Parameters taken from literature are indicated by the source, the rest are identified in this work
Full size table
Table 3 Mechanical material parameters used in all simulations of this work. Parameters taken from literature are indicated by the source, the rest are identified in this work
Full size table
Fig. 3
figure 3

a Equilibrium water content c in \(\,\textrm{wt}\%\) when PA 6 is exposed to an environment with humidity content \(\phi \) for three Flory–Huggins parameters. At \(\phi = 50\,\%\textrm{RH}\) and \(\phi _\textrm{max}\), the model predictions are marked by a dot as these data points are used to identify the Flory–Huggins parameter \(\chi \) as outlined in the text. b Relaxation modulus over time for both an experimental and simulated result of a relaxation experiment conducted at \(80^\circ \,\textrm{C}\) under HC

Full size image

All mechanical and chemical material parameters of the model outlined above have to be identified in order to study water uptake or drying of PA 6 coupled to it’s deformation. All parameters used in subsequent simulations are summarized in Tables 2 and 3. Due to the modeling assumptions outlined above, most of the chemical parameters can be taken directly from literature. The only unknown chemical parameter is the Flory–Huggins parameter \(\chi \). To identify both \(\chi \) and the mechanical parameters we rely on two sets of data. We use sorption curves of PA 6 exposed to an atmosphere with given relative humidity \(\phi \) to determine \(\chi \). For the isotropic equilibrium stiffness \({\mathbb { C}}_0\) as well as Maxwell element parameters \(G_\alpha \) and \(\tau _\alpha \) we use the experimental results of a relaxation test conducted under HC at \(80^\circ \,\textrm{C}\), c.f. Fig. 1.

To identify the Flory–Huggins parameter \(\chi \), both the maximum concentration \(c_\textrm{max} = 0.09\) of water in PA 6 as well as the mass fraction \(c\in \left[ 2.5\,\textrm{wt}\%, 3\,\textrm{wt}\%\right] \) of water in PA 6 after conditioning in an atmosphere with \(\phi = 50\,\%\textrm{RH}\) are considered to be given [3]. We then determine \(\chi \) in such a way, that our model reproduces the maximum concentration \(c_\textrm{max}\). In addition, the mass fraction should result in a value from the interval \(c\in \left[ 2.5\,\textrm{wt}\%, 3\,\textrm{wt}\%\right] \) obtained experimentally. To this end, we equate the boundary condition of the chemical potential, Eq. 31, with the chemical potential of water in PA 6, Eq. 25 (2), and neglect mechanical contributions. We vary \(\chi \) and study both the water uptake at \(\phi = 50\,\%\textrm{RH}\) as well as \(\phi \approx 100 \, \%\textrm{RH}\). The results are shown in Fig. 3a, where the water uptake as a function of the relative humidity is depicted. Both the model prediction for \(\phi = 50\,\%\textrm{RH}\) and \(\phi = 100\,\%\textrm{RH}\) are depicted as dots. For \(\chi = 1.64\), both \(c(\phi = 50\,\%\textrm{RH}) \approx 3\,\textrm{wt}\%\) as well as \(c_\textrm{max} \approx 9\,\textrm{wt}\%\) are predicted with satisfying accuracy. The shape of the sorption curve, i.e., the equilibrium water content plotted against the relative humidity as predicted by our model was investigated experimentally in, e.g., [3, 33]. The curves determined published in these works qualitatively match the shape of our model curve.

The mechanical material parameters are the equilibrium compression and shear moduli \(K_0\) and \(G_0\) as well as the shear and relaxation moduli of the Maxwell elements \(G_\alpha , \tau _\alpha \). As no experimental evidence is at hand, the Poisson ratio of PA 6 is chosen to be \(\nu = 0.4\) [37]. All other parameters are determined by fitting to the experimentally obtained relaxation curve under HC at \(80^\circ ~\textrm{C}\) depicted in Fig. 3b. This is achieved by means of a least square fit of a one-dimensional linear viscoelastic model to the experimental data. The number of Maxwell elements \(N_\textrm{MW} = 5\) and the relaxation times \(\tau _\alpha \in \left[ 10^0, 10^1, 10^2, 10^3, 10^4\right] \, ~\mathrm{1/s}\) are previously fixed [7, 38, 39]. The optimization allows us to identify the equilibrium elastic modulus \(E_0\) as well as elastic moduli \(E_\alpha \) for the Maxwell elements. Using \(G_\alpha = E_\alpha / 2 / (1 - \nu )\) all shear moduli of the Maxwell elements are determined. The result of the determined relaxation curve is depicted in Fig. 3b, where the model prediction is compared to experimental results. As can be seen, the identified set of mechanical parameters allows us to capture the typical decrease in relaxation modulus R(t).

Before we proceed to conduct Finite-Element simulations of diffusion and coupled diffusion-deformation processes, we comment on two material parameters summarized in Tables 2 and 3.

Diffusion coefficient: An experimental investigation showed that the dependency of the diffusion coefficient of water in PA 6 strongly depends on temperature [3]. An explicit relation for this was proposed as

$$\begin{aligned} D = D_0 \text {exp}\left( - \frac{E_\textrm{s}}{k_\textrm{B} \theta }\right) , \end{aligned}$$
(32)

where \(E_\textrm{s} = 0.49\,~\textrm{eV}\) is an activation energy and \(k_\textrm{B}\) the Boltzmann constant. The diffusion coefficient \(D_{70^\circ \text {C}} = 3 \times 10^{-6}\,~\mathrm {mm^2 / s}\) was determined experimentally [3]. Using these measurements and Eq. 32, we determine a diffusion coefficient for water in PA 6 at \(80^\circ \textrm{C}\) as \(D_{80^\circ \textrm{C}} = 5\times 10^{-6}\,\mathrm{mm^2 / s}\).

Expansion coefficient: In [6, 11, 40] and [10] measurements were conducted to identify the swelling coefficient \({\alpha _\textrm{c}}\) leading to a volume change of PA 6 for increasing water content. To obtain the parameter, specimen are allowed to absorb the maximum amount of water and the change in length is measured. In the mentioned works, the swelling coefficient lies in the range \({\alpha _\textrm{c}} \in \left[ 0.018, 0.05\right] \). This range is explained by differing processing conditions of specimens [11], by differing volume to surface ratios [13] and by differing boundary conditions [6]. As no experiments were conducted in this study, we use a swelling factor of \({\alpha _\textrm{c}} = 0.045\). We note that this choice is coupled to the choice of the Flory–Huggins parameter \(\chi \) due to the fact that \({\alpha _\textrm{c}}\) also enters Eq. 25 (2). Thus, the choice of \({\alpha _\textrm{c}}\) and \(\chi \) are, in our model, coupled in such a way that the water uptake experimentally observed in [3] is influenced by them.

3.2 Finite-element solution of the coupled balance equations

In order to study diffusion deformation behavior of PA 6 relying on the model outlined in in the previous section, we rely on the commercial Finite-Element solver ABAQUS. To implement the derived model equations in ABAQUS, the similarity between the diffusion equation and the heat-transfer equation is recognized, i.e. both equations are partial differential equations with an instationary term on the left hand side and the Laplacian of the unknown field on the right hand side. This so called heat-transfer analogy was first used in the context of hydrogen diffusion in metal lattices, see, e.g., [41, 42], where the concentration was used as chemical degree of freedom. In this work, however, we rely upon the chemical potential as degree of freedom, as outlined above. That implies, that in our implementation scheme, the chemical potential is considered to be the temperature. This allows us to use either the ABAQUS built-in heat-transer step for pure diffusion without deformations or a coupled temperature-displacement step to solve the chemo-mechanically coupled process. Two subroutines are necessary, namely UMAT and UMATHT. In UMAT, the viscoelastic behavior coupled to chemical strains is computed, while in UMATHT water flux and the update of the left hand side of the diffusion equation have to be computed. Details of this newly proposed scheme are outlined in “Appendix”.

3.3 Drying of preconditioned specimens

Fig. 4
figure 4

a Water concentration c in \(\textrm{wt}\%\) along the thickness of three specimens for varying relative humidity \(\phi \) at \(80^\circ \textrm{C}\). All specimens are preconditioned to \(c = 3\,\textrm{wt}\%\) at an ambient humidity of \(\phi = 50\,\%\textrm{RH}\). Dashed lines depict the water concentration after the specimen is exposed to an environment with lower ambient humidity. Dotted lines show the concentration after \(1\,~\textrm{h}\) of drying while solid lines show the concentration after \(7\,~\textrm{h}\). b Water concentration c in \(\textrm{wt}\%\) along a single specimen’s thickness for \(\phi = 35\,\%\textrm{RH}\). The black arrow indicates increasing drying time

Full size image

We first use the derived and identified model to study the drying of PA 6 specimens preconditioned to \(c = 3\,\textrm{wt}\%\) at an ambient relative humidity of \(\phi = 50\,\%\textrm{RH}\) and \(\theta = 80^\circ \textrm{C}\). We therefore expose specimens to a varying ambient humidity \(\phi = \left[ 35, 25, 15\right] \%\textrm{RH}\) for \(7\,~\textrm{h}\), which corresponds to the total exposure time during the relaxation experiment depicted in Fig. 1. The specimen dimensions presented in Sect. 1 are used in the simulation. However, we want to point out, that [7, Tab. 10] documents slight variation in specimen thickness for each specimen, which results from the injection molding process. We focus solely on the drying process and, at this stage, do not solve the balance of linear momentum. Instead, we solve Eq. 30 (2) for given boundary and initial conditions using a heat-transfer step in ABAQUS. Initially, the chemical potential is homogeneous, \(\hat{\mu } = -2.04\times 10^3\, ~\mathrm{J / mol}\) based on Eq. 31 for \(\theta = 80^\circ ~\textrm{C}\) and \(\phi = 50\,\%\textrm{RH}\). This leads to an initial concentration of \(\hat{c} = 3\,\textrm{wt}\%\). For the drying process, the boundary chemical potential on all surfaces of the specimen is adjusted to \(\bar{\mu } = \left[ -3.08, -4.07, -5.57\right] \times 10^3\, ~\mathrm{J / mol}\) according to Eq. 31 for \(\phi = \left[ 35, 25, 15\right] \%\textrm{RH}\). Before that, in an initial simulation step, the preconditioned specimen is initialized in a homogeneous state. The boundary conditions are subsequently applied within \(0.3\,~\textrm{s}\), i.e. instantaneously in comparison with the duration of the experiment. However, we note that this choice is of \(0.3\,~\textrm{s}\) is arbitrary. This mimics the removal of the specimen from a controlled environment and its placement in a testing chamber with a lower ambient humidity. Subsequently, the water diffusion or drying is allowed to take place for \(7\,~\textrm{h}\). The specimen geometry is discretized using linear hexahedral DC3D8 elements with an edge length of \(0.5\,~\textrm{mm}\) in length and width direction and \(0.1\,~\textrm{mm}\) in thickness direction, which leads to 20 elements over the specimen thickness.

Results of the three simulations are depicted in Fig. 4a as concentration profiles along the thickness (z-direction) in the specimen center. Both the initial concentration profile after applying the corresponding chemical potential boundary condition (dashed lines), after \(1\,~\textrm{h}\) of drying (dotted lines), as well as the final profile (solid lines) after \(7\,~\textrm{h}\) of drying are depicted. As observed in previous publications, see, e.g., [6, 10], after \(1\,~\textrm{h}\) a significant concentration gradient occurs within the specimen. In fact, the lower the ambient humidity, the stronger the heterogeneity of the concentration along the specimen thickness. As is to be expected, a lower ambient humidity leads to a lower concentration of water close to the surface. After \(7\,~\textrm{h}\) of drying at \(80^\circ ~\textrm{C}\), the specimen is almost in equilibrium with it’s environment, regardless of the ambient humidity content. To study the water distribution as a function of time, the concentration profile at \(\phi = 35\,\%\textrm{RH}\) is depicted for increasing simulation time in Fig. 4b. The sharp initial concentration gradient along z flattens out with increasing exposure time, as the system moves towards an equilibrium between the boundary and initial chemical potentials.

In addition to the concentration heterogeneity along the specimen thickness, the drying simulation allows to study the weight loss due to drying during the experiment. In [7], weight loss of a preconditioned specimen tested in a relaxation test at \(80^\circ ~\textrm{C}\) at a relative humidity of \(\phi \approx 35\,\%\textrm{RH}\) is reported to be \(- 1.115\,\%\). In Table 4 results from the three drying simulations are compared to the experimentally obtained mass. To this end, the mean water concentration \(c_\textrm{mean}\) in \(\textrm{wt}\%\) is computed for the entire specimen, i.e.

$$\begin{aligned} c_\textrm{mean} = \frac{1}{V}\sum _{\alpha } c_\alpha v_\alpha , \end{aligned}$$
(33)

where \(c_\alpha \) is the concentration at integration point \(\alpha \), \(v_\alpha \) its volume and V denotes the volume of the entire specimen. The mass of water then follows as \(m_\textrm{w} = c_\textrm{mean} m_\textrm{P}\), c.f. Eq. 1, where \(m_\textrm{P}\) is the mass of the PA 6 specimen. The result from the simulation with a relative humidity \(\phi = 35\,\%\textrm{RH}\) is close to the experimentally obtained values, which allows us to conclude, that the relative humidity during the relaxation experiment without HC is indeed \(\phi = 35\,\%\textrm{RH}\). We consider the slight deviation between experiment and simulation to be due to the fact that the exact shape of the specimen used in the experiments scatters [7, Tab. 10] due to the injection molding process, which is not reproduced in the simulations.

To summarize, the drying simulation does lead to a mass loss in close agreement with the one observed in experiments. In addition, the heterogeneous water profile along the specimen thickness is in qualitative agreement with previously published simulative and experimental studies. We now proceed to study the model response in a relaxation experiment.

Table 4 The initial total mass before testing and final total mass after testing of the specimens (i.e. PA 6 and water) is summarized for both experiments (no HC and HC) and the simulations for varying ambient humidity levels. The relative deviation \(\Delta m = (m_\textrm{end} - m_\textrm{initial}) / m_\textrm{initial}\) is also displayed
Full size table

3.4 Comparison of relaxation experiments and simulation results

Fig. 5
figure 5

Relaxation modulus for two relaxation experiments conducted on PA 6 at \(80^\circ ~\textrm{C}\). Both specimens were conditioned at a humidity level of \(\phi = 50\,\%\textrm{RH}\). In the HC experiment, a controlled humidity level of \(\phi = 50\,\%\textrm{RH}\) was enforced, while the other specimen was tested without humidity control. In addition, the results of Finite-Element simulations based on the model outlined in this publications are depicted

Full size image

Finally we use the fully chemo-mechanically coupled model to study relaxation experiments and compare numerically obtained results with the experimentally obtained data depicted in Fig. 1. We therefore reproduce the simulation setup outlined in [7]. The geometry of the specimen is the same as described above. However, as we consider four nodal degrees of freedom, a coupled temperature-displacement step is used to model the coupling of the drying process to the viscoelastic behavior of PA 6 in ABAQUS. We use linear hexahedral C3D8T elements with an identical size to the one used in the drying simulation. In the experimental setup, the preconditioned specimen is placed in the testing chamber of the DMA. The test protocol starts with a rest period of \(1\,~\textrm{h}\) during which the length of the specimen is recorded continuously and the strain amplitude is kept at \(\varepsilon _0 = 0\,\%\). After the rest period, a strain \(\varepsilon _0 = 0.1\,\%\) is applied with a rate of \(\dot{\varepsilon }_0 = \,~\mathrm{1/s}\). This strain is subsequently held constant for \(6\,~\textrm{h}\). To mimic this setup in the simulation, we apply an initial chemical potential of \(\hat{\mu } = -2.04\times 10^3\, ~\mathrm{J / mol}\) which leads to an initially homogeneous water concentration of \(\hat{c} = 3\,\textrm{wt}\%\) analogously to the drying simulation. We use this initial concentration as the swelling free normalized concentration \(\tilde{c}_0 = \hat{c} /c_\textrm{max}\). The specimen surface is then exposed to a boundary chemical potential \(\bar{\mu } = -3.08 \times 10^3\, ~\mathrm{J / mol}\). This boundary condition is ramped up in \(0.3\,~\textrm{s}\) and held constant for \(1\,~\textrm{h}\). As above, this mimics the placing of the specimen in the testing chamber and the rest period. During this time, one end of the specimen is restrained from moving, i.e. \(\bar{{\varvec{ u}}} = \textbf{0}\). Due to the onset of drying, the length of the specimen decreases, as the concentration falls below the swelling free concentration. After the rest period, a displacement \(\bar{{\varvec{ u}}}\) leading to a strain of \(\varepsilon = 0.1\,\%\) is applied with the same rate as in the experiment, which is held constant for \(6\,~\textrm{h}\).

The result of the simulation is depicted in Fig. 5. The experiment conducted in a humidity controlled environment is, as shown during the parameter identification, reproduced accurately. In addition, the simulation of a relaxation experiment without HC closely matches the experimental results. Especially the initial decline and subsequent increase in relaxation modulus R(t) during the first \(4\,~\textrm{h}\) of simulation time matches the experimentally obtained curve. In fact, the slope of increasing R(t) in simulation and experiment are almost identical. This is, in our simulation framework, entirely due to the drying of the specimen. As shown in Fig. 4b, the mean water concentration decreases significantly due to the onset of drying. This leads to a compressive chemical strain as the concentration falls below the swelling free concentration \(\tilde{c}_0\). Due to the applied mechanical boundary conditions, \(\varvec{\varepsilon }\) is constant in the specimen and Eq. 25 (1) therefore predicts an increasing stress and relaxation modulus R(t). After about \(5\,~\textrm{h}\) in the relaxation experiment (which is equivalent to \(6\,~\textrm{h}\) of drying), the specimen is almost dry (c.f. Fig. 4b) and only negligible changes in chemical strains occur. This leads to a slight flattening of the relaxation modulus R(t), and the simulation results deviate from the experimentally obtained curve which shows a further increase in R(t).

3.5 Discussion of the results

Before concluding this work, several remarks regarding the results are given, in order to make the results and their limitations more clear:

Chemical parameters. The chosen chemical part of the free energy, based on the Flory–Huggins theory, introduces only a single unknown parameter. This interaction parameter was identified by studying the absorption of water exposed to a humid atmosphere as depicted in Fig. 3a. All other chemical parameters in the model are taken from literature.

Mass loss. As shown during the drying simulation, c.f. Table 4, the mass loss of the PA 6 specimen observed in the experiment is reproduced based on the derived chemical model.

Relaxation modulus. When the fully chemo-mechanically coupled model is used to study the behavior in a relaxation experiment, only the drying of the PA 6 specimen leads to an increase in the relaxation modulus R(t). The experimentally observed increase in R(t) is reproduced by the chemo-mechanically coupled model derived in this work.

Glass transition. As outlined in Sect. 2, both experimental [13, 32] and numerical studies [14, 33] indicate that the glass transition temperature \(\theta _\textrm{g}\) of PA 6 strongly varies with the water content. This is due to an increasing chain mobility caused by the presence of water molecules. This fact is not considered in our model. However, the model outlined in [14] can be used as a starting point to include such a transition.

Temperature dependency. In this work, we consider the temperature to be constant at all times. In order to incorporate non isothermal cases, the derivation of a heat-equation in a thermo-chemo-mechanical setting would be required. This has been done in other works, see, e.g., [21, 22]. In addition, each node in the Finite-Element scheme would have 5 degrees of freedom, i.e. three displacement degrees of freedom, a chemical one and temperature. This would require a more involved implementation scheme, relying on the UEL of ABAQUS.

Statistical relevance. In experimental studies on PA 6, such as [6, 10, 13] and many other, scatterings have been observed in both parameters and material response to applied loads and boundary conditions. Due to the fact that our model predictions are compared with results of only a single specimen, no statement regarding the statistical relevance of our data can be given. To quantify this, further experimental investigations are necessary in future work.

4 Conclusion and outlook

In the present work, a chemo-mechanically coupled continuum model is derived with the goal of predicting changes in water concentration in PA 6 during mechanical testing using Finite-Element simulations and its influence on mechanical behavior. The main results are:

  • The coupling between chemical and mechanical fields is derived by means of a thermodynamically consistent constitutive theory. To this end, a free energy for the mixture of water and PA 6 is additively decomposed into mechanical and chemical parts. While the former part is based on standard linear-viscoelastic Maxwell elements, the chemical part relies on the Flory–Huggins theory of mixing of monomers with solvent molecules. Thereby, a parameter for the interaction during mixing is introduced. The coupling of chemical fields to mechanical fields arises due to chemical strains, while the mechanical stress leads to a water flux and thus couples mechanical to chemical fields.

  • The derived model is implemented in the commercial Finite-Element program ABAQUS, relying on a newly proposed version of the heat-transfer analogy, exploiting the similarity of heat-equation and diffusion equation. Parameters for the chemical part of the model are mostly taken from literature, while the Flory–Huggins interaction parameter is identified to match experimentally obtained water uptake curves of polyamide exposed to humid environments. The Maxwell elements are identified by fitting to an experiment, where no water diffusion is involved.

  • The identified model is capable of reproducing mass loss due to drying as well as an increasing relaxation modulus R(t) during a prolonged relaxation test, where the specimen exhibits significant drying.

In future work, the authors plan to extend the outlined model by incorporating parameter changes depending on the local water concentration, inspired by [14]. In this setting, all parameters depend on the difference of current temperature \(\theta \) and glass transition temperature \(\theta _\textrm{g}(c)\), which is itself a function of local water content c. Such an approach would, in the opinion of the authors, not only increase the accuracy of the model predictions, but also allow the usage of the model at other temperatures levels or in settings with non constant temperature. Furthermore, an extension to account for nonlinear viscoelastic behavior can be incorporated, see, e.g., [34].