Setting of forced oscillations of viscoelastic coating

Abstract

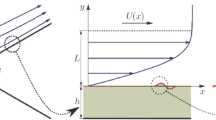
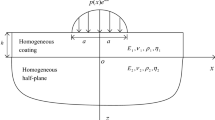
This paper formulates the problem of determining the response of a flat monolithic viscoelastic coating to traveling pressure and shear waves in two-dimensional formulation. Examples of corresponding numerical computations for coating parameters typical for laboratory experiments on the reduction in turbulent viscous drag are presented. The coating parameters are demonstrated, which provide the setting time less than one period of the forced oscillations. It is shown that the time to reach the regime is practically the same for both the shear and the pressure forcing, the time being increased with a decrease in relative thickness of the coating, as well as with an increase in the forcing frequency, particularly at frequencies above the first resonance frequency.

Appendix: Spatial discretization

We construct a nonuniform grid in $0 \le y \le 1$ with nodes $y_{j} = (x_{j}-1)/2$, $j=0, \dots n+1$, where $x_{j}$, $j=1, \dots n$, are the roots of the derivatives of the Legendre polynomials of degree $n+1$ and $x_{0}=-1$ and $x_{n+1}=1$ (Gauss–Lobatto nodes) [26]. Recall that ${\varvec{\xi }}$ and ${\varvec{\eta }}$ are the $n+1$—component vector columns containing, respectively, the values of the tangent and normal components of the displacement at all nodes $y_{j}$, excluding the boundary node $y=0$ due to the zero boundary conditions. In addition, let $D_{y}$ and $D_{yy}$ be the square matrices of order $n+2$, which are discrete analogs of the first and second derivative operators on y at nodes $y_{j}$, $j=0, \dots n+1$, respectively. We compute these matrices using the algorithms described in [35]. Given the zero boundary conditions for the displacement components at node $y_{0}=0$, we discard the first column and the first row in $D_{y}$. In the resulting matrix, denote the first n rows by $D_{1}$, and the last one by $d_{1}$. Similarly, we obtain a matrix $D_{2}$ based on $D_{yy}$. The matrices $D_{1}$ and $D_{2}$ of size $n \times n+1$ are the discrete analogs of the first and second derivative operators at nodes $y_{j}$, $j=1, \dots n$, respectively, for the displacements given at nodes $j=1, \dots n+1$, and the $n+1$-element row $d_{1}$ is a discrete analogue of the first derivative operator at node $y_{n+1}=1$ for displacements given at nodes $j=1, \dots n+1$.

Using the differentiation matrices, the spatially approximated equations (13) can be written as follows:

$$\begin{aligned} \begin{aligned} \hat{I} \frac{{\text {d}}^{2} {\varvec{\xi }}}{{\text {d}} t^{2}} =&\left( 2\mathrm {i}\omega \hat{I} + \theta L_{tl} \right) \frac{{\text {d}} {\varvec{\xi }}}{{\text {d}} t} + \mathrm {i}\theta k c_{lt} D_{1} \frac{{\text {d}} {\varvec{\eta }}}{{\text {d}} t} \\&+ \left( \omega ^{2} \hat{I} + (1 - \mathrm {i}\theta \omega ) L_{tl} \right) {\varvec{\xi }} + \mathrm {i}(1 - \mathrm {i}\theta \omega ) k c_{lt} D_{1} {\varvec{\eta }}, \\ \hat{I} \frac{{\text {d}}^{2} {\varvec{\eta }}}{{\text {d}} t^{2}} =\,&\mathrm {i}\theta k c_{lt} D_{1} \frac{{\text {d}} {\varvec{\xi }}}{{\text {d}} t} + \left( 2\mathrm {i}\omega \hat{I} + \theta L_{lt} \right) \frac{{\text {d}} {\varvec{\eta }}}{{\text {d}} t}\\&+ \mathrm {i}(1 - \mathrm {i}\theta \omega ) k c_{lt} D_{1} {\varvec{\xi }} + \left( \omega ^{2} \hat{I} + (1 - \mathrm {i}\theta \omega ) L_{lt} \right) {\varvec{\eta }}, \end{aligned} \end{aligned}$$

where $\hat{I}$ is the matrix obtained from the identity matrix of order $n+1$ after discarding its last row, $c_{lt} = c_{l}^{2}-c_{t}^{2}$, and $L_{tl} = c_{t}^{2} D_{2} - k^{2} c_{l}^{2} \hat{I}$ and $L_{lt} = c_{l}^{2} D_{2} - k^{2} c_{t}^{2} \hat{I}$. For the boundary conditions (15) at $y=1$, we have:

$$\begin{aligned} \begin{aligned} 0&= \theta c_{t}^{2} d_{1} \frac{{\text {d}} {\varvec{\xi }}}{{\text {d}} t} + \mathrm {i}\theta k c_{t}^{2} i_{1} \frac{{\text {d}} {\varvec{\eta }}}{{\text {d}} t} + (1 - \mathrm {i}\theta \omega ) c_{t}^{2} d_{1} {\varvec{\xi }} + \mathrm {i}(1 - \mathrm {i}\theta \omega ) k c_{t}^{2} i_{1} {\varvec{\eta }} - S, \\ 0&= \mathrm {i}\theta k \left( c_{l}^{2} - 2 c_{t}^{2}\right) i_{1} \frac{{\text {d}} {\varvec{\xi }}}{{\text {d}} t} + \theta c_{l}^{2} d_{1} \frac{{\text {d}} {\varvec{\eta }}}{{\text {d}} t} + \mathrm {i}(1 - \mathrm {i}\theta \omega ) k \left( c_{l}^{2} - 2 c_{t}^{2}\right) i_{1} {\varvec{\xi }} + (1 - \mathrm {i}\theta \omega ) c_{l}^{2} d_{1} {\varvec{\eta }} - P, \end{aligned} \end{aligned}$$

where $i_{1}$ is the last row of the identity matrix of order $n+1$.

Thus, Eqs. (13) approximated in space, taking into account the boundary conditions (14), (15), can be written as system (19) with matrices

$$\begin{aligned} M = \left[ \begin{array}{cc} \hat{I} &{}\quad 0\\ 0 &{}\quad 0 \\ 0 &{}\quad \hat{I}\\ 0 &{}\quad 0 \end{array} \right] , \; A = \left[ \begin{array}{cc} L_{tl} &{}\quad \mathrm {i}k c_{lt} D_{1}\\ c_{t}^{2} d_{1} &{}\quad \mathrm {i}k c_{t}^{2} i_{1}\\ \mathrm {i}k c_{lt} D_{1} &{}\quad L_{lt}\\ \mathrm {i}k \left( c_{l}^{2} - 2 c_{t}^{2}\right) i_{1} &{}\quad c_{l}^{2} d_{1} \end{array} \right] , \; f = \left[ \begin{array}{r} 0\\ -S\\ 0\\ -P \end{array} \right] . \end{aligned}$$