1 Introduction

Peridynamics (PD) has been introduced by Silling [1] to overcome the problems and limitations of classical continuum mechanics (CCM). Amongst these problems, the governing equations of CCM are in partial differential equation form which are not valid along crack surfaces since the displacement field is not continuous at those locations. On the other hand, the governing equations of PD are in integro-differential equation form and do not contain any spatial derivatives. Therefore, they are always applicable regardless of discontinuity in the displacement field. Moreover, CCM does not have a length scale parameter. Hence, it cannot represent non-classical material behaviour which usually appears at micro-scale. Instead, peridynamics is a non-local continuum mechanics formulation and it has a length scale parameter called horizon. As mentioned by dell’Isola et. al. [2, 3], the origins of peridynamics go back to Piola.

Since its introduction, there has been a rapid progress in peridynamics research. Since it is a general continuum mechanics formulation, any material system can be analysed by using peridynamics including metals [4], composites [5,6,7], polycrystalline materials [8,9,10], concrete [11], ceramics [12], ice [13], graphene [14], etc. It is also possible to perform fatigue analysis in PD theory [15]. Moreover, any type of material behaviour can be incorporated, such as plasticity [16], viscoelasticity [17], and viscoplasticity [18]. In addition, PD can be used for multiphysics analysis since peridynamics equations are also available for thermal field [19, 20], electrical field [21], diffusion field [22,23,24,25], porous flow [26], etc. PD can also be used for fluid flow simulations [27, 28]. Peridynamic formulations for simplified structures, including beams [29, 30], plates [31] and shells [32], are also available in the literature. With the advancement of additive manufacturing technologies, fabrication of complex materials such as microstructured materials [33,34,35,36,37,38,39,40,41,42,43,44] is possible. PD theory can be a suitable alternative for the analysis of microstructured materials.

Analytical solutions of PD equations are not usually possible. Therefore, numerical techniques, especially meshless method, are widely utilised. In majority of the publications in the literature, uniform discretisation is used for spatial discretisation. Although uniform discretisation is simple to implement, for certain applications, it unnecessarily increases computational time since only some parts of the solution domain require a finer discretisation and other parts can be discretised by using a coarser grid. Hence, non-uniform discretisation can be very beneficial in terms of computational time. In addition to non-uniform discretisation, horizon size can also be different at different parts of the solution domain either to reduce the computational time or to capture correct physics of the problem. However, this requires extra care especially to satisfy conservation laws. To accomplish these requirements, Ren et. al. [45, 46] introduced dual-horizon peridynamics concept. In this study, we present a different way to derive dual-horizon peridynamics formulation for state-based peridynamics by utilising Euler–Lagrange equations. Moreover, application of boundary conditions and determination of surface correction factors are also explained. Finally, the current formulation is verified by considering two benchmark problems including plate under tension and vibration of a plate.

2 Dual-horizon peridynamics formulation based on Euler–Lagrange equation

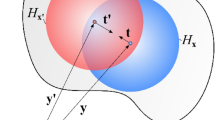
In this study, dual-horizon peridynamics formulation is derived based on Euler–Lagrange equation. Peridynamics is a non-local continuum mechanics formulation. Therefore, the body is composed of small volumes called “material points” as shown in Fig. 1.

Fig. 1
figure 1

Material points and the horizon concept [4]

Full size image

The equation of motion of a particular material point k at location \(\mathbf{x }_{(k)} \) in the initial configuration can be obtained by using Euler–Lagrange equation as [4]

$$\begin{aligned} \frac{d}{dt}\left( {\frac{\partial L}{\partial {{\dot{\mathbf{u }}}}_{(k)} }} \right) -\frac{\partial L}{\partial \mathbf{u }_{(k)} }=0 \end{aligned}$$
(1)

where L is the Lagrangian which represents the difference between the total kinetic energy of the body and the total potential energy of the body, t represents time, \(\mathbf{u }_{(k)} \) and \({{\dot{\mathbf{u }}}}_{(k)} \) are the displacement and velocity of the material point k. The total kinetic energy of the body can be calculated by summing the kinetic energies of all material points in the body as

$$\begin{aligned} T=\sum \limits _{i=1}^ {\frac{1}{2}} \rho _{(i)} {{\dot{\mathbf{u }}}}_{(i)} \cdot {{\dot{\mathbf{u }}}}_{(i)} V_{(i)} \end{aligned}$$
(2)

where \(\rho \) is the density and \(V_{(i)} \) is the volume of the material point i. On the other hand, the total potential energy of the body is the difference between the total strain energy of the body and the energy due to external forces which can be written as

$$\begin{aligned} U=\sum \limits _{i=1} {W_{(i)} } \,V_{(i)} -\sum \limits _{i=1} {\left( {\mathbf{b }_{(i)} \cdot \mathbf{u }_{(i)} } \right) } \,V_{(i)} \end{aligned}$$
(3)

where W is the strain energy density which can be defined for the material point k as

$$\begin{aligned} W_{(k)} =\frac{1}{2}\sum \limits _{j=1}^{N_{k} } {\frac{1}{2}\left( {\omega _{(k)(j)} \left( {\mathbf{y }_{(1^{k})} -\mathbf{y }_{(k)} ,...,\mathbf{y }_{(N_{k}^{k})} -\mathbf{y }_{(k)} } \right) +\omega _{(j)(k)} \left( {\mathbf{y }_{(1^{j})} -\mathbf{y }_{(j)} ,...,\mathbf{y }_{(N_{j}^{j})} -\mathbf{y }_{(j)} } \right) } \right) } \,V_{(j)}\nonumber \\ \end{aligned}$$
(4)

with \(\omega \) being the micropotential arising due to interaction between material points k and j, \(N_{k}\) and \(N_{j}\) represent the number of family members within the horizon of material points k and j, respectively, and \(\mathbf{y }\) is the position of the material point in the deformed configuration. Note that micropotentials \(\omega _{(k)(j)}\) and \(\omega _{(j)(k)}\) do not need to be equal to each other since they have a different domain of influence, horizon (Fig. 1). In Eq. (3), \(\mathbf{b }\) is the body load acting on a particular material point. Substituting Eqs. (2) and (3) in Euler–Lagrange equation given in Eq. (1), the equation of motion of the material point kcan be obtained as

$$\begin{aligned} \rho _{(k)} {{\ddot{\mathbf{u }}}}_{(k)} =\sum \limits _{j=1}^{N_{k} } {\left( {\mathbf{t }_{(k)(j)} -\mathbf{t }_{(j)(k)} } \right) } \,V_{(j)} +\mathbf{b }_{(k)} \end{aligned}$$
(5)

where peridynamic forces given in Eq. (5) can be written in terms of micropotentials between interacting material points, \(\omega \), as

$$\begin{aligned} \mathbf{t }_{kj}= & {} \frac{1}{2}\frac{1}{V_{j} }\left( {\sum \limits _{i=1}^{N_{k} } {\frac{\partial \omega _{ki} }{\partial \left( {\mathbf{y }_{j} -\mathbf{y }_{k} } \right) }V_{i} } } \right) \end{aligned}$$
(6)
$$\begin{aligned} \mathbf{t }_{jk}= & {} \frac{1}{2}\frac{1}{V_{k} }\left( {\sum \limits _{i=1}^{N_{j} } {\frac{\partial \omega _{ji} }{\partial \left( {\mathbf{y }_{k} -\mathbf{y }_{j} } \right) }V_{i} } } \right) . \end{aligned}$$
(7)

For ordinary state-based peridynamics, peridynamic forces can be rewritten for variable size horizon case as

$$\begin{aligned} \mathbf{t }_{kj}= & {} \alpha _{kj} \left( {\frac{2ad\delta _{k} }{\left| {\mathbf{x }_{j} -\mathbf{x }_{k} } \right| }\theta _{k} \left( {\mathbf{x }_{k} ,t} \right) +b\,s_{kj} } \right) \,\frac{\mathbf{y }_{j} -\mathbf{y }_{k} }{\left| {\mathbf{y }_{j} -\mathbf{y }_{k} } \right| } \end{aligned}$$
(8)
$$\begin{aligned} \mathbf{t }_{jk}= & {} \alpha _{jk} \left( {\frac{2ad\delta _{j} }{\left| {\mathbf{x }_{j} -\mathbf{x }_{k} } \right| }\theta _{j} \left( {\mathbf{x }_{j} ,t} \right) +b\,s_{kj} } \right) \,\frac{\mathbf{y }_{k} -\mathbf{y }_{j} }{\left| {\mathbf{y }_{k} -\mathbf{y }_{j} } \right| } \end{aligned}$$
(9)

with

$$\begin{aligned} \alpha _{kj}= & {} \left\{ {{\begin{array}{*{20}c} {1,\omega _{kj} \ne 0} \\ {0,\omega _{kj} =0} \\ \end{array} }} \right. \end{aligned}$$
(10)
$$\begin{aligned} \alpha _{jk}= & {} \left\{ {{\begin{array}{*{20}c} {1,\omega _{jk} \ne 0} \\ {0,\omega _{jk} =0} \\ \end{array} }} \right. \end{aligned}$$
(11)

and the stretch term can be expressed as

$$\begin{aligned} s_{kj} =\frac{\left| {\mathbf{y }_{j} -\mathbf{y }_{k} } \right| -\left| {\mathbf{x }_{j} -\mathbf{x }_{k} } \right| }{\left| {\mathbf{x }_{j} -\mathbf{x }_{k} } \right| }. \end{aligned}$$
(12)

The peridynamic dilatation in Eqs. (8,9) for the material points k and j is defined as

$$\begin{aligned} \theta _{k}= & {} \sum \limits _{i=1}^{N_{k} } {d\delta _{k} s_{ki} V_{i} } \end{aligned}$$
(13)
$$\begin{aligned} \theta _{j}= & {} \sum \limits _{i=1}^{N_{j} } {d\delta _{j} s_{ji} V_{i} }. \end{aligned}$$
(14)

The parameters a, b and d are peridynamic parameters which can be expressed in terms of material constants of CCM for an isotropic material as

$$\begin{aligned} a= & {} \frac{1}{2}\left( {\kappa -2\mu } \right) \end{aligned}$$
(15)
$$\begin{aligned} b= & {} \frac{6\mu }{\pi h\delta ^{4}} \end{aligned}$$
(16)
$$\begin{aligned} d= & {} \frac{2}{\pi h\delta ^{3}} \end{aligned}$$
(17)

with \(\kappa \) and \(\mu \) being the bulk and shear moduli, respectively, h is the thickness of the two-dimensional domain and \(\delta \) is the horizon size of a particular material point.

Fig. 2
figure 2

Non-uniform discretisation with different horizon sizes

Full size image

Note that in Eqs. (10) and (11), the micropotential being zero means one of the material points is not within the horizon of the other material point. As shown in Fig. 2, although the material point with a blue (smaller) horizon is inside the horizon of the material point with red (larger) horizon, the material point with a red horizon is outside of the horizon of the material point with a blue horizon.

For non-ordinary state-based peridynamics, peridynamic forces for variable horizon can be expressed as

$$\begin{aligned} \mathbf{t }_{kj}= & {} \alpha _{kj} \left\{ {\mathbf{P }\left[ {\mathbf{x }_{k} } \right] \mathbf{K }^{-1}\left[ {\mathbf{x }_{k} } \right] \left( {\mathbf{x }_{j} -\mathbf{x }_{k} } \right) } \right\} \end{aligned}$$
(18)
$$\begin{aligned} \mathbf{t }_{jk}= & {} \alpha _{jk} \left\{ {\mathbf{P }\left[ {\mathbf{x }_{j} } \right] \mathbf{K }^{-1}\left[ {\mathbf{x }_{j} } \right] \left( {\mathbf{x }_{k} -\mathbf{x }_{j} } \right) } \right\} \end{aligned}$$
(19)

where \(\mathbf{P }\) is the first Piola–Kirchhoff stress tensor. The shape tensor, \(\mathbf{K }\), for the material points k and j is defined as

$$\begin{aligned}&\mathbf{K }\left[ {\mathbf{x }_{k} } \right] =\sum \limits _{i=1}^{N_{k} } {\left( {\mathbf{x }_{i} -\mathbf{x }_{k} } \right) \otimes \left( {\mathbf{x }_{i} -\mathbf{x }_{k} } \right) V_{i} } \end{aligned}$$
(20)
$$\begin{aligned}&\mathbf{K }\left[ {\mathbf{x }_{j} } \right] =\sum \limits _{i=1}^{N_{j} } {\left( {\mathbf{x }_{i} -\mathbf{x }_{j} } \right) \otimes \left( {\mathbf{x }_{i} -\mathbf{x }_{j} } \right) V_{i} } \end{aligned}$$
(21)

where the symbol \(\otimes \) represents the dyadic product. Note that non-ordinary state-based formulation can suffer from the zero-energy mode problem. In this study, the zero-energy mode problem is prevented by following the approach given in Silling [47].

For bond-based peridynamics, peridynamic force between two interacting material points is only influenced by the motion of these two material points. In other words, only micropotentials which belong to both interacting points exist, i.e. \(\omega _{ik} =\omega _{ki} =0,\,\text{ if }\,i\ne j\). Therefore, peridynamic forces given in Eqs. (6) and (7) can be simplified as

$$\begin{aligned}&\mathbf{t }_{kj} =\frac{1}{2}\left( {\frac{\partial \omega _{kj} }{\partial \left( {\mathbf{y }_{j} -\mathbf{y }_{k} } \right) }} \right) \end{aligned}$$
(22)
$$\begin{aligned}&\mathbf{t }_{jk} =\frac{1}{2}\left( {\frac{\partial \omega _{jk} }{\partial \left( {\mathbf{y }_{k} -\mathbf{y }_{j} } \right) }} \right) . \end{aligned}$$
(23)

These forces can also be expressed as

$$\begin{aligned}&\mathbf{t }_{kj} =\alpha _{kj} \left( {\frac{c}{2}\,s_{kj} } \right) \,\frac{\mathbf{y }_{j} -\mathbf{y }_{k} }{\left| {\mathbf{y }_{j} -\mathbf{y }_{k} } \right| } \end{aligned}$$
(24)
$$\begin{aligned}&\mathbf{t }_{jk} =\alpha _{jk} \left( {\frac{c}{2}\,s_{kj} } \right) \,\frac{\mathbf{y }_{k} -\mathbf{y }_{j} }{\left| {\mathbf{y }_{k} -\mathbf{y }_{j} } \right| } \end{aligned}$$
(25)

where c is the bond constant which can be written for an isotropic material and two-dimensional domain as

$$\begin{aligned} c=\frac{9E}{\pi h\delta ^{3}} \end{aligned}$$
(26)

with E being the elastic modulus.

3 Boundary condition

Since PD equations are in the form of integro-differential equations, the way to apply boundary conditions in PD is different than CCM. Boundary conditions in PD are applied through volumes, and these volumes are sometimes created as fictitious regions outside the actual solution domain. In this study, boundary volumes are chosen as fictitious regions, \(\mathfrak {R}_{f} \), outside of the main solution domain, \(\mathfrak {R}\), as shown in Fig. 3, which is an effective procedure suggested in [14].

3.1 Displacement constraints

In this study, the size of the fictitious region is specified as twice the horizon size, i.e. \(2\delta \), and only two-dimensional problems are considered. However, the presented approach can be easily extended to three-dimensional models. The prescribed boundary value of the displacements \(U^{*}\) and \(V^{*}\) in the \(x-\) and \(y-\) directions can be applied by specifying the displacements of the material points in the fictitious region, \(u_{f}\) and \(v_{f}\), in terms of displacements of the material points in the actual domain, u and v, as (Fig. 3)

$$\begin{aligned}&u_{f} \left( {x_{f} ,y_{f} ,t+\Delta t} \right) =2U^{*}\left( {x^{*},y^{*},t+\Delta t} \right) -u\left( {x,y,t} \right) \end{aligned}$$
(27)
$$\begin{aligned}&v_{f} \left( {x_{f} ,y_{f} ,t+\Delta t} \right) =2V^{*}\left( {x^{*},y^{*},t+\Delta t} \right) -v\left( {x,y,t} \right) . \end{aligned}$$
(28)
Fig. 3
figure 3

Application of displacement constraints in PD introducing a fictitious region [14]

Full size image

3.2 Traction boundary conditions

Traction boundary conditions can also be applied similar to displacement constraints by using a fictitious region as shown in Fig. 4. The displacements of the material points in the fictitious region depend on the unit normal of the boundary on which the traction boundary condition, \(\sigma _{ij}^{*} ,\text{ with }\,i,j=x,y\), is exerted.

Fig. 4
figure 4

Application of traction boundary conditions on a surface with a normal vector (a) in the x-direction and (b) in the y-direction in PD introducing a fictitious region [14]

Full size image

For the traction boundary with a unit normal in the \(x-\)direction, they can be written as [14]

$$\begin{aligned}&u_{f} \left( {x_{f} ,y_{f} ,t+\Delta t} \right) =\left[ {\frac{\sigma _{xx}^{*} \left( {1-\upsilon ^{2}} \right) }{E}-\upsilon \frac{v\left( {x,y^{+},t} \right) -v\left( {x,y^{-},t} \right) }{y^{+}-y^{-}}} \right] \left( {x_{f} -x} \right) +u\left( {x,y,t} \right) \end{aligned}$$
(29)
$$\begin{aligned}&v_{f} \left( {x_{f} ,y_{f} ,t+\Delta t} \right) =\left[ {\frac{2\left( {1+\upsilon } \right) \sigma _{xy}^{*} }{E}-\frac{u\left( {x,y^{+},t} \right) -u\left( {x,y^{-},t} \right) }{y^{+}-y^{-}}} \right] \left( {x_{f} -x} \right) +v\left( {x,y,t} \right) . \end{aligned}$$
(30)

Similarly, for the traction boundary with a unit normal in the \(y-\)direction, they can be written as

$$\begin{aligned}&u_{f} \left( {x_{f} ,y_{f} ,t+\Delta t} \right) =\left[ {\frac{2\left( {1+\upsilon } \right) \sigma _{xy}^{*} }{E}-\frac{v\left( {x^{+},y,t} \right) -v\left( {x^{-},y,t} \right) }{x^{+}-x^{-}}} \right] \left( {y_{f} -y} \right) +u\left( {x,y,t} \right) \end{aligned}$$
(31)
$$\begin{aligned}&v_{f} \left( {x_{f} ,y_{f} ,t+\Delta t} \right) =\left[ {\frac{\sigma _{yy}^{*} \left( {1-\upsilon ^{2}} \right) }{E}-\upsilon \frac{u\left( {x^{+},y,t} \right) -v\left( {x^{-},y,t} \right) }{x^{+}-x^{-}}} \right] \left( {y_{f} -y} \right) +v\left( {x,y,t} \right) . \end{aligned}$$
(32)
Fig. 5
figure 5

Square plate subjected to uniaxial tension loading

Full size image
Fig. 6
figure 6

Geometry and discretisation of the square plate

Full size image
Fig. 7
figure 7

Discretisation and horizons for refined grid–coarse grid case

Full size image
Fig. 8
figure 8

Variation of horizontal displacements along the central axis (x, \(y \quad =\) 0)

Full size image
Fig. 9
figure 9

Variation of vertical displacement along the central axis (\(x = \)0, y)

Full size image
Fig. 10
figure 10

Discretisation and horizons for refined grid–coarse grid case

Full size image
Fig. 11
figure 11

Variation of horizontal displacements along the central axis (x, \(y \quad =\) 0)

Full size image
Fig. 12
figure 12

Variation of vertical displacements along the central axis (\(x = \)0, y)

Full size image

4 Surface correction

Determination of surface correction factors for ordinary state-based peridynamics is important not only for material points close to the surfaces due to lack of interactions, but also for material points inside the solution domain since spatial numerical integration scheme based on meshless approach introduces numerical error to the solution. These errors can be corrected by using surface correction factors and modifying the peridynamic dilatation terms and peridynamic force expressions given in Eqs. (8,9,13,14) as

$$\begin{aligned} \theta _{k}= & {} \sum \limits _{i=1}^{N_{k} } {\beta _{k} d\delta _{k} s_{ki} V_{i} } \end{aligned}$$
(33)
$$\begin{aligned} \theta _{j}= & {} \sum \limits _{i=1}^{N_{j} } {\beta _{j} d\delta _{j} s_{ji} V_{i} } \end{aligned}$$
(34)

and

$$\begin{aligned} \mathbf{t }_{kj}= & {} \alpha _{kj} \left( {\frac{2ad\delta _{k} }{\left| {\mathbf{x }_{j} -\mathbf{x }_{k} } \right| }\theta _{k} \left( {\mathbf{x }_{k} ,t} \right) +\lambda _{k} b\,s_{kj} } \right) \,\frac{\mathbf{y }_{j} -\mathbf{y }_{k} }{\left| {\mathbf{y }_{j} -\mathbf{y }_{k} } \right| } \end{aligned}$$
(35)
$$\begin{aligned} \mathbf{t }_{jk}= & {} \alpha _{jk} \left( {\frac{2ad\delta _{j} }{\left| {\mathbf{x }_{j} -\mathbf{x }_{k} } \right| }\theta _{j} \left( {\mathbf{x }_{j} ,t} \right) +\lambda _{j} bs_{kj} } \right) \,\frac{\mathbf{y }_{k} -\mathbf{y }_{j} }{\left| {\mathbf{y }_{k} -\mathbf{y }_{j} } \right| } \end{aligned}$$
(36)

where \(\beta \) and \(\lambda \) represent the surface correction terms for the dilatation and peridynamic force expressions, respectively. As explained in Madenci and Oterkus [4], surface correction factors can be obtained by considering a simple loading condition and determining the ratio of the dilatation and strain energy density of a particular material point calculated from CCM and PD. Note that surface correction factors are not necessary for the non-ordinary state-based formulation since correction is automatically done within the formulation.

Fig. 13
figure 13

Discretisation and horizons for refined grid–coarse grid case

Full size image
Fig. 14
figure 14

Variation of horizontal displacements along the central axis (x, \(y \quad =\) 0)

Full size image
Fig. 15
figure 15

Variation of vertical displacements along the central axis (\(x = \)0, y)

Full size image
Fig. 16
figure 16

Discretisation and horizons for refined grid–coarse grid case

Full size image
Fig. 17
figure 17

Variation of horizontal displacements along the central axis (x, \(y \quad =\) 0)

Full size image
Fig. 18
figure 18

Variation of vertical displacements along the central axis (\(x = \)0, y)

Full size image
Fig. 19
figure 19

Square plate subjected to initial uniaxial strain condition

Full size image
Fig. 20
figure 20

Geometry and discretisation of the square plate

Full size image
Fig. 21
figure 21

Discretisation and horizons for refined grid–coarse grid case

Full size image

5 Numerical results

As mentioned earlier, although uniform discretisation is widely used in the peridynamic studies available in the scientific literature, it can be computationally advantageous to have flexibility to use different grid sizes at different parts of the solution domain which is a common procedure used in other numerical methods such as finite element method (FEM). Hence, in this section, we present the capability of dual-horizon peridynamics using variable grid sizes and horizons based on the formulation given in Sects. 2, 3 and 4. The solution domain is split into two regions so that each of these regions can have different grid sizes and horizon sizes. In the first problem case, plate under tension problem is considered in Sect. 5.1 to validate the dual-horizon peridynamic formulation for static problems. As the second validation case, vibration of a plate problem considered in Sect. 5.2 is investigated to validate the dual-horizon peridynamic formulation for dynamic problems.

5.1 Plate under tension

In the first problem case, a square plate with dimensions of \(L = \quad W =\) 1m is considered. The plate has a thickness of 0.01 m and subjected to a uniaxial tension loading of \(\upsigma * =\) 200 MPa at the right edge as shown in Fig. 5. The applied loading is specified by creating a fictitious region at the right edge as demonstrated in Fig. 6. Elastic modulus and density of the plate are specified as 200 GPa and 7850 kg/m\(^{\mathrm {3}}\), respectively. The left edge of the plate is fully fixed by using a fictitious region (Fig. 6). The steady-state solution is obtained by utilising the adaptive dynamic relaxation technique [48].

Fig. 22
figure 22

Variation of horizontal displacement of the material point located at (0.255 m, 0.255 m) with time

Full size image
Fig. 23
figure 23

Variation of vertical displacement of the material point located at (0.255 m, 0.255 m) with time

Full size image
Fig. 24
figure 24

Discretisation and horizons for a Case 1 and b Case 2

Full size image

5.1.1 Ordinary state-based peridynamics

A plate under tension is first analysed by using ordinary state-based peridynamics. The solution domain is split into two equal regions as Region 1 and Region 2 as shown in Fig. 7. The discretisation size in Region 1, \(\Delta x_{\mathrm {1}} \quad =\) 0.005 m, is half of the discretisation size of Region 2, \(\Delta x_{\mathrm {2}} \quad =\) 0.01 m. Material points in both regions are interacting with the same number of material points. This also means that the horizon size of material points in Region 1, \(\updelta _{\mathrm {1}}\), is half of the horizon size in Region 2, \(\updelta _{\mathrm {2}}\). Note that dual-horizon peridynamics formulation is especially effective for the material points close to the interface of Regions 1 and 2 since material points in one of these regions are interacting with material points in the other region.

Fig. 25
figure 25

Variation of horizontal displacement of the material point located at (0.255 m, 0.255 m) with time

Full size image
Fig. 26
figure 26

Variation of vertical displacement of the material point located at (0.255 m, 0.255 m) with time

Full size image
Fig. 27
figure 27

Discretisation and horizons for refined grid–coarse grid case

Full size image

Five different horizon size values are considered, i.e. \(\updelta _{\mathrm {1}}= n\Delta x_{\mathrm {1}}\), \(\updelta _{\mathrm {2}}=n\Delta x_{\mathrm {2}}\), \(n=\)1,…5. Variation of horizontal displacements along the central axes is shown in Figs. 8 and 9. The horizon size values of \(\updelta _{\mathrm {1}}=\)3\(\Delta x_{\mathrm {1}}\) & \(\updelta _{\mathrm {2}}=3\Delta x_{\mathrm {2}}\), \(\updelta _{\mathrm {1}}=4\Delta x_{\mathrm {1}}\) & \(\updelta _{\mathrm {2}}=4\Delta x_{\mathrm {2}}\) and \(\updelta _{\mathrm {1}}=5\Delta x_{\mathrm {1}}\) & \(\updelta _{\mathrm {2}}=5\Delta x_{\mathrm {2}}\) have better agreement with FEM results obtained by using ANSYS, a commercial finite element software.

In addition, the effect of the horizon size is investigated by considering the same horizon sizes for Regions 1 and 2 as shown in Fig. 10, i.e. \(\updelta _{\mathrm {1}}=\updelta _{\mathrm {2}}=6\Delta x_{\mathrm {1}}=3\Delta x_{\mathrm {2}}\), and compared against the different horizon case considered earlier with the horizon size in Region 1, \(\updelta _{\mathrm {1}}=3\Delta x_{\mathrm {1}}\), and the horizon size in Region 2, \(\updelta _{\mathrm {2}}=3\Delta x_{\mathrm {2}}\). As shown in Figs. 11 and 12, although both cases provide good agreement with FEM results for horizontal displacements, equal horizon case yields better vertical displacement results with respect to FEM results since there are more material points inside the horizon in Region 1 for this case.

5.1.2 Non-ordinary state-based peridynamics

In this section, a plate under tension problem is analysed by using non-ordinary state-based peridynamics. As in the previous section, the horizon size and discretisation size of Region 1 are half of the Region 2 (Fig. 13). Five different horizon size cases are considered, i.e. \(\updelta _{\mathrm {1}}= n\Delta x_{\mathrm {1}}\), \(\updelta _{\mathrm {2}}=n\Delta x_{\mathrm {2}}\), \(n=\)1,…5, and the variation of horizontal and vertical displacements along the central axes is shown in Figs. 14 and 15. According to these figures, the horizon size value of \(\updelta _{\mathrm {1}}=2\Delta x_{\mathrm {1}}\) & \(\updelta _{\mathrm {2}}=2\Delta x_{\mathrm {2}}\) has better agreement with FEM results since it provides smoother transition between the two regions which is a different outcome than ordinary state-based case. As the horizon size increases, error at the interface region increases.

Next, equal size horizon for both Regions 1 and 2 is considered and compared against the case with different horizon sizes in Regions 1 and 2 where the horizon size in Region 1, \(\updelta _{\mathrm {1}}=2\Delta x_{\mathrm {1}}\), is half of the horizon size in Region 2, \(\updelta _{\mathrm {2}}=2\Delta x_{\mathrm {2}}\) (Fig. 16). As shown in Figs. 17 and 18, both cases yield good agreement with FEM results.

5.2 Vibration of a plate

In the second problem case, the square plate considered in the previous case is subjected to an initial condition in the form of uniaxial strain of 0.001 in the x-direction as shown in Fig. 19. The solution is obtained using explicit time integration [4] with a time step size of \(1\times 10^{\mathrm {-7}}\) s (Fig. 20).

Fig. 28
figure 28

Variation of horizontal displacement of the material point located at (0.255 m, 0.255 m) with time

Full size image

5.2.1 Ordinary state-based peridynamics

As in the plate under tension problem, first solution is obtained by using ordinary state-based peridynamics. The solution domain is split into two equal regions as Region 1 and Region 2 as shown in Fig. 21. The discretisation size in Region 1, \(\Delta x_{\mathrm {1}} \quad =\) 0.005 m, is half of the discretisation size of Region 2, \(\Delta x_{\mathrm {2}} \quad =\) 0.01 m. Moreover, the horizon size of material points in Region 1, \(\updelta _{\mathrm {1}}\), is half of the horizon size in Region 2, \(\updelta _{\mathrm {2}}\).

Five different horizon size values are considered, \(\updelta _{\mathrm {1}}= n\Delta x_{\mathrm {1}}\), \(\updelta _{\mathrm {2}}=n\Delta x_{\mathrm {2}}\), \(n=\)1,…5. To analyse the results, a suitable point which is located far from the surfaces and the central axes is selected which is located at (0.255 m, 0.255 m). The variation of horizontal and vertical displacements at this point as the time progresses is shown in Figs. 22 and 23 for five different horizon size values. According to these results, the horizon size values of \(\updelta _{\mathrm {1}}=3\Delta x_{\mathrm {1}}\) & \(\updelta _{\mathrm {2}}=3\Delta x_{\mathrm {2}}\) and \(\updelta _{\mathrm {1}}=4\Delta x_{\mathrm {1}}\) & \(\updelta _{\mathrm {2}}=4\Delta x_{\mathrm {2}}\) provide better agreement with FEM results.

Next, the effect of discretisation size is investigated. By keeping the same horizon sizes as before, the discretisation size in Region 1 is specified as half of the previous case as shown in Fig. 24. Therefore, the grid size in Region 2 is \(\Delta x_{\mathrm {2}} \quad =\) 0.01, whereas the grid size in Region 1 is \(\Delta x_{\mathrm {1}} \quad =\) 0.005 for Case 1 and \(\Delta x_{\mathrm {1}} \quad =\) 0.025 for Case 2. The horizon size in Region 1 is half of the horizon size in Region 2, \(\updelta _{\mathrm {2}}=3\Delta x_{\mathrm {2}}\). As shown in Figs. 25 and 26, although horizontal displacements in both cases are similar to each other, Case 2 yields better vertical displacement results with respect to Case 1 since there are more material points inside the horizon of Region 1 in Case 2.

Fig. 29
figure 29

Variation of horizontal displacement of the material point located at (0.255 m, 0.255 m) with time

Full size image
Fig. 30
figure 30

Discretisation and horizons for a Case 1 and b Case 2

Full size image
Fig. 31
figure 31

Variation of horizontal displacement of the material point located at (0.255 m, 0.255 m) with time

Full size image

5.2.2 Non-ordinary state-based peridynamics

Finally, the vibration of a plate problem is analysed by using non-ordinary state-based peridynamics.

Five different horizon sizes are considered, \(\updelta _{\mathrm {1}}= n\Delta x_{\mathrm {1}}\), \(\updelta _{\mathrm {2}}=n\Delta x_{\mathrm {2}}\), \(n=\)1,…5. The horizon size in Region 1 is half of the horizon size in Region 2 (Fig. 27). As shown in Figs. 28 and 29, the horizon size value of \(\updelta _{\mathrm {1}}=2\Delta x_{\mathrm {1}}\) & \(\updelta _{\mathrm {2}}=2\Delta x_{\mathrm {2}}\) has better agreement with FEM results.

Next, two different non-uniform discretisation cases are compared (Fig. 30). The grid size in Region 2 is \(\Delta x_{\mathrm {2}} \quad =\) 0.01, whereas the grid size in Region 2 is \(\Delta x_{\mathrm {1}} \quad =\) 0.005 for Case 1 and \(\Delta x_{\mathrm {1}} \quad =\) 0.025 for Case 2. The horizon size in Region 1 is half of the horizon size in Region 2, \(\updelta _{\mathrm {2}}=2\Delta x_{\mathrm {2}}\). As shown in Figs. 31 and 32, both cases provide similar results and good agreement with FEM solution.

Fig. 32
figure 32

Variation of horizontal displacement of the material point located at (0.255 m, 0.255 m) with time

Full size image

6 Conclusions

In this study, dual-horizon peridynamics formulation was derived by using Euler–Lagrange equation. Dual-horizon peridynamics is an effective methodology when non-uniform discretisation and variable horizon sizes are considered either due to computational efficiency purposes and/or due to physical requirement of the problem. After deriving the dual-horizon peridynamic formulation for both ordinary and non-ordinary state-based peridynamics, two benchmark problems were analysed to investigate the effect of discretisation size and horizon size. By comparing PD results against FEM results, non-ordinary state-based peridynamics provides better agreement for smaller horizons sizes and error at the interface becomes larger as the horizon size increases. On the other hand, for ordinary state-based peridynamics results, the results at the interface are smoother and the results are getting better as the horizon size increases. Moreover, as the number of points inside the horizon is increasing, a better agreement is obtained for a constant horizon size in the solution domain. Finally, with the advancement of additive manufacturing technologies, fabrication of complex materials such as microstructured materials is possible. PD theory can be a suitable alternative for the analysis of microstructured materials to some other approaches presented in the literature [49,50,51], especially for damage prediction.