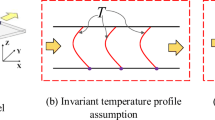
Abstract
This paper proposes an integrated two-step strategy for an optimal design of liquid-cooled channel layout based on the moving morphable component (MMC)-density approach. The proposed strategy intends to take the advantage of both the MMC approach for its high flexibility in searching a physically reasonable layout and the density approach for its better capacity of topology description. On the basis of the above-mentioned strategy, an intermediate layout is obtained through MMC approach and further optimized as initial solution of density approach step. Through density approach step, the final layout shows smoother boundary while retaining reasonable feature size. The original contributions of this paper are as follows: (i) An assembled quadratic Bézier curves component is proposed to describe the largely curved channel with limited numbers of optimization variables and computation order. (ii) Benefited from explicit geometric description, adaptive mesh refinement (AMR) is applied in MMC approach step for the first time. The application of AMR, from the numerical point of view, has two key ingredients to be highlighted: (i) the accuracy of solution in fluid–solid boundary region can be ensured with relatively limited computational cost. (ii) The contradiction that the difference step of MMC updating needs to be both as small as possible and integer multiple of the mesh size can be avoided. The performance of our methodology is demonstrated by numerical examples aiming for maximal heat exchange with power dissipation constraint. The main finding reveals that the proposed strategy can offer reasonable channel layout with better thermal performance, compared with conventional density approach. The whole numerical implementation relies on OpenFOAM and PETSc open-source software packages.



















Similar content being viewed by others
Notes
The pressure p is regulated through being divided by density \(\rho\) when solving N–S equations in OpenFOAM.
References
Alexandersen J, Andreasen CS (2020) A review of topology optimisation for fluid-based problems. Fluids 5(1):29
Alexandersen J, Sigmund O, Aage N (2016) Large scale three-dimensional topology optimisation of heat sinks cooled by natural convection. Int J Heat Mass Transf 100:876–891
Barber RW, Emerson DR (2008) Optimal design of microfluidic networks using biologically inspired principles. Microfluid Nanofluid 4(3):179–191
Bello-Ochende T, Liebenberg L, Meyer JP (2007) Constructal cooling channels for micro-channel heat sinks. Int J Heat Mass Transf 50(21–22):4141–4150
Bello-Ochende T, Olakoyejo OT, Meyer JP, Bejan A, Lorente S (2013) Constructal flow orientation in conjugate cooling channels with internal heat generation. Int J Heat Mass Transf 57(1):241–249
Borrvall T, Petersson J (2003) Topology optimization of fluids in Stokes flow. Int J Numer Methods Fluids 41(1):77–107
Cornolti L (2018) 2D adaptive Mesh Refinement. CFD-online. https://www.cfd-online.com/Forums/openfoam-community-contributions/118870-2d-adaptive-mesh-refinement-2.html
Dang X-P, Park H-S (2011) Design of U-shape milled groove conformal cooling channels for plastic injection mold. Int J Precis Eng Manuf 12(1):73–84
Dede EM (2009) Multiphysics topology optimization of heat transfer and fluid flow systems. In: Proceedings of the COMSOL users conference
Dilgen SB, Dilgen CB, Fuhrman DR, Sigmund O, Lazarov BS (2018) Density based topology optimization of turbulent flow heat transfer systems. Struct Multidisc Optim 57(5):1905–1918
Feppon F, Allaire G, Dapogny C, Jolivet P (2020) Topology optimization of thermal fluid–structure systems using body-fitted meshes and parallel computing. J Comput Phys 417:109574
Gersborg-Hansen A, Sigmund O, Haber RB (2005) Topology optimization of channel flow problems. Struct Multidisc Optim 30(3):181–192
Guo X, Zhang W, Zhong W (2014) Doing topology optimization explicitly and geometrically—a new moving morphable components based framework. J Appl Mech 81(8):081009
Huo W, Liu C, Du Z, Liu Z, Guo X (2022) Topology optimization on complex surfaces based on the moving morphable components (MMCs) method and computational conformal mapping (CCM). arXiv preprint arXiv:2201.08190
Jarrett A, Kim IY (2011) Design optimization of electric vehicle battery cooling plates for thermal performance. J Power Sources 196(23):10359–10368
Koga AA, Lopes ECC, Villa Nova HF, De Lima CR, Silva ECN (2013) Development of heat sink device by using topology optimization. Int J Heat Mass Transf 64:759–772
Kreissl S, Maute K (2012) Level set based fluid topology optimization using the extended finite element method. Struct Multidisc Optim 46(3):311–326
Lam YC, Zhai LY, Tai K, Fok SC (2004) An evolutionary approach for cooling system optimization in plastic injection moulding. Int J Prod Res 42(10):2047–2061
Lazarov BS, Sigmund O (2011) Filters in topology optimization based on Helmholtz-type differential equations. Int J Numer Methods Eng 86(6):765–781
Li CG, Li CL (2008) Plastic injection mould cooling system design by the configuration space method. Comput Aided Des 40(3):334–349
Li H, Ding X, Jing D, Xiong M, Meng F (2019a) Experimental and numerical investigation of liquid-cooled heat sinks designed by topology optimization. Int J Therm Sci 146:106065
Li H, Ding X, Meng F, Jing D, Xiong M (2019b) Optimal design and thermal modelling for liquid-cooled heat sink based on multi-objective topology optimization: an experimental and numerical study. Int J Heat Mass Transf 144:118638
Li H, Yamada T, Jolivet P, Furuta K, Kondoh T, Izui K, Nishiwaki S (2021) Full-scale 3D structural topology optimization using adaptive mesh refinement based on the level-set method. Finite Elem Anal Des 194:103561
Li H, Kondoh T, Jolivet P, Furuta K, Yamada T, Zhu B, Izui K, Nishiwaki S (2022a) Three-dimensional topology optimization of a fluid–structure system using body-fitted mesh adaption based on the level-set method. Appl Math Model 101:276–308
Li H, Kondoh T, Jolivet P, Furuta K, Yamada T, Zhu B, He Zhang, Izui K, Nishiwaki S (2022b) Optimum design and thermal modeling for 2D and 3D natural convection problems incorporating level set-based topology optimization with body-fitted mesh. Int J Numer Methods Engi 123(9):1954–1990
Matsumori T, Kondoh T, Kawamoto A, Nomura T (2013) Topology optimization for fluid–thermal interaction problems under constant input power. Struct Multidisc Optim 47(4):571–581
Olesen LH, Okkels F, Bruus H (2006) A high-level programming-language implementation of topology optimization applied to steady-state Navier–Stokes flow. Int J Numer Methods Eng 65(7):975–1001
Park H-S, Dang X-P (2010) Optimization of conformal cooling channels with array of baffles for plastic injection mold. Int J Precis Eng Manuf 11(6):879–890
Rettenmaier D, Deising D, Ouedraogo Y, Gjonaj E, De Gersem H, Bothe D, Tropea C, Marschall H (2019) Load balanced 2D and 3D adaptive mesh refinement in OpenFOAM. SoftwareX 10:100317
Sato Y, Yaji K, Izui K, Yamada T, Nishiwaki S (2018) An optimum design method for a thermal–fluid device incorporating multiobjective topology optimization with an adaptive weighting scheme. J Mech Des 140(3):031402
Svanberg K (1987) The method of moving asymptotes—a new method for structural optimization. Int J Numer Methods Eng 24(2):359–373
Svanberg K (2002) A class of globally convergent optimization methods based on conservative convex separable approximations. SIAM J Optim 12(2):555–573
Tang LQ, Chassapis C, Manoochehri S (1997) Optimal cooling system design for multi-cavity injection molding. Finite Elem Anal Des 26(3):229–251
Wein F, Dunning PD, Norato JA (2020) A review on feature-mapping methods for structural optimization. Struct Multidisc Optim 62:1–42
Wiker N, Klarbring A, Borrvall T (2007) Topology optimization of regions of Darcy and Stokes flow. Int J Numer Methods Eng 69(7):1374–1404
Xu S, Cai Y, Cheng G (2010) Volume preserving nonlinear density filter based on Heaviside functions. Struct Multidisc Optim 41(4):495–505
Yaji K, Yamada T, Kubo S, Izui K, Nishiwaki S (2015) A topology optimization method for a coupled thermal–fluid problem using level set boundary expressions. Int J Heat Mass Transf 81:878–888
Yoon GH (2010) Topological design of heat dissipating structure with forced convective heat transfer. J Mech Sci Technol 24(6):1225–1233
Yoon GH (2016) Topology optimization for turbulent flow with Spalart–Allmaras model. Comput Methods Appl Mech Eng 303:288–311
Yu M, Ruan S, Wang X, Li Z, Shen C (2019) Topology optimization of thermal–fluid problem using the MMC-based approach. Struct Multidisc Optim 60(1):151–165
Yu M, Ruan S, Gu J, Ren M, Li Z, Wang X, Shen C (2020) Three-dimensional topology optimization of thermal–fluid–structural problems for cooling system design. Struct Multidisc Optim 62(6):3347–3366
Zeng S, Kanargi B, Lee PS (2018) Experimental and numerical investigation of a mini channel forced air heat sink designed by topology optimization. Int J Heat Mass Transf 121:663–679
Zhang W, Chen J, Zhu X, Zhou J, Xue D, Lei X, Guo X (2017) Explicit three dimensional topology optimization via moving morphable void (MMV) approach. Comput Methods Appl Mech Eng 322:590–614
Zhou Y, Zhang W, Zhu J, Xu Z (2016) Feature-driven topology optimization method with signed distance function. Comput Methods Appl Mech Eng 310:1–32
Zhou Y, Zhu J, Zhan H, Zhang W, Gu Y (2021) A bio-inspired B-spline offset feature for structural topology optimization. Comput Methods Appl Mech Eng 386:114081
Zhu B, Wang R, Wang N, Li H, Zhang X, Nishiwaki S (2021) Explicit structural topology optimization using moving wide Bezier components with constrained ends. Struct Multidisc Optim 64(1):53–70
Acknowledgments
Sheng Pan and Minghao Yu have contributed equally to this work.
Funding
The present work was supported by the National Natural Science Foundation of China (Grant Nos. 11602050, and 11702053), the 111 Project (Grant No. B14013), the Fundamental Research Funds for the Central Universities (Grant No. DUT2019TD37), and Japan Society for the Promotion of Science (No. JP21J13418).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no competing financial interests for this paper.
Replication of results
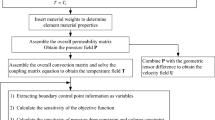
A detailed procedure and flowchart of the proposed method have been presented in Sects. 2 and 3 and one can follow them and reproduce the results. In case of further queries, please contact the corresponding authors.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Responsible Editor: Kentaro Yaji
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Topical Collection: Flow-driven Multiphysics
Guest Editors: J Alexandersen, C S Andreasen, K Giannakoglou, K Maute, K Yaji.
Appendix: Sensitivity analysis
Appendix: Sensitivity analysis
In this paper, the adjoint equations and adjoint BCs are derived by continuous adjoint method and subsequently discretized and solved. Using Lagrange’s method, the optimization problem given by Eqs. (17) and (18) can be substituted by an unconstrained optimization problem. The Lagrangian \({\mathcal {L}}({\varvec{u}}, p, T, \gamma )\) can be formulated as (Sato et al. 2018):
where \({\varvec{v}}, q, t, {\varvec{v}}_{\text {in}},{\varvec{v}}_{\text {wall}}, {\varvec{v}}_{\text {out}}, t_{\text {in}}, t_{\text {wall}}\) represent the corresponding Lagrangian multipliers. Through partial integration, Eq. (27) can be inferred as
In such case, the Karush–Kuhn–Tucker conditions for PDE constrained optimization problems should be satisfied:
where \({\varvec{w}}, r, e\) are the direction of Gâteaux derivative; R, C represent primal governing equations and primal BCs, respectively. Thus, the derivative versus pseudo density of objective function can be inferred as
The Gâteaux derivative of the Lagrangian with respect to state variables is given as
which can be reformulated as
Due to the arbitrary of Gáteaux derivative direction, all integral items but Gáteaux derivative parts ought to equal zero. Then, the adjoint equations, the adjoint BCs can be derived by merging Gateaux derivative parts, respectively. Now consider a generic integral-type objective function of the following form:
where A, \(B_{\text {f}}\), \(B_{\text {t}}\) are objective function defined in the domain, the fluid and temperature boundary, respectively. The derivatives versus state variables of the objective function are
After substituting Eq. (34) into Eq. (32), the adjoint equations can be derived:
with adjoint BCs:
Using the adjoint variables, the stationary conditions meet the following conditions for the Lagrangian multipliers:
In this paper, the objective function is set as \(\int \limits _{\varOmega }T{\text {d}}\varOmega /\left| \varOmega \right|\), that is \(A=T\); \(B_{\text {f}}=0\), \(B_{t}=0\). Substituting above equation into Eqs. (35) and (36), Eqs. (22) and (23) can be derived eventually.
Rights and permissions
About this article
Cite this article
Pan, S., Yu, M., Li, H. et al. An integrated two-step strategy for an optimal design of liquid-cooled channel layout based on the MMC–density approach. Struct Multidisc Optim 65, 221 (2022). https://doi.org/10.1007/s00158-022-03315-9
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00158-022-03315-9