Blood flow topology optimization considering a thrombosis model

Abstract

In the field of topology optimization for fluid flow design, there is a specific class of formulations directed to non-Newtonian fluids. One prominent case is when the fluid is blood. In this case, in addition to the non-Newtonian effect, the damage caused by the flow to the blood (i.e., blood damage) should be taken into account. Blood damage is essentially given by two types: hemolysis, which corresponds to the breakdown of Red Blood Cells (RBCs), and thrombosis, which corresponds to the formation of blood clotting. More specifically, in terms of thrombosis, blood clotting is formed by the aggregation of platelets and RBCs in vessels. Furthermore, in order to model thrombosis, there are essentially two approaches—platelet activation (initiation of thrombosis) and platelet aggregation. However, the computational cost of the second approach is still considered impractical for real applications. In the topology optimization field, hemolysis and thrombosis have been normally assumed to be indirectly minimized by considering the shear stress (or even energy dissipation or vorticity). However, a recent work has considered the direct minimization of hemolysis from a differential equation model. In terms of thrombosis, the stress levels for damage are 10 times lower than hemolysis, which means that it may not be sufficient to consider only the minimization of hemolysis in the design. Therefore, in this work, the topology optimization is formulated in order to take thrombosis into account, computed by a platelet activation model. The resulting formulation is also set to consider hemolysis and relative energy dissipation (as a way to indirectly maximize efficiency). In terms of thrombosis, the shear-induced platelet activation model is here rewritten for a finite elements approach, while also considering the necessary adjustments for the topology optimization formulation. The topology optimization is also formulated for a non-Newtonian fluid model for blood, and the optimization solver is IPOPT (Interior Point Optimization algorithm). Some numerical examples are presented considering 2D swirl flow configurations and a 2D configuration.

Appendices

Appendix A: Finite element formulation for the fluid flow problem

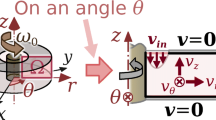
In order to define the finite element formulation, it is necessary to first define the corresponding boundary value problem. By considering the types of computational domains illustrated in Fig. 29, (Alonso et al. 2019)

$$\begin{aligned} \begin{aligned} \rho \nabla \varvec{v}{\cdot }\varvec{v} = \nabla {\cdot }{\varvec{T}}&(\mu ({\dot{\gamma }}_{\text {m}})) + \rho {\varvec{f}} - 2\rho ({\varvec{\omega }}{\wedge }\varvec{v}) \\&- \rho {\varvec{\omega }}{\wedge }({\varvec{\omega }}{\wedge }{\varvec{r}}) + {\varvec{f}}_{r}(\alpha ) \qquad \qquad \text { in } {\Omega }\\ \nabla {\cdot }\varvec{v}&= 0 \qquad \qquad \qquad \qquad \qquad \qquad \text { in } {\Omega }\\ \varvec{v}&= \varvec{v}_{in} \qquad \qquad \qquad \qquad \qquad \quad \text { on } {\Gamma }_{\text {in}}\\ \varvec{v}&= {\varvec{0}} \qquad \qquad \qquad \qquad \qquad \,\,\,\,\,\,\,\,\,\, \text { on } {\Gamma }_{\text {wall}} \\ {\varvec{T}}(\mu (&{\dot{\gamma }}_{\text {m}})) {\cdot } {\varvec{n}} = {\varvec{0}} \qquad \qquad \qquad \qquad \,\,\,\,\, \text { on } {\Gamma }_{\text {out}}\\ {v_r} = {0} \text { and } \frac{\partial v_{r}}{\partial r }&= \frac{\partial v_{\theta }}{\partial r } = \frac{\partial v_{z}}{\partial r } = \frac{\partial p}{\partial r } = {0} \qquad \quad \,\, \text { on } {\Gamma }_{\text {sym}}\\ \end{aligned} \end{aligned}$$

(52)

Figure 29 shows the interior of the computational domain (${\Omega }$), and the boundaries (${\Gamma }_{\text {in}}$, ${\Gamma }_{\text {wall}}$, ${\Gamma }_{\text {out}}$, and ${\Gamma }_{\text {sym}}$). On the inlet boundary (${\Gamma }_{\text {in}}$), the velocity profile is fixed, while, on the walls (${\Gamma }_{\text {wall}}$), the no-slip condition is set. On the outlet boundary (${\Gamma }_{\text {out}}$), the stress free Neumann boundary condition is set, while ${\varvec{n}}$ is the unit vector that is normal to the boundaries—i.e., pointing outside the computational domain, and being given, in the 2D swirl flow model, as ${\varvec{n}} = (n_r,\ 0,\ n_z)$, and, in the 2D model, as ${\varvec{n}} = (n_x,\ n_y)$. On the symmetry axis (${\Gamma }_{\text {sym}}$, used in one of the 2D swirl flow cases in Fig. 29), there is a symmetry axis boundary condition: the derivatives in relation to the r coordinate are zero, and the radial velocity is also zero. The stress tensor (${\varvec{T}}$) is indicated as ${\varvec{T}}(\mu ({\dot{\gamma }}_{\text {m}}))$, when considering the fluid being modeled from the non-Newtonian fluid model, in Eq. (6).

Fig. 29

Examples of boundaries for the fluid flow problems

From the formulation presented in Eq. (52), the finite element method is considered to solve the equilibrium equations for the 2D swirl flow model, by considering the weighted-residual and the Galerkin methods for the velocity-pressure (mixed) formulation, (Reddy and Gartling 2010; Alonso and Silva 2021)

$$\begin{aligned}&{R}_{c} = \int _{{\Omega }}[\nabla {\cdot }\varvec{v}]{{w}}_{p}rd{\Omega }\end{aligned}$$

(53)

(54)

where the equations are indicated by subscripts: c (denoting the continuity equation), and m (denoting the linear momentum equation—i.e., the Navier-Stokes equations). The corresponding test functions are indicated as: ${{w}}_{p}$ (pressure test function), and ${{{\varvec{w}}}}_{v} =\left[ \begin{matrix}{{w}}_{v,r}\\ {{w}}_{v,\theta }\\ {{w}}_{v,z}\end{matrix}\right]$ (velocity test function). Since the integration domain ($2\pi r d{\Omega }$) includes a constant multiplier ($2\pi$), which exerts no influence when solving the weak form, Eqs. (53) and (54) are given including a division by $2\pi$ (Alonso et al. 2019).

In the case of a 2D model, the integration domain is different (i.e., in Cartesian coordinates), meaning that, in Eqs. (53) and (54), $rd{\Omega }$ should be replaced by $d{\Omega }$, while $rd{\Gamma }$ should be replaced by $d{\Gamma }$.

The test functions (${{w}}_{p}$ and ${{{\varvec{w}}}}_{v}$) in Eqs. (53) and (54) are mutually independent. This means that the corresponding equations may be summed, resulting in a single equation

$$\begin{aligned} F = {R}_{c} + {R}_{m} = 0 \end{aligned}$$

(55)

Appendix B: LSFEM formulation for the thrombosis model

The resulting LSFEM (Least Squares Finite Element Method) formulation from Eqs. (27), (28), (29) and (30) becomes:

$$\begin{aligned}&\int _{\Omega }\left[ \frac{(\varvec{v}{\cdot }\nabla )S_{\tau }}{\tau _{\mathrm {m}}} - 1 \right] \left[ (\varvec{v}{\cdot }\nabla ){{w}}_{S_{\tau }} \right] r d{\Omega }= 0 \end{aligned}$$

(56)

$$\begin{aligned}&\begin{aligned} \int _{\Omega }&\left[ \frac{(\varvec{v}{\cdot }\nabla )D_{PAS,sl}}{\tau _{\mathrm {m}}^{\frac{\alpha _s}{\alpha _t}}} - 1 \right] \left[ (\varvec{v}{\cdot }\nabla ){{w}}_{D_{PAS,sl}} \right] r d{\Omega }= 0 \end{aligned} \end{aligned}$$

(57)

$$\begin{aligned}&\begin{aligned} \int _{\Omega }&\left[ \frac{(\varvec{v}{\cdot }\nabla )D_{PAS,sr}}{{|(\varvec{v}{\cdot }\nabla )\tau _{\mathrm {m}}|}^{\frac{\delta _s}{\delta _t}}} - 1 \right] \left[ (\varvec{v}{\cdot }\nabla ){{w}}_{D_{PAS,sr}} \right] r d{\Omega }= 0 \end{aligned} \end{aligned}$$

(58)

$$\begin{aligned}&\begin{aligned}&\left\{ \frac{(\varvec{v}\cdot \nabla )I_{\text{PAS}}}{S_{\tau }} - \left[C_{PAS,S} I_{\text{PAS}} \right. \right. \\&\left. \left. \quad + \frac{C_{PAS,sl} \alpha _t D_{PAS,sl}^{\alpha _t - 1} (\varvec{v}{\cdot }\nabla )D_{PAS,sl}}{S_{\tau }} \right. \right. \\&\left. \left. \quad + \frac{C_{PAS,sr} \delta _t D_{PAS,sr}^{\delta _t - 1} (\varvec{v}{\cdot }\nabla )D_{PAS,sr}}{S_{\tau }} \right] (1 - I_{\text{PAS}}) \right. \\&\left. \quad - \kappa _{\text{PAS}}(\alpha ) (I_{\text{PAS}} - I_{PAS, \mathrm {mat}}) \right\} \left\{(\varvec{v}\cdot \nabla ){{w}}_{I_{\text{PAS}}} \right. \\&\left. - \left[C_{PAS,S} {{w}}_{I_{\text{PAS}}} S_{\tau } (1 - I_{\text{PAS}}) + \left(C_{PAS,S} I_{\text{PAS}} S_{\tau } \right. \right. \right. \\&\left. \left. \left. \quad + C_{PAS,sl} \alpha _t D_{PAS,sl}^{\alpha _t - 1} (\varvec{v}{\cdot }\nabla )D_{PAS,sl} \right. \right. \right. \\&\left. \left. \left. \quad + C_{PAS,sr} \delta _t D_{PAS,sr}^{\delta _t - 1} (\varvec{v}{\cdot }\nabla )D_{PAS,sr} \right) (-{{w}}_{I_{\text{PAS}}}) \right] \right. \\&\left. - \kappa _{\text{PAS}}(\alpha ) {{w}}_{I_{\text{PAS}}} \right\} r d{\Omega }= 0 \end{aligned} \end{aligned}$$

(59)

where ${{w}}_{S_{\tau }}$, ${{w}}_{D_{PAS,sl}}$, ${{w}}_{D_{PAS,sr}}$ and ${{w}}_{I_{\text{PAS}}}$ are the test functions.

Notice that $(\varvec{v}{\cdot }\nabla )D_{PAS,sl}$ and $(\varvec{v}{\cdot }\nabla )D_{PAS,sr}$ in Eq. (30) can be substituted from Eqs. (28) and (29), but the resulting system of equations would achieve a worse numerical conditioning (as has been observed in some tests). The numerical conditioning was observed to be much better when using the formulation presented in Eq. (30).