Abstract
A theoretical development is carried to establish fundamental results about rank-initial embeddings and automorphisms of countable non-standard models of set theory, with a keen eye for their sets of fixed points. These results are then combined into a “geometric technique” used to prove several results about countable non-standard models of set theory. In particular, back-and-forth constructions are carried out to establish various generalizations and refinements of Friedman’s theorem on the existence of rank-initial embeddings between countable non-standard models of the fragment \({\mathrm {KP}}^{{\mathcal {P}}}\) + \(\Sigma _1^{{\mathcal {P}}}\)-Separation of \({\mathrm {ZF}}\); and Gaifman’s technique of iterated ultrapowers is employed to show that any countable model of \({\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\text { is weakly compact''}\) can be elementarily rank-end-extended to models with well-behaved automorphisms whose sets of fixed points equal the original model. These theoretical developments are then utilized to prove various results relating self-embeddings, automorphisms, their sets of fixed points, strong rank-cuts, and set theories of different strengths. Two examples: The notion of “strong rank-cut” is characterized (i) in terms of the theory \({\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\text { is weakly compact''}\), and (ii) in terms of fixed-point sets of self-embeddings.
Similar content being viewed by others
1 Introduction
In [10] Friedman famously invented an ingenious back-and-forth construction to show that every non-standard countable model of a certain fragment of \({\mathrm {ZF}}\) (or \({\mathrm {PA}}\)) has a proper self-embedding. He actually proved a more general result, and his technique was later used to prove sharper results on non-standard models of arithmetic under additional assumptions. On a parallel track, Ramsey’s theorem was used in [4] to show that any first-order theory with an infinite model has a model with a non-trivial automorphism. In particular, there are models of \({\mathrm {PA}}\), \({\mathrm {ZFC}}\), etc. with non-trivial automorphisms. Later on, Gaifman refined this technique considerably in the domain of models of arithmetic, showing that any countable model \({\mathcal {M}}\) of \({\mathrm {PA}}\) can be elementarily end-extended to a model \({\mathcal {N}}\) with an automorphism \(j : {\mathcal {N}} \rightarrow {\mathcal {N}}\) whose set of fixed points is precisely \({\mathcal {M}}\) [11]. This was facilitated by the technical break-through of iterated ultrapowers, introduced by Gaifman and later adapted by Kunen to a set theoretical setting.
This paper generalizes and refines these two theorems in the domain of non-standard models of set theory, and combines them into a geometric machinery which is used to prove several new results. In the course of this project we also take the opportunity to generalize some more related results from arithmetic to set theory.
These results require a few definitions.
The Takahashi hierarchy, presented e.g. in [23] (and in Sect. 3 of the present paper), is similar to the well-known Lévy hierarchy, but any quantifiers of the forms \(\exists x \in y, \exists x \subseteq y, \forall x \in y, \forall x \subseteq y\) are considered bounded. \(\Delta _0^{{\mathcal {P}}}\) is the set of set-theoretic formulae with only bounded quantifiers in that sense, and \(\Sigma _n^{{\mathcal {P}}}\) and \(\Pi _n^{{\mathcal {P}}}\) are then defined recursively in the usual way for all \(n \in {\mathbb {N}}\). \({\mathrm {KP}}^{{\mathcal {P}}}\) (presented in Sect. 4) is the set theory axiomatized by Extensionality, Pair, Union, Powerset, Infinity, \(\Delta _0^{{\mathcal {P}}} \text {-Separation}\), \(\Delta _0^{{\mathcal {P}}} \text {-Collection}\) and \(\Pi _1^{{\mathcal {P}}} \text {-Foundation}\).
Let us now go through some notions of substructure relevant to set theory (these are explained in more detail in Sect. 6). Let \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}}\). A rank-initial substructure \({\mathcal {S}}\) of \({\mathcal {M}}\) is a submodel that is downwards closed in ranks (so if \(s \in {\mathcal {S}}\) and \({\mathcal {M}} \models {\mathrm {rank}}(m) \le {\mathrm {rank}}(s)\), then \(m \in {\mathcal {S}}\)). It is a rank-cut if, moreover, there is an infinite strictly descending downwards cofinal sequence of ordinals in \({\mathcal {M}} {\setminus } {\mathcal {S}}\). It is a strong rank-cut if, moreover, for every function \(f : {\mathrm {Ord}}^{\mathcal {S}} \rightarrow {\mathrm {Ord}}^{\mathcal {M}}\) coded in \({\mathcal {M}}\) (in the sense that \({\mathcal {M}}\) believes there is a function \({\hat{f}}\) whose externalization restricted to \({\mathrm {Ord}}^{\mathcal {S}}\) equals f), there is an ordinal \(\mu \in {\mathcal {M}} {\setminus } {\mathcal {S}}\) such that \(f\quad (\xi ) \not \in {\mathcal {S}} \Leftrightarrow f\quad (\xi ) > \mu \). Note that these notions for substructures also make sense for embeddings.
If (the interpretation of the element-relation in) \({\mathcal {M}}\) is well-founded, then we say that \({\mathcal {M}}\) is a standard model, and otherwise we say that it is non-standard. The largest well-founded rank-initial substructure of \({\mathcal {M}}\) exists. It is called the well-founded part of \({\mathcal {M}}\) and is denoted \({\mathrm {WFP}}({\mathcal {M}})\). It turns out that \({\mathrm {WFP}}({\mathcal {M}})\) is a rank-cut of \({\mathcal {M}}\).
Suppose that \({\mathcal {M}}\) is a model of \({\mathrm {KP}}^{{\mathcal {P}}}\) with a proper rank-cut \({\mathcal {S}}\). If \(A \subseteq {\mathcal {S}}\), then A is coded in \({\mathcal {M}}\) if there is \(a \in {\mathcal {M}}\) such that \(\{x \in {\mathcal {S}} \mid {\mathcal {M}} \models x \in a\} = A\). The standard system of \({\mathcal {M}}\) over \({\mathcal {S}}\), denoted \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}})\) is the second-order structure obtained by expanding \({\mathcal {S}}\) with all the subsets of \({\mathcal {S}}\) coded in \({\mathcal {M}}\). We define \({\mathrm {SSy}}({\mathcal {M}}) = {\mathrm {SSy}}_{{\mathrm {WFP}}({\mathcal {M}})}({\mathcal {M}})\).
Section 7 is concerned with proving various existence results for embeddings between countable non-standard models of fragments of \({\mathrm {ZFC}}\). Friedman showed that for any countable non-standard models \({\mathcal {M}}\) and \({\mathcal {N}}\) of
and \({\mathcal {S}}\) such that
there is a proper rank-initial embedding of \({\mathcal {M}}\) into \({\mathcal {N}}\) iff the \(\Sigma _1^{{\mathcal {P}}}\)-theory of \({\mathcal {M}}\) with parameters in \({\mathcal {S}}\) is included in the corresponding theory of \({\mathcal {N}}\) and \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}}) = {\mathrm {SSy}}_{\mathcal {S}}({\mathcal {N}})\).Footnote 1
Theorem 7.2 and Corollary 7.7, refine Friedman’s result in multiple ways. Firstly, we show that it holds for any common rank-cut \({\mathcal {S}}\) of \({\mathcal {M}}\) and \({\mathcal {N}}\) (not just for the standard cut); secondly, we show that it holds for all countable non-standard models of \({\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1 \text {-Separation}\); thirdly we show that continuum many such embeddings can be obtained (generalizing a result from [24] for models of \({\mathrm {PA}}\)); and fourthly, we show that the embedding can be constructed so as to yield a rank-cut of the co-domain. Moreover, Theorem 7.8 establishes that for every model \({\mathcal {M}}\) of \({\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1 \text {-Separation}\) and every rank-cut \({\mathcal {S}}\) of \({\mathcal {M}}\), there is a rank-initial topless self-embedding of \({\mathcal {M}}\) which fixes \({\mathcal {S}}\) pointwise but moves some element on every rank above \({\mathcal {S}}\).
Friedman’s insight lead to further developments in this direction in the model-theory of arithmetic. In particular, it was established for countable non-standard models of \({\mathrm {I}}\Sigma _1\). Ressayre showed, conversely, that if \({\mathcal {M}} \models {\mathrm {I}}\Sigma _0 + {\mathrm {exp}}\), and for every \(a \in {\mathcal {M}}\) there is a proper initial self-embedding of \({\mathcal {M}}\) which fixes every element \({\mathcal {M}}\)-below a, then \({\mathcal {M}} \models {\mathrm {I}}\Sigma _1\) [21]. Theorem 7.16 is a set theoretic version of this optimality result, to the effect that if \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}}\), and for every \(a \in {\mathcal {M}}\) there is a proper rank-initial self-embedding of \({\mathcal {M}}\) which fixes every element that is an \({\mathcal {M}}\)-member of a, then \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1 \text {-Separation}\).
Wilkie showed that for every countable non-standard model \({\mathcal {M}} \models {\mathrm {PA}}\) and for every element a of \({\mathcal {M}}\), there is a proper initial self-embedding whose image includes a [25]. Theorem 7.10 and Corollary 7.12 generalize this result to set theory in refined form, e.g.: For every countable non-standard model \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _2^{{\mathcal {P}}}\text {-Separation} + \Pi _2^{{\mathcal {P}}}\text {-Foundation}\) and for every element a of \({\mathcal {M}}\), there is a proper initial self-embedding whose image includes a.
Yet another result in this vein is that the isomorphism types of countable recursively saturated models of \({\mathrm {PA}}\) only depends on the theory and standard system. A generalization of this result for \({\mathrm {PA}}\) (allowing common \(\omega \)-toplessFootnote 2 initial segments to be fixed) was proved in [17]. Theorem 7.14 is an analogous result for \({\mathrm {ZF}}\).
Theorem 7.15 states that every countable recursively saturated model \({\mathcal {M}}\) of \({\mathrm {ZF}}\), with a rank-cut \({\mathcal {S}}\), has an arbitrarily high rank-initial self-embedding j, fixing \({\mathcal {S}}\) pointwise, such that \(j({\mathcal {M}}) \prec {\mathcal {M}}\). This was originally proved in [20], but we provide a new proof that is conceptually simpler.
The gist of our generalization of Gaifman’s result is that any countable model \(({\mathcal {M}}, {\mathcal {A}})\) of the theory \({\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\text { is weakly compact''}\)Footnote 3 has an elementary rank-end-extension \({\mathcal {N}}\), such that \({\mathrm {SSy}}_{\mathcal {M}}({\mathcal {N}}) = ({\mathcal {M}}, {\mathcal {A}})\). This result was actually obtained in [6], but in this paper a more detailed result is proved, see Theorem 8.6.
Once these refined and generalized Friedman- and Gaifman-style results have been established, we combine them in numerous ways to prove a number of new results about non-standard models of set theory. This is carried out in Sect. 9.
Kirby and Paris essentially showed in [16] that any cut \({\mathcal {S}}\) of a model \({\mathcal {M}} \models {\mathrm {I}}\Delta _0\) is strong iff \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}}) \models {\mathrm {ACA}}_0\). Theorem 9.1 generalizes this to set theory. It turns out that any rank-cut \({\mathcal {S}}\) including \(\omega ^{\mathcal {M}}\) of an ambient model \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + {\mathrm {Choice}}\) is strong iff \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}}) \models {\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\text { is weakly compact''}\). This result is given a new proof relying on our refined and generalized versions of the Friedman and Gaifman theorems. A similar technique was used in [7] to reprove the result of Kirby and Paris in the context of arithmetic.
Using the above characterization of strong rank-cuts we show (Theorem 9.5) that for any countable model \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}}\), and any rank-cut \({\mathcal {S}}\) of \({\mathcal {M}}\): there is a self-embedding of \({\mathcal {M}}\) whose set of fixed points is precisely \({\mathcal {S}}\) iff \({\mathcal {S}}\) is a \(\Sigma _1^{{\mathcal {P}}}\)-elementary strong rank-cut of \({\mathcal {M}}\). In [1] the analogous result is shown for models of the fragment \({\mathrm {I}}\Sigma _1\) of \({\mathrm {PA}}\).
The latter result of Bahrami and Enayat was inspired by an analogous result in the context of countable recursively saturated models of \({\mathrm {PA}}\) [15], namely that any cut of such a model is the fixed point set of an automorphism iff it is an elementary strong cut. Theorem 9.8 generalizes this result to set theory by means of a new proof, again relying on a combination of our Friedman- and Gaifman-style theorems. It is shown that for any rank-cut \({\mathcal {S}}\) of a countable recursively saturated model of \({\mathrm {ZFC}} + V = {\mathrm {HOD}}\):Footnote 4\({\mathcal {S}}\) is the fixed point set of an automorphism of \({\mathcal {M}}\) iff it is an elementary strong rank-cut.
Finally, we combine the Friedman- and Gaifman-style theorems to show (Theorem 9.9) that for any countable non-standard \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1^{{\mathcal {P}}} \text {-Separation} + \text {Choice}\): \({\mathcal {M}}\) has a strong rank-cut isomorphic to \({\mathcal {M}}\) iff \({\mathcal {M}}\) expands to a model of \({\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\) is weakly compact”.
2 Motivation
It is a common theme throughout mathematics to study structures and how these structures relate to each other. Usually structures are related to each other by functions from one structure (the domain) to another (the co-domain), which preserve some of the structure involved. Since the study of such functions has turned out to be very fruitful in many branches of mathematics, it makes sense to apply this methodology to models of set theory as well.
When we consider models of such expressive theories as set theories, it is natural to compare structures by means of embeddings. Any embedding exhibits the domain as a substructure of the co-domain, but we can ask various questions about “how nicely” the domain can be embedded in the co-domain: Firstly, for any first-order structure we can ask if the embedding is elementary, i.e. whether the truth of every first-order sentence with parameters in the domain is preserved by the embedding. Secondly, for structures of set theory we can ask whether the domain is embedded “initially” in the co-domain. For set theory, the intuition of “initiality” may be captured by various different formal notions, of different strengths (see Sect. 6). The weakest notion of this form is called initiality and requires simply that the image of the embedding is downwards closed under \(\in \), i.e. if b is in the image, and the co-domain satisfies that \(c \in b\), then c is also in the image. This paper is concerned with rank-initial embeddings, defined by the stronger property that for every value of the embedding, every element of the co-domain of rank less than or equal to the rank of that value is also a value of the embedding. As noted in Sect. 4, \({\mathrm {KP}}^{{\mathcal {P}}}\) proves that the function \((\alpha \mapsto V_\alpha )\) is total on the ordinals, so it makes sense to consider a notion of embedding which preserves this structure \((\alpha \mapsto V_\alpha )\). And indeed, an embedding \(i : {\mathcal {M}} \rightarrow {\mathcal {N}}\) is rank-initial iff i is initial and \(i(V_\alpha ^{{\mathcal {M}}}) = V_{i(\alpha )}^{{\mathcal {N}}}\), for every ordinal \(\alpha \) in \({\mathcal {M}}\) (see Corollary 6.11), so the choice to study the notion of rank-initial embedding is quite a natural in the setting of \({\mathrm {KP}}^{{\mathcal {P}}}\).
Between well-founded structures, all initial embeddings are trivial: This follows from the Mostowski collapse theorem (see Theorem 6.8 and Proposition 6.10 (a)). In particular, if \(i : {\mathcal {M}} \rightarrow {\mathcal {N}}\) is an initial embedding between well-founded extensional structures, then \({\mathcal {M}}\) and \({\mathcal {N}}\) are isomorphic to transitive sets (with the inherited \(\in \)-structure) \({\mathcal {M}}'\) and \({\mathcal {N}}'\), respectively, and i is induced by the inclusion function of \({\mathcal {M}}'\) into \({\mathcal {N}}'\). So for a study of initial embeddings of models of set theory to yield any insight, we must turn our attention to non-standard models. As explained in the introduction, for non-standard models of arithmetic, several interesting results have been obtained that are either directly about initial embeddings between such models, or are proved by means of considering such embeddings. Thus a motivation for this work is to determine whether these generalize to the set theoretic setting, and if so, for which particular set theory. We give positive answers for suitable extensions of \({\mathrm {KP}}^{{\mathcal {P}}}\).
A deeper motivation lies in combining the techniques of Friedman and Gaifman into a geometric machinery. Several results and proofs of Sect. 9 testify to the versatility of this approach, where relationships are established between the theory \({\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\text { is weakly compact''}\), strong cuts, rank-initial embeddings, and fixed point sets of rank-initial embeddings.
3 Basic logic and model theory
This section contains basic material on logic and model theory typically found in introductory textbooks such as [3]. An expanded version of this section with proofs of the results is found as §4.1 of [12].
We work with the usual first-order logic. A signature is a set of constant, function and relation symbols. The language of a signature is the set of well-formed formulas in the signature. The arity of function symbols, f, and relation symbols, R, are denoted \({\mathrm {arity}}(f)\) and \({\mathrm {arity}}(R)\), respectively. Models in a language are written as \({\mathcal {M}}\), \({\mathcal {N}}\), etc. They consist of interpretations of the symbols in the signature; for each symbol S in the signature, its interpretation in \({\mathcal {M}}\) is denoted \(S^{\mathcal {M}}\). If X is a term, relation or function definable in the language over some theory under consideration, then \(X^{\mathcal {M}}\) denotes its interpretation in \({\mathcal {M}}\).
The domain of \({\mathcal {M}}\) is also denoted \({\mathcal {M}}\), so \(a \in {\mathcal {M}}\) means that a is an element of the domain of \({\mathcal {M}}\). Finite tuples are written as \(\vec {a}\), and the tuple \(\vec {a}\) considered as a set (forgetting the ordering of the coordinates) is also denoted \(\vec {a}\). Moreover, \(\vec {a} \in {\mathcal {M}}\) means that each coordinate of \(\vec {a}\) is an element of the domain of \({\mathcal {M}}\). \(\mathrm {length}(\vec {a})\) denotes the number of coordinates in \(\vec {a}\). For each natural number \(k \in \{ 1, \dots , \mathrm {length}(\vec {a}) \}\), \(\pi _k(\vec {a})\) is the k-th coordinate of \(\vec {a}\). When a function \(f : A \rightarrow B\) is applied as \(f(\vec {a})\) to a tuple \(\vec {a} \in A^n\), where \(n \in {\mathbb {N}}\), then it is evaluated coordinate-wise, so \(f(a_1, \dots , a_{n}) = (f(a_1), \dots , f\,(a_n))\). If \(\Gamma \) is a set of formulae in a language and \(n \in {\mathbb {N}}\), then \(\Gamma [x_1, \dots , x_n]\) denotes the subset of \(\Gamma \) of formulae all of whose free variables are in \(\{x_1, \dots , x_n\}\).
The theory of a model \({\mathcal {M}}\), denoted \({\mathrm {Th}}({\mathcal {M}})\), is the set of formulae in the language satisfied by \({\mathcal {M}}\). If \(\Gamma \) is a subset of the language and \(S \subseteq {\mathcal {M}}\), then
The standard model of arithmetic is denoted \({\mathbb {N}}\).
\({\mathcal {L}}^0\) is the language of set theory, i.e. the set of all well-formed formulae generated by \(\{\in \}\).
\({\mathcal {L}}^1\) is defined as a two-sorted language in the single binary relation symbol \(\{\in \}\); we have a sort \({\mathsf {Class}}\) of classes (which covers the whole domain and whose variables and parameters are written in uppercase X, Y, Z, A, B, C, etc.) and a sort \({\mathsf {Set}}\) of sets (which is a subsort of \({\mathsf {Class}}\) and whose variables and parameters are written in lowercase x, y, z, a, b, c, etc.). The relation \(\in \) is a predicate on the derived sort \({\mathsf {Set}} \times {\mathsf {Class}}\).
Models in \({\mathcal {L}}^1\) are usually written in the form \(({\mathcal {M}}, {\mathcal {A}})\), where \({\mathcal {M}}\) is an \({\mathcal {L}}^0\)-structure on the domain of sets, and \({\mathcal {A}}\) is a set of classes. It is sometimes convenient to regard an \({\mathcal {L}}^1\)-structure \(({\mathcal {M}}, {\mathcal {A}})\) simply as its reduct \({\mathcal {M}}\) to the language \({\mathcal {L}}^0\); for example, if \(({\mathcal {M}}, {\mathcal {A}})\) is an \({\mathcal {L}}^1\)-structure, then (unless otherwise stated), by an element of\(({\mathcal {M}}, {\mathcal {A}})\), is meant an element of sort \({\mathsf {Set}}\).
The notions of substructure, embedding and isomorphism are defined in the usual way. An embedding is proper if it is not onto. We write \({\mathcal {M}} \cong {\mathcal {N}}\) if \({\mathcal {M}}\) and \({\mathcal {N}}\) are isomorphic. If \({\mathcal {S}}\) is a common subset of \({\mathcal {M}}\) and \({\mathcal {N}}\), and there is an isomorphism between \({\mathcal {M}}\) and \({\mathcal {N}}\) fixing \({\mathcal {S}}\) pointwise, then we write \({\mathcal {M}} \cong _{\mathcal {S}} {\mathcal {N}}\).
An embedding \(f : {\mathcal {M}} \rightarrow {\mathcal {N}}\) of \({\mathcal {L}}\)-structures is \(\Gamma \)-elementary, for some \(\Gamma \subseteq {\mathcal {L}}\), if for each formula \(\phi (\vec {x})\) in \(\Gamma \), and for each \(\vec {m} \in {\mathcal {M}}\),
If there is such an embedding we write \({\mathcal {M}} \preceq _\Gamma {\mathcal {N}}\). f is elementary if it \({\mathcal {L}}\)-elementary.
It is also of interest to consider partial embeddings. \(\llbracket {\mathcal {M}} \preceq _{\Gamma , {\mathcal {S}}}^{< \omega } {\mathcal {N}} \rrbracket \) denotes the set of partial functions f from \({\mathcal {M}}\) to \({\mathcal {N}}\), with finite domain, fixing \({\mathcal {S}}\) pointwise, and such that for all \(\phi (\vec {x}) \in \Gamma \) and for all \(\vec {m} \in {\mathcal {M}}\),
PLEASE NOTE!: This definition uses ‘\(\Rightarrow \)’, as opposed to the ‘\(\Leftrightarrow \)’ used in the definition of ‘\(\preceq \)’.
If \(\Gamma \) is omitted, then it is assumed to be \({\mathcal {L}}^0\), and if \({\mathcal {S}}\) is omitted, then it is assumed to be \(\varnothing \). Let \({\mathbb {P}} = \llbracket {\mathcal {M}} \preceq _{\Gamma , {\mathcal {S}}}^{<\omega } {\mathcal {N}} \rrbracket \). We endow \({\mathbb {P}}\) with the following partial order. For any \(f,g \in {\mathbb {P}}\),

In Sect. 6 we will introduce definitions for more types of embeddings that are relevant to the study of models of set theory.
The uniquely existential quantifier\(\exists ! x \cdot \phi (x)\) is defined as \(\exists x \cdot (\phi (x) \wedge (\forall y \cdot \phi (y) \rightarrow y = x)).\) The bounded quantifiers, \(\forall u \in y \cdot \phi (u, y)\) and \(\exists u \in y \cdot \phi (u, y)\), are defined as \(\forall u \cdot (u \in y \rightarrow \phi (u, y))\) and \(\exists u \cdot (u \in y \wedge \phi (u, y))\), respectively. \({\hat{\Delta }}_0 \subseteq {\mathcal {L}}^0\) is the set of formulae all of whose quantifiers are bounded. \({\hat{\Sigma }}_0\) and \({\hat{\Pi }}_0\) are defined as equal to \({\hat{\Delta }}_0\). Recursively, for every \(n \in {\mathbb {N}}\): \({\hat{\Sigma }}_{n+1} \subseteq {\mathcal {L}}^0\) is the set of formulae of the form \(\exists x \cdot \phi \), where \(\phi \) is in \({\hat{\Pi _n}}\); and dually, \({\hat{\Pi }}_{n+1} \subseteq {\mathcal {L}}^0\) is the set of formulae of the form \(\forall x \cdot \phi \), where \(\phi \) is in \({\hat{\Sigma _n}}\). For each \(n \in {\mathbb {N}}\), \(\hat{{\mathrm {B}}}_n\) is defined as the closure of \({\hat{\Sigma }}_n\) under Boolean connectives and bounded quantifiers.
Suppose a background \({\mathcal {L}}^0\)-theory T is given. For each \(n \in {\mathbb {N}}\) and each symbol ‘\(\Gamma \)’ \(\in \)\(\{\) ‘\(\Sigma \)’, ‘\(\Pi \)’, ‘\({\mathrm {B}}\)’\(\}\), \(\Gamma _n\) is defined as the set of formulae provably equivalent (in T) to a formula in \(\hat{\Gamma }_n\). Moreover, for each \(n \in {\mathbb {N}}\), \(\Delta _{n} =_{\mathrm {df}}\Sigma _{n} \cap \Pi _{n}\). These sets of formulae are collectively called the Lévy hierarchy, and we say that they measure a formula’s Lévy complexity. This hierarchy is developed in [18].
If \(\phi \) is an \({\mathcal {L}}^0\)-formula and t is an element of a model or an \({\mathcal {L}}^0\)-term, such that none of the variables of t occur in \(\phi \), then \(\phi ^t\) denotes the formula obtained from \(\phi \) by replacing each quantifier of the form ‘\(\boxminus x\)’ by ‘\(\boxminus x \in t\)’, where \(\boxminus \in \{\exists , \forall \}\).
The \({{\mathcal {P}}}\)-bounded quantifiers\(\forall x \subseteq y \cdot \phi (x, y)\) and \(\exists x \subseteq y \cdot \phi (x, y)\) are defined as \(\forall x \cdot (x \subseteq y \rightarrow \phi (x, y))\) and \(\exists x \cdot (x \subseteq y \wedge \phi (x, y))\), respectively. For each \(n \in {\mathbb {N}}\), we define sets \({\hat{\Sigma }}^{\mathcal {P}}_n\), \({\hat{\Pi }}^\mathcal {P}_n\), \({\hat{\Delta }}^\mathcal {P}_n\), \(\hat{{\mathrm {B}}}^{{\mathcal {P}}}_n\), \(\Sigma ^{{\mathcal {P}}}_n\), \(\Pi ^{{\mathcal {P}}}_n\), \(\Delta ^{{\mathcal {P}}}_n\) and \(\mathrm B^{{\mathcal {P}}}_n\) analogously as above, but replacing “bounded” by “bounded or \({{\mathcal {P}}}\)-bounded”. These sets of formulae are called the Takahashi hierarchy, and we say that they measure a formula’s Takahashi complexity. Many facts about this hierarchy (in the context of \({\mathrm {ZFC}}\)) are established in [23]. It appears like these results also hold in the context of \({\mathrm {KP}}^{{\mathcal {P}}}\) (apart from its Theorem 6, which might require \({\mathrm {KP}}^{{\mathcal {P}}} + \text {Choice}\)).
When a set of formulae is denoted with a name that includes free variables, for example \(p(\vec {x})\), then it is assumed that each formula in the set has at most the free variables \(\vec {x}\). Moreover, if \(\vec {a}\) are terms or elements of a model, then \(p(\vec {a}) = \{\phi (\vec {a}) \mid \phi (\vec {x}) \in p(\vec {x})\}\).
A type\(p(\vec {x})\)over a theoryT or over a model\({\mathcal {M}}\), are defined in the usual way. Given a tuple \(\vec {a} \in {\mathcal {M}}\), a subset \(\Gamma \subseteq {\mathcal {L}}\) and a subset \(S \subseteq {\mathcal {M}}\), the\(\Gamma \)-type of\(\vec {a}\)over\({\mathcal {M}}\)with parameters inS is the set \(\{\phi (\vec {x}, \vec {b}) \mid \phi \in \Gamma \wedge \vec {b} \in S \wedge {\mathcal {M}} \models \phi (\vec {a}, \vec {b})\}\), denoted \({\mathrm {tp}}_{\Gamma , S}(\vec {a})\).
We fix a Gödel numbering of the syntactical objects in the languages \({\mathcal {L}}^0\) and \({\mathcal {L}}^1\), and assume that any syntactic object in these languages equals its Gödel number. A type \(p(\vec {x}, \vec {b})\) over \({\mathcal {M}}\) is recursive if \(\{ \ulcorner \phi (\vec {x}, \vec {y}) \urcorner \mid \phi (\vec {x}, \vec {b}) \in p(\vec {x}, \vec {b})\}\) is a recursive set, where \(\ulcorner \phi (\vec {x}, \vec {y}) \urcorner \) denotes the Gödel code of \(\phi (\vec {x}, \vec {y})\) (henceforth formulae will be identified with their Gödel codes). \({\mathcal {M}}\) is recursively\(\Gamma \)-saturated if it realizes every recursive \(\Gamma \)-type over \({\mathcal {M}}\).
The notions of poset (or partial order) and linear order are defined in the usual way.
Let \({\mathbb {P}}\) be a poset. We say that a formula \(\phi (x)\)holds for unboundedly many\(x \in {\mathbb {P}}\), if for any \(a \in {\mathbb {P}}\), there is \(b >^{\mathbb {P}} a\) such that \(\phi (b)\).
An embedding\(i : {\mathbb {P}} \rightarrow {\mathbb {P}}'\)of posets, is just a special case of embeddings of structures, i.e. it is an embedding of \(\{\le \}\)-structures. Let \(i : {\mathbb {P}} \rightarrow {\mathbb {P}}'\) be an embedding of posets. \(y \in {\mathbb {P}}'\) is an upper bound of i if \(\forall x \in {\mathbb {P}} \cdot i(x) < y\). If such a y exists then i is bounded above. i is topless if it is bounded above but does not have a \({\mathbb {P}}'\)-least upper bound.
A self-embedding \(i : {\mathbb {P}} \rightarrow {\mathbb {P}}\) is contractive if for all \(x \in {\mathbb {P}}\), we have \(i(x) <_{\mathbb {P}} x\).
Let \({\mathbb {P}}\) be a poset. Given \(x \in {\mathbb {P}}\), define \({\mathbb {P}}_{\le x}\) as the substructure of \({\mathbb {P}}\) on \(\{y \in {\mathbb {P}} \mid y \le _{\mathbb {P}} x\}\); and similarly, if \(X \in {\mathbb {P}}\), define \({\mathbb {P}}_{\le X}\) as the substructure of \({\mathbb {P}}\) on \(\{y \in {\mathbb {P}} \mid \exists x \in X \cdot y \le _{\mathbb {P}} x\}\). We have analogous definitions for when ‘\(\le \)’ is replaced by ‘<’, ‘\(\ge \)’ or ‘>’.
For any ordinal \(\alpha \) and linearly ordered set \(({\mathbb {L}}, <^{\mathbb {L}})\), the lexicographic ordering on the set \({\mathbb {L}}^{<\alpha }\) is defined in the usual way and denoted \(<^{\mathrm {lex}}\).
Let \({\mathbb {P}}\) be a poset. A subset \({\mathcal {D}} \subseteq {\mathbb {P}}\) is dense if for any \(x \in {\mathbb {P}}\) there is \(y \in {\mathcal {D}}\) such that \(y \le x\). A filter\({\mathcal {F}}\) on \({\mathbb {P}}\) is a non-empty subset of \({\mathbb {P}}\), such that \(\forall x, y \in {\mathbb {P}} \cdot ((x \in {\mathcal {F}} \wedge x \le y) \rightarrow y \in {\mathcal {F}})\) (upwards closed) and \(\forall x, y \in {\mathcal {F}} \cdot \exists z \in {\mathcal {F}} \cdot (z \le x \wedge z \le y)\) (downwards directed). A filter \({\mathcal {F}}\) is an ultrafilter if it is maximal, i.e. if there is no filter \({\mathcal {F}}'\) on \({\mathbb {P}}\) such that \({\mathcal {F}} \subsetneq {\mathcal {F}}'\). Let \({\mathbf {D}}\) be a set of dense subsets of \({\mathbb {P}}\). A filter \({\mathcal {F}}\) is \({\mathbf {D}}\)-generic, if \(\forall {\mathcal {D}} \in {\mathbf {D}}\cdot {\mathcal {D}} \cap {\mathcal {F}} \ne \varnothing \).
Lemma 3.1
Let \({\mathbb {P}}\) be a poset with an element p. If \({\mathbf {D}}\) is a countable set of dense subsets of \({\mathbb {P}}\), then there is a \({\mathbf {D}}\)-generic filter \({\mathcal {F}}\) on \({\mathbb {P}}\) containing p.
Lemma 3.2
Let \({\mathbb {P}}\) be a poset and let \({\mathcal {F}}\) be a filter on \({\mathbb {P}}\). There is an ultrafilter \({\mathcal {U}}\) such that \({\mathcal {F}} \subseteq {\mathcal {U}}\).
4 Power Kripke–Platek set theory
The set theory \({\mathrm {KP}}^{{\mathcal {P}}}\) may be viewed as the natural extension of Kripke–Platek set theory \({\mathrm {KP}}\) “generated” by adding the Powerset axiom.
Axioms 4.1
(Power Kripke–Platek set theory, \({\mathrm {KP}}^{{\mathcal {P}}}\)) \({\mathrm {KP}}^{{\mathcal {P}}}\) is the \({\mathcal {L}}^0\)-theory given by these axioms and axiom schemata:
Above and in the following, if a schema named \(\Gamma \)-[name] is specified by a formula involving a meta-variable for a subformula (e.g. \(\phi \) above), then this meta-variable ranges over \(\Gamma \). If \(\Gamma \) is omitted from such a name, then the formula ranges over \({\mathcal {L}}^0\).
We also consider these axioms and schemata:
Apart from adding the Powerset axiom, \({\mathrm {KP}}^{{\mathcal {P}}}\) differs from \({\mathrm {KP}}\) in that the schemata of Separation, Collection and Foundation are extended to broader sets of formulae, using the Takahashi hierarchy instead of the Lévy hierarchy. (\({\mathrm {KP}}\) has \(\Delta _0 \text {-Separation}\), \(\Delta _0 \text {-Collection}\) and \(\Pi _1 \text {-Foundation}\).) Since
the Takahashi hierarchy treats the powerset operation as a bounded operation. It is in this sense that \({\mathrm {KP}}^{{\mathcal {P}}}\) is “generated” from \({\mathrm {KP}}\) by adding powersets.
The theory \({\mathrm {KP}}\) has received a great deal of attention, because of its importance to Gödel’s L (the hierarchy of constructible sets), definability theory, recursion theory and infinitary logic. The “bible” on this subject is [2]. The main sources on \({\mathrm {KP}}^{{\mathcal {P}}}\) seem to be the papers by Friedman and Mathias that are discussed later on in this section.
There is of course much to say about what can and cannot be proved in these theories. \({\mathrm {KP}}\) proves \(\Delta _1\)-Separation, \(\Sigma _1\)-Collection and \(\Sigma _1\)-Replacement. \({\mathrm {KP}}^{{\mathcal {P}}}\) proves \(\Delta _1^{{\mathcal {P}}}\)-Separation, \(\Sigma _1^{{\mathcal {P}}}\)-Collection and \(\Sigma _1^{{\mathcal {P}}}\)-Replacement. Both theories enjoy a decent recursion theorem. In \({\mathrm {KP}}\) we have \(\Sigma _1\)-Recursion and in \({\mathrm {KP}}^{{\mathcal {P}}}\) we have \(\Sigma _1^{{\mathcal {P}}}\)-Recursion. \(\Gamma \)-Recursion is the statement in the meta-theory (in relation to an object base theory) that for any \(\psi (x, y) \in \Gamma \) provably defining a total function G on the universe, there is \(\phi (x, y) \in \Gamma \) provably defining a a total function F on the universe, such that provably  .
.
\(\Sigma _1\)-Recursion is quite important in that it enables development of first-order logic and model theory. Moreover, it enables \({\mathrm {KP}}\) to prove the totality of the rank-function, but (in the absence of Powerset) it is not sufficient to establish that the function \(\alpha \mapsto V_\alpha \) is total on the ordinals. However, thanks to \(\Sigma _1^{{\mathcal {P}}}\)-Recursion, \({\mathrm {KP}}^{{\mathcal {P}}}\) does prove the latter claim, and this is needed for certain arguments in Sect. 7, particularly in the proof of our Friedman-style embedding theorem. Also of interest, though not used in this paper, is that neither of the theories proves the existence of an uncountable ordinal. (This may be seen from the short discussion about the Church–Kleene ordinal later on in the section.) However, \({\mathrm {KP}}^{{\mathcal {P}}}\) augmented with the axiom of Choice proves the existence of an uncountable ordinal, essentially because Choice gives us that \({{\mathcal {P}}}(\omega )\) can be well-ordered.
There is also a philosophical reason for considering \({\mathrm {KP}}\) and \({\mathrm {KP}}^{{\mathcal {P}}}\), in that they encapsulate a more parsimonious ontology of sets than \({\mathrm {ZF}}\). If a is an element of an \({\mathcal {L}}^0\)-structure \({\mathcal {M}}\), then \(a_{\mathcal {M}}\) denotes the set \(\{x \in {\mathcal {M}} \mid {\mathcal {M}} \models x \in a\}\). A set x is transitive if \(\forall u \in x \cdot u \subseteq x\). It is supertransitive if additionally \(\forall u \in x \cdot \forall v \subseteq u \cdot v \in x\). The transitive closure\({\mathrm {TC}}(x)\) of a set x is its closure under elements of elements, i.e. the least superset of x such that \(\forall u \in {\mathrm {TC}}(x) \cdot \forall r \in u \cdot r \in {\mathrm {TC}}(x)\). The supertransitive closure\({\mathrm {STC}}(x)\) of a set x is its closure under elements of elements and subsets of elements, i.e. the least superset of x such that \(\forall u \in {\mathrm {STC}}(x) \cdot \forall r \in u \cdot r \in {\mathrm {STC}}(x)\) and \(\forall u \in {\mathrm {STC}}(x) \cdot \forall v \subseteq u \cdot v \in {\mathrm {STC}}(x)\). \({\mathrm {KP}}\) proves that \({\mathrm {TC}}(x)\) exists for all x, and \({\mathrm {KP}}^{{\mathcal {P}}}\) proves that \({\mathrm {STC}}(x)\) exists for all x.
If \({\mathcal {M}}\) is a model of \({\mathrm {KP}}\), a is an element of \({\mathcal {M}}\), and \(\phi (x)\) is a \(\Delta _0\)-formula of set theory, then it is straightforward to show that
The reason for this equivalence is that a quantifier in a \(\Delta _0\)-formula can only range over a subset of the transitive closure of \(\{a\}\).
Similarly, if \({\mathcal {M}}\) is a model of \({\mathrm {KP}}^{{\mathcal {P}}}\), a is an element of \({\mathcal {M}}\), and \(\phi (x)\) is a \(\Delta _0^{{\mathcal {P}}}\)-formula of set theory, then
Thus, the Separation and Collection schemata of \({\mathrm {KP}}\) and \({\mathrm {KP}}^{{\mathcal {P}}}\) only apply to formulae whose truth depends exclusively on the part of the model which is “below” the parameters and free variables appearing in the formula (in the respective senses specified above).
Friedman’s groundbreaking paper [10], established several important results in the model theory of \({\mathrm {KP}}^{{\mathcal {P}}}\). Section 7 is concerned with generalizing and refining one of these results (Theorem 4.1 of that paper), as well as related results. In its simplest form, this result is that every countable non-standard model of \({\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1^{{\mathcal {P}}} \text {-Separation}\) has a proper self-embedding.
A second important result of Friedman’s paper (its Theorem 2.3) is that every countable standard model of \({\mathrm {KP}}^{{\mathcal {P}}}\) is the well-founded part of a non-standard model of \({\mathrm {KP}}^{{\mathcal {P}}}\).
Thirdly, let us also consider Theorem 2.6 of Friedman’s paper. This theorem says that any countable model of \({\mathrm {KP}}\) can be extended to a model of \({\mathrm {KP}}^{{\mathcal {P}}}\) with the same ordinals. The ordinal height of a standard model of \({\mathrm {KP}}\) is the ordinal representing the order type of the ordinals of the model. An ordinal is said to be admissible if it is the ordinal height of some model of \({\mathrm {KP}}\). This notion turns out to be closely connected with recursion theory. For example, the first admissible ordinal is the Church–Kleene ordinal\(\omega _1^{\mathrm {CK}}\), which may also be characterized as the least ordinal which is not order-isomorphic to a recursive well-ordering of the natural numbers. So in particular, Friedman’s theorem shows that every countable admissible ordinal is also the ordinal height of some model of \({\mathrm {KP}}^{{\mathcal {P}}}\).
Another important paper on \({\mathrm {KP}}^{{\mathcal {P}}}\) is Mathias’s [19], which contains a large body of results on weak set theories. See its Sect. 6 for results on \({\mathrm {KP}}^{{\mathcal {P}}}\). One of many results established there is its Theorem 6.47, which shows that \({\mathrm {KP}}^{{\mathcal {P}}} + V = L\) proves the consistency of \({\mathrm {KP}}^{{\mathcal {P}}}\), where \(V = L\) is the statement that every set is Gödel constructible.
From the perspective of this paper, the main \({\mathrm {KP}}^{{\mathcal {P}}}\)-style set theory of interest is \({\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1^{{\mathcal {P}}} \text {-Separation}\), because it is for non-standard countable models of this theory that Friedman’s embedding theorem holds universally. Returning to the philosophical discussion on parsimony above, this theory of affirms the existence of more sets, as arising from applying Separation to \(\Sigma _1^{{\mathcal {P}}}\)-formulae. The truth of such formulae can be given a similar characterization as we gave for \(\Delta _0^{{\mathcal {P}}}\)-formulae: If \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}}\), \(p \in {\mathcal {M}}\) and \(\delta (x, y) \in \Delta _0^{{\mathcal {P}}}\), then
Proposition 4.2
Useful relationships between axioms to be considered:
-
(a)
\({\mathrm {KP}}^{{\mathcal {P}}} \vdash \Delta _1^{{\mathcal {P}}}\text {-Separation}, \Sigma _1^{{\mathcal {P}}}\text {-Collection}, \Sigma _1^{{\mathcal {P}}}\text {-Replacement}.\)
-
(b)
\({\mathrm {KP}}^{{\mathcal {P}}} \vdash \) “the function \(\alpha \mapsto V_\alpha \) is total on the ordinals”.
-
(c)
\({\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1^{{\mathcal {P}}} \text {-Separation} \vdash \text {Strong }\Sigma _1^{{\mathcal {P}}}\text {-Collection}\).
-
(d)
For each \(n \in {\mathbb {N}}\), \({\mathrm {KP}}^{{\mathcal {P}}} \vdash \Sigma _n^{{\mathcal {P}}} \text {-Separation} \leftrightarrow \mathrm B_n^{{\mathcal {P}}} \text {-Separation}.\)
Proof
For (a) we refer to [19]. The others are routine. \(\square \)
We shall now establish some basic closure properties in the Takahashi hierarchy. These will often be used without explicit reference to this proposition.
Proposition 4.3
Take \({\mathrm {KP}}^{{\mathcal {P}}}\) as base theory.
-
(a)
\(\Delta _1^{{\mathcal {P}}}\) is closed under boolean connectives. Moreover, if f is a \(\Sigma _1^{{\mathcal {P}}}\)-function and \(\phi \in \Delta _1^{{\mathcal {P}}}\), then the formulae \(\forall x \in f(y) \cdot \phi \), \(\exists x \in f(y) \cdot \phi \), \(\forall x \subseteq f(y) \cdot \phi \) and \(\exists x \subseteq f(y) \cdot \phi \) are all in \(\Delta _1^{{\mathcal {P}}}\).
-
(b)
\(\Sigma _1^{{\mathcal {P}}}\) is closed under disjunction and conjunction. Moreover, if f is a \(\Sigma _1^{{\mathcal {P}}}\)-function and \(\phi \in \Sigma _1^{{\mathcal {P}}}\), then the formulae \(\forall x \in f(y) \cdot \phi \), \(\exists x \in f(y) \cdot \phi \), \(\forall x \subseteq f(y) \cdot \phi \) and \(\exists x \subseteq f(y) \cdot \phi \) are all in \(\Sigma _1^{{\mathcal {P}}}\).
-
(c)
If f is a \(\Sigma _1^{{\mathcal {P}}}\)-function, then it is a \(\Delta _1^{{\mathcal {P}}}\)-function.
Proof
We follow the proof of Theorem 1 in [23]. Let \(\phi \), \(\psi \) be \({\mathcal {L}}^0\)-formulae. By mere logic,
Assume that \(\phi \) and \(\psi \) are in \(\Sigma _1^{{\mathcal {P}}}\). By set-theory,
In particular, the first equivalence follows from Pair, the second follows from \(\Sigma _1^{{\mathcal {P}}}\)-Collection, and the third follows from Powerset and \(\Sigma _1^{{\mathcal {P}}}\)-Collection.
Suppose that f is defined by a \(\Sigma _1^{{\mathcal {P}}}\)-formula F(x, y), such that \(f(x) = y \leftrightarrow F(x, y)\). By considering the formula
we see that f is actually a \(\Delta _1^{{\mathcal {P}}}\)-function. Now note that by logic, for any \(\phi \in {\mathcal {L}}^0\),
With all these equivalences at hand, the proposition is easily verified. \(\square \)
The fact that \({\mathrm {KP}}^{{\mathcal {P}}}\) proves the existence of the V-hierarchy is very useful. For example, it enables the following result.
Proposition 4.4
For each \(1 \le k < \omega \), \({\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _k^{{\mathcal {P}}} \text {-Separation} \vdash {\mathrm {B}}_k^{{\mathcal {P}}} \text {-Foundation}\).
Proof
Recall that \(\Sigma _k^{{\mathcal {P}}} \text {-Separation}\) implies \({\mathrm {B}}_k^{{\mathcal {P}}} \text {-Separation}\). Let \(\phi (x) \in {\mathrm {B}}_k^{{\mathcal {P}}}[x]\). Suppose there is a such that \(\phi (a)\). By \({\mathrm {B}}_k^{{\mathcal {P}}}\)-Separation, let
and note that \(a \in A.\) By \(\Sigma _1\)-Separation, let
Since R is a non-empty set of ordinals, it has a least element \(\rho \). Let \(a' \in A\) such that \({\mathrm {rank}}(a') = \rho \). Then we have \(\forall x \in a \cdot \lnot \phi (x)\), as desired. \(\square \)
5 ZFC, GBC and “Ord is weakly compact”
A set s is ordinal definable if there is \(n \in {\mathbb {N}}\), ordinals \(\alpha , \beta _1, \dots , \beta _n\), and a formula \(\phi \), for which s is the unique set such that  . \({\mathrm {OD}}\) is defined as the class of ordinal definable sets. A set t is hereditarily ordinal definable if every element in the transitive closure of \(\{t\}\) is ordinal definable. \({\mathrm {HOD}}\) is defined as the class of hereditarily ordinal definable sets.
. \({\mathrm {OD}}\) is defined as the class of ordinal definable sets. A set t is hereditarily ordinal definable if every element in the transitive closure of \(\{t\}\) is ordinal definable. \({\mathrm {HOD}}\) is defined as the class of hereditarily ordinal definable sets.
\({\mathrm {ZFC}}\) plus the axiom
has definable Skolem functions.
If \({\mathcal {L}}\) is an expansion of \({\mathcal {L}}^0\) with more symbols, then \({\mathrm {ZF}}({\mathcal {L}})\) denotes the theory
by which is meant that the schemata of Separation and Replacement are extended to all formulae in \({\mathcal {L}}\). \({\mathrm {ZFC}}({\mathcal {L}})\) is defined analogously.
We will also consider the axiom “\({\mathrm {Ord}}\) is weakly compact”, in the context of \({\mathrm {GBC}}\). It is defined as “Every binary tree of height \({\mathrm {Ord}}\) has a branch.” The new notions used in the definiens are now to be defined. Let \(\alpha \) be an ordinal. A binary tree is a (possibly class) structure \({\mathcal {T}}\) with a binary relation \(<_{\mathcal {T}}\), such that:
-
(i)
Every element of \({\mathcal {T}}\) (called a node) is a function from an ordinal to 2;
-
(ii)
For every \(f \in {\mathcal {T}}\) and every ordinal \(\xi < \mathrm {dom}(f)\), we have
 ;
; -
(iii)
For all \(f, g \in {\mathcal {T}}\),

Suppose that \({\mathcal {T}}\) is a binary tree. The height of \({\mathcal {T}}\), denoted \({\mathrm {height}}({\mathcal {T}})\), is \(\{ \xi \mid \exists f \in {\mathcal {T}} \cdot \mathrm {dom}(f) = \xi \}\) (which is either an ordinal or the class \({\mathrm {Ord}}\)). A branch in \({\mathcal {T}}\) is a (possibly class) function \(F : {\mathrm {Ord}} \rightarrow {\mathcal {T}}\), such that for all ordinals \(\xi \in {\mathrm {height}}({\mathcal {T}})\), \(\mathrm {dom}(F(\alpha )) = \alpha \), and for all ordinals \(\alpha < \beta \in {\mathrm {height}}({\mathcal {T}})\), \(F(\alpha ) <_{\mathcal {T}} F(\beta )\). Moreover, for each ordinal \(\alpha \in {\mathrm {height}}({\mathcal {T}})\), we define

Proposition 5.1
\({\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\text { is weakly compact''} \vdash \text {Global Choice}\), where
Proof-sketch
Consider the class tree of well-orderings of \(V_\alpha \), for all ordinals \(\alpha \): The well-orderings are ordered by  . Using \(\text {``}{\mathrm {Ord}}\text { is weakly compact''}\), one can show that this tree has a branch. From this branch a class-function witnessing global choice can be constructed. \(\square \)
. Using \(\text {``}{\mathrm {Ord}}\text { is weakly compact''}\), one can show that this tree has a branch. From this branch a class-function witnessing global choice can be constructed. \(\square \)
In [6] it is shown that the \({\mathcal {L}}^0\)-consequences of \({\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\text { is weakly compact''}\) are the same as for \({\mathrm {ZFC}} + \Phi \), where
In particular, they are equiconsistent. Let us therefore define n-Mahlo and explain why \(V_\kappa \prec _{\Sigma _n} V\) can be expressed as a sentence.
\(V_\kappa \prec _{\Sigma _n} V\) is expressed by a sentence saying that for all \(\Sigma _n\)-formulae \(\phi (\vec {x})\) of set theory and for all \(\vec {a} \in V_\kappa \) matching the length of \(\vec {x}\), we have  . Here we utilize the partial satisfaction relations \({\mathrm {Sat}}_{\Sigma _n}\), introduced to set theory in [18].
. Here we utilize the partial satisfaction relations \({\mathrm {Sat}}_{\Sigma _n}\), introduced to set theory in [18].
In contrast to the result above, Enayat has communicated to the author that there are countable models of \({\mathrm {ZFC}} + \Phi \) that do not expand to models of \({\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\text { is weakly compact''}\). In particular, such is the fate of Paris models, i.e. models of \({\mathrm {ZFC}}\) each of whose ordinals is definable in the model. An outline of a proof: Let \({\mathcal {M}}\) be a Paris model. There is no ordinal \(\alpha \) in \({\mathcal {M}}\), such that \({\mathcal {M}}_\alpha \prec {\mathcal {M}}\), where  , because that would entail that a correct satisfaction relation is definable in \({\mathcal {M}}\) contradicting Tarski’s well-known theorem on the undefinability of truth. Suppose that \({\mathcal {M}}\) expands to a model \(({\mathcal {M}}, {\mathcal {A}}) \models {\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\text { is weakly compact''}\). Then by the proof of Theorem 4.5(i) in [5], \({\mathcal {M}}\) has a safe satisfaction relation \({\mathrm {Sat}} \in {\mathcal {A}}\) (see the definition preceding Lemma 6.14) below. But then there is, by Lemma 6.14, unboundedly many ordinals \(\alpha \) in \({\mathcal {M}}\) such that \({\mathcal {M}}_\alpha \prec {\mathcal {M}}\).
, because that would entail that a correct satisfaction relation is definable in \({\mathcal {M}}\) contradicting Tarski’s well-known theorem on the undefinability of truth. Suppose that \({\mathcal {M}}\) expands to a model \(({\mathcal {M}}, {\mathcal {A}}) \models {\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\text { is weakly compact''}\). Then by the proof of Theorem 4.5(i) in [5], \({\mathcal {M}}\) has a safe satisfaction relation \({\mathrm {Sat}} \in {\mathcal {A}}\) (see the definition preceding Lemma 6.14) below. But then there is, by Lemma 6.14, unboundedly many ordinals \(\alpha \) in \({\mathcal {M}}\) such that \({\mathcal {M}}_\alpha \prec {\mathcal {M}}\).
Moreover, it is shown in [8] that for every model \({\mathcal {M}} \models {\mathrm {ZFC}}\) and the collection \({\mathcal {A}}\) of definable subsets of \({\mathcal {M}}\), we have \(({\mathcal {M}}, {\mathcal {A}}) \models {\mathrm {GBC}} + \lnot \text {``}{\mathrm {Ord}}\text { is weakly compact''}\).
6 Non-standard models of set theory
This section contains basic material on non-standard models of set theory. An expanded version of this section with more proofs is found as §4.6 of [12].
If \({\mathcal {M}}\) is an \({\mathcal {L}}^0\)-structure, and a is a set or class in \({\mathcal {M}}\), then the externalization of a, denoted \(a_{\mathcal {M}}\), is defined as \(\{x \in {\mathcal {M}} \mid x \in ^{\mathcal {M}} a\}\). If \(E = \in ^{\mathcal {M}}\), then the notation \(a_E\) is also used for \(a_{\mathcal {M}}\). If \(f \in {\mathcal {M}}\) and \({\mathcal {M}} \models ``f\text { is a function''}\), then we say that f is a function internal to \({\mathcal {M}}\). If \(f \in {\mathcal {M}}\) is a function internal to \({\mathcal {M}}\), then \(f_{\mathcal {M}}\) also denotes the externalization of this function: \(\forall x, y \in {\mathcal {M}}. (f_{\mathcal {M}}(x) = y \leftrightarrow {\mathcal {M}} \models f\,(x) = y)\). Moreover, if \(a \in {\mathcal {M}}\) codes a structure internal to \({\mathcal {M}}\), then \(a_{\mathcal {M}}\) also denotes the externalization of this structure; in particular, if R codes a relation in \({\mathcal {M}}\), then \(\forall x, y \in {\mathcal {M}} \cdot ( x R_{\mathcal {M}} y \leftrightarrow {\mathcal {M}} \models \langle x, y \rangle \in R)\). For example, recall that \({\mathbb {N}}^{\mathcal {M}}\) denotes the interpretation of \({\mathbb {N}}\) in \({\mathcal {M}}\) (assuming that \({\mathcal {M}}\) satisfies that the standard model of arithmetic exists); then \({\mathbb {N}}^{\mathcal {M}}_{\mathcal {M}}\) denotes the externalization of this model (which might be non-standard).
Let \({\mathcal {M}} \models {\mathrm {KP}}\). Then every element of \({\mathcal {M}}\) has a rank; so for any \(\alpha \in {\mathrm {Ord}}^{\mathcal {M}}\), we can define
We say that an embedding \(i : {\mathcal {S}} \rightarrow {\mathcal {M}}\) of an \({\mathcal {L}}^0\)-structure \({\mathcal {S}}\) into \({\mathcal {M}}\) is bounded (by\(\alpha \in {\mathrm {Ord}}^{\mathcal {M}}\)) if \(i({\mathcal {S}}) \subseteq {\mathcal {M}}_\alpha \).
Definition 6.1
Let \({\mathcal {M}} = (M, E)\) be a model in \({\mathcal {L}}^0\). It is standard if E is well-founded. Assume that \({\mathcal {M}}\) is a model of \({\mathrm {KP}}\). Then the usual rank-function \({\mathrm {rank}}: M \rightarrow {\mathrm {Ord}}^{\mathcal {M}}\) is definable in \({\mathcal {M}}\). Therefore \({\mathcal {M}}\) is non-standard iff  is not well-founded. \(m \in {\mathcal {M}}\) is standard in\({\mathcal {M}}\) if
is not well-founded. \(m \in {\mathcal {M}}\) is standard in\({\mathcal {M}}\) if  is standard.
is standard.
-
The ordinal standard part of \({\mathcal {M}}\), denoted \({\mathrm {OSP}}({\mathcal {M}})\), is defined:

We say that \({\mathcal {M}}\) is \(\omega \)-non-standard if \({\mathrm {OSP}}({\mathcal {M}}) = \omega \).
-
The well-founded part of \({\mathcal {M}}\), denoted \({\mathrm {WFP}}({\mathcal {M}})\), is the substructure of \({\mathcal {M}}\) on the elements of standard rank:

-
A set of the form \(c_E \cap A\), where \(c \in M\) and \(A \subseteq M\), is said to be a subset of Acoded in\({\mathcal {M}}\). This notion is extended in the natural way to arbitrary injections into M. We define:
$$\begin{aligned} {\mathrm {Cod}}_A({\mathcal {M}}) =_{\mathrm {df}}\{c_E \cap A \mid c \in M\}. \end{aligned}$$ -
The standard system of\({\mathcal {M}}\)over\(A \subseteq {\mathcal {M}}\), denoted \({\mathrm {SSy}}_A({\mathcal {M}})\), is obtained by expanding
 to an \({\mathcal {L}}^1\)-structure, adding \({\mathrm {Cod}}_A({\mathcal {M}})\) as classes:
to an \({\mathcal {L}}^1\)-structure, adding \({\mathrm {Cod}}_A({\mathcal {M}})\) as classes: 
for any \(x \in A\), \(c \in {\mathcal {M}}\) and \(C \in {\mathrm {Cod}}_A({\mathcal {M}})\), such that \(C = c_E \cap A\).
Moreover, we define
$$\begin{aligned} {\mathrm {SSy}}({\mathcal {M}}) =_{\mathrm {df}}{\mathrm {SSy}}_{{\mathrm {WFP}}({\mathcal {M}})}({\mathcal {M}}). \end{aligned}$$
Definition 6.2
Let \(i : {\mathcal {M}} \rightarrow {\mathcal {N}}\) be an embedding of models of \({\mathrm {KP}}\).
-
i is initial, if
$$\begin{aligned} \forall m \in {\mathcal {M}} \cdot \forall n \in {\mathcal {N}} \cdot (n \in ^{\mathcal {N}} i(m) \rightarrow n \in i({\mathcal {M}})). \end{aligned}$$This is equivalent to:
$$\begin{aligned} \forall m \in {\mathcal {M}} \cdot i(m_{\mathcal {M}}) = i(m)_{\mathcal {N}}. \end{aligned}$$ -
i is \({{\mathcal {P}}}\)-initial (or power-initial), if it is initial and powerset preserving in the sense:
$$\begin{aligned} \forall m \in {\mathcal {M}} \cdot \forall n \in {\mathcal {N}} \cdot (n \subseteq ^{\mathcal {N}} m \rightarrow n \in i({\mathcal {M}})). \end{aligned}$$ -
i is rank-initial, if
$$\begin{aligned} \forall m \in {\mathcal {M}} \cdot \forall n \in {\mathcal {N}} \cdot ({\mathrm {rank}}^{\mathcal {N}}(n) \le ^{\mathcal {N}} {\mathrm {rank}}^{\mathcal {N}}(i(m)) \rightarrow n \in i({\mathcal {M}})). \end{aligned}$$ -
i is topless, if it is bounded and
$$\begin{aligned} \forall \beta \in {\mathrm {Ord}}^{\mathcal {N}} {\setminus } i({\mathcal {M}}) \cdot \exists \beta ' \in {\mathrm {Ord}}^{\mathcal {N}} {\setminus } i({\mathcal {M}}) \cdot \beta ' <^{\mathcal {N}} \beta . \end{aligned}$$ -
i is strongly topless, if it is bounded and for each \(f \in {\mathcal {N}}\) with \(\alpha , \beta \in {\mathrm {Ord}}^{\mathcal {N}}\) satisfying
$$\begin{aligned} ({\mathcal {N}} \models f : \alpha \rightarrow \beta ) \wedge \alpha _{\mathcal {N}} \supseteq i({\mathrm {Ord}}^{\mathcal {M}}), \end{aligned}$$there is \(\nu \in {\mathrm {Ord}}^{\mathcal {N}} {\setminus } i({\mathcal {M}})\) such that for all \(\xi \in i({\mathrm {Ord}}^{\mathcal {M}})\),
$$\begin{aligned} f_{\mathcal {N}}(\xi ) \not \in i({\mathcal {M}}) \Leftrightarrow {\mathcal {N}} \models f\,(\xi ) > \nu . \end{aligned}$$ -
i is \(\omega \)-topless, if it is bounded and not \(\omega \)-coded from above, meaning that for each \(f \in {\mathcal {N}}\) with \(\alpha , \beta \in {\mathrm {Ord}}^{\mathcal {N}}\) satisfying
$$\begin{aligned} ({\mathcal {N}} \models f : \alpha \rightarrow \beta ) \wedge \alpha _{\mathcal {N}} \supseteq \omega \wedge \forall k < \omega . f_{\mathcal {N}}(k) \in {\mathrm {Ord}}^{\mathcal {N}} {\setminus } i({\mathcal {M}}), \end{aligned}$$there is \(\nu \in {\mathrm {Ord}}^{\mathcal {N}} {\setminus } i({\mathcal {M}})\) such that \(\nu <^{\mathcal {N}} f_{\mathcal {N}}(k)\), for all \(k < \omega \).
The notions of initiality are often combined with some notion of toplessness, yielding notions of cut. In particular, an embedding i is a rank-cut if it is topless and rank-initial, and i is a strong rank-cut if it is strongly topless and rank-initial.
It is easily seen that if i is rank-initial and proper, then it is bounded, so the first condition of toplessness is satisfied. Moreover, we immediately obtain the following implications:
Proofs of the following results are found in §4.6 of [12].
Lemma 6.3
(\(\Sigma _n^{{\mathcal {P}}}\)-Overspill) Let \(n \in {\mathbb {N}}\) and suppose that \({\mathcal {S}}\) is a rank-cut of \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Pi _n^{{\mathcal {P}}} \text {-Foundation}\), that \(m \in {\mathcal {M}}\), and that \(\sigma (x, y) \in \Sigma _n^{{\mathcal {P}}}[x, y]\). If for every ordinal \(\xi \in {\mathcal {S}}\), there is an ordinal \(\xi <^{\mathcal {M}} \zeta \in {\mathcal {S}}\) such that \({\mathcal {M}} \models \sigma (\zeta , m)\), then for every ordinal \(\nu \in {\mathcal {M}} {\setminus } {\mathcal {S}}\) there is an ordinal \(\nu >^{\mathcal {M}} \mu \in {\mathcal {M}} {\setminus } {\mathcal {S}}\), such that \({\mathcal {M}} \models \sigma (\mu , m)\).
Proposition 6.4
Let \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}}\) and suppose that \(i : {\mathcal {M}} \rightarrow {\mathcal {N}}\) is an elementary embedding. Then i is initial if, and only if, it is rank-initial.
Proposition 6.5
Let \({\mathcal {M}} \models {\mathrm {KP}}\). An element \(m_0 \in {\mathcal {M}}\) is standard iff \({\mathrm {rank}}^{\mathcal {M}}(m_0)\) is standard. If \({\mathcal {M}}\) is non-standard, then \({\mathrm {WFP}}({\mathcal {M}})\) is a rank-cut of \({\mathcal {M}}\).
Proposition 6.6
Let \(i : {\mathcal {M}} \rightarrow {\mathcal {N}}\) and \(j : {\mathcal {N}} \rightarrow {\mathcal {O}}\) be embeddings of models of \({\mathrm {KP}}\).
-
(a)
If i is topless and j is initial, then \(j \circ i : {\mathcal {M}} \rightarrow {\mathcal {O}}\) is topless.
-
(b)
If i is strongly topless and j is rank-initial, then \(j \circ i : {\mathcal {M}} \rightarrow {\mathcal {O}}\) is strongly topless.
Proof
-
(a)
Let \(\gamma \in {\mathrm {Ord}}({\mathcal {O}}) {\setminus } j\circ i({\mathcal {M}})\). By toplessness, there are \(\beta ' <^{\mathcal {N}} \beta \in {\mathrm {Ord}}({\mathcal {N}}) {\setminus } i({\mathcal {M}})\). If \(j(\beta ') <^{\mathcal {O}} \gamma \), then we are done. Otherwise, \(\gamma <^{\mathcal {O}} j(\beta )\), so that by initiality \(\gamma \in j({\mathcal {N}})\). By toplessness, this yields \(\beta '' \in {\mathrm {Ord}}^{\mathcal {N}} {\setminus } i({\mathcal {M}})\) such that \(j(\beta '') < \gamma \).
-
(b)
Let \(f \in {\mathcal {O}}\) with \(\alpha , \beta \in {\mathrm {Ord}}^{\mathcal {O}}\) satisfying
$$\begin{aligned} ({\mathcal {O}} \models f : \alpha \rightarrow \beta ) \wedge \alpha _{\mathcal {O}} \supseteq (j \circ i)({\mathrm {Ord}}^{\mathcal {M}}). \end{aligned}$$By toplessness of i and initiality of j, there is \(\gamma \in {\mathrm {Ord}}^{\mathcal {N}}\), such that \(\gamma _{\mathcal {N}} \supseteq i({\mathrm {Ord}}^{\mathcal {M}})\) and \(j(\gamma ) \le ^{\mathcal {O}} \alpha \). In \({\mathcal {O}}\), let \(f' : j(\gamma ) \rightarrow j(\gamma )\) be the “truncation” of f defined by \(f'(\xi ) = f(\xi )\), if \(f(\xi ) < j(\gamma )\), and by \(f'(\xi ) = 0\), if \(f(\xi ) \ge j(\gamma )\). Note that \({\mathcal {O}} \models {\mathrm {rank}}(f') \le j(\gamma ) + 2\). So by rank-initiality, there is \(g' \in {\mathcal {N}}\), such that \(j(g') = f'\). Consequently, \({\mathcal {N}} \models g' : \gamma \rightarrow \gamma \), and by initiality of j, \((j(g'))_{\mathcal {O}} = f'_{\mathcal {O}}\). By strong toplessness of i, there is \(\nu \in {\mathrm {Ord}}^{\mathcal {N}} {\setminus } i({\mathcal {M}})\) such that for all \(\xi \in i({\mathrm {Ord}}^{\mathcal {M}})\),
$$\begin{aligned} g'_{\mathcal {N}}(\xi ) \not \in i({\mathcal {M}}) \Leftrightarrow {\mathcal {N}} \models g'(\xi ) > \nu . \end{aligned}$$It follows that for all \(\xi \in (j \circ i)({\mathrm {Ord}}^{\mathcal {M}})\),
$$\begin{aligned} f_{\mathcal {O}}(\xi ) \not \in (j \circ i)({\mathcal {M}}) \Leftrightarrow {\mathcal {O}} \models f(\xi ) > j(\nu ). \end{aligned}$$So \(j \circ i\) is strongly topless. \(\square \)
Lemma 6.7
Let \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}}\) be \(\omega \)-non-standard and let \(\alpha _0 \in {\mathrm {Ord}}^{\mathcal {M}}\). For each \(k < \omega \), let \(\alpha _k \in {\mathrm {Ord}}^{\mathcal {M}}\) such that \({\mathcal {M}} \models \alpha _k = \alpha _0 + k^{\mathcal {M}}\). Then \(\bigcup _{k < \omega } {\mathcal {M}}_{\alpha _k}\) is an \(\omega \)-topless rank-initial substructure of \({\mathcal {M}}\).
Proof
\(\bigcup _{k < \omega } {\mathcal {M}}_{\alpha _k}\) is obviously rank-initial in \({\mathcal {M}}\). Let \(m \in ^{\mathcal {M}} \omega ^{\mathcal {M}}\) be non-standard. Since \(\alpha _0 +^{\mathcal {M}} m \in {\mathcal {M}}\), we have that \(\bigcup _{k < \omega } {\mathcal {M}}_{\alpha _k}\) is bounded in \({\mathcal {M}}\). Moreover, \(\bigcup _{k < \omega } {\mathcal {M}}_{\alpha _k}\) is topless, because otherwise \(\gamma =_{\mathrm {df}}\sup \{\alpha _k \mid k < \omega \}\) exists in \({\mathcal {M}}\) and \({\mathcal {M}} \models \gamma - \alpha _0 = \omega \), which contradicts that \({\mathcal {M}}\) is \(\omega \)-non-standard.
Let \(f : \alpha \rightarrow \beta \) be a function in \({\mathcal {M}}\), where \(\alpha , \beta \in {\mathrm {Ord}}^{\mathcal {M}}\) and
Note that for all \(k < \omega \),
So by \(\Delta _0^{{\mathcal {P}}}\)-Overspill, there is a non-standard \({\mathring{k}} \in ^{\mathcal {M}} \omega ^{\mathcal {M}}\), such that
Hence, \(\alpha _0 +^{\mathcal {M}} {\mathring{k}}\) witnesses \(\omega \)-toplessness of \(\bigcup _{k < \omega } {\mathcal {M}}_{\alpha _k}\). \(\square \)
The following classic result is proved as Theorem 6.15 in [14]:
Theorem 6.8
(Mostowski’s Collapse) If \({\mathcal {M}}\) is a well-founded model of \(\text {Extensionality}\), then there is a unique isomorphism  , such that T is transitive. Moreover,
, such that T is transitive. Moreover,
This theorem motivates the following simplifying assumption:
Assumption 6.9
Every well-founded \({\mathcal {L}}^0\)-model \({\mathcal {M}}\) of \(\text {Extensionality}\) is a transitive set, or more precisely, is of the form  where T is transitive and unique. Every embedding between well-founded \({\mathcal {L}}^0\)-models of \(\text {Extensionality}\) is an inclusion function.
where T is transitive and unique. Every embedding between well-founded \({\mathcal {L}}^0\)-models of \(\text {Extensionality}\) is an inclusion function.
In particular, for any model \({\mathcal {M}}\) of \({\mathrm {KP}}\), \({\mathrm {WFP}}({\mathcal {M}})\) is a transitive set and \({\mathrm {OSP}}({\mathcal {M}})\) is an ordinal.
Proposition 6.10
If \(i : {\mathcal {M}} \rightarrow {\mathcal {N}}\) is an initial embedding between models of \({\mathrm {KP}}\), then:
-
(a)
\(i(x) = x\), for all \(x \in {\mathrm {WFP}}({\mathcal {M}})\).
-
(b)
i is \(\Delta _0\)-elementary. More sharply, for every \(\sigma (\vec {x}) \in \Sigma _1[\vec {x}]\), and for every \(\vec {a} \in {\mathcal {M}}\),
$$\begin{aligned} {\mathcal {M}} \models \sigma (\vec {a}) \Rightarrow {\mathcal {N}} \models \sigma (i(\vec {a})). \end{aligned}$$ -
(c)
If i is \({{\mathcal {P}}}\)-initial, then it is \(\Delta _0^{{\mathcal {P}}}\)-elementary. More sharply, for every \(\sigma (\vec {x}) \in \Sigma _1^{{\mathcal {P}}}[\vec {x}]\), and for every \(\vec {a} \in {\mathcal {M}}\),
$$\begin{aligned} {\mathcal {M}} \models \sigma (\vec {a}) \Rightarrow {\mathcal {N}} \models \sigma (i(\vec {a})). \end{aligned}$$ -
(d)
If i is rank-initial and \({\mathcal {S}}\) is a common bounded substructure of \({\mathcal {M}}\) and \({\mathcal {N}}\), pointwise fixed by i, then \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}}) = {\mathrm {SSy}}_{{\mathcal {S}}}({\mathcal {N}})\).
The proof is routine.
Corollary 6.11
If \(i: {\mathcal {M}} \rightarrow {\mathcal {N}}\) is an embedding between models of \({\mathrm {KP}}^{{\mathcal {P}}}\), then the following are equivalent:
-
(a)
i is rank-initial.
-
(b)
i is \({{\mathcal {P}}}\)-initial.
-
(c)
i is initial, and for each ordinal \(\xi \) in \({\mathcal {M}}\), \(i(V_\xi ^{\mathcal {M}}) = V_{i(\xi )}^{\mathcal {M}}\).
Proof
(a) \(\Rightarrow \) (b) is immediate from the definition.
(b) \(\Rightarrow \) (c): The formula \(x = V_\alpha \) is \(\Sigma _1^{{\mathcal {P}}}\), so by Proposition 6.10 (c), \(i(V_\alpha ^{\mathcal {M}}) = V_{i(\alpha )}^{\mathcal {N}}\), for all ordinals \(\alpha \) in \({\mathcal {M}}\).
(c) \(\Rightarrow \) (a): Let \(a \in {\mathcal {M}}\) with \({\mathcal {M}}\)-rank \(\alpha \), let \(b = i(a)\) with \({\mathcal {N}}\)-rank \(\beta \), and let \(c \in {\mathcal {N}}\) be of \({\mathcal {N}}\)-rank \(\gamma \le ^{\mathcal {N}} \beta \). Since i is an embedding preserving \((\xi \mapsto V_\xi )\), we have that \(b \in ^{\mathcal {N}} i(V_{\alpha + 1})\) and \(i(V_{\alpha + 1}) = V_{\beta '}\), for some \(\beta ' >^{\mathcal {N}} \beta \). Therefore \(c \in i(V_{\alpha +1})\), so since i is initial, we get that \(c \in i({\mathcal {M}})\). \(\square \)
We shall now introduce partial satisfaction relations for the Takahashi hierarchy. The details of this are worked out in §4.4 of [12]. Recall that we have assumed that each \({\mathcal {L}}^0\)-formula is identical to its Gödel code. Moreover, recall that for each \(n \in {\mathbb {N}}\), \({\hat{\Sigma }}^{\mathcal {P}}_n\) and \({\hat{\Pi }}^\mathcal {P}_n\) are defined recursively by: \({\hat{\Delta }}^\mathcal {P}_0 = {\hat{\Sigma }}^{\mathcal {P}}_0 = {\hat{\Pi }}^\mathcal {P}_n\) is the set of \({\mathcal {L}}^0\)-formulae such that every quantifier is of the form ‘\(\exists x \in y\)’, ‘\(\exists x \subseteq y\)’, ‘\(\forall x \in y\)’ or ‘\(\forall x \subseteq y\)’; if \(\phi \) is \({\hat{\Sigma }}^{\mathcal {P}}_n\), then \(\exists x \cdot \phi \) is \({\hat{\Sigma }}^{\mathcal {P}}_n\) and \(\forall x \cdot \phi \) is \({\hat{\Pi }}^\mathcal {P}_{n+1}\); and dually, if \(\phi \) is \({\hat{\Pi }}^\mathcal {P}_n\), then \(\exists x \cdot \phi \) is \({\hat{\Sigma }}^{\mathcal {P}}_{n+1}\) and \(\forall x \cdot \phi \) is \({\hat{\Pi }}^\mathcal {P}_{n}\).
Theorem 6.12
For each \(n \in {\mathbb {N}}\), there are formulae \({\mathrm {Sat}}_{\Sigma _n^{{\mathcal {P}}}}(\sigma , \vec {x}) \in {\hat{\Sigma }}_{\mathrm {max}(1, n)}^{{\mathcal {P}}}\) and \({\mathrm {Sat}}_{\Pi _n^{{\mathcal {P}}}}(\pi , \vec {x}) \in {\hat{\Pi }}_{\mathrm {max}(1, n)}^{{\mathcal {P}}}\), such that for any model \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}}\), any \(\sigma \in {\hat{\Sigma }}_n^\mathcal {P}[\vec {u}]\) and any \(\pi \in {\hat{\Pi }}_n^\mathcal {P}[\vec {u}]\),
We write \({\mathrm {Sat}}_{\Delta _0^{{\mathcal {P}}}}\) for \({\mathrm {Sat}}_{\Sigma _0^{{\mathcal {P}}}}\) and \({\mathrm {Sat}}_{\Pi _0^{{\mathcal {P}}}}\), as they are equivalent. By the theorem, \({\mathrm {Sat}}_{\Delta _0^{{\mathcal {P}}}} \in \Delta _1^{{\mathcal {P}}}\).
Lemma 6.13
Let \(n \in {\mathbb {N}}\), suppose that \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _n^{{\mathcal {P}}}\text {-Separation}\) is non-standard, and let \({\mathcal {S}}\) be a bounded substructure of \({\mathcal {M}}\). For each \(\vec {a} \in {\mathcal {M}}\), we have that \({\mathrm {tp}}_{{\hat{\Sigma }}_n^\mathcal {P}, {\mathcal {S}}}(\vec {a})\) and \({\mathrm {tp}}_{{\hat{\Pi }}_n^\mathcal {P}, {\mathcal {S}}}(\vec {a})\) are coded in \({\mathcal {M}}\).
Proof
Let \(\alpha \) be an ordinal in \({\mathcal {M}}\), such that \({\mathcal {S}} \subseteq {\mathcal {M}}_\alpha \). Note that if \(n = 0\), then \({\mathcal {M}} \models \Delta _1^{{\mathcal {P}}}\text {-Separation}\), and for any \(n \in {\mathbb {N}}\) we have both \(\Sigma _n^{{\mathcal {P}}}\)-Separation and \(\Pi _n^{{\mathcal {P}}}\)-Separation in \({\mathcal {M}}\). So by Theorem 6.12, we have these sets in \({\mathcal {M}}\):
By Theorem 6.12, s codes \({\mathrm {tp}}_{{\hat{\Sigma }}_n^\mathcal {P}, {\mathcal {S}}}(\vec {a})\), and p codes \({\mathrm {tp}}_{{\hat{\Pi }}_n^\mathcal {P}, {\mathcal {S}}}(\vec {a})\). \(\square \)
Theorem 6.15 below characterizing recursively saturated models of \({\mathrm {ZF}}\) is useful. To state it we introduce this definition: Let \({\mathcal {L}}^0_{\mathrm {Sat}}\) be the language obtained by adding a new binary predicate \({\mathrm {Sat}}\) to \({\mathcal {L}}^0\). We say that \({\mathcal {M}}\)admits a safe satisfaction relation if \({\mathcal {M}}\) expands to an \({\mathcal {L}}^0_{\mathrm {Sat}}\)-structure \(({\mathcal {M}}, {\mathrm {Sat}}^{\mathcal {M}})\), such that
-
(i)
\(({\mathcal {M}}, {\mathrm {Sat}}^{\mathcal {M}}) \models {\mathrm {ZF}}({\mathcal {L}}^0_{\mathrm {Sat}})\),
-
(ii)
For each \(n \in {\mathbb {N}}\):
$$\begin{aligned} ({\mathcal {M}}, {\mathrm {Sat}}^{\mathcal {M}})&\models \forall \sigma \in {\hat{\Sigma _n}} \cdot ({\mathrm {Sat}}(\sigma , x) \leftrightarrow {\mathrm {Sat}}_{\Sigma _n}(\sigma , x)) \\ ({\mathcal {M}}, {\mathrm {Sat}}^{\mathcal {M}})&\models \forall \pi \in {\hat{\Pi _n}} \cdot ({\mathrm {Sat}}(\pi , x) \leftrightarrow {\mathrm {Sat}}_{\Pi _n}(\pi , x)) \end{aligned}$$
We say that \({\mathrm {Sat}}^{\mathcal {M}}\) is a safe satisfaction relation on \({\mathcal {M}}\). For the second condition considered alone, we say that \({\mathrm {Sat}}^{\mathcal {M}}\) is correct for standard formulae.
The following result is found as Theorem 3.2 (and the remark preceding it) in [22].
Theorem 6.14
Let \({\mathcal {M}}\) be a model of \({\mathrm {ZF}}\) that admits a safe satisfaction relation. There are unboundedly many \(\alpha \in {\mathrm {Ord}}^{\mathcal {M}}\), such that \({\mathcal {M}}_\alpha \preceq {\mathcal {M}}.\)
The forward direction of the following result follows from Theorems 1.3 and 3.4 in [22]. The converse is easier, it follows by overspill from the observation that a model of \({\mathrm {ZF}}\) with a safe satisfaction relation codes any recursive type.
Theorem 6.15
Let \({\mathcal {M}} \models {\mathrm {ZF}}\) be countable. The following conditions are equivalent:
-
(a)
\({\mathcal {M}}\) is recursively saturated.
-
(b)
\({\mathcal {M}}\) is \(\omega \)-non-standard and admits a safe satisfaction relation.
Moreover, even if \({\mathcal {M}}\) is not assumed countable, we have (b) \(\Rightarrow \) (a).
Definition 6.16
Let \(i : {\mathcal {M}} \rightarrow {\mathcal {M}}\) be a self-embedding of a model \({\mathcal {M}}\) of \({\mathrm {KP}}\).
-
\(x \in {\mathcal {M}}\) is a fixed point of i, if \(i(x) = x\). The substructure of \({\mathcal {M}}\) of fixed points of i is denoted \({\mathrm {Fix}}(i)\).
-
\(X \subseteq {\mathcal {M}}\) is pointwise fixed by i, if every \(x \in X\) is fixed by i. \(x \in {\mathcal {M}}\) is pointwise fixed by i (or an initial fixed point of i), if \(x_{\mathcal {M}}\) is pointwise fixed by i. The substructure of \({\mathcal {M}}\) of elements pointwise fixed by i, is denoted \({\mathrm {Fix}}^\mathrm {initial}(i)\).
-
\(x \in {\mathcal {M}}\) is a rank-initial fixed point of \({\mathcal {M}}\), if \(\{y \in {\mathcal {M}} \mid {\mathrm {rank}}(y) \le {\mathrm {rank}}(x)\}\) is pointwise fixed by i. The substructure of \({\mathcal {M}}\) of rank-initial fixed points of i is denoted \({\mathrm {Fix}}^{\mathrm {rank}}(i)\).
We say that i is contractive on\(A \subseteq {\mathcal {M}}\) if for all \(x \in A\), we have \({\mathcal {M}} \models {\mathrm {rank}}(i(x)) < {\mathrm {rank}}(x)\).
Assume that \({\mathcal {M}}\) is extensional and \(i : {\mathcal {M}} \rightarrow {\mathcal {M}}\) is initial. Then \(x \in {\mathcal {M}}\) is a fixed point of i if it is pointwise fixed by i. It follows that
Lemma 6.17
Suppose that \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}}\) and that i is a rank-initial self-embedding of \({\mathcal {M}}\) such that  is a rank-initial substructure of \({\mathcal {M}}\). Then \({\mathcal {S}} \preceq _{\Sigma _1^{{\mathcal {P}}}} {\mathcal {M}}\).
is a rank-initial substructure of \({\mathcal {M}}\). Then \({\mathcal {S}} \preceq _{\Sigma _1^{{\mathcal {P}}}} {\mathcal {M}}\).
Proof
We verify \({\mathcal {S}} \preceq _{\Sigma _1^{{\mathcal {P}}} } {\mathcal {M}}\) using the Tarski-Vaught Test (it applies since \(\Sigma _1^{{\mathcal {P}}}\) is closed under subformulae). Let \(\delta (x, \vec {y}) \in \Delta _0^{{\mathcal {P}}}[x, \vec {y}]\), let \(\vec {s} \in {\mathcal {S}}\), and assume that \({\mathcal {M}} \models \exists x \cdot \delta (x, \vec {s})\). We shall now work in \({\mathcal {M}}\): Let \(\xi \) be the least ordinal such that \(\exists x \in V_{\xi + 1} \cdot \delta (x, \vec {s})\). We shall show that \(i(\xi ) = \xi \). Suppose not, then either \(i(\xi ) < \xi \) or \(i(\xi ) > \xi \). If \(i(\xi ) < \xi \), then \(\exists x \in V_{i(\xi ) + 1} \cdot \delta (x, \vec {s})\), contradicting that \(\xi \) is the least ordinal with this property. If \(i(\xi ) > \xi \), then by rank-initiality there is an ordinal \(\zeta < \xi \) such that \(i(\zeta ) = \xi \). But then \(\exists x \in V_{\zeta + 1} \cdot \delta (x, \vec {s})\), again contradicting that \(\xi \) is the least ordinal with this property.
By \(\Delta _0^{{\mathcal {P}}}\)-Separation in \({\mathcal {M}}\), let \(D = \{ x \in V_{\xi + 1} \mid \delta (x, \vec {s}) \}^{\mathcal {M}}\). Since i is \(\Delta _0^{{\mathcal {P}}}\)-elementary and \(\xi , \vec {s} \in {\mathrm {Fix}}(i)\), we have
It immediately follows that \(i(D) \subseteq D\). But by rank-initiality, every x of rank \(\xi \) in \({\mathcal {M}}\) is a value of i, so we even get that \(i(D) = D\). Let \(d \in D\). By initiality and \(D \in {\mathrm {Fix}}(i)\), we have \(d \in {\mathrm {Fix}}(i)\); and by construction of D, \({\mathcal {M}} \models \delta (d, \vec {s})\), as desired. \(\square \)
Lemma 6.18
Suppose that \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}}\) has definable Skolem functions and that i is an automorphism of \({\mathcal {M}}\) such that  . Then \({\mathcal {S}} \preceq {\mathcal {M}}\).
. Then \({\mathcal {S}} \preceq {\mathcal {M}}\).
Proof
Again, we apply The Tarski Test. Let \(\phi (x, \vec {y}) \in {\mathcal {L}}^0\), let \(\vec {s} \in {\mathcal {S}}\), and assume that \({\mathcal {M}} \models \exists x \cdot \phi (x, \vec {s})\). Let \(m \in {\mathcal {M}}\) be a witness of this fact. Let f be a Skolem function for \(\phi (x, \vec {y})\), defined in \({\mathcal {M}}\) by a formula \(\psi (x, \vec {y})\). Then \({\mathcal {M}} \models \psi (m, \vec {s})\), and since i is an automorphism fixing \({\mathcal {S}}\) pointwise, \({\mathcal {M}} \models \psi (i(m), \vec {s})\). But \(\psi \) defines a function, so \({\mathcal {M}} \models m = i(m)\), whence \(m \in {\mathcal {S}}\) as desired. \(\square \)
7 Embeddings between models of set theory
In §4 of [10], a back-and-forth technique was pioneered that utilizes partial satisfaction relations and the ability of non-standard models to code types over themselves (as indicated in Lemma 6.13). Here we will prove refinements of set theoretic results in §4 of [10], as well as generalizations of arithmetic results in [1] and [21] to set theory. We will do so by casting the results in the conceptual framework of forcing. We do so because:
-
The conceptual framework of forcing allows a modular design of the proofs, clarifying which assumptions are needed for what, and whereby new pieces can be added to a proof without having to re-write the other parts. So it serves as an efficient bookkeeping device.
-
It enables us to look at these results from a different angle, and potentially apply theory that has been developed for usage in forcing.
Lemma 7.1
Let \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1^{{\mathcal {P}}}\text {-Separation}\) and \({\mathcal {N}} \models {\mathrm {KP}}^{{\mathcal {P}}}\) be countable and non-standard, and let \({\mathcal {S}}\) be a common rank-cut of \({\mathcal {M}}\) and \({\mathcal {N}}\). Moreover, let \({\mathbb {P}} = \llbracket {\mathcal {M}} \preceq _{\Sigma _1^{{\mathcal {P}}}, {\mathcal {S}}}^{<\omega } {\mathcal {N}}_\beta \rrbracket \) and let \(\beta \in {\mathrm {Ord}}^{\mathcal {N}} {\setminus } {\mathcal {S}}\).
-
(a)
If \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}}) \subseteq {\mathrm {SSy}}_{{\mathcal {S}}}({\mathcal {N}})\), then
$$\begin{aligned} {\mathcal {C}}_{m} =_{\mathrm {df}}\big \{ f \in {\mathbb {P}} \mid m \in \mathrm {dom}(f) \big \} \end{aligned}$$is dense in \({\mathbb {P}}\), for each \(m \in {\mathcal {M}}\).
-
(b)
If \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}}) = {\mathrm {SSy}}_{{\mathcal {S}}}({\mathcal {N}})\), then
$$\begin{aligned} {\mathcal {D}}_{m, n} =_{\mathrm {df}}\big \{ f \in {\mathbb {P}} \mid&m \in \mathrm {dom}(f) \wedge (({\mathcal {N}} \models {\mathrm {rank}}(n) \le {\mathrm {rank}}(f(m))) \rightarrow n \in {\mathrm {image}}(f)) \big \} \end{aligned}$$is dense in \({\mathbb {P}}\), for each \(m \in {\mathcal {M}}\) and \(n \in {\mathcal {N}}\).
-
(c)
If \({\mathcal {N}} = {\mathcal {M}}\), then
$$\begin{aligned} {\mathcal {E}}_{\alpha } =_{\mathrm {df}}\big \{ f \in {\mathbb {P}} \mid \exists m \in \mathrm {dom}(f) \cdot (f\,(m) \ne m \wedge {\mathcal {M}} \models {\mathrm {rank}}(m) = \alpha ) \big \} \end{aligned}$$is dense in \({\mathbb {P}}\), for each \(\alpha \in {\mathrm {Ord}}^{\mathcal {M}} {\setminus } {\mathcal {S}}\).
Note that \({\mathcal {N}}_\beta \) is rank-initial in \({\mathcal {N}}\), so by absoluteness of \(\Delta _0^{{\mathcal {P}}}\)-formulas over rank-initial substructures, we have for any \(n \in {\mathcal {N}}_\beta \), for any \(s \in {\mathcal {S}}\) and for any \(\delta (x, y, z) \in \Delta _0^{{\mathcal {P}}}[x, y, z]\), that

Proof
If \({\mathbb {P}} = \varnothing \), then the result is trivial, so assume that \({\mathbb {P}} \ne \varnothing \). This means in particular that \({\mathrm {Th}}_{\Sigma _1^{{\mathcal {P}}}, {\mathcal {S}}}({\mathcal {M}}) \subseteq {\mathrm {Th}}_{\Sigma _1^{{\mathcal {P}}}, {\mathcal {S}}}({\mathcal {N}}_\beta )\).
(a) Let \(g \in {\mathbb {P}}\). Unravel g as a \(\gamma \)-sequence of ordered pairs \(\langle m_\xi , n_\xi \rangle _{\xi < \gamma }\), where \(\gamma < \omega \). Let \(m_\gamma \in {\mathcal {M}}\) be arbitrary. We need to find f in \({\mathbb {P}}\) extending g, such that \(m_\gamma \in \mathrm {dom}(f)\).
Using \({\mathrm {Sat}}_{\Sigma _1^{{\mathcal {P}}}}\), we have by Lemma 6.13 and \(\Sigma _1^{{\mathcal {P}}}\)-Separation that there is a code c in \({\mathcal {M}}\) for
By \({\mathrm {SSy}}({\mathcal {M}}) \subseteq {\mathrm {SSy}}({\mathcal {N}}_\beta )\), this set has a code d in \({\mathcal {N}}_\beta \) as well. We define the formula
Since \({\mathrm {Sat}}_{\Delta _0^{{\mathcal {P}}}} \in \Delta _1^{{\mathcal {P}}}\), we have \(\phi \in \Sigma _1^{{\mathcal {P}}}\). For every ordinal \(\zeta \in {\mathcal {S}}\), we have \(c \cap V_\zeta = d \cap V_\zeta \in {\mathcal {S}}\), and as witnessed by \(m_{\gamma }\), we have \({\mathcal {M}} \models \phi (\zeta , c, \langle m_\xi \rangle _{\xi < \gamma })\). So by \(g \in {\mathbb {P}}\), we have \({\mathcal {N}}_\beta \models \phi (\zeta , d, \langle n_\xi \rangle _{\xi < \gamma })\) for every ordinal \(\zeta \in {\mathcal {S}}\). Since \({\mathcal {S}}\) is topless in \({\mathcal {N}}_\beta \), there is by \(\Sigma _1^{{\mathcal {P}}}\)-Overspill an ordinal \(\nu \) in \({\mathcal {N}}_\beta {\setminus } {\mathcal {S}}\), such that \({\mathcal {N}}_\beta \models \phi (\nu , d, \langle n_\xi \rangle _{\xi < \gamma })\). Set \(n_{\gamma }\) to some witness of this fact. Put \(f = g \cup \{\langle m_\gamma , n_\gamma \rangle \}\). We proceed to verify that f is \(\Sigma _1^{{\mathcal {P}}}\)-elementary. Let \(s \in {\mathcal {S}}\) and let \(\delta (x, \langle y_\xi \rangle _{\xi< \gamma +1}, z) \in \Delta _0^{{\mathcal {P}}}[x, \langle y_\xi \rangle _{\xi < \gamma +1}, z]\). Now, as desired,
The second implication follows from the choice of \(n_\gamma \) and Theorem 6.12.
(b) Let \(g \in {\mathbb {P}}\). Unravel g as a \(\gamma \)-sequence of ordered pairs \(\langle m_\xi , n_\xi \rangle _{\xi < \gamma }\), where \(\gamma < \omega \). Let \(\xi _0 < \gamma \), and suppose that \(n_\gamma \in {\mathcal {N}}_\beta \), such that \({\mathcal {N}}_\beta \models {\mathrm {rank}}(n_\gamma ) \le {\mathrm {rank}}(g(m_{\xi _0}))\). By (a), it suffices to find f in \({\mathbb {P}}\) extending g, such that \(n_\gamma \in {\mathrm {image}}(f)\).
By \({\mathcal {N}} \models \Delta _1\text {-Separation}\), (\(\dagger \)) and Lemma 6.13, there is a code \(d'\) in \({\mathcal {N}}_\beta \) for
By \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}}) \supseteq {\mathrm {SSy}}_{\mathcal {S}}({\mathcal {N}})\), let \(c'\) be its code in \({\mathcal {M}}\). We define the formula

Since \({\mathrm {Sat}}_{\Delta _0^{{\mathcal {P}}}}\) and the function \((u \mapsto V_{{\mathrm {rank}}(u)})\) are \(\Delta _1^{{\mathcal {P}}}\), we have that \(\psi \) is \(\Pi _1^{{\mathcal {P}}}\). Moreover, \(d' \cap V_\zeta = c' \cap V_\zeta \). Note that for every ordinal \(\zeta \in {\mathcal {S}}\), we have \({\mathcal {N}}_\beta \models \psi (\zeta , d', \langle n_\xi \rangle _{\xi < \gamma })\), as witnessed by \(n_{\gamma }\). It follows from \(g \in {\mathbb {P}}\) that \(\psi (\zeta , c', \langle m_\xi \rangle _{\xi < \gamma })\) is satisfied in \({\mathcal {M}}\) for every ordinal \(\zeta \in {\mathcal {S}}\), whence by \(\Pi _1^{{\mathcal {P}}}\)-Overspill we have \({\mathcal {M}} \models \psi (\mu , c', \langle m_\xi \rangle _{\xi < \gamma })\), for some ordinal \(\mu \in {\mathcal {M}} {\setminus } {\mathcal {S}}\). (It follows from \(\Sigma _1\)-Separation, Proposition 4.4 and Lemma 6.3 that \({\mathcal {M}}\) satisfies \(\Pi _1^{{\mathcal {P}}}\)-Overspill.) Let \(m_\gamma \) be some witness of this fact, and put \(f = g \cup \{\langle m_\gamma , n_\gamma \rangle \}\). We proceed to verify that \(f \in {\mathbb {P}}\). Let \(s \in {\mathcal {S}}\) and let \(\delta (x, \langle y_\xi \rangle _{\xi< \gamma +1}, z) \in \Delta _0^{{\mathcal {P}}}[x, \langle y_\xi \rangle _{\xi < \gamma +1}, z]\). Now, as desired,
The second implication follows from the choice of \(m_\gamma \) and Theorem 6.12.
(c) Let \(\alpha \in {\mathrm {Ord}}^{\mathcal {M}} {\setminus } {\mathcal {S}}\), and let \(g \in {\mathbb {P}}\). Unravel g as a \(\gamma \)-sequence of ordered pairs \(\langle m_\xi , n_\xi \rangle _{\xi < \gamma }\), where \(\gamma < \omega \). We need to find \(m_\gamma \ne n_\gamma \), such that \({\mathcal {M}} \models {\mathrm {rank}}(m_\gamma ) = \alpha \) and \(g \cup \{\langle m_\gamma , n_\gamma \rangle \} \in {\mathbb {P}} = \llbracket {\mathcal {M}} \preceq _{\Sigma _1^{{\mathcal {P}}}, {\mathcal {S}}}^{< \omega } {\mathcal {N}}_\beta \rrbracket \). Note that by rank-initiality and toplessness, there is \(\alpha ' \in {\mathrm {Ord}}^{\mathcal {M}} {\setminus } {\mathcal {S}}\), such that \((\alpha ' + 3 \le \alpha )^{\mathcal {M}}\) and \({\mathcal {M}}_{\alpha '} \supseteq {\mathcal {S}}\).
We proceed to work in \({\mathcal {M}}\): The set \(V_{\alpha +1} {\setminus } V_\alpha \) of sets of rank \(\alpha \) has cardinality \(\beth _{\alpha +1}\), while the set \({{\mathcal {P}}}(V_{\alpha '} \times V_{\alpha '}) \subseteq V_{\alpha ' + 3}\) is strictly smaller, of cardinality less than or equal to \(\beth _{\alpha ' + 3}\). (Here we used \({\mathcal {M}} \models \text {Powerset}\), and the recursive definition \(\beth _0 = 0\), \(\beth _{\xi + 1} = 2^{\beth _\xi }\), \(\beth _\xi = \sup \{\beth _\zeta \mid \zeta < \xi \}\) for limits \(\xi \).) We define a function \(t : V_{\alpha +1} {\setminus } V_\alpha \rightarrow V_{\alpha '+3}\) by
for each \(v \in V_{\alpha +1} {\setminus } V_\alpha \). t exists by \(\Sigma _1^{{\mathcal {P}}}\)-Separation. Since t has a domain of strictly larger cardinality than its co-domain, there are \(m, m'\) of rank \(\alpha \), such that \(m \ne m'\) and \(t(m) = t(m')\).
We return to working in the meta-theory: m and \(m'\) have the same \(\Sigma _1^{{\mathcal {P}}}\)-type with parameters in \({\mathcal {S}} \cup \langle m_\xi \rangle _{\xi < \gamma }\). In other words, for every \(s \in {\mathcal {S}}\) and every \(\delta (x, \langle y_\xi \rangle _{\xi< \gamma }, y_\gamma , z) \in \Delta _0^{{\mathcal {P}}}[x, \langle y_\xi \rangle _{\xi < \gamma }, y_\gamma , z]\), we have ’

On the other hand, by (a) and by \(g \in {\mathbb {P}}\), there are n, \(n'\), such that for every \(s \in {\mathcal {S}}\) and every \(\delta (x, \langle y_\xi \rangle _{\xi< \gamma }, y_\gamma , y_{\gamma + 1}, z) \in \Delta _0^{{\mathcal {P}}}[x, \langle y_\xi \rangle _{\xi < \gamma }, y_\gamma , y_{\gamma + 1}, z]\), we have

By (\(\ddagger \)), \(n \ne n'\), whence \(m \ne n\) or \(m \ne n'\). If \(m \ne n\), then \(g \cup \{ \langle m, n \rangle \} \in {\mathcal {E}}_\alpha \) by (\(\ddagger \)). If \(m \ne n'\), then by (\(\dagger \)) and (\(\ddagger \)),
so \(g \cup \{ \langle m, n' \rangle \} \in {\mathcal {E}}_\alpha \). In either case we are done. \(\square \)
Based on this Lemma, we can prove a theorem that refines results in §4 of [10]. If \(i, j : {\mathcal {M}} \rightarrow {\mathcal {N}}\) are rank-initial embeddings between models of \({\mathrm {KP}}^{{\mathcal {P}}}\), then we write \(i <^{\mathrm {rank}} j\) to indicate that  is a rank-initial substructure of
is a rank-initial substructure of  .
.
Theorem 7.2
(Friedman-style) Let \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1^{{\mathcal {P}}}\text {-Separation}\) and \({\mathcal {N}} \models {\mathrm {KP}}^{{\mathcal {P}}}\) be countable and non-standard, and let \({\mathcal {S}}\) be a shared rank-cut of \({\mathcal {M}}\) and \({\mathcal {N}}\). Moreover, let \(m_0 \in {\mathcal {M}}\), let \(n_0 \in {\mathcal {N}}\), and let \(\beta \in {\mathrm {Ord}}^{\mathcal {N}}\). Then the following are equivalent:
-
(a)
There is a rank-initial embedding \(i : {\mathcal {M}} \rightarrow {\mathcal {N}}\), fixing \({\mathcal {S}}\) pointwise, such that \(i(m_0) = n_0\) and \(i({\mathcal {M}}) \subseteq {\mathcal {N}}_\beta \).
-
(b)
\({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}}) = {\mathrm {SSy}}_{{\mathcal {S}}}({\mathcal {N}})\), and for all \(s \in {\mathcal {S}}\) and \(\delta (x, y, z) \in \Delta _0^{{\mathcal {P}}}[x, y, z]\):
$$\begin{aligned} {\mathcal {M}} \models \exists x \cdot \delta (x, m_0, s) \Rightarrow {\mathcal {N}} \models \exists x \in V_\beta \cdot \delta (x, n_0, s). \end{aligned}$$ -
(c)
There is a map \(g \mapsto i_g\), from sequences \(g : \omega \rightarrow 2\), to embeddings \(i_g : {\mathcal {M}} \rightarrow {\mathcal {N}}\) satisfying (a), such that for any \(g <^{\mathrm {lex}} g' : \omega \rightarrow 2\), we have \(i_g <^{\mathrm {rank}}i_{g'}\).
-
(d)
There is a topless embedding \(i : {\mathcal {M}} \rightarrow {\mathcal {N}}\) satisfying (a).
Proof
Most of the work has already been done for (a) \(\Leftrightarrow \) (b). The other equivalences are proved as Lemma 7.6 below.
(a) \(\Rightarrow \) (b): The first conjunct follows from Proposition 6.10(d). The second conjunct follows from Proposition 6.10(c) and that \(i({\mathcal {M}})\) is rank-initial in \({\mathcal {N}}_\beta \).
(b) \(\Rightarrow \) (a): Let \({\mathbb {P}} = \llbracket {\mathcal {M}} \preceq _{\Sigma _1^{{\mathcal {P}}}, {\mathcal {S}}}^{<\omega } {\mathcal {N}}_\beta \rrbracket \). By the second conjunct of (b), the function \(f_0\) defined by \((m_0 \mapsto n_0)\), with domain \(\{m_0\}\), is in \({\mathbb {P}}\). Using Lemma 3.1 and Lemma 7.1 (a, b), we obtain a filter \({\mathcal {I}}\) on \({\mathbb {P}}\) which contains \(f_0\) and is \(\{{\mathcal {D}}_{m, n} \mid m \in {\mathcal {M}} \wedge n \in {\mathcal {N}}\}\)-generic (and hence \(\{{\mathcal {C}}_m \mid m \in {\mathcal {M}}\}\)-generic as well). Let \(i = \bigcup {\mathcal {I}}\). Since \({\mathcal {I}}\) is downwards directed, i is a function. Clearly \({\mathrm {image}}(i) \subseteq {\mathcal {N}}_\beta \). Since \({\mathcal {I}}\) is \(\{{\mathcal {C}}_m \mid m \in {\mathcal {M}}\}\)-generic, i has domain \({\mathcal {M}}\); and since \(f_0 \in {\mathcal {I}}\), \(i(m_0) = n_0\). To see that i is rank-initial, let \(m \in {\mathcal {M}}\), and let \(n \in {\mathcal {N}}\) such that \({\mathcal {N}} \models {\mathrm {rank}}(n) \le {\mathrm {rank}}(i(m))\). Since \({\mathcal {I}} \cap {\mathcal {D}}_{m, n} \ne \varnothing \), we have that n is in the image of i. \(\square \)
Friedman’s theorem is especially powerful in conjunction with the following lemmata.
Lemma 7.3
Let \({\mathcal {N}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1^{{\mathcal {P}}}\text {-Separation}\), let \(n \in {\mathcal {N}}\) and let \({\mathcal {S}}\) be a bounded substructure of \({\mathcal {N}}\). Then there is an ordinal \(\beta \in {\mathcal {N}}\), such that for each \(s \in {\mathcal {S}}\), and for each \(\delta (x, y, z) \in \Delta _0^{{\mathcal {P}}}[x, y, z]\):
Proof
Let \(\nu \) be an infinite ordinal in \({\mathcal {N}}\) such that \({\mathcal {S}} \subseteq {\mathcal {N}}_\nu \). We work in \({\mathcal {N}}\): Let \(A = \Delta _0^{{\mathcal {P}}}[x, y, z] \times V_\nu \). By Strong \(\Sigma _1^{{\mathcal {P}}}\)-Collection there is a set B, such that for all \(\langle \delta , t\rangle \in A\), if \(\exists x \cdot {\mathrm {Sat}}_{\Delta _0^{{\mathcal {P}}}}( \delta , x, n, t)\), then there is \(b \in B\) such that \({\mathrm {Sat}}_{\Delta _0^{{\mathcal {P}}}}(\delta , b, n, t)\). Setting \(\beta = {\mathrm {rank}}(B)\), the claim of the lemma follows from the properties of \({\mathrm {Sat}}_{\Delta _0^{{\mathcal {P}}}}\). \(\square \)
Lemma 7.4
Let \({\mathcal {N}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _2^{{\mathcal {P}}}\text {-Separation}\), let \(n \in {\mathcal {N}}\) and let \({\mathcal {S}}\) be a bounded substructure of \({\mathcal {N}}\). Then there are unboundedly many ordinals \(\beta \in {\mathcal {N}}\), such that for each \(s \in {\mathcal {S}}\), and for each \(\delta (x, x', y, z) \in \Delta _0^{{\mathcal {P}}}[x, x', y, z]\):
Proof
Let \(\alpha \) be an ordinal in \({\mathcal {N}}\). Let \(\beta _0 >^{\mathcal {N}} \alpha \) be an infinite ordinal in \({\mathcal {N}}\) such that \({\mathcal {S}} \subseteq {\mathcal {N}}_{\beta _0}\). We work in \({\mathcal {N}}\): By \(\Sigma _2^{{\mathcal {P}}}\)-Separation (which is equivalent to \(\Pi _2^{{\mathcal {P}}}\)-Separation), let
Recursively, for each \(k < \omega \), let \(\beta _{k+1}\) be the least ordinal such that
The existence of the set \(\{ \beta _k \mid k < \omega \}\) follows from \(\Sigma _1^{{\mathcal {P}}}\)-Recursion, because the functional formula defining the recursive step is \(\Sigma _1^{{\mathcal {P}}}\), as seen when written out as \(\phi (\beta _k, \beta _{k+1}) \wedge \forall \gamma < \beta _{k+1} \cdot \lnot \phi (\beta _k, \gamma ),\) where \(\phi (\beta _k, \beta _{k+1})\) is the formula \(\forall \langle \delta , t \rangle \in D \cdot \big ( \forall x \in V_{\beta _k} \cdot \exists x' \in V_{\beta _{k+1}} \cdot {\mathrm {Sat}}_{\Delta _0^{{\mathcal {P}}}}(\delta , x, x', n, s) \big )\). Put \(\beta = {\mathrm {sup}}\{ \beta _k \mid k < \omega \}\).
Let \(s \in {\mathcal {S}}\) and let \(\delta (x, x', y, z) \in \Delta _0^{{\mathcal {P}}}[x, x', y, z]\). To verify that
we work in \(({\mathcal {N}}, n, s)\): Suppose that \(\forall x \cdot \exists x' \cdot \delta (x, x', n, s)\), and let \(x \in V_\beta \). Then \(x \in V_{\beta _k}\) for some \(k < \omega \). By construction, there is \(x' \in V_{\beta _{k+1}}\), such that \({\mathrm {Sat}}_{\Delta _0^{{\mathcal {P}}}}(\delta , x, x', n, s)\). So by the properties of \({\mathrm {Sat}}_{\Delta _0^{{\mathcal {P}}}}\), we have \(\delta (x, x', n, s)\), as desired. \(\square \)
Lemma 7.5
Under the assumptions of Theorem 7.2, for each embedding \(i_1 : {\mathcal {M}} \rightarrow {\mathcal {N}}\) satisfying (a) of Theorem 7.2, there is an embedding \(i_0 <^{\mathrm {rank}}i_1\) satisfying (a).
Proof
By Lemma 7.3, there is \(\alpha \in {\mathrm {Ord}}^{\mathcal {M}}\), such that for all \(s \in {\mathcal {S}}\) and all \(\delta (x, y, z) \in \Delta _0^{{\mathcal {P}}}[x, y, z]\):
By Proposition 6.10(c) applied to \(i_1\), we have for all \(s \in {\mathcal {S}}\) and all \(\delta (x, y, z) \in \Delta _0^{{\mathcal {P}}}[x, y, z]\) that
and consequently that
So by (b) \(\Rightarrow \) (a) of Theorem 7.2, there is a rank-initial embedding \(i_0 : {\mathcal {M}} \rightarrow {\mathcal {N}}\), such that \(i_0(m) = n\) and \(i_0({\mathcal {M}}) \subseteq V_{i_1(\alpha )}^{\mathcal {N}}\). Since \(i_1(\alpha ) \in i_1({\mathcal {M}}) {\setminus } i_0({\mathcal {M}})\), we are done. \(\square \)
Lemma 7.6
These statements are equivalent to (a) in Theorem 7.2:
-
(a)
There is a map \(g \mapsto i_g\), from sequences \(g : \omega \rightarrow 2\), to embeddings \(i_g : {\mathcal {M}} \rightarrow {\mathcal {N}}\) satisfying (a), such that for any \(g <^{\mathrm {lex}} g' : \omega \rightarrow 2\), we have \(i_g <^{\mathrm {rank}}i_{g'}\).
-
(b)
There is a topless embedding \(i : {\mathcal {M}} \rightarrow {\mathcal {N}}\) satisfying (a).
Proof
It suffices to show that (a) \(\Rightarrow \) (c) \(\Rightarrow \) (d).
(a) \(\Rightarrow \) (c): Let \((a_\xi )_{\xi < \omega }\) and \((b_\xi )_{\xi < \omega }\) be enumerations of \({\mathcal {M}}\) and \({\mathcal {N}}\), respectively, with infinitely many repetitions of each element. For each \(g : \omega \rightarrow 2\), we shall construct a distinct \(i_g : {\mathcal {M}} \rightarrow {\mathcal {N}}\). To do so, we first construct approximations of the \(i_g\).
For any \(\gamma < \omega \), we allow ourselves to denote any function \(f : \gamma \rightarrow 2\) as an explicit sequence of values \(f(0),f(1), \dots , f(\gamma - 1)\). For each \(\gamma < \omega \), we shall construct a finite subdomain \(D_\gamma \subseteq {\mathcal {M}}\), and for each \(f : \gamma \rightarrow 2\), we shall construct an embedding \(i_f\). We do so by this recursive construction on \(\gamma < \omega \):
-
1.
For \(i_\varnothing : {\mathcal {M}} \rightarrow {\mathcal {N}}\), choose any embedding satisfying (a).
-
2.
Put \(D_\varnothing = \{m\}\).
-
3.
Suppose that \(i_f\) has been constructed for some \(f : \gamma \rightarrow 2\), where \(\gamma < \omega \). Put \(i_{f, 1} = i_f\). Applying Lemma 7.5 to \(i_{f,1}\), with \(D_\gamma ^{\mathcal {M}}\) in place of m and with \(i_f(D_\gamma ^{\mathcal {M}})\) in place of n, we choose an embedding \(i_{f, 0} : {\mathcal {M}} \rightarrow {\mathcal {N}}\) such that :
-
(i)
\(i_{f, 0}, i_{f, 1}\) are rank-initial, with all values of rank below \(\beta \) in \({\mathcal {N}}\);
-
(ii)
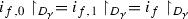 ;
; -
(iii)
\(i_{f,0} <^{\mathrm {rank}}i_{f,1}\).
-
(i)
-
4.
Put \(D_{\gamma + 1}\) to be a finite subdomain of \({\mathcal {M}}\), such that:
-
(i)
\(D_{\gamma } \subseteq D_{\gamma + 1}\);
-
(ii)
\(a_\gamma \in D_{\gamma + 1}\);
-
(iii)
For each \(f : \gamma +1 \rightarrow 2\), if \(\big ( {\mathrm {rank}}(b_\gamma ) \le \sup \{{\mathrm {rank}}(i_f(a)) \mid a \in D_\gamma \} \big )^{\mathcal {N}}\), then \(i_{f}^{-1}(b_\gamma ) \in D_{\gamma + 1}\) (note that \(i_{f}^{-1}(b_\gamma )\) exists by rank-initiality of \(i_f\));
-
(iv)
For each \(f : \gamma \rightarrow 2\), we have that \(i_{f, 1}^{-1}(\nu ) \in D_{\gamma + 1}\), for some \(\nu \in i_{f, 1}({\mathrm {Ord}}^{\mathcal {M}}) {\setminus } i_{f, 0}({\mathrm {Ord}}^{\mathcal {M}})\).
-
(i)
Note that every \(a \in {\mathcal {M}}\) is in \(D_\gamma \) for some \(\gamma < \omega \). Moreover, for every \(\gamma < \omega \), if \(f <^{\mathrm {lex}} f' : \gamma \rightarrow 2\), then \(i_f <^{\mathrm {rank}}i_{f'}\).
Now, for each \(g : \omega \rightarrow 2\), define \(i_g : {\mathcal {M}} \rightarrow {\mathcal {N}}\) by

for each \(a \in {\mathcal {M}}\), where \(\gamma < \omega \) is such that \(a \in D_\gamma \). Note that for each \(\gamma < \omega \),  . We now verify that these \(i_g\) have the desired properties. Let \(g : \omega \rightarrow 2\).
. We now verify that these \(i_g\) have the desired properties. Let \(g : \omega \rightarrow 2\).
-
\(i_g\) is an embedding: Let \(\phi (x)\) be a quantifier free formula and let \(a \in {\mathcal {M}}\). Then \(a \in D_\gamma \) for some \(\gamma < \omega \), so since
 is an embedding, \({\mathcal {M}} \models \phi (a) \Rightarrow {\mathcal {N}} \models \phi (i_g(a)).\)
is an embedding, \({\mathcal {M}} \models \phi (a) \Rightarrow {\mathcal {N}} \models \phi (i_g(a)).\) -
\(i_g(m) = n\): \(m \in D_\varnothing \) and
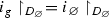 .
. -
\(i_g({\mathcal {M}}) \subseteq {\mathcal {N}}_\beta \): Let \(a \in {\mathcal {M}}\) and pick \(\gamma < \omega \) such that \(a \in D_\gamma \). Then
 .
. -
\(i_g\) is rank-initial: Let \(a \in {\mathcal {M}}\) and \(b \in {\mathcal {N}}\), such that \({\mathcal {N}} \models {\mathrm {rank}}(b) \le {\mathrm {rank}}(i_g(a))\). Pick \(\gamma < \omega \) such that \(a \in D_\gamma \). By (iii),
 . So \(b \in i_g({\mathcal {M}})\).
. So \(b \in i_g({\mathcal {M}})\). -
If \(g <^{\mathrm {lex}} g' : \omega \rightarrow 2\), then \(i_g <^{\mathrm {rank}}i_{g'}\): Let \(\gamma < \omega \) be the least such that \(g(\gamma ) < g'(\gamma )\). By (iv),
 .
.
(c) \(\Rightarrow \) (d): Since \({\mathcal {N}}\) is countable, there are only \(\aleph _0\) many ordinals in \({\mathcal {N}}\) which top a substructure, so by (c) we are done. \(\square \)
The following two results sharpen results in §4 of [10].
Corollary 7.7
Let \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1^{{\mathcal {P}}}\text {-Separation}\) and \({\mathcal {N}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1^{{\mathcal {P}}}\text {-Separation}\) be countable and non-standard. Let \({\mathcal {S}}\) be a common rank-cut of \({\mathcal {M}}\) and \({\mathcal {N}}\). Then the following are equivalent:
-
(a)
There is a rank-initial \(i : {\mathcal {M}} \rightarrow {\mathcal {N}}\), fixing \({\mathcal {S}}\) pointwise.
-
(a’)
There is a rank-cut \(i : {\mathcal {M}} \rightarrow {\mathcal {N}}\), fixing \({\mathcal {S}}\) pointwise.
-
(b)
\({\mathrm {SSy}}({\mathcal {M}}) = {\mathrm {SSy}}({\mathcal {N}})\), and \({\mathrm {Th}}_{\Sigma _1^{{\mathcal {P}}}, S}({\mathcal {M}}) \subseteq {\mathrm {Th}}_{\Sigma _1^{{\mathcal {P}}}, S}({\mathcal {N}})\).
Proof
(a) \(\Rightarrow \) (b) is proved just as for Theorem 7.2.
(b) \(\Rightarrow \) (a’) follows from Theorem 7.2 by letting \(\beta \in {\mathcal {N}}\) be as obtained from Lemma 7.3, and setting \(m_0 = \varnothing ^{\mathcal {M}}\) and \(n_0 = \varnothing ^{\mathcal {N}}\). \(\square \)
Theorem 7.8
Let \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1^{{\mathcal {P}}}\text {-Separation}\) be countable and non-standard. Let \({\mathcal {S}}\) be a rank-cut of \({\mathcal {M}}\). Then there is a rank-cut \(i : {\mathcal {M}} \rightarrow {\mathcal {M}}\), fixing \({\mathcal {S}}\) pointwise, such that
Proof
Let \(\beta \in {\mathcal {M}}\) be be the ordinal bound obtained from Lemma 7.3, and let \({\mathbb {P}} = \llbracket {\mathcal {M}} \preceq _{\Sigma _1^{{\mathcal {P}}}, {\mathcal {S}}}^{<\omega } {\mathcal {M}}_\beta \rrbracket \). Put \(m_0 = n_0 = \varnothing ^{\mathcal {M}}\). We adjust the proof of (b) \(\Rightarrow \) (a) in Theorem 7.2, by setting \({\mathcal {I}}\) to be a \(\{{\mathcal {C}}_m \mid m \in {\mathcal {M}}\} \cup \{{\mathcal {D}}_{m, n} \mid m \in {\mathcal {M}} \wedge n \in {\mathcal {N}}\} \cup \{{\mathcal {E}}_{\alpha } \mid \alpha \in {\mathrm {Ord}}^{\mathcal {M}} {\setminus } {\mathcal {S}}\}\)-generic filter on \({\mathbb {P}}\) (utilizing Lemma 7.1 (c)). Put \(i = \bigcup {\mathcal {I}}\). It only remains to verify that
But this follows from that \({\mathcal {I}}\) intersects \({\mathcal {E}}_\alpha \), for each \(\alpha \in {\mathrm {Ord}}^{\mathcal {M}} {\setminus } {\mathcal {S}}\). \(\square \)
The result above says in particular that every countable non-standard model of \({\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1^{{\mathcal {P}}}\text {-Separation}\) has a proper rank-initial self-embedding. As a remark, there is a related theorem by Hamkins, where no initiality is required from the embedding. In particular, it is shown in [13] that every countable model \({\mathcal {M}}\) of KP has a self-embedding \(i : {\mathcal {M}} \rightarrow L^{\mathcal {M}}\), where \(L^{\mathcal {M}} \subseteq {\mathcal {M}}\) is the Gödel constructible universe of \({\mathcal {M}}\).
The extra clause in the above Corollary, ensuring that something is moved on every rank above the cut, enables the following characterization.
Theorem 7.9
(Bahrami–Enayat-style) Let \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1^{{\mathcal {P}}}\text {-Separation}\) be countable and non-standard, and let \({\mathcal {S}}\) be a topless substructure of \({\mathcal {M}}\). The following are equivalent:
-
(a)
\({\mathcal {S}} = {\mathrm {Fix}}^{\mathrm {rank}}(i)\), for some rank-initial self-embedding \(i : {\mathcal {M}} \rightarrow {\mathcal {M}}\).
-
(a)’
\({\mathcal {S}} = {\mathrm {Fix}}^{\mathrm {rank}}(i)\), for some proper topless rank-initial self-embedding \(i : {\mathcal {M}} \rightarrow {\mathcal {M}}\).
-
(b)
\({\mathcal {S}}\) is rank-initial in \({\mathcal {M}}\).
Proof
(a) \(\Rightarrow \) (b) is immediate from the definition of \({\mathrm {Fix}}^{\mathrm {rank}}\).
(b) \(\Rightarrow \) (a’) follows from Corollary 7.8. \(\square \)
Theorem 7.10
(Wilkie-style) Suppose that \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1^{{\mathcal {P}}}\text {-Separation}\)\(+ \Pi _2^{{\mathcal {P}}}\text {-Foundation}\) and \({\mathcal {N}} \models {\mathrm {KP}}^{{\mathcal {P}}}\) are countable and non-standard. Let \({\mathcal {S}}\) be a common rank-cut of \({\mathcal {M}}\) and \({\mathcal {N}}\), and let \(\beta \in {\mathrm {Ord}}^{{\mathcal {N}}}\). Then the following are equivalent:
-
(a)
For any ordinal \(\alpha <^{\mathcal {N}} \beta \), there is a rank-initial embedding \(i : {\mathcal {M}} \rightarrow {\mathcal {N}}\), fixing \({\mathcal {S}}\) pointwise, such that \({\mathcal {N}}_\alpha \subseteq i({\mathcal {M}}) \subseteq {\mathcal {N}}_\beta \).
-
(a’)
For any ordinal \(\alpha <^{\mathcal {N}} \beta \), there is a rank-cut \(i : {\mathcal {M}} \rightarrow {\mathcal {N}}\), fixing \({\mathcal {S}}\) pointwise, such that \({\mathcal {N}}_\alpha \subseteq i({\mathcal {M}}) \subseteq {\mathcal {N}}_\beta \).
-
(b)
\({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}}) = {\mathrm {SSy}}_{\mathcal {S}}({\mathcal {N}})\), and for all \(s \in {\mathcal {S}}\) and \(\delta (x, y, z) \in \Delta _0^{{\mathcal {P}}}[x, y, z]\):
$$\begin{aligned} ({\mathcal {M}}, s) \models \forall x \cdot \exists y \cdot \delta (x, y, s) \Rightarrow ({\mathcal {N}}, s) \models \forall x \in V_\beta \cdot \exists y \in V_\beta \cdot \delta (x, y, s). \end{aligned}$$
Proof
(a) \(\Rightarrow \) (b): It is easy to see that (a) \(\Rightarrow \)\(\beta \) is a limit ordinal in \({\mathcal {N}}\). Let \(s \in {\mathcal {S}}\). Let \(\delta (x, y, z)\) be \(\Delta _0^{{\mathcal {P}}}[x, y, z]\) and assume that \({\mathcal {M}} \models \forall x \cdot \exists y \cdot \delta (x, y, s)\). Given Theorem 7.2, it only remains to show that \({\mathcal {N}} \models \forall x \in V_\beta \cdot \exists y \in V_\beta \cdot \delta (x, y, s)\). Let \(a \in {\mathcal {N}}_\beta \) be arbitrary and set \(\alpha = ({\mathrm {rank}}(a)+1)^{\mathcal {N}}\). Since \(\beta \) is a limit, \(\alpha < \beta \). By (a), there is a rank-initial embedding \(i : {\mathcal {M}} \rightarrow {\mathcal {N}}\), such that \(a \in i({\mathcal {M}}) \subseteq {\mathcal {N}}_\beta \). Pick \(m \in {\mathcal {M}}\) such that \({\mathcal {M}} \models \delta (i^{-1}(a), m, s)\). Then \(i(m) \in {\mathcal {N}}_\beta \), and by Proposition 6.10, \({\mathcal {N}} \models \delta (a, i(m), s)\), as desired.
(b) \(\Rightarrow \) (a’): Let \(\alpha <^{\mathcal {N}} \beta \) and let \(n = V_\alpha ^{\mathcal {N}}\). Using Lemma 6.13 and \(\Delta _1^{{\mathcal {P}}}\)-Collection, let d be a code in \({\mathcal {N}}\) for the following set:
Using \({\mathrm {SSy}}({\mathcal {M}}) = {\mathrm {SSy}}({\mathcal {N}})\) let c be a code for this set in \({\mathcal {M}}\). Define the formulae
Note that \(\phi \) is \(\Sigma _2^{{\mathcal {P}}}\). Moreover, \(c \cap V_\zeta = d \cap V_\zeta \) and n witnesses \(\phi _{<\beta }(\zeta )\), for all ordinals \(\zeta \in {\mathcal {S}}\). So by the second conjunct of (b), \({\mathcal {M}} \models \phi (\zeta )\) for all ordinals \(\zeta \in {\mathcal {S}}\), whence by \(\Sigma _2^{{\mathcal {P}}}\)-Overspill, \({\mathcal {M}} \models \phi (\mu )\) for some ordinal \(\mu \in {\mathcal {M}} {\setminus } {\mathcal {S}}\). Letting \(m \in {\mathcal {M}}\) be a witness of this fact, we have \({\mathcal {M}} \models \forall x \cdot \delta (x, m, s)\), for all \(\delta (x, y, s) \in D\). Now (a) is obtained by plugging m and n into Theorem 7.2. \(\square \)
Corollary 7.11
Let \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1^{{\mathcal {P}}}\text {-Separation} + \Pi _2^{{\mathcal {P}}}\text {-Foundation}\) and \({\mathcal {N}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _2^{{\mathcal {P}}}\text {-Separation}\) be countable and non-standard. Let \({\mathcal {S}}\) be a common rank-cut of \({\mathcal {M}}\) and \({\mathcal {N}}\). Then the following are equivalent:
-
(a)
For any ordinal \(\alpha \in {\mathcal {N}}\), there is a rank-initial embedding \(i : {\mathcal {M}} \rightarrow {\mathcal {N}}\), fixing \({\mathcal {S}}\) pointwise, such that \({\mathcal {N}}_\alpha \subseteq i({\mathcal {M}})\).
-
(a’)
For any ordinal \(\alpha \in {\mathcal {N}}\), there is a rank-cut \(i : {\mathcal {M}} \rightarrow {\mathcal {N}}\), fixing \({\mathcal {S}}\) pointwise, such that \({\mathcal {N}}_\alpha \subseteq i({\mathcal {M}})\).
-
(b)
\({\mathrm {SSy}}({\mathcal {M}}) = {\mathrm {SSy}}({\mathcal {N}})\), and \({\mathrm {Th}}_{\Pi _2^{{\mathcal {P}}}, S}({\mathcal {M}}) \subseteq {\mathrm {Th}}_{\Pi _2^{{\mathcal {P}}}, S}({\mathcal {N}})\).
Proof
(a) \(\Rightarrow \) (b) is proved just as for Theorem 7.10.
(b) \(\Rightarrow \) (a’) follows from Theorem 7.10 by letting \(\beta >^{\mathcal {N}} \alpha \) be as obtained from Lemma 7.4. \(\square \)
Corollary 7.12
Let \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _2^{{\mathcal {P}}}\text {-Separation} + \Pi _2^{{\mathcal {P}}}\text {-Foundation}\) be countable and non-standard. Let \({\mathcal {S}}\) be a rank-cut of \({\mathcal {M}}\). For any \(\alpha \in {\mathrm {Ord}}^{\mathcal {M}}\), there is a rank-cut \(i : {\mathcal {M}} \rightarrow {\mathcal {M}}\), fixing \({\mathcal {S}}\) pointwise, such that \({\mathcal {M}}_\alpha \subseteq i({\mathcal {M}})\) and
Proof
Let \({\mathcal {N}} = {\mathcal {M}}\) and let \(\beta >^{\mathcal {M}} \alpha \) be as obtained from Lemma 7.4. Then condition (b) of Theorem 7.10 is satisfied. Repeat the proof of Theorem 7.10 (b) \(\Rightarrow \) (a’) with \({\mathcal {N}} = {\mathcal {M}}\), except that at the last step: apply Theorem 7.8 instead of Theorem 7.2. \(\square \)
Now that we have explored necessary and sufficient conditions for constructing embeddings between models, we turn to the question of constructing isomorphisms between models. For this purpose we shall restrict ourselves to recursively saturated models of \({\mathrm {ZF}}\).
Lemma 7.13
Let \({\mathcal {M}}\) and \({\mathcal {N}}\) be countable recursively saturated models of \({\mathrm {ZF}}\), and let \({\mathcal {S}}\) be a common rank-initial \(\omega \)-topless substructure of \({\mathcal {M}}\) and \({\mathcal {N}}\). Moreover, let \({\mathbb {P}} = \llbracket {\mathcal {M}} \preceq _{\mathcal {S}}^{< \omega } {\mathcal {N}} \rrbracket \).
If \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}}) \subseteq {\mathrm {SSy}}_{\mathcal {S}}({\mathcal {N}})\), then
is dense in \({\mathbb {P}}\), for each \(m \in {\mathcal {M}}\).
Proof
By Theorem 6.15, \({\mathcal {M}}\) and \({\mathcal {N}}\) are \(\omega \)-non-standard and there are expansions \(({\mathcal {M}}, {\mathrm {Sat}}^{\mathcal {M}})\) and \(({\mathcal {N}}, {\mathrm {Sat}}^{\mathcal {N}})\) satisfying condition (b) of that theorem. Recall that this condition says that these are satisfaction classes that are correct for all formulae in \({\mathcal {L}}^0\) of standard complexity, and that the expanded structures satisfy Separation and Replacement for all formulae in the expanded language \({\mathcal {L}}^0_{\mathrm {Sat}}\).
Let \(g \in {\mathbb {P}}\). We unravel it as \(g = \{\langle m_\xi , n_\xi \rangle \mid \xi < \gamma \}\), for some \(\gamma < \omega \). Let \(m_\gamma \in {\mathcal {M}}\) be arbitrary. By \({\mathcal {L}}^0_{\mathrm {Sat}}\)-Separation, there is a code c in \({\mathcal {M}}\) for the set
Since \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}}) = {\mathrm {SSy}}_{\mathcal {S}}({\mathcal {N}})\), this set is also coded by some d in \({\mathcal {N}}\).
We define a formula:
By construction of c and correctness of \({\mathrm {Sat}}^{\mathcal {M}}\), we have that
for each \(\zeta \in {\mathrm {Ord}}^{\mathcal {M}} \cap {\mathcal {S}}\) and each \(k < \omega = {\mathrm {OSP}}({\mathcal {M}})\). So since g is elementary, and since \({\mathcal {M}}_\zeta = {\mathcal {N}}_\zeta \) and \(c_{\mathcal {M}} \cap {\mathcal {M}}_\zeta = d_{\mathcal {N}} \cap {\mathcal {N}}_\zeta \) for each \(\zeta \in {\mathrm {Ord}}^{\mathcal {N}} \cap {\mathcal {S}}\), we also have that \({\mathcal {N}} \models \phi (\zeta , k, \langle n_\xi \rangle _{\xi < \gamma }, d)\) for each \(\zeta \in {\mathrm {Ord}}^{\mathcal {N}} \cap {\mathcal {S}}\) and each \(k < \omega \). Pick some \(\nu \in {\mathrm {Ord}}^{\mathcal {N}} {\setminus } {\mathcal {S}}\). Now by Overspill on \({\mathcal {S}}\), for each \(k < \omega \) there is \(\nu '_k \in {\mathrm {Ord}}^{\mathcal {N}} {\setminus } {\mathcal {S}}\) such that \(({\mathcal {N}}, {\mathrm {Sat}}^{\mathcal {N}}) \models \nu '_k< \nu \wedge \phi (\nu '_k, k, \langle n_\xi \rangle _{\xi < \gamma }, d)\).
Pick some non-standard \(o <^{\mathcal {N}} \omega ^{\mathcal {N}}\). Working in \({\mathcal {N}}\), we construct a partial function \((k \mapsto \nu _k) : o \rightarrow \nu + 1\), such that for each \(k < o\),
We return to reasoning in the meta-theory. By the Overspill-argument above, this function is total on \(\omega \), and \(\nu _k \not \in {\mathcal {S}}\) for each \(k < \omega \). Moreover, by logic, \(\nu _k \ge \nu _l\) for all \(k \le l < \omega \). So by \(\omega \)-toplessness, there is \(\nu _\infty \in {\mathrm {Ord}}^{\mathcal {N}} {\setminus } {\mathcal {S}}\), such that for each \(k < \omega \), \(\nu _\infty <^{\mathcal {N}} \nu _k\). So for each \(k < \omega \), we have \(({\mathcal {N}}, {\mathrm {Sat}}^{\mathcal {N}}) \models \phi (\nu _\infty , k, \langle n_\xi \rangle _{\xi < \gamma }, d)\), whence by Overspill on \({\mathrm {WFP}}({\mathcal {N}})\), there is a non-standard \(k_\infty \in ^{\mathcal {N}} \omega ^{\mathcal {N}}\) such that \(({\mathcal {N}}, {\mathrm {Sat}}^{\mathcal {N}}) \models \phi (\nu _\infty , k_\infty , \langle n_\xi \rangle _{\xi < \gamma }, d)\). Let \(n_\gamma \in {\mathcal {N}}\) be a witness of this fact. Note that for all \(s \in {\mathcal {S}}\) and for all \(\delta \in {\mathcal {L}}^0[\langle x_\xi \rangle _{\xi < \gamma }, x_\gamma , z]\),
Let \(f = g \cup \{\langle m_\gamma , n_\gamma \rangle \}\). We need to show that \(f \in {\mathcal {C}}'_{m_\gamma }\); it only remains to verify that f is elementary. Now observe that for any \(s \in {\mathcal {S}}\), and any formula \(\delta (\langle x_\xi \rangle _{\xi< \gamma + 1}, z) \in {\mathcal {L}}^0[\langle x_\xi \rangle _{\xi < \gamma + 1}, z]\),
Therefore, \(f \in {\mathcal {C}}'_{m_\gamma }\) as desired. \(\square \)
Theorem 7.14
Let \({\mathcal {M}}\) and \({\mathcal {N}}\) be countable recursively saturated models of \({\mathrm {ZF}}\), and let \({\mathcal {S}}\) be a common rank-initial \(\omega \)-topless substructure of \({\mathcal {M}}\) and \({\mathcal {N}}\). Let \(m_0 \in {\mathcal {M}}\) and let \(n_0 \in {\mathcal {N}}\). The following are equivalent:
-
(a)
There is an isomorphism \(i : {\mathcal {M}} \rightarrow {\mathcal {N}}\), fixing \({\mathcal {S}}\) pointwise, such that \(i(m_0) = n_0\).
-
(b)
\({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}}) = {\mathrm {SSy}}_{\mathcal {S}}({\mathcal {N}})\) and \({\mathrm {Th}}_{\mathcal {S}}(({\mathcal {M}}, m_0)) = {\mathrm {Th}}_{\mathcal {S}}(({\mathcal {N}}, n_0))\).
Proof
The forward direction is clear since i is an isomorphism.
Let \({\mathbb {P}} = \llbracket {\mathcal {M}} \preceq _{\mathcal {S}}^{< \omega } {\mathcal {N}} \rrbracket \). Since \({\mathrm {Th}}_{\mathcal {S}}(({\mathcal {M}}, m_0)) = {\mathrm {Th}}_{\mathcal {S}}(({\mathcal {N}}, n_0))\), the function \((m_0 \mapsto n_0)\) is in \({\mathbb {P}}\). For each \(m \in {\mathcal {M}}\) and each \(n \in {\mathcal {N}}\), let
By Lemma 7.13, \({\mathcal {C}}'_m\) and \({\mathcal {D}}'_n\) are dense in \({\mathbb {P}}\) for all \(m \in {\mathcal {M}}\) and all \(n \in {\mathcal {N}}\). By Lemma 3.1, there is a \({\mathcal {C}}'_m \cup {\mathcal {D}}'_n\)-generic filter \({\mathcal {I}}\) on \({\mathbb {P}}\) containing \((m_0 \mapsto n_0)\). Let \(i = \bigcup {\mathcal {I}}\).
By the genericity, \(\mathrm {dom}(i) = {\mathcal {M}}\) and \({\mathrm {image}}(i) = {\mathcal {N}}\). Moreover, by the filter properties, for any \(\vec {m} \in {\mathcal {M}}\), some finite extension \(f \in {\mathbb {P}}\) of  is in \({\mathcal {I}}\). So by elementarity of f and arbitrariness of \(\vec {m}\), we have that i is an isomorphism. \(\square \)
is in \({\mathcal {I}}\). So by elementarity of f and arbitrariness of \(\vec {m}\), we have that i is an isomorphism. \(\square \)
The following Theorem is an improvement of Theorem 6.14. The proof given here is meant to be simpler and more accessible than the one given in [20].
Theorem 7.15
(Ressayre) Let \({\mathcal {M}}\) be a countable recursively saturated model of \({\mathrm {ZF}}\). There are unboundedly many \(\alpha \in {\mathrm {Ord}}^{\mathcal {M}}\), such that for all \(S \in {\mathcal {M}}_\alpha \) we have \({\mathcal {M}} \cong _{S_{\mathcal {M}}} {\mathcal {M}}_\alpha \preceq {\mathcal {M}}\).
Proof
Let \(\alpha >^{\mathcal {M}} \omega ^{\mathcal {M}}\) be as obtained from Theorem 6.14. Thus \({\mathcal {M}}_\alpha \preceq {\mathcal {M}}\). Let \(S \in {\mathcal {M}}_\alpha \) be arbitrary. For each \(m \in ^{\mathcal {M}} \omega ^{\mathcal {M}}\), let \(\sigma _m = {\mathrm {rank}}(S) + m\) as evaluated in \({\mathcal {M}}\). Since \({\mathcal {M}}_\alpha \preceq {\mathcal {M}}\), we have \(\sigma _m < \alpha \) for each \(m \in ^{\mathcal {M}} \omega ^{\mathcal {M}}\).
Since \({\mathcal {M}}\) is recursively saturated, it is \(\omega \)-non-standard. Let \({\mathcal {M}}_{S, \omega } = \bigcup _{k < \omega } {\mathcal {M}}_{\sigma _k}\) (note that we take this union only over standard k). By Lemma 6.7, \({\mathcal {M}}_{S, \omega }\) is a common rank-initial \(\omega \)-topless substructure of \({\mathcal {M}}\) and \({\mathcal {M}}_\alpha \); and obviously \(S_{\mathcal {M}} \subseteq {\mathcal {M}}_{S, \omega }\).
By rank-initiality, \({\mathrm {SSy}}_{{\mathcal {M}}_{S, \omega }}(\mathcal {M_\alpha }) = {\mathrm {SSy}}_{{\mathcal {M}}_{S, \omega }}({\mathcal {M}})\), and by \({\mathcal {M}}_\alpha \preceq {\mathcal {M}}\), we have \({\mathrm {Th}}_{{\mathcal {M}}_{S, \omega }}(\mathcal {M_\alpha }) = {\mathrm {Th}}_{{\mathcal {M}}_{S, \omega }}({\mathcal {M}})\). So it follows from Theorem 7.14 that \({\mathcal {M}} \cong _{S_{\mathcal {M}}} {\mathcal {M}}_\alpha \). \(\square \)
Theorem 7.16
(Ressayre-style) Let \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}}\) be countable and non-standard. The following are equivalent:
-
(a)
\({\mathcal {M}} \models \Sigma _1^{{\mathcal {P}}} \text {-Separation}.\)
-
(b)
For every \(\alpha \in {\mathrm {Ord}}^{\mathcal {M}}\), there is a proper rank-initial self-embedding of \({\mathcal {M}}\) which fixes \({\mathcal {M}}_\alpha \) pointwise.
Proof
(a) \(\Rightarrow \) (b): Let \({\mathcal {N}} = \bigcup _{\xi \in {\mathrm {OSP}}({\mathcal {M}})} {\mathcal {M}}_{\alpha + \xi }.\) Note that \({\mathcal {N}}\) is a rank-cut of \({\mathcal {M}}\). So by Theorem 7.8, we are done.
(b) \(\Rightarrow \) (a): Let \(\phi (x) \in \Sigma _1^{{\mathcal {P}}}[x]\) and let \(a \in {\mathcal {M}}\). Let i be a rank-initial self-embedding of \({\mathcal {M}}\) which fixes \({\mathcal {M}}_{({\mathrm {rank}}(a) + 1)^{\mathcal {M}}}\) pointwise and which satisfies \(i({\mathcal {M}}) \subseteq {\mathcal {M}}_\mu \), for some \(\mu \in {\mathrm {Ord}}^{\mathcal {M}}\). Let us write \(\phi (x)\) as \(\exists y \cdot \delta (y, x)\), where \(\delta \in \Delta _0^{{\mathcal {P}}}\). Since i fixes \(a_{\mathcal {M}}\) pointwise, we have
So \(\{ x \in a \mid \phi (x) \} = \{ x \in a \mid \exists y \in V_\mu \cdot \delta (y, x)) \}\), which exists by \(\Delta _0^{{\mathcal {P}}}\)-Separation. \(\square \)
8 Iterated ultrapowers with special self-embeddings
It is convenient to fix some objects which will be discussed throughout this section. Fix a countable model \(({\mathcal {M}}, {\mathcal {A}}) \models {\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\text { is weakly compact''}\). Fix \({\mathbb {B}}\) to be the boolean algebra \(\{A \subseteq {\mathrm {Ord}}^{\mathcal {M}} \mid A \in {\mathcal {A}}\}\) induced by \({\mathcal {A}}\). Fix \({\mathbb {P}}\) to be the partial order of unbounded sets in \({\mathbb {B}}\) ordered under inclusion. Fix a filter \({\mathcal {U}}\) on \({\mathbb {P}}\). Note that by Proposition 5.1, \(({\mathcal {M}}, {\mathcal {A}}) \models \text {Global Choice}\).
\({\mathcal {U}}\) is \({\mathbb {P}}\)-generic over\(({\mathcal {M}}, {\mathcal {A}})\), or simply \(({\mathcal {M}}, {\mathcal {A}})\)-generic, if it intersects every dense subset of \({\mathbb {P}}\) that is parametrically definable in \(({\mathcal {M, A}})\). \({\mathcal {U}}\) is \(({\mathcal {M, A}})\)-complete if for every \(a \in {\mathcal {M}}\) and every \(f : {\mathrm {Ord}}^{\mathcal {M}} \rightarrow a_{\mathcal {M}}\) that is coded in \({\mathcal {A}}\), there is \(b \in a_{\mathcal {M}}\) such that \(f^{-1}(b) \in {\mathcal {U}}\). Considering the characteristic functions of the classes in \({\mathcal {A}}\), we can easily see that if \({\mathcal {U}}\) is \(({\mathcal {M, A}})\)-complete, then it is an ultrafilter on \({\mathbb {B}}\), i.e. for any \(A \in {\mathbb {B}}\), we have \(A \in {\mathcal {U}}\) or \({\mathrm {Ord}}^{\mathcal {M}} {\setminus } A \in {\mathcal {U}}\).
Let \(P : {\mathrm {Ord}}^{\mathcal {M}} \times {\mathrm {Ord}}^{\mathcal {M}} \rightarrow {\mathrm {Ord}}^{\mathcal {M}}\) be a bijection coded in \({\mathcal {A}}\). For each \(g : {\mathrm {Ord}}^{\mathcal {M}} \rightarrow \{0,1\}^{\mathcal {M}}\) coded in \({\mathcal {A}}\), and each \(\alpha \in {\mathrm {Ord}}^{\mathcal {M}}\), define \(S^g_\alpha =_{\mathrm {df}} \{\xi \in {\mathrm {Ord}}^{\mathcal {M}} \mid g(P(\alpha , \xi )) = 1\}\). Thus, g may be thought of as coding an \({\mathrm {Ord}}^{\mathcal {M}}\)-sequence of sets; indeed \((\alpha \mapsto S^g_\alpha ) : {\mathrm {Ord}}^{\mathcal {M}} \rightarrow {\mathbb {B}}\). \({\mathcal {U}}\) is \(({\mathcal {M, A}})\)-iterable if for every \(g : {\mathrm {Ord}}^{\mathcal {M}} \rightarrow \{0,1\}^{\mathcal {M}}\) coded in \({\mathcal {A}}\), we have \(\{\alpha \mid S^g_\alpha \in {\mathcal {U}}\} \in {\mathcal {A}}\).
A filter \({\mathcal {U}}\) is \(({\mathcal {M, A}})\)-canonically Ramsey if for every \(n \in {\mathbb {N}}\) and \(f : [{\mathrm {Ord}}^{\mathcal {M}}]^n \rightarrow {\mathrm {Ord}}^{\mathcal {M}}\) coded in \({\mathcal {A}}\), there is \(H \in {\mathcal {U}}\) and \(S \subseteq \{1, \dots , n\}\), such that for any \(\alpha _1, \dots , \alpha _n\) and \(\beta _1, \dots , \beta _n\) in H,
We say that f is canonical on H.
The following theorem is proved in [6, p. 48]. Combined with Lemma 3.1, it establishes the existence of an ultrafilter on \({\mathbb {B}}\), which is \(({\mathcal {M, A}})\)-complete, \(({\mathcal {M, A}})\)-iterable and \(({\mathcal {M, A}})\)-canonically Ramsey, under the assumption that \(({\mathcal {M, A}}) \models \text {``}{\mathrm {Ord}}\text { is weakly compact''}\).
Theorem 8.1
Let \(({\mathcal {M, A}})\) a model of \({\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\text { is weakly compact''}\). If \({\mathcal {U}}\) is \(({\mathcal {M, A}})\)-generic, then \({\mathcal {U}}\) is
-
(a)
\(({\mathcal {M, A}})\)-complete,
-
(b)
\(({\mathcal {M, A}})\)-iterable, and
-
(c)
\(({\mathcal {M, A}})\)-canonically Ramsey.
Using such an ultrafilter, we shall now construct an iterated ultrapower of \(({\mathcal {M}}, {\mathcal {A}}\)). A more detailed account of this construction is found in [9].
Construction 8.2
Suppose that \({\mathcal {U}}\) is a non-principal \(({\mathcal {M}}, {\mathcal {A}})\)-iterable ultrafilter on \({\mathbb {B}}\). Then for any \(n \in {\mathbb {N}}\), an ultrafilter \({\mathcal {U}}^n\) can be recursively constructed on \({\mathbb {B}}^n =_{\mathrm {df}} \{A \subseteq ({\mathrm {Ord}}^{\mathcal {M}})^n \mid A \in {\mathcal {A}}\}\) as follows:
First, we extend the definition of iterability. An ultrafilter \({\mathcal {V}}\) on \({\mathbb {B}}^n\) is \(({\mathcal {M}}, {\mathcal {A}})\)-iterable if for any function \((\alpha \mapsto S_\alpha ) : {\mathrm {Ord}}^{\mathcal {M}} \rightarrow {\mathbb {B}}^n\) coded in \({\mathcal {A}}\), we have \(\{\alpha \mid S_\alpha \in {\mathcal {V}}\} \in {\mathcal {A}}\).
\({\mathcal {U}}^0\) is the trivial (principal) ultrafilter \(\{\{\langle \rangle \}\}\) on the boolean algebra \(\{\langle \rangle , \{\langle \rangle \}\}\), where \(\langle \rangle \) is the empty tuple.
For any \(n \in {\mathbb {N}}\), \(X \in {\mathbb {B}}^{n+1}\) and any \(\alpha \in {\mathrm {Ord}}^{\mathcal {M}}\), define
Note that there are other equivalent definitions:
By the setup, \({\mathcal {U}}^1 = {\mathcal {U}}\), which is an \(({\mathcal {M}}, {\mathcal {A}})\)-iterable ultrafilter on \({\mathbb {B}}^1\) by assumption. Assuming that \({\mathcal {U}}^n\) is an \(({\mathcal {M}}, {\mathcal {A}})\)-iterable ultrafilter on \({\mathbb {B}}^n\), we shall show that \({\mathcal {U}}^{n+1}\) is an \(({\mathcal {M}}, {\mathcal {A}})\)-iterable ultrafilter on \({\mathbb {B}}^{n+1}\).
Let \(X \in {\mathcal {U}}^{n+1}\). If \(X \subseteq Y \in {\mathbb {B}}^{n+1}\), then \(X_\alpha \subseteq Y_\alpha \), for each \(\alpha \in {\mathrm {Ord}}^{\mathcal {M}}\), and by iterability of \({\mathcal {U}}^{n}\), \(\{\alpha \mid Y_\alpha \in {\mathcal {U}}\} \in {\mathcal {A}}\). So \(Y \in {\mathcal {U}}^{n+1}\) by upwards closure of \({\mathcal {U}}^n\) and \({\mathcal {U}}\). Similarly, the iterability of \({\mathcal {U}}^n\) and the finite intersection and maximality properties of \({\mathcal {U}}^n\) and \({\mathcal {U}}\) imply that \({\mathcal {U}}^{n+1}\) has the finite intersection and maximality properties, respectively. To show iterability, suppose that the function \((\xi \mapsto S^g_\xi ) : {\mathrm {Ord}}^{\mathcal {M}} \rightarrow {\mathbb {B}}^{n+1}\) is coded in \({\mathcal {A}}\). Then

by iterability of \({\mathcal {U}}\). So \({\mathcal {U}}^{n+1}\) is also \(({\mathcal {M}}, {\mathcal {A}})\)-iterable. We have proved:
Lemma 8.3
If \({\mathcal {U}}\) is an \(({\mathcal {M, A}})\)-iterable ultrafilter on \({\mathbb {B}}\), then \({\mathcal {U}}^n\) is an \(({\mathcal {M, A}})\)-iterable ultrafilter on \({\mathbb {B}}^n\), for every \(n \in {\mathbb {N}}\).
Since \({\mathcal {U}}\) is a non-principal ultrafilter, it contains all final segments of \({\mathrm {Ord}}^{\mathcal {M}}\). So by induction, we have
for every \(n \in {\mathbb {N}}\).
Lastly, we shall extend the definition of completeness and show that each \({\mathcal {U}}^n\) has this property. An ultrafilter \({\mathcal {V}}\) on \({\mathbb {B}}^n\) is \(({\mathcal {M, A}})\)-complete if for any \(m < n\) and any functions \(f : ({\mathrm {Ord}}^{\mathcal {M}})^m \rightarrow M\) and \(g : ({\mathrm {Ord}}^{\mathcal {M}})^n \rightarrow M\) coded in \({\mathcal {A}}\), such that
we have that \({\mathcal {A}}\) codes a function \(f' : ({\mathrm {Ord}}^{\mathcal {M}})^m \rightarrow M\), such that
Lemma 8.4
If \({\mathcal {U}}\) is an \(({\mathcal {M, A}})\)-complete and \(({\mathcal {M, A}})\)-iterable ultrafilter, then \({\mathcal {U}}^n\) is \(({\mathcal {M, A}})\)-complete, for every \(n \in {\mathbb {N}}\).
Proof
Suppose that \(m < n\) and that
satisfy
We may assume that \(m + 1 = n\). The above is equivalent to
Moreover, by completeness of \({\mathcal {U}}\), for any \(\langle \alpha _1, \dots , \alpha _m \rangle \in A\), there is \(y \in f(\alpha _1, \dots , \alpha _m)\) such that

On the other hand, we have by iterability of \({\mathcal {U}}\) (utilizing a bijection coded in \({\mathcal {A}}\) between \({\mathrm {Ord}}^{\mathcal {M}}\) and \({\mathcal {M}}^n\)) that
Since \({\mathcal {U}}\) is an ultrafilter, \(f'\) is a function whose domain is a superset of \(A \in {\mathcal {U}}\), and by extending it arbitrarily we may assume its domain is \(({\mathrm {Ord}}^{\mathcal {M}})^m\). Now by (\(\dagger \)), we have
Thus
as desired. \(\square \)
Construction 8.5
Let \({\mathcal {L}}^0_{\mathcal {A}}\) be the language obtained from \({\mathcal {L}}^0\) by adding constant symbols for all elements of \({\mathcal {M}}\) and adding relation and function symbols for all relations and functions on \({\mathcal {M}}\) coded in \({\mathcal {A}}\). \(({\mathcal {M}}, A)_{A \in {\mathcal {A}}}\) denotes the canonical expansion of \({\mathcal {M}}\) to \({\mathcal {L}}^0_{\mathcal {A}}\) determined by \(({\mathcal {M}}, {\mathcal {A}})\). Assume that \({\mathcal {U}}\) is a non-principal \(({\mathcal {M}}, {\mathcal {A}})\)-iterable ultrafilter on \({\mathrm {Ord}}^{\mathcal {M}}\) and let \({\mathbb {L}}\) be a linear order. We construct \({\mathrm {Ult}}_{{\mathcal {U}}, {\mathbb {L}}}({\mathcal {M}}, {\mathcal {A}})\) as follows:
For each \(n \in {\mathbb {N}}\), define
Since \({\mathcal {U}}^n\) is an ultrafilter on \(({\mathrm {Ord}}^{\mathcal {M}})^n\), each \(\Gamma _n\) is a complete n-type over \({\mathcal {M}}\) in the language \({\mathcal {L}}^0_{\mathcal {A}}\). Moreover, each \(\Gamma _n\) contains the elementary diagram of \(({\mathcal {M}}, A)_{A \in {\mathcal {A}}}\).
For each \(l \in {\mathbb {L}}\), let \(c_l\) be a new constant symbol, and let \({\mathcal {L}}^0_{{\mathcal {A}}, {\mathbb {L}}}\) be the language generated by \({\mathcal {L}}^0_{\mathcal {A}} \cup \{c_l \mid l \in {\mathbb {L}}\}\). Define
\(T_{{\mathcal {U}}, {\mathbb {L}}}\) is complete and contains the elementary diagram of \(({\mathcal {M}}, {\mathcal {A}})\), because the same holds for each \(\Gamma _n\). By Construction 8.2,

Moreover, \(T_{{\mathcal {U}}, {\mathbb {L}}}\) has definable Skolem functions: For each \({\mathcal {L}}^0_{{\mathcal {A}}, {\mathbb {L}}}\)-formula \(\exists x \cdot \phi (x)\), we can prove in \(T_{{\mathcal {U}}, {\mathbb {L}}}\) that the set of witnesses of \(\exists x . \phi (x, y)\) of least rank exists, and provided this set is non-empty an element is picked out by a global choice function coded in \({\mathcal {A}}\). Thus we can define the iterated ultrapower of\(({\mathcal {M, A}})\)modulo\({\mathcal {U}}\)along\({\mathbb {L}}\) as
In particular, every element of \({\mathrm {Ult}}_{{\mathcal {U}}, {\mathbb {L}}}({\mathcal {M}}, {\mathcal {A}})\) is of the form \(f(c_{l_1}, \dots , c_{l_n})\), where \(l_1< \dots < l_n \in {\mathbb {L}}\) and \(f \in {\mathcal {A}}\) (considered as a function symbol of \({\mathcal {L}}^0_{{\mathcal {A}}, {\mathbb {L}}}\)). Note that for any \(A \in {\mathcal {A}}\), any function f coded in \({\mathcal {A}}\) and for any \(l_1, \dots , l_n \in {\mathbb {L}}\), where \(n \in {\mathbb {N}}\), we have
A different way of saying the same thing:
Since \(T_{{\mathcal {U}}, {\mathbb {L}}}\) contains the elementary diagram of \(({\mathcal {M}}, {\mathcal {A}})\), the latter embeds elementarily in \({\mathrm {Ult}}_{{\mathcal {U}}, {\mathbb {L}}}({\mathcal {M}}, {\mathcal {A}})\). For simplicity of presentation, we assume that this is an elementary extension. Note that if \({\mathbb {L}}\) is empty, then \({\mathrm {Ult}}_{{\mathcal {U}}, {\mathbb {L}}}({\mathcal {M}}, {\mathcal {A}}) = ({\mathcal {M, A}})\). If \({\mathcal {U}}\) is non-principal, then it is easily seen from Construction 8.2 that for any \(l, l' \in {\mathbb {L}}\) and any \(\alpha \in {\mathrm {Ord}}^{\mathcal {M}}\),
where \({\mathbb {O}} = {\mathrm {Ord}}^{{\mathrm {Ult}}_{{\mathcal {U}}, {\mathbb {L}}}({\mathcal {M}}, {\mathcal {A}})}\). So \({\mathbb {L}}\) embeds into the linear order of the ordinals in \({\mathrm {Ult}}_{{\mathcal {U}}, {\mathbb {L}}}({\mathcal {M}}, {\mathcal {A}})\), above the ordinals of \({\mathcal {M}}\).
It will be helpful to think of the ultrapower as a function (actually functor) of \({\mathbb {L}}\) rather than as a function of \(({\mathcal {M, A}})\), so we introduce the alternative notation
Suppose that \(({\mathcal {M, A}})\) is a countable model of \({\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\text { is weakly compact''}\) and let \({\mathcal {U}}\) be an iterable non-principal ultrafilter on \({\mathbb {B}}\). Given an embedding \(i : {\mathbb {K}} \rightarrow {\mathbb {L}}\), we construct an embedding
as follows: Note that any \(a \in {\mathcal {G}}_{{\mathcal {U}}, ({\mathcal {M, A}})}({\mathbb {K}})\) is of the form \(f(c_{k_1}, \dots , c_{k_n})\) for some \(f \in {\mathcal {A}}\), \(n \in {\mathbb {N}}\) and \(k_1, \dots , k_n \in {\mathbb {K}}\). Define \({\mathcal {G}}_{{\mathcal {U}}, ({\mathcal {M, A}})}(i)(a) = f(c_{i(k_1)}, \dots , c_{i(k_n)})\).
As shown in Theorem 8.6, \({\mathcal {G}}_{{\mathcal {U}}, ({\mathcal {M, A}})}(i)\) is an elementary embedding, and further more, \({\mathcal {G}}_{{\mathcal {U}}, ({\mathcal {M, A}})}\) is a functor from the category of linear orders, with embeddings as morphisms, to the category of models of the \({\mathcal {L}}^0_{\mathcal {A}}\)-theory of \(({\mathcal {M}}, A)_{A \in {\mathcal {A}}}\), with elementary embeddings as morphisms. We call this the Gaifman functor of \({\mathcal {U}}, ({\mathcal {M, A}})\) and denote it by \({\mathcal {G}}_{{\mathcal {U}}, ({\mathcal {M, A}})}\), or just \({\mathcal {G}}\) for short.
Gaifman [11] essentially proved the theorem below for models of arithmetic. A substantial chunk of its generalization to models of set theory was proved for specific needs in [6].
Theorem 8.6
(Gaifman-style) Suppose that \(({\mathcal {M}}, {\mathcal {A}}) \models {\mathrm {GBC}} + \)“\({\mathrm {Ord}}\) is weakly compact” is countable and let \({\mathcal {U}}\) be an \(({\mathcal {M}}, {\mathcal {A}})\)-generic ultrafilter. Write \({\mathcal {G}} = {\mathcal {G}}_{{\mathcal {U}}, ({\mathcal {M, A}})}\) for the corresponding Gaifman functor. Let \(i : {\mathbb {K}} \rightarrow {\mathbb {L}}\) be an embedding of linear orders.
-
(a)
For each \(n \in {\mathbb {N}}\) and each \(\phi (x_1, \dots , x_n) \in {\mathcal {L}}^0_{{\mathcal {A}}, {\mathbb {L}}}\):
$$\begin{aligned}&{\mathcal {G}}({\mathbb {L}}) \models \phi (c_{l_1}, \dots , c_{l_n}) \Leftrightarrow \\&\quad \big \{ \langle \alpha _1, \dots , \alpha _n \rangle \in ({\mathrm {Ord}}^{\mathcal {M}})^n \mid ({\mathcal {M}}, A)_{A \in {\mathcal {A}}} \models \phi (\alpha _1, \dots , \alpha _n) \big \} \in {\mathcal {U}}^n. \end{aligned}$$ -
(b)
\({\mathcal {G}}(i) : {\mathcal {G}}({\mathbb {K}}) \rightarrow {\mathcal {G}}({\mathbb {L}})\) is an elementary embedding.
-
(c)
\({\mathcal {G}}\) is a functor.
-
(d)
If \({\mathbb {L}} \ne \varnothing \), then \({\mathrm {SSy}}_{\mathcal {M}}({\mathcal {G}}({\mathbb {L}})) = ({\mathcal {M}}, {\mathcal {A}})\).
-
(e)
\(|{\mathcal {G}}({\mathbb {L}})| = |{\mathbb {L}}| + \aleph _0\).
-
(f)
i is initial iff \({\mathcal {G}}(i)\) is rank-initial.
-
(g)
i is an isomorphism iff \({\mathcal {G}}(i)\) is an isomorphism.
-
(h)
Let \(l_0 \in {\mathbb {L}}\). i is strictly bounded above by \(l_0\) iff
 is strictly bounded above by \(c_{l_0}\).
is strictly bounded above by \(c_{l_0}\). -
(i)
If \({\mathbb {L}} {\setminus } i({\mathbb {K}})\) has no least element, then \(\{ c_l \mid l \in {\mathbb {L}} {\setminus } i({\mathbb {K}})\}\) is downwards cofinal in \({\mathrm {Ord}}^{{\mathcal {G}}({\mathbb {L}})} {\setminus } {\mathrm {Ord}}^{{\mathcal {G}}(i({\mathbb {K}}))}\).
-
(j)
Let \({\mathbb {L}}'\) be a linear order and let \(j, j' : {\mathbb {L}} \rightarrow {\mathbb {L}}'\) be embeddings. i is an equalizer of \(j, j' : {\mathbb {L}} \rightarrow {\mathbb {L}}'\) iff \({\mathcal {G}}(i)\) is an equalizer of \({\mathcal {G}}(j), {\mathcal {G}}(j') : {\mathcal {G}}({\mathbb {L}}) \rightarrow {\mathcal {G}}({\mathbb {L}}')\).
-
(k)
Let \(i' : {\mathbb {K}} \rightarrow {\mathbb {L}}\) be an embedding. We have \(\forall k \in {\mathbb {K}} . i(k) < i'(k)\) iff \(\forall \xi \in {\mathrm {Ord}}^{{\mathcal {G}}({\mathbb {K}})} {\setminus } {\mathrm {Ord}}^{\mathcal {M}} . {\mathcal {G}}(i)(\xi ) < {\mathcal {G}}(i')(\xi )\).
Remark
(b) and (f) imply that \(({\mathcal {M, A}})\) is a rank-initial elementary substructure of \({\mathcal {G}}({\mathbb {L}})\). It follows from (j) that if \(j : {\mathbb {L}} \rightarrow {\mathbb {L}}\) is a self-embedding with no fixed point, then the fixed point set of \({\mathcal {G}}(j)\) is \({\mathcal {M}}\) (consider the equalizer of j and \(\mathrm {id}_{\mathbb {L}}\)). It follows from (k) that \(i : {\mathbb {L}} \rightarrow {\mathbb {L}}\) is contractive iff \({\mathcal {G}}(i)\) is contractive on \({\mathcal {M}} {\setminus } {\mathcal {S}}\).
Proof
(a) This is immediate from Construction 8.5.
(b) We may assume that \({\mathbb {K}} \subseteq {\mathbb {L}}\) and that i is the corresponding inclusion function. This has the convenient consequence that \({\mathcal {L}}^0_{{\mathcal {A}}, {\mathbb {K}}} \subseteq {\mathcal {L}}^0_{{\mathcal {A}}, {\mathbb {L}}}\). Let \(\phi (\vec {c}) \in {\mathcal {L}}^0_{{\mathcal {A}}, {\mathbb {K}}}\) be a sentence, where \(\vec {c}\) is a tuple of constants. By (a),
Since every element of \({\mathcal {G}}({\mathbb {K}})\) interprets a term, this equivalence establishes \({\mathcal {G}}({\mathbb {K}}) \preceq {\mathcal {G}}({\mathbb {L}})\), as \({\mathcal {L}}^0_{{\mathcal {A}}, {\mathbb {K}}}\)-structures.
(c) It is clear that \({\mathcal {G}}(\mathrm {id}_{\mathbb {L}}) = \mathrm {id}_{{\mathcal {G}}({\mathbb {L}})}\). It only remains to verify that composition is preserved. Let \(j : {\mathbb {L}} \rightarrow {\mathbb {L}}'\) and \(j' : {\mathbb {L}}' \rightarrow {\mathbb {L}}''\) be embeddings of linear orders. Let a be an arbitrary element of \({\mathcal {G}}({\mathbb {L}})\). Then \(a = f(c_{l_1}, \dots , c_{l_n})\), for some \(f \in {\mathcal {A}}\), \(n \in {\mathbb {N}}\) and \(l_1, \dots , l_n \in {\mathbb {L}}\). \({\mathcal {G}}(j'\circ j)(a) = f(c_{j'\circ j(l_1)}, \dots , c_{j'\circ j(l_n)}) = f(c_{j'(j(l_1))}, \dots , c_{j'(j(l_n))}) = ({\mathcal {G}}(j') \circ {\mathcal {G}}(j))(a)\), as desired.
(d) We start with \({\mathcal {A}} \subseteq {\mathrm {Cod}}_{\mathcal {M}}({\mathcal {G}}({\mathbb {L}}))\): Let \(A \in {\mathcal {A}}\). Since \(({\mathcal {M}}, {\mathcal {A}}) \models {\mathrm {GBC}}\), the function \(f_A : {\mathrm {Ord}}^{\mathcal {M}} \rightarrow {\mathcal {M}}\), defined by \(f_A(\xi ) = V_\xi \cap A\) for all \(\xi \in {\mathrm {Ord}}^{\mathcal {M}}\), is coded in \({\mathcal {A}}\). Since \({\mathbb {L}} \ne \varnothing \), let \(l \in {\mathbb {L}}\). Now by (a), for each \(a \in {\mathcal {M}}\),
so \(f_A(c_l)\) codes A.
We proceed with \({\mathrm {Cod}}_{\mathcal {M}}({\mathcal {G}}({\mathbb {L}})) \subseteq {\mathcal {A}}\): Let \(b \in {\mathcal {G}}({\mathbb {L}})\). Then \({\mathcal {G}}({\mathbb {L}}) \models b = f(c_{l_1}, \dots , c_{l_n})\), for some \(n \in {\mathbb {N}}\) and \(l_1, \dots , l_n \in {\mathbb {L}}\). We need to show that
By (a), this amounts to showing that
Letting \(w : {\mathrm {Ord}}^{\mathcal {M}} \rightarrow {\mathcal {M}}\) be a well-ordering of \({\mathcal {M}}\) coded in \({\mathcal {A}}\), the above is equivalent to

This last statement holds since \({\mathcal {U}}^n\) is \(({\mathcal {M}}, {\mathcal {A}})\)-iterable on \({\mathbb {B}}^n\).
(e) Since \(({\mathcal {M}}, {\mathcal {A}})\) is countable, \(|{\mathbb {L}}| + \aleph _0 = |{\mathcal {L}}^0_{{\mathcal {A}}, {\mathbb {L}}}|\). So since \({\mathcal {G}}({\mathbb {L}})\) is a prime model in that language, we have \(|{\mathcal {G}}({\mathbb {L}})| = |{\mathbb {L}}| + \aleph _0\).
(f) We may assume that \({\mathbb {L}}\) extends \({\mathbb {K}}\) and that \({\mathcal {G}}({\mathbb {L}})\) extends \({\mathcal {G}}({\mathbb {K}})\). By Proposition 6.4, it suffices to show that i is initial. Let \(a \in {\mathcal {G}}({\mathbb {K}})\) and \(b \in {\mathcal {G}}({\mathbb {L}})\), such that \({\mathcal {G}}({\mathbb {L}}) \models b \in a\). We need to show that \(b \in {\mathcal {G}}({\mathbb {K}})\). Note that \({\mathcal {G}}({\mathbb {K}}) \models a = f(c_{l_1}, \dots , c_{l_m})\) and \({\mathcal {G}}({\mathbb {L}}) \models b = g(c_{l_1}, \dots , c_{l_n})\), for some \(m \le n \in {\mathbb {N}}\), \(l_1, \dots , l_m \in {\mathbb {K}}\), \( l_{m+1}, \dots , l_n \in {\mathbb {L}}\) and \(f, g \in {\mathcal {A}}\). By (a), we have that
So by \(({\mathcal {M, A}})\)-completeness of \({\mathcal {U}}\) and Lemma 8.4, there is \(f' : ({\mathrm {Ord}}^{\mathcal {M}})^m \rightarrow {\mathcal {M}}\) in \({\mathcal {A}}\), such that
whence \({\mathcal {G}}({\mathbb {L}}) \models b = f'(c_{l_1}, \dots , c_{l_m})\). But \(f'(c_{l_1}, \dots , c_{l_m}) \in {\mathcal {G}}({\mathbb {K}})\). So i is initial.
(g) (\(\Leftarrow \)) follows from that the orderings embed into the respective sets of ordinals of the models, and that any isomorphism of the models preserves the order of their ordinals. (\(\Rightarrow \)) follows from that functors preserve isomorphisms.
(h) (\(\Leftarrow \)) is obvious. For (\(\Rightarrow \)), we may assume that \({\mathbb {K}}\) is a linear suborder of \({\mathbb {L}}\) that is strictly bounded above by \(l_0 \in {\mathbb {L}}\). Note that \({\mathcal {G}}({\mathbb {K}}) \prec {\mathcal {G}}({\mathbb {L}}_{< l_0}) \prec {\mathcal {G}}({\mathbb {L}})\). So every ordinal of \({\mathcal {G}}({\mathbb {K}})\) is an ordinal of \({\mathcal {G}}({\mathbb {L}}_{< l_0})\), and by (f), every ordinal of \({\mathcal {G}}({\mathbb {L}}_{< l_0})\) is an ordinal of \({\mathcal {G}}({\mathbb {L}})\) below \(c_{l_0}\).
(i) We may assume that \({\mathbb {K}} \subseteq {\mathbb {L}}\). Suppose that \({\mathbb {L}} {\setminus } {\mathbb {K}}\) has no least element. Let \(\alpha \in {\mathrm {Ord}}^{{\mathcal {G}}({\mathbb {L}})} {\setminus } {\mathrm {Ord}}^{{\mathcal {G}}({\mathbb {K}})}\). Then \({\mathcal {G}}({\mathbb {L}}) \models \alpha = f(c_{l_1}, \dots , c_{l_n})\), for some \(n \in {\mathbb {N}}\) and \(l_1< \dots < l_n \in {\mathbb {L}}\). Let \(1 \le n^\circ \le n\) be the least natural number such that there is \(l \in {\mathbb {L}}{\setminus } {\mathbb {K}}\) with \(l < l_{n^\circ }\). Let \(l^* \in {\mathbb {L}}{\setminus } {\mathbb {K}}\) witness this for \(n^\circ \). To show that \({\mathcal {G}}({\mathbb {L}}) \models l^* < \alpha \), it suffices to show that
Suppose not. Then
so by completeness
Hence, by iterability, we can code a function \(f' : ({\mathrm {Ord}}^{\mathcal {M}})^{n^\circ -1} \rightarrow {\mathrm {Ord}}^{\mathcal {M}}\) by the class
and \({\mathcal {G}}({\mathbb {L}}) \models f'(l_{c_1}, \dots , l_{c_{n^\circ - 1}}) = \alpha \). But this means that \(\alpha \in {\mathcal {G}}({\mathbb {K}})\), contradicting assumption.
(j) (\(\Leftarrow \)) is obvious. For (\(\Rightarrow \)), assume that \(i : {\mathbb {K}} \rightarrow {\mathbb {L}}\) is an equalizer of \(j, j' : {\mathbb {L}} \rightarrow {\mathbb {L}}'\), i.e. we may assume that \({\mathbb {K}}\) is the linear suborder of \({\mathbb {L}}\) on \(\{l \in {\mathbb {L}} \mid j(l) = j'(l)\}\). It suffices to show that for all elements x of \({\mathcal {G}}({\mathbb {L}})\), we have \({\mathcal {G}}(j)(x) = {\mathcal {G}}(j')(x) \leftrightarrow x \in {\mathcal {G}}({\mathbb {K}})\). (\(\leftarrow \)) is obvious. For (\(\rightarrow \)), suppose that \(a \in {\mathcal {G}}({\mathbb {L}}) {\setminus } {\mathcal {G}}({\mathbb {K}})\). Let \(n^*\) be the least natural number such that \({\mathcal {G}}({\mathbb {L}}) \models a = f(c_{l_1}, \dots , c_{l_{n^*}})\), for some \(f \in {\mathcal {A}}\) and \(l_1< \dots < l_{n^*} \in {\mathbb {L}}\). Suppose towards a contradiction that \({\mathcal {G}}({\mathbb {L}}) \models f(c_{j(l_1)}, \dots , c_{j(l_{n^*})}) = f(c_{j'(l_1)}, \dots , c_{j'(l_{n^*})})\). Since \({\mathcal {U}}\) is \(({\mathcal {M, A}})\)-canonically Ramsey, since f is coded in \({\mathcal {A}}\) and since there is a bijection between the universe and the ordinals coded in \({\mathcal {A}}\), there is \(H \in {\mathcal {U}}\) and \(S \subseteq \{1, \dots , n^*\}\), such that for any \(\alpha _1< \dots < \alpha _{n^*}\) and \(\beta _1< \dots < \beta _{n^*}\) in H,
Since \(a \not \in {\mathcal {G}}({\mathbb {K}})\), there is \(1 \le n^\circ \le n^*\), such that \(l_{n^\circ } \in {\mathbb {L}} {\setminus } {\mathbb {K}}\) and consequently \(j(l_{n^\circ }) \ne j'(l_{n^\circ })\). So since \(f(c_{j(l_1)}, \dots , c_{j(l_{n^*})}) = f(c_{j'(l_1)}, \dots , c_{j'(l_{n^*})})\), we have \(n^\circ \not \in S\). Note that \(f' : ({\mathrm {Ord}}^{\mathcal {M}})^{n^*-1} \rightarrow {\mathcal {M}} \), defined by
is coded in \({\mathcal {A}}\); and by \(n^\circ \not \in S\),
for all \(\alpha _1< \dots < \alpha _{n^*} \in H\). Since \(H \in {\mathcal {U}}\), it follows that
contradicting minimality of \(n^*\).
(k) (\(\Leftarrow \)) is obvious. For (\(\Rightarrow \)), let \(\alpha \) be an arbitrary ordinal in \({\mathcal {G}}({\mathbb {K}})\) not in \({\mathcal {M}}\). Let \(k^*\) be the least element of \({\mathbb {K}}\), such that \({\mathcal {G}}({\mathbb {K}}) \models \alpha = f(c_{k_1}, \dots , c_{k_n})\), where \(f \in {\mathcal {A}}\), \(n \in {\mathbb {N}}\) and \(k_1< \dots < k_n = k^* \in {\mathbb {K}}\). Note that \(i'(\alpha )\) is in \({\mathcal {G}}({\mathbb {L}}_{\le i'(k^*)})\) and that \(i(\alpha )\) is in \({\mathcal {G}}({\mathbb {L}}_{\le i(k^*)})\). On the other hand, since \(i(k^*) < i'(k^*)\), we have by minimality of \(k^*\) that \(i'(\alpha )\) is not in \({\mathcal {G}}({\mathbb {L}}_{\le i(k^*)})\). So by (b) and (f), \({\mathcal {G}}({\mathbb {L}}) \models i(\alpha ) < i'(\alpha )\). \(\square \)
As seen in the proofs of the Corollaries below, this theorem is quite powerful when applied to the set of rational numbers \({\mathbb {Q}}\), with the usual ordering \(<_{\mathbb {Q}}\). For any structure \({\mathcal {K}}\), and \(S \subseteq {\mathcal {K}}\), we define \({\mathrm {End}}_S({\mathcal {K}})\) as the monoid of endomorphisms of \({\mathcal {K}}\) that fix S pointwise, and we define \({\mathrm {Aut}}_S({\mathcal {K}})\) as the group of automorphisms of \({\mathcal {K}}\) that fix S pointwise.
Corollary 8.7
If \({\mathcal {M}} \models {\mathrm {ZFC}}\) expands to a countable model \(({\mathcal {M}}, {\mathcal {A}})\) of \({\mathrm {GBC}} + \) “\({\mathrm {Ord}}\) is weakly compact”, then there is \({\mathcal {M}} \prec ^\text {rank-cut} {\mathcal {N}}\), such that \({\mathrm {SSy}}_{\mathcal {M}}({\mathcal {N}}) = ({\mathcal {M}}, {\mathcal {A}})\), and such that for any countable linear order \({\mathbb {L}}\), there is an embedding of \({\mathrm {End}}({\mathbb {L}})\) into \({\mathrm {End}}_{\mathcal {M}}({\mathcal {N}})\). Moreover, this embedding sends every automorphism of \({\mathbb {L}}\) to an automorphism of \({\mathcal {N}}\), and sends every contractive self-embedding of \({\mathbb {L}}\) to a self-embedding of \({\mathcal {N}}\) that is contractive on \({\mathrm {Ord}}^{\mathcal {N}} {\setminus } {\mathcal {M}}\) and whose fixed-point set is \({\mathcal {M}}\).
Proof
Since \(({\mathcal {M}}, {\mathcal {A}})\) is countable, Lemma 3.1 tells us that there is an \(({\mathcal {M}}, {\mathcal {A}})\)-generic ultrafilter \({\mathcal {U}}\). Let \({\mathcal {N}} = {\mathcal {G}}_{{\mathcal {U}}, ({\mathcal {M}}, {\mathcal {A}})}({\mathbb {Q}})\). By Theorem 8.6 (b), (d) and (f), \({\mathcal {M}} \prec ^\text {rank-cut} {\mathcal {N}}\) and \({\mathrm {SSy}}_{\mathcal {M}}({\mathcal {N}}) = ({\mathcal {M}}, {\mathcal {A}})\). By Theorem 8.6 (c) and (j), there is an embedding of \({\mathrm {End}}({\mathbb {Q}})\) into \({\mathrm {End}}_{\mathcal {M}}({\mathcal {N}})\). Moreover, it is well-known that for any countable linear order \({\mathbb {L}}\), there is an embedding of \({\mathrm {End}}({\mathbb {L}})\) into \({\mathrm {End}}({\mathbb {Q}})\). Composing these two embeddings gives the result. The last sentence in the statement follows from Theorem 8.6 (g), (j) and (k). \(\square \)
Lemma 8.8
For any \(q \in {\mathbb {Q}}\), there is an initial topless contractive self-embedding of the usual linear order on \({\mathbb {Q}}\) that is strictly bounded by q.
Proof
It suffices to show that there is an initial topless contractive self-embedding of \({\mathbb {Q}}\), because by toplessness that would be bounded by some \(q' \in {\mathbb {Q}}\) and we can compose it with the self-embedding \((x \mapsto x - |q' - q|)\) to obtain an initial topless contractive self-embedding bounded by q. Thus, we proceed to show that the usual linear order on \({\mathbb {Q}}\) can be expanded to a model of the following theory T, in the language of a binary relation < and a unary function f:
Let \({\mathcal {R}}\) be the expansion of the order of the punctured reals \({\mathbb {R}} {\setminus } \{0\}\) inherited from the usual order of \({\mathbb {R}}\), interpreting f by the function \(f^{\mathcal {R}} : {\mathbb {R}} {\setminus } \{0\} \rightarrow {\mathbb {R}} {\setminus } \{0\}\), defined by \(f^{\mathcal {R}}(x) = -2^{-x}\), for all \(x \in {\mathbb {R}} {\setminus } \{0\}\). Note that \({\mathcal {R}} \models T\). Now by the Downward Löwenheim-Skolem Theorem, there is a countable model \({\mathcal {Q}}\) of T. Since every countable dense linear order without endpoints is isomorphic to \(({\mathbb {Q}}, <_{\mathbb {Q}})\), it follows that \(f^{\mathcal {Q}}\) induces an initial topless contractive self-embedding of \({\mathbb {Q}}\). \(\square \)
Corollary 8.9
Suppose that \({\mathcal {M}} \models {\mathrm {ZFC}}\) expands to a countable model \(({\mathcal {M}}, {\mathcal {A}})\) of \({\mathrm {GBC}} + \)“\({\mathrm {Ord}}\) is weakly compact”. Then there is a model \({\mathcal {M}} \prec ^\text {rank-cut} {\mathcal {N}}\), with \({\mathrm {SSy}}_{\mathcal {M}}({\mathcal {N}}) = ({\mathcal {M}}, {\mathcal {A}})\), such that for any \(\nu \in {\mathrm {Ord}}^{\mathcal {N}} {\setminus } {\mathcal {M}}\), there is a rank-initial topless elementary self-embedding j of \({\mathcal {N}}\), which is contractive on \({\mathrm {Ord}}^{\mathcal {N}} {\setminus } {\mathcal {M}}\), bounded by \(\nu \), and satisfies \({\mathcal {M}} = {\mathrm {Fix}}(j)\).
Proof
Let \({\mathcal {U}}\) be an \(({\mathcal {M}}, {\mathcal {A}})\)-generic ultrafilter, and let \({\mathcal {N}}\) be the model \({\mathcal {G}}_{{\mathcal {U}}, ({\mathcal {M}}, {\mathcal {A}})}({\mathbb {Q}})\). As in Corollary 8.7, \({\mathcal {M}} \prec ^\text {rank-cut} {\mathcal {N}}\) and \({\mathrm {SSy}}_{\mathcal {M}}({\mathcal {N}}) = ({\mathcal {M}}, {\mathcal {A}})\). Let \(\nu \in {\mathrm {Ord}}^{\mathcal {N}} {\setminus } {\mathcal {M}}\). By Theorem 8.6 (i), there is \(q \in {\mathbb {Q}}\), such that \({\mathcal {N}} \models c_q < \nu \). Using Lemma 8.8, let \({\hat{j}}\) be an initial topless contractive self-embedding of \({\mathbb {Q}}\) that is strictly bounded by q. Let \(j = {\mathcal {G}}({\hat{j}})\). The result now follows from Theorem 8.6: By (b), j is an elementary embedding; by (f), j is rank-initial; by (h), j is bounded by \(\nu \); by toplessness of \({\hat{j}}\) and by (i) applied to \({\mathcal {N}} {\setminus } {\mathcal {G}}({\hat{j}}({\mathbb {Q}}))\), j is topless; by (k), j is contractive on \({\mathcal {N}} {\setminus } {\mathcal {M}}\); and by (j) \({\mathcal {M}} = {\mathrm {Fix}}(j)\). \(\square \)
9 Geometric results
Theorem 9.1
(Kirby-Paris-style) Let \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \text {Choice}\) be countable and let \({\mathcal {S}} \le ^\text {rank-cut} {\mathcal {M}}\). The following are equivalent:
-
(a)
\({\mathcal {S}}\) is a strong rank-cut in \({\mathcal {M}}\) and \(\omega ^{\mathcal {M}} \in {\mathcal {S}}\).
-
(b)
\({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}}) \models {\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\text { is weakly compact''}\).
Proof
The two directions are proved as Lemmata 9.3 and 9.6 below. \(\square \)
Lemma 9.2
Let \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \text {Choice}\), let \({\mathcal {S}}\) be a strongly topless rank-initial substructure of \({\mathcal {M}}\) and let us write \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}})\) as \(({\mathcal {S}}, {\mathcal {A}})\). For any \(\phi (\vec {x}, \vec {Y}) \in {\mathcal {L}}^1\) and for any \(\vec {A} \in {\mathcal {A}}\), there is a formula \(\theta _\phi (\vec {x}, \vec {y}) \in \Delta _0^{{\mathcal {P}}} \subseteq {\mathcal {L}}^0\) and parameters \(\vec {p} \in {\mathcal {M}}\), such that for all \(\vec {s} \in {\mathcal {S}}\),
Proof
We construct \(\theta _\phi \) recursively on the structure of \(\phi \). Let \(\vec {A} \in {\mathcal {A}}\) be arbitrary and let \(\vec {a}\) be a tuple of codes in \({\mathcal {M}}\) for \(\vec {A}\). In the base cases, given a coordinate A in \(\vec {A}\) and its code a in \(\vec {a}\), put:
It is clear that the result holds in the first two cases, and also in the third case since a codes A.
Assume inductively that the result holds for \(\phi (\vec {x}, \vec {Y}), \psi (\vec {x}, \vec {Y}) \in {\mathcal {L}}^1\) and \(\theta _\phi (\vec {x}, \vec {y}), \theta _\psi (\vec {x}, \vec {y}) \in \Delta _0^{{\mathcal {P}}}\), and put:
where \(b \in {\mathcal {M}}\) is next to be constructed. But before doing so, note that the result holds for the first two cases, simply because the connectives commute with \(\models \).
Let us write \(\vec {x}\) as \(x, \vec {x}'\), and let \(k = {\mathrm {arity}}(\vec {x}')\). Since \({\mathcal {S}}\) is bounded in \({\mathcal {M}} \models \text {Infinity}\), there is a limit \(\mu \in {\mathrm {Ord}}^{\mathcal {M}} {\setminus } {\mathcal {S}}\). Therefore, by letting \(d = V_\mu ^{\mathcal {M}}\), we obtain \(d \in {\mathcal {M}}\), \({\mathcal {S}} \subseteq d_{\mathcal {M}}\), and \({\mathcal {M}} \models d^k \subseteq d\). Working in \({\mathcal {M}}\), by Choice and \(\Delta _0^{{\mathcal {P}}}\)-Separation, there is a function \(f : d \rightarrow d\), such that for all \(\vec {t} \in d^k\),

By strong toplessness and rank-initiality, there is \(\beta \in {\mathrm {Ord}}^{\mathcal {M}} {\setminus } {\mathcal {S}}\) such that for all \(s \in {\mathcal {S}}\),

Put \(b = V_\beta ^{\mathcal {M}}\). Note that by toplessness, \({\mathcal {S}}\) is closed under ordered pair. Putting (\(\dagger \)) and (\(\ddagger \)) together, we have that, for all \(\vec {s} \in {\mathcal {S}}\),
and by induction hypothesis,
Putting these equivalences together yields the desired result for \(\exists x . \phi \). The parameters \(\vec {p}\) appearing in \(\theta _{\exists x . \phi }\) are b together with \(\vec {a}\). \(\square \)
Lemma 9.3
Let \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \text {Choice}\). If \({\mathcal {S}}\) is strong rank-cut in \({\mathcal {M}}\) and \(\omega ^{\mathcal {M}} \in {\mathcal {S}}\), then \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}}) \models {\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\text { is weakly compact''}\).
Proof
Let us write \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}})\) as \(({\mathcal {S}}, {\mathcal {A}})\). By toplessness and rank-initiality, there is \(d \in {\mathcal {M}}\) such that \(d_{\mathcal {M}} \supset {\mathcal {S}}\).
\(({\mathcal {S}}, {\mathcal {A}}) \models \text {Class Extensionality, Pair, Union, Powerset, Infinity}\) are inherited from \({\mathcal {M}}\), because \(\omega ^{\mathcal {M}} \in {\mathcal {S}}\) and for any \(\alpha \in {\mathrm {Ord}}^{\mathcal {S}}\), \(\alpha +^{\mathcal {M}} 2 \in {\mathcal {S}}\) by toplessness, and \({\mathcal {M}}_{\alpha +^{\mathcal {M}} 2} \subseteq {\mathcal {S}}\) by rank-initiality.
\(({\mathcal {S}}, {\mathcal {A}}) \models \text {Class Foundation}\): Let \(A \in {\mathcal {A}}\) such that \(({\mathcal {S}}, {\mathcal {A}}) \models A \ne \varnothing \). Let a be a code for A in \({\mathcal {M}}\). By \(\Pi _1^{{\mathcal {P}}}\)-Foundation, there is an \(\in ^{\mathcal {M}}\)-minimal element \(m \in ^{\mathcal {M}} a\). Since A is non-empty, we have by rank-initiality that \(m \in {\mathcal {S}}\). If there were \(s \in {\mathcal {S}}\) such that \(({\mathcal {S}}, {\mathcal {A}}) \models s \in m \cap A\), then we would have \({\mathcal {M}} \models s \in m \cap a\), contradicting \(\in ^{\mathcal {M}}\)-minimality of m. Hence, m is an \(\in \)-minimal element of A in \(({\mathcal {S}}, {\mathcal {A}})\).
\(({\mathcal {S}}, {\mathcal {A}}) \models \text {Global Choice}\): By Choice in \({\mathcal {M}}\), there is a choice function f on \((d {\setminus } \{\varnothing \})^{\mathcal {M}}\). Note that f codes a global choice function \(F \in {\mathcal {A}}\) on \((V {\setminus } \{\varnothing \})^{({\mathcal {M}}, {\mathcal {A}})} \in {\mathcal {A}}\).
\(({\mathcal {S}}, {\mathcal {A}}) \models \text {Class Comprehension}\): Let \(\phi (x, \vec {Y}) \in {\mathcal {L}}^1\), in which all variables of sort \({\mathsf {Class}}\) are free, and let \(\vec {A} \in {\mathcal {A}}\). By Lemma 9.2, there are \(\theta _\phi \in \Delta _0^{{\mathcal {P}}}\) and \(\vec {a} \in {\mathcal {M}}\), such that for all \(s \in {\mathcal {S}}\),
Working in \({\mathcal {M}}\), let \(c = \{ t \in d \mid \theta _\phi (t, \vec {a}) \}\). Let \(C \in {\mathcal {A}}\) be the class coded by c. It follows that
\(({\mathcal {S}}, {\mathcal {A}}) \models \text {Extended Separation}\): Simply observe that if \(s \in {\mathcal {S}}\), \(\vec {A} \in {\mathcal {A}}\) and \(\phi (x, \vec {Y}) \in {\mathcal {L}}^1\), in which all variables of sort \({\mathsf {Class}}\) are free, then by Class Comprehension, the class \(\{ x \mid \phi (x, \vec {A}) \}^{({\mathcal {S}}, {\mathcal {A}})}\) exists in \({\mathcal {A}}\) and is coded in \({\mathcal {M}}\) by c, say. So by rank-initiality, \(c \cap s \in {\mathcal {S}}\), and \(c \cap s\) clearly witnesses the considered instance of \(\text {Extended Separation}\).
\(({\mathcal {S}}, {\mathcal {A}}) \models \text {Class Replacement}\): Let \(F \in {\mathcal {A}}\) be a class function such that \(\mathrm {dom}(F) \in {\mathcal {S}}\), and let f be a code in \({\mathcal {M}}\) for F. In \({\mathcal {M}}\), using \(\mathrm {dom}(F)\) and f as parameters, we can construct a function \(f'\) such that

Note that  . Suppose that
. Suppose that
Then we have for all \(\xi \in {\mathrm {Ord}}^{\mathcal {S}}\) that
So by Overspill, there is \(\mu \in {\mathrm {Ord}}^{\mathcal {M}} {\setminus } {\mathcal {S}}\) such that
But this contradicts that  . Therefore,
. Therefore,
Now it follows by \(\text {Extended Separation}\) that \({\mathrm {image}}^{({\mathcal {S}}, {\mathcal {A}})}(F) \in {\mathcal {S}}\).
\(({\mathcal {S}}, {\mathcal {A}}) \models \) “\({\mathrm {Ord}}\) is weakly compact”: Let \({\mathcal {T}}\) be a binary tree of height \({\mathrm {Ord}}\) in \({\mathcal {S}}\), coded in \({\mathcal {M}}\) by \(\tau \in {\mathcal {M}} {\setminus } {\mathcal {S}}\). Note that for all \(\zeta \in {\mathrm {Ord}}^{\mathcal {S}}\), \(\tau _\zeta \) is a binary tree of height \(\zeta \). So by \(\Delta _0\)-Overspill, there is \(\mu \in {\mathrm {Ord}}^{\mathcal {M}} {\setminus } {\mathcal {S}}\), such that \(\tau _\mu \) is a binary tree of height \(\mu \). Let \(f \in ^{\mathcal {M}} \tau _\mu \) such that \(\mathrm {dom}^{\mathcal {M}}(f) \in {\mathrm {Ord}}^{\mathcal {M}} {\setminus } {\mathcal {S}}\). Let \(F \in {\mathcal {A}}\) be the class coded by f. Since \({\mathcal {S}}\) is rank-initial in \({\mathcal {M}}\), we have for each \(\zeta \in {\mathrm {Ord}}^{\mathcal {S}}\), that  . It follows that F is a branch in \({\mathcal {T}}\). \(\square \)
. It follows that F is a branch in \({\mathcal {T}}\). \(\square \)
Lemma 9.4
Let \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1^{{\mathcal {P}}}\text {-Separation}\) be countable and non-standard, and let \({\mathcal {S}}\) be a \(\Sigma _1^{{\mathcal {P}}}\)-elementary rank-cut of \({\mathcal {M}}\), such that
Then there is a structure \({\mathcal {N}} \succ {\mathcal {S}}\), and a self-embedding \(i : {\mathcal {N}} \rightarrow {\mathcal {N}}\), such that \({\mathrm {Fix}}(i) = {\mathcal {S}}\), i is contractive on \({\mathcal {N}} {\setminus } {\mathcal {S}}\), and
Proof
Let us write \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}})\) as \(({\mathcal {S}}, {\mathcal {A}})\). Since
we can apply Corollary 8.9 to obtain a model \({\mathcal {N}}\), such that \({\mathcal {S}} \preceq ^{{\mathrm {rank}}} {\mathcal {N}}\) and for each \(\nu \in {\mathrm {Ord}}^{\mathcal {N}} {\setminus } {\mathcal {S}}\), there is a topless rank-initial self-embedding \(i_\nu \) of \({\mathcal {N}}\), which is contractive on \({\mathcal {N}} {\setminus } {\mathcal {S}}\) and which satisfies \({\mathrm {image}}(i_\nu ) \subseteq {\mathcal {N}}_\nu \) and \({\mathrm {Fix}}(i_\nu ) = {\mathcal {S}}\).
Since \({\mathcal {S}} \preceq {\mathcal {M}}\) and \({\mathcal {S}} \preceq {\mathcal {N}}\), we have \({\mathrm {Th}}_{\Sigma _1^{{\mathcal {P}}}, {\mathcal {S}}}({\mathcal {M}}) = {\mathrm {Th}}_{\Sigma _1^{{\mathcal {P}}}, {\mathcal {S}}}({\mathcal {N}})\). So by Corollary 7.7, there is a topless rank-initial embedding \(j : {\mathcal {M}} \rightarrow {\mathcal {N}}\) which fixes \({\mathcal {S}}\) pointwise. Identify \({\mathcal {M}}\), pointwise, with the image of this embedding, and pick \(\mu \in {\mathrm {Ord}}^{\mathcal {M}} {\setminus } {\mathcal {S}}\). Let \(i = i_\mu \). It now follows from Proposition 6.6 that \(i({\mathcal {M}}) <^{\text {rank-cut}} i({\mathcal {N}})\), so
as desired. \(\square \)
Theorem 9.5
(Bahrami–Enayat-style) Let \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1^{{\mathcal {P}}}\text {-Separation} + \text {Choice}\) be countable and non-standard, and let \({\mathcal {S}}\) be a proper rank-initial substructure of \({\mathcal {M}}\). The following are equivalent:
-
(a)
\({\mathcal {S}} = {\mathrm {Fix}}(i)\), for some self-embedding \(i : {\mathcal {M}} \rightarrow {\mathcal {M}}\).
-
(a’)
\({\mathcal {S}} = {\mathrm {Fix}}(i)\), for some topless rank-initial self-embedding \(i : {\mathcal {M}} \rightarrow {\mathcal {M}}\), which is contractive on \({\mathcal {M}} {\setminus } {\mathcal {S}}\).
-
(b)
\({\mathcal {S}}\) is a \(\Sigma _1^{{\mathcal {P}}}\)-elementary strong rank-cut of \({\mathcal {M}}\).
Proof
(a) \(\Rightarrow \) (b): It follows from Lemma 6.17 that \({\mathcal {S}} \preceq _{\Sigma _1^{{\mathcal {P}}}} {\mathcal {M}}\). Next we observe that \({\mathcal {S}}\) is topless: It is assumed to be a proper substructure. If there were a least \(\lambda \in {\mathrm {Ord}}^{\mathcal {M}} {\setminus } {\mathcal {S}}\), then by initiality of i and \({\mathcal {S}} \subseteq {\mathrm {Fix}}(i)\), we would have \(i(\lambda ) = \lambda \), contradicting \({\mathcal {S}} \supseteq {\mathrm {Fix}}(i)\) and \(\lambda \not \in {\mathcal {S}}\).
Let \(\alpha , \beta \in {\mathrm {Ord}}^{\mathcal {M}}\), with \({\mathrm {Ord}}^{\mathcal {M}} \cap {\mathcal {S}} \subseteq \alpha _{\mathcal {M}}\), and let \(f \in {\mathcal {M}}\) code a function from \(\alpha \) to \(\beta \) in \({\mathcal {M}}\). Note that \({\mathrm {Ord}}^{\mathcal {M}} \cap {\mathcal {S}} \subseteq i(\alpha )_{\mathcal {M}}\) and that i(f) codes a function from \(i(\alpha )\) to \(i(\beta )\) in \({\mathcal {M}}\). By \({\mathcal {S}} = {\mathrm {Fix}}(i)\), for all \(\zeta \in {\mathrm {Ord}}^{\mathcal {M}} \cap {\mathcal {S}}\) we have

We define a formula, with f and i(f) as parameters:
Note that \(\phi \) is \(\Pi _1\) and that \({\mathcal {M}} \models \phi (\zeta )\), for all \(\zeta \in {\mathrm {Ord}}^{\mathcal {M}} \cap {\mathcal {S}}\). So by \(\Pi _1^{{\mathcal {P}}} \text {-Overspill}\) and toplessness of \({\mathcal {S}}\), there is \(\mu \in {\mathrm {Ord}}^{\mathcal {M}} {\setminus } {\mathcal {S}}\) such that \({\mathcal {M}} \models \phi (\mu )\). Combining \({\mathcal {M}} \models \phi (\mu )\) with (\(\dagger \)), we have for all \(\zeta \in {\mathrm {Ord}}^{\mathcal {M}} \cap {\mathcal {S}}\) that
On the other hand, by \(\mu \in {\mathrm {Ord}}^{\mathcal {M}} {\setminus } {\mathcal {S}}\), the converse is obvious. Hence, \({\mathcal {S}}\) is strongly topless.
(b) \(\Rightarrow \) (a’): By Lemma 9.3, we can apply Lemma 9.4. The restriction  of \(i : {\mathcal {N}} \rightarrow {\mathcal {N}}\) (from Lemma 9.4) to \({\mathcal {M}}\), is a topless rank-initial self-embedding of \({\mathcal {M}}\) with fixed-point set \({\mathcal {S}}\), which is contractive on \({\mathcal {M}} {\setminus } {\mathcal {S}}\). \(\square \)
of \(i : {\mathcal {N}} \rightarrow {\mathcal {N}}\) (from Lemma 9.4) to \({\mathcal {M}}\), is a topless rank-initial self-embedding of \({\mathcal {M}}\) with fixed-point set \({\mathcal {S}}\), which is contractive on \({\mathcal {M}} {\setminus } {\mathcal {S}}\). \(\square \)
Lemma 9.6
Let \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \text {Choice}\) be countable and let \({\mathcal {S}}\) be a rank-cut of \({\mathcal {M}}\). If \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}}) \models {\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\text { is weakly compact''}\), then \({\mathcal {S}}\) is a strong rank-cut of \({\mathcal {M}}\).
Proof
Write \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}})\) as \(({\mathcal {S}}, {\mathcal {A}})\). Let \({\mathcal {S}} \preceq {\mathcal {N}}\) be the elementary extension obtained from Corollary 8.9, with a topless rank-initial self-embedding i that is contractive on \({\mathcal {N}} {\setminus } {\mathcal {S}}\). It follows from Theorem 9.5 that \({\mathcal {S}}\) is a strong rank-cut of \({\mathcal {N}}\).
Since \({\mathcal {S}}\) is rank-initial in \({\mathcal {M}}\), we have by Proposition 6.10(c) that \({\mathrm {Th}}_{\Sigma _1^{{\mathcal {P}}}, {\mathcal {S}}}(S) \subseteq {\mathrm {Th}}_{\Sigma _1^{{\mathcal {P}}}, {\mathcal {S}}}(M)\). So since \({\mathcal {S}} \preceq {\mathcal {N}}\), we have \({\mathrm {Th}}_{\Sigma _1^{{\mathcal {P}}}, {\mathcal {S}}}(N) \subseteq {\mathrm {Th}}_{\Sigma _1^{{\mathcal {P}}}, {\mathcal {S}}}(M)\), whence by Corollary 7.7, there is a topless rank-initial embedding \(j : {\mathcal {N}} \rightarrow {\mathcal {M}}\) which fixes \({\mathcal {S}}\) pointwise. Now it follows from Proposition 6.6 that \({\mathcal {S}}\) is also a strong rank-cut of \({\mathcal {M}}\). \(\square \)
Lemma 9.7
Let \({\mathcal {M}}\) be a countable recursively saturated model of \({\mathrm {ZFC}}\). If \({\mathcal {S}}\) is a strongly topless rank-initial elementary substructure of M, then \(S \cong {\mathcal {M}}\), and a safe satisfaction relation on \({\mathcal {S}}\) is coded in \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}})\).
Proof
We start by showing that a safe satisfaction relation on \({\mathcal {S}}\) is coded in \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}})\). By the forward direction of Theorem 6.15, \({\mathcal {M}}\) is \(\omega \)-non-standard and admits a safe satisfaction relation \({\mathrm {Sat}}^{\mathcal {M}}\). Put \({\mathrm {Sat}}^{\mathcal {S}} = {\mathrm {Sat}}^{\mathcal {M}} \cap {\mathcal {S}}\). Note that \({\mathrm {Sat}}^{\mathcal {S}}\) is coded in \({\mathcal {M}}\), so the relation \({\mathrm {Sat}}^{\mathcal {S}}\) is coded as a class in \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}})\). Since \({\mathcal {S}} \prec {\mathcal {M}}\), we have \(\omega ^{\mathcal {S}} = \omega ^{\mathcal {M}}\). So since \({\mathcal {S}}\) is rank-initial in \({\mathcal {M}}\) and \({\mathcal {M}}\) is \(\omega \)-non-standard, \({\mathcal {S}}\) is \(\omega \)-non-standard.
Since \({\mathcal {S}}\) is a strongly topless rank-initial elementary substructure of M, we have by Lemma 9.3 that \({\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}}) \models {\mathrm {GBC}}\). Therefore we have \(({\mathcal {S}}, {\mathrm {Sat}}^{\mathcal {S}}) \models {\mathrm {ZF}}({\mathcal {L}}^0_{\mathrm {Sat}})\). To establishes that \({\mathrm {Sat}}^{\mathcal {S}}\) is a safe satisfaction relation on \({\mathcal {S}}\), it remains only to check that \(({\mathcal {S}}, {\mathrm {Sat}}^{\mathcal {S}}) \models \forall \sigma \in {\bar{\Sigma }}_n[x] . ({\mathrm {Sat}}(\sigma , x) \leftrightarrow {\mathrm {Sat}}_{\Sigma _n}(\sigma , x)\) and \(({\mathcal {S}}, {\mathrm {Sat}}^{\mathcal {S}}) \models \forall \pi \in {\bar{\Pi }}_n[x] . {\mathrm {Sat}}(\pi , x) \leftrightarrow {\mathrm {Sat}}_{\Pi _n}(\pi , x))\), for each standard \(n \in {\mathbb {N}}\). But this follows from that \({\mathrm {Sat}}_{\Sigma _n}^{\mathcal {S}} = {\mathrm {Sat}}_{\Sigma _n}^{\mathcal {M}} \cap {\mathcal {S}}^2\) and \({\mathrm {Sat}}_{\Pi _n}^{\mathcal {S}} = {\mathrm {Sat}}_{\Pi _n}^{\mathcal {M}} \cap {\mathcal {S}}^2\), for each standard \(n \in {\mathbb {N}}\), which in turn follows from that \({\mathcal {S}} \prec {\mathcal {M}}\).
By the backward direction of Theorem 6.15, it now follows that \({\mathcal {S}}\) is recursively saturated. Since recursively saturated models are \(\omega \)-non-standard, we have by Lemma 6.7 that \({\mathrm {WFP}}({\mathcal {M}})\) is \(\omega \)-topless in \({\mathcal {M}}\) and in \({\mathcal {S}}\). So by Theorem 7.14, \({\mathcal {S}} \cong {\mathcal {M}}\). \(\square \)
Theorem 9.8
(Kaye–Kossak–Kotlarski-style) Let \({\mathcal {M}} \models {\mathrm {ZFC}} + V = {\mathrm {HOD}}\) be countable and recursively saturated, and let \({\mathcal {S}}\) be a proper rank-initial substructure of \({\mathcal {M}}\). The following are equivalent:
-
(a)
\({\mathcal {S}} = {\mathrm {Fix}}(i)\), for some automorphism \(i : {\mathcal {M}} \rightarrow {\mathcal {M}}\).
-
(b)
\({\mathcal {S}}\) is a strongly topless elementary substructure of \({\mathcal {M}}\).
-
(b’)
\({\mathcal {S}}\) is a strongly topless elementary substructure of \({\mathcal {M}}\) isomorphic to \({\mathcal {M}}\).
Proof
(a) \(\Rightarrow \) (b’): Since \({\mathcal {M}} \models V = {\mathrm {HOD}}\), it has definable Skolem functions, whence Lemma 6.18 may be applied to the effect that \({\mathcal {S}} \prec {\mathcal {M}}\). Strong toplessness of \({\mathcal {S}}\) follows from the forward direction of Theorem 9.5. By Lemma 9.7, we also have that \({\mathcal {S}} \cong {\mathcal {M}}\).
(b) \(\Rightarrow \) (a): Let \(({\mathcal {S}}, {\mathcal {A}}) = {\mathrm {SSy}}_{\mathcal {S}}({\mathcal {M}})\). Since \({\mathcal {S}} \prec {\mathcal {M}}\), we have \(\omega ^{\mathcal {M}} \in {\mathcal {S}}\). Now, by Lemma 9.3, \(({\mathcal {S}}, {\mathcal {A}}) \models {\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\text { is weakly compact''}\). Thus, we may apply Theorem 8.6 (say with \({\mathbb {L}} = {\mathbb {Q}}\)) to obtain a countable model \({\mathcal {S}} \prec {\mathcal {N}}\) with an automorphism \(j : {\mathcal {N}} \rightarrow {\mathcal {N}}\) such that \({\mathrm {Fix}}(j) = {\mathcal {S}}\). By Lemma 9.6, \({\mathcal {S}}\) is strongly topless in \({\mathcal {N}}\).
Moreover, we have by Lemma 9.7 that \({\mathcal {S}}\) is recursively saturated with a safe satisfaction relation \({\mathrm {Sat}}^{\mathcal {S}}\) coded in \({\mathcal {A}}\). By part (b) of Theorem 8.6, \({\mathrm {Sat}}^{\mathcal {S}}\) corresponds to a safe satisfaction class \({\mathrm {Sat}}^{\mathcal {N}}\) on \({\mathcal {N}}\). So by Theorem 6.15, \({\mathcal {N}}\) is recursively saturated. Since \({\mathcal {S}}\) is strongly topless in both \({\mathcal {M}}\) and \({\mathcal {N}}\), it now follows from Theorem 7.14 that there is an isomorphism \(k \in \llbracket {\mathcal {M}} \cong _{\mathcal {S}} {\mathcal {N}} \rrbracket \). The desired automorphism of \({\mathcal {M}}\) is now obtained as \(i = k^{-1} \circ j \circ k\). \(\square \)
Theorem 9.9
Suppose that \({\mathcal {M}} \models {\mathrm {KP}}^{{\mathcal {P}}} + \Sigma _1^{{\mathcal {P}}}\text {-Separation} + \text {Choice}\) is countable and non-standard. The following are equivalent:
-
(a)
There is a strongly topless rank-initial self-embedding i of \({\mathcal {M}}\).
-
(b)
\({\mathcal {M}}\) expands to a model \(({\mathcal {M}}, {\mathcal {A}})\) of \({\mathrm {GBC}} + \text {``}{\mathrm {Ord}}\text { is weakly compact''}\).
Proof
(a) \(\Rightarrow \) (b): If i is strongly topless and rank-initial, then by the Lemma 9.3, we have \({\mathrm {SSy}}_{i({\mathcal {M}})}({\mathcal {M}}) \models {\mathrm {GBC}} + ``{\mathrm {Ord}}\text { is weakly compact''}\). So since \({\mathcal {M}} \cong i({\mathcal {M}})\), we have that \({\mathcal {M}}\) expands to a model of \({\mathrm {GBC}} + \)“\({\mathrm {Ord}}\) is weakly compact”.
(b) \(\Rightarrow \) (a): Expand \({\mathcal {M}}\) to a countable model \(({\mathcal {M}}, {\mathcal {A}})\) of \({\mathrm {GBC}} + \) “\({\mathrm {Ord}}\) is weakly compact”. Let \({\mathcal {N}} \succ ^\text {rank-cut} {\mathcal {M}}\) be a model obtained from Theorem 8.6 by putting \({\mathbb {L}}\) to be a countable linear order without a least element, e.g. \({\mathbb {Q}}\). By Theorem 9.5, \({\mathcal {M}}\) is strongly topless in \({\mathcal {N}}\). Note that \({\mathrm {Th}}({\mathcal {N}}) = {\mathrm {Th}}({\mathcal {M}})\) and \({\mathrm {SSy}}({\mathcal {N}}) = {\mathrm {SSy}}({\mathcal {M}})\). So by Theorem 7.2, there is a rank-initial embedding \(i : {\mathcal {N}} \rightarrow {\mathcal {M}}\). By Proposition 6.6, it now follows that \(i({\mathcal {M}})\) is strongly topless in \({\mathcal {M}}\). \(\square \)
Notes
Here Foundation is the axiom schema \(\exists x \cdot \phi (x) \rightarrow \exists y \cdot (\phi (y) \wedge \forall v \in y \cdot \lnot \phi (v))\), where \(\phi \) ranges over formulae in the language of set theory.
\(\omega \)-toplessness is a strong notion of toplessness; see Sect. 6 for details.
Here \({\mathrm {GBC}}\) is the Gödel–Bernays theory of classes with the axiom of choice, and “\({\mathrm {Ord}}\) is weakly compact” denotes a formal statement to the effect that every binary class-tree as high as the class of ordinals \({\mathrm {Ord}}\) has a branch going all the way to the top.
\(V = {\mathrm {HOD}}\) is the statement that every set is hereditarily ordinal definable; see Sect. 5 for details.
References
Bahrami, S., Enayat, A.: Fixed points of self-embeddings of models of arithmetic. Ann. Pure Appl. Log. 169(6), 487–513 (2018)
Barwise, J.: Admissible Sets and Structures. Springer, Berlin (1975)
Chang, C.C., Keisler, H.J.: Model Theory. Elsevier Science Publishers, Amsterdam (1990)
Ehrenfeucht, A., Mostowski, A.: Models of axiomatic theories admitting automorphisms. Fundamenta Mathematicae 43, 50–68 (1956)
Enayat, A.: Power like models of set theory. J. Symb. Log. 66(2), 1766–1782 (2001)
Enayat, A.: Automorphisms, Mahlo Cardinals, and NFU. In: Nonstandard Models of Arithmetic and Set Theory, Contemporary Mathematics, vol. 361, American Mathematical Society, pp. 37-59 (2004)
Enayat, A.: Automorphisms of models of arithmetic: a unified view. Ann. Pure Appl. Log. 145, 16–36 (2007)
Enayat, A., Hamkins, J.D.: ZFC proves that the class of ordinals is not weakly compact for definable classes. arXiv:1610.02729 [math.LO]. Forthcoming in The Journal of Symbolic Logic
Enayat, A., Kaufmann, M., McKenzie, Z.: Iterated ultrapowers for the masses. Archive for Mathematical Logic, Published online (2017)
Friedman, H.: Countable models of set theories. In: Mathias, A.R.D., Rogers, H. (eds.) Cambridge Summer School in Mathematical Logic. Springer, Berlin (1973)
Gaifman, H.: Models and types of arithmetic. Ann. Math. Log. 9, 223–306 (1976)
Gorbow, P.K.: Self-similarity in the foundations. Ph.D. Thesis. Acta Philosophica Gothoburgensia 32. University of Gothenburg (2018). On-line: 1806.11310
Hamkins, J.D.: Every countable model of set theory embeds into its own constructible universe. J. Math. Log. 13, (2013)
Jech, T.: Set Theory. Springer, Berlin (2002)
Kaye, R., Kossak, R., Kotlarski, H.: Automorphisms of recursively saturated models of arithmetic. Ann. Pure Appl. Log. 55, 67–99 (1991)
Kirby, L., Paris, J.: Initial segments of models of Peano’s axioms, In: Lecture Notes in Mathematics, Vol. 619, Springer-Verlag, pp. 211-226 (1977)
Kossak, R., Kotlarski, H.: Results on automorphisms of recursively saturated models of PA. Fund. Math. 129, 9–15 (1988)
Lévy, A.: A Hierarchy of Formulas in Set Theory. American Mathematical Society, Providence (1965)
Mathias, A.R.D.: The strength of Mac Lane set theory. Ann. Pure Appl. Log. 110, 107–234 (2001)
Ressayre, J.-P.: Modèles non Standard et Sous-Systèmes Remarquables de ZF. In: Modèles non Standard en arithmétique et théorie des ensambles. Publications mathématiques de l’Université Paris VII, no. 22, U.E.R. de Mathématiques, Paris, pp. 47-147 (1987)
Ressayre, J.-P.: Non standard universes with strong embeddings, and their finite approximations. Logic and Combinatorics. Contemp. Math. 65. Amer. Math. Soc. Providence, RI, pp. 333-358 (1987)
Schlipf, J.S.: Toward model theory through recursive saturation. J. Symb. Log. 43(2), 183–206 (1978)
Takahashi, M.: \(\tilde{\Delta }_1\)-definability in set theory. In: Hodges, W. ed., Conference in mathematical logic —London ’70, Springer Lecture Notes in Mathematics 255 , pp. 281-304 (1972)
Wilkie, A.J.: Models of Number Theory. Doctoral dissertation, University of London, (1973)
Wilkie, A.J.: On the theories of end-extensions of models of arithmetic. In: Lachlan, A., Srebrny, M., Zarach, A. (eds.) Set Theory and Model Theory V. Springer, Heidelberg (1977)
Acknowledgements
Open access funding provided by University of Gothenburg. This paper presents a portion of the results in the author’s Ph.D. Thesis [12], which was carried out at The University of Gothenburg, under close supervision of Ali Enayat.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kindvall Gorbow, P. Rank-initial embeddings of non-standard models of set theory. Arch. Math. Logic 59, 517–563 (2020). https://doi.org/10.1007/s00153-019-00699-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00153-019-00699-2
Keywords
- Set theory
- KP
- ZF
- GBC
- Weakly compact
- Nonstandard model
- Embedding
- Self-embedding
- Automorphism
- Fixed point
- Strong cut
- Iterated ultrapower
- Recursively saturated



 ;
;


 to an
to an 
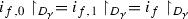 ;
; is an embedding,
is an embedding, 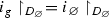 .
. .
. . So
. So  .
. is strictly bounded above by
is strictly bounded above by