Spatial Filter for the Pseudo-spectral Implementation of Fractional Derivative Wave Equation

Abstract

The viscoelasticity of the subsurface media varies spatially, and such viscoelasticity can be represented concisely by a wave equation in the form of fractional temporal derivative (FTD). We have developed a strategy for simulating seismic waves propagating through a heterogeneous viscoelastic model. The FTD is transferred to fractional spatial derivatives (FSDs), and the FSDs are implemented through the fast Fourier transform (FFT), for improving the computational efficiency. However, the FFT implementation is not rigorously applicable to the heterogeneous model. In this paper, we have reformulated the FSD wave equation by introducing a spatial-position dependent filter. This spatial filter corrects the errors that are caused by the assumption of non-heterogeneity in the FFT implementation. This formulation appropriately represents the viscoelastic effect in seismic wave propagation, leading to the improvement on the accuracy of numerical simulation.

1 Introduction

The anelasticity of subsurface media causes seismic dissipation effect including the energy absorption and velocity dispersion, and has a significant impact on field seismic records and subsequent seismic images (Wang, 2008). Conventional models for describing viscoelasticity include Kjartansson’s constant-Q model (Kjartansson, 1979), the Kosky model (Kolsky, 1953), the Kelvin-Voigt model, the standard linear solid model (Zener, 1948), the Cole–Cole model (Cole & Cole, 1941) etc. These models can lead to viscoelastic wave equations in the form of fractional temporal derivative (FTD).

The FTD was introduced to describe the viscoelasticity of the Earth media by Caputo (1967). The FTD form was used also for the fractional Zener model to describe the mechanic combination of the viscoelasticity (Liu & Greenhalgh, 2019). However, directly solving the FTD wave equation presents a numerical challenge in seismic wave simulation. The FTD might be solved in the frequency domain, but the computation is extremely intensive because it requires to solve numerous Helmholtz equations (Vasilyeva et al., 2019). An alternative, but still expensive, method is to solve a convolution equation in the time domain (Carcione et al., 2002). The Grünwald-Letnikov expansion can also be used to calculate the FTD, but this expansion requires large computational memory to store the wavefield history, even the expansion is truncated (Podlubny, 1999).

A practical way to reduce the computational cost of the FTD wave equation is that, when the attenuation is weak, one can transfer the FTD to fractional spatial derivatives (FSDs), and then solve FSDs by Fourier pseudo-spectral method, which greatly lowers the computation memory threshold (Carcione, 2010; Chen & Holm, 2004; Treeby & Cox, 2010). The FSDs in the wave equation can also be decoupled into velocity dispersion and energy dissipation, respectively (Zhu & Harris, 2014), and this decoupled wave equation can be further expanded to viscoelastic and tilted transversely isotropic (TTI) media (Qiao et al., 2019; Zhu & Bai, 2019; Zhu & Carcione, 2014). The accuracy of the FSDs for wave simulation in high-attenuation media can further be improved by Taylor series expansion (Mu et al., 2021).

When using the pseudo-spectral method to solve the FSDs in the wave equation, it requires that the viscoelastic parameter $\beta ({\mathbf{x}})$ is a constant in the space. In practice, the viscoelastic parameter $\beta ({\mathbf{x}})$ is averaged over the space ${\mathbf{x}}$, to generate a constant $\overline{\beta }$ for the purpose of spatial Fourier transform. This averaging process will cause errors in numerical calculation. Based on the locality principle, Zhu and Harris (2014) propose to interpolate the solutions generated with every single constant parameter for whole model. The spatially varying order of FSD is a function of $\beta ({\mathbf{x}})$. Chen et al. (2016) and Xing and Zhu (2019) use either the Taylor expansion or a polynomial approximation to transfer the spatial-varying order FSD into the constant order FSDs, and then implement the pseudo-spectral method directly. Yao et al. (2017) apply the Hermite distributed approximation to transfer the spatial-varying FSD to an integral of the fractional derivative of delta function, and this fractional derivative can be solved locally. But all these schemes aforementioned scarify the efficiency for accuracy to some extent. For example, when using the polynomial approximation to derive the constant-order wave equation (Xing & Zhu, 2019), the resultant wave equation includes six fractional Laplacian operators. This scheme greatly lowers the efficiency, if compared with the original two-operator equation.

In this paper, we propose a strategy to solve the FSDs for wave simulation in heterogeneous media, that would be straightforward in philosophy and simpler in realization. The strategy is to build a spatially varying correction function, and to insert this spatial filter directly into the averaging scheme. Because this spatial filter is frequency-independent, it is efficiently implemented as a coefficient multiplied to the wave equation. Therefore, this filter improves the accuracy and maintains the high efficiency of FFT implementation.

2 The Equation Formed with Fractional Spatial Derivatives

The wave equation presented in terms of FTD may be transferred to a wave equation formed with FSDs. The ultimate purpose of this paper is to have an efficient implementation of wave equation with FSDs.

We consider the FTD wave equation (Wang, 2016), as the following

$$ \frac{{\partial^{2} u}}{{\partial t^{2} }} = c^{2} (\beta )\nabla^{2} \left( {1 + \frac{\beta }{{\omega_{0}^{\beta } }}\frac{{{\text{d}}^{\beta } }}{{{\text{d}}t^{\beta } }}} \right)u, $$

(1)

where u is the scalar wavefield, $\omega_{0}$ is the reference frequency, $\beta$ is the viscoelastic parameter, and $c(\beta )$ is the viscoelastic velocity, which means the phase velocity at zero frequency. Assuming the medium parameters to be spatially invariant, we can rewrite it in the frequency-wavenumber domain as

$$ \left[ {\frac{{\omega^{2} }}{{c^{2} }} - k^{2} \left( {1 + \beta \left( {\frac{\omega }{{\omega_{0} }}} \right)^{\beta } \cos \frac{\beta \pi }{2} + i\beta \left( {\frac{\omega }{{\omega_{0} }}} \right)^{\beta } \sin \frac{\beta \pi }{2}} \right)} \right]\hat{u} = 0, $$

(2)

where k is the wavenumber, and $\hat{u}$ is the frequency-wavenumber domain wavefield. Now, making an approximation based on weak attenuation assumption (Zhu & Harris, 2014)

$$ \frac{\omega }{{c_{0} }} \approx k, $$

(3)

where $c_{0}$ is the reference velocity, Eq. (2) is approximated to

$$ \left( {\frac{{\omega^{2} }}{{c^{2} }} - k^{2} - k^{2 + \beta } C_{1} (\beta ) - i\omega k^{1 + \beta } C_{2} (\beta )} \right)\hat{u} = 0, $$

(4)

$$ \begin{gathered} C_{1} (\beta ) = \beta \left( {\frac{{c_{0} }}{{\omega_{0} }}} \right)^{\beta } \cos \frac{\beta \pi }{2}, \hfill \\ C_{2} (\beta ) = \frac{\beta }{{\omega_{0} }}\left( {\frac{{c_{0} }}{{\omega_{0} }}} \right)^{\beta - 1} \sin \frac{\beta \pi }{2}. \hfill \\ \end{gathered} $$

(5)

Applying an inverse Fourier transform to Eq. (4), the generalized wave equation in the temporal-spatial domain may be presented as FSDs:

$$ \frac{1}{{c^{2} }}\frac{{\partial^{2} u}}{{\partial t^{2} }} + \left( {( - \nabla^{2} ) + C_{1} (\beta )( - \nabla^{2} )^{1 + \beta /2} + C_{2} (\beta )( - \nabla^{2} )^{(1 + \beta )/2} \frac{\partial }{\partial t}} \right)u = 0, $$

(6)

where $u$ is the time–space domain wavefield. Equation (6) decouples the dissipation effect, as the $C_{1}$ term is from the real part of FTD, which represents the velocity dispersion and the $C_{2}$ term is from the imaginary part of the FTD, which represents the amplitude absorption (Zhu & Harris, 2014). In this equation, $C_{1} (\beta )$ and $C_{2} (\beta )$ are assumed to be spatially independent. However, when forming the FSDs for a general viscoelastic case, both terms are spatially variable, because $\beta ({\mathbf{x}})$ is a spatial function.

For the derivation above, the approximation Eq. (3) is a key condition, so that the complex wavenumber $\tilde{k}$ could be replaced with the real wavenumber $k = \tilde{k}_{{\text{Re}}}$. This approximation to the complex wavenumber is made based on the weak-attenuation assumption. For the complex wavenumber $\tilde{k}$, the real and imaginary part may be written analytically as (Wang, 2019)

$$ \tilde{k}_{{\text{Re}}} = \frac{\omega }{v(\beta , \, \omega )} = \frac{\left| \omega \right|}{{\sqrt 2 c(\beta )}}\frac{{\sqrt {A + B} }}{A}, $$

(7)

$$\tilde{k}_{{\text{Im}}} = \alpha (\beta , \, \omega ) = \frac{\left| \omega \right|}{{\sqrt 2 c(\beta )}}\frac{{\sqrt {A - B} }}{A},$$

(8)

where $v(\beta ,\omega )$ is the phase velocity, $\alpha (\beta ,\omega )$ is the attenuation coefficient, and the absolute value is for satisfying the anti-Hermitian property of the complex wavenumber. The factors A and B were given by Wang (2019).

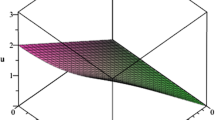
Figure 1 illustrates the accuracy of this weak-attenuation assumption with the ratio $R = k/|\tilde{k}|$. The reference frequency $\omega_{0}$ is set as 500 Hz, which is the highest possible frequency of exploration seismology (Wang & Guo, 2004), and then $\omega /\omega_{0} \le 1$. Figure 1 shows that the ratio R is close to 1, for $\beta \le 0.75$, and the relative error is less than 0.5%. When $\beta \le 0.351$, the ratio R is approaching to 1 with decreasing $\beta$. But when $\beta > 0.351$, the ratio R is increasing with an increasing $\beta$. Therefore, the weak-attenuation assumption is valid for $\beta \le 0.351$, to the most areas interested by seismic application (Kolsky, 1953; Futterman, 1962; Mason, 1956; Wang, 2019).

Fig. 1

Variation of the weak-attenuation assumption, illustrated by the ratio $R = k_{{\text{Re}}} /|\tilde{k}|$ versus the viscoelastic parameter $\beta$. The upper side of the yellow square represent $R = 1.0$

To evaluate the accuracy of FSDs of Eq. (6), the wavenumber domain Eq. (4) is treated as a non-linear equation $f(k) = 0$. The numerically solved wavenumber is compared to the exact wavenumber of FTD presented analytically in Eqs. (7) and (8).

Figure 2 demonstrates the accuracy evaluation using an arbitrarily designed pure acoustic velocity $c_{0} =$ 2500 m/s, and considering cases of weak, median, and strong attenuation with $\beta =$(0.010, 0.183, 0.351). The accuracy of the phase velocity is high in general, as the root-mean-square (RMS) error in three cases together is 4.169 m/s. The accuracy of the attenuation depends on the $\beta$ value. The RMS errors in the attenuation coefficient are $0.0501 \times 10^{ - 3} {\text{m}}^{{ - {1}}}$ for $\beta = 0.010$ and $0.3405 \times 10^{ - 3} {\text{m}}^{{ - {1}}}$ for $\beta = 0.190$. However, the RMS error in the attenuation coefficient is $6.769 \times 10^{ - 3} {\text{m}}^{ - 1}$ for the extreme case with $\beta = 0.351$. This error existed in the most attenuating case is caused by the approximation $\omega /c_{0} \approx k$ (Eq. 3) used in the transformation from FTD to FSDs.

Fig. 2

Comparison between the wave equations formed with FTD (solid black curves) and with FSDs (dashed red curves). a The attenuation $\alpha (\omega )$. b The phase velocity $v(\omega )$

To investigate the reliability of the FSDs, we compare the analytical solutions of two types of wave equations presented as FTD and FSDs, respectively. Considering a homogeneous case with constant $\beta$, the one-dimensional analytical solution for FTD in frequency domain is derived as

$$ \hat{u}(\omega ,x) = - \frac{{ie^{{i\omega \Omega_{1} \left\| {x - x_{0} } \right\|}} }}{2\omega }\Omega_{1} \hat{f}(\omega ), $$

(9)

with

$$\Omega_{1} = \frac{1}{c(\beta )}\left( {1 + \beta \left( {\frac{i\omega }{{\omega_{0} }}} \right)^{\beta } } \right)^{ - 1/2} ,$$

(10)

where $\hat{u}(\omega ,x)$ is the wavefield in the frequency domain, and $\hat{f}(\omega )$ is the source signature in the frequency domain. For FSDs, the corresponding analytical solution is formed using the Green’s function $G(t,k,\tau )$ as

$$\hat{u}(t,k) = \int_{0}^{t} {G(t,k,\tau )f(\tau ){\text{d}}\tau ,}$$

(11)

where $\hat{u}(t,k)$ is the wavefield in the wavenumber domain. The Green’s function is

$$ G(t,k,\tau ) = H(t - \tau )\frac{{\sin \left[ {\left( {t - \tau } \right)\Omega_{2} } \right]}}{{\Omega_{2} }}e^{{ - \frac{1}{2}(t - \tau )c^{2} (\beta )k^{1 + \beta } C_{2} }} , $$

(12)

where $H(t - \tau )$ is the Heaviside step function, and

$$\Omega_{2} = c(\beta )k\sqrt {1 + k^{\beta } C_{1} - \frac{1}{4}c^{2}(\beta ) k^{2\beta } C_{2}^{2} } .$$

(13)

An inverse Fourier transform of $\hat{u}(t,k)$ with respect to the wavenumber $k$ produces the time–space domain wavefield $u(t,x)$. Note that the Green’s function in Eq. (12) is presented in terms of a sinc function.

We set a model with the velocity of 2500 m/s, and assume the source signature be a Ricker wavelet with the peak frequency of 20 Hz (Wang, 2015). Figure 3 displays the waveform at travel distance 200 m, and demonstrates that two equations match well in general, and only a minor discrepancy exists in the strong attenuation case. The RMS differences corresponding to the cases with $\beta$ = (0.010, 0.144, 0.190, 0.351) are ($5.276 \times 10^{ - 2}$, $6.538 \times 10^{ - 2}$, $7.295 \times 10^{ - 2}$, $22.878 \times 10^{ - 2}$), respectively. This observation is consistent with that shown in Fig. 2.

Fig. 3

Comparison between the wave equation formed with the FTD (solid black curves) and one with FSDs (dashed red curves). The travel distance is 200 m. The Q value and the corresponding RMS differences are listed in the plots

Noted that the above equation with FSDs (Eq. 6) is derived based on homogeneous media where the viscoelastic parameter $\beta$ is constant. When forming the FSDs for a general viscoelastic case, $\beta ({\mathbf{x}})$ is a spatial function. Based on the small perturbation assumption, FSDs is still approximated valid for a general viscoelastic case (Xing & Zhu, 2019; Zhu & Harris, 2014).

3 The Spatial Filter for the Heterogeneous Media

For the numerical calculation of Eq. (6), we use a pseudo-spectral method to solve the FSD. In practice, the viscoelastic parameter $\beta ({\mathbf{x}})$ in the heterogeneous media is assumed to be smoothly varied and then the average parameter $\overline{\beta }$ is adopted for calculating the FSD:

$$ ( - \nabla^{2} )^{{\overline{\beta }/2}} u({\mathbf{x}}) = {\mathbf{F}}_{{\text{x}}}^{ - 1} \left\{ {k^{{\overline{\beta }}} {\mathbf{F}}_{{\text{x}}} {[}u({\mathbf{x}})]} \right\}, $$

(14)

where ${\mathbf{F}}_{{\text{x}}}$ is the Fourier transform with respect to vector x, and ${\mathbf{F}}_{{\text{x}}}^{ - 1}$ is the inverse of ${\mathbf{F}}_{{\text{x}}}$. The wavefield in the space domain and in the wavenumber domain are listed in pairs as the following:

$$ \begin{gathered} u({\mathbf{x}}) \, \leftrightarrow \, {\mathbf{F}}_{{\text{x}}} {[}u({\mathbf{x}})], \\ - \nabla^{2} u({\mathbf{x}}) \, \leftrightarrow \, k^{2} {\mathbf{F}}_{{\text{x}}} {[}u({\mathbf{x}})], \\ ( - \nabla^{2} )^{\beta /2} u({\mathbf{x}}) \, \leftrightarrow \, k^{\beta } {\mathbf{F}}_{{\text{x}}} {[}u({\mathbf{x}})]. \\ \end{gathered} $$

(15)

The pseudo-spectral method has been used widely in the wave simulation (Carcione, 2010). Therefore, the numerical advantage of the FSD is to overcome the memory issue related to the numerical calculation of the FTD in the original wave equation.

In order to correct the errors caused by the averaging scheme of the FFT implementation, we introduce a correction function $f(\beta ({\mathbf{x}}))$ as a spatial filter to correct the wavenumber as

$$ k^{{\beta ({\mathbf{x}})}} = k^{{\overline{\beta }}} f(\beta ({\mathbf{x}})). $$

(16)

Multiplying either $k$ or $k^{2}$ to both sides, we have $k^{{1 + \beta ({\mathbf{x}})}} = f(\beta ({\mathbf{x}}))k^{{1 + \overline{\beta }}}$ and $k^{{2 + \beta ({\mathbf{x}})}} = f(\beta ({\mathbf{x}}))k^{{2 + \overline{\beta }}}$. Therefore, a corrected wave equation which corresponds to Eq. (6) is

$$ \frac{1}{{c^{2} }}\frac{{\partial^{2} u}}{{\partial t^{2} }} + \left( {( - \nabla^{2} ) + ( - \nabla^{2} )^{{1 + \overline{\beta }/2}} C_{1} (\beta ({\mathbf{x}}))f(\beta ({\mathbf{x}})) + ( - \nabla^{2} )^{{(1 + \overline{\beta })/2}} C_{2} (\beta ({\mathbf{x}}))f(\beta ({\mathbf{x}}))\frac{\partial }{\partial t}} \right)u = 0. $$

(17)

For constructing the spatial filter, we assume the case of weak attenuation with $k_{{{\text{Im}}}} /|\tilde{k}| \, \ll 1$ and make approximation $\tilde{k} \approx k_{{\text{Re}}}$. The real wavenumber $k_{{\text{Re}}}$ in Eq. (7) can be expanded to the first order as

$$k_{{\text{Re}}} \approx \frac{\omega }{c}\left( {1{ + }\frac{{\beta(\mathbf{x}) }}{8}\cos \left( {\frac{{\pi \beta (\mathbf{x})}}{2}} \right)} \right).$$

(18)

Then, the spatial filter $f(\beta ({\mathbf{x}}))$ is evaluated at each grid by

$$\begin{aligned} &f(\beta ({\mathbf{x}})) \approx k_{{\text{Re}}}^{{\beta ({\mathbf{x}}) - \overline{\beta }}} \\ &\qquad \quad = \left( {\frac{\omega }{c}} \right)^{{\beta ({\mathbf{x}}) - \overline{\beta }}} \left( {1{ + }\frac{{\beta ({\mathbf{x}})}}{8}\cos \left( {\frac{{\pi \beta ({\mathbf{x}})}}{2}} \right)} \right)^{{\beta ({\mathbf{x}}) - \overline{\beta }}} \\ &\qquad \quad \approx \left( {\frac{{\omega_{m} }}{c}} \right)^{{\beta ({\mathbf{x}}) - \overline{\beta }}} \left( {1{ + }\frac{{\beta ({\mathbf{x}})}}{8}\cos \left( {\frac{{\pi \beta ({\mathbf{x}})}}{2}} \right)} \right)^{{\beta ({\mathbf{x}}) - \overline{\beta }}} , \\ \end{aligned}$$

(19)

where $\omega_{m}$ is the mean frequency. The central-frequency approximation in the last line is made based on an assumption $\left| {\beta ({\mathbf{x}}) - \overline{\beta }} \right| \ll 1$, so that the spatial filter $f(\beta ({\mathbf{x}}))$ is frequency independent and avoids any extra Fourier transform. Thus, this spatial filter does not affect the efficiency of the algorithm, but greatly improve the accuracy in heterogeneous media.

4 Numerical Examples

In this paper, we present two numerical examples. The first example is for validating the effectiveness of the spatial filter.

We set the constant velocity to be 2500 m/s, and consider a model with the viscoelastic parameter values $\beta =$(0.351, 0.190, 0.131). We use the same source signature of 20-Hz Ricker wavelet (Wang, 2015a, b), and calculate the waveforms at distances of 500 m and 2000 m. These two accurate waveforms are plotted in a single trace in Fig. 4 (black solid curves).

Fig. 4

The correction function of wave equation for heterogeneous media. a Comparison between the averaging scheme without correction (red dots) and the accurate solution (black solid curves). b Comparison between the averaging plus correction scheme (blue dots) and the accurate solution

To mimic the approximation in the viscoelastic wave equation, we assume a “heterogeneous” model with the average value of $\overline{\beta } =$(0.237, 0.152, 0.112). The approximated solutions (in red dots) are overlaid with the accurate trace, as shown in Fig. 4a. Three cases have RMS differences of 23.95 $\times 10^{ - 2}$, 9.09 $\times 10^{ - 2}$, and 4.74 $\times 10^{ - 2}$. These differences are caused mainly due to the phase discrepancy but is also due to the amplitude difference at large $\beta$ value case.

Adopting the correction with the spatial filter, calculated waveforms (in blue dots) are close to the accurate waveforms, as shown in Fig. 4b. The RMS differences are (2.85 $\times 10^{ - 2}$, 1.05 $\times 10^{ - 2}$, 0.52 $\times 10^{ - 2}$) for the three cases, respectively. Both the phase and the amplitude are corrected remarkably. This example shows that the correction function can improve the accuracy of waveform simulation in the heterogeneous media, especially in a high-attenuation area.

Next, we validate our scheme in a two-layer model. The model is shown in Fig. 5a. A reference is set by directly solving Eq. (1) using Grünwald-Letnikov expansion (Podlubny, 1999) as follows:

$$ \frac{{{\text{d}}^{\beta } u}}{{{\text{d}}t^{\beta } }} \approx \frac{1}{{\Delta t^{\beta } }}\sum\limits_{m = 0}^{t/\Delta t} {( - 1)^{m} \left( {\begin{array}{*{20}c} \beta \\ m \\ \end{array} } \right)u(t - m\Delta t)} $$

(20)

Fig. 5

A layered model and wavefield snapshots at 0.35 s. a The model parameter and reference wavefield; b the wavefield without correction and its residual to reference; c the wavefield with correction and its residual to reference

where $\Delta t$ is the time interval. A 20-Hz Ricker wavelet is emitted the centre of the model. The model is discretized into 801 × 801 grids with grid spacings of 2.5 m. This fine spacing is equivalent to 16 nodes per wavelength ($\lambda_{\min } = v_{\min } /(2.5f_{p} )$ = 40 m). The time step is set as $\Delta t$ = 0.25 ms, which is also finer than the numerical requirement $\Delta t < \Delta x/(\sqrt 2 v_{\max } ) = 0.59$. Setting fine intervals in spatial and temporal axes is for minimizing discrepancy between Grünwald-Letnikov expansion and the pseudo-spectral method.

Figure 5 also displays the wavefield snapshots at 0.35 s of the layered model. The result without correction by the spatial filter (Fig. 5b) shows significant discrepancy from the reference, which proves that the conventional averaging scheme causes errors. However, after correction (Fig. 5c), the accuracy is significantly improved. This example further demonstrates the importance of spatial filter for seismic sim ulation in heterogeneous media. Any remaining weak residual in Fig. 5c is attributed to the transformation from FTD to FSDs.

In the second example, we apply FSDs of Eq. (17) to simulate the wavefield of the Marmousi model. Figure 6 displays the acoustic velocity of the Marmousi model, and the $\beta$ model. The $\beta$ model is built based on an analysis of the attenuation versus velocity from a field 3D seismic data in Tarim basin. The model is discretized into 751 × 301 grid points with regular vertical and horizontal grid spacings of 10 m. The source signature is a 20-Hz Ricker wavelet and is emitted at (3800, 150) m. The receivers are located at a depth of 150 m and in a spatial range of 0–7500 m with 10 m spacing. The time step is 1 ms.

Fig. 6

The Marmousi model. a The P-wave velocity model. b The $\beta$ model, generated through an empirical formula

Figure 7 shows snapshots of the wavefield without attenuation and the wavefield with attenuation at 0.6 s, 0.8 s and 1.0 s, respectively. There are no free-surface reflections from the top boundary and other three boundaries, since a convolutional perfectly matched layer (CPML) absorbing condition is adopted in numerical calculation. However, there are clear reflections from the interfaces within the model, for both cases; this observation indicates the high quality of the simulation with ignorable numerical dispersion. More importantly, these snapshots demonstrate that the attenuating wavefields have a clearly delayed wavefront and reduced amplitude, if compared to its non-attenuation counterparts.

Fig. 7

Seismic wave simulation. a Snapshots of non-attenuating wavefield at 0.6 s, 0.8 s and 1.0 s. b Snapshots of attenuating wavefield at 0.6 s, 0.8 s and 1.0 s

Comparison between the non-attenuating and attenuating shot gathers (Fig. 8a and b) demonstrates the accumulative effect of attenuation. Moreover, comparison between residuals of the conventional averaging scheme and the corrected scheme with the proposed spatial filter (Fig. 9a and b) demonstrates the significance of the spatial filter. The residual shown in Fig. 9 is the discrepancy from the Grünwald-Letnikov expansion. Whereas the proposed wave equation is applicable to complex geological models, the reflection events from the interior interfaces are very weak in amplitude. The accurate wave simulation will lead to correct subsurface image from seismic migration, as it leads to correct compensation to the viscoelasticity of the subsurface media.

Fig. 8

The effect of attenuation in seismic wavefield. a The non-attenuating shot gather. b The attenuating shot gather, generated by the corrected scheme

Fig. 9

The significance of the correction function. a The residual of the conventional averaging scheme. b The residual of the corrected averaging scheme. The reference is the solution of Grünwald-Letnikov expansion

5 Conclusions

When transferring the wave equation in the FTD form to the FSDs form, the wave simulation can be implemented in the wavenumber domain. In this paper, we have proposed to insert a frequency-independent correction function into the wave equation as a spatial filter to correct the error caused by the heterogeneity of the model. This spatial filter can be easily implemented and an equation including the correction improves the accuracy of the simulation. Numerical examples have demonstrated that this strategy may properly represent the dissipation effect of the viscoelasticity on waveforms and improve accuracy and maintains the high efficiency of FFT implementation.