Simulating Seismic Wave Propagation in Viscoelastic Media with an Irregular Free Surface

Abstract

In seismic numerical simulations of wave propagation, it is very important for us to consider surface topography and attenuation, which both have large effects (e.g., wave diffractions, conversion, amplitude/phase change) on seismic imaging and inversion. An irregular free surface provides significant information for interpreting the characteristics of seismic wave propagation in areas with rugged or rapidly varying topography, and viscoelastic media are a better representation of the earth’s properties than acoustic/elastic media. In this study, we develop an approach for seismic wavefield simulation in 2D viscoelastic isotropic media with an irregular free surface. Based on the boundary-conforming grid method, the 2D time-domain second-order viscoelastic isotropic equations and irregular free surface boundary conditions are transferred from a Cartesian coordinate system to a curvilinear coordinate system. Finite difference operators with second-order accuracy are applied to discretize the viscoelastic wave equations and the irregular free surface in the curvilinear coordinate system. In addition, we select the convolutional perfectly matched layer boundary condition in order to effectively suppress artificial reflections from the edges of the model. The snapshot and seismogram results from numerical tests show that our algorithm successfully simulates seismic wavefields (e.g., P-wave, Rayleigh wave and converted waves) in viscoelastic isotropic media with an irregular free surface.

Appendices

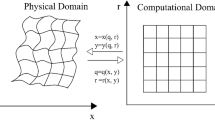
Appendix A: Relationship Between Cartesian and Curvilinear Coordinates

The grid point $\left( {x,z} \right)$ in Cartesian coordinates is determined from the grid point $\left( {q,r} \right)$ in curvilinear coordinates with the equations:

$$ x = x(q,r), $$

(22)

$$ z = z(q,r). $$

(23)

The spatial derivatives in the Cartesian coordinate system can be obtained from the curvilinear coordinate system following the chain rule (Lan and Zhang 2011; Lan et al. 2016):

$$ \partial_{x} = q_{x} \partial_{q} + r_{x} \partial_{r} , $$

(24)

$$ \partial_{z} = q_{z} \partial_{q} + r_{z} \partial_{r} , $$

(25)

where $q_{x}$, $q_{z}$, $r_{x}$ and $r_{z}$ denote $\partial_{q} \left( {x,z} \right)/\partial_{x}$, $\partial_{q} \left( {x,z} \right)/\partial_{z}$,$\partial_{r} \left( {x,z} \right)/\partial_{x}$ and $\partial_{r} \left( {x,z} \right)/\partial_{z}$, respectively. Similarly, we can express the spatial derivatives in the curvilinear coordinate system $\left( {q,r} \right)$ as

$$ \partial_{q} = x_{q} \partial_{x} + z_{q} \partial_{z} , $$

(26)

$$ \partial_{r} = x_{r} \partial_{x} + z_{r} \partial_{z} . $$

(27)

These kinds of derivatives are called metric derivatives (Lan and Zhang 2011):

$$ q_{x} = \frac{{z_{r} }}{J},\quad q_{z} = \frac{{ - x_{r} }}{J}, $$

(28)

$$ r_{x} = \frac{{ - z_{q} }}{J},\quad r_{z} = \frac{{x_{q} }}{J}, $$

(29)

where $z_{r}$, $z_{q}$, $x_{r}$ and $x_{r}$ denote $\partial_{z} \left( {q,r} \right)/\partial_{r}$, $\partial_{z} \left( {q,r} \right)/\partial_{q}$,$\partial_{x} \left( {q,r} \right)/\partial_{r}$ and $\partial_{x} \left( {q,r} \right)/\partial_{r}$, respectively. The Jacobian of the transformation $J$ is given by

$$ J = {\text{x}}_{q} z_{r} - x_{r} z_{q} . $$

(30)

Appendix B: Viscoelastic Equations with the CPML Boundary Condition

The viscoelastic equations with the CPML boundary condition in curvilinear coordinates can be written as

$$ \rho \frac{{\partial^{ 2} u}}{{\partial t^{2} }} = u_{1} + u_{2} + u_{3} + u_{4} , $$

(31)

$$ \rho \frac{{\partial^{ 2} v}}{{\partial t^{2} }} = v_{1} + v_{2} + v_{3} + v_{4} , $$

(32)

where

$$ u_{1} = q_{x} \cdot \left[ \begin{aligned} \left( {\lambda + 2\mu } \right)q_{x} \left( {\frac{1}{{k_{q} }}\frac{{\partial u_{q} }}{\partial q} + \phi_{{q,u_{q} }} } \right) + \left( {\lambda + 2\mu } \right)r_{x} \left( {\frac{1}{{k_{q} }}\frac{{\partial u_{r} }}{\partial q} + \phi_{{{\text{q}},u_{r} }} } \right) + \frac{1}{2}\frac{{\partial \sum\nolimits_{l = 1}^{{L_{1} }} {e_{1l} } }}{\partial q} \hfill \\ + \lambda q_{z} \left( {\frac{1}{{k_{q} }}\frac{{\partial v_{q} }}{\partial q} + \phi_{{q,v_{q} }} } \right) + \lambda r_{z} \left( {\frac{1}{{k_{q} }}\frac{{\partial v_{r} }}{\partial q} + \phi_{{{\text{q}},v_{r} }} } \right) + \frac{{\partial \sum\nolimits_{l = 1}^{{L_{2} }} {e_{11l} } }}{\partial q} \hfill \\ \end{aligned} \right], $$

(33)

$$ u_{2} = q_{z} \cdot \left[ \begin{aligned} \mu q_{x} \left( {\frac{1}{{k_{q} }}\frac{{\partial v_{q} }}{\partial q} + \phi_{{q,v_{q} }} } \right) + \mu r_{x} \left( {\frac{1}{{k_{q} }}\frac{{\partial v_{r} }}{\partial q} + \phi_{{q,v_{r} }} } \right) + \frac{{\partial \sum\nolimits_{l = 1}^{{L_{2} }} {e_{12l} } }}{\partial q} \hfill \\ + \mu q_{z} \left( {\frac{1}{{k_{q} }}\frac{{\partial u_{q} }}{\partial q} + \phi_{{q,u_{q} }} } \right) + \mu r_{z} \left( {\frac{1}{{k_{q} }}\frac{{\partial u_{r} }}{\partial q} + \phi_{{q,u_{r} }} } \right) \hfill \\ \end{aligned} \right], $$

(34)

$$ u_{3} = r_{x} \cdot \left[ \begin{aligned} \left( {\lambda + 2\mu } \right)q_{x} \left( {\frac{1}{{k_{r} }}\frac{{\partial u_{q} }}{\partial r} + \phi_{{q,u_{q} }} } \right) + \left( {\lambda + 2\mu } \right)r_{x} \left( {\frac{1}{{k_{r} }}\frac{{\partial u_{r} }}{\partial r} + \phi_{{q,u_{r} }} } \right) + \frac{1}{2}\frac{{\partial \sum\nolimits_{l = 1}^{{L_{1} }} {e_{1l} } }}{\partial r} \hfill \\ + \lambda q_{z} \left( {\frac{1}{{k_{r} }}\frac{{\partial v_{q} }}{\partial r} + \phi_{{q,v_{q} }} } \right) + \lambda r_{z} \left( {\frac{1}{{k_{r} }}\frac{{\partial v_{r} }}{\partial r} + \phi_{{q,v_{r} }} } \right) + \frac{{\sum\nolimits_{l = 1}^{{L_{2} }} {e_{11l} } }}{\partial r} \hfill \\ \end{aligned} \right], $$

(35)

$$ u_{4} = r_{z} \cdot \left[ \begin{aligned} \mu q_{x} \left( {\frac{1}{{k_{r} }}\frac{{\partial v_{q} }}{\partial r} + \phi_{{q,v_{q} }} } \right) + \mu r_{x} \left( {\frac{1}{{k_{r} }}\frac{{\partial v_{r} }}{\partial r} + \phi_{{q,v_{r} }} } \right) + \frac{{\partial \sum\nolimits_{l = 1}^{{L_{2} }} {e_{12l} } }}{\partial r} \hfill \\ + \mu q_{z} \left( {\frac{1}{{k_{r} }}\frac{{\partial u_{q} }}{\partial r} + \phi_{{q,u_{q} }} } \right) + \mu r_{z} \left( {\frac{1}{{k_{r} }}\frac{{\partial u_{r} }}{\partial r} + \phi_{{q,u_{r} }} } \right) \hfill \\ \end{aligned} \right], $$

(36)

$$ v_{1} = q_{z} \cdot \left[ \begin{aligned} \left( {\lambda + 2\mu } \right)q_{z} \left( {\frac{1}{{k_{q} }}\frac{{\partial v_{q} }}{\partial q} + \phi_{{q,v_{q} }} } \right) + \left( {\lambda + 2\mu } \right)r_{z} \left( {\frac{1}{{k_{q} }}\frac{{\partial v_{r} }}{\partial q} + \phi_{{q,v_{r} }} } \right) + \frac{1}{2}\frac{{\partial \sum\nolimits_{l = 1}^{{L_{1} }} {e_{1l} } }}{\partial q} \hfill \\ + \lambda q_{x} \left( {\frac{1}{{k_{q} }}\frac{{\partial u_{q} }}{\partial q} + \phi_{{q,u_{q} }} } \right) + \lambda r_{x} \left( {\frac{1}{{k_{q} }}\frac{{\partial u_{r} }}{\partial q} + \phi_{{q,u_{r} }} } \right) - \frac{{\partial \sum\nolimits_{l = 1}^{{L_{2} }} {e_{11l} } }}{\partial q} \hfill \\ \end{aligned} \right], $$

(37)

$$ v_{2} = q_{x} \cdot \left[ \begin{aligned} \mu q_{x} \left( {\frac{1}{{k_{q} }}\frac{{\partial v_{q} }}{\partial q} + \phi_{{q,v_{q} }} } \right) + \mu r_{x} \left( {\frac{1}{{k_{q} }}\frac{{\partial v_{r} }}{\partial q} + \phi_{{q,v_{r} }} } \right) + \frac{{\partial \sum\nolimits_{l = 1}^{{L_{2} }} {e_{12l} } }}{\partial q} \hfill \\ + \mu q_{z} \left( {\frac{1}{{k_{q} }}\frac{{\partial u_{q} }}{\partial q} + \phi_{{q,u_{q} }} } \right) + \mu r_{z} \left( {\frac{1}{{k_{q} }}\frac{{\partial u_{r} }}{\partial q} + \phi_{{q,u_{r} }} } \right) \hfill \\ \end{aligned} \right], $$

(38)

$$ v_{3} = r_{z} \cdot \left[ \begin{aligned} \left( {\lambda + 2\mu } \right)q_{z} \left( {\frac{1}{{k_{r} }}\frac{{\partial v_{q} }}{\partial r} + \phi_{{q,v_{q} }} } \right) + \left( {\lambda + 2\mu } \right)r_{z} \left( {\frac{1}{{k_{r} }}\frac{{\partial v_{r} }}{\partial r} + \phi_{{q,v_{r} }} } \right) + \frac{1}{2}\frac{{\partial \sum\nolimits_{l = 1}^{{L_{1} }} {e_{1l} } }}{\partial r} \hfill \\ + \lambda q_{x} \left( {\frac{1}{{k_{r} }}\frac{{\partial u_{q} }}{\partial r} + \phi_{{q,u_{q} }} } \right) + \lambda r_{x} \left( {\frac{1}{{k_{r} }}\frac{{\partial u_{r} }}{\partial r} + \phi_{{q,u_{r} }} } \right) - \frac{{\partial \sum\nolimits_{l = 1}^{{L_{2} }} {e_{11l} } }}{\partial r} \hfill \\ \end{aligned} \right], $$

(39)

$$ v_{4} = r_{x} \cdot \mu \left[ \begin{aligned} c_{44} q_{x} \left( {\frac{1}{{k_{r} }}\frac{{\partial v_{q} }}{\partial r} + \phi_{{q,v_{q} }} } \right) + \mu r_{x} \left( {\frac{1}{{k_{r} }}\frac{{\partial v_{r} }}{\partial r} + \phi_{{q,v_{r} }} } \right) + \frac{{\partial \sum\nolimits_{l = 1}^{{L_{2} }} {e_{12l} } }}{\partial r} \hfill \\ + \mu q_{z} \left( {\frac{1}{{k_{r} }}\frac{{\partial u_{q} }}{\partial r} + \phi_{{q,u_{q} }} } \right) + \mu r_{z} \left( {\frac{1}{{k_{r} }}\frac{{\partial u_{r} }}{\partial r} + \phi_{{q,u_{r} }} } \right) \hfill \\ \end{aligned} \right]. $$

(40)

In $e_{1l}$, $e_{11l}$, $e_{12l}$ and in the viscoelastic equations (33)–(40), the first-order derivatives $u_{q}$, $u_{r}$, $v_{q}$ and $v_{r}$ are given by the following:

$$ u_{q} = \frac{1}{{k_{q} }}\frac{\partial u}{\partial q} + \phi_{q} , $$

(41)

$$ u_{r} = \frac{1}{{k_{r} }}\frac{\partial u}{\partial r} + \phi_{r} , $$

(42)

$$ v_{q} = \frac{1}{{k_{q} }}\frac{\partial v}{\partial q} + \phi_{q} , $$

(43)

$$ v_{r} = \frac{1}{{k_{r} }}\frac{\partial v}{\partial r} + \phi_{r} , $$

(44)

Appendix C: CPML Parameters

In the stretched-coordinate metrics, the parameters of the CPML in the $q$ and $r$ directions are (Komatitsch and Tromp 1999):

$$ d_{0} = - \left( {N + 1} \right) \cdot \sqrt {\frac{\lambda + 2\mu }{\rho }} \cdot \frac{\ln R}{2L}, $$

(45)

$$ d_{q} = d_{0} \left( {\frac{q}{L}} \right)^{N} , $$

(46)

$$ d_{r} = d_{0} \left( {\frac{r}{L}} \right)^{N} , $$

(47)

$$ b_{q} = {\text{e}}^{{ - \left( {\frac{{d_{q} }}{{k_{q} }} + \alpha_{q} } \right) \cdot \Delta t}} , $$

(48)

$$ b_{r} = {\text{e}}^{{ - \left( {\frac{{d_{r} }}{{k_{r} }} + \alpha_{r} } \right) \cdot \Delta t}} , $$

(49)

$$ a_{q} = \frac{{d_{q} }}{{k_{q} \cdot d_{q} + k_{q}^{2} \cdot \alpha_{q} }}\left( {b_{q} - 1} \right), $$

(50)

$$ a_{r} = \frac{{d_{r} }}{{k_{r} \cdot d_{r} + k_{r}^{2} \cdot \alpha_{r} }}\left( {b_{r} - 1} \right), $$

(51)

where $N$ is a constant. $N$ is normally set to 2. $R$ is the theoretical reflection coefficient. Here we use $R = 0.0001$. $L$ is the thickness of the CPML boundary. $d_{q}$ and $d_{r}$ are attenuation factors, and $a_{q}$, $a_{r}$, $b_{q}$, and $b_{r}$ are parameters used for the memory variables.