1 Introduction and Motivation

Einstein’s equation

$$\begin{aligned} Ric[g]-\Lambda g=0 \end{aligned}$$
(1.1)

in the absence of matter with non-negative cosmological constant \(\Lambda \ge 0\) has been extensively studied by both the mathematics and physics communities over the past century. Black hole solutions of (1.1) are of particular interest. We will specifically here consider the Schwarzschild–de Sitter spacetime \((\mathcal {M}_\textit{ext},g_{M,\Lambda })\) with

$$\begin{aligned} g_{M,\Lambda }=-\left( 1-\frac{2M}{r}-\frac{1}{3}\Lambda r^2\right) \textrm{d}t^2+\left( 1-\frac{2M}{r}-\frac{1}{3}\Lambda r^2\right) ^{-1}\textrm{d}r^2+r^2 \textrm{d}\sigma _{\mathbb {S}^2}, \end{aligned}$$
(1.2)

where \(\textrm{d}\sigma _{\mathbb {S}^2}\) is the standard metric of the unit sphere. This represents a black hole in an expanding cosmological universe, see [22, 31, 35]. Making contact with a recent result of Holzegel–Kauffman [20], we shall also consider the \(\Lambda =0\) case, i.e., the Schwarzschild spacetime \((\mathcal {M}_\textit{S},g_M)\) with \(g_M=g_{M,\Lambda =0}\). The aim of this paper will be to revisit the study of the scalar wave equation

$$\begin{aligned} \Box _g \psi =0, \end{aligned}$$
(1.3)

on the background (1.2), studied in [3, 10, 13, 26, 33, 34].

To give some motivation, we recall that over the years a number of methods have been developed to attack problems governed by linear and non-linear equations of hyperbolic type, including (1.1). A fundamental insight is the central role of generalizations of the energy concept as a tool for the global analysis of (1.1). To a large extent, this concept can be understood directly in physical space, i.e., in the ‘time domain’. Physical space energy-based methods have the advantage of displaying incredible resilience when passing from statements concerning linear equations, e.g., the scalar wave equation (1.3), to understanding nonlinear problems, e.g., Einstein’s equation (1.1). A spectacular example of the success of this approach is the proof of the stability of Minkowski spacetime by Christodoulou and Klainerman, see the monograph [7], and the more recent alternative proof [23]. Therefore, it is desirable, when possible, to have a physical space, purely energy based, understanding of boundedness and decay properties of (1.3). This is the goal of the present work.

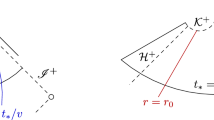
In the present paper we are specifically interested in the exterior region of subextremal Schwarzschild–de Sitter bounded between the event \(\mathcal {H}^+\) and cosmological \(\bar{\mathcal {H}}^+\) horizons, see already the dark shaded region of Fig. 1. For an analysis of linear waves on the cosmological region, see [30], and analysis of linear waves on the black hole interior see [15, 16, 18]. The extremal case has not been studied systematically for \(\Lambda >0\). It is subject to the Aretakis instability [1].

Fig. 1
figure 1

The Schwarzschild–de Sitter spacetime

Full size image

The wave equation (1.3) on the subextremal Schwarzschild–de Sitter exterior with \(\Lambda >0\) has been studied in the past by two different, though related, approaches.

One approach was initiated in [10] by Dafermos–Rodnianski, where the wave equation (1.3) was studied using only energy estimates. Their energy estimates, which can in fact be expressed exclusively in physical space, prove faster than any polynomial decay in the shaded region of Fig. 1, along a suitable foliation. Specifically, by assigning data on a spacelike hyperboloidal hypersurface

$$\begin{aligned} \Sigma , \end{aligned}$$
(1.4)

that connects the event \(\mathcal {H}^+\) and cosmological horizon \(\bar{\mathcal {H}}^+\), they prove faster than any polynomial decay, in \(\tau \), of the energy flux through the hypersurface

$$\begin{aligned} \phi _\tau (\Sigma ), \end{aligned}$$
(1.5)

which is the push forward of \(\Sigma \) by the Killing vector field \(\partial _t\). This decay result, in turn, follows from a Morawetz estimate, which is of the form

(1.6)

where \((r,\bar{t},\theta ,\phi )\) are suitably defined hyperboloidal coordinates. Here, \(\psi _\infty \) is a constant which can also be bounded from initial data. Note that the estimate (1.6) manifestly already excludes finite frequency growing modes and, finally, is non-degenerate at the horizons \(\mathcal {H}^+,\bar{\mathcal {H}}^+\), exploiting thus the red-shift. The estimate, however, degenerates at \(r=3M\) due to the presence of trapped null geodesics, as necessitated by [29, 32].

Another approach was initiated in [3] by Bony–Häfner, where they proved exponential decay for (1.3), restricted, however, away from the horizons \(\mathcal {H}^+, \bar{\mathcal {H}}^+\), based on results concerning the asymptotic distribution of quasinormal modes shown previously by Sá Barreto and Zworski in [28]. Following these proofs, a number of authors worked on the problem, see [26, 33], and finally exponential decay was proved for the slowly rotating Kerr–de Sitter black hole by Dyatlov in [12, 13] without restriction away from the horizons. The papers of Dyatlov appeal to resolvent estimates in the complex plane and further machinery developed in microlocal analysis. Remarkably, building on all these results, Hintz and Vasy [19] proved nonlinear stability for the slowly rotating Kerr–de Sitter spacetime.

For nonlinear applications, arbitrarily fast polynomial decay is in fact more than sufficient, in principle, to obtain stability. Nonetheless, it is curious that the physical space argument of [10] only seemed to give this type of decay and not the full exponential decay. Indeed, this is connected precisely with the degeneration at \(r=3M\) in the Morawetz estimate (1.6), referred to above.

The purpose of our paper is to overcome this difficulty and to show exponential decay for (1.3) on Schwarzschild–de Sitter, by an elementary additional physical space argument. We do so by proving a different type of local energy estimate, which, though still degenerate at \(r=3M\), is relativelynonspsdegenerate, i.e., its bulk term is not degenerate with respect to its boundary term, see already (1.13). One ingredient of our proof is the Morawetz estimate (1.6). However, on top of the Morawetz estimate (1.6), we will require an additional commutation by a vector field which can again be thought to capture some of the properties of trapping, see already (1.9). In the \(\Lambda =0\) case, this will recover a recent construction of Holzegel–Kauffman [20]. Our physical space commutation, in the high frequency limit, connects with the work of previous authors on ‘lossless estimates’ and ‘non-trapping estimates’, e.g., see [2, 4, 5, 14, 17, 21, 26, 27].

In our companion [24], we use the results of the present paper to prove global well posedness and exponential decay for the solutions of quasilinear wave equation and semilinear wave equations on Schwarzschild–de Sitter.

Before stating our main results, we introduce the commutation and the energies which are of fundamental importance to this paper.

1.1 The Commutation Vector Fields and the Energy

We use a system of regular hyperboloidal coordinates \((r,\bar{t},\theta ,\phi )\), see already Sect. 2, in which the metric takes the form

$$\begin{aligned} g_{M,\Lambda }= & {} -\left( 1-\frac{2M}{r}-\frac{\Lambda }{3}r^2\right) (\textrm{d}\bar{t})^2-2\frac{1-\frac{3M}{r}}{\sqrt{1-9M^2\Lambda }}\sqrt{1+\frac{6M}{r}} \textrm{d}\bar{t}\textrm{d}r \nonumber \\{} & {} +\frac{27M^2}{1-9M^2\Lambda }\frac{1}{r^2} (\textrm{d}r)^2+r^2 \textrm{d}\sigma _{\mathbb {S}^2}. \end{aligned}$$
(1.7)

The leaf

$$\begin{aligned} \Sigma =\{\bar{t}=0\} \end{aligned}$$
(1.8)

connects the event horizon \(\mathcal {H}^+\) with the cosmological horizon \(\bar{\mathcal {H}}^+\), as depicted in Fig. 2.

We introduce the commutation vector field

$$\begin{aligned} \begin{aligned} \mathcal {G} = r\sqrt{1-\frac{2M}{r}-\frac{\Lambda }{3}r^2}\frac{\partial }{\partial r}, \end{aligned} \end{aligned}$$
(1.9)

where \(\partial _r\) is the coordinate vector field associated to \((r,\bar{t},\theta ,\phi )\). (The simple form of this vector field is intimately related to the precise choice of coordinate \(\bar{t}\). Note that \(\mathcal {G}\) is orthogonal to the Killing vector field \(\partial _{\bar{t}}\) at \(r=3M\).)

Fig. 2
figure 2

The vector field \(\mathcal {G}\)

Full size image

We define the energy density

$$\begin{aligned} \begin{aligned} \mathcal {E}(\mathcal {G}\psi ,\psi )\,\dot{=}\, \mathbb {T}(\partial _{\bar{t}},n)[\mathcal {G}\psi ]+\mathbb {T}(n,n)[\psi ], \end{aligned} \end{aligned}$$
(1.10)

where \(\mathbb {T}\) is the energy momentum tensor of the wave equation, and n is the normal to the foliation \(\phi _\tau (\Sigma )\), see already Sect. 2.

The energy density (1.10) is a non-negative definite quantity which contains up to second derivatives of \(\psi \). We have the property

(1.11)

In particular, we note that \(\mathcal {E}(\mathcal {G}\psi ,\psi )\) controls the \(H^1\) energy density. Note, however, that \(\mathcal {E}(\mathcal {G}\psi ,\psi )\) does not control the full \(H^2\) energy density.

1.2 The Main Result

Let

$$\begin{aligned} \phi _\tau (\Sigma )=\{\bar{t}=\tau \}, \end{aligned}$$
(1.12)

for \(\tau \ge 0\). We shall refer below to the energy density (1.10) and the commutation vector field (1.9). Our main theorem is an energy estimate without relative degeneration.

Theorem 1

(Rough version). Solutions of the wave equation (1.3) on the exterior of the subextremal Schwarzschild–de Sitter \((\Lambda >0)\) black hole background \(\left( \mathcal {M}_\textit{ext},g_{M,\Lambda }\right) \), dark shaded region of Fig. 1, satisfy

$$\begin{aligned} \int _{\phi _{\tau _2}(\Sigma )}\mathcal {E}\left( \mathcal {G}\psi ,\psi \right) +\int _{\tau _1}^{\tau _2} \textrm{d}\tau \int _{\phi _{\tau }(\Sigma )}\mathcal {E}(\mathcal {G}\psi ,\psi )\lesssim \int _{\phi _{\tau _1}(\Sigma )} \mathcal {E}\left( \mathcal {G}\psi ,\psi \right) , \end{aligned}$$
(1.13)

for \(0\le \tau _1<\tau _2\).

Remark 1.1

Theorem 1 remains true with \(\Sigma \) replaced by a general spacelike hypersurface connecting the event with the cosmological horizons.

Remark 1.2

The estimate (1.13) differs from the Morawetz estimate (1.6) in that, in the former, the same energy density appears in both the bulk term on the left-hand side and the initial hypersurface flux term on the right-hand side, while in the latter, certain derivatives in the bulk term have \(\left( 1-\frac{3M}{r}\right) \) weights relative to their flux terms. In this sense, estimate (1.13) is relatively non-degenerate. Note that this is still compatible with the obstructions of [29, 32] due to trapping at \(r=3M\). It is this relative non-degeneracy that will allow us to immediately obtain exponential decay.

As a corollary of Theorem 1, we have exponential decay:

Corollary 1

(Rough version). With the assumptions of Theorem 1, we have the exponential decay estimates

$$\begin{aligned} \int _{\phi _{\tau }(\Sigma )} \mathcal {E}(\mathcal {G}\psi ,\psi ) \lesssim e^{-c\tau }\int _{\Sigma }\mathcal {E}\left( \mathcal {G}\psi ,\psi \right) \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&\sup _{\phi _{\tau }(\Sigma )}|\psi -\psi _\infty |\lesssim \sqrt{E}e^{-c \tau }, \end{aligned} \end{aligned}$$

for \(0\le \tau \). Here E is an appropriate higher-order energy of the initial data of \(\psi \), and \(\psi _\infty \) is a constant that can be controlled by initial data.

We can apply the arguments of Theorem 1 to obtain a second corollary, concerning small first-order perturbations of the wave operator.

Corollary 2

(Rough version). Let \(\psi \) be a solution of

$$\begin{aligned} \Box _{g_{M,\Lambda }}\psi =\epsilon a^j\partial _j\psi , \end{aligned}$$
(1.14)

where the vector field \(a=a^j\partial _j\) is suitably bounded to first order, and \(\epsilon \) sufficiently small. Then, the following estimate holds

$$\begin{aligned} \int _{\phi _{\tau }(\Sigma )} \mathcal {E}(\mathcal {G}\psi ,\psi ) \lesssim e^{-c\tau }\int _{\Sigma }\mathcal {E}\left( \mathcal {G}\psi ,\psi \right) . \end{aligned}$$

Also, if \(a=a^j\partial _j\) is suitably bounded up to second order, we obtain

$$\begin{aligned} \begin{aligned}&\sup _{\phi _{\tau }(\Sigma )}|\psi -\psi _\infty |\lesssim \sqrt{E} e^{-c \tau }, \end{aligned} \end{aligned}$$

for \(0\le \tau \), where E is an appropriate integral quantity defined on \(\Sigma \), and \(\psi _\infty \) is a constant that can be controlled by initial data.

In our forthcoming [25], we prove a Morawetz estimate on Kerr–de Sitter spacetimes with parameters \((a,M,\Lambda )\) for the wave equation (1.3), and more generally for the Klein–Gordon equation, and use it in conjunction with a generalization of the methods introduced here, to again prove an analogue of Theorem 1 and exponential decay. We specifically establish exponential decay for slow rotation (\(|a|\ll M,\Lambda \)), or alternatively, in the full subextremal case of parameters but where the solution is assumed axisymmetric.

1.3 The \(\Lambda =0\) Schwarzschild Limit

In the Schwarzschild limit \(\Lambda =0\) the commutation vector field \(\mathcal {G}\) (2.18) reduces to the vector field introduced in [20], see already Sect. 7. Note, however, that in [20] the commutation vector field \(\mathcal {G}\) was expressed in coordinates that were there denoted as \((t,R^\star ,\theta ,\phi )\). Those coordinates, although regular at \(\mathcal {H}^+\), do not coincide with our regular hyperboloidal coordinates. Thus, in those coordinates, \(\mathcal {G}\) did not have the simple form 1.9 for \(\Lambda =0\).

2 Preliminaries

2.1 The Subextremality Conditions

We will use the following notation extensively.

Definition 2.1

Let \(M>0\) and \(\Lambda \ge 0\). Then, we define the function \(\mu \) by

$$\begin{aligned} 1-\mu _{M,\Lambda }=1-\frac{2M}{r}-\frac{1}{3}\Lambda r^2. \end{aligned}$$
(2.1)

We will often simply denote it as \(\mu \).

We define the following.

Definition 2.2

Let \(\Lambda \ge 0\). Then, the set of sub-extremal black hole parameters is

$$\begin{aligned} \begin{aligned} \mathcal {B}_\Lambda&=\{M>0:\,1-\mu =0\textit{ admits only distinct real roots}\}\\&=\left\{ M:0< M<\frac{1}{3\sqrt{\Lambda }}\right\} . \end{aligned} \end{aligned}$$

For \(M\in \mathcal {B}_\Lambda \), we denote the two positive real roots of \(1-\mu \) as

$$\begin{aligned} r_+(M,\Lambda )<\bar{r}_+(M,\Lambda ), \end{aligned}$$
(2.2)

which will correspond to the area radius of the event and cosmological horizons, respectively, see Definition 2.4. We shall often denote these simply as \(r_+,\bar{r}_+\).

2.2 The Spacetimes in Regular Hyperboloidal Coordinates

We now define the metric of Schwarzschild–de Sitter.

Definition 2.3

Let \(\Lambda > 0\) and \(M\in \mathcal {B}_\Lambda \). We define the following manifold with boundary

$$\begin{aligned} \begin{aligned} \mathcal {M}_\textit{ext}=[r_+,\bar{r}_+]_r\times \mathbb {R}_{\bar{t}}\times \mathbb {S}^2_{(\theta ,\phi )},\,\, \mathcal {M}_{\textit{ext},\delta }=[r_+-\delta ,\bar{r}_+ +\delta ]_r\times \mathbb {R}_{\bar{t}}\times \mathbb {S}^2_{(\theta ,\phi )} \end{aligned} \end{aligned}$$
(2.3)

for a \(\delta >0\) sufficiently small, and the metric

$$\begin{aligned} g_{M,\Lambda } =-(1-\mu )(\textrm{d} \bar{t})^2-2 \xi (r) \textrm{d} \bar{t} \textrm{d}r +\frac{1-\xi ^2(r)}{1-\mu }(\textrm{d}r)^2+r^2 \textrm{d}\sigma _{\mathbb {S}^2} \end{aligned}$$
(2.4)

where \(\textrm{d}\sigma _{\mathbb {S}^2}\) is the standard metric of the unit sphere and

$$\begin{aligned} \xi (r)= \frac{1-\frac{3M}{r}}{\sqrt{1-9M^2\Lambda }}\sqrt{1+\frac{6M}{r}},\quad \frac{1-\xi ^2(r)}{1-\mu }=\frac{27M^2}{1-9M^2\Lambda }\frac{1}{r^2}. \end{aligned}$$
(2.5)

We refer to the tuple \((r,\bar{t},\theta ,\phi )\) as regular hyperboloidal coordinates. Note the inverse metric components

$$\begin{aligned} \begin{aligned} g^{rr}=(1-\mu ),\quad g^{\bar{t}\bar{t}}=-\frac{1-\xi ^2(r)}{1-\mu },\quad g^{\bar{t}r}=-\xi (r). \end{aligned} \end{aligned}$$
(2.6)

See also “Appendix A” for the Christoffel symbols of the metric (2.4).

2.3 The Time Orientation

We take the vector field

$$\begin{aligned} \frac{\partial }{\partial \bar{t}}. \end{aligned}$$
(2.7)

to be future oriented. This defines a time orientation for \(\mathcal {M}_\textit{ext}\).

2.4 The Event \(\mathcal {H}^+\) and Cosmological \(\bar{\mathcal {H}}^+\) Horizons

Now we can define the following boundaries.

Definition 2.4

We define the following boundaries to the manifolds \(\mathcal {M}_{\textit{ext}},\mathcal {M}_{\textit{ext},\delta }\)

$$\begin{aligned} \begin{aligned}&\mathcal {H}^+=\{(r, \bar{t},\theta ,\phi ): \bar{t}>-\infty ,r=r_+ \},\, \bar{\mathcal {H}}^+=\{(r, \bar{t},\theta ,\phi ): \bar{t}>-\infty ,r=\bar{r}_+\},\\&\mathcal {H}^+_\delta =\{(r, \bar{t},\theta ,\phi ): \bar{t}>-\infty ,r=r_+-\delta \},\, \bar{\mathcal {H}}^+_\delta =\{(r, \bar{t},\theta ,\phi ): \bar{t}>-\infty ,r=\bar{r}_++\delta \} \end{aligned} \end{aligned}$$
(2.8)

which we call future event horizon and future cosmological horizon, respectively.

2.5 The Photon Sphere

The hypersurface \(\{r=3M\}\) is called the ‘photon sphere’. All future directed null geodesics either cross \(\mathcal {H}^+\), cross \(\bar{\mathcal {H}}^+\), or asymptote to \(r=3M\). We will refer to the ones asymptoting to \(r=3M\) as ‘future trapped null geodesics’.

2.6 The Schwarzschild–de Sitter Coordinates

We define the following coordinates.

Definition 2.5

From regular hyperboloidal coordinates, Definition 2.3, we define the Schwarzschild–de Sitter coordinates, \((r,t,\theta ,\phi )\in (r_+,\bar{r}_+)\times \mathbb {R}\times \mathbb {S}^2\), by the following transformation

$$\begin{aligned} t= \bar{t}+H(r),\quad H(r)=\int _{3M}^r\frac{\xi (\tilde{r})}{1-\mu }\textrm{d}\tilde{r}, \end{aligned}$$
(2.9)

where \(\xi (r)\) is given by (2.5). These coordinates cover the region \(\mathcal {M}_{\textit{ext}}^o\).

We rewrite the metric (2.4) by using the transformation (2.9) to obtain

$$\begin{aligned} g_{M,\Lambda }=-\left( 1-\mu \right) \textrm{d}t^2+\left( 1-\mu \right) ^{-1}\textrm{d}r^2+r^2\textrm{d}\sigma _{\mathbb {S}^2}. \end{aligned}$$
(2.10)

We distinguish between the coordinate vector field

$$\begin{aligned} \varvec{\frac{\partial }{\partial r}} \end{aligned}$$
(2.11)

with respect to the Schwarzschild–de Sitter coordinate system \((r,t,\theta ,\phi )\), and the coordinate vector field

$$\begin{aligned} \frac{\partial }{\partial r} \end{aligned}$$
(2.12)

with respect to the regular hyperboloidal coordinates \((r,\bar{t},\theta ,\phi )\).

The following equality holds

$$\begin{aligned} \frac{\partial }{\partial \bar{t}}=\frac{\partial }{\partial t}, \end{aligned}$$
(2.13)

in the region \(\mathcal {M}^o_\textit{ext}\) that the Schwarzschild–de Sitter coordinates are defined.

2.7 Tortoise Coordinate

We define the tortoise coordinate

$$\begin{aligned} r^\star \,\dot{=}\,\int _{3M}^r\frac{1}{1-\mu } \textrm{d}r. \end{aligned}$$
(2.14)

The expression

$$\begin{aligned} \frac{\partial }{\partial r^\star } \end{aligned}$$
(2.15)

will denote the vector field taken in \((r^\star ,t,\theta ,\phi )\) coordinates. Note that \(\frac{\partial }{\partial r^\star }=(1-\mu )\varvec{\frac{\partial }{\partial r}}\). The vector field (2.15) extends smoothly to a tangential vector field along \(\mathcal {H}^+\) and \(\bar{\mathcal {H}}^+\).

2.8 Chain Rule Between Coordinate Vector Fields

By a simple chain rule, we have

$$\begin{aligned} \varvec{\frac{\partial }{\partial r}}=\frac{\partial }{\partial r}+\frac{\textrm{d}\bar{t}}{\textrm{d} r}\frac{\partial }{\partial \bar{t}}. \end{aligned}$$
(2.16)

We have

$$\begin{aligned} \frac{\textrm{d}\bar{t}}{\textrm{d}r}=-\frac{\textrm{d}H}{\textrm{d}r}(r), \end{aligned}$$

where, for H(r), see Sect. 2.6. Note that at \(r=3M\) the vector field \(\partial _r\) is in the direction of \(\partial _{r^\star }\), since

$$\begin{aligned} \frac{\partial }{\partial r}=\sqrt{\frac{27M^2}{1-9M^2\Lambda }}\frac{\partial }{\partial r^\star }. \end{aligned}$$
(2.17)

2.9 The Vector Field \(\mathcal {G}\) in Schwarzschild–de Sitter Coordinates

We define the vector field

$$\begin{aligned} \mathcal {G}=r\sqrt{1-\mu }\frac{\partial }{\partial r}. \end{aligned}$$
(2.18)

Note that \(\mathcal {G}\) is \(C^0\) on the horizons \(\mathcal {H}^+,\bar{\mathcal {H}}^+\), but not \(C^1\). We extend the vector field \(\mathcal {G}\), of (2.18), beyond the horizons \(\mathcal {H}^+,\bar{\mathcal {H}}^+\) such that

$$\begin{aligned} \mathcal {G}\equiv 0,\quad \text {in } \{r\le r_+\}\cup \{r\ge \bar{r}_+\}. \end{aligned}$$
(2.19)

This vector field is suggested by the good commutation property of Proposition 4.1. Note that in view of (2.17), at \(r=3M\) the vector field \(\mathcal {G}\) is in the direction of \(\partial _{r^\star }\) and is thus orthogonal to \(\partial _{\bar{t}}\). This is significant because this is precisely the derivative that does not degenerate in estimate (1.6).

We express the vector field (2.18) in Schwarzschild–de Sitter coordinates.

Lemma 2.1

In \(\mathcal {M}^o_{\textit{ext}}\) the vector field (2.18) can be written as

$$\begin{aligned} \mathcal {G}=G_1(r)\frac{\partial }{\partial r^\star }+G_2(r)\frac{\partial }{\partial t}, \end{aligned}$$
(2.20)

in Schwarzschild–de Sitter coordinates. The functions \(G_1,G_2\) are defined as follows

$$\begin{aligned} G_1(r)=\sqrt{\frac{r^2}{1-\mu }},\,\,G_2(r)=\frac{r}{\sqrt{1-\mu }}\left( 1-\frac{3M}{r}\right) \frac{1}{\sqrt{1-9M^2\Lambda }}\sqrt{1+\frac{6M}{r}}. \end{aligned}$$

Proof

We note

$$\begin{aligned} \left( G_1\frac{\partial }{\partial r^\star }+G_2\frac{\partial }{\partial t}\right)= & {} r\sqrt{1-\mu }\frac{\partial }{\partial r} \nonumber \\{} & {} +\frac{r}{\sqrt{1-\mu }}\left( -(1-\mu )\frac{d H}{d r}+\frac{(1-\frac{3M}{r})}{\sqrt{1-9M^2\Lambda }}\sqrt{1+\frac{6M}{r}}\right) \frac{\partial }{\partial t} \nonumber \\{} & {} = r\sqrt{1-\mu }\frac{\partial }{\partial r}, \end{aligned}$$
(2.21)

since \((1-\mu )\frac{d H}{d r}=\frac{1-\frac{3\,M}{r}}{\sqrt{1-9\,M^2\Lambda }}\sqrt{1+\frac{6\,M}{r}}\). \(\square \)

2.10 Wave Operator

We denote by the covariant derivative with respect to \(r^2 \textrm{d}\sigma _{\mathbb {S}^2}\).

The wave operator is

(2.22)

where . Note, moreover, that we define the following expression

(2.23)

Furthermore, we denote as \(\Omega _\alpha \), for \(\alpha =1,2,3\) the standard vector fields

$$\begin{aligned} \Omega _1=\partial _\phi ,\quad \Omega _2=\cos {\phi }\,\partial _\theta -\sin {\phi }\cot {\theta }\,\partial _\phi ,\quad \Omega _3=-\left( \sin {\phi }\,\partial _{\theta }+\cos {\phi }\cot {\theta }\,\partial _\phi \right) , \end{aligned}$$
(2.24)

that generate the lie algebra so(3). Note \([\Box _{g_{M,\Lambda }},\Omega _\alpha ]=0, [\Box _{g_{M,\Lambda }},\partial _{\bar{t}}]=0\).

2.11 Spacelike Hypersurfaces

In Schwarzschild–de Sitter a prototype hypersurface that is spacelike and connects the event horizon \(\mathcal {H}^+\) with the cosmological horizon \(\bar{\mathcal {H}}^+\) would be

$$\begin{aligned} \Sigma =\{\bar{t}=0\}. \end{aligned}$$
(2.25)

Our results also hold for general spacelike hypersurfaces connecting \(\mathcal {H}^+\) and \(\bar{\mathcal {H}}^+\). (For convenience, however, we always work with \(\Sigma \) fixed as above.)

2.12 Spacelike Foliations and Causal Domains

We push forward the hypersurface \(\Sigma \), see Sect. 2.11, under the flow \(\phi _\tau \) of the vector field \(\partial _{\bar{t}}\) to obtain the family of hypersurfaces

$$\begin{aligned} \phi _\tau (\Sigma )=\{\bar{t}=\tau \}. \end{aligned}$$
(2.26)

We define the following spacetime domains.

Definition 2.6

For \(\tau _1<\tau _2\) define the spacetime domain

$$\begin{aligned} D(\tau _1,\tau _2)\,\dot{=}\,J^+(\phi _{\tau _1}(\Sigma ))\cap J^-(\phi _{\tau _2}(\Sigma ))=\{(r,\bar{t},\theta ,\phi ):\tau _1\le \bar{t}\le \tau _2\}, \end{aligned}$$
(2.27)

and

$$\begin{aligned} D(\tau ,\infty )\,\dot{=}\,J^+(\phi _\tau (\Sigma ))=\{(r,\bar{t},\theta ,\phi ):\tau \le \bar{t}<\infty \}. \end{aligned}$$
(2.28)

The domains of Definition 2.6 are both globally hyperbolic, with \(\phi _{\tau _1}(\Sigma )\) and \(\phi _{\tau }(\Sigma )\), respectively, as Cauchy hypersurfaces.

2.13 Normals of Spacelike Hypersurfaces

The unit normal vector fields of the foliation of Sect. 2.11 can be computed from the gradient \(\nabla \bar{t}\) which in regular hyperboloidal coordinates is

$$\begin{aligned} \nabla \bar{t}\!=\!-\frac{1-\xi ^2(r)}{1-\mu }\frac{\partial }{\partial \bar{t}}\!-\!\xi (r)\frac{\partial }{\partial r}\!=\!- \frac{27M^2}{1-9M^2\Lambda }\frac{1}{r^2}\frac{\partial }{\partial \bar{t}}\!-\!\frac{1-\frac{3M}{r}}{\sqrt{1-9M^2\Lambda }}\sqrt{1+\frac{6M}{r}}\frac{\partial }{\partial r}. \nonumber \\ \end{aligned}$$
(2.29)

Note moreover that \(g(\nabla \bar{t},\nabla \bar{t})\le b(M,\Lambda )<0\) on \([r_+,\bar{r}_+]\). The normal of the relevant foliation will be

$$\begin{aligned} n_{\phi _{\tau }(\Sigma )}=-\frac{\nabla \bar{t}}{\sqrt{-g(\nabla \bar{t},\nabla \bar{t})}}=\sqrt{\frac{1-\xi ^2}{1-\mu }}\frac{\partial }{\partial \bar{t}}+\frac{\xi (r)}{\sqrt{\frac{1-\xi ^2}{1-\mu }}}\frac{\partial }{\partial r}, \end{aligned}$$
(2.30)

often denoted simply as n.

2.14 Volume Forms

The volume form of a spacetime domain is

$$\begin{aligned} \textrm{d}g=r^2\sin \theta \textrm{d}\bar{t} \textrm{d}r \textrm{d}\theta \textrm{d}\phi \end{aligned}$$
(2.31)

with respect to the \(\left( r,\bar{t},\theta ,\phi \right) \) coordinates.

By pulling back the spacetime volume form (2.31) into hypersurfaces of constant \(\bar{t}\), we obtain that the \(\{\bar{t}=\tau \}\) hypersurfaces admit the volume form

$$\begin{aligned} \textrm{d}g_{\{\bar{t}=c\}}=r\sqrt{\frac{27M^2}{1-9M^2\Lambda }}\sin \theta \textrm{d}r \textrm{d}\theta \textrm{d}\phi . \end{aligned}$$
(2.32)

We define the normals of the event and cosmological horizons respectively as

$$\begin{aligned} n_{\mathcal {H}^+}=\partial _{\bar{t}},\,n_{\bar{\mathcal {H}}^+}=\partial _{\bar{t}}. \end{aligned}$$
(2.33)

With the above choice of normals, the corresponding volume forms of the respective null hypersurfaces take the form

$$\begin{aligned} \textrm{d}g_{\mathcal {H}^+}=r^2\sin \theta \textrm{d}\bar{t}\textrm{d}\sigma _{\mathbb {S}^2},\,\, \textrm{d}g_{\bar{\mathcal {H}}^+}=r^2\sin \theta \textrm{d}\bar{t}\textrm{d}\sigma _{\mathbb {S}^2}. \end{aligned}$$

In all integrals without explicit volume form, it is to be understood that the volume forms are taken to be the ones defined in this section.

2.15 Coarea Formula

Let f be a continuous non-negative function. Then, note the coarea formula

$$\begin{aligned} \int _{0}^\tau \textrm{d}\tau \int _{\phi _\tau (\Sigma )} f \textrm{d}g_{\{\bar{t}=\tau \}}\sim \int \int _{D(0,\tau )}\frac{1}{r} f \textrm{d}g, \end{aligned}$$
(2.34)

where the constants in the above similarity depend only on the black hole mass M and do not degenerate in the limit \(\Lambda \rightarrow 0\). For fixed \(\Lambda >0\) the r factor of (2.34) is of course inessential.

2.16 Penrose Diagrams

The reader familiar with the Penrose diagrammatic representation may wish to refer to Fig. 3.

Fig. 3
figure 3

The foliation of the Schwarzschild–de Sitter exterior

Full size image

2.17 Currents and the Divergence Theorem

We will employ the energy momentum tensor and the relevant current it produces.

Definition 2.7

Let g be a smooth Lorentzian metric. For \(\psi \) a solution of

$$\begin{aligned} \Box _g\psi =F, \end{aligned}$$
(2.35)

we define the energy momentum tensor

$$\begin{aligned} \mathbb {T}_{\mu \nu }[\psi ]\,\dot{=}\,\partial _{\mu }\psi \partial _{\nu }\psi -\frac{1}{2}g_{\mu \nu }\Big (g^{\gamma \epsilon }\partial _{\gamma }\psi \partial _{\epsilon }\psi \Big ). \end{aligned}$$
(2.36)

The energy current with respect to a vector field X is

$$\begin{aligned} J^{X}_{\mu }[\psi ]\,\dot{=}\, \mathbb {T}_{\mu \nu }[\psi ]X^{\nu }, \end{aligned}$$
(2.37)

with divergence

$$\begin{aligned} \nabla ^{\mu }J^{X}_{\mu } =X(\psi ) F+\frac{1}{2}\mathbb {T}_{\mu \nu }\,^{(X)}\pi ^{\mu \nu }, \end{aligned}$$
(2.38)

where

$$\begin{aligned} ^{(X)}\pi ^{\mu \nu }\dot{=}\,\frac{1}{2}\big ( \nabla ^{\mu }X^{\nu }+\nabla ^{\nu }X^{\mu } \big ) \end{aligned}$$
(2.39)

is the deformation tensor.

Lastly, for X, n future causal vector fields, we have that

$$\begin{aligned} J^X_\mu [\psi ]n^\mu =\mathbb {T}(X,n)[\psi ]\ge 0 \end{aligned}$$
(2.40)

We apply the divergence theorem in the region \(D(\tau _1,\tau _2)\) to obtain the following Proposition.

Proposition 2.1

Let \(\psi \) satisfy the Eq. (2.35) on \(D(\tau _1,\tau _2)\). Then, with the notation above, the following holds

$$\begin{aligned} \begin{aligned}&\int _{\phi _{\tau _2}(\Sigma )}J^{X}_{\mu }[\psi ]n^{\mu }_{\phi _{\tau _2}(\Sigma )}+\int _{\mathcal {H}^{+}\cap D(\tau _1,\tau _2)}J^{X}_{\mu }[\psi ]n^{\mu }_{\mathcal {H}^{+}}+\int _{\bar{\mathcal {H}}^{+}\cap D(\tau _1,\tau _2)}J^{X}_{\mu }[\psi ]n^{\mu }_{\bar{\mathcal {H}}^{+}}\\&\quad +\int \int _{D(\tau _1,\tau _2)}\nabla ^{\mu }J^{X}_{\mu }[\psi ] =\int _{\phi _{\tau _1}(\Sigma )} J^{X}_{\mu }[\psi ]n^{\mu }. \end{aligned} \end{aligned}$$
(2.41)

In the above, in accordance with our conventions from Sect. 2.14, all integrals are taken with respect to the volume form of the respective hypersurfaces or spacetime domain.

For a further study on currents related to partial differential equations, see the monograph of Christodoulou [6].

3 The Main Theorems

3.1 The Homogeneous Wave Equation

The following is the central theorem of this paper.

Theorem 1

(Detailed version). We fix the parameters \(M,\Lambda >0\). Then, there exists a constant \(C=C(M,\Lambda )>0\), such that for \(\psi \) a sufficiently regular solution of the wave equation (1.3) on \(D(\tau _1,\tau _2)\), we have

$$\begin{aligned} \int _{\phi _{\tau _2}(\Sigma )}\mathcal {E}\left( \mathcal {G}\psi ,\psi \right){} & {} +\int \int _{D(\tau _1,\tau _2)}\left( \frac{1}{(1-\mu )}(\partial _t\mathcal {G}\psi )^2+\mathcal {E}(\mathcal {G}\psi ,\psi )\right) \nonumber \\{} & {} \quad \le C \int _{\phi _{\tau _1}(\Sigma )} \mathcal {E}\left( \mathcal {G}\psi ,\psi \right) , \end{aligned}$$
(3.1)

for all \(0\le \tau _1<\tau _2\), where \(\mathcal {E}\left( \mathcal {G}\psi ,\psi \right) \) is defined in (1.10).

Since \(\int \int _{D(\tau _1,\tau _2)} \mathcal {E}(\mathcal {G}\psi ,\psi )\sim \int _{\tau _1}^{\tau _2}\textrm{d}\tau \int _{\phi _\tau (\Sigma )}\mathcal {E}(\mathcal {G}\psi ,\psi )\) we in particular have

$$\begin{aligned} \int _{\phi _{\tau _2}(\Sigma )}\mathcal {E}\left( \mathcal {G}\psi ,\psi \right) +\int _{\tau _1}^{\tau _2}\textrm{d}\tau \int _{\phi _\tau (\Sigma )}\mathcal {E}(\mathcal {G}\psi ,\psi )\le C \int _{\phi _{\tau _1}(\Sigma )} \mathcal {E}\left( \mathcal {G}\psi ,\psi \right) . \end{aligned}$$
(3.2)

Note that this Theorem also holds for the domain \(D_\delta (\tau _1,\tau _2)\) in the place of \(D(\tau _1,\tau _2)\), for a sufficiently small \(\delta >0\), where the constant C is independent of \(\delta \).

As an immediate corollary we have exponential decay.

Corollary 1

(Detailed version). There exist positive constants \(c(M,\Lambda )>0, C(M,\Lambda )>0\), such that for \(\psi \) a sufficiently regular solution of the wave equation (1.3) on \(D(0,\tau )\), we have

$$\begin{aligned} \begin{aligned} \int _{\phi _{\tau }(\Sigma )}\mathcal {E}(\mathcal {G}\psi ,\psi ) \le C e^{-c\tau } \int _{\Sigma } \mathcal {E}\left( \mathcal {G}\psi ,\psi \right) , \end{aligned} \end{aligned}$$

and also the pointwise decay

$$\begin{aligned} \begin{aligned}&\sup _{\phi _{\tau }(\Sigma )}|\psi -\psi _\infty |\le C\sqrt{E}e^{-c \tau }, \end{aligned} \end{aligned}$$

where \(\psi _\infty \) is a constant satisfying \(|\psi _\infty |\le C\left( \sup _{\Sigma }|\psi |+ \sqrt{\int _{\Sigma }\mathbb {T}(n,n)[\psi ]}\right) \), and

$$\begin{aligned} E=\sum _{0\le i\le 1}\sum _{1\le \alpha \le 3}\int _\Sigma \mathcal {E}(\mathcal {G}\Omega _\alpha ^i\psi ,\Omega _\alpha ^i\psi ), \end{aligned}$$
(3.3)

where \(\Omega _\alpha \) are defined in (2.24).

3.2 The Inhomogeneous Wave Equation and Absorption of Small Error Terms

The following theorem concerns the inhomogeneous wave equation on the Schwarzschild–de Sitter background.

Theorem 2

(Detailed version). Let F be a sufficiently regular function on \(D(\tau _1,\tau _2)\). We have that, for sufficiently regular solutions of

$$\begin{aligned} \Box _{g_{M,\Lambda }}\psi =F \end{aligned}$$
(3.4)

on \(D(\tau _1,\tau _2)\), the following holds

$$\begin{aligned} \begin{aligned}&\int _{\phi _{\tau _2}(\Sigma )}\mathcal {E}(\mathcal {G}\psi ,\psi )+\int \int _{D(\tau _1,\tau _2)}\left( \frac{1}{(1-\mu )}(\partial _t\mathcal {G}\psi )^2+\mathcal {E}(\mathcal {G}\psi ,\psi )\right) \\&\quad \le C\int _{\phi _{\tau _1}(\Sigma )}\mathcal {E}(\mathcal {G}\psi ,\psi )+C\int \int _{D(\tau _1,\tau _2)}(1-\mu )\left| \mathcal {G}F\right| ^2+|F|^2, \end{aligned} \end{aligned}$$
(3.5)

for all \(0\le \tau _1<\tau _2\), and for some constant \(C(M,\Lambda )\).

Note that this theorem also holds for the domain \(D_\delta (\tau _1,\tau _2)\) in the place of \(D(\tau _1,\tau _2)\) for a sufficiently small \(\delta >0\), where the constant C is independent of \(\delta \).

We have the following Corollary.

Corollary 2

(Detailed version). Let \(a=a^j\partial _j\) be a vector field, where

$$\begin{aligned} a^{\bar{t}}, a^r, g^{\theta \theta }(a^\theta )^2+g^{\phi \phi }(a^\phi )^2, [\mathcal {G},a]^{\bar{t}}, [\mathcal {G},a]^r, g^{\theta \theta }([\mathcal {G},a]^{\theta })^2+g^{\phi \phi }([\mathcal {G},a]^\phi )^2 \end{aligned}$$
(3.6)

are smooth and bounded functions on \(D(0,\infty )\). For \(\epsilon >0\) sufficiently small, there exists a constant \(C(M,\Lambda )>0\) such that sufficiently regular solutions of the equation

$$\begin{aligned} \Box _{g_{M,\Lambda }}\psi =\epsilon a^j\partial _j\psi \end{aligned}$$
(3.7)

satisfy the following estimate

$$\begin{aligned}{} & {} \int _{\phi _{\tau _2}(\Sigma )}\mathcal {E}\left( \mathcal {G}\psi ,\psi \right) +\int \int _{D(\tau _1,\tau _2)}\left( \frac{1}{(1-\mu )}(\partial _t\mathcal {G}\psi )^2+\mathcal {E}(\mathcal {G}\psi ,\psi )\right) \nonumber \\{} & {} \qquad \qquad \le C\int _{\phi _{\tau _1}(\Sigma )}\mathcal {E}\left( \mathcal {G}\psi ,\psi \right) . \end{aligned}$$
(3.8)

Also, there exist constants \(C(M,\Lambda )>0\), \(c(M,\Lambda )>0\) depending only on the black hole parameters such that

$$\begin{aligned} \int _{\phi _{\tau }(\Sigma )}\mathcal {E}(\mathcal {G}\psi ,\psi )\le C e^{-c \tau } \int _{\Sigma } \mathcal {E}(\mathcal {G}\psi ,\psi ). \end{aligned}$$
(3.9)

Moreover, let \([\Omega _\alpha \mathcal {G},a]^{\bar{t}}, [\Omega _\alpha \mathcal {G},a]^r, g^{\theta \theta }([\Omega _\alpha \mathcal {G},a]^\theta )^2+g^{\phi \phi }([\Omega _\alpha \mathcal {G},a]^\phi )^2 \) be bounded for all \(\alpha \), where \(\Omega _\alpha \) are defined in Eq. (2.24). Then, we obtain

$$\begin{aligned} \sup _{\phi _{\tau }(\Sigma )}|\psi -\psi _\infty |\le C\sqrt{E}e^{-c\tau }, \end{aligned}$$
(3.10)

where \(\psi _\infty \) is a constant satisfying \(|\psi _\infty |\le C\left( \sup _{\Sigma }|\psi |+ \sqrt{\int _{\Sigma }\mathbb {T}(n,n)[\psi ]+\mathbb {T}(n,n)[\mathcal {G}\psi ]}\right) \), and

$$\begin{aligned} E=\sum _{0\le i\le 1}\sum _{1\le \alpha \le 3} \int _{\Sigma } \mathcal {E}(\mathcal {G}\Omega _\alpha ^i \psi ,\Omega _\alpha ^i\psi ). \end{aligned}$$
(3.11)

3.3 The Higher-Order Statement

The following theorem is the higher-order statement of Theorem 2. We will use the following result in our companion paper [24] to prove stability of solutions of the quasilinear wave equation.

Theorem 3

Let F be a sufficiently regular function on \(D(\tau _1,\tau _2)\). We have that, for a sufficiently regular solution of

$$\begin{aligned} \Box _{g_{M,\Lambda }}\psi =F \end{aligned}$$
(3.12)

on \(D(\tau _1,\tau _2)\), and for any \(j\ge 3\), there exists a constant \(C=C(j,M,\Lambda )\) such that the following higher-order estimate holds

$$\begin{aligned} \begin{aligned}&E_{\mathcal {G},j}[\psi ](\tau _2) +\int \int _{D(\tau _1,\tau _2)} \frac{1}{1-\mu }\sum _{0\le i_1+i_2\le j-2}\sum _\alpha \left( \partial _{\bar{t}}^{1+i_1}\Omega _\alpha ^{i_2}\mathcal {G}\psi \right) ^2\\&\quad +\int _{\tau _1}^{\tau _2}\textrm{d}\tau E_{\mathcal {G},j}[\psi ](\tau )\\&\quad \le C E_{\mathcal {G},j}[\psi ](\tau _1)+C\int \int _{D(\tau _1,\tau _2)} (1-\mu )\sum _{0\le i_1+i_2\le j-2}\sum _\alpha \left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\mathcal {G}F\right) ^2\\&\quad \quad +\sum _{0\le i_1+i_2+i_3\le j-2}\sum _\alpha \left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\partial _r^{i_3}F\right) ^2\\&\quad \quad +C \int _{\{\bar{t}=\tau _2\}} \sum _{0\le i_1+i_2+i_3\le j-3}\sum _\alpha (1-\mu )^{2i_3+1}\left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\partial _r^{i_3}\mathcal {G}F\right) ^2\\&\quad \quad +\sum _{0\le i_1+i_2+i_3\le j-3}\sum _\alpha \left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\partial _r^{i_3}F\right) ^2 \end{aligned} \end{aligned}$$
(3.13)

for all \(0\le \tau _1\le \tau _2\), where

$$\begin{aligned} \begin{aligned} E_{\mathcal {G},j}[\psi ](\tau )&=\sum _\alpha \int _{\{\bar{t}=\tau \}}\sum _{1\le i_1+i_2+i_3\le j-1,i_3\ge 1}(1-\mu )^{2i_3-1}\left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\partial _r^{i_3}\mathcal {G}\psi \right) ^2\\&\quad +\sum _{1\le i_1+i_2\le j-1}\left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\mathcal {G}\psi \right) ^2 \\&\quad +\sum _{1\le i_1+i_2+i_3\le j-1}\left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\partial _r^{i_3}\psi \right) ^2. \end{aligned} \end{aligned}$$
(3.14)

The \(j=2\) case is the same without the hypersurface error terms in the right-hand side of (3.13).

Note that this theorem also holds for the domain \(D_\delta (\tau _1,\tau _2)\) in the place of \(D(\tau _1,\tau _2)\), for a sufficiently small \(\delta >0\), where the constant C is independent of \(\delta \).

Proof

See Sect. 6. \(\square \)

4 Proof of Theorem 1

4.1 The Morawetz Estimate of [10]

As mentioned earlier, this proof utilizes a Morawetz estimate for the wave equation on Schwarzschild–de Sitter, which we find in [10].

Theorem 4.1

(Theorem 1.1 in [10]). There exists a constant \(B=B(\Sigma ,M,\Lambda )>0\) such that, for \(\psi \) satisfying the wave equation (1.3) in \(D(\tau _1,\tau _2)\)

(4.1)

and

$$\begin{aligned} \left( \int _{\phi _{\tau _2}(\Sigma )}+\int _{\mathcal {H}^+\cap D(\tau _1,\tau _2)}+\int _{\bar{\mathcal {H}}^+\cap D(\tau _1,\tau _2)}\right) J^n_\mu [\psi ] n^\mu \le B\int _{\phi _{\tau _1}(\Sigma )}J^n_\mu [\psi ] n^\mu \nonumber \\ \end{aligned}$$
(4.2)

where the constant \(\psi _\infty \) satisfies \(|\psi _\infty |\le C\left( \sup _{\phi _{\tau _1}(\Sigma )}|\psi |+ \sqrt{\int _{\phi _{\tau _1}(\Sigma )}J^n_\mu [\psi ] n^\mu }\right) \).

Remark 4.1

At \(r=3M\), corresponding to trapping, note that the vector field \(\partial _r\) does not degenerate and is, in fact, in the direction of \(\partial _{r^\star }\) by (2.17). We have used this relation to translate Theorem 4.1 from the coordinates of [10].

Remark 4.2

The proof of Theorem 4.1 of Dafermos–Rodnianski actually made use of a spherical harmonics decomposition. It would be interesting to give a completely physical space proof, as has been done for Schwarzschild, see [9].

Remark 4.3

For a solution of the inhomogeneous equation

$$\begin{aligned} \Box _{g_{M,\Lambda }}\psi =F, \end{aligned}$$
(4.3)

one sees that the same estimate applies, with an additional term

$$\begin{aligned} \int \int _{D(\tau _1,\tau _2)}|\partial _{\bar{t}}\psi \cdot F|+|F|^2, \end{aligned}$$
(4.4)

on the right-hand side of both equations of Theorem 4.1. Moreover, in this case, \(\psi _\infty \) is bounded by

$$\begin{aligned} |\psi _\infty |\le C \left( \sup _{\phi _{\tau _1}(\Sigma )} |\psi | +\sqrt{\int _{\phi _{\tau _1(\Sigma )}} J^n_\mu [\psi ] n^\mu + \int \int _{D(0,\infty )}|\partial _{\bar{t}}\psi \cdot F|+|F|^2} \right) . \end{aligned}$$
(4.5)

4.2 The Equation for \(\mathcal {G}\psi \) and the \(\partial _{\bar{t}}\) Energy Identity

Before we begin the proof, we derive the equation satisfied by \(\mathcal {G}\psi \).

Proposition 4.1

Let \(\psi \) satisfy the wave equation (1.3). Then, the following holds

$$\begin{aligned} \Box _{g_{M,\Lambda }}\mathcal {G}\psi =\big [\Box _{g_{M,\Lambda }},\mathcal {G}\big ]\psi =\frac{2\sqrt{1-9M^2\Lambda }}{(1-\mu )r\sqrt{1+\frac{6M}{r}}}\partial _{\bar{t}}\mathcal {G}\psi + E_1(r)\partial _{\bar{t}}\psi + E_2(r)\partial _r\psi \end{aligned}$$
(4.6)

where

$$\begin{aligned} \begin{aligned} E_1(r)&=\frac{2\sqrt{1-\mu }(-1+2\Lambda r^2)}{r}, \\ E_2(r)&= \frac{9M^2-24M\Lambda r^3+r^4\Lambda (9-2r^2\Lambda )}{9r^3\sqrt{1-\mu }}. \end{aligned} \end{aligned}$$
(4.7)

Proof

For convenience let

$$\begin{aligned} f(r)=r\sqrt{1-\mu }. \end{aligned}$$
(4.8)

Let \(\varphi \) be a smooth function on \(\mathcal {M}_{\textit{ext}}\), and note the commutation

$$\begin{aligned} \begin{aligned} \left[ \Box _{g_{M,\Lambda }},f(r)\frac{\partial }{\partial r}\right] \varphi&=\Box (f(r)\partial _r\varphi )-f(r)\partial _r\Box _{g_{M,\Lambda }}\varphi \\&=\Box _{g_{M,\Lambda }} f \partial _r\varphi +2\nabla ^cf(r)\nabla _c \partial _r\varphi \\&\quad +f(r)\left( \Box _{g_{M,\Lambda }}\partial _r\varphi -\partial _r\Box _{g_{M,\Lambda }}\varphi \right) \\&= \Box _{g_{M,\Lambda }} f(r)\partial _r\varphi +2g^{rr}\partial _r f(r)\partial _r^2\varphi +2g^{r\bar{t}}\partial _r f(r)\partial _{\bar{t}}\partial _r\varphi \\&\quad + f(r)\left( \Box _{g_{M,\Lambda }}\partial _r\varphi -\partial _r\Box _{g_{M,\Lambda }}\varphi \right) , \end{aligned} \end{aligned}$$
(4.9)

where

(4.10)

Now, by computing the right-hand side of Eq. (4.10) for \(\psi \), a solution of the wave equation (1.3), we obtain

(4.11)

Finally, by using Eq. (4.9) for \(\psi \), a solution of the wave equation (1.3), together with (4.11), we obtain

$$\begin{aligned} \big [\Box _{g_{M,\Lambda }},f(r)\frac{\partial }{\partial r}\big ]\psi= & {} \left( 2\partial _r f(r) -f(r)\left( \partial _r g^{rr}+\frac{2}{r}g^{rr}\right) \right) \partial _r^2\psi \nonumber \\{} & {} \quad +\left( 2g^{r\bar{t}}\partial _r f(r) -2 f(r)\left( \partial _rg^{r\bar{t}} +\frac{2}{r}g^{r\bar{t}}\right) \right) \partial _{{\bar{t}}}\partial _r\psi \nonumber \\{} & {} \quad -f(r)\left( \partial _rg^{\bar{t}\bar{t}}+\frac{2}{r}g^{\bar{t}\bar{t}} \right) \partial _{{\bar{t}}}^2\psi +\Box _{g_{M,\Lambda }} f(r) \partial _r\psi \nonumber \\{} & {} \quad -\frac{2}{r}f(r)g^{ab}\Gamma ^c\,_{ab}\partial _c\psi -f(r)\partial _r\left( g^{ab}\Gamma ^c\,_{ab}\right) \partial _c\psi . \end{aligned}$$
(4.12)

By revisiting the metric in regular hyperboloidal coordinates, see (2.4), we note

$$\begin{aligned} \begin{aligned} \partial _rg^{\bar{t}\bar{t}}+\frac{2}{r}g^{\bar{t}\bar{t}}=0, \end{aligned} \end{aligned}$$
(4.13)

also

$$\begin{aligned} \begin{aligned} 2\partial _r f(r)g^{rr} -f(r)\left( \partial _r g^{rr}+\frac{2}{r}g^{rr}\right) =0, \end{aligned} \end{aligned}$$
(4.14)

and finally

$$\begin{aligned} 2g^{r\bar{t}}\partial _r f(r)-2f(r)\left( \partial _rg^{r\bar{t}}+\frac{2}{r}g^{r\bar{t}}\right) = \frac{2\sqrt{1-9M^2\Lambda }}{\sqrt{1-\mu }\sqrt{1+\frac{6M}{r}}}. \end{aligned}$$
(4.15)

Therefore, we conclude

$$\begin{aligned} \big [\Box _{g_{M,\Lambda }},f(r)\frac{\partial }{\partial r}\big ]\psi= & {} \frac{2\sqrt{1-9M^2\Lambda }}{\sqrt{1-\mu }\sqrt{1+\frac{6M}{r}}}\partial _r\partial _{{\bar{t}}}\psi + \Box _{g_{M,\Lambda }} f(r) \partial _r\psi \nonumber \\{} & {} \quad -\frac{2}{r}f(r)g^{ab}\Gamma ^c\,_{ab}\partial _c\psi -f(r)\partial _r\left( g^{ab}\Gamma ^c\,_{ab}\right) \partial _c\psi \nonumber \\= & {} \frac{2\sqrt{1-9M^2\Lambda }}{r(1-\mu )\sqrt{1+\frac{6M}{r}}}\partial _{{\bar{t}}}\mathcal {G}\psi + \Box _{g_{M,\Lambda }} f(r) \partial _r\psi \nonumber \\{} & {} \quad -\frac{2}{r}f(r)g^{ab}\Gamma ^c\,_{ab}\partial _c\psi -f(r)\partial _r\left( g^{ab}\Gamma ^c\,_{ab}\right) \partial _c\psi . \nonumber \\ \end{aligned}$$
(4.16)

Now, by revisiting the wave operator (2.22), we compute

$$\begin{aligned} g^{ab}\Gamma ^c\,_{ab}\partial _c\psi =\left( -\partial _r\xi +2r^{-1}\xi (r)\right) \partial _t\psi +\left( 2r^{-1}(1-\mu ) +\partial _r(1-\mu )\right) \partial _r\psi , \end{aligned}$$
(4.17)

and

$$\begin{aligned} \partial _r(g^{ab}\Gamma ^c\,_{ab})\partial _c\psi =\partial _r\left( -\partial _r\xi +2r^{-1}\xi (r)\right) \partial _{\bar{t}}\psi +\partial _r\left( 2r^{-1}(1-\mu )+\partial _r(1-\mu )\right) \partial _r\psi . \end{aligned}$$
(4.18)

By examining equations (4.16) and (4.17), (4.18) we conclude the result. \(\square \)

Remark 4.4

From relations (4.13), (4.14) we can see how we arrived at our choice of coordinates, Definition 2.3, and our vector field (2.18). Specifically, in the class of coordinate transformations \(\bar{t}=t-H(r)\) we select H(r) such that equation (4.13) holds. Moreover, we select the function f, such that (4.14) holds. By this choice of coordinates \((r,\bar{t}, \theta ,\phi )\) and vector field \(\mathcal {G}\), the expression of Eq. (4.15) is positive. This reflects the good unstable structure of trapping.

We apply a \(\partial _{\bar{t}}\)-multiplier estimate to the Eq. (4.6).

Proposition 4.2

Let \(\psi \) satisfy the wave equation (1.3). Then, we have the following

$$\begin{aligned}{} & {} \left( \int _{\mathcal {H}^+\cap D(\tau _1,\tau _2)}+\int _{\bar{\mathcal {H}}^+\cap D(\tau _1,\tau _2)} +\int _{\phi _{\tau _2}(\Sigma )}\right) J_\mu ^{\partial _{\bar{t}}}[\mathcal {G}\psi ]n^\mu \nonumber \\{} & {} \quad +\int \int _{D(\tau _1,\tau _2)}\frac{2\sqrt{1-9M^2\Lambda }}{(1-\mu )r\sqrt{1+\frac{6M}{r}}}\left( \partial _{{\bar{t}}}\mathcal {G}\psi \right) ^2 \nonumber \\{} & {} \quad =\int _{\phi _{\tau _1}(\Sigma )} J_\mu ^{\partial _{\bar{t}}}[\mathcal {G}\psi ]n^\mu -\int \int _{D(\tau _1,\tau _2)}\left( E_1(r) \partial _{r}\psi +E_2(r)\partial _{{\bar{t}}}\psi \right) \partial _{{\bar{t}}}\mathcal {G}\psi . \nonumber \\ \end{aligned}$$
(4.19)

Proof

We have

$$\begin{aligned} \nabla ^\mu J_\mu ^{\partial _{\bar{t}}}[\mathcal {G}\psi ]=\partial _{{\bar{t}}} \mathcal {G}\psi \Box _{g_{M,\Lambda }}\mathcal {G}\psi , \end{aligned}$$
(4.20)

and we have already computed

$$\begin{aligned} \Box _{g_{M,\Lambda }}\mathcal {G}\psi =\frac{2\sqrt{1-9M^2\Lambda }}{(1-\mu )r\sqrt{1+\frac{6M}{r}}}\partial _{{\bar{t}}}\mathcal {G}\psi + E_1(r)\partial _{r}\psi + E_2(r)\partial _{{\bar{t}}}\psi \end{aligned}$$
(4.21)

in Proposition 4.1. We apply the divergence theorem, see Eq. (2.41), to \(\mathcal {G}\psi \) and conclude the result. \(\square \)

4.3 Auxiliary Estimates

Remark 4.5

In the proof of this section we shall keep track of the powers of r in our estimates, such that the constants in our estimates do not degenerate as \(\Lambda \rightarrow 0\). This shall be useful in the next Sect. 7, where we treat the \(\Lambda =0\) Schwarzschild case.

We will also need the following elementary pointwise lemma later.

Lemma 4.1

Let \(E_1(r),E_2(r)\) be defined as in Proposition 4.1. Then, we have the following

$$\begin{aligned} \Big |\int \int _{D(\tau _1,\tau _2)}{} & {} \left( E_1(r)\partial _{{\bar{t}}}\psi +E_2(r)\partial _{r}\psi \right) \partial _{{\bar{t}}}\mathcal {G}\psi \Big | \nonumber \\{} & {} \le \int \int _{D(\tau _1,\tau _2)}\left( \frac{r}{2\epsilon }(1-\mu )\left( E_2(r)\partial _{r}\psi \right) ^2+\frac{\epsilon }{2}\frac{1}{(1-\mu )r}(\partial _{{\bar{t}}}\mathcal {G}\psi )^2\right) \nonumber \\{} & {} \quad +\int \int _{D(\tau _1,\tau _2)}|\partial _r(1-\mu )|(\partial _{\bar{t}}\psi )^2. \end{aligned}$$
(4.22)

We want to generate all the derivatives of \(\mathcal {G}\psi \) from terms appearing in Eq. (4.19).

Lemma 4.2

There exists a constant \(C(M,\Lambda )>0\), which does not degenerate as \(\Lambda \rightarrow 0\), such that, if \(\psi \) solves the wave equation (1.3), then we obtain

(4.23)

Proof

We begin from the equation for \(\mathcal {G}\psi \), see the commutation (4.6)

(4.24)

and multiply it with \(\frac{1}{r}\mathcal {G}\psi \)

(4.25)

where \(\textit{RHS}\) is the right-hand side of Eq. (4.24).

We integrate (4.25) over \(D(\tau _1,\tau _2)\). Then, we perform the necessary integration by parts and Young’s inequalities to get the result. \(\square \)

We want to generate a non-degenerate \((\partial _t\psi )^2\) from terms appearing in Eq. (4.19).

Lemma 4.3

There exists a constant \(C(M,\Lambda )>0\) that does not degenerate as \(\Lambda \rightarrow 0\), such that for all \(\epsilon >0\), if \(\psi \) satisfies the wave equation (1.3), then we have

$$\begin{aligned} \begin{aligned} \frac{C}{\epsilon }\int \int _{D(\tau _1,\tau _2)} \frac{1-\mu }{r^3}(\partial _{{\bar{t}}}\psi )^2&\le \frac{1}{2}\int \int _{D(\tau _1,\tau _2)}\frac{2\sqrt{1-9M^2\Lambda }}{r^4(1-\mu )\sqrt{1+\frac{6M}{r}}}(\partial _{{\bar{t}}}\mathcal {G}\psi )^2 \\&\quad +\frac{C}{\epsilon ^2}\left( \int \int _{D(\tau _1,\tau _2)}\frac{(r-3M)^2}{r^4\sqrt{1-9M^2\Lambda }}(\partial _{{\bar{t}}}\psi )^2\right) . \end{aligned} \end{aligned}$$

Proof

We begin by

$$\begin{aligned} \int \int _{D(\tau _1,\tau _2)}\frac{1-\mu }{r^2}(\partial _{\bar{t}}\psi )^2\frac{1}{r}\textrm{d}g= \int _{\mathbb {S}^2}\int _0^\tau \int _{r_+}^{\bar{r}_+}\frac{1-\mu }{r^2}\frac{\partial }{\partial r} (r-3M) (\partial _t\psi )^2 \sin {\theta }\textrm{d}r \textrm{d}\bar{t}\textrm{d}\sigma . \end{aligned}$$

We perform an integration by parts and write the right-hand side of the above as

$$\begin{aligned}{} & {} \int _{\mathbb {S}^2}\int _0^\tau \left[ \frac{1-\mu }{r^2}(r-3M)(\partial _{\bar{t}}\psi )^2\right] _{r_+}^{\bar{r}_+}\\{} & {} \quad -\int \int _{D(\tau _1,\tau _2)}\left( \frac{\partial }{\partial r} \left( \frac{1-\mu }{r^2}\right) (r-3M)(\partial _{\bar{t}}\psi )^2\right. \\{} & {} \quad \left. +(r-3M)\frac{1-\mu }{r^2}2\partial _{\bar{t}}\psi \frac{\partial }{\partial r} \partial _{\bar{t}}\psi \right) r\sin {\theta }\textrm{d}r \textrm{d}\bar{t}\textrm{d}\sigma \\{} & {} \quad =-\int \int _{D(\tau _1,\tau _2)}\left( \frac{\partial }{\partial r} \left( \frac{1-\mu }{r^2}\right) (r-3M)(\partial _{\bar{t}}\psi )^2\right. \\{} & {} \quad \quad \left. +(r-3M)\frac{1-\mu }{r^2}2\partial _{\bar{t}}\psi \frac{\partial }{\partial r} \partial _{\bar{t}}\psi \right) r\sin {\theta }\textrm{d}r \textrm{d}\bar{t}\textrm{d}\sigma \\{} & {} \quad \le C\int \int _{D(\tau _1,\tau _2)} \frac{1}{r^6}(r-3M)^2 (\partial _{\bar{t}}\psi )^2+\frac{1}{\epsilon r^8\sqrt{1-9M^2\Lambda }}(r-3M)^2(\partial _{\bar{t}}\psi )^2\\{} & {} \quad \quad +\epsilon \frac{\sqrt{1-9M^2\Lambda }}{r^4(1-\mu )\sqrt{1+\frac{6M}{r}}}(\partial _{\bar{t}}\mathcal {G}\psi )^2. \end{aligned}$$

We conclude the proof. \(\square \)

4.4 Proofs of Theorem 1 and Corollary 1

We are now ready to conclude Theorem 1 and the exponential decay Corollary 1.

Proof of Theorem 1

We first use Lemma 4.1 on Eq. (4.19), in conjunction with Lemmata 4.1, 4.3 to obtain

$$\begin{aligned}{} & {} \left( \int _{\mathcal {H}^+\cap D(\tau _1,\tau _2)}+\int _{\bar{\mathcal {H}}^+\cap D(\tau _1,\tau _2)} +\int _{\phi _{\tau _2}(\Sigma )}\right) J_\mu ^{\partial _{\bar{t}}}[\mathcal {G}\psi ]n^\mu \nonumber \\{} & {} \quad \quad +\int \int _{D(\tau _1,\tau _2)}\frac{2\sqrt{1-9M^2\Lambda }}{(1-\mu )r\sqrt{1+\frac{6M}{r}}}\left( \partial _{{\bar{t}}}\mathcal {G}\psi \right) ^2+\frac{1-\mu }{r^4}(\partial _{\bar{t}}\psi )^2 \nonumber \\{} & {} \quad \lesssim \int _{\phi _{\tau _1}(\Sigma )} J_\mu ^{\partial _{\bar{t}}}[\mathcal {G}\psi ]n^\mu +\int \int _{D(\tau _1,\tau _2)}r^{-2}(\partial _{\bar{t}}\psi )^2+r^{-2}(\partial _r\psi )^2 \end{aligned}$$
(4.26)

Note that the horizon hypersurface terms on \(\mathcal {H}^+,\bar{\mathcal {H}}^+\), on the left-hand side of Eq. (4.26), are non-negative, see (2.40), so we may drop them from our estimates. We multiply the estimate of Lemma 4.2 with a smallness parameter and add it to (4.26) to obtain

(4.27)

Finally, we add in the Morawetz estimate (4.1) of Theorem 4.1, multiplied with a large parameter and use the boundedness estimate (4.2), to conclude

(4.28)

We recall the definition of \(\mathcal {E}(\mathcal {G}\psi ,\psi )\) in Eq. (1.10) and note Eq. (1.11). We conclude (3.1).

Moreover, we conclude (3.2), in view of the relation of the coarea formula of Sect. 2.15, namely

$$\begin{aligned} \int \int _{D(\tau _1,\tau _2)}\mathcal {E}(\mathcal {G}\psi ,\psi )\sim \int _{\tau _1}^{\tau _2}\textrm{d}\tau \int _{\phi _\tau (\Sigma )}\mathcal {E}(\mathcal {G}\psi ,\psi ). \end{aligned}$$
(4.29)

\(\square \)

We need the following lemma.

Lemma 4.4

Let \(f:[0,\infty )\rightarrow \mathbb {R}\) a nonnegative continuous function satisfying

$$\begin{aligned} f(\tau _2)+\int _{\tau _1}^{\tau _2}f(\tau ) \textrm{d}\tau \le k f(\tau _1), \end{aligned}$$

for all \(\tau _2>\tau _1\ge 0\) and some \(k> 0\). Then, there exists constants \(c,C>0\) depending only on k such that:

$$\begin{aligned} f(\tau )\le C e^{- c\tau }f(0), \end{aligned}$$

for all \(\tau \ge 0\).

Proof

This is elementary. See for example [10]. \(\square \)

Now we can infer exponential decay.

Proof of Corollary 1

The estimate

$$\begin{aligned} \int _{\phi _{\tau }(\Sigma )}\mathcal {E}(\mathcal {G}\psi ,\psi )\lesssim e^{-c\tau }\int _{\Sigma }\mathcal {E}(\mathcal {G}\psi ,\psi ) \end{aligned}$$
(4.30)

is an immediate consequence of Eq. (3.2) of Theorem 1 and Lemma 4.4, where \(f(\tau )=\int _{\phi _\tau (\Sigma )}\mathcal {E}(\mathcal {G}\psi ,\psi )\).

We note that inequality (4.30) holds for \(\partial _{\bar{t}}^i\Omega _\alpha ^j\psi \), for all indices i, j, in the place of \(\psi \), where \(\Omega _\alpha \) are defined in Eq. (2.24), since the following hold: \([\Box _{g_{M,\Lambda }},\partial _{\bar{t}}]=0, [\Box _{g_{M,\Lambda }},\Omega _\alpha ]=0\).

Therefore, one can prove, by commuting with \(\Omega _\alpha \) and then a Sobolev estimate, the pointwise estimate

$$\begin{aligned} \sup _{\phi _{\tau }(\Sigma )} |\psi -\psi _\infty |^2{} & {} \lesssim \int _{\phi _\tau (\Sigma )} \sum _{0\le i\le 1}\sum _{0\le \alpha \le 3} \mathcal {E}(\mathcal {G}\Omega _\alpha ^i\psi ,\Omega _\alpha \psi )\nonumber \\{} & {} \lesssim e^{-c{\tau }} \int _\Sigma \sum _{0\le i\le 1}\sum _{0\le \alpha \le 3} \mathcal {E}(\mathcal {G}\Omega _\alpha ^i\psi ,\Omega _\alpha \psi ), \end{aligned}$$
(4.31)

where \(\psi _\infty \) is from Theorem 4.1, and satisfies \(|\psi _\infty |\!\le \! C\left( \sup _{\Sigma }|\psi |\!+\!\sqrt{\int _{\Sigma }J^n_\mu [\psi ]n^\mu } \right) \).

\(\square \)

Remark 4.6

Note that from Theorem 3 and the use of Sobolev estimates we can obtain pointwise estimates for arbitrary regular higher-order derivatives

$$\begin{aligned} \sup _{\phi _\tau (\Sigma )}\sum _{1\le i+j+l\le k} |\partial _r^i\partial _{\bar{t}}^j\Omega _\alpha ^l\psi |^2\lesssim E_{\mathcal {G},k+3} e^{-c\tau }, \end{aligned}$$
(4.32)

where for \(E_{\mathcal {G},k+3}\) see (3.14).

5 Proof of Theorem 2

We recall

$$\begin{aligned} \big [\Box _{g_{M,\Lambda }},\mathcal {G}\big ]\psi =\frac{2\sqrt{1-9M^2\Lambda }}{(1-\mu )r\sqrt{1+\frac{6M}{r}}}\partial _{{\bar{t}}}\mathcal {G}\psi + E_1(r)\partial _{\bar{t}}\psi + E_2(r)\partial _r\psi \end{aligned}$$
(5.1)

from which we easily deduce

$$\begin{aligned} \Box _{g_{M,\Lambda }}\mathcal {G}\psi = \frac{2\sqrt{1-9M^2\Lambda }}{(1-\mu )r\sqrt{1+\frac{6M}{r}}}\partial _{{\bar{t}}}\mathcal {G}\psi +E_1(r)\partial _{\bar{t}}\psi + E_2(r)\partial _r\psi +\mathcal {G} F. \end{aligned}$$
(5.2)

Now, we follow the arguments of Sect. 4. Specifically, we conclude that there exists a constant \(C=C(M,\Lambda )>0\), such that for \(\psi \) a sufficiently regular solution of the inhomogeneous wave equation (3.4) on \(D(\tau _1,\tau _2)\), we obtain

$$\begin{aligned} \begin{aligned}&\int _{\phi _{\tau _2}(\Sigma )} J_\mu ^{\partial _{\bar{t}}}[\mathcal {G}\psi ]n^\mu +\int \int _{D(\tau _1,\tau _2)}\frac{1}{r(1-\mu )}(\partial _{{\bar{t}}}\mathcal {G}\psi )^2\\&\quad \le C\int _{\phi _{\tau _1}(\Sigma )} J_\mu ^{\partial _{\bar{t}}}[\mathcal {G}\psi ]n^\mu + C\int \int _{D(\tau _1,\tau _2)} \left| \partial _{\bar{t}}\mathcal {G}\psi \mathcal {G}F \right| \\&\quad \quad +C\int \int _{D(\tau _1,\tau _2)} \left| \partial _{\bar{t}}\mathcal {G}\psi \left( E_1(r)\partial _{\bar{t}}\psi +E(r)\partial _r\psi \right) \right| . \end{aligned} \end{aligned}$$
(5.3)

Then, we use appropriate Young’s inequalities on the right-hand side of (5.3) to conclude

$$\begin{aligned}{} & {} \int _{\phi _{\tau _2}(\Sigma )} J_\mu ^{\partial _{\bar{t}}}[\mathcal {G}\psi ]n^\mu +\int \int _{D(\tau _1,\tau _2)}\frac{1}{r(1-\mu )}(\partial _{{\bar{t}}}\mathcal {G}\psi )^2 \nonumber \\{} & {} \quad \le C\int _{\phi _{\tau _1}(\Sigma )} J_\mu ^{\partial _{\bar{t}}}[\mathcal {G}\psi ]n^\mu + C\int \int _{D(\tau _1,\tau _2)} (1-\mu )\left| \mathcal {G}F \right| ^2 \nonumber \\{} & {} \quad \quad +C\int \int _{D(\tau _1,\tau _2)} (1-\mu )\left| E_1(r)\partial _{\bar{t}}\psi +E_2(r)\partial _r\psi \right| ^2. \end{aligned}$$
(5.4)

Now, we sum in (5.4) the Morawetz estimate of Theorem 4.1, (in the inhomogeneous form given by Remark 4.3), to conclude

(5.5)

where we generated all the derivatives of \(\mathcal {G}\psi \) and \(\psi \) on the left-hand side of our estimate (5.5), by Lemmata 4.2, 4.3. We apply a Young’s inequality on the last term on the right-hand side of (5.5) and conclude

(5.6)

Now, Theorem 2 is a trivial consequence of Eq. (5.6), since we have the property (1.11).

Proof of Corollary 2

Suppose that

$$\begin{aligned} F=\epsilon a^j\partial _j\psi , \end{aligned}$$

where \(a^j\) are smooth and bounded with \(\mathcal {G}a^j\) bounded, for all j. Now, we use Eq. (5.5) to obtain

(5.7)

since

$$\begin{aligned} \begin{aligned} \mathcal {G} F&= \epsilon \left( \partial _j\psi \mathcal {G} a^j\right) + \epsilon \left( a^j\mathcal {G}\partial _j\psi \right) . \end{aligned} \end{aligned}$$

If \(\epsilon \) is sufficiently small the terms on the right-hand side can be absorbed, after also using a Hardy inequality.

Finally, for the pointwise result, we commute the inhomogeneous Eq. (3.4) with the vector fields \(\Omega _\alpha \), see Eq. (2.24), to conclude that (5.7) holds for \(\Omega _\alpha \psi \) in the place of \(\psi \). Moreover, we know that \([\Omega _\alpha \mathcal {G}, a]^{\bar{t}},[\Omega _\alpha \mathcal {G}, a]^{r},g^{\theta \theta }([\Omega _\alpha \mathcal {G}, a]^{\theta })^2+g^{\phi \phi }([\Omega _\alpha \mathcal {G}, a]^{\phi })^2\) are bounded. We use a Sobolev inequality and conclude that

$$\begin{aligned} \sup _{\phi _\tau (\Sigma )}|\psi -\psi _\infty |\le C\sqrt{E}e^{-c\tau } \end{aligned}$$
(5.8)

where, in view of Eq. (4.5), the following holds

$$\begin{aligned} |\psi _\infty |\le C\left( \sup _\Sigma |\psi |+\sqrt{\int _\Sigma \mathbb {T}(n,n)[\psi ]+\mathbb {T}(\partial _{\bar{t}},n)[\mathcal {G}\psi ]}\right) \end{aligned}$$
(5.9)

and

$$\begin{aligned} E=\sum _{0\le i\le 1}\sum _{1\le \alpha \le 3}\int _{\Sigma }\mathcal {E}(\mathcal {G}\Omega _\alpha ^i\psi ,\Omega _\alpha ^i\psi ). \end{aligned}$$
(5.10)

\(\square \)

6 Proof of Theorem 3

We define the auxiliary energy

$$\begin{aligned} E_{j}[\psi ](\tau )= \sum _{1\le i_1+i_2+i_3\le j}\sum _{\alpha =1,2,3}\int _{\phi _\tau (\Sigma )}\left( \partial _{\bar{t}}^{i_1}\partial _r^{i_2}\Omega _\alpha ^{i_3}\psi \right) ^2. \end{aligned}$$
(6.1)

We begin by noting the following Proposition, which is a higher-order analogue of the inhomogeneous version of Theorem 4.1

Proposition 6.1

Let \(\psi \) satisfy the inhomogeneous wave equation (3.12). Then, we obtain the following higher-order Morawetz estimate

$$\begin{aligned}{} & {} E_j[\psi ](\tau _2) + \int \int _{D(\tau _1,\tau _2)} \left( 1-\frac{3M}{r}\right) ^2\sum _{i_1+i_2=j}\sum _{\alpha } \left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\psi \right) ^2 \nonumber \\{} & {} \qquad +\sum _{i_1+i_2+i_3=j,i_3\ge 1}\sum _\alpha \left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\partial _r^{i_3}\psi \right) ^2 \nonumber \\{} & {} \qquad +\sum _{1\le i_1+i_2+i_3\le j-1}\sum _\alpha \left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\partial _r^{i_3}\psi \right) ^2 \nonumber \\{} & {} \quad \le C E_j[\psi ](\tau _1) +C\int \int _{D(\tau _1,\tau _2)}\left| \partial _{\bar{t}}^{j}\psi \cdot \partial _{\bar{t}}^{j-1}F\right| \nonumber \\{} & {} \quad \quad +\sum _{1\le i_1+i_2+i_3\le j-2}\sum _\alpha \left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\partial _r^{i_3}F\right) ^2 \nonumber \\{} & {} \quad \quad +C\int _{\phi _{\tau _2}(\Sigma )} \sum _{0\le i_1+i_2+i_3\le j-2}\sum _\alpha \left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\partial _r^{i_3}F\right) ^2 \end{aligned}$$
(6.2)

for a constant \(C(j,M,\Lambda )>0\).

Proof

The proof of this Proposition follows from Theorem 4.1 and additional redshift commutations of the Lecture notes [11] and elliptic estimates. \(\square \)

Now we prove Theorem 3.

Proof of Theorem 3

We start by recalling the result of Theorem 2, namely

(6.3)

where we have kept certain r factor explicitly for integrands related to \(\mathcal {G}\), for comparison with the case \(\Lambda =0\). (We note, however, that we drop the r factor in the lower-order terms.) The inequality (6.3) already gives the result of the Theorem for \(j=2\).

Now, for any \(j\ge 3\), by commuting the inhomogeneous wave equation (3.12) with

$$\begin{aligned} \partial _{\bar{t}}^k\Omega _\alpha ^l,\qquad k+l\le j-2 \end{aligned}$$
(6.4)

we obtain

(6.5)

Then, to obtain all the lower-order terms on the bulk of the left-hand side of (6.5) we sum in the Morawetz estimate (6.2) of Proposition 6.1, at order \(j-1\), and after appropriate Young’s inequalities on the contribution of the F error term we obtain

(6.6)

where we used the auxiliary energy

$$\begin{aligned} E^\prime _{\mathcal {G},j}[\psi ](\tau ) =\int _{\{\bar{t}=\tau \}}\sum _{0\le i_1+i_2= j-2}\sum _\alpha J_\mu ^{\partial _{\bar{t}}}[\partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\mathcal {G}\psi ]n^\mu +E_{j-1}[\psi ](\tau ). \end{aligned}$$
(6.7)

Note that in the energy estimate (6.6) there is no degeneration, at the low order, on the photon sphere \(r=3M\), because we repeated a Poincare-type argument at top order, see Lemma 4.3.

Note that we control all the desired higher-order derivatives (at order j) related to \(\mathcal {G}\), on the left-hand side of (6.6), except for

$$\begin{aligned} \partial _r^{i_3}\mathcal {G}\psi ,\qquad i_3=j-1 \end{aligned}$$
(6.8)

with the appropriate degenerative weight. For that purpose, we return to the equation satisfied by \(\mathcal {G}\psi \), see (4.6), which reads

(6.9)

where recall \(g^{rr}=1-\mu \). We differentiate (6.9) by

$$\begin{aligned} \partial _r^{i_3-2}, \end{aligned}$$
(6.10)

and then we square the result and note that there exists a constant \(C(j,M,\Lambda )>0\) such that

$$\begin{aligned} \begin{aligned}&(1-\mu )^2(\partial _r^{i_3}\mathcal {G}\psi )^2 \le C(j,M,\Lambda ) \\&\quad \left( \left( \partial _r^{i_3-2}\left( \frac{1}{\sqrt{1-\mu }}\right) \frac{2\sqrt{1-9M^2\Lambda }}{\sqrt{1+\frac{6M}{r}}} (\partial _r\partial _{\bar{t}}\psi )\right) ^2+\dots +\left( \partial _r^{i_3-2}\mathcal {G}F\right) ^2\right) \\ \end{aligned} \end{aligned}$$
(6.11)

where, in inequality (6.11) the three terms displayed are from left to right the highest \(\partial _r\) derivative term, the fastest degenerating \((1-\mu )\) term and the contribution of the inhomogeneity F. We rewrite (6.11) as

$$\begin{aligned} \begin{aligned} (1-\mu )^2(\partial _r^{i_3}\mathcal {G}\psi )^2&\le C(j,M,\Lambda )\left( \frac{1}{(1-\mu )^{2i_3-3}}\left( \partial _r\partial _{\bar{t}}\psi \right) ^2+\dots + \left( \partial _r^{i_3-2}\mathcal {G}F\right) ^2\right) \\ \end{aligned} \end{aligned}$$
(6.12)

and therefore, by multiplying (6.12) with \(\frac{(1-\mu )^{2i_3-3}}{r}\), so that no terms blow up at the roots of \(1-\mu =0\), we obtain

$$\begin{aligned} \begin{aligned}&\frac{(1-\mu )^{2i_3-1}}{r}(\partial _r^{i_3}\mathcal {G}\psi )^2 \le C(j,M,\Lambda )\left( \frac{1}{r^3(1-\mu )}\right. \\&\quad \left. \left( \partial _{\bar{t}}\mathcal {G}\psi \right) ^2+\dots +\frac{(1-\mu )^{2i_3-3}}{r}\left( \partial _r^{i_3-2}\mathcal {G}F\right) ^2\right) . \end{aligned} \end{aligned}$$
(6.13)

For the \(j=3\) case of inequality (6.13) with all its terms displayed see already Remark 6.1. Therefore, by using the integrated inequality (6.6) and the pointwise estimate (6.13) we obtain

(6.14)

for all \(\tau _1\le \tau _2\) and for all \(j\ge 2\).

Now, we want to estimate from below \(E^\prime _{\mathcal {G},j}[\psi ](\tau _2)\) by \(E_{\mathcal {G},j}[\psi ](\tau _2)\), in the energy estimate (6.14), for all orders \(j\ge 3\) at the expense of producing hypersurface error terms. We note that there exists a constant \(c(j,M,\Lambda )\) such that

(6.15)

Then, we want to obtain the top order derivatives

$$\begin{aligned} \partial _r^{i_3}\mathcal {G}\psi ,\qquad i_3=j-1, \end{aligned}$$
(6.16)

on the left-hand side, with the appropriate degenerative weights of \((1-\mu )\). Therefore, we multiply the pointwise estimate (6.12) with \((1-\mu )^{2i_3-3}\) and sum it to (6.15) to obtain that there exist constants

$$\begin{aligned} c(j,M,\Lambda ),C(j,M,\Lambda )>0 \end{aligned}$$
(6.17)
$$\begin{aligned}{} & {} c(j,M,\Lambda )\int _{\{\bar{t}=\tau \}} \sum _{0\le i_1+i_2\le j-2 }\sum _\alpha \mathcal {E}\left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\mathcal {G}\psi ,\partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\psi \right) \nonumber \\{} & {} \qquad +\sum _{1\le i_1+i_2+i_3\le j-1,i_3\ge 1}\sum _\alpha r(1-\mu )^{2i_3-1}\left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\partial _r^{i_3}\mathcal {G}\psi \right) ^2 \nonumber \\{} & {} \qquad +\sum _{1\le i_1+i_2+i_3\le j-1,i_3\ge 1}\sum _\alpha r\left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\partial _r^{i_3}\psi \right) ^2 \nonumber \\{} & {} \quad \le E^\prime _{\mathcal {G},j}[\psi ](\tau ) \nonumber \\{} & {} \quad \quad + C(j,M,\Lambda )\int _{\{\bar{t}=\tau \}} \sum _{0\le i_1+i_2+i_3\le j-3}\sum _\alpha (1-\mu )^{2i_3+1}r\left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\partial _r^{i_3}\mathcal {G}F\right) ^2 \nonumber \\{} & {} \quad \quad +\sum _{0\le i_1+i_2+i_3\le j-3}\sum _\alpha r\left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\partial _r^{i_3}F\right) ^2. \end{aligned}$$
(6.18)

Note that the left-hand side of (6.18) is similar to \(E_{\mathcal {G},j}[\psi ](\tau )\).

Finally, by using the energy estimate (6.14) in conjunction with the pointwise estimate (6.18) we conclude the result of the Corollary. \(\square \)

Remark 6.1

For an example of the computation (6.13) note that at order \(j=3\) we obtain

(6.19)

where the constant \(C(M,\Lambda )\) does not degenerate in the limit \(\Lambda \rightarrow 0\).

7 The Schwarzschild Case \(\Lambda =0\)

We can also prove the equivalent of Theorem 2 on the asymptotically flat Schwarzschild exterior. This result had been obtained previously by [20]. For completeness, we give a treatment here in our set up.

We study the inhomogeneous wave equation

$$\begin{aligned} \Box _{g_M} \psi =F. \end{aligned}$$
(7.1)

Before stating the theorem let us introduce some preliminary notions, specifically for the Schwarzschild case.

First, we define regular hyperboloidal coordinates \((\bar{t},r,\theta ,\phi )\) on which the metric takes the form

$$\begin{aligned} g_{M}=-\left( 1-\frac{2M}{r}\right) (\textrm{d}\bar{t})^2-2\left( 1-\frac{3M}{r}\right) \sqrt{1+\frac{6M}{r}} \textrm{d}\bar{t}\textrm{d}r +\frac{27M^2}{r^2} (\textrm{d}r)^2+r^2 \textrm{d}\sigma _{\mathbb {S}^2}. \end{aligned}$$
(7.2)

These correspond to the regular hyperboloidal coordinates of Sect. 2.2, when we take \(\Lambda =0\). Moreover, we can define the Schwarzschild coordinates \((t,r,\theta ,\phi )\) similarly to the Schwarzschild–de Sitter coordinates, see Sect. 2.

We may attach null infinity

$$\begin{aligned} \mathcal {I}^+=\{(\bar{t},r=+ \infty ,\theta ,\phi )\in \mathbb {R}\times \{+\infty \}\times \mathbb {S}^2\}, \end{aligned}$$
(7.3)

as a boundary in the obvious way. Formally, we consider its normal to be \(n_{\mathcal {I}^+}=\frac{\partial }{\partial \bar{t}}\) and note

$$\begin{aligned} J^T_\mu [\psi ]n_{\mathcal {I}^+}^\mu =\left( \partial _{\bar{t}}\psi \right) ^2. \end{aligned}$$
(7.4)

Let

$$\begin{aligned} \tilde{\Sigma }=\{\bar{t}=0\}. \end{aligned}$$
(7.5)

Then the leaves of the foliation

$$\begin{aligned} \phi _\tau (\tilde{\Sigma })=\{\bar{t}=\tau \} \end{aligned}$$
(7.6)

connect the event horizon \(\mathcal {H}^+\) with future null infinity \(\mathcal {I}^+\). Also, we define the spacetime domain

$$\begin{aligned} \tilde{D}(\tau _1,\tau _2)=\{\tau _1\le \bar{t}\le \tau _2\}. \end{aligned}$$
(7.7)

The reader familiar with the Penrose diagram may want to consult Fig. 4.

Fig. 4
figure 4

The foliation of the Schwarzschild exterior

Full size image

Note that the volume form of (7.7) is

$$\begin{aligned} \textrm{d}g=r^2\sin {\theta }\textrm{d}\bar{t}\textrm{d}\theta \textrm{d}\phi \end{aligned}$$
(7.8)

and the volume form of (7.6) is

$$\begin{aligned} \textrm{d}g_{\{\bar{t}=c\}}=3\sqrt{3}Mr\sin {\theta }\textrm{d}r \textrm{d}\theta \textrm{d}\phi . \end{aligned}$$
(7.9)

and the normal of the \(\{\bar{t}=c\}\) hypersurface is

$$\begin{aligned} n_{\phi _{\tau }(\Sigma )}=\frac{\sqrt{27}M}{r}\frac{\partial }{\partial \bar{t}}+r\frac{\xi (r)}{\sqrt{27}M}\frac{\partial }{\partial r}, \end{aligned}$$
(7.10)

where \(\xi (r)=\left( 1-\frac{3M}{r}\right) \sqrt{1+\frac{6M}{r}}\).

The vector field \(\mathcal {G}\) here takes the form

$$\begin{aligned} \mathcal {G}\!=\!r\sqrt{1-\frac{2M}{r}}\frac{\partial }{\partial r}\!=\!\frac{r}{\sqrt{1-\mu }}\frac{\partial }{\partial r^\star }\!+\!\frac{r}{\sqrt{1-\mu }}\left( 1-\frac{3M}{r}\right) \sqrt{1\!+\!\frac{6M}{r}}\frac{\partial }{\partial t}\qquad \end{aligned}$$
(7.11)

and the energy density,

$$\begin{aligned} \tilde{\mathcal {E}}(\mathcal {G}\psi ,\psi )\,\dot{=}\, \mathbb {T}(\partial _{\bar{t}},n)[\mathcal {G}\psi ]+\mathbb {T}(N,n)[\psi ], \end{aligned}$$
(7.12)

is now defined with \(\mathcal {G}\) as in (7.11), where N is a time translation invariant strictly timelike vector field, see the Lecture notes [11] that away from the horizon \(\mathcal {H}^+\) is equal to \(\partial _{\bar{t}}\). We also obtain

(7.13)

Remark 7.1

Note that the vector field (7.11) coincides with the vector field already described by Holzegel–Kauffman [20].

Note that the divergence theorem of Eq. (2.41), holds with \(\mathcal {I}^+\) in the place of \(\bar{\mathcal {\mathcal {H}}}^+\). The energy flux at null infinity \(\mathcal {I}^+\), and the event horizon \(\mathcal {H}^+\), are nonnegative and we will may drop them from our estimates, see Eq. (7.4).

The Morawetz estimate we will need was proved in [8] by Dafermos–Rodnianski.

Theorem 7.1

(Theorem 1.1 in [8]). Let \(\psi \) satisfy Eq. (7.1) on a fixed Schwarzschild background. Then, for initial data vanishing at infinity, for all \(0<\eta \le 1\) there exists a constant \(C=C(M,\eta )\) such that

(7.14)

and

$$\begin{aligned} \int _{\phi _\tau (\tilde{\Sigma })}J^N_\mu [\psi ]n^\mu \le C \int _{\tilde{\Sigma }}J^N_\mu [\psi ]n^\mu +C\int \int _{\tilde{D}(0,\tau )}|\partial _{\bar{t}}\psi \cdot F|+r^{1+\eta }|F|^2 \nonumber \\ \end{aligned}$$
(7.15)

where N is the redshift vector field of Dafermos–Rodnianski, see the Lecture notes [11].

Recalling Remark 4.5, we repeat similar arguments to the ones used in the previous Sect. 4, up to estimate (4.27). Note, however, that we use the commutation vector field (7.11) and the energy density (1.10) with \(\Lambda =0\). Now, adding the Morawetz estimate of Theorem 7.1, noting the weights and absorbing relevant terms, we conclude the following.

Theorem 7.2

There exists a constant \(C(M,\eta )>0\), such that if \(\psi \) satisfies

$$\begin{aligned} \Box _{g_M}\psi =F \end{aligned}$$

on the spacetime domain \(\tilde{D}(0,\tau )\), the following holds

(7.16)

for any \(\eta \in (0,1]\).

Proof

By repeating the arguments of Sect. 4, and by keeping track of the weights in r, we conclude the following estimate

$$\begin{aligned} \begin{aligned}&\int _{\phi _\tau (\tilde{\Sigma })}J^{\partial _{\bar{t}}}_\mu [\mathcal {G}\psi ]n^\mu +\int \int _{\tilde{D}(0,\tau )} \frac{1}{r(1-\mu )}(\partial _{\bar{t}}\mathcal {G}\psi )^2\\&\quad \lesssim \int _{\tilde{\Sigma }}J^{\partial _{\bar{t}}}_\mu [\mathcal {G}\psi ]n^\mu +\int \int _{\tilde{D}(0,\tau )}\partial _{\bar{t}}\mathcal {G}\psi \cdot \mathcal {G}F+\partial _{\bar{t}}\mathcal {G}\psi \left( E_2(r)\partial _t\psi +E_1(r)\partial _r\psi \right) , \end{aligned} \end{aligned}$$
(7.17)

where for \(E_1(r),E_2(r)\) see Proposition 4.6. Then, to obtain all of the derivatives of \(\mathcal {G}\psi \) on the left-hand side of (7.17) we use Lemma 4.2, by keeping the weights in r and by an additional F error term to obtain

(7.18)

To control all the first-order terms on the right-hand side of (7.18), we use the boundedness estimate and the Morawetz estimate of Theorem 7.1 and obtain

(7.19)

for any \(\eta \in (0,1]\), where we used Young’s inequalities in the lower-order terms on the right-hand side of (7.17). Note that no degeneration is present on the photon sphere \(r=3M\) since we repeated the Poincare-type inequality of Lemma 4.3. Finally, by using the appropriate Young’s inequalities on the right-hand side of (7.19), we conclude the result. \(\square \)

Moreover, we have the Corollary.

Corollary 7.1

Under the assumptions of the above theorem, and the additional assumptions that, for the vector field \(a=a^j\partial _j\) and the scalar function b the following

$$\begin{aligned} a^{\bar{t}},a^r,g^{\theta \theta }(a^\theta )^2+g^{\phi \phi }(a^\phi )^2,b(r) \end{aligned}$$
(7.20)

are smooth functions on \(\tilde{D}(0,\infty )\), with

$$\begin{aligned} a^{\bar{t}}(r,\cdot ),a^r(r,\cdot ),\left( g^{\theta \theta }(a^\theta )^2+g^{\phi \phi }(a^\phi )^2\right) (r,\cdot ),|[\mathcal {G}, a]^{\bar{t}}(r,\cdot )|\le \frac{C}{r^2} \end{aligned}$$
(7.21)

and

$$\begin{aligned} b(r,\cdot ), |\mathcal {G}b|(r,\cdot )\le \frac{C}{r^3}, \end{aligned}$$
(7.22)

then we have the following.

There exists a constant \(C=C(M,\eta )\) such that for solutions of

$$\begin{aligned} \Box _{g_{M}}\psi =\epsilon a^j\partial _j\psi +\epsilon b(r)\psi , \end{aligned}$$
(7.23)

and for \(\epsilon \) sufficiently small, we have

(7.24)

and

(7.25)

since by the relation of the volume forms, see Sect. 2.14, we have

$$\begin{aligned} \int _{0}^\tau \textrm{d}\tau \int _{\phi _\tau (\Sigma )} \left( \cdot \right) \sim \int \int _{D(0,\tau )}\frac{1}{r}\left( \cdot \right) , \end{aligned}$$
(7.26)

where the constants in the above similarity depend only on the black hole mass M.

Remark 7.2

The bulk term, on the left-hand side of inequality (7.25), and the hypersurface term, on the right-hand side of inequality (7.25), have different weights in r. Specifically, some of the terms of the right-hand side, have larger weights in r. It is because of this reason that one does not obtain exponential decay for \(\psi \), on a Schwarzschild exterior.

Remark 7.3

The reason we can include the zeroth-order term, with component b(r), in Eq. (7.23), as opposed to Eq. (3.7) on the Schwarzschild–de Sitter case, is the lack of the \(\psi _\infty \) term in (7.14) for initial data vanishing at infinity.

Remark 7.4

Our Corollary 7.1, without the \(\frac{1}{r(1-\mu )}(\partial _{\bar{t}}\mathcal {G}\psi )^2\) term and slightly different weights of r on the left-hand side, coincides with Theorem 4.1 of [20].

Note that we have the following higher-order theorem.

Theorem 7.3

Under the assumption of Theorem 7.2, for all \(j\ge 3\) there exists a positive constant \(C=C(j,M,\eta )>0\) such that

(7.27)

for all \(0\le \tau _1\le \tau _2\), where

$$\begin{aligned} \begin{aligned} \tilde{E}_{\mathcal {G},j}[\psi ](\tau )&= \int _{\{\bar{t}=\tau \}} \sum _{0\le i_1+i_2\le j-2 }\sum _\alpha \tilde{\mathcal {E}}\left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\mathcal {G}\psi ,\partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\psi \right) \\&\quad +\sum _{1\le i_1+i_2+i_3\le j-1,i_3\ge 1}\sum _\alpha r(1-\mu )^{2i_3-1}\left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\partial _r^{i_3}\mathcal {G}\psi \right) ^2\\&\quad +\sum _{1\le i_1+i_2+i_3\le j-1,i_3\ge 1}\sum _\alpha r\left( \partial _{\bar{t}}^{i_1}\Omega _\alpha ^{i_2}\partial _r^{i_3}\psi \right) ^2 \end{aligned} \end{aligned}$$
(7.28)

where N is the redshift vector field of Dafermos–Rodnianski, see the Lecture notes [11]. The \(j=2\) case is the same without the hypersurface error terms on the right-hand side of (7.27). For the volume forms of the spacetime domains and of the hypersurface terms see Sect. 2.14.

Proof

The proof of this Theorem is essentially the same as Theorem 3 of the Schwarzschild–de Sitter case. Note that in the proof of Theorem 3 we kept some ‘key’ weights in r so that the proof can be read for the asymptotically flat case. \(\square \)

Remark 7.5

In order to write inequality (7.27) in its most compact form, we had to slightly differ its presentation from the relevant inequality of Theorem 3, since the weights in r are now significant.