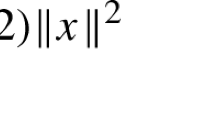Abstract
The minimax spherical location problem is formulated in the Cartesian coordinate system using the Euclidean norm, instead of the spherical coordinate system using spherical arc distance measures. It is shown that minimizing the maximum of the spherical arc distances between the facility point and the demand points on a sphere is equivalent to minimizing the maximum of the corresponding Euclidean distances. The problem formulation in this manner helps to reduce Karush-Kuhn-Tucker necessary optimality conditions into the form of a set of coupled nonlinear equations, which is solved numerically by using a method of factored secant update with a finite difference approximation to the Jacobian. For a special case when the set of demand points is on a hemisphere and one or more point-antipodal point pair(s) are included in the demand points, a simplified approach gives a minimax point in a closed form.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
A.A. Aly, D.C. Kay and D.W. Litwhiler, “Location Dominance on Spherical Surfaces,”Operations Research 27, 972–981 (979).
T. Aykin and A.J.G. Babu, “Constrained Large-Region Multifacility Location Problems,”Journal of Operations Research Society 38, 241–252 (1987).
J.E. Dennis, Jr. and R.B. Schnabel,Numerical Methods for Unconstrained Optimization and Nonlinear Equations, Prentice-Hall, Englewood Cliffs, New Jersey, 1983.
U.R. Dhar and J.R. Rao, “Domain Approximation Method for Solving Multifacility Location Problems on a Sphere,”Journal of Operations Research Society 33, 639–645 (1982).
U.R. Dhar and J.R. Rao, “An Efficient Algorithm for Solving Area-Constrained Location Problems on a Sphere,”Opsearch 19, 23–32 (1982).
Z. Drezner, “On Location Dominance on Spherical Surfaces,”Operations Research 29, 1218–1219 (1981).
Z. Drezner and G.O. Wesolowsky, “Facility Location on a Sphere,”Journal of Operations Research Society 29, 997–1004 (1978).
I.N. Katz and L. Copper, “Optimal Location on a Sphere,”Computational Mathematics and Applications 6, 175–196 (1980).
D.W. Litwhiler and A.A. Aly, “Large Region Location Problems”Computers and Operations Research 6, 1–12 (1979).
R. Love, J.G. Morris and G.O. Wesolowsky,Facilities Location: Models and Methods, North-Holland, New York, New York, 1988.
G.O. Wesolowsky, “Location Problems on a Sphere,”Regional Science and Urban Economics 12, 495–508 (1982).
Z. Drezner and G.O. Wesolowsky, “Minimax and Maximin Facility Location Problems on a Sphere,”Naval Research Logistics Quarterly,30, 305–312 (1983).
R.K. Chakraborty and P.K. Chaudhuri, “Note on Geometrical Solution for Some Minimax Location Problems,”Transportation Science 15, 164–166 (1981).
R. Chandrasekaran and M.J.A.P. Pacca, “Weighted Min-Max Location Problems: Polynomially Bounded Algorithms,”Opsearch 17, 172–180 (1980).
R. Chen and G.Y. Handler, “Relaxation Method for the Solution of the Minimax Location-Allocation Problem in Euclidean Space,”Naval Research Logistics 34, 775–788 (1987).
V.F. Demjanov, “Algorithms for Some Minimax Problems,”Journal of Computers and System Science 2, 342–380 (1968).
J. Elzinga and D.W. Hearn, “Geometrical Solutions for Some Minimax Location Problems,”Transporation Science 6, 379–394 (1972).
D.W. Hearn and J. Vijay, “Efficient Algorithms for the (Weighted) Minimum Circle Problem,”Operations Research 30, 777–795 (1982).
Z. Drezner and G.O. Wesolowsky, “A Maximin Location Problem With Maximum Distance Constraints,”AIIE Transactions 12, 249–252 (1980).
W.-H. Tsai, M.-S. Chern and T.-M. Lin, “An Algorithm for Determining Whetherm Given Demand Points Are on a Hemisphere or Not,”Transportation Science 25, 91–97 (1991).
M.H., D.L. Nettles and S.J. Deutsch, “A Linear Programming-Based Method for Determining Whether or Notn Demand Points are on a Hemisphere,Naval Research Logistics 40, 543–552 (1993).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Patel, M.H. Spherical minimax location problem using the Euclidean norm: Formulation and optimization. Comput Optim Applic 4, 79–90 (1995). https://doi.org/10.1007/BF01299160
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01299160