Skip to main content
SpringerLink
Log in

Liquid flow in foams

  • Published:
Fluid Dynamics Aims and scope Submit manuscript

Abstract

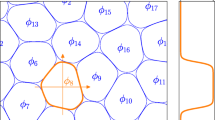
A model equation for describing liquid motion in a foam of polyhedral structure is proposed. A dimensionless parameter characterizing the structure of the foam, namely, the ratio of the volume energy densities of the capillary and gravitational forces, is introduced. When the gravitational forces predominate over the capillary forces, the out-flow process may be regarded as a kinematic wave that can be described by the Burgers equation. In the opposite case, the capillary absorption can be described by a quasilinear parabolic equation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Literature cited

  1. V. V. Krotov, “Structure, syneresis and breakdown kinetics of polyhedral disperse systems,” in: Problems of Thermodynamics of Heterogeneous Systems and the Theory of Surface Effects, No. 6 [in Russian], Izd. LGU, Leningrad (1982), p. 110.

    Google Scholar 

  2. K. B. Kann, “Steady flow of liquid through a foam,” Izv. Akad. Nauk SSSR, Mekh. Zhidk. Gaza, No. 3, 98 (1986).

    Google Scholar 

  3. R. I. Nigmatulin, Fundamentals of the Mechanics of Heterogeneous Media [in Russian], Nauka, Moscow (1978).

    Google Scholar 

  4. V. G. Levich, Physicochemical Hydrodynamics [in Russian], Fizmatgiz, Moscow (1959).

    Google Scholar 

  5. V. K. Tikhomirov, Foams: Theory and Practice of their Production and Breakdown [in Russian], Khimiya, Moscow (1983).

    Google Scholar 

  6. L. D. Landau and E. M. Lifshitz, Theoretical Physics. Vol. 6. Hydrodynamics [in Russian], Nauka, Moscow (1986).

    Google Scholar 

  7. R. A. Leonard and R. Lemlich, “Laminar longitudinal flow between close-packed cylinders,” Chem. Eng. Sci.,20, 790 (1965).

    Google Scholar 

  8. V. I. Karpman, Nonlinear Waves in Dispersive Media [in Russian], Nauka, Moscow (1973).

    Google Scholar 

  9. G. I. Barenblatt, V. M. Entov, and V. M. Ryzhik, Theory of Unsteady Flow of Liquids and Gases Through Porous Media [in Russian], Nedra, Moscow (1972).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Tyumen'

    I. I. Gol'dfarb, K. B. Kann & I. R. Shreiber

Authors
  1. I. I. Gol'dfarb
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. B. Kann
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. I. R. Shreiber
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Izvestiya Akademii Nauk SSSR, Mekhanika Zhidkosti i Gaza, No. 2, pp. 103–108, March–April, 1988.

The authors are grateful to A. V. Berlyand for discussing the problems associated with the solution of Eq. (3. 4).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gol'dfarb, I.I., Kann, K.B. & Shreiber, I.R. Liquid flow in foams. Fluid Dyn 23, 244–249 (1988). https://doi.org/10.1007/BF01051894

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01051894

Keywords

Search

Navigation