Skip to main content
SpringerLink
Log in

A maximum entropy priority approximation for a stableG/G/1 queue

  • Published:
Acta Informatica Aims and scope Submit manuscript

Summary

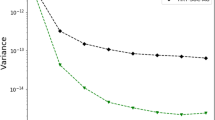
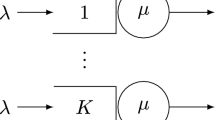
The principle of maximum entropy is used under two different sets of mean value constraints to analyse a stableG/G/1 queue withR priority classes under preemptive-resume (PR) and non-preemptive head-of-line (HOL) scheduling disciplines. New one-step recursions for the maximum entropy state probabilities are established and closed form approximations for the marginal queue length distribution per priority class are derived. To expedite the utility of the maximum entropy solutions exact analysis, based on the generalised exponential (GE) distribution, is used to approximate the marginal mean queue length and idle state probability class constraints for both the PR and HOLG/G/1 priority queues. Moreover, these results are used as building blocks in order to provide new approximate formulae for the mean and coefficient of variation of the effective priority service-time and suggest a maximum entropy algorithm for general open queueing networks with priorities in the context of the reduced occupancy approximation (ROA) method. Numerical examples illustrate the accuracy of the proposed maximum entropy approximations in relation to simulations involving different interarrival-time and service-time distributions per class. Comments on the extension of the work to more complex types of queueing systems are included.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Baskett, F., Chandy, S.C., Muntz, R.R., Palacios, F.G.: Open, closed and mixed networks of queues with different classes of customers. J. ACM22, 248–260 (1975)

    Google Scholar 

  2. Bondi, B., Chuang, Y.M.: A new MVA based approximation for closed queueing networks with a preemptive priority server. Performance Eval.8, 195–221 (1988)

    Google Scholar 

  3. Bryant, R.M., Krzesinski, E., Seetha Lakshmi, M., Chandy, K.M.: The MVA priority approximation. ACM Trans. Comput. Syst.2, 335–359 (1984)

    Google Scholar 

  4. Buzen, J.P., Denning, P.J.: Measuring and calculating queue length distributions. IEEE Comput.13, 33–44 (1980)

    Google Scholar 

  5. Buzen, J.P., Bondi, A.B.: The response times of priority classes under preemptive resume inM/M/m queues. Oper. Res.31, 456–465 (1983)

    Google Scholar 

  6. Chaudhry, K.M., Templeton, J.G.C.: A first course in bulk queues, 1st Ed. New York: Wiley 1983

    Google Scholar 

  7. Chow, W.M.:M/M/1 priority queues with state dependent arrival and service rates. IBM Thomas J. Watson Res. Center Rept. Re 8570 (1980)

  8. El-Affendi, M.A., Kouvatsos, D.D.: A maximum entropy analysis of theM/G/1 andG/M/1 queueing systems at equilibrium. Acta Inf.,19, 339–355 (1983)

    Google Scholar 

  9. Jaiswal, N.K.: Priority queues, 1st Ed. New York: Academic Press 1968

    Google Scholar 

  10. Jaynes, E.T.: Prior probabilities. IEEE Trans. Syst. Sci. Cyber. SSC4, 227–241 (1968)

    Google Scholar 

  11. Kaufman, J.S.: Approximation methods for networks of queues with priorities. performance Eval.4, 183–198 (1984)

    Google Scholar 

  12. Kelly, F.P.: Reversibility and stochastic networks, 1st Ed. New York: Wiley 1979

    Google Scholar 

  13. Kouvatsos, D.D.: Maximum entropy methods for general queueing networks. Proc. Int. Conf. Modelling Techniques and Tools for Performance Analysis. Potier, D. (ed.), pp. 589–608. Amsterdam: North-Holland 1985

    Google Scholar 

  14. Kouvatsos, D.D.: A maximum entropy analysis of theG/G/1 queue at equilibrium. J. Oper. Res. Soc.39, 183–200 (1988a)

    Google Scholar 

  15. Kouvatsos, D.D., Georgatsos, P.H.E., Tabet-Aouel, N.M.: A universal maximum entropy algorithm for general multiple class open networks with mixed service disciplines. Proc. 4th Int. Conf. on Modelling Techniques and Tools for Computer Performance Evaluation, pp. 473–492. Palma de Mallorca (Balaeric Islands, Spain) Sept. 1988b

    Google Scholar 

  16. Lazowska, E.D., Zahorjan, J., Sevcik, K.C.: Computer systems performance evaluation using queueing network models. Computer Syst. Research Institute, University of Toronto. Tech. Rep. 86-02-07 (1986)

    Google Scholar 

  17. Marks, B.I.: State probabilities ofM/M/1 priority queues. Oper. Res.21, 974–987 (1973)

    Google Scholar 

  18. Miller, D.R.: Computation of steady-state probabilities forM/M/1 priority queues. Oper. Res.29, 945–958 (1981)

    Google Scholar 

  19. Kleinrock, L.: Queueing systems, Vols. 1, 2. New York: Wiley 1975, 1976

    Google Scholar 

  20. Mitrani, I., King, P.J.B.: Multiprocessor systems with preemptive priorities. Perf. Eval., 118–125 (1981)

  21. Neuse, D., Chandy, K.M.: Ham: The heuristic algorithm method for solving general closed queueing models of computer systems. Perf. Eval. Rev.11, 195–1212 (1982)

    Google Scholar 

  22. Sauer, C.: Configuration of computing systems: An approach using queueing network models. PhD Thesis, Univ. of Texas, Austin, USA 1975

    Google Scholar 

  23. Sevcik, K,.C.: Priority scheduling disciplines in queueing network models of computer systems. In: Gilchrist, B. (ed.) Proc. IFIP Congress '77, pp. 565–570. Amsterdam: North-Holland 1977

    Google Scholar 

  24. Shore, J.E., Johnson, R.W.: Axiomatic derivation of the principle of maximum entropy and the principle of minimum cross entropy. IEEE Trans. Inf. Theory.26, 26–37 (1980)

    Google Scholar 

  25. Schmitt, W.: Approximate analysis of markovian queueing networks with priorities. Proc. of 10th Int. Tel. Congress, Montreal 1983

  26. Schmitt, W.: On decompositions of markovian priority queues and their application to the analysis of closed priority queueing networks. In: Gelenbe, E. (ed.) Proc. 10th Int. Symp. on Comp. Perf., pp. 393–407. Amsterdam: North-Holland 1984

    Google Scholar 

  27. Tabet-Aouel, N.: General queueing networks with priorities. Forthcoming PhD Thesis, University of Bradford, 1989

  28. Veran, M, Potier, D., QNAP-2: A portable environment for queueing network modelling. Proc. Int. Conf. on Modelling Techniques and Tools for Performance Analysis, INRIA (1984)

  29. Zahorjan, J., Lazowska, E.D., Sevcik, K.C.: The use of approximations in production performance evaluation software. Proc. Int. Workshop on modelling techniques and performance evaluation. Paris 1987

Download references

Author information

Authors and Affiliations

  1. Computer Systems Modelling Research Group, University of Bradford, Bradford, UK

    Demetres Kouvatsos & Nasreddine Tabet-Aouel

Authors
  1. Demetres Kouvatsos
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Nasreddine Tabet-Aouel
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

This work is sponsored in part by the Science and Engineering Research Council (SERC), UK, under grant GR/D/12422 and in part by the Ministry of Higher Education of the Algerian Government

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kouvatsos, D., Tabet-Aouel, N. A maximum entropy priority approximation for a stableG/G/1 queue. Acta Informatica 27, 247–286 (1989). https://doi.org/10.1007/BF00572990

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00572990

Keywords

Search

Navigation